2,467
просмотров
Текст этой презентации
Слайд 1
Расчет корреляционных зависимостей в MS Excel
Подготовила учитель информатики
Яценко Е.В.
Слайд 2
Множественная корреляция в MS Excel При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства получаемые коэф-фициенты сводят в таблицы, называемые корреляционными матрицами.
Слайд 3
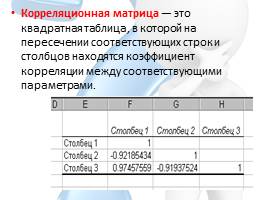
Корреляционная матрица — это квадратная таблица, в которой на пересечении соответствующих строк и столбцов находятся коэффициент корреляции между соответствующими параметрами.
Слайд 4
В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.
Слайд 5
Для реализации процедуры необходимо:
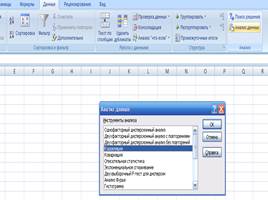
выполнить команду Данные — Анализ данных; 2. в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК; 3. в появившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов. 4. в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам); 5. указать выходной интервал, то есть ввести ссылку на ячейку, начиная с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.
Слайд 6
Слайд 7
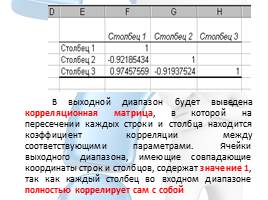
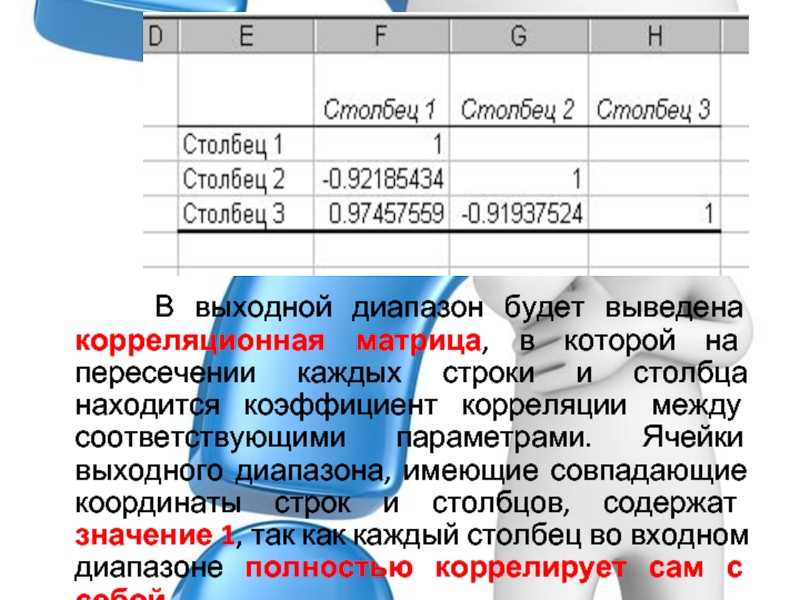
В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой
Слайд 8
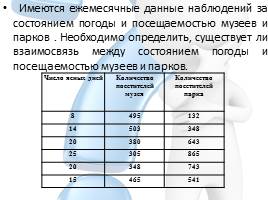
Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков . Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.
Число ясных дней Количество посетителей музея Количество посетителей парка
8 495 132
14 503 348
20 380 643
25 305 865
20 348 743
15 465 541
Слайд 9
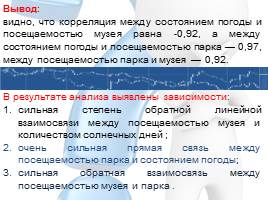
Решение. Для выполнения корреляционного анализа введите в диапазон A1:G3 исходные данные . Затем в меню Сервис выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал (А2:С7). Укажите, что данные рассматриваются по столбцам. Укажите выходной диапазон (Е1) и нажмите кнопку ОК.
Слайд 10
Вывод:
видно, что корреляция между состоянием погоды и посещаемостью музея равна -0,92, а между состоянием погоды и посещаемостью парка — 0,97, между посещаемостью парка и музея — 0,92. В результате анализа выявлены зависимости: сильная степень обратной линейной взаимосвязи между посещаемостью музея и количеством солнечных дней ;
очень сильная прямая связь между посещаемостью парка и состоянием погоды;
сильная обратная взаимосвязь между посещаемостью музея и парка .
1.
Расчёт корреляционных
зависимостей в Excel
2. Корреляция
Зависимости между величинами, каждая из
которых подвергается не контролируемому
полностью разбросу, называются
корреляционными зависимостями.
Мерой корреляционной зависимости является
величина, которая называется коэффициентом
корреляции.
3. Коэффициент корреляции
• Мерой корреляционной зависимости является величина,
которая называется коэффициентом корреляции.
• Коэффициент корреляции обозначается греческой
буквой
ρ («ро»).
• Это число, заключенное в диапазоне от -1 до +1 (если
это число по модулю близко к 1, то имеет место сильная
корреляция, если к 0, то слабая).
• Близость ρ к +1 означает, что возрастанию одного
набора значений соответствует возрастание другого
набора, близость к -1 означает обратное.
• Значение ρ легко найти с помощью Excel без всяких
формул (разумеется, потому, что в Excel они встроены).
4. Функция КОРРЕЛ
• В Excel имеется функция вычисления коэффициента
корреляции КОРРЕЛ , входит в группу
статистических функций.
Для вычисления коэффициента корреляции необходимо:
• на том же листе Excel, где находится таблица, надо
установить курсор на любую свободную ячейку и запустить
функцию КОРРЕЛ.
• указать два диапазона значений по которым
устанавливается зависимость
• после их ввода выведется ответ. Эта величина говорит о
среднем уровне корреляции
5. Пример
Рассмотрим зависимость успеваемости учащихся
старших классов от двух факторов:
• обеспеченности школьной библиотеки
учебниками
• обеспеченности школы компьютерами.
6. Результаты измерения обоих факторов в 11 разных школах
7. Выводы и результаты
• Для обеих зависимостей получены
коэффициенты линейной корреляции.
• Как видно из таблицы, корреляция между
обеспеченностью учебниками и успеваемостью
сильнее, чем корреляция между компьютерным
обеспечением и успеваемостью (хотя и тот и
другой коэффициенты корреляции не очень
большие).
• Отсюда можно сделать вывод, что пока еще книга
остается более значительным источником знаний,
чем компьютер.
8.
Как можно отформатировать ответ?
Если в результате получилось значение с длинной
дробной частью, вроде 0,892857142857143,
его следует отформатировать.
Пусть, например, результат в ячейке D9, и его требуется
представить в виде
ρ=0,892857
Для этого в ячейке можно написать формулу
Ну а в нашем случае результат вычисляется с помощью
функции КОРРЕЛ, то есть в качестве аргумента
используем эту функцию.
9.
Обратите внимание
Указать все единицы измерения.
Грамотно использовать знаки препинания и пробелы в
текстах.
Заголовки таблиц и столбцов выделить.
Заголовки выровнять по центру как по вертикали, так и по
горизонтали, включить для заголовков перенос по словам.
Ячейки выровнять грамотно.
Обратите внимание на выравнивание однотипных чисел
в столбце.
Удачно разместить материал в ячейках и на страницах
бумаги.
Выводы и результаты!
Слайд 1
Расчет корреляционных зависимостей в MS Excel
Подготовила учитель информатики
Яценко Е.В.

Слайд 2Множественная корреляция в MS Excel
При большом числе наблюдений, когда
коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства
получаемые коэф-фициенты сводят в таблицы, называемые корреляционными матрицами.

Слайд 3Корреляционная матрица — это квадратная таблица, в которой на пересечении
соответствующих строк и столбцов находятся коэффициент корреляции между соответствующими параметрами.

Слайд 4В MS Excel для вычисления корреляционных матриц используется процедура Корреляция
из пакета Анализ данных.
Процедура позволяет получить корреляционную матрицу, содержащую
коэффициенты корреляции между различными параметрами.
Слайд 5Для реализации процедуры необходимо:
выполнить команду Данные — Анализ данных;
2. в
появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку
ОК;
3. в появившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов.
4. в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам);
5. указать выходной интервал, то есть ввести ссылку на ячейку, начиная с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.

Слайд 7В выходной диапазон будет выведена корреляционная матрица, в которой на
пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими
параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой
Слайд 8 Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью
музеев и парков . Необходимо определить, существует ли взаимосвязь между
состоянием погоды и посещаемостью музеев и парков.

Слайд 9Решение. Для выполнения корреляционного анализа введите в диапазон A1:G3 исходные
данные .
Затем в меню Сервис выберите пункт Анализ данных
и далее укажите строку Корреляция.
В появившемся диалоговом окне укажите Входной интервал (А2:С7).
Укажите, что данные рассматриваются по столбцам. Укажите выходной диапазон (Е1) и нажмите кнопку ОК.
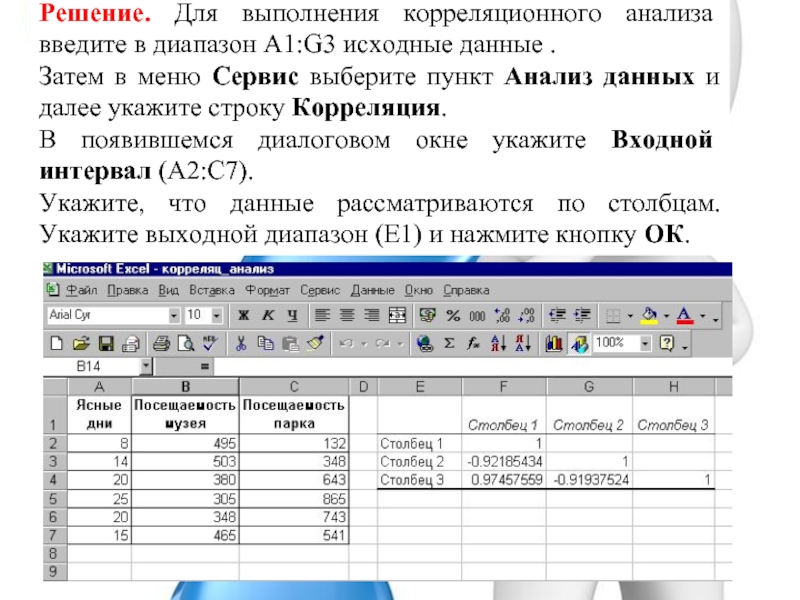
Слайд 10Вывод:
видно, что корреляция между состоянием погоды и посещаемостью музея равна
-0,92, а между состоянием погоды и посещаемостью парка — 0,97,
между посещаемостью парка и музея — 0,92.
В результате анализа выявлены зависимости:
сильная степень обратной линейной взаимосвязи между посещаемостью музея и количеством солнечных дней ;
очень сильная прямая связь между посещаемостью парка и состоянием погоды;
сильная обратная взаимосвязь между посещаемостью музея и парка .

Тема: Практическая работа №17
«Расчет корреляционных зависимостей в Microsoft Excel»
Тип урока: практическая работа
Цели:
Получение представления о корреляционной зависимости величин;
Освоение способа вычисления коэффициента корреляции с помощью функции КОРРЕЛ;
Формирование навыка по работе в MS Excel;
Развитие системного мышления, позволяющего выделять в окружающей действительности системы, элементы систем, адекватные поставленной задаче;
Формирование профессиональных навыков работы.
Оборудование:
ПК;
Интерактивная доска;
MS Excel
Ход урока:
I. Организационный момент (5 мин.)
Приветствие. Сообщение темы.
II. Актуализация знаний (5 мин.)
Проверка домашнего задания.
III. Практическая работа (30 мин.)
Практическая работа №17
Задание 1
Требуется выполнить расчеты корреляционной зависимости успеваемости учащихся от хозяйственных расходов школы, описанные в § 38 учебника.
1. Заполнить электронную таблицу следующими данными:
|
А |
В |
С |
|
№ п/п |
Затраты (руб./чел.) |
Успеваемость (средний балл) |
|
1 |
50 |
3,81 |
|
2 |
345 |
4,13 |
|
3 |
79 |
4,30 |
|
4 |
100 |
3,96 |
|
5 |
203 |
3,87 |
|
6 |
420 |
4,33 |
|
7 |
210 |
4 |
|
8 |
137 |
4,21 |
|
9 |
463 |
4,4 |
|
10 |
231 |
3,99 |
|
11 |
134 |
3,9 |
|
12 |
100 |
4,07 |
|
18 |
294 |
4,15 |
|
14 |
396 |
4,1 |
|
15 |
77 |
3,76 |
|
16 |
480 |
4,25 |
|
17 |
450 |
3,88 |
|
18 |
496 |
4,50 |
|
19 |
102 |
4,12 |
|
20 |
150 |
4,32 |
2. Построить точечную диаграмму зависимости величин (ее вид показан в учебнике на рис. 6.7).
3. Выполнить статистическую функцию КОРРЕЛ, указав в диалоговом окне диапазоны значений: В2:В21 и С2:С21.
4. Выписать значение коэффициента корреляции.
Задание 2
Выполнить расчеты корреляционных зависимостей успеваемости учащихся от обеспеченности учебниками и от обеспеченности компьютерами, представленными в следующей таблице.
|
Обеспечение учебного процесса |
||||
|
Номер школы |
Обеспеченность учебниками (%) |
Успеваемость (средний балл) |
Обеспеченность компьютерами (%) |
Успеваемость (средний балл) |
|
1 |
50 |
3,81 |
10 |
3,98 |
|
2 |
78 |
4,15 |
25 |
4,01 |
|
3 |
94 |
4,69 |
19 |
4,34 |
|
4 |
65 |
4,37 |
78 |
4,41 |
|
5 |
99 |
4,53 |
45 |
3,94 |
|
6 |
87 |
4,23 |
32 |
3,62 |
|
7 |
100 |
4,73 |
90 |
4,6 |
|
8 |
63 |
3,69 |
21 |
4,24 |
|
9 |
79 |
4,08 |
34 |
4,36 |
|
10 |
94 |
4,2 |
45 |
3,99 |
|
11 |
93 |
4,32 |
67 |
4,5 |
Полученные значения коэффициентов корреляции сопоставить с приведенными в § 38 учебника.
Задание для самостоятельного выполнения по теме
«Корреляционные зависимости»
Придумать таблицу парных измерений значений некоторых величин, между которыми существует гипотетическая корреляционная зависимость. Провести анализ этой зависимости на наличие линейной корреляции.
Примерами соответствующих связанных величин могут служить:
уровень образования (измеренный, например, в годах обучения в целом) и уровень месячного дохода;
уровень образования и уровень занимаемой должности (для последней придумайте условную шкалу);
количество компьютеров в школе, приходящихся на одного учащегося, и средняя оценка при тестировании на уровень владения стандартными технологиями обработки информации;
количество часов, затрачиваемых старшеклассниками на выполнение домашних заданий, и средняя оценка;
количество удобрений, вносимых в почву, и урожайность той или иной сельскохозяйственной культуры.
При этом вы можете идти двумя путями. Первый, более серьезный и практически полезный: вы не просто придумываете гипотетическую корреляционную зависимость, но и находите в литературе действительные данные о ней. Второй путь, более легкий: вы рассматриваете это как игру, необходимую для понимания того, что такое корреляционная зависимость, и выработки технических навыков ее анализа, и придумываете соответствующие данные, стараясь делать это наиболее правдоподобным образом.
IV. Итог урока (2 мин.) Объявляются оценки.
V. Домашнее задание (3 мин.) Повторить § 38
Курс «Информационные системы и базы данных», а так же курс «Математическое моделирование в планировании и управлении» разработан для учащихся 11 класса. Для данного курса были разработаны и апробированы тематическое планирование и презентационное сопровождение уроков. Для проведения занятий используется учебник, разработанный авторами Семакин И.Г., Хеннер Е.К., Информатика. 11-й класс. Учебник включает в себя не только теоретические выкладки, а так же 16 компьютерных практикумов. Предложенный урок разработан по теме данного учебника §2.11 «Корреляционные зависимости».
В управлении и планировании существует целый ряд типовых задач, которые можно переложить на плечи компьютера. В данном курсе мы рассматриваем только три типа задач, которые часто приходится решать специалистам в области планирования и управления:
1.прогнозирование – поиск ответа на вопросы «Что будет через какое-то время?», или «Что будет, если…?»;
2.определение влияния одних факторов на другие – поиск ответа на вопрос «Как сильно влияет фактор на фактор А?», или «Какой фактор или — влияет сильнее на фактор А?»;
3.поиск оптимальных решений – поиск ответа на вопрос «Как спланировать производство, чтобы достичь оптимального значения некоторого показателя (Например, максимума прибыли, или минимума расхода электроэнергии)?».
Работа по освоению данного курса позволяет улучшить навыки работы c приложениями Microsoft Office, обогащает новыми знаниями по использованию информационных технологий. Надеюсь, что предложенная разработка урока будет полезна тем учителям, которые работают по учебнику Семакин И.Г., Хеннер Е.К., Информатика. 11-й класс.