Расчет корреляции по спирмену в excel - Word и Excel - помощь в работе с программами

17 авг. 2022 г.
читать 3 мин

В статистике корреляция относится к силе и направлению связи между двумя переменными. Значение коэффициента корреляции может варьироваться от -1 до 1 со следующими интерпретациями:

-1: идеальная отрицательная связь между двумя переменными
0: нет связи между двумя переменными
1: идеальная положительная связь между двумя переменными

Один особый тип корреляции называется ранговой корреляцией Спирмена и используется для измерения корреляции между двумя ранжированными переменными. (например, оценка балла учащегося на экзамене по математике и оценка его оценки на экзамене по естественным наукам в классе).

В этом руководстве объясняется, как рассчитать ранговую корреляцию Спирмена между двумя переменными в Excel.

Пример: ранговая корреляция Спирмена в Excel

Выполните следующие шаги, чтобы вычислить ранговую корреляцию Спирмена между результатами экзамена по математике и результатами экзамена по естественным наукам 10 учащихся в определенном классе.

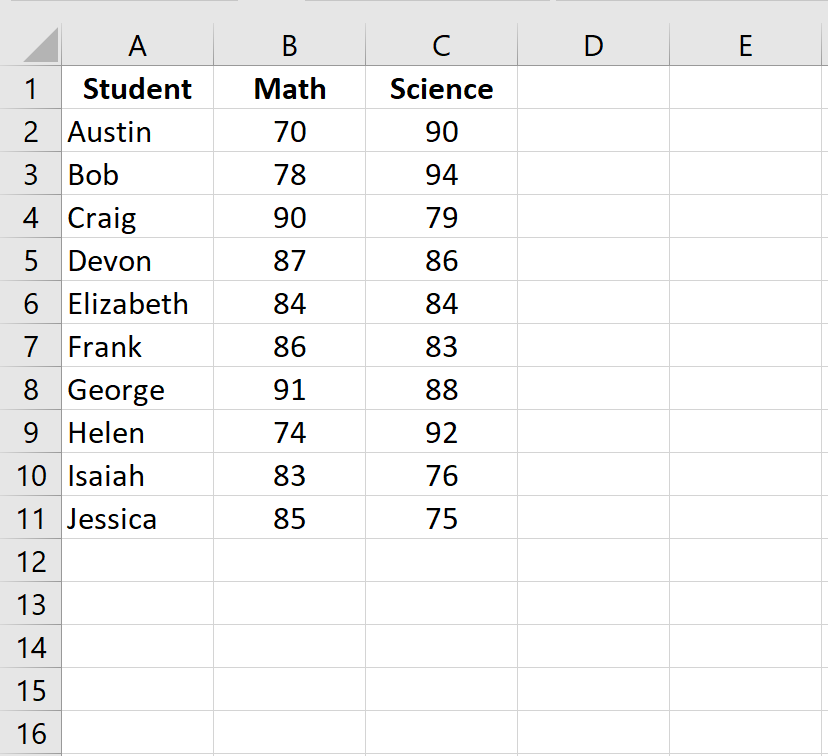
Шаг 1: Введите данные.

Введите экзаменационные баллы для каждого учащегося в два отдельных столбца:

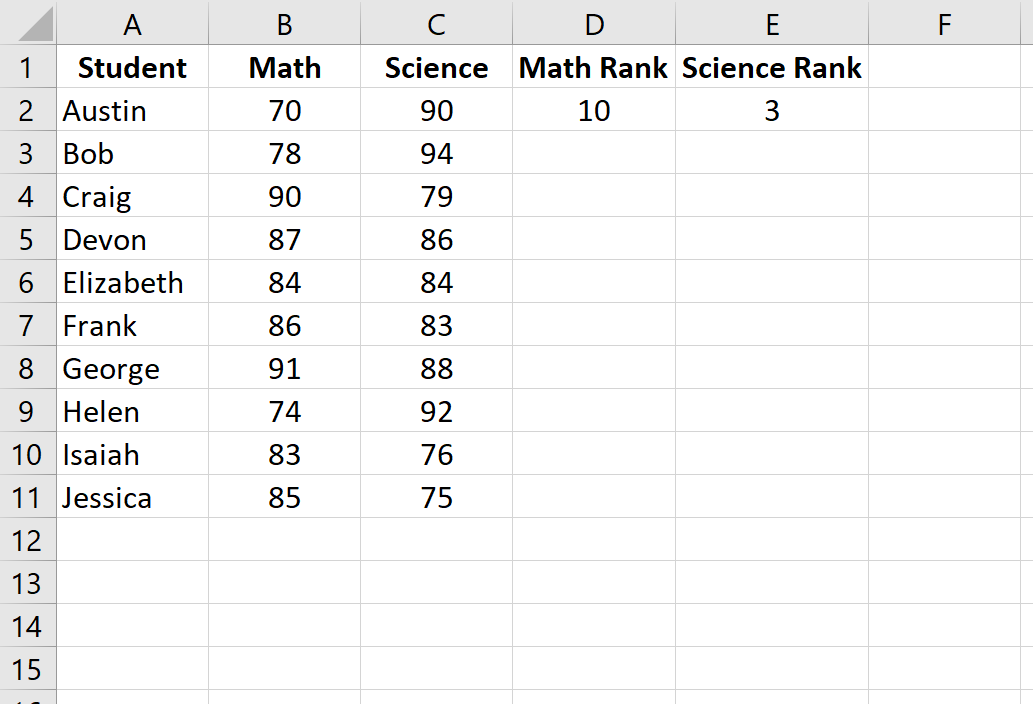
Шаг 2: Рассчитайте ранги для каждого экзаменационного балла.

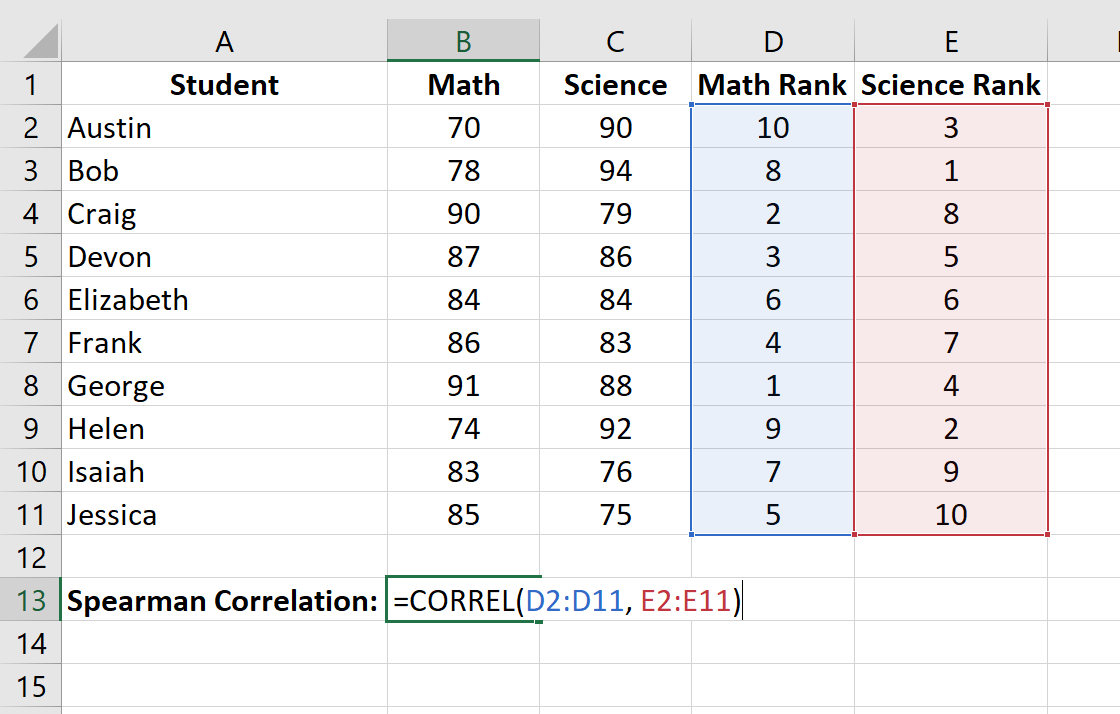
Далее мы рассчитаем рейтинг для каждого экзаменационного балла. Используйте следующие формулы в ячейках D2 и E2, чтобы вычислить рейтинги по математике и естественным наукам для первого ученика, Остина:

Ячейка D2: =RANK.AVG(B2, $B$2:$B$11, 0)

Ячейка E2: =RANK.AVG(C2, $C$2:$C$11, 0)

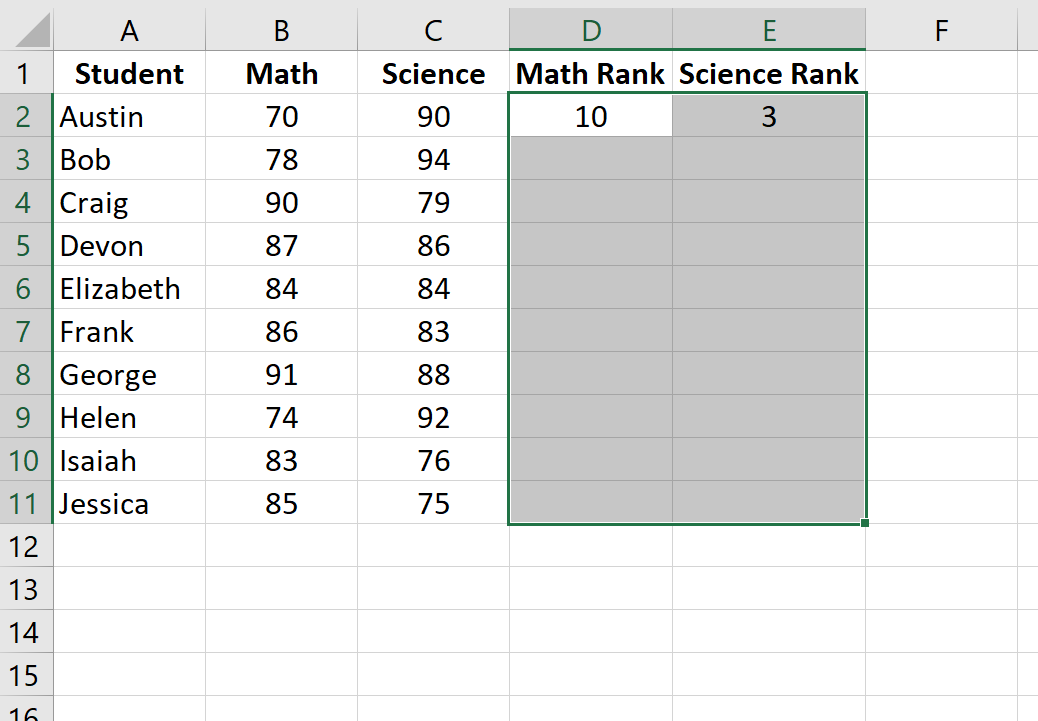
Затем выделите оставшиеся ячейки для заполнения:

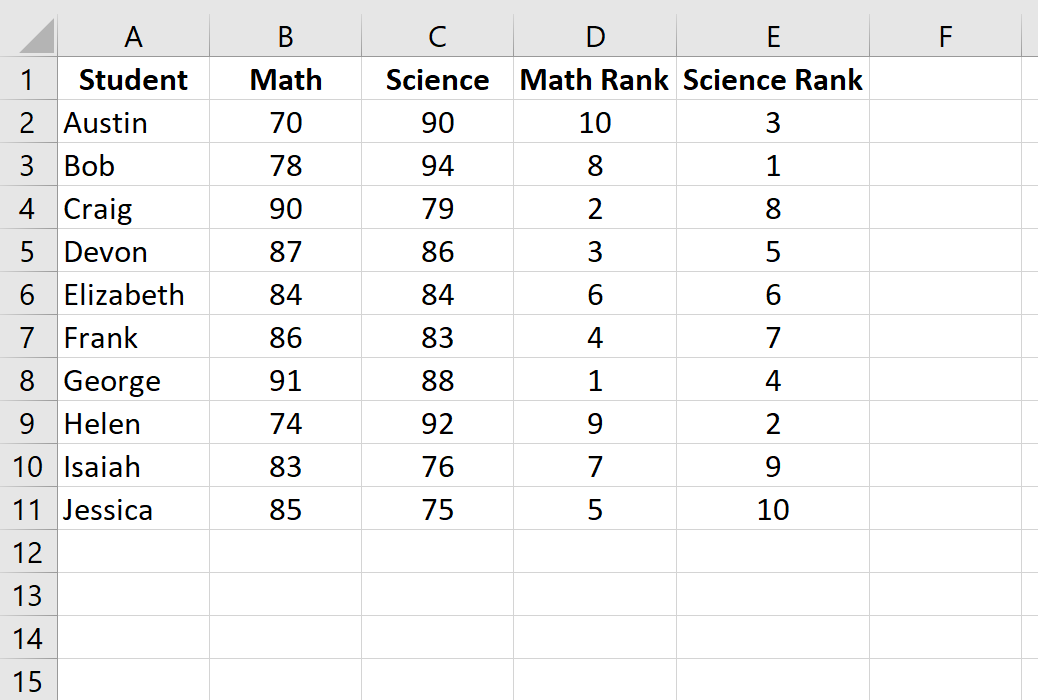
Затем нажмите Ctrl+D, чтобы заполнить ранги для каждого ученика:

Шаг 3: Рассчитайте коэффициент ранговой корреляции Спирмена.

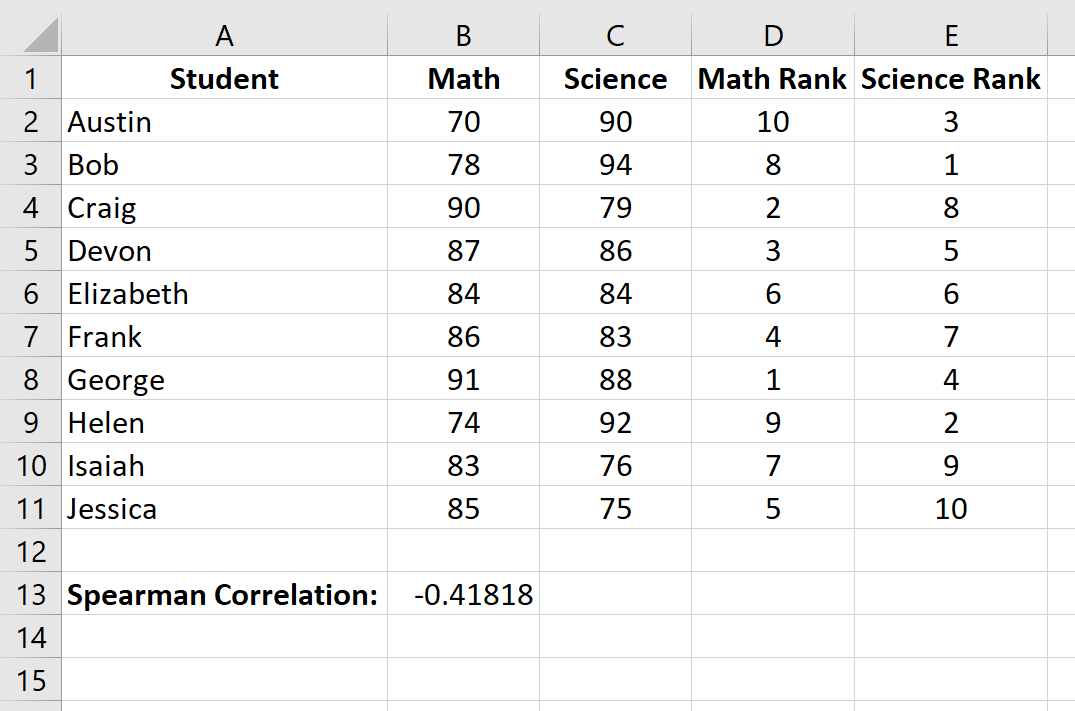
Наконец, мы рассчитаем коэффициент ранговой корреляции Спирмена между оценками по математике и по естественным наукам с помощью функции CORREL() :

Ранговая корреляция Спирмена оказывается равной -0,41818 .

Шаг 4 (необязательно): Определите, является ли ранговая корреляция Спирмена статистически значимой.

На предыдущем шаге мы обнаружили, что ранговая корреляция Спирмена между результатами экзаменов по математике и естественным наукам составляет -0,41818 , что указывает на отрицательную корреляцию между двумя переменными.

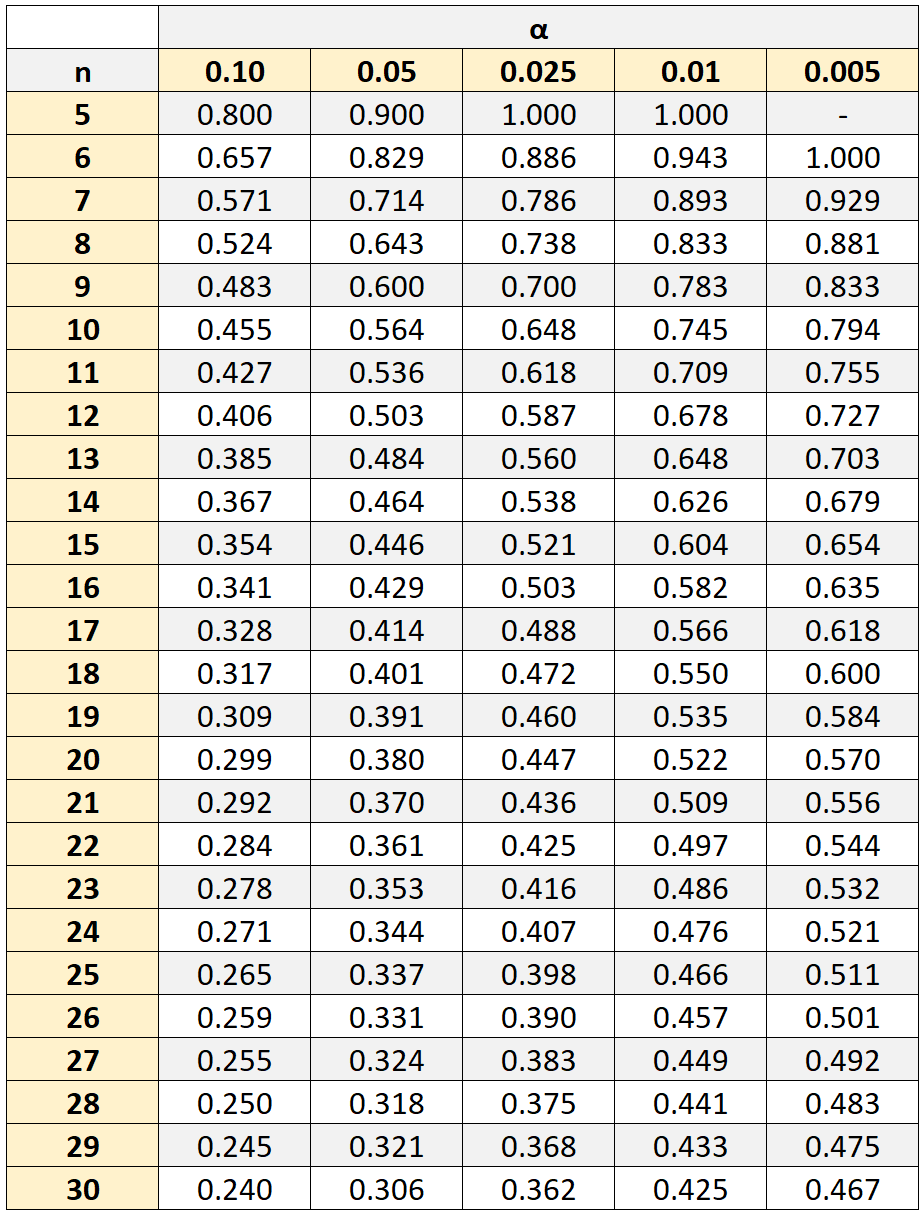
Однако, чтобы определить, является ли эта корреляция статистически значимой, нам нужно будет обратиться к таблице ранговой корреляции Спирмена критических значений, которая показывает критические значения, связанные с различными размерами выборки (n) и уровнями значимости (α).

Если абсолютное значение нашего коэффициента корреляции больше критического значения в таблице, то корреляция между двумя переменными является статистически значимой.

В нашем примере размер выборки составлял n = 10 студентов. Используя уровень значимости 0,05, мы находим, что критическое значение равно 0,564 .

Поскольку рассчитанное нами абсолютное значение рангового коэффициента корреляции Спирмена ( 0,41818 ) не превышает этого критического значения, это означает, что корреляция между баллами по математике и естественным наукам не является статистически значимой.

Источник

We have noticed a general trend that with an increase in the height of a person, its weight also increases. This happens because there is a positive correlation between height and weight. As one variable increases, the other one also increases, but with this, we only get the quality measure of the data and not quantity, that by how much they are related. To solve this problem, we have a Spearman Rank Correlation coefficient whose value will tell by how two variables are related. In this article, we will learn how to calculate Spearman Rank Correlation Coefficient in excel.

What is Spearman Rank Correlation Coefficient?

Spearman rank correlation coefficient is a non-parametric measure by which we can have a numerical value of how much two variables are related. Spearman’s rank correlation coefficient works on the ranks and not the data set provided. It would be better to say that Spearman works on ordinal data.

Range of Spearman Rank Correlation Coefficient

If the graph is monotonically increasing, then the spearman coefficient tends to 1.
If the graph is monotonically decreasing, then the spearman coefficient tends to -1.
If the graph is both increasing and decreasing, the spearman coefficient tends to be 0.
A perfect 1 value signifies that data is said to have a perfect positive correlation.
A perfect -1 value signifies that data is said to have a perfect negative correlation.
A perfect 0 value signifies that data is said to have no relation between two variables.

Hence, the spearman coefficient value lies in the range of [-1, 1], where -1 and 1 are included.

Advantages of Spearman Rank Correlation Coefficient

As spearman works on ordinal data, so it’s a non-parametric test. The test has no relation to the actual values in the data set. This coefficient test works well with outliers. The correlation value is not distorted if there are significant outliers in the data set.

The formula for Spearman Rank Correlation Coefficient

A formula has been provided to calculate the Spearman rank coefficient. The formula is:

$r_s = 1 - frac{6Σd_i^2}{n(n^2-1)}$

Where,

r_s= Spearman Rank Correlation Coefficient,

d_i = Difference of the rank of the values in the data set,

n = Size of the data set.

Note: The Formula works only if there are no tie ranks in your data set, i.e. there should be only distinct values for each Variable.

For example:

DataSet 1: Variable1: [1, 4, 3, 5], Variable2: [3, 4, 2, 5]

DataSet 2: Variable1: [1, 2, 2, 2], Variable2: [3, 4, 2, 5]

In the above two given data sets, DataSet1 satisfies the condition, and hence the formula could be applied to find spearman coefficient, but DataSet2 do not satisfies the condition, as there are duplicate values in Variable1 of second data set, hence the formula could not be applied to find spearman coefficient.

How to Calculate Spearman Rank Correlation in Excel?

Before following the procedure to calculate the spearman coefficient, we need to understand two functions in excel, which will be helpful in calculating the coefficient.

Rank Function

=RANK.AVG(number, ref, order)

The rank specifies the rank of a given number in a dataset; one can also select the order in which rank has to appear. =RANK.AVG() takes three arguments: number, ref, and order.

Argument 1: Number is the first argument in the rank function, which specifies for which number rank has to be estimated.

Argument 2: Reference is the second argument in the rank function. One needs to provide the absolute range of the data set.

Argument 3: Order is the third argument in the rank function. The order can be either ascending(1) or descending(0).

Correl function

=CORREL(array1, array2)

Similar to the spearman rank correlation coefficient, we also have the Pearson correlation coefficient. Pearson correlation coefficient is a parametric test to calculate the correlation value of two variables. Both the test is nearly the same. Just the difference lies in that spearman works on ranks of the data, and Pearson works on the actual data. The =CORREL() function calculates the Pearson correlation coefficient. This could be very useful in finding the spearman correlation coefficient, which we will talk about in the later stage of the article. =CORREL() function takes two arguments, array1 and array2.

Argument 1: Array1 is the first argument in the correlation function. It takes the entire data set of the variable1.

Argument 2: Array2 is the second argument in the correlation function. It takes the entire data set of the variable2.

Different methods to find Spearman Coefficient in Excel

There are two different methods by which we can find the Spearman correlation rank coefficient.

Method 1: Using the Formula

Spearman rank coefficient can be found with the help of a formula, as we have mentioned in the above article, but this formula can only be used if each data set does not contain duplicate values so that the rank of each value is unique. For example, Arushi is an aspiring Chartered Accountant, daily, she used to spend her entire day either studying or playing. For 7 days, she kept track of how many hours does she study and play. On a daily basis, her study hours and playing hours vary. Arushi wants to find whether her playing hours and studying hours are positively or negatively correlated with the help of the Spearman correlation rank coefficient.

Dataset

Following are the steps

Step 1: Create a new column name Study Rank. In cell D3, use the formula =RANK.AVG(B3, $B$3:$B$9, 1). This finds the rank of cell B3 for Study Hours. Press Enter.

Step 2: The number 4 appears in cell D3. This number has ranked 4 in the Study Hours data set.

Step 3: Copy the same formula of D3 to cells D4:D9.

Step 4: Create a new column name Play Rank. In cell E3, use the formula =RANK.AVG(C3, $C$3:$C$9, 1). This finds the rank of cell C3 for Play Hours. Press Enter.

Step 5: The number 3 appears in cell E3. This number has ranked 3 in the Play Hours data set.

Step 6: Copy the same formula of E3 to cells E4:E9.

Step 7: Create a new column, name, d. In cell F3, use the formula =D3-E3. This calculates the difference in the ranks. Press Enter.

Step 8: Copy the same formula of F3 to cells F4:F9.

Step 9: Create a new column, name, d{square}. In cell G3, use the formula =F3^2. This calculates the square of the difference. Press Enter.

Step 10: Copy the same formula of G3 to cells G4:G9.

Step 11: Use =COUNT(C3:C9) function to calculate the size of the data set. Press Enter.

Step 12: In the cell, J3, 7 appears, which is the size of the data set.

Step 13: Use =SUM(G3:G9) function to calculate the sum of the difference between the ranks. Press Enter.

Step 14: In the cell, G10, 110 appears.

Step 15: In cell J5, apply the Spearman formula as mentioned above in the article, i.e., =1-(6*G10/(J3*(J3^2-1))). Press Enter.

Step 16: We get the spearman correlation rank coefficient as -0.96429, which proves that studying hours and playing hours are negatively correlated.

Method 2: Using =CORREL() function

We previously saw that correlated function finds the value of Pearson correlated coefficient by using arguments as data set values. We also know that the spearman coefficient works on the ranks and is a non-parametric test. The correlated function can also be used to find the spearman correlation coefficient by using arguments as data set rank values. For example, Arushi is an aspiring Chartered Accountant, daily she used to spend her entire day either studying or playing. For 7 days, she kept track of how many hours does she study and play. On a daily basis, her study hours and playing hours vary. Arushi wants to find whether her playing hours and studying hours are positively or negatively correlated with the help of the Spearman correlation rank coefficient.

Dataset

Following are the steps

Step 1: Create a new column, name Study Rank. In cell D3, use the formula =RANK.AVG(B3, $B$3:$B$9, 1). This finds the rank of cell B3 for Study Hours. Press Enter.

Step 2: The number 4 appears in cell D3. This number has ranked 4 in the Study Hours data set.

Step 3: Copy the same formula of D3 to cells D4:D9.

Step 4: Create a new column, name Play Rank. In cell E3, use the formula =RANK.AVG(C3, $C$3:$C$9, 1). This finds the rank of cell C3 for Play Hours. Press Enter.

Step 5: The number 3 appears in cell E3. This number has ranked 3 in the Play Hours data set.

Step 6: Copy the same formula of E3 to cells E4:E9.

Step 7: In cell H4, use =CORREL(D3:D9, E3:E9) function to find the spearman correlation rank coefficient. Press Enter.

Step 8: We get the spearman correlation rank coefficient as -0.96429, which proves that studying hours and playing hours are negatively correlated.

Источник

Для того, чтобы рассчитать коэффициент корреляции в Excell необходимо сделать следующие шаги:

1.Вносим значения для двух переменных в таблицу (Например Переменная 1 и Переменная 2)

2. Ставим курсор в пустую ячейку

3. На панеле инструментов нажимаем кнопку fx (вставить формулу)

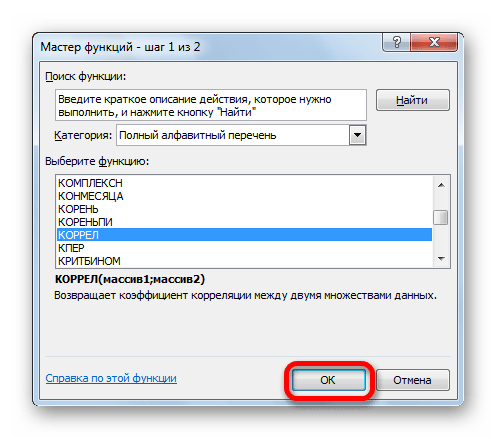
4. В открывшемся окне «Мастер функций» в поле «Категории» выбираем Полный алфавитный перечень

5. Затем в поле «Выберите функцию» находим функцию КОРЕЛЛ

5.1. Нажимаем Ок

6. В открывшемся окне «Аргументы функции» в поле Массив1 вносим номера ячеек, содержащие значения Переменной 1, в поле Массив2 вносим номера ячеек, содержащие значения Переменной2.

7. Нажимаем Ок

8. Смотрим получившийся результат

Источник

Загрузить PDF

Коэффициент корреляции ранга Спирмена позволяет определить, существует ли между двумя переменными зависимость, выражаемая монотонной функцией (то есть при росте одной переменной увеличивается и вторая, и наоборот). Приведенные в статье простые шаги позволят вам производить расчеты вручную, а также вычислять коэффициент корреляции при помощи программ Excel и R.

1
Составьте таблицу данных. Таким образом вы упорядочите информацию, необходимую для расчета коэффициента корреляции ранга Спирмена. При этом вам понадобится:
- 6 колонок, озаглавленных так, как показано выше на рисунке.
- Количество строк, соответствующее числу пар переменных.
2

Заполните первые две колонки парами переменных.
3

В третьей колонке запишите номера (ранги) пар переменных от 1 до n (общее число пар). Присвойте номер 1 паре с наименьшим значением в первой колонке, 2 — следующему за ним значению, и так по возрастанию величин переменной из первой колонки.
4
В четвертой колонке сделайте то же, что и в третьей, но на этот раз пронумеруйте пары переменных по второй колонке таблицы.
- Если два (или более) значения переменной в одной колонке одинаковы, расположите их один за другим и найдите среднее значение их номеров, затем пронумеруйте их этим средним значением.
  В приведенном справа примере два значения переменной совпадают и равны 5; в случае нормальной нумерации эти данные получили бы ранги 2 и 3. Поскольку значения одинаковы, находим среднюю величину их рангов. Среднее 2 и 3 равно 2,5, поэтому обеим величинам присваиваем ранг 2,5.
5

В колонке «d» вычислите разность между двумя рангами из предыдущих двух колонок. Например, если ранг в третьей колонке равен 1, а в четвертой – 3, то разница между ними составит 2. Знак не имеет значения, поскольку на следующем шаге эти числа будут возведены в квадрат.
6

Возведите каждое значение из колонки «d» в квадрат и запишите полученные величины в колонку «d²«.
7

Просуммируйте все значения из колонки «d²«. Вы определите сумму Σd².
8

Воспользуйтесь одной из следующих формул:
9
Проанализируйте результат. Полученное значение находится между -1 и 1.
- Если оно близко к -1, корреляция отрицательна.
- Если близко к 0, корреляция отсутствует.
- Если близко к 1, наблюдается положительная корреляция.
- Не забудьте поделить на сумму переменных и взять корень. После этого поделите на Σd².
Реклама

1

Создайте новые колонки с рангами, соответствующими колонкам данных. Например, если данные внесены в Колонку A2:A11, используйте функцию «=RANK(A2,A$2:A$11)» и занесите результаты для всех строк в новую колонку.
2

Найдите ранги для одинаковых величин, как описано в шагах 3 и 4 метода 1.
3

В новой ячейке определите корреляцию между двумя колонками рангов с помощью функции «=CORREL(C2:C11,D2:D11)». В данном случае C и D – это колонки, содержащие ранги. Таким образом, в данной ячейке вы получите коэффициент ранговой корреляции Спирмена.

Реклама

1

Если у вас еще нет программы R для обработки статистических данных, приобретите ее (см. http://www.r-project.org).
2

Сохраните данные в формате CSV, расположив их в двух колонках, корреляцию между которыми вы собираетесь исследовать. Сохранить файл в данном формате легко посредством опции «Сохранить как».
3

Откройте редактор R. Если вы еще не вошли в программу R, просто запустите ее. Для этого достаточно нажать иконку R на рабочем столе.
4
Наберите команды:
- d <- read.csv(«NAME_OF_YOUR_CSV.csv») и нажмите клавишу ввода
- cor(rank(d[,1]),rank(d[,2]))
Реклама

Советы

Как правило, набор данных должен состоять не менее чем из 5 пар для того, чтобы можно было достоверно установить какую-либо корреляцию (3 пары было использовано в примере выше для простоты).

Предупреждения

Коэффициент ранговой корреляции Спирмена позволяет установить лишь то, растут ли обе переменные или уменьшаются одновременно. Если разброс данных слишком велик, этот коэффициент не даст точного значения корреляции.
Приведенная функция даст верный результат при отсутствии одинаковых значений в массиве данных. Если такие значения существуют, как в рассмотренном нами примере, необходимо использовать следующее определение: коэффициент корреляции, основанный на рангах.

Об этой статье

Эту страницу просматривали 68 172 раза.

Была ли эта статья полезной?

Источник

Содержание

Суть корреляционного анализа
Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
Вопросы и ответы

Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

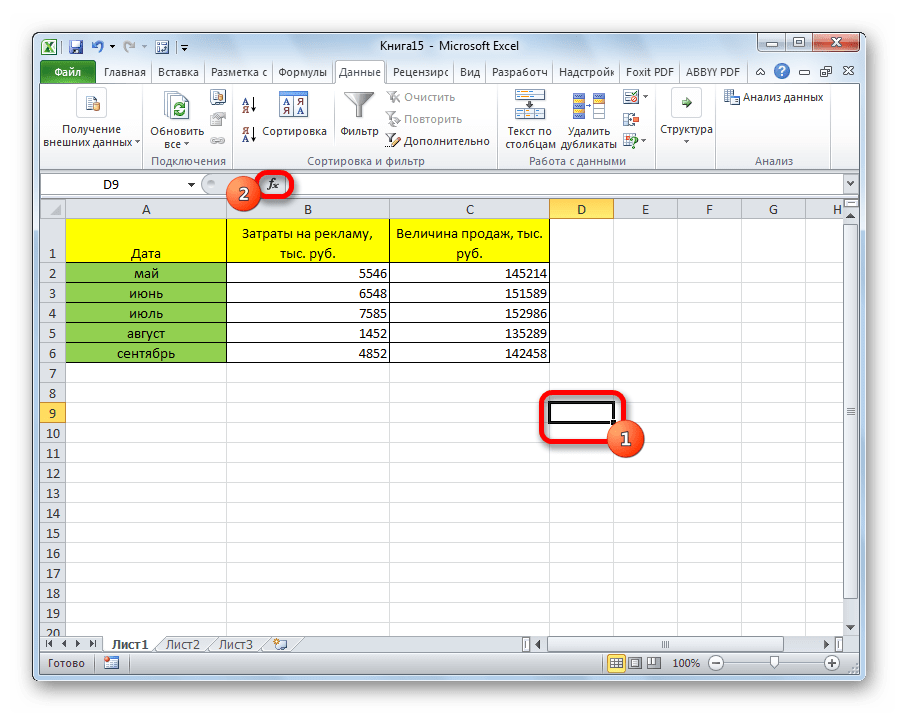
Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

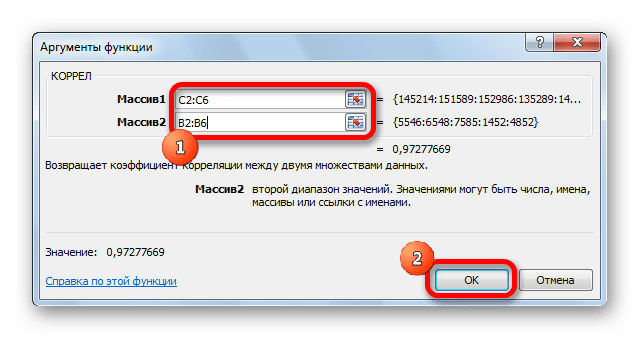
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

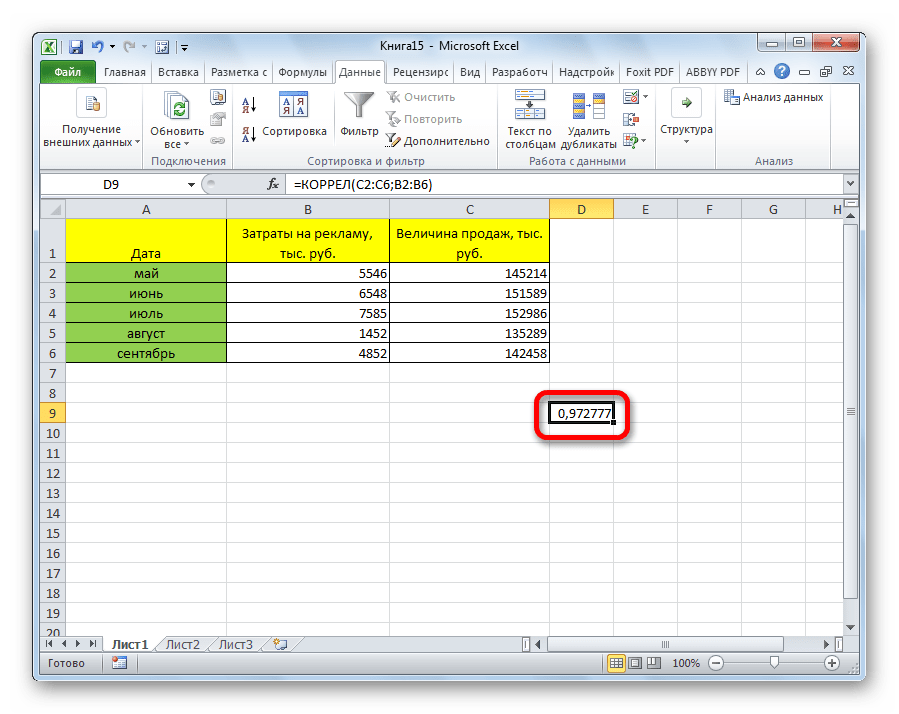
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

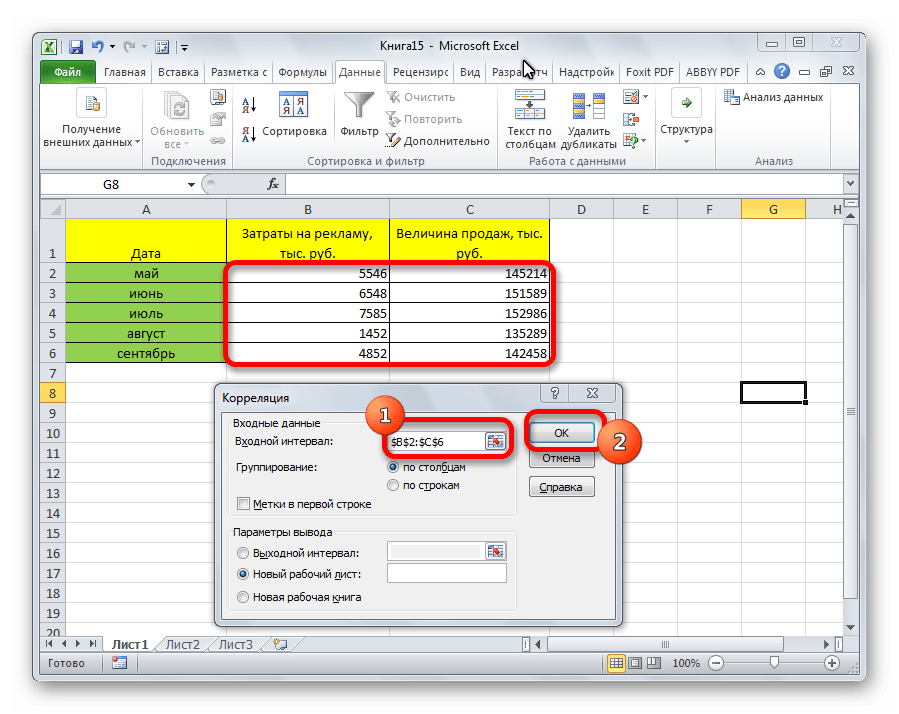
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

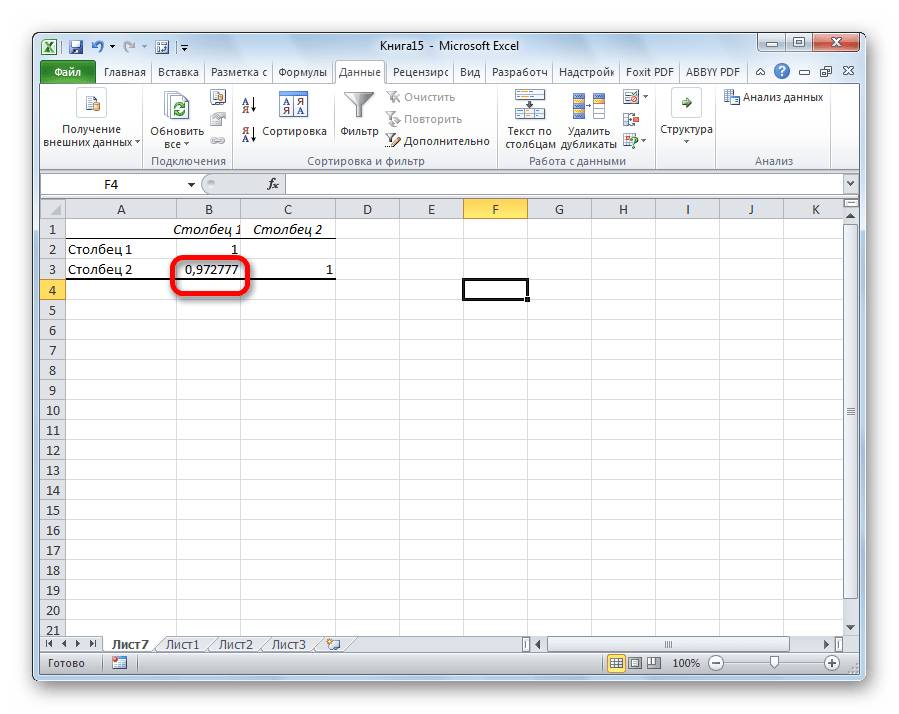
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник