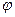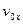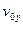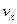Практическая работа № 2
Тема: Моделирование ситуаций
Задача 2. Обои и комната
1 этап. Постановка задачи
В магазине продаются обои. Наименования, длина и ширина рулона известны. Для удобства обслуживания надо составить таблицу, которая позволит определить необходимое количество рулонов для оклейки любой комнаты.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
D |
Е |
|
|
1 |
Обои и комната |
||||
|
2 |
|||||
|
3 |
Исходные данные |
||||
|
4 |
Комната |
||||
|
5 |
Высота |
2,6 |
|||
|
6 |
Длина |
5 |
|||
|
7 |
Ширина |
3 |
|||
|
8 |
Неоклеив. пов-ть |
15% |
|||
|
9 |
Площадь стен |
Формула 1 |
|||
|
10 |
|||||
|
11 |
Обои |
Промежуточные расчеты |
|||
|
12 |
Обрезки |
10% |
Результаты |
||
|
13 |
Наименования |
Длина |
Ширина |
Площадь рулона |
Количество рулонов |
|
14 |
Образец 1 |
10,5 |
0,5 |
Формула 2 |
Формула 3 |
|
15 |
Образец 2 |
10,5 |
0,6 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
|
16 |
Образец 3 |
10,5 |
0,7 |
||
|
17 |
Образец 4 |
13 |
0,5 |
||
|
18 |
Образец 5 |
13 |
0,6 |
||
|
19 |
Образец 6 |
13 |
0,7 |
Расчетные формулы:
|
Ячейка |
Формула |
|
А10 |
=2*($B$6+$B$7)* $B$5*(1-$B$8) |
|
D14 |
=(1-$B$12)*В14* С14 |
|
Е14 |
=ЦЕЛОЕ($B$9/ D14+1 |
3 этап. Компьютерный эксперимент
Эксперимент 1.
Провести расчет количества рулонов обоев для помещений вашей квартиры
Эксперимент 2.
Изменить данные некоторых образцов обоев и проследить за пересчетом результатов
Эксперимент 3.
Добавить строки с образцами и дополнить модель расчетом по новым образцам.
Задача 3. Компьютерный магазин
1 этап. Постановка задачи
Магазин компьютерных аксессуаров продает товары, указанные в прайс-листе. Стоимость указана в долларах. Если стоимость товара превышает некоторую сумму, покупателю предоставляется скидка. Составить таблицу-шаблон, позволяющую быстро рассчитать стоимость произвольной покупки. В расчете учесть текущий курс доллара.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
D |
Е |
|
|
1 |
Компьютерный магазин |
||||
|
2 |
Дата покупки |
Формула 1 |
|||
|
3 |
|||||
|
4 |
Курс доллара |
30,38 |
|||
|
5 |
Скидки |
5% |
|||
|
6 |
Сумма для учета скидки |
1000 |
|||
|
7 |
Прайс-лист |
||||
|
8 |
Наименование товара |
Цена, $ |
Количества |
Цена, руб. |
Стоимость |
|
9 |
Дискеты 3.5” BASF |
0,12 |
10 |
Формула 2 |
Формула 3 |
|
10 |
Дискеты 3.5” Verbatim |
0,14 |
10 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
|
11 |
Дискеты 3.5”TDK |
0,16 |
0 |
||
|
12 |
CD-R BASF 700 Mb/80 min |
1,7 |
1 |
||
|
13 |
CD-RW Intense 650 Mb/74 min |
2,7 |
0 |
||
|
14 |
Мышь Mitsumi |
5 |
0 |
||
|
15 |
Мышь Genius |
3,5 |
1 |
||
|
16 |
Мышь оптическая |
14 |
0 |
||
|
17 |
Держатель листа (холдер) |
3 |
1 |
||
|
18 |
ИТОГО |
Стоимость покупки без скидки |
Формула 4 |
||
|
19 |
Стоимость покупки со скидкой |
Формула 5 |
Расчетные формулы:
|
Ячейка |
Формула |
|
|
Формула 1 |
B2 |
Команда Вставка – Дата и время |
|
Формула 2 |
D9 |
=B9*$B$4 |
|
Формула 3 |
Е9 |
=С9* D9 |
|
Формула 4 |
Е18 |
=СУММ(Е9:Е17) |
|
Формула 5 |
Е19 |
=ЕСЛИ(Е18$B$6;Е18*(1-$B$5);Е18) |
3 этап. Компьютерный эксперимент
Эксперимент 1.
Ввести курс доллара на текущий день, размер скидки и провести расчет покупки со своим количеством товара.
Эксперимент 2.
Добавить строки другими видами товаров и дополнить модель расчетом по этим данным.
Задача 4. Сберкасса
1 этап. Постановка задачи
За 2 часа до обеденного перерыва 40 бабушек встали в очередь за пенсией. Кассирша обслуживает клиента в среднем одну минуту.
Первая бабушка «мучила» кассиршу вопросами 9 мин. 15 с. Каждая следующая бабушка, частично «мотая на ус» ответы, адресованные предыдущим бабушкам, «мучает» кассиршу на 10 с меньше. Построить модель ситуации и исследовать ее.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
|
|
1 |
Очередь в сберкассе |
||
|
2 |
|||
|
3 |
Исходные данные |
||
|
4 |
Кассир |
||
|
5 |
Время обслуживания одного клиента |
00:01:00 |
|
|
6 |
Очередь |
||
|
7 |
Время общения |
00:09:15 |
|
|
8 |
Уменьшение времени |
00:00:10 |
|
|
9 |
Количество бабушек |
40 |
|
|
10 |
|||
|
11 |
Результаты |
||
|
12 |
№ бабушки |
Время обслуживания бабушки |
Время ожидания бабушки |
|
13 |
1 |
Формула 2 |
Формула 4 |
|
14 |
Формула 1 |
Формула 3 |
Формула 5 |
|
15 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
Расчетные формулы:
|
Ячейка |
Формула |
|
|
Формула 1 |
А14 |
=А13+1 |
|
Формула 2 |
В13 |
=$B$5+$B$7 |
|
Формула 3 |
В14 |
=В13-+$B$8 |
|
Формула 4 |
С13 |
= В13 |
|
Формула 5 |
С14 |
= С13+ В14 |
3 этап. Компьютерный эксперимент
Эксперимент 1.
Изменяя значения ячеек В5, В7, В8, исследовать, влияние этих характеристик на скорость движения очереди.
Проведение исследования
-
Введите в таблицу контрольные исходные данные и скопируйте расчетные формулы в две-три строки.
-
Заполните формулами ячейки на 40 строк.
-
Определите по таблице, сколько времени понадобиться кассиру, чтобы обслужить всю очередь.
-
Найдите в таблице строку, которая соответствует наступлению обеденного перерыва.
Задача 5. Расчет кривой падения электрика
1 этап. Постановка задачи
Электрик Петров приставил к стене лестницу и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать вниз электрик Петров.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
||
|
1 |
Электрик Петров |
|||
|
2 |
||||
|
3 |
Исходные данные |
|||
|
4 |
Длина лестницы, м |
|||
|
5 |
Количество ступенек |
|||
|
6 |
Номер ступеньки, на которой стоит электрик |
|||
|
7 |
Шаг изменения угла |
|||
|
8 |
Промежуточные расчеты и результаты |
|||
|
9 |
Расстояние между соседними ступеньками |
Формула 1 |
||
|
10 |
Расстояние от ступеньки электрика до пола |
Формула 2 |
||
|
11 |
Расстояние от ступеньки электрика до стены |
Формула 3 |
||
|
12 |
Угол в градусах |
Угол в радианах |
Координата Х |
Координата Y |
|
13 |
Формула 4 |
Формула 6 |
Формула 7 |
Формула 8 |
|
14 |
Формула 5 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
|
15 |
Заполнить вниз с помощью маркера автозаполнения |
Расчетные формулы:
|
Ячейка |
Формула |
|
|
Формула 1 |
C9 |
=$С$4/$С$5 |
|
Формула 2 |
C10 |
=$С$6*$С$9 |
|
Формула 3 |
C11 |
=$С$4-$С$10 |
|
Формула 4 |
А13 |
0 |
|
Формула 5 |
А14 |
= А13+ $С$7 |
|
Формула 6 |
В13 |
=А13/180*ПИ() |
|
Формула 7 |
С13 |
=$С$11*СИН(В13) |
|
Формула 8 |
D13 |
=$С$10*КОС(В13) |
3 этап. Компьютерный эксперимент
Эксперимент 1.
-
Исследовать вид кривой падения электроника в зависимости от номера ступеньки.
-
Исследовать вид кривой в зависимости от номера ступеньки.
Проведение исследования
-
По столбцам С и D постройте диаграмму кривой, по которой движется ступенька с электриком.

Главная Контакты Случайная статья
|
||||
|
Лабораторная работа 13. Решение задач с помощью MS Excel. Задание 1. Рассчитать количество рулонов, необходимое для оклейки стен комнаты.
Расчет необходимого количества рулонов обоев |
||||
|
Исходные данные |
||||
|
Комната |
||||
|
Высота(h) |
2,6 |
|||
|
Длина(a) |
||||
|
Ширина(b) |
||||
|
Площадь стен |
35,36 |
|||
|
Образцы обоев |
||||
|
Названия |
Длина |
Ширина |
Площадь |
Необходим. кол-во |
|
Образец 1 |
10,5 |
0,5 |
||
|
Образец 2 |
10,5 |
0,6 |
||
|
Образец 3 |
10,5 |
0,7 |
||
|
Образец 4 |
0,5 |
|||
|
Образец 5 |
0,6 |
|||
|
Образец 6 |
0,7 |
2. Рассчитать Площадь и Необходимое кол – во по формулам, добавив в таблицу столбцы для расчета Sкомн и Sр:
Фактическая площадь стен минус площади окон и дверей (15%) Sкомн.=0,85*2*(a+b)*h
Фактическая площадь рулона за вычетом 10% на обрезки Sp = 0.9*l*d
Количество необходимых рулонов N= ЦЕЛОЕ(Sкомн/Sp)+2
Задание 2. Рассчитать параметры падения парашютиста.
- Заготовить таблицу с исходными данными:
Исходные данные
Масса человека
Приращение времени
0,5
Ускорение свободного падения
9,81
Расчет
Время
Скорость
Расстояние
Ускорение
9,81
- Задать начальное время равное 0 с. и по формуле = А8+$B$4 рассчитать отрезок времени до 20 с.
- Рассчитать скорость падения парашютиста по формуле: = В8+ $B$4*A8
- Рассчитать расстояние по формуле: = A8*B8+$B4$4*A8*A8/2
- Построить график зависимости скорости падения от времени.
Движение тела, брошенного под углом к горизонту.
1.Заполните таблицу исходных данных по образцу.
Поражение цели
Исходные данные
Ускорение свободного падения, g
9,81
Начальная скорость, v0
Угол бросания в градусах ,
Шаг изменения времени
0,2
координаты цели:
xц
yц
Точность попадания
1,5
Данные для расчетов:
Начальная горизонтальная скорость,
15,32089
Начальная вертикальная скорость,
12,85575
2. Заготовьте таблицу для расчетов:
|
время |
Горизонтальная скорость |
Вертикальная скорость |
x |
y |
Sx=х-хц |
Sy=y-yц |
Полное смещение |
3. Задать начальное время 0
4. Рассчитать промежуток времени по формуле: = время + шаг изменения времени и с помощью маркера заполнения протяните до значения времени =3.
5. Рассчитайте горизонтальную и вертикальную скорости:
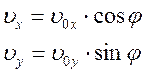
переведя их на язык Excel, где 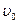
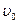
6. Аналогично рассчитайте координаты тела по формулам:
7. Рассчитайте полное смещение тела: Sx=х-хц Sy=y-yц
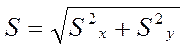
8. По координатам x, y построить график движения.
9. Определите по таблице расчетов:
— наибольшую высоту подъема;
— время движения до наивысшей точки;
— расстояние от точки броска до точки падения на землю;
-время движения до падения.
10. Проведите расчеты на Лист 2 , увеличив угол бросания 850 и оставляя неизменной начальную скорость. По координатам x, y построить график движения.
11. Сделайте анализ как в п.9
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна. |
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
47
Добавлен:
22.03.2015
Размер:
136.19 Кб
Скачать
В
магазине продаются обои. Наименования,
длина и ширина рулона известны. Провести
исследование, которое позволит
автоматически определить необходимое
количество рулонов для оклейки любой
комнаты. Размеры комнаты задаются
высотой (h),
длиной (а) и шириной (b).
При этом учесть, что 15% площади стен
комнаты занимают окна и двери, а при
раскрое 10% площади рулона уходит на
обрезки.
-
Составьте
информационную и математическую модель
предложенной ситуации. -
Заполните по
образцу расчетную таблицу.
|
A |
B |
C |
D |
E |
|
|
1 |
Расчет |
||||
|
2 |
|||||
|
3 |
Исходные |
Промежуточные |
Результаты |
||
|
4 |
|||||
|
5 |
Обои |
||||
|
6 |
Наименование |
Длина |
Ширина |
Площадь |
Кол-во |
|
7 |
Образец |
10,5 |
0,5 |
||
|
8 |
Образец |
10,5 |
0,6 |
||
|
9 |
Образец |
10,5 |
0,7 |
||
|
10 |
Образец |
13 |
0,5 |
||
|
11 |
Образец |
13 |
0,6 |
||
|
12 |
Образец |
13 |
0,7 |
||
|
13 |
|||||
|
14 |
Комната |
Площадь |
|||
|
15 |
Высота |
2,6 |
|||
|
16 |
Ширина |
3 |
|||
|
17 |
Длина |
5 |
-
Введите формулы
в расчетные ячейки, используя относительные
и абсолютные ссылки. -
Название таблицы
выполните подчеркнутым полужирным
шрифтом
16 размера.
-
Сохраните таблицу
под именем OBOI.xls
на дискете.
-
Под функцией в
EXCEL понимают
программу с уникальным именем, для
которой пользователь должен задать
конкретные значения аргументов функции,
стоящих в скобках после ее имени. -
Функции вводят в
таблицу в составе формул либо отдельно. -
В электронных
таблицах могут быть представлены
следующие виды функций:
-
Математические
-
Статистические
-
Текстовые
-
Логические
-
Финансовые
-
Функции даты и
времени и др.
-
Функции вводятся
с помощью диалогового окна «Мастер
функций», которое вызывается командой
ВСТАВКА, Функция или кнопкой -
Для каждой категории
функции справа в окне Мастера функций
показан их состав. Выбирается категория
функции (слева), имя функции (справа),
внизу дается краткий синтаксис функции. -
Правила построения
формул с помощью «Мастера функций»:
-
Активизировать
ячейку, в которой необходимо получить
результат -
Вызвать Мастер
функций -
В диалоговом окне
Мастера функций выбрать необходимую
для расчета функцию -
В диалоговом окне
выбранной функции ввести адрес
блока ячеек используемых в расчете
При копировании
или перемещении формулы в другое место
таблицы необходимо организовать
управление формированием адресов
исходных данных. Поэтому в электронной
таблице при написании формул наряду с
введенным ранее понятием ссылки
используются понятия Относительной
и Абсолютной ссылок.
-
Абсолютная
ссылка – это не изменяющийся
при копировании и перемещении формулы
адрес ячейки, содержащий исходное
данное (операнд).
Для указания
абсолютной адресации вводится символ
$ . Различают два типа абсолютной
ссылки: полная и частичная.
-
Полная абсолютная
ссылка указывается, если при копировании
и перемещении адрес клетки, содержащий
исходное данное, не меняется. Для этого
символ $ ставится перед наименованием
столбца и номером строки.
Например: $B$5
; $D$12 — полные
абсолютные ссылки
-
Частичная абсолютная
ссылка указывается, если при копировании
и перемещении не меняется номер строки
или наименование столбца. При этом
символ $ в первом случае ставится
перед номером строки, а во втором –
перед наименованием столбца.
Например: B$5
; D$12 — частичная
абсолютные ссылка, где не меняется номер
строки;
Например: $B5
; $D12 — частичная
абсолютные ссылка, где не меняется
наименование столбца.
-
Относительная
ссылка – это изменяющийся при
копировании и перемещении формулы
адрес ячейки, содержащий исходное
данное (операнд). Изменение адреса
происходит по правилу
относительной ориентации
клетки с исходной формулой и клеток
с операндами. Форма написания относительной
ссылки совпадает с обычной записью.
Соседние файлы в папке Информатика_лабы
- #
- #
- #
- #
- #
Содержание
- Необходимо покрасить краской стены кухни сколько потребуется банок краски если известно что
- Практическая работа тема: «Компьютерное моделирование в среде тп мs excel»
- Как рассчитать расход краски.
- Основа при расчетах краски.
- Правила расчета краски.
- Нормы расхода краски.
- Примеры вычислений расхода краски.
- Советы как можно экономить на краске.
- Поверхности для окрашивания.
- Влияет ли способ нанесения на расход краски?
- Тема. Использование электронных таблиц MS Excel для компьютерного моделирования Курбанов Р.Р. КГС 9-211 КГС 9-211. — презентация
- Презентация на тему: » Тема. Использование электронных таблиц MS Excel для компьютерного моделирования Курбанов Р.Р. КГС 9-211 КГС 9-211.» — Транскрипт:
- Использование возможностей MS Excel для решения профессиональных задач
- Просмотр содержимого документа «Использование возможностей MS Excel для решения профессиональных задач»
Необходимо покрасить краской стены кухни сколько потребуется банок краски если известно что
Практическая работа тема: «Компьютерное моделирование в среде тп мs excel»
Цель: освоить технологию моделирования в среде ТП МS Excel.
- размеры кухни 405 × 310 × 285 см;
- 88% площади стен занимает кафельная плитка;
- 1 банка краски предназначена для покраски площади 5 м 2 ?
Дано: a = 405 см – длина комнаты, b = 310 см – ширина комнаты,
c = 285 см – высота комнаты,
1 – 0,88 = 0,12 – часть комнаты для покраски (без кафеля),
5 м 2 – площадь покраски при использовании 1 банки краски.
Найти: необходимое для покраски стен кухни количество банок краски.
2. Математическая модель.
Sстен с кафелем =2(a + b)•c, Sстен для покраски = 2(a + b)•c * 0,12.
Чтобы определить, сколько потребуется банок краски, надо площадь для покраски разделить на 5 м 2 , т. е. Sстен для покраски : 5 и результат округлить до целых.
3
Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул.
Электронная таблица в режиме отображения значений.
4. ВЫВОД: С помощью ТП MS Excel мы определили, что для покраски стен кухни необходимо взять ______________________________________.
Задача 2. Через иллюминатор корабля требуется вытащить сундук с драгоценностями. Удастся ли это сделать?
И
2. Математическая модель.
Пусть r – радиус иллюминатора,
a, b, c – размеры сундука,
d1, d2, d3 – диагонали боковых поверхностей сундука
Сундук можно вытаскивать через иллюминатор одной из трех боковых граней, следовательно, достаточно, чтобы диагональ иллюминатора оказалась меньше одной из трех диагоналей сундука, т.е. должно быть истинно хотя бы одно из условий:
3
Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул.
Э
4. Компьютерный эксперимент.
Как рассчитать расход краски.
В процессе любого ремонта поднимается вопрос, сколько должно уйти расходного материала и как рассчитать расход краски? В особенности это относится к краске для окрашивания помещений. Многим может показаться, что это просто. Но как только дело дойдет до расчетов, многие начинают теряться. А нужно только соблюдать определенные правила при расчетах.
Для расчета расхода краски, вы можете воспользоваться калькулятором расхода краски.
Основа при расчетах краски.
Чтобы узнать как рассчитать расход краски, понадобится следующее: карандаш, рулетка, знание таблицы умножения, лист бумаги. Разделим все поэтапно:
1. Сначала измеряется длина стен в помещении с помощью рулетки, далее вычисляется периметр по формуле. Например, длина одной стены — 4 метра, тогда как ширина — 3 метра. В таком случае периметр составит: Р=(3*2)+(4*2)=14 метров.
2. На следующем этапе измеряется высота помещения либо высота уровня, до которого стены будут окрашены. Если высота составляет 2,5 метра, то площадь высчитывается следующим образом: S=2,5*14=35 метров квадратных.
3. Далее вычисляется высота и ширина дверных и оконных проемов, а также их периметры и общая площадь.
4. Из общей площади помещения необходимо вычесть площадь дверных и оконных проемов.
5. Для расчета расхода количества краски пользуемся нормами, которые указаны на упаковке. При расчете учитывается качество поверхности, подготовка поверхности и свойства материала.
После выполненных расчетов нужно только купить краску, размешать ее и приступать к покраске помещения. Если нужно будет красить декоративные детали, окна, дверные полотна, то расчеты соответственно усложнятся, хотя будут базироваться на перечисленных выше простых правилах.
Правила расчета краски.
Точно рассчитать краску можно после определения площади, которая будет окрашиваться, ее расположения, от типа применяемой краски. Для проведения расчетов нужно знать 2 значения:
- Нормативный расход для определенного вида краски;
- Площадь окрашиваемой поверхности.
Как необходимо рассчитывать площадь уже было написано выше, а вот расход краски рассчитывается следующим образом: нужно площадь разделить на нормативный расход. Мы получим в итоге цифру количества краски, которую нужно будет нанести в один слой.
Нормы расхода краски.
До того как производить расчеты краски, нужно учитывать тот факт, что норма будет меняться в зависимости от окрашиваемой поверхности:
- Если красится металл, то на 14-16 квадратных метров уходит 1 литр краски;
- На покраску 16 квадратных метров свежей штукатурки уходит 1 литр краски;
- Если красится шлифованное дерево, то 1 литр краски уходит на 16 квадратных метров;
- На покраску 10 квадратных метров рельефных обоев уходит 1 литр краски;
- При покраске 8-10 квадратных метров свежеспиленного дерева уходит 1 литр краски;
- На 15-17 кв. метров загрунтованной штукатурки уходит 1 литр краски.
При этом нужно учитывать следующий фактор: отечественные производители расход краски указывают в граммах, а не в литрах на 1 метр квадратный. Также нужно учитывать, что 1 килограмм краски и 1 литр — разные вещи, так как вода легче краски и имеет другой объем.
На норму расхода существенно влияет метод нанесения краски. Можно наносить краску пистолетом-пульверизатором, кистью либо валиком.
Примеры вычислений расхода краски.
Пример №1: Как рассчитать расход краски при покраске стен обычного помещения.
Как уже говорилось раньше нужно сначала рассчитать общую площадь помещения, после чего вычесть площади оконных и дверных проемов. В нашем случае нужно красить одну стену. При этом высота стены составляет 3 метра, а ширина 4 метра. Площадь такой стены составит 12 кв. метров.
Далее нужно вычислить площадь проема двери на данной стене, в нашем случае это 2 кв. метра. По общим правилам нужно от общей площади (12 кв. метров) отнять площадь двери (2 кв. метра).
В итоге мы получим следующие результаты: площадь поверхности для окраски составит 10 квадратных метров. Далее нужно рассчитать нужный объем краски. Например, если банка вмещает 2,5 литра, которой должно хватить на окраску площади в 25 квадратных метров, учитывая что будет красится 1 слой. Если красить стену необходимо в 2 слоя, то понадобится только 1 банка.
Пример №2: Окрашивание с учетом окон и дверей.
Если есть необходимость окрашивания пола, потолка, дверей, то используется такая же формула, как и в примере №1. При этом общая площадь окрашиваемой поверхности будет состоять из нескольких составляющих.
Площади всех стен, подоконников, дверей, потолка, пола рассчитываются отдельно, которые нужно потом сложить. Далее нужно найти расход краски, указанный на упаковке, и высчитать сколько потребуется краски. Если разные типы красок будут использоваться для отдельных элементов, то сначала вычисляется площадь, а только потом расход каждого из них.
Советы как можно экономить на краске.
Для расчета расходов можно использовать не только данные указанные на упаковке, площадь и свойства поверхности. На расход краски также влияют дополнительные факторы, которым также следует уделить внимание.
Укрывистость краски — такое свойство представляет собой способность целиком перекрывать собственным цветом предыдущий слой. С увеличением данного показателя уменьшается и расход краски. Такой показатель можно пересчитать, для этого нужно размеры площади окрашиваемой поверхности умножить на число слоев, и полученную сумму округлить в большую сторону. Также нужно учитывать качество поверхности, метод нанесения краски и степень подготовленности.
Часто бывает так, что 2-х слоев краски бывает недостаточно для качественного и полного окрашивания. Помимо этого еще нужно учесть следующий момент: изготовители краски на упаковках всегда указывают значения для подготовленных и ровных поверхностей. Часто после расчетов оказывается, что краски по факту может не хватить. В связи с этим рассчитывая расход краски, следует прибавить к полученному значению небольшой процент.
Поверхности для окрашивания.
Если учтены все факторы, то сделать расчеты достаточно просто. Чем лучше поверхность под окрашивание подготовлена, тем расход краски будет меньше. Когда стена уже окрашена в более яркий или темный цвет, а окраска будет происходить в светлых тонах, то расход значительно вырастет. В таком случае есть 2 выхода.
- Первый выход — избавиться от старого покрытия, удалить старую краску, а поверхность подготовить для окраски в светлый цвет;
- Второй выход — увеличить количество слоев, которые будут наноситься на поверхность.
Стоит отметить, что второй способ не такой эффективный, так как с увеличением слоев краска будет сохнуть намного дольше, при этом ее качества ухудшаться.
Влияет ли способ нанесения на расход краски?
Наиболее экономичным является метод нанесения краски специальным краскопультом, с помощью которого краска разбрызгивается. В итоге на поверхности остается аккуратная тонкая пленка краски.
К самому расточительному методу нанесения относится нанесение краски кистью (разная толщина слоев, потеки, неравномерность). Перечисленные факторы увеличивают расход. Идеальным вариантом буду малярные валики, они доступные и недорогие, легко чистятся, а краска экономично расходуется и ложится ровно.
Тема. Использование электронных таблиц MS Excel для компьютерного моделирования Курбанов Р.Р. КГС 9-211 КГС 9-211. — презентация
Презентация на тему: » Тема. Использование электронных таблиц MS Excel для компьютерного моделирования Курбанов Р.Р. КГС 9-211 КГС 9-211.» — Транскрипт:
1 Тема. Использование электронных таблиц MS Excel для компьютерного моделирования Курбанов Р.Р. КГС9-211 КГС9-211
2 Microsoft Office Excel позволяет группировать данные и выполнять различные действия над связанными данными. В этой презентаций будет показано как с помощью Microsoft Office Excel можно решать математические задачи разной сложности.
3 Задача 1 Необходимо покрасить краской стены кухни. Сколько потребуется банок краски, если известно, что размеры кухни 405×310×285 см ; 88% площади стен занимает кафельная плитка ; 1 банка краски предназначена для покраски площади 5 м 2.
4 Задача 1 Решение Постановка задачи Дано : a=405 см – длина комнаты, b=310 см – ширина комнаты, c=285 см – высота комнаты, 1- 0,88=0,12 – часть комнаты для покраски ( без кафеля ), 5 м 2 – площадь покраски при использовании 1 банки краски. Найти : необходимое для покраски стен кухни количество банок краски.
5 Задача 1 Моделирование в среде ЭТ В режиме отображения формул :
6 Задача 1 Моделирование в среде ЭТ В режиме отображения значений :
7 Задача 2 Через иллюминатор корабля требуется вытащить сундук с драгоценностями. Удастся ли это сделать ? Решение Постановка задачи Иллюминатор корабля имеет форму круга. Будем считать, что сундук имеет форму параллелепипеда. Чтобы вытащить сундук, необходимо, чтобы диаметр иллюминатора был больше любой из трех диагоналей поверхности сундука.
8 c R Задача 2 Пусть r – радиус иллюминатора, a, b, c – размеры сундука, d 1, d 2, d 3 – диагонали боковых поверхностей сундука. a b d1d1 d2d2 d3d3 с Математическая модель
9 Задача 2 Сундук можно вытаскивать через иллюминатор одной из трех боковых граней, следовательно, достаточно, чтобы диагональ иллюминатора оказалась меньше одной из трех диагоналей сундука, т. е. должно быть истинно хотя бы одно из условий : ЕСЛИ ((2*R> КОРЕНЬ (a^2+b^2));1;0) ЕСЛИ ((2*R> КОРЕНЬ (a^2+c^2));1;0) ЕСЛИ ((2*R> КОРЕНЬ ( с ^2+b^2));1;0).
10 Задача 2 Моделирование в среде ЭТ В режиме отображения формул :
11 Задача 2 Моделирование в среде ЭТ В режиме отображения значений :
12 Задача 3 Решить уравнение х 4 -4 х х х -14=0. Решение Необходимо построить график функции у = х 4 -4 х х х -14. Точки пересечения графика с осью Х будут решениями данного уравнения.
13 Задача 3 Таблица значений функции
14 Задача 3 Строим диаграмму.
16 Промежутки, в которых находятся корни : С помощь Подбора параметра уточняются значения корней
17 Задача 3 Уточненные корни
18 Задача 4 Решить уравнение log 2 (x·(1-x))-sin( π /x)+2=0 область определения которого : x принадлежит промежутку [0;1].
19 Задача 4 В MS Excel составляем таблицу значений функции с шагом аргумента h=0,04:
21 X 1 =0,1 8 X 2 =0,19 X 3 =0,2 6 X 4 =0, 33 X 5 =0, 50 X 6 =0,8 1
22 Вывод С помощью электронных таблиц MS Excel можно решать математические задачи и уравнения ; При этом отрабатываются навыки работы в электронных таблицах, а именно : оформление таблицы, работа с формулами, построение диаграмм.
Источник
Использование возможностей MS Excel для решения профессиональных задач

Работа представлена в виде презентации, в которой рассматривается пример решения практической задачи по строительным специальностям, а также приводится задание для самостоятельной работы. Ссылка на электронные ресурсы позволит самостоятельно проработать нужный материал.
Просмотр содержимого документа
«Использование возможностей MS Excel для решения профессиональных задач»
Использование возможностей MS Excel для решения профессиональных задач
Использование возможностей программы MS Excel
облегчает и ускоряет решение профессиональных задач .
Пример. Необходимо покрасить краской стены помещения. Сколько потребуется банок краски, если известны:
- Размеры помещения;
- Неокрашиваемая площадь (в процентах от общей);
- Расход краски (площадь)
Результат вычисления оформить в таблицу:
1 . Запустить Microsoft Excel 2007.
2. Выделить диапазон ячеек А1:D1.
3. Объединить эти ячейки щелчком по пиктограмме Объединить и поместить в центре
4. Ввести в объединённую ячейку текст Расход краски
5. Аналогично объединить ячейки А2:В2 и С2:D2. Ввести текст в эти ячейки Размеры помещения и Неокрашиваемая поверхность.
6. В диапазоны ячеек А3:В6 и С3:D4 ввести данные согласно заданию, изменяя при необходимости ширину столбцов. Перед вводом данных в ячейку D3 задать ей процентный формат.
7. Объединить ячейки С5:D5. Ввести текст Расход краски (площадь в кв. м).
8. Заполнить ячейки С6, D6.
9. Задать границы
диапазон А2:D6 и
щелкнуть по пиктограмме Все границы .
10. Объединить ячейки А8:С8 , ввести текст Требуемое количество банок.
11. Задать границы диапазона А8:D8.
12. В ячейку В6 ввести формулу вычисления площади стен помещения. Формула должна начинаться со знака «=». Это обязательное условие:
13. В ячейку D4 ввести формулу вычисления площади неокрашиваемой поверхности: = В6*D3.
14. Для нахождения количества
банок надо поделить
окрашиваемую площадь на
расход краски. Требуемое
количество банок краски должно
быть целочисленным значением.
Поэтому для вычисления
используем функцию ОКРВВЕРХ
из категории Математические,
которая округляет число до
Обратите внимание, что в указанных ячейках отображается не формула, а вычисленное значение!
Задание . Рассчитать количество рулонов обоев для оклейки трех комнат отдельной квартиры.
Следует учесть обрезку обоев при совмещении рисунка (вычесть из площади рулона площадь на обрезку).
Результат вычислений оформит в таблицу.
- Как адресуется ячейка?
- Как ввести информацию в ячейку?
- Для чего используется строка формул?
- Что такое «автозаполнение» ячеек?
- Каким образом можно изменить формат и тип вводимых данных?
- Что такое «диапазон ячеек»? Как он адресуется?
- Как выделить диапазон ячеек?
- Как объединить ячейки?
- Как вставить или удалить столбцы таблицы?
- Как вставить или удалить строки таблицы
- Как изменить ширину столбцов и высоту строк в электронной таблице?
- Как задать границы таблицы?
- Как установить в ячейке перенос текста?
- Как выполнить вычисления в электронной таблице?
- Что такое «абсолютный адрес» ячейки?
- Как выполнить автосуммирование ячеек?
- Как вставить функцию и аргументы функции?
- Как скопировать формулу с помощью маркера автозаполнения?
- Для чего используется команда Специальная вставка?
- Как отобразить на листе не вычисляемые значения, а формулы?
- Как отсортировать данные в таблице?
- Как графически отобразить данные таблицы?
- Как называются элементы диаграммы?
- Как изменить тип диаграммы?
- Как отформатировать диаграмму?
Источник
Опубликовано 11 Июн 2019
Рубрика: Справочник Excel | 14 комментариев

…из свободно распространяемого офисного пакета LibreOffice. При этом ни к созданию макросов, ни к написанию пользовательских функций, ни к программированию вообще обращаться нет необходимости!
«Решатель» Calc — это NLPSolver (wiki.openoffice.org/wiki/NLPSolver).
Предложенное далее решение прекрасно работает и в Calc, и в Excel. Причем даже переписывать формулы не нужно! Достаточно просто скопировать ячейки с формулами и данными и вставить на лист Excel, а вместо «Решателя» использовать надстройку «Поиск решения» — Excel Solver (solver.com/excel-solver-online-help) или лучше – надстройку OpenSolver (opensolver.org).
И все-таки – почему в данном случае стоит попробовать использовать не Excel, а Calc?
- Во-первых (и это важно), в «Решателе» Calc нет ограничения по количеству переменных. В Excel «Поиск решения» может принять для поиска оптимального раскройного плана только 200 схем раскроев. (Но, если скачать и в Excel подключить OpenSolver, то получите еще более широкие возможности, чем в LibreOffice Calc!)
- Во-вторых, интерфейс «Решателя» — на русском языке. Интерфейс OpenSolver — на английском языке.
- В-третьих, в «Решателе» Calc представлены 5 различных алгоритмов поиска решения. В Excel без надстройки OpenSolver набор алгоритмов скромнее.
- В-четвертых, LibreOffice Calc, в отличие от MS Excel, бесплатен для коммерческого использования.
- В-пятых, LibreOffice Calc не обязательно устанавливать на компьютер. На официальном сайте можно скачать полнофункциональную версию — LibreOffice Portable (libreoffice.org/download/portable-versions/).
Структура задачи и терминология.
Данная тема уже была подробно рассмотрена на блоге в статье «Линейный раскрой в Excel» 4 года назад. Вновь обратиться к ней побудило желание автоматизировать генерацию схем раскроев и сравнить результаты работы «Решателя» и OpenSolver.
Полную «задачу о распиле» можно разделить на две значительные подзадачи:
- Генерация всех возможных схем раскроев.
- Поиск на основе сгенерированных схем оптимального раскройного плана.
Первая подзадача в статье «Линейный раскрой в Excel» решалась методом составления схем раскроев «вручную» по определенному алгоритму.
Вторая подзадача решалась автоматически с использованием надстройки Excel «Поиск решения» (Excel Solver).
В представленной далее программе генерация схем раскроев выполняется автоматически! Это существенно упрощает работу, защищает от ошибок и экономит время при значительном количестве типоразмеров деталей и схем раскроев.
Поиск плана раскроя осуществим тремя способами:
- В LibreOffice Calc с помощью «Решателя» (NLPSolver).
- В MS Office Excel посредством штатного «Поиска решения» (Excel Solver).
- В MS Office Excel при помощи надстройки OpenSolver.
Определимся с терминологией и ограничениями:
- Заготовки – это исходный материал в виде рулонов, прутков, полос, стержней и т.д. одинаковой длины.
- Детали – это элементы, которые необходимо получить, разрезав исходные заготовки на части.
- Схема раскроя – один из вариантов раскроя заготовки, при котором длина отхода всегда меньше длины самой короткой детали.
- План раскроя – это перечень схем раскроя с количеством их повторений.
- *Ширина реза равна нулю.
Пример.

Условие задачи:
Бумагоделательная машина производит рулоны (заготовки) шириной 5600 мм.
Нужно найти план раскроя для нарезки 13 типоразмеров конечных рулонов (деталей), используя минимальное количество исходных рулонов (заготовок).
Ширины конечных рулонов (размеры деталей) и их необходимое количество — в таблице слева.
Скриншот программы:
Область для генерации схем раскроев имеет размер 13×213 ячеек, что обусловлено исключительно условиями этой конкретной задачи, и может быть изменена и в ширину и в высоту в сторону увеличения или уменьшения по желанию пользователя с соответствующей корректировкой формул.
К сожалению, качественно показать на скриншоте всю область программы для раскроя затруднительно. Скачайте файлы по ссылке под рисунком для детального просмотра листов Calc и Excel с программами.
В ячейках с желтой заливкой – не защищенные от изменений формулы!!! Будьте внимательны! Изменять значения можно только в ячейках со светло-бирюзовой заливкой.
Прошу уважающих труд автора скачать файлы с программой после подписки на анонсы статей. Подписные окна расположены в конце статьи и наверху страницы.
Ссылки на скачивание файлов с программой:
- linejnyj-raskroj-2 (ods 106,4KB);
- linejnyj-raskroj-2 (xlsx 60,3KB).
Правила ввода исходных данных:
В светло-бирюзовые ячейки записываем исходные данные из условия задачи:
- длину исходных рулонов – заготовок — Lз;
- длины конечных рулонов – деталей — Lдi;
- количество конечных рулонов – деталей — Nдi.
Длины деталей Lдi следует вписывать в порядке уменьшения размеров, слева – направо:
Lд1 > Lд2 > Lд3 > … > Lд12 > Lд13
Внимание! Если типоразмеров деталей в другой вашей задаче будет меньше 13, например 10, то, чтобы не переделывать каждый раз поле схем раскроев, в первые 3 ячейки для длин деталей следует записать значения больше размера заготовки, а их количество указать равным нулю:
Lд1 = Lд2 = Lд3 = А
А > Lз
Nд1= Nд2= Nд3=0
Решение:
После ввода всех исходных данных программа для раскроя автоматически сгенерирует 213 схем, решив, таким образом, первую подзадачу.
Действия пользователя при решении второй подзадачи – поиск оптимального плана раскроя — подробно описаны в статье о линейном раскрое в Excel. Эти действия полностью идентичны при работе со всеми тремя вышеназванными надстройками. Повторять их здесь нет смысла, так как, перейдя по ссылке, можно получить подробную, развернутую инструкцию.
Единственное, что следует дополнительно настроить:
- Из окна «Решателя» нужно перейти в окно «Параметры» и выбрать в выпадающем списке «Механизма решателя»: LibreOffice CoinMP линейный решатель.
- Там же в окне «Настройки» рекомендую проставить все галочки, так как переменные у нас в примере неотрицательные и целочисленные.
Ответ:
Минимум из 73 заготовок (исходных рулонов) можно изготовить все детали (конечные рулоны) с долей отходов всего 0,401%! В плане раскроя используется 12 схем раскроев. Время поиска решения – менее 10 секунд! (План раскроя показан выше на скриншоте программы.)
Ответ в Википедии: 73 заготовки; 0,401% отходов; в плане – 10 схем раскроев.
Итоги.
Существует несколько решений — планов раскроя с 13, 12, 11, 10 схемами раскроев, состоящих из 73 заготовок.
В таблице ниже представлены решения, найденные с использованием разных программ и надстроек. При расчетах в Excel и Calc использовались линейные механизмы поиска.
Все программы справились с поставленной задачей – нашли раскройные планы, обеспечивающие минимальное количество отходов.
Для обеспечения работоспособности стандартного «Поиска решения» (Excel Solver) в Excel пришлось удалить из поиска 13 схем раскроев с большими длинами остатков.
Если для этой задачи применить прямолинейный «жадный» алгоритм, традиционно используемый на многих производствах (сначала режем широкие рулоны, а узкие – в конце, используя по возможности отходы), то потребуется 82 исходных рулона-заготовки. Более 11,3% материала уйдет в отходы. При этом в плане будет 15 схем раскроев.
В случае необходимости минимизировать количество схем раскроев в плане стоит применить нелинейные алгоритмы надстроек из списков механизмов поиска решения.
Не используя специальных программ с помощью свободной программы LibreOffice Calc или MS Excel можно эффективно решать весьма громоздкие задачи по линейному раскрою погонажных материалов.
Возможности программы для раскроя можно существенно расширить под соответствующие задачи, увеличив количество типоразмеров деталей и пространство для схем раскроя. Ограничивающими факторами расширения являются только размеры листа программы Calc или Excel, производительность процессора и … здравый смысл.
Другие статьи автора блога
На главную