Расчет колебаний в excel

Муниципальное автономное общеобразовательное учреждение

«Средняя общеобразовательная школа №1» г. Боровичи

Проект

«Моделирование гармонических колебаний в среде табличного процессора Microsoft Excel»

	Подготовила: Ученица 11 «А» класса Январева Мария Руководитель: Васильева Надежда Владимировна 2021г. г. Боровичи
Содержание Введение         1. Теоретическая часть         1.1 Гармонические колебания: понятие, основные параметры         1.2 Уравнение гармонического колебания         1.3 Табличный процессор MS Excel: понятие, основные инструменты         2. Практическая часть         2.1 Заполнение исходных параметров колебаний в таблице         2.2 Создание полосы прокрутки в MS Excel         2.3 Создание графика в MS Excel         Заключение         Список Литературы

Введение

В школьной программе по предмету «физика» изучаются гармонические колебания. Однако в действительности осуществить эксперименты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно.  Microsoft Excel является отличным средством для моделирования различных динамических процессов. В этой работе с помощью функций MS Excel можно исследовать влияние параметров колебательного процесса на график колебаний.

Цель: смоделировать гармонические колебания с помощью табличного процессора Microsoft Excel.

Гипотеза: если изучить инструментарий табличного процессора Microsoft Excel, то с его помощью можно моделировать физические процессы.

Предмет: программа Microsoft Excel, как среда моделирования гармонических процессов.

Объект: График гармонических колебаний.

Задачи:

1) Изучить теоретический материал по теме Гармонические колебания.

2) Изучить теоретический материал о табличном процессоре Microsoft Excel.

3)Практически смоделировать Гармонические колебания в табличном процессоре Microsoft Excel.

1. Теоретическая часть

1.1 Гармонические колебания: понятие, основные параметры

Колебательное движение — это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени, при котором тело многократно и в разных направлениях проходит положение  равновесия.

Гармонические колебания – колебания,  при которых физическая величина изменяется с течением времени по гармоническому закону.

Рис 1. График синусоиды

1.2 Уравнение гармонического колебания

x = a*sin*(ω*t+φ0)

• x – смещение тела
• a – амплитуда колебаний
• ω – циклическая частота колебаний
•  t – время
• φ0 – начальная фаза колебаний

Период колебаний (T) – это минимальный промежуток времени, через который происходит повторение движения тела.

Τ= t / n

Начальная фаза колебания (φ0) — это фаза колебаний в начальный момент времени.  

Циклическая (круговая) частота (ω) — это число колебаний тела за 2π с.

ω0 = 2π/T = 2πν

Амплитуда колебаний (a) — максимальное смещение от положения равновесия.

Это уравнение дает зависимость «x» от времени «t».

1.3 Табличный процессор MS Excel: понятие, основные инструменты

Microsoft Excel – это универсальная программа для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию. В ней можно вести домашний бюджет, производить простые или сложные расчеты, организовывать дневники, составлять отчеты, строить графики, диаграммы и многое другое.

Основные инструменты MS Excel: рабочее поле, ячейка, диапазон ячеек, символьные и строковые величины, логические величины, формулы.

Рабочее поле – это экран дисплея, на котором электронная таблица предоставляется в виде прямоугольника, разделенного на строки и столбцы.

Ячейка – минимальный элемент электронной таблицы, над которым можно выполнять те или иные операции. Каждая ячейка имеет уникальное имя. Например: B2, C17, G150 и т.д.

Диапазон ячеек – его можно выделить из подряд идущих ячеек в строке, столбце или прямоугольнике. При задании диапазона указывают его начальную и конечную ячейки. Примеры диапазонов – A1:A100, B15:AZ12.

Для моделирования гармонических колебаний можно использовать:

 1)Формулы

      2)Полосы прокрутки

 3)График

2. Практическая часть

2.1 Заполнение исходных параметров колебаний в таблице

Ячейки электронной таблицы заполнены следующим образом: в ячейке B6 — значение амплитуды (a); B8 – значение круговой частоты (ω); B10 – значение фазы колебаний (α). Каждая из этих ячеек имеет формулу: B6 (=C6/10); B8 (=C8); B10 (=C10/100). (Заменим «φ0» на «α»).  

В столбце G вычисляются значения времени, возрастающие на 0,02, для этого в G4 введена формула (=G3+0,02).

В столбце H вычисляются значения X по формуле (=$B$6*SIN($B$8*G…+$B$10)) , где G меняется в зависимости от выбранной ячейки (заполняем с H3 вниз аналогичным способом). Для наглядности в ячейках G и H значения времени и координаты продолжены до 160 строчки.

В режиме отображения формул таблица выглядит следующим образом:

Рис.2. Режим отображения формул

В режиме отображения значений:

Рис.3. Режим отображения значений

2.2 Создание полосы прокрутки в MS Excel

С целью исследования влияния параметров гармонических колебаний на график колебательного процесса используем такую возможность как полосы прокрутки. Для каждой полосы прокрутки установлены максимальное и минимальное значение. Каждая полоса прокрутки привязана к соответствующей ячейке. Поправка положения ползунка на полосе прокрутки приводит к изменению значения в ячейке. Таким образом, изменяя значения амплитуды, круговой частоты и начальной фазы колебаний, можно наблюдать изменение графика.

1. Через меню Разработчик (Вставить/Элементы ActiveX) выбираем элемент «Полоса прокрутки».
2. Выбрав нужные ячейки, нужно вставить туда полосу прокрутки (меняем размер).
3. После вставки Полосы прокрутки она становится выделенной. Если нажать на любое другое место листа, то Полоса прокрутки перестанет быть выделенной.
4. Нажимаем на Полосу прокрутки правой кнопкой мыши и выбираем «Свойства».
5. В свойствах меняем значения «Max» и «Min» на те, которые необходимы (на 10 и 0, соответственно).
6. Чтобы привязать полосу прокрутки в строке «LinkedCell» выбираем ячейку, где будут находиться значения колебания.
7. Также можно изменить цвет полосы, для этого нужно найти строчки «BackColor» и «ForeColor». «BackColor» меняет фон полосы, а «ForeColor» цвет стрелок и ползунка.
8. Полоса прокрутки готова.

Полосы прокрутки находятся в ячейках D6E6, D8E8, D10E10 и привязаны к ячейкам C6, C8, C10. Полосы прокрутки меняют значения в этих ячейках от 0 до 10, так как установлено максимальное и минимальное значение.

2.3 Создание графика в MS Excel

1. Выделяем таблицу от G3 и H3 до G160 и H160, и переходим во вкладку «Вставка». Нажимаем на кнопку «График» и выбираем самый простой из них (находится на первом месте).
2. Программа произвела построения графика, но как видим, появилось две линии, нужно удалить одну из них (удалим линию «t»).
3. Легенда тоже не нужна, так как на графике всего одна линия. Поэтому нужно удалить легенду.
4. Теперь нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «t» в таблице.
5. Нажимаем правой кнопки мыши на график. В меню перемещаемся по значению «Выбрать данные…».
6. В активировавшемся окне выбора источника нажать на правую кнопку «Изменить».
7. Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «t». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».
8. В окне выбора источника данных нажимаем на «ОК».
9. Далее выбираем «Режим Конструктора» и нажимаем на график левой кнопкой мыши. Находим и нажимаем на «Макет», переходим во вкладку «Оси». В самом низу находится «Дополнительные параметры основной горизонтальной оси…». Меняем параметры горизонтальной оси. Аналогично делаем и с вертикальной осью.
10. После этого программа произведет редактирование ранее построенного графика согласно тем изменениям, которые были произведены в настройках.

Рис. 4. График колебательного процесса.

Заключение

Таким образом, данный график может применяться на уроках физики, что позволит ученикам явно проследить изменение графика колебаний при изменении различных параметров. А ученикам, увлекающимся информатикой, эта работа поможет для моделирования гармонических колебаний, поможет еще больше узнать о возможностях табличного процессора MS Excel.

Список литературы

1. Мякишев Г.Я. Учебник Физики 11 класса. Гармонические колебания. Просвещение, 2010. – 399с.

  2. Фаза колебаний. https://www.calc.ru/Faza-Kolebaniy.html

3. Гарнаев А.Ю. Самоучитель VBA. СПб: БХВ, Санкт Петербург, 1999.

4. Веденеева Е.А. Функции и формулы Excel 2007. Библиотека пользователя. – Санкт Петербург, 2008. –384с.

5. Полосы прокрутки. https://excel2.ru/articles/polosa-prokrutki-element-upravleniya-formy-v-ms-excel

6. График. https://exceltable.com/grafiki/grafiki-i-diagrammi-v-excel

Практическая работа Гармонические колебания.

«Построение графика функции в Excel»

1. Построить таблицу:

а) в первой строке необходимо задать аргумент функции от xn до xk с шагом h, используя автозаполнение (т.е. задаём интервал функции [-10;10] с шагом 0,5).

б) Во вторую строку вводим выражение (например: f(x)=sin x), точно также используя автозаполнение копируем его.

2. Выделить диапазон из двух строк.

3. Вкладка Вставка – панель Диаграммы – инструмент Точечная с гладкими кривыми.

Рисунок 1. Примерный график функции cos x в диапазоне [-10;10].

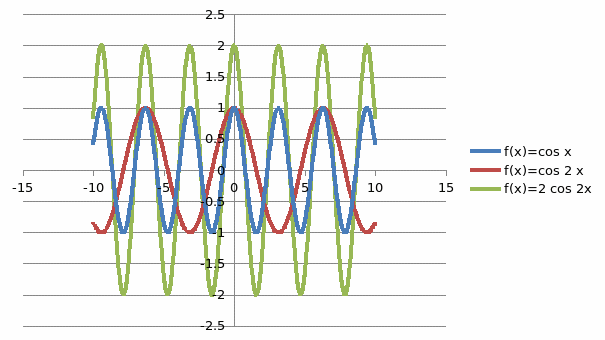
Построить диаграммы для функций:

1. f(x) = cos x;

2. f(x) = cos 2 x;

3. f(x) = 2 cos 2 x;

4. f(x) = sin x;

5. f(x) = sin 2 x;

6. f(x) = 2 sin 2 x.

Сравнить полученные графики.

Рисунок 2. Сравнение функций cos x; cos 2 x; 2 cos 2 x;

1. Моделирование гармонических колебаний в среде табличного процессора MS Excel

Работа ученицы 10 класса
МОУ СОШ пос. Мизур
Цогоевой Ирины

2. Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются

ГАРМОНИЧЕСКИМИ
КОЛЕБАНИЯМИ
x
xm
0
xm
π/2
π
3π/2
T/4
T/2
3T/4
2π
T
φ
t

3. Уравнение гармонического колебания

x = xm cos(ω0 t + φ0)
x – смещение тела
t – время
xm – амплитуда колебаний
φ0- начальная фаза колебаний
ω – циклическая частота колебаний

4. Период колебаний

X
xm
t
T
Минимальный промежуток времени, через который
происходит повторение движения тела, называется
периодом колебаний T.
= t / n

5. Амплитуда колебания

X
xm
t
xm – амплитуда колебаний, т. е. максимальное
смещение от положения равновесия

6. Частота колебаний

X
1
Т
xm
T
Физическая величина, обратная периоду колебаний,
называется частотой колебаний. Частота колебаний
показывает, сколько колебаний совершается за 1 с.
Единица частоты – герц (Гц).

7. Циклическая частота колебаний

Циклическая или круговая частота — это число
колебаний тела за 2π с.
ω0 = 2π/T = 2π

8. Исследование влияния параметров гармонических колебаний на график колебательного процесса

9. Сложение колебаний

a1
a
a2
α
0
x1
a2
α1
x2
x
x1 = а1 cos (ω1t + α)
cos (ωt + α)
x2 = a2 cos (ω2t +α)
а² = а1² + а2² + 2 а1а2 cos (α2 – α1)
X
x=a

10. Сложение колебаний в MS Excel

11. Биения

12. Информатика, физика, математика – это не скучно!