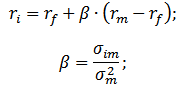Расчет коэффициента бета capm excel - Word и Excel - помощь в работе с программами

КУРС

ИНВЕСТИЦИОННЫЙ АНАЛИТИК

Модель CAPM часто используется как дополнение к портфельной теории Г. Марковица. В практике построения инвестиционных портфелей модель САРМ, как правило, используется для выбора активов из всего множества, далее уже с помощью модели Г. Марковица формируется оптимальный портфель.

Модель CAPM связывает такие составляющие как будущая доходность ценной бумаги и риск этой бумаги. Рассмотрим модель САРМ (ее также называют модель Шарпа) более подробно.

Если вы хотите детальнее познакомиться с другими концепциями финансовой и экономической теории, то рекомендуем записаться на наш открытый онлайн-курс «Финансы с нуля».

Формула Шарпа связи будущей доходности ценной бумаги и риска

R — ожидаемая норма доходности;
Rf — безрисковая ставка доходности, как правило, ставка по государственным облигациям;
Rd — доходность рынка;
β — коэффициент бета, который является мерой рыночного риска (недиверсифицируемого риска) и отражает чувствительность доходности ценной бумаги к изменениям доходности рынка в целом.

Итак, ожидаемая норма доходности — это та доходность ценной бумаги, на которую рассчитывает инвестор. Другими словами — это прибыль этой ценной бумаги.

Безрисковая ставка доходности — это доходность, полученная по безрисковым ценным бумагам. Как правило, берут ставку по государственным облигациям. Чтобы посмотреть ставки по государственным облигациям, можно зайти на сайт центрального банка РФ. В России на данный момент она составляет 5.04%.

Под доходностью рынка понимают доходность индекса данного рынка, в нашем случае индекс РТС (RTSI). Для Американских акций берут индекс S&P 500.

Бета — коэффициент, показывающий рискованность ценной бумаги.

Применение модели оценки капитальных активов

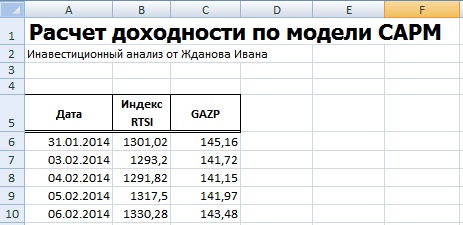
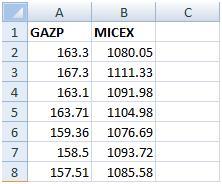
Итак, попытаемся рассчитать будущую доходность акции Газпрома GAZP. Возьмем котировки этой акции и индекса РТС (RTSI) или ММВБ (MICEX) по месяцам за период с 27 августа 2009 года по 27 августа 2010 года (котировки можно экспортировать в Excel с сайта).

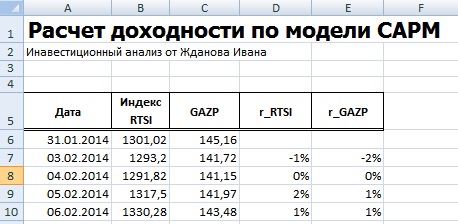
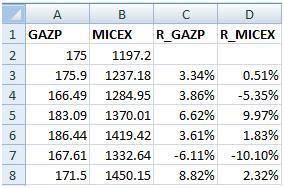
Далее рассчитаем дневные доходности по акции Газпрома и индексу ММВБ.

=(A3-A2)/A2
=(B3-B2)/B2

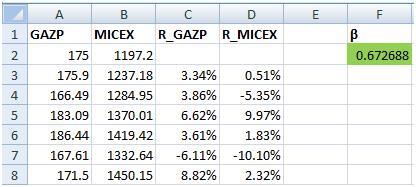
В итоге получится следующая таблица.

Для того, чтобы рассчитать коэффициент бета, необходимо рассчитать коэффициент линейной регрессии между доходностями акции Газпрома и индекса ММВБ. Можно пойти двумя путями.

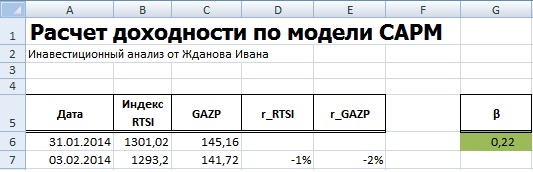
Расчет беты через формулу

В ячейке F2 введем следующую формулу:

=ИНДЕКС(ЛИНЕЙН(C3:C13;D3:D13);1)

Коэффициент бета будет равен 1,043.

Расчет беты через надстройку «Анализ данных»

Для расчета коэффициента вторым способом необходимо установить надстройку Excel «Анализ Данных». Если вы хотите лучше разбираться в функционале Excel, то рекомендуем записаться на наш открытый онлайн-курс «Аналитика в Excel».

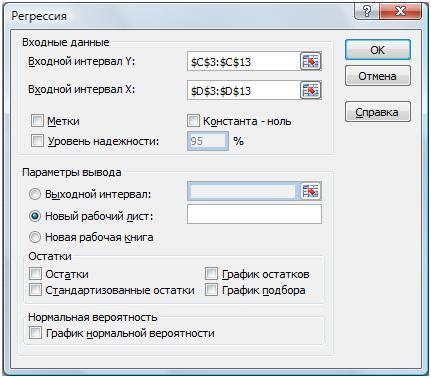
В ней выбрать раздел «Регрессия» и установить входные интервалы, которые соответствуют доходностям акции Газпрома и индекса ММВБ. В новом рабочем листе появится отчет.

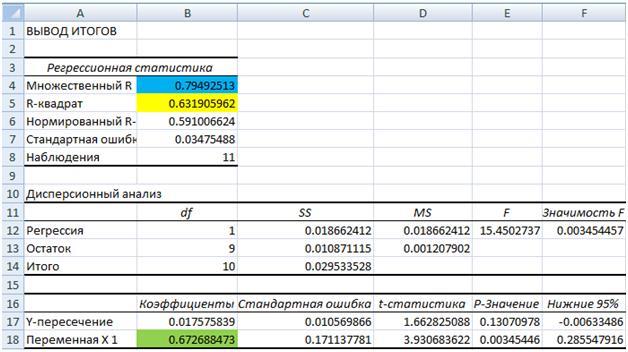
Отчет по регрессии выглядит следующим образом. В ячейке В18 находится расчет коэффициента линейной регрессии — необходимый коэффициент бета. Коэффициент бета равен 0,67.

Также в отчете есть показатель «R-квадрат» (коэффициент детерминированности), значение которого равно 0,63. Он показывает силу зависимости между независимыми переменными (зависимость между доходностью акции и индексом).

Показатель «Множественный R» является коэффициентом корреляции. Как видим, коэффициент корреляции составляет 0,79, что говорит о сильной связи между доходностью индекса и доходностью акции Газпрома.

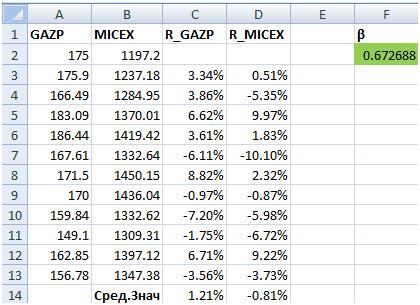
Осталось рассчитать месячную доходность рынка — доходность индекса ММВБ. Она рассчитывается как среднеарифметическая доходность индекса. Доходность индекса ММВБ составляет в среднем за месяц -0,81%, а среднемесячная доходность акции Газпрома — 1,21%.

Мы рассчитали все необходимые параметры модели САРМ.

Теперь рассчитаем справедливую норму доходности акции Газпрома на следующий месяц:

Норма доходности акции Газпрома на следующий месяц равняется 1,12%. Можно сказать, что это прогнозная цена будущей доходности в следующем отчетном периоде (у нас месяц).

Модель оценки капитальных активов (CAPM) — мощный инструмент оценки акций и ценных бумаг, который позволит составить прибыльный инвестиционный портфель.

Автор: Жданов Иван, эксперт SF Education

КУРС

ИНВЕСТИЦИОННЫЙ АНАЛИТИК

Источник

На чтение 8 мин Просмотров 67.3к.

Рассмотрим практические аспекты построения модели оценки капитальных активов CAPM с помощью Excel для отечественных акций ОАО «Газпром».

Модель оценки капитальных активов (англ. Capital Assets Price Model, CAPM) – модель оценки (прогнозирования) будущей доходности актива для инвесторов. Подход оценки активов был теоретически разработана еще в 50-е годы Г.Марковицем, и окончательно сформирован в виде модели в 60-е годы У.Шарпом (1964), Дж. Трейнором (1962), Дж. Линтнером (1965), Ж. Мосином (1966).

★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут

Модель CAPM основывается на гипотезе эффективного рынка капитала (Efficient Market Hypothesis, EMH), созданной еще в начале 20-го века Л. Башелье и активно продвигаемую Ю.Фамой в 60-е годы. Данная гипотеза имеет ряд условий по способу распространению информации и действию инвесторов на эффективном рынке капитала:

Информация свободно распространяется и доступно всем инвесторам, рынок имеет совершенную конкуренцию. Другими словами, отсутствуют инсайдеры, которые обладают большим преимуществом в принятии решений и получении сверхдоходности (выше среднерыночной).
Любое изменение информации о компании сразу приводит к изменению стоимости ее активов (акций). Это исключает возможность использования любой активной стратегии инвестирования для получения сверхприбыли. Данная предпосылка исключает возможность арбитражных сделок, когда инвестор заранее имеет полезную информацию, тогда как цена на активы компании еще не изменилась.
Инвесторы на эффективном рынке имеют долгосрочный горизонт вложения. Это исключает возникновение резких изменений цен на активы (акции) и кризисов.
Активы имеют высокую ликвидность и абсолютно делимы.

Исходя из гипотезы эффективного рынка, У. Шарп сделал предположение, что на будущую доходность акции будут оказывать влияние только рыночные (системные) риски. Другими словами, будущую доходность акции будут определять общее настроение рынка. Поэтому, кстати, он и был сторонником пассивного инвестирования, когда инвестиционный портфель не пересматривается от получения новой информации. Следует отметить, что на эффективном рынке невозможно получить сверхприбыль. Это делает любое активное управление инвестициями (инвестиционным портфелем) не целесообразным и ставит под сомнение эффективность вложения в ПИФы. В результате, модель У. Шарпа имеет всего один фактор – рыночный риск (коэффициент бета). Анализируя данные постулаты эффективного рынка, можно заметить, что в современной экономике многие из них не выполняются. Модель CAPM в большей степени является теоретической моделью и может использоваться на практике в общем случае.

Содержание

Модель CAPM. Формула расчета
Расчет модели CAPM в Excel
Расчет коэффициента бета с помощью формул Excel
Расчет коэффициента бета через надстройку «Регрессия»
Что показывает коэффициент бета в модели CAPM?
Расчет безриковой ставки для модели CAPM
Расчет средней доходности рынка
Расчет будущей доходности по модели CAPM
Преимущества и недостатки модели CAPM

Модель CAPM. Формула расчета

Формула оценки будущей доходности актива (акции) по модели CAPM имеет следующий аналитический вид:

где:

r – ожидаемая доходность актива (акций);

r_f – доходность по безрисковому активу;

r_m – среднерыночная доходность;

β – коэффициент бета (мера рыночного риска), который отражает чувствительность изменения стоимости активов в зависимости от доходности рынка. Данный коэффициент иногда называют коэффициент Шарпа.

Модель представляет собой уравнение линейной регрессии и показывает линейную взаимосвязь между доходностью (r) и рыночным риском (β);

σ_im – стандартное отклонение изменения доходности акции от изменения доходности рынка;

σ²_m – дисперсия рыночной доходности.

Расчет модели CAPM в Excel

Для того чтобы лучше понять модель CAPM разберем ее на реальном примере акций предприятия ОАО «Газпром». Для этого воспользуемся программой Excel. Получить котировки акций можно на сайте finam.ru в разделе «Про рынок» → «Экспорт данных».

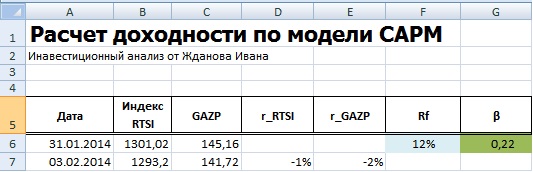
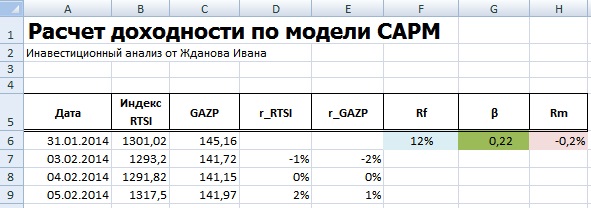
В нашей формуле за рыночную доходность будем брать изменения индекса РТС (RTSI), также это может быть индекс ММВБ (MICECX). Для американских акций зачастую берут изменения индекса S&P500. Были взяты ежедневные котировки акции и индекса за 1 год (250 данных), начиная с 31.01.2014 по 30.01.2015 г.
Далее необходимо рассчитать доходности акции (E) и индекса (D), по формулам:

=(B7-B6)/B6

=(C7-C6)/C6

Хочется заметить, что для оценки доходностей могла быть использована также формула расчета через натуральный логарифм:

=LN(B7/B6)

=LN(C7/C6)

Итоговый результат расчета доходности одинаковый.

На следующем этапе необходимо рассчитать значение коэффициента бета, отражающего рыночный риск акции. Для этого есть два варианта расчета.

Расчет коэффициента бета с помощью формул Excel

Для расчета коэффициента бета можно воспользоваться формулой ИНДЕКС и ЛИНЕЙН, первая позволяет взять индекс b из формулы линейной регрессии между доходностями акции и индекса, который соответствует коэффициенту бета. Формула расчета будет следующая:

=ИНДЕКС(ЛИНЕЙН(E7:E256;D7:D256);1)

Расчет коэффициента бета через надстройку «Регрессия»

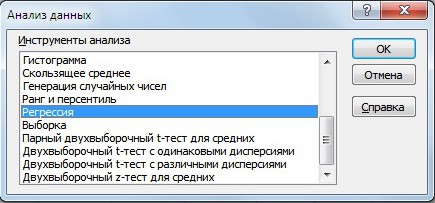
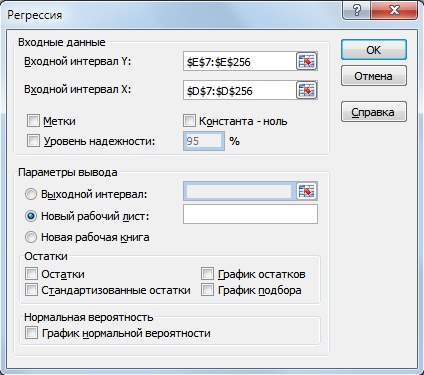
Второй вариант расчета рыночного риска модели заключается в использовании надстройки в разделе «Главное меню» → «Данные» →«Анализ данных» → «Регрессия».

В открывшемся окне необходимо заполнить два поля: «Входной интервал Y» и «Входной интервал Х» доходностями индекса и акции соответственно.

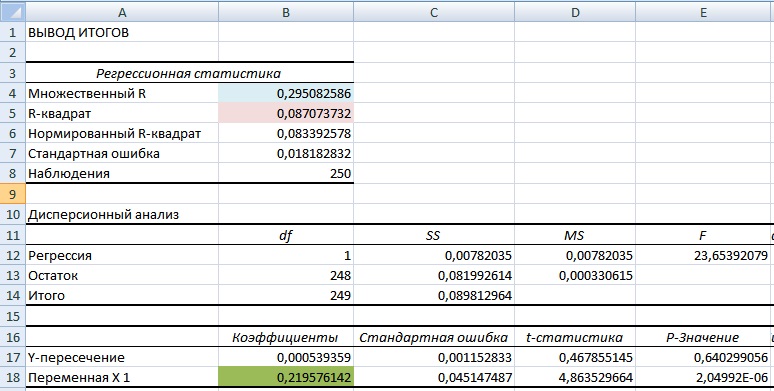
На новом листе Excel появится основные параметры модели линейной регрессии. В ячейке В18 отразится рассчитанный коэффициент линейной регрессии – коэффициент бета. Рассмотрим другие полученные параметры анализа. Так показатель Множественной R (коэффициента корреляции) между доходностью акции и индекса составляет 0,29, что показывает низкую степень зависимости доходности акции от доходности индекса. Коэффициент R-квадрат (коэффициент детерминированности) отражает точность полученной модели. Точность составляет 0,08, что очень мало для того чтобы принимать адекватные решения о прогнозировании будущей доходности на основе взаимосвязи только с уровнем риска рынка.

Что показывает коэффициент бета в модели CAPM?

Коэффициент бета показывает чувствительность изменения доходности акции и доходности рынка. Другими словами, отражает рискованность вложения в тот или иной актив. Коэффициент бета служит мерой рыночного риска. Знак перед показателем отражает их однонаправленное или разнонаправленное движение. Рассмотрим более подробно значение бета в таблице ниже:

Значение коэффициента бета	Комментарии
β > 1	Доходность акция более чувствительная к изменению, доходности рынка
β = 1	Доходность акции совпадает доходности рынка
0 < β < 1	Доходность акции менее чувствительна к изменениям доходности рынка
β = 0	Доходность акции не зависит от доходности рынка полностью

В нашем примере, мы получили значение бета равной 0,22 – это показывает малую степень влияния рыночного риска на доходность акции ОАО «Газпром». На следующем этапе необходимо рассчитать безрисковую ставку (r_f).

Расчет безриковой ставки для модели CAPM

Безрисковая ставка представляет собой гарантированный уровень доходности, который получил бы инвестор при осуществлении альтернативного инвестирования. На практике за безрисковую процентную ставку берут процентные ставки государственных ценных бумаг (ГКО – государственные краткосрочные бескупонные облигации, ОФЗ – облигации федерального займа ) и (доходность 30-летних облигаций США). Доходности по российским ценным бумагам можно посмотреть на сайте ЦБ РФ «Ставки рынка ГКО-ОФЗ». На текущий момент, процентная ставка составляет около 12% годовых. Отразим полученные данные в таблице Excel.

Расчет средней доходности рынка

Расчет средней доходности рынка (индекса РТС) проходит простой формуле Excel:

=СРЗНАЧ(D6:D256)

Расчет будущей доходности по модели CAPM

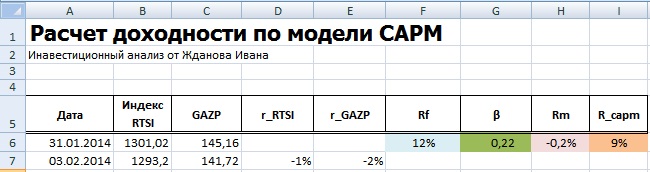
Рассчитаем будущую доходность акции ОАО «Газпром» на основе модели CAPM (R_capm). Формула оценки следующая:

=F6+G6*(H6-F6)

Как мы видим, что по модели CAPM ожидается доходность акции ОАО «Газпром» в размере 9%, что ниже, чем доходность по безрисковому активу. Доходность рынка составила отрицательное значение (-0,2%). Это объясняется тем, что сейчас наблюдается кризис на фондовом рынке, что приводит к оттоку капитала и созданию неустойчивой инвестиционной среды. Современные методы оценки инвестиций и инвестиционных портфелей вы можете прочитать в моей статье: «Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel«.

Преимущества и недостатки модели CAPM

К преимуществам модели можно отнести ее фундаментальный принцип о взаимосвязи между уровнем рыночного риска (системного риска) и уровнем будущей доходности акции.

Рассмотрим недостатки модели CAPM.

Во-первых, модель оперирует только одним фактором, влияющим на будущую доходность акции. В 1992 году Ю. Фама К. Френч доказали, что на будущую доходность также влияют такие факторы как: размер компании и отраслевая принадлежность.

Во-вторых, модель имеет ряд ограничений: модель не учитывает налоги, трансакционные затраты, непрозрачность финансового рынка и т.д.

В-третьих, для прогнозирования будущей доходности используют ретроспективный уровень рыночного риска, что приводит к ошибке прогноза.

Резюме

В данной статье мы рассмотрели на практическом примере расчет будущей доходности акции ОАО «Газпром» в Excel. Следует отметить, что модель CAPM может применяться в условиях эффективного рынка капитала. В настоящее время увеличивается количество кризисов на финансовых рынках, это делает затруднительным использование модели в долгосрочной оценки активов. Несмотря на это, модель может быть использована как метод анализа силы влияния рыночного риска на будущую доходность акции. Спасибо за внимание, с вами был Иван Жданов.

Автор: к.э.н. Жданов Иван Юрьевич

Источник

What Is Beta?

Peering through Yahoo (YHOO) Finance, Google (GOOG) Finance, or other financial data feeders, one may see a variable called beta amid other financial data, such as stock price or market value.

In finance, the beta of a firm refers to the sensitivity of its share price with respect to an index or benchmark. Generally, the index of 1.0 is selected for the market index (usually the S&P 500 index), and if the stock behaved with more volatility than the market, its beta value will be greater than one. If the opposite is the case, its beta will be a value less than one. A company with a beta of greater than one will tend to amplify market movements (for instance the case for the banking sector), and a business with a beta of less than one will tend to ease market movements.

Beta can be seen as a measure of risk: the higher the beta of a company, the higher the expected return should be to compensate for the excess risk caused by volatility.

Therefore, from a portfolio management or investment perspective, one wants to analyze any measures of risk associated with a company to gain a better estimation of its expected return.

Key Takeaways

Beta is a measure of how sensitive a firm’s stock price is to an index or benchmark.
A beta greater than 1 indicates that the firm’s stock price is more volatile than the market, and a beta less than 1 indicates that the firm’s stock price is less volatile than the market.
A beta may produce different results because of the variations in estimating it, such as different time spans used to calculate data.
Microsoft Excel serves as a tool to quickly organize data and calculate beta.
Low beta stocks are less volatile than high beta stocks and offer more protection during turbulent times.

How Do You Calculate Beta In Excel?

Different Results for the Same Beta

Incidentally, it is important to differentiate the reasons why the beta value that is provided on Google Finance may be different from the beta on Yahoo Finance or Reuters.

This is because there are several ways to estimate beta. Multiple factors, such as the duration of the period taken into account, are included in the computation of the beta, which creates various results that could portray a different picture. For example, some calculations base their data on a three-year span, while others may use a five-year time horizon. Those two extra years may be the cause of two vastly different results. Therefore, the idea is to select the same beta methodology when comparing different stocks.

Calculation of Beta Using Excel

It’s simple to calculate the beta coefficient over a certain time period. The beta coefficient needs a historical series of share prices for the company that you are analyzing. In our historical example, we will use Apple (AAPL) stock prices from 2012 through 2015 as our object of analysis and the S&P 500 as our historical index. To get this data, go to:

Yahoo! Finance –> Historical prices, and download the time series «Adj Close» for the S&P 500 and the firm Apple.

We only provide a small snippet of the data over 750 rows as it is extensive:

Once we have the Excel table, we can reduce the table data to three columns: the first is the date, the second is the Apple stock, and the third is the price of the S&P 500.

There are then two ways to determine beta. The first is to use the formula for beta, which is calculated as the covariance between the return (r_a) of the stock and the return (r_b) of the index divided by the variance of the index (over a period of three years).

Cov

(

)

Var

(

)

begin{aligned} &beta_a = frac { text{Cov} ( r_a, r_b ) }{ text{Var} ( r_b ) } \ end{aligned}

βa=Var(rb)Cov(ra,rb)

To do so, we first add two columns to our spreadsheet; one with the index return r (daily in our case), (column D in Excel), and with the performance of Apple stock (column E in Excel).

At first, we only consider the values of the last three years (about 750 days of trading) and a formula in Excel, to calculate beta.

BETA FORMULA = COVAR (D1: D749; E1: E749) / VAR (E1: E749)

The second method is to perform a linear regression, with the dependent variable performance of Apple stock over the last three years as an explanatory variable and the performance of the index over the same period.

Now that we have the results of our regression, the coefficient of the explanatory variable is our beta (the covariance divided by variance).

With Excel, we can pick a cell and enter the formula: «SLOPE» which represents the linear regression applied between the two variables; the first for the series of daily returns of Apple (here: 750 periods), and the second for the daily performance series of the index, which follows the formula:

BETA FORMULA = SLOPE (E1: E749; D1:D749)

Here, we have just computed a beta value for Apple’s stock (0.77 in our example, taking daily data and an estimated period of three years, from April 9, 2012, to April 9, 2015).

Low Beta–High Beta

Many investors found themselves with heavy losing positions as part of the global financial crisis that began in 2007. As part of those collapses, low beta stocks dove down much less than higher beta stocks during periods of market turbulence. This is because their market correlation was much lower, and thus the swings orchestrated through the index were not felt as acutely for those low beta stocks.

However, there are always exceptions given the industry or sectors of low beta stocks, and so, they might have a low beta with the index but a high beta within their sector or industry.

Therefore, incorporating low beta stocks versus higher beta stocks could serve as a form of downside protection in times of adverse market conditions. Low beta stocks are much less volatile; however, another analysis must be done with intra-industry factors in mind.

On the other hand, higher beta stocks are selected by investors who are keen and focused on short-term market swings. They wish to turn this volatility into profit, albeit with higher risks. Such investors would select stocks with a higher beta, which offer more ups and downs and entry points for trades than stocks with lower beta and lower volatility.

What Does a Stock’s Beta Tell You?

The Beta of a stock indicates its relative volatility compared to the broader equity market, as measured by the S&PO 500 (which has a beta of 1.0). A beta greater than one would indicate that the stock will go up more (in percentage terms) than the index when the index goes up, but also fall more than the index when it declines. A beta of less than one would suggest more muted movements relative to the index.

How Is Beta Computed?

Beta is essentially the regression coefficient of a stock’s historical returns compared to those of the S&P 500 index. This coefficient represents the slope of a line of best fit correlating the stock’s returns against the index’s. Because regression coefficients are called «betas» (β) in statistics, the terminology was carried over to investing.

How Is Beta Used in Practice?

Beta is used to gauge the relative riskiness of a stock. As an example, consider the hypothetical firm US CORP (USCS). Financial websites provide a current beta for this company at 5.48, which means that with respect to the historical variations of the stock compared to the Standard & Poor’s 500, US CORP increased on average by 5.48% if the S&P 500 rose by 1%. Conversely, when the S&P 500 is down 1%, US CORP Stock would tend to average a decline of 5.48%. If the index rose by 0,2%, USGC rose, on average, by 1.1%. As a result, one may conclude that USGC is a fairly risky investment.

The Bottom Line

It is important to follow strict trading strategies and rules and apply a long-term money management discipline in all beta cases. Employing beta strategies can be useful as part of a broader investment plan to limit downside risk or realize short-term gains, but it’s important to remember that it is also subject to the same levels of market volatility as any other trading strategy.

Источник

Построение модели CAPM в Excel для российского фондового рынка

Модель оценки капитальных активов или как ее английская аббревиатура CAPM (Capital Assets Price Model) была создана в 70-х годах прошлого века для оценки финансовых активов предприятия: денежные средства и ценные бумаги. Эта модель была разработана и сформирована такими известными учеными как: Шарпом, Линтнером и Моссиным. Модель CAPM предназначена для определения цены акции или стоимости компании в будущем, другими словами, текущая оценка перекупленности или перепроданности компании.

Модель CAPM часто используется как дополнение к портфельной теории Г. Марковица. В практике построения инвестиционных портфелей, модель CAPM, как правило, используется для выбора активов из всего множества, далее уже с помощью модели Г. Марковица формируется оптимальный портфель. Модель CAPM связывает такие составляющие как будущая доходность ценной бумаги и риск этой бумаги. Рассмотрим модель CAPM (ее так же называют модель Шарпа) более подробно.

{module 297} Формула Шарпа связи будущей доходности ценной бумаги и риска Где:R- ожидаемая норма доходности;R_f — безрисковая ставка доходности, как правило, ставка по государственным облигациям;R_d— доходность рынка;β- коэффициент бета, который является мерой рыночного риска (недиверсифицируемого риска) и отражает чувствительность доходности ценной бумаги к изменениям доходности рынка в целом.И так, ожидаемая норма доходности — эта та доходность ценной бумаги, на которую рассчитывает инвестор. Другими словами- эта прибыль этой ценной бумаги.Безрисковая ставка доходности — эта доходность, полученная по безрисковым ценным бумагам. Как правило, берут ставку по государственным облигациям. Что бы посмотреть ставки по государственным облигациям можно зайти на сайт центрального банка РФ. http://cbr.ru/hd_base/OpenMarket.asp . В России, на данный момент, она составляет 5.04%.Под доходностью рынка понимают доходность индекса данного рынка, в нашем случае индекс РТС (RTSI). Для Американских акций берут индекс S&P500. Бета — коэффициент показывающий рискованность ценной бумаги.Пример применения модели оценки капитальных активовИ так, попытаемся рассчитать будущую доходность акции Газпрома GAZP. Возьмем котировка по месяцам этой акции и индекса РТС (RTSI) или ММВБ (MICEX) за период с 27 августа 2009 года по 27 августа 2010 года (котировки можно экспортировать в Excel с сайта finam.ru).

Далее рассчитаем дневные доходности по акции Газпрома и индексу ММВБ. =(A3-A2)/A2 =(B3-B2)/B2В итоге получится следующая таблица.

Для того что бы рассчитать коэффициент бета необходимо рассчитать коэффициент линейной регрессии между доходностями акции Газпрома и доходностью индекса ММВБ. Можно пойти двумя путями.Расчет беты через формулу В ячейке F2 введем следующую формулу:=ИНДЕКС(ЛИНЕЙН(C3:C13;D3:D13);1)Коэффициент бета будет равен 1,043.

Расчет беты через надстройку «Анализ данных«Для расчета коэффициента беты через «Анализ данных» необходимо установить надстройку Excel «Анализ Данных». В ней выбрать раздел «Регрессия» и установить входные интервалы, которые соответствую доходностям акции Газпрома и индекса ММВБ. В новом рабочем листе появится отчет.

Отчет по регрессии выглядит следующим образом. В ячейке В18 находится расчет коэффициента линейной регрессии, как раз необходимый коэффициент бета. Коэффициент бета равен 0,67. Так же в отчете есть показатель R- квадрат (коэффициент детерминированности), значение которого равно 0,63. Он показывает силу зависимости меду независимыми переменными (зависимость между доходностью акции и индексом). Показатель Множественный R —является коэффициентом корреляции. Как видим коэффициент корреляции составляет 0,79, что говорит о сильной связи между доходностью индекса и доходностью акции Газпрома.

Осталось рассчитать месячную доходность рынка, доходность индекса ММВБ, которая рассчитывается как среднеарифметическая доходность индекса. Доходность индекса ММВБ составляет в среднем за месяц −0,81%, а среднемесячная доходность акции Газпрома 1,21%.

{module 297}

Мы рассчитали все необходимые параметры модели CAPM. Теперь рассчитаем справедливую норму доходности акции Газпрома на следующий месяц. R_f=5.04%, β=0.67, R_d=-0.81%. R_GAZP=5,04%+0,67*(-0,81%-5,04%)=1,12%Норма доходности акции Газпрома равняется 1,12% на следующий месяц. Можно сказать, что это прогнозная цена будущей доходности в следующем отчетном периоде (у нас месяц). Модель оценки капитальных активов (CAPM) мощный инструмент оценки акций и ценных бумаг, позволит составить прибыльный инвестиционный портфель.

Источник

Построение модели CAPM в Excel для российского фондового рынка

{module 297}

Источник