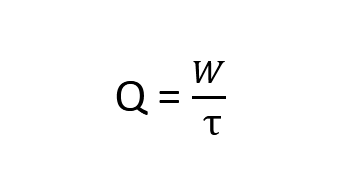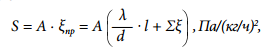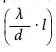Расчет гидравлического сопротивления трубопровода в excel - Word и Excel

Гидравлический расчет трубопроводов

Опубликовано 08 Апр 2014
Рубрика: Теплотехника | 66 комментариев

Системы отопления зданий, теплотрассы, водопроводы, системы водоотведения, гидравлические схемы станков, машин – все это примеры систем, состоящих из трубопроводов. Гидравлический расчет трубопроводов — особенно сложных, разветвленных…

… — является очень непростой и громоздкой задачей. Сегодня в век компьютеров решать ее стало существенно легче при использовании специального программного обеспечения. Но хорошие специальные программы дорого стоят и есть они, как правило, только у специалистов-гидравликов.

В этой статье мы рассмотрим гидравлический расчет трубопроводов на примере расчета в Excel горизонтального участка трубопровода постоянного диаметра по двум методикам и сравним полученные результаты. Для «неспециалистов» применение представленной ниже программы позволит решить несложные «житейские» и производственные задачи. Для специалистов применение этих расчетов возможно в качестве проверочных или для выполнения быстрых простых оценок.

Как правило, гидравлический расчет трубопроводов включает в себя решение двух задач:

1. При проектировочном расчете требуется по известному расходу жидкости найти потери давления на рассматриваемом участке трубопровода. (Потери давления – это разность давлений между точкой входа и точкой выхода.)

2. При проверочном расчете (при аудите действующих систем) требуется по известному перепаду давления (разность показаний манометров на входе в трубопровод и на выходе) рассчитать расход жидкости, проходящей через трубопровод.

Приступаем к решению первой задачи. Решить вторую задачу вы сможете легко сами, используя сервис программы MS Excel «Подбор параметра». О том, как использовать этот сервис, подробно описано во второй половине статьи «Трансцендентные уравнения? «Подбор параметра» в Excel!».

Предложенные далее расчеты в Excel, можно выполнить также в программе OOo Calc из свободно распространяемого пакета Open Office.

Правила цветового форматирования ячеек листа Excel, которые применены в статьях этого блога, детально описаны на странице «О блоге».

Расчет в Excel трубопроводов по формулам теоретической гидравлики.

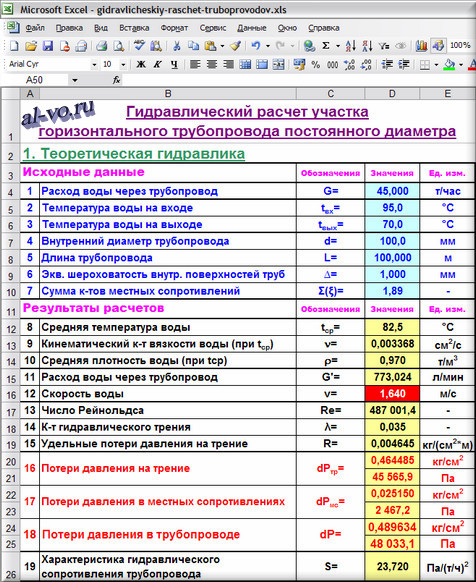
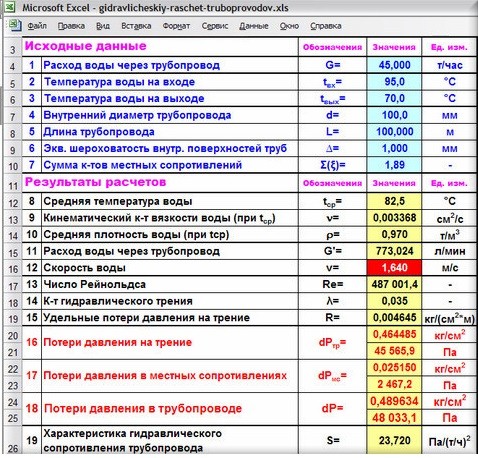
Рассмотрим порядок и формулы расчета в Excel на примере прямого горизонтального трубопровода длиной 100 метров из трубы ø108 мм с толщиной стенки 4 мм.

Исходные данные:

1. Расход воды через трубопровод G в т/час вводим

в ячейку D4: 45,000

2. Температуру воды на входе в расчетный участок трубопровода t_вх в °C заносим

в ячейку D5: 95,0

3. Температуру воды на выходе из расчетного участка трубопровода t_вых в °C записываем

в ячейку D6: 70,0

4. Внутренний диаметр трубопровода d в мм вписываем

в ячейку D7: 100,0

5. Длину трубопровода L в м записываем

в ячейку D8: 100,000

6. Эквивалентную шероховатость внутренних поверхностей труб ∆ в мм вносим

в ячейку D9: 1,000

Выбранное значение эквивалентной шероховатости соответствует стальным старым заржавевшим трубам, находящимся в эксплуатации много лет.

Эквивалентные шероховатости для других типов и состояний труб приведены на листе «Справка» расчетного файла Excel «gidravlicheskiy-raschet-truboprovodov.xls», ссылка на скачивание которого дана в конце статьи.

7. Сумму коэффициентов местных сопротивлений Σ(ξ) вписываем

в ячейку D10: 1,89

Мы рассматриваем пример, в котором местные сопротивления присутствуют в виде стыковых сварных швов (9 труб, 8 стыков).

Для ряда основных типов местных сопротивлений данные и формулы расчета представлены на листах «Расчет коэффициентов» и «Справка» файла Excel «gidravlicheskiy-raschet-truboprovodov.xls».

Результаты расчетов:

8. Среднюю температуру воды t_ср в °C вычисляем

в ячейке D12: =(D5+D6)/2 =82,5

t_ср=(t_вх+t_вых)/2

9. Кинематический коэффициент вязкости воды n в cм²/с при температуре t_ср рассчитываем

в ячейке D13: =0,0178/(1+0,0337*D12+0,000221*D12^2) =0,003368

n=0,0178/(1+0,0337*t_ср+0,000221*t_ср²)

10. Среднюю плотность воды ρ в т/м³ при температуре t_ср вычисляем

в ячейке D14: =(-0,003*D12^2-0,1511*D12+1003,1)/1000 =0,970

ρ=(-0,003*t_ср²-0,1511*t_ср+1003, 1)/1000

11. Расход воды через трубопровод G’ в л/мин пересчитываем

в ячейке D15: =D4/D14/60*1000 =773,024

G’=G*1000/(ρ*60)

Этот параметр пересчитан нами в других единицах измерения для облегчения восприятия величины расхода.

12. Скорость воды в трубопроводе v в м/с вычисляем

в ячейке D16: =4*D4/D14/ПИ()/(D7/1000)^2/3600 =1,640

v=4*G/(ρ*π*(d/1000)²*3600)

К ячейке D16 применено условное форматирование. Если значение скорости не попадает в диапазон 0,25…1,5 м/с, то фон ячейки становится красным, а шрифт белым.

Предельные скорости движения воды приведены на листе «Справка» расчетного файла Excel «gidravlicheskiy-raschet-truboprovodov.xls».

13. Число Рейнольдса Re определяем

в ячейке D17: =D16*D7/D13*10 =487001,4

Re=v*d*10/n

14. Коэффициент гидравлического трения λ рассчитываем

в ячейке D18: =ЕСЛИ(D17<=2320;64/D17;ЕСЛИ(D17<=4000; 0,0000147*D17;0,11* (68/D17+D9/D7)^0,25)) =0,035

λ=64/Re при Re≤2320

λ=0,0000147*Re при 2320≤Re≤4000

λ=0,11*(68/Re+∆/d)^0,25 при Re≥4000

15. Удельные потери давления на трение R в кг/(см²*м) вычисляем

в ячейке D19: =D18*D16^2*D14/2/9,81/D7*100 =0,004645

R=λ*v²*ρ*100/(2*9,81*d)

16. Потери давления на трение dP_тр в кг/см² и Па находим соответственно

в ячейке D20: =D19*D8 =0,464485

dP_тр=R*L

и в ячейке D21: =D20*9,81*10000 =45565,9

dP_тр=dP_тр*9,81*10000

17. Потери давления в местных сопротивлениях dP_мс в кг/см² и Па находим соответственно

в ячейке D22: =D10*D16^2*D14*1000/2/9,81/10000 =0,025150

dP_мс=Σ(ξ)*v²*ρ/(2*9,81*10)

и в ячейке D23: =D22*9,81*10000 =2467,2

dP_тр=dP_мс*9,81*10000

18. Расчетные потери давления в трубопроводе dP в кг/см² и Па находим соответственно

в ячейке D24: =D20+D22 =0,489634

dP=dP_тр+dP_мс

и в ячейке D25: =D24*9,81*10000 =48033,1

dP=dP*9,81*10000

19. Характеристику гидравлического сопротивления трубопровода S в Па/(т/ч)² вычисляем

в ячейке D26: =D25/D4^2 =23,720

S=dP/G²

Гидравлический расчет в Excel трубопровода по формулам теоретической гидравлики выполнен!

Гидравлический расчет трубопроводов в Excel по формулам СНиП 2.04.02-84.

Этот расчет определяет потери на трение в трубопроводах по эмпирическим формулам без учета коэффициентов местных сопротивлений, но с учетом сопротивлений, вносимых стыками.

На длинных трубопроводах, каковыми являются водопроводы и теплотрассы, влияние местных сопротивлений мало по сравнению с шероховатостью стенок труб и перепадами высот, и часто коэффициентами местных сопротивлений можно пренебречь при оценочных расчетах.

Исходные данные:

Этот расчет использует ранее введенные в предыдущем расчете значения внутреннего диаметра трубопровода d и длины трубопровода L, а также рассчитанное значение скорости движения воды v.

1. Выбираем из выпадающего списка, расположенного над ячейками A30…E30 вид трубы:

Неновые стальные и неновые чугунные без внутр. защитного покр. или с битумным защитным покр., v > 1,2м/c

Результаты расчетов:

По выбранному виду трубы Excel автоматически извлекает из таблицы базы данных значения эмпирических коэффициентов. Таблица базы данных, взятая из СНиП 2.04.02–84, расположена на этом же рабочем листе «РАСЧЕТ».

2. Коэффициент m извлекается

в ячейку D32: =ИНДЕКС(H31:H42;H29) =0,300

3. Коэффициент A₀ извлекается

в ячейку D33: =ИНДЕКС(I31:I42;I29) =1,000

4. Коэффициент 1000A₁ извлекается

в ячейку D34: =ИНДЕКС(J31:J42;J29) =21,000

5. Коэффициент 1000A₁/(2g) извлекается

в ячейку D35: =ИНДЕКС(K31:K42;K29) =1,070

6. Коэффициент С извлекается

в ячейку D36: =ИНДЕКС(L31:L42;L29) =0,000

7. Коэффициент гидравлического сопротивления i в м.вод.ст./м рассчитываем

в ячейке D37: =D35/1000*((D33+D36/D16)^D32)/((D7/1000)^(D32+1))*D16^2 =0,057

i=((1000A1/(2g))/1000)*(((A0+C/v)^m)/((d/1000)^(m+1)))*v²

8. Расчетные потери давления в трубопроводе dP в кг/см² и Па находим соответственно

в ячейке D38: =D39/9,81/10000 =0,574497

dP=dP/9,81/10000

и в ячейке D39: =D37*9,81*1000*D8 =56358,1

dP=i*9,81*1000*L

Гидравлический расчет трубопровода по формулам Приложения 10 СНиП 2.04.02–84 в Excel завершен!

Итоги.

Полученные значения потерь давления в трубопроводе, рассчитанные по двум методикам отличаются в нашем примере на 15…17%! Рассмотрев другие примеры, вы можете увидеть, что отличие иногда достигает и 50%! При этом значения, полученные по формулам теоретической гидравлики всегда меньше, чем результаты по СНиП 2.04.02–84. Я склонен считать, что точнее первый расчет, а СНиП 2.04.02–84 «подстраховывается». Возможно, я ошибаюсь в выводах. Следует отметить, что гидравлические расчеты трубопроводов тяжело поддаются точному математическому моделированию и базируются в основном на зависимостях, полученных из опытов.

В любом случае, имея два результата, легче принять нужное правильное решение.

При гидравлическом расчете трубопроводов с перепадом высот входа и выхода не забывайте добавлять (или отнимать) к результатам статическое давление. Для воды – перепад высот в 10 метров ≈ 1 кг/см².

Уважаемые читатели, Ваши мысли, замечания и предложения всегда интересны коллегам и автору. Пишите их внизу, в комментариях к статье!

Ссылка на скачивание файла: gidravlicheskiy-raschet-truboprovodov (xls 57,5KB).

Важное и, думаю, интересное продолжение темы читайте здесь.

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Источник

Опубликовано 24 Июн 2022 Рубрика: Теплотехника | 32 комментария

Выполнение расчета гидравлического сопротивления отдельного трубопровода и всей системы в комплексе является ключевой задачей в гидравлике, решение которой позволяет подобрать сечения труб и насос с необходимыми значениями давления и расхода в рабочем режиме.

В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно. В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати. Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.

Постановка задачи

Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

Многолетний практический опыт эксплуатации систем трубопроводов показал, что трубы, имеющие круглое сечение, обладают определенными преимуществами перед трубопроводами, имеющими поперечное сечение любой другой геометрической формы:

минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
процесс изготовления труб круглой формы относительно простой и доступный.

Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.

Основными параметрами, характеризующими трубопровод являются:

условный (номинальный) диаметр – DN;
давление номинальное – PN;
рабочее допустимое (избыточное) давление;
материал трубопровода, линейное расширение, тепловое линейное расширение;
физико-химические свойства рабочей среды;
комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
изоляционные материалы трубопровода.

Условный диаметр (проход) трубопровода (DN) – это условная безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.

Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.

Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.

Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.

Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.

Как работать в EXCEL

Использование таблиц Excel очень удобно, поскольку результаты гидравлического расчёта всегда сводятся к табличной форме. Достаточно определить последовательность действий и подготовить точные формулы.

Ввод исходных данных

Выбирается ячейка и вводится величина. Вся остальная информация просто принимается к сведению.

Ячейка	Величина	Значение, обозначение, единица выражения
D4	45,000	Расход воды G в т/час
D5	95,0	Температура на входе tвх в °C
D6	70,0	Температура на выходе tвых в °C
D7	100,0	Внутренний диаметр d, мм
D8	100,000	Длина, L в м
D9	1,000	Эквивалентная шероховатость труб ∆ в мм
D10	1,89	Сумма коэф. местных сопротивлений — Σ(ξ)

Пояснения:

значение в D9 берётся из справочника;
значение в D10 характеризует сопротивления в местах сварных швов.

Формулы и алгоритмы

Выбираем ячейки и вводим алгоритм, а также формулы теоретической гидравлики.

Ячейка	Алгоритм	Формула	Результат	Значение результата
D12	!ERROR! D5 does not contain a number or expression	tср=(tвх+tвых)/2	82,5	Средняя температура воды tср в °C
D13	!ERROR! D12 does not contain a number or expression	n=0,0178/(1+0,0337tср+0,000221tср2)	0,003368	Кинематический коэф. вязкости воды — n, cм2/с при tср
D14	!ERROR! D12 does not contain a number or expression	ρ=(-0,003tср2-0,1511tср+1003, 1)/1000	0,970	Средняя плотность воды ρ,т/м3 при tср
D15	!ERROR! D4 does not contain a number or expression	G’=G1000/(ρ60)	773,024	Расход воды G’, л/мин
D16	!ERROR! D4 does not contain a number or expression	v=4G:(ρπ(d:1000)23600)	1,640	Скорость воды v, м/с
D17	!ERROR! D16 does not contain a number or expression	Re=vd10/n	487001,4	Число Рейнольдса Re
D18	!ERROR! Cell D17 does not exist	λ=64/Re при Re≤2320 λ=0,0000147Re при 2320≤Re≤4000 λ=0,11(68/Re+∆/d)0,25 при Re≥4000	0,035	Коэффициент гидравлического трения λ
D19	!ERROR! Cell D18 does not exist	R=λv2ρ100/(29,81*d)	0,004645	Удельные потери давления на трение R, кг/(см2*м)
D20	!ERROR! Cell D19 does not exist	dPтр=R*L	0,464485	Потери давления на трение dPтр, кг/см2
D21	!ERROR! Cell D20 does not exist	dPтр=dPтр9,8110000	45565,9	и Па соответственно D20
D22	!ERROR! D10 does not contain a number or expression	dPмс=Σ(ξ)v2ρ/(29,8110)	0,025150	Потери давления в местных сопротивлениях dPмс в кг/см2
D23	!ERROR! Cell D22 does not exist	dPтр=dPмс9,8110000	2467,2	и Па соответственно D22
D24	!ERROR! Cell D20 does not exist	dP=dPтр+dPмс	0,489634	Расчетные потери давления dP, кг/см2
D25	!ERROR! Cell D24 does not exist	dP=dP9,8110000	48033,1	и Па соответственно D24
D26	!ERROR! Cell D25 does not exist	S=dP/G2	23,720	Характеристика сопротивления S, Па/(т/ч)2

Пояснения:

значение D15 пересчитывается в литрах, так легче воспринимать величину расхода;
ячейка D16 — добавляем форматирование по условию: «Если v не попадает в диапазон 0,25…1,5 м/с, то фон ячейки красный/шрифт белый».

Для трубопроводов с перепадом высот входа и выхода к результатам добавляется статическое давление: 1 кг/см2 на 10 м.

Оформление результатов

Авторское цветовое решение несёт функциональную нагрузку:

Светло-бирюзовые ячейки содержат исходные данные – их можно менять.
Бледно-зелёные ячейка — вводимые константы или данные, мало подверженные изменениям.
Жёлтые ячейки — вспомогательные предварительные расчёты.
Светло-жёлтые ячейки — результаты расчётов.
Шрифты: синий — исходные данные;
чёрный — промежуточные/неглавные результаты;
красный — главные и окончательные результаты гидравлического расчёта.

Пример от Александра Воробьёва

Пример несложного гидравлического расчёта в программе Excel для горизонтального участка трубопровода.

Исходные данные:

длина трубы100 метров;
ø108 мм;
толщина стенки 4 мм.

Основные положения гидравлического расчета

Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.

Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:

ламинарный поток (Re<2300), при котором носитель-жидкость движется тонкими слоями, практически не смешивающимися друг с другом;
переходный режим (2300
турбулентный поток (Re>4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.

Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.

Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.

Начальные условия примера

Для более конкретного пояснения всех деталей гидравлического просчёта возьмем конкретный пример обычного жилищного помещения. В наличии имеем классическую 2-комнатную квартиру панельного дома, общей площадью 65,54 м2, которая включает две комнаты, кухню, раздельные туалет и ванная, двойной коридор, спаренный балкон.

После сдачи в эксплуатацию получили следующую информацию относительно готовности квартиры. Описываемая квартира включает обработанные шпаклевкой и грунтом стены из монолитных железо-бетонных конструкций, окна из профиля с двух камерными стеклами, тырсо-прессованные межкомнатные двери, керамическая плитка на полу санузла.

Кроме того, представленное жильё уже оснащено медной проводкой, распределителями и отдельным щитком, газовой плитой, ванной, умывальником, унитазом, полотенцесушителем, мойкой.

И самое главное в жилых комнатах, ванной и кухне уже имеются алюминиевые отопительные радиаторы. Вопрос относительно труб и котла остаётся открытым.

Подбор оптимального диаметра трубопровода

Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.

Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:

При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).

Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:

Задвижка

При расчете трубопроводных систем коэффициент сопротивления открытой задвижки принимается ζзадв = 0,1 — 0,2. Если задвижка прикрыта на определенную величину, то коэффициент сопротивления напрямую зависит от степени закрытия. Ниже представлена таблица зависимости коэффициента сопротивления задвижки от степени закрытия. Чем больше степень закрытия — тем больше коэффициент сопротивления.

Степень закрытия (d-h)/d	1/8	2/8	3/8	1/2	5/8	3/4	7/8
ζзадв	0,07	0,26	0,81	2,06	5,52	17,0	97,8

Расчет падения напора и гидравлического сопротивления

Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.

Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.

Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.

Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.

Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:

В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы:

Обзор программ

Для удобства расчётов применяются любительские и профессиональные программы вычисления гидравлики.

Самой популярной является Excel.

Можно воспользоваться онлайн-расчётом в Excel Online, CombiMix 1.0, или онлайн-калькулятором гидравлического расчёта. Стационарную программу подбирают с учётом требований проекта.

Главная трудность в работе с такими программами — незнание основ гидравлики. В некоторых из них отсутствуют расшифровки формул, не рассматриваются особенности разветвления трубопроводов и вычисления сопротивлений в сложных цепях.

Особенности программ:

HERZ C.O. 3.5 – производит расчёт по методу удельных линейных потерь давления.
DanfossCO и OvertopCO – умеют считать системы с естественной циркуляцией.
«Поток» (Potok) — позволяет применять метод расчёта с переменным (скользящим) перепадом температур по стоякам.

Следует уточнять параметры ввода данных по температуре — по Кельвину/по Цельсию.

Расчет потерь давления

Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.

Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:

Выводы и полезное видео по теме

Особенности, преимущества и недостатки естественной и принудительной систем циркуляции теплоносителя для систем отопления:

Подводя итого вычислений гидравлического расчёта, в результате получили конкретные физические характеристики будущей системы отопления.

Естественно, что это упрощенная схема расчёта, которая даёт приблизительные данные относительно гидравлического расчёта для системы отопления типичной двухкомнатной квартиры.

Пытаетесь самостоятельно провести гидравлический расчет отопительной системы? А может, не согласны с изложенным материалом? Ждем ваших комментариев и вопросов — блок для обратной связи расположен ниже.

Источник

Библиографическое описание:

Кислякова, Е. В. Алгоритм расчета короткого напорного трубовода средствами MS Excel / Е. В. Кислякова. — Текст : непосредственный // Молодой ученый. — 2016. — № 21 (125). — С. 149-153. — URL: https://moluch.ru/archive/125/34527/ (дата обращения: 17.04.2023).

В статье приводится алгоритм расчета короткого напорного трубопровода и его реализация в MSExcel. Задача нахождения диаметра трубопровода, обеспечивающего требуемый расход, решается методом подбора.

Ключевые слова: короткий трубопровод, гидравлические сопротивления, число Рейнольдса, режим движения жидкости

Введение. Одной из основных задач курса гидравлики является расчет короткого напорного трубопровода. Важность задачи обусловлена широким применением коротких трубопроводов, к которым можно отнести сифонные трубопроводы, всасывающие трубы насосов, дюкеры, части трубопроводов внутри зданий и сооружений и пр.

Короткий трубопровод — трубопровод достаточной малой длины, в котором потери напора в местных сопротивлениях составляют более 10 % от потерь напора по длине [1, с. 215]. В связи с этим при расчете короткого трубопровода необходимо учитывать как потери напора по длине, так и местные потери напора.

Расчет короткого трубопровода сводится к решению одной из трех задач (рис. 1).

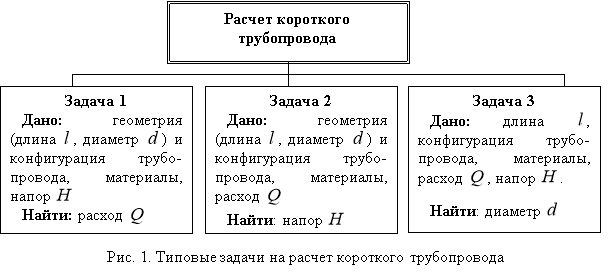
Наибольшие сложности вызывает решение третьей задачи, так как в большинстве случаев определить диаметр короткого трубопровода можно только методом подбора.

Алгоритм расчета диаметра короткого напорного трубопровода методом подбора. Рассмотрим общий алгоритм решения поставленной задачи. Вычисления в соответствии с представленным алгоритмом в ручном режиме являются достаточно затратными по времени. Существенно упростить работу по расчету диаметра трубопровода методом подбора позволяет реализация алгоритма в какой-либо программной среде. При этом самым простым вариантом, не требующим специальных навыков в области программирования, является MSExcel.

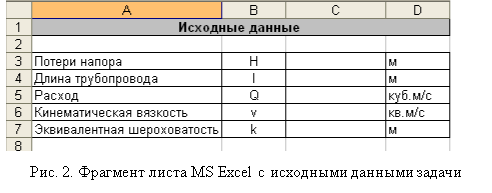
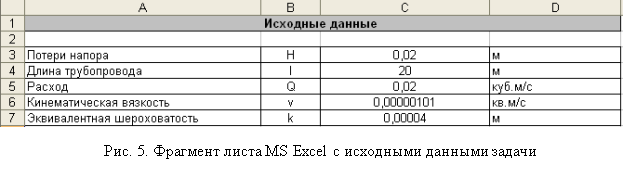
Этап 1. Зададим исходные данные, известные по условию задачи. К исходным данным следует отнести (рис. 2): потери напора (перепад уровней жидкости) (, м); длину трубопровода (, м); пропускную способность трубопровода (расход) (, м); кинематическую вязкость жидкости (, м2/с); эквивалентную шероховатость стенок трубопровода (, м).

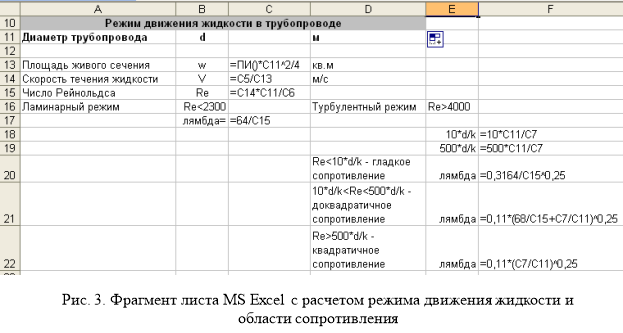
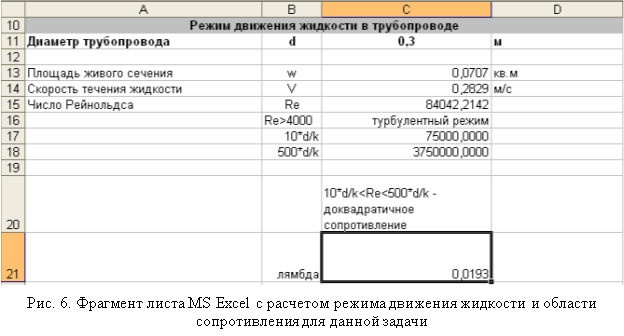
Этап 2. Зададим произвольным образом диаметр трубопровода и определим режим движения жидкости.

Вычислим площадь живого сечения трубопровода. Для упрощения рассуждений будем считать, что диаметр трубопровода по его длине не меняется, трубопровод имеет круглое сечение, полностью заполненное жидкостью:

(1)

Рассчитаем скорость течения жидкости в трубопроводе:

(2)

Определим режим движения жидкости в трубопроводе, для чего вычислим число Рейнольдса:

(3)

При режим движения жидкости ламинарный, при – турбулентный.

Рассчитаем коэффициент гидравлического трения . Если режим движения ламинарный, то коэффициент определяют по формуле:

(4)

Если режим движения турбулентный, то дополнительно нужно определить область сопротивления. Для этого по материалу, из которого изготовлен трубопровод, и сроку его службы нужно найти эквивалентную шероховатость стенок трубопровода [2, с. 72].

Если , то трубопровод следует отнести к области гладкого сопротивления. В этом случае коэффициент может быть рассчитан по формуле Блазиуса:

(5)

Если , то область сопротивления является доквадратичной и для расчета коэффициента используется формула Альтшуля:

(6)

Если , то область сопротивления квадратичная и для нахождения коэффициента можно применить формулу Шифринсона:

(7)

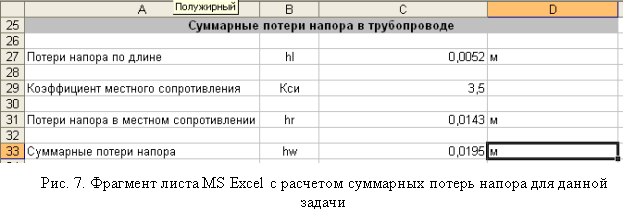
Этап 3. Рассчитаем потери напора в трубопроводе при заданном диаметре. Полные потери напора в трубопроводе состоят из потерь напора по длине и потерь напора в местных сопротивлениях:

(8)

Потери напора по длине определим по формуле Вейсбаха-Дарси:

(9)

Потери напора в местных сопротивлениях вычислим по формуле Вейсбаха:

(10)

где — коэффициент местного сопротивления, который зависит от вида местного сопротивления и его геометрии.

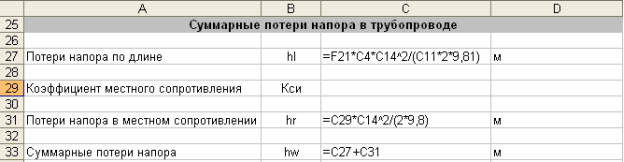
Рис. 4. Фрагмент листа MS Excel с расчетом суммарных потерь напора

Этап 4. Сравним рассчитанные суммарные потери напора в трубопроводе с потерями напора , заданными по условию задачи. Если , то значение диаметра выбрано верно. Если же , то значение диаметра нужно изменить и повторить все вычисления.

Пример решения задачи на расчет короткого напорного трубопровода.

Задача. Трубопровод из стальных новых труб длиной 20 м присоединен к напорному баку, заполненному водой при температуре 20ºС. После полного открытия вентиля расход воды в трубопроводе оказался равным 20 л/с, а разность уровней воды в напорном резервуаре и пьезометре составила 2 см. Определите диаметр трубопровода.

Для решения задачи воспользуемся приведенным выше алгоритмом.

Зададим исходные данные. Коэффициент кинематической вязкости воды при приведен по справочнику [2, с. 16], коэффициент эквивалентной шероховатости стальных новых труб — по справочнику [2, с. 72].

Зададим произвольным образом диаметр трубопровода и определим для указанного диаметра режим движения жидкости.

Так как число Рейнольдса , то режим движения турбулентный. Далее, используя значение эквивалентной шероховатости, определим область сопротивлений. Так как , то область сопротивления доквадратичная и для расчета коэффициента гидравлического трения следует использовать формулу Альтшуля (6). В итоге расчетов получаем .

По формулам (8), (9), (10) рассчитаем потери напора в трубопроводе. В рассматриваемой задаче имеются два местных сопротивления: внезапное сужение потока при переходе из напорного резервуара в трубопровод () и вентиль, который полностью открыт ().

Из проведенного расчета видно, что суммарные потери напора по длине трубопровода примерно совпадают с потерями напора (разностью уровней воды в резервуаре и пьезометре), заданными по условию задачи . Следовательно, диаметр трубопровода выбран верно.

Однако найденное значение диаметра можно уточнить. Если задать значение диаметра , то расчетные суммарные потери напора в трубопроводе составят .

Выводы. Представленный в статье алгоритм определения диаметра короткого напорного трубопровода и его реализация в MSExcel предназначены в первую очередь для студентов строительных направлений подготовки, изучающих гидравлику. Реализация алгоритма средствами MSExcel достаточно проста и позволяет наглядно проследить основные этапы расчета трубопровода. Вместе с тем, применение табличного редактора существенно экономит время проведения типовых расчетов.

Литература:

Чугаев Р. Р. Гидравлика: учебник для вузов. — Л.: Энергоиздат, 1982.
Вильнер Я. М. Справочное пособие по гидравлике, гидромашинам и гидроприводам / Я. М. Вильнер, Я. Т. Ковалев, Б. Б. Некрасов, под ред. Б. Б. Некрасова. — Минск, 1976.

Основные термины (генерируются автоматически): потеря напора, диаметр трубопровода, короткий напорный трубопровод, короткий трубопровод, режим движения жидкости, трубопровод, метод подбора, область сопротивления, суммарная потеря напора, значение диаметра.

Источник

Экономичность теплового комфорта в доме обеспечивают расчет гидравлики, её качественный монтаж и правильная эксплуатация. Главные компоненты отопительной системы — источник тепла (котёл), тепловая магистраль (трубы) и приборы теплоотдачи (радиаторы). Для эффективного теплоснабжения необходимо сохранить первоначальные параметры системы при любых нагрузках независимо от времени года.

Перед началом гидравлических расчётов выполняют:

Сбор и обработку информации по объекту с целью:
- определения количества требуемого тепла;
- выбора схемы отопления.
Тепловой расчёт системы отопления с обоснованием:
- объёмов тепловой энергии;
- нагрузок;
- теплопотерь.

Если водяное отопление признаётся оптимальным вариантом, выполняется гидравлический расчёт.

Для расчёта гидравлики с помощью программ требуется знакомство с теорией и законами сопротивления. Если приведенные ниже формулы покажутся вам сложными для понимания, можно выбрать параметры, которые мы предлагаем в каждой из программ.

Расчёты проводились в программе Excel. Готовый результат можно посмотреть в конце инструкции.

Что такое гидравлический расчёт

Это третий этап в процессе создания тепловой сети. Он представляет собой систему вычислений, позволяющих определить:

диаметр и пропускную способность труб;
местные потери давления на участках;
требования гидравлической увязки;
общесистемные потери давления;
оптимальный расход воды.

Согласно полученным данным осуществляют подбор насосов.

Для сезонного жилья, при отсутствии в нём электричества, подойдёт система отопления с естественной циркуляцией теплоносителя (ссылка на обзор).

Основная цель гидравлического расчёта — обеспечить совпадение расчётных расходов по элементам цепи с фактическими (эксплуатационными) расходами. Количество теплоносителя, поступающего в радиаторы, должно создать тепловой баланс внутри дома с учётом наружных температур и тех, что заданы пользователем для каждого помещения согласно его функциональному назначению (подвал +5, спальня +18 и т.д.).

Комплексные задачи — минимизация расходов:

капитальных – монтаж труб оптимального диаметра и качества;
эксплуатационных:
- зависимость энергозатрат от гидравлического сопротивления системы;
- стабильность и надёжность;
- бесшумность.

Замена централизованного режима теплоснабжения индивидуальным упрощает методику вычислений

Для автономного режима применимы 4 метода гидравлического расчёта системы отопления:

по удельным потерям (стандартный расчёт диаметра труб);
по длинам, приведённым к одному эквиваленту;
по характеристикам проводимости и сопротивления;
сопоставление динамических давлений.

Два первых метода используются при неизменном перепаде температуры в сети.

Два последних помогут распределить горячую воду по кольцам системы, если перепад температуры в сети перестанет соответствовать перепаду в стояках/ответвлениях.

Расчет гидравлики системы отопления

Нам потребуются данные теплового расчёта помещений и аксонометрической схемы.

Аксонометрическая схема

Вынесите данные в эту таблицу:

№ расчётного участка	Тепловая нагрузка	Длина
записать	записать	записать

Шаг 1: считаем диаметр труб

В качестве исходных данных используются экономически обоснованные результаты теплового расчёта:

1а. Оптимальная разница между горячим (tг) и охлаждённым( tо) теплоносителем для двухтрубной системы – 20º

Δtco=tг- tо=90º-70º=20ºС

1б. Расход теплоносителя G, кг/час — для однотрубной системы.

2. Оптимальная скорость движения теплоносителя – ν 0,3-0,7 м/с.

Чем меньше внутренний диаметр труб — тем выше скорость. Достигая отметки 0,6 м/с, движение воды начинает сопровождаться шумом в системе.

3. Расчётная скорость теплопотока – Q, Вт.

Выражает количество тепла (W, Дж), переданного в секунду (единицу времени τ):

Формула для расчёта скорости теплопотока

4. Расчетная плотность воды: ρ = 971,8 кг/м3 при tср = 80 °С

5. Параметры участков:

Участок	Длина участка, м	Число приборов N, шт
1 — 2	1.78	1
2 — 3	2.60	1
3 — 4	2.80	2
4 — 5	2.80	2
5 — 6	2.80	4
6 — 7	2.80
7 — 8	2.20
8 — 9	6.10	1
9 — 10	0.5	1
10 — 11	0.5	1
11 — 12	0.2	1
12 — 13	0.1	1
13 — 14	0.3	1
14 — 15	1.00	1

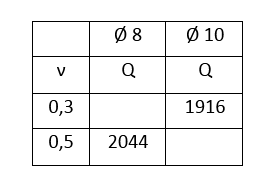
Для определения внутреннего диаметра по каждому участку удобно пользоваться таблицей.

Расшифровка сокращений:

зависимость скорости движения воды — ν, с

теплового потока — Q, Вт

расхода воды G, кг/час от внутреннего диаметра труб

Ø 8	Ø 10	Ø 12	Ø 15	Ø 20	Ø 25	Ø 50
ν	Q	G	v	Q	G	v	Q	G	v	Q	G	v	Q	G	v	Q	G	v	Q	G
0.3	1226	53	0.3	1916	82	0.3	2759	119	0.3	4311	185	0.3	7664	330	0.3	11975	515	0.3	47901	2060
0.4	1635	70	0.4	2555	110	0.4	3679	158	0.4	5748	247	0.4	10219	439	0.4	15967	687	0.4	63968	2746
0.5	2044	88	0.5	3193	137	0.5	4598	198	0.5	7185	309	0.5	12774	549	0.5	19959	858	0.5	79835	3433
0.6	2453	105	0.6	3832	165	0.6	5518	237	0.6	8622	371	0.6	15328	659	0.6	23950	1030	0.6	95802	4120
0.7	2861	123	0.7	4471	192	0.7	6438	277	0.7	10059	433	0.7	17883	769	0.7	27942	1207	0.7	111768	4806

Пример

Задача: подобрать диаметр трубы для отопления гостиной площадью 18 м², высота потолка 2,7 м.

Данные проекта:

двухтрубная схема разводки;
циркуляция — принудительная (насос).

Среднестатистические данные:

расход мощности – 1 кВт на 30 м³
запас тепловой мощности – 20%

Расчёт:

объём помещения: 18 * 2,7 = 48,6 м³
расход мощности: 48,6 / 30 = 1,62 кВт
запас на случай морозов: 1,62 * 20% = 0,324 кВт
итоговая мощность: 1,62 + 0,324 = 1,944 кВт

Находим в таблице наиболее близкое значения Q:

Получаем интервал внутреннего диаметра: 8-10 мм.
Участок: 3-4.
Длина участка: 2.8 метров.

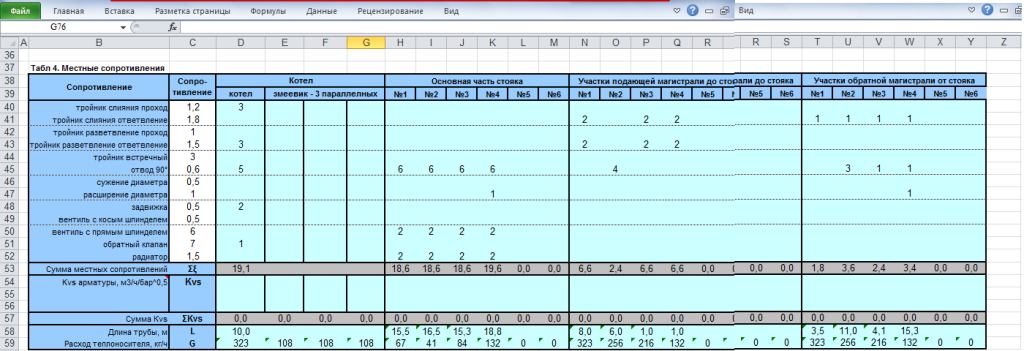
Шаг 2: вычисление местных сопротивлений

Чтобы определиться с материалом труб, необходимо сравнить показатели их гидравлического сопротивления на всех участках отопительной системы.

Факторы возникновения сопротивления:

Трубы для отопления

в самой трубе:
- шероховатость;
- место сужения/расширения диаметра;
- поворот;
- протяжённость.
в соединениях:
- тройник;
- шаровой кран;
- приборы балансировки.

Расчетным участком является труба постоянного диаметра с неизменным расходом воды, соответствующим проектному тепловому балансу помещения.

Для определения потерь берутся данные с учётом сопротивления в регулирующей арматуре:

длина трубы на расчётном участке/l,м;
диаметр трубы расчётного участка/d,мм;
принятая скорость теплоносителя/u, м/с;
данные регулирующей арматуры от производителя;
справочные данные:
- коэффициент трения/λ;
- потери на трение/∆Рl, Па;
- расчетная плотность жидкости/ρ = 971,8 кг/м3;
технические характеристики изделия:
- эквивалентная шероховатость трубы/kэ мм;
- толщина стенки трубы/dн×δ, мм.

Для материалов со сходными значениями kэ производители предоставляют значение удельных потерь давления R, Па/м по всему сортаменту труб.

Чтобы самостоятельно определить удельные потери на трение/R, Па/м, достаточно знать наружный d трубы, толщину стенки/dн×δ, мм и скорость подачи воды/W, м/с (или расход воды/G, кг/ч).

Для поиска гидросопротивления/ΔP в одном участке сети подставляем данные в формулу Дарси-Вейсбаха:

Для стальных и полимерных труб (из полипропилена, полиэтилена, стекловолокна и т.д.) коэффициент трения/ λ наиболее точно вычисляется по формуле Альтшуля:

Re — число Рейнольдса, находится по упрощённой формуле (Re=v*d/ν) или с помощью онлайн-калькулятора:

Шаг 3: гидравлическая увязка

Для балансировки перепадов давления понадобится запорная и регулирующая арматура.

Исходные данные:

проектная нагрузка (массовый расход теплоносителя — воды или низкозамерзающей жидкости для систем отопления);
данные производителей труб по удельному динамическому сопротивлению/А, Па/(кг/ч)²;
технические характеристики арматуры.
количество местных сопротивлений на участке.

Задача: выровнять гидравлические потери в сети.

В гидравлическом расчёте для каждого клапана задаются установочные характеристики (крепление, перепад давления, пропускная способность). По характеристикам сопротивления определяют коэффициенты затекания в каждый стояк и далее — в каждый прибор.

Фрагмент заводских характеристик поворотного затвора

Выберем для вычислений метод характеристик сопротивления S,Па/(кг/ч)².

Потери давления/∆P, Па прямо пропорциональны квадрату расхода воды по участку/G, кг/ч:

В физическом смысле S — это потери давления на 1 кг/ч теплоносителя:

где:

ξпр — приведенный коэффициент для местных сопротивлений участка;
А — динамическое удельное давление, Па/(кг/ч)².

Удельным считается динамическое давление, возникающее при массовом расходе 1 кг/ч теплоносителя в трубе заданного диаметра (информация предоставляется производителем).

Σξ — слагаемое коэффициентов по местным сопротивлениям в участке.

Приведенный коэффициент:

Он суммирует все местные сопротивления:

С величиной:

которая соответствует коэффициенту местного сопротивления с учётом потерь от гидравлического трения.

Шаг 4: определение потерь

Гидравлическое сопротивление в главном циркуляционном кольце представлено суммой потерь его элементов:

первичного контура/ΔPIк ;
местных систем/ΔPм;
теплогенератора/ΔPтг;
теплообменника/ΔPто.

Сумма величин даёт нам гидравлическое сопротивление системы/ΔPсо:

Обзор программ

Для удобства расчётов применяются любительские и профессиональные программы вычисления гидравлики.

Самой популярной является Excel.

Особенности программ:

HERZ C.O. 3.5 – производит расчёт по методу удельных линейных потерь давления.
DanfossCO и OvertopCO – умеют считать системы с естественной циркуляцией.
«Поток» (Potok) — позволяет применять метод расчёта с переменным (скользящим) перепадом температур по стоякам.

Следует уточнять параметры ввода данных по температуре — по Кельвину/по Цельсию.

Как работать в EXCEL

Ввод исходных данных

Выбирается ячейка и вводится величина. Вся остальная информация просто принимается к сведению.

Ячейка	Величина	Значение, обозначение, единица выражения
D4	45,000	Расход воды G в т/час
D5	95,0	Температура на входе tвх в °C
D6	70,0	Температура на выходе tвых в °C
D7	100,0	Внутренний диаметр d, мм
D8	100,000	Длина, L в м
D9	1,000	Эквивалентная шероховатость труб ∆ в мм
D10	1,89	Сумма коэф. местных сопротивлений — Σ(ξ)

Пояснения:

значение в D9 берётся из справочника;
значение в D10 характеризует сопротивления в местах сварных швов.

Формулы и алгоритмы

Выбираем ячейки и вводим алгоритм, а также формулы теоретической гидравлики.

Ячейка	Алгоритм	Формула	Результат	Значение результата
D12	387332	tср=(tвх+tвых)/2	82,5	Средняя температура воды tср в °C
D13	!ERROR! B3 -> Formula Error: Unexpected ,	n=0,0178/(1+0,0337tср+0,000221tср2)	0,003368	Кинематический коэф. вязкости воды — n, cм2/с при tср
D14	!ERROR! B4 -> Formula Error: Unexpected ,	ρ=(-0,003tср2-0,1511tср+1003, 1)/1000	0,970	Средняя плотность воды ρ,т/м3 при tср
D15	0.03301785959853	G’=G1000/(ρ60)	773,024	Расход воды G’, л/мин
D16	#NAME?	v=4G:(ρπ(d:1000)23600)	1,640	Скорость воды v, м/с
D17	46820984.143969	Re=vd10/n	487001,4	Число Рейнольдса Re
D18	!ERROR! B8 -> Formula Error: An unexpected error occurred	λ=64/Re при Re≤2320 λ=0,0000147Re при 2320≤Re≤4000 λ=0,11(68/Re+∆/d)0,25 при Re≥4000	0,035	Коэффициент гидравлического трения λ
D19	!ERROR! B9 -> Formula Error: Unexpected ,	R=λv2ρ100/(29,81*d)	0,004645	Удельные потери давления на трение R, кг/(см2*м)
D20	0	dPтр=R*L	0,464485	Потери давления на трение dPтр, кг/см2
D21	!ERROR! B11 -> Formula Error: Unexpected ,	dPтр=dPтр9,8110000	45565,9	и Па соответственно D20
D22	!ERROR! B12 -> Formula Error: Unexpected ,	dPмс=Σ(ξ)v2ρ/(29,8110)	0,025150	Потери давления в местных сопротивлениях dPмс в кг/см2
D23	!ERROR! B13 -> Formula Error: Unexpected ,	dPтр=dPмс9,8110000	2467,2	и Па соответственно D22
D24	0	dP=dPтр+dPмс	0,489634	Расчетные потери давления dP, кг/см2
D25	!ERROR! B15 -> Formula Error: Unexpected ,	dP=dP9,8110000	48033,1	и Па соответственно D24
D26	0	S=dP/G2	23,720	Характеристика сопротивления S, Па/(т/ч)2

Пояснения:

значение D15 пересчитывается в литрах, так легче воспринимать величину расхода;
ячейка D16 — добавляем форматирование по условию: «Если v не попадает в диапазон 0,25…1,5 м/с, то фон ячейки красный/шрифт белый».

Оформление результатов

Авторское цветовое решение несёт функциональную нагрузку:

Светло-бирюзовые ячейки содержат исходные данные – их можно менять.
Бледно-зелёные ячейка — вводимые константы или данные, мало подверженные изменениям.
Жёлтые ячейки — вспомогательные предварительные расчёты.
Светло-жёлтые ячейки — результаты расчётов.
Шрифты:
- синий — исходные данные;
- чёрный — промежуточные/неглавные результаты;
- красный — главные и окончательные результаты гидравлического расчёта.

Результаты в таблице Эксель

Пример от Александра Воробьёва

Пример несложного гидравлического расчёта в программе Excel для горизонтального участка трубопровода.

Исходные данные:

длина трубы100 метров;
ø108 мм;
толщина стенки 4 мм.

Excel

Таблица результатов расчёта местных сопротивлений

Усложняя шаг за шагом расчёты в программе Excel, вы лучше осваиваете теорию и частично экономите на проектных работах. Благодаря грамотному подходу, ваша система отопления станет оптимальной по затратам и теплоотдаче.

Источник

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Трубопровод – это промышленное сооружение, предназначенное для транспортировки жидких, газообразных и твердых веществ, а также их смесей за счет разницы давлений в поперечных сечениях трубы.

При гидравлическом расчете трубопроводы подразделяют на простые и сложные. Простым называют трубопровод, состоящий из одной линии труб с постоянным расходом пути и передающий жидкость из резервуара в атмосферу или в другой резервуар. Сложные трубопроводы состоят из системы (сети) труб, подающей жидкость сразу в несколько точек.

Гидравлический расчет трубопровода позволяет определить его диаметр, пропускную способность или необходимый перепад давления. Такие расчеты трубопроводов проводят на основе уравнения Бернулли, которое имеет вид:

Где: величина, которая зависит от расчетного диаметра трубы и которая определяется по специальным справочным таблицам;

коэффициент местных сопротивлений;

удельное сопротивление;

длины участков трубопроводов;

пьезометрические напоры в начале и конце трубопровода. Они определяются по формуле:

где: геодезическая отметка какой-либо точки трубопровода;

избыточное давление в этой точке;

пьезометрическая высота (свободный напор).

Расчет потерь на трение ведется по формуле:

где  диаметр трубопровода;

 коэффициент трения;

 скоростной напор.

Потери напора в местном сопротивлении рассчитываются следующим образом:

При расчетах гидравлического процесса применяют различные эмпирические зависимости и формулы, полученные экспериментально-опытным путем, позволяющие определить коэффициент гидравлического трения:

для гидравлических гладких труб используют формулу Блазиуса:

где число Рейнольдса, (  динамическая вязкость);

в области смешанного режима течения используют формулу:

где e  относительная шероховатость трубы;

для шероховатых труб применяют формулу Шифринсона:

где k – средняя высота выступов шероховатости на внутренне поверхности трубопровода.

При расчетах коротких трубопроводов из уравнения Бернулли (1) находят, в зависимости от условий задачи, расход Q,необходимый напор H трубопровода или диаметр трубопровода d и т.д.

В среде электронной таблицы MS Excel решим следующую задачу на гидравлический расчет трубопровода.

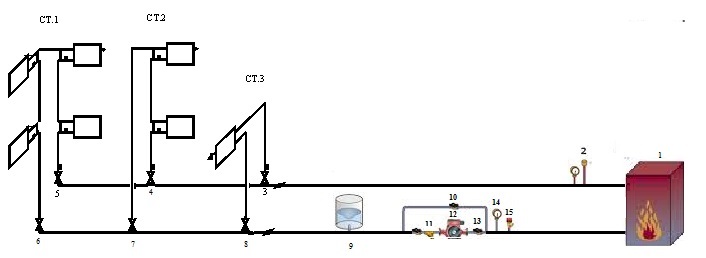
Дан трубопровод, с областью смешанного режима течения, внутренний диаметр которого равен 42 мм. К этому трубопроводу подключен насос, перекачивающий воду с расходом 10 м³/час и создающий напор 12 м. Температура перекачиваемой среды 20 °C. Конфигурация трубопровода представлена на рисунке 1. Необходимо рассчитать потери напора и проверить способность имеющегося насоса перекачивать воду при заданных параметрах трубопровода. Относительную шероховатость труб принять равной 0,15 мм. (Справочный материал приведен в таблице 1).

Рисунок 1 – Конфигурация трубопровода.

Таблица 1 – Табличные значения коэффициентов местных сопротивлений.

Колено (угол 90°)
Диаметр трубы, мм	12,5	25	37	50	Более 50
Коэффициент местного сопротивления	2,2	2	1,6	1,1	1,1
Нормальный вентиль (полное открытие)
Диаметр трубы, мм	13	20	40	80	100	150	200	250	350
Коэффициент местного сопротивления	10,8	8,0	4,9	4,0	4,1	4,4	4,7	5,1	5,5

Решение:

1. Введем исходные данные в ЭТ Ms Excel.

Рисунок 2 – Исходные данные.

2. Рассчитаем скорость течения жидкости, используя формулу:

Рисунок 3 – Скорость течения жидкости в трубопроводе.

3. Рассчитаем потери на трение в трубах и коэффициент трения, используя формулы (3) и (6) соответственно:

Рисунок 4 – Потери на трение в трубопроводе.

4. Найдем потери напора на местные сопротивления.

Из схемы трубопровода на рисунке 1 известно что, из местных сопротивлений присутствуют два вентиля, четыре прямоугольных колена и один выход из трубы. Так как в таблице 1 нет значений коэффициентов местных сопротивлений для нормальных вентилей и прямоугольных колен при диаметре трубы 42 мм, поэтому будем использовать один из методов приближенного расчета необходимых нам значений.

Возьмем табличные значения коэффициентов местных сопротивлений нормального вентиля для диаметров 40 и 80 мм. Положим, что график значений коэффициентов на этом промежутке представляет собой прямую линию. Составим и решим систему уравнений, матричным методом, с целью найти график функции зависимости коэффициента местного сопротивления от диаметра трубы:

Рисунок 4 — Коэффициент местного сопротивления нормального вентиля.

Аналогично найдем значение коэффициента местного сопротивления для прямоугольного колена. Возьмем табличные значения для диаметров 37 и 50 мм и составим и решим систему уравнений, вновь сделав аналогичное допущение о характере графика на данном участке:

Рисунок 5 – Коэффициент местного сопротивления для прямоугольного колена.

Для выхода из трубы коэффициент местного сопротивления принимается равным единице.

Следовательно, потери напора на местные сопротивления вычисляем по формуле (4):

Рисунок 6  Потери напора на местные сопротивления.

5. Найдем суммарные потери напора в системе:

Таким образом, проанализировав полученные результаты, можно сделать вывод, данный насос подходит для перекачивания воды по данному трубопроводу, так как создаваемый им напор больше суммарных потерь напора в системе, и скорость тока жидкости укладывается в границы оптимума.

Библиографический список

Альтшуль А.Д. , Киселев П.Г. Гидравлика и аэродинамика. Основы механики жидкости /Альтшуль А.Д. , Киселев П.Г. – Москва: Изд-во Стройиздат, Москва, 1975 г.  327 стр.

Галдин Н.С. Основы гидравлики и гидропривода: учебное пособие /Н.С.Галдин. – Омск: Изд-во СибАДИ, 2010. – 145 с.

Чугаев Р.Р. Гидравлика (техническая механика жидкости): учебник /Р.Р.Чугаев. – М.: Бастет, 2008. — 672 с.

Источник