Диаграммы позволяют нам комфортно воспринимать информацию. Excel обладает широкими возможностями для создания диаграмм и графиков. А если добавить к диаграммам формулы, то тогда появляется дополнительная возможность для создания динамических отчетов и презентаций.
Рассмотрим, как применять формулы и условное форматирование в диаграммах Excel.
Примеры формул в диаграммах
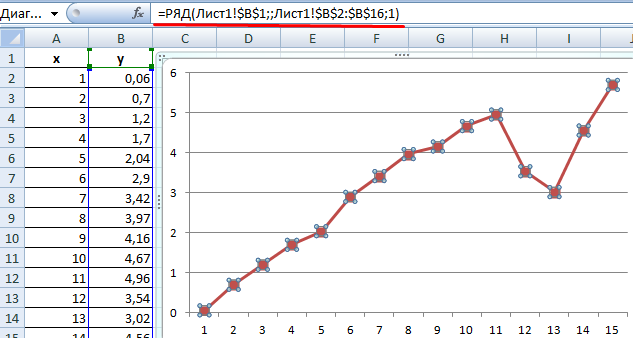
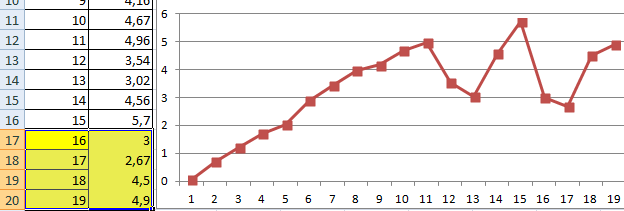
Построим на основе ряда данных простой график с маркерами:
Если щелкнуть по любой точке графика, то в строке формул появится функция РЯД. Именно с ее помощью генерируются ряды данных всех диаграмм. Эта функция применяется только для определения значений точек на графиках. Просто использовать ее на рабочем листе невозможно.
Аргументы функции РЯД:
- Имя (название ряда данных, отображается в легенде; не обязательный аргумент);
- Подписи категорий (метки, появляющиеся на оси категорий; не обязательный аргумент);
- Значения (которые применяются для построения графика; обязательный параметр);
- Порядок (порядок значений в ряду данных; обязательный параметр).
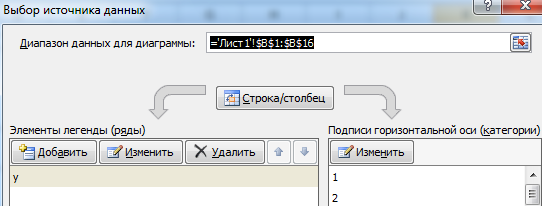
Аргументы функции РЯД можно найти и изменить в диалоговом окне «Выбрать данные»:
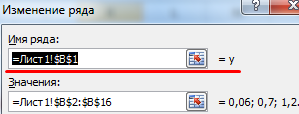
Выделим элемент легенды «y» и щелкнем по кнопке изменить. В поле «Имя ряда» содержится аргумент функции «Имя»:
Название ряда данных – «y». Его можно менять.
В поле «Значения» — аргумент значений ряда данных.
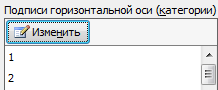
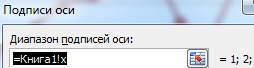
Подписи горизонтальной оси – это аргумент функции РЯД «Подписи категорий»:
Так как наш график построен на основе одного ряда данных, то порядок равняется единице. Данный аргумент отражается в списке «Элементы легенды».
Аргументы функции РЯД допускают применение именованных диапазонов. Если воспользоваться данной возможностью, то можно создать динамическую диаграмму, быстро переключаться между данными одного ряда.
Присмотримся поближе к применению именованных динамических диапазонов при построении диаграмм.
Создание динамических диаграмм
Для имеющейся исходной таблицы с данными создадим именованные диапазоны: для первого столбца – категорий – «х»; для второго – точек данных – «у».
Открываем вкладку «Формулы» — нажимаем кнопку «Диспетчер имен».
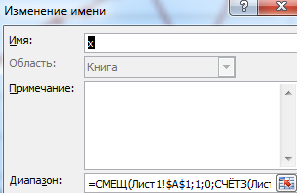
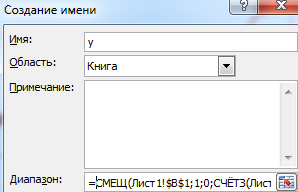
В диалоговом окне жмем «Создать». Откроется окно «Создание имени». В поле «Имя» вводим имя диапазона. В поле «Диапазон» — формулу для ссылки на данные в первом столбце (=СМЕЩ(Лист1!$A$1;1;0;СЧЁТЗ(Лист1!$A$1:$A$20)-1;1)).
Чтобы заголовок ряда данных не включался в именованный диапазон, за аргументами функции СЧЕТЗ ставим «-1». В качестве диапазона можно указывать весь столбец А – Excel быстро определяет пустые ячейки. В примере мы поставили лишь первые 20 ячеек.
Создаем именованный диапазон для второго столбца. По такому же принципу.
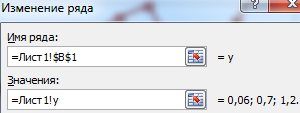
Теперь поменяем ссылки на ряд данных в графике именами динамических диапазонов. Вызываем диалоговое окно «Выбор источника данных». Выделяем элемент легенды и нажимаем «Изменить». Меняем ссылки в поле «Значения» на имя диапазона.
Далее жмем «Изменить подписи горизонтальной оси». Задаем для диапазона назначенной имя.
График остается прежним. Но если мы добавим в имеющуюся таблицу новые данные, они тут же попадут на диаграмму.
При работе с огромным массивом данных иногда нужно создать диаграмму только на основе некоторого количества последних значений в ряду. Чтобы формула выбирала только их, при формировании динамического именованного диапазона прописываем следующее: =СМЕЩ(Лист1!$A$1;СЧЁТЗ(Лист1!$A$1:$A$1000)-40;0;40;1). По такому же принципу – для столбца В.
Сколько бы данных мы ни добавляли в исходную таблицу, на графике будет показано только последние 40 значений.
Условное форматирование в диаграмме
Данный инструмент достаточно просто используется для обычных данных. Для диаграмм в Excel применить встроенное условное форматирование невозможно. Нужно идти другим путем.
Зачем это? Для улучшения восприятия информации. При изменении значений в исходных ячейках автоматически будет меняться цветовое исполнение диаграммы.
Выполнить условное форматирование в диаграммах можно с помощью макросов и формул. Рассмотрим второй способ.
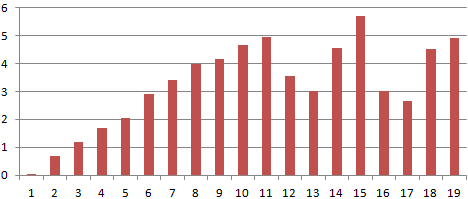
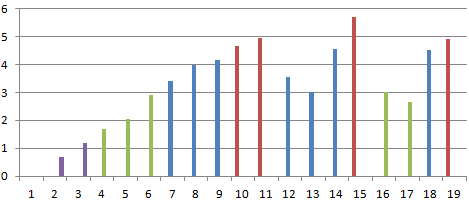
На основании тех же исходных данных составим гистограмму:
Так выглядит диаграмма без форматирования. Нужно сделать следующим образом: отдельные столбики должны закрашиваться в определенный цвет в зависимости от значения.
Для условного форматирования требуется формула, которая определяет отформатированные ячейки.
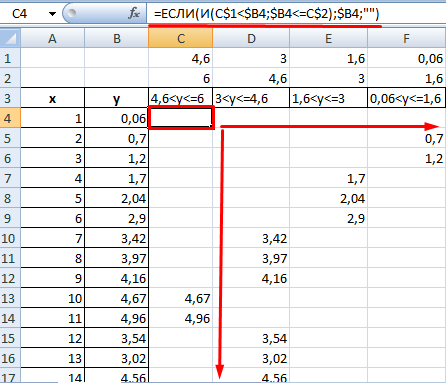
Для каждого условия создадим отдельный ряд данных. Значения в исходной таблице находятся в диапазоне от 0,06 до 5,7. Создадим ряд для периодов 0-0,6; 0,6-1,6; 1,6-3; 3-4,6; 4,6-6.
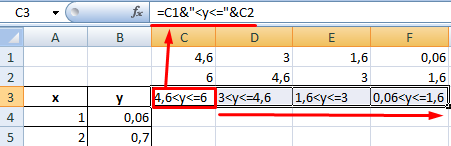
Сформируем данные для гистограммы с условным форматированием. Диапазон условий внесем в строки 1 и 2. Заголовки – в строку 3. Формулы для заголовков:
Заполним колонки для диаграммы с условным форматированием. Воспользуемся формулой, которая будет отображать значения, находящиеся в диапазонах заголовков.
Источник данных для гистограммы – столбцы А и В. Нужно исключить колонку В и добавить вновь созданный диапазон С:F.
Теперь столбики диаграммы окрашены в разные цвета в зависимости от значения.
Содержание
Подбор
формул по графику. Линия тренда
Подбор
формул со многими неизвестными
Расчет
стоимости недвижимости
Оценка
эффективности рекламы
Подбор
формул по графику. Линия тренда
Для
всех рассмотренных выше задач удавалось
построить уравнение или систему
уравнений. Но во многих случаях при
решении практических задач имеются
лишь экспериментальные (результаты
измерений, статистические, справочные,
опытные) данные. По ним с определенной
мерой близости пытаются восстановить
эмпирическую формулу (уравнение), которая
может быть использована для поиска
решения, моделирования, оценки решений,
прогнозов.
Процесс
подбора эмпирической формулы P(x)
для опытной зависимости F(x)
называется аппроксимацией
(сглаживанием).
Для зависимостей с одним неизвестным
в Excel
используются графики, а для зависимостей
со многими неизвестными – пары функций
из группы Статистические
ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ.
В
настоящем разделе рассматривается
аппроксимация экспериментальных данных
с помощью графиков Excel:
на основе данных стоится график, к нему
подбирается линия
тренда, т.е.
аппроксимирующая функция, которая с
максимальной степенью близости
приближается к опытной зависимости.
Excel
предоставляет 5 видов аппроксимирующих
функций:
-
Линейная
– y=cx+b.
Это простейшая функция, отражающая
рост и убывание данных с постоянной
скоростью. -
Полиномиальная
– y=c0+c1x+c2x2+…+c6x6.
Функция описывает попеременно
возрастающие и убывающие данные. Полином
2-ой степени может иметь один экстремум
(min
или max),
3-ей степени – до 2-х экстремумов, 4-ой
степени – до 3-х и т.д. -
Логарифмическая
– y=clnx+b.
Эта функция описывает быстро возрастающие
(убывающие) данные, которые затем
стабилизируются. -
Степенная
– y=cxb,
(х>0
и
y>0).
Функция отражает данные с постоянно
увеличивающейся (убывающей) скоростью
роста. -
Экспоненциальная
– y=cebx,
(e
– основание натурального логарифма).
Функция описывает быстро растущие
(убывающие) данные, которые затем
стабилизируются.
Степень
близости подбираемой функции оценивается
коэффициентом
детерминации
R2.
Если нет других теоретических соображений,
то выбирают функцию с коэффициентом
R2,
стремящимся к 1. Отметим, что подбор
формул с использованием линии тренда
позволяет установить как вид эмпирической
формулы, так и определить численные
значения неизвестных параметров.
Для
всех 5 видов функций используется
аппроксимация данных по методу наименьших
квадратов. Подробнее о формулах расчета
линии тренда и коэффициента детерминации
смотрите в справке по F1,
введя поиск слов «линия тренда».
В
качестве примера рассмотрим зависимость
продаж от рекламы, заданную следующими
статистическими данными по некоторой
фирме:
|
Реклама |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
|
Продажи |
3 |
13 |
25 |
35 |
40 |
45 |
48 |
50 |
51 |
Необходимо
построить функцию, наилучшим образом
отражающую эту зависимость. Кроме того,
необходимо оценить продажи для рекламных
вложений в 6 тыс. руб.
Приступим
к решению: в первую очередь введите эти
данные в Excel
и постройте график, как на рис. 2.48. Как
видно, график построен на основании
диапазона B2:J2.
Далее, щелкнув правой кнопкой мыши по
графику, добавьте линию тренда, как
показано на рис. 2.48.
В
открывшемся окне настройки (рис. 2.49), в
закладке Тип
выберите для аппроксимации логарифмическую
линию тренда (по виду графика). В закладке
Параметры
установите флажки, отображающие на
графике уравнение и коэффициент
детерминации.
После
нажатия ОК
Вы получите результат, как на рис. 2.50.
Коэффициент детерминации R2=0.9846,
что является неплохой степенью близости.
Для подтверждения правильности выбранной
функции (поскольку других теоретических
соображений нет) спрогнозируйте развитие
продаж на 10 периодов вперед. Для этого
щелкните правой кнопкой по линии тренда
– измените формат – после этого в поле
Прогноз: вперед
на: (рис. 2.49)
установите значение 10.
Рис.
2.48
Рис.
2.49
Рис.
2.50
После
установки прогноза Вы увидите изменение
кривой графика на 10 периодов наблюдения
вперед, как на рис. 2.51. Он с большой долей
вероятности отражает дальнейшее
увеличение продаж с увеличением рекламных
вложений.
Рис.
2.51
Теперь
вернитесь к состоянию рис. 2.50, нажав
кнопку
Отменить
на Панели инструментов. Попробуйте
изменить формат линии тренда – установите
полиномиальную
линию тренда полиномом 2-ой степени –
получите рис. 2.52.
Рис.
2.52
Как
видно, полученная формула аппроксимирует
исходную зависимость (на отрезке B2:J2)
с большей степенью близости, т.к.
R2=0.9973.
В то же время, если сделать прогноз на
10 периодов вперед, то он будет не совсем
верно отражать реальность: продажи не
могут уменьшаться с увеличением рекламных
вложений. Убедитесь в этом: сделайте
прогноз на 10 периодов наблюдения вперед
и получите график.
Опять
вернитесь к состоянию рис. 2.50, нажав
кнопку
Отменить.
Для вычисления продаж при рекламе в 6
тыс. руб. запишите в ячейку К2 формулу
=23,796*LN(K1)+0,5961: должно получиться 43,2 тыс.
штук.
В
Excel
имеется функция ПРЕДСКАЗ, которая
вычисляет будущее значение Y
по существующим парам значений X и Y
значениям с использованием линейной
регрессии. Функция Y
по возможности должна быть линейной,
т.е. описываться уравнением типа c+bx.
Функция предсказания для нашего примера
запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1).
Запишите – должно получится значение
64.4.
Обратите
внимание, что
на
рис. 2.50 ось Х подписана номерами периодов
наблюдения, а на рис. 2.52 — значениями в
точках наблюдения. Для нанесения значений
на ось Х щелкните правой кнопкой мыши
по графику и в выпавшем меню выберите
пункт Исходные
данные:
В
открывшемся одноименном окне, в закладке
Ряд,
в поле Подписи
оси Х,
укажите диапазон ячеек, где записаны
значения Х (здесь $B$1:$K$1).
Задачи
для самостоятельного выполнения:
-
Постройте
функцию, наилучшим образом отражающую
зависимость и спрогнозируйте значения
для следующего периода наблюдения со
значением 5, основываясь на следующих
данных:
|
Цена |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
|
Спрос |
1300 |
700 |
500 |
200 |
100 |
70 |
50 |
40 |
-
Концентрация
ядовитого вещества в водоеме изменялась
во времени согласно таблице:
|
Время после |
1 |
3 |
5 |
8 |
|
Концентрация |
8 |
2.8 |
1 |
0.3 |
Определите
вид зависимости концентрации от времени
и расчетную концентрацию в момент
выброса.
Подбор
формул со многими неизвестными
Использование
линии тренда графиков Excel
– наиболее наглядный и информативный
способ восстановления зависимости и
исследования связи между двумя
переменными. Для зависимостей со многими
неизвестными подбор формул выполняют
с помощью специальных функций из группы
Статистические
— ЛИНЕЙН и ЛГРФПРИБЛ. Кроме того, функции
ТЕНДЕНЦИЯ и РОСТ позволяют вычислить
значения аппроксимирующей функции в
диапазоне наблюдения. Еще один инструмент
для подбора формул со многими неизвестными
Регрессия,
входящий в Пакет
анализа (СервисАнализ
данных…),
будет рассмотрен в следующем разделе.
В
настоящем разделе рассматривается
аппроксимация экспериментальных данных
с помощью функций ЛИНЕЙН, ТЕНДЕНЦИЯ,
ЛГРФПРИБЛ и РОСТ. Функции ЛИНЕЙН и
ТЕНДЕНЦИЯ применяют для восстановления
линейных зависимостей вида
y=b+a1x1+a2x2+…+anxn,
а функции ЛГРФПРИБЛ и РОСТ — для нелинейных
(показательных) зависимостей вида
y=ba1X1a2X2…anXn.
Функции
ЛИНЕЙН и ЛГРФПРИБЛ возвращают массив
с т.н. регрессионной статистикой, в
котором содержатся вычисленные значения
параметров (b,a1,a2,…an),
коэффициент детерминации
R2
и другие данные, характеризующие
аппроксимирующую функцию. Формат функций
ЛИНЕЙН, ЛГРФПРИБЛ и их применение
поясним на примере.
Расчет
стоимости недвижимости
Агентство
недвижимости оценивает однокомнатные
квартиры по трем переменным: х1 – общая
площадь, х2 – площадь кухни, х3 – этаж
квартиры, предполагая, что между каждой
переменной х1, х2, х3 и зависимой переменной
y
(стоимость) существует линейная
зависимость. Подобрать формулу для
вычисления стоимости однокомнатных
квартир и вычислить стоимость квартиры
с данными: х1=42кв.м, х2=11кв.м, х3=5эт. Собранные
рекламные данные занесены в приведенную
ниже таблицу.
Последовательность
действий для решения задачи следующая:
-
Заведите
приведенную таблицу в Excel,
в ячейки A1:D14. -
Выделите
диапазон ячеек B17:E21
(рис. 2.54) для сохранения результатов
вычислений функции ЛИНЕЙН – массива
регрессионной статистики. -
Вызовите
мастер функций, выберите статистическую
функцию ЛИНЕЙН и заполните параметры
функции как на рис. 2.53. Параметр Изв_знач_y
содержит диапазон D2:D14,
т.е. известные значения y.
Параметр Изв_знач_х
содержит диапазон A2:C14,
т.е. известные значения х. Параметр
Стат=1,
поскольку мы хотим получить дополнительную
статистику.
Рис.
2.53
-
После
нажатия ОК встаньте на строку формул
и нажмите Ctrl+Shift+Enter.
В результате должен получиться массив
значений, показанный на рис. 2.54.
Интересующие нас коэффициенты выделены
на рисунке (подробнее см. справку F1).
Коэффициент детерминации
R2=0.9725
вполне удовлетворителен. Таким образом,
искомая формула имеет вид:
Y
= 1,36*х1 + 0,1*х2 – 0,21*х3 – 19,27
Рис.
2.54
-
После
подбора формулы осталось вычислить
стоимость при х1=42, х2=11, х3=5. В любую
ячейку запишите выражение
=1,36*42+0,1*11–0,21*5–19,27. В результате получится
y=37.9
тыс. $.
Использование
функции ТЕНДЕНЦИЯ покажем на этом же
примере для расчета стоимостей различных
вариантов квартир, как показано на рис.
2.55.
Рис.
2.55
Новые
значения Х, для которых надо рассчитать
стоимость, следует ввести в ячейки
F2:H14.
Диапазон I2:I14
используйте для записи рассчитанных
значений y,
Вызовите мастер функций и функцию
ТЕНДЕНЦИЯ. Параметры функции заполните
как на рис. 2.56. Как видно параметр
Нов_знач_х
содержит диапазон F2:H14,
т.е. новые значения х. После нажатия ОК
встаньте на строку формул и нажмите
Ctrl+Shift+Enter
– результат, заполненный диапазон
I2:I14
на рис. 2.55.
Рис.
2.56
Оценка
эффективности рекламы
Следующий
пример. Подобрать формулу для вычисления
процента увеличения оборота при различных
затратах на рекламу. Экспериментально
известны проценты увеличения оборота
при затратах в 5, 10, 15, 20 тыс.$ в 3-х масс-медиа
— на телевидении, радио и в прессе:
|
5 тыс. |
10 тыс. |
15 |
20 тыс. |
|
|
1. |
28% |
43% |
61% |
95% |
|
2. |
15% |
24% |
34% |
50% |
|
3. |
6% |
9% |
13% |
20% |
Кроме
этого, надо вычислить процент увеличения
оборота в прессе при затратах 2 тыс.$ и
на телевидении при затратах в 22 тыс.$.
Дополнительно вычислите проценты для
всех масс-медиа при затратах 2, 17 и 25
тыс.$.
Для
решения задачи в первую очередь следует
правильно разместить данные – рис.
2.57.
Рис.
2.57
Затем
вычислите массив с регрессионной
статистикой функцией ЛИНЕЙН: выделите
диапазон ячеек F2:H6
и проделайте известные из предыдущего
примера действия. В итоге должен
получиться массив:
Как
видно, коэффициент детерминации
R2=0.8757
не удовлетворителен. Поэтому выполните
подбор формулы с помощью функции для
нелинейных зависимостей ЛГРФПРИБЛ:
выделите диапазон ячеек F2:H6
и проделайте известные из предыдущего
примера действия. В итоге должен
получиться массив:
В
этом случае коэффициент детерминации
R2=0.989
вполне удовлетворителен и можно записать
искомую аппроксимирующую формулу
показательного типа (т.к. использована
функция ЛГРФПРИБЛ):
Y
= 0,44 * 0,46х1
* 1,08х2
Теперь
вычислите проценты увеличения оборота
из условия задачи: введите формулы и не
забудьте установить процентный формат
отображения значений в ячейках. Результаты
приведены в таблице:
|
Пресса, |
5,0% |
=0,44*0,46^3*1,08^2 |
|
TV, |
110,0% |
=0,44*0,46^1*1,08^22 |
В
заключении, вычислите проценты для всех
масс-медиа при затратах 2, 17 и 25 тыс.$.
Подготовьте данные, колонки J
и K,
как на рис. 2.58.
Для
вычисления значений Y
используем функцию РОСТ, поскольку уже
известно, что зависимость нелинейная,
показательная. Выделите диапазон ячеек
L2:L10
и введите функцию РОСТ; заполнение
параметров функции показано на рис.
2.59.
Рис.
2.58
Рис.
2.59
После
нажатия ОК и Ctrl+Shift+Enter
на строке формул, колонка L
будет заполнена как на рис. 2.58. Сравните
результаты с результатами вычисления
по подобранной формуле.
Задачи
для самостоятельного выполнения:
-
Источник
радиоактивного излучения помещен в
жидкость. Датчик расположен на расстоянии
(х1) 20, 50 и 100 см от источника. Измерения
интенсивности излучения (y,
мРн) проводились через 1, 5 и 10 суток (х2)
после установки источника. Необходимо
подобрать аппроксимирующее уравнение.
Результаты измерений приведены в
таблице:
|
х1 |
1 |
5 |
10 |
|
20 |
61.2 |
43.6 |
28.3 |
|
50 |
33.6 |
24.0 |
15.6 |
|
100 |
12.3 |
8.8 |
5.7 |
-
В
бассейне проводится ежедневная частичная
смена воды. Необходимо подобрать формулу
для вычисления уровня воды в бассейне,
которая зависит от двух переменных: х1
– длительность впуска воды, х2 –
длительность выпуска воды. Кроме этого,
необходимо вычислить значения уровня
воды для х1[90;140]
с шагом 10 и х2[10;30]
с шагом 5. Исходные данные — результаты
наблюдений за неделю приведены в
таблице:
|
х1 |
х2 |
y |
|
120 |
20 |
3.2 |
|
100 |
25 |
2.8 |
|
130 |
20 |
3.3 |
|
100 |
15 |
3.3 |
|
110 |
23 |
3.0 |
|
105 |
26 |
2.8 |
|
112 |
13 |
3.3 |
9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сравнение показателей в таблице за определенный период – одна из популярных задач, которая стоит перед пользователями Microsoft Excel. Чаще всего это осуществляется путем вывода вспомогательного столбца, где значения указаны в процентах, и сразу становится понятно, насколько сильной была позитивная или негативная динамика.
В этой статье я на простом примере предлагаю разобраться с соответствующим оформлением таблицы.
Предварительные действия
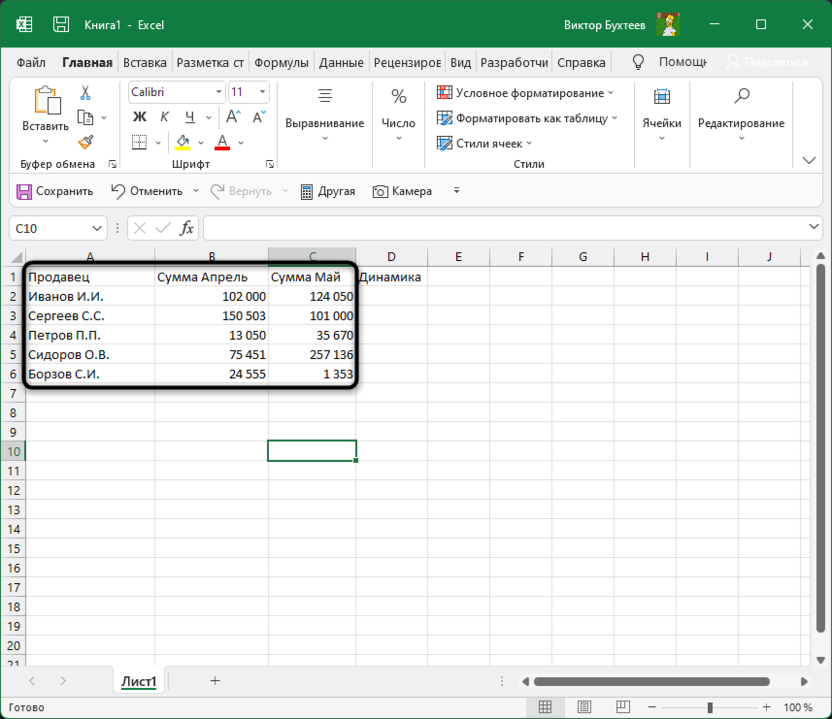
Сначала понадобится подготовить таблицу, чтобы кроме ввода функций далее от вас ничего не требовалось. Выберите два общих значения, которые будете сравнивать. Если это должна быть, например, месячная выручка, сначала сделайте сводную таблицу по дням и ссылайтесь на нее при создании общей суммы. Выведите два значения, динамику между которыми нужно сравнивать, чтобы перейти далее. На изображении ниже показан самый простой пример подходящей таблицы.
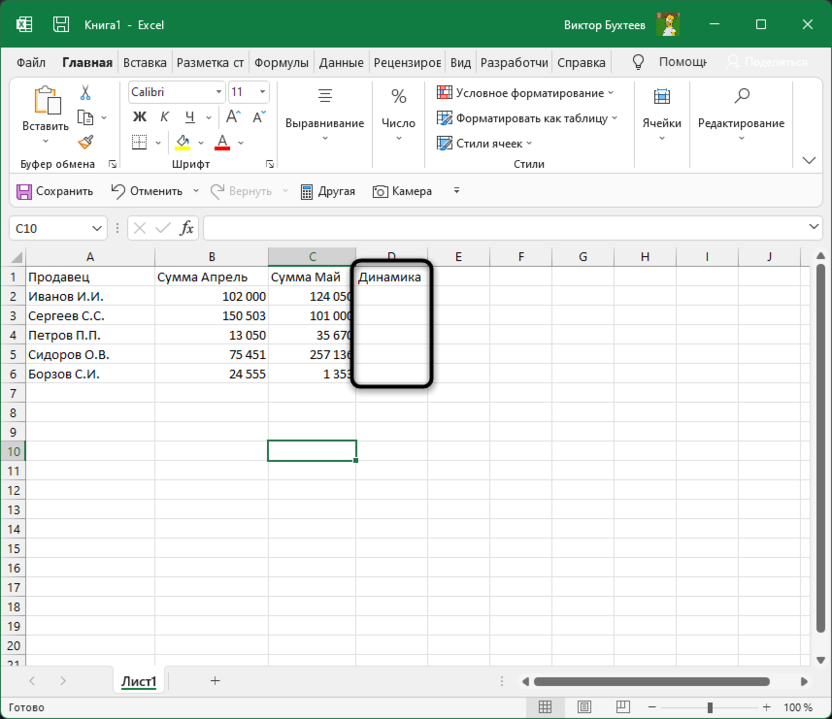
Создайте вспомогательный столбец для вывода процентов. Введите для него совершенно любое удобное для вас название и задайте визуальное оформление в соответствии со стилем основной таблицы.
Сейчас стоит учитывать, что тип ячейки, в которой будут отображаться проценты, является общим. При расчетах в таком случае появится очень большое значение в виде обычного числа. Поэтому понадобится изменить формат ячеек, чтобы проценты выводились корректно.
-
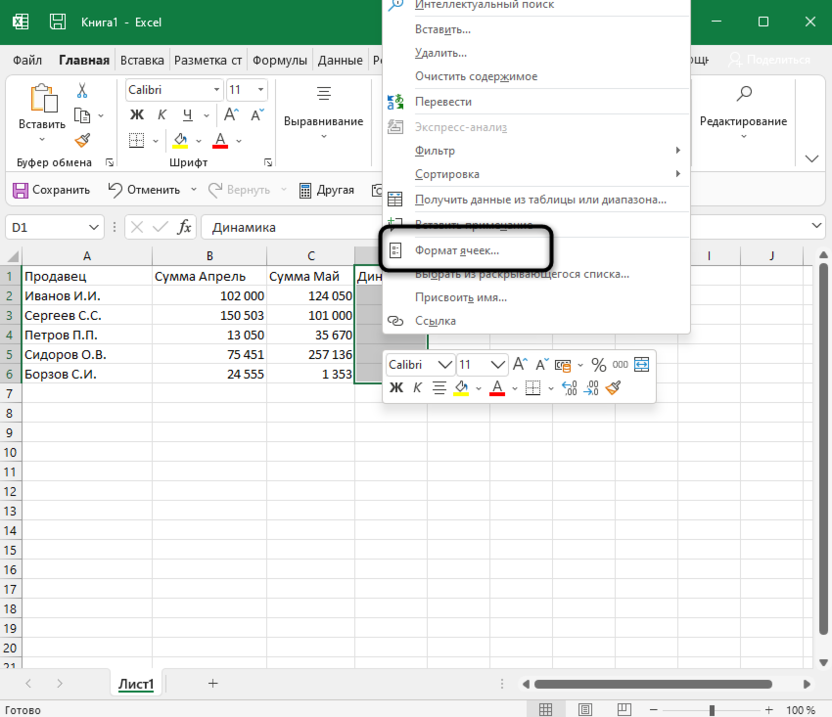
Для этого выделите необходимые ячейки и щелкните по любой из них правой кнопкой мыши. Из контекстного меню выберите пункт «Формат ячеек».
-
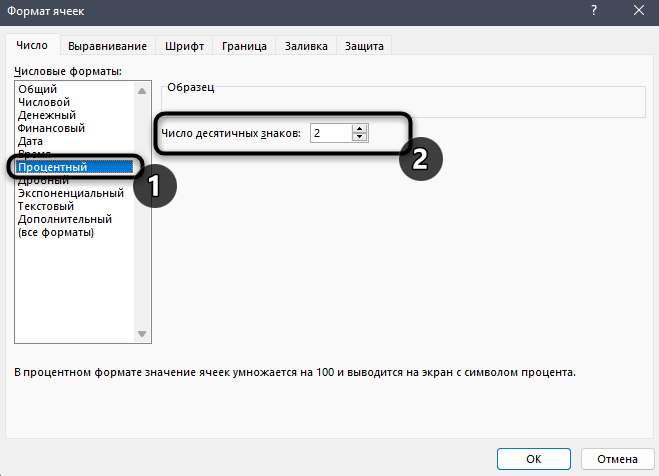
Отобразится отдельное окно, в котором будет выбрана вкладка «Число». На ней выберите «Процентный» и определите количество знаков после запятой или оставьте его по умолчанию. После этого сохраните новый формат ячейки.
На этом подготовительные действия завершены, поэтому можно приступить к заполнению формул и вычислении положительной или негативной динамики.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
Создание формулы отслеживания динамики роста
В следующей инструкции я постараюсь наглядно описать каждое действие при написании функции, чтобы вы понимали, какие значения берутся, как они сравниваются и что получается в итоге. Если вы сделали таблицу такого же формата, как и в примере, достаточно будет выполнить точно такие же действия, чтобы отследить динамику роста в процентах.
-
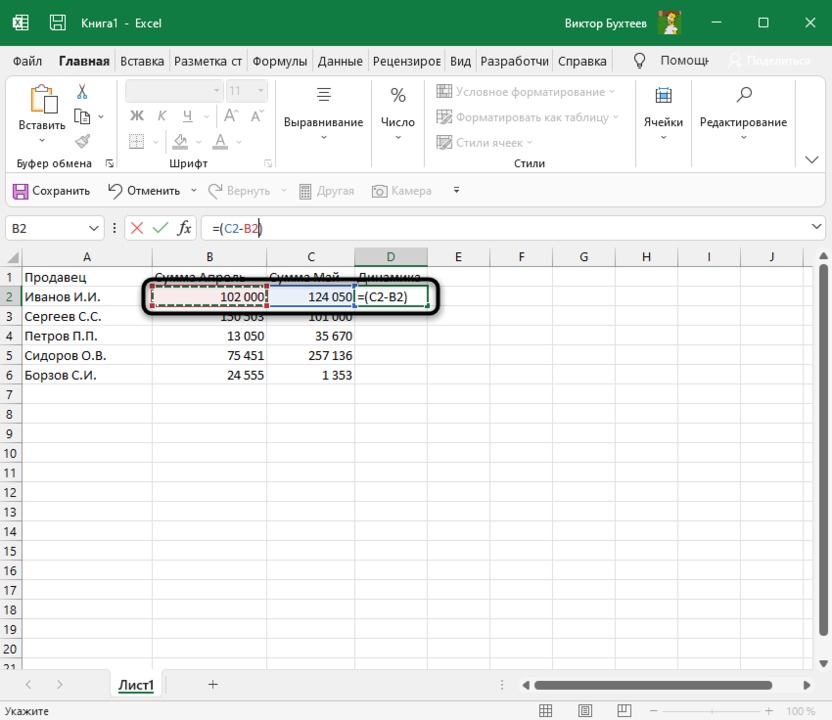
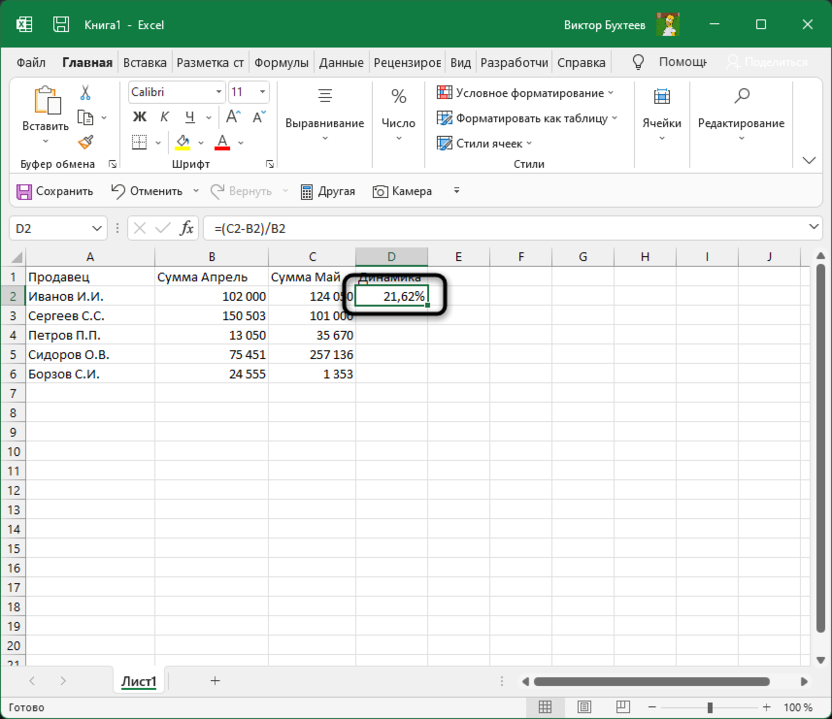
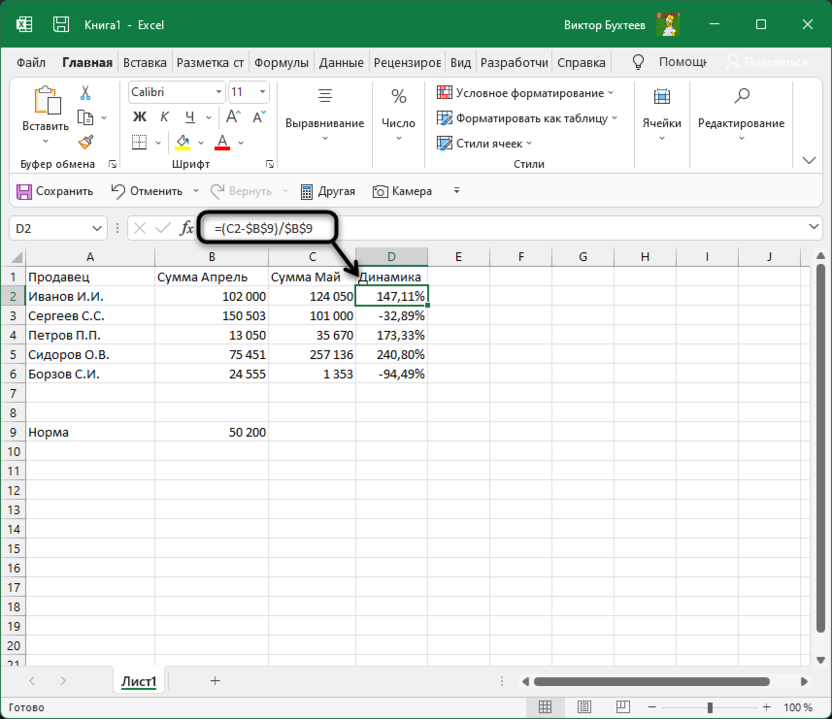
Выделите ячейку, где должны выводиться проценты и напишите первую часть формулы =(C2 — B2). Это поможет определить разницу между суммами за два разных месяца. Соответственно, если номера ячеек в вашей таблице другие, замените их, отняв сумму второго значения от первого.
-
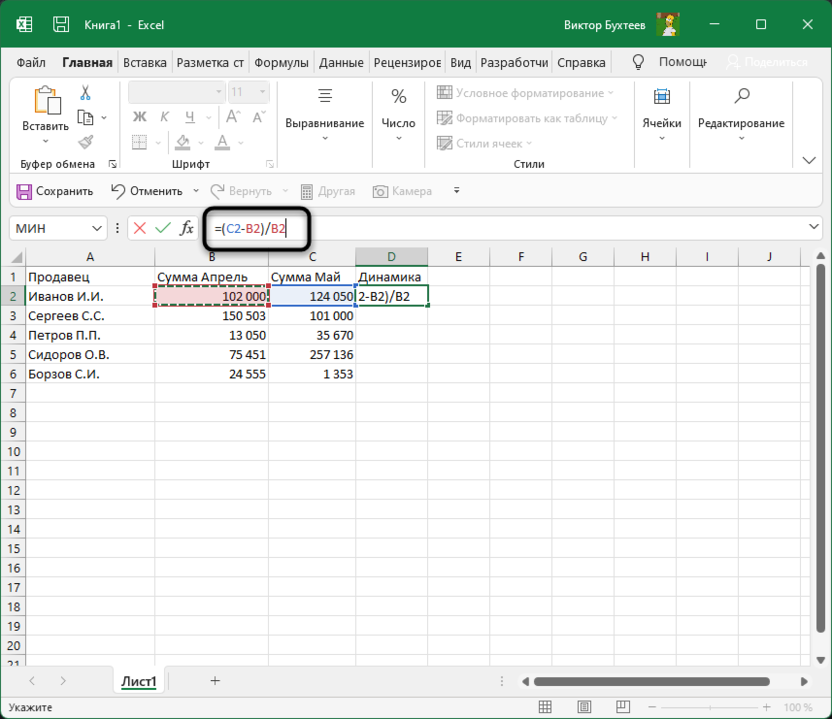
После скобок добавьте /B2, чтобы разделить это все на сумму первого значения, то есть на 100%, если говорить о стандартных математических операциях с процентами.
-
Нажмите Enter и посмотрите на результат. В моем случае сумма за первый месяц была 102 000, за второй — 124 000, а разница – 22 000. Получается, динамика роста является положительной и равняется 21,62%. У вас значение будет другим, в соответствии с суммами в таблице.
-
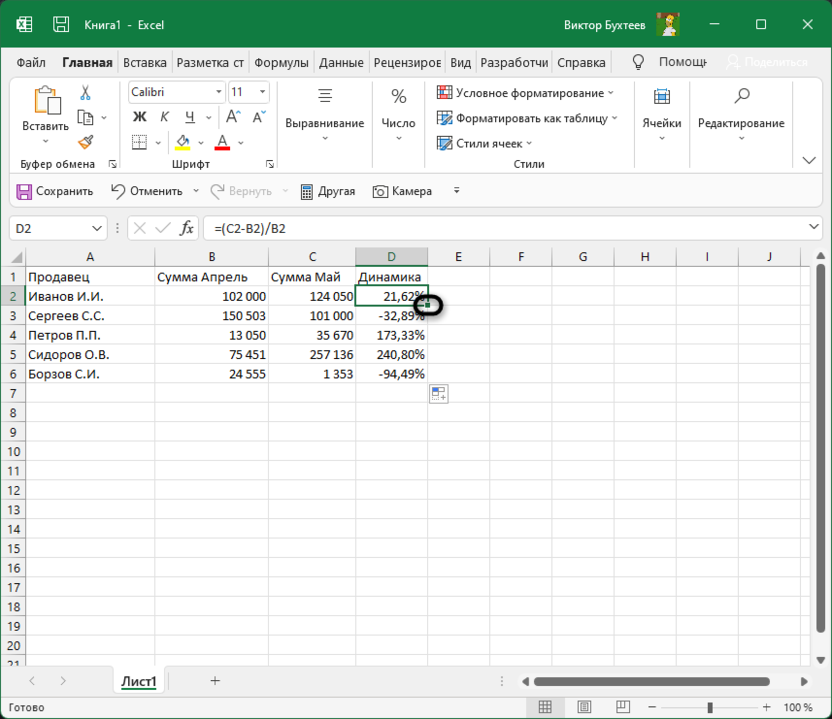
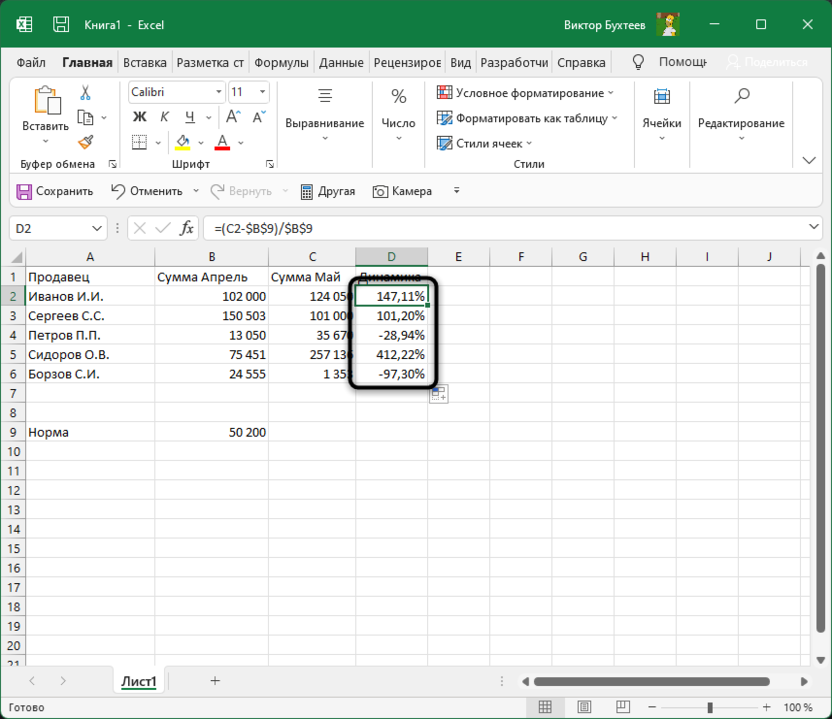
Если далее в таблице должно происходить такое же сравнение значений и вывод процентов, просто зажмите левой кнопкой мыши правый угол текущей ячейки и растяните ее вниз.
-
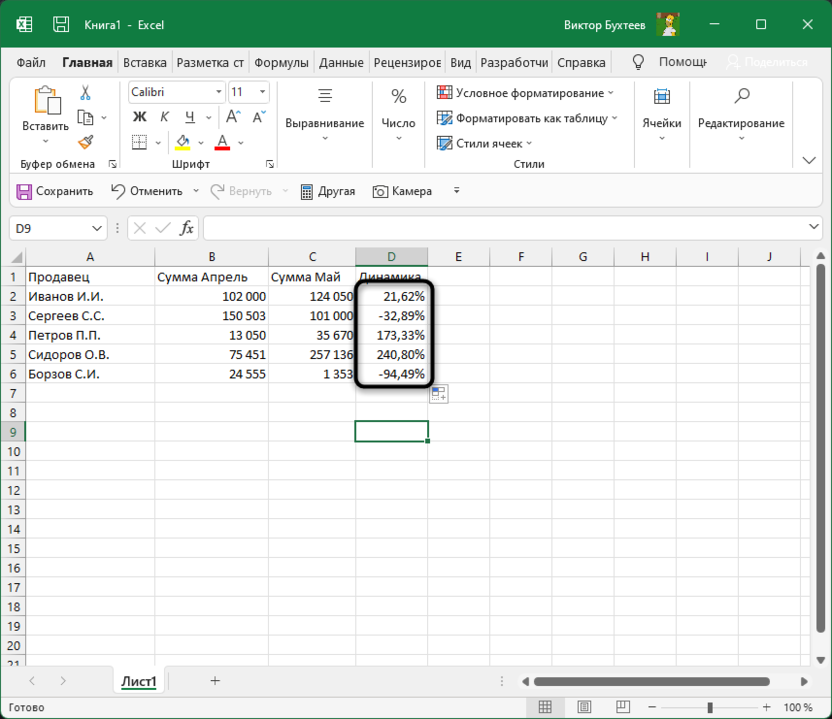
В итоге таблица сама заполнится, и на экране появится список всех процентов, характеризующих положительную или отрицательную динамику роста.
Далее ничего вас не ограничивает, вы можете сравнивать показатели бесконечное количество раз. Отнимать и добавлять проценты, чтобы понять общую сумму изменений и заниматься дальнейшим взаимодействием с электронной таблицей для своих целей.
Формула отслеживания динамики роста по норме
Иногда расчеты подразумевают наличие нормы, то есть средневзвешенной суммы, которая является оптимальной. Вы можете использовать только это значение, чтобы сравнить его с другими показателями и вычислить проценты. Давайте наглядно разберемся с изменениями, которые вносятся в этом типе расчетов.
-
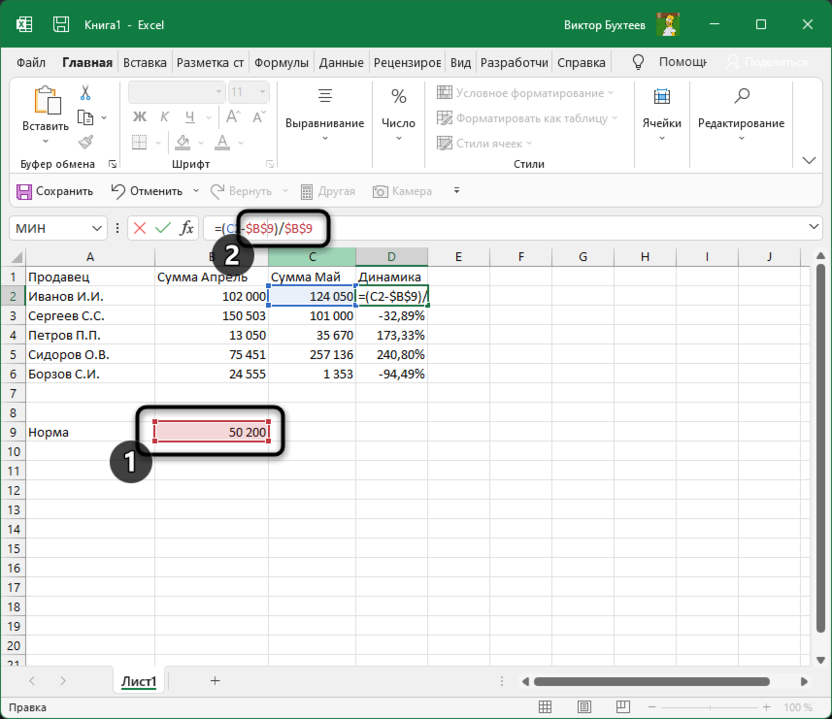
Найдите ту ячейку, где будет указана норма. Если ее еще нет, создайте и введите необходимое число. Формула будет немного отличаться от предыдущей. Вам нужно в качестве первого значения как раз и задать эту ячейку, полностью закрепив ее при помощи знаков $.
-
Больше никаких изменений вводить не нужно, достаточно нажать Enter, чтобы ознакомиться с результатом.
-
При растягивании формула тоже будет считаться корректно, поскольку ранее вы полностью закрепили одну ячейку.
В этом случае формула обретает вид =(C2-$B$9)/$B$9, где $B$9 – номер той самой закрепленной ячейки, а C2 – сумма второго месяца, от которой и отнимается норма для вычисления процентов.
На основе созданной таблицы вы можете добавлять наглядный график, визуально демонстрирующий динамику роста. Детальнее о его создании рассказано в другой моей статье по ссылке ниже.
Подробнее: Как создать диаграмму темпов роста в Microsoft Excel
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
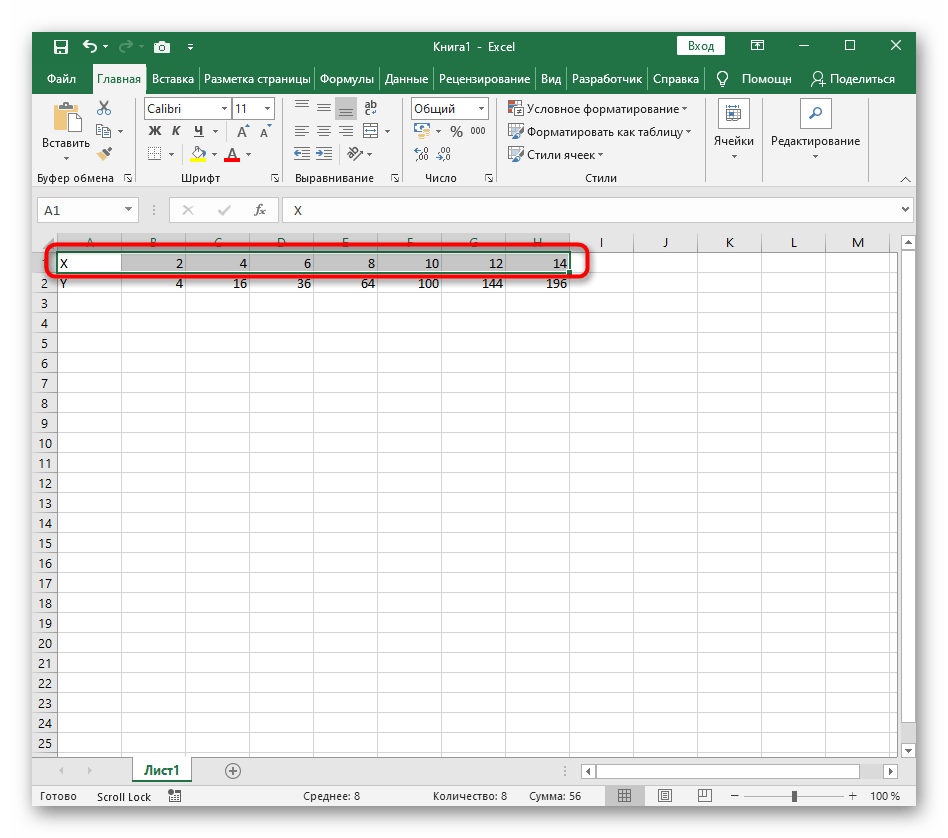
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
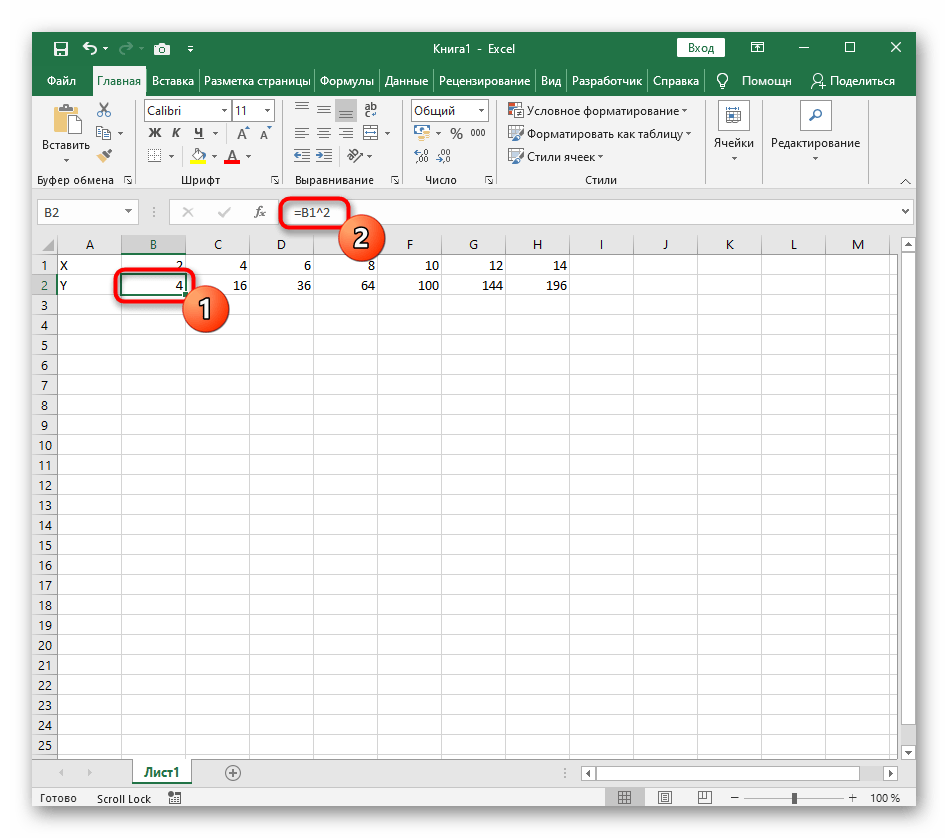
- Нажмите по первой ячейке и впишите
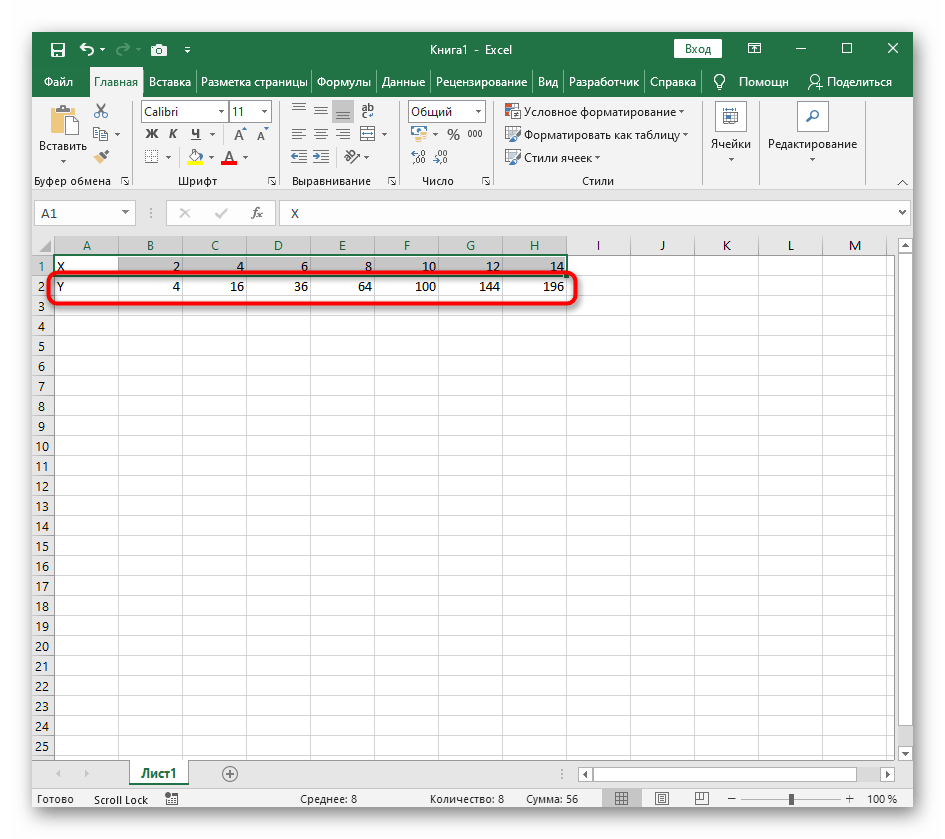
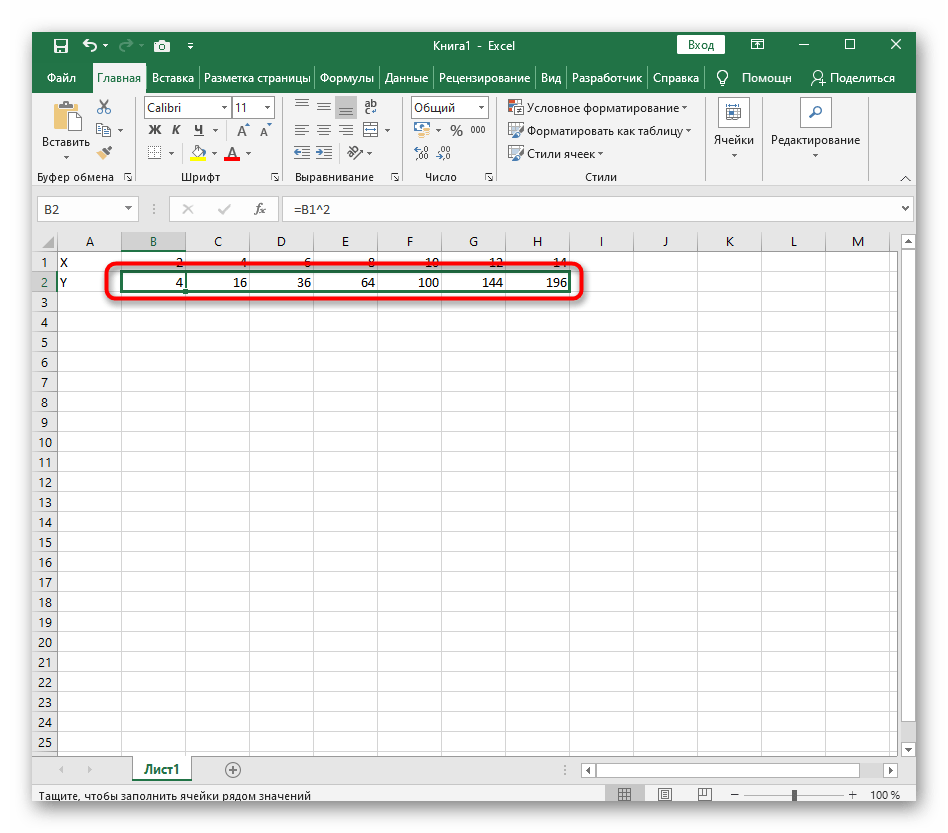
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
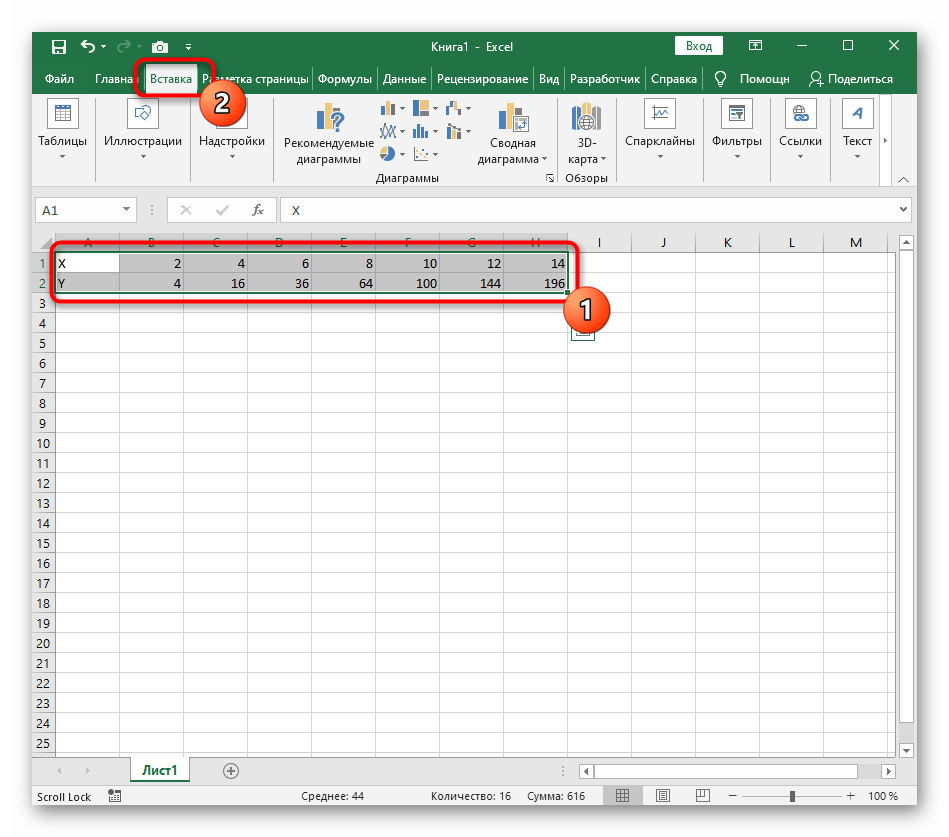
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
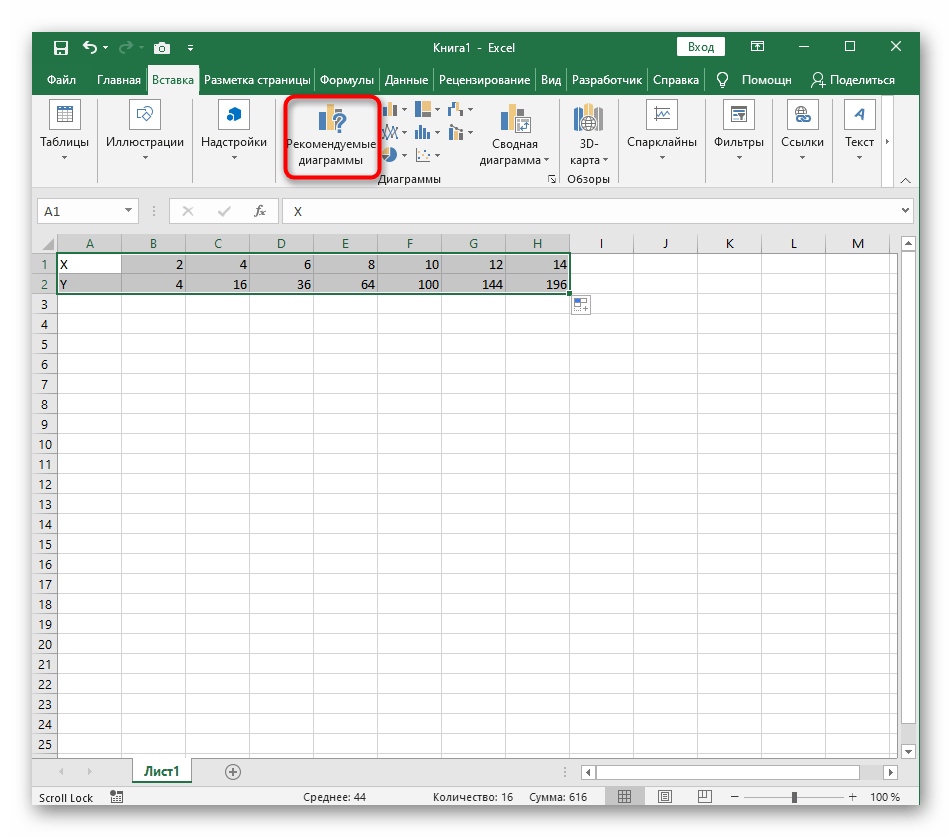
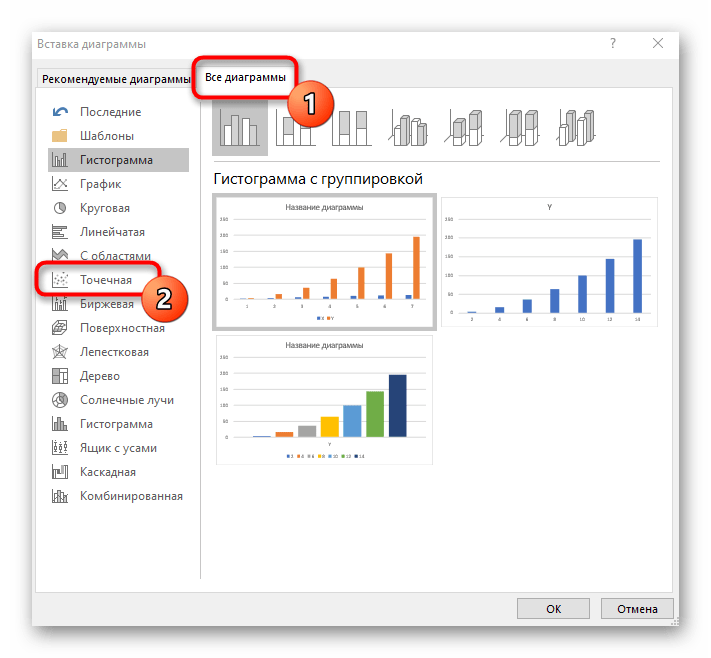
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
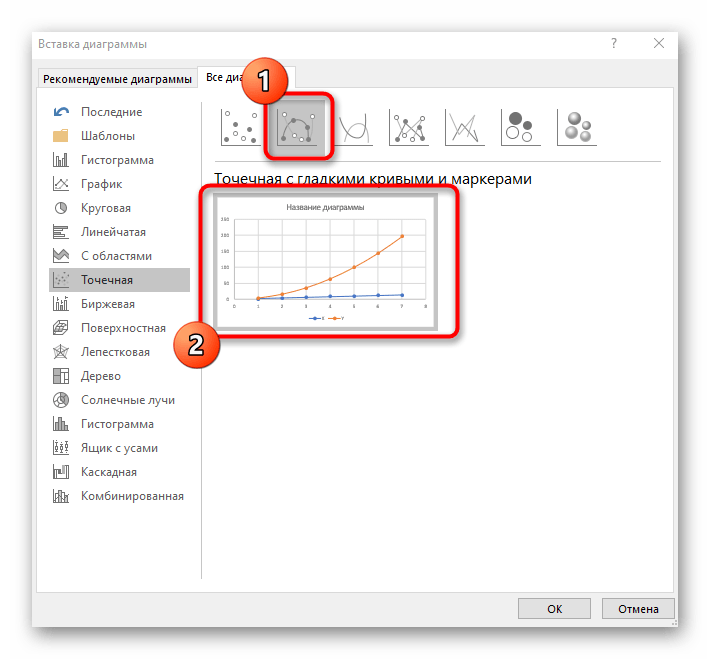
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
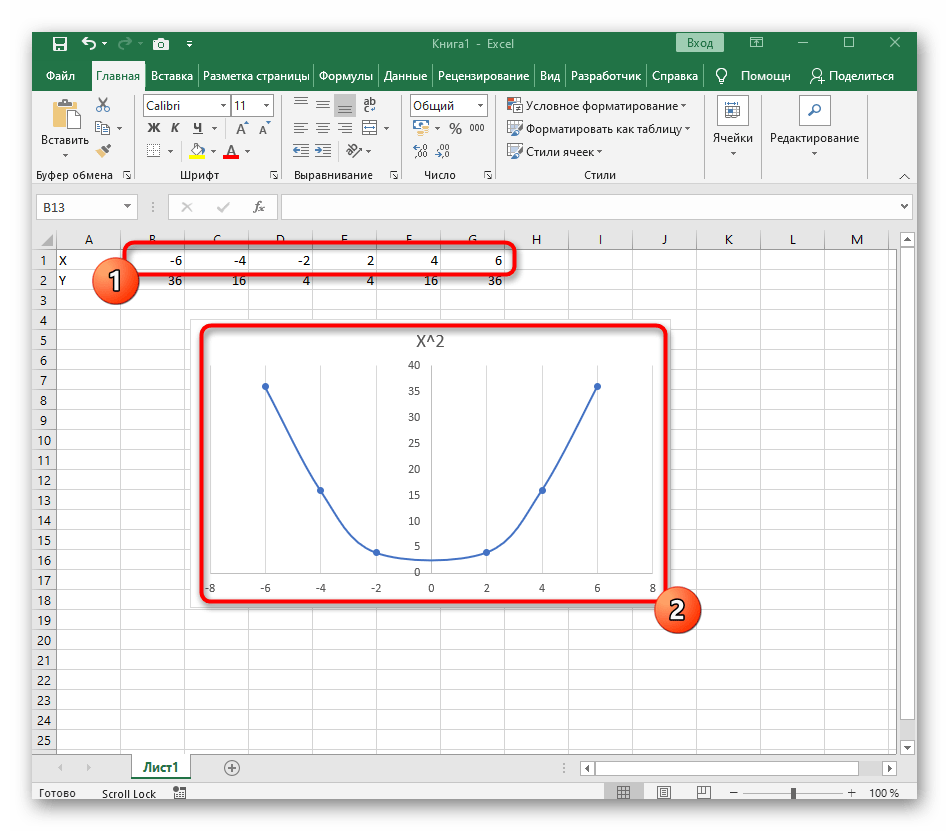
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
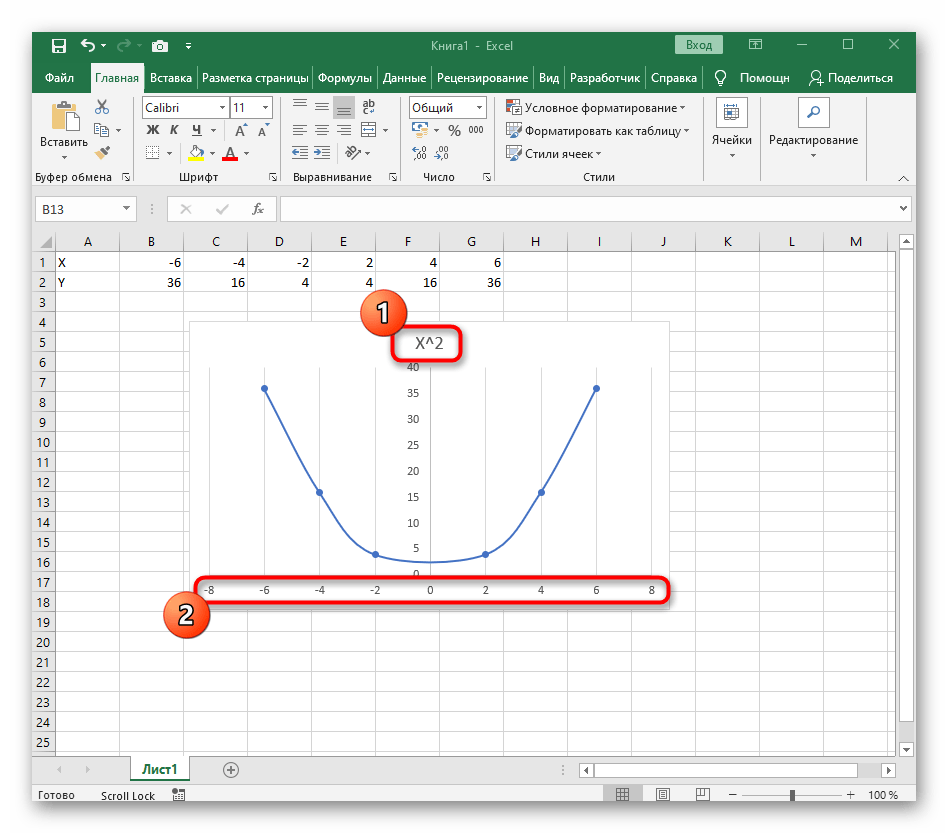
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
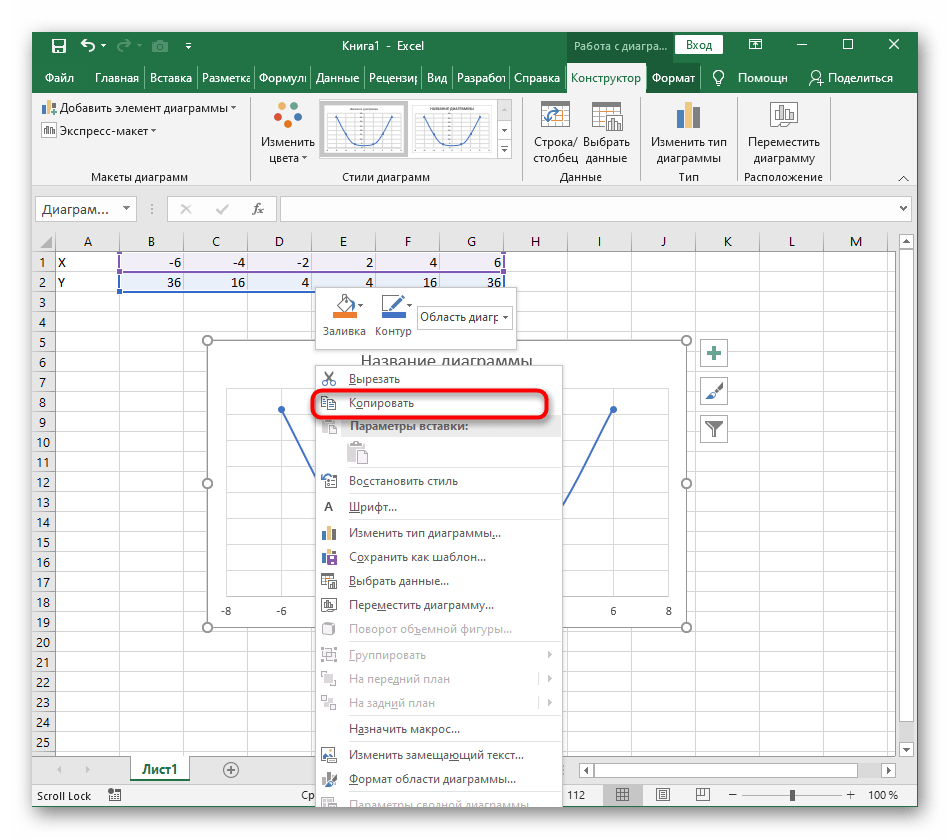
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
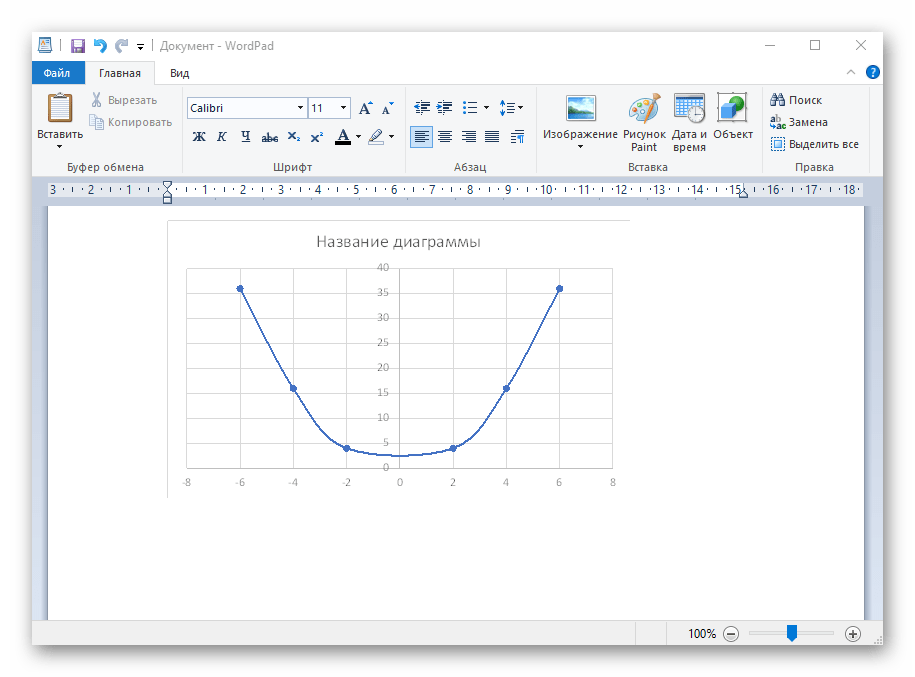
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
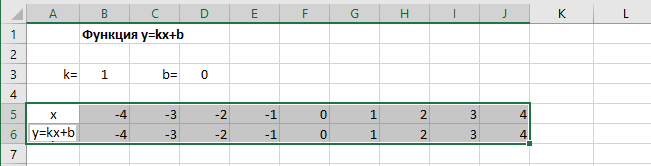
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
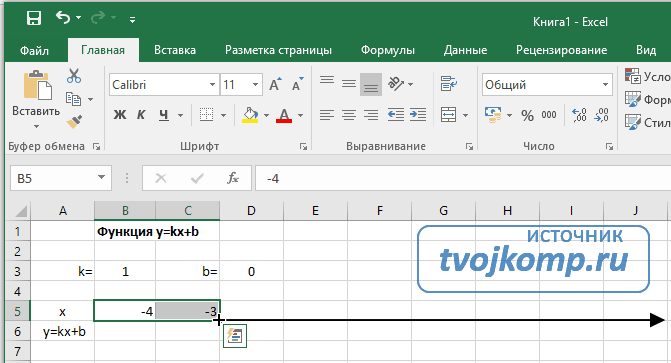
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
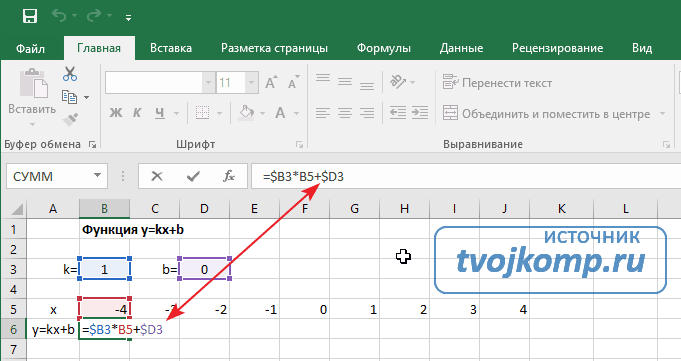
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
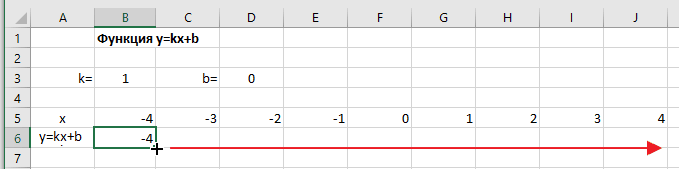
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
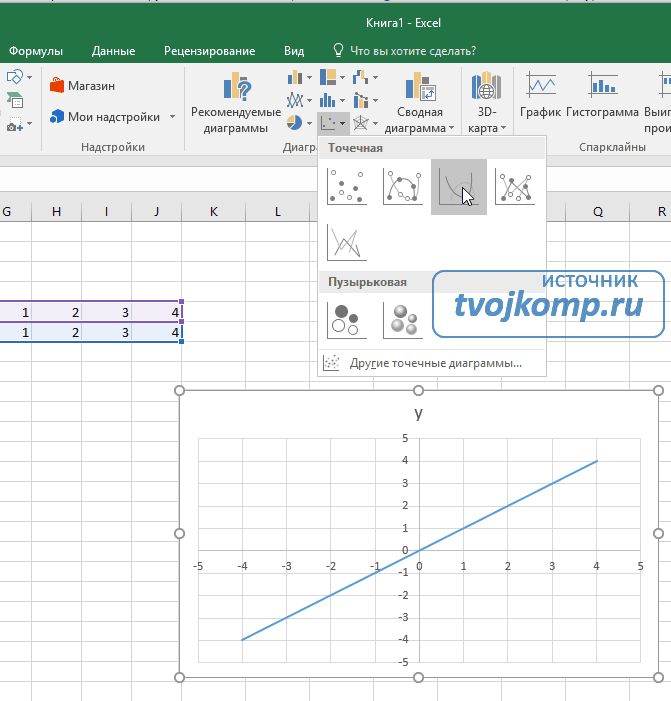
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
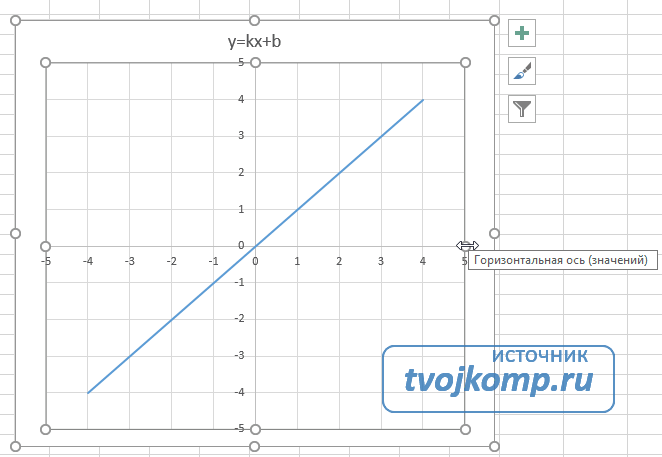
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
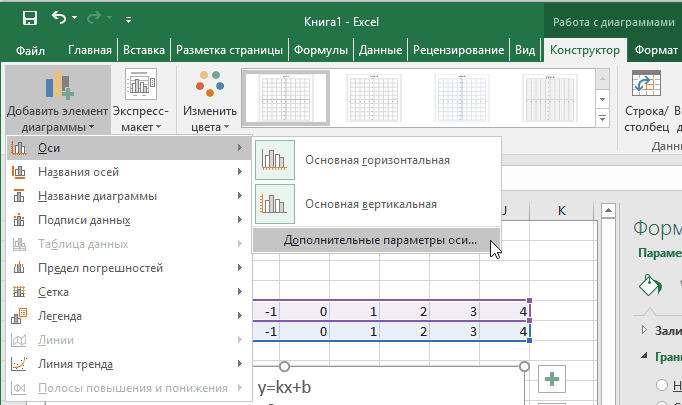
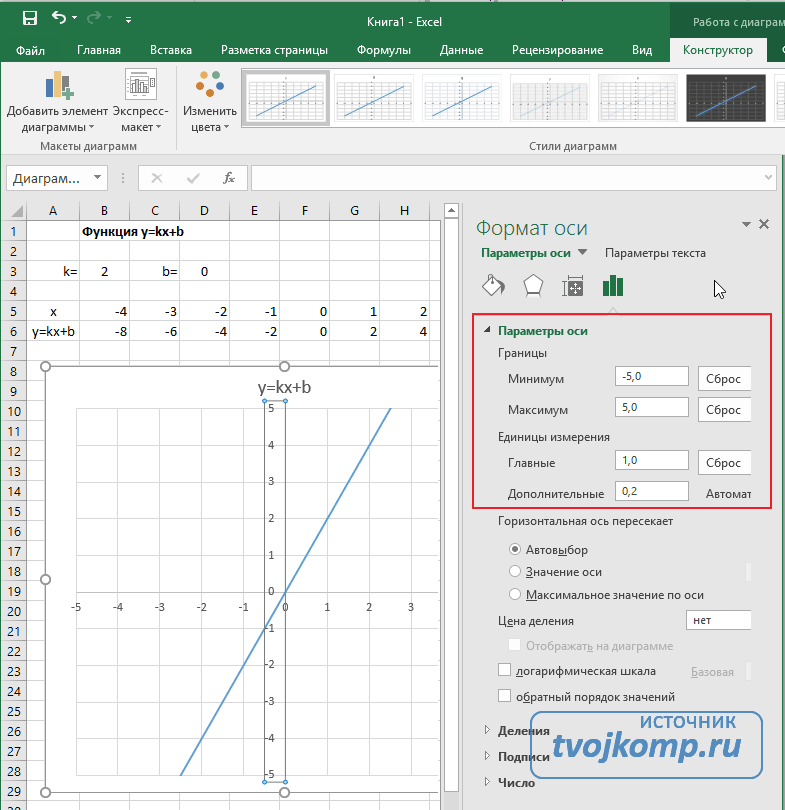
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
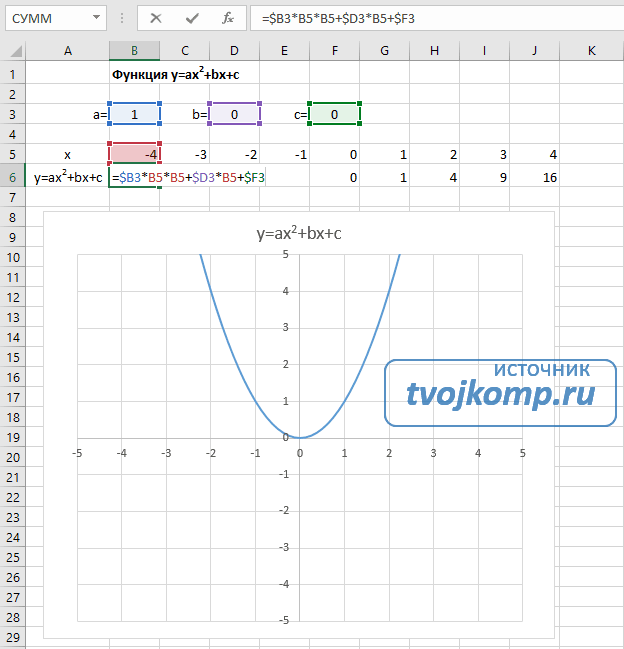
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
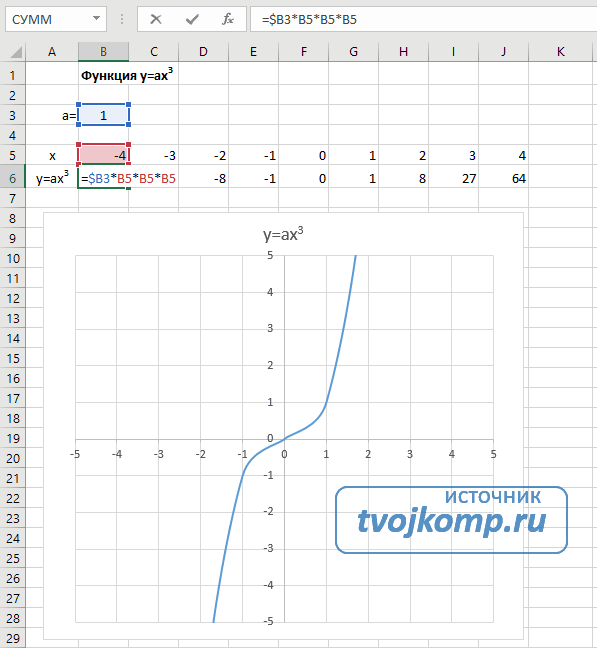
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
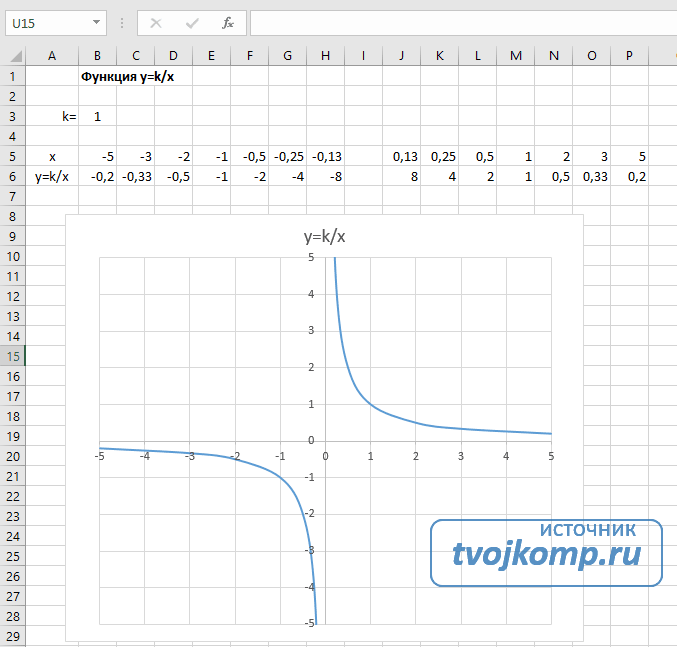
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
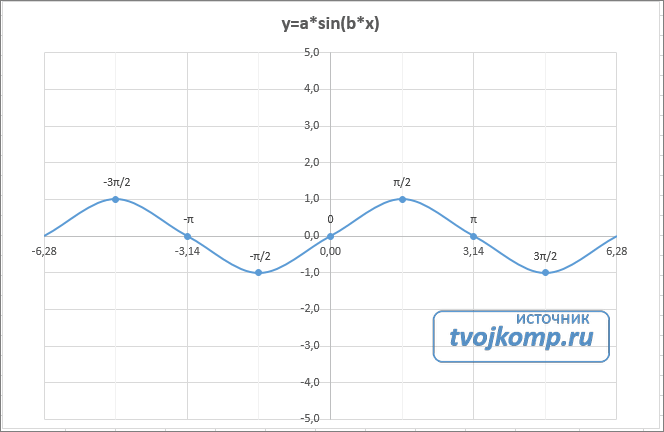
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
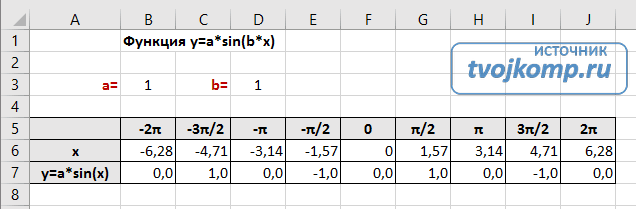
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
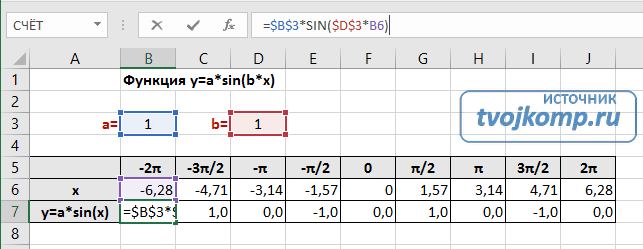
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
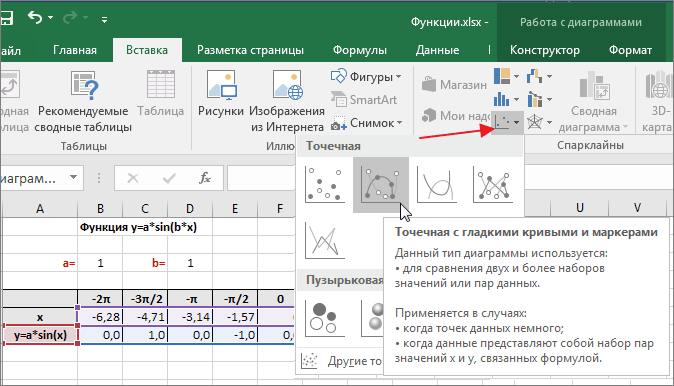
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
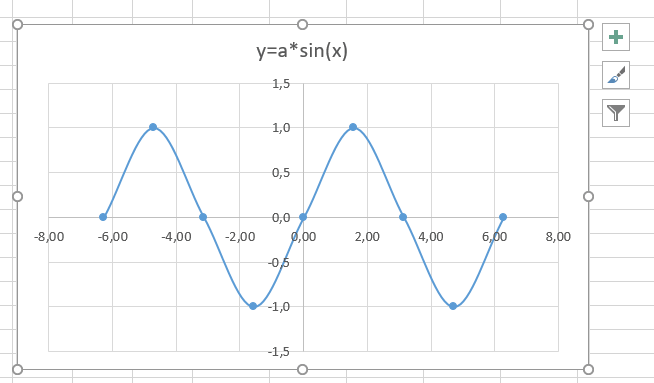
В итоге получим диаграмму.
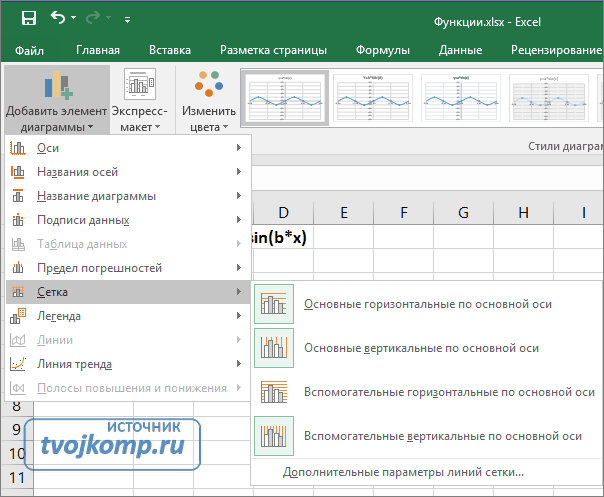
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
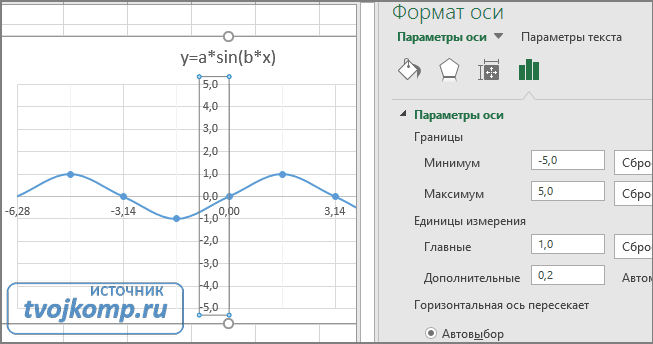
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
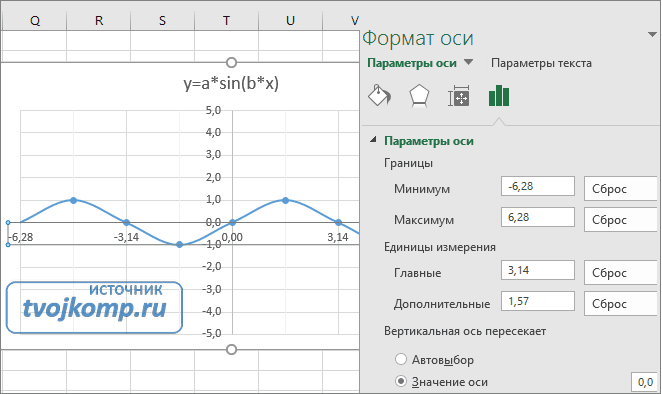
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
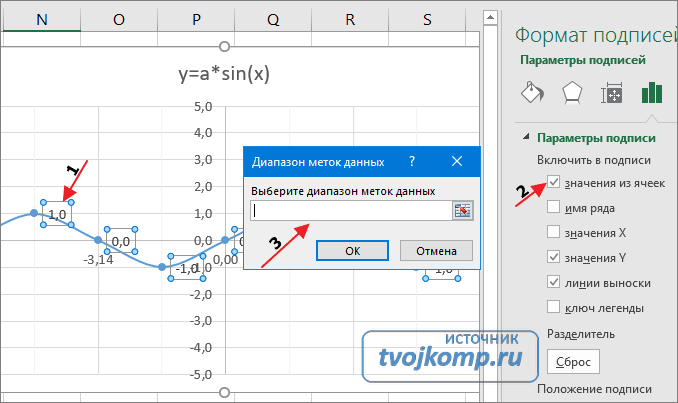
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!