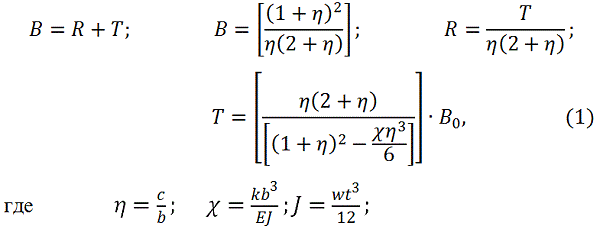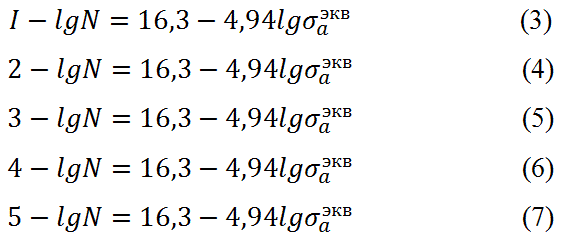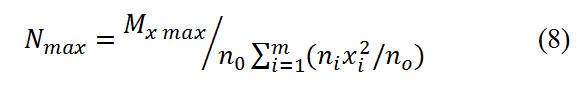Tyhig
размещено: 04 Апреля 2015
обновлено: 12 Января 2019
Расчёт фланцевого соединения на 4 высокопрочных болтах для квадратных и прямоугольных труб с центральным растяжением (и, местами, внецентренным растяжением) от 04.04.2015 по СП и Рекомендациям.
Ключевые слова: фланец, ферма, tyhig, болт, высокопрочные болты, фланцевое соединение, соединение на высокопрочных болтах, болтовое соединение, трубы, труб, ексель, MS Excel 2013.
Ничего не надо включать, ексель 2013 без макросов. Если включить макросы, то файл будет испорчен.
Ограничения расчёта: только 4 высокопрочных болта, только квадратные и прямоугольные трубы (хотя это влияет только на сварные швы), толщина фланца 20…40 мм (сделано для всех, но другие толщины незаконно экстраполированы), внецентренное растяжение учитывается только при расчёте болтов (и, видимо, толщины фланца), а прочие проверки (в том числе сварные швы) не годятся.
Версия от 04.04.2015 г.
Нормативные документы (указаны в файле): новый СП 2011 г. и «Рекомендации…» 1989 г.
Формат zip, так как сюда допускается загружать только djvu, pdf, zip.
Вирусов быть не должно. Можете проверить ещё сами.
0.05 МБ
СКАЧАТЬ
Может пригодиться в расчетах студентам и инженерам, сам я довольно часто использую некоторые из этих расчётов.

хоть бы намекнули в чем суть расчетов. а то качать и смотреть всем то не хочется 
Список вложенных файлов
___________________________
1. algebra.XLS Расчет квадратного уравнения несколькими способами
2. boltkruk.XLS Расчет прочности нагруженных болтовых соединений
3. circle.XLS Расчет параметров круга
4. dm1cepr.XLS Расчет цепной передачи по методике Чернавского
5. dm1cher.XLS Расчет червячного редуктора Чернавского
6. dm1klrem.XLS Расчет клиноременной передачи по методике Чернавского
7. dm1kon.XLS Расчет конического прямозубого редуктора по методике Чернавского
8. dm1kos.XLS Расчет цилиндрического косозубого редуктора по методике Чернавского
9. dm1plrem.XLS Расчет плоскоременной передачи по методике Чернавского
10. dm1podc.XLS Расчет подшипников цилиндрического редуктора по методике Чернавского
11. dm1porem.XLS Расчет поликлиновой передачи по методике Чернавского
12. dm1pr.XLS Расчет цилиндрического прямозубого редуктора по методике Чернавского
13. dm1privd.XLS Расчет КПД привода и мощности электродвигателя по методике Чернавского
14. dm1shpon.XLS Расчет прочности шпоночного соединения по методике Чернавского
15. dm1val1.XLS Предварительный расчет валов по методике Чернавского
16. dm2cher.XLS Расчет червячного редуктора по методике Дунаева
17. dm2kon.XLS Расчет конического прямозубого редуктора по методике Дунаева
18. dm2kos.XLS Расчет цилиндрического косозубого редуктора по методике Дунаева
19. dm2privd.XLS Расчет КПД и мощности электродвигателя по методике Дунаева
20. dm2shpon.XLS Расчет прочности шпоночного соединения по методике Дунаева
21. dm3podc.XLS Расчет подшипников цилиндрического редуктора по методике Шейнблита
22. dm3privd.XLS Расчет КПД и мощности электродвигателя по методике Шейнблита
23. dm4klrem.XLS Расчет клиноременной передачи по методике Эрдеди
24. dm4plrem.XLS Расчет плоскоременной передачи по методике Эрдеди
25. dm4shpon.XLS Расчет прочности шпоночного соединения по методике Эрдеди
26. dm5klrem.XLS Расчет клиноременной передачи по методике Иванова
27. dmmufta.XLS Расчет муфты
28. electro.XLS Электротехника — расчет сопротивления резистора
29. manyangl.XLS Геометрия — расчет многоугольников
30. mechanic.XLS Механика — расчет реакций опор
31. physic.XLS Физика — расчет движения тела, брошенного под углом к горизонту
32. piramida.XLS Геометрия — расчет пирамиды
33. plita.XLS Механика — расчет нагрузок кронштейновых и балочных конструкций
34. rezba.XLS Расчет резьбовых соединений
35. ring.XLS Геометрия — расчет кольца
36. romb.XLS Геометрия — расчет ромба
37. square.XLS Геометрия — расчет квадрата
38. svarka.XLS Расчет сварных соединений
39. vint4.XLS Расчет передачи винт-гайка
40. zaklepka.XLS Расчет клепаных соединений
___________________________________________________
Один файл
GPM.XLS Расчет узлов грузоподъемных машин по методике Казака
Не могу отправить из-за ограничений размеров файлов, если Администратор мне поможет это исправить, то и его выложу.
Или предложите куда его выложить, чтобы смогли скачать.
Цитата: VIO от 22.03.08, 10:32:09
…
Один файлGPM.XLS Расчет узлов грузоподъемных машин по методике Казака
Не могу отправить из-за ограничений размеров файлов, если Администратор мне поможет это исправить, то и его выложу.
Или предложите куда его выложить, чтобы смогли скачать.
Да хоть куда: _www.slil.ru например.
Пожалуйста, там он будет висеть 1 месяц
http://slil.ru/25613893
GPM.XLS Расчет узлов грузоподъемных машин по методике Казака
Расчёт для общего развития хороший 
Только жаль, что разбросан. Но это на мой вкус.
Не знаю что и предложить?
Может администратор, что предложит?
VIO
Спасибо за файлы!
Как я понял это из книги А.Дубина «Машиностроительные расчеты в среде Excel 97/2000»
Просто книга у меня есть, а дискету куда-то потерял.
Ещё раз спасибо!
Цитата: Игорьтек от 26.03.08, 14:15:41
VIO
Спасибо за файлы!
Как я понял это из книги А.Дубина «Машиностроительные расчеты в среде Excel 97/2000»
Просто книга у меня есть, а дискету куда-то потерял.
Ещё раз спасибо!
Правильно, купил думал освою VBA, но как-то времени не хватает.

Народ
Может кто обновит ссылку ?
Вы не могли бы залить все одним файлом
В том числе и самый большой ?
VIO!
Перезалейте, пожалуйста, GPM.XLS Расчет узлов грузоподъемных машин по методике Казака ( Расчет8.zip ), а то ссылки уже не работают.
- Форум пользователей ПО АСКОН
-
►
Профессиональные вопросы -
►
Конструирование -
►
Расчеты в Excel
Расчет болтового соединения за одну минуту!
Опубликовано 20 Апр 2013
Рубрика: Механика | 19 комментариев

…нагружено сдвигающей силой, то ее должна компенсировать сила трения между деталями, возникающая при затяжке. Если сдвигающая сила значительна и превосходит силу трения, то необходимо при проектировании узла применить штифты, шпонки, сухари или иные элементы, которые должны воспринять на себя сдвиг. Болт в «правильном» с точки зрения инженера-механика соединении никогда не должен работать на смятие и тем более на срез. У проектировщиков-строителей – это не аксиома, а «болт – на срез» — в порядке вещей и обыденность… Но да ладно – болт он и в Африке болт – хоть у механика, хоть у строителя!
Рассмотрим три схемы, изображенные на рисунке.
На левой схеме показано собранное болтовое соединение до затяжки Fo=0 и до приложения внешней нагрузки F=0.
На средней схеме изображено соединение после затяжки – Fo>0; F=0. Обратите внимание, что пакет из соединяемых деталей стал тоньше, он сжался, как пружина, а болт удлинился тоже как пружина и запасся потенциальной энергией.
Болтовое соединение, изображенное на правой схеме, показано после затяжки и приложения внешней силы (рабочее состояние соединения) — Fo>0; F>0. Болт еще больше удлинился, при этом пакет из деталей стал толще, чем на средней схеме, но тоньше, чем на левой. Если внешняя сила F будет нарастать и достигнет критического значения, то произойдет раскрытие стыка, при этом болт может еще не начать разрушаться.
Запускаем Excel – приступаем к расчету болтового соединения!
Итак, приступим непосредственно к расчетам. На рисунке, расположенном ниже, представлен общий вид листа Excel с программой для расчета болтового соединения.
В левой таблице в бирюзовых и светло-зеленых ячейках записываем исходные данные. В правой таблице в светло-желтых ячейках считываем промежуточные и окончательные результаты расчетов.
Общий список исходных данных содержит двадцать значений.
При наведении курсором мыши на ячейки для записи значений исходных параметров «всплывают» подсказки, разнообразные таблицы, рекомендации позволяющие облегчить определение этих значений. Вам не придется «рыскать» по справочникам или каким-то иным источникам информации. Вся необходимая информация для заполнения таблицы исходных данных – в примечаниях к ячейкам!
Одно важное замечание: при задании усилия в болте от предварительной затяжки в ячейке D23 необходимо контролировать значение в ячейке J29 — оно не должно превышать 80%!
Общий список результатов расчетов содержит двадцать семь значений.
При наведении курсором мыши на ячейки с результатами расчетов, в примечаниях увидите формулы, по которым и был выполнен расчет.
В примере, показанном на рисунках, произведен расчет болтового соединения двух стальных деталей (например, фланцев) толщиной по 80 мм каждая при помощи высокопрочного болта М24 х 200 ГОСТ22353-77 из стали 40Х «селект» с использованием шайб 24 ГОСТ22355-77.
В результатах расчета вы видите, что для того, что бы создать усилие в болте от предварительной затяжки 24400 кг (ячейка D23) необходимо на ключе создать момент 114,4 кг х м (ячейка J24)!
Болт разрушится без приложения внешней нагрузки, если создать усилие от предварительной затяжки 31289 кг (ячейка J27).
При создании усилия в болте от предварительной затяжки 28691 кг (ячейка J26) раскрытие стыка и разрушение болта произойдут одновременно при действии максимальной внешней нагрузки величиной 27138 кг (ячейка J30).
И последнее и самое главное — рассмотренное болтовое соединение способно воспринимать внешние нагрузки растягивающего характера до 27138 кг (ячейка J30) из условия нераскрытия стыка.
Ссылка на скачивание файла: raschet-stalnogo-boltovogo-soyedineniya-na-rastyazheniye (xls 1,43 МB).
P. S. (11.03.2017)
В дополнение к теме выкладываю глубоко переработанный и расширенный файл, присланный мне одним из читателей. Серые поля – формулы и константы, бесцветные – для заполнения. Прочие цвета – выделение по смыслу. Начинается с выбора материала. Размещаю ссылку на файл в том виде, в каком мне его любезно прислал Viktor Ganapoler (vganapoler@haprotec.de): Schraubenberechnung_VG-ru (xls 1,72MB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
- Фланцы: трубопроводные и аппаратные
- Сравнение трубопроводных и аппаратных фланцев
- Соединение фланцев
- Прочность и герметичность
- Нагрузки, учитываемые при расчете фланцевых соединений:
- Этапы расчета фланцевых соединений на прочность и герметичность
- Температура
- Приведенное давление
- Видео про штуцера, про фланцы, про люки
Тема материала – расчет фланцевого соединения. Видео про фланцы, штуцера и люки, про их типы и условия их применения в в конце статьи. Далее мы рассмотрим расчет: в чем заключается расчет, от каких нагрузок и для каких условий.
Содержание
- Устал крутить гайки? Переходи на БРС!
- Фланцы: трубопроводные и аппаратные
- Сравнение трубопроводных и аппаратных фланцев
- Соединение фланцев
- Прочность и герметичность
- Нагрузки, учитываемые при расчете фланцевых соединений:
- Этапы расчета фланцевых соединений на прочность и герметичность
- Температура
- Приведенное давление
- Видео про штуцера, про фланцы, про люки
Содержание +
Фланцы: трубопроводные и аппаратные
Вспомним типы основных фланцев и разделим их на две группы: трубопроводные и аппаратные фланцы.
|
СРАВНЕНИЕ DN 500 мм; PN 2,5 МПа |
Размерный ряд |
D gab |
Н габ |
Масса |
Размер и Кол-во крепежа |
|
трубопроводные ГОСТ 33259-2015 |
DN10-2000 (4000) |
730 |
104 |
89 |
М36, 20 шт |
|
аппаратные ГОСТ 28759.(1-5)-90 |
400 — 4000 |
640 |
80 |
45 |
М20, 28 шт |
Они стандартизованы по разным нормативным документам и имеют разный размерный ряд.
Трубопроводные фланцы могут иметь номинальный диаметр от 10 до 2000 мм, предложений на которые довольно много. Имеются также трубопроводные фланцы до 4000 мм, но их совсем мало, и они рассчитаны на очень ограниченный ряд давления.
Аппаратные фланцы могут быть стандартными – диаметром от 400 до 4000 мм. Причем, если трубопроводные фланцы стандартизованы по номинальному диаметру, то аппаратные фланцы – по внутреннему. Аппаратные фланцы применяются для соединения частей аппаратов: для соединения частей обечаек, либо аппарата с крышкой или с днищем на фланцевом соединении, либо, как у теплообменника, для соединения разных частей аппаратов распределительной камеры и кожуха.
Сравнение трубопроводных и аппаратных фланцев
Рассмотрим сравнение трубопроводных и аппаратных фланцев для номинального диаметра 500 мм и номинального давления 2,5 МПа. При сопоставлении можно отметить, что трубопроводные фланцы массивнее, габаритнее и тяжелее, чем аппаратные фланцы. Соответственно, есть различие по размеру и количеству крепежных элементов. С чем это связано? Зачем необходимы эти различия?
- Аппаратные фланцы работают преимущественно только от воздействия внутреннего давления. Нагрузки от осевых сил и изгибающих моментов у них минимальны, поэтому при одинаковых размерах они могут быть меньше и легче.
- Трубопроводные фланцы, предназначенные для соединения частей трубопроводов или трубопроводов с аппаратом на штуцере, могут также испытывать нагрузки от трубопроводов, ветрового воздействия на трубопроводы, веса трубопроводов, осевых и поперечных сил, изгибающих моментов. Соответственно, для обеспечения прочности фланца потребуются бо́льшие сечения.
Следует также напомнить, что на люках устанавливаются аппаратные, а не трубопроводные фланцы, поскольку люк соединяется не с трубопроводом, а с крышкой, то есть работает только на внутреннее давление, несмотря на то, что люк внешне очень похож на штуцер.
Это означает, что указанные размеры рассчитываются только от внутреннего давления. Соответственно, если на фланец оказывается какая-то внешняя нагрузка, и вы ее не учли при выборе фланца, то прочность и надежность фланца, а также ваша репутация как расчетчика могут серьезно пострадать.
То есть, если фланец имеет значительный диаметр, или даже если действует только давление, но диаметр больше чем 600 мм, или если есть остальные фланцы с учетом конкретных условий эксплуатации (т.е. внешних нагрузок), все они обязательно должны подтверждаться расчетом.
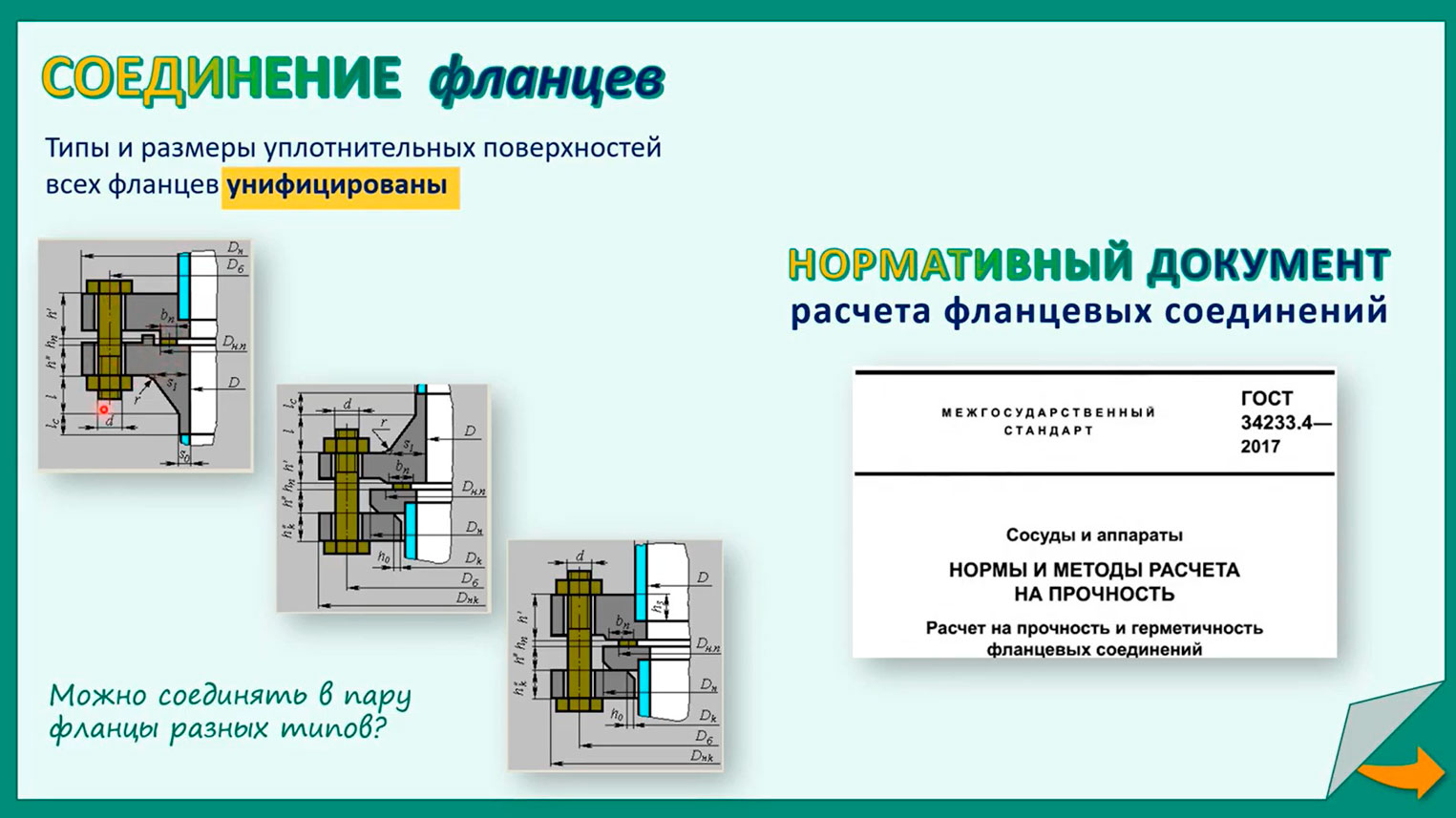
Соединение фланцев
Можно ли соединять в пару фланцы разных типов, как показано на этих рисунках , и почему возникла необходимость соединять разные типы фланцев?
Ответы на данный вопрос могут быть индивидуальны для каждой конкретной задачи. Зачастую на практике возникает необходимость соединения фланцев разных типов. Главное – методика расчета позволяет проводить расчет такого фланцевого соединения.
Соединение фланцев возможно, потому что типы и размеры всех уплотнительных поверхностей разных типов фланцев унифицированы. Соответственно, фланцы подойдут друг другу по размерам уплотнительных поверхностей и по количеству и размерам крепежных деталей, если они подобраны на одинаковый номинальный диаметр и на одинаковые давления.
Расчет фланцевых соединений производится по нормативному документу ГОСТ 34233.4-2017. Сосуды и аппараты. Нормы и методы расчета на прочность. Расчет на прочность и герметичность фланцевых соединений.
Прочность и герметичность
Прочность и герметичность – два основных требования к фланцевым соединениям, где под прочностью понимается способность выдерживать нагрузки без разрушения, под герметичностью – способность обеспечивать непроникновение рабочей среды. Поскольку фланцевые соединения – это разъемные соединения, обеспечить герметичность на стыке фланцев – очень важная задача, особенно в условиях пожаро-, взрывоопасных и токсичных рабочих сред.
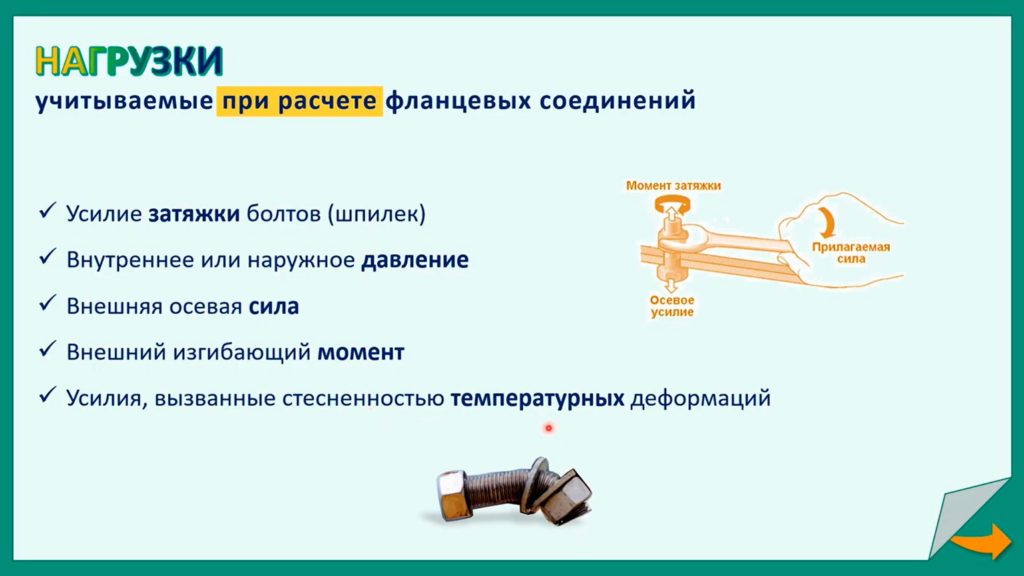
Нагрузки, учитываемые при расчете фланцевых соединений:
- Усилие затяжки болтов (шпилек),
- Внутреннее или наружное давление,
- Внешняя осевая сила,
- Внешний изгибающий момент,
- Усилия, вызванные стесненностью температурных деформаций.
Помимо затяжки болтов, внешнего и внутреннего давления, осевых сил и изгибающих моментов фланцевое соединение может испытывать усилия от стесненных температурных деформаций: если разные элементы фланцевых соединений имеют значительно различающиеся коэффициенты температурных удлинений, то элементы будут испытывать стесненность от температурной деформации. То есть, поскольку разные элементы стремятся удлиняться на разную величину деформации, но при этом они соединены, они не имеют возможность свободно удлиняться и испытывают стесненность.
Этапы расчета фланцевых соединений на прочность и герметичность
Расчет фланцевых соединений на прочность и герметичность состоит из 5 этапов:
- Расчет усилия на прокладку, необходимого для ее сжатия и обеспечения герметичности;
- Расчет усилия в болтах (шпильках) в рабочих условиях и при затяжке для обеспечения герметичности фланцевого соединения;
- Проверка прочности болтов (шпилек) и прокладки
- Расчет на прочность элементов фланцев при затяжке и в рабочих условиях;
- Проверка углов поворота фланцев. В описании этапов упоминаются термины «при затяжке» и «в рабочих условиях».
Для аппаратов мы использовали понятие «расчетных условий» (монтаж, рабочие условия, гидроиспытания), а для расчета фланцевых соединений – «затяжка» (затягивание крепежных элементов – болтов или шпилек). Это и есть условия монтажа, но в терминологии расчета фланцевых соединений используются термин «при затяжке»
Расчет фланцевых соединений на прочность и герметичность состоит из 5 этапов:
1-й пункт: расчет усилия на прокладку
На эскизе представлено фланцевое соединение, состоящее из двух приварных встык фланцев с зажатой между ними прокладкой, соединенных шпилькой.
Усилие, необходимое для смятия прокладки при затяжке:
Для расчета усилия на прокладке при затяжке первоначально требуется обжать (смять) прокладку с определенным усилием, а затем рассчитать давление обжатия. Давление обжатия определяется по формуле Pобж= 0,5πDсп b0 qобж , где 0,5πDсп b0 – площадь прокладки, а qобж – удельное давление обжатия прокладки. Удельное давление обжатия прокладки зависит от ее материала и конструкции. Удельное давление – это стандартизованная величина, таблицу которой можно найти как в приложении по расчету фланцевых соединений, так и в нормативном документе на сами прокладки.
Усилие на прокладке в рабочих условиях:
При обжатии прокладки возникает реакция, ответная сила. Реакция прокладки – это и есть усилие в рабочих условиях. Оно определяется по формуле Rп=πDспb0mp, где mp – удельное давление в рабочих условиях, которое и вызывает реакцию прокладки. Коэффициент m здесь означает не массу, а прокладочный коэффициент, который тоже зависит от материала прокладки.
Dсп – серединный диаметр прокладки
b0 – эффективная ширина прокладки
m – прокладочный коэффициент
qобж – удельное давление обжатия прокладки
2-й пункт: расчет усилия в болтах (шпильках)
Расчетная нагрузка на болты (шпильки) при затяжке:
Сила на болты при монтаже определяется как большее из трех компонентов по формуле Pбм=max{αQд+Rп; Pобж; 0,4Aб[σ]0б}, где αQд+Rп – нагрузка от внутреннего давления;
Qд=0,785D2сп p – равнодействующая нагрузка от давления, которая определяется по серединному диаметру прокладки и внутреннему давлению;
Pобж – давление обжатия прокладки при монтаже;
0,4Aб[σ]0б – условие прочности болтов (где 0,4Aб – площадь сечения болтов, а [σ]0б – допускаемая нагрузка на болты); α – коэффициент жесткости фланцевого соединения.
Расчетная нагрузка на болты (шпильки) при рабочих условиях:
Расчетная нагрузка на болты (шпильки) при рабочих условиях рассчитывается по формуле
Pбp=Pбм+(1-α) Qд. Нагрузка на болты Pбp по сравнению с нагрузкой при монтаже Pбм при затяжке увеличивается также на равнодействующую от давления (1-α) Qд. Данные формулы упрощены и указаны без учета внешних сил и моментов, а также стесненности температурных деформаций. Полный вариант этих формул можно найти в нормативном документе по расчету фланцевых соединений.
3-й пункт: проверка прочности болтов (шпилек) и прокладки
Условие прочности болтов (шпилек) при затяжке и при рабочих условиях:
Прочность болтов определяется очень просто по формуле Pбм/Aб ≤[σ]мб, где усилие в болтах Pбм соотносится с суммарной площадью сечения болтов Aб и сопоставляется с допускаемым напряжением для материала болтов в условиях монтажа [σ]мби в рабочих условиях [σ]рб.
Условие прочности прокладок:
Для определения условия прочности рассчитывается расчетное давление на прокладку и затем сопоставляется с удельным допускаемым давлением на прокладку: q=max{Pбм;Pбр}/πDспbп≤[q].
Все характеристики основных типов прокладок, в том числе допускаемое удельное давление на прокладку, которое также зависит от ее конструкции и материала, есть в ГОСТ 34233.4-2017 в «приложении И», а также указаны в нормативных документах в специальных таблицах.
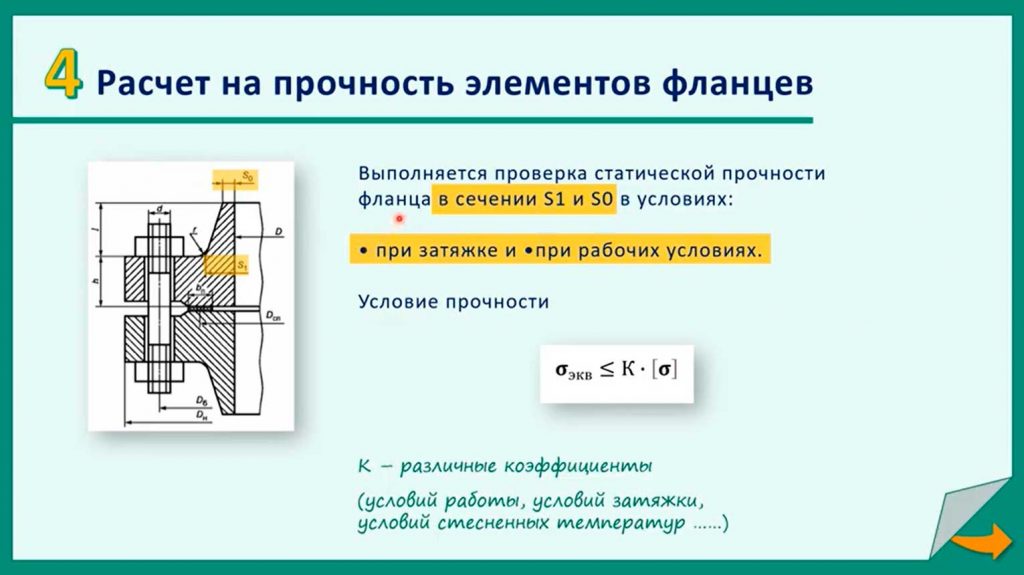
4-й пункт: расчет на прочность элементов фланцев
Прочность элементов фланцев проверяется в двух сечениях – S1 и S0. Сечение S1 – это сечение соединения кольца фланца с втулкой, то есть там, где идет переход от цилиндрической части к фланцевому кольцу. Сечение S0 – это минимальное сечение (толщина) втулки фланца. В каждом из этих сечений определяются три типа напряжения – меридиональное, тангенциальное, радиальное. Из этих значений трех типов напряжений определяется эквивалентное напряжение в указанном сечение σэкв и сопоставляется с допускаемым напряжением [σ], которое может быть увеличено на различные сочетания коэффициентов: σэкв≤K∙[σ].
Для упрощения восприятия теории здесь представлен только один коэффициент, но на самом деле их несколько, и они перемножаются. Это могут быть коэффициент условий работы, условий затяжки, условий стесненности температурных деформаций и т.д.
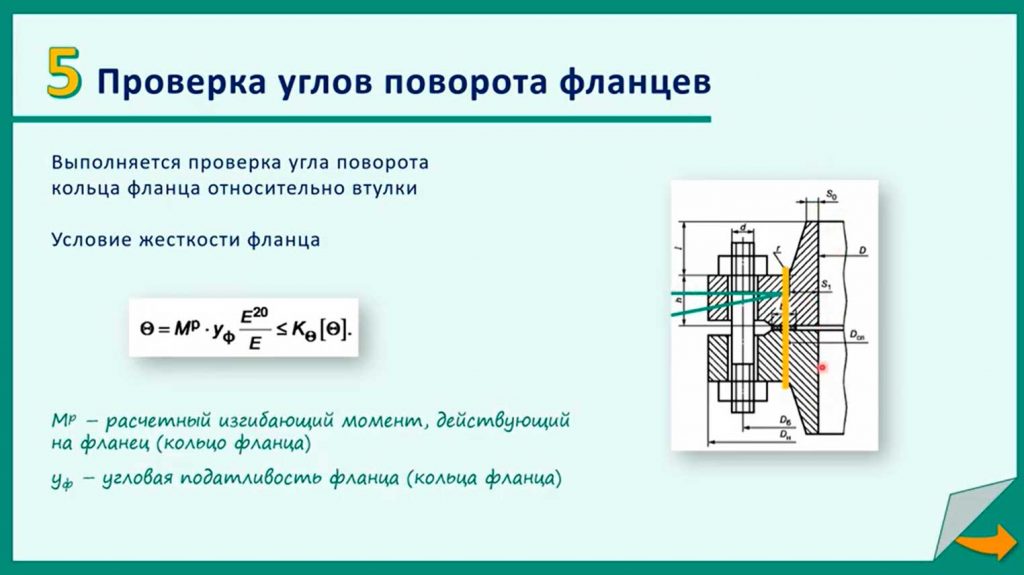
5-й пункт: проверка углов поворота фланцев
При затяжке крепежных элементов (шпилек или болтов) фланцевые кольца стягиваются между собой или отклоняются друг к другу. На рисунке увеличенными голубыми линиями показан условно возможный угол поворота фланцевого кольца, которое не поворачивается вокруг трубы (вокруг трубы могут поворачиваться свободные фланцы), а отгибается относительно втулки. Оранжевой линией показано расчетное сечение, в котором проверяется жесткость фланца.
Условие жесткости фланца θ определяется как расчетный угол поворота Mр∙yф E20/Eв сопоставлении с допускаемым углом поворота Kθ [θ], где учитывается расчетный изгибающий момент, который действует на кольцо фланца Mр и угловая податливость фланца yф: θ= Mр∙yф E20/E≤ Kθ [θ].
Расчетный изгибающий момент возникает, в том числе, от усилия затяжки крепежных элементов. При возникновении поворота нарушаются жесткость фланца, герметичность и условия смятия прокладки и смыкания уплотнительной поверхности. Угловая податливость фланца и жесткость – взаимообратные величины.
Температура
Расчетная температура фланцевых соединений должна определяться теплотехническим расчетом и подтверждаться экспериментально либо на эксплуатации. Но если нет точных данных о температуре элемента фланцевых соединений, допускается определять расчет температуры по нижеприведенной таблице, где t – это расчетная температура в самом аппарате.
|
Тип фланцевого соединения |
Изолированные фланцы |
Неизолированные фланцы |
||||
| т ф | t x | т б | т ф | t x | т б | |
|
Плоские, приварные встык |
т |
— |
0,97т |
0,96т |
— |
0,95т |
|
Со свободными кольцами |
т |
0,97т |
0,90т |
0,96т |
0,90т |
0,81 т |
Из таблицы видно, что расчетная температура неизолированных фланцев, болтов или кольца фланца меньше, чем расчетная температура корпуса аппарата. Если фланец изолирован, то расчетная температура фланца равна расчетной температуре корпуса, а температура свободного кольца или болтов остается чуть меньшей, чем температура корпуса.
Приведенное давление
Возможно сочетание внешних нагрузок: это могут быть осевые и поперечные нагрузки, изгибающие и крутящие моменты на фланец. Сочетание и величина этих нагрузок всегда индивидуальны и не могут быть унифицированы. В каждом конкретном случае нужно четко понимать и очень точно определять эти внешние нагрузки. Конечно, их желательно минимизировать и обеспечивать все трубопроводы и элементы необходимым количеством опор, чтобы как можно меньше внешних нагрузок воздействовало на фланцевое соединение.
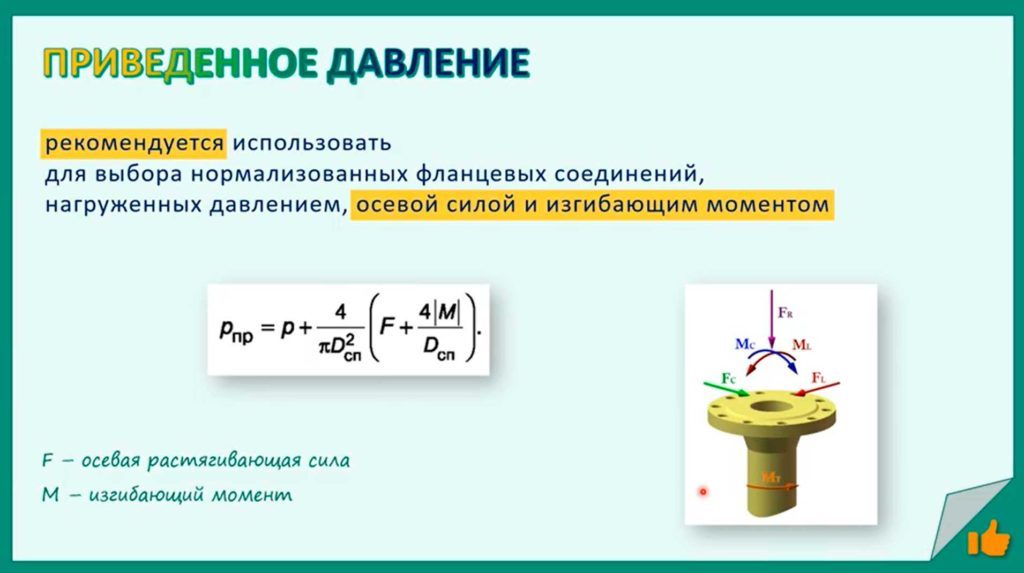
Если эти нагрузки определены, то есть если известны осевая растягивающая сила F и изгибающий момент M, возможен подбор стандартизованного фланцевого соединения по нормативному документу, в котором приведены размеры фланцев, но только от приведенного давления. Приведенное давление – это некая условная величина, которая учитывает внутреннее давление и внешние нагрузки. То есть внешние нагрузки расчетным методом приводятся к параметру давления, увеличивают внутреннее давление на некоторую величину, что позволяет подобрать фланцевые соединения по параметру давления и по размерам стандарта с использованием большего значения: pпр=p+4/(πDсп2 ) (F+4|M|/Dсп ).
Указанная формула и методика не обязательны, но рекомендуются при выборе нормализованных фланцевых соединений, нагруженных не только давлением, но осевой силой и изгибающим моментом.
Спасибо за внимание!
Видео про штуцера, про фланцы, про люки


Читать далее
Добавлено в список желанийУдалено из списка желаний 0

Добавлено в список желанийУдалено из списка желаний 0

Добавлено в список желанийУдалено из списка желаний 0

Добавлено в список желанийУдалено из списка желаний 0

Введение
В настоящее время наиболее универсальными и удобными при монтаже стальных строительных конструкций являются болтовые соединения. Их применение позволяет получить исключительно высокую точность установки и исключить «человеческий фактор». Из болтовых соединений наиболее эффективными являются фланцевые соединения. Их использование в различных конструкциях существенно повышает производительность труда при монтаже и соответственно его скорость. Также фланцевые соединения крайне удобны при ремонте строительных конструкций, они позволяют быстро вычленить один элемент и заменить его другим.
До настоящего времени достаточно большое число ученых изучало фланцевые соединения и особенности их применения. Среди них можно отметить работу В.В. Каленова, В.М. Горпинченко, А.Г. Соскина, О.И. Ганиза, Глауберман В. Б. и др..
В основном вышеперечисленными учеными проводились работ по изучению прочностных характеристик фланцевых соединений. В результате исследований были разработаны рекомендации по расчету, проектированию, изготовлению и монтажу фланцевых соединений стальных строительных конструкций [1] и глава 27 пособия по проектированию стальных конструкций (к СНиП II-23-81*). Пособие и рекомендации не распространяются на фланцевые соединения:
-воспринимающие знакопеременные нагрузки, а также многократно действующие подвижные, вибрационные или другого вида нагрузки с числом циклов свыше 105 при коэффициенте асимметрии напряжений в соединяемых элементах r = (smin/smax)³ * 0,8;
-эксплуатируемые в сильноагрессивной среде. К этим соединениям можно отнести фланцевые соединения подкрановых балок. Подкрановые балки можно отнести к элементам открытого профиля.
Глава 1. Прочность фланцевых соединений элементов открытого профиля
Вопрос прочность фланцевых соединений элементов открытого профиля изучался профессором Грудевым И. Д. [2].
Им была разработана полуэмпирическая методика рачета на прочность фланцевых соединений элементов отрытого профиля: двутавров, тавров, уголков. Четко сформулированы допущения, которые легли в основу решаемой задачи. Составлена замкнутая система уравнений, включающая несколько подгоночных параметров. Решение получено численно, а подгоночные параметры определены по данным эксперимента. Для удобства пользования методикой предложена аппроксимационная формула.
Определение прочности и долговечности фланцевых соединений элементов открытого профиля: двутавров, тавров и уголков, яаляется основным неразработанным вопросом. В данных соединениях деформации различных болтов существенно неодинаковы, т.к. фланец деформируется сложным образом и кроме того прочность самих болтов имеет статистический разброс и определяется функцией плотности вероятности разрушения.
В основу исследования положены следующие положения:
- Все болты имеют одинаковое предварительное натяжение.
- Болты в составе соединения работают неравномерно, и по характеру своей работы разделяются на две группы: болты внутренней зоны, расположенные в углах сечения и более нагруженные, отмеченные ниже индексом В, и болты наружной зоны с индексом Н.
- Наружная зона разбивается на элементарные Т-образные соединения.
- Последние описываются балочной моделью с учетом только геометрической нелинейности.
- Соотношение между усилиями в болтах внутренней и наружной зон описывается кусочно-линейной функцией, полученной путем аппроксимации экспериментальных данных.
- Если разрушение происходит по болтам, оно имеет вероятностную природу и определяется несущей способностью совокупности болтов внутренней зоны.
- Изгиб болта, наличие отверстий под болты, неравномерность предварительного натяжения, наличие внешних изгибающих моментов, приводит к необходимости введения подгоночных параметров.
Усилия, возникающие во фланцевом соединении в соответствии с балочной моделью описываются следующими соотношениями:
k – жесткость болта на растяжение с учетом контактных перемещений, — значение предварительного натяжения. Остальные обозначения приведены на рис. 1.
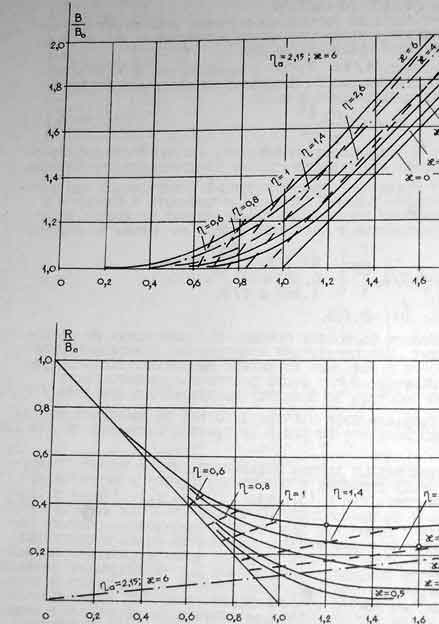
Безразмерные величины в зависимости от
и параметра
показаны на рис.2. Безразмерная жесткость болта может быть также представлена в виде
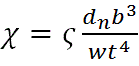
Причем параметр целесообразно оставить в качестве подгоночного, т.к. определить его теоретически не представляется возможным.
Рис. 1
Отношение между усилиями в болтах наружной и внутренней зон зависит от безразмерного усилия , приложенного к фланцу и в пределах существующих конструкций слабо зависит от других параметров. Оно определяется по данным эксперимента.
Разрушение по болтам фланцевых соединений, работающих на растяжение, происходит, как показывает эксперимент, практически мгновенно, что говорит о лавинном характере разрушения болтов, причем лавина начинается обычно после разрушения первого болта, т.е. соединение работает по принципу наислабейшего элемента.
Рис.2
Анализ экспериментальных данных показывает, что к моменту разрушения разница между усилиями в болтах внутренней и наружной зон составляет в соответствии с [3] около 20-30%, т.к. усилия в болтах наружной зоны не превосходят 37т. При этом они не могут дать заметного вклада в суммарную вероятность разрушения, поэтому последняя определяется исключительно прочностью более нагруженных болтов внутренней зоны, а болты наружной зоны разрываются на заключительной стадии лавинного разрушения. Для двутаврового сечения, а также для таврового с ребром, к внутренней зоне относятся четыре болта.
Глава 2. Напряженно-деформированное состояние фланцевых соединений
Инженером Соскиным А. Г. [4] было проведено исследование напряженно-деформированного состояния фланцевых соединений элементов открытого профиля, воспринимающих статические растягивающие усилия с целью получения зависимости между толщиной фланцев и соотношением усилий, воспринимаемых болтами внутренней и наружной зон от действия внешней нагрузки.
Фланцевые соединения на высокопрочных болтах являются наиболее эффективными по сравнению с другими типами монтажных соединений элементов стальных строительных конструкций. Эффект достигается, главным образом, за счет практически полного использования несущей способности болтов на растяжение, что обеспечивает их минимальное количество в соединениях и, как следствие, существенно понижает затраты труда на монтаже конструкций. В этой связи, расчет болтов, основанный на допущениях, отражающих их действительное поведение, приобретает особое значение.
С точки зрения поведения болтов среди конструктивных форм фланцевых соединений растянутых элементов следует различать такие, в которых болты находятся в одинаковых условиях («элементарные» Т-образные соединения, ФС круглых и квадратных труб) и соединения, в которых условия работы болтов не одинаковы (фланцевые соединения элементов открытого профиля: парных и непарных уголков, тавров, двутавров и т.п.). Исследования показали, что поведение последних весьма сложно, характеризуется геометрической и физической нелинейностью.
С целью изучения закономерностей напряженно-деформированного состояния таких соединений были проведены испытания опытных образцов натурных фланцевых соединений (табл. 1):
— типовых стропильных ферм пролетом 24 метра с нижним поясом из парных равнополочных уголков 110х12, 125х8 и 140х12мм;
— широкополочные тавры 15Шт4;
Материал уголков, тавров, фаооиок, ребер жесткости и фланцев — стали с расчетным сопротивлением разрыву по пределу текучести от 225 до 400 МПа. Фланцы опытных образцов толщиной 20, 25 и 30 мм приваривали к соединяемым элементам без разделки кромок, вручную электродами типа Э50А по ГОСТ 9467-75. Болты высокопрочные М24 из стали 40Х «Селект» с нормативным сопротивлением разрыву 1100 МПа Опытные образцы испытывали на специальном стенде, позволяющим развивать растягивающие усилия в соединяемых элементах до 4000 кн. Измерение относительных деформаций проводили тензометрированием с использованием датчиков с базой 5, 10 и 20 мм. Все образцы доводили до разрушения, характер которого фиксировали.
Анализ экспериментальных данных показал, что распределение нормальных напряжений в сечениях соединяемых элементов, расположенных в непосредственной близости от фланцев, носит практически равномерный характер. Вместе с тем, усилия в болтах и изгибные напряжения на характерных участках фланцев испытанных соединений развиваются неравномерно.
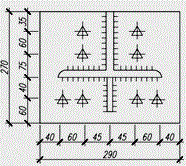
На рис. 3 представлена усредненная диаграмма усилий в болтах образца Т-4, типичная для опытных ФС с числом болтов 6 и более. Из диаграммы следует, что гораздо более интенсивный прирост усилий происходит в болтах №№ 1,2,3,4, расположенных на участках фланцев внутренней зоны – ВЗ (см. схему соединения — заштрихованная область) . Внешняя нагрузка раскрытия внутренней зоны фланцев ТР в = 1236 кН, наружной зоны (НЗ) — ТРН= 1688 кН. Соответствующий прирост усилий в болтах ВЗ относительно усилия предварительного натяжения Вов= 216 кН составил ?Вв = 29 кН. В момент разрушения соединения при Траз= 1962 кН усилия в болтахВЗ Враз = 392 кН. Ддя болтов НЗ эти значения равны: В0 = 216 кН, ?Вн = 15 кН, Враз= 260 кН. Полученные экспериментально усилия в болтах, соответствующие им значения внешней нагрузки и данные о характере разрушения опытных ФС приведены в табл. 2, Из таблицы следует, что выявленная закономерность развития усилий в болтах Т-4 прослеживается и в других опытных соединениях.
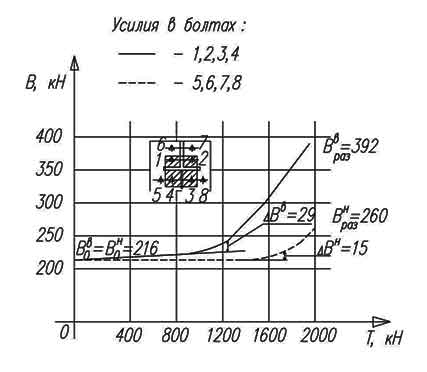
Раскрытие фланцев ВЗ наступает раньше НЗ ( ТР в < ТРН ), а усилия в болтах ВЗ — Вв (после раскрытия фланцев) всегда больше Вн. Причина этого заключается в различной жесткости внутренней и наружной зоны фланцев. Анализ напряженно-деформированного состояния показал, что изгибные напряжения во ВЗ фланцев развиваются заметно слабее, чем в НЗ, более жесткая на изгиб внутренняя зона фланцев передает на болты большую часть внешней нагрузки — Тв по сравнению с наружной, передающей на болты нагрузку Тн (Т = Тв + Тн). Но этой же причине рычажные усилия — R, действующие на болты ВЗ и НЗ также неодинаковы.
Отметим, что экспериментальные значения напряжений в опасных сечениях фланцев при толщине t ? 20мм и достижении в болтах расчетных усилий — Вр, не превышали значений расчетных сопротивлений стали фланцев изгибу по пределу текучести.
Таблица 1. Геометрические параметры опытных соединений
|
Обозначение соединения |
Схема соединения |
Сечение (марка) профиля ммхмм |
Толщи- на флан- ца мм |
Катет сварно-го шва мм |
Толщина фасон-ки (ребра) мм |
|
У-1 У-2 |
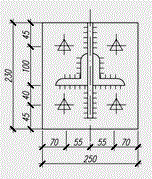 |
110х12 |
20 |
10 |
8 |
|
У-4 |
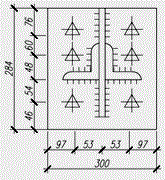 |
125х8 |
25 |
12 |
10 |
|
У-5 |
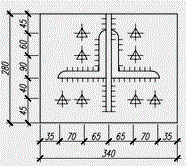 |
140х12 |
25 |
14 |
16 |
|
Т-1 |
 |
15Шт4 |
20 |
10 |
10 |
|
Т-2 |
25 |
||||
|
Т-3 |
30 |
Глава 3. Усталостная прочность фланцевых соединений растянутых элементов
Исследованиями усталостной прочности фланцевых соединений растянутых элементов конструкций занимались Каленов В. В., Соскин А. Г. и Евдокимов В. В. [5]. Ими были представлены результаты экспериментальных исследований циклической долговечности монтажных фланцевых соединений элементов конструкций, воспринимающих циклически изменяющиеся, растягивающие нагрузки. Получены расчетные кривые усталости высокопрочных болтов и сварных соединений фланцев с профилем. Показано, что циклическую долговечность соединений следует определять по амплитуде номинальных напряжений. При этом, в качестве расчетного должно быть принято наименьшее значение долговечности, полученное для болтов, или сварных соединений с различными типами исполнения и дефектами швов.
В период эксплуатации фланцевые соединения воспринимают как статические, так и циклические воздействия.
В одной из первых работ, посвященных исследованию характеристик сопротивления усталости ФС, приведены результаты испытаний 12 двухбайтовых Т-образных соединений. Получены кривые усталости болтов А325 и А490, установленных с усилием предварительного натяжения То — (0,7 + 0,8) Tu., где Тu — разрушающее усилие болтов при растяжении. Сделан вывод о том, что высокая долговечность болтов может быть обеспечена высоким уровнем То, что при прочих равных условиях ведет к значительному уменьшению амплитуды переменных напряжений в болтах. Также приведены исследования усталостной долговечности высокопрочных болтов М22 типа F9T и FIIT, работающих в составе ФС. Опытные соединения испытывали сериями из 6+13 образцов с одинаковыми геометрическими характеристиками. Показано, что долговечность болтовой группы в значительной степени зависит от величины предварительного натяжения болтов. Следует отметить, что испытанные болты по механическим свойствам и химическому составу существенно отличаются от отечественных.
Для этих и других исследований характерно, что циклическую долговечность ФС в целом определяют, главным образом, сопротивлением усталости болтов. Вместе с тем, очевидно, что не менее опасным с точки зрения усталостного разрушения ФС являются сварные соединения фланцев с профилем.
В этой связи авторами исследования был выполнен комплекс исследований, целью которых являлось изучение закономерностей сопротивления усталости ФС элементов конструкций, воспринимающих циклические растягивающие нагрузки и разработка инженерной методики расчета ФС на усталость. Исследования предусматривали с одной стороны – построение расчетной кривой усталости для болтов, учтановленных с высоким уровнем предварительного натяжения В0 = 0,9Вр, с другой – построение построение расчетных кривых усталости для сварных соединений ФС с различными типами исполнения (бездефектными и с дефектами) швов, выполненных в соответствии с ГОСТ 5264-69, ГОСТ 14771-76, ГОСТ 8713-70 и СНиП 3.03.01-87 (с разделкой и без разделки кромок, с подрезом, с механической обработкой и т.д.).
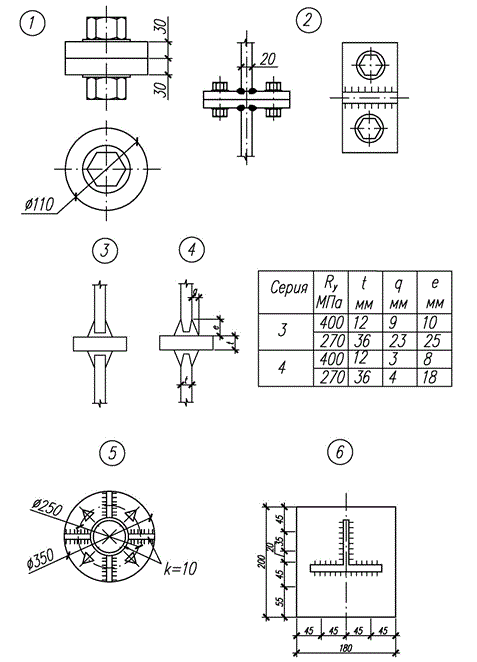
На рис. 4 показаны подготовленные для испытания на усталость модели и натурные образцы опытных ФС (всего 6 серий). 1 серия – 12 одноболтовых ФС, вторая – 13 Т-образных двухболтовых ФС. Сварное соединение стенки с фланцем выполняли вручную, с разделкой кромок (угол фаски — 50°, притупление – 2мм) электродами марки УОНИ – 13/55 по ГОСТ 9467-75, третья серия – 7 образцов тавровых сварных соединений без разделки кромок, четвертая – то же с разделкой кромок. Пятая серия – 4 соединения крулых труб 168х8 мм, усиленных ребрами жесткости толщиной 10 мм . Фланцы толщиной 22 и 25 мм. Шестая серия – 6 ФС широкополочных тавров 150х96х13х10 мм с фланцами толщиной 25 мм. Материал фланцев и соединяемых элементов опытных образцов – стали с расчетным сопротивлением растяжению, сжатию, изгибу по пределу текучести от 225 до 400 МПа (09Г2С, 10Г2С1, 16Г2АФ) по ГОСТ 19282-73,
Рис.4. Схемы моделей и опытных образцов ФС.
ГОСТ 19281-73. Болты высокопрочные М24 из стали 40Х «Селект» с временным сопротивлению разрыву не менее 1100 МПа Сварка ручная. Расчетное сопротивление угловых сварных швов срезу по металлу шва 215 МПа. Измерение относительных деформаций (напряжений) в болтах при количестве циклов нагружения N=1,5,1000,10000 осуществляли тензометрированием.
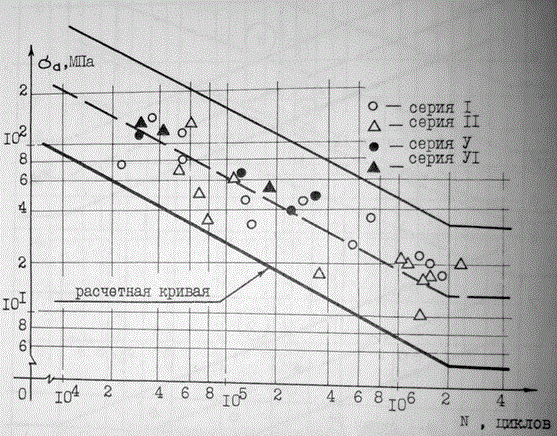
На рис. 5 представлена зависимость между амплитудой номинальных упругих напряжений в болтах различных серий опытных соединений и их циклической долговечностью N. Для аналитического выражения расчетной кривой усталости по параметру среднего напряжения цикла
= 727 МПа использовано уравнение Веллера
. Полученное методами математической статистики уравнение нижней огибающей трехстандартного диапозона долговечности болтов ФС имеет вид
(1)
Средне-квадратическое отклонение по lg N равно 0, 256; коэффициент корреляции — 0,91. Как следует из графика, усталостное разрушение болтов, предварительно напряженных на усилие В0 = (0,8+1,0) Вр, происходит в области малоцикловой и ограниченней усталости в диапазоне от 104 до циклов нагружения. При этом, максимальные внешние нагрузки вызывают усилия в болтах приблизительно равные Вр.
Рис.5. Циклическая долговечность и кривые усталости высокопрочных болтов опытных соединений.
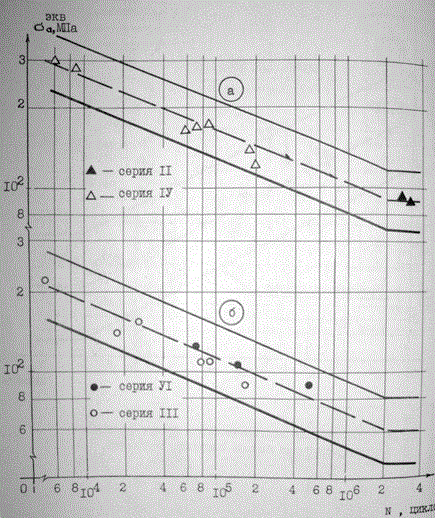
На рис.6 показаны экспериментальные точки, отражающие зависимость циклической долговечности сварных соединений опытных образцов различных серий с разделкой и без разделки кромок от эквивалентной амплитуды номинальных напряжений – в соединяемых элементах. Для определения
использована зависимость С. В Серенсена
(2)
, где — среднее напряжение цикла в соединяемых элементах;
— коэффициент чувствительности материала к асимметрии цикла нагружения. Для низколегированных сталей принят равным 0,25.
Рис.6. Циклическая долговечность и кривые усталости сварных соединений фланцев с профилем опытных образцов различных серий;
а — соединения с разделкой кромок, б – без разделки.
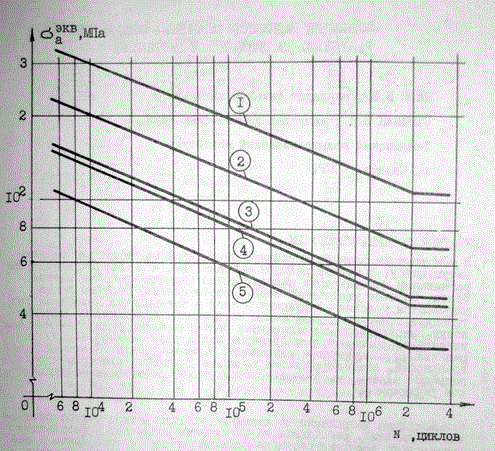
На этом же графике пунктирными линиями обозначены экспериментальные кривые усталости, а сплошными линиями – границы трехстандартного диапазона рассеивания возможных значений долговечности сварных соединений ФС. Нижние огибающие диапазонов приняты за расчетные кривые усталости (рис.7, кривые 2,4). Аналогичным образом на основе экспериментальных исследований получены расчетные кривые усталости №№1,3,5, математическое выражение которых имеет вид
На основе результатов исследований разработана инженерная методика расчета на усталость ФС элементов конструкций, воспринимающих циклические растягивающие нагрузки. Циклическую долговечность соединений исследуемых конструктивных форм следует определять как наименьшую из расчетных значений по болтам и сварным соединениям фланцев с профилем. Расчет рекомендуется проводить по амплитуде номинальных напряжений цикла с использованием представленных выше расчетных кривых усталости и уравнений (1)-(7).
Рис.7. Расчетные кривые усталости
сварных соединений фланцев с профилем;
1- с разделкой кромок и последующей
механической обработкой сварного шва;
2 — с разделкой и без обработки;
3 – то же с подрезом шва;
4 – без разделки кромок с необработанным швом.
5 – то же с подрезом шва.
Доктором технический наук В. В. Бирюлевым был рассмотрен вопрос конструирования и расчета балок с фланцевыми стыками [6].
Монтажные стыки как в обычных, так и в облегченных балках имеют три конструктивных решения — сварные (без накладок и с накладками), сдвигоустойчивые (с накладками на сдвигоустойчивых высокопрочных болтах), фланцевые (на высокопрочных болтах).
Сварные стыки без накладок наименее металлоемки, но требуют значительных затрат труда высококвалифицированных сварщиков. Кроме того, при сварке стыков в холодное время года необходимо проводить дополнительные мероприятия для обеспечения качества и надежности соединений.
Сдвигоустойчивые соединения менее трудоемки в изготовлении, не требуют высокой квалификации монтажников, проще выполняются при низких температурах, более надежны в работе при динамических и циклических нагрузках, так как не создают концентраций напряжений и остаточных температурных напряжений, как сварные швы.
Фланцевые соединения, в свою очередь, имеют ряд преимуществ по сравнению со сдвигоустойчивыми. Во фланцевых стыках уменьшается расход металла на соединение, в 3 … 3,5 раза снижается количество болтов (в сдвигоустойчивых соединениях болты ставятся с двух сторон и нагружены одинаково в сжатой и растянутой зонах, несущая способность на сдвиг меньше несущей способности на растяжение. Количество болтов в сжатой зоне во фланцевых соединениях может быть уменьшено, поскольку нормальных усилий они не передают, а только обеспечивают передачу поперечных сил за счет трения поверхностей фланцев. Основное количество болтов сосредоточено в зоне растянутого пояса, причем болты работают с большей отдачей, чем при сдвиге. Отсюда следует, что трудоемкость монтажа фланцевых соединений снижается в 3,5 … 4 раза. Кроме того, уменьшается трудоемкость изготовления балок, главным образом за счет резкого сокращения числа отверстий в стенке и поясах.
Болты во фланцевых стыках устанавливаются на одинаковом расстоянии или концентрируются в растянутой зоне у пояса. Толщина и ширина фланца в этом месте иногда увеличиваются, причем часть фланца в растянутой зоне выполняется из более прочной стали, а в сжатой малонагруженной растянутой зонах — из малоуглеродистой стали. При мощных поясах количество болтов с каждой стороны стенки в ряду доводится до 3 … 4 штук.
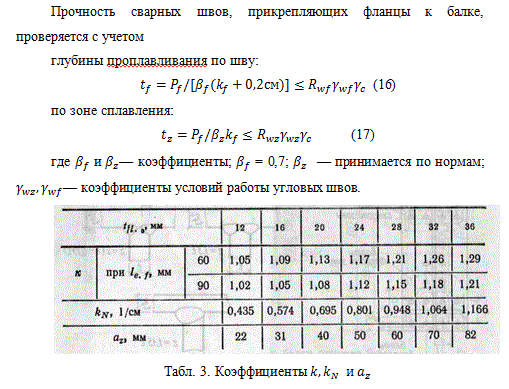
При расчете фланцевого соединения должна быть проверена прочность в четырех зонах — в высокопрочных болтах, во фланцах, в сварных швах, прикрепляющих фланцы, в основном сечении балок у сварных швов. Во фланцах проверяется прочность при их изгибе, а также при возможном поверхностном отрыве в околошовной зоне.
Весьма приближенный расчет фланцевого соединения в балках ведется из предположения, что усилия в болтах распределяются пропорционально расстоянию от точки приложения равнодействующей силы в сжатой зоне, например от центра сжатого пояса до болта. Тогда усилие в наиболее напряженном крайнем болте будет
где — расстояние до i-ro ряда и до крайнего ряда болтов;
— количество болтов в i-м и крайнем ряду; m — число рядов.
Такое распределение усилий может быть только при очень толстых фланцах.
Действительная работа фланцев сложна. Если во фланце вырезать полоску, то ее можно представить как своеобразную балку, находящуюся под действием системы сил Pf, Nb, V. Сила Pf передается от балки (стенки или пояса) на фланец, Nb — это сила, которая возникает в болте после приложения внешней нагрузки. Силу V обычно называют рычажной. Это — равнодействующая, возникающая от совместного прижатия двух фланцев друг к другу; положение равнодействующей зависит от ряда факторов, в первую очередь от толщины фланцев.
Если представить себе, что фланец не деформируется, то под нагрузкой возникает изгибающий момент (у стенки или полки), равный Nbc. Наличие рычажной силы уменьшает величину этого момента, следовательно, требуемую толщину фланца. Влияние рычажной силы учитывается при расчете фланцевых соединений.
Имеется предложение использовать резервы несущей способности фланцевого соединения, если допустить развитие пластических деформаций в сечении балки и во фланцах и применить для их оценки метод предельного равновесия.
Определяемая толщина фланца в этом случае будет минимальной. К тому же развитие пластических деформаций во фланцах вызовет повышение прогиба балки, как свидетельствуют эксперименты, на 5… 15%. Поэтому до накопления дополнительных экспериментальных данных такой метод можно использовать для расчета фланцевых соединений лишь в малоответственных конструкциях.
Предполагается, что с деформируемой поверхности фланца на сечение балки, примыкающей к нему, передаются реактивные усилия, ограниченные в сжатой зоне сопротивлением металла балки Ru, а в растянутой зоне предельным усилием, необходимым для образования пластического механизма в расчетной полоске фланца. Принято, что полоска жестко защемлена по линии размещения болтов и эти полоски у стенки и полки балки работают независимо.
До начала расчета устанавливаются: размеры фланцев с учетом габаритов балок, диаметр высокопрочных болтов, минимальное количество болтов, необходимое для восприятия растягивающего усилия пояса двутавра. Болты размещаются на минимально возможных расстояниях от полок и стенок.
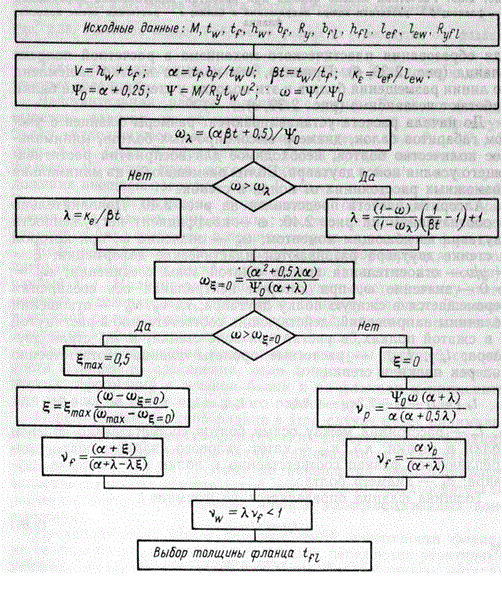
Алгоритм расчета представлен на рис. 8. Дополнительно к обозначениям на рис.8 : — коэффициент нагруженности двутавра изгибающим моментом;
— значение
, при котором в стенке двутавра развиваются пластические деформации;
— относительная высота сжатой зоны соединения;
— значение , при котором нейтральная ось соединения перемещается в сжатую полку двутавра;
— отношения величины напряжений, действующих соответственно в растянутой и в сжатой полках, в растянутой зоне стенки, к Ry стали двутавра;
расчетные пролеты фланца соответственно поперек полки и стенки:
— расстояния между осями болтов соответственно поперек полки и стенки; — катет углового сварного шва, прикрепляющего фланец соответственно к полке или к стенке двутавра;
— диаметр болта.
Толщина фланца определяется по формуле
коэффициент k принимается по табл. 2.8. В этой же таблице указано минимальное расстояние от оси болтов до края фланца , при котором обеспечивается рычажный эффект.
Найденная по (9) толщина фланца будет минимальная. Если же вести расчет по упругой стадии работы фланца, то, естественно, толщину его потребуется увеличить. При передаче фланцевым соединением, кроме изгибающего момента, еще и поперечной силы следует выполнить дополнительные расчеты.
Рис. 8 Блок-схема расчета фланцевого соединения на изгиб с учетом различия деформаций.
Необходимое минимальное количество болтов в зоне растянутой полки:
Заключение
Подводя итоги, можно заметить, что в области исследования фланцевых соединений скрывается еще много вопросов и одним из них является вопрос о динамической выносливости фланцевых соединений при разнозначных видах нагружения и применения их при устройстве подкрановых балок.
Литература
- Рекомендации по расчету, проектированию, изготовлению и монтажу фланцевых соединений стальных строительных конструкций. М. , ЦБНТИ Минмонтажспецстроя СССР, 1989, с. 53.
- Грудев И. Д. Прочность фланцевых соединений элементов открытого профиля. Болтовые и специальные монтажные соединения в стальных строительных конструкциях. Международный коллоквиум. – 1989. – Труды. Т.2 – С. 7-13.
- Фланцевые соединения. Расчет и проектирование. Бугов А. У. – Л. Машиностроение, 1975. – с. 191.
- Соскин А. Г. Особенности поведения и расчет болтов фланцевых соединений. Болтовые и специальные монтажные соединения в стальных строительных конструкциях. Международный коллоквиум. – 1989. – Труды. Т.2 – С. 24-31.
- Каленов В. В, Соскин А. Г., Евдокимов В. В. Исследования и расчет усталостной прочности фланцевых соединений растянутых элементов конструкций. Болтовые и специальные монтажные соединения в стальных строительных конструкциях. Международный коллоквиум. – 1989. – Труды. Т.2 – С. 41-17.
- Проектирование металлических конструкций: Спец.курс. Учебное пособие для вузов/ В. В. Бирюлев, И. И. Кошин, И. И. Крылов, А. В. Сильвестров. – Л.: Стройиздат, 1990 – 432 с.