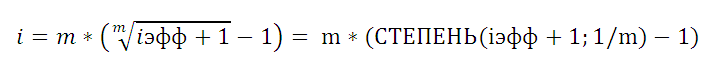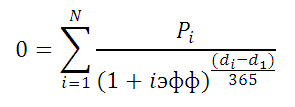Рассчитаем в MS EXCEL эффективную годовую процентную ставку и эффективную ставку по кредиту.
Эффективная ставка возникает, когда имеют место
Сложные проценты
. Понятие эффективная ставка встречается в нескольких определениях. Например, есть Эффективная (фактическая)
годовая
процентная ставка, есть Эффективная ставка
по вкладу
(с учетом капитализации), есть Эффективная процентная ставка
по потребительским кредитам
. Разберемся, что эти ставки из себя представляют и как их рассчитать в MS EXCEL.
Эффективная (фактическая) годовая процентная ставка
В MS EXCEL есть функция ЭФФЕКТ(номинальная_ставка, кол_пер), которая возвращает эффективную (фактическую)
годовую
процентную ставку, если заданы номинальная годовая процентная ставка и
количество периодов в году
, в которые начисляются сложные проценты. Под номинальной ставкой здесь понимается, годовая ставка, которая прописывается, например, в договоре на открытие вклада. Предположим, что
сложные проценты
начисляются m раз в год. Эффективная годовая процентная ставка дает возможность увидеть, какая годовая ставка
простых процентов
позволит достичь такого же финансового результата, что и m-разовое наращение в год по ставке i/m, где i – номинальная ставка. При сроке контракта 1 год по
формуле наращенной суммы
имеем: S = Р*(1+i/m)^m – для сложных процентов, где Р – начальная сумма вклада. S = Р*(1+iэфф) – для простых процентов
Так как финансовый результат S должен быть, по определению, одинаков для обоих случаев, приравниваем оба уравнения и после преобразования получим формулу, приведенную в справке MS EXCEL для функции
ЭФФЕКТ()
iэфф =((1+i/m)^m)-1
Примечание
. Если задана эффективная годовая процентная ставка, то величина соответствующей ей годовой номинальной процентной ставки рассчитывается по формуле
или с помощью функции НОМИНАЛ(эффективная_ставка, кол_периодов). См.
файл примера
.
Эффективная ставка по вкладу
Если договор вклада длится, скажем, 3 года, с ежемесячным начислением по сложным процентам по ставке i, то Эффективная ставка по вкладу вычисляется по формуле: iэфф =((1+i/12)^(12*3)-1)*(1/3) или через функцию
ЭФФЕКТ(
): iэфф= ЭФФЕКТ(i*3;3*12)/3 Для вывода формулы справедливы те же рассуждения, что и для годовой ставки: S = Р*(1+i/m)^(3*m) – для сложных процентов, где Р – начальная сумма вклада. S = 3*Р*(1+iэфф) – для простых процентов (ежегодной капитализации не происходит, проценты начисляются раз в год (всего 3 раза) всегда на первоначальную сумму вклада). Если срок вклада =1 году, то Эффективная ставка по вкладу = Эффективной (фактической) годовой процентной ставке (См.
файл примера
).
Эффективная процентная ставка по потребительским кредитам
Эффективная ставка по вкладу и Эффективная годовая ставка используются чаще всего для сравнения доходности вкладов в различных банках. Несколько иной смысл закладывается при расчете Эффективной ставки по кредитам, прежде всего по потребительским. Эффективная процентная ставка по кредитам используется для сравнения различные кредитных предложений банков. Эффективная процентная ставка по кредиту отражает реальную стоимость кредита с точки зрения заёмщика, то есть учитывает все дополнительные выплаты, непосредственно связанные с кредитом (помимо платежей по самому кредиту). Такими дополнительными выплатами являются банковские комиссии — комиссии за открытие и ведение счёта, за приём в кассу наличных денег и т.п., а также страховые выплаты. По закону банк обязан прописывать в договоре эффективную ставку по кредиту. Но дело в том, что заемщик сразу не видит кредитного договора и поэтому делает свой выбор, ориентируясь лишь на номинальную ставку, указанную в рекламе банка. Для создания расчетного файла в MS EXCEL воспользуемся Указаниями Центробанка РФ от 13 мая 2008 года № 2008-У «О порядке расчета и доведения до заемщика — физического лица полной стоимости кредита» (приведена Формула и порядок расчета эффективной процентной ставки), а также разъяснительным письмом ЦБ РФ № 175-Т от 26 декабря 2006 года, где можно найти примеры расчета эффективной ставки (см. здесь
http://www.cbr.ru/publ/VesnSearch.aspx
). Эффективную ставку по кредиту рассчитаем используя функцию
ЧИСТВНДОХ()
. Для этого нужно составить график платежей по кредиту и включить в него все дополнительные платежи.
Пример
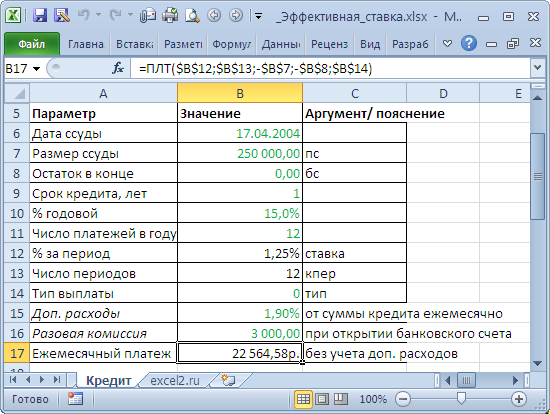
. Рассчитаем Эффективную ставку по кредиту со следующими условиями: Сумма кредита — 250 тыс. руб., срок — 1 год, дата договора (выдачи кредита) – 17.04.2004, годовая ставка – 15%, число платежей в году по аннуитетной схеме – 12 (ежемесячно). Дополнительные расходы – 1,9% от суммы кредита ежемесячно, разовая комиссия – 3000р. при открытии банковского счета.
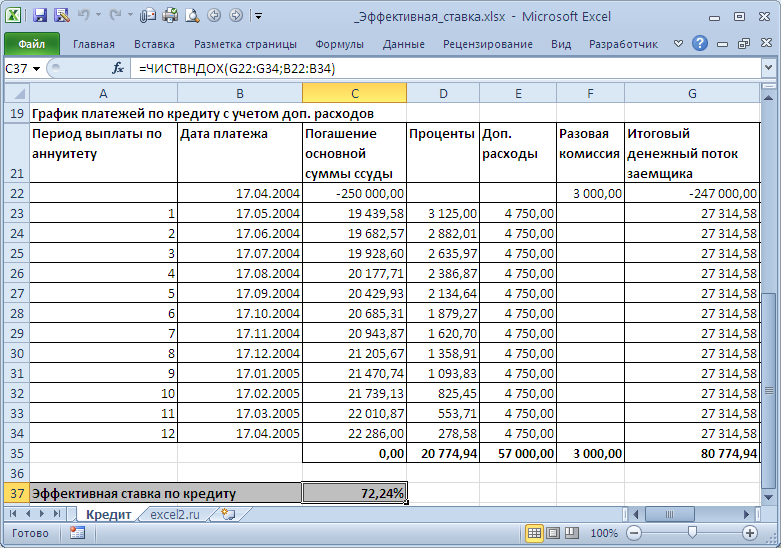
Сначала составим График платежей по кредиту с учетом дополнительных расходов (см.
файл примера Лист Кредит
). Затем сформируем Итоговый денежный поток заемщика (суммарные платежи на определенные даты).
Эффективную ставку по кредиту iэфф определим используя функцию ЧИСТВНДОХ (значения, даты, [предп]). В основе этой функции лежит формула:
Где, Pi = сумма i-й выплаты заемщиком; di = дата i-й выплаты; d1 = дата 1-й выплаты (начальная дата, на которую дисконтируются все суммы).
Учитывая, что значения итогового денежного потока находятся в диапазоне
G22:G34
, а даты выплат в
B22:B34
, Эффективная ставка по кредиту для нашего случая может быть вычислена по формуле
=ЧИСТВНДОХ(G22:G34;B22:B34)
. Получим 72,24%. Значения Эффективных ставок используются при сравнении нескольких кредитов: чья ставка меньше, тот кредит и более выгоден заемщику. Но, что за смысл имеет 72,24%? Может быть это соответствующая ставка по простым процентам? Рассчитаем ее как мы делали в предыдущих разделах: Мы переплатили 80,77т.р. (в виде процентов и дополнительных платежей) взяв кредит в размере 250т.р. Если рассчитать ставку по методу простых процентов, то она составит 80,77/250*100%=32,3% (срок кредита =1 год). Это значительно больше 15% (ставка по кредиту), и гораздо меньше 72,24%. Значит, это не тот подход, чтобы разобраться в сути эффективной ставке по кредиту. Теперь вспомним принцип временной стоимости денег: всем понятно, что 100т.р. сегодня – это значительно больше, чем 100т.р. через год при 15% инфляции (или, наоборот — значительно меньше, если имеется альтернатива положить эту сумму в банк под 15%). Для сравнения сумм, относящихся к разным временным периодам используют дисконтирование, т.е.
приведение их к одному моменту времени
. Вспомнив формулу Эффективной ставки по кредитам, увидим, что для всех платежей по кредитам рассчитывается их приведенная стоимость к моменту выдачи кредита. И, если мы хотим взять в 2-х банках одну и туже сумму, то стоит выбрать тот банк, в котором получается наименьшая приведенная стоимость всех наших платежей в погашение кредита. Почему же тогда не сравнивают более понятные приведенные стоимости, а используют Эффективную ставку? А для того, чтобы сравнивать разные суммы кредита: Эффективная ставка поможет, если в одном банке дают 250т.р. на одних условиях, а в другом 300т.р. на других. Итак, у нас получилось, что сумма всех наших платежей в погашение основной суммы кредита дисконтированных по ставке 72,24% равна размеру кредита (это из определения эффективной ставки). Если в другом банке для соблюдения этого равенства потребуется дисконтировать суммы платежей идущих на обслуживание долга по б
о
льшей ставке, то условия кредитного договора в нем менее выгодны (суммы кредитов могут быть разными). Поэтому, получается, что важнее не само значение Эффективной ставки, а результат сравнения 2-х ставок (конечно, если эффективная ставка значительно превышает ставку по кредиту, то это означает, что имеется значительное количество дополнительных платежей: убрав файле расчета все дополнительные платежи получим эффективную ставку 16,04% вместо 72,24%!).
Примечание
.
Функция
ЧИСТВНДОХ()
похожа на
ВСД()
(используется для расчета
ставки внутренней доходности, IRR
), в которой используется аналогичное дисконтирование регулярных платежей, но на основе номера периода выплаты, а не от количества дней.
Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения
Представим себе ситуацию, когда в 2-х разных банках нам предлагают взять в кредит одинаковую сумму на одинаковых условиях, но выплата кредита в одном будет осуществляться
дифференцированными платежами
, а в другом по
аннуитетной схеме
(равновеликими платежами). Для простоты предположим, что дополнительные платежи не взимаются. Зависит ли значение эффективной ставки от графика погашения? Сразу даем ответ: зависит, но незначительно.
В
файле примера на листе
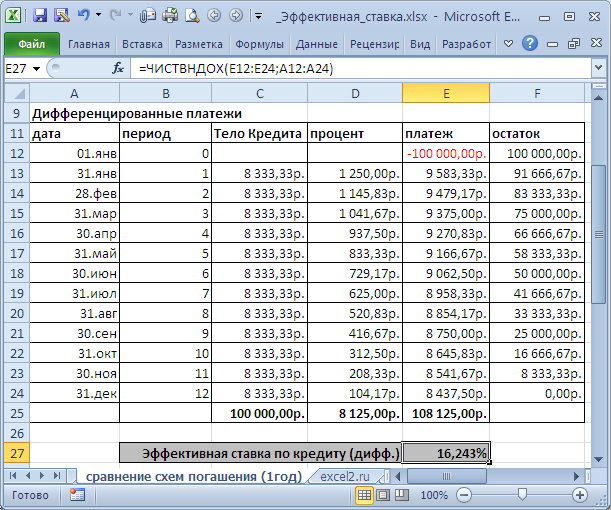
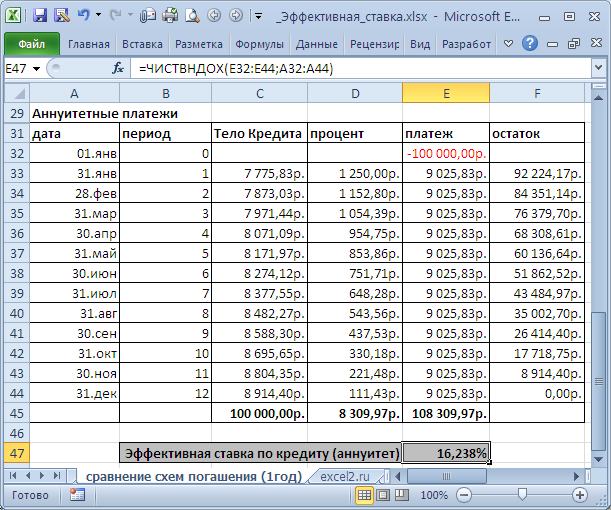
Сравнение схем погашения (1год)
приведен расчет для 2-х различных графиков погашения (сумма кредита 250 т.р., срок =1 год, выплаты производятся ежемесячно, ставка = 15%).
В случае дифференцированных платежей Эффективная ставка по кредиту = 16,243%, а в случае аннуитета – 16,238%. Разница незначительная, чтобы на ее основании принимать решение. Необходимо определиться какой график погашения больше Вам подходит.
При увеличении срока кредита разница между Эффективными ставками практически не изменяется (см.
файл примера Лист
Сравнение схем погашения (5лет)
).
Примечание
.
Эффективная годовая ставка, рассчитанная с помощью функции
ЭФФЕКТ()
, дает значение 16,075%. При ее расчете не используются размеры фактических платежей, а лишь номинальная ставка и количество периодов капитализации. Если грубо, то получается, что в нашем частном случае (без дополнительных платежей) отличие эффективной ставки по кредиту от номинальной (15%) в основном обусловлено наличием периодов капитализации (самой сутью сложных процентов).
Примечание
. Сравнение графиков погашения дифференцированными платежами и по аннуитетной схеме
приведено в этой статье
.
Примечание.
Эффективную ставку по кредиту можно рассчитать и без функции
ЧИСТВНДОХ()
— с помощью Подбора параметра. Для этого в
файле примера на Листе
Кредит
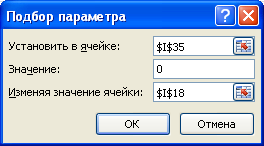
создан столбец I (Дисконтированный денежный поток (для Подбора параметра)). В окне инструмента
Подбор параметра
введите значения указанные на рисунке ниже.
После нажатия кнопки ОК, в ячейке
I18
будет рассчитана Эффективная ставка совпадающая, естественно, с результатом формулы
ЧИСТВНДОХ()
.
Эффективная процентная ставка по кредиту (как и практически любому другому финансовому инструменту) – это выражение всех будущих денежных платежей (поступлений от финансового инструмента), содержащихся в условиях договора, в приведенном к годовой процентной ставке показателе. То есть это та реальная ставка, которую заемщик будет платить за пользование деньгами банка (инвестор – получать). Здесь учитывается сама процентная ставка, указанная в договоре, все комиссии, схемы погашения, срок кредита (вклада).
Расчет эффективной ставки по кредиту в Excel
В Excel существует ряд встроенных функций, которые позволяют рассчитать эффективную процентную ставку как с учетом дополнительных комиссий и сборов, так и без учета (с опорой только на номинальную ставку и срок кредитования).
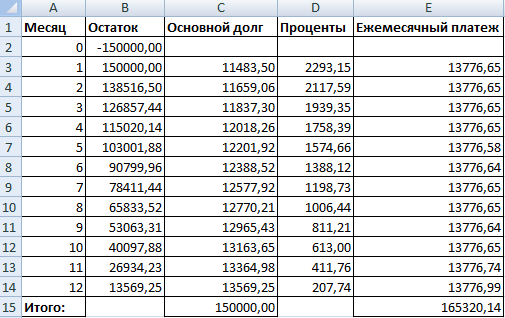
Заемщик взял кредит на сумму 150 000 рублей. Срок – 1 год (12 месяцев). Номинальная годовая ставка – 18%. Выплаты по кредиту укажем в таблице:
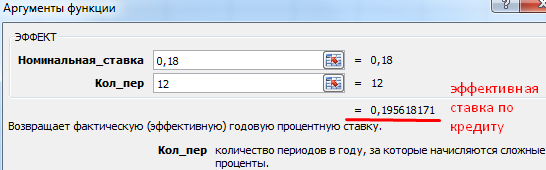
Поскольку в примере не предусмотрено дополнительных комиссий и сборов, определим годовую эффективную ставку с помощью функции ЭФФЕКТ.
Вызываем «Мастер функций». В группе «Финансовые» находим функцию ЭФФЕКТ. Аргументы:
- «Номинальная ставка» — годовая ставка по кредиту, указанная в договоре с банком. В примере – 18% (0,18).
- «Количество периодов» — число периодов в году, за которые начисляются проценты. В примере – 12 месяцев.
Эффективная ставка по кредиту – 19,56%.
Усложним задачу, добавив единовременную комиссию при выдаче кредита в размере 1% от суммы 150 000 рублей. В денежном выражении – 1500 рублей. Заемщик на руки получит 148 500 рублей.
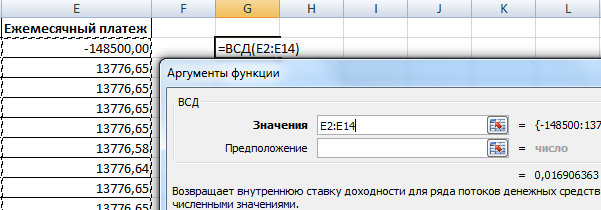
Чтобы рассчитать эффективную ежемесячную ставку, воспользуемся функцией ВСД (возвращает внутреннюю ставку доходности для потока денежных средств):
Мы внесли в столбец с ежемесячными платежами 148 500 со знаком «-», т.к. эти деньги банк сначала отдает. Платежи, которые вносит заемщик в кассу впоследствии, являются для банка положительными. Внутреннюю ставку доходности считаем с точки зрения банка: он выступает в качестве инвестора.
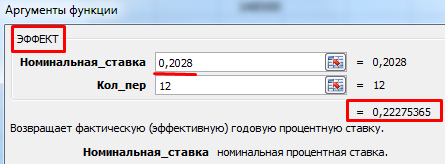
Функция дала эффективную ежемесячную ставку 1,69%. Для расчета номинальной ставки результат умножим на 12 (срок кредитования): 1,69% * 12 = 20,28%. Пересчитаем эффективную процентную ставку:
Единовременная комиссия в размере 1% повысила фактическую годовую процентную ставку на 2,72%. Стало: 22,28%.
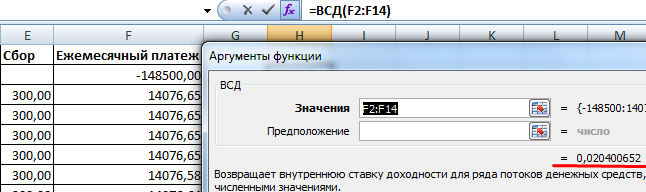
Добавим в схему выплат по кредиту ежемесячный сбор за обслуживание счета в размере 300 рублей. Ежемесячная эффективная ставка будет равна 2,04%.
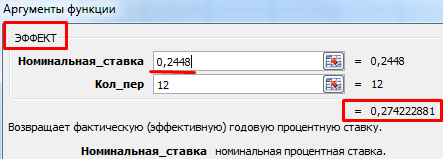
Номинальная ставка: 2,04% * 12 = 24,48%. Эффективная годовая ставка:
Ежемесячные сборы увеличили ее до 27,42%. Но в кредитном договоре по-прежнему будет стоять цифра 18%. Правда, новый закон обязует банки указывать в кредитном договоре эффективную годовую процентную ставку. Но заемщик увидит эту цифру после одобрения и заключения договора.
Чем отличается лизинг от кредита
Лизинг – это долгосрочная аренда транспорта, объектов недвижимости, оборудования с возможностью их дальнейшего выкупа. Лизингодатель приобретает имущество и передает его на основании договора физическому / юридическому лицу на определенных условиях. Лизингополучатель пользуется имуществом (в личных / предпринимательских целях) и платит лизингодателю за право пользования.
По сути, это тот же кредит. Только имущество будет принадлежать лизингодателю до тех пор, пока лизингополучатель полностью не погасит стоимость приобретенного объекта плюс проценты за пользование.
Расчет эффективной ставки по лизингу в Excel проводится по той же схеме, что и расчет годовой процентной ставки по кредиту. Приведем пример с другой функцией.
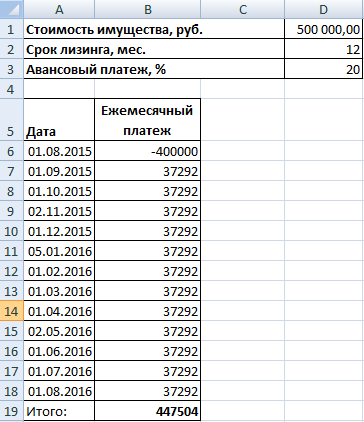
Входные данные:
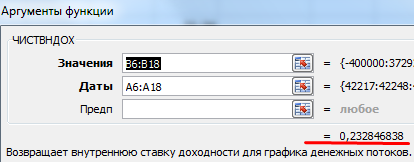
Можно пойти по уже проторенному пути: рассчитать внутреннюю ставку доходности, а потом умножить результат на 12. Но мы используем функцию ЧИСТВНДОХ (возвращает внутреннюю ставку доходности для графика денежных потоков).
Аргументы функции:
Эффективная ставка по лизингу составила 23,28%.
Расчет эффективной ставки по ОВГЗ в Excel
ОВГЗ – облигации внутреннего государственного займа. Их можно сравнить с депозитами в банке. Так как точно также вкладчик получает возврат всей суммы вложенных средств плюс дополнительный доход в виде процентов. Гарантом сохранности средств выступает центральный банк.
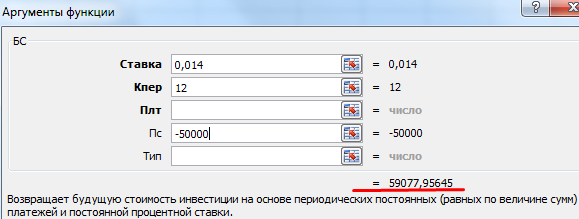
Эффективная ставка позволяет оценить настоящий доход, т.к. учитывает капитализацию процентов. Для примера «приобретем» годичные облигации на сумму 50 000 под 17%. Чтобы рассчитать свой доход, используем функцию БС:
Предположим, что проценты капитализируются ежемесячно. Поэтому 17% делим на 12. Результат в виде десятичной дроби вносим в поле «Ставка». В поле «Кпер» вводим число периодов капитализации. Ежемесячные фиксированные выплаты получать не будем, поэтому поле «Плт» оставляем свободным. В графу «Пс» вносим сумму вложенных средств со знаком «-».
Скачать пример расчета эффективной процентной ставки в Excel
В окошке сразу видна сумма, которую можно выручить за облигации в конце периода. Это и есть денежное выражение начисленных сложных процентов.
В данном уроке будем создавать кредитный калькулятор Аннуитета (оплата кредита равными платежами) в Excelе для расчета по таких параметров как:
- ежемесячный платеж;
- сумму оплаты за пользованием кредита;
- эффективную ставку по кредиту.
Важно понимать, что данные, которые рассчитаем, будут близки к банковским расчетам, но все же могут незначительно отличаться.
Шаг 1. Создаем таблицу значений
В новом документе Excel создаем таблицу с данными, которые будем использовать для расчета:
- Сумма кредита;
- Процентная ставка (годовая);
- Ежемесячная комиссия;
- Единоразовая комиссия;
- Срок кредита в месяцах.
Ячейки для ввода данных обозначим желтым.
Данные которые будем рассчитывать:
- Ежемесячный платеж;
- Сумма переплаты по кредиту;
- Процент переплаты;
- Эффективнаяставка.
Шаг 2. Рассчитываем ежемесячный платеж
Для того, чтобы рассчитать ежемесячный платеж используем функцию «ПЛТ», она находится в категории «Финансовые».
Аргументы функции «ПЛТ»
- Ставка — Выбираем ячейку процентной ставки и делим ее на 12. Это связано с тем, что процентную ставку указываем годовую, а платеж мы рассчитываем ежемесячный
- Кпер — срок кредитования;
- ПС — сумма кредита, обязательно ставим знак «-» перед значением. Так как в параметрах есть Единоразовая комиссия Сумма долга = Сумма кредита + Сумма кредита * Единоразовою комиссию. Все кредитные учреждения Единоразовою комиссию включают в основной долг и насчитывают на них годовую процентную ставку.
После использования формулы расчета ежемесячного платежа по аннуитету «ПЛТ» с учетом «Единоразовой комиссии», остается учесть еще ежемесячную комиссию. Таким образом, в строке формулы к функции добавляем расчет суммы ежемесячной комиссии.
Шаг 3. Расчет оплаты за кредит.
Расчет суммы оплаты по кредиту производит путем умножение ежемесячного платежа по кредиту на срок кредита и вычитаем основную сумму кредита.
Процент переплаты по кредиту рассчитывается как сумма оплаты деленная на сумму кредита и умноженная на 100.
Шаг 4. Расчет эффективной ставки по кредиту
Эффективная ставка по кредиту включает в себя все проценты и все платежи по кредиту:
- Процентная ставка;
- Единоразовая комиссия;
- Ежемесячная комиссия.
Для расчет эффективной ставки используем функцию «СТАВКА» в категории функций «ФИНАНСОВЫЕ».
Аргументы функции:
- Кпер — срок кредитования;
- Плт — рассчитанный ежемесячный платеж, который включает в себя все проценты и комиссии;
- Пс — сумма кредита, обязательно со знаком «-«.
После использования функции «СТАВКА» необходимо в строке формулы умножить данную функцию на 12, чтобы вычислить годовую эффективную ставку.
С помощью данного калькулятора, легко, просто и быстро рассчитать ежемесячный платеж по любому кредиту, а также высчитать эффективную ставку.
людей нашли эту статью полезной. А Вы?
В наш век высоких технологий и автоматизации как-то неприлично вручную выполнять сложные расчёты. Хоть аннуитетные платежи рассчитать не так и трудно, но как говорит Юрий Ашер:
«Не надо напрягать свой мозг там, где это могут сделать за вас другие!»
В нашей ситуации к вам на помощь придут: компьютер и программа Microsoft Excel.
Хотим предупредить, что команда портала temabiz.com поставила перед собой цель не просто дать вам «халяву» в виде «экселевского» файла с готовыми расчетами. Нет, в этой публикации мы вас научим самостоятельно рассчитывать аннуитетные платежи, а также составлять в программе Excel графики погашения аннуитетных кредитов. Ну а для ленивых мы, конечно же, выложим готовые файлы кредитных калькуляторов.
Содержание
- Как рассчитать аннуитетный платеж в Excel
- Расчет в Excel суммы кредита для заданного аннуитетного платежа
- Кредитный калькулятор в Excel по расчету графика аннуитетных платежей
Как рассчитать аннуитетный платеж в Excel
Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.
Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.
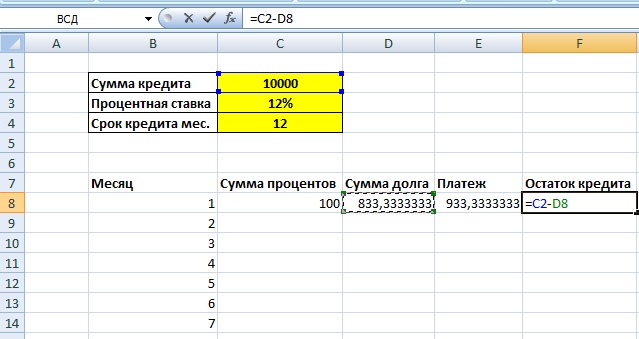
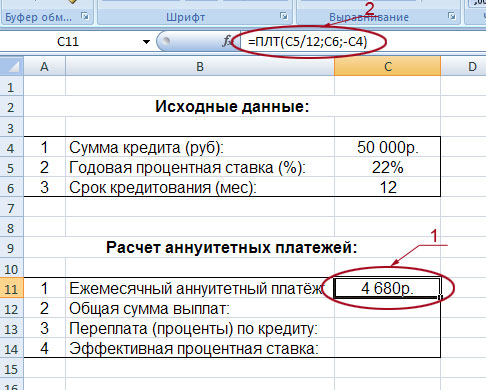
Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:
Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.
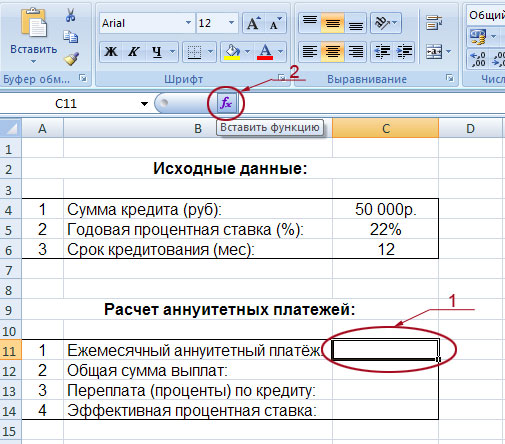
Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:
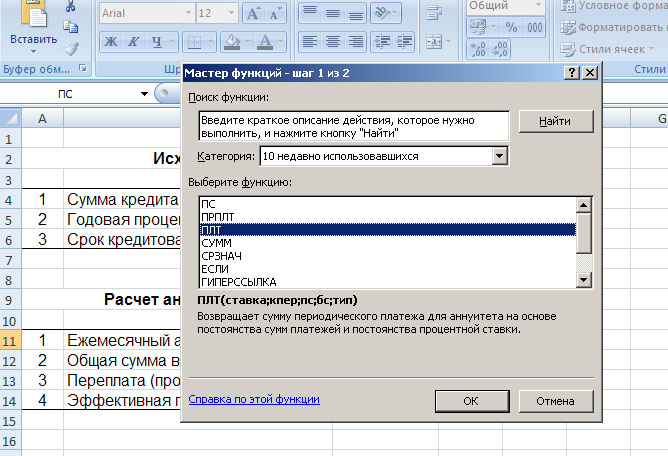
Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:
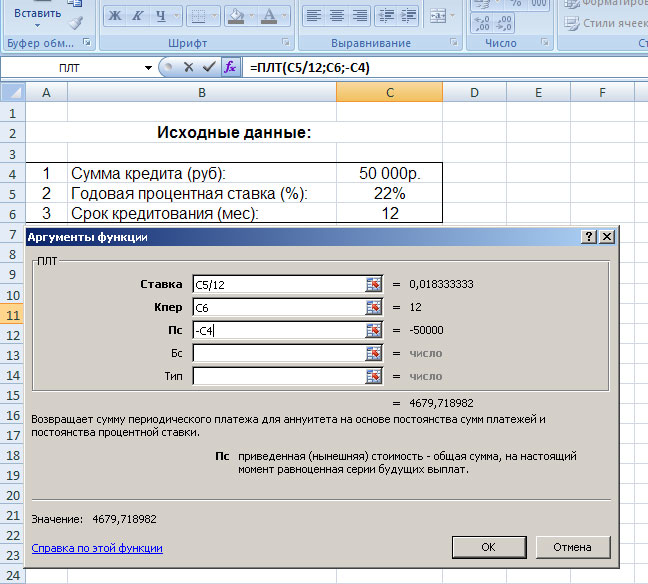
Здесь нам требуется заполнить три поля:
- «Ставка» – годовая процентная ставка по кредиту делённая на 12.
- «Кпер» – общий срок кредитования.
- «Пс» – сумма кредита (указывается со знаком минус).
Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.
После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:
Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.
Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.
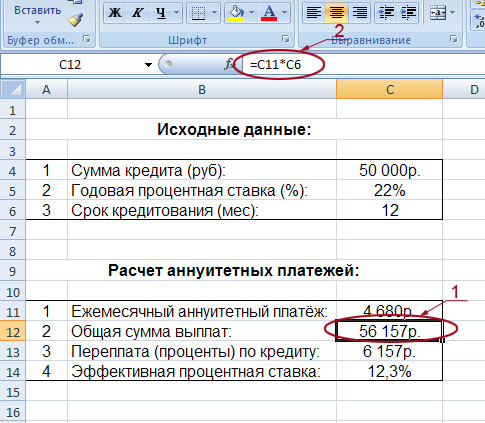
Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:
На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.
Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.
Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.
Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:
Расчет в Excel суммы кредита для заданного аннуитетного платежа
В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.
Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!
Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.
Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:
- «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
- «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
- «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).
Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.
Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4). Те самые параметры, которые мы вводили в таблице функции ПС.
Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:
- Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
- Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
- Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).
Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:
Кредитный калькулятор в Excel по расчету графика аннуитетных платежей
Два предыдущих кредитных калькулятора очень удобны, но они выполняют краткие (общие) расчёты. А иногда заёмщику нужна расширенная информация – график ежемесячных аннуитетных платежей с детальной расшифровкой каждой выплаты (с указанием сумм, идущих на погашение процентов, и сумм, погашающих тело кредита). В общем, сейчас мы сделаем в программе Excel ещё один кредитный калькулятор, который будет автоматически рассчитывать график аннуитетных платежей. Щёлкаем мышкой по рисунку:
Перед вами расширенная и доработанная версия нашего первого кредитного калькулятора (того, который рассчитывает размер ежемесячного аннуитетного платежа по кредиту). Здесь кроме стандартных блоков с исходными данными и расчётами, появилась таблица, в которой детально расписаны все наши будущие ежемесячные выплаты. Таблица имеет пять колонок:
- 1. Месяцы. В этой колонке по порядку указаны номера месяцев, в которые будут осуществляться выплаты. Обратите внимание, что речь идёт не о календарных, а о порядковых номерах. То есть, если первая выплата припадает на сентябрь месяц, то ему присваивается порядковый номер «1», как первому месяцу, а не «9», как календарному.
- 2. Ежемесячный платёж. Это тот самый аннуитетный платёж, который не меняется на протяжении всего срока кредитования. В сноске к одной из ячеек вы можете увидеть данные, которые внесены в строку формул: =ПЛТ(B3/12;B4;-H14). Вы уже знаете, что за расчёт аннуитетного платежа в экселе отвечает функция ПЛТ. Координаты необходимых значений для расчёта можно внести, как через строку формул, так и заполнив таблицу, которая появится при нажатии на кнопку «fx», находящуюся слева от строки формул.
- 3. Погашение процентов. Здесь рассчитывается доля процентов в аннуитетных платежах (в каждой новой выплате она будет уменьшаться). В программе Excel за расчёт данного показателя отвечает функция ПРПЛТ. Опять же, задать необходимые параметры для расчётов можно либо нажав на кнопку «fx» и заполнив таблицу, либо просто внеся нужную информацию в строку формул. В нашем примере для расчёта доли процентов в первом платеже, в строке формул записано следующее: =ПРПЛТ(A15/12;D15;B15;-C15).
- 4. Погашение тела кредита. Та самая выплата, которая вытягивает нас из долговой ямы и избавляет от банковского рабства. Мы рассчитали её просто: из суммы аннуитетного платежа вычли долю процентов, которую рассчитали в предыдущей колонке. Собственно, в строке формул по первому платежу так и записано: =E15-F15. Но можно пойти и другим, более изощрённым, путём. В программе Excel за расчёт этого платежа отвечает функция ОСПЛТ. Можете для интереса нажать кнопку «fx», выбрать функцию ОСПЛТ, внести все необходимые данные и получить сумму, идущую на погашение тела кредита в выбранном платеже.
- 5. Долг на конец месяца. Ну, здесь всё просто! В данной колонке отображается сумма вашего долга перед банком на конец текущего месяца. Из текущего остатка мы отнимаем долю, идущую на погашение тела кредита. А вот уплаченные проценты просто уходят в казну банка и никак не влияют на сумму вашего текущего долга по кредиту.
Вот так легко и непринуждённо мы разработали кредитный калькулятор по расчёту графика аннуитетных платежей. Скачать его можно ссылке ниже:
Итак, друзья, теперь у вас есть целых три кредитных калькулятора по расчёту аннуитетных платежей, разработанных в программе Microsoft Excel. В следующей публикации мы расскажем о досрочном погашении аннуитетного кредита.
⇧
Выбирая наиболее выгодные условия кредитования, каждый клиент ориентируется именно на процентную ставку. Это неправильный подход. У одного банка ставка может быть ниже, чем у другого, а в кредитной программе скрыты дополнительные комиссии. Все это нужно учитывать. Так как же правильно рассчитать эффективную процентную ставку? В чем ее суть?
Содержание статьи
- 1 Что такое эффективная ставка по кредиту
- 2 Расчет ЭКС (эффективной кредитной ставки)
- 2.1 Расчет эффективной кредитной ставки по специальной формуле
- 2.2 Проведем пример расчета.
- 2.3 Расчет эффективной кредитной ставки в Excel
- 2.4 Специальный калькулятор для расчета ЭКС
- 3 Итоги
Что такое эффективная ставка по кредиту
Это ставка, которая отображает реальную стоимость кредита. Она должна учитывать все дополнительные выплаты при оформлении займа. К ним относят следующее:
- плата за открытие и ведение счета;
- плата за внесение наличных через кассу или специальные устройства;
- комиссия за снятие со счета и прочее.
Несмотря на то, что Центральный Банк РФ обязал коммерческие банки раскрывать информацию об эффективной процентной ставке по кредиту, многие из них не соблюдают такие условия.
Расчет ЭКС (эффективной кредитной ставки)
Есть несколько методов:
- с помощью специальной формулы;
- в программе Excel;
- с помощью кредитного калькулятора.
Рассмотрим каждый из них.
Расчет эффективной кредитной ставки по специальной формуле
Для удобства расчетов была разработана определенная формула:
ЭКС = СКР / t / ССК, где
ЭКС – эффективная кредитная ставка,
СКР – полная сумма кредитных расходов с учетом дополнительных выплат и комиссий,
t – срок кредитования в годах,
ССК – средневзвешенная сумма кредита.
Последний показатель (ССК) определяют по дополнительным формулам в зависимости от типа погашения кредита.
При классической схеме погашения ССК определяют по формуле:
ССК = СК * (t+1) / (t+2), где
СК – сумма кредита,
t – срок кредита в месяцах.
При аннуитетной схеме погашения ССК определяют по такой формуле:
ССК = СК ((((1+%/12)^t-1) / (%*t/12)) — ((((1+%/12)^t-1) / (%/12))-t) / (t*(1-(1+%/12))^t)))), где
СК – сумма кредита,
t – срок кредита в месяцах.
Исходя из вышеуказанной информации, можно сделать вывод, что гораздо сложнее производить расчет эффективной кредитной ставки именно с аннуитетной формой погашения. Также стоит отметить, что стоимость кредитов с аннуитетами гораздо выше, чем с классический схемой погашения. Последняя заключается в том, что проценты начисляют не на общую сумму кредита, а на ее остаток.
Проведем пример расчета.
Клиент хочет оформить кредит на сумму 50 тыс. руб. на срок 12 месяцев. Ему нужно заплатить при выдаче займа страховку в размере 1000 руб., за оформление кредита — 250 руб., Процентная ставка по кредиту — 18,5% годовых. Размер платежей рассчитывается по классической схеме.
Изначально нам нужно определить, сколько клиент должен заплатить за 12 месяцев кредита. Для этого вычисляем:
50 000 * 18,5% годовых = 9250 руб.
Это будет переплата по кредиту за весь период пользования. К этой сумме прибавляем другие расходы:
9250 + 250 + 1000 = 10500 руб.
Итак, полная сумма кредитных расходов (СКР) составит 10500 руб.
Теперь определяем ССК (средневзвешенную сумму кредита) по вышеуказанной формуле:
ССК = 50 000 (СК) * (12+1)/(12+2) = 46428,57 руб.
Можно переходить к расчету эффективной кредитной ставки по формуле:
10500 (СКР)/12(t)/46428,57(ССК) = 0,0188
Теперь эту сумму умножаем на 100%. Получается 1,88% в месяц, так как мы использовали в формуле временной промежуток в 12 месяцев. Если клиент будет погашать кредит на протяжении всего срока действия, ЭКС составит 22,56% годовых, а не заявленные 18,5% годовых.
Расчет эффективной кредитной ставки в Excel
Такой метод считается самым популярным. Нужно воспользоваться программой Ексель. В ней есть огромное количество встроенных функций, которые помогают сделать правильные расчеты.
Давайте рассмотрим все на примере.
Клиент оформляет кредит на сумму 100 000 руб. Срок кредитования 24 месяца. Заявленная банком процентная ставка составляет 17% годовых. Клиент должен единоразово внести комиссию в размере 15 000 руб.
Строим в Екселе таблицу следующего вида:
- первый столбец — нумерация месяцев;
- второй — дата погашения в каждом месяце;
- третий — сумма ежемесячного погашения.
| Месяц | Дата погашения | Сумма ежемесячного платежа |
|---|---|---|
| 1 | 22.09.2016 | -85000 (15000 — комиссия) |
| 2 | 22.10.2016 | 4944,22 |
| 3 | 22.11.2016 | 4944,22 |
| 4 | 22.12.2016 | 4944,22 |
И так до окончания срока действия кредита.
После этого в любой свободной ячейке программы вводим значение: =ЧИСТВНДОХ (значения; даты). Значения — суммы платежей, а даты — расписание погашений в каждом месяце.
После того, как набрали =ЧИСТВНДОХ, выделяем в таблице весь столбец с суммами платежей. Не выделяя при этом название этого столбца. Иначе расчет не получится. Также выделяем столбец с датами. Затем закрываем скобку в формуле, нажимаем на Enter. Полученное значение умножаем на 100%.
В нашем примере сумма получится сумма 0,40244. Умножаем ее на 100%. Получаем 40,2%. Эта и будет эффективная процентная ставка по кредиту.
Специальный калькулятор для расчета ЭКС
Эти приложения разработаны для удобства пользователей. В них имеется огромное количество встроенных функций, а также дополнительных параметров, с помощью которых можно без особых усилий автоматически рассчитать эффективную ставку по кредиту.
Вот пример одного из них.
Программа предлагает проводить расчеты по двум схемам:
- классической;
- аннуитетной.
Клиент выбирает на основании какой суммы ему нужно произвести подсчет: по стоимости покупки или сумме кредита. Обязательно нужно внести общую сумму кредита, срок кредита, заявленную банком процентную ставку. Далее, выбрать вид погашения кредита, указать единоразовую сумму комиссии, если она есть, проставить дату начала выплат. Затем нажать на кнопку «Рассчитать». Программа выдаст результат в течение нескольких секунд.
Итоги
При выборе кредита нужно обращать внимание не только на процентную ставку, которую предлагает банк. Нужно учитывать комиссии и дополнительные выплаты. Они могут быть единовременными или постоянными на протяжении всего срока кредитования. А с их учетом эффективная процентная ставка будет гораздо выше, чем ставка, заявленная банком.
Методика расчета основана на классической теории финансирования. Современные банки могут применять другие методы начисления процентов, например, с учетом точного количества дней в каждом месяце, или не применять сложные процентные ставки, а использовать метод 360 дней. Если вам нужен точный расчет – стройте точную модель платежей и используйте функцию Goal seek (Подбор значения).
Этот калькулятор подойдет вам только если кредит – аннуитетный (равные платежи, в составе которых меняется сумма погашения и сумма выплаты процентов, но общая сумма остается неизменной).
Если вы захотите внести какие-то изменения, то снимите защиту листа. Лист защищен без пароля.
В приложенном файле корректируйте синие ячейки. Желтые ячейки содержат формулы.
Расчет эффективной процентной ставки
Исходные данные:
- Сумма кредита: 100 000 руб
- Ставка: 18% годовых
- Ежемесячная комиссия за обслуживание кредита: 1% от суммы кредита
- Срок кредита: 12 месяцев
- Метод погашения: аннуитетные платежи.
Так как платежи у нас аннуитетные, то погашать кредит будем равными долями в течение всего срока, другими словами, ежемесячный платёж – одна и та же сумма. Это удобно заёмщику.
A = K*S,
где S – сумма кредита (в нашем случае S = 100 000);
K – коэффициент аннуитета, считается по формуле, зависящей от i и n.
В нашем случае i = 0,015 n = 12, подставляем их в формулу, получаем, что К = 0,09168.
А = 9168 рублей.
Способ 2.
Можно сделать проще. Чтобы рассчитать сумму аннуитетного платежа, воспользуемся встроенной в Excel функцией ПЛТ.
Вводим в ячейку формулу вида:
и получаем ту же сумму: 9168 руб.
Примечание к формуле.
0,015 – месячная процентная ставка i = 18 / 12 / 100;
12 – количество выплат n;
-100000 – сумма кредита S
Далее составляем таблицу выплат по месяцам.
Итоги расчёта процентной ставки
Взяли кредит на 100 000 руб.
Выплатили 122015,99 руб.
Переплата составила 22015,99 руб.
Ставка 22015,99 / 100000 = 22%.
Ежемесячная комиссия в 1% обошлась нам в 12000 рублей, что даже больше, чем основные выплаты по кредиту! Это объясняется тем, что комиссию мы платили каждый раз от полной суммы кредита (100 тыщ), а проценты – от оставшейся суммы (то есть за вычетом того, что уже уплатили), которая с каждым месяцем уменьшается. Подобные хитрости со стороны банка могут в конечном итоге дорого обойтись.
Сегодня всё больше клиентов банка стали интересоваться расчетами максимальной суммы кредита, эффективной процентной ставки, а также заниматься поисками формулы расчёта аннуитетного платежа и т.д. Это связанно не только с тем, что они не хотят быть обманутыми, но и с их желанием найти наиболее подходящий для себя вид кредита. Кроме того, заранее произведённые расчеты самими заёмщиками помогают им при обращении в банк сэкономить кучу времени, которое им пришлось бы затратить на обход огромного количества финансовых учреждений, а также максимально снизить переплату по кредиту. Как же рассчитать эффективную процентную ставку самому?
Что нужно для правильного расчета ставки
Итак, начать следует с воспоминаний школьной программы по математике. Далее следует вооружится калькулятором, бумагой и ручкой. Ну, а кто предпочитает считать на компьютере, расчет реально произвести и при помощи программы Microsoft Exel. Кроме того, нам понадобятся несколько стандартных формул, которыми так любят орудовать банковские менеджеры. Ну и конечно мало просто написать саму формулу и расшифровать её буквенное значение, а также провести предварительно расчёт реальной процентной ставки. Необходимо ещё и привести конкретный пример, чтобы вы знали с чего начать при своём самостоятельном пересчёте.
Примеры расчёта
Для наглядности приведём реальный пример из жизни. Клиент банка взял потребкредит (потребительский кредит) на сумму 200 000 долларов США на неотложные нужды. Годовая ставка по такому виду банковского займа составила 19%, а банковская комиссия за пользование кредитом составляет 2% от всей суммы банковской ссуды. При выборе схемы оплаты заёмщик выбирает аннуитетные платежи. Таким образом, погашение займа будет происходить в течение всего оговоренного в договоре кредитного срока равными суммами. Для расчета эффективной процентной ставки по кредиту нам понадобиться предварительно, рассчитать размер платежа по кредиту, который заёмщик и будет оплачивать ежемесячно. Воспользуемся формулой расчёта аннуитетных платежей, напоминаем, как она выглядит: A = K*S
- S – общая сумма кредита (согласно данным нашего примера, она равна S = 200 000);
- K — коэффициент аннуитета (он зависит напрямую от других величин n и i) и рассчитывается по следующей формуле:

K=0,092252 Следовательно А=0,092252*200 000, отсюда А=18 450.41 долларов.
Способ второй
Второй способ расчета ежемесячного платежа по кредиту можно сделать, как уже говорилось выше в файле Exel. Для этого в верхней строке после fx вписываете следующие данные: =ПЛТ(0,016;12;-200000) Благодаря встроенной функции ПЛТ расчет происходит автоматически. Проверяем наш предыдущий ответ и получаем такую же сумму — 18 450.41 долларов, как при расчёте первым способом. После того, как два варианта совпали, внесём некоторые корректировки и можем приступать к дальнейшим действиям, а именно к составлению таблицы ежемесячных выплат. Пояснения: 0,015 – размер ежемесячной процентной ставки, i = 19/12/100$ 12 – количество месяцев, входящих в состав кредитного периода = n; -200000 – общая сумма займа = S (пишется со знаком минус). А теперь составляем таблицу:
По итогам данной таблицы можно отметить, что в каждом месяце уменьшалось количество процентных выплат по кредиту, а выплаты основной кредитной части росли. Это и является характерной особенностью для схемы аннуитетного платежа.
Согласно полученным цифрам в таблице, можно сделать следующие выводы:
- Клиент брал кредит в размере 200 000 долларов США, а выплатил 269404,80 долларов США;
- Сумма переплаты по кредиту составила – 69404,80 долларов США;
- А сумма процентной ставки увеличилась до 34%;
- Сумма ежемесячной комиссии за пользование кредитом с 2% выросла до 48000 долларов США (получилось, что данная сумма выплаты по кредиту превысила сумму выплат по основной сумме кредита).
Следовательно, сумма переплаты возникла по большей части из-за ежемесячной оплаты комиссии банка.