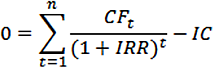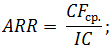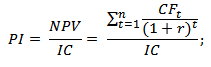IRR (Internal Rate of Return), или ВНД – показатель внутренней нормы доходности инвестиционного проекта. Часто применяется для сопоставления различных предложений по перспективе роста и доходности. Чем выше IRR, тем большие перспективы роста у данного проекта. Рассчитаем процентную ставку ВНД в Excel.
Экономический смысл показателя
Другие наименования: внутренняя норма рентабельности (прибыли, дисконта), внутренний коэффициент окупаемости (эффективности), внутренняя норма.
Коэффициент IRR показывает минимальный уровень доходности инвестиционного проекта. По-другому: это процентная ставка, при которой чистый дисконтированный доход равен нулю.
Формула для расчета показателя вручную:
, где
- CFt – денежный поток за определенный промежуток времени t;
- IC – вложения в проект на этапе вступления (запуска);
- t – временной период.
На практике нередко коэффициент IRR сравнивают со средневзвешенной стоимостью капитала:
- ВНД выше – следует внимательно рассмотреть данный проект.
- ВНД ниже – нецелесообразно вкладывать средства в развитие проекта.
- Показатели равны – минимально допустимый уровень (предприятие нуждается в корректировке движения денежных средств).
Часто IRR сравнивают в процентами по банковскому депозиту. Если проценты по вкладу выше, то лучше поискать другой инвестиционный проект.
Пример расчета IRR в Excel
Быстро рассчитать IRR можно с помощью встроенной функции ВСД. Синтаксис:
- диапазон значений – ссылка на ячейки с числовыми аргументами, для которых нужно посчитать внутреннюю ставку доходности (хотя бы один денежный поток должен иметь отрицательное значение);
- предположение – величина, которая предположительно близка к значению ВСД (аргумент необязательный; но если функция выдает ошибку, аргумент нужно задать).
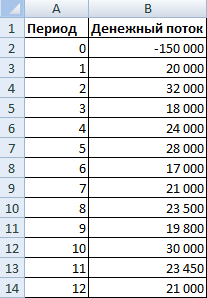
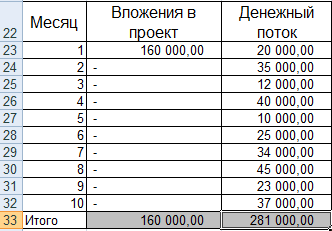
Возьмем условные цифры:
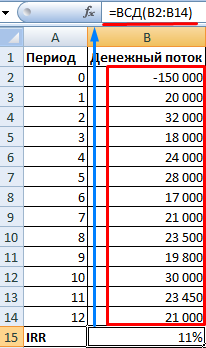
Первоначальные затраты составили 150 000, поэтому это числовое значение вошло в таблицу со знаком «минус». Теперь найдем IRR. Формула расчета в Excel:
Расчеты показали, что внутренняя норма доходности инвестиционного проекта составляет 11%. Для дальнейшего анализа значение сравнивается с процентной ставкой банковского вклада, или стоимостью капитала данного проекта, или ВНД другого инвестиционного проекта.
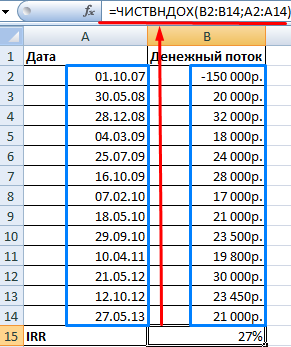
Мы рассчитали ВНД для регулярных поступлений денежных средств. При несистематических поступлениях использовать функцию ВСД невозможно, т.к. ставка дисконтирования для каждого денежного потока будет меняться. Решим задачу с помощью функции ЧИСТВНДОХ.
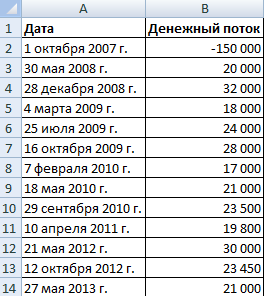
Модифицируем таблицу с исходными данными для примера:
Обязательные аргументы функции ЧИСТВНДОХ:
- значения – денежные потоки;
- даты – массив дат в соответствующем формате.
Формула расчета IRR для несистематических платежей:
Существенный недостаток двух предыдущих функций – нереалистичное предположение о ставке реинвестирования. Для корректного учета предположения о реинвестировании рекомендуется использовать функцию МВСД.
Аргументы:
- значения – платежи;
- ставка финансирования – проценты, выплачиваемые за средства в обороте;
- ставка реинвестирования.
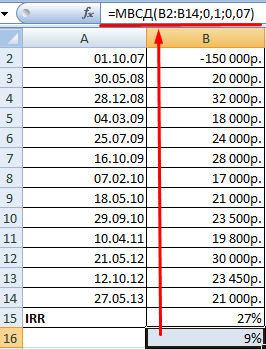
Предположим, что норма дисконта – 10%. Имеется возможность реинвестирования получаемых доходов по ставке 7% годовых. Рассчитаем модифицированную внутреннюю норму доходности:
Полученная норма прибыли в три раза меньше предыдущего результата. И ниже ставки финансирования. Поэтому прибыльность данного проекта сомнительна.
Графический метод расчета IRR в Excel
Значение IRR можно найти графическим способом, построив график зависимости чистой приведенной стоимости (NPV) от ставки дисконтирования. NPV – один из методов оценки инвестиционного проекта, который основывается на методологии дисконтирования денежных потоков.
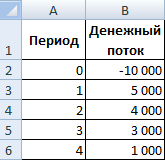
Для примера возьмем проект со следующей структурой денежных потоков:
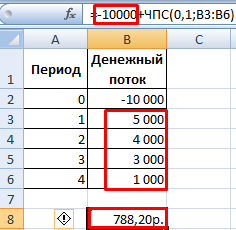
Для расчета NPV в Excel можно использовать функцию ЧПС:
Так как первый денежный поток происходил в нулевом периоде, то в массив значений он не должен войти. Первоначальную инвестицию нужно прибавить к значению, рассчитанному функцией ЧПС.
Функция дисконтировала денежные потоки 1-4 периодов по ставке 10% (0,10). При анализе нового инвестиционного проекта точно определить ставку дисконтирования и все денежные потоки невозможно. Имеет смысл посмотреть зависимость NPV от этих показателей. В частности, от стоимости капитала (ставки дисконта).
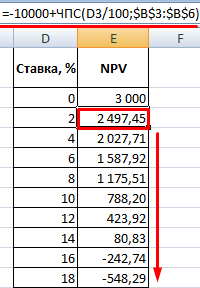
Рассчитаем NPV для разных ставок дисконтирования:
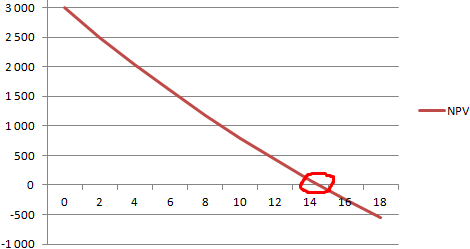
Посмотрим результаты на графике:
Напомним, что IRR – это ставка дисконтирования, при которой NPV анализируемого проекта равняется нулю. Следовательно, точка пересечения графика NPV с осью абсцисс и есть внутренняя доходность предприятия.
Инвестиционная модель в EXCEL с NPV-анализом
Уважаемые посетители!
Перечень всех финансовых и инвестиционных моделей нашего сайта, которые можно бесплатно скачать,
Вы найдете здесь.
В современном социуме вопросы финансовой безопасности как отдельного человека – физического лица, так и каждого предприятия –
юридического лица в структуре жизненно важных приоритетов находятся далеко не на последних местах.
Долгосрочный стабильный прирост капитала обеспечивает при прочих равных условиях уверенность в завтрашнем дне
и готовность ко многим форс-мажорным происшествиям, влекущим потребность в финансовых средствах для их нейтрализации, конечно же,
когда речь не идет о глобальных потрясениях.
По отношению к уже накопленному капиталу задачей-минимум, которую решает его обладатель, является сохранение капитала.
Где под «сохранением капитала» мы понимаем сохранение его рыночной ликвидности во времени, т.е., если на данный момент
времени преобразовав весь свой капитал в максимально возможный относительно рыночной конъюнктуры объем денежных средств
(в чистые финансы), обладатель этого капитала делает все возможное, чтобы и через год и через десять лет его капитал
оценивался или, что тоже самое, мог быть конвертирован на рынке в такой же или больший объем денежных средств, но только
не с точки зрения номинала (суммы), а сточки зрения покупательной способности в натуральных объемах некоторой
«продуктовой корзины», ну, или, по крайней мере, с точки зрения официальной инфляции.
Наиболее доступный способ, к которому прибегают, чтобы сохранить капитал в виде денежных средств,
это положить деньги в банк на депозит. Но по известным причинам в надежных банках процент по депозитам обычно не
покрывает инфляцию, а в ненадежных банках можно просто потерять весь капитал. Поэтому при таком способе долгосрочного
сохранения капитала необходимо иметь дополнительные источники дохода, которые будут покрывать потери капитала в связи
с инфляцией, т.е. необходима постоянная «подпитка капитала извне».
Но пожалуй, более заманчивой, а возможно и более популярной формой не только сохранения капитала, но и его преумножения
являются инвестиции, о чем в данном разделе и пойдет речь.
Пример реально действующей системы комплексного инвестиционного анализа и комплексной оценки финансово-хозяйственного
состояния предприятия или будущего инвестиционного проекта/стартапа с расчетом всех ключевых финансовых и инвестиционных показателей,
а также оценки стоимости бизнеса или компании в целом можно посмотреть, скачав универсальную финансовую модель поколения 4.0
для анализа всевозможных инвестиционных проектов и принятия решений об инвестировании в них ниже в синей рамке.
СКАЧАТЬ
ФИНМОДЕЛЬ С ИНВЕСТИЦИОННЫМ АНАЛИЗОМ БИЗНЕС-ПРОЕКТА

Для целей настоящей статьи под инвестициями или инвестиционными вложениями мы будем понимать направление капитала в
виде денежных средств в производственную инфраструктуру с целью создания в будущем серийного производства нового продукта
или расширения производства для создания бОльшего объема продукции, и через продажу которой предполагается возврат вложенных
инвестиционных средств. Где в свою очередь в качестве производственной инфраструктуры будем рассматривать все составляющие
цикла создания продукта потребления от идей, научных исследований и проектных работ до разработки, строительства,
внедрения и запуска мощностей серийного производства и сбыта.
Как обычно, сразу выкладываем для скачивания соответствующую финансовую модель инвестиционного проекта (инвестмодель)
в виде EXCEL-файла:
СКАЧАТЬ
Классическая базовая инвестиционная модель

Чтобы на начальном этапе знакомства с методами инвестиционного анализа не перегружать читателя разнообразной спецификой типов
объектов капитальных вложений, представленный для скачивания EXCEL-файл содержит, так сказать, базовую инвестиционную модель
схематичного вида, где капитальные вложения рассматриваются, как простой инвестиционный поток во времени.
Для удобства ознакомления и в качестве примера данная инвестмодель уже наполнена конкретными данными исходных финансово-экономических
показателей, которые пользователь вносит для расчета ключевых показателей эффективности инвестиционного проекта.
Эта же модель, но только незаполненная, приведена в виде такого же EXCEL-файла для скачивания в конце раздела.
Прежде чем перейти к описанию финмодели инвестиционного проекта, для полноты содержания раздела «управление финансами»
мы познакомим с основными широко известными и подробно представленными, например, в Интернете показателями эффективности
инвестиционных проектов такими, как NPV, IRR, PP, PI, ROI и т.д., а также коснемся принципов достаточно нового современного
подхода к управлению коммерческой структурой, который носит емкую аббревиатуру «EVA» — Economic Value Added;
авторами концепции EVA являются американцы Б.Стюарт и Д.Стерн.
Для любого инвестора при вложении денег в тот или иной проект, инвестиционный проект, естественно важно, чтобы,
как минимум, произошел возврат инвестиционных вложений в полном объеме и более того, чтобы возврат этого самого «полного объема»
был произведен, как в народе говорят, «с учетом стоимости денег» или, как говорят, специалисты «с учетом уровня потери
покупательной способности денежных средств».
Учет покупательной способности денег в инвестиционном анализе происходит путем введения коэффициента дисконтирования,
с помощью которого производится дисконтирование будущих финансовых потоков или, что тоже самое, приведение финансового потока будущих
периодов к некоторому определенному моменту времени, например, к моменту начала инвестиционного проекта.
Чтобы понять, как работает дисконтирование разберемся сначала с процессом того, как происходит изменение покупательной
способности денежных средств. Допустим, Вы ходите в магазин и покупаете систематически за 1000руб. один и тот же набор товаров,
составляющих Вашу собственную «потребительскую корзину», т.е. Ваш средний чек на протяжении некоторого периода времени равен 1000руб.
Далее пусть также по прошествии еще некоторого периода времени происходят изменения цен на товары Вашей потребительской корзины и
Вам приходится покупать тот же набор товаров уже за 1100руб., т.е. на 10% дороже. Тогда если предположить, что у Вас нет 1100руб.
на покупку полной корзины, а Вы все также располагаете ровно «той же» тысячью рублей, тогда Вы сможете купить лишь только некоторую долю,
обозначим ее через D, от той продуктовой корзины, которую привыкли покупать до повышения цен. И эта доля, как легко посчитать, равна
D = 1 / (1 + 10%).
То есть покупательная способность денег относительно Вашей продуктовой корзины или Ваша личная покупательская способность снизилась на
10% / (1 + 10%) = 9,(09)%.
Получается, что инфляция в размере 10% «съедает» чуть более 9% Вашей продуктовой потребительской корзины.
Или обобщая, получаем, что при Вашем финансовом бездействии в течение инфляционного периода инфляция в размере i процентов «съест»
i * D(i) * 100%
процентов Ваших повседневных потребительских возможностей, которыми Вы обладаете в настоящий момент, где
D(i) = 1 / (1 + i).
Значит, если не бездействовать с точки зрения Вашего финансового положения, т.е. для того чтобы иметь и в будущем возможность
потреблять на том же уровне, Вам необходимо позаботиться о том, чтобы либо Ваш доход (например, заработная плата)
со временем увеличился на инфляционный процент, либо Ваши накопления прирастали со скоростью инфляции.
На самом деле и то и другое означает создание условий, при которых прирост Вашего капитала в широком смысле будет не ниже уровня инфляции,
ведь получая заработную плату, Вы взамен отдаете свой «трудовой капитал».
В случае же если деньги есть сейчас, а потратить их придется в будущем через определенный срок, тогда необходимо найти такую
возможность вложить эти денежные средства, чтобы через этот срок они не потеряли покупательную способность.
Например, если банк предлагает процент по депозиту на указанный срок в размере ожидаемой инфляции по продукции,
которую предполагается купить по истечение срока, то при понятных рисках можно положить деньги на депозит в этот банк.
Но, как мы уже заметили выше, такое положение дел встречается крайне редко.
Для нас же здесь важным является то, что при вложении свободных денежных средств сегодня в какой-либо (долгосрочный) проект
инвестор должен рассчитать/оценить будущий возврат вложенных средств, как минимум, с точки зрения потери покупательной способности.
Или, говоря научным языком, необходимо продисконтировать будущий финансовый поток инвестиционного проекта
(без учета возврата инвестиционных вливаний), тем самым, привести все движения денежных средств в рамках одноименного отчета
финансовой модели инвестпроекта к настоящему моменту, после чего сравнить итог с вложенной суммой инвестиций, также приведенной
к настоящему моменту, в случае если инвестиционные вложения происходят не единовременно в начальный момент,
а как-то распределены в рамках периода реализации проекта (в соответствии с графиком инвестирования).
Классическая формула такого расчета, а именно расчета приведенного к настоящему моменту финансового потока инвестиционного п
роекта без учета возврата инвестиционных вливаний имеет следующий вид:
PV = ∑t=1,2,…,n CFt / (1 + d)t.
Здесь через PV (Present Value) обозначен приведенный к «настоящему» моменту (моменту начала инвестиционного проекта) объем
финансового потока инвестпроекта. Через CFt обозначена величина финансового потока периода t в номинале, которая в
свою очередь равна разнице между притоком CF+t и оттоком CF—t
денежных средств (ДС) за период t при реализации проекта:
CFt = CF+t — CF—t, для каждого t=1,2,…,n.
Наконец через d мы обозначили ставку дисконтирования, выражаемую в процентах, и через n – количество базовых периодов,
на которые разделен период реализации (рассмотрения реализации) нашего инвестиционного проекта.
Для простейшей оценки состоятельности или просто окупаемости проекта очевидно, что необходимо произвести сравнение полученной
приведенной стоимости PV инвестпроекта с объемом инвестиционных вложений в него, также приведенных к начальной точке проекта –
обозначим приведенный инвестиционный поток через PIV или, что тоже самое, необходимо сравнить разницу между PV и PIV с нулем.
Эта разница между приведенным (дисконтированным) финансовым потоком проекта и соответствующим инвестиционным потоком обычно
обозначается через NPV и называется чистой приведенной стоимостью проекта или чистым дисконтированным доходом проекта,
и имеет свое выражение в виде следующей формулы:
NPV = PV — PIV = ∑ t=1,2,…,n CFt / (1 + d)t — ∑ t=1,2,…,n It / (1 + d)t,
где через It обозначен объем инвестиционных средств, которые предполагается вложить в проект за период t.
Таким образом, если NPV > 0, то проект окупается и, как минимум, его можно рассматривать.
На практике ставка дисконтирования может «плавать» год от года. Например, ЦБ может для макроэкономики страны устанавливать
стратегическую цель, в соответствии с которой предполагается «борьба с инфляцией» и которая буквально формулируется так:
«в течение следующих пяти лет мы планируем добиться снижения инфляции с нынешних 12% до 4% через пять лет, так чтобы в следующем
году инфляция составила 10%, через два года 7% и далее в течение очередных трех лет снижение инфляции происходило ежегодно на один
процентный пункт до целевого уровня в размере 4%». Стратегия? Да, конечно, стратегия и вполне себе определенная…
В таком случае, обладая, так сказать, сегодня таким знанием странно было бы не учитывать его (знание о стратегии государства)
для планирования инвестиционных проектов будущего.
Тогда формула расчета NPV будет иметь следующий вид:
NPV = ∑ t=1,2,…,n CFt / Dt — ∑ t=1,2,…,n It / Dt,
где для каждого t=1,2,…,n через Dt обозначается произведение
Dt = (1 + d1) * (1 + d2) * … * (1 + dt),
где в свою очередь di — ставка дисконтирования i-того периода.
Приведем пару примеров. Пусть «на руках» имеются 10 млн. руб., которые их владелец планирует сохранить для своего однолетнего
ребенка для его обучения (поступления, оплаты обучения, проживания и т.п.) в ВУЗе через 15 лет. Допустим в первом случае он (владелец)
кладет эти деньги в банк под 9% годовых, а во втором случае – покупает квартиру в Москве для сдачи ее в аренду, денежные средства от
которой он также кладет в банк под 9% годовых, постепенно накапливая депозит. Также будем предполагать, что согласно условиям
депозитного договора и в том и другом случае период капитализации депозита составляет один год, причем во втором случае владелец
собирает в течение года денежные средства, поступающие от сдачи в аренду квартиры и потом общую сумму кладет на депозит в начале очередного года.
Для начала будем считать, что финансовые условия в течение 15 лет не меняются и общая официальная инфляция составляет 10%.
Тогда в первом случае на конец 15-ого года владелец 10 млн. руб. в номинале получит сумму из банка в размере:
10млн.руб. * (1 + 9%)15 = 36,4млн.руб.
Если в качестве коэффициента дисконтирования рассмотреть инфляцию в размере 10% и привести к начальному моменту,
полученные через 15 лет 36,4 миллиона, то получим:
36,4млн.руб. / (1 + 10%)15 = 8,7млн.руб.
То есть с точки зрения покупательной способности денежных средств потери составят разницу между 10-тью изначальными миллионами
рублей и приведенными к начальному моменту 8,7 млн.руб., равную 1,3млн.руб.
Теперь возвращаемся к сформулированной выше цели вложения денежных средств на 15 лет – сохранение денег для обучения ребенка в ВУЗе.
Это значит, что такое вложение является целевым, под покупку конкретного продукта (образовательных услуг) через 15 лет, и поэтому не
совсем корректным является применение общего показателя инфляции в качестве ставки дисконтирования.
Следовательно необходимо, как минимум, изучить и спрогнозировать средний уровень инфляции в сфере предоставления услуг обучения ВУЗами,
и если он окажется ниже 9% (ставки банковского депозита), то вложение очевидно является состоятельным по отношению к выбранной цели.
Причем имеет смысл рассмотреть в том числе и вариант, когда инфляция услуг обучения, которая в нашем случае берется за
коэффициент дисконтирования, ниже годовой ставки банковского депозита. В этом случае родитель ребенка получает доход, что немаловажно.
Если, например, стоимость услуг обучения в ВУЗе растет год от года в среднем на 7%, то «родитель-инвестор» может рассчитывать на доход,
размер которого с точки зрения его приведенной стоимости составит:
(36,4млн.руб. — 10млн.руб. * (1 + 7%)15) / (1 + 10%)15 =
= (36,4млн.руб. – 27,6млн.руб.) / (1 + 10%)15 =
= 8,8млн.руб. / (1 + 10%)15 = 2,1млн.руб.
Здесь мы естественно для дисконтирования применяем общий показатель инфляции (10%), поскольку не знаем на что родитель-инвестор
собирается потратить свой дополнительный доход. Заметим, что воспользоваться рассчитанной приведенной суммой в размере 2,1 миллиона
в полном объеме наш заботливый инвестор сможет только через 15 лет – как видно из расчетов, тогда это уже будет сумма в номинале
в размере 8,8 млн.руб.
Если же наш владелец начального капитала пожелает каждый год выводить свой дополнительный доход при начислении процентов и
не оставлять далее на депозите эти 2%, например, будет тратить на свою текущую жизнь, то в таком случае его приведенный к
начальному моменту времени дополнительный доход составит 2,3 млн.руб. – предлагаем читателю самому произвести необходимые расчеты,
чтобы убедиться в этом. То есть получается, что при таком подходе родитель получит больший доход (с точки зрения стоимости денег)
и при этом еще и сможет им воспользоваться в течение 15-ти лет, а не после их прошествия, что на первый взгляд кажется странным и
логически неверным, но именно расчеты показывают верность такого заключения.
Теперь обратимся ко второму из рассмотренных вариантов сохранения денежных средств – к инвестпроекту вложения капитала в квартиру
с целью ее сдачи в аренду. Допустим за 10 млн. руб. покупается «двушка» в Москве в районе, где ее можно сдавать ежемесячно за 50 тыс. руб.,
и денежные средства, получаемые в качестве оплаты услуг аренды, накапливаются в течение года и кладутся на депозит со ставкой 9%
и с такими же прочими условиями по депозиту, как и выше.
При условии, что купленная квартира будет продана через 15-ть лет, получаем следующую формулу для номинального дохода
нашего второго «инвестпроекта»:
I * (1+i1)n + RY * ∑ t=0,1,…,n-1 (1+i2)t * (1+r)n-t-1.
В этой формуле через I обозначен объем начальных инвестиций, равный 10 млн.руб., через i1 и i2обозначены
прогнозные уровни инфляции для стоимости квартир и стоимости услуг аренды соответственно в рассматриваемом регионе,
через RY обозначен годовой доход от сдачи квартиры, в нашем случае он равен 600 тысяч рублей (50т.р./мес. умножить на 12 месяцев),
наконец, через r обозначена годовая ставка по депозиту, равная в нашем случае 9%, и n – период инвестиционного проекта в количестве лет,
составляющий 15 лет согласно наших предпосылок.
Теперь если предположить, что в среднем ежегодный прирост стоимости купленной квартиры составит i1=3%,
и уровень прироста ставки ее аренды также будет i2=3%, то не сложно посчитать по приведенной формуле,
что в конце 15-ого года объем денег на руках инвестора составит ровно те же 36,4 млн. руб. – столько же сколько при вложении начальных
10-ти миллионов на депозит под 9% годовых, см. расчет выше.
Встроив, например, в EXCEL-файл все приведенные здесь формулы можно получить удобный финансовый калькулятор,
с помощью которого легко будут просчитываться и сравниваться между собою результаты возможных вариантов вложений
денежных средств и пользователь сможет принимать соответствующие решения.
Итак, уже на этом этапе рассмотрения основ NPV-анализа понятно, что вопрос об уровне ставки дисконтирования не такой уж и тривиальный.
В отношении ставки дисконтирования важно то, чтобы «потребности инвестора совпадали с его возможностями», поскольку ставку дисконтирования
еще определяют, как уровень средней ежегодной доходности альтернативного инвестиционного проекта или альтернативного вложения капитала.
Инвестор конечно же может для себя определять/рассчитывать ставку дисконтирования по какой-либо из известных классических формул,
общая суть которых сводится к следующей (формуле):
d = i + r + σ.
Которая «читается» так: ставка дисконтирования равна уровню инфляции i плюс «желаемый» уровень чистой (с учетом инфляции)
доходности вложенного капитала r плюс премия за риск σ. И, если опять же обыденно смотреть на эти вещи, то означает это
примерно то, что инвестор не желает потерять покупательную способность инвестированных денежных средств в связи с инфляцией i,
т.е. необходимо сохранить капитал, и при этом желает получить чистый, очищенный от инфляции доход r, другими словами,
успешная реализация инвестиционного проекта должна привести к приросту капитала с точки зрения его реальной рыночной ликвидности,
ну и третье слагаемое σ в этой формуле означает, что инвестор не прочь получить еще и «небольшой» бонус или сверхдоход за то,
что «отважился на вход» в проект с определенной долей риска, который оценивается в размере σ.
Вполне себе нормальное желание, если не брать в расчет того факта, что с такой «желаемой» доходностью у инвесторов чаще
всего нет альтернативных инвестпроектов, поэтому в результате ставку дисконтирования просто-напросто приводят к уровню ставки
банковского депозита, усредненной по, например, первой десятке банков и от этого отталкиваются.
Если рассмотреть чистый дисконтированный доход проекта, как функцию от ставки дисконтирования NPV(d)и решить уравнение
NPV(d) = 0,
т.е. найти такой уровень ставки дисконтирования d, при котором приведенный финансовый поток проекта сравняется с приведенными
инвестиционными вложениями в него. То мы получим крайне важный показатель, характеризующий эффективность инвестиционного проекта,
а именно внутреннюю норму доходностиинвестпроекта, обозначаемую через IRR — Internal Rate of Return, и, как мы уже сказали выше,
получаемую из уравнения:
NPV(IRR) = 0.
В общем случае данное уравнение согласно хорошо известной теореме Абеля из курса алгебры, которая говорит о том,
что уравнения, начиная с пятой степени, не имеют представления корней в радикалах, нельзя решить так, чтобы прописать
единую формулу, например, для расчета IRR в EXCEL в рамках финансовой модели инвестиционного проекта. Поэтому обычно
используется итерационный метод дихотомии нахождения приближенного значения внутренней нормы доходности IRR проекта с наперед заданной точностью.
Например, в приведенной нами в начале этой страницы финансовой модели инвестиционного проекта в EXCEL внутренняя норма
доходности IRR инвестпроекта рассчитывается во вкладке «NPV» в строках с 61ой по 160тую путем применения метода дихотомии с
50-тью итерациями.
Суть метода дихотомии нахождения внутренней нормы доходности IRR состоит в том, чтобы заключить ставку IRR между двумя
такими аргументами d0 и d1, что выполняются одновременно два неравенства:
NPV(d0) > 0 и NPV(d1) < 0.
После чего отрезок (d0,d1) делится пополам – обозначим соответствующий аргумент через d2,
и в случае если NPV(d2)>0, то в качестве отрезка (d0,d1) при следующей итерации рассматривается
отрезок (d2,d1) или если NPV(d2)<0, то в качестве отрезка (d0,d1)
при следующей итерации рассматривается отрезок (d0,d2). И так далее, проведя достаточное количество
подобных итераций, мы можем получить приближение к значению внутренней нормы доходности IRR с любой наперед заданной точностью.
В случае если внутренняя норма доходности IRR инвестиционного проекта оказалась выше рассматриваемой инвестором,
«комфортной» для него ставки дисконтирования dI, т.е.
IRR > dI,
то считается, что проект имеет смысл рассматривать.
Или если анализируются одновременно несколько возможностей инвестирования в различные проекты, то при прочих равных возможностях
предпочтение отдается тому инвестпроекту, у которого внутренняя норма доходности выше или, что тоже самое, тому проекту,
который выдерживает больший уровень дисконтирования.
В приведенных выше двух примерах при вложении 10-ти миллионов рублей родителем-инвестором предполагалось,
что в конце периода инвестирования денежные средства в полном объеме выводились «на руки» либо с банковского депозита,
либо при продаже квартиры через 15 лет, так сказать, инвестиционный проект имел некое завершение для инвестора.
Но, вообще говоря, можно рассматривать вложения в инвестиционные проекты, при которых не предполагается окончания действия проекта,
т.е. проект можно рассматривать, как бесконечно действующий с точки зрения жизни инвестора и в том числе его наследников,
что означает предположение о том, что активы в которые вложены инвестиционные денежные средства или соответствующий капитал
будут неограниченно долго генерировать постоянный, например, ежегодный доход.
В случае с банковским депозитом этот доход будет ежегодно составлять 900 тыс. руб., при условии что не происходит капитализации
по депозиту, если, например, вкладчик выводит проценты на текущие нужды. В случае со сдачей квартиры в аренду ежегодный доход составит
600 тыс. руб., умноженные на инфляционный коэффициент, в нашем случае это 1+i2, где i2 –
инфляция арендных ставок на рынке сдачи жилья в рассматриваемом регионе.
Мы же рассмотрим в этой связи вложения в акции на фондовом рынке с целью систематического получения дивидендов,
т.е. без цели их перепродажи по более высокой цене. Пусть дивиденды по купленным акциям какого-либо эмитента составляют p рублей,
пусть также ежегодно прогнозируется увеличение объема дивидендов по данному эмитенту на i процентов, тогда приведенный финансовый
поток при таком инвестиционном вложении будет иметь следующий вид:
∑ t=0,1,…,∞ p * ( 1 + i )t / ( 1 + d )t,
где, как обычно, d – ставка дисконтирования.
Соответственно мы получаем бесконечную сумму геометрической прогрессии со знаменателем
q = ( 1 + i ) / ( 1 + d ).
Из математики хорошо известно, что такая сумма имеет конечное значение, если знаменатель qположителен и меньше единицы,
т.е. в нашем случае если ставка дисконтирования d больше ожидаемого среднегодового прироста размера дивидендов i.
Предположим, что именно так и есть в рассматриваемом нами случае: 0 < q < 1 или i < d.
Посчитаем чему равна указанная сумма или чему равен в этом примере приведенный финансовый поток неограниченных
по сроку дивидендных выплат. Для этого сначала посчитаем чему равна сумма первых n+1членов геометрической прогрессии
Sn = ∑ t=0,1,…,n p * qt.
Имеет место система двух уравнений:
Sn+1 — Sn = p * qn+1,
q * Sn — Sn+1 = -p.
Из первого уравнения получаем
Sn+1 = Sn + p * qn+1.
Подставляем полученное выражение для Sn+1 во второе уравнение и получаем искомую сумму первых n+1членов нашей геометрической прогрессии:
Sn = p * ( qn+1 — 1 ) / ( q – 1 )
или, как чаще она (формула) выглядит:
Sn = p * ( 1 — qn+1 ) / ( 1 — q ).
Теперь устремляя n в бесконечность получаем приведенный финансовый поток PV дивидендных выплат по акциям нашего эмитента:
PV = p / ( 1 — q ),
куда вместо q подставляем выражение ( 1 + i ) / ( 1 + d ) и имеем окончательную формулу приведенного финансового потока для нашего примера:
PV = p * ( 1+ d ) / ( d — i ).
В заключение предположим, что родитель-инвестор из нашего второго примера не собирается продавать через 15-ть лет квартиру,
купленную за 10-ть миллионов, да и вообще никогда не собирается продавать, а просто планирует получать арендные платежи с
квартиросъемщиков и тратить их на текущую жизнь, т.е. по аналогии с вложениями в акции в качестве дивидендного дохода p он
имеет 600 тысяч рублей. Тогда если общая инфляция d, как было рассмотрено выше и которая считалась в качестве ставки дисконтирования,
составляет 10%, а инфляция по арендным платежам i предполагается равной 3%, то наш родитель получит от вложения в квартиру сумму равную
PV = p * ( 1+ d ) / ( d — i ) = 600 тыс. руб. * ( 1 + 10% ) / ( 10% — 3% ) = 9 429 тыс. руб.
То есть прогнозный приведенный доход будет вполне себе сравним с изначально вложенными 10-тью миллионами рублей.
Аналогично каждому инвестору приходится рано или поздно принимать решение о том, чтобы остаться в инвестпроекте и
получать бессрочный, рассчитываемый по подобным формулам, приведенный дисконтированный доход на вложенный инвестиционный капитал,
или выйти из него взяв свою долю здесь и сейчас по текущей рыночной цене.
Вообще говоря, финансовая и инвестиционная математика – дело заманчивое и интересное. Но, как мы видим из примеров этого раздела,
помимо всего прочего еще и важное. Приведем еще один простой пример наглядно иллюстрирующий место высшей математики
в сфере принятия инвестиционных решений.
Как обычно, сформулируем начальные предпосылки для очередного нашего примера.
Допустим Вы решили сажать картошку в Подмосковье, собирать урожай и потом его продавать.
Для этого Вам предположим необходимо купить лопату и землю, т.е. произвести инвестиционные вложения
во внеоборотные активы для производства картофеля.
Пусть также при выборе лопаты Вам предлагают два экземпляра за одну и ту же цену, отличающиеся между собой только длиной черенка.
Тогда естественно Вы выбрать должны более длинный экземпляр при прочих равных условиях.
Как в этом случае принять решение без прибегания к математическим расчетам?
Очевидно, необходимо приложить обе лопаты к общему началу отсчета кончиками черенков и визуально сравнить их длины,
и соответственно принять решение о покупке той лопаты, которая оказалась на Ваш взгляд в буквальном смысле длиннее.
Итак, одно инвестиционное решение принято.
Теперь предположим, что Вам за одну и ту же цену предлагают два участка земли, один из которых на юге Подмосковья,
а другой – на севере. Понятно, что в этом случае приложить их друг к другу, чтобы увидеть какой больше, а какой меньше, не получится,
да и предположим еще, что «на глаз с вертолета» их тоже невозможно оценить, поскольку их границы не квадратные или прямоугольные, а какие-то
разнообразно кривые. Естественно для принятия решения без математики здесь уже не обойтись – для принятия решения о покупке,
о втором принципиальном инвестиционном вложении средств, Вам необходимо рассчитать площадь каждого участка,
т.е. поставить в соответствие каждому объекту вложения некоторое число, а именно число гектаров земли, после чего сравнить эти
два числа на предмет больше-меньше.
Если Вы сами не владеете методами расчета площади земли, то Вам придется нанять специального оценщика,
который рассчитает площади каждого из участков. Отметим здесь, что за расчет площадей в математике отвечают интегралы,
ну а на практике, например, метод триангуляции.
Отлично! Оценщик посчитал и «принес Вам на блюдечке» две цифры, Вы заплатили за участок, который имеет бОльшую площадь, и
Ваш проект стартанул.
Здесь-то и возникает главный вопрос: математика-то математикой, а вдруг оценщик ошибся в расчетах или хуже того по каким-либо
причинам оказался недобросовестным и специально произвел расчеты так, что по факту меньший участок земли получил в соответствие
при расчетах оценщика большую площадь, и Вы в результате приняли неверное решение, а это значит, что, как минимум,
Вам придется дольше «отбивать» свои инвестиционные вложения.
Конечно же математика важна, но вопрос доверия при инвестировании не менее важен. Жизнь знает огромное количество самых разных
примеров: и когда инвестиционные расчеты заведомо были неверными, а инвестор принимал решение в пользу таких проектов,
доверяя представившим эти расчеты инвестиционным аналитикам, после чего «вылетал в трубу», и когда расчеты были верными,
а люди представлявшие такие расчеты и желающие запустить свой «супермега» проект были профессионалами своего дела и
кристально честными, но инвестор отказывался от вложений, поскольку по причинам известным только ему самому он не доверял
этим людям и, тем самым, упускал прекрасную возможность хорошо заработать.
Никакая премия за риск в рамках расчетов ставки дисконтирования не защитит Вас от лопнувшего недобросовестного банка,
в который Вы положите деньги в сумме, большей, чем максимальный размер застрахованного вклада по системе страхования вкладов,
или от сгоревшей квартиры, которую Вы сдадите недобросовестному квартиросъемщику, или от недобросовестных топ-менеджеров инвестиционного
проекта, куда Вы вложили Ваши кровные, откуда, упомянутые топ-менеджеры выведут в оффшоры оборотные средства предприятия,
а точнее просто своруют их.
Вопросы доверия находятся в области, так называемых, неявных факторов, изучением нивелирования негативного влияния которых
занимается теория управления рисками. И если кратко, то основной вывод этой теории состоит в том, что главным спасением от этих
самых неявных факторов или главным спасением от реализации рисков негативного воздействия является выстраивание такой системы
принятия решений, при которой своевременно принимаются компетентные и правильные решения, короче говоря, необходимо «держать нос по ветру»,
а «ухо востро».
Данная тема, равно как управление рисками, так и формирование эффективной системы принятия решений, будет рассмотрена нами подробно
в других одноименных разделах сайта, а сейчас мы переходим к изложению методологии финансового моделирования инвестиционного
проекта или просто – методологии инвестиционного моделирования, на примере финмодели, EXCEL-файл с которой был выложен для
скачивания в начале настоящей статьи и который можно также
скачать здесь.
Легенда инвестиционного проекта, моделирование которого представлено в EXCEL-файле, заключается в следующем.
Инвестиционные средства вкладываются в создание производства некоторых товаров, в проекте они названы готовой продукцией,
прибыль от продажи которых направляется на погашение задолженности производственного предприятия перед инвесторами.
Срок инвестирования рассматривается в размере 10-ти лет, расчеты финмодели производятся в ежемесячной динамике, начало периода
пользователь может задавать сам из выпадающего списка первых чисел различных годов.
С точки зрения специфики объектов капитальных затрат финмодель различает только то, что на инвестиционные средства
приобретается производственная инфраструктура, без уточнения способа приобретения – будь то строительство с нуля или покупка
готовых производственных мощностей (зданий, сооружений, оборудования и т.п.), включающая в себя склад сырья и материалов и
склад готовой продукции, а также площади для персонала, в том числе офисные для управленческого персонала,
т.е. аренды офисов не предполагается, также как не предполагается капитальных вложений в торговую и логистическую
инфраструктуру – нет своих магазинов и транспортных средств – логистика на аутсорсинге.
Финмодель позволяет задавать уровень максимальной выработки готовой продукции в месяц, при этом план продаж в количестве
готовой продукции задается независимо от максимальной выработки производства. Поэтому в инвестиционной модели предусмотрена
возможность расширения или масштабирования производства путем капитальных вложений в дополнительные производственные модули,
подобные изначальному, источником финансирования которых также являются инвестиции.
То есть предполагается, что если в какой-либо будущий период для выполнения плана продаж необходимо производство продукции
в объеме превосходящем максимальную выработку одного производственного модуля, то финмодель автоматически рассчитывает
инвестиционные капитальные затраты на создание дополнительных производственных мощностей, тем самым, формируется инвестиционный поток модели.
EXCEL-файл с инвестиционной моделью состоит из 10-ти вкладок, в первой из которых, во вкладке «оглавление» представлен список с
указанием содержания оставшихся 9-ти вкладок и гиперссылками на них (в файле финмодели предусмотрена возможность перемещения между
вкладками посредством гиперссылок через оглавление), кратко это выглядит так:

В листе «условия» пользователь финмодели задает основные исходные условия для моделирования инвестиционного проекта.
Начинается все с задания даты старта проекта в ячейке M11 из выпадающего списка дат (набор дат этого списка можно поменять во вкладке «структура»,
в столбце D). После чего в строках 7, 8 и 9 происходит автоматическая разбивка инвестиционного периода на 10-ть последующих лет.
В строке 13 «условий» задаются общие ежегодные объемы капитальных затрат в тысячах рублей на инфраструктуру одного
производственного модуля, с которого проект начинает операционное функционирование.
В строках с 15-той по 48-ую производится ежемесячная разбивка общих сумм капитальных затрат из 13-той строки.
Здесь предусмотрены следующие три способа разбивки, выбор которых осуществляется через выпадающий список ячейки M11
со следующими значениями (названия которых можно поменять во вкладке «структура» в столбце G):
— равномерно по году;
— равномерно с…по…;
— вручную.
При выборе способа «равномерно по году» в строках с 35-той по 46-ую общие суммы из 13-той строки просто делятся на 12
для каждого месяца соответствующего года. При выборе способа «равномерно с…по…» в строках 17 и 18 необходимо выбрать
из списка номера месяцев начала и окончания капитальных вложений данного года, после чего финмодель автоматически распределит
равномерно по выбранным месяцам общие объемы капитальных вложений в блоке строк с 35-ой по 46-ую. Наконец при выборе способа «вручную»
Вам будет предложено в строках с 21-ой по 32-ую просто задать процентное распределение по месяцам года общих сумм капзатрат.
В строке 48 задается номер месяца ввода в эксплуатацию объектов капитальных затрат, причем если этот номер не совпадает
с номером месяца последних ненулевых ежемесячных объемов капзатрат, то ввод в эксплуатацию будет рассчитан в два этапа:
сначала будет введен в эксплуатацию весь объем до указанного месяца, включая его, потом в последний месяц ненулевых объемов
будет введен в эксплуатацию оставшийся объем внеоборотных активов.
В ячейке Q50 задается количество лет амортизации производственных объектов.
В строках с 52-ой по 56-тую задаются ограничения на производственные и складские мощности одного производственного модуля:
максимальный ежемесячный объем выпуска готовой продукции задается в ячейке Q52, объем собственного склада готовой продукции
задается в ячейке Q54, как процент от максимальной ежемесячной выработки, объем собственного склада сырья и материалов – в ячейке Q56
(в удельном пересчете на единицы готовой продукции).
В блоке строк с 58-ой по 77-ую задается план продаж в количестве единиц готовой продукции,
как произведение количества потенциальных клиентов/покупателей в регионе продаж (строка 58), прогнозной целевой доли рынка сбыта,
которую планирует занять предприятие в регионе, (строка 60) и среднее количество единиц продукции, которое будет покупать клиент,
(строка 62).
Операционный цикл нашего предприятия состоит из производственного цикла и торгового цикла, первый из которых
начинается покупкой сырья и материалов и заканчивается выпуском готовой продукции и размещением ее на собственный склад.
Торговый цикл начинается с размещения готовой продукции на склад предприятия и заканчивается ее продажей клиентам.
Соответствующие периоды оборачиваемости или длины указанных циклов задаются в строках 79 и 81.
Такие показатели, как бюджет закупки сырья и материалов, бюджет производства готовой продукции, остатки на конец периода запасов
сырья и материалов, а также готовой продукции, рассчитываются в рассматриваемой финансовой модели с точки зрения классического подхода,
через коэффициенты оборачиваемости, отталкиваясь от бюджета продаж.
Например, для того чтобы рассчитать план производства готовой продукции за период мы используем формулу:
ГП = ГП1 — ГП0 + S,
где ГП1 и ГП0 – соответственно остатки готовой продукции на конец и начало периода, S – продажи готовой продукции за период.
При этом расчет объема готовой продукции ГП1 на конец периода производится по такой формуле (можно посмотреть в любом учебнике):
ГП1 = [ 2 * S * Поб(ГП) / кол-во дней периода ] — ГП0,
которая вытекает из классического определения коэффициента и периода оборачиваемости запасов готовой продукции, где Поб(ГП) –
заданный в строке 79 вкладки «условия» период оборачиваемости готовой продукции.
Естественно задавая объем запасов ГП0 для первого периода нашей инвестмодели равным нулю, мы последовательно
применяя вышеприведенные формулы для каждого очередного периода, а в нашем случае это месяцы (см. вкладку «monthly»),
получаем объемы производства за период и остатки запасов ГП на конец периода.
Аналогично рассчитываются объемы закупки сырья и материалов за период, а также запасы на конец периодов сырья и материалов
через заранее рассчитанный план производства готовой продукции и заданный в строке 81 период оборачиваемости запасов сырья и
материалов относительно выпуска готовой продукции.
Заметим лишь то, что формулы с оборачиваемостью запасов и готовой продукции мы применяем в финмодели для продаж выраженных в натуральных
величинах, т.е. в количестве единиц готовой продукции, после чего задавая в строках 83, 85 и 104 соответственно плановую себестоимость
продукции, прогнозную инфляцию в рамках стоимости сырья и материалов, а также наценку при продажах, получаем бюджет закупок,
план производства и остатки запасов сырья и материалов и готовой продукции в деньгах, в нашем случае в тысячах рублей.
Все расчеты инвестиционной модели происходят в ежемесячной детализации во вкладке «monthly», после чего данные поступают в
листы нашего EXCEL-файла с итоговыми формами финансовой управленческой отчетности, см. оглавление выше по тексту.
Отчет о прибылях и убытках или как сейчас стало принятым говорить, «отчет о финансовом результате (P&L) в финмодели представлен
в двух вариантах, а именно в виде маржинального P&L и функционального P&L – вкладки «PL_m» и «PL_f».
В маржинальном отчете о прибылях и убытках все расходы разделяются на переменные и постоянные, т.е. на те статьи, которые
зависят от тех или иных доходных показателей и на статьи, прямо не зависящие от них. С шаблоном/форматом маржинального P&L
можно ознакомиться ниже:

В функциональном отчете о прибылях и убытках все расходы разделяются по принципу функциональной принадлежности,
т.е. разделение статей расходов происходит согласно утвержденной оргструктуры предприятия, с шаблоном/форматом функционального P&L
можно ознакомиться ниже:
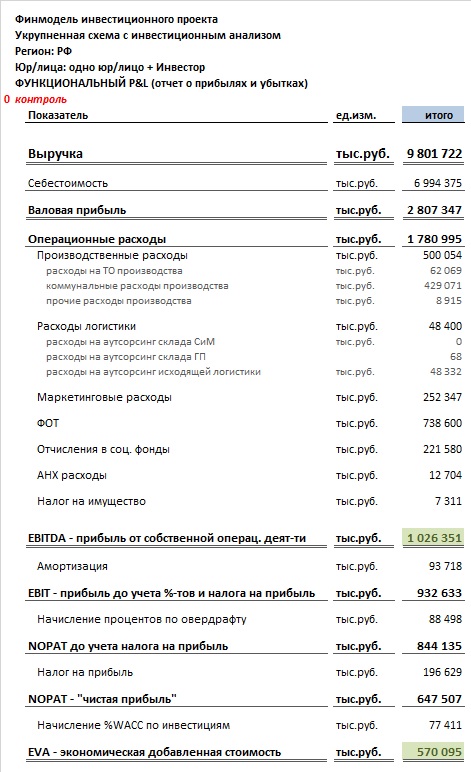
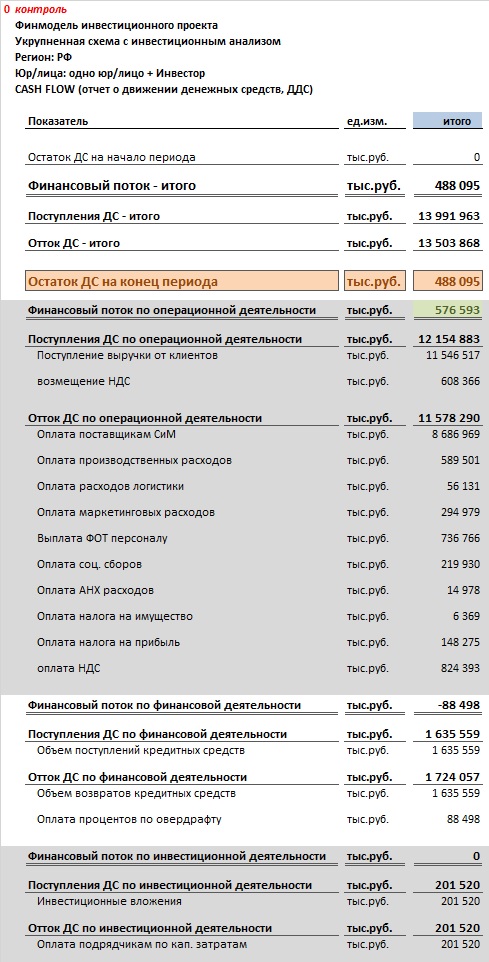
Шаблон/формат отчета о движении денежных средств (Cash Flow), который используется в финмодели выглядит следующим образом:
Формат баланса мы не будем выкладывать, потому как если читателя уже заинтересовала наша финансовая модель инвестиционного проекта,
то наверняка Вы ее скачаете и самостоятельно ознакомитесь с ним (с форматом/шаблоном баланса).
Мы же обратимся к рассмотрению вкладки «NPV», в которой как раз таки с использованием EXCEL-формул проводится NPV-анализ,
где рассчитываются такие показатели, как:
— NPV инвестиционных вложений (Inv);
— NPV потока ДС (CF);
— возврат инвестиций;
— PP — период окупаемости;
— NPV CF после инвестиционного периода;
— PI инвестиционного периода;
— NPV полный;
— PI полный;
— ROI инвестиционного периода;
— ROI полный;
— средняя ставка дисконтирования инвестпроекта;
— IRR — внутренняя норма доходности.
Формат отчета с NPV-анализом инвестпроекта следующий:
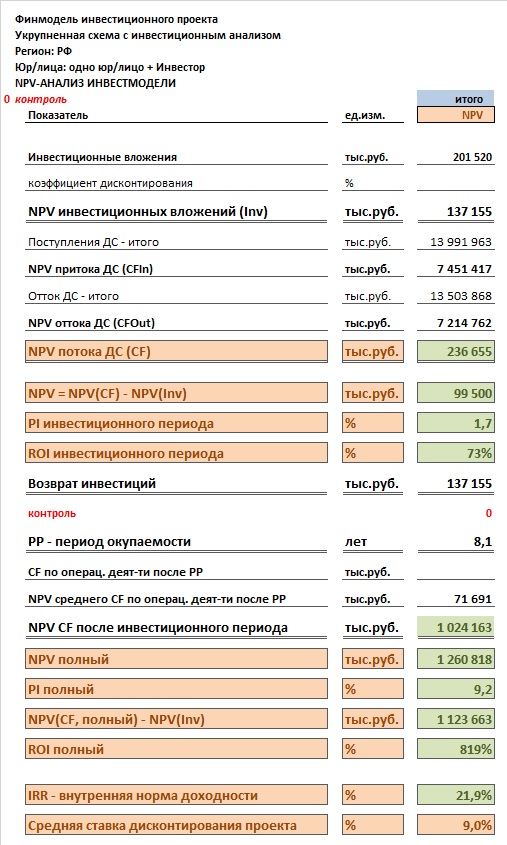
Итак, мы рассматриваем вкладку «NPV». В 12-тую строку этой вкладки мы из отчета Cash Flow вкладки «CF» вносим с помощью
EXCEL-формул данные о потоке инвестиционных вложений в проект на капитальные затраты для создания того количества производственных модулей,
которое необходимо в соответствии с планом продаж готовой продукции.
В строке 14 производится расчет коэффициентов дисконтирования для каждого года на основе данных из строки 188
вкладки «условия», куда пользователь в свою очередь вносит вручную прогнозные ставки дисконтирования финансового потока
отдельно для каждого года инвестпроекта, напоминаем, что эти ставки в общем случае могут быть различными от года к году.
Приведенная стоимость инвестиционных вложений рассчитывается в строке 16 путем суммирования последовательных частных
от деления для каждого года строки 12 с номинальными объемами инвестиций на соответствующие коэффициенты дисконтирования из строки 14.
Далее в строках 20 и 24 рассчитываются аналогичным образом приведенные стоимости притоков и оттоков денежных средств проекта
без учета возврата инвестиционных займов, но с учетом финансовой деятельности предприятия, если топ-менеджменту последнего
пришлось привлекать кредиты на пополнение оборотных средств операционной деятельности.
Рассматриваемая модель предполагает, что инвестиции направляются только на производственную инфраструктуру,
а на поддержание операционной деятельности в случае возникновения кассовых разрывов топ-менеджмент предприятия должен сам
найти возможность привлечения соответствующих кредитов и займов, объемы которых наша финмодель рассчитывает автоматически
через модель овердрафтного кредитования и учитывает эти операции в рамках блока с движением денежных средств по финансовой
деятельности в отчете Cash Flow.
Другими словами, в строке 26 рассчитывается приведенный финансовый поток по основной и финансовой деятельности или, что тоже самое,
финансовый поток по операционной деятельности предприятия, который как раз таки и необходимо сравнить с приведенным потоком инвестиций
из строки 16, что и делается в ячейке M29, в которой считается указанная разница. С помощью условного форматирования EXCEL
ячейка M29закрашивается в зеленый цвет, если значение в ней больше нуля, т.е. проект состоятелен (приведенный финпоток
по операционной деятельности больше приведенного инвестпотока), и окрашивается в красный, если наоборот – проект убыточен
при прочих равных условиях с точки зрения инвестора.
В ячейках M31 и M33 рассчитываются значения показателей PI и ROI:
PI — Profitability Index — Индекс прибыльности инвестиций — равен отношению приведенного финансового потока по операционной
деятельности к приведенной стоимости инвестиционных вложений – очевидно, что должен быть больше единицы, чтобы проект был
предложен к рассмотрению;
ROI — Return On Investment — Рентабельность инвестиций — равен отношению NPV к приведенной стоимости инвестиций.
В строке 35 производится расчет потока возврата инвестиций, в связи с чем в ячейке M39 рассчитывается показатель
PP — Payback Period — Период возврата или окупаемости инвестиций — равен средневзвешенному по суммам возврата количеству лет,
по прошествии которых инвестору вернутся все вложенные в проект денежные средства с учетом заданного уровня дисконтирования.
Далее в блоке строк с 41-ой по 53-тью рассчитываются все уже приведенные ранее показатели эффективности инвестиционного
проекта для случая, если инвестор решит не выходить из проекта, а оставить его для себя «навсегда», см. соответствующие формулы
в первой части этого раздела. Здесь в качестве ежегодного финансового потока на период после 10-ти лет существования проекта
рассматривается средний финансовый поток рассчитанный по периоду следующему после периода окупаемости PP.
Наконец в ячейке M56, а на самом деле в блоке строк с 61-ой по 160-тую путем применения метода дихотомии,
как мы уже отмечали выше, рассчитывается приближенное значение показателя эффективности инвестпроекта IRR —
внутренней нормы доходности. И чтобы его было с чем сравнивать, в случае если от года к году пользователем модели
задаются различные ставки дисконтирования, мы приводим в ячейке M56, с расчетом в блоке строк со 161-ой по 260-тую
среднюю единую для каждого года ставку дисконтирования инвестиционного проекта.
В заключение отметим, что за скобки представленного в настоящей статье материала мы осознанно выносим обсуждение
таких важнейших понятий, как EBITDA и EVA, а также рыночная стоимость чистых активов, философия которых формирует адекватное
понимание того, что такое эффективное управление с точки зрения системы принятия инвестиционных, да и не только, решений.
Также отметим, что взгляд на управление через эти понятия подобен, например, системе управления, называемой «бережливое производство»,
которая сформировалась в Японии. В данном случае речь идет не просто о формулах, через которые формально дается представление
обывателю об этих показателях и связанных с ними понятиях, речь идет о том, как в реальной жизни предприятия внедрить соответствующие
высоко эффективные системы управления, что является базовой отправной точкой для любого инвестора при формировании команды
топ-менеджеров для управления проектом. Указанный материал мы разместим в ближайшем будущем в разделе, посвященном законам
эффективного управления.
Незаполненная инвестиционная модель
СКАЧАТЬ
Незаполненная финмодель инвестиционного проекта, NPV-анализ

Читать далее —
Финмодель инвестпроекта в EXCEL, версия 2.0
Управление финансами
-
Предел потребительского спроса
-
Финансовая стратегия
-
Бюджетирование продаж и закупок
-
Финансовый поток и структура финансового цикла
-
Маржинальный отчет о прибылях и убытках P&L
-
Типовые финансово-хозяйственные операции. Баланс
-
Учет расходов в трех формах финансовой отчетности
-
Отражение бизнес-процесса в балансе предприятия
-
Эффективность операционной деятельности. EBITDA
-
БДДС-Финансовый поток-Кассовые разрывы-Cash Flow
-
Итоговый БДР. Итоговый прогнозный баланс
-
Примеры классических форм бухгалтерской отчетности
-
Финансово-экономический анализ предприятия
-
Период оборачиваемости продаж и товарных запасов
-
Разработка финансовой модели ритейла в EXCEL
-
Инвестиционная модель в EXCEL с NPV-анализом
-
Финмодель инвестпроекта в EXCEL, версия 2.0
-
Финансовые модели бюджетирования
Содержание
- Инвестиционный проект в Excel c примерами для расчетов
- Финансовая модель инвестиционного проекта в Excel
- Расчет экономической эффективности инвестиционного проекта в Excel
- Рентабельность инвестиций
- Что характеризует индекс по доходности и как рассчитать его формулу
- Понятие рентабельности или индекса доходности
- Индекс рентабельности инвестпроекта: методика и формулы
- Значение показателей индекса по доходности
- Роль индекса по доходности в оценке бизнес-плана
- Расчёт доходности в таблице Excel
- Достоинства и проблемы показателя доходности
- Индекс доходности (рентабельности) инвестиций — PI. Формула. Пример расчета в Excel
- Инфографика: Индекс доходности (рентабельности) инвестиций
- Индекс доходности инвестиции. Формула расчета
- Дисконтированный индекс доходности инвестиций. Формула расчета
- Сложности оценки индекса доходности на практике
- Что показывает индекс доходности?
- Мастер-класс: «Как рассчитать индекс доходности для бизнес плана»
- Оценка индекса доходности инвестиции в Excel
- Как произвести экспресс-оценку любого бизнес плана?
- Преимущества и недостатки индекса доходности инвестиционного проекта
Инвестиционный проект в Excel c примерами для расчетов
Для привлечения и вложения средств в какое-либо дело инвестору необходимо тщательно изучить внешний и внутренний рынок.
На основании полученных данных составить смету проекта, инвестиционный план, спрогнозировать выручку, сформировать отчет о движении денежных средств. Наиболее полно всю нужную информацию можно представить в виде финансовой модели.
Финансовая модель инвестиционного проекта в Excel
Составляется на прогнозируемый период окупаемости.
- описание макроэкономического окружения (темпы инфляции, проценты по налогам и сборам, требуемая норма доходности);
- прогнозируемый объем продаж;
- прогнозируемые затраты на привлечение и обучение персонала, аренду площадей, закупку сырья и материалов и т.п.;
- анализ оборотного капитала, активов и основных средств;
- источники финансирования;
- анализ рисков;
- прогнозные отчеты (окупаемость, ликвидность, платежеспособность, финансовая устойчивость и т.д.).
Чтобы проект вызывал доверие, все данные должны быть подтверждены. Если у предприятия несколько статей доходов, то прогноз составляется отдельно по каждой.
Финансовая модель – это план снижения рисков при инвестировании. Детализация и реалистичность – обязательные условия. При составлении проекта в программе Microsoft Excel соблюдают правила:
- исходные данные, расчеты и результаты находятся на разных листах;
- структура расчетов логичная и «прозрачная» (никаких скрытых формул, ячеек, цикличных ссылок, ограниченное количество имен массивов);
- столбцы соответствуют друг другу;
- в одной строке – однотипные формулы.
Расчет экономической эффективности инвестиционного проекта в Excel
Для оценки эффективности инвестиций применяются две группы методов:
- статистические (PP, ARR);
- динамические (NPV, IRR, PI, DPP).
Коэффициент PP (период окупаемости) показывает временной отрезок, за который окупятся первоначальные вложения в проект (когда вернутся инвестированные деньги).
Экономическая формула расчета срока окупаемости:
где IC – первоначальные вложения инвестора (все издержки),
CF – денежный поток, или чистая прибыль (за определенный период).
Расчет окупаемости инвестиционного проекта в Excel:
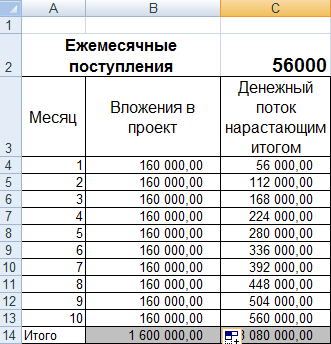
- Составим таблицу с исходными данными. Стоимость первоначальных инвестиций – 160000 рублей. Ежемесячно поступает 56000 рублей. Для расчета денежного потока нарастающим итогом была использована формула: =C4+$C$2.
- Рассчитаем срок окупаемости инвестированных средств. Использовали формулу: =B4/C2 (сумма первоначальных инвестиций / сумма ежемесячных поступлений).
Так как у нас дискретный период, то срок окупаемости составит 3 месяца.
Данная формула позволяет быстро найти показатель срока окупаемости проекта. Но использовать ее крайне сложно, т.к. ежемесячные денежные поступления в реальной жизни редко являются равными суммами. Более того, не учитывается инфляция. Поэтому показатель применяется вкупе с другими критериями оценки эффективности.
Рентабельность инвестиций
ARR, ROI – коэффициенты рентабельности, показывающие прибыльность проекта без учета дисконтирования.
где CFср. – средний показатель чистой прибыли за определенный период;
IC – первоначальные вложения инвестора.
Пример расчета в Excel:
- Изменим входные данные. Первоначальные вложения в размере 160 000 рублей вносятся только один раз, на старте проекта. Ежемесячные платежи – разные суммы.
- Рассчитаем средние поступления по месяцам и найдем рентабельность проекта. Используем формулу: =СРЗНАЧ(C23:C32)/B23. Формат ячейки с результатом процентный.
Чем выше коэффициент рентабельности, тем привлекательнее проект. Главный недостаток данной формулы – сложно спрогнозировать будущие поступления. Поэтому показатель часто применяется для анализа существующего предприятия.
Примеры инвестиционне6ого проекта с расчетами в Excel:
Статистические методы не учитывают дисконтирование. Зато позволяют быстро и просто найти необходимые показатели.
Источник
Что характеризует индекс по доходности и как рассчитать его формулу
Инвестор, прежде чем вкладывать средства в какое-либо предприятие, стремится проанализировать, какая прибыль может быть получена в результате. К числу параметров, посредством которых оцениваются перспективы развития бизнес-проекта, относится PI — индекс доходности. Термин имеет несколько названий — Present value index или прибыльности, DPI или рентабельности.
Понятие рентабельности или индекса доходности
Рентабельность проекта обозначает его прибыльность. С помощью этого показателя оценивают потенциальную доходность любого бизнеса. На практике понятие рентабельности широко применяют для оценки экономического состояния предприятия, конкурентоспособности выпускаемой продукции или оказываемых услуг. Для этого отдельный вид продукции сравнивают с таковым у конкурирующих компаний или с другим видом товара, выпускаемого предприятием.
Этот индекс, как показатель, является универсальным. С его помощью можно сравнивать эффективность и прибыльность проектов различного масштаба. Если выразить индекс как понятие в числах, оно отобразит цифру чистой прибыли, делённую на количество затраченных ресурсов. Поэтому возникло понятие — рентабельности вложенного капитала или, простыми словами, доходности.
Индекс рентабельности инвестпроекта: методика и формулы
Profitability Index для оценки инвестиций задействую, оценивая относительную доходность различных вложений средств. Рассчитать его величину можно с помощью матформулы:
NPV это чистая стоимость входящих инвестпотоков в реальном времени в рублях. I — величина вкладов в инвестпроект в рублях. Для инвестиций Индекс по доходности используют при оценке относительной отдачи предназначенных для идеи финансов. Если вливания капитала в крупный бизнес-проект разнесены на длительный период, в формулу вводится величина дисконтирования по средней норме отдачи за год.
Значение показателей индекса по доходности
Рассчитывать индекс доходности нужно, чтобы определить возможную эффективность от инвестиции в конкретный бизнес-проект, и успешно ли составлен бизнес-план. Чем выше цифра индекса рентабельности для вложений, тем больший доход способна принести идея в перспективе. Результаты анализа полученных данных характеризуются следующим образом:
- Когда значение индекса прибыльности получается менее 1, проект признается не доходным, и делать дальнейшие вливания нецелесообразно.
- Когда индекс равен единице, считается, что финансовые потоки будут равны прибыли от проекта. Для этого случая возможен запуск бизнес-процессов, но требуется его существенная доработка.
- Если показатель индекса доходности превышает единицу, такой бизнес-план признается перспективным и принимается к рассмотрению.
- Если сравниваются 2 показателя от 2 разных планов, к работе принимается тот, у которого выше значение индекса. Считается, что он обладает большим потенциалом к получению прибыли.
Роль индекса по доходности в оценке бизнес-плана
Любой бизнес-план требует проведения серии расчётов в финансовой части. Здесь учитывается несколько главных показателей. На их основании судят о пригодности проекта к воплощению в жизнь. К числу показателей относятся:
- чистая дисконтированная прибыль;
- внутренняя норма доходности;
- индекс доходности;
- дисконтированное время вероятной окупаемости.
Чтобы бизнес-план был принят и одобрен, необходимо, чтобы чистая дисконтированная прибыль была выше 0, а время окупаемости проекта было минимальным. Оценить ставку дисконта можно разными способами. Если планируется вложить кредитные деньги, то минимальной величиной дисконтирования должна быть процентная ставка по кредиту. Здесь полученная прибыль позволит покрыть расходы. Иначе инвестору гораздо выгоднее направить финансы на счёт в банковское учреждение и не рисковать ими в инвестпроектах.
Если же инвестиции проводятся из собственных финансов, ставка доходности вложений должна равняться или быть большей, чем уровень уже имеющейся доходности бизнесмена. Кроме того, цифра ставки дисконтирования нужна меньшей величины налога на прибыль с имеющегося капитала.
Исходя из этих факторов, проводить оценку рентабельности предприятия всегда нужно по нескольким параметрам — индексу доходности, дисконтной ставке и текущей стоимости всех инвестиций. Определение индекса доходности требуется проводить не только перед принятием бизнес-проекта в момент выбора, но и в ходе реализации и после завершения.
Большое значение имеет и величина, обратная индексу. Она называется сроком окупаемости для инвестиций (РР — Pay-Back-Period). Этот показатель позволяет определить, как скоро инвестор получит доход от вложения своего капитала. В России доходы от инвестиционных проектов можно ожидать спустя 3 года. Это связано с особенностями экономических процессов в стране. Для кредитных средств предельным сроком окупаемости считается 5 лет. В странах с развитой экономикой период составляет 7 лет.
Расчёт доходности в таблице Excel
Один из наиболее простых способов расчёта индекса — оценка с помощью Excel. Ее использует большинство инвесторов, так как она отличается простотой, высокой точностью и скоростью операций. С помощью таких таблиц можно подсчитать дисконтированные расходы и прибыль.
Разработано 2 варианта расчётов доходности. Первый из них отличается простым алгоритмом для индекса:
- финансовый поток определяется с помощью формулы CF = С8-D8;
- дисконтированный финансовый поток рассчитывается Е8/(1+ (1+$C4 $)) А8;
- чистый дисконтированный финансовый поток вычисляется как (F8: F16)—B7;
- с помощью отношения F17/B7 можно вычислить индекс прибыльности.
Для доходности существует второй вариант — более сложный. В нем используется встроенная формула, которая помогает рассчитывать параметры, необходимые для определения дисконтированной прибыли.
Достоинства и проблемы показателя доходности
Индекс доходности даёт вкладчику большое количество преимуществ. Можно сравнивать несколько инвестпроектов различных по объёму вложений. Показатель позволяет также применять ставку дисконтирования к инвестидеям, когда трудно прогнозировать и формализовать часть данных. Формулы для обработки довольно просты и не требуют установки дополнительного программного обеспечения. Достаточно внести все исходные в таблицу Excel.
Наряду с этим, индекс имеет некоторые недостатки, которые проявляются во время его использования:
Не всегда получается спрогнозировать уровень влияния различных факторов на финпотоки.
Для некоторых идей норму дисконта бывает сложно вычислить.
Это касается и расчёта планируемых финпотоков.
Стабильность финансовых поступлений обусловлена несколькими внешними факторами. Среди них ведущую роль играют ключевая ставка Центробанка, затраты на приобретение материалов и сырья, а также объёмы реализации готовой продукции. Немаловажную роль играет также действующая финансовая политика компании, и какая экономическая обстановка на тот или иной момент наблюдается в государстве. Все эти факторы оказывают непосредственное влияние на ставку дисконта, следовательно, доходность.
Спрогнозировать их бывает не всегда легко. Чем больше предполагаемый срок жизни проекта, тем выше неопределённость при расчётах. В качестве примера можно привести наложение санкций на некоторые российские предприятия, что негативно отразилось на их экономическом состоянии.
Таким образом, при внешней простоте расчётов по формуле индекса доходности могут возникать неожиданные затруднения, снижающие точность показателя.
По каким формулам и в какой программе вы рассчитываете показатель доходности?
Источник
Индекс доходности (рентабельности) инвестиций — PI. Формула. Пример расчета в Excel
Рассмотрим такой важный инвестиционный показатель как индекс доходности, данный показатель используется для оценки эффективности инвестиций, бизнес-планов компаний, инвестиционных и инновационных проектов.
Индекс доходности (англ. PI, DPI, Present value index, Profitability Index, benefit cost ratio) – показатель эффективности инвестиции, представляющий собой отношение дисконтированных доходов к размеру инвестиционного капитала. Другие синонимы индекса доходности, которые несут аналогичный экономический смысл: индекс прибыльности и индекс рентабельности.
Инфографика: Индекс доходности (рентабельности) инвестиций
Индекс доходности инвестиции. Формула расчета
PI (Profitability Index) – индекс доходности инвестиционного проекта;
NPV (Net Present Value) – чистый дисконтированный доход;
n – срок реализации (в годах, месяцах);
r – ставка дисконтирования (%);
CF (Cash Flow) – денежный поток;
IC (Invest Capital) – первоначальный затраченный инвестиционный капитал.
 |
★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Дисконтированный индекс доходности инвестиций. Формула расчета
Существует модификация формулы индекса доходности инвестиционного проекта, которая позволяет учесть не единовременные затраты (вложения) в первом периоде времени, а вложения в течение всего срока реализации проекта. Для этого все последующие инвестиционные затраты дисконтируются. В результате формула будет иметь следующий вид:
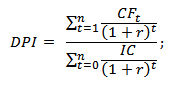
DPI (Discounted Profitability Index) –дисконтированный индекс доходности; NPV – чистый дисконтированный доход; n – срок реализации (в годах, месяцах); r – ставка дисконтирования (%) инвестиции; IC – первоначальный затраченный инвестиционный капитал.
Сложности оценки индекса доходности на практике
Основная сложность расчета индекса доходности или дисконтированного индекса доходности заключается в оценке размера будущих денежных поступлений и нормы дисконта (ставки дисконтирования).
На устойчивость будущих денежных потоков оказывают влияние множество макро-, микроэкономических факторов: сезонность спроса и предложения, процентные ставки ЦБ РФ, стоимость сырья и материалов, объем продаж и т.д. В настоящее время на размер будущих денежных потоков ключевое значение оказывает уровень продаж, на который влияет маркетинговая стратегия фирмы.
Существует множество различных подходов оценки ставки дисконтирования. Сама по себе ставка дисконтирования отражает временную стоимость денег и позволяет привести будущие денежные платежи к настоящему времени. Так если проект финансируется только на основе собственных средств, то за ставку дисконтирования принимают доходности по альтернативным инвестициям, которая может быть рассчитана как доходность по банковскому вкладу, доходность ценных бумаг (CAPM), доходность от вложения в недвижимость и т.д. При финансировании проекта за счет собственных и заемных средств используют метод WACC. Более подробно методы оценки ставки дисконтирования рассмотрены в статье «Ставка дисконтирования. 10 современных методов расчета».
Что показывает индекс доходности?
Показатель индекс доходности показывает эффективность использования капитала в инвестиционном проекте или бизнес плане. Оценка аналогична как для индекса доходности (PI) так и для дисконтированного индекса доходности (DPI). В таблице ниже приводится оценка инвестиционного проекта в зависимости от значения показателя DPI.
| Значение показателя | Оценка инвестиционного проекта |
| DPI 1 | Инвестиционный проект принимается для дальнейшего инвестиционного анализа |
| DPI1>DPI2 | Уровень эффективности управления капиталом в первом проекте выше, нежели во втором. Первый проект имеет большую инвестиционную привлекательность |
Мастер-класс: «Как рассчитать индекс доходности для бизнес плана»
Оценка индекса доходности инвестиции в Excel
Рассмотрим пример оценки индекса доходности с помощью программы Excel. Для этого необходимо рассчитать две составляющие показателя: чистый дисконтированных доход и чистые дисконтированные затраты (если они присутствовали в течение срока реализации проекта). Рассмотрим два варианта расчета в Excel индекса доходности.
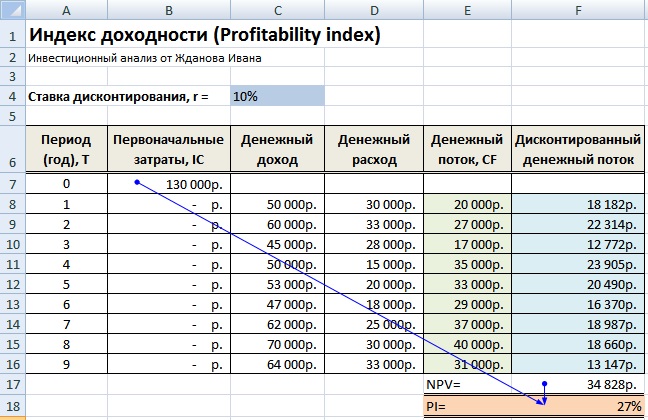
Первый вариант расчета индекса доходности следующий:
- Денежный потокCF (CashFlow) =C8-D8
- Дисконтированный денежный поток =E8/(1+$C$4)^A8
- Чистый дисконтированный денежный поток (NPV) =СУММ(F8:F16)-B7
- Индекс доходности (PI)=F17/B7
На рисунке ниже показан итоговый результат расчета PI в Excel.
Второй вариант расчета индекса доходности инвестиционного проекта заключается в использовании встроенной финансовой формулы в Excel — ЧПС (чистая приведенная стоимость) для расчета чистого дисконтированного дохода (NPV). В результате формулы расчета будут иметь следующий вид:
- Дисконтированный денежный поток (NPV) =ЧПС(C4;E7:E16)-B7
- Индекс прибыльности (PI) =E17/B7
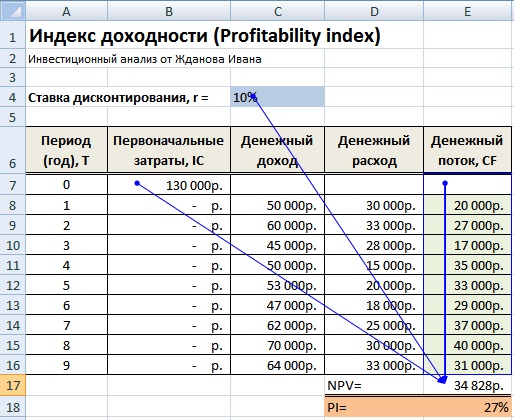
Как видно, расчет по двум методам привел к аналогичным результатам.
 |
★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Как произвести экспресс-оценку любого бизнес плана?
Все бизнес-планы включают в себя финансовый план, который оценивают с помощью инвестиционных показателей эффективность вложения для инвестора. Финансовый план и его показатели являются самыми значимыми для принятия решения о финансировании проекта. Чтобы быстро оценить любой бизнес-проект на уровень инвестиционной привлекательности следует рассмотреть четыре показателя: чистый дисконтированный доход, внутренняя норма прибыли, индекс доходности и дисконтированный период окупаемости. Если выполняются условия по данным показателям, то инвестиционный проект может быть уже более детально проанализирован на характер и природу получения денежных потоков, систему менеджмента, маркетинга и продаж.
Показатели экспресс оценки
Значения показателей
Чистый дисконтированный доход (NPV) Дисконтированный индекс доходности (DPI) Дисконтированный период окупаемости (DPP)
Индекс доходности входит в четыре основных показателя, которые оценивает любой инвестор при вложении в проект. Помимо данных показателей существуют другие коэффициенты оценки эффективности инвестиций, которые более подробно рассмотрены в статье: «6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI» .
Преимущества и недостатки индекса доходности инвестиционного проекта
Преимущества индекса доходности следующие:
- Возможность сравнительного анализа инвестиционных проектов различных по масштабу.
- Использование ставки дисконтирования для учета различных трудноформализуемых факторов риска проекта.
К недостаткам индекса доходности можно отнести:
- Прогнозирование будущих денежных потоков в инвестиционном проекте.
- Сложность точной оценки ставки дисконтирования для различных проектов.
- Сложность оценки влияния нематериальных факторов на будущие денежные потоки проекта.
 |
★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Резюме
В современной экономике возрастает роль оценки инвестиционных проектов, которые становятся драйверами для увеличения будущей стоимости компаний и получения дополнительной прибыли. В данной статье мы рассмотрели показатель индекс прибыльности, который является фундаментальным в системе выбора инвестиционного проекта. Так же на примере разобрали, как использовать Excel для быстрого расчета данного показателя для проекта или бизнес-плана.
Автор: к.э.н. Жданов Иван Юрьевич
Источник
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
В статье будет приведен расчет показателей эффективности проекта, с учетом дисконтирования.
- ЧДД или чистый дисконтированный доход от инвестиционного проекта;
- Внутренняя норма доходности.
Рассмотрим эти два показателя подробнее и рассчитаем пример работы с ними в Excel. Еще больше о возможностях Excel можно узнать на нашем открытом курсе «Аналитика в Excel».
Net Present Value (NPV, чистый дисконтированный доход) — один из самых распространенных показателей эффективности инвестиционного проекта.
Это разность между дисконтированными по времени поступлениями от проекта и инвестиционными затратами на него.
Метод расчета NPV:
- Определяем текущую стоимость затрат (инвестиции в проект)
- Производим расчет текущей стоимости денежных поступлений от проекта, для этого доходы за каждый отчетный период приводятся к текущей дате

CF – денежный поток;
r – ставка дисконта.
3. Сравниваем текущую стоимость инвестиций (наши затраты) в проект (Io) с текущей стоимостью доходов (PV). Разница между ними будет чистый дисконтированный доход — NPV.

NPV показывает инвестору доход или убыток от вложений средств в проект по сравнению с доходом от хранения денег в банке.
Если NPV больше 0, то инвестиции принесут больше дохода, нежели чем аналогичный вклад в банке.
Формула 1 модифицируется если инвестиционные вложения в проект осуществляются в несколько этапов (периодов).

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
r – ставка дисконтирования;
n – количество периодов.
Internal Rate of Return (Внутренняя норма доходности, IRR) определяет ставку дисконтирования при которой инвестиции равны 0 (NPV=0), или другими словами затраты на проект равны его доходам.
IRR = r, при которой NPV = f(r) = 0, находим из формулы:

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
n – количество периодов.
Этот показатель показывает норму доходности или возможные затраты при вложении денежных средств в проект (в процентах).
Пример расчета NPV в Excel
В MS Excel 2010 для расчета NPV используется функция =ЧПС().
Найдем чистый дисконтированный доход (NPV) проекта, требующего вложений инвестиций на 90 тыс. руб., и денежный поток которого распределен по времени рис 1. , и ставка дисконта равна 10%.

Рассчитаем показатель NPV по формуле Excel:
=ЧПС(D3;C3;C4:C11)
D3 – ставка дисконта;
C3 – вложения в 0 периоде (наши инвестиционные затраты в проект);
C4:C11 – денежный поток проекта за 8 периодов.

В итоге показатель чистого дисконтированного дохода равен 51,07 >0, это говорит о том, что в проект стоит инвестировать.

Расчет IRR в Excel
Для определения IRR в Excel используется встроенная функция
=ЧИСТВНДОХ()
Но так как у нас в примере данные поступали в равные интервалы времени можно использовать функцию
=ВСД(C3:C11)

Доходность вложения в проект равна 38%.
В завершение картинка финансового анализа проекта целиком.

КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Содержание:
- Разъяснение внутренней нормы прибыли (IRR)
- Функция IRR в Excel — синтаксис
- Расчет IRR для различных денежных потоков
- Узнайте, когда инвестиции принесут положительную внутреннюю норму доходности
- Использование функции IRR для сравнения нескольких проектов
- Расчет IRR для нерегулярных денежных потоков
- IRR против NPV — что лучше?
При работе с капитальным бюджетом IRR (внутренняя норма доходности) используется для понимания общей нормы доходности, которую проект будет генерировать на основе его будущих рядов денежных потоков.
В этом уроке я покажу вам, как рассчитать IRR в Excel, чем он отличается от другого популярного показателя NPV и различных сценариев, в которых вы можете использовать встроенные формулы IRR в Excel.
Разъяснение внутренней нормы прибыли (IRR)
IRR — это ставка дисконтирования, которая используется для измерять доходность инвестиций на основе периодических доходов. IRR отображается в процентах и может использоваться для определения прибыльности проекта (инвестиции) для компании.
Позвольте мне объяснить IRR на простом примере:
Предположим, вы планируете купить компанию за 50 000 долларов, которая будет приносить 10 000 долларов ежегодно в течение следующих 10 лет. Вы можете использовать эти данные для расчета IRR этого проекта, которая представляет собой норму прибыли, которую вы получаете от своих инвестиций в размере 50 000 долларов США.
В приведенном выше примере IRR составляет 15% (мы увидим, как рассчитать это позже в руководстве). Это означает, что вы вкладываете свои деньги со ставкой 15% или доходом в течение 10 лет.
Получив значение IRR, вы можете использовать его для принятия решений. Поэтому, если у вас есть какой-либо другой проект, в котором IRR составляет более 15%, вам следует вместо этого инвестировать в этот проект.
Или, если вы планируете взять ссуду или привлечь капитал и купить этот проект за 50 000 долларов, убедитесь, что стоимость капитала составляет менее 15% (иначе вы заплатите больше как стоимость капитала, чем вы зарабатываете из проект).
Функция IRR в Excel — синтаксис
Excel позволяет рассчитать внутреннюю норму прибыли с помощью функции IRR. Эта функция имеет следующие параметры:
= IRR (значения; [предположить])
- значения — массив ячеек, содержащих числа, для которых вы хотите рассчитать внутреннюю норму доходности.
- предполагать — число, которое, по вашему мнению, близко к результату IRR (не является обязательным и по умолчанию составляет 0,1–10%). Это используется, когда есть возможность получить несколько результатов, и в этом случае функция возвращает результат, наиболее близкий к значению аргумента предположения.
Вот некоторые важные предпосылки для использования функции
- Функция IRR будет рассматривать только числа в указанном диапазоне ячеек. Любые логические значения или текстовые строки в массиве или ссылочном аргументе будут проигнорированы.
- Суммы в параметре значений должны быть отформатированы как числа
- Параметр «guess» должен быть в процентах в десятичном формате (если он предусмотрен).
- Ячейка, в которой отображается результат функции, должна быть отформатирована как процент
- Суммы происходят в регулярные временные интервалы (месяцы, кварталы, годы)
- Одна сумма должна быть отрицательный денежный поток (представляющий первоначальные инвестиции), а другие суммы должны быть положительный денежные потоки, представляющие периодические доходы
- Все суммы должны быть в хронологический порядок потому что функция вычисляет результат на основе порядка сумм
Если вы хотите рассчитать значение IRR, когда денежный поток поступает в разные промежутки времени, вы должны использовать Функция XIRR в Excel, который также позволяет указать даты для каждого денежного потока. Пример этого будет рассмотрен позже в руководстве.
Теперь давайте рассмотрим пример, чтобы лучше понять, как использовать функцию IRR в Excel.
Расчет IRR для различных денежных потоков
Предположим, у вас есть набор данных, как показано ниже, где у нас есть начальные инвестиции в размере 30 000 долларов США, а затем варьируемый денежный поток / доход от них в течение следующих шести лет.
Для этих данных нам нужно рассчитать IRR, что можно сделать, используя следующую формулу:
= IRR (D2: D8)
Результат функции: 8.22%, которая представляет собой IRR денежного потока через шесть лет.
Примечание: Если функция возвращает # ЧИСЛО! ошибка, вам следует указать в формуле параметр «предположение». Это происходит, когда формула считает, что несколько значений могут быть правильными, и ей необходимо иметь значение предположения, чтобы вернуть IRR, ближайшую к предположению, которое мы предоставили. В большинстве случаев вам не нужно использовать это
Узнайте, когда инвестиции принесут положительную внутреннюю норму доходности
Вы также можете рассчитать IRR за каждый период в денежном потоке и посмотрите, когда именно инвестиции начинают иметь положительную внутреннюю норму доходности.
Предположим, у нас есть приведенный ниже набор данных, где у меня есть все денежные потоки, перечисленные в столбце C.
Идея здесь состоит в том, чтобы определить год, в котором IRR этой инвестиции станет положительной (с указанием, когда проект окупится и станет прибыльным).
Для этого вместо расчета IRR для всего проекта мы найдем IRR для каждого года.
Это можно сделать, используя приведенную ниже формулу в ячейке D3, а затем скопировав ее для всех ячеек в столбце.
= IRR ($ C $ 2: C3)
Как видите, IRR после года 1 (значения D2: D3) составляет -80%, после года 2 (D2: D4) -52% и т. Д.
Этот обзор показывает нам, что инвестиции в размере 30 000 долларов США с заданным денежным потоком имеют положительную внутреннюю норму доходности после пятого года.
Это может быть полезно, когда вам нужно выбрать один из двух проектов с одинаковой внутренней доходностью. Было бы более прибыльным выбрать проект, в котором IRR быстрее станет положительным, поскольку это означает меньший риск возврата вашего первоначального капитала.
Обратите внимание, что в приведенной выше формуле ссылка на диапазон смешана, то есть первая ссылка на ячейку ($ C $ 2) заблокирована знаками доллара перед номером строки и буквой столбца, а вторая ссылка (C3) не является заблокирован.
Это гарантирует, что при копировании формулы вниз всегда учитывается весь столбец до строки, в которой применяется формула.
Использование функции IRR для сравнения нескольких проектов
Функцию IRR в Excel также можно использовать для сравнения инвестиций и прибылей нескольких проектов и определения наиболее прибыльного проекта.
Предположим, у вас есть набор данных, как показано ниже, где у вас есть три проекта с начальными инвестициями (которые показаны отрицательными, поскольку это отток), а затем серией положительных денежных потоков.
Чтобы получить лучший проект (с самым высоким IRR, нам нужно будет рассчитать IRR для каждого проекта, используя простую формулу IRR:
= IRR (C2: C8)
Приведенная выше формула даст IRR для проекта 1. Аналогичным образом вы можете рассчитать IRR для двух других проектов.
Как вы видете:
- Проект 1 имеет IRR в размере 5.60%
- Проект 2 имеет IRR в размере 1.75%
- Проект 3 имеет IRR в размере 14.71%.
Если мы предположим, что стоимость капитала составляет 4,50%, мы можем сделать вывод, что вложение 2 неприемлемо (так как приведет к убыткам), в то время как вложение 3 является наиболее прибыльным с самой высокой внутренней нормой доходности.
Поэтому, если вам нужно принять решение об инвестировании только в один проект, вам следует выбрать проект 3, а если вы можете инвестировать более чем в один проект, вы можете инвестировать в проекты 1 и 3.
Определение: Если вам интересно, какова стоимость капитала, это деньги, которые вам придется заплатить, чтобы получить доступ к деньгам. Например, если вы берете в долг 100 тысяч долларов под 4,5% годовых, ваша стоимость капитала составляет 4,5%. Аналогичным образом, если вы выпускаете привилегированные акции, обещая Возврат 5%, чтобы получить 100K, ваша стоимость капитала будет 5%. В реальных сценариях компания обычно привлекает деньги из различных источников, и ее Стоимость капитала — это средневзвешенная величина всех этих источников капитала.
Расчет IRR для нерегулярных денежных потоков
Одним из ограничений функции IRR в Excel является то, что денежные потоки должны быть периодическими с одинаковым интервалом между ними.
Но в реальной жизни могут быть случаи, когда ваши проекты окупаются нерегулярно.
Например, ниже представлен набор данных, в котором денежные потоки происходят с нерегулярными интервалами (см. Даты в столбце A).
В этом примере мы не можем использовать обычную функцию IRR, но есть еще одна функция, которая может это сделать — Функция XIRR.
Функция XIRR принимает денежные потоки, а также даты, что позволяет учитывать нерегулярные денежные потоки и давать корректирующую IRR.
В этом примере IRR можно рассчитать по следующей формуле:
= XIRR (B2: B8; A2: A8)
В приведенной выше формуле денежные потоки указаны как первый аргумент, а даты указаны как второй аргумент.
Если эта формула возвращает # ЧИСЛО! ошибку, вы должны ввести третий аргумент с приблизительной IRR, которую вы ожидаете. Не волнуйтесь, оно не обязательно должно быть точным или даже очень близким, это просто приблизительная оценка IRR, которую, по вашему мнению, он принесет. Это поможет улучшить повторение формулы и даст результат.
IRR против NPV — что лучше?
Когда дело доходит до оценки проектов, используются как NPV, так и IRR, но NPV — более надежный метод.
NPV — это метод чистой приведенной стоимости, при котором вы оцениваете все будущие денежные потоки и вычисляете, какой будет чистая приведенная стоимость всех этих денежных потоков.
Если это значение окажется выше вашего первоначального оттока, значит, проект прибыльный, иначе проект не прибыльный.
С другой стороны, когда вы рассчитываете IRR для проекта, он сообщает вам, какой будет норма прибыли для всего будущего денежного потока, чтобы вы получили сумму, эквивалентную текущему оттоку. Например, если вы сегодня тратите 100 тысяч долларов на проект с IRR или 10%, это означает, что если вы дисконтируете все будущие денежные потоки по ставке дисконтирования 10%, вы получите 100 тысяч долларов.
Хотя при оценке проектов используются оба метода, более надежным является метод NPV. Существует вероятность того, что вы можете получить противоречивые результаты при оценке проекта с использованием метода NPV и IRR.
В таком случае лучше всего воспользоваться рекомендацией, полученной с помощью метода NPV.
В целом метод IRR имеет ряд недостатков, которые делают метод NPV более надежным:
- Более высокий метод или предполагает, что все будущие денежные потоки, полученные от проекта, будут реинвестированы с той же нормой прибыли (то есть IRR проекта). в большинстве случаев это необоснованное предположение, поскольку большая часть денежных потоков будет реинвестирована в другие проекты, которые могут иметь другой IR или ненадежность, такие как облигации, которые будут иметь гораздо более низкую норму доходности.
- Если у вас есть несколько оттоков и притоков в проекте, для этого проекта будет несколько IRR. Это снова сильно затрудняет сравнение.
Несмотря на свои недостатки, IRR является хорошим способом оценки проекта и может использоваться в сочетании с методом NPV, когда вы решаете, какой проект (ы) выбрать.
В этом уроке я показал вам, как использовать Функция ВНД в Excel. Я также рассказал, как рассчитать IRR в случае нерегулярных денежных потоков с помощью функции XIRR.
Надеюсь, вы нашли этот урок полезным!