Расчет длины развертки
Опубликовано 09 Июн 2013
Рубрика: Механика | 74 комментария

…квадратного сечений, гнут и все прокатные профили – уголки, швеллеры, двутавры, трубы. Однако холодная гибка деталей из листового металлопроката, безусловно, является наиболее распространенной.
Для обеспечения минимальных радиусов, детали перед гибкой иногда нагревают. При этом повышается пластичность материала. Используя гибку с калибрующим ударом, добиваются того, что внутренний радиус детали становится абсолютно равным радиусу пуансона. При свободной V-образной гибке на листогибе внутренний радиус получается на практике больше радиуса пуансона. Чем более у материала детали ярко выражены пружинные свойства, тем более отличаются друг от друга внутренний радиус детали и радиус пуансона.
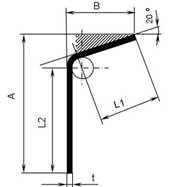
На рисунке, представленном ниже, изображен согнутый из листа толщиной s и шириной b уголок. Необходимо найти длину развертки.
Расчет развертки выполним в программе MS Excel.
В чертеже детали заданы: величина внутреннего радиуса R, угол a и длина прямолинейных участков L1 и L2. Вроде все просто – элементарная геометрия и арифметика. В процессе изгиба заготовки происходит пластическая деформация материала. Наружные (относительно пуансона) волокна металла растягиваются, а внутренние сжимаются. В середине сечения – нейтральная поверхность…
Но вся проблема в том, что нейтральный слой располагается не в середине сечения металла! Для справки: нейтральный слой – поверхность расположения условных волокон металла, не растягивающихся и не сжимающихся при изгибе. Более того – эта поверхность (вроде как) не является поверхностью кругового цилиндра. Некоторые источники предполагают, что это параболический цилиндр…
Я более склонен доверять классическим теориям. Для сечения прямоугольной формы по классическому сопромату нейтральный слой располагается на поверхности кругового цилиндра с радиусом r.
r = s/ln(1+s/R)
На базе этой формулы и создана программа расчета развертки листовых деталей из сталей марок Ст3 и 10…20 в Excel.
В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные. В ячейке со светло-желтой заливкой считываем результат расчета.
1. Записываем толщину листовой заготовки s в миллиметрах
в ячейку D3: 5,0
2. Длину первого прямого участка L1 в миллиметрах вводим
в ячейку D4: 40,0
3. Внутренний радиус сгиба первого участка R1 в миллиметрах записываем
в ячейку D5: 5,0
4. Угол сгиба первого участка a1 в градусах пишем
в ячейку D6: 90,0
5. Длину второго прямого участка детали L2 в миллиметрах вводим
в ячейку D7: 40,0
6. Все, результат расчета — длина развертки детали L в миллиметрах
в ячейке D17: =D4+ЕСЛИ(D5=0;0;ПИ()/180*D6*D3/LN ((D5+D3)/D5))+ +D7+ЕСЛИ(D8=0;0;ПИ()/180*D9*D3/LN ((D8+D3)/D8))+D10+ +ЕСЛИ(D11=0;0;ПИ()/180*D12*D3/LN ((D11+D3)/D11))+D13+ +ЕСЛИ(D14=0;0;ПИ()/180*D15*D3/LN ((D14+D3)/D14))+D16=91.33
L = ∑(Li+3.14/180*ai*s/ln((Ri+s)/Ri)+L(i+1))
Используя предложенную программу, можно рассчитать длину развертки для деталей с одним сгибом – уголков, с двумя сгибами – швеллеров и Z-профилей, с тремя и четырьмя сгибами. Если необходимо выполнить расчет развертки детали с большим числом сгибов, то программу очень легко доработать, расширив возможности.
Важным преимуществом предложенной программы (в отличие от многих аналогичных) является возможность задания на каждом шаге различных углов и радиусов гибки.
А «правильные» ли результаты выдает программа? Давайте, сравним полученный результат с результатами расчетов по методике изложенной в «Справочнике конструктора-машиностроителя» В.И. Анурьева и в «Справочнике конструктора штампов» Л.И. Рудмана. Причем в расчет возьмем только криволинейный участок, так как прямолинейные участки все, надеюсь, считают одинаково.
Проверим рассмотренный выше пример.
«По программе»: 11,33 мм – 100,0%
«По Анурьеву»: 10,60 мм – 93,6%
«По Рудману»: 11,20 мм – 98,9%
Увеличим в нашем примере радиус гибки R1 в два раза — до 10 мм. Еще раз произведем расчет по трем методикам.
«По программе»: 19,37 мм – 100,0%
«По Анурьеву»: 18,65 мм – 96,3%
«По Рудману»: 19,30 мм – 99,6%
Таким образом, предложенная методика расчетов выдает результаты на 0,4%…1,1% больше, чем «по Рудману» и на 6.4%…3,7% больше, чем «по Анурьеву». Понятно, что погрешность существенно уменьшится, когда мы добавим прямолинейные участки.
«По программе»: 99,37 мм – 100,0%
«По Анурьеву»: 98,65 мм – 99,3%
«По Рудману»: 99,30 мм – 99,9%
Возможно Рудман составлял свои таблицы по этой же формуле, которую использую я, но с погрешностью логарифмической линейки… Конечно, сегодня «на дворе» двадцать первый век, и рыскать по таблицам как-то не с руки!
В заключение добавлю «ложку дегтя». Длина развертки — это очень важный и «тонкий» момент! Если конструктор гнутой детали (особенно высокоточной (0,1 мм)) надеется расчетом точно и с первого раза определить ее, то он зря надеется. На практике в процесс гибки вмешается масса факторов – направление проката, допуск на толщину металла, утонение сечения в месте изгиба, «трапециевидность сечения», температура материала и оснастки, наличие или отсутствие смазки в зоне гибки, настроение гибщика… Короче, если партия деталей большая и дорого стоит – уточните практическими опытами длину развертки на нескольких образцах. И только после получения годной детали рубите заготовки на всю партию. А для изготовления заготовок для этих образцов, точности, которую обеспечивает программа расчета развертки, хватит с лихвой!
Программы расчета «по Анурьеву» и «по Рудману» в Excel можете найти в Сети.
Ссылка на скачивание файла: raschet-dliny-razvertki (xls 36,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Файл в формате Excel. На одном листе расчет разверток из листового металла по справочнику Анурьева, на другом — по «Справочнику конструктора штампов», Л.И.Рудман. Буду благодарен, если кто-нибудь сможет на основе этого создать какое-нибудь приложение к ACAD для упрощения жизни конструкторов. Пишите [email protected]
Комментарии
Комментарии могут оставлять только зарегистрированные
участники
Авторизоваться
Комментарии 1-7 из 7
Волков Ю.В.
, 07 сентября 2005 в 16:49
#1
Отличная таблица. Очень помогла. Огромное спасибо!
Kuznetsov
, 30 сентября 2005 в 09:32
#2
Spasibo tebe za etu tablitsu.
Василий Данилов
, 22 октября 2005 в 13:43
#3
Ребята, молодцы!
Здорово оформлено.
Только вот размер С на практике обычно дают по внутренним поверхностям, хотя как у вас тоже встречается, но редко.
Флаг вам в руки! Рад видеть хорошую работу!
Алексей
, 25 октября 2005 в 12:55
#4
Табл то хороший, но все таки внимательнее надо, дабы другие ошибок не понаделали!!! Автор, ПОСМОТРИ внимательнее справочник Анурьева, коэфициенты на толщину 0,5 у тебя неправильные, а также коэфициент при S=5мм&R=8мм тоже неправильный. Так что товарищи Данилов и Кузнецов теперь могут попасть!
Инженер-конструктор
, 27 октября 2005 в 10:41
#5
Спасибо за замечание. Все исправлено. Мои извинения, тем кто мог ошибиться.
Сергей
, 23 ноября 2005 в 11:40
#6
Очень хороший расчет. Очень короткий,красивый и простой. Огромное спасибо
Kaha251184
, 04 февраля 2019 в 22:55
#7
Спасибо!
Расчет длины развертки

. квадратного сечений, гнут и все прокатные профили – уголки, швеллеры, двутавры, трубы. Однако холодная гибка деталей из листового металлопроката, безусловно, является наиболее распространенной.
Для обеспечения минимальных радиусов, детали перед гибкой иногда нагревают. При этом повышается пластичность материала. Используя гибку с калибрующим ударом, добиваются того, что внутренний радиус детали становится абсолютно равным радиусу пуансона. При свободной V-образной гибке на листогибе внутренний радиус получается на практике больше радиуса пуансона. Чем более у материала детали ярко выражены пружинные свойства, тем более отличаются друг от друга внутренний радиус детали и радиус пуансона.
На рисунке, представленном ниже, изображен согнутый из листа толщиной s и шириной b уголок. Необходимо найти длину развертки.
Расчет развертки выполним в программе MS Excel.
В чертеже детали заданы: величина внутреннего радиуса R , угол a и длина прямолинейных участков L1 и L2 . Вроде все просто – элементарная геометрия и арифметика. В процессе изгиба заготовки происходит пластическая деформация материала. Наружные (относительно пуансона) волокна металла растягиваются, а внутренние сжимаются. В середине сечения – нейтральная поверхность…
Но вся проблема в том, что нейтральный слой располагается не в середине сечения металла! Для справки: нейтральный слой – поверхность расположения условных волокон металла, не растягивающихся и не сжимающихся при изгибе. Более того – эта поверхность (вроде как) не является поверхностью кругового цилиндра. Некоторые источники предполагают, что это параболический цилиндр…
Я более склонен доверять классическим теориям. Для сечения прямоугольной формы по классическому сопромату нейтральный слой располагается на поверхности кругового цилиндра с радиусом r .
На базе этой формулы и создана программа расчета развертки листовых деталей из сталей марок Ст3 и 10…20 в Excel.
В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные. В ячейке со светло-желтой заливкой считываем результат расчета.
1. Записываем толщину листовой заготовки s в миллиметрах
в ячейку D 3 : 5,0
2. Длину первого прямого участка L1 в миллиметрах вводим
в ячейку D 4 : 40,0
3. Внутренний радиус сгиба первого участка R1 в миллиметрах записываем
в ячейку D 5 : 5,0
4. Угол сгиба первого участка a1 в градусах пишем
в ячейку D 6 : 90,0
5. Длину второго прямого участка детали L2 в миллиметрах вводим
в ячейку D 7 : 40,0
6. Все, результат расчета — длина развертки детали L в миллиметрах
в ячейке D 17 : =D4+ЕСЛИ(D5=0;0;ПИ()/180*D6*D3/LN ((D5+D3)/D5))+ +D7+ЕСЛИ(D8=0;0;ПИ()/180*D9*D3/LN ((D8+D3)/D8))+D10+ +ЕСЛИ(D11=0;0;ПИ()/180*D12*D3/LN ((D11+D3)/D11))+D13+ +ЕСЛИ(D14=0;0;ПИ()/180*D15*D3/LN ((D14+D3)/D14))+D16 =91.33
Используя предложенную программу, можно рассчитать длину развертки для деталей с одним сгибом – уголков, с двумя сгибами – швеллеров и Z-профилей, с тремя и четырьмя сгибами. Если необходимо выполнить расчет развертки детали с большим числом сгибов, то программу очень легко доработать, расширив возможности.
Важным преимуществом предложенной программы (в отличие от многих аналогичных) является возможность задания на каждом шаге различных углов и радиусов гибки.
А «правильные» ли результаты выдает программа? Давайте, сравним полученный результат с результатами расчетов по методике изложенной в «Справочнике конструктора-машиностроителя» В.И. Анурьева и в «Справочнике конструктора штампов» Л.И. Рудмана. Причем в расчет возьмем только криволинейный участок, так как прямолинейные участки все, надеюсь, считают одинаково.
Проверим рассмотренный выше пример.
«По программе» : 11,33 мм – 100,0%
«По Анурьеву» : 10,60 мм – 93,6%
«По Рудману» : 11,20 мм – 98,9%
Увеличим в нашем примере радиус гибки R1 в два раза — до 10 мм. Еще раз произведем расчет по трем методикам.
«По программе» : 19,37 мм – 100,0%
«По Анурьеву» : 18,65 мм – 96,3%
«По Рудману» : 19,30 мм – 99,6%
Таким образом, предложенная методика расчетов выдает результаты на 0,4%…1,1% больше, чем «по Рудману» и на 6.4%…3,7% больше, чем «по Анурьеву». Понятно, что погрешность существенно уменьшится, когда мы добавим прямолинейные участки.
«По программе» : 99,37 мм – 100,0%
«По Анурьеву» : 98,65 мм – 99,3%
«По Рудману» : 99,30 мм – 99,9%
Возможно Рудман составлял свои таблицы по этой же формуле, которую использую я, но с погрешностью логарифмической линейки… Конечно, сегодня «на дворе» двадцать первый век, и рыскать по таблицам как-то не с руки!
В заключение добавлю «ложку дегтя». Длина развертки — это очень важный и «тонкий» момент! Если конструктор гнутой детали (особенно высокоточной (0,1 мм)) надеется расчетом точно и с первого раза определить ее, то он зря надеется. На практике в процесс гибки вмешается масса факторов – направление проката, допуск на толщину металла, утонение сечения в месте изгиба, «трапециевидность сечения», температура материала и оснастки, наличие или отсутствие смазки в зоне гибки, настроение гибщика… Короче, если партия деталей большая и дорого стоит – уточните практическими опытами длину развертки на нескольких образцах. И только после получения годной детали рубите заготовки на всю партию. А для изготовления заготовок для этих образцов, точности, которую обеспечивает программа расчета развертки, хватит с лихвой!
Программы расчета «по Анурьеву» и «по Рудману» в Excel можете найти в Сети.
Жду ваших комментариев, коллеги.
Для УВАЖАЮЩИХ труд автора — скачать файл можно ПОСЛЕ ПОДПИСКИ НА АНОНСЫ СТАТЕЙ (подписная форма — чуть ниже и наверху страницы).
Для ОСТАЛЬНЫХ — можно скачать просто так.
Ссылка на скачивание файла: raschet-dliny-razvertki (xls 36,5KB).
Продолжение темы — в статье о К-факторе.
О расчете развертки при гибке труб и прутков читайте здесь.
Расчет длины развертки детали
Расчет размеров заготовки при гибке
14.05.2015 Опубликовал Mehanolog 1
Рассмотрим ситуацию, которая нередко возникает на гибочном производстве. Особенно это касается небольших цехов, которые обходятся средствами малой и средней механизации. Под малой и средней механизацией я подразумеваю использование ручных или полуавтоматических листогибов. Оператор суммирует длину полок, получает общую длину заготовки для требуемого изделия, отмеряет нужную длину, отрезает и.. после гибки получает неточное изделие. Погрешности размеров конечного изделия могут быть весьма значительными (зависит от сложности изделия, количества гибов и т.д.). Все потому, что при расчетах длины заготовки нужно учитывать толщину металла, радиус гибки, коэффициент положения нейтральной линии (К-фактор). Именно этому и будет посвящена данная статья.
Честно говоря, произвести расчет размеров заготовки несложно. Нужно только понять, что нужно брать в расчет не только длины полок (прямых участков), но и длины криволинейных участков, получившихся ввиду пластических деформаций материала при гибке.
Притом, все формулы уже давно выведены «умными людьми», книги и ресурсы которых я постоянно указываю в конце статей (оттуда вы, при желании, можете получить дополнительные сведения).
Таким образом, для расчета правильной длины заготовки (развертки детали), обеспечивающей после гибки получение заданных размеров, необходимо, прежде всего, понять, по какому варианту мы будем производить расчет.
Таким образом, если вам нужна поверхность полки А без деформаций (например для расположения отверстий), то вы ведете расчет по варианту 1. Если же вам важна общая высота полки А, тогда, без сомнения, вариант 2 более подходящий.
Вариант 1 (с припуском)
а) Определить К-фактор (см Справочную);
б) Разбить контур изгибаемой детали на элементы, представляющие собой отрезки прямой и части окружностей;
в) Суммировать длины этих отрезков. При этом, длины прямых участков суммируются без изменения, а длины криволинейных участков – с учетом деформации материала и соответственного смещения нейтрального слоя.
Так, например, для заготовки с одним гибом, формула будет выглядеть следующим образом:
Где X1 – длина первого прямого участка, Y1– длина второго прямого участка, φ – внешний угол, r – внутренний радиус гибки, k – коэффициент положения нейтральной линии (К-фактор), S – толщина металла.
Причем, нам придется считать длину каждой полки отдельно, прежде чем задавать точку перемещения заднего упора станка. Надеюсь, это понятно.
Таким образом, ход расчета будет следующим..
Y1 + BA1 + X1 + BA2 +..т.д
Длина формулы зависит от количества переменных.
Вариант 2 (с вычетом)
По моему опыту, это самый распространенный вариант расчетов для гибочных станков с поворотной балкой. Поэтому, давайте рассмотрим этот вариант.
Нам также необходимо:
а) Определить К-фактор (см таблицу).
б) Разбить контур изгибаемой детали на элементы, представляющие собой отрезки прямой и части окружностей;
в) Рассчитать необходимые вычеты. При этом, длины прямых участков суммируются без изменения, а длины вычетов – соответственно, вычитаются.
Здесь необходимо рассмотреть новое понятие – внешняя граница гибки.
Чтобы было легче представить, см рисунок:
Внешняя граница гибки – вот эта воображаемая пунктирная линия.
Так вот, чтобы найти длину вычета, нужно от длины внешней границы отнять длину криволинейного участка.
Таким образом, формула длины заготовки по варианту 2:
Где Y2, X2 – полки, φ – внешний угол, r – внутренний радиус гибки, k – коэффициент положения нейтральной линии (К-фактор), S – толщина металла.
Вычет у нас (BD), как вы понимаете:
Внешняя граница гибки (OS):
И в этом случае также необходимо каждую операцию рассчитывать последовательно. Ведь нам важна точная длина каждой полки.
Схема расчета следующая:
(Y2 – BD1 / 2) + (X2 – (BD1 / 2 + BD2 / 2)) + (M2 – (BD2 / 2 + BD3 /2)) +.. и т.д.
Графически это будет выглядеть так:
И еще, размер вычета (BD) при последовательном расчете считать надо правильно. То есть, мы не просто сокращаем двойку. Сначала считаем весь BD, и только после этого получившийся результат делим пополам.
Надеюсь, что этой своей ремаркой я никого не обидел. Просто я знаю, что математика забывается и даже элементарные вычисления могут таить в себе никому не нужные сюрпризы.
На этом все. Всем спасибо за внимание.
При подготовке информации я использовал: 1. Статья «BendWorks. The fine-art of Sheet Metal Bending» Olaf Diegel, Complete Design Services, July 2002; 2. Романовский В.П. «Справочник по холодной штамповке» 1979г; материалы англоязычного ресурса SheetMetal.Me (раздел “Fabrication formulas”, ссылка: http://sheetmetal.me/formulas-and-functions/)
Расчет длины развертки детали
Упрощенно развертка рассчитывается следующим образом:
Допустим, имеется деталь как на рисунке.
Считаем суммарно развертку по СРЕДНЕЙ линии….. примерно так :
Затем считаем гибы. У нас получается 6 гибов. Каждый гиб уменьшает длину развертки примерно на толщину материала. У нас деталь из листа 3 мм. Из полученной суммарной длины развертки (284 мм) вычитаем 3х6=18 мм …. Получаем длину развертки 284-18 = 266. Цифра достаточно эмпирическая , но позволяет достаточно точно посчитать размер.
Еще необходимо учесть следующее ограничение – минимальное расстояние между гибами или от гиба до края заготовки должно быть не менее 15 мм. Это технологическое ограничение листогиба. Можно и меньше, но это необходимо обсудить. Есть и другие ограничения, но это уже будем решать вместе.
Расчет разверток деталей из листа под углом N°
где каэффициент K определяется по таблице. Он зависит от отношения внутреннего радиуса гибки и толщины материала r/t
Lр = L1 + L2 + Lдуги
Lдуги = pi * G/180 * Rср
Как мы видим r/t (на рисунке r/s) равно1,5.Выбираем из таблицы 1,5 получаем K=0,441
Ну вот получилась прожка.Данный файл xlРасчет разверткиВы можете скачать прямо с сайта.Он сам все расчитает.Нужно только ввести размеры. Если хотите посмотреть как работают формулы,снимите защиту с листа.Пароля нет.
Расчет разверток данным калькулятором
Выберите нужный профиль:
Введите значения: толщины материала S, радиуса гиба R, величин A, B, C, D, E.
Значения R и S — выбираются из выпадающего списка; A, B, C, D, E — вводятся вручную. Значения S — от 0.1 до 10 мм, значения R — от 0.1 до 20 мм.
Нажмите кнопку ‘Рассчитать’.
*Дробные значения вводятся через точку.
Длина развертки рассчитывается по формуле:
L = L1+L2+. +Ln + n*Li,
где L1, L2. Ln — длины прямых участков;
Li — длина изогнутого участка;
n — количество изогнутых участков.
Длина изогнутого участка: Li = π/2*(R+x*S),
где x — коэффициент, выбираемый в зависимости от отношения R/S.
Все ваши замечания, предложения, пожелания будут учтены. Пробуйте, тестируйте. По всем вопросам сюда.
А ещё можно загрузить моё приложение на андроид-устройство:
источники:
http://poisk-ru.ru/s8461t7.html
http://onlinerazvertka.ru/

Продолжая тему расчета длины разверток деталей, согнутых из листового металла прямоугольного сечения, представляю расчет в Excel длины развертки деталей из прутков и труб круглого сечения.
Программа расчета написана по формуле классического сопромата! Практические результаты будут немного отличаться от рассчитанных значений из-за целого ряда факторов, о которых уже упоминалось в статье о гибке листовых заготовок (ссылку на эту статью найдете, перейдя по ссылке в низу анонса). Однако точность при гибке трубы для изготовления опытного образца представленная ниже программа обеспечит.
Читать полностью.
28.07.2015 , обновлено 28.07.2015
В избранное
Пожаловаться
Просмотров: 2628
Обновлено: 16.04.2023
Как я и обещал в комментариях к статье «Расчет усилия листогиба», сегодня поговорим о расчете длины развертки детали, согнутой из листового металла. Конечно, процессу гибки подвергают не только детали из листов. Гнут детали круглого и.
. квадратного сечений, гнут и все прокатные профили – уголки, швеллеры, двутавры, трубы. Однако холодная гибка деталей из листового металлопроката, безусловно, является наиболее распространенной.
Для обеспечения минимальных радиусов, детали перед гибкой иногда нагревают. При этом повышается пластичность материала. Используя гибку с калибрующим ударом, добиваются того, что внутренний радиус детали становится абсолютно равным радиусу пуансона. При свободной V-образной гибке на листогибе внутренний радиус получается на практике больше радиуса пуансона. Чем более у материала детали ярко выражены пружинные свойства, тем более отличаются друг от друга внутренний радиус детали и радиус пуансона.
На рисунке, представленном ниже, изображен согнутый из листа толщиной s и шириной b уголок. Необходимо найти длину развертки.
Расчет развертки выполним в программе MS Excel.
В чертеже детали заданы: величина внутреннего радиуса R , угол a и длина прямолинейных участков L1 и L2 . Вроде все просто – элементарная геометрия и арифметика. В процессе изгиба заготовки происходит пластическая деформация материала. Наружные (относительно пуансона) волокна металла растягиваются, а внутренние сжимаются. В середине сечения – нейтральная поверхность…
Но вся проблема в том, что нейтральный слой располагается не в середине сечения металла! Для справки: нейтральный слой – поверхность расположения условных волокон металла, не растягивающихся и не сжимающихся при изгибе. Более того – эта поверхность (вроде как) не является поверхностью кругового цилиндра. Некоторые источники предполагают, что это параболический цилиндр…
Я более склонен доверять классическим теориям. Для сечения прямоугольной формы по классическому сопромату нейтральный слой располагается на поверхности кругового цилиндра с радиусом r .
r = s /ln(1+ s / R )
На базе этой формулы и создана программа расчета развертки листовых деталей из сталей марок Ст3 и 10…20 в Excel.
В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные. В ячейке со светло-желтой заливкой считываем результат расчета.
1. Записываем толщину листовой заготовки s в миллиметрах
в ячейку D 3 : 5,0
2. Длину первого прямого участка L1 в миллиметрах вводим
в ячейку D 4 : 40,0
3. Внутренний радиус сгиба первого участка R1 в миллиметрах записываем
в ячейку D 5 : 5,0
4. Угол сгиба первого участка a1 в градусах пишем
в ячейку D 6 : 90,0
5. Длину второго прямого участка детали L2 в миллиметрах вводим
в ячейку D 7 : 40,0
6. Все, результат расчета — длина развертки детали L в миллиметрах
в ячейке D 17 : =D4+ЕСЛИ(D5=0;0;ПИ()/180*D6*D3/LN ((D5+D3)/D5))+ +D7+ЕСЛИ(D8=0;0;ПИ()/180*D9*D3/LN ((D8+D3)/D8))+D10+ +ЕСЛИ(D11=0;0;ПИ()/180*D12*D3/LN ((D11+D3)/D11))+D13+ +ЕСЛИ(D14=0;0;ПИ()/180*D15*D3/LN ((D14+D3)/D14))+D16 =91.33
L = ∑( Li +3.14/180* ai * s /ln(( Ri + s )/ Ri )+ L(i +1) )
Используя предложенную программу, можно рассчитать длину развертки для деталей с одним сгибом – уголков, с двумя сгибами – швеллеров и Z-профилей, с тремя и четырьмя сгибами. Если необходимо выполнить расчет развертки детали с большим числом сгибов, то программу очень легко доработать, расширив возможности.
Важным преимуществом предложенной программы (в отличие от многих аналогичных) является возможность задания на каждом шаге различных углов и радиусов гибки.
А «правильные» ли результаты выдает программа? Давайте, сравним полученный результат с результатами расчетов по методике изложенной в «Справочнике конструктора-машиностроителя» В.И. Анурьева и в «Справочнике конструктора штампов» Л.И. Рудмана. Причем в расчет возьмем только криволинейный участок, так как прямолинейные участки все, надеюсь, считают одинаково.
Проверим рассмотренный выше пример.
«По программе» : 11,33 мм – 100,0%
«По Анурьеву» : 10,60 мм – 93,6%
«По Рудману» : 11,20 мм – 98,9%
Увеличим в нашем примере радиус гибки R1 в два раза — до 10 мм. Еще раз произведем расчет по трем методикам.
«По программе» : 19,37 мм – 100,0%
«По Анурьеву» : 18,65 мм – 96,3%
«По Рудману» : 19,30 мм – 99,6%
Таким образом, предложенная методика расчетов выдает результаты на 0,4%…1,1% больше, чем «по Рудману» и на 6.4%…3,7% больше, чем «по Анурьеву». Понятно, что погрешность существенно уменьшится, когда мы добавим прямолинейные участки.
«По программе» : 99,37 мм – 100,0%
«По Анурьеву» : 98,65 мм – 99,3%
«По Рудману» : 99,30 мм – 99,9%
Возможно Рудман составлял свои таблицы по этой же формуле, которую использую я, но с погрешностью логарифмической линейки… Конечно, сегодня «на дворе» двадцать первый век, и рыскать по таблицам как-то не с руки!
В заключение добавлю «ложку дегтя». Длина развертки — это очень важный и «тонкий» момент! Если конструктор гнутой детали (особенно высокоточной (0,1 мм)) надеется расчетом точно и с первого раза определить ее, то он зря надеется. На практике в процесс гибки вмешается масса факторов – направление проката, допуск на толщину металла, утонение сечения в месте изгиба, «трапециевидность сечения», температура материала и оснастки, наличие или отсутствие смазки в зоне гибки, настроение гибщика… Короче, если партия деталей большая и дорого стоит – уточните практическими опытами длину развертки на нескольких образцах. И только после получения годной детали рубите заготовки на всю партию. А для изготовления заготовок для этих образцов, точности, которую обеспечивает программа расчета развертки, хватит с лихвой!
Программы расчета «по Анурьеву» и «по Рудману» в Excel можете найти в Сети.
Жду ваших комментариев, коллеги.
Для УВАЖАЮЩИХ труд автора — скачать файл можно ПОСЛЕ ПОДПИСКИ НА АНОНСЫ СТАТЕЙ (подписная форма — чуть ниже и наверху страницы).
К-фактор в расчете развертки
Возвращение к старой теме расчета длины развертки детали из листового металла при гибке обусловлено необходимостью консолидации некоторой новой и старой информации по этому вопросу. Обобщение и анализ имеющихся данных, думаю, будут полезными для принятия.
. правильных решений на практике.
Длину развертки криволинейного участка принято определять как длину дуги окружности радиусом r по известной со школы формуле:
Lг =π* r * α /180, где
π =3,14…
r – радиус нейтрального слоя, который не растягивается и не сжимается при изгибе
α – угол изгиба в градусах
Главная проблема – как максимально точно вычислить этот радиус r ? Ведь просто взять и измерить его по понятным и очевидным причинам нельзя!
Если представить радиус r в виде суммы R и t (смотри рисунок выше), а размер t в виде произведения толщины материала s на некоторый коэффициент K , то получим формулы:
r = R + t
t = K * s
r = R + K * s
Задача сведена к тому, что для ее решения необходимо знать значение коэффициента К .
Коэффициент смещения условного нейтрального слоя K во многих источниках принято ныне называть коротко: К-фактором.
K =f ( R / s )
На графиках ниже наглядно представлена информация, собранная из ряда доступных популярных источников.
Значения К-фактора, как видите, несколько отличаются у разных авторов.
АСКОН (в старых версиях) «согласен» с немецким стандартом DIN 6935, наш РТМ 34-65 опирается на данные Рудмана и Романовского, Анурьев и «примкнувший» к нему T-flex занимают свою позицию в этом вопросе.
Формула из классического сопромата:
K =1/ln(1+ s / R ) — R / s
— кривая красного цвета, которой, к слову, я раньше пользовался всегда, близка к значениям Рудмана, но всё же выдает несколько большие значения К-фактора в зоне наиболее распространенных на практике отношений R / s .
Данные Рудмана считаются многими коллегами и экспертами в Сети наиболее точными. Возможно. Несколько смущает странный непонятный перегиб кривой Рудмана в весьма интересной для практики области 0,8< R / s . Если данные – результат опытов, то, что такое происходит нестандартное с металлом в этой области?
Некоторые CAD-программы, работающие с листовыми телами, «ждут» решения от пользователя по вводу и подтверждению значения К-фактора. На сегодня, видимо, есть два варианта действий по принятию решения. Первый – поверить какому-либо из вышеназванных источников. Второй – на опыте в результате эксперимента определить значение К-фактора для конкретного материала и условий гибки.
Избравшие второй путь при обеспечении чистоты эксперимента и высокой точности замеров получат истинное значение К-фактора для конкретной детали при строгом соблюдении и повторении определенной технологии.
В помощь решившимся идти по пути эксперимента могу порекомендовать небольшую простую программу BendWorks Олафа Дигеля из Новой Зеландии написанную ещё в 2003 году.
Во-первых, программа считает длину развертки по заданной вами величине К-фактора.
Длина изогнутого участка в развернутом состоянии определяется по формуле:
Lг =π*( R + K * s )* α /180
Во-вторых, если вы не знаете значения K , то программа, определяя длину развертки, в зависимости от способа гибки и жесткости материала предлагает приближенные значения К-фактора согласно таблице, приведенной ниже.
С одной стороны учет свойств металла и способов гибки детали – это несомненный шаг вперед. Но, с другой стороны, жестко фиксированные значения К-фактора в достаточно широких диапазонах R / s – это «минус» точности расчета развертки. Хотя для случаев, не требующих особой точности, определение К-фактора по предложенной автором таблице может быть успешно применено на практике.
В-третьих, программа помогает легко вычислить по результатам экспериментальных замеров реальное значение К-фактора для вашего материала, инструмента, оснастки, технологии. Именно этот вариант определения коэффициента смещения нейтрального слоя K настоятельно рекомендует автор при жестких допусках на размеры гнутой детали.
K =( Lг *180/(π* α ) — R )/ s
Обратите внимание: на графике в начале статьи область, выделенная зеленым цветом, соответствует данным из вышеприведенной таблицы программы. Все-таки она ближе к данным Рудмана, Романовского и классического сопромата в диапазоне 0 < R / s !
В Сети программа легко находится по поисковому запросу «BendWorks».
На старинной страничке автора сказано, что программа «абсолютно бесплатна», и помещены координаты для связи и адрес электронной почты:
Хотя английский интерфейс программы прост и интуитивно понятен, для упрощения работы прилагаю ссылку на файл с переводом статьи-справки автора «The fine-art of Sheet Metal Belding»:
Гибка трубы. Длина развертки в Excel!
При проектировании и изготовлении гнутых деталей из труб и прутков всегда возникает задача определения длины развертки – длины прямолинейной заготовки до начала технологического процесса гибки.
. расчета длины разверток деталей, согнутых из листового металла прямоугольного сечения, представляю расчет в Excel длины развертки деталей из прутков и труб круглого сечения.
Программа расчета написана по формуле классического сопромата! Практические результаты будут немного отличаться от рассчитанных значений из-за целого ряда факторов, о которых уже упоминалось в статье о гибке листовых заготовок (ссылка на эту статью в предыдущем абзаце). Однако точность при гибке трубы для изготовления опытного образца представленная ниже программа обеспечит.
Ниже этого текста на рисунке представлена расчетная схема.
Радиусы нейтральных слоев каждого из изогнутых участков рассчитываются по формуле:
rni =((4* Ri 2 — D 2 ) 0,5 +(4* Ri 2 — d 2 ) 0,5 )/4
Нейтральный слой – это поверхность, ближе которой к центру радиуса изгиба материал трубы при гибке сжимается, а дальше которой от центра радиуса изгиба – растягивается.
Длина кривых участков при гибке трубы определяется по формуле:
Здесь угол αi должен быть в градусах.
Общая длина развертки вычисляется суммированием длин прямых и изогнутых участков:
L = ∑( Li + li )
Программа расчета в Excel длины развертки при гибке труб.
Для выполнения расчетов используем программу MS Excel. Можно воспользоваться табличным процессором Calc из свободно распространяемых пакетов Apache OpenOffice или LibreOffice.
Исходные данные:
Положим, что в рассматриваемом примере деталь состоит из трех прямых и двух изогнутых участков (как на схеме вверху).
1. Записываем наружный диаметр трубы D в миллиметрах
в ячейку D4: 57,0
2. Значение внутреннего диаметра трубы d в миллиметрах заносим
в ячейку D5: 50,0
Внимание. Если рассчитывается длина развертки прутка сплошного круглого сечения, то d =0!
3. Длину первого прямого участка L1 в миллиметрах вводим
в ячейку D6: 200,0
4. Осевой радиус сгиба первого кривого участка R1 в миллиметрах записываем
в ячейку D7: 300,0
5. Угол сгиба первого кривого участка α1 в градусах пишем
в ячейку D8: 90,0
6. Длину второго прямого участка детали L2 в миллиметрах вводим
в ячейку D9: 100,0
7. Осевой радиус сгиба второго изогнутого участка R2 в миллиметрах записываем
в ячейку D10: 200,0
8. Угол сгиба второго изогнутого участка α2 в градусах пишем
в ячейку D11: 135,0
9. Длину третьего прямого участка детали L3 в миллиметрах вводим
в ячейку D12: 300,0
10-15. Ввод исходных данных в Excel для нашего примера завершен. Ячейки D13…D18 оставляем пустыми.
Программа позволяет рассчитывать развертки деталей, содержащих до пяти прямых участков и до четырех изогнутых. Гибка трубы с большим количеством участков требует для расчета развертки незначительной модернизации программы.
Результаты расчетов:
16. Длину первого изогнутого участка L1 в миллиметрах вычисляем
в ячейке D20: =ЕСЛИ(D7=0;0;ПИ()*D8/180*((4*D7^2-$D$4^2)^0,5+(4*D7^2-$D$5^2)^0,5)/4) =469,4
17. Длину второго изогнутого участка L2 в миллиметрах вычисляем
в ячейке D21: =ЕСЛИ(D10=0;0;ПИ()*D11/180*((4*D10^2-$D$4^2)^0,5+(4*D10^2-$D$5^2)^0,5)/4) =467,0
в ячейке D22: =ЕСЛИ(D13=0;0;ПИ()*D14/180*((4*D13^2-$D$4^2)^0,5+(4*D13^2-$D$5^2)^0,5)/4) =0,0
в ячейке D23: =ЕСЛИ(D16=0;0;ПИ()*D17/180*((4*D16^2-$D$4^2)^0,5+(4*D16^2-$D$5^2)^0,5)/4) =0,0
20. Общая длина развертки детали L в миллиметрах суммируется
в ячейке D24: =D6+D9+D12+D15+D18+D20+D21+D22+D23 =1536,3
Длина развертки изогнутой трубы рассчитана с помощью программы MS Excel.
Заключение.
УВАЖАЮЩИМ труд автора скачать файл можно ПОСЛЕ ПОДПИСКИ НА АНОНСЫ СТАТЕЙ (подписные формы — чуть ниже и наверху страницы).
Определение длины развертки при гибке
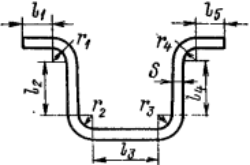
Элементы заготовки, расположенные в деформируемой зоне и прилегающие к внутренней поверхности изгибаемой детали (со стороны пуансона), подвергаются сжатию, а прилегающие к внешней поверхности (со стороны матрицы)—растяжению. Между растянутыми и сжатыми волокнами находится нейтральная линия длина которой не изменяется (Черт. 106).
Черт. 106
Радиус нейтральной линии R в мм (черт. 106) определяется по формуле
где r — радиус гибки, мм;
s— толщина материала мм;
x — коэффициент, величина которого зависит от отношения r/s (табл. 48).
Таблица 48
При завивке шарниров (петель) вследствие наличия внешних сил трения, препятствующих деформированию, коэффициент х определяется по табл. 48а.
Таблица 48а
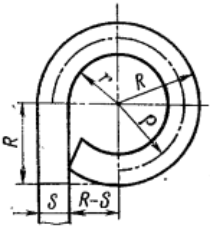
Длина развертки изгибаемой детали Lр в мм (черт. 107) определяется по формуле
R1; R2; R3 — радиусы нейтральной линии, определяемые по формуле (46).
Черт. 107
При гибке материалов толщиной свыше 3 мм под углом 90° с радиусом гибки r≤s радиус нейтральной линии R, рассчитанный по формуле (46), должен быть скорректирован до величины R1 (черт. 108), исходя из условия целостности материала и сопряжения в точках а и а1 криволинейного участка радиусом R1 с прямыми а—а и а1—а1, преходящими через середину толщины s. На участке С—С1 пунктиром показан внешний контур при расчете без учета утонения материала. В связи с утонением при гибке толщина s1 на этом участке меньше исходной s.
Черт. 108
Значения R1 радиуса скорректированной нейтральной линии и длину дуги abа1, следует подсчитать по формулам
R — определяется по формуле (46); r — радиус гибки, мм; остальные обозначения показаны на черт. 108.
Элементы для определения размеров разверток часто применяемых гнутых деталей приведены в табл. 49.
Таблица 49
- y, y1, y2 — величины, учитывающие изменение длины развертки при гибке под углом 90°. При толщине материала до 2,5 мм принимаются по табл. 50, а при толщине 3 и более мм при r
- х — коэффициент, принимается по табл. 48а.
Таблица 50
Таблица 50а
Пример. Определить длину развертки для детали, изображенной нa черт. 109.
Черт. 109
где l и l1 —длины прямых участков гнутой детали;
у —находим по табл. 50а
При s=4 мм и r= 3,5 мм
Если в рабочем чертеже детали заданы односторонние допуски, то для подсчета длины развертки эти допуски должны быть пересчитаны на двухсторонние, с сохранением заданного поля допуска. При этом должны быть также пересчитаны номинальные размеры детали (черт. 110).
Черт. 110
В табл. 51 и 52 приведены формулы для расчета длины развертки гнутых деталей при различных исходных данных на рабочем чертеже и различных формах сопряжения.
Таблица 51
Примечание: х — коэффициент, определяется по табл. 48.
Таблица 52
Размеры разверток гнутых деталей, рассчитанных по формуле (47), следует уточнить опытным путем в случаях:
- когда в одном штампе совмещены две или несколько гибочных операций (черт. 111 и 112,а).
- при гибке ушков, петель и т. п. (черт. 112,б);
- когда допуски на размеры гнутых деталей меньше допусков 5-го класса точности.
Необходимость уточнения размеров разверток вызывается смешением нейтральной линии в процессе гибки вследствие колебания механических свойств материала, различных условий трения на контактных поверхностях обрабатываемого материала и рабочих деталей штампа и т.п.
13. Определение размеров заготовок при гибке
Определение размеров плоских заготовок, подлежащих гибке, основано на равенстве длины заготовки длине нейтрального слоя изогнутой детали и сводится к определению положения и длины нейтрального слоя в зависимости от относительного радиуса изгиба r/S.
Различают два основных случая определения размеров заготовки:
1) при гибке с закруглением (по радиусу);
2) при гибке под углом без закругления (с калибровкой угла).
В первом случае длина заготовки равна сумме длин прямых участков и длины нейтрального слоя в изогнутом участке.
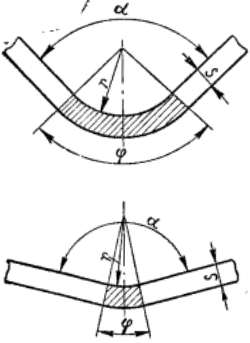
Рис.59. Соотношение между
углом изогнутого
участка и углом гибки
(φ = 180° — α)
Длина нейтрального слоя в изогнутом участке определяется по формуле:
или при φ = 90°
,где l — длина нейтрального слоя изогнутого участка; φ — угол изогнутого участка; х — коэффициент, определяющий положение нейтрального слоя (см. табл.16).
Угол изогнутого участка только при φ = 90° равен углу гибки; во всех же других случаях он составляет (рис.59):
В табл.21 приведены примеры определения размеров заготовок для наиболее распространенных случаев гибки по радиусу.
Таблица 21. Определение размеров заготовки при
гибке с закруглением (по радиусу).
| Тип гибки | Эскиз | Длинна заготовки, в мм |
| Одноугловая | 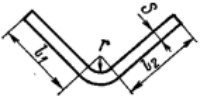 |
L = l1 + l2 + ln = l1 + l2 + π/2(r+xS) |
| Двухугловая |  |
L = l1 + l2 + l3 + π(r+xS) = l1 + l2 + l3 +2lH |
| Четырехугловая (за две операции) |
 |
L = l1 + 2l2 + l3 + l4 + 2lH1 + 2lH2 = = l1 + 2l2 + l3 + l4 + π(r1+x1S) + π(r2+x2S) |
| Полукгуглая (U образная) |
 |
L = 2l + 2lH = 2l + π(r+xS) |
| Торцовая (закатная) |
 |
L = 1,5πρ + 2R — S; ρ = R — yS |
1. Коэффициент х — см. табл.16;
2. Значение lH брать по табл.22.
Расположение нейтральной линии (xS) определяется в зависимости от отношения r/S и находится по табл.16 или по рис.56.
Для упрощения подсчетов и удобства пользования в производственных условиях в табл.22 приведена вычисленная длина нейтрального слоя угловых закруглений в зависимости от толщины материала и радиуса гибки:
Таблица 22. Длина нейтрального слоя угловых закруглений lH = π/2 • (r + xS)
| r, мм |
Толщина материалa S, мм | ||||||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,8 | 1 | 1,2 | 1,3 | 1,5 | 1,6 | 1,8 | 2 | 2,5 | 3 | 3,5 | 4 | 5 | |
| 0,2 | 0,39 | 0,45 | 0,50 | 0,55 | 0,60 | 0,65 | 0,75 | 0,83 | 0,93 | 0,98 | 1,08 | 1,12 | 1,19 | 1,26 | — | — | — | — | — |
| 0,3 | 0,55 | 0,61 | 0,67 | 0,73 | 0,78 | 0,83 | 0,93 | 1,03 | 1,13 | 1,16 | 1,25 | 1,31 | 1,40 | 1,50 | 1,70 | 1,88 | — | — | — |
| 0,4 | 0,70 | 0,77 | 0,83 | 0,89 | 0,95 | 1,00 | 1,11 | 1,21 | 1,30 | 1,35 | 1,46 | 1,48 | 1,58 | 1,67 | 1,90 | 2,14 | 2,36 | 2,52 | — |
| 0,5 | 0,86 | 0,93 | 1,00 | 1,06 | 1,12 | 1,17 | 1,28 | 1,38 | 1,48 | 1,54 | 1,63 | 1,68 | 1,78 | 1,85 | 2,10 | 2,30 | 2,54 | 2,80 | 3,14 |
| 0,6 | 1,02 | 1,09 | 1,16 | 1,22 | 1,28 | 1,34 | 1,45 | 1,56 | 1,66 | 1,71 | 1,81 | 1,85 | 1,95 | 2,06 | 2,30 | 2,50 | 2,75 | 3,00 | 3,46 |
| 0,8 | 1,33 | 1,41 | 1,47 | 1,54 | 1,61 | 1,67 | 1,78 | 1,90 | 2,00 | 2,06 | 2,16 | 2,21 | 2,31 | 2,42 | 2,67 | 2,92 | 3,15 | 3,35 | 3,80 |
| 1,0 | 1,65 | 1,73 | 1,79 | 1,86 | 1,93 | 1,99 | 2,11 | 2,23 | 2,35 | 2,40 | 2,51 | 2,56 | 2,68 | 2,76 | 3,02 | 3,26 | 3,51 | 3,77 | 4,20 |
| 1,5 | 2,43 | 2,51 | 2,58 | 2,65 | 2,73 | 2,79 | 2,93 | 3,06 | 3,17 | 3,23 | 3,35 | 3,41 | 3,51 | 3,63 | 3,89 | 4,15 | 4,41 | 4,65 | 5,14 |
| 2,0 | 3,22 | 3,30 | 3,37 | 3,44 | 3,52 | 3,59 | 3,73 | 3,86 | 3,99 | 4,05 | 4,17 | 4,22 | 4,34 | 4,46 | 4,74 | 5,00 | 5,27 | 5,53 | 6,05 |
| 2,5 | 4,01 | 4,08 | 4,16 | 4,23 | 4,30 | 4,37 | 4,52 | 4,66 | 4,79 | 4,85 | 4,99 | 5,05 | 5,17 | 5,28 | 5,58 | 5,86 | 6,13 | 6,40 | 6,91 |
| 3,0 | 4,79 | 4,87 | 4,95 | 5,02 | 5,09 | 5,16 | 5,31 | 5,45 | 5,59 | 5,66 | 5,78 | 5,85 | 5,98 | 6,11 | 6,39 | 6,69 | 6,98 | 7,26 | 7,78 |
| 3,5 | 5,58 | 5,65 | 5,73 | 5,80 | 5,88 | 5,95 | 6,10 | 6,24 | 6,38 | 6,45 | 6,59 | 6,65 | 6,78 | 6,91 | 7,51 | 7,51 | 7,81 | 8,11 | 8,64 |
| 4,4 | 6,36 | 6,44 | 6,51 | 6,60 | 6,66 | 6,74 | 6,88 | 7,03 | 7,17 | 7,24 | 7,38 | 7,45 | 7,59 | 7,71 | 8,04 | 8,34 | 8,63 | 8,92 | 9,48 |
| 4,5 | 7,15 | 7,23 | 7,30 | 7,38 | 7,45 | 7,52 | 7,67 | 7,82 | 7,96 | 8,03 | 8,18 | 8,25 | 8,38 | 8,52 | 8,84 | 9,17 | 9,44 | 9,74 | 10,34 |
| 5,0 | 7,93 | 8,01 | 8,09 | 8,16 | 8,24 | 8,31 | 8,46 | 8,62 | 8,75 | 8,82 | 8,97 | 9,04 | 9,18 | 9,32 | 9,64 | 9,97 | 10,27 | 10,56 | 11,15 |
| 6 | 9,50 | 9,58 | 9,66 | 9,73 | 9,81 | 9,90 | 10,03 | 10,18 | 10,32 | 10,40 | 10,54 | 10,61 | 10,76 | 10,90 | 11,25 | 11,57 | 11,90 | 12,23 | 12,78 |
| 7 | 11,07 | 11,15 | 11,23 | 11,31 | 11,38 | 11,45 | 11,61 | 11,80 | 11,90 | 11,97 | 12,12 | 12,19 | 12,33 | 12,48 | 12,83 | 13,18 | 13,50 | 13,83 | 14,45 |
| 8 | 12,64 | 12,72 | 12,80 | 12,88 | 12,95 | 13,03 | 13,20 | 13,33 | 13,47 | 13,55 | 13,69 | 13,77′ | 13,91 | 14,06 | 14,42 | 14,76 | 15,11 | 15,43 | 16,08 |
| 9 | 14,22 | 14,29 | 14,37 | 14,45 | 14,53 | 14,60 | 14,75 | 14,90 | 15,05 | 15,12 | 15,27 | 15,34 | 15,49 | 15,68 | 16,00 | 16,35 | 16,69 | 17,05 | 17,69 |
| 10 | 15,79 | 15,87 | 15,94 | 16,02 | 16,10 | 16,17 | 16,32 | 16,50 | 16,62 | 16,69 | 16,84 | 16,92 | 17,09 | 17,29 | 17,59 | 17,93 | 18,29 | 18,63 | 19,28 |
| 11 | 17,36 | 17,44 | 17,51 | 17,59 | 17,67 | 17,75 | 17,90 | 18,04 | 18,19 | 18,27 | 18,41 | 18,49 | 18,64 | 18,78 | 19,15 | 19,51 | 19,86 | 20,22 | 20,90 |
| 12 | 18,93 | 19,01 | 19,09 | 19,16 | 19,24 | 19,32 | 19,47 | 19,62 | 19,77 | 19,84 | 19,99 | 20,06 | 20,21 | 20,36 | 20,72 | 21,09 | 21,44 | 21,80 | 22,49 |
| 13 | 20,50 | 20,58 | 20,66 | 20,73 | 20,81 | 20,89 | 21,04 | 21,19 | 21,34 | 21,41 | 21,56 | 21,63 | 21,78 | 21,93 | 22,30 | 22,66 | 23,02 | 23,38 | 24,09 |
| 14 | 22,07 | 22,15 | 22,23 | 22,31 | 22,38 | 22,46 | 22,61 | 22,76 | 22,91 | 22,99 | 23,13 | 23,21 | 23,35 | 23,50 | 23,87 | 24,26 | 24,60 | 24,96 | 25,67 |
| 15 | 23,63 | 23,70 | 23,77 | 23,84 | 23,90 | 24,03 | 24,18 | 24,33 | 24,48 | 24,57 | 24,70 | 24,76 | 24,91 | 25,06 | 25,47 | 25,86 | 26,18 | 26,55 | 27,25 |
Примечение.
Приведение величины lH подсчитаны для угла в 90° при значениях х по табл. 16 и округлены до 0,01 мм.
Приведенные в таблице значения lH подсчитаны для гибки под углом 90°.
В случае необходимости найти длину нейтрального слоя для другого угла гибки, найденные из табл. 22, следует умножить на отношение φ/90 (где φ — требуемый угол гибки, град).
Если размеры гнутых деталей заданы, включая радиусы закруглений (рис. 60), то подсчет длины развертки производится по заданным размерам с введением поправки, приведенной в четвертом издании справочника (табл. 40). При подсчете длины развертки точных деталей с двусторонним допуском (±) расчет производится по номинальным размерам детали.
Рис.60. Схема пересчета односторонних допусков на двусторонние.
Если размеры детали заданы с односторонним допуском (рис. 60,а), то для того, чтобы деталь не вышла из поля допуска, необходимо односторонние допуски пересчитать на двусторонние (рис. 60,б). Расчет развертки производится по пересчитанным номинальным размерам детали на технологические размеры.
Необходимо сделать следующие технологические указания, без которых невозможно получить точные гнутые детали.
1. Размеры деталей будут соответствовать расчетным лишь в том случае, если гибка происходит без растяжения и утонения отгибаемых полок.
2. Двухугловая гибка должна производиться в штампах с сильным прижимом (см. рис.51). В противном случае средний участок, отжимая слабый прижим, выгибается и имеет длину, большую ширины матрицы. Без калибровки деталь получается некачественной, а при калибровке происходит осадка выпуклости и утолщение материала. Вследствие этого деталь получается с более короткими полками, чем предусматривалось по расчету. При гибке с сильным прижимам (0,3 — 0,5 РИЗГ) деталь получается качественной.
3. Четырехугловая деталь должна гнуться за две операции, или за два перехода последовательного штампа. При одновременной гибке всех четырех углов происходит растяжение верхних полок и деталь получается больших размеров, чем по расчету, и неправильной формы.
В случае гибки под углом без закругления размеры заготовки находят исходя из равенства объемов заготовки и изогнутой детали с учетом утонения в месте изгиба. Длина заготовки определяется как сумма длин прямых участков и прибавки на образование углов:
,где n — число прямых участков;
l1, l2, . ln — длины прямых участков, мм;
k — коэффициент, составляющий 0,38—0,40 при закруглении пуансона радиусом r = 0,05S
и 0,45—0,48 при закруглении пуансона радиусом r = 0,1S;
причем меньшие значения относятся к толщине материала S
Пример 1.
Определить длину заготовки для двухугловой гибки скобы размерами:
l1 = l2 = 40 мм, l3 = 30 мм, r = 1 мм и S = 2 мм
По табл. 22 находим длину нейтрального слоя lH = 2,76 мм.
Длина заготовки: L = 2l1 + l3 + 2lH = 80 + 30 4 + 5,52 ≈ 115,5 мм.
Пример 2.
Определить длину заготовки для шарнирной петли (нижняя схема табл. 21) при R = 3 мм, S = 1,5 мм.
Находим радиус нейтрального слоя ρ = R — уS; по табл. 17 для R/S = 2,0 и у = 0,44
ρ = 3 — 0,44 • 1,5 = 2,34 мм.
Длина развернутой заготовки: L = 1,5πρ + 2R — S = 11,0 + 6 — 1,5 = 15,5 мм.
Читайте также:
- Из чего сделан жесткий диск металл какой
- Переходная сварочная проволока для сварки нержавейки с черным металлом марка
- Типовая инструкция по контролю металла и продлению срока службы основных элементов котлов
- Изготовление скамеек из металла
- Металлическая стяжка 4 6х150
Содержание
- Расчет разверток гнутых изделий. Гибка трубы. Длина развертки в Excel!
- Программа расчета в Excel длины развертки при гибке труб.
- Исходные данные:
- Онлайн калькулятор развертки листового металла. Расчет развертки выполним в программе MS Excel.
- Расчет размеров заготовки при гибке онлайн. Расчеты параметров гибки изделий из листового металла для гибочного пресса
- Процесс гибки: простые факты
- Простое заключение
- Как радиус влияет на заготовки
- Допуск на гибку
- Расчет допуска на гибку
- Формула допуска на гибку (ВА)
- Расчет длины развертки листа онлайн. Внутренняя поверхность
- Гибка листового металла расчет. Гибка листового металла — методы и советы по проектированию [часть 2]
- Формула коэффициента K:
- Формулы припусков на изгиб:
- Расчет допуска на изгиб:
- Советы по гибке листового металла:
- Минимальная длина фланца:
- Боковые стороны с фаской:
- Расстояние от отверстия до изгиба:
- Симметрия:
- Заклепочные гайки:
- Маленькие фланцы для больших деталей:
- Сгибы рядом друг с другом:
Расчет разверток гнутых изделий. Гибка трубы. Длина развертки в Excel!
При проектировании и изготовлении гнутых деталей из труб и прутков всегда возникает задача определения длины развертки – длины прямолинейной заготовки до начала технологического процесса гибки.
Продолжая тему…
… расчета длины разверток деталей, согнутых из листового металла прямоугольного сечения , представляю расчет в Excel длины развертки деталей из прутков и труб круглого сечения.
Программа расчета написана по формуле классического сопромата! Практические результаты будут немного отличаться от рассчитанных значений из-за целого ряда факторов, о которых уже упоминалось в статье о гибке листовых заготовок (ссылка на эту статью в предыдущем абзаце). Однако точность при гибке трубы для изготовления опытного образца представленная ниже программа обеспечит.
Ниже этого текста на рисунке представлена расчетная схема.
Радиусы нейтральных слоев каждого из изогнутых участков рассчитываются по формуле:
Нейтральный слой – это поверхность, ближе которой к центру радиуса изгиба материал трубы при гибке сжимается, а дальше которой от центра радиуса изгиба – растягивается.
Длина кривых участков при гибке трубы определяется по формуле:
Здесь угол αi должен быть в градусах.
Общая длина развертки вычисляется суммированием длин прямых и изогнутых участков:
Программа расчета в Excel длины развертки при гибке труб.
Для выполнения расчетов используем программу MS Excel. Можно воспользоваться табличным процессором Calc из свободно распространяемых пакетов Apache OpenOffice или LibreOffice .
Исходные данные:
Положим, что в рассматриваемом примере деталь состоит из трех прямых и двух изогнутых участков (как на схеме вверху).
1. Записываем наружный диаметр трубы D в миллиметрах
в ячейку D4: 57,0
2. Значение внутреннего диаметра трубы d в миллиметрах заносим
в ячейку D5: 50,0
Внимание!!! Если рассчитывается длина развертки прутка сплошного круглого сечения, то d =0!
в ячейку D6: 200,0
в ячейку D7: 300,0
в ячейку D8: 90,0
в ячейку D9: 100,0
в ячейку D10: 200,0
в ячейку D11: 135,0
в ячейку D12: 300,0
10-15. Ввод исходных данных в Excel для нашего примера завершен. Ячейки D13…D18 оставляем пустыми.
Программа позволяет рассчитывать развертки деталей, содержащих до пяти прямых участков и до четырех изогнутых. Гибка трубы с большим количеством участков требует для расчета развертки незначительной модернизации программы.
Онлайн калькулятор развертки листового металла. Расчет развертки выполним в программе MS Excel.
В чертеже детали заданы: величина внутреннего радиуса R , угол a и длина прямолинейных участков L1 и L2 . Вроде все просто – элементарная геометрия и арифметика. В процессе изгиба заготовки происходит пластическая деформация материала. Наружные (относительно пуансона) волокна металла растягиваются, а внутренние сжимаются. В середине сечения – нейтральная поверхность…
Но вся проблема в том, что нейтральный слой располагается не в середине сечения металла! Для справки: нейтральный слой – поверхность расположения условных волокон металла, не растягивающихся и не сжимающихся при изгибе. Более того – эта поверхность (вроде как) не является поверхностью кругового цилиндра. Некоторые источники предполагают, что это параболический цилиндр…
Я более склонен доверять классическим теориям. Для сечения прямоугольной формы по классическому сопромату нейтральный слой располагается на поверхности кругового цилиндра с радиусом r .
На базе этой формулы и создана программа расчета развертки листовых деталей из сталей марок Ст3 и 10…20 в Excel.
В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные. В ячейке со светло-желтой заливкой считываем результат расчета.
1. Записываем толщину листовой заготовки s в миллиметрах
в ячейку D 3 : 5,0
в ячейку D 4 : 40,0
в ячейку D 5 : 5,0
в ячейку D 6 : 90,0
в ячейку D 7 : 40,0
6. Все, результат расчета — длина развертки детали L в миллиметрах
в ячейке D 17 : =D4+ЕСЛИ(D5=0;0;ПИ()/180*D6*D3/LN ((D5+D3)/D5))+ +D7+ЕСЛИ(D8=0;0;ПИ()/180*D9*D3/LN ((D8+D3)/D8))+D10+ +ЕСЛИ(D11=0;0;ПИ()/180*D12*D3/LN ((D11+D3)/D11))+D13+ +ЕСЛИ(D14=0;0;ПИ()/180*D15*D3/LN ((D14+D3)/D14))+D16 =91.33
Используя предложенную программу, можно рассчитать длину развертки для деталей с одним сгибом – уголков, с двумя сгибами – швеллеров и Z-профилей, с тремя и четырьмя сгибами. Если необходимо выполнить расчет развертки детали с большим числом сгибов, то программу очень легко доработать, расширив возможности.
Важным преимуществом предложенной программы (в отличие от многих аналогичных) является возможность задания на каждом шаге различных углов и радиусов гибки .
А «правильные» ли результаты выдает программа? Давайте, сравним полученный результат с результатами расчетов по методике изложенной в «Справочнике конструктора-машиностроителя» В.И. Анурьева и в «Справочнике конструктора штампов» Л.И. Рудмана. Причем в расчет возьмем только криволинейный участок, так как прямолинейные участки все, надеюсь, считают одинаково.
Проверим рассмотренный выше пример.
«По программе» : 11,33 мм – 100,0%
«По Анурьеву» : 10,60 мм – 93,6%
«По Рудману» : 11,20 мм – 98,9%
Увеличим в нашем примере радиус гибки R 1 в два раза — до 10 мм. Еще раз произведем расчет по трем методикам.
«По программе» : 19,37 мм – 100,0%
«По Анурьеву» : 18,65 мм – 96,3%
«По Рудману» : 19,30 мм – 99,6%
Таким образом, предложенная методика расчетов выдает результаты на 0,4%…1,1% больше, чем «по Рудману» и на 6.4%…3,7% больше, чем «по Анурьеву». Понятно, что погрешность существенно уменьшится, когда мы добавим прямолинейные участки.
«По программе» : 99,37 мм – 100,0%
«По Анурьеву» : 98,65 мм – 99,3%
«По Рудману» : 99,30 мм – 99,9%
Возможно Рудман составлял свои таблицы по этой же формуле, которую использую я, но с погрешностью логарифмической линейки… Конечно, сегодня «на дворе» двадцать первый век, и рыскать по таблицам как-то не с руки!
В заключение добавлю «ложку дегтя». Длина развертки — это очень важный и «тонкий» момент! Если конструктор гнутой детали (особенно высокоточной (0,1 мм)) надеется расчетом точно и с первого раза определить ее, то он зря надеется. На практике в процесс гибки вмешается масса факторов – направление проката, допуск на толщину металла, утонение сечения в месте изгиба, «трапециевидность сечения», температура материала и оснастки, наличие или отсутствие смазки в зоне гибки, настроение гибщика… Короче, если партия деталей большая и дорого стоит – . И только после получения годной детали рубите заготовки на всю партию. А для изготовления заготовок для этих образцов, точности, которую обеспечивает программа расчета развертки, хватит с лихвой!
Расчет размеров заготовки при гибке онлайн. Расчеты параметров гибки изделий из листового металла для гибочного пресса
Понимание соотношения между V-образной выемкой, радиусом, допуском на гибку и К-фактором для лучшего выполнения расчетов плоской развертки детали из листового металла.
Иногда на производстве бывают случаи, когда детали из листового металла, вырезанные лазером, полученные путем пробивки или обрезки кажутся «слишком длинными» или «слишком короткими» после их гибки на листогибочном прессе. Бывает также, что изделия, спроектированные на компьютере, не соответствуют реальным размерам после гибки. Производитель инструмента для гибки Rolleri предлагает больше узнать о факторах, которые следует учитывать для достижения наилучших результатов в подобных ситуациях.
Процесс гибки: простые факты
1) Радиус, получающийся за счет гибки металлического листа, влияет на длину, на которую следует обрезать изделие перед гибкой.
2) Полученный радиус гибки на 99% зависит от V-образной выемки, которую мы выбираем для работы.
Простое заключение
До начала проектирования изделия и резки заготовок, следует обязательно знать, какая V-образная выемка будет использоваться для гибки детали на листогибочном станке.
Как радиус влияет на заготовки
Больший радиус раздвинет изделие в сторону внешнего края, оставляя впечатление того, что была отрезана слишком длинная заготовка.
Меньший радиус потребует заготовки, обрезанной «немного длиннее», чем в случае большего радиуса.
Допуск на гибку
Развернутая плоская заготовка профиля, указанного выше на изображении рассчитывается следующим образом:
B = 150 + 100 + 60 + BA1 + BA2
Далее последует обьяснение, как рассчитать параметры ВА1 и ВА2.
Расчет допуска на гибку
Участок, на который нужно укоротить обе стороны, которые совпадут после расплющивания детали, является тем, что обычно называется «допуском на гибку» и обозначаем ВА в формуле.
Формула допуска на гибку (ВА)
Формула BA для сгибов менее 90°
Формула АВ для сгибов от 91°до 165°
iR= внутренний радиус
S=толщина
Β = угол
Π = 3,14159265….
Расчет длины развертки листа онлайн. Внутренняя поверхность
Такой показатель применяется в процессе гидродинамических расчетов, когда определяется площадь поверхности трубы, которая постоянно контактирует с водой.
При определении данного параметра следует учитывать:
- Чем больше диаметр водопроводных труб, тем меньше скорость проходящего потока зависит от шероховатости стенок конструкции.
На заметку! Если трубопроводы с большим диаметром характеризуются малой протяженностью, то величиной сопротивления стенок можно пренебречь.
- При гидродинамических расчетах шероховатости поверхности стенок придается не меньшее значение, чем ее площади. Если вода проходит по ржавому внутри водопроводу, то ее скорость меньше скорости жидкости, которая протекает по сравнительно гладкой полипропиленовой конструкции.
- Сети, которые монтируются из не оцинкованной стали, отличаются непостоянной площадью внутренней поверхности. При эксплуатации они покрываются ржавчиной и зарастают минеральными отложениями, из-за чего сужается просвет трубопровода.
Важно! Обратите внимание на этот факт, если захотите сделать холодное водоснабжение из стального материала. Проходимость такого водопровода сократится в два раза уже после десяти лет эксплуатации.
Расчет развертки трубы в данном случае делается с учетом того, что внутренний диаметр цилиндра определяется, как разность внешнего диаметра профиля и увеличенной вдвое толщины его стенок.
В результате площадь поверхности цилиндра определяется по формуле:
S= π (D-2N)L, где к уже известным параметрам добавляется показатель N, определяющий толщину стенок.
Формула развертки заготовки помогает рассчитать количество необходимой теплоизоляции
Чтобы знать, как посчитать развертку трубы, достаточно вспомнить курс геометрии, которую осваивают в средних классах. Приятно, что школьная программа находит применение во взрослой жизни и помогает решать серьезные задачи, связанные со строительством. Пусть они окажутся полезными и для вас!
Как я и обещал в комментариях к статье , сегодня поговорим о расчете длины развертки детали, согнутой из листового металла. Конечно, процессу гибки подвергают не только детали из листов. Гнут детали круглого и…
Квадратного сечений, гнут и все прокатные профили – уголки, швеллеры, двутавры, трубы. Однако холодная гибка деталей из листового металлопроката, безусловно, является наиболее распространенной.
Для обеспечения минимальных радиусов, детали перед гибкой иногда нагревают. При этом повышается пластичность материала. Используя гибку с калибрующим ударом, добиваются того, что внутренний радиус детали становится абсолютно равным радиусу пуансона. При свободной V-образной гибке на листогибе внутренний радиус получается на практике больше радиуса пуансона. Чем более у материала детали ярко выражены пружинные свойства, тем более отличаются друг от друга внутренний радиус детали и радиус пуансона.
Гибка листового металла расчет. Гибка листового металла — методы и советы по проектированию [часть 2]
Если вы сами создаете чертежи, вам нужно знать следующее. Процесс гибки удлиняет материал. Это означает, что нейтральная линия или ось, о которой мы говорили в предыдущей статье, на самом деле находится не посередине материала. Но плоская деталь должна быть сформирована в соответствии с нейтральной линией. И для нахождения ее положения требуется коэффициент k.
Коэффициент K — это эмпирическая константа, то есть его значение было определено в результате испытаний. Он варьируется в зависимости от материала, его толщины, радиуса изгиба и метода гибки. По сути, коэффициент k смещает нейтральную линию, чтобы обеспечить плоский рисунок, отражающий реальность. Используя его, вы получаете допуск на изгиб, который, по сути, является длиной изогнутой нейтральной оси.
Первую часть данной статьи вы можете найти в нашем блоге по ссылке . Примечание: данная статья является переводом.
Формула коэффициента K:
k — коэффициент k, постоянный; ir — внутренний радиус (мм); t — толщина листа (мм)
Формулы припусков на изгиб:
Для изгибов от 0 до 90 градусов формула выглядит следующим образом:
ß — угол изгиба (°)
Для изгибов от 90 до 165 градусов формула имеет вид:
Для изгибов более 165° нет необходимости рассчитывать припуски на изгиб, так как нейтральная ось остается практически посередине детали.
Расчет допуска на изгиб:
Допустим, у вас есть деталь, похожая на ту, что на изображении выше — у нее прямая ножка 20 мм и другая 70 мм. Угол изгиба составляет 90°, толщина листа — 5 мм, а внутренний радиус — 6 мм. Мы хотим узнать конечную длину детали. Во-первых, мы должны начать с коэффициента k:
Другой способ определения коэффициента k — следовать «правилу большого пальца». Просто выберите коэффициент k в соответствии с вашим материалом из приведенной ниже таблицы. Это дает достаточно точные результаты для большинства случаев.
Для получения окончательной длины мы просто прибавляем две длины ног к припуску на подгибку:
Советы по гибке листового металла:
Итак, я поговорил с нашим опытным менеджером по продажам, который знает толк в гибке листового металла. Он загорелся и решил воспользоваться возможностью и поделиться своими знаниями о гибке листового металла. Таким образом, он привел список распространенных ошибок и решений, как их избежать.
Минимальная длина фланца:
Существует минимальная длина фланца, как уже говорилось ранее. Для ориентировки смотрите таблицу изгибающих усилий. В зависимости от толщины выбирается ширина штампа. Если вы разработаете слишком короткий фланец, он будет неловко «проваливаться» в щель, и вы не получите желаемого результата.
Боковые стороны с фаской:
Если вы хотите сделать фланец с фаской на одном или двух концах, предыдущее правило о минимальной длине фланца остается в силе. Фаски должны оставлять достаточно места для выполнения правильных изгибов, иначе фланец будет выглядеть деформированным, и никто не будет удовлетворен.
Расстояние от отверстия до изгиба:
Если отверстия расположены слишком близко к изгибу, они могут деформироваться. Круглые отверстия не так проблематичны, как другие типы, но болты все равно могут не пройти. Опять же, смотрите диаграмму изгибающего усилия для минимальных размеров фланца и размещайте отверстия дальше, чем минимальные.
Симметрия:
Существует большая опасность при изготовлении деталей, которые почти симметричны. Если возможно, делайте их симметричными. Если деталь почти симметрична, оператор гибочного пресса может запутаться. Результат? Ваша деталь будет согнута в неправильном направлении.
Заклепочные гайки:
Если вы используете заклепочные гайки вблизи линии изгиба, известно, что их установка перед изгибом хороша для обеспечения его применимости. После изгиба отверстия могут деформироваться. Тем не менее, убедитесь, что гайки не будут мешать инструментам при гибке.
Маленькие фланцы для больших деталей:
Лучше отказаться от маленьких фланцев на больших и тяжелых деталях. Это очень усложняет производство, и может потребоваться ручная обработка, которая обойдется дороже, чем простая механическая. В результате, если есть возможность, лучше выбрать альтернативное решение.
Сгибы рядом друг с другом:
Если вы хотите включить последовательные изгибы, проверьте, выполнимо ли это. Проблема возникает, когда вы не можете установить уже согнутую деталь на штамп. Если изгибы направлены в одну сторону — U-образный изгиб, — то общее правило заключается в том, что промежуточная часть должна быть длиннее фланцев.
Содержание
- Гибка трубы. Длина развертки в Excel!
- Программа расчета в Excel длины развертки при гибке труб.
- Исходные данные:
- Результаты расчетов:
- Заключение.
- Статьи с близкой тематикой
- Отзывы
- Расчет длины развертки
- Расчет развертки выполним в программе MS Excel.
Гибка трубы. Длина развертки в Excel!

. расчета длины разверток деталей, согнутых из листового металла прямоугольного сечения, представляю расчет в Excel длины развертки деталей из прутков и труб круглого сечения.
Программа расчета написана по формуле классического сопромата! Практические результаты будут немного отличаться от рассчитанных значений из-за целого ряда факторов, о которых уже упоминалось в статье о гибке листовых заготовок (ссылка на эту статью в предыдущем абзаце). Однако точность при гибке трубы для изготовления опытного образца представленная ниже программа обеспечит.
Ниже этого текста на рисунке представлена расчетная схема.
Радиусы нейтральных слоев каждого из изогнутых участков рассчитываются по формуле:
rni =((4* Ri 2 — D 2 ) 0,5 +(4* Ri 2 — d 2 ) 0,5 )/4
Нейтральный слой – это поверхность, ближе которой к центру радиуса изгиба материал трубы при гибке сжимается, а дальше которой от центра радиуса изгиба – растягивается.
Длина кривых участков при гибке трубы определяется по формуле:
Здесь угол αi должен быть в градусах.
Общая длина развертки вычисляется суммированием длин прямых и изогнутых участков:
L = ∑( Li + li )
Программа расчета в Excel длины развертки при гибке труб.
Для выполнения расчетов используем программу MS Excel. Можно воспользоваться табличным процессором Calc из свободно распространяемых пакетов Apache OpenOffice или LibreOffice.
Исходные данные:
Положим, что в рассматриваемом примере деталь состоит из трех прямых и двух изогнутых участков (как на схеме вверху).
1. Записываем наружный диаметр трубы D в миллиметрах
в ячейку D4: 57,0
2. Значение внутреннего диаметра трубы d в миллиметрах заносим
в ячейку D5: 50,0
Внимание. Если рассчитывается длина развертки прутка сплошного круглого сечения, то d =0!
3. Длину первого прямого участка L1 в миллиметрах вводим
в ячейку D6: 200,0
4. Осевой радиус сгиба первого кривого участка R1 в миллиметрах записываем
в ячейку D7: 300,0
5. Угол сгиба первого кривого участка α1 в градусах пишем
в ячейку D8: 90,0
6. Длину второго прямого участка детали L2 в миллиметрах вводим
в ячейку D9: 100,0
7. Осевой радиус сгиба второго изогнутого участка R2 в миллиметрах записываем
в ячейку D10: 200,0
8. Угол сгиба второго изогнутого участка α2 в градусах пишем
в ячейку D11: 135,0
9. Длину третьего прямого участка детали L3 в миллиметрах вводим
в ячейку D12: 300,0
10-15. Ввод исходных данных в Excel для нашего примера завершен. Ячейки D13…D18 оставляем пустыми.
Программа позволяет рассчитывать развертки деталей, содержащих до пяти прямых участков и до четырех изогнутых. Гибка трубы с большим количеством участков требует для расчета развертки незначительной модернизации программы.
Результаты расчетов:
16. Длину первого изогнутого участка L1 в миллиметрах вычисляем
в ячейке D20: =ЕСЛИ(D7=0;0;ПИ()*D8/180*((4*D7^2-$D$4^2)^0,5+(4*D7^2-$D$5^2)^0,5)/4) =469,4
17. Длину второго изогнутого участка L2 в миллиметрах вычисляем
в ячейке D21: =ЕСЛИ(D10=0;0;ПИ()*D11/180*((4*D10^2-$D$4^2)^0,5+(4*D10^2-$D$5^2)^0,5)/4) =467,0
18-19. Так как в рассматриваемом примере нет третьего и четвертого кривых участков, то
в ячейке D22: =ЕСЛИ(D13=0;0;ПИ()*D14/180*((4*D13^2-$D$4^2)^0,5+(4*D13^2-$D$5^2)^0,5)/4) =0,0
в ячейке D23: =ЕСЛИ(D16=0;0;ПИ()*D17/180*((4*D16^2-$D$4^2)^0,5+(4*D16^2-$D$5^2)^0,5)/4) =0,0
20. Общая длина развертки детали L в миллиметрах суммируется
в ячейке D24: =D6+D9+D12+D15+D18+D20+D21+D22+D23 =1536,3
Длина развертки изогнутой трубы рассчитана с помощью программы MS Excel.
Заключение.
Гибка трубы и/или прутка – не простая технологическая задача, таящая целый ряд «подводных камней». Надеюсь, предложенный расчет в Excel упростит вам, уважаемые читатели, ее решение. Возможность задания на каждом шаге различных длин прямых участков, углов и радиусов гибки, несомненно, расширит область применения представленной программы.
Уважаемые читатели! Вопросы, отзывы, и замечания оставляйте, пожалуйста, в комментариях внизу страницы.
УВАЖАЮЩИМ труд автора скачать файл можно ПОСЛЕ ПОДПИСКИ НА АНОНСЫ СТАТЕЙ (подписные формы — чуть ниже и наверху страницы).
ОСТАЛЬНЫМ — можно скачать просто так.
Ссылка на скачивание файла: raschet-dliny-razvertki-truby (xls 103KB).
Статьи с близкой тематикой
Отзывы
29 комментариев на «Гибка трубы. Длина развертки в Excel!»
Как хорошо, что такие люди как Вы есть. Спасибо за Ваше неравнодушие.
Александр спасибо вам огромное, что подробно расказываете и выкладываете расчет. Гибка труб — действительно нужное знание для инженеров и конструкторов. Пригодится даже в дом. хозяйстве. Успехов.
Большое спасибо за ценный материал.
А можно ли применить этот подход, если пруток — квадратного сечения? Например пересчитать площадь сечения в эквивалентный диаметр?
Александр, конечно, можно. Вы только что читали статью «Расчет длины развертки», где приведена формула для прямоугольного сечения. Квадрат — это тоже прямоугольник!
Доброе время суток. А как насчет материала 316 (нерж).
Так как формула расчета взята из классического сопромата, то применима для любых материалов, обладающих упругостью и пластичностью.
Перечитайте третий абзац статьи.
Большое Вам спасибо за безвозмездную помощь.
Гнем трубу буквой П. Исходные данные:
Внутренний диаметр — 42,6мм (стенка трубы 1,2мм)
Длина первого прямого участка — 375,5мм
Длина второго прямого участка — 175мм
Длина третьего прямого участка — 375,5мм
По Вашим расчетам получаем длину разверки — 1203,3мм
Если считать развертку по длине осевой линии: 375,5мм х 2шт + 175мм + 109,95 (длина дуги=пирн/180) х 2шт = 1145,9мм
1203,3-1145,9 = 57,4мм — расхождение
По моим расчетам получаем длину развертки — 1134,9мм!
Не знаю откуда Вы взяли 1203,3?
Если считать по осевой линии — 1145,9.
Заготовку следует взять на 11,0 мм короче, чем получается по осевой линии.
Добрый день! Как рассчитать длину трубы, имея уже согнутую заготовку. Исходные данные:
Диаметр трубы — 32мм, толщина стенки 1,2мм, согнута в одной плоскости буквой П. Если рулеткой измерять периметр по наруже, получаем 1147мм(сумма трех сторон с радиусами).
Добрый день! Владимир, вспомните геометрию.
Не зная радиусов и линейных размеров ответить на Ваш вопрос нельзя.
В формуле используются какие либо коэффициенты привязаные к материалу? Нужно рассчитать длину медной трубы.
Если Вы внимательно посмотрите на входящие в формулу параметры, то увидите, что они все чисто геометрические. Нет и намека на характеристики материала.
Дело в том, что классический сопромат рассматривает (в основном) материалы, обладающие при растяжении зоной упругой деформации, площадкой текучести, участком пластической деформации приводящим к точке разрушения. Так вот схожими по виду (не по величинам нагрузок и деформаций) диаграммами растяжения обладают все, так называемые, пластичные материалы. К ним относятся многие металлы, а вот закаленные стали, стекло, бетон — нет. Так их никто и не гнет!
Эта формула — теоретически выведенная для материалов с идеальной площадкой текучести. Но как и идеального газа (помните физику?), так и идеального металла в природе нет. Но с очень близкими диаграммами растяжения — полно.
Если точность в 3. 5% Вас не устраивает, то можно найти массу таблиц разных исследователей, которые определяют длину разверток для различных материалов опытным путем.
Резюме: эта формула для всех пластичных металлов. Её можно найти во многих учебниках по сопромату.
На практике многие вообще считают развертки труб по средней линии. Полученные погрешности «съедаются» низкой точностью оборудования и еще десятком факторов.
Спасибо Вам! За изложенный материал, где все так доходчиво расписано.
Расчет точен только при сгибе на 90 градусов. Если угол выше 90, длина кривого участка в 1,5-2 больше реальной длины.
Андрей, приведите свой пример.
В примере, приведенном в статье, 2-ой кривой участок с углом 135 градусов считается верно!
Может подскажите какие формулы использовать для расчета длинны развертки не круглой, а квадратной или прямоугольной трубы.
Если нужны формулы для очень точного расчета с учетом смещения нейтрального слоя относительно центра тяжести сечения, то — не подскажу.
5 и более раз больше размера сечения и не требуется точность «до миллиметра», то — считайте по осевой линии (линии центров тяжести сечений).
Спасибо, вы мне помогли сохранить время!))
Спасибо огромное за ваши труды!
А не подскажите в каком учебнике можно посмотреть вывод формулы для расчёта радиусов нейтральных слоёв у труб?
В каком-то из учебников по сопромату. По-быстрому вспомнить и найти в каком именно — не получилось.
Добрый день, мне необходимо согнуть круглую трубу (диаметр 25, стенка 1мм) в форму прямоугольника 50*40 см. Как произвести расчет?
Как посчитать? Так, как написано выше в статье.
Только для такой тонкостенной трубы необходимо задать достаточно большой радиус изгиба, иначе сечение при изгибе деформируется. В итоге такой небольшой прямоугольник Вам получить будет трудно. В углах будут слишком большие радиусы.
Решения — горячая штамповка, гибка с дорном, гибка с набивкой сечения песком, вварка в углы горячештампованных крутых отводов.
Последний вариант — самый простой и дешевый.
(Минимальные радиусы холодной гибки труб из различных металлов смотрите в справочниках.)
Задайте угрл 359 градусов, должно получить длина первого участка приблизительно в 2 раза больше радиуса, но не как в 5 раз больше радиуса
Смеющийся Архимед по ночам не снится? 🙂
Чисто практические решения повседневных (спонтанно появляющихся) задач. Но — проработанные, и не на глазок.
Вопрос смежный с темой этой странички: Расчёт роликов для гибки трубы с учётом свойств материала и диапазонов деформации (На грани смятия маленькие) (большие, практически без остаточной упругой деформации).
Материалы: от мельхиора и меди, до нержавейки и жаропрочной стали.
На данный момент подгонка осуществляется корректирующим точением заведомо большего огибаемого ролика (долго зачастую).
Борис, спасибо за высокую оценку материалов сайта.
Но в чем вопрос? Не очень понятно без схемы.
Собственно схема не нужна.
Диаметр обкатываемого ролика отличается от искомого на величину упругой деформации (чаще речь идёт о гибке на 180 градусов). Причём просто подгонка межосевого расстояния не всегда возможна, поскольку гнутые элементы «вложены» друг в друга и зазор между трубами лимитирован по всей длине, в том числе и в радиусной части.
Приходится ловить радиус гибки с точностью до десяток.
Применение «в лоб» коэффициента упругости из свойств материала не помогает. И коэффициент соотношения радиуса гибки к радиусу ролика плавает в зависимости от крутизны гиба.
Собственно пока писал — осознал, что вывести зависимость поможет только собственная статистика.
Источник
Расчет длины развертки

. квадратного сечений, гнут и все прокатные профили – уголки, швеллеры, двутавры, трубы. Однако холодная гибка деталей из листового металлопроката, безусловно, является наиболее распространенной.
Для обеспечения минимальных радиусов, детали перед гибкой иногда нагревают. При этом повышается пластичность материала. Используя гибку с калибрующим ударом, добиваются того, что внутренний радиус детали становится абсолютно равным радиусу пуансона. При свободной V-образной гибке на листогибе внутренний радиус получается на практике больше радиуса пуансона. Чем более у материала детали ярко выражены пружинные свойства, тем более отличаются друг от друга внутренний радиус детали и радиус пуансона.
На рисунке, представленном ниже, изображен согнутый из листа толщиной s и шириной b уголок. Необходимо найти длину развертки.
Расчет развертки выполним в программе MS Excel.
В чертеже детали заданы: величина внутреннего радиуса R , угол a и длина прямолинейных участков L1 и L2 . Вроде все просто – элементарная геометрия и арифметика. В процессе изгиба заготовки происходит пластическая деформация материала. Наружные (относительно пуансона) волокна металла растягиваются, а внутренние сжимаются. В середине сечения – нейтральная поверхность…
Но вся проблема в том, что нейтральный слой располагается не в середине сечения металла! Для справки: нейтральный слой – поверхность расположения условных волокон металла, не растягивающихся и не сжимающихся при изгибе. Более того – эта поверхность (вроде как) не является поверхностью кругового цилиндра. Некоторые источники предполагают, что это параболический цилиндр…
Я более склонен доверять классическим теориям. Для сечения прямоугольной формы по классическому сопромату нейтральный слой располагается на поверхности кругового цилиндра с радиусом r .
На базе этой формулы и создана программа расчета развертки листовых деталей из сталей марок Ст3 и 10…20 в Excel.
В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные. В ячейке со светло-желтой заливкой считываем результат расчета.
1. Записываем толщину листовой заготовки s в миллиметрах
в ячейку D 3 : 5,0
2. Длину первого прямого участка L1 в миллиметрах вводим
в ячейку D 4 : 40,0
3. Внутренний радиус сгиба первого участка R1 в миллиметрах записываем
в ячейку D 5 : 5,0
4. Угол сгиба первого участка a1 в градусах пишем
в ячейку D 6 : 90,0
5. Длину второго прямого участка детали L2 в миллиметрах вводим
в ячейку D 7 : 40,0
6. Все, результат расчета — длина развертки детали L в миллиметрах
в ячейке D 17 : =D4+ЕСЛИ(D5=0;0;ПИ()/180*D6*D3/LN ((D5+D3)/D5))+ +D7+ЕСЛИ(D8=0;0;ПИ()/180*D9*D3/LN ((D8+D3)/D8))+D10+ +ЕСЛИ(D11=0;0;ПИ()/180*D12*D3/LN ((D11+D3)/D11))+D13+ +ЕСЛИ(D14=0;0;ПИ()/180*D15*D3/LN ((D14+D3)/D14))+D16 =91.33
Используя предложенную программу, можно рассчитать длину развертки для деталей с одним сгибом – уголков, с двумя сгибами – швеллеров и Z-профилей, с тремя и четырьмя сгибами. Если необходимо выполнить расчет развертки детали с большим числом сгибов, то программу очень легко доработать, расширив возможности.
Важным преимуществом предложенной программы (в отличие от многих аналогичных) является возможность задания на каждом шаге различных углов и радиусов гибки.
А «правильные» ли результаты выдает программа? Давайте, сравним полученный результат с результатами расчетов по методике изложенной в «Справочнике конструктора-машиностроителя» В.И. Анурьева и в «Справочнике конструктора штампов» Л.И. Рудмана. Причем в расчет возьмем только криволинейный участок, так как прямолинейные участки все, надеюсь, считают одинаково.
Проверим рассмотренный выше пример.
«По программе» : 11,33 мм – 100,0%
«По Анурьеву» : 10,60 мм – 93,6%
Увеличим в нашем примере радиус гибки R1 в два раза — до 10 мм. Еще раз произведем расчет по трем методикам.
«По программе» : 19,37 мм – 100,0%
«По Анурьеву» : 18,65 мм – 96,3%
Таким образом, предложенная методика расчетов выдает результаты на 0,4%…1,1% больше, чем «по Рудману» и на 6.4%…3,7% больше, чем «по Анурьеву». Понятно, что погрешность существенно уменьшится, когда мы добавим прямолинейные участки.
«По программе» : 99,37 мм – 100,0%
«По Анурьеву» : 98,65 мм – 99,3%
Возможно Рудман составлял свои таблицы по этой же формуле, которую использую я, но с погрешностью логарифмической линейки… Конечно, сегодня «на дворе» двадцать первый век, и рыскать по таблицам как-то не с руки!
В заключение добавлю «ложку дегтя». Длина развертки — это очень важный и «тонкий» момент! Если конструктор гнутой детали (особенно высокоточной (0,1 мм)) надеется расчетом точно и с первого раза определить ее, то он зря надеется. На практике в процесс гибки вмешается масса факторов – направление проката, допуск на толщину металла, утонение сечения в месте изгиба, «трапециевидность сечения», температура материала и оснастки, наличие или отсутствие смазки в зоне гибки, настроение гибщика… Короче, если партия деталей большая и дорого стоит – уточните практическими опытами длину развертки на нескольких образцах. И только после получения годной детали рубите заготовки на всю партию. А для изготовления заготовок для этих образцов, точности, которую обеспечивает программа расчета развертки, хватит с лихвой!
Программы расчета «по Анурьеву» и «по Рудману» в Excel можете найти в Сети.
Жду ваших комментариев, коллеги.
Для УВАЖАЮЩИХ труд автора — скачать файл можно ПОСЛЕ ПОДПИСКИ НА АНОНСЫ СТАТЕЙ (подписная форма — чуть ниже и наверху страницы).
Для ОСТАЛЬНЫХ — можно скачать просто так.
Ссылка на скачивание файла: raschet-dliny-razvertki (xls 36,5KB).
Продолжение темы — в статье о К-факторе.
О расчете развертки при гибке труб и прутков читайте здесь.
Источник



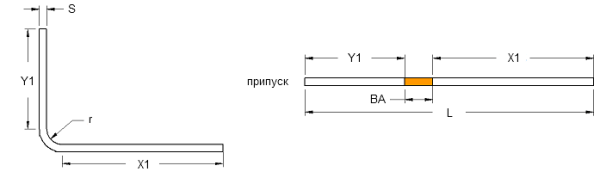
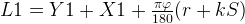
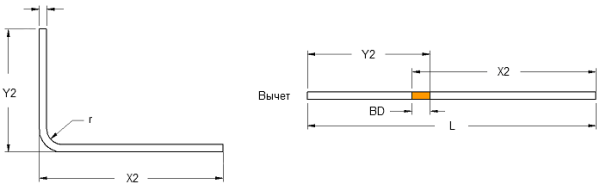
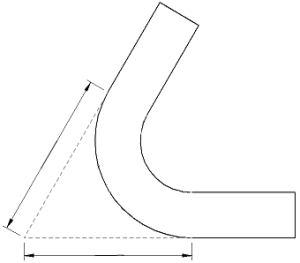
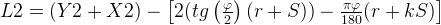
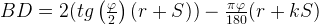

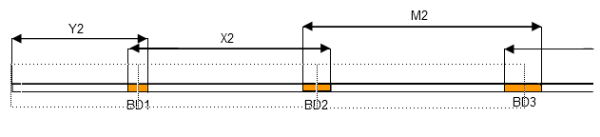
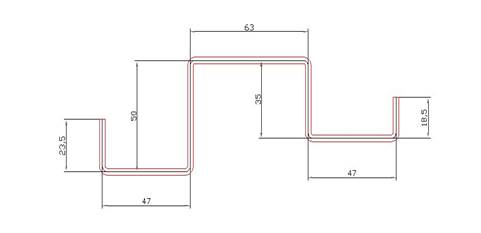
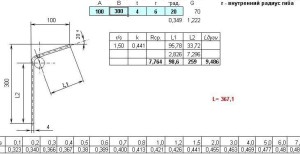






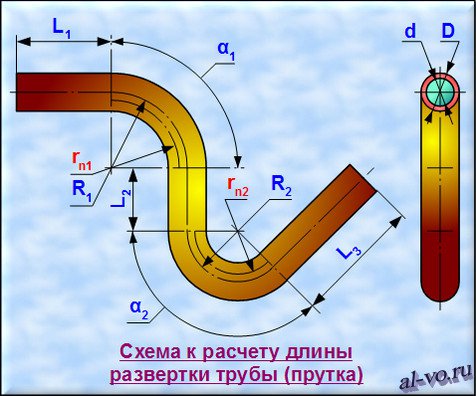
















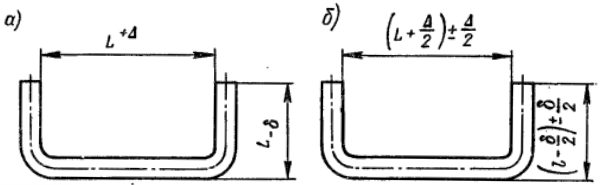
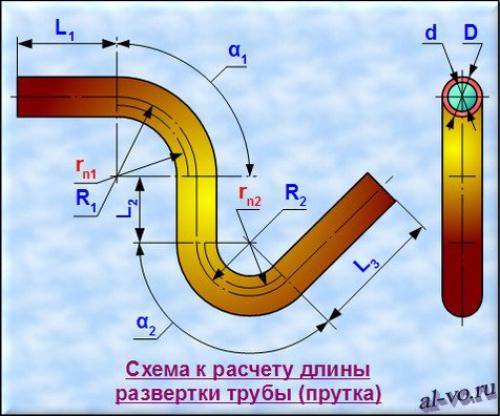
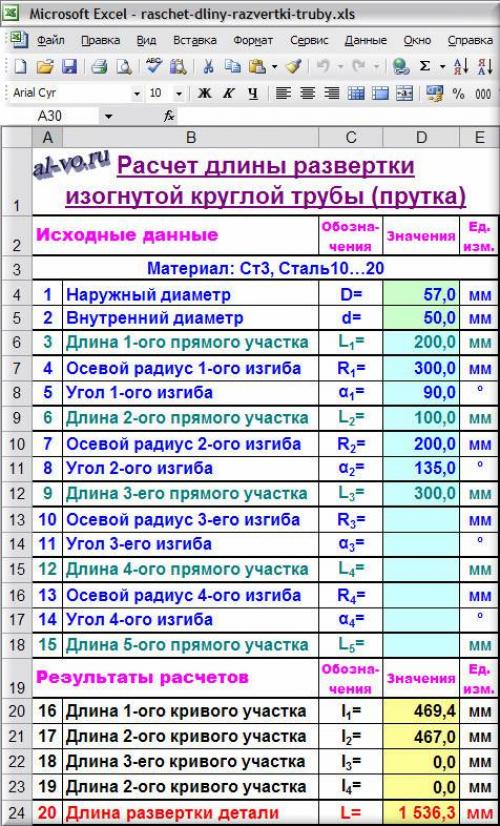
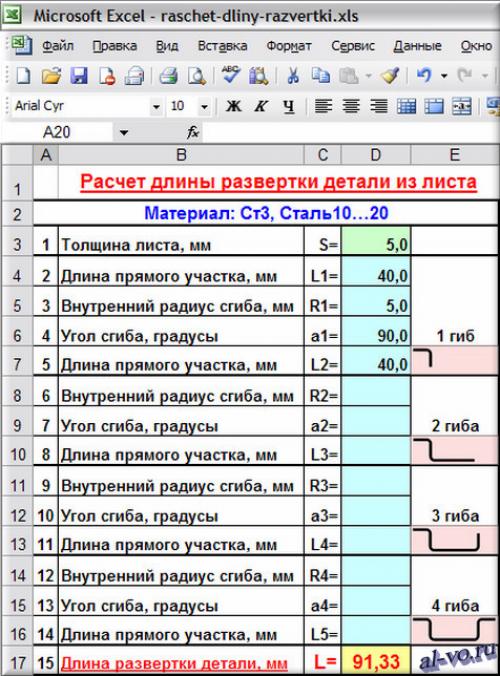
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/631337185852.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/33c5aaaf8f55.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/afbf76d5c59c.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/7626776df2e4.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/aa64dfdcc577.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/60022c01892b.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/c683e1dd6838.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/019fd92c2a46.jpg)
![Гибка листового металла расчет. Гибка листового металла - методы и советы по проектированию [часть 2]](https://baget-bez-stusla.aystroika.info/sites/default/files/i/baget-bez-stusla.aystroika.info/25022/4-9/24c70806539a.jpg)