Содержание
- Применение математических функций
- СУММ
- СУММЕСЛИ
- ОКРУГЛ
- ПРОИЗВЕД
- ABS
- СТЕПЕНЬ
- КОРЕНЬ
- СЛУЧМЕЖДУ
- ЧАСТНОЕ
- РИМСКОЕ
- Вопросы и ответы
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
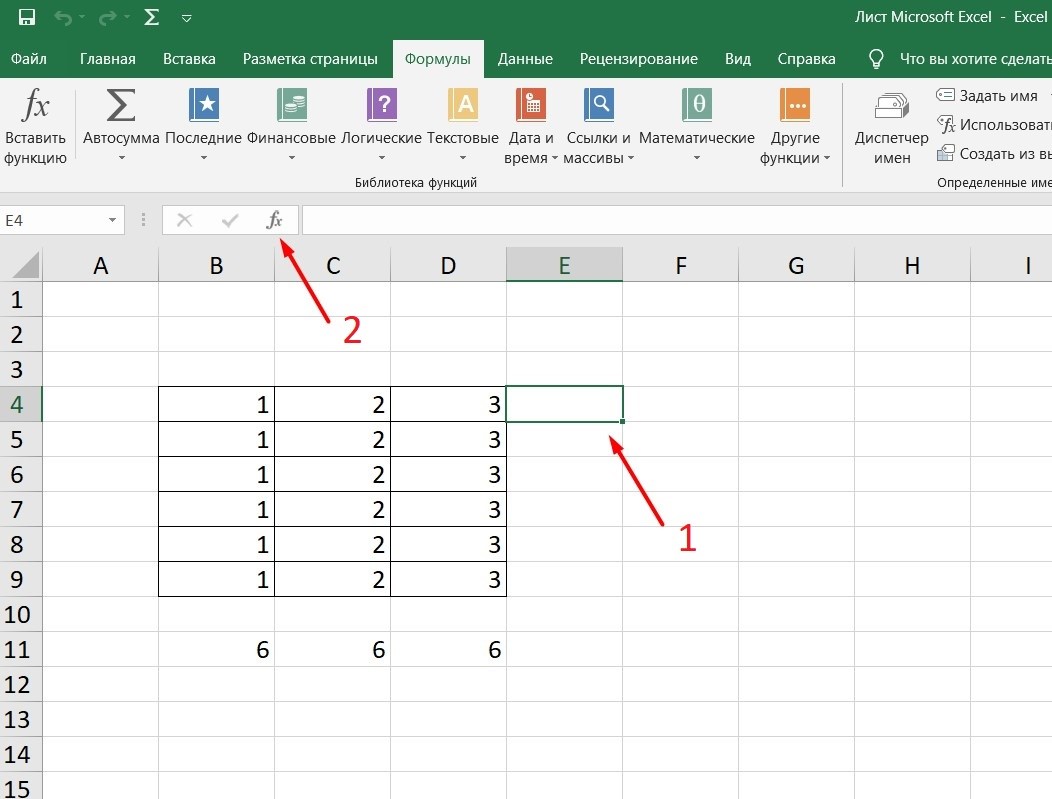
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.
Урок: Мастер функций в Excel
СУММ
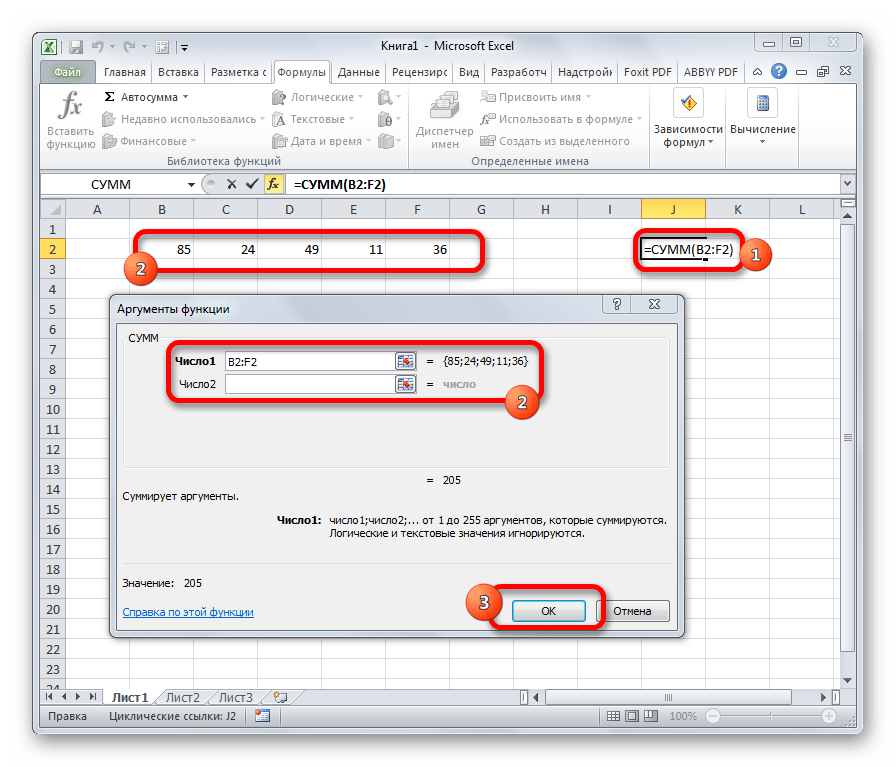
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
=СУММ(число1;число2;…)
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
Урок: Как посчитать сумму в Экселе
СУММЕСЛИ
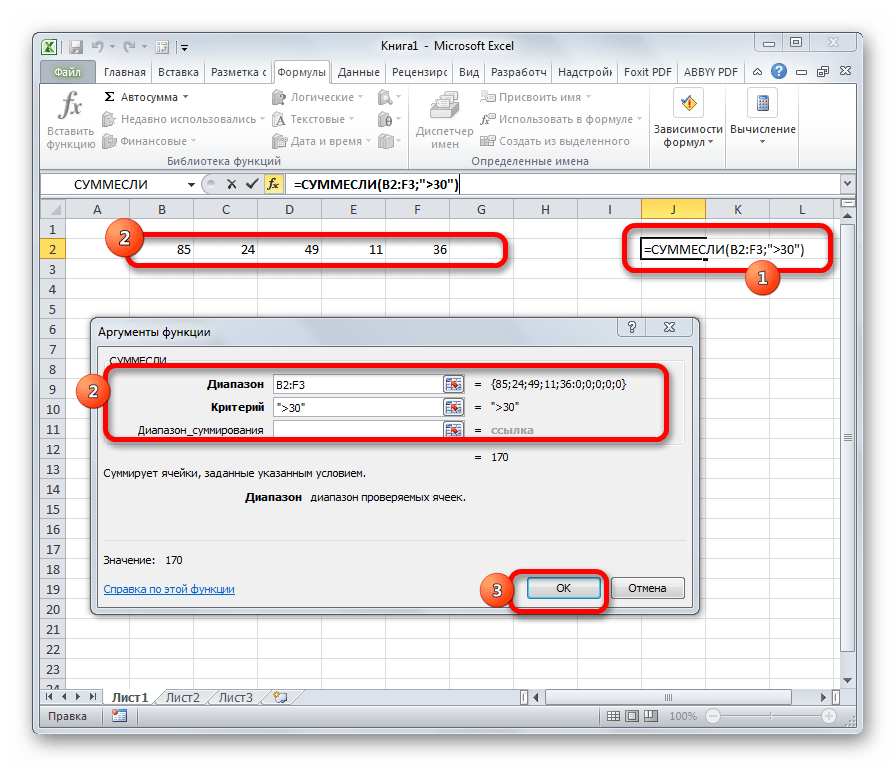
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
ОКРУГЛ
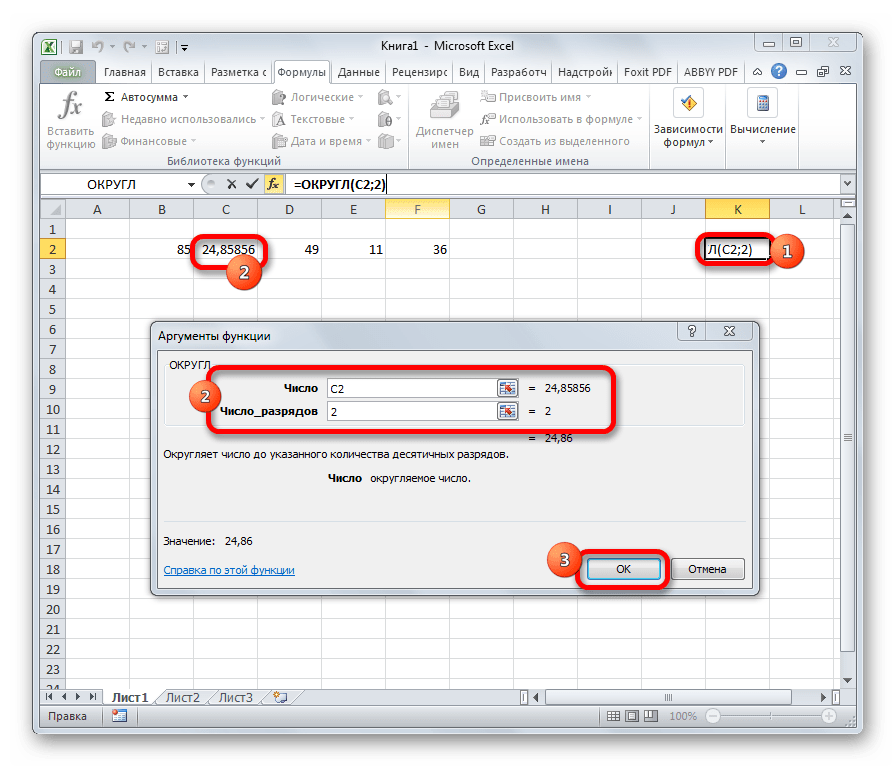
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
=ОКРУГЛ(число;число_разрядов)
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
Урок: Округление чисел в Excel
ПРОИЗВЕД
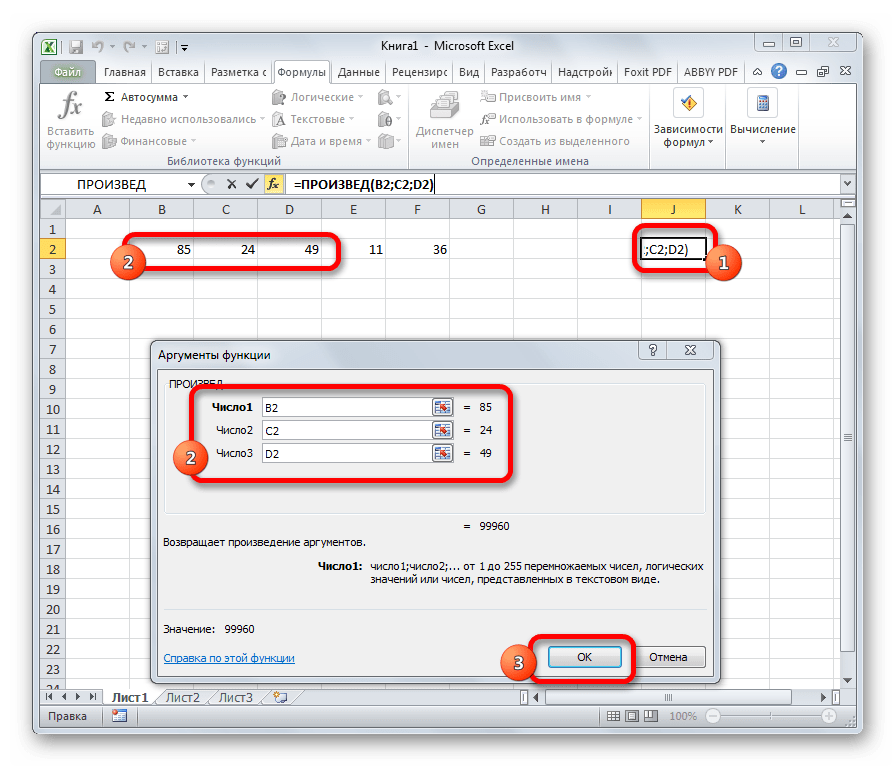
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
=ПРОИЗВЕД(число;число;…)
Урок: Как правильно умножать в Excel
ABS
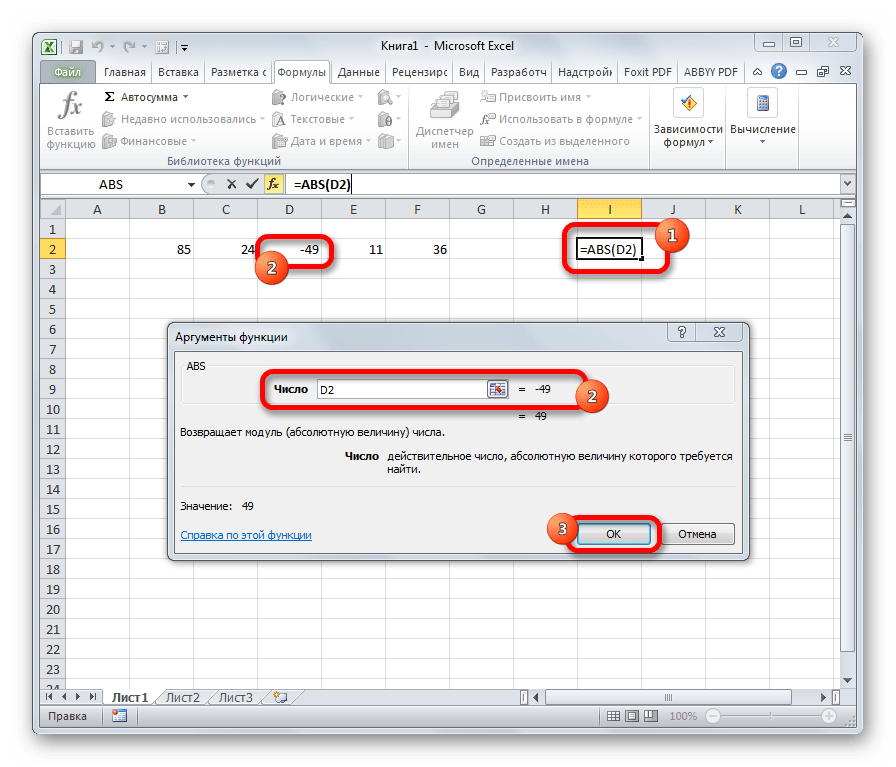
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
Урок: Функция модуля в Excel
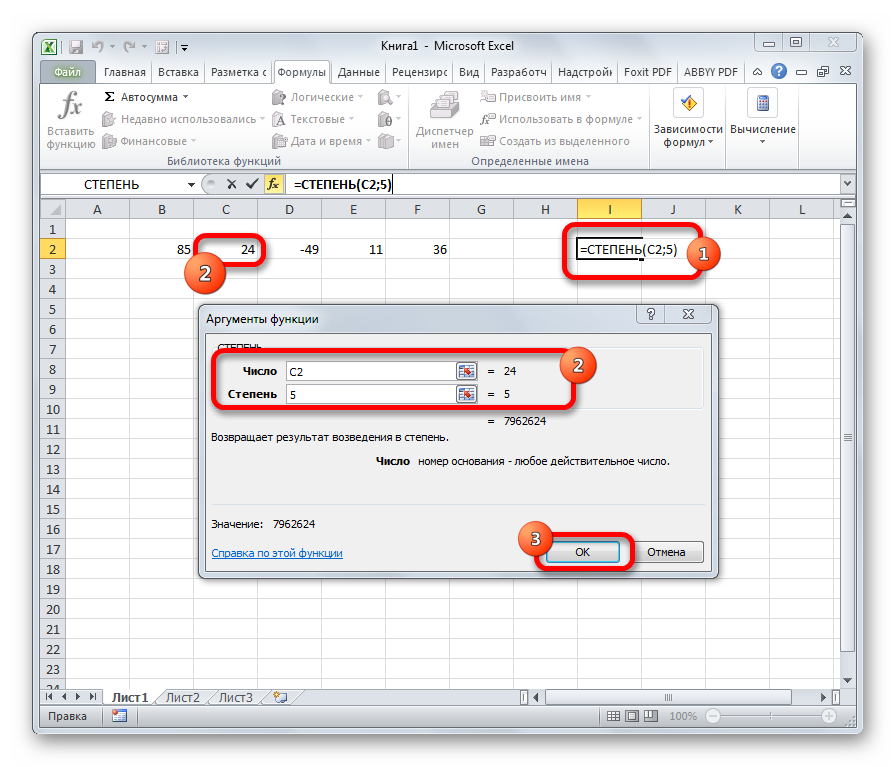
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
Урок: Как возводить в степень в Экселе
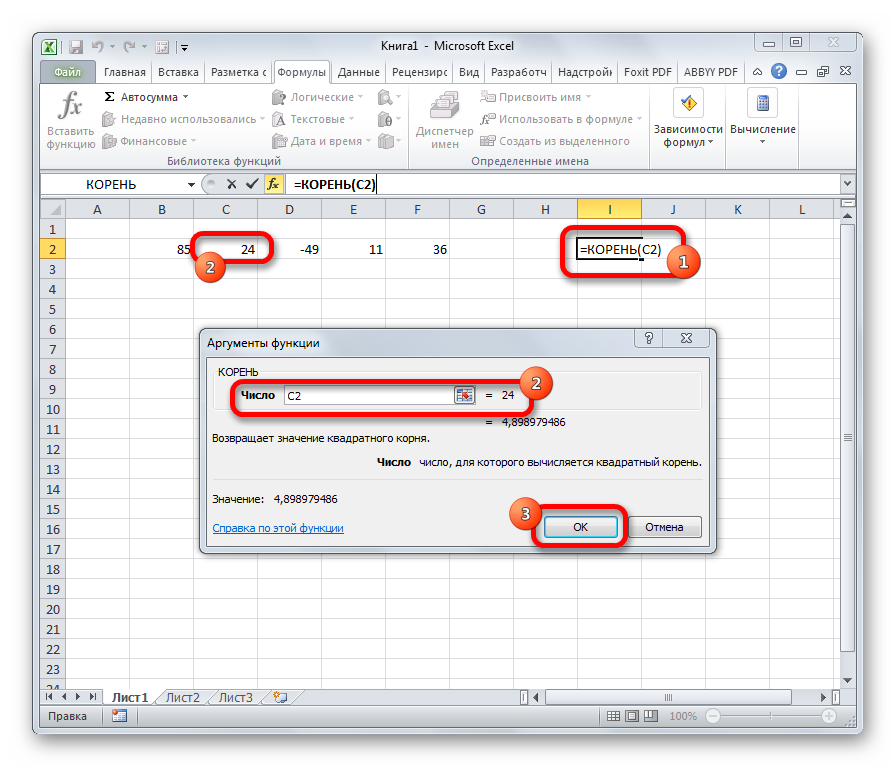
КОРЕНЬ
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
=КОРЕНЬ(число)
Урок: Как посчитать корень в Экселе
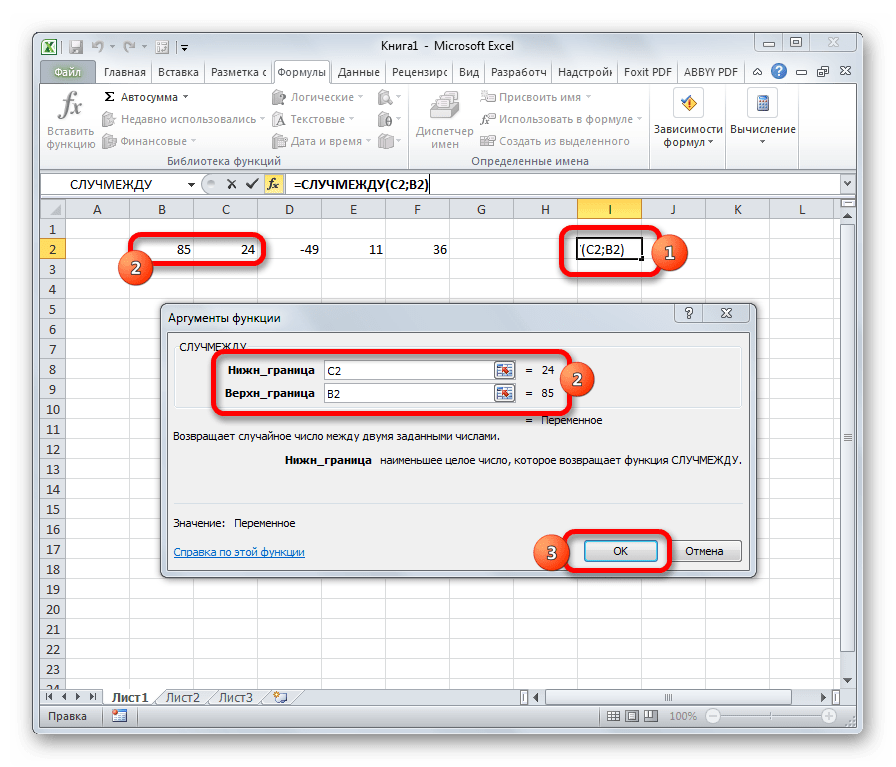
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
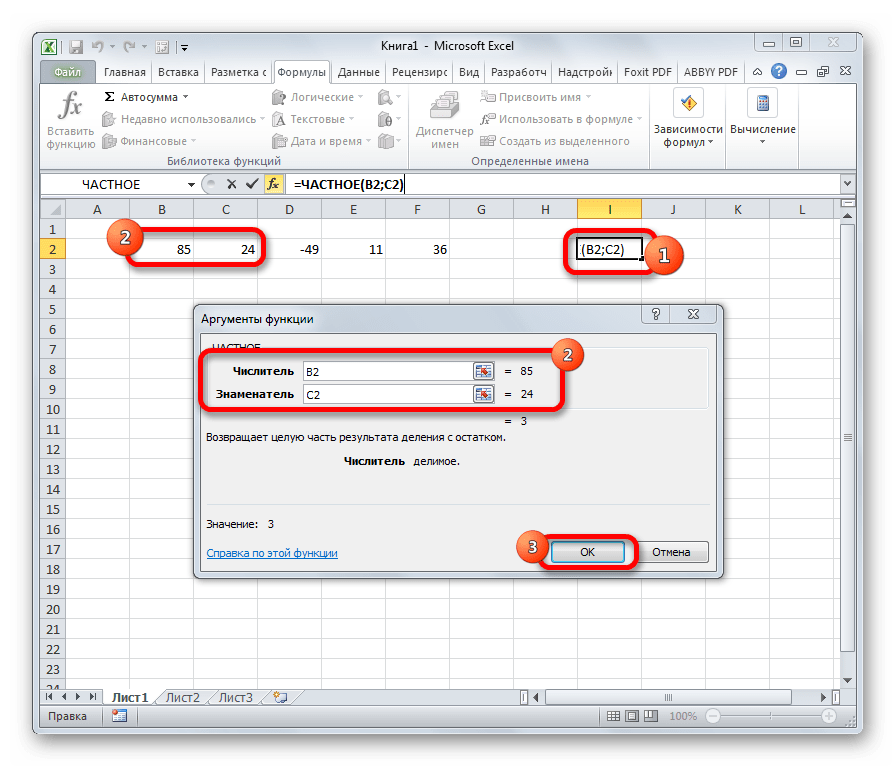
ЧАСТНОЕ
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
=ЧАСТНОЕ(Числитель;Знаменатель)
Урок: Формула деления в Экселе
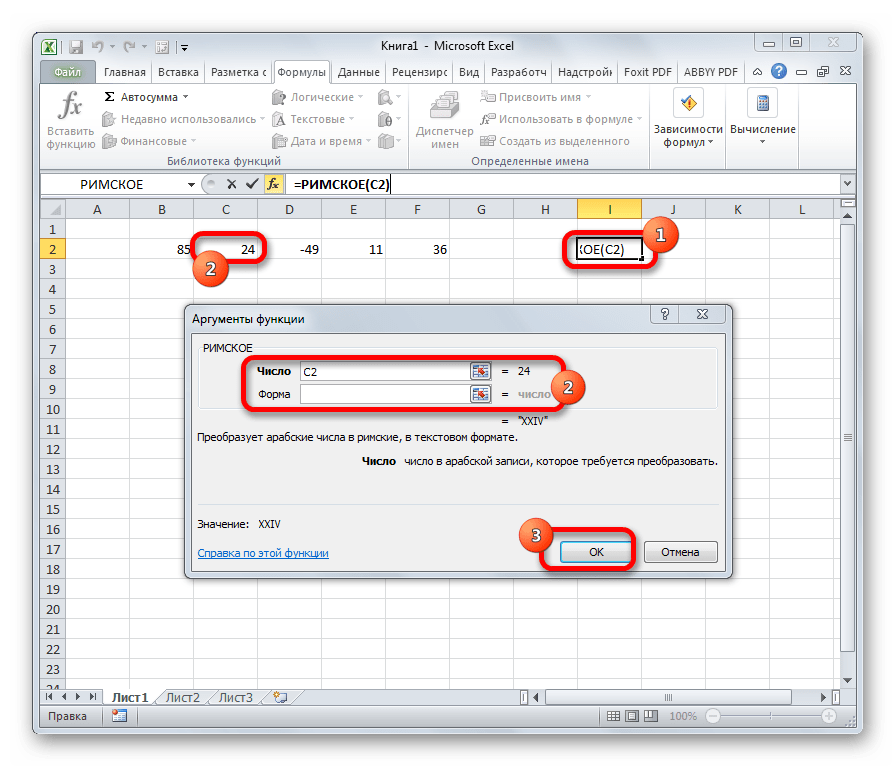
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Иногда трудно понять, как вложенная формула вычисляет конечный результат, поскольку в ней выполняется несколько промежуточных вычислений и логических проверок. Но с помощью диалогового окна Вычисление формулы вы можете увидеть, как разные части вложенной формулы вычисляются в заданном порядке. Например, формулу =ЕСЛИ(СПБ(F2:F5)>50;СУММ(G2:G5);0) проще понять, если вы увидите промежуточные результаты:
|
Шаги, показанные в диалоговом окне |
Описание |
|
=ЕСЛИ(СРЗНАЧ(F2:F5)>50;СУММ(G2:G5);0) |
Сначала выводится вложенная формула. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ. |
|
=ЕСЛИ(40>50;СУММ(G2:G5);0) |
Диапазон ячеек F2:F5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(F2:F5) возвращает результат 40. |
|
=ЕСЛИ(Ложь;СУММ(G2:G5);0) |
40 не больше 50, поэтому выражение в первом аргументе функции ЕСЛИ (аргумент logical_test) ложно. |
|
0 |
Функция ЕСЛИ возвращает значение третьего аргумента (аргумент значение_если_ложь). Функция СУММ не вычисляется, так как она является вторым аргументом функции ЕСЛИ (value_if_true) и возвращается только в том случае, если выражение истинно. |
-
Выделите ячейку, которую нужно вычислить. За один раз можно вычислить только одну ячейку.
-
На вкладке Формулы в группе Зависимости формул нажмите кнопку Вычислить формулу.
-
Нажмите кнопку Вычислить, чтобы проверить значение подчеркнутой ссылки. Результат вычисления отображается курсивом.
Если подчеркнутая часть формулы является ссылкой на другую формулу, нажмите кнопку Шаг с заходом, чтобы отобразить другую формулу в поле Вычисление. Нажмите кнопку Шаг с выходом, чтобы вернуться к предыдущей ячейке и формуле.
Примечание: Кнопка Шаг с заходом недоступна для ссылки, если ссылка используется в формуле во второй раз или если формула ссылается на ячейку в отдельной книге.
-
Продолжайте этот процесс, пока не будут вычислены все части формулы.
-
Чтобы посмотреть вычисление еще раз, нажмите кнопку Начать сначала.
Чтобы закончить вычисление, нажмите кнопку Закрыть.
Примечания:
-
Некоторые части формул, в которые используются функции ЕСЛИ и ВЫБОР, не вычисляются, и в поле «Оценка» #N/Д.
-
Если ссылка пуста, в поле Вычисление отображается нулевое значение (0).
-
Формулы с циклыми ссылками могут не оцениваться, как ожидалось. При желании можно включить итеративные вычисления.
-
Следующие функции пересчитываются каждый раз при внесении изменений в ячейку и могут привести к тому, что инструмент «Вычислите формулу» дает результаты, отличаные от результатов в ячейке: СЛЧИС, СМЕДЕН, ЯЧЕЙКА, ДВЕ, СЕГОДНЯ, СЛЧИСЛО, МНИМ.СТ.ЕСЛИ (в некоторых случаях).
-
Нужна дополнительная помощь?
Формула, она же функция, – одна из основных составляющих электронных таблиц, создаваемых при помощи программы Microsoft Excel. Разработчики добавили огромное количество разных функций, предназначенных для выполнения как простых, так и сложных расчетов. К тому же пользователю разрешено самостоятельно производить математические операции, что тоже можно назвать своеобразной реализацией формул. Именно о работе с этими компонентами и пойдет речь далее.
Я разберу основы работы с формулами и полезные «фишки», способные упростить процесс взаимодействия с таблицами.
Поиск перечня доступных функций в Excel
Если вы только начинаете свое знакомство с Microsoft Excel, полезно будет узнать, какие функции существуют, для чего предназначены и как происходит их создание. Для этого в программе есть графическое меню с отображением всего списка формул и кратким описанием действия расчетов.
-
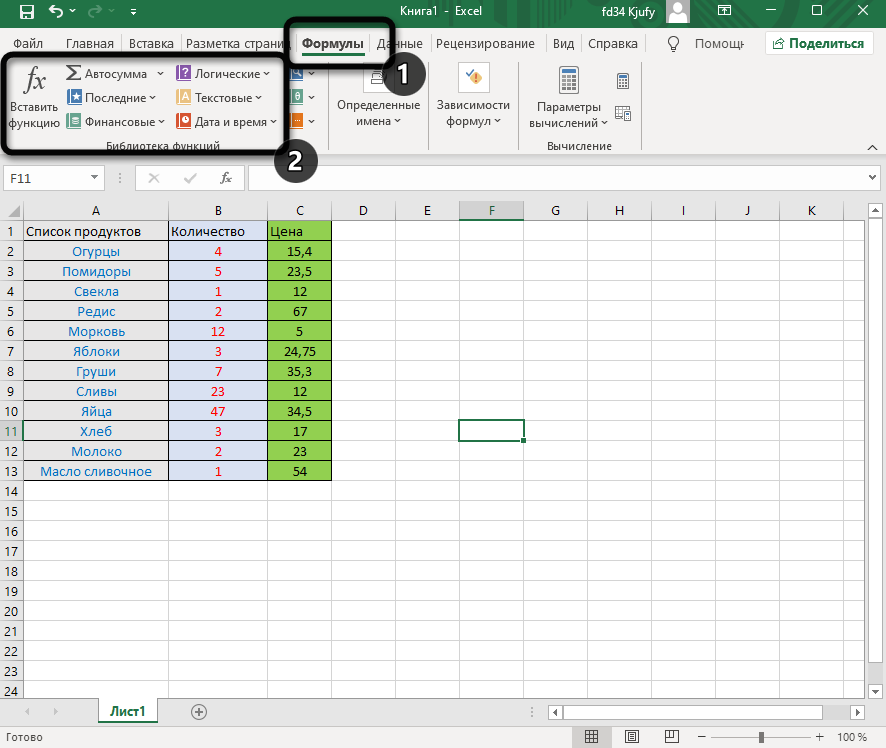
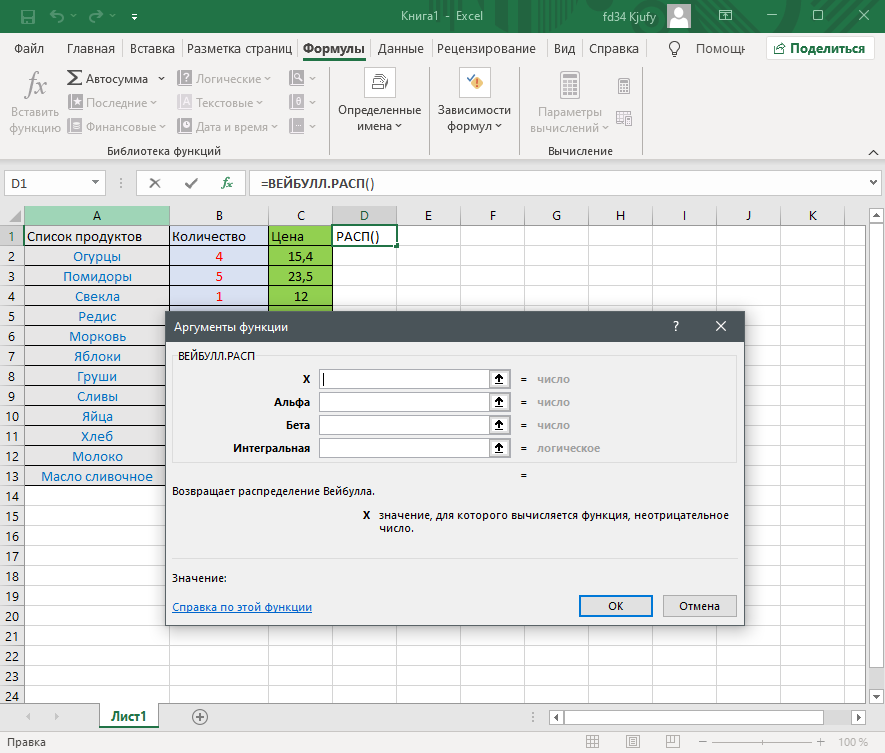
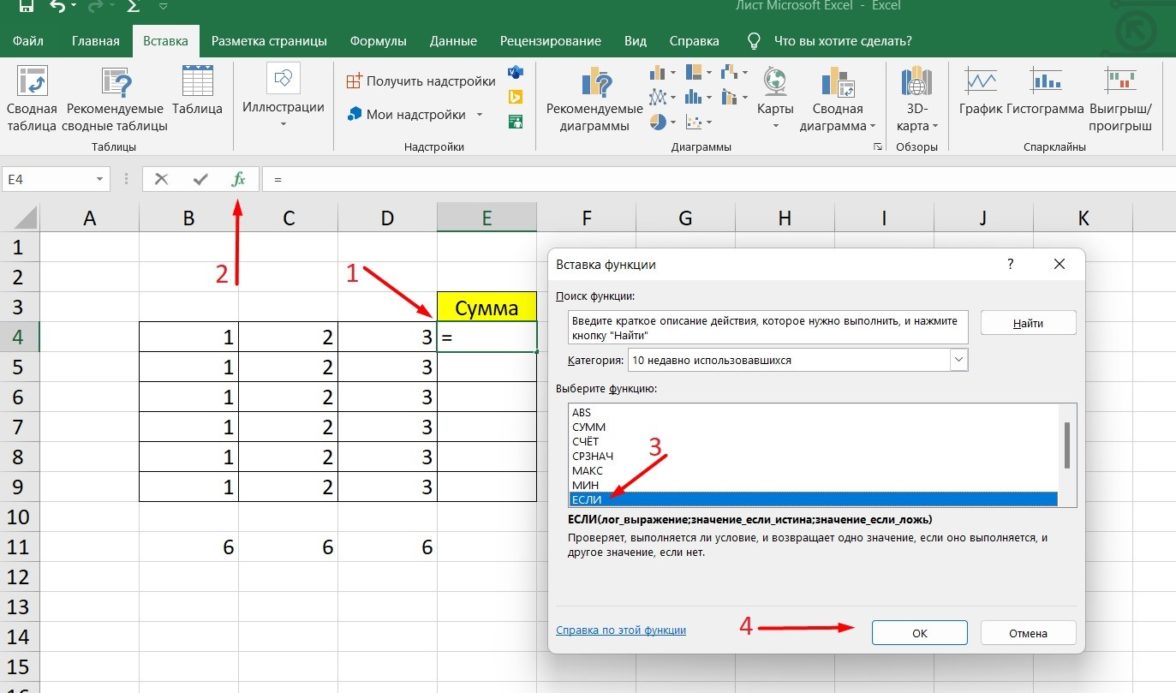
Откройте вкладку «Формулы» и нажмите на кнопку «Вставить функцию» либо разверните список с понравившейся вам категорией функций.
-
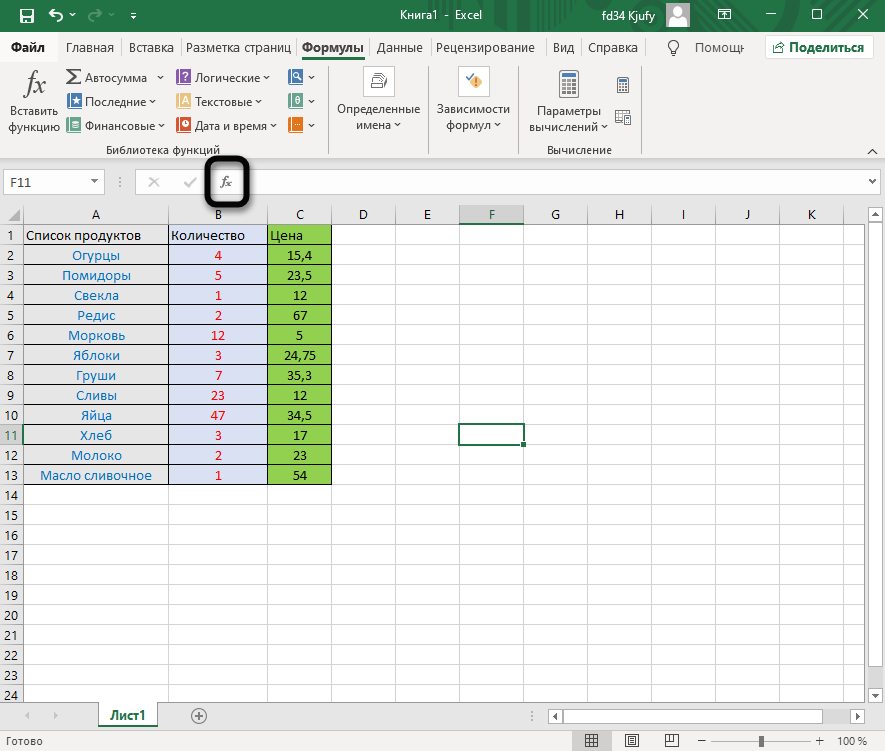
Вместо этого всегда можно кликнуть по значку с изображением «Fx» для открытия окна «Вставка функции».
-
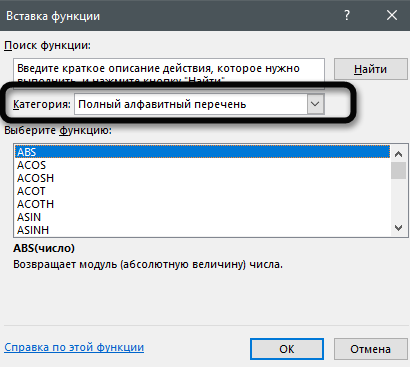
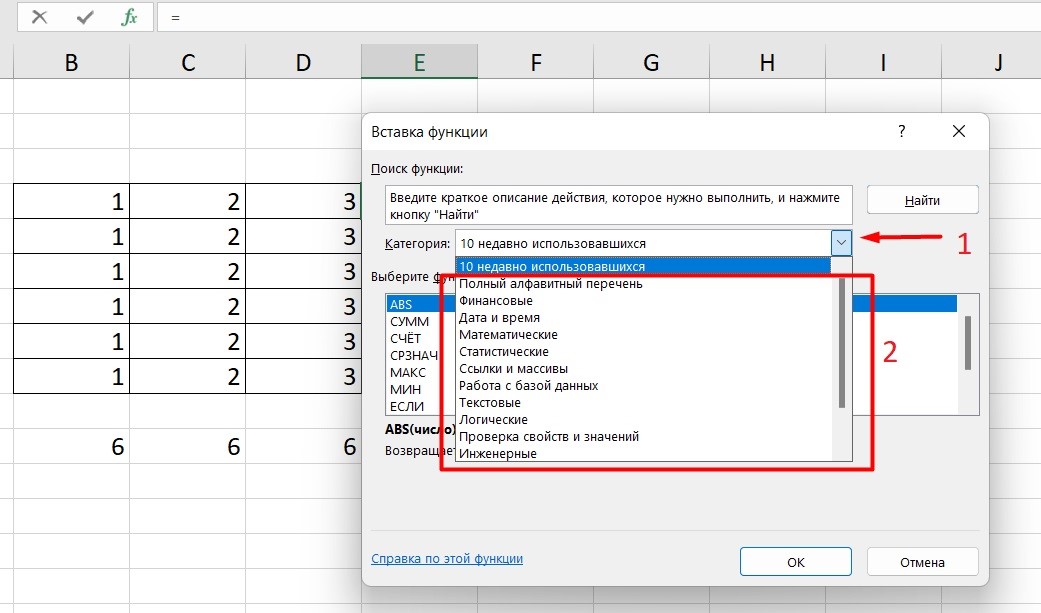
В этом окне переключите категорию на «Полный алфавитный перечень», чтобы в списке ниже отобразились все доступные формулы в Excel, расположенные в алфавитном порядке.
-
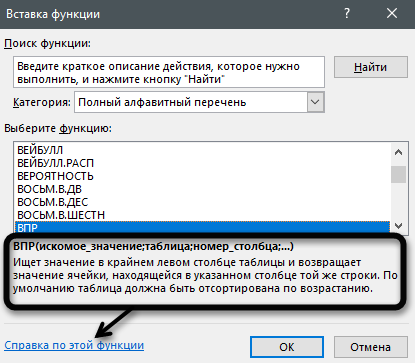
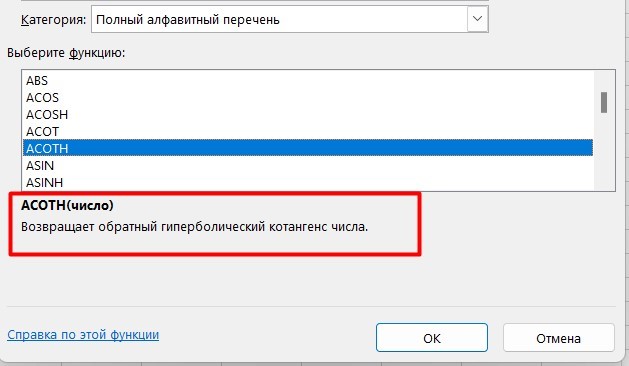
Выделите любую строку левой кнопкой мыши и прочитайте краткое описание снизу. В скобках показан синтаксис функции, который необходимо соблюдать во время ее написания, чтобы все аргументы и значения совпадали, а вычисления происходило корректно. Нажмите «Справка по этой функции», если хотите открыть страницу о ней в официальной документации Microsoft.
-
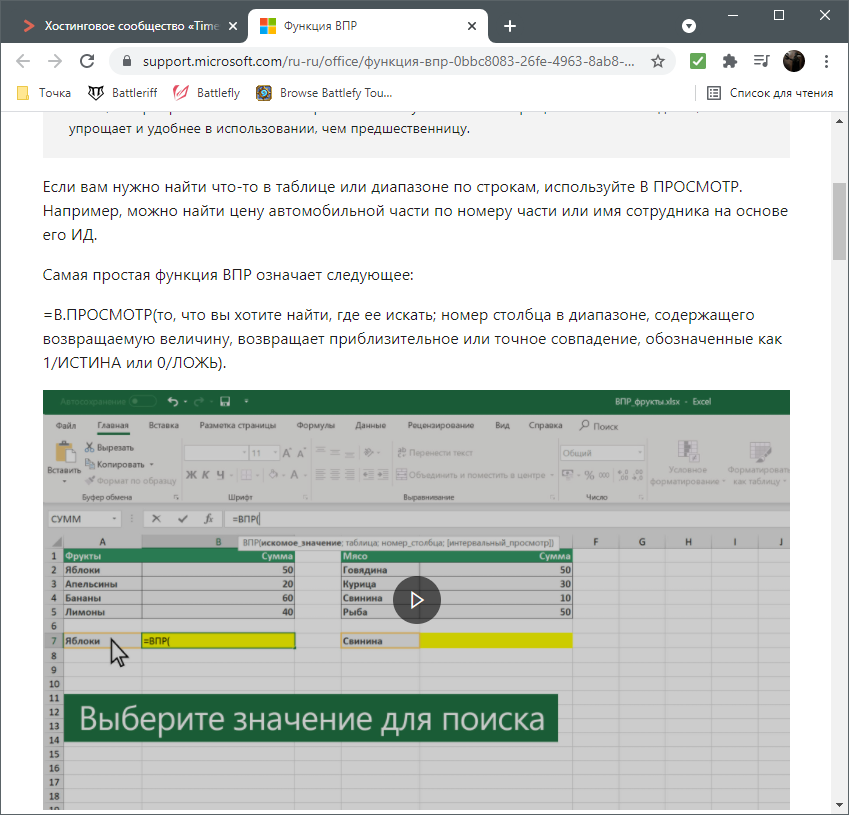
В браузере вы увидите большое количество информации по выбранной формуле как в текстовом, так и в формате видео, что позволит самостоятельно разобраться с принципом ее работы.
Отмечу, что наличие подобной информации на русском языке, еще и в таком развернутом виде, делает процесс знакомства с ПО еще более простым, особенно когда речь идет о переходе к более сложным функциям, действующим не совсем очевидным образом. Не стесняйтесь и переходите на упомянутые страницы, чтобы получить справку от специалистов и узнать что-то новое, что хотя бы минимально или даже значительно ускорит рабочий процесс.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
Вставка функции в таблицу
Теперь давайте разберемся с тем, как в Excel задать формулу, то есть добавить ее в таблицу, обеспечив вычисление определенных значений. Вы можете писать функции как самостоятельно, объявляя их название после знака «=», так и использовать графическое меню, переход к которому осуществляется так, как это было показано выше. В Комьюнити уже есть статья «Как вставить формулу в Excel», поэтому я рекомендую нажать по выделенной ссылке и перейти к прочтению полезного материала.
Использование математических операций в Excel
Если необходимо выполнить математические действия с ячейками или конкретными числами, в Excel тоже создается формула, поскольку все записи, начинающиеся с «=» в ячейке, считаются функциями. Все знаки для математических операций являются стандартными, то есть «*»– умножить, «/» – разделить и так далее. Следует отметить, что для возведения в степень используется знак «^». Вкратце рассмотрим объявление подобных функций.
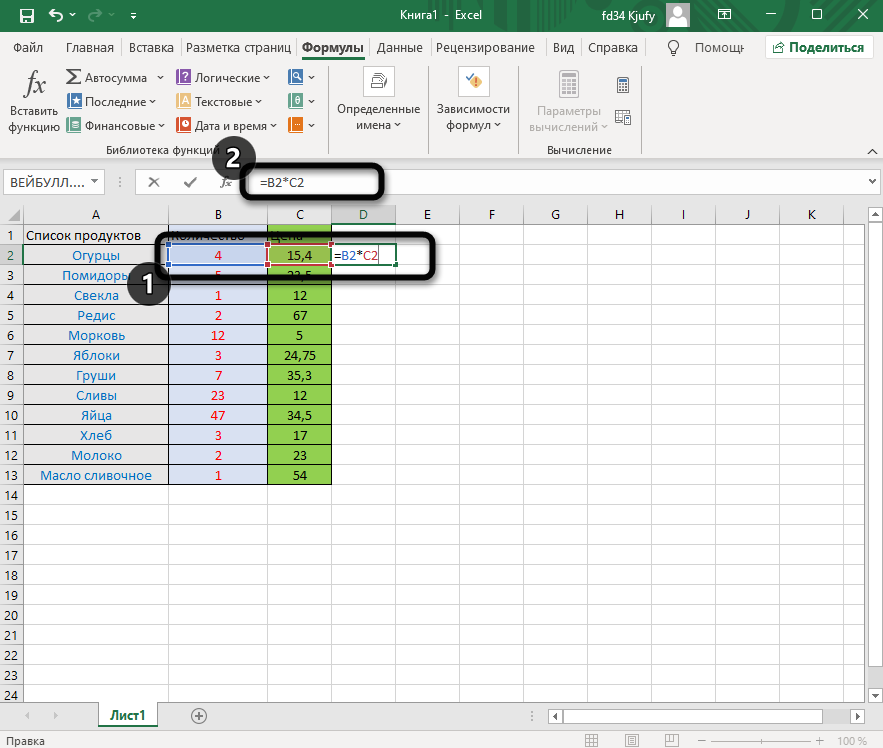
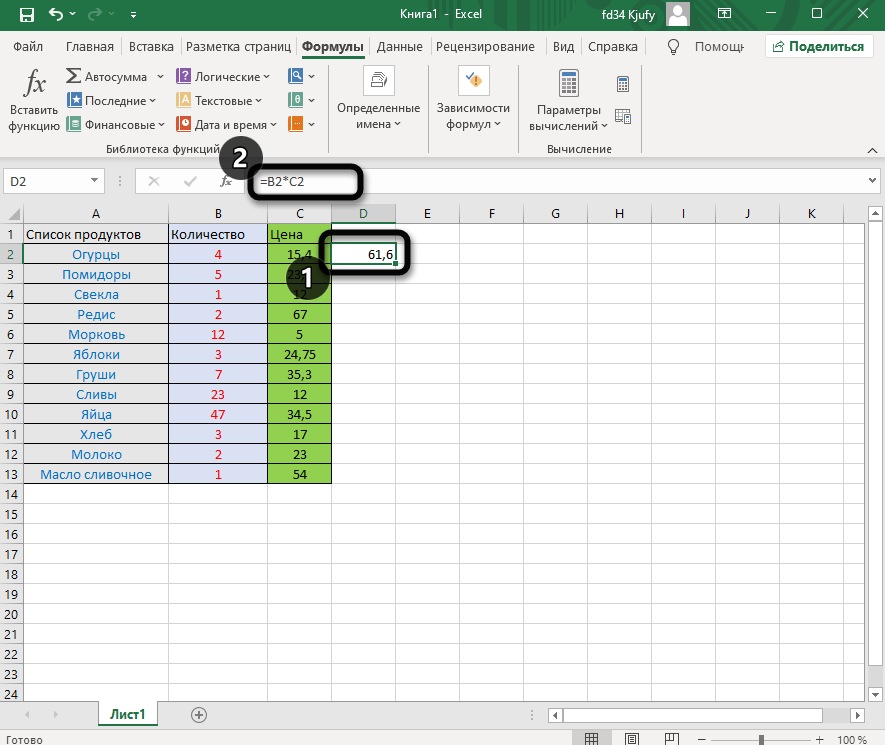
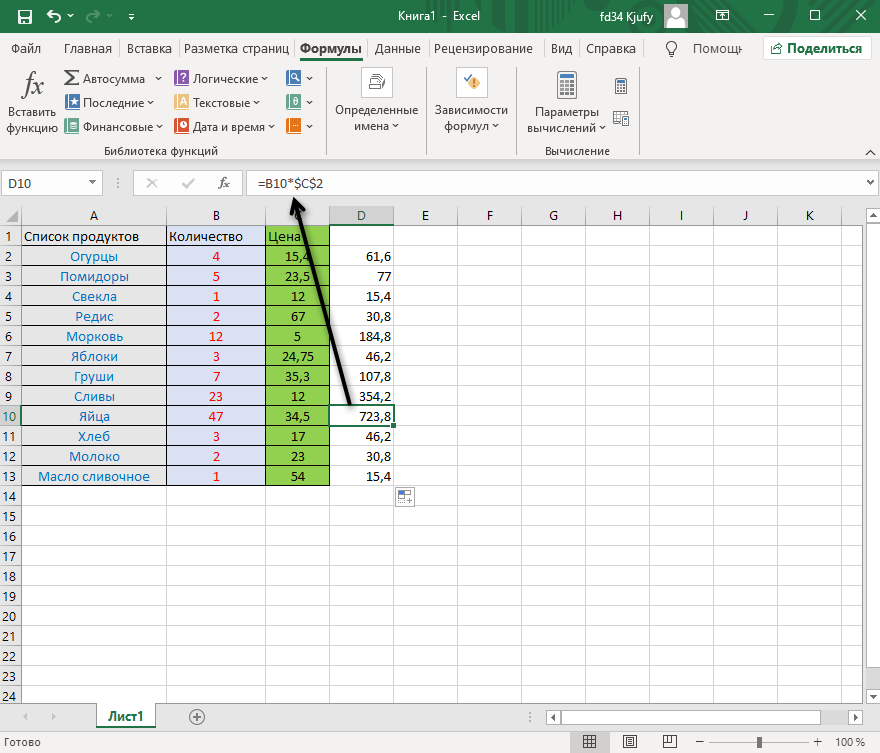
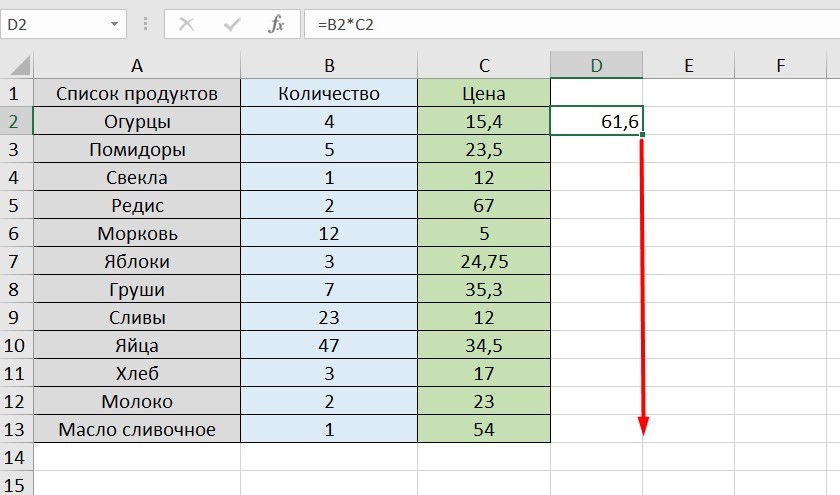
Выделите любую пустую ячейку и напишите в ней знак «=», объявив тем самым функцию. В качестве значения можете взять любое число, написать номер ячейки (используя буквенные и цифровые значения слева и сверху) либо выделить ее левой кнопкой мыши. На следующем скриншоте вы видите простой пример =B2*C2, то есть результатом функции будет перемножение указанных ячеек друг на друга.
После заполнения данных нажмите Enter и ознакомьтесь с результатом. Если синтаксис функции соблюден, в выбранной ячейке появится число, а не уведомление об ошибке.
Попробуйте самостоятельно использовать разные математические операции, добавляя скобки, чередуя цифры и ячейки, чтобы быстрее разобраться со всеми возможностями математических операций и в будущем применять их, когда это понадобится.
Растягивание функций и обозначение константы
Работа с формулами в Эксель подразумевает и выполнение более сложных действий, связанных с заполнением строк всей таблицы и связыванием нескольких разных значений. В этом разделе статьи я объединю сразу две разных темы, поскольку они тесно связаны между собой и обе упрощают взаимодействие с открытым в программе проектом.
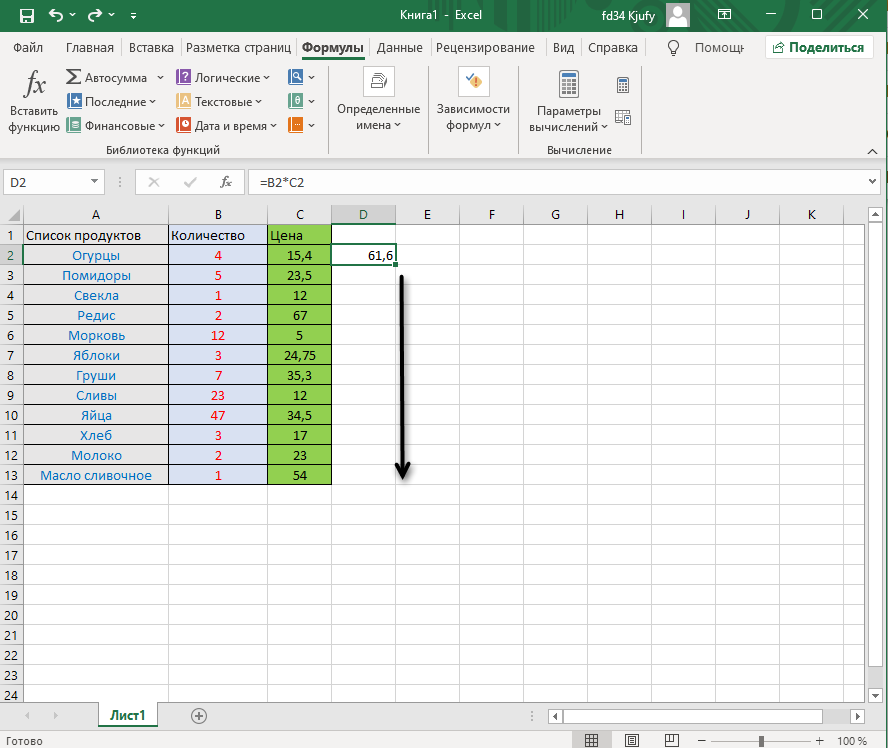
Для начала остановимся на растягивании функции. Для этого вам необходимо ввести ее в одной ячейке и убедиться в получении корректного результата. Затем зажмите точку в правом нижнем углу ячейки и проведите вниз.
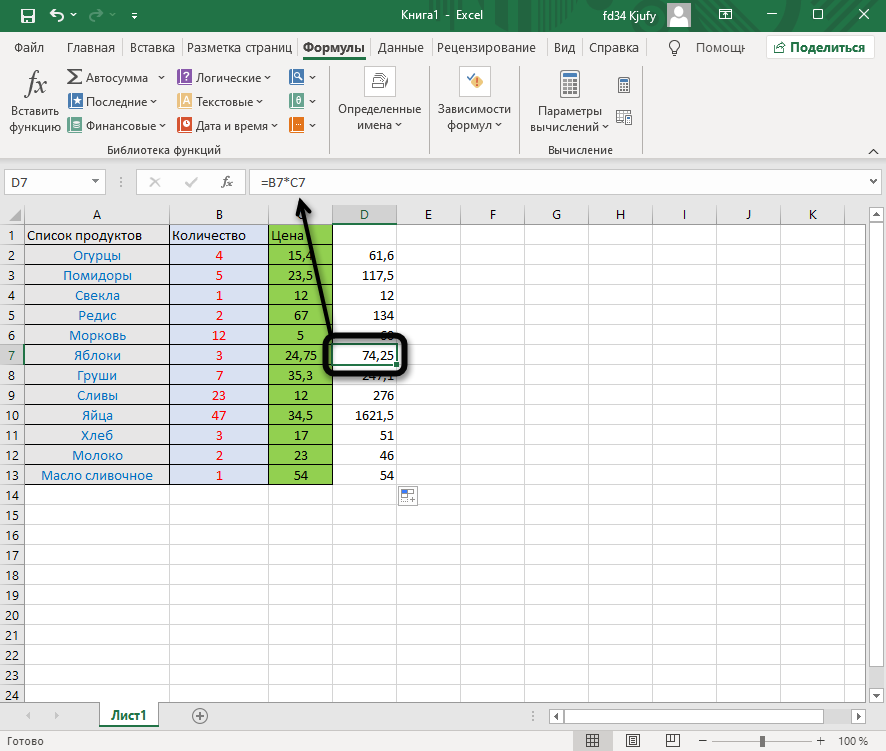
В итоге вы должны увидеть, что функция растянулась на выбранный диапазон, а значения в ней подставлены автоматически. Так, изначальная функция имела вид =B2*C2, но после растягивания вниз последующие значения подставились автоматически (от B3*C3 до B13*C13, что видно на следующем изображении). Точно так же растягивание работает с СУММ и другими простыми формулами, где используется несколько аргументов.
Константа, или абсолютная ссылка, – обозначение, закрепляющее конкретную ячейку, столбец или строку, чтобы при растягивании функции выбранное значение не заменялось, а оставалось таким же.
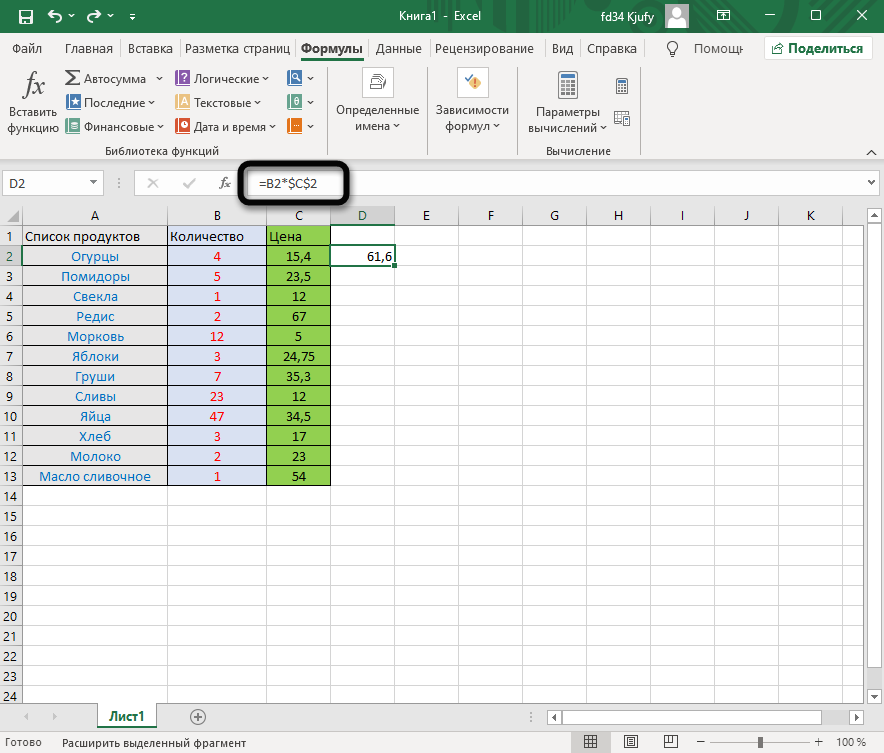
Сначала разберемся с тем, как задать константу. В качестве примера сделаем постоянной и строку, и столбец, то есть закрепим ячейку. Для этого поставьте знак «$» как возле буквы, так и цифры ячейки, чтобы в результате получилось такое написание, как показано на следующем изображении.
Растяните функцию и обратите внимание на то, что постоянное значение таким же и осталось, то есть произошла замена только первого аргумента. Сейчас это может показаться сложным, но стоит вам самостоятельно реализовать подобную задачу, как все станет предельно ясно, и в будущем вы вспомните, что для выполнения конкретных задач можно использовать подобную хитрость.
В закрепление темы рассмотрим три константы, которые можно обозначить при записи функции:
-
$В$2 – при растяжении либо копировании остаются постоянными столбец и строка.
-
B$2 – неизменна строка.
-
$B2 – константа касается только столбца.
Построение графиков функций
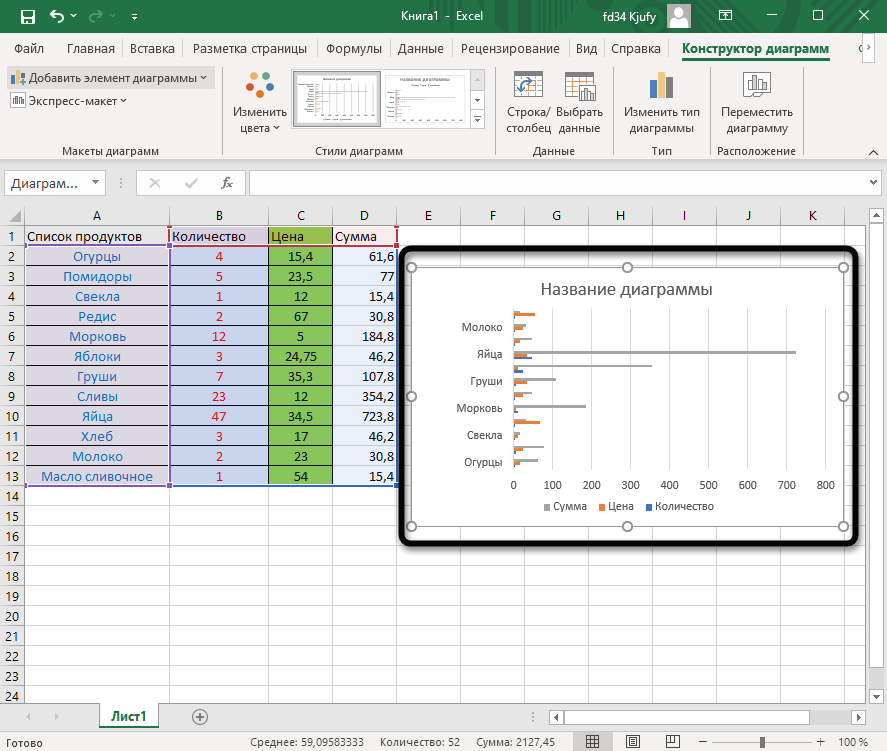
Графики функций – тема, косвенно связанная с использованием формул в Excel, поскольку подразумевает не добавление их в таблицу, а непосредственное составление таблицы по формуле, чтобы затем сформировать из нее диаграмму либо линейный график. Сейчас детально останавливаться на этой теме не будем, но если она вас интересует, перейдите по ссылке ниже для прочтения другой моей статьи по этой теме.
Читайте также: Как построить график функции в Excel
В этой статье вы узнали, какие есть функции в Excel, как сделать формулу и использовать полезные возможности программы, делающие процесс взаимодействия с электронными таблицами проще. Применяйте полученные знания для самостоятельной практики и поставленных задач, требующих проведения расчетов и их автоматизации.
Самая популярная программа для работы с электронными таблицами «Microsoft Excel» упростила жизнь многим пользователям, позволив производить любые расчеты с помощью формул. Она способна автоматизировать даже самые сложные вычисления, но для этого нужно знать принципы работы с формулами. Мы подготовили самую подробную инструкцию по работе с Эксель. Не забудьте сохранить в закладки 😉
Содержание
-
Кому важно знать формулы Excel и где выучить основы.
-
Элементы, из которых состоит формула в Excel.
-
Основные виды.
-
Примеры работ, которые можно выполнять с формулами.
-
22 формулы в Excel, которые облегчат жизнь.
-
Использование операторов.
-
Использование ссылок.
-
Использование имён.
-
Использование функций.
-
Операции с формулами.
-
Как в формуле указать постоянную ячейку.
-
Как поставить «плюс», «равно» без формулы.
-
Самые распространенные ошибки при составлении формул в редакторе Excel.
-
Коды ошибок при работе с формулами.
-
Отличие в версиях MS Excel.
-
Заключение.
Кому важно знать формулы Excel и где изучить основы
Excel — эффективный помощник бухгалтеров и финансистов, владельцев малого бизнеса и даже студентов. Менеджеры ведут базы клиентов, а маркетологи считают в таблицах медиапланы. Аналитики с помощью эксель формул обрабатывают большие объемы данных и строят гипотезы.
Эксель довольно сложная программа, но простые функции и базовые формулы можно освоить достаточно быстро по статьям и видео-урокам. Однако, если ваша профессиональная деятельность подразумевает работу с большим объемом данных и требует глубокого изучения возможностей Excel — стоит пройти специальные курсы, например тут или тут.
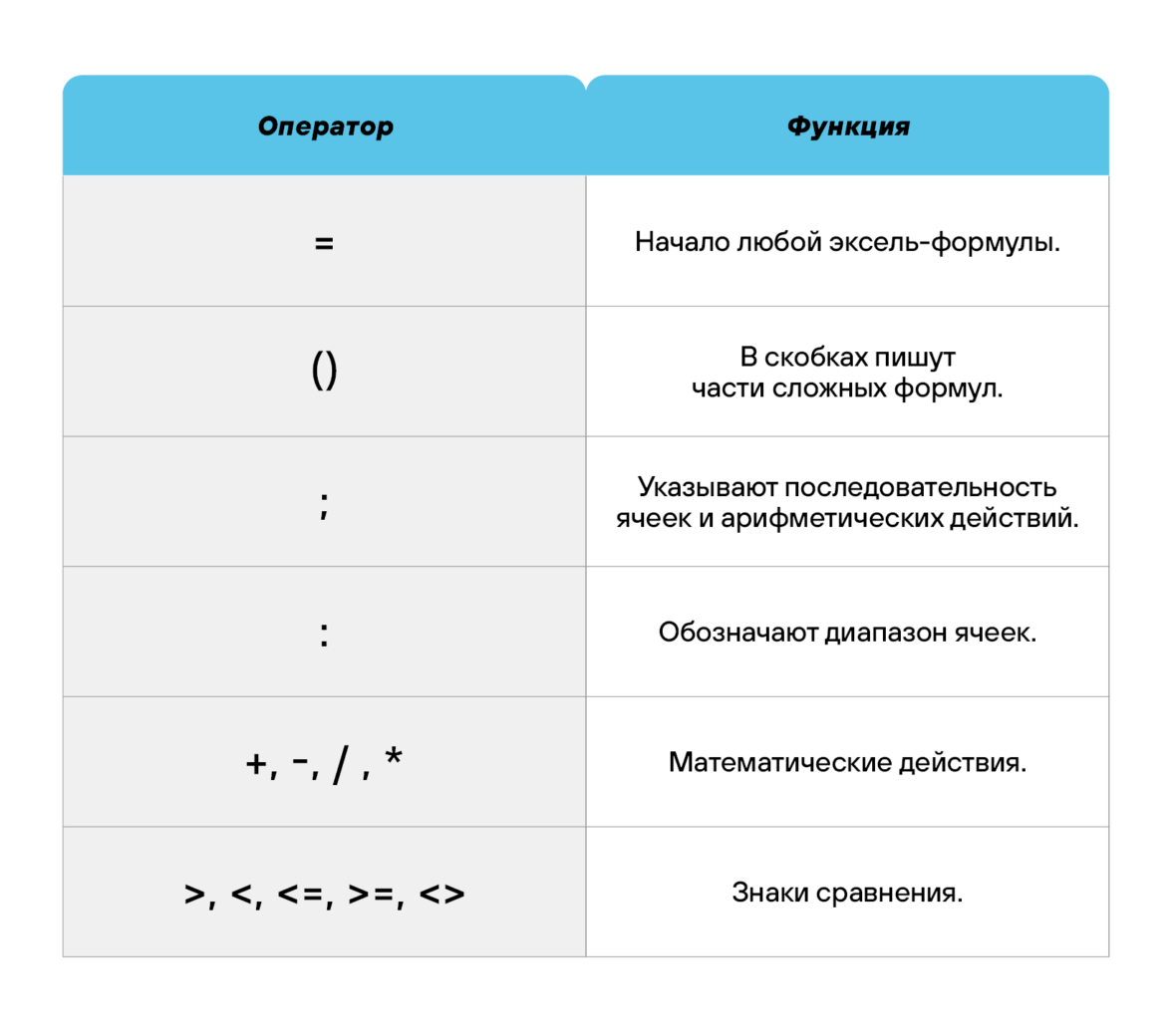
Элементы, из которых состоит формула в Excel
Формулы эксель: основные виды
Формулы в Excel бывают простыми, сложными и комбинированными. В таблицах их можно писать как самостоятельно, так и с помощью интегрированных программных функций.
Простые
Позволяют совершить одно простое действие: сложить, вычесть, разделить или умножить. Самой простой является формула=СУММ.
Например:
=СУММ (A1; B1) — это сумма значений двух соседних ячеек.
=СУММ (С1; М1; Р1) — сумма конкретных ячеек.
=СУММ (В1: В10) — сумма значений в указанном диапазоне.
Сложные
Это многосоставные формулы для более продвинутых пользователей. В данную категорию входят ЕСЛИ, СУММЕСЛИ, СУММЕСЛИМН. О них подробно расскажем ниже.
Комбинированные
Эксель позволяет комбинировать несколько функций: сложение + умножение, сравнение + умножение. Это удобно, когда, например, нужно вычислить сумму двух чисел, и, если результат будет больше 100, его нужно умножить на 3, а если меньше — на 6.
Выглядит формула так ↓
=ЕСЛИ (СУММ (A1; B1)<100; СУММ (A1; B1)*3;(СУММ (A1; B1)*6))
Встроенные
Новичкам удобнее пользоваться готовыми, встроенными в программу формулами вместо того, чтобы писать их вручную. Чтобы найти нужную формулу:
-
кликните по нужной ячейке таблицы;
-
нажмите одновременно Shift + F3;
-
выберите из предложенного перечня нужную формулу;
-
в окошко «Аргументы функций» внесите свои данные.
Примеры работ, которые можно выполнять с формулами
Разберем основные действия, которые можно совершить, используя формулы в таблицах Эксель и рассмотрим полезные «фишки» для упрощения работы.
Поиск перечня доступных функций
Перейдите в закладку «Формулы» / «Вставить функцию». Или сразу нажмите на кнопочку «Fx».
Выберите в категории «Полный алфавитный перечень», после чего в списке отобразятся все доступные эксель-формулы.
Выберите любую формулу и прочитайте ее описание. А если хотите изучить ее более детально, нажмите на «Справку» ниже.
Вставка функции в таблицу
Вы можете сами писать функции в Excel вручную после «=», или использовать меню, описанное выше. Например, выбрав СУММ, появится окошко, где нужно ввести аргументы (кликнуть по клеткам, значения которых собираетесь складывать):
После этого в таблице появится формула в стандартном виде. Ее можно редактировать при необходимости.
Использование математических операций
Начинайте с «=» в ячейке и применяйте для вычислений любые стандартные знаки «*», «/», «^» и т.д. Можно написать номер ячейки самостоятельно или кликнуть по ней левой кнопкой мышки. Например: =В2*М2. После нажатия Enter появится произведение двух ячеек.
Растягивание функций и обозначение константы
Введите функцию =В2*C2, получите результат, а затем зажмите правый нижний уголок ячейки и протащите вниз. Формула растянется на весь выбранный диапазон и автоматически посчитает значения для всех строк от B3*C3 до B13*C13.
Чтобы обозначить константу (зафиксировать конкретную ячейку/строку/столбец), нужно поставить «$» перед буквой и цифрой ячейки.
Например: =В2*$С$2. Когда вы растяните функцию, константа или $С$2 так и останется неизменяемой, а вот первый аргумент будет меняться.
Подсказка:
-
$С$2 — не меняются столбец и строка.
-
B$2 — не меняется строка 2.
-
$B2 — константой остается только столбец В.
22 формулы в Эксель, которые облегчат жизнь
Собрали самые полезные формулы, которые наверняка пригодятся в работе.
МАКС
=МАКС (число1; [число2];…)
Показывает наибольшее число в выбранном диапазоне или перечне ячейках.
МИН
=МИН (число1; [число2];…)
Показывает самое маленькое число в выбранном диапазоне или перечне ячеек.
СРЗНАЧ
=СРЗНАЧ (число1; [число2];…)
Считает среднее арифметическое всех чисел в диапазоне или в выбранных ячейках. Все значения суммируются, а сумма делится на их количество.
СУММ
=СУММ (число1; [число2];…)
Одна из наиболее популярных и часто используемых функций в таблицах Эксель. Считает сумму чисел всех указанных ячеек или диапазона.
ЕСЛИ
=ЕСЛИ (лог_выражение; значение_если_истина; [значение_если_ложь])
Сложная формула, которая позволяет сравнивать данные.
Например:
=ЕСЛИ (В1>10;”больше 10″;»меньше или равно 10″)
В1 — ячейка с данными;
>10 — логическое выражение;
больше 10 — правда;
меньше или равно 10 — ложное значение (если его не указывать, появится слово ЛОЖЬ).
СУММЕСЛИ
=СУММЕСЛИ (диапазон; условие; [диапазон_суммирования]).
Формула суммирует числа только, если они отвечают критерию.
Например:
=СУММЕСЛИ (С2: С6;»>20″)
С2: С6 — диапазон ячеек;
>20 —значит, что числа меньше 20 не будут складываться.
СУММЕСЛИМН
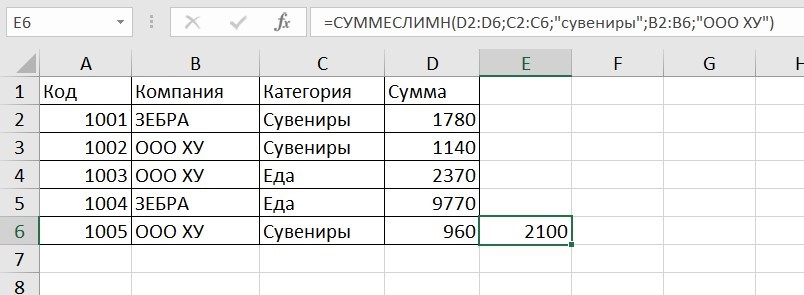
=СУММЕСЛИМН (диапазон_суммирования; диапазон_условия1; условие1; [диапазон_условия2; условие2];…)
Суммирование с несколькими условиями. Указываются диапазоны и условия, которым должны отвечать ячейки.
Например:
=СУММЕСЛИМН (D2: D6; C2: C6;”сувениры”; B2: B6;”ООО ХУ»)
D2: D6 — диапазон, где суммируются числа;
C2: C6 — диапазон ячеек для категории; сувениры — обязательное условие 1, то есть числа другой категории не учитываются;
B2: B6 — дополнительный диапазон;
ООО XY — условие 2, то есть числа другой компании не учитываются.
Дополнительных диапазонов и условий может быть до 127 штук.
СЧЕТ
=СЧЁТ (значение1; [значение2];…)Формула считает количество выбранных ячеек с числами в заданном диапазоне. Ячейки с датами тоже учитываются.
=СЧЁТ (значение1; [значение2];…)
Формула считает количество выбранных ячеек с числами в заданном диапазоне. Ячейки с датами тоже учитываются.
СЧЕТЕСЛИ и СЧЕТЕСЛИМН
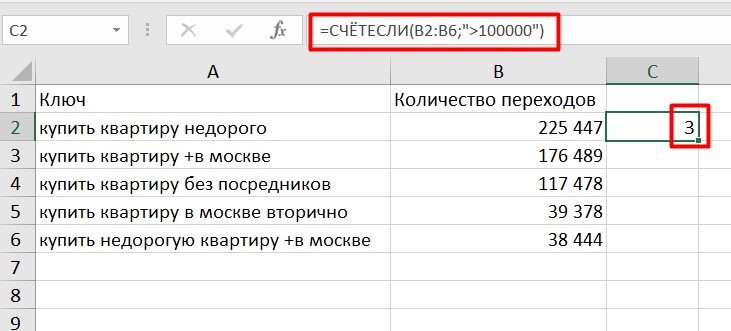
=СЧЕТЕСЛИ (диапазон; критерий)
Функция определяет количество заполненных клеточек, которые подходят под конкретные условия в рамках указанного диапазона.
Например:
=СЧЁТЕСЛИМН (диапазон_условия1; условие1 [диапазон_условия2; условие2];…)
Эта формула позволяет использовать одновременно несколько критериев.
ЕСЛИОШИБКА
=ЕСЛИОШИБКА (значение; значение_если_ошибка)
Функция проверяет ошибочность значения или вычисления, а если ошибка отсутствует, возвращает его.
ДНИ
=ДНИ (конечная дата; начальная дата)
Функция показывает количество дней между двумя датами. В формуле указывают сначала конечную дату, а затем начальную.
КОРРЕЛ
=КОРРЕЛ (диапазон1; диапазон2)
Определяет статистическую взаимосвязь между разными данными: курсами валют, расходами и прибылью и т.д. Мах значение — +1, min — −1.
ВПР
=ВПР (искомое_значение; таблица; номер_столбца;[интервальный_просмотр])
Находит данные в таблице и диапазоне.
Например:
=ВПР (В1; С1: С26;2)
В1 — значение, которое ищем.
С1: Е26— диапазон, в котором ведется поиск.
2 — номер столбца для поиска.
ЛЕВСИМВ
=ЛЕВСИМВ (текст;[число_знаков])
Позволяет выделить нужное количество символов. Например, она поможет определить, поместится ли строка в лимитированное количество знаков или нет.
ПСТР
=ПСТР (текст; начальная_позиция; число_знаков)
Помогает достать определенное число знаков с текста. Например, можно убрать лишние слова в ячейках.
ПРОПИСН
=ПРОПИСН (текст)
Простая функция, которая делает все литеры в заданной строке прописными.
СТРОЧН
Функция, обратная предыдущей. Она делает все литеры строчными.
ПОИСКПОЗ
=ПОИСКПОЗ (искомое_значение; просматриваемый_массив; тип_сопоставления)
Дает возможность найти нужный элемент в заданном блоке ячеек и указывает его позицию.
ДЛСТР
=ДЛСТР (текст)
Данная функция определяет длину заданной строки. Пример использования — определение оптимальной длины описания статьи.
СЦЕПИТЬ
=СЦЕПИТЬ (текст1; текст2; текст3)
Позволяет сделать несколько строчек из одной и записать до 255 элементов (8192 символа).
ПРОПНАЧ
=ПРОПНАЧ (текст)
Позволяет поменять местами прописные и строчные символы.
ПЕЧСИМВ
=ПЕЧСИМВ (текст)
Можно убрать все невидимые знаки из текста.
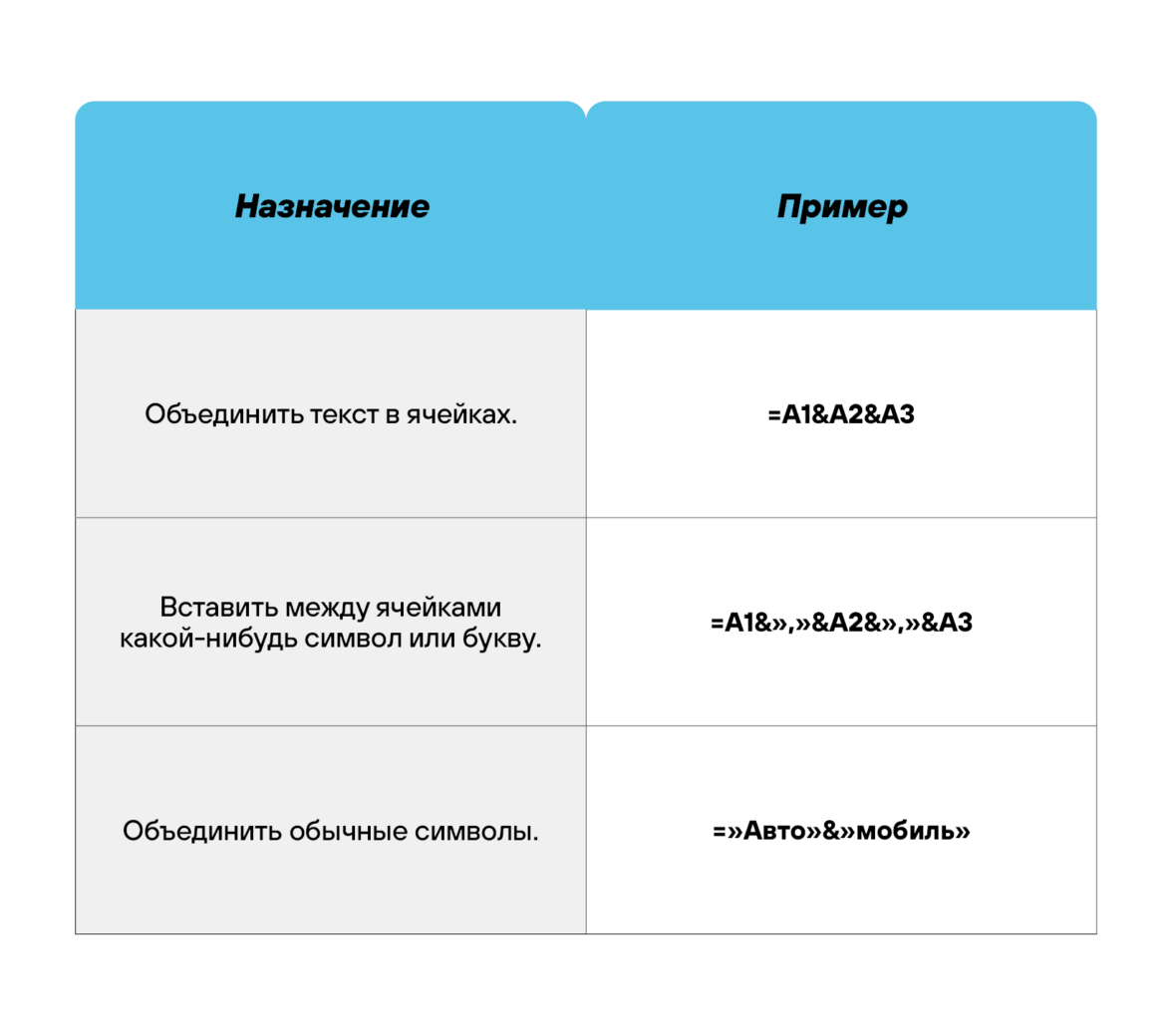
Использование операторов
Операторы в Excel указывают, какие конкретно операции нужно выполнить над элементами формулы. В вычислениях всегда соблюдается математический порядок:
-
скобки;
-
экспоненты;
-
умножение и деление;
-
сложение и вычитание.
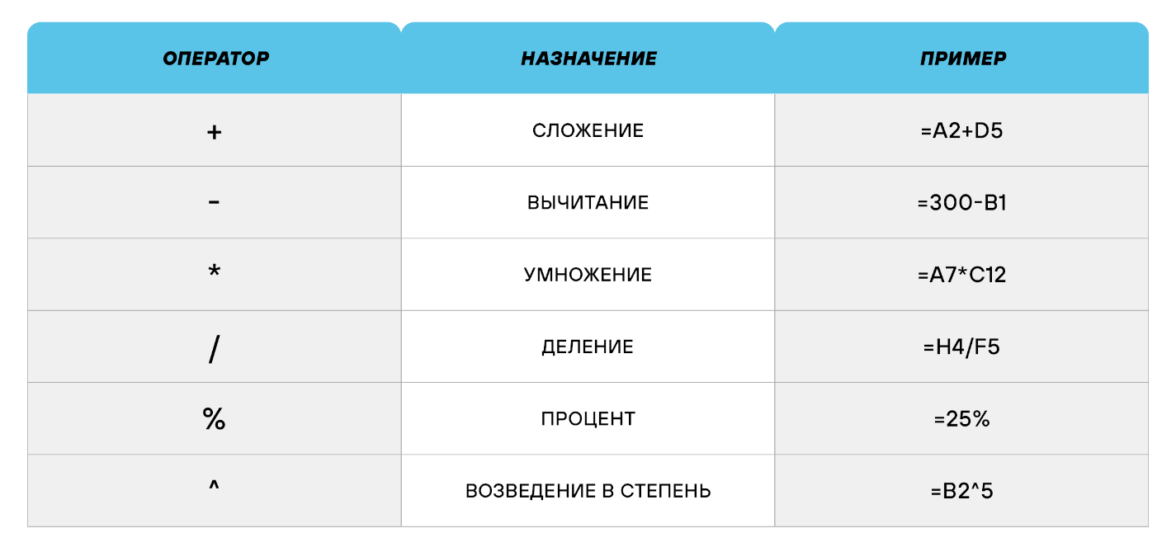
Арифметические
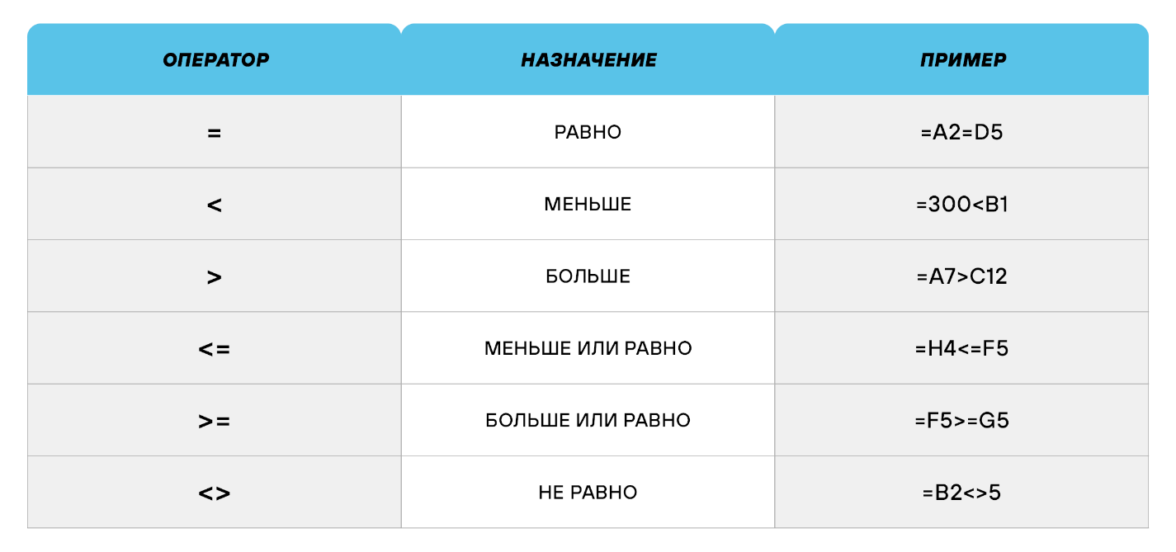
Операторы сравнения
Оператор объединения текста
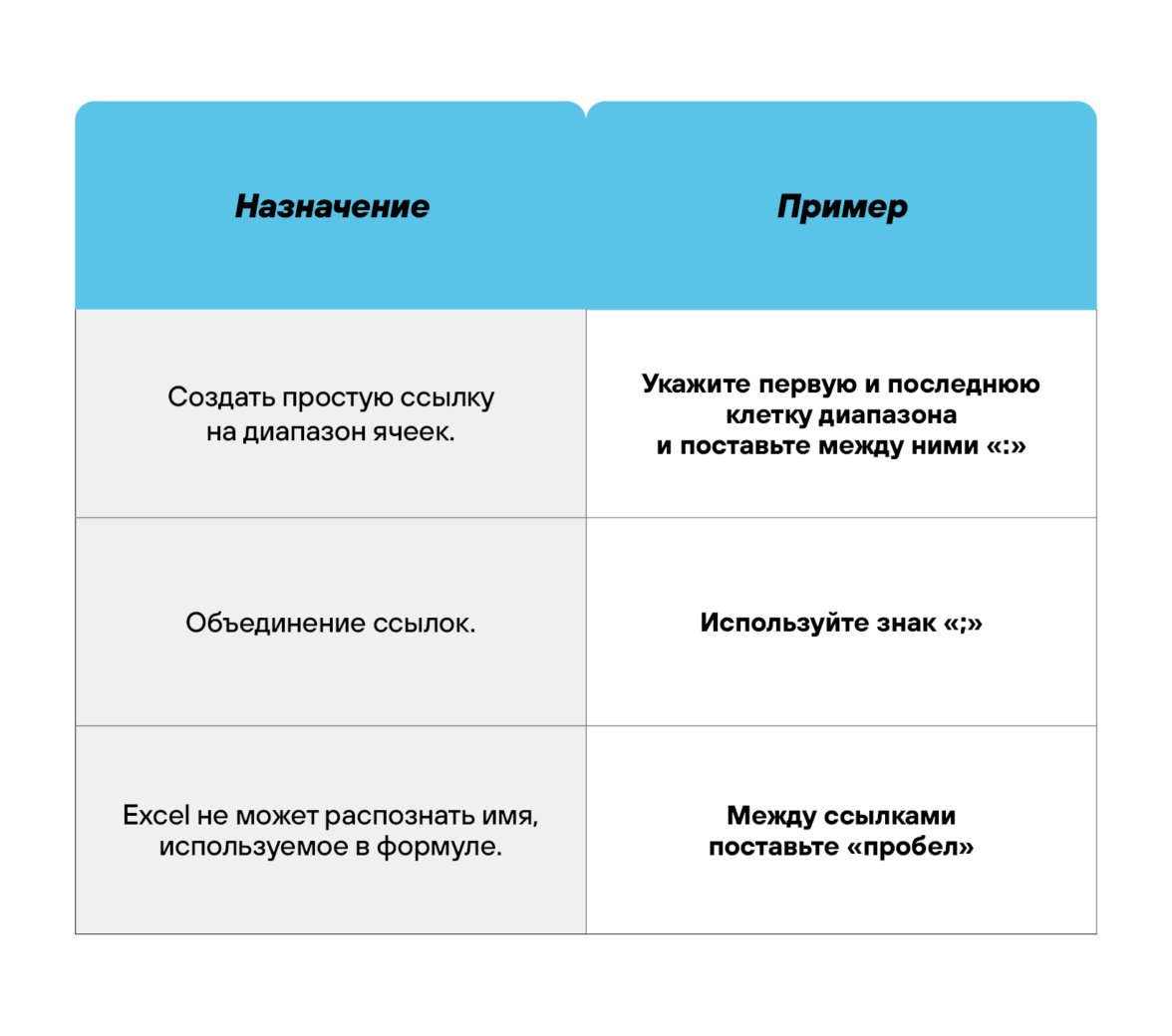
Операторы ссылок
Использование ссылок
Начинающие пользователи обычно работают только с простыми ссылками, но мы расскажем обо всех форматах, даже продвинутых.
Простые ссылки A1
Они используются чаще всего. Буква обозначает столбец, цифра — строку.
Примеры:
-
диапазон ячеек в столбце С с 1 по 23 строку — «С1: С23»;
-
диапазон ячеек в строке 6 с B до Е– «B6: Е6»;
-
все ячейки в строке 11 — «11:11»;
-
все ячейки в столбцах от А до М — «А: М».
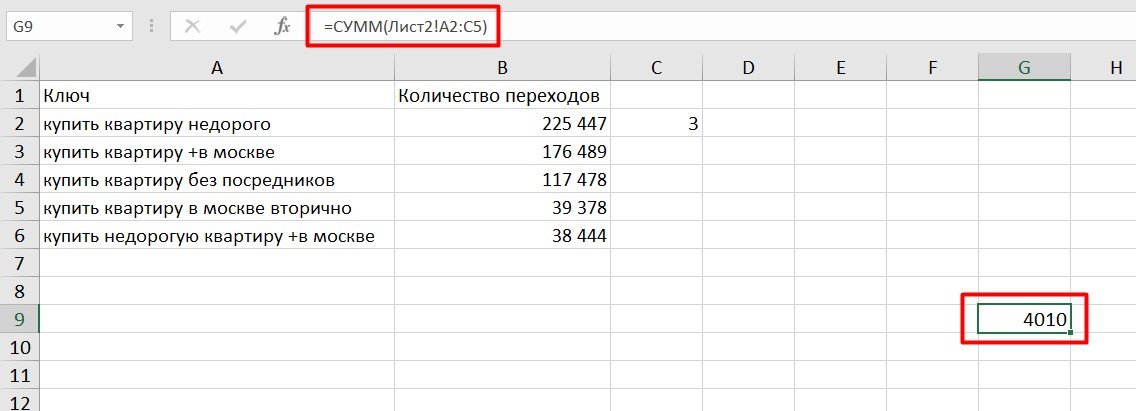
Ссылки на другой лист
Если необходимы данные с других листов, используется формула: =СУММ (Лист2! A5: C5)
Выглядит это так:
Абсолютные и относительные ссылки
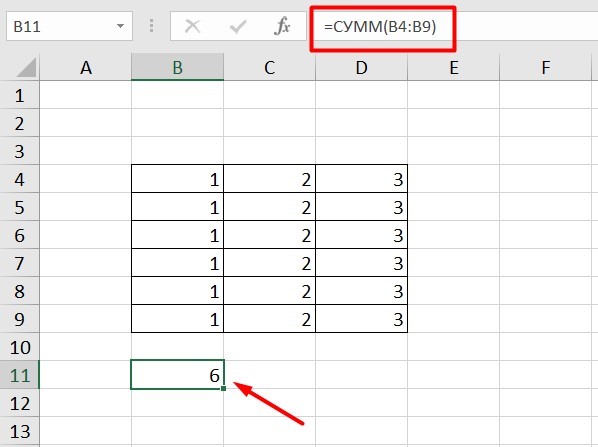
Относительные ссылки
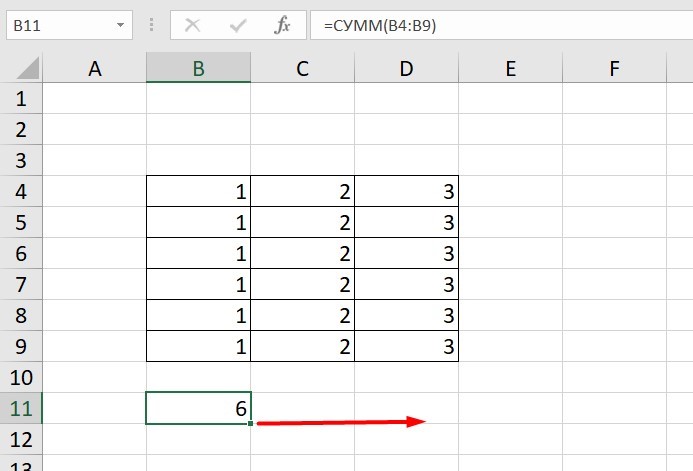
Рассмотрим, как они работают на примере: Напишем формулу для расчета суммы первой колонки. =СУММ (B4: B9)
Нажимаем на Ctrl+C. Чтобы перенести формулу на соседнюю клетку, переходим туда и жмем на Ctrl+V. Или можно просто протянуть ячейку с формулой, как мы описывали выше.
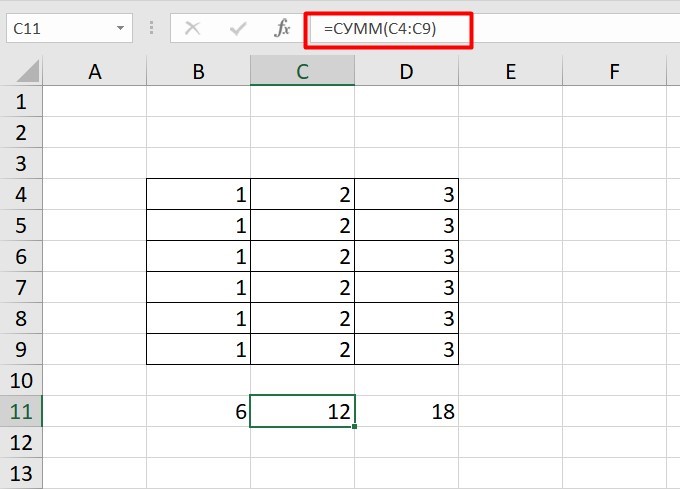
Индекс таблицы изменится автоматически и новые формулы будут выглядеть так:
Абсолютные ссылки
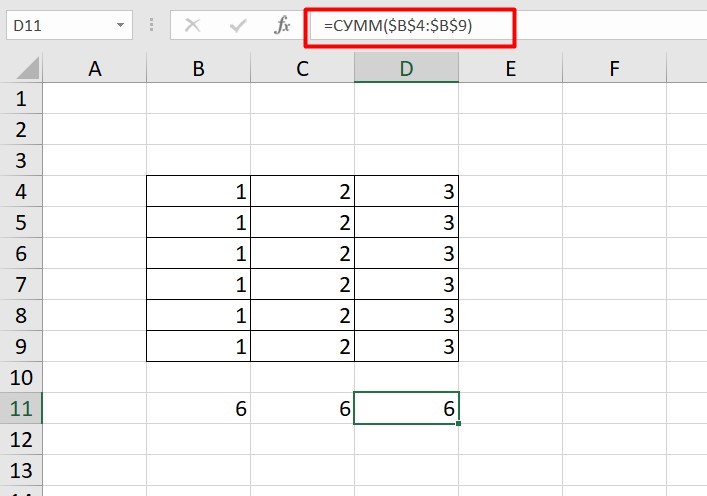
Чтобы при переносе формул ссылки сохранялись неизменными, требуются абсолютные адреса. Их пишут в формате «$B$2».
Например, есть поставить знак доллара в предыдущую формулу, мы получим: =СУММ ($B$4:$B$9)
Как видите, никаких изменений не произошло.
Смешанные ссылки
Они используются, когда требуется зафиксировать только столбец или строку:
-
$А1– сохраняются столбцы;
-
А$1 — сохраняются строки.
Смешанные ссылки удобны, когда приходится работать с одной постоянной строкой данных и менять значения в столбцах. Или, когда нужно рассчитать результат в ячейках, не расположенных вдоль линии.
Трёхмерные ссылки
Это те, где указывается диапазон листов.
Формула выглядит примерно так: =СУММ (Лист1: Лист5! A6)
То есть будут суммироваться все ячейки А6 на всех листах с первого по пятый.
Ссылки формата R1C1
Номер здесь задается как по строкам, так и по столбцам.
Например:
-
R9C9 — абсолютная ссылка на клетку, которая расположена на девятой строке девятого столбца;
-
R[-2] — ссылка на строчку, расположенную выше на 2 строки;
-
R[-3]C — ссылка на клетку, которая расположена на 3 ячейки выше;
-
R[4]C[4] — ссылка на ячейку, которая распложена на 4 клетки правее и 4 строки ниже.
Использование имён
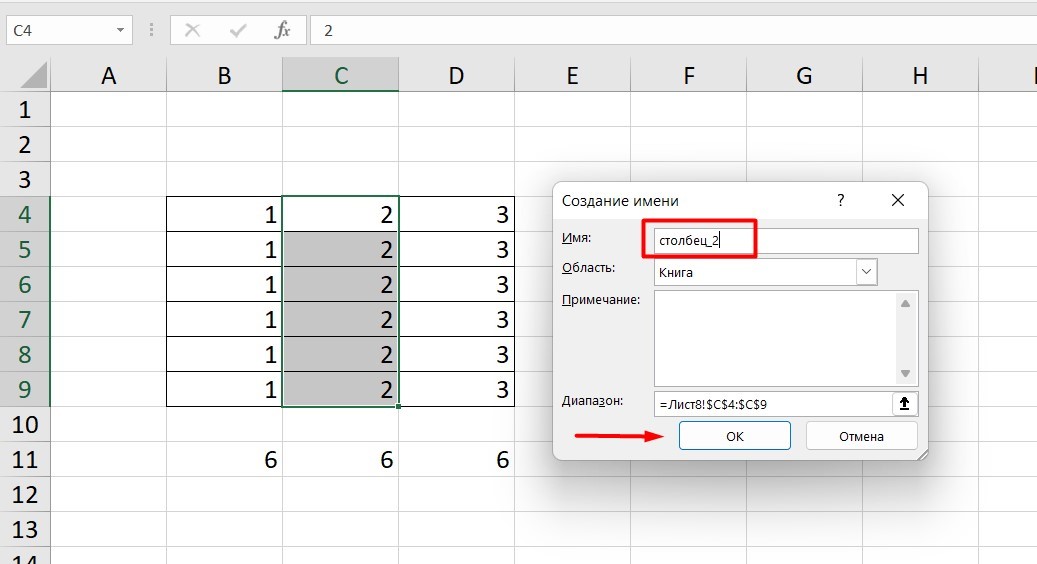
Функционал Excel позволяет давать собственные уникальные имена ячейкам, таблицам, константам, выражениям, даже диапазонам ячеек. Эти имена можно использовать для совершения любых арифметических действий, расчета налогов, процентов по кредиту, составления сметы и табелей, расчётов зарплаты, скидок, рабочего стажа и т.д.
Все, что нужно сделать — заранее дать имя ячейкам, с которыми планируете работать. В противном случае программа Эксель ничего не будет о них знать.
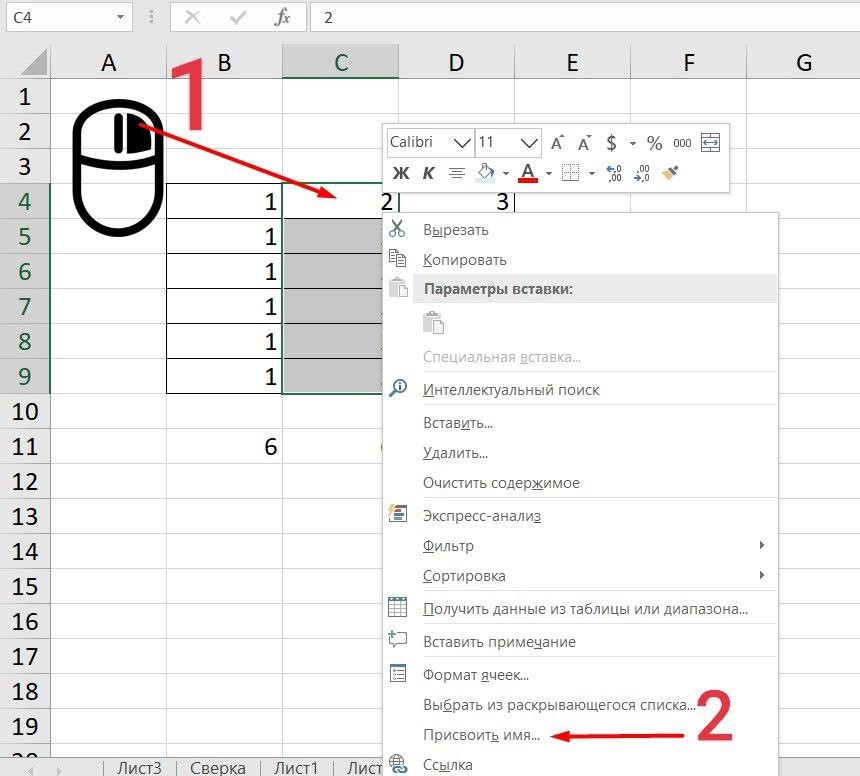
Как присвоить имя:
-
Выделите нужную ячейку/столбец.
-
Правой кнопкой мышки вызовите меню и перейдите в закладку «Присвоить имя».
-
Напишите желаемое имя, которое должно быть уникальным и не повторяться в одной книге.
-
Сохраните, нажав Ок.
Использование функций
Чтобы вставить необходимую функцию в эксель-таблицах, можно использовать три способа: через панель инструментов, с помощью опции Вставки и вручную. Рассмотрим подробно каждый способ.
Ручной ввод
Этот способ подойдет тем, кто хорошо разбирается в теме и умеет создавать формулы прямо в строке. Для начинающих пользователей и новичков такой вариант покажется слишком сложным, поскольку надо все делать руками.
Панель инструментов
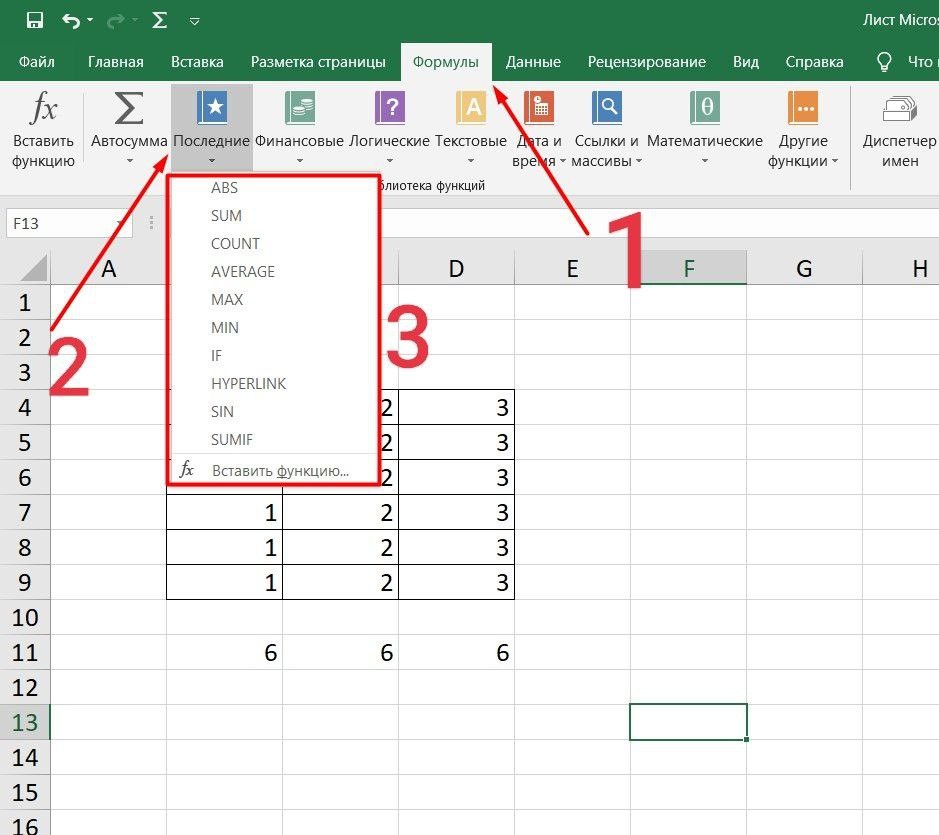
Это более упрощенный способ. Достаточно перейти в закладку «Формулы», выбрать подходящую библиотеку — Логические, Финансовые, Текстовые и др. (в закладке «Последние» будут наиболее востребованные формулы). Остается только выбрать из перечня нужную функцию и расставить аргументы.
Мастер подстановки
Кликните по любой ячейке в таблице. Нажмите на иконку «Fx», после чего откроется «Вставка функций».
Выберите из перечня нужную категорию формул, а затем кликните по функции, которую хотите применить и задайте необходимые для расчетов аргументы.
Вставка функции в формулу с помощью мастера
Рассмотрим эту опцию на примере:
-
Вызовите окошко «Вставка функции», как описывалось выше.
-
В перечне доступных функций выберите «Если».
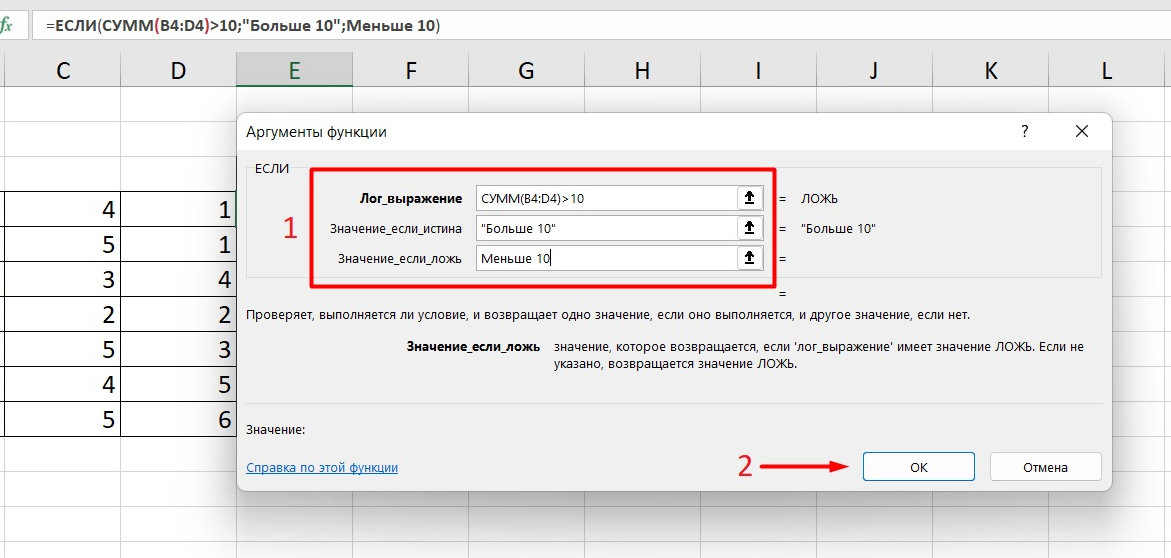
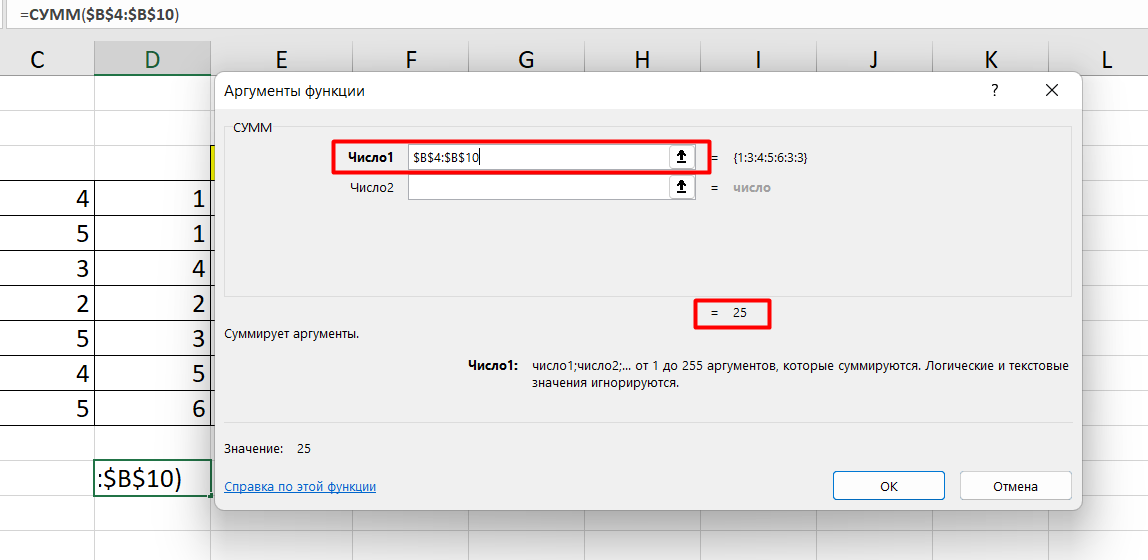
Теперь составим выражение, чтобы проверить, будет ли сумма трех ячеек больше 10. При этом Правда — «Больше 10», а Ложь — «Меньше 10».
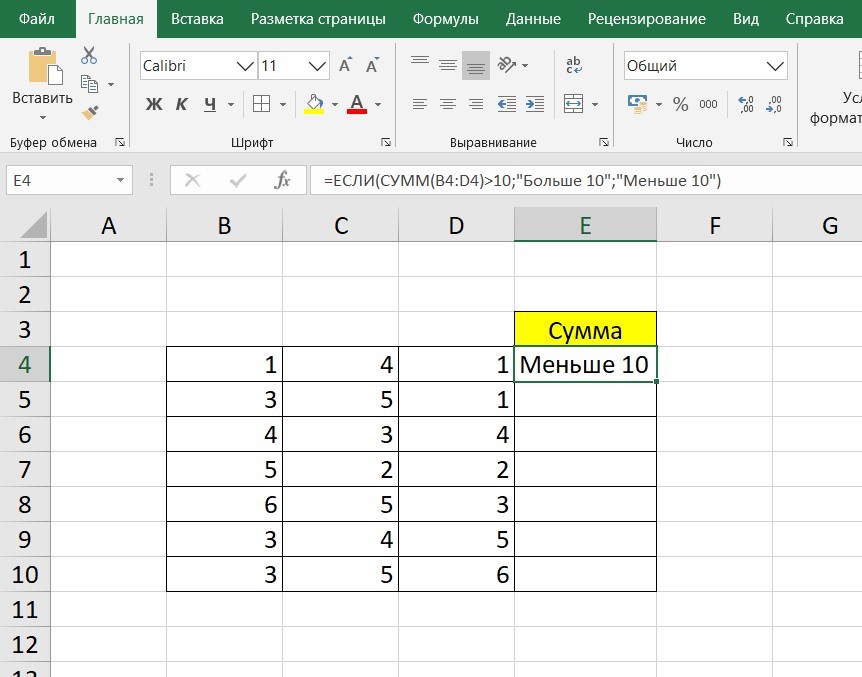
=ЕСЛИ (СУММ (B3: D3)>10;”Больше 10″;»Меньше 10″)
Программа посчитала, что сумма ячеек меньше 10 и выдала нам результат:
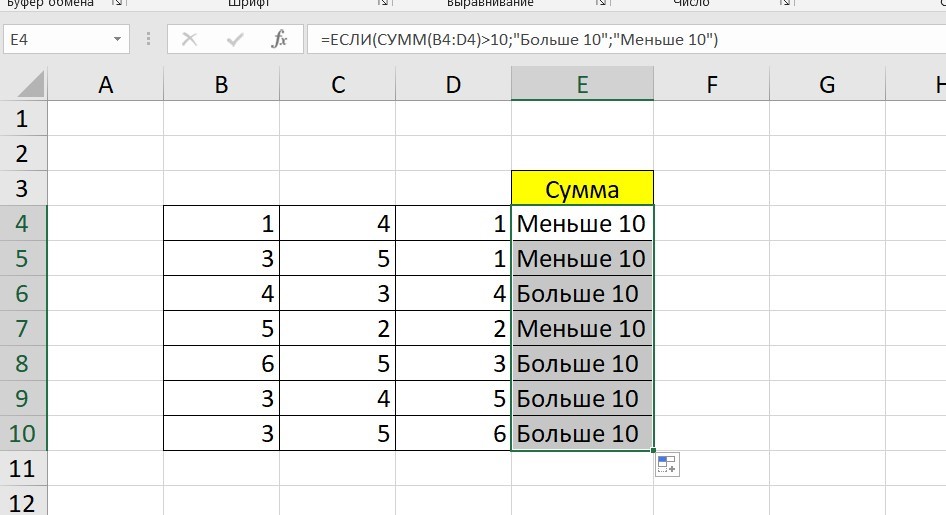
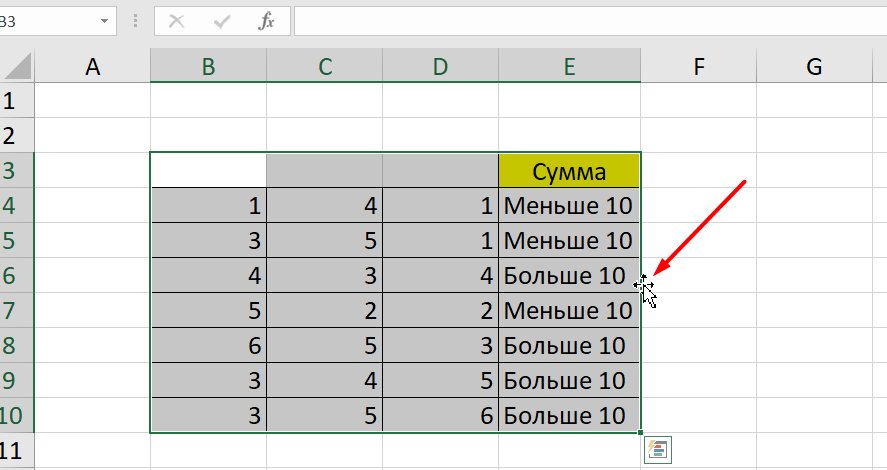
Чтобы получить значение в следующих ячейках столбца, нужно растянуть формулу (за правый нижний уголок). Получится следующее:
Мы использовали относительные ссылки, поэтому программа пересчитала выражение для всех строк корректно. Если бы нам нужно было зафиксировать адреса в аргументах, тогда мы бы применяли абсолютные ссылки, о которых писали выше.
Редактирование функций с помощью мастера
Чтобы отредактировать функцию, можно использовать два способа:
-
Строка формул. Для этого требуется перейти в специальное поле и вручную ввести необходимые изменения.
-
Специальный мастер. Нажмите на иконку «Fx» и в появившемся окошке измените нужные вам аргументы. И тут же, кстати, сможете узнать результат после редактирования.
Операции с формулами
С формулами можно совершать много операций — копировать, вставлять, перемещать. Как это делать правильно, расскажем ниже.
Копирование/вставка формулы
Чтобы скопировать формулу из одной ячейки в другую, не нужно изобретать велосипед — просто нажмите старую-добрую комбинацию (копировать), а затем кликните по новой ячейке и нажмите (вставить).
Отмена операций
Здесь вам в помощь стандартная кнопка «Отменить» на панели инструментов. Нажмите на стрелочку возле нее и выберите из контекстного меню те действия. которые хотите отменить.
Повторение действий
Если вы выполнили команду «Отменить», программа сразу активизирует функцию «Вернуть» (возле стрелочки отмены на панели). То есть нажав на нее, вы повторите только что отмененную вами операцию.
Стандартное перетаскивание
Выделенные ячейки переносятся с помощью указателя мышки в другое место листа. Делается это так:
-
Выделите фрагмент ячеек, которые нужно переместить.
-
Поместите указатель мыши над одну из границ фрагмента.
-
Когда указатель мыши станет крестиком с 4-мя стрелками, можете перетаскивать фрагмент в другое место.
Копирование путем перетаскивания
Если вам нужно скопировать выделенный массив ячеек в другое место рабочего листа с сохранением данных, делайте так:
-
Выделите диапазон ячеек, которые нужно скопировать.
-
Зажмите клавишу и поместите указатель мыши на границу выбранного диапазона.
-
Он станет похожим на крестик +. Это говорит о том, что будет выполняться копирование, а не перетаскивание.
-
Перетащите фрагмент в нужное место и отпустите мышку. Excel задаст вопрос — хотите вы заменить содержимое ячеек. Выберите «Отмена» или ОК.
Особенности вставки при перетаскивании
Если содержимое ячеек перемещается в другое место, оно полностью замещает собой существовавшие ранее записи. Если вы не хотите замещать прежние данные, удерживайте клавишу в процессе перетаскивания и копирования.
Автозаполнение формулами
Если необходимо скопировать одну формулу в массив соседних ячеек и выполнить массовые вычисления, используется функция автозаполнения.
Чтобы выполнить автозаполнение формулами, нужно вызвать специальный маркер заполнения. Для этого наведите курсор на нижний правый угол, чтобы появился черный крестик. Это и есть маркер заполнения. Его нужно зажать левой кнопкой мыши и протянуть вдоль всех ячеек, в которых вы хотите получить результат вычислений.
Как в формуле указать постоянную ячейку
Когда вам нужно протянуть формулу таким образом, чтобы ссылка на ячейку оставалась неизменной, делайте следующее:
-
Кликните на клетку, где находится формула.
-
Наведите курсор в нужную вам ячейку и нажмите F4.
-
В формуле аргумент с номером ячейки станет выглядеть так: $A$1 (абсолютная ссылка).
-
Когда вы протяните формулу, ссылка на ячейку $A$1 останется фиксированной и не будет меняться.
Как поставить «плюс», «равно» без формулы
Когда нужно указать отрицательное значение, поставить = или написать температуру воздуха, например, +22 °С, делайте так:
-
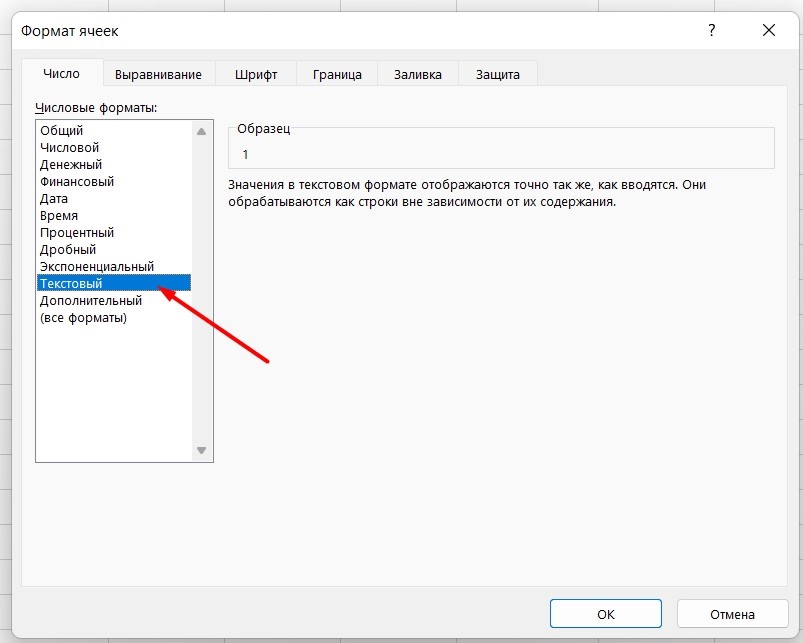
Кликаете правой кнопкой по ячейке и выбираете «Формат ячеек».
-
Отмечаете «Текстовый».
Теперь можно ставить = или +, а затем нужное число.
Самые распространенные ошибки при составлении формул в редакторе Excel
Новички, которые работают в редакторе Эксель совсем недавно, часто совершают элементарные ошибки. Поэтому рекомендуем ознакомиться с перечнем наиболее распространенных, чтобы больше не ошибаться.
-
Слишком много вложений в выражении. Лимит 64 штуки.
-
Пути к внешним книгам указаны не полностью. Проверяйте адреса более тщательно.
-
Неверно расставленные скобочки. В редакторе они обозначены разными цветами для удобства.
-
Указывая имена книг и листов, пользователи забывают брать их в кавычки.
-
Числа в неверном формате. Например, символ $ в Эксель — это не знак доллара, а формат абсолютных ссылок.
-
Неправильно введенные диапазоны ячеек. Не забывайте ставить «:».
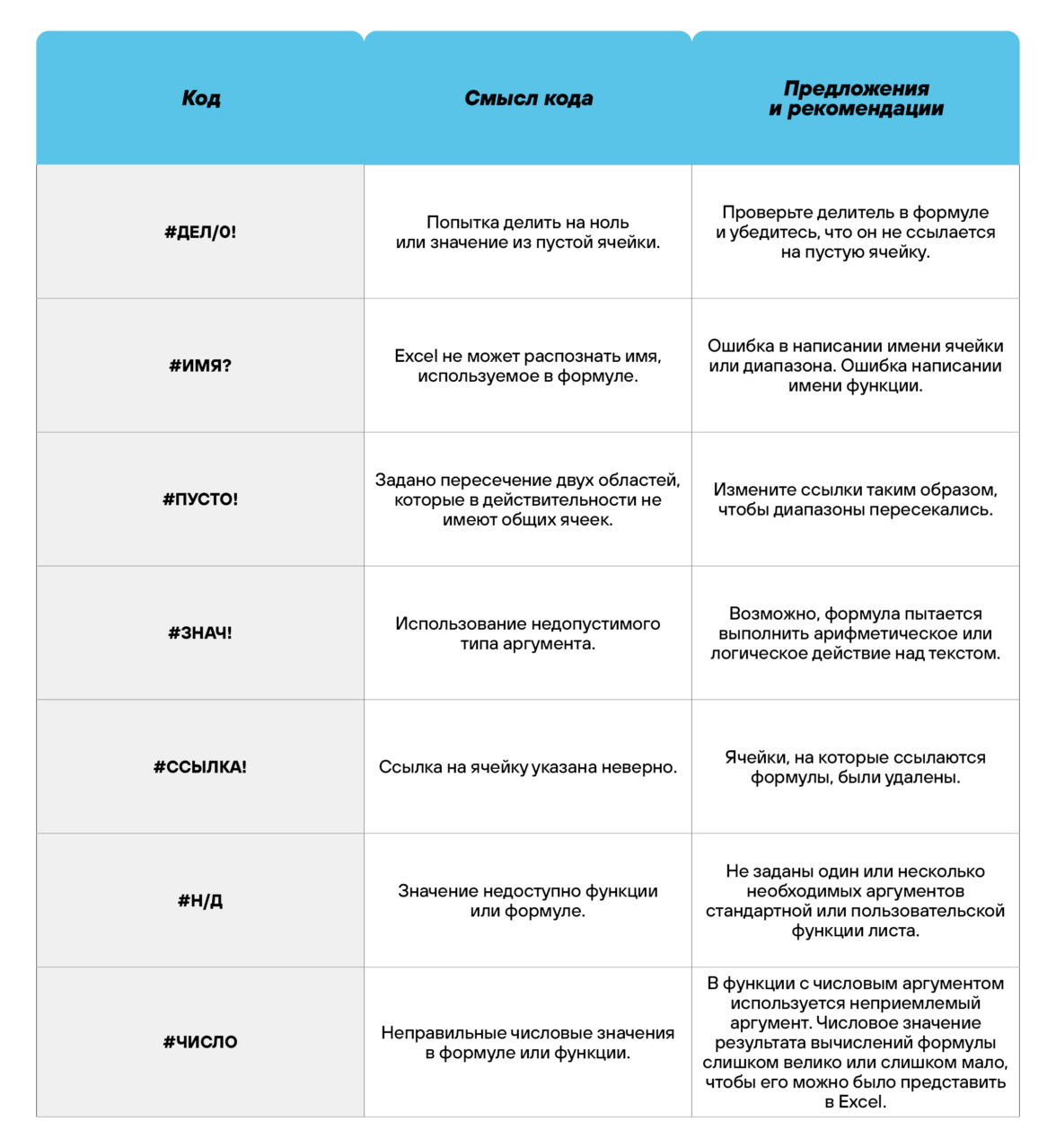
Коды ошибок при работе с формулами
Если вы сделаете ошибку в записи формулы, программа укажет на нее специальным кодом. Вот самые распространенные:
Отличие в версиях MS Excel
Всё, что написано в этом гайде, касается более современных версий программы 2007, 2010, 2013 и 2016 года. Устаревший Эксель заметно уступает в функционале и количестве доступных инструментов. Например, функция СЦЕП появилась только в 2016 году.
Во всем остальном старые и новые версии Excel не отличаются — операции и расчеты проводятся по одинаковым алгоритмам.
Заключение
Мы написали этот гайд, чтобы вам было легче освоить Excel. Доступным языком рассказали о формулах и о тех операциях, которые можно с ними проводить.
Надеемся, наша шпаргалка станет полезной для вас. Не забудьте сохранить ее в закладки и поделиться с коллегами.
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html