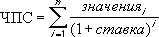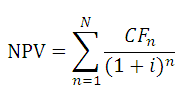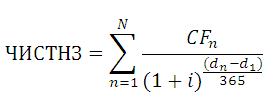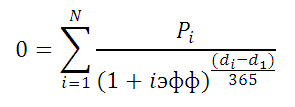Расчет чпс в excel примеры

В этой статье описаны синтаксис формулы и использование функции ЧПС в Microsoft Excel.

Описание

Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).

Синтаксис

ЧПС(ставка; значение1; [значение2],…)

Аргументы функции ЧПС описаны ниже.

• Ставка    Обязательный аргумент. Ставка дисконтирования за один период.

• Значение1, значение2,…    Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 254 аргументов, представляющих выплаты и поступления.

  • Аргументы «значение1, значение2, …» должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

  • Функция ЧПС использует порядок аргументов «значение1, значение2, …» для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.

  • Аргументы, которые являются пустыми ячейками, логическими значениями или текстовыми представлениями чисел, значениями ошибок или текстом, который невозможно преобразовать в числа, игнорируются.

  • Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.

Замечания

• Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса «значение1» и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Дополнительные сведения см. в приведенных ниже примерах.

• Если n — количество денежных потоков в списке значений, формула для функции ЧПС имеет следующий вид:

  

• ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. Сведения о функциях платежей по ссуде и финансовых функциях см. в описании функции ПС.

• ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,1	Годовая ставка дисконтирования
-10 000	Начальная стоимость инвестиции через один год
3000	Доход за первый год
4200	Доход за второй год
6800	Доход за третий год
Формула	Описание	Результат
=ЧПС(A2; A3; A4; A5; A6)	Чистая приведенная стоимость данной инвестиции	1 188,44 ₽

Пример 2

Данные	Описание
0,08	Годовая ставка дисконтирования. Она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям.
-40 000	Начальная стоимость инвестиции
8000	Доход за первый год
9200	Доход за второй год
10000	Доход за третий год
12000	Доход за четвертый год
14500	Доход за пятый год
Формула	Описание	Результат
=ЧПС(A2; A4:A8)+A3	Чистая приведенная стоимость данной инвестиции	1 922,06 ₽
=ЧПС(A2; A4:A8; -9000)+A3	Чистая приведенная стоимость данной инвестиции с учетом убытка (9000) на шестом году	(3 749,47 ₽)

К началу страницы

Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул

MS

EXCEL.

Начнем с определения, точнее с определений.

Чистой приведённой стоимостью (Net present value, NPV) называют

сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню

(взято из Википедии). Или так:

Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт

cfin.

ru)

Или так:

Текущая

стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика

.

Толковыйсловарь

. —

М

.

:

»

ИНФРА

—

М

«,

Издательство

»

ВесьМир

«.

Дж

.

Блэк

.)

Примечание1

. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется

ЧПС()

, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с

Приведенной стоимостью

.

Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма

Приведенных стоимостей

денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.

Совет

: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи

Приведенная стоимость

.

Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу

сложных процентов

.

Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция

ЧПС()

(английский вариант — NPV()). В ее основе используется формула:

CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).

Примечание2

. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:

Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)

. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).

Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.

Выбор периода дисконтирования для функции ЧПС()

При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.

Примечание3

. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.

Определившись со сроками денежных потоков, для функции

ЧПС()

нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы  ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.

файл примера, лист NPV

).

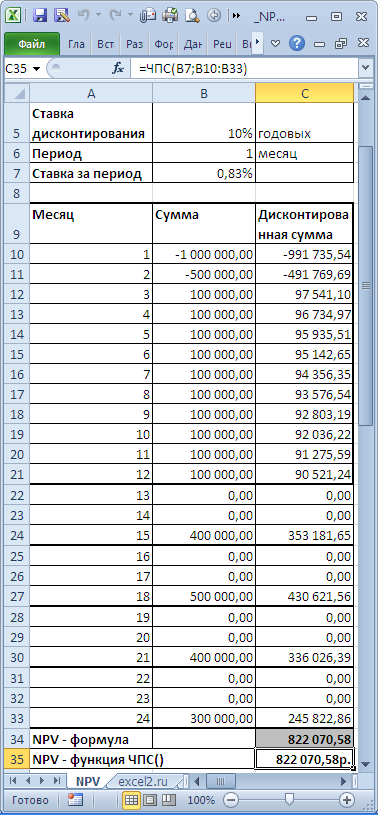
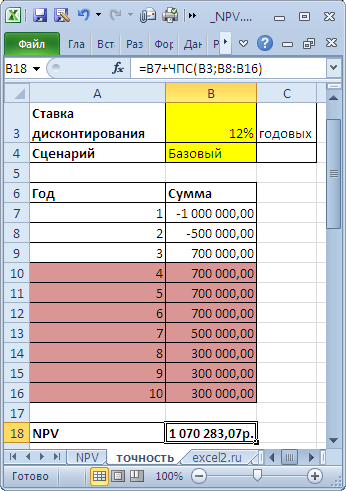
В таблице NPV подсчитан двумя способами: через функцию

ЧПС()

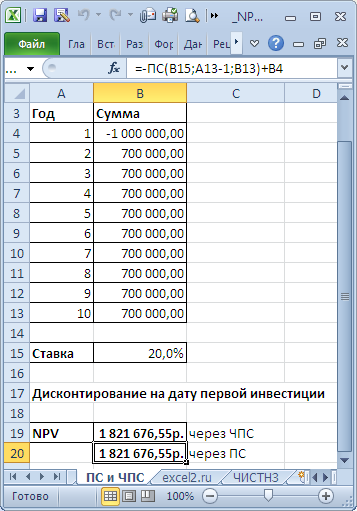
и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции

ЧПС()

, а нужно просто прибавить к получившемуся результату (см.

файл примера

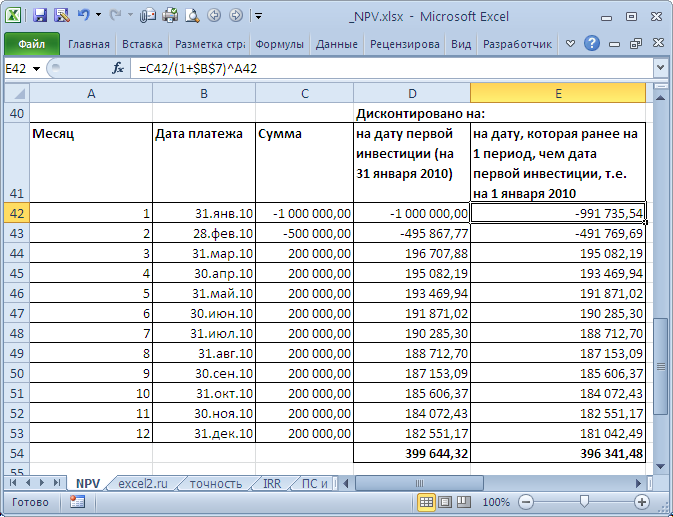
). Сравнение 2-х вариантов дисконтирования приведено в

файле примера

, лист NPV:

О точности расчета ставки дисконтирования

Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.

файл примера, лист Точность

).

Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.

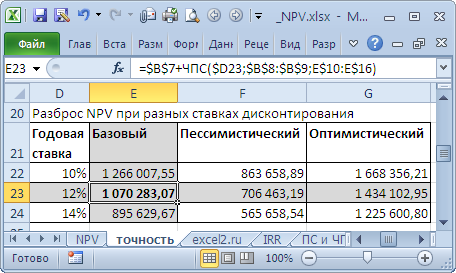
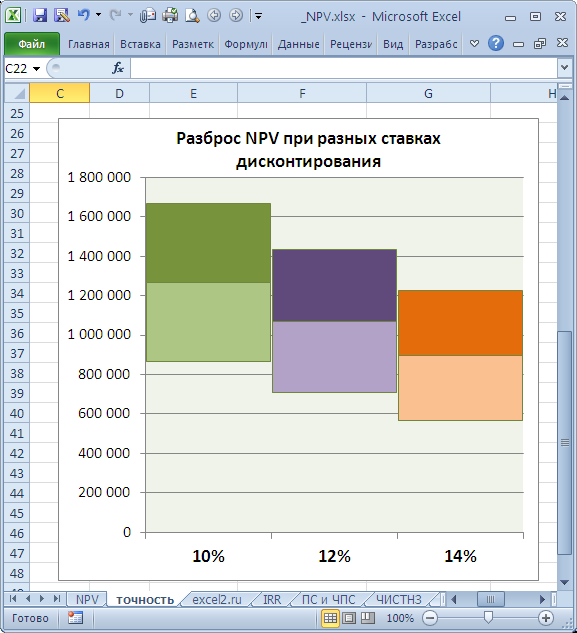
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):

Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.

Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.

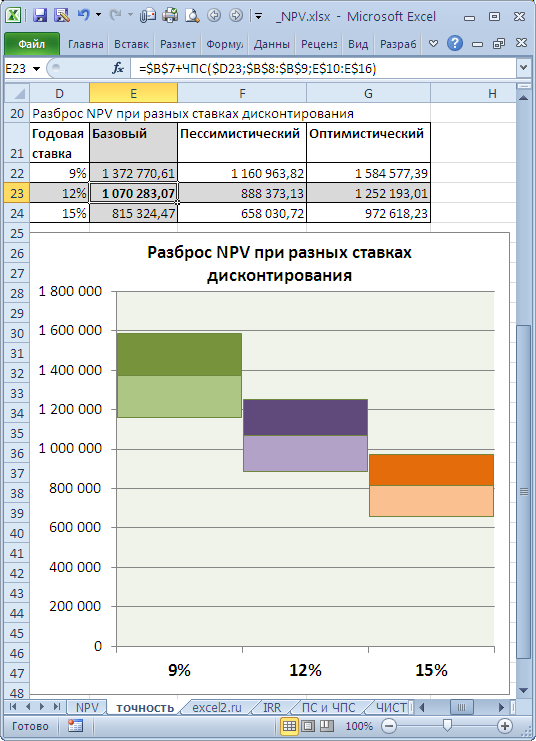
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0

Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.

Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.

После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.

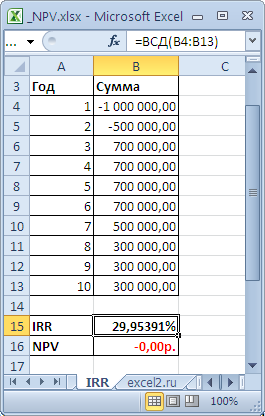
Внутренняя ставка доходности

IRR

(ВСД)

Внутренняя ставка доходности (англ.

internal rate of return

, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.

файл примера, лист IRR

).

Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.

Для расчета IRR используется функция

ВСД()

(английский вариант – IRR()). Эта функция тесно связана с функцией

ЧПС()

. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией

ВСД()

, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:

=ЧПС(ВСД(B5:B14);B5:B14)

Примечание4

. IRR можно рассчитать и без функции

ВСД()

: достаточно иметь функцию

ЧПС()

. Для этого нужно использовать инструмент

Подбор параметра

(поле «Установить в ячейке» должно ссылаться на формулу с

ЧПС()

, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).

Расчет NPV при постоянных денежных потоках с помощью функции ПС()

Напомним, что

аннуитет

представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию

ПС()

(см.

файл примера, лист ПС и ЧПС

).

В этом случае все денежные потоки (диапазон

В5:В13

, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке

В4

. Ставка дисконтирования расположена в ячейке

В15

со знаком минус. В этом случае формула

=B4+ЧПС(B15;B5:B13)

дает тот же результат, что и

= B4-ПС(B15;9;B13)

Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени

Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за

любые

промежутки времени, то используется функция

ЧИСТНЗ()

(английский вариант – XNPV()).

Функция

ЧИСТНЗ()

возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:

Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.

Принципиальным отличием от

ЧПС()

является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у

ЧИСТНЗ()

всегда годовая, т.к. указана база 365 дней, а не за период, как у

ЧПС()

. Еще отличие от

ЧПС()

: все денежные потоки всегда дисконтируются на дату первого платежа.

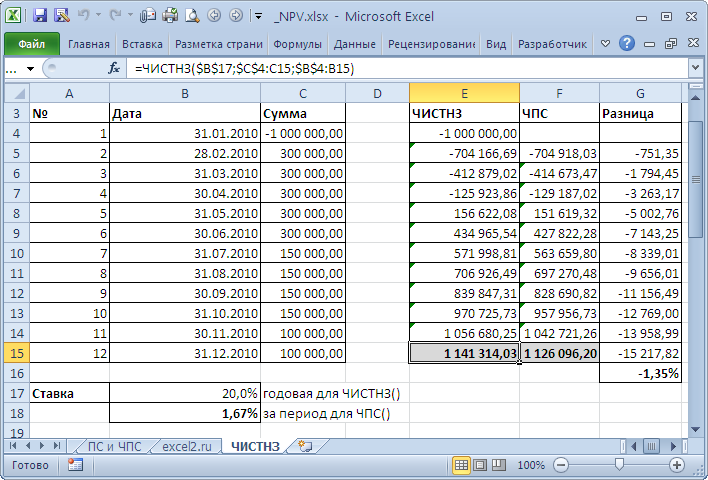
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций

ЧИСТНЗ()

и

ЧПС()

. Эти функции возвращают несколько отличающиеся результаты. Для задачи из

файла примера, Лист ЧИСТНЗ

разница составила порядка 1% (период = 1 месяцу).

Это связано с тем, что у

ЧИСТНЗ()

длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у

ЧПС()

указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет

високосного

года).

Внутренняя ставка доходности ЧИСТВНДОХ()

По аналогии с

ЧПС()

, у которой имеется родственная ей функция

ВСД()

, у

ЧИСТНЗ()

есть функция

ЧИСТВНДОХ()

, которая вычисляет годовую ставку дисконтирования, при которой

ЧИСТНЗ()

возвращает 0.

Расчеты в функции

ЧИСТВНДОХ()

производятся по формуле:

Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).

Примечание5

. Функция

ЧИСТВНДОХ()

используется для

расчета эффективной ставки по потребительским кредитам

.

Функция ЧПС возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).

Как работает функция ЧПС в Excel?

ЧПС определяет сумму приведенных к нынешнему дню дисконтированных значений платежей произвольной величины, которые являются разностью между поступлениями и выплатами. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех выплат после того, как окупится первоначальный вклад.

Функция ЧПС аналогична функции ПС (текущее значение), но различие между этими функциями заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода и они должны быть постоянными на протяжении всего периода инвестиции (аннуитетными платежами). В функции ЧПС денежные взносы могут быть переменной величиной. ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД – это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.

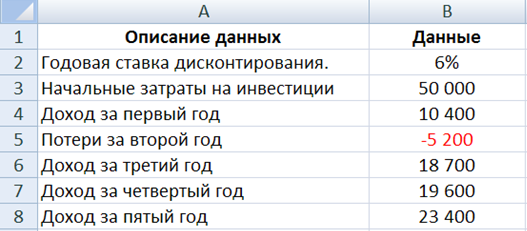
Пусть имеется проект: срок реализации – 5 лет, ставка дисконтирования – 6%, период денежных потоков – 1 год. Пример такой таблицы изображен ниже на рисунке:

Задача следующая: необходимо определить какую сумму прибыли может получить инвестор за вычетом потерь после того, как окупятся начальные затраты.



Функция ЧПС в Excel пошаговая инструкция

1. Ниже таблицы данных, например, в ячейку А10 запишите название вычисляемого показателя:



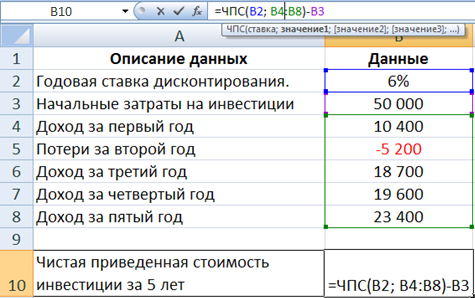
2. В ячейке B10 введите следующую формулу:

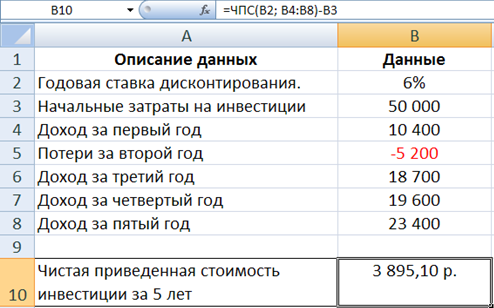
В данной формуле первоначально затраченная сумма, стоящая в ячейке В3 учитывается со знаком «минус». Однако эта сумма не включается в диапазон В4:В8 и ставится за скобками функции поскольку выплата производилась в начале первого периода:

В результате получаем значение 3 895,10 р.

Описание примера как работает функция ЧПС

В первом аргументе функции указывается процент ставки (она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям). Во втором и последующих аргументах указываются поступлениями и выплатами. На основе этих данных функция вычисляет значение чистой прибыли, из которой, разумеется, нужно вычесть начальные затраты. Поскольку начальная сумма была затрачена в начале первого периода, то к ней не применяется дисконтная ставка и, соответственно, она не включается в диапазон значений поступлений и выплат.

Внимание! Для функции ЧПС значения поступлений – положительные, а значения выплат – отрицательные. Поэтому во избежание ошибок и для удобства работы можно применять условное форматирование, окрашивающее шрифт отрицательных чисел в красный цвет.

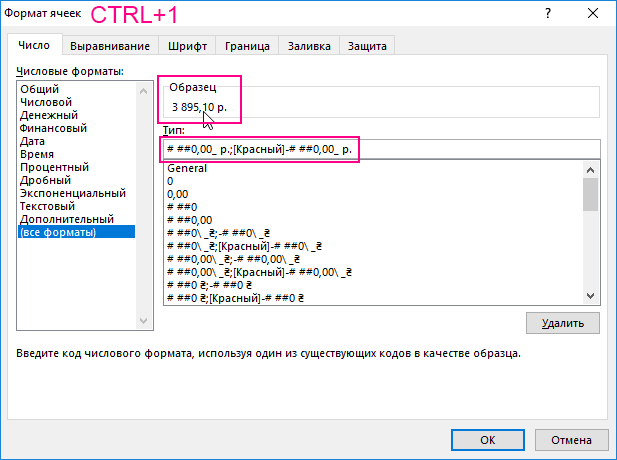
Многие русифицированные версии Excel выводят денежный рублевый формат без пробела между последней цифрой числа и символами «р.». Чтобы избавиться от этого досадной ошибки и вдобавок получить красный шрифт отрицательных чисел без использования условного форматирования, можно применить дополнительный формат. Для этого выберите «Главная» → «Ячейки» → «Формат» → «Формат ячеек» (CTRL+1) → «Число» → «Все форматы» в поле «Тип:» следует ввести следующую строку символов:

# ##0,00_ р.;[Красный]-# ##0,00_ р.

Расчет чистой приведенной стоимости в Excel подводит закономерный итог нашим обстоятельным публикациям, посвященным теме приведенной стоимости вообще и чистой приведенной стоимости (NPV) – в частности.

Помимо специальных калькуляторов и таблиц, наиболее эффективным на текущий момент представляется расчет чистой приведенной стоимости именно средствами Excel, хотя бы потому, что это легко, удобно и отвечает современным представлениям об эффективных расчетах.

В сегодняшней статье мы разберем стандартную функцию ЧПС, используемую для нахождения значений чистой приведенной стоимости в таблицах Microsoft Excel, уделив внимание ее синтаксису и приведя несколько наглядных примеров ее практического применения.

Предварительные данные о чистой приведенной стоимости

Освежить свои представления о приведенной и чистой приведенной стоимости можно соответственно здесь и здесь.

Ради экономии вашего (прежде всего) времени ограничусь лишь напоминанием общеизвестной формулы, которую нам придется впоследствии увязывать со стандартной функцией Excel.

Как мы помним, когда речь идет о расчете чистой приведенной стоимости n-ного количества денежных потоков, мы прибегаем к помощи следующей весьма изящной математической конструкции:

Здесь P_i обозначает численное значение денежного потока (которое, кстати говоря, может иметь и отрицательное значение, когда речь идет об оттоках денежных средств), а r – некоторая процентная ставка (ставка дисконтирования).

Разработчики Excel позаботились о том, чтобы предельно упростить стоящую перед нами задачу расчета данного показателя, разработав функцию ЧПС, имеющую следующий формат:

=ЧПС (r, P₁, P₂, …).

Обязательными в этой функции являются только два параметра: r – размер процентной ставки и P₁ – денежный поток в 1-ом периоде. Остальными параметрами можно пренебречь.

Всего формула позволяет обработать 254 значения P_i.

Значения P₁, P₂, …, P_nмогут быть положительными (в случае ПОСТУПЛЕНИЯ денежных средств) или отрицательными (когда имеют место будущие ВЫПЛАТЫ).

В свою очередь, результат функции ЧПС будет напрямую зависеть от исследуемых эмпирических данных и, как следствие, может принимать как положительные, так и отрицательные значения.

Особенности использования функции ЧПС

Ввести одномоментно 254 значения в одну ячейку бывает весьма утомительно.

Лучше заранее заполнить численными значениями некоторый диапазон, а затем подставлять в формулу ЧПС ссылки на входящие в диапазон ячейки.

Такой подход позволит легко комбинировать данные и исправлять возможные ошибки.

Следует помнить, что для расчета функции ЧПС важен ПОРЯДОК, в котором следуют значения P₁, P₂, …, P_n. Изменение этого порядка приведет к разным значениям нашей функции.

Предполагается также, что расчет производится для случая, когда выплаты или поступления отстоят друг от друга на один и тот же период (неделя, месяц, год и т.д.), то есть имеет место равномерное распределение денежных потоков во времени.

Все аргументы должны иметь численный формат. Ошибочно введенные в формулу ЧПС буквенные значения или символы при расчетах будут проигнорированы.

Пример расчета чистой приведенной стоимости

Не смею больше испытывать ваше терпение и предлагаю немедля окунуться в завораживающий мир расчета чистой приведенной стоимости с помощью функции ЧПС.

Итак, обещанный пример. Внимательно смотрим на иллюстрацию ниже:

Организуйте на листе вашей таблицы Excel размещение данных, аналогичных вышеприведенным.

Здесь важно заполнить ячейки A1, A2, A3, A4 и A5 конкретными числовыми данными, а в ячейку A7 поместить (важен каждый символ) выражение =ЧПС(A1; A2; A3; A4; A5).

Значение ячейки A7 как раз и будет содержать результат вычисления чистой приведенной стоимости ряда A2:A5.

Соответствующий диапазон, естественно, вы можете расширить или сузить, как вам заблагорассудится, а результирующее значение поместить в любую другую удобную для вас ячейку.

Здесь главное – понять принцип.

Обратите внимание, что значение в ячейке A3 имеет отрицательное значение (-5350).

Это означает, что имеет место выплата денежных средств (что в данном случае соответствует размеру первоначальных инвестиций).

Значения всех следующих аргументов являются положительными, так как мы имеем дело с поступлениями, символизирующими отдачу от наших инвестиций.

Заметим также, что наша функция в ячейке A7 может иметь и более краткий вид: =ЧПС(A1; A2:A5).

Такая запись соответствует синтаксическим стандартам Excel и позволяет сэкономить в ряде случаев и время, и нервы…

Итоговое значение (4110,00р) в денежном формате отображено во все той же ячейке A7.

Обязательно ВРУЧНУЮ проработайте приведенный выше пример.

Вы получите очень важный навык расчета реального финансового показателя – чистой приведенной стоимости – с помощью таблиц Excel.

Если вы планируете серьезно погрузиться в мир инвестиций, вам придется кое-что уметь и кое в чем разбираться.

Умение считать не на бумажке, а с использованием современного программного обеспечения – один из таких навыков.

Дополнительная информация по теме представлена в статье Расчет NPV в Excel (пример).

Удачных инвестиций!

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

В статье будет приведен расчет показателей эффективности проекта, с учетом дисконтирования.

• ЧДД или чистый дисконтированный доход от инвестиционного проекта;
• Внутренняя норма доходности.

Рассмотрим эти два показателя подробнее и рассчитаем пример работы с ними в Excel. Еще больше о возможностях Excel можно узнать на нашем открытом курсе «Аналитика в Excel».

Net Present Value (NPV, чистый дисконтированный доход) — один из самых распространенных показателей эффективности инвестиционного проекта.

Это разность между дисконтированными по времени поступлениями от проекта и инвестиционными затратами на него.

Метод расчета NPV:

1. Определяем текущую стоимость затрат (инвестиции в проект)
2. Производим расчет текущей стоимости денежных поступлений от проекта, для этого доходы за каждый отчетный период приводятся к текущей дате

CF – денежный поток;
r – ставка дисконта.

3. Сравниваем текущую стоимость инвестиций (наши затраты) в проект (Io) с текущей стоимостью доходов (PV). Разница между ними будет чистый дисконтированный доход — NPV.

NPV показывает инвестору доход или убыток от вложений средств в проект по сравнению с доходом от хранения денег в банке.

Если NPV больше 0, то инвестиции принесут больше дохода, нежели чем аналогичный вклад в банке.

Формула 1 модифицируется если инвестиционные вложения в проект осуществляются в несколько этапов (периодов).

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
r – ставка дисконтирования;
n – количество периодов.

Internal Rate of Return (Внутренняя норма доходности, IRR) определяет ставку дисконтирования при которой инвестиции равны 0 (NPV=0), или другими словами затраты на проект равны его доходам.

IRR = r, при которой NPV = f(r) = 0, находим из формулы:

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
n – количество периодов.

Этот показатель показывает норму доходности или возможные затраты при вложении денежных средств в проект (в процентах).

Пример расчета NPV в Excel

В MS Excel 2010 для расчета NPV используется функция =ЧПС().

Найдем чистый дисконтированный доход (NPV) проекта, требующего вложений инвестиций на 90 тыс. руб., и денежный поток которого распределен по времени рис 1. , и ставка дисконта равна 10%.

Рассчитаем показатель NPV по формуле Excel:

=ЧПС(D3;C3;C4:C11)

D3 – ставка дисконта;
C3 – вложения в 0 периоде (наши инвестиционные затраты в проект);
C4:C11 – денежный поток проекта за 8 периодов.

В итоге показатель чистого дисконтированного дохода равен 51,07 >0, это говорит о том, что в проект стоит инвестировать.

Расчет IRR в Excel

Для определения IRR в Excel используется встроенная функция

=ЧИСТВНДОХ()

Но так как у нас в примере данные поступали в равные интервалы времени можно использовать функцию

=ВСД(C3:C11)

Доходность вложения в проект равна 38%.

В завершение картинка финансового анализа проекта целиком.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.