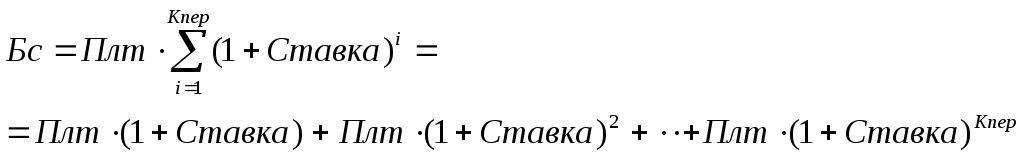Расчет будущей стоимости вклада в excel

Рассчитаем Будущую стоимость инвестиции для различных способов начисления процента: по формуле простых процентов, сложных процентов и формуле аннуитета.

Будущая стоимость (Future Value), является суммой, в которую в будущем превратится определенная сумма денег, инвестированная ранее под известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Будущей стоимости, также как и

Приведенной (Текущей) стоимости

важен, так как, платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту.

Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты:

простые проценты

,

сложные проценты

или

аннуитет

(в

файле примера

приведено решение задачи для каждого из методов).

Простые проценты

Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты, начисленные  за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).

При начислении простых процентов формула для расчета будущей стоимости (FV) инвестиций имеет следующий вид:

FV = PV * (1+i*n)

где PV —

настоящая (приведенная) стоимость

(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц (=годовая ставка/12)); n – количество периодов времени, в течение которых начисляются проценты.

Как видно из формулы FV (в MS EXCEL используется аббревиатура БС) это ни что иное, как

наращенная сумма

с использованием простых процентов. Про вычисление наращенной суммы при постоянной и переменной ставке можно прочитать в статье

Простые проценты в MS EXCEL

.

Примечание

. В MS EXCEL нет отдельной функции для расчета Будущей стоимости по методу Простых процентов. Функция

БС()

используется только для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить

БС()

рассчитать Будущую стоимость и по методу простых процентов (см.

файл примера

).

Сложные проценты

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент» (см.

файл примера

). Формула для расчета Будущей стоимости в случае начисления по сложным процентам имеет следующий вид:

FV = PV * (1+i)^n

где PV —

настоящая (приведенная) стоимость

(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). Предполагается, что процентная ставка не изменяется в течение всего срока инвестирования; n – количество периодов времени, в течение которого начисляются проценты.

Про вычисление Будущей стоимости по сложным процентам можно прочитать в статье

Сложные проценты в MS EXCEL

. В этой статье разобраны случаи применения функции

БС()

и формула капитализации m раз в год. В статье

Сложные проценты в MS EXCEL. Переменная ставка

разобраны случаи применения функции

БЗРАСПИС()

для расчета будущей стоимости при переменной ставке. В статье

Непрерывные проценты

Будущая стоимость рассчитывается при непрерывном начислении процентов.

Аннуитет

Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Будущей стоимости существенно усложняется См. статью

Аннуитет. Определяем в MS EXCEL Будущую Стоимость

.

В случае, если сумма начальной инвестиции =0 и нужно определить Будущую стоимость периодических равновеликих платежей, то это можно сделать по формуле (см.

файл примера

):

FV = PMT * (((1+i)^n)-1) / i

где PMT – размер платежа при аннуитете; i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). В формуле предполагается, что проценты начисляются в конце периода; n – количество периодов времени, в течение которых начисляются проценты (и делаются платежи).

Функция БС в Excel рассчитывает будущую стоимость инвестиции при условии, что процентная ставка является константой (не меняется с течением времени), и возвращает соответствующее значение. Функцию можно использовать в случаях, когда по окончанию срока выполняется единый платеж, а также при разбиении общей суммы на несколько фиксированных платежей.

Примеры использования финансовой функции БС в Excel

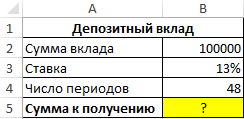
Пример 1. Вкладчик сделал депозит с ежемесячной капитализацией на сумму 100 000 рублей под 13% годовых сроком на 4 года. Какую сумму средств он сможет снять со своего депозитного счета по окончанию действия договора с банком?

Исходные данные:

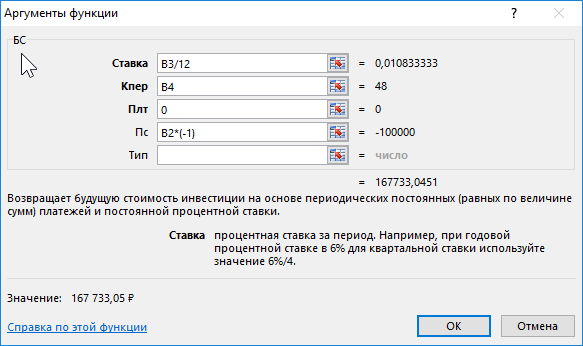
Формула для расчета:

Описание аргументов:

• B3/12 – ставка за период (капитализация выполняется ежемесячно);
• B4 – число периодов капитализации вклада;
• 0 – сумма выплаты за период капитализации (неизвестная величина в рамках данной задачи, поэтому значение 0);
• B2*(-1) – начальная сумма вклада (инвестиция, которая должна являться отрицательным числом).

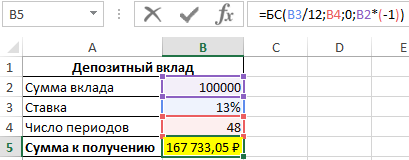
Результаты расчета:

Спустя 4 года вкладчик получит 167 733 рубля.



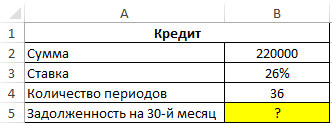
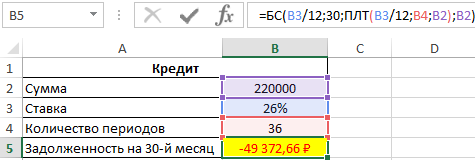
Расчет суммы долга по кредиту по состоянию на 30-й период погашения

Пример 2. Заемщик взял кредит в банке под 26% годовых на сумму 220 000 рублей сроком на 3 года с ежемесячным фиксированным платежом. Какой будет сумма задолженности заемщика по окончанию 30-го периода выплат?

Исходные данные:

Формула для расчета:

=БС(B3/12;30;ПЛТ(B3/12;B4;B2);B2)

Описание аргументов:

• B3/12 – месячная процентная ставка;
• 30 – номер периода для расчета остатка задолженности;
• ПЛТ(B3/12;B4;B2) – функция, возвращающая сумму ежемесячного платежа;
• B2 – тело кредита.

Полученный результат:

Фактическая задолженность за кредит по окончанию 30-го месяца составит примерно 49372 рубля.

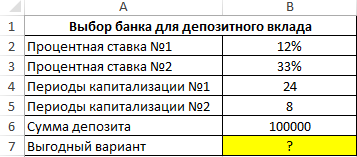
Сравнительный инвестиционный анализ условий депозита в банке

Пример 3. Вкладчик получил предложения по депозитному вкладу от двух банков с различными условиями:

1. Ставка – 12% годовых, капитализация – ежемесячная.
2. Ставка – 33% годовых, капитализация – ежеквартальная.

Определить, какое из предложений является более выгодным, если сумма вклада – 100000 рублей, срок действия договора – 2 года.

Исходные данные:

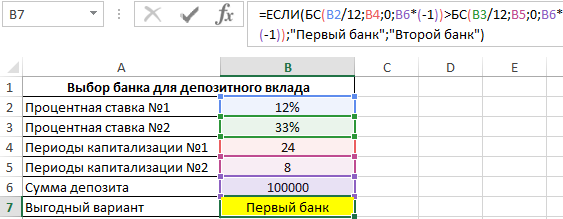
Формула для расчета:

С помощью функции ЕСЛИ определяем, в каком случае будущая стоимость окажется больше и возвращаем соответствующее значение. Полученный результат:

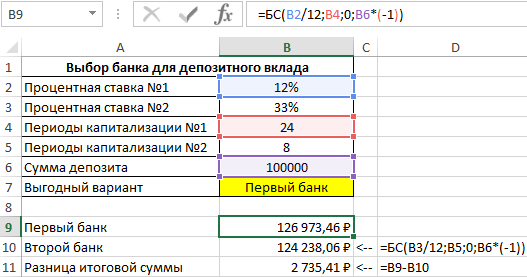
Выведем результаты расчетов функций БС и разницу сумм:

Как видно, несмотря на высокую годовую ставку, первый банк сделал более выгодное предложение, поскольку по условиям предложенного договора капитализация является ежемесячной. То есть, чем чаще происходит капитализация, тем быстрее увеличивается сумма вклада.

Особенности использования финансовой функции БС в Excel

Функция БС используется наряду с прочими финансовыми функциями (ПС, ПЛТ, КПЕР и другими) и имеет следующий синтаксис:

=БС(ставка;кпер;плт;[пс];[тип])

Описание аргументов:

• ставка – аргумент, принимающий числовое или процентное значение ставки за указанный период. Обязательный для заполнения. Если по условию используется годовая ставка, необходимо выполнить пересчет по следующей формуле: R=Rg/n, где Rg – годовая ставка, n – число периодов.
• кпер – числовое значение, характеризующее число периодов оплаты. Аргумент обязателен для заполнения. Если кредит был взят на период 3 года, выплаты по которому должны производиться каждый месяц, аргумент кпер должен принять значение 3*12=36 (12 – месяцы в году).
• плт – числовое значение, характеризующее фиксированную сумму выплаты за каждый период. Аргумент обязателен для заполнения. Если выплата за период является неизвестной величиной, аргумент плт может принимать значение 0, но при этом следующий аргумент задается явно.
• [пс] – приведенная стоимость на данный момент. Например, когда заемщик берет кредит у финансовой организации, тело кредита является приведенной на текущий момент стоимостью. По умолчанию аргумент [пс] принимает значение 0, а плт должен иметь отличное от нуля значение.
• [тип] – числовое значение, характеризующее тип выплат: в конце или начале периода. Принимает только два значения: 0 (если явно не указан) и 1.

Примечание 1:

1. При указании аргумента ставка можно использовать процентный формат данных (например 17%) и числовой аналог (0,17).
2. Расходные операции (текущая стоимость, выплата за период) должны быть указаны со знаком «-», то есть являться отрицательными числами.
3. Функция БС использует в расчетах следующую формулу:



4. Данная функция может быть использована для расчета баланса на конец периода и остаточной суммы задолженности по кредиту на текущий момент.
5. Если процентная ставка меняется со временем, для расчетов следует использовать формулу БЗРАСПИС.
6. Аргументы функции могут являться числовыми значениями или текстовыми данными, которые могут быть преобразованы в числа. Если один или несколько аргументов функции БС принимают текстовые строки, не содержащие числовые значения, будет возвращен код ошибки #ЗНАЧ!.

Примечание 2: функция БС также применяется для определения остатка задолженности по кредиту с аннуитетным графиком выплат, при этом дополнительные проценты и комиссии учтены не будут. Аннуитетный график предполагает фиксированную сумму погашения для каждого периода выплат (состоит из процентов и тела кредита).

В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала – выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.

За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) – о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f _{x ,} слева от строки ввода значений и адресов ячеек.

В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.

Составляющим формулы расчета будущей стоимости FV = PV(1+r)ⁿ в Excel соответствуют следующие функции:

Общее название	Функция в Excel	Краткое описание
FV (Future Value)	БС (Будущая Стоимость)	Будущая сумма вклада
PV (Present Value)	ПС (Текущая Стоимость)	Текущая стоимость вклада
n	КПЕР (Количество Периодов)	Число периодов начисления процентов по вкладу
r	СТАВКА	Процентная ставка по вкладу

Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.

Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет – у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком “минус”, т.к. мы эти деньги отдаем, а не получаем.

Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:

• если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим “0” или оставляем поле пустым;
• если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим “1”.

В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном – 20 (4 кв. х 5 лет).

А теперь: внимание – вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем “ОК”.

Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда – вывод. Проценты по вашему вкладу должны:

• капитализироваться;
• капитализироваться ежемесячно.

Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.

• Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.

А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!

А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.

Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать – это подумать о завтра сегодня.

• Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои курсы и вебинары.

Обучение торговле на бирже

БС — одна из финансовых функций, возвращающая будущую стоимость инвестиции на основе постоянной процентной ставки. В функции БС можно использовать как периодические постоянные платежи, так и единый общий платеж.

Воспользуйтесь средством Excel Formula Coach для расчета будущей стоимости серии платежей. При этом вы узнаете, как использовать функцию БС в формуле.

Excel Formula Coach также можно использовать для расчета будущей стоимости единого общего платежа.

Синтаксис

БС(ставка;кпер;плт;[пс];[тип])

Дополнительные сведения об аргументах функции БС и других функциях, связанных с аннуитетами, см. в описании функции ПС.

Аргументы функции БС описаны ниже.

• Ставка    — обязательный аргумент. Процентная ставка за период.

• Кпер    — обязательный аргумент. Общее количество периодов платежей по аннуитету.

• Плт    — обязательный аргумент. Выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.

• Пс    — необязательный аргумент. Приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент «пс» опущен, предполагается значение 0. В этом случае аргумент «плт» является обязательным.

• Тип    Необязательный. Число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.

Тип	Выплата
0	В конце периода
1	В начале периода

Замечания

• Убедитесь, что единицы измерения аргументов «ставка» и «кпер» используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента «ставка» и 4*12 — в качестве аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% в качестве аргумента «ставка» и 4 — в качестве аргумента «кпер».

• Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.

Примеры

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,06	Годовая процентная ставка
10	Количество платежей
-200	Объем платежей
-500	Стоимость на текущий момент
1	Платежи осуществляются в начале периода (0 означает, что платежи осуществляются в конце периода)
Формула	Описание	Результат
=БС(A2/12; A3; A4; A5; A6)	Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5.	2 581,40 ₽

Пример 2

Данные	Описание
0,12	Годовая процентная ставка
12	Количество платежей
-1000	Объем платежей
Формула	Описание	Результат
=БС(A2/12; A3; A4)	Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A4.	12 682,50 ₽

Пример 3

Данные	Описание
0,11	Годовая процентная ставка
35	Количество платежей
-2000	Объем платежей
1	Платежи осуществляются в начале года (0 означает конец года)
Формула	Описание	Результат
=БС(A2/12; A3; A4;; A5)	Будущая стоимость инвестиций с условиями, указанными в ячейках A2:A4.	82 846,25 ₽

Пример 4

Данные	Описание
0,06	Годовая процентная ставка
12	Количество платежей
-100	Объем платежей
-1000	Стоимость на текущий момент
1	Платежи осуществляются в начале года (0 означает конец года)
Формула	Описание	Результат
=БС(A2/12; A3; A4; A5; A6)	Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5.	2 301,40 ₽

Определение будущей стоимости на основе постоянной процентной ставки

Задача
1.

Постановка
задачи.

На
банковский счет под 11,5% годовых внесли
37000 руб. Определить размер вклада по
истечении 3 лет, если проценты начисляются
каждые полгода.

Алгоритм
решения задачи.

Поскольку
необходимо рассчитать единую сумму
вклада на основе постоянной процентной
ставки, то используем функцию БС
(ставка;
кпер;
плт;
пс; тип). Опишем способы задания
аргументов данной функции.

В связи
с тем, что проценты начисляются каждые
полгода, аргумент ставка
равен 11,5%/2. Общее число периодов
начисления равно 3*2 (аргументкпер).
Если решать данную задачу с точки зрения
вкладчика, то аргументпс(начальная стоимость вклада) равный 37
000 руб., задается в виде отрицательной
величины (- 37 000), поскольку для вкладчика
это отток его денежных средств (вложение
средств). Если рассматривать решение
данной задачи с точки зрения банка, то
данный аргумент (пс)
должен быть задан в виде
положительной величины, т.к. означает
поступление средств в банк.

Аргумент
плтотсутствует, т.к. вклад не пополняется.
Аргументтиправен 0, т.к. в подобных операциях проценты
начисляются в конце каждого периода
(задается по умолчанию). Тогда к концу
3-го года на банковском счете имеем:

=
БС (11,5%/2;3*2;;-37 000) = 51 746,86 руб., с
точки зрения вкладчика это доход,

=
БС (11,5%/2;3*2;;37 000) = — 51 746,86 руб., с
точки зрения банка это расход, т.е.
возврат денег банком вкладчику.

На
практике, в зависимости от условий
финансовой сделки проценты могут
начисляться несколько раз в год, например,
ежемесячно, ежеквартально и т.д. Если
процент начисляется несколько раз в
год, то необходимо определение общего
числа периодов начисления процентов и
ставки процента за период начисления.
В таблице 4.3 приведены данные для наиболее
распространенных методов внутригодового
учета процентов.

Таблица 4.3.

Расчет данных для различных вариантов начисления процентов

Метод начисления процентов	Общее число периодов начисления процентов	Процентная ставка за период начисления, %
Ежегодный	N	K
Полугодовой	N*2	K/2
Квартальный	N*4	K/4
Месячный	N*12	K/12
Ежедневный	N*365	K/365

Этот
же расчет можно выполнить по формуле:

(4.1),

где: Бс – будущая стоимость (значение)
вклада;

Пс– текущая стоимость вклада;

Кпер– общее число периодов
начисления процентов;

Ставка– процентная ставка по
вкладу за период.

Подставив
в формулу числовые данные, получим:

Примечания.

1. При
аналитических вычислениях в Excelс помощью функций, связанных с аннуитетом,
–БЗРАСПИС,
БС, ОБЩДОХОД, ОБЩПЛАТ, ОСПЛТ, ПЛТ, ПРПЛТ,
ПС, СТАВКА, ЧИСТВНДОХ, ЧИСТНЗ–
используется следующее основное
уравнение:

(4.2),

в котором наименования параметров Пс,
Ставка, Кпер, Плт, Бс соответствуют
описаниям из таблицы 4.2 (и, соответственно,
одноименным встроенным функциям), а
параметрТипопределяет обязательность
выплаты платежей в начале периода (1)
или выплату обычных платежей в конце
периода (0).

2. Из
уравнения (4.2) могут быть выражены
значения бс, пс, ставка, кпер, плт через
другие параметры. Эти выражения
используются соответствующими функциямиExcel.

3. Если
ставкаравна 0, вместо уравнения
(4.2) используется уравнение:

(4.3)

4. Если
формула (4.1) не предусматривает задание
денежных потоков, идущих от клиента, со
знаком минус, то в формулах (4.2) и (4.3) это
учтено.

Нахождение
решения задачи 1 по формуле (4.2) дает тот
же результат. Иллюстрация решения
приведена на рис. 4.1.

Рис.
4.1. Фрагмент листа Excel
с решением задачи о нахождении будущего
размера вклада

Задача
2.

Постановка
задачи.

Определить,
сколько денег окажется на банковском
счете, если ежегодно в течение 5 лет под
17% годовых вносится 20 тыс. руб. Взносы
осуществляются в начале каждого года.

Алгоритм
решения задачи.

Поскольку
следует рассчитать будущую стоимость
фиксированных периодических выплат на
основе постоянной процентной ставки,
то воспользуемся функцией БСсо следующими аргументами:

=
БС(17%;5;-20000;;1) = 164 136,96 руб.

Если
бы взносы осуществлялись в конце каждого
года, результат был бы:

=
БС(17%;5;-20000) = 140 288 руб.

В
рассмотренной функции не используется
аргумент пс,
т.к. первоначально на счете денег не
было.

Решение
задачи может быть найдено с использованием
формулы:

(4.4),

где: Бс– будущая стоимость потока
фиксированных периодических платежей;

Плт– фиксированная периодическая
сумма платежа;

Кпер– общее число периодов выплат;

Ставка– постоянная процентная
ставка;

i– номер текущего
периода выплаты платежа.

Результат
аналитического вычисления:

Задача
3.

Постановка
задачи.

Достаточно
ли положить на счет 85 000 руб. для
приобретения через 5 лет легкового
автомобиля стоимостью 160 000 руб.? Банк
начисляет проценты ежеквартально,
годовая ставка 12%.

Произвести
расчеты при разных вариантах процентной
ставки.

Алгоритм
решения задачи.

Поскольку
требуется найти будущее значение суммы
вклада через 5 лет, для решения поставленной
задачи воспользуемся функцией БС.
Получим:

=БС(12%/4;5*4;;-85000;
0)= 153 519,45р.

Как
видим, найденная сумма недостаточна
для совершения покупки. Чтобы осуществить
мечту, существует два варианта:
первоначально положить на счет большую
сумму или воспользоваться банком, где
предусмотрена большая процентная
ставка. Внесение дополнительных платежей
рассматривать не будем.

1 вариант.

Для
определения необходимой суммы исходные
данные задачи представим в виде таблицы
и воспользуемся средством Подборпараметраиз меню командыСервис.

Иллюстрация решения представлена на
рис. 4.2.

Рис.
4.2. Фрагмент окна Excel
с заполненными полями подбора параметров

После
подтверждения введенных данных в ячейке
В7
установится значение 160 000,00р.,
а в ячейкеB3
отобразится результат –
88 588,12р.

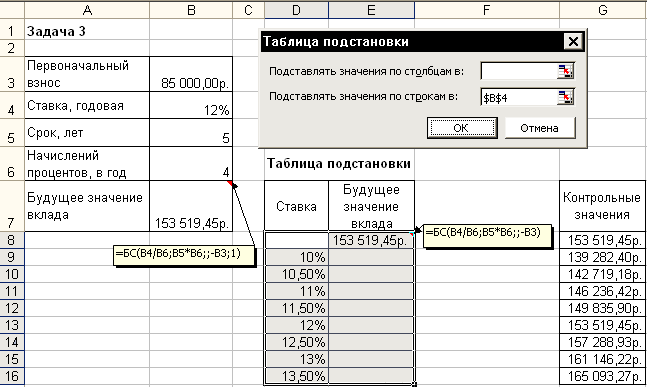
2 вариант.

В данном
случае также можно применить средство
Подбор параметра, изменяя ячейку,
в которой находится процентная ставка.
Однако для анализа влияния процентной
ставки на зависящую от нее формулу
расчета будущей суммы вклада воспользуемся
другим средством –Таблицей подстановки
из меню командыСервис.

В
дополнение к исходным данным задачи,
представленным в виде таблицы, наметим
контуры будущей таблицы подстановки:
укажем наименования столбцов, в ячейки
D9:D16введем процентные ставки (входы в нашу
таблицу подстановки будут размещаться
слева в строках), а в ячейкуЕ8введем формулу расчета будущего значения
единой суммы вклада. Затем выполним
необходимые действия по инициализации
средства Таблица подстановки и внесения
в соответствующее поле подстановки по
строкам значения адреса ячейки с
процентной ставкой.

Иллюстрация
окна Excelпосле задания
параметров для таблицы подстановки, а
также контрольные значения искомых
результатов представлены на рис. 4.3.

Рис.
4.3. Фрагмент окна Excel
с заполненными полями таблицы подстановки

После
подтверждения в диалоговом окне заданных
параметров таблицы подстановки в
диапазоне ячеек Е9:Е16автоматически появятся результаты,
полностью совпадающие с контрольными
значениями.

Из
результатов следует, что годовые ставки
менее 13% не обеспечивают рост вклада до
требуемой величины, равной 160 000 р.

При
ставке 13% значение вклада вырастет до
161 146,22р., а
ставка 13,5% обеспечивает рост вклада до
165 093,27р.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #