Расчет будущей стоимости платежа в excel

Рассчитаем Будущую стоимость инвестиции для различных способов начисления процента: по формуле простых процентов, сложных процентов и формуле аннуитета.

Будущая стоимость (Future Value), является суммой, в которую в будущем превратится определенная сумма денег, инвестированная ранее под известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Будущей стоимости, также как и

Приведенной (Текущей) стоимости

важен, так как, платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту.

Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты:

простые проценты

,

сложные проценты

или

аннуитет

(в

файле примера

приведено решение задачи для каждого из методов).

Простые проценты

Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты, начисленные  за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).

При начислении простых процентов формула для расчета будущей стоимости (FV) инвестиций имеет следующий вид:

FV = PV * (1+i*n)

где PV —

настоящая (приведенная) стоимость

(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц (=годовая ставка/12)); n – количество периодов времени, в течение которых начисляются проценты.

Как видно из формулы FV (в MS EXCEL используется аббревиатура БС) это ни что иное, как

наращенная сумма

с использованием простых процентов. Про вычисление наращенной суммы при постоянной и переменной ставке можно прочитать в статье

Простые проценты в MS EXCEL

.

Примечание

. В MS EXCEL нет отдельной функции для расчета Будущей стоимости по методу Простых процентов. Функция

БС()

используется только для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить

БС()

рассчитать Будущую стоимость и по методу простых процентов (см.

файл примера

).

Сложные проценты

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент» (см.

файл примера

). Формула для расчета Будущей стоимости в случае начисления по сложным процентам имеет следующий вид:

FV = PV * (1+i)^n

где PV —

настоящая (приведенная) стоимость

(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). Предполагается, что процентная ставка не изменяется в течение всего срока инвестирования; n – количество периодов времени, в течение которого начисляются проценты.

Про вычисление Будущей стоимости по сложным процентам можно прочитать в статье

Сложные проценты в MS EXCEL

. В этой статье разобраны случаи применения функции

БС()

и формула капитализации m раз в год. В статье

Сложные проценты в MS EXCEL. Переменная ставка

разобраны случаи применения функции

БЗРАСПИС()

для расчета будущей стоимости при переменной ставке. В статье

Непрерывные проценты

Будущая стоимость рассчитывается при непрерывном начислении процентов.

Аннуитет

Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Будущей стоимости существенно усложняется См. статью

Аннуитет. Определяем в MS EXCEL Будущую Стоимость

.

В случае, если сумма начальной инвестиции =0 и нужно определить Будущую стоимость периодических равновеликих платежей, то это можно сделать по формуле (см.

файл примера

):

FV = PMT * (((1+i)^n)-1) / i

где PMT – размер платежа при аннуитете; i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). В формуле предполагается, что проценты начисляются в конце периода; n – количество периодов времени, в течение которых начисляются проценты (и делаются платежи).

Функция ПЛТ в Excel входит в категорию «Финансовых». Она возвращает размер периодического платежа для аннуитета с учетом постоянства сумм платежей и процентной ставки. Рассмотрим подробнее.

Синтаксис и особенности функции ПЛТ

Синтаксис функции: ставка; кпер; пс; [бс]; [тип].

Расшифровка аргументов:

• Ставка – это проценты по займу.
• Кпер – общее количество платежей по ссуде.
• Пс – приведенная стоимость, равноценная ряду будущих платежей (величина ссуды).
• Бс – будущая стоимость займа после последнего платежа (если аргумент опущен, будущая стоимость принимается равной 0).
• Тип – необязательный аргумент, который указывает, выплата производится в конце периода (значение 0 или отсутствует) или в начале (значение 1).

Особенности функционирования ПЛТ:

1. В расчете периодического платежа участвуют только выплаты по основному долгу и платежи по процентам. Не учитываются налоги, комиссии, дополнительные взносы, резервные платежи, иногда связываемые с займом.
2. При задании аргумента «Ставка» необходимо учесть периодичность начисления процентов. При ссуде под 6% для квартальной ставки используется значение 6%/4; для ежемесячной ставки – 6%/12.
3. Аргумент «Кпер» указывает общее количество выплат по кредиту. Если человек совершает ежемесячные платежи по трехгодичному займу, то для задания аргумента используется значение 3*12.



Примеры функции ПЛТ в Excel

Для корректной работы функции необходимо правильно внести исходные данные:

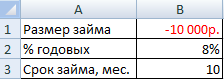
Размер займа указывается со знаком «минус», т.к. эти деньги кредитная организация «дает», «теряет». Для записи значения процентной ставки необходимо использовать процентный формат. Если записывать в числовом, то применяется десятичное число (0,08).

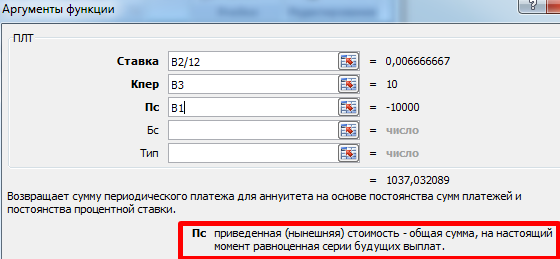
Нажимаем кнопку fx («Вставить функцию»). Откроется окно «Мастер функций». В категории «Финансовые» выбираем функцию ПЛТ. Заполняем аргументы:

Когда курсор стоит в поле того или иного аргумента, внизу показывается «подсказка»: что необходимо вводить. Так как исходные данные введены в таблицу Excel, в качестве аргументов мы использовали ссылки на ячейки с соответствующими значениями. Но можно вводить и числовые значения.

Обратите внимание! В поле «Ставка» значение годовых процентов поделено на 12: платежи по кредиту выполняются ежемесячно.

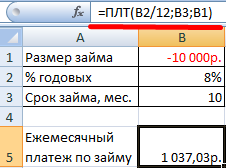
Ежемесячные выплаты по займу в соответствии с указанными в качестве аргументов условиями составляют 1 037,03 руб.

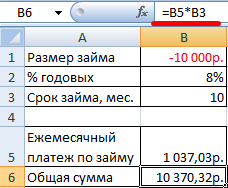
Чтобы найти общую сумму, которую нужно выплатить за весь период (основной долг плюс проценты), умножим ежемесячный платеж по займу на значение «Кпер»:

Исключим из расчета ежемесячных выплат по займу платеж, произведенный в начале периода:

Для этого в качестве аргумента «Тип» нужно указать значение 1.

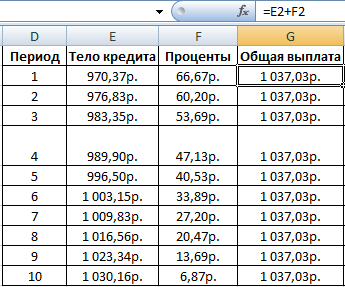
Детализируем расчет, используя функции ОСПЛТ и ПРПЛТ. С помощью первой покажем тело кредита, посредством второй – проценты.

Для подробного расчета составим таблицу:

Рассчитаем тело кредита с помощью функции ОСПЛТ. Аргументы заполняются по аналогии с функцией ПЛТ:

В поле «Период» указываем номер периода, для которого рассчитывается основной долг.

Заполняем аргументы функции ПРПЛТ аналогично:

Дублируем формулы вниз до последнего периода. Для расчета общей выплаты суммируем тело кредита и проценты.

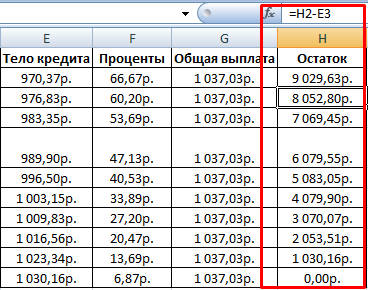
Рассчитываем остаток по основному долгу. Получаем таблицу следующего вида:

Общая выплата по займу совпадает с ежемесячным платежом, рассчитанным с помощью функции ПЛТ. Это постоянная величина, т.к. пользователь оформил аннуитетный кредит.

Таким образом, функция ПЛТ может применяться для расчета ежемесячных выплат по вкладу или платежей по кредиту при условии постоянства процентной ставки и сумм.

Прежде, чем брать заем, неплохо было бы рассчитать все платежи по нему. Это убережет заёмщика в будущем от различных неожиданных неприятностей и разочарований, когда выяснится, что переплата слишком большая. Помочь в данном расчете могут инструменты программы Excel. Давайте выясним, как рассчитать аннуитетные платежи по кредиту в этой программе.

Расчет оплаты

Прежде всего, нужно сказать, что существует два вида кредитных платежей:

• Дифференцированные;
• Аннуитетные.

При дифференцированной схеме клиент вносит в банк ежемесячно равную долю выплат по телу кредита плюс платежи по процентам. Величина процентных выплат каждый месяц уменьшается, так как уменьшается тело займа, с которого они рассчитываются. Таким образом и общий ежемесячный платеж тоже уменьшается.

При аннуитетной схеме используется несколько другой подход. Клиент ежемесячно вносит одинаковую сумму общего платежа, который состоит из выплат по телу кредита и оплаты процентов. Изначально процентные взносы насчитываются на всю сумму займа, но по мере того, как тело уменьшается, сокращается и начисление процентов. Но общая сумма оплаты остается неизменной за счет ежемесячного увеличения величины выплат по телу кредита. Таким образом, с течением времени удельный вес процентов в общем ежемесячном платеже падает, а удельный вес оплаты по телу растет. При этом сам общий ежемесячный платеж на протяжении всего срока кредитования не меняется.

Как раз на расчете аннуитетного платежа мы и остановимся. Тем более, это актуально, так как в настоящее время большинство банков используют именно эту схему. Она удобна и для клиентов, ведь в этом случае общая сумма оплаты не меняется, оставаясь фиксированной. Клиенты всегда знают сколько нужно заплатить.

Этап 1: расчет ежемесячного взноса

Для расчета ежемесячного взноса при использовании аннуитетной схемы в Экселе существует специальная функция – ПЛТ. Она относится к категории финансовых операторов. Формула этой функции выглядит следующим образом:

=ПЛТ(ставка;кпер;пс;бс;тип)

Как видим, указанная функция обладает довольно большим количеством аргументов. Правда, последние два из них не являются обязательными.

Аргумент «Ставка» указывает на процентную ставку за конкретный период. Если, например, используется годовая ставка, но платеж по займу производится ежемесячно, то годовую ставку нужно разделить на 12 и полученный результат использовать в качестве аргумента. Если применяется ежеквартальный вид оплаты, то в этом случае годовую ставку нужно разделить на 4 и т.д.

«Кпер» обозначает общее количество периодов выплат по кредиту. То есть, если заём берется на один год с ежемесячной оплатой, то число периодов считается 12, если на два года, то число периодов – 24. Если кредит берется на два года с ежеквартальной оплатой, то число периодов равно 8.

«Пс» указывает приведенную стоимость на настоящий момент. Говоря простыми словами, это общая величина займа на начало кредитования, то есть, та сумма, которую вы берете взаймы, без учета процентов и других дополнительных выплат.

«Бс» — это будущая стоимость. Эта величина, которую будет составлять тело займа на момент завершения кредитного договора. В большинстве случаев данный аргумент равен «0», так как заемщик на конец срока кредитования должен полностью рассчитаться с кредитором. Указанный аргумент не является обязательным. Поэтому, если он опускается, то считается равным нулю.

Аргумент «Тип» определяет время расчета: в конце или в начале периода. В первом случае он принимает значение «0», а во втором – «1». Большинство банковских учреждений используют именно вариант с оплатой в конце периода. Этот аргумент тоже является необязательным, и если его опустить считается, что он равен нулю.

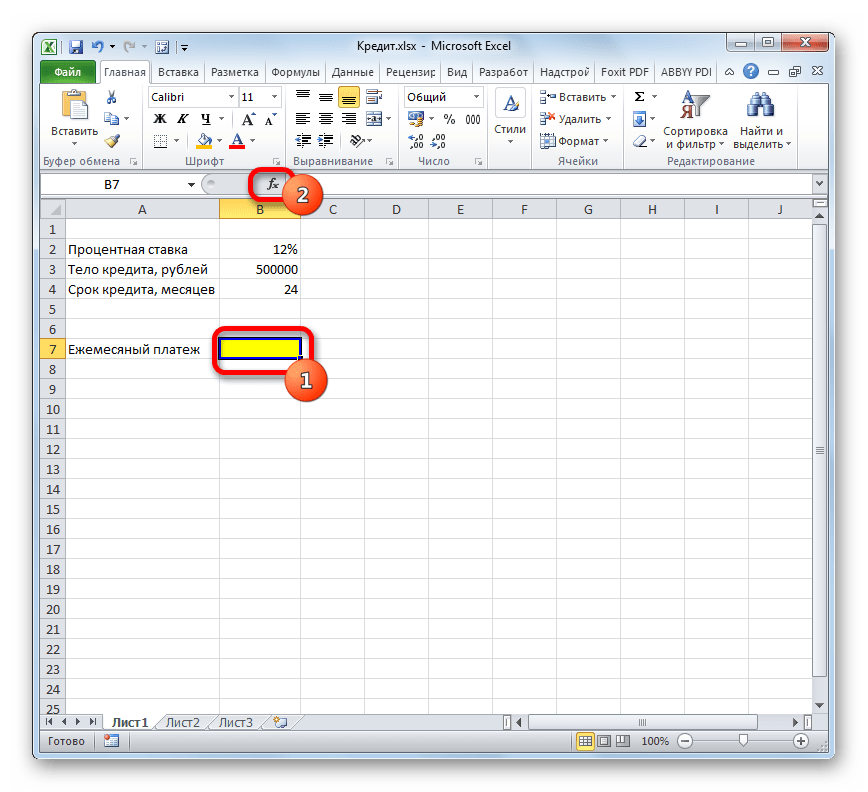
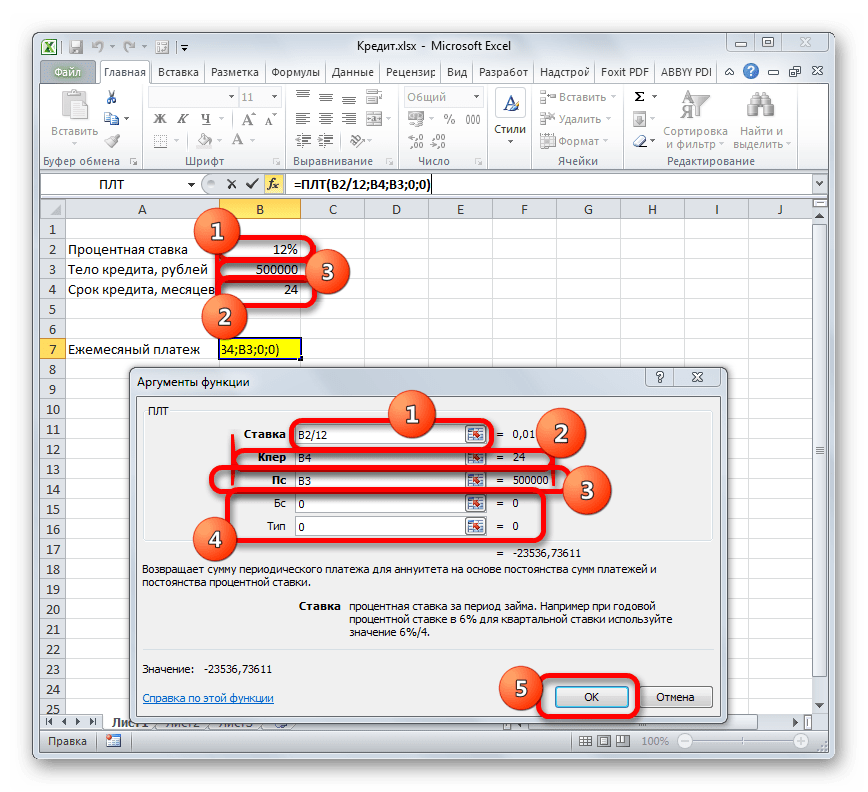
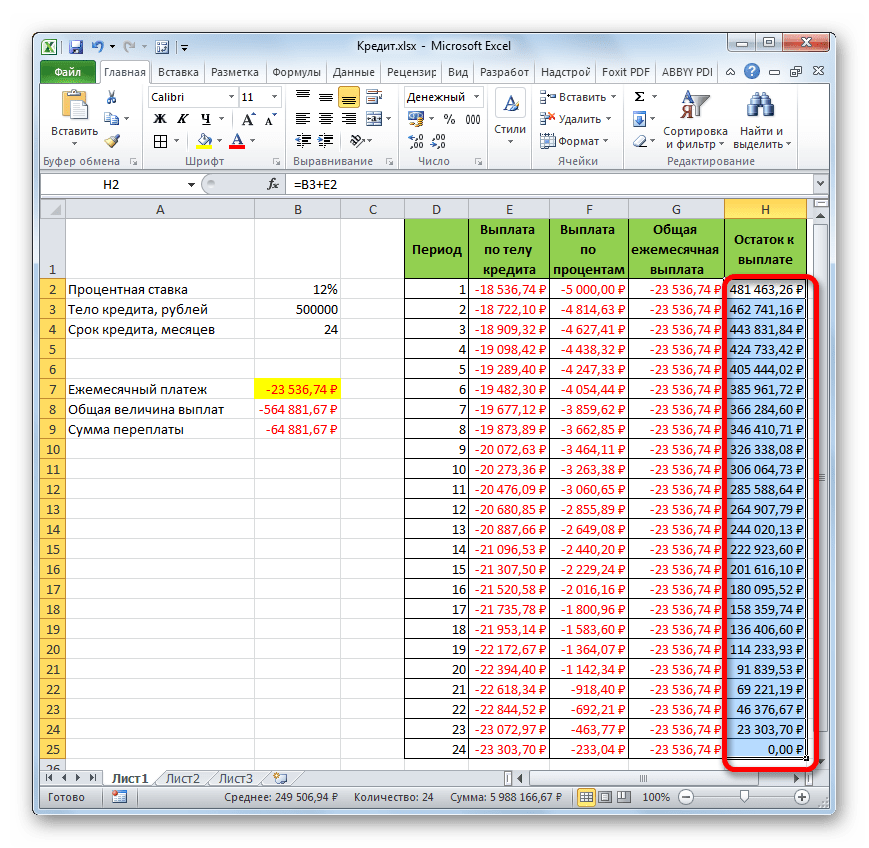
Теперь настало время перейти к конкретному примеру расчета ежемесячного взноса при помощи функции ПЛТ. Для расчета используем таблицу с исходными данными, где указана процентная ставка по кредиту (12%), величина займа (500000 рублей) и срок кредита (24 месяца). При этом оплата производится ежемесячно в конце каждого периода.

1. Выделяем элемент на листе, в который будет выводиться результат расчета, и щелкаем по пиктограмме «Вставить функцию», размещенную около строки формул.



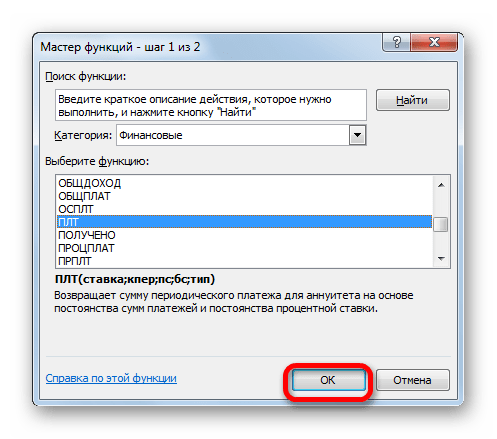
2. Производится запуск окошка Мастера функций. В категории «Финансовые» выделяем наименование «ПЛТ» и жмем на кнопку «OK».



3. После этого открывается окно аргументов оператора ПЛТ.

   В поле «Ставка» следует вписать величину процентов за период. Это можно сделать вручную, просто поставив процент, но у нас он указан в отдельной ячейке на листе, поэтому дадим на неё ссылку. Устанавливаем курсор в поле, а затем кликаем по соответствующей ячейке. Но, как мы помним, у нас в таблице задана годовая процентная ставка, а период оплаты равен месяцу. Поэтому делим годовую ставку, а вернее ссылку на ячейку, в которой она содержится, на число 12, соответствующее количеству месяцев в году. Деление выполняем прямо в поле окна аргументов.

   В поле «Кпер» устанавливается срок кредитования. Он у нас равен 24 месяцам. Можно занести в поле число 24 вручную, но мы, как и в предыдущем случае, указываем ссылку на месторасположение данного показателя в исходной таблице.

   В поле «Пс» указывается первоначальная величина займа. Она равна 500000 рублей. Как и в предыдущих случаях, указываем ссылку на элемент листа, в котором содержится данный показатель.

   В поле «Бс» указывается величина займа, после полной его оплаты. Как помним, это значение практически всегда равно нулю. Устанавливаем в данном поле число «0». Хотя этот аргумент можно вообще опустить.

   В поле «Тип» указываем в начале или в конце месяца производится оплата. У нас, как и в большинстве случаев, она производится в конце месяца. Поэтому устанавливаем число «0». Как и в случае с предыдущим аргументом, в данное поле можно ничего не вводить, тогда программа по умолчанию будет считать, что в нем расположено значение равное нулю.

   После того, как все данные введены, жмем на кнопку «OK».



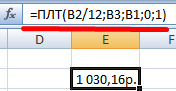
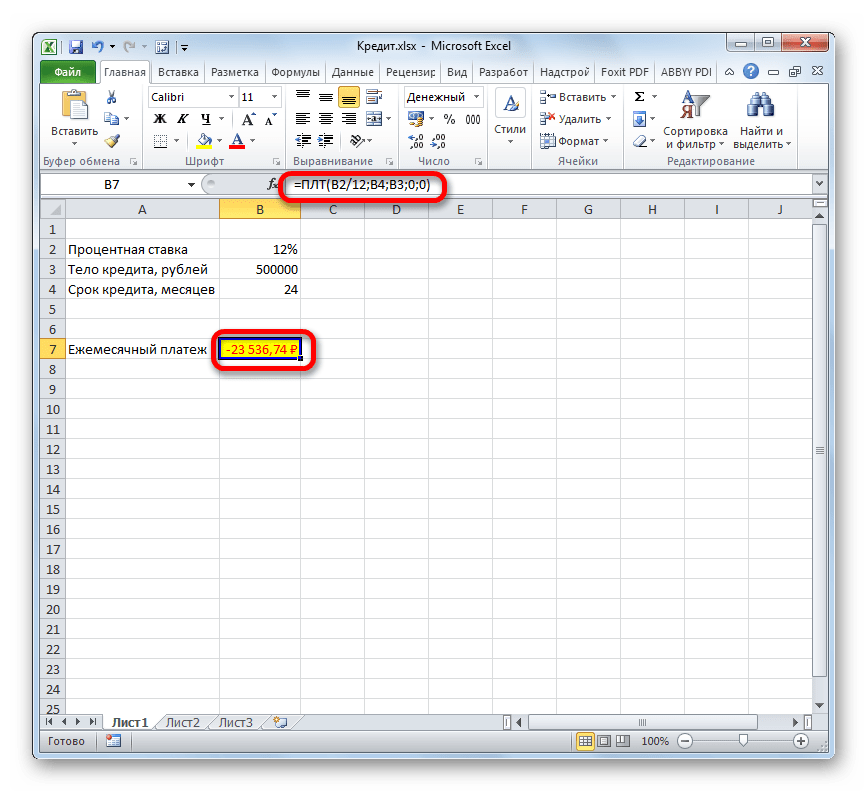
4. После этого в ячейку, которую мы выделили в первом пункте данного руководства, выводится результат вычисления. Как видим, величина ежемесячного общего платежа по займу составляет 23536,74 рубля. Пусть вас не смущает знак «-» перед данной суммой. Так Эксель указывает на то, что это расход денежных средств, то есть, убыток.



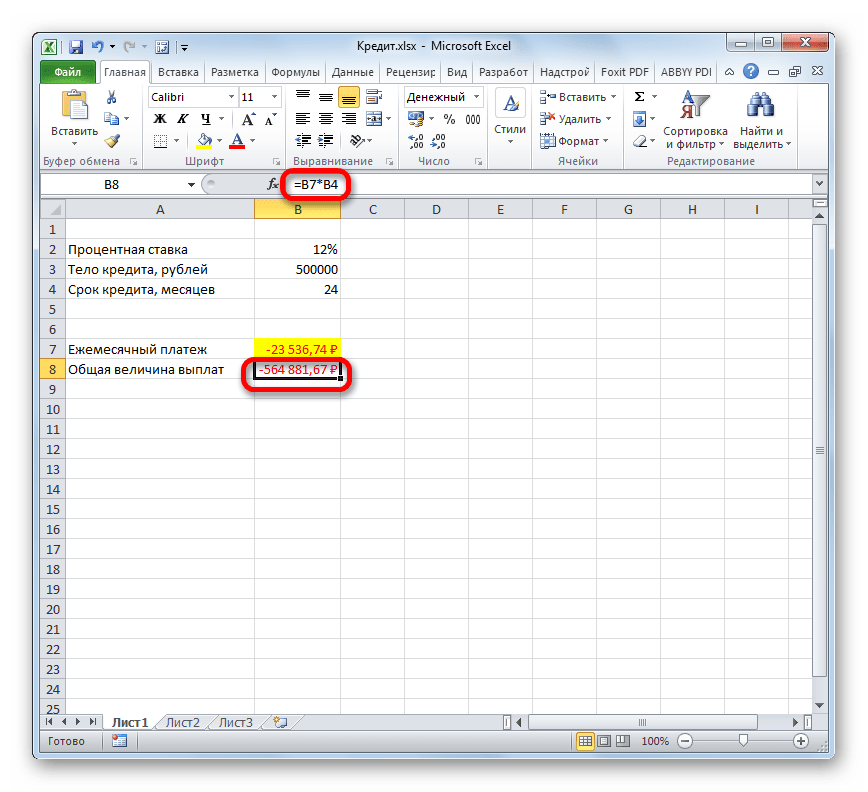
5. Для того, чтобы рассчитать общую сумму оплаты за весь срок кредитования с учетом погашения тела займа и ежемесячных процентов, достаточно перемножить величину ежемесячного платежа (23536,74 рубля) на количество месяцев (24 месяца). Как видим, общая сумма платежей за весь срок кредитования в нашем случае составила 564881,67 рубля.



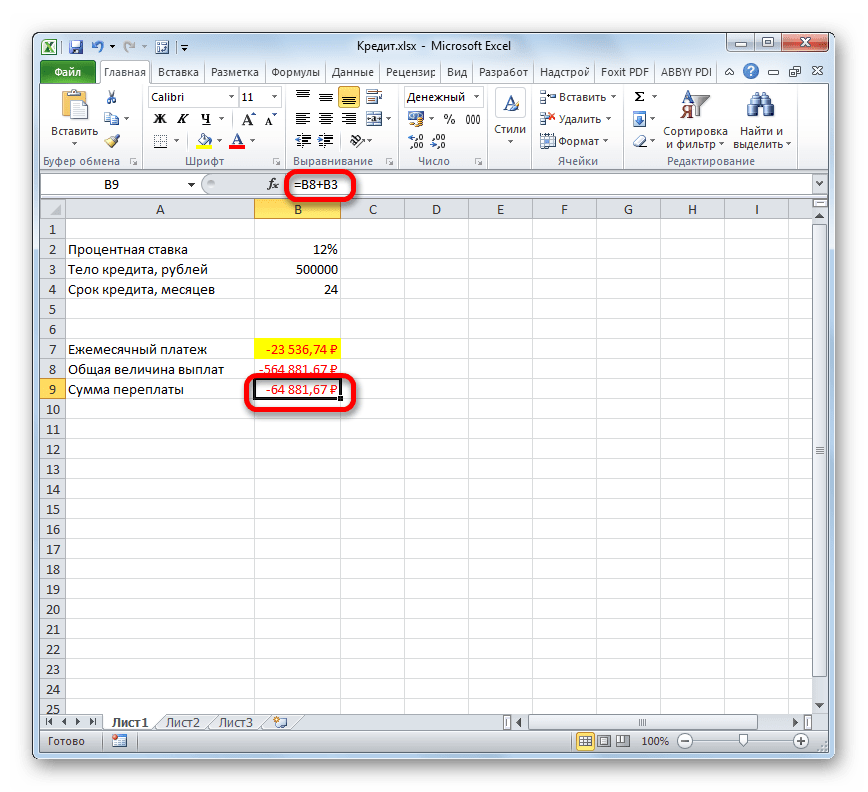
6. Теперь можно подсчитать сумму переплаты по кредиту. Для этого нужно отнять от общей величины выплат по кредиту, включая проценты и тело займа, начальную сумму, взятую в долг. Но мы помним, что первое из этих значений уже со знаком «-». Поэтому в конкретно нашем случае получается, что их нужно сложить. Как видим, общая сумма переплаты по кредиту за весь срок составила 64881,67 рубля.

Урок: Мастер функций в Эксель

Этап 2: детализация платежей

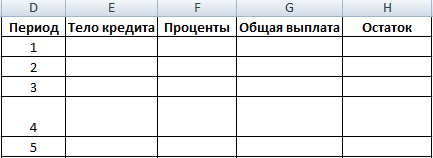
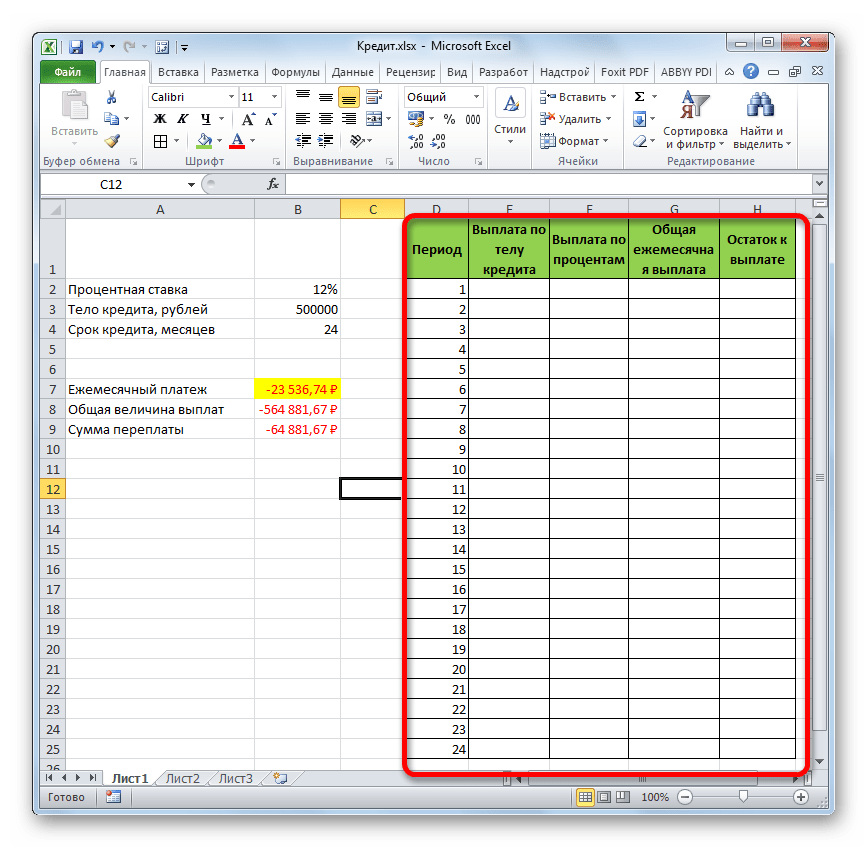
А теперь с помощью других операторов Эксель сделаем помесячную детализацию выплат, чтобы видеть, сколько в конкретном месяце мы платим по телу займа, а сколько составляет величина процентов. Для этих целей чертим в Экселе таблицу, которую будем заполнять данными. Строки этой таблицы будут отвечать соответствующему периоду, то есть, месяцу. Учитывая, что период кредитования у нас составляет 24 месяца, то и количество строк тоже будет соответствующим. В столбцах указана выплата тела займа, выплата процентов, общий ежемесячный платеж, который является суммой предыдущих двух колонок, а также оставшаяся сумма к выплате.

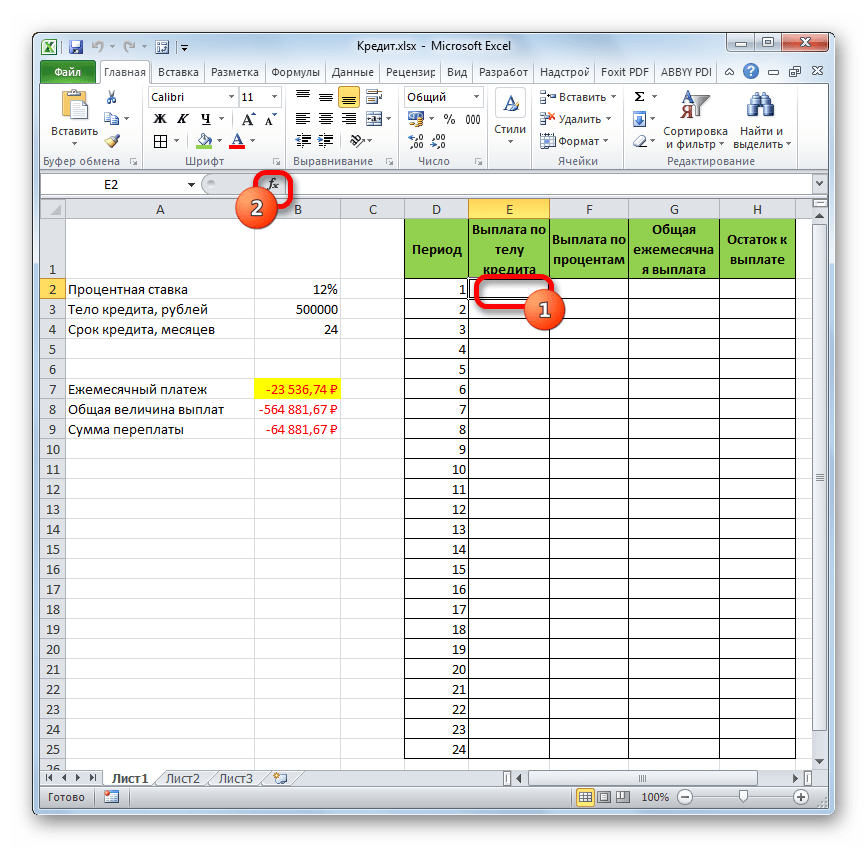
1. Для определения величины оплаты по телу займа используем функцию ОСПЛТ, которая как раз предназначена для этих целей. Устанавливаем курсор в ячейку, которая находится в строке «1» и в столбце «Выплата по телу кредита». Жмем на кнопку «Вставить функцию».



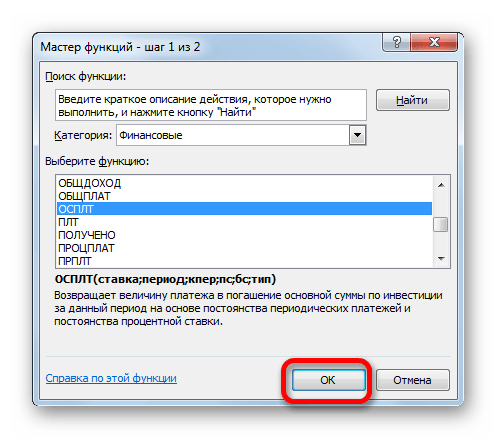
2. Переходим в Мастер функций. В категории «Финансовые» отмечаем наименование «ОСПЛТ» и жмем кнопку «OK».



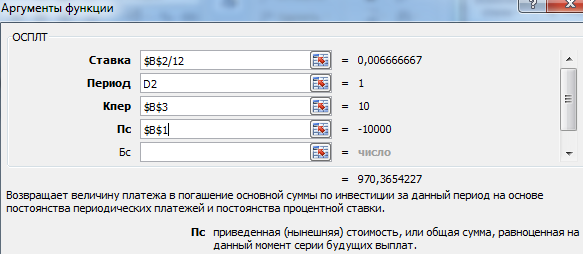
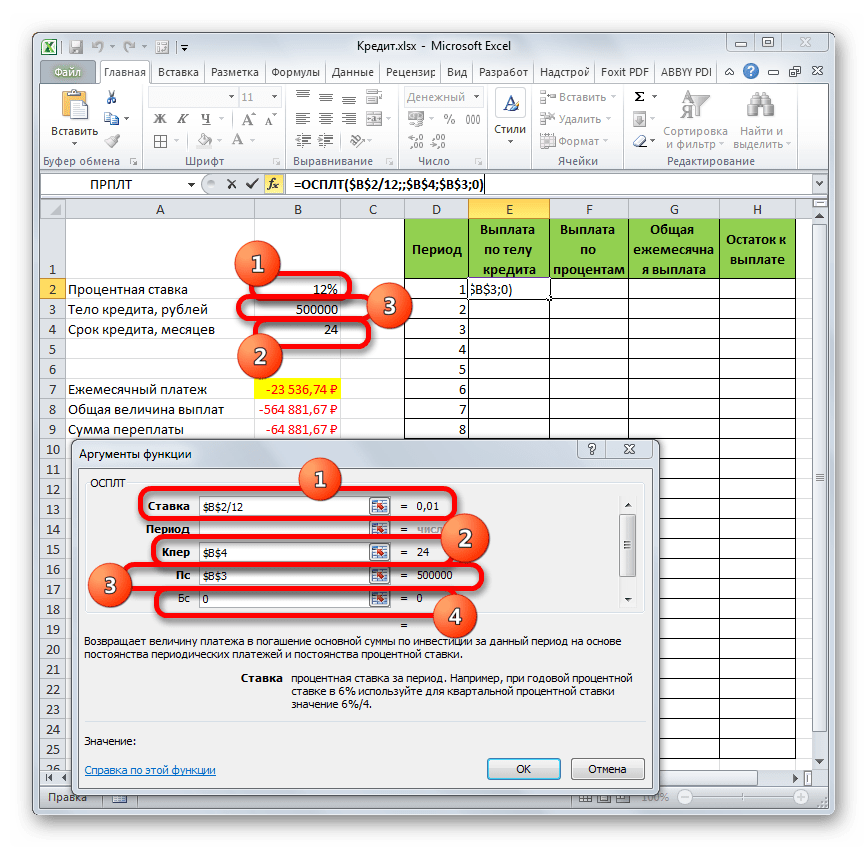
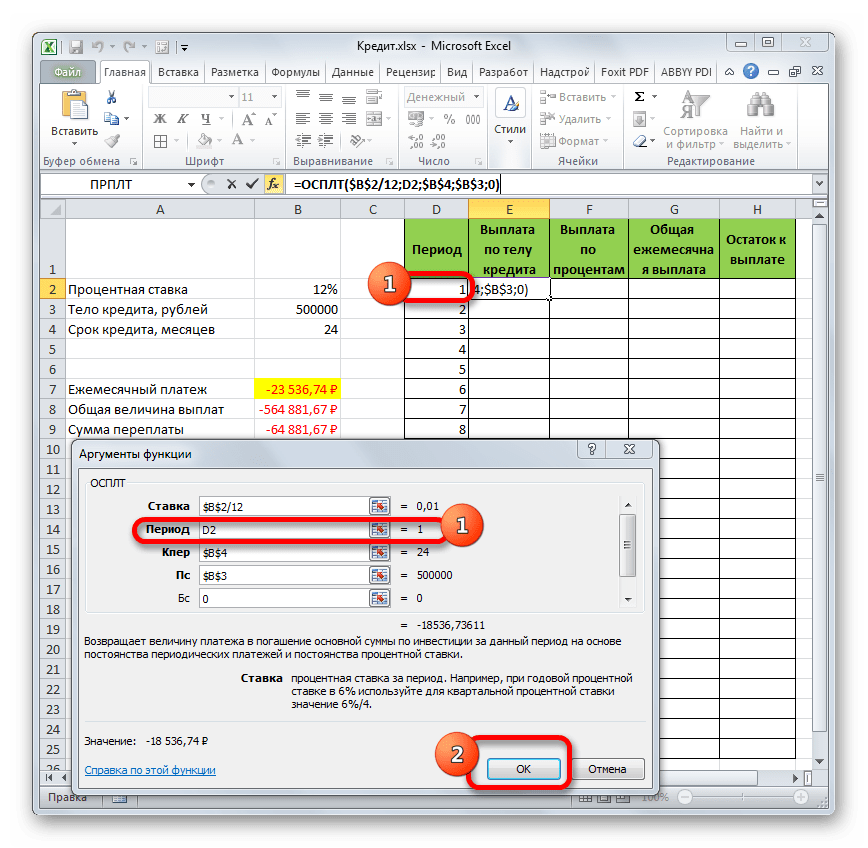
3. Запускается окно аргументов оператора ОСПЛТ. Он имеет следующий синтаксис:

   =ОСПЛТ(Ставка;Период;Кпер;Пс;Бс)

   Как видим, аргументы данной функции почти полностью совпадают с аргументами оператора ПЛТ, только вместо необязательного аргумента «Тип» добавлен обязательный аргумент «Период». Он указывает на номер периода выплаты, а в нашем конкретном случае на номер месяца.

   Заполняем уже знакомые нам поля окна аргументов функции ОСПЛТ теми самыми данными, что были использованы для функции ПЛТ. Только учитывая тот факт, что в будущем будет применяться копирование формулы посредством маркера заполнения, нужно сделать все ссылки в полях абсолютными, чтобы они не менялись. Для этого требуется поставить знак доллара перед каждым значением координат по вертикали и горизонтали. Но легче это сделать, просто выделив координаты и нажав на функциональную клавишу F4. Знак доллара будет расставлен в нужных местах автоматически. Также не забываем, что годовую ставку нужно разделить на 12.



4. Но у нас остается ещё один новый аргумент, которого не было у функции ПЛТ. Этот аргумент «Период». В соответствующее поле устанавливаем ссылку на первую ячейку столбца «Период». Данный элемент листа содержит в себе число «1», которое обозначает номер первого месяца кредитования. Но в отличие от предыдущих полей, в указанном поле мы оставляем ссылку относительной, а не делаем из неё абсолютную.

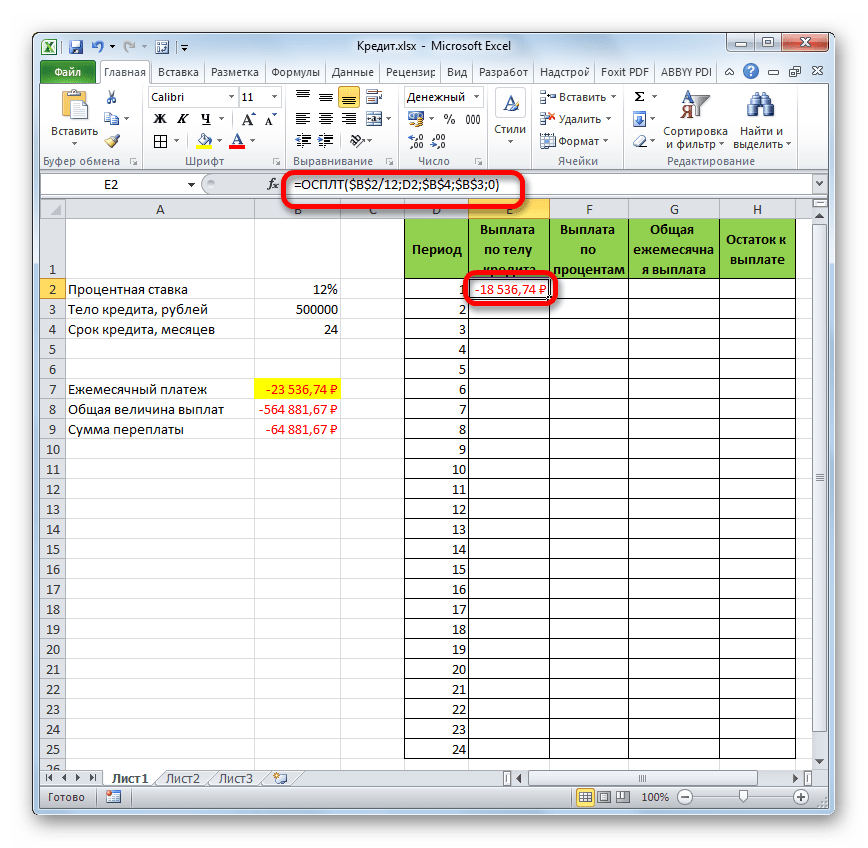
   После того, как все данные, о которых мы говорили выше, введены, жмем на кнопку «OK».



5. После этого в ячейке, которую мы ранее выделили, отобразится величина выплаты по телу займа за первый месяц. Она составит 18536,74 рубля.



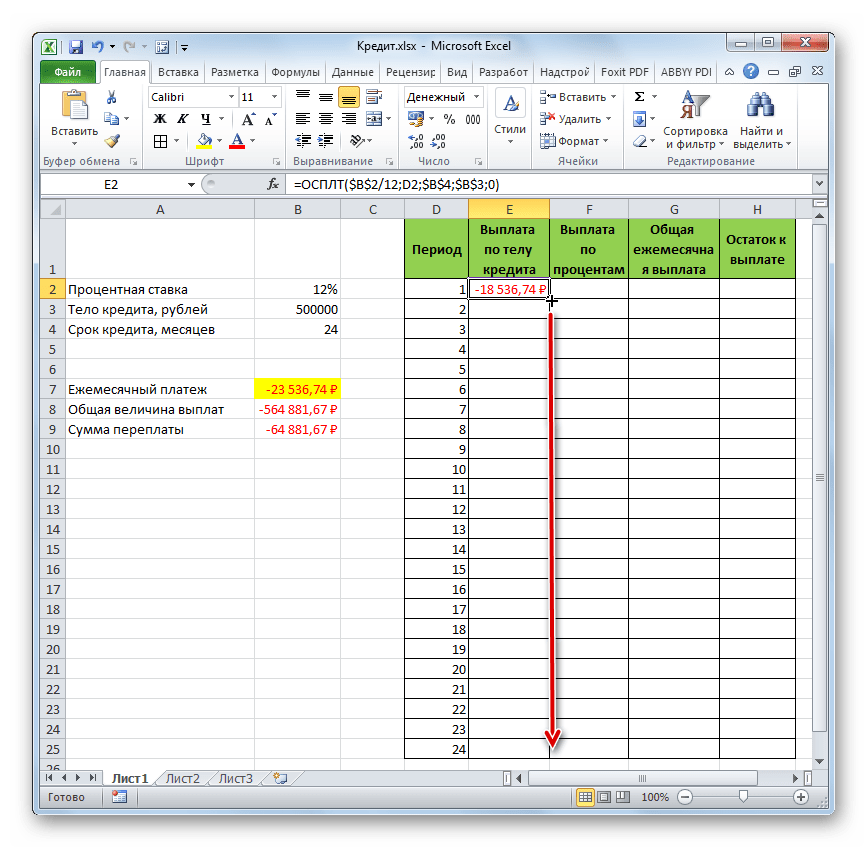
6. Затем, как уже говорилось выше, нам следует скопировать данную формулу на остальные ячейки столбца с помощью маркера заполнения. Для этого устанавливаем курсор в нижний правый угол ячейки, в которой содержится формула. Курсор преобразуется при этом в крестик, который называется маркером заполнения. Зажимаем левую кнопку мыши и тянем его вниз до конца таблицы.



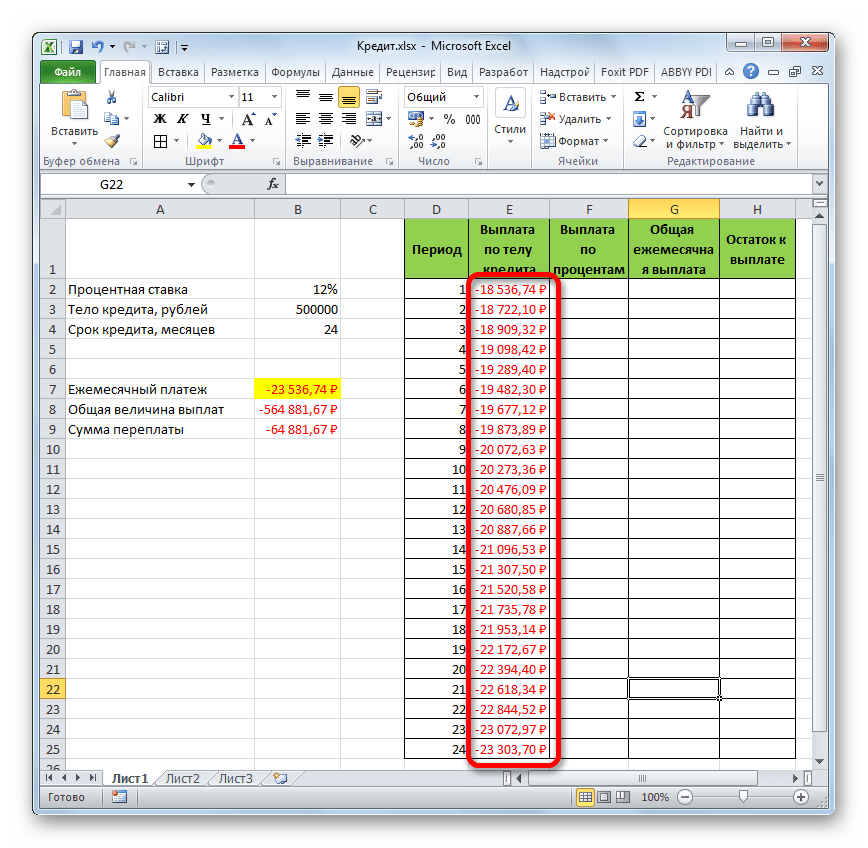
7. В итоге все ячейки столбца заполнены. Теперь мы имеем график выплаты тела займа помесячно. Как и говорилось уже выше, величина оплаты по данной статье с каждым новым периодом увеличивается.



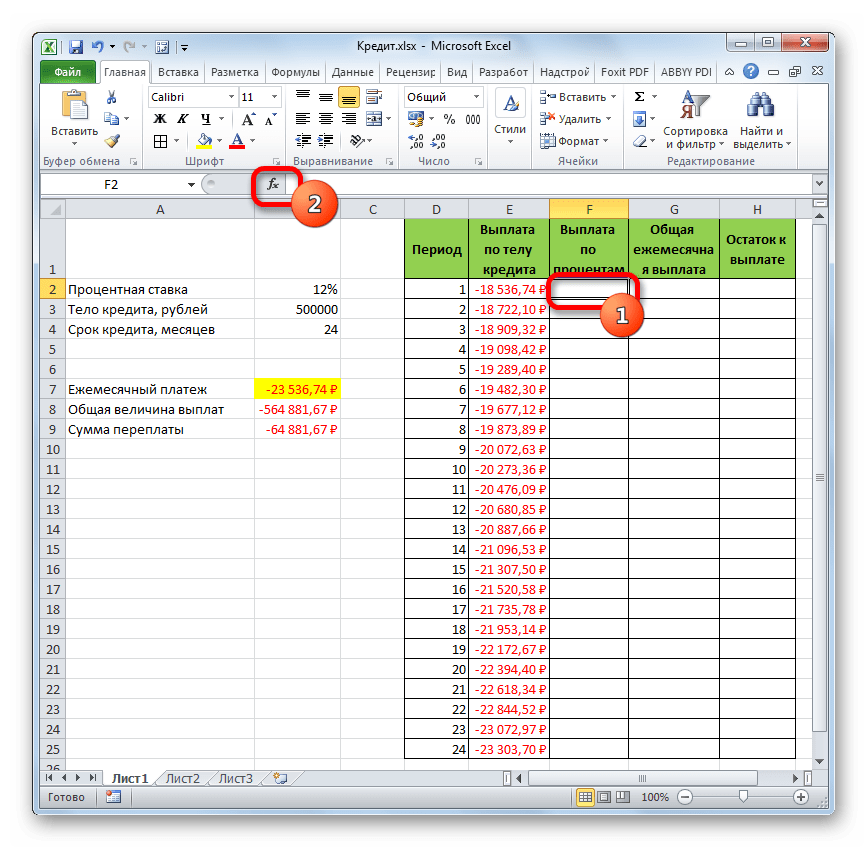
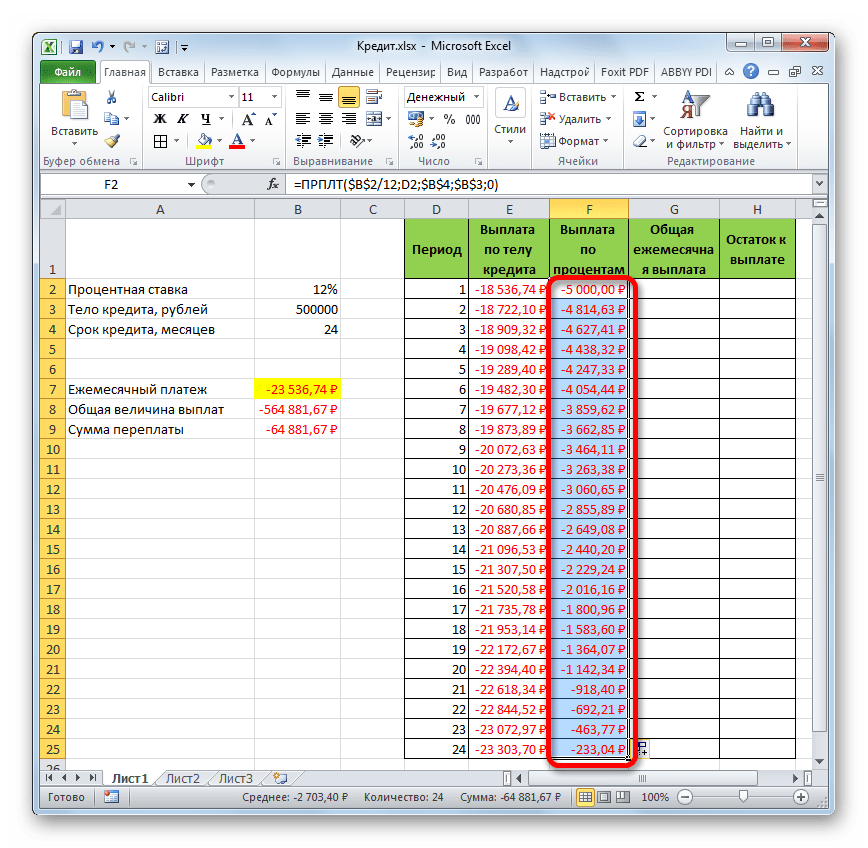
8. Теперь нам нужно сделать месячный расчет оплаты по процентам. Для этих целей будем использовать оператор ПРПЛТ. Выделяем первую пустую ячейку в столбце «Выплата по процентам». Жмем на кнопку «Вставить функцию».



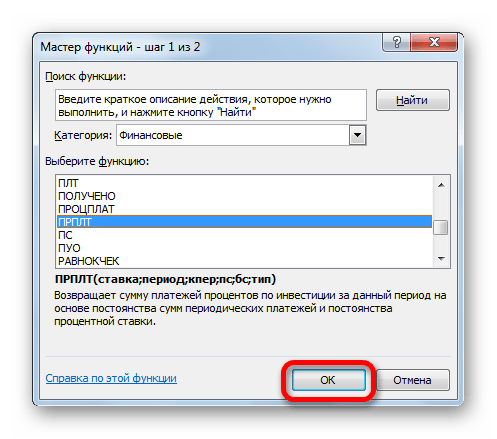
9. В запустившемся окне Мастера функций в категории «Финансовые» производим выделение наименования ПРПЛТ. Выполняем щелчок по кнопке «OK».



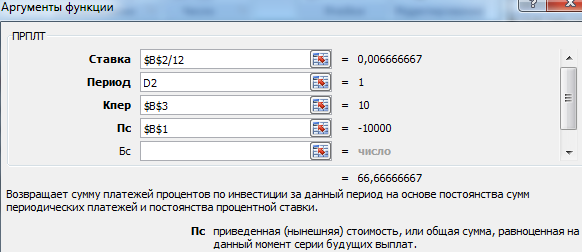
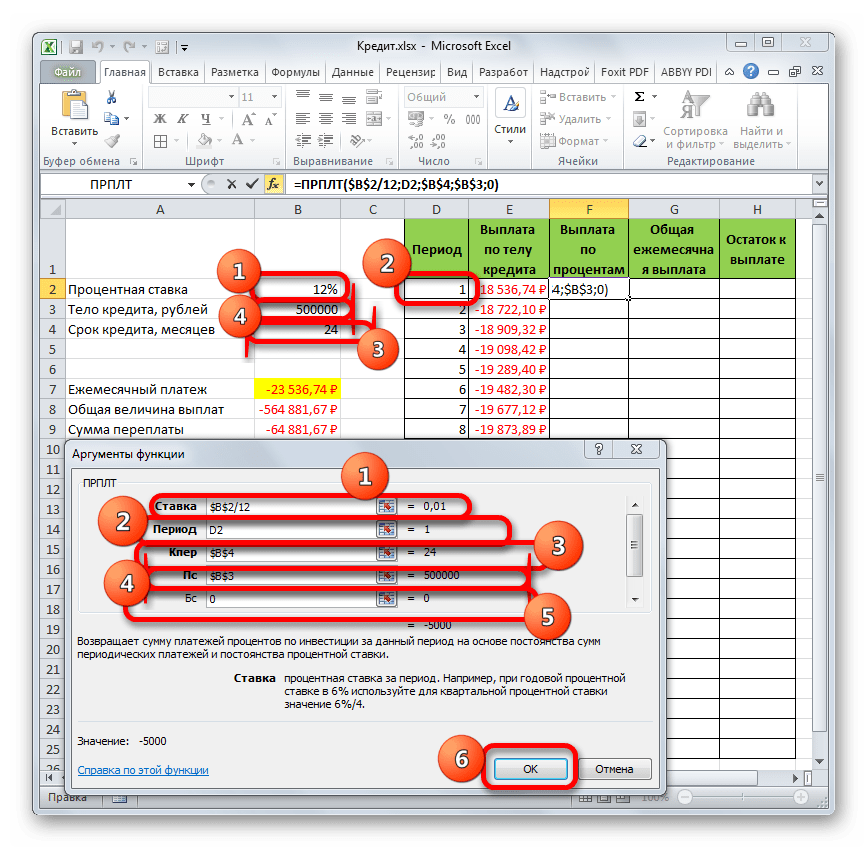
10. Происходит запуск окна аргументов функции ПРПЛТ. Её синтаксис выглядит следующим образом:

    =ПРПЛТ(Ставка;Период;Кпер;Пс;Бс)

    Как видим, аргументы данной функции абсолютно идентичны аналогичным элементам оператора ОСПЛТ. Поэтому просто заносим в окно те же данные, которые мы вводили в предыдущем окне аргументов. Не забываем при этом, что ссылка в поле «Период» должна быть относительной, а во всех других полях координаты нужно привести к абсолютному виду. После этого щелкаем по кнопке «OK».



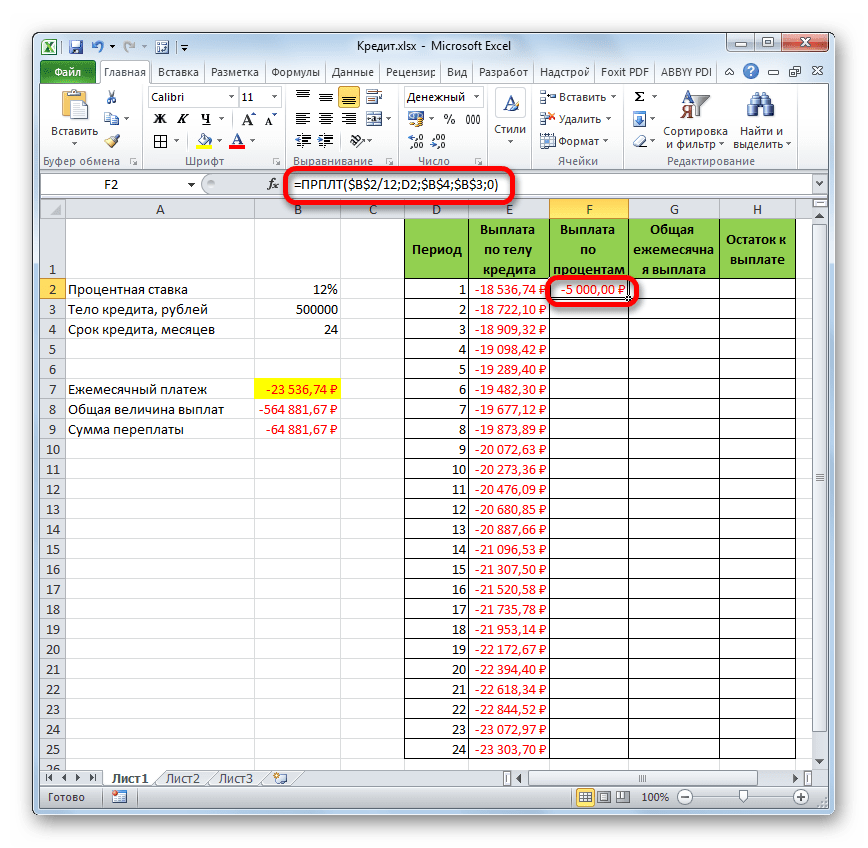
11. Затем результат расчета суммы оплаты по процентам за кредит за первый месяц выводится в соответствующую ячейку.



12. Применив маркер заполнения, производим копирование формулы в остальные элементы столбца, таким способом получив помесячный график оплат по процентам за заём. Как видим, как и было сказано ранее, из месяца в месяц величина данного вида платежа уменьшается.



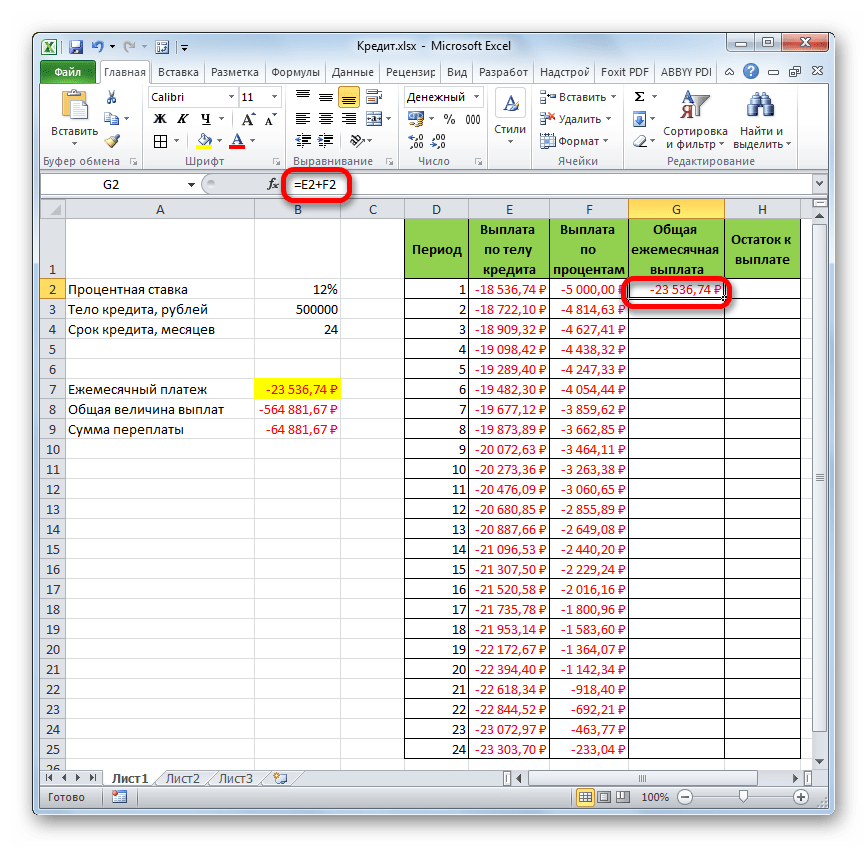
13. Теперь нам предстоит рассчитать общий ежемесячный платеж. Для этого вычисления не следует прибегать к какому-либо оператору, так как можно воспользоваться простой арифметической формулой. Складываем содержимое ячеек первого месяца столбцов «Выплата по телу кредита» и «Выплата по процентам». Для этого устанавливаем знак «=» в первую пустую ячейку столбца «Общая ежемесячная выплата». Затем кликаем по двум вышеуказанным элементам, установив между ними знак «+». Жмем на клавишу Enter.



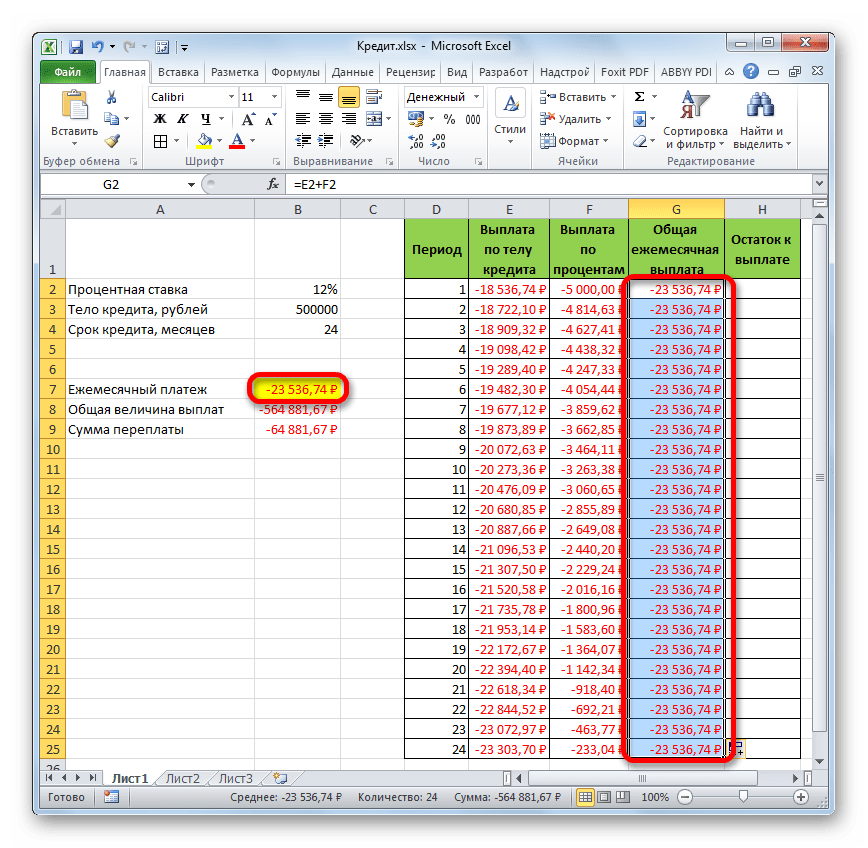
14. Далее с помощью маркера заполнения, как и в предыдущих случаях, заполняем колонку данными. Как видим, на протяжении всего действия договора сумма общего ежемесячного платежа, включающего платеж по телу займа и оплату процентов, составит 23536,74 рубля. Собственно этот показатель мы уже рассчитывали ранее при помощи ПЛТ. Но в данном случае это представлено более наглядно, именно как сумма оплаты по телу займа и процентам.



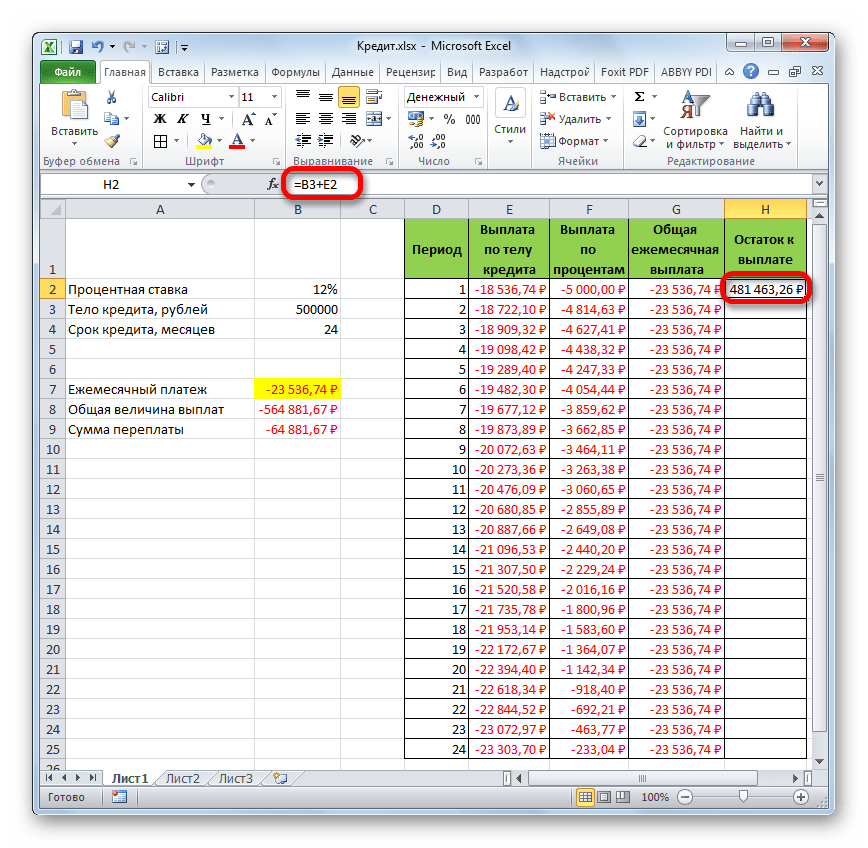
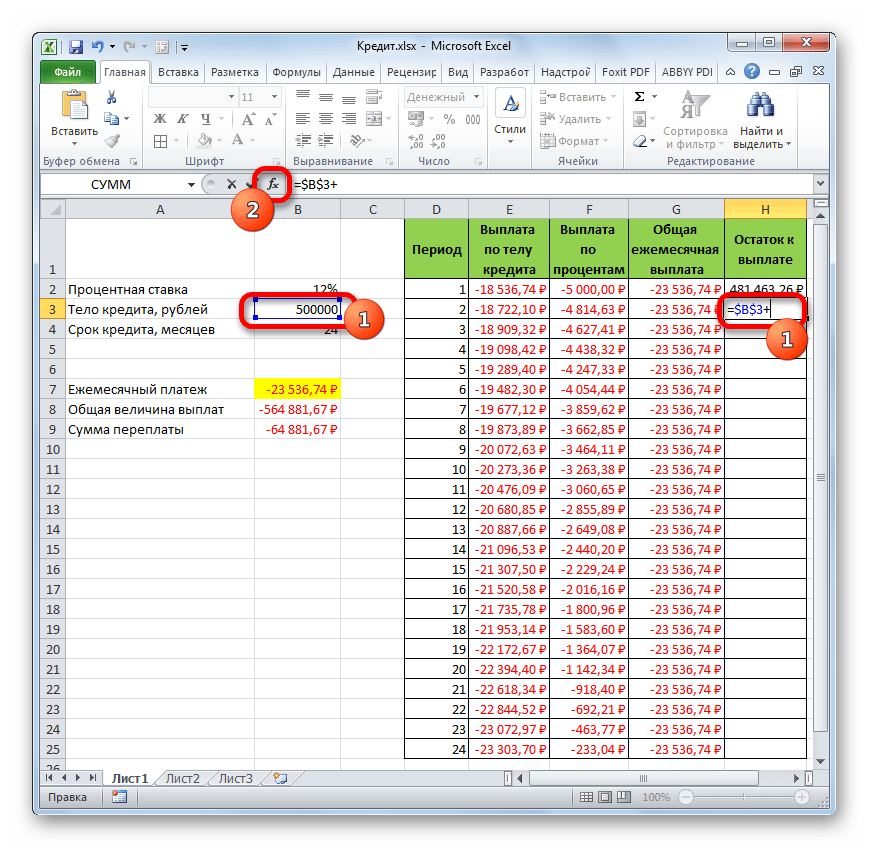
15. Теперь нужно добавить данные в столбец, где будет ежемесячно отображаться остаток суммы по кредиту, который ещё требуется заплатить. В первой ячейке столбца «Остаток к выплате» расчет будет самый простой. Нам нужно отнять от первоначальной величины займа, которая указана в таблице с первичными данными, платеж по телу кредита за первый месяц в расчетной таблице. Но, учитывая тот факт, что одно из чисел у нас уже идет со знаком «-», то их следует не отнять, а сложить. Делаем это и жмем на кнопку Enter.



16. А вот вычисление остатка к выплате после второго и последующих месяцев будет несколько сложнее. Для этого нам нужно отнять от тела кредита на начало кредитования общую сумму платежей по телу займа за предыдущий период. Устанавливаем знак «=» во второй ячейке столбца «Остаток к выплате». Далее указываем ссылку на ячейку, в которой содержится первоначальная сумма кредита. Делаем её абсолютной, выделив и нажав на клавишу F4. Затем ставим знак «+», так как второе значение у нас и так будет отрицательным. После этого кликаем по кнопке «Вставить функцию».



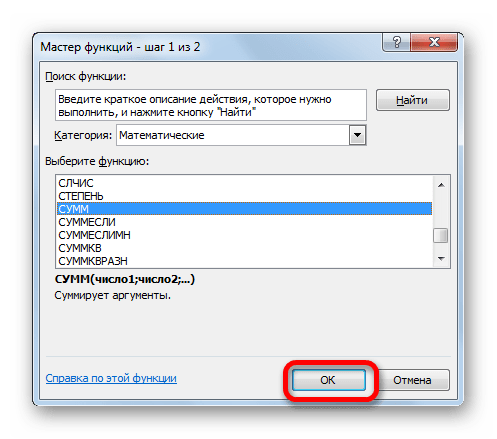
17. Запускается Мастер функций, в котором нужно переместиться в категорию «Математические». Там выделяем надпись «СУММ» и жмем на кнопку «OK».



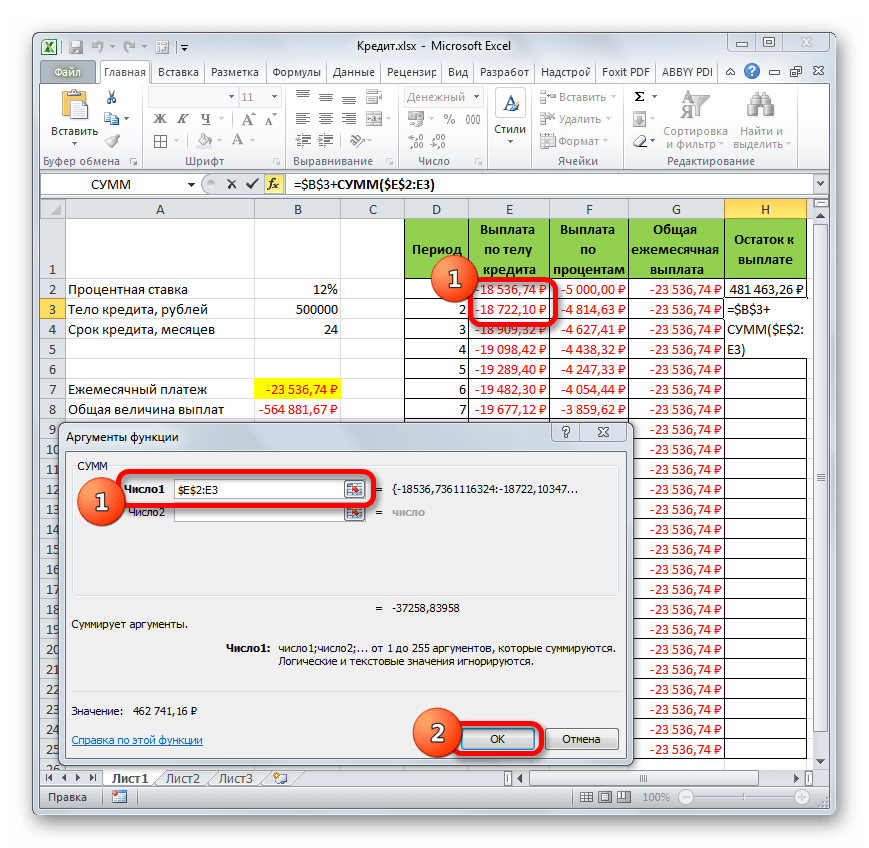
18. Запускается окно аргументов функции СУММ. Указанный оператор служит для того, чтобы суммировать данные в ячейках, что нам и нужно выполнить в столбце «Выплата по телу кредита». Он имеет следующий синтаксис:

    =СУММ(число1;число2;…)

    В качестве аргументов выступают ссылки на ячейки, в которых содержатся числа. Мы устанавливаем курсор в поле «Число1». Затем зажимаем левую кнопку мыши и выделяем на листе первые две ячейки столбца «Выплата по телу кредита». В поле, как видим, отобразилась ссылка на диапазон. Она состоит из двух частей, разделенных двоеточием: ссылки на первую ячейку диапазона и на последнюю. Для того, чтобы в будущем иметь возможность скопировать указанную формулу посредством маркера заполнения, делаем первую часть ссылки на диапазон абсолютной. Выделяем её и жмем на функциональную клавишу F4. Вторую часть ссылки так и оставляем относительной. Теперь при использовании маркера заполнения первая ячейка диапазона будет закреплена, а последняя будет растягиваться по мере продвижения вниз. Это нам и нужно для выполнения поставленных целей. Далее жмем на кнопку «OK».



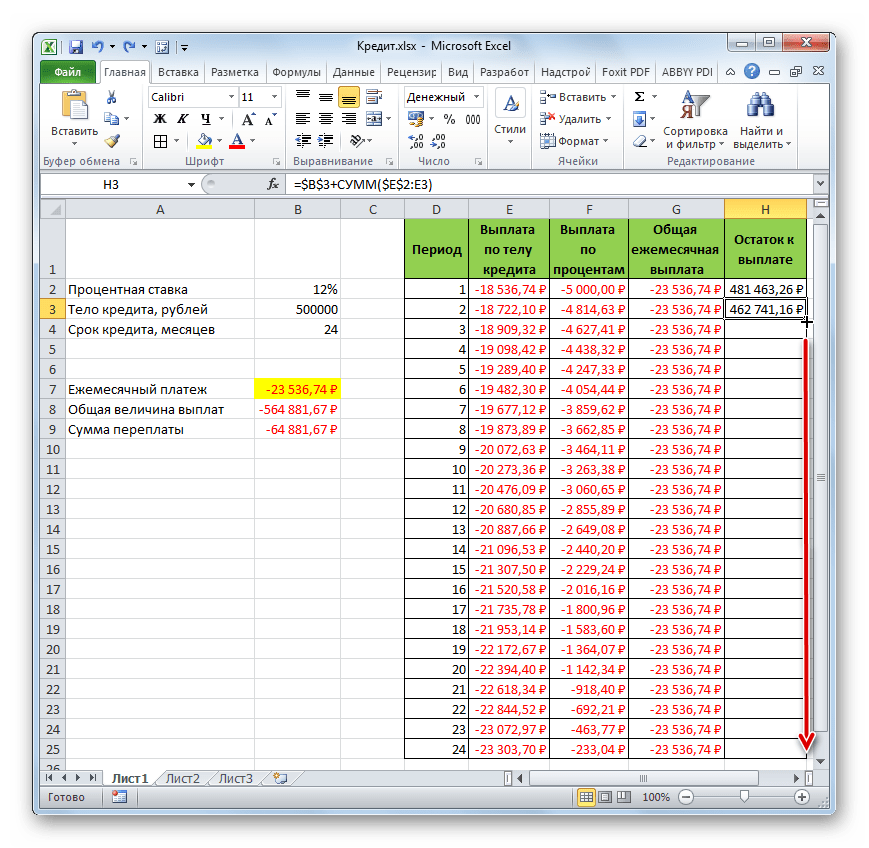
19. Итак, результат остатка кредитной задолженности после второго месяца выводится в ячейку. Теперь, начиная с данной ячейки, производим копирование формулы в пустые элементы столбца с помощью маркера заполнения.



20. Помесячный расчет остатков к оплате по кредиту сделан за весь кредитный период. Как и положено, на конец срока эта сумма равна нулю.

Таким образом, мы произвели не просто расчет оплаты по кредиту, а организовали своеобразный кредитный калькулятор. Который будет действовать по аннуитетной схеме. Если в исходной таблице мы, например, поменяем величину займа и годовой процентной ставки, то в итоговой таблице произойдет автоматический пересчет данных. Поэтому её можно использовать не только один раз для конкретного случая, а применять в различных ситуациях для расчета кредитных вариантов по аннуитетной схеме.

Урок: Финансовые функции в Excel

Как видим, при помощи программы Excel в домашних условиях можно без проблем рассчитать общий ежемесячный кредитный платеж по аннуитетной схеме, используя для этих целей оператор ПЛТ. Кроме того, при помощи функций ОСПЛТ и ПРПЛТ можно произвести расчет величины платежей по телу кредита и по процентам за указанный период. Применяя весь этот багаж функций вместе, существует возможность создать мощный кредитный калькулятор, который можно будет использовать не один раз для вычисления аннуитетного платежа.