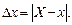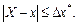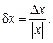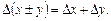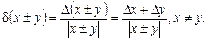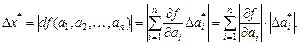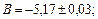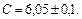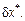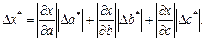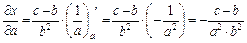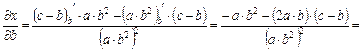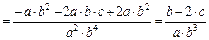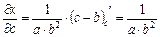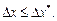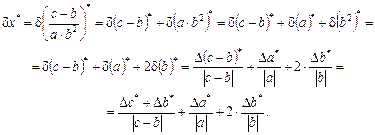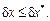ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ
Пусть 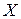
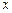
Абсолютная погрешность приближенного числа равна модулю разности между его точным и приближенным значениями:
Довольно часто точное значение 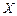
Число 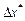
Основной характеристикой точности числа является относительная погрешность.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
1.
2.
3.
4.
Общая формула для оценки предельной абсолютной погрешности функции нескольких переменных 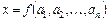
где 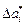
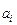
Пример: Известно, что 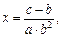
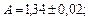
Найти 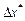
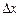
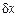
Для оценки предельной абсолютной погрешности воспользуемся формулой:
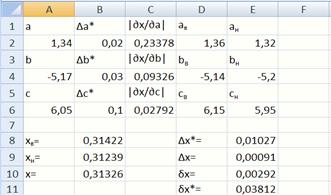
Рис. 1. Вид экрана для вычисления абсолютной и относительной погрешностей
Исходные данные вводятся в блок А1:B6 (рис. 1). В ячейки С1:С6вводятся формулы для вычисления частных производных искомой функции. В ячейку Е8записывается формула 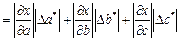
В ячейках D1:E6рассчитываются верхние и нижние оценки значений переменных по формулам 
В ячейках B8:B10вычисляются верхняя и нижняя оценки значений функции и само значение функции 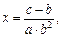
В ячейку Е9записывается формула для вычисления абсолютной погрешности 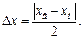
В ячейку Е10записывается формула для вычисления относительной погрешности
Предельную относительную погрешность заданной функции 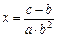
Полученную формулу записывают в ячейку Е11. Найденная относительная погрешность не должна превышать значение предельной относительной погрешности, т.е.
Задания для самостоятельного выполнения.
Из таблицы 1 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Вычислить частные производные, верхнюю и нижнюю оценки значений функции и само значение функции, изменить формулу вычисления предельной относительной погрешности. Все остальные ячейки пересчитаются автоматически.
Контрольные вопросы
1. Как записать основные математические функции в Excel.
2. Сформулируйте определение абсолютной и относительной погрешностей.
3. Запишите формулы для вычисления предельной абсолютной и предельной относительной погрешностей.
4. Основные правила вычисления абсолютной и относительной погрешностей.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8833 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
С использованием встроенных функций Excel расчет доверительного интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа — уровень значимости используемый для вычисления уровня надежности.
( 


станд_откл — стандартное отклонение, предполагается известным;
размер — размер выборки.
Задание: Обработать заданный набор экспериментальных данных методом Стьюдента, построить экспериментальные кривые методом наименьших квадратов.
Предположим, в ходе эксперимента по измерению электросопротивления были получены следующие данные:
Используя для определения сопротивления закон Ома 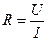
| Используемуе формулы |
 |
| Результат расчета |
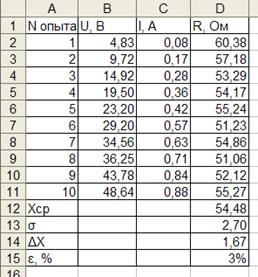 |
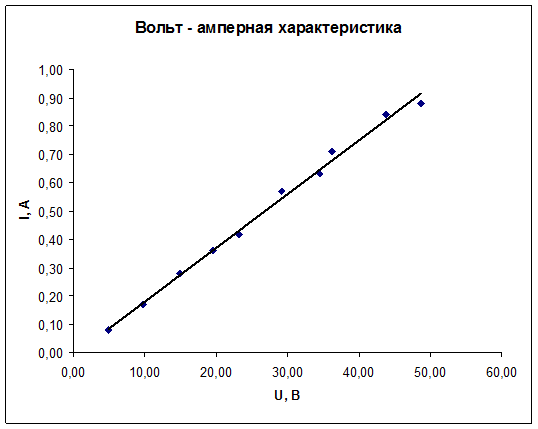
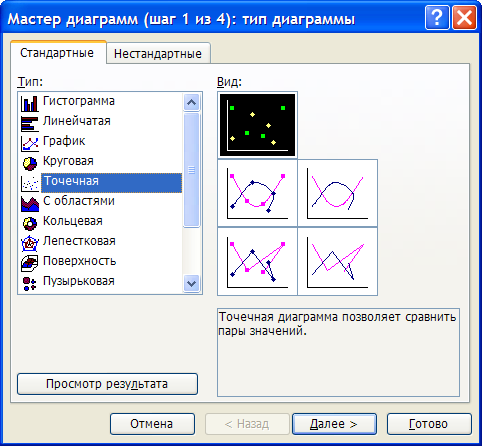
Для построения графика используем мастер диаграмм.
Полученные экспериментальные данные следует аппроксимировать. Для выполнения этой процедуры в Excel предусмотрен мастер, добавляющий линию тренда, производящий аппроксимацию и сглаживание.
В меню «Диаграмма» выберите пункт «Добавить линию тренда…».
В результате, должен получиться следующий график.
Задание 1.
Просчитать погрешность измерений и построить график ее распределения.
| Задание 1 | Задание 2 | Задание 3 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 4 | Задание 5 | Задание 6 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
| Задание 7 | Задание 8 | Задание 9 |
| № опыта | № опыта | № опыта |
| 10,3 | 13,55 | 12,65 |
| 10,277 | 13,527 | 12,627 |
| 10,325 | 13,575 | 12,675 |
| 10,285 | 13,535 | 12,635 |
| 10,297 | 13,547 | 12,647 |
| 10,31 | 13,56 | 12,66 |
| 10,35 | 13,6 | 12,7 |
| 10,35 | 13,6 | 12,7 |
| 10,29 | 13,54 | 12,64 |
| 10,38 | 13,63 | 12,73 |
| Задание 10 | Задание 11 | Задание 12 |
| № опыта | №опыта | № опыта |
| 26,65 | 24,65 | 18,3 |
| 26,627 | 24,627 | 18,277 |
| 26,675 | 24,675 | 18,325 |
| 26,635 | 24,635 | 18,285 |
| 26,647 | 24,647 | 18,297 |
| 26,66 | 24,66 | 18,31 |
| 26,7 | 24,7 | 18,35 |
| 26,7 | 24,7 | 18,35 |
| 26,64 | 24,64 | 18,29 |
| 26,73 | 24,73 | 18,38 |
| Задание 13 | Задание 14 | Задание 15 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 16 | Задание 17 | Задание 18 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
Задание 2.
Определить является ли 3-е измерение промахом.
Доброго дня, друзья.
Так как в после прошлого поста несколько человек заинтересовались моей таблицей, решил поделиться с вами еще одной своей таблицей.
Есть у нас лаборатория, и мы постоянно сверяем результаты наших исследований с результатами контрагентов. По нормативным документам нужно придерживаться определенных пределов расхождений в результатах.
Чтобы постоянно не открывать таблицу с значениями пределов воспроизведения, селал себе такую таблчку.
Чтобы было понятно, Результаты испытаний записываются в виде X±Δ
где X – результат анализа;
±Δ – погрешность результатов анализа, в нашем случае воспроизводимость..
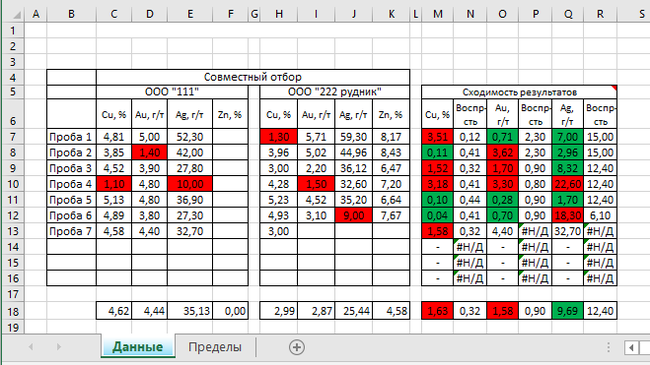
То есть для первого испытания на медь для Пробы 1 результат у нас (H7) 1,30±0,12, а у контрагентов (ячейка C7) 4,81±0,12. А разница между результатами 4,81-1,30=3,51
Мы не входим в предел воспроизведения, ячейка M7 окрасилась в красный и сразу видим, что и один из нас хочет другого немного обмануть)) Если бы ячейка стала зеленой, то все норм.
Вот чтобы такие расчеты постоянно не делать, была создана данная таблица.
Данные вычисления могут быть полезны чтобы узнать и в других областях, где нужно узнать, вписываемся мы в пределы или нет.
Вот так выглядит рабочая таблица на странице Данные:
Левая табличка разделена на две чати — наши данные при отгрузке продукта и данные контрагента при приемке продкта. В правой табличке, соответственно производятся все вычисления и ячейка окрашивается в определенный цвет при выполнении и невыполнении условий.
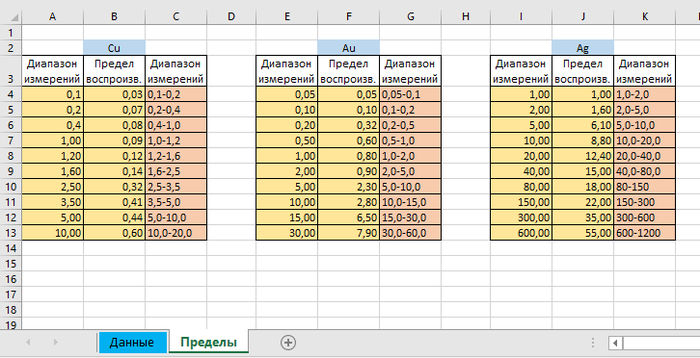
Также имеется вторая табличка на странице Пределы, где расписаны пределы по диапазонам:
Вычисления производятся по желтым ячейкам, а розовые для информации. Первый и третий столбци по сути одно и то же.
Итак погнали. Что тут творится вообще ))
Буду объяснять для пробы 1, результаты Cu, ячейки M7 и N7. Остальное аналогично
Сперва вычислим раницу между нашими результатами испытаний. Нам нужны только абсолютные значения, так как разность может быть отрицательной. В M7 ввоим формулу:
В N7 вводим следующую формулу:
Тут остановимся, разберем формулу по частям:
Берем значение из ячейки H7 (это наш результат) и ищем на странице Пределы в массиве для Cu пределы значений, куда входит наш результат. Находим, что походит диапазон 1,2-1,6
Ищем номер строки значениея из ячейки H7 в таблице на листе Пределы. В предыдущей формуле мы нашли, что значение относится к пределам 1,2-1,6 и теперь легком можем найти номер строки, где он находится.
Так, номер строки нашли, и нам надо узнать значение погрешности или воспроизведения. Тут нам поможет функция ИНДЕКС, который возвращает значение на пересечении указанных номеров строки и столбца в массиве.Номер строки мы узнали из предыдущей формулы, номер столбца, где нужно искать результат укажем вручную:
Тут Пределы!$B$4:$C$13 это массив где мы делаем поиск
ПОИСКПОЗ(ВПР(Данные!H7;Пределы!$A$4:$C$13;3;ИСТИНА);Пределы!$C$4:$C$13;0) — номер строки.
И единичка в конце — номер столбца.
Теперь мы узнали, что наш результат должен быть 1,30±0,12
А разница результатов двух предприятий 3,51. Это означает, что мы не входим в предел воспроизведения.
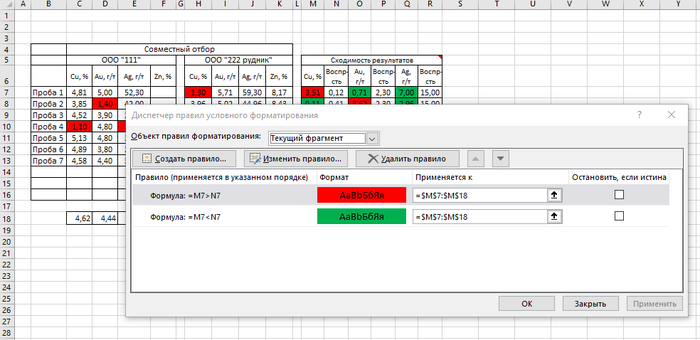
Чтобы визуально сразу увидеть это, окрасим эту ячейку в красный. Делается это через меню Условное форматирование
Выбираем в меню Условное форматирование — Правила выделения ячеек — Больше (Меньше) и задаем форматирование — окрасить ячейку в красный или зеленый цвет.
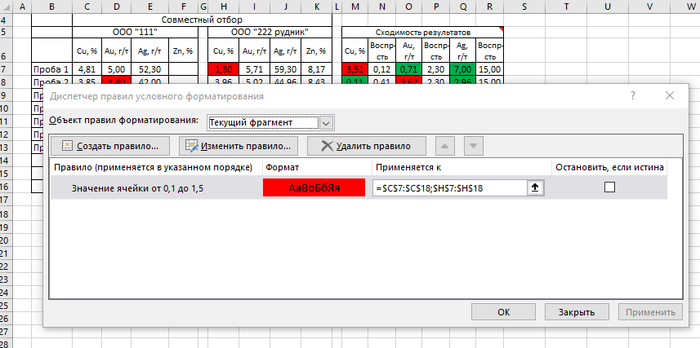
Также у нас есть ограничение в поставке продукта. Качество должно быть не менее определенного значения. Чтобы тоже сразу наглядно это увидеть, я через Условное форматирование выбрал пункт Между.. и задал нужные значения
Если отгрузим товар с качеством по меди меньше 1,5%, то ячейка окрашивается в красный цвет.
Спасибо что дочитали, надеюсь кому-нибудь пригодится данная таблица или формулы.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Mean absolute error is the measure of error between the observed and the expected values in a given data set.
Where,
- O stands for Observed values,
- E stands for Expected values,
- n stands for total no. of observations.
Now let us understand it with the help of an example.
Example:
Follow the below steps to calculate MAE in Excel:
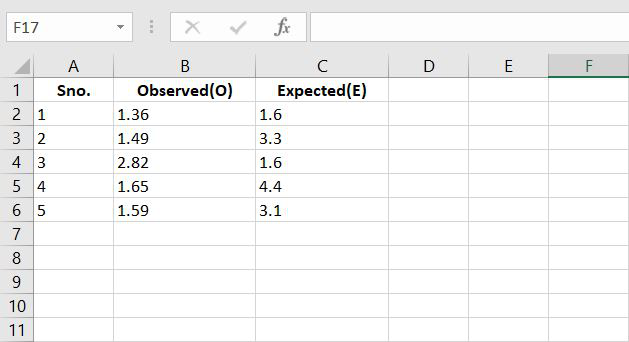
Step 1: Suppose we have the following data:
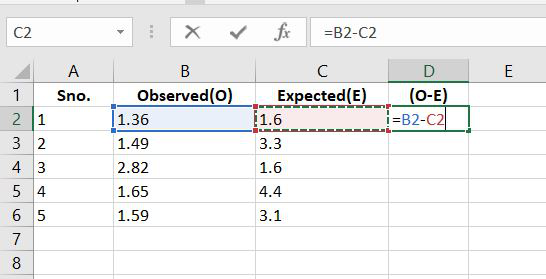
Step 2: According to formulae, let’s calculate the difference between the observed and the expected values.
Step 3: Now let’s calculate the absolute values.
Step 4: Now we know from the data that n= no of observations and in this the value of n=5. And also the let’s calculate the total sum of |O-E|.
Step 5: Now we have the value of Sum of |O-E| and the value of n. Now according to formulae, the Mean Absolute Error is calculated as:
Step 6: So the value of MAE is:
Like Article
Save Article
С использованием встроенных функций Excel расчет доверительного интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа — уровень значимости используемый для вычисления уровня надежности.
( , т.е. означает надежности );
станд_откл — стандартное отклонение, предполагается известным;
размер — размер выборки.
Задание: Обработать заданный набор экспериментальных данных методом Стьюдента, построить экспериментальные кривые методом наименьших квадратов.
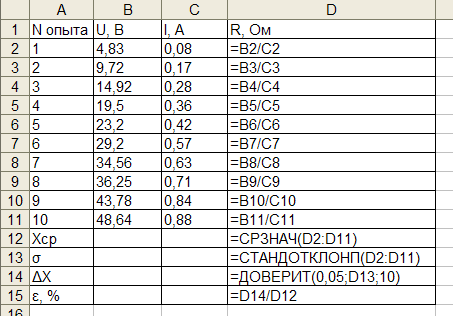
Предположим, в ходе эксперимента по измерению электросопротивления были получены следующие данные:
Используя для определения сопротивления закон Ома произведем обработку данной серии экспериментальных данных.
| Используемуе формулы |
 |
| Результат расчета |
 |
Для построения графика используем мастер диаграмм.
Полученные экспериментальные данные следует аппроксимировать. Для выполнения этой процедуры в Excel предусмотрен мастер, добавляющий линию тренда, производящий аппроксимацию и сглаживание.
В меню «Диаграмма» выберите пункт «Добавить линию тренда…».
В результате, должен получиться следующий график.
Задание 1.
Просчитать погрешность измерений и построить график ее распределения.
| Задание 1 | Задание 2 | Задание 3 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 4 | Задание 5 | Задание 6 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
| Задание 7 | Задание 8 | Задание 9 |
| № опыта | № опыта | № опыта |
| 10,3 | 13,55 | 12,65 |
| 10,277 | 13,527 | 12,627 |
| 10,325 | 13,575 | 12,675 |
| 10,285 | 13,535 | 12,635 |
| 10,297 | 13,547 | 12,647 |
| 10,31 | 13,56 | 12,66 |
| 10,35 | 13,6 | 12,7 |
| 10,35 | 13,6 | 12,7 |
| 10,29 | 13,54 | 12,64 |
| 10,38 | 13,63 | 12,73 |
| Задание 10 | Задание 11 | Задание 12 |
| № опыта | №опыта | № опыта |
| 26,65 | 24,65 | 18,3 |
| 26,627 | 24,627 | 18,277 |
| 26,675 | 24,675 | 18,325 |
| 26,635 | 24,635 | 18,285 |
| 26,647 | 24,647 | 18,297 |
| 26,66 | 24,66 | 18,31 |
| 26,7 | 24,7 | 18,35 |
| 26,7 | 24,7 | 18,35 |
| 26,64 | 24,64 | 18,29 |
| 26,73 | 24,73 | 18,38 |
| Задание 13 | Задание 14 | Задание 15 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 16 | Задание 17 | Задание 18 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
Задание 2.
Определить является ли 3-е измерение промахом.
Формула погрешности
- Формула погрешности
Формула погрешности (оглавление)
- Формула погрешности
- Примеры формулы допустимой погрешности (с шаблоном Excel)
- Калькулятор формулы ошибки поля
Формула погрешности
В статистике мы рассчитываем доверительный интервал, чтобы увидеть, куда упадет значение данных выборочной статистики. Диапазон значений, которые находятся ниже и выше выборочной статистики в доверительном интервале, называется границей ошибки. Другими словами, это в основном степень ошибки в статистике выборки. Чем выше погрешность, тем меньше будет достоверность результатов, поскольку степень отклонения в этих результатах очень высока. Как следует из названия, погрешность — это диапазон значений выше и ниже фактических результатов. Например, если мы получаем ответ в опросе, в котором 70% людей ответили «хорошо», а допустимая погрешность составляет 5%, это означает, что в целом от 65% до 75% населения считают, что ответ «хороший»,
Margin of Error = Z * S / √n
- Z — Z счет
- S — стандартное отклонение населения
- n — Размер выборки
Другая формула для расчета погрешности:
Margin of Error = Z * √((p * (1 – p)) / n)
- p — доля образца (доля образца, которая является успешной)
Теперь, чтобы найти желаемую оценку z, вам нужно знать доверительный интервал выборки, потому что оценка Z зависит от этого. Ниже приведена таблица, чтобы увидеть отношение доверительного интервала и z балла:
| Доверительный интервал | Z — Оценка |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Как только вы знаете доверительный интервал, вы можете использовать соответствующее значение z и рассчитать предел погрешности оттуда.
Примеры формулы допустимой погрешности (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчёт Margin of Error.
Вы можете скачать этот шаблон Margin of Error здесь — Шаблон Margin of Error
Формула погрешности — пример № 1
Допустим, мы проводим опрос, чтобы увидеть, каков балл, который получают студенты университетов. Мы выбрали 500 учеников случайным образом и задали их оценку. Среднее значение составляет 2, 4 из 4, а стандартное отклонение составляет, скажем, 30%. Предположим, что доверительный интервал составляет 99%. Рассчитайте погрешность.
Решение:
Погрешность рассчитывается по формуле, приведенной ниже
Граница ошибки = Z * S / √n
- Погрешность = 2, 58 * 30% / √ (500)
- Погрешность = 3, 46%
Это означает, что с вероятностью 99% средний балл учащихся составляет 2, 4 плюс или минус 3, 46%.
Формула погрешности — пример № 2
Допустим, вы запускаете новый продукт для здоровья на рынке, но вы не знаете, какой вкус понравится людям. Вы путаетесь между ароматом банана и ванили и решили провести опрос. Для вас это 500 000 человек, что является вашим целевым рынком, и из этого вы решили спросить мнение 1000 человек, и это будет образец. Предположим, что доверительный интервал составляет 90%. Рассчитайте погрешность.
Решение:
Как только опрос закончен, вы узнали, что банану понравился 470 человек, а 530 попросили аромат ванили.
Погрешность рассчитывается по формуле, приведенной ниже
Граница ошибки = Z * √ ((p * (1 — p)) / n)
- Погрешность = 1, 65 * √ ((0, 47 * (1 — 0, 47)) / 1000)
- Погрешность = 2, 60%
Таким образом, мы можем сказать, что с 90% уверенностью, что 47% всех людей любили банановый аромат плюс или минус 2, 60%.
объяснение
Как обсуждалось выше, предел погрешности помогает нам понять, подходит ли размер выборки для вашего опроса или нет. В случае, если погрешность слишком велика, возможно, размер нашей выборки слишком мал, и нам нужно его увеличить, чтобы результаты выборки более точно соответствовали результатам совокупности.
Существуют некоторые сценарии, в которых предел погрешности не будет иметь большого значения и не поможет нам в отслеживании ошибки:
- Если вопросы опроса не разработаны и не помогают получить требуемый ответ
- Если люди, отвечающие на опрос, имеют некоторую предвзятость в отношении продукта, для которого проводится опрос, то и результат будет не очень точным
- Если выбранная выборка является надлежащим представителем населения, в этом случае также результаты будут далеко.
Кроме того, одно большое предположение здесь состоит в том, что население обычно распределено. Таким образом, если размер выборки слишком мал и распределение населения не является нормальным, z-оценка не может быть рассчитана, и мы не сможем найти предел погрешности.
Актуальность и использование формулы ошибки
Всякий раз, когда мы используем выборочные данные, чтобы найти какой-то релевантный ответ для набора населения, возникает некоторая неопределенность и вероятность того, что результат может отличаться от фактического результата. Допустимая погрешность скажет нам, что каков уровень отклонения, это образец выборки. Нам необходимо минимизировать погрешность, чтобы результаты наших выборок отражали реальную историю данных о населении. Поэтому, чем ниже погрешность, тем лучше будут результаты. Запас погрешности дополняет и дополняет имеющуюся у нас статистическую информацию. Например, если опрос показал, что 48% людей предпочитают проводить время дома в выходные дни, мы не можем быть настолько точными, и в этой информации отсутствуют некоторые элементы. Когда мы ввели здесь предел погрешности, скажем, 5%, то результат будет интерпретирован как 43-53% людей, которым понравилась идея быть дома в выходные дни, что имеет полный смысл.
Калькулятор формулы ошибки поля
Вы можете использовать следующий калькулятор Margin of Error
Рекомендуемые статьи
Это было руководство по формуле ошибки. Здесь мы обсудим, как рассчитать погрешность, а также на практических примерах. Мы также предоставляем калькулятор Margin of Error с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
- Руководство по формуле амортизации прямой линии
- Примеры формулы удвоения времени
- Как рассчитать амортизацию?
- Формула для центральной предельной теоремы
- Альтман Z Оценка | Определение | Примеры
- Формула амортизации | Примеры с шаблоном Excel
С использованием встроенных функций
Excel расчет доверительного
интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа —
уровень значимости используемый для
вычисления уровня надежности.
(,
т.е.
означает надежности);
станд_откл
— стандартное отклонение, предполагается
известным;
размер — размер выборки.
Лабораторная работа
1
Тема: Обработка прямых
измерений в Excel (2 часа ).
Задание:
Обработать заданный набор экспериментальных
данных методом Стьюдента, построить
экспериментальные кривые методом
наименьших квадратов.
|
Пример |
Используемуе |
|
|
|
Для построения графика используем
мастер диаграмм.
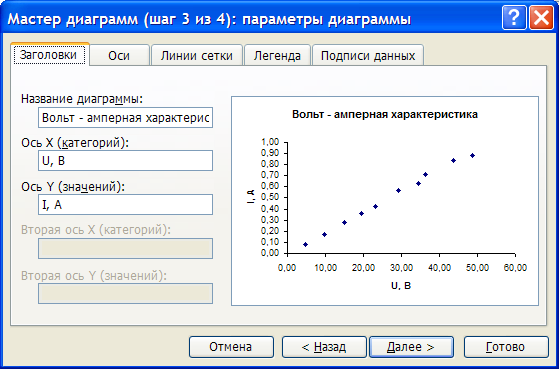
Расчет
погрешности при косвенных измерениях
При измерении
величины косвенным методом предполагается,
что известна математическая модель
связывающая искомую
величину
с величинами
,
измеряемыми непосредственно. Далее
предполагается, выполнена обработка
всех прямых измерений, т. е. определены
доверительные интервалы для величин
:
Погрешность величины у
определяется по формуле:
где
.
Расчет косвенной
погрешности в Maple
Рассмотрим расчет погрешности на примере
функции одной переменной
,
где
Таким образом, найден доверительный
интервал величины
.
В случае, если определяемая в косвенном
измерении величина, является функцией
нескольких переменных, рекомендуем:
-
вычисление погрешности оформить в виде
процедуры
>dy:=proc(y, dx) ……код
процедуры
…… end proc
Код процедуры учащийся должен составить
самостоятельно на основе примера,
рассмотренного выше.
-
параметр dx считать массивом из N
переменных -
для определения списка аргументов и
их количества величины y
можно использовать операторы op() и
nops():
-
Лабораторная работа 2 Тема: Обработка косвенных измерений в Maple (4 часа).
Задание:
Написать программу нахождения погрешности
косвенного измерения в среде Maple.
Выполнение задания
1. Ввести выборку значений измеряемых
величин в матричном виде
2. Определить размерность выборки
3. Задать уровень значимости и определить
степень доверия:
4. Вычислить среднее значение выборки
измеряемой величины:
a) с помощью операций
суммирования
б) с помощью встроенных функций
5. Вычислить значения среднеквадратичного
отклонения.
а) с помощью операций суммирования
,
в) с помощью встроенных функций
6. Вычислить доверительный интервал:
а) Задать коэффициент Стьюдента для
данных размерности выборки и степени
доверия:
.
б) Вычислить абсолютную случайную
погрешность
.
в) Вычислить верхнюю и нижнюю границы
доверительного интервала.
.
7. Учесть приборные погрешности:
а) Задать приборные погрешности
.
б) Вычислить абсолютную случайную
погрешность с учетом приборных
погрешностей
.
8. Представить результат:
а) Абсолютная погрешность:
,
б) Относительная погрешность:
,
в) Верхняя и нижняя границы доверительного
интервала.
.
Примечание. Вычисления провести:
а) в обычном виде,
(См. Дов_инт_01)
б) с помощью операций суммирования,
(См. Дов_инт_02)
в) с помощью встроенных функций.
(См. Дов_инт_03)
2. Вычисление косвенных погрешностей
Выполнение задания
1. Провести аналитические вычисления:
а) Ввести выражение для исследуемой
функции:
,
б) Получить выражение для среднего
значения величины исследуемой функции:
,
в) Получить выражение косвенной
погрешности исследуемой функции в общем
виде и для значения :
,
,
1. Провести численные вычисления:
а) Ввести численные значения постоянных,
б) Ввести средние значения и доверительные
интервалы переменных,
в) Вычислить относительные погрешности
переменных,
г) Вычислить среднее значение исследуемой
функции:
,
г) Вычислить косвенную погрешность
(абсолютную погрешность) исследуемой
функции
,
г) Вычислить относительную погрешность
исследуемой функции
,
в) Вычислить верхнюю и нижнюю границы
доверительного интервала исследуемой
функции:
.
(См. Косв_погр).
3. Построение графиков. Полиномиальная
регрессия
Выполнение задания
1. Ввод выборок значений величин :
2. Вычислить верхнюю и нижнюю границы
доверительного величины Y:
.
3. Полиномиальная регрессия:
а) Задать степень полинома k:
б) Задать число точек данных:
.
в) Задать регрессионную зависимость:
.
г) Определить коэффициенты уравнения
регрессии
:
,
.
4. Построить графики:
а) точечных график данных,
б) кривую регрессии,
в) доверительные интервалы величины Y.
(См. Постр_граф).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17 авг. 2022 г.
читать 1 мин
В статистике средняя абсолютная ошибка (MAE) — это способ измерения точности данной модели. Он рассчитывается как:
MAE = (1/n) * Σ|y i – x i |
куда:
- Σ: греческий символ, означающий «сумма».
- y i : Наблюдаемое значение для i -го наблюдения
- x i : Прогнозируемое значение для i -го наблюдения
- n: общее количество наблюдений
В следующем пошаговом примере показано, как рассчитать среднюю абсолютную ошибку в Excel.
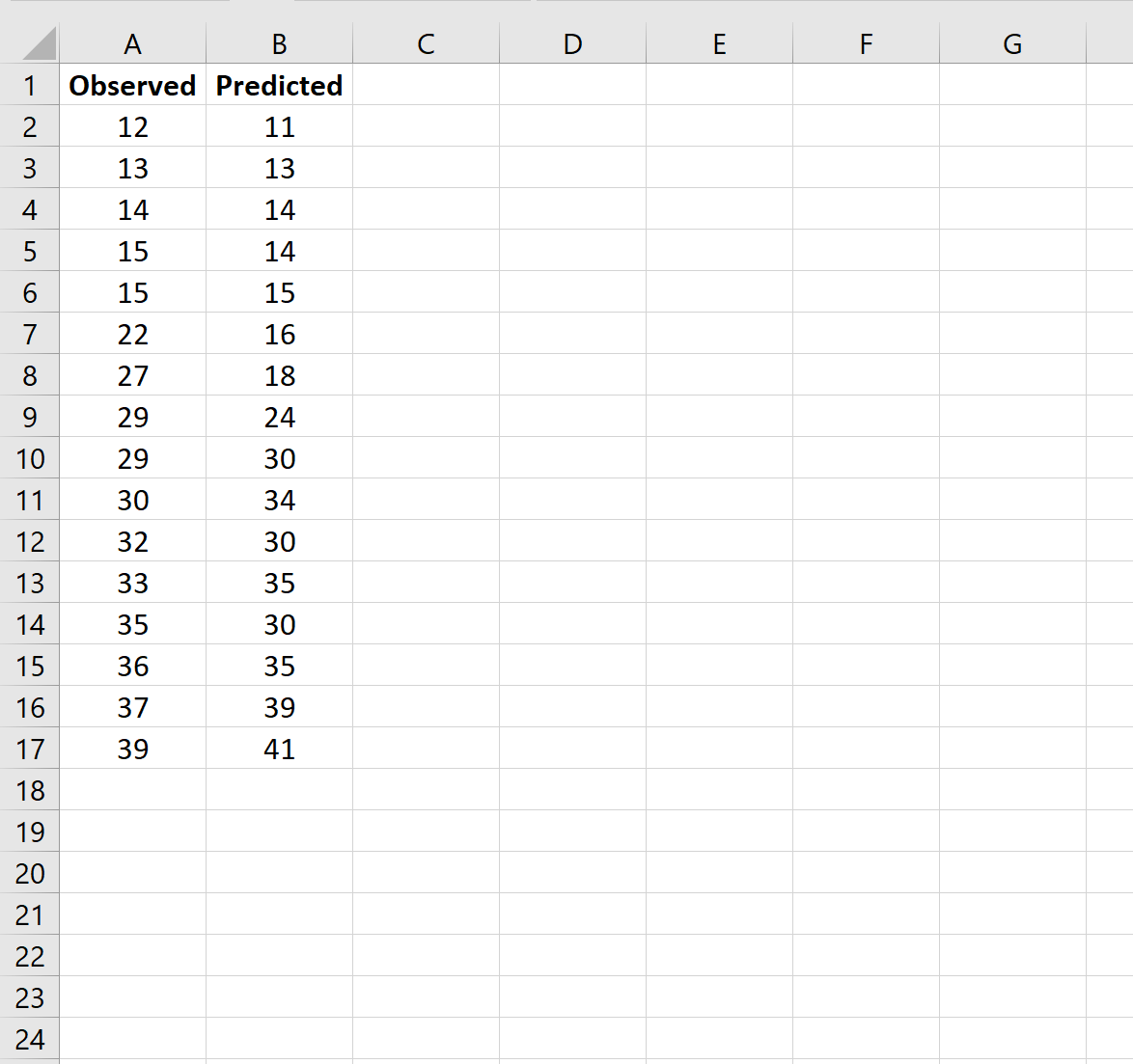
Шаг 1: введите данные
Во-первых, давайте введем список наблюдаемых и прогнозируемых значений в два отдельных столбца:
Примечание. Используйте это руководство , если вам нужно научиться использовать модель регрессии для расчета прогнозируемых значений.
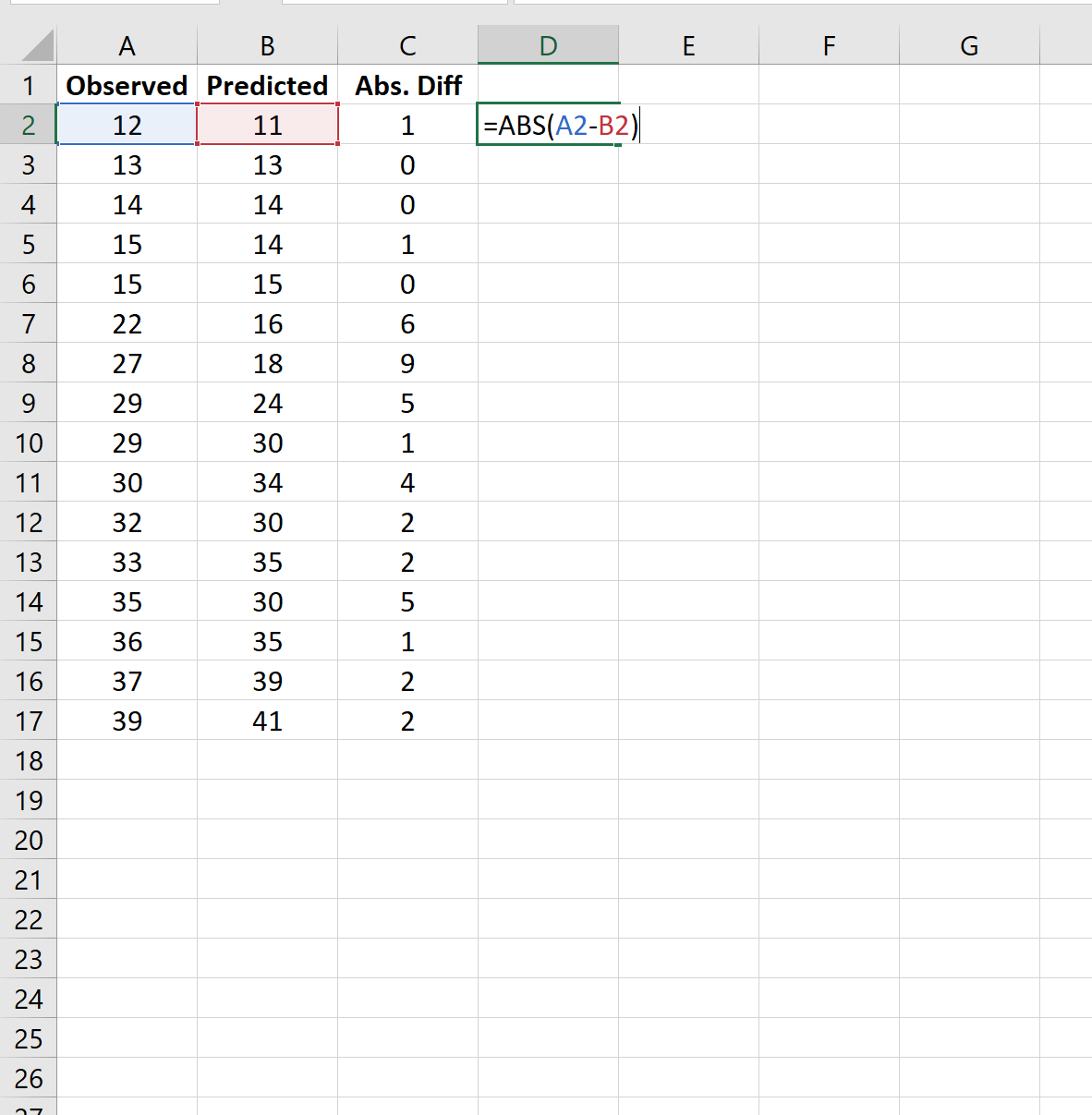
Шаг 2: Рассчитайте абсолютные разницы
Далее мы будем использовать следующую формулу для расчета абсолютных различий между наблюдаемыми и прогнозируемыми значениями:
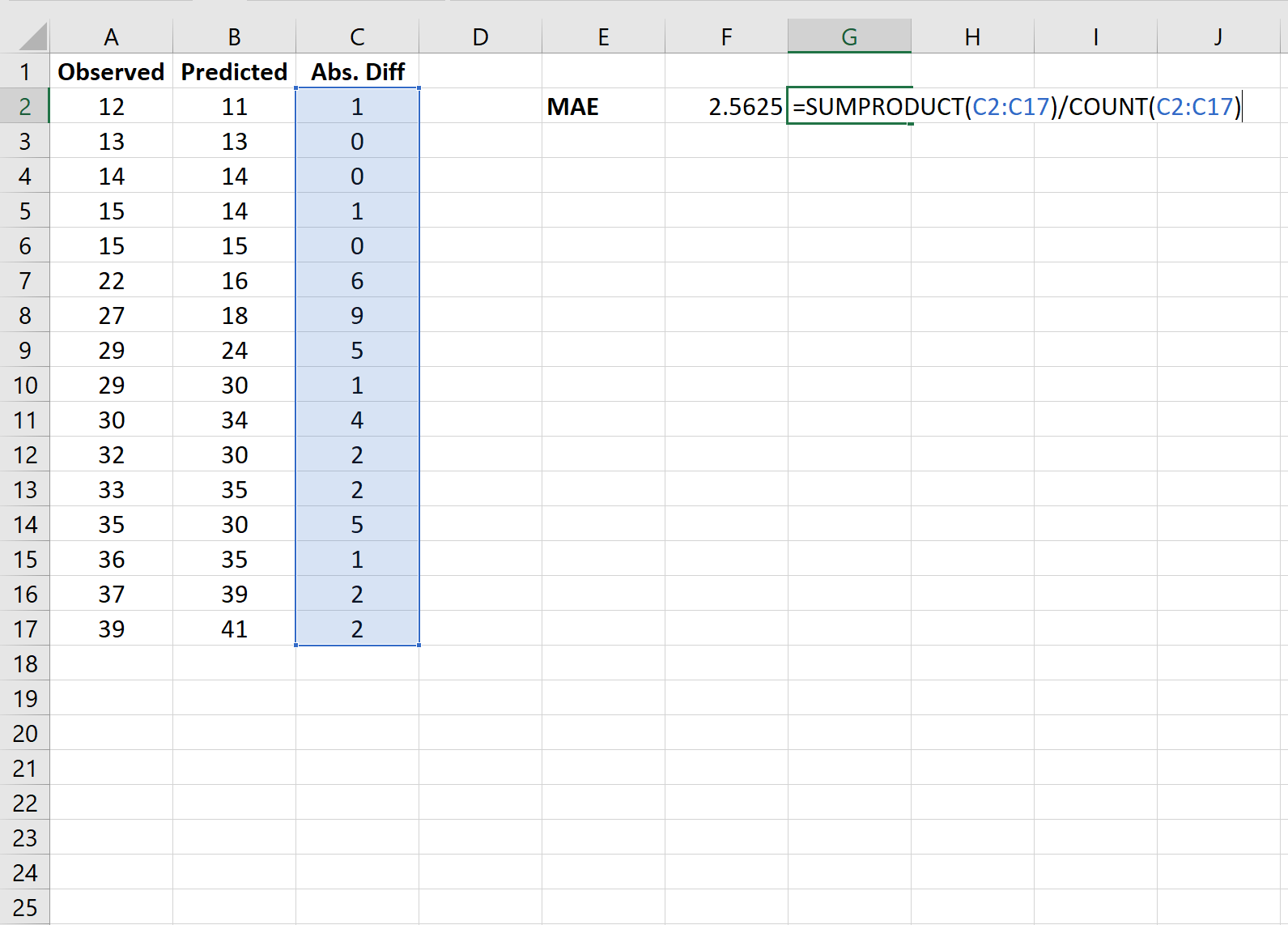
Шаг 3: Рассчитайте MAE
Далее мы будем использовать следующую формулу для расчета средней абсолютной ошибки:
Средняя абсолютная ошибка (MAE) оказывается равной 2,5625 .
Это говорит нам о том, что средняя абсолютная разница между наблюдаемыми значениями и предсказанными значениями составляет 2,5625.
Как правило, чем ниже значение MAE, тем лучше модель соответствует набору данных. При сравнении двух разных моделей мы можем сравнить MAE каждой модели, чтобы узнать, какая из них лучше подходит для набора данных.
Бонус: не стесняйтесь использовать этот Калькулятор средней абсолютной ошибки для автоматического расчета MAE для списка наблюдаемых и прогнозируемых значений.
Дополнительные ресурсы
Как рассчитать MAPE в Excel
Как рассчитать SMAPE в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.