Quantile regression in excel

Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в

MS

EXCEL

.

Понятие

Квантиля

основано на определении

Функции распределения

. Поэтому, перед изучением

Квантилей

рекомендуем освежить в памяти понятия из статьи

Функция распределения вероятности

.

Содержание статьи:

• Определение
• Квантили специальных видов
• Квантили стандартного нормального распределения
• Квантили распределения Стьюдента
• Квантили распределения ХИ-квадрат
• Квантили F-распределения
• Квантили распределения Вейбулла
• Квантили экспоненциального распределения

Сначала дадим формальное определение

квантиля,

затем приведем примеры их вычисления в MS EXCEL.

Определение

Пусть случайная величина

X

, имеет

функцию распределения

F

(

x

).

α-квантилем

(

альфа-

квантиль,

x

_a

,

квантиль

порядка

α, нижний

α-

квантиль

) называют решение уравнения

x

_a

=F

^-1

(α), где

α

— вероятность, что случайная величина х примет значение меньшее или равное x

_a

, т.е. Р(х<= x

_a

)=

α.

Из определения ясно, что нахождение

квантиля

распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении

функции распределения

мы находим вероятность

α,

зная x

_a

, то при нахождении

квантиля

мы, наоборот, ищем

x

_a

зная

α

.

Чтобы пояснить определение, используем график функции

стандартного нормального распределения

(см.

файл примера Лист Определение

):

Примечание

: О построении графиков в MS EXCEL можно прочитать статью

Основные типы диаграмм в MS EXCEL

.

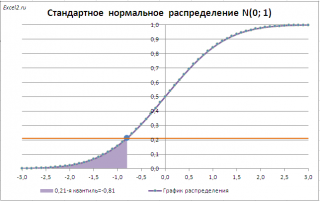
Например, с помощью графика вычислим 0,21-ю

квантиль

, т.е. такое значение случайной величины, что Р(X<=x

_0,21

)=0,21.

Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с

функцией распределения

. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я

квантиль

равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная

стандартному нормальному закону,

примет значение

меньше

-0,81, равна 0,21 (21%).

Примечание

: При вычислении

квантилей

в MS EXCEL используются

обратные функции распределения

:

НОРМ.СТ.ОБР()

,

ЛОГНОРМ.ОБР()

,

ХИ2.ОБР(),

ГАММА.ОБР()

и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Точное значение

квантиля

в нашем случае можно найти с помощью формулы

=НОРМ.СТ.ОБР(0,21)

СОВЕТ

: Процедура вычисления

квантилей

имеет много общего с вычислением

процентилей

выборки

(см. статью

Процентили в MS EXCEL

).

Квантили специальных видов

Часто используются

Квантили

специальных видов:

• процентили

  x
  
  _p/100
  
  , p=1, 2, 3, …, 99

• квартили

  x
  
  _p/4
  
  , p=1, 2, 3

• медиана

  x
  
  _1/2
  

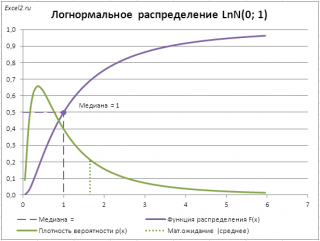
В качестве примера вычислим

медиану (0,5-квантиль)

логнормального распределения

LnN(0;1) (см.

файл примера лист Медиана

).

Это можно сделать с помощью формулы

=ЛОГНОРМ.ОБР(0,5; 0; 1)

Квантили стандартного нормального распределения

Необходимость в вычислении квантилей

стандартного нормального распределения

возникает при

проверке статистических гипотез

и при

построении доверительных интервалов.

Примечание

: Про

проверку статистических гипотез

см. статью

Проверка статистических гипотез в MS EXCEL

. Про

построение доверительных интервалов

см. статью

Доверительные интервалы в MS EXCEL

.

В данных задачах часто используется специальная терминология:

• 
  Нижний квантиль уровня
  
  альфа
  
  (
  
  α
  
  percentage point)
  
  ;
• 
  Верхний квантиль уровня альфа (upper
  
  α
  
  percentage point)
  
  ;
• 
  Двусторонние квантили уровня
  
  альфа
  
  .

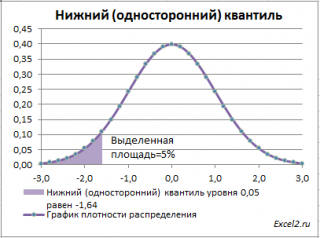
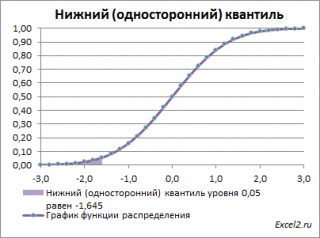
Нижний квантиль уровня альфа

— это обычный

α-квантиль.

Чтобы пояснить название «

нижний» квантиль

, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

(см.

файл примера лист Квантили

).

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше

α-квантиля

. Из определения

квантиля

эта вероятность равна

α

. Из графика

функции распределения

становится понятно, откуда происходит название »

нижний квантиль» —

выделенная область расположена в нижней части графика.

Для

α=0,05,

нижний 0,05-квантиль

стандартного нормального распределения

равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:

=НОРМ.СТ.ОБР(0,05)

Однако, при

проверке гипотез

и построении

доверительных интервалов

чаще используется «верхний»

α-квантиль.

Покажем почему.

Верхним

α

—

квантилем

называют такое значение x

_α

, для которого вероятность, того что случайная величина X примет значение

больше или равное

x

_α

равна

альфа:

P(X>= x

_α

)=

α

. Из определения понятно, что

верхний альфа

—

квантиль

любого распределения равен

нижнему (1-

α)

—

квантилю.

А для распределений, у которых

функция плотности распределения

является четной функцией,

верхний

α

—

квантиль

равен

нижнему

α

—

квантилю

со знаком минус

.

Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.

Действительно, для

α=0,05,

верхний 0,05-квантиль

стандартного нормального распределения

равен 1,645. Т.к.

функция плотности вероятности

стандартного нормального

распределения

является четной функцией, то вычисления в MS EXCEL

верхнего квантиля

можно сделать по двум формулам:

=НОРМ.СТ.ОБР(1-0,05)

=-НОРМ.СТ.ОБР(0,05)

Почему применяют понятие

верхний

α

—

квантиль?

Только из соображения удобства, т.к. он при

α<0,5

всегда положительный (в случае

стандартного нормального

распределения

). А при проверке гипотез

α

равно

уровню значимости

, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре

проверки гипотез

пришлось бы записывать условие отклонения

нулевой гипотезы

μ>μ

₀

как Z

₀

>Z

<sub>1-

α</sub>

, подразумевая, что Z

<sub>1-

α</sub>

–

обычный

квантиль

порядка

1-

α

(или как Z

₀

>-Z

_α

). C верхнем квантилем эта запись выглядит проще Z

₀

>Z

_α

.

Примечание

: Z

₀

— значение

тестовой статистики

, вычисленное на основе

выборки

. Подробнее см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

.

Чтобы пояснить название «

верхний»

квантиль

, построим график

плотности вероятности

и

функцию вероятности

стандартного нормального

распределения

для

α=0,05.

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше

верхнего 0,05-квантиля

, т.е.

больше

значения 1,645. Эта вероятность равна 0,05.

На графике

плотности вероятности

площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика

функции распределения

становится понятно, откуда происходит название «верхний»

квантиль

—

выделенная область расположена в верхней части графика. Если Z

₀

больше

верхнего квантиля

, т.е. попадает в выделенную область, то

нулевая гипотеза

отклоняется.

Также при

проверке двухсторонних гипотез

и построении соответствующих

доверительных интервалов

иногда используется понятие «двусторонний»

α-квантиль.

В этом случае условие отклонения

нулевой гипотезы

звучит как |Z

₀

|>Z

<sub>α

/2</sub>

, где Z

<sub>α

/2</sub>

–

верхний

α/2-квантиль

. Чтобы не писать

верхний

α/2-квантиль

, для удобства используют «двусторонний»

α-квантиль.

Почему двусторонний? Как и в предыдущих случаях, построим график

плотности вероятности стандартного нормального распределения

и график

функции распределения

.

Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение

между

нижним квантилем уровня α

/2 и

верхним квантилем

уровня α

/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z

₀

попадает в одну из выделенных областей, то

нулевая гипотеза

отклоняется.

Вычислить

двусторонний

0,05

—

квантиль

это можно с помощью формул MS EXCEL:

=НОРМ.СТ.ОБР(1-0,05/2)

или

=-НОРМ.СТ.ОБР(0,05/2)

Другими словами,

двусторонние α-квантили

задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.

Квантили распределения Стьюдента

Аналогичным образом

квантили

вычисляются и для

распределения Стьюдента

. Например, вычислять

верхний

α/2-

квантиль

распределения Стьюдента с

n

-1 степенью свободы

требуется, если проводится

проверка двухсторонней гипотезы

о

среднем значении

распределения при

неизвестной

дисперсии

(

см. эту статью

).

Для

верхних квантилей

распределения Стьюдента

часто используется запись t

_α/2,n-1

. Если такая запись встретилась в статье про

проверку гипотез

или про построение

доверительного интервала

, то это именно

верхний квантиль

.

Примечание

:

Функция плотности вероятности распределения Стьюдента

, как и

стандартного нормального распределения

, является четной функцией.

Чтобы вычислить в MS EXCEL

верхний

0,05/2

—

квантиль

для t-распределения с 10 степенями свободы (или тоже самое

двусторонний

0,05-квантиль

), необходимо записать формулу

=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)

или

=СТЬЮДРАСПОБР(0,05; 10)

или

=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)

или

=-СТЬЮДЕНТ.ОБР(0,05/2; 10)

.2X означает 2 хвоста, т.е.

двусторонний квантиль

.

Квантили распределения ХИ-квадрат

Вычислять

квантили

распределения ХИ-квадрат

с

n

-1 степенью свободы

требуется, если проводится

проверка гипотезы

о

дисперсии нормального распределения

(см. статью

Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения

).

При

проверке таких гипотез

также используются

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

распределения

ХИ

²

: χ

²

_α/2,n-1

и

χ

²

<sub>1-

α/2,n-1</sub>

. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

, где используется

стандартное нормальное распределение

или

t-распределение

?

Дело в том, что в отличие от

стандартного нормального распределения

и

распределения Стьюдента

, плотность распределения

ХИ

²

не является четной (симметричной относительно оси х). У него все

квантили

больше 0, поэтому

верхний альфа-квантиль

не равен

нижнему (1-альфа)-квантилю

или по-другому:

верхний альфа-квантиль

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2

—

квантиль

для

ХИ

²

-распределения

с

числом степеней свободы

10, т.е.

χ

²

_0,05/2,n-1

, необходимо в MS EXCEL записать формулу

=ХИ2.ОБР.ПХ(0,05/2; 10)

или

=ХИ2.ОБР(1-0,05/2; 10)

Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Чтобы вычислить

верхний

(1-0,05/2)-

квантиль

при том же

числе степеней свободы

, т.е.

χ

²

_1-0,05/2,n-1

и необходимо записать формулу

=ХИ2.ОБР.ПХ(1-0,05/2; 10)

или

=ХИ2.ОБР(0,05/2; 10)

Результат равен 3,25.

Квантили F-распределения

Вычислять

квантили

распределения Фишера

с

n

₁

-1 и

n

₂

-1 степенями свободы

требуется, если проводится

проверка гипотезы

о равенстве

дисперсий двух нормальных распределений

(см. статью

Двухвыборочный тест для дисперсии: F-тест в MS EXCEL

).

При

проверке таких гипотез

используются, как правило,

верхние квантили.

Например, при

двухсторонней гипотезе

требуется вычислить 2

верхних

квантиля

F

-распределения:

F

<sub>α/2,n1-1,

n

2

-1</sub>

и

F

<sub>1-α/2,n1-1,

n

2

-1</sub>

. Почему требуется вычислить два

квантиля

, не один, как при

проверке гипотез о среднем

? Причина та же, что и для распределения ХИ

²

– плотность

F-распределения

не является четной

.

Эти

квантили

нельзя выразить один через другой как для

стандартного нормального распределения

.

Верхний альфа-квантиль

F

-распределения

не равен

нижнему альфа-квантилю

со знаком минус.

Чтобы вычислить

верхний

0,05/2-квантиль

для

F

-распределения

с

числом степеней свободы

10 и 12, необходимо записать формулу

=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)

Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике

функции распределения

.

Квантили распределения Вейбулла

Иногда

обратная функция распределения

может быть представлена в явном виде с помощью элементарных функций, например как для

распределения Вейбулла

. Напомним, что функция этого распределения задается следующей формулой:

После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p

—

квантиль.

Суть от этого не меняется.

Это и есть обратная функция, которая позволяет вычислить

P

—

квантиль

(

p

—

quantile

). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х

_p

(вероятность того, что случайная величина Х примет значение меньше или равное х

_p

равна P).

Квантили экспоненциального распределения

Задача

:

Случайная величина имеет

экспоненциальное распределение

:

Требуется выразить

p

-квантиль

x

_p

через параметр распределения λ и заданную вероятность

p

.

Примечание

: Вместо обозначения

α-квантиль

может использоваться

p-квантиль

. Суть от этого не меняется.

Решение

: Вспоминаем, что

p

-квантиль

– это такое значение x

_p

случайной величины X, для которого P(X<=x

_p

)=

p

. Т.е. вероятность, что случайная величина X примет значение меньше или равное x

_p

равна

p

. Запишем это утверждение с помощью формулы:

По сути, мы записали

функцию вероятности экспоненциального распределения

: F(x

_p

)=

p

.

Из определения

квантиля

следует, что для его нахождения нам потребуется

обратная функция распределения

.

Проинтегрировав вышеуказанное выражение, получим:

Используя это уравнение, выразим x

_p

через λ и вероятность

p

.

Конечно, явно выразить

обратную функцию распределения

можно не для всех

функций распределений

.

Основная статья: Медиана (статистика)

• 0,25-квантиль называется первым (или нижним) квартилем (от лат. quarta — четверть);
• 0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым квартилем
  
• 0,75-квантиль называется третьим (или верхним) квартилем.

Интерквартильным размахом (англ. Interquartile range) называется разность между третьим и первым квартилями. Интерквартильный размах является характеристикой разброса распределения величины и является робастным аналогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.

Математическое описание

Смотря на закон распределения, мы можем понять, какова вероятность того или иного события, можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы “на глаз” перевести в математически обоснованное утверждение.

Крайне важное определение: математическое ожидание – это площадь под графиком распределения. Если мы говорим о дискретном распределении – это сумма событий умноженных на соответсвующие вероятности, также известно как момент:

(2) E(X) = Σ(p_i•X_i) E – от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:
(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)

Момент степени k:

(5) ν_k = E(X^k)

Центральный момент степени k:

(6) μ_k = E[X – E(X)]^k

Среднее значение

Среднее значение (μ) закона распределения – это математическое ожидание случайной величины (случайная величина – это событие), например, сколько в среднем посетителей заходит в магазин в час:

Кол-во посетителей	0	1	2	3	4	5	6
Количество наблюдений	114	115	52	52	24	13	30
Таблица 1. Количество посетителей в час

График 1. Количество посетителей в час

Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:

μ = (114 • 0 + 115 • 1 + 52 • 2 + 52 • 3 + 24 • 4 + 13 • 5 + 30 • 6) / 400 = 716/400 = 1.79

То же самое мы можем проделать используя формулу 2:

μ = M(X) = Σ(X_i•p_i) = 0 • 0.29 + 1 • 0.29 + 2 • 0.13 + 3 • 0.13 + 4 • 0.06 + 5 • 0.03 + 6 • 0.08 = 1.79 Момент первой степени, формула (5)

Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 1.79 посетителя в час

Количество посетителей	0	1	2	3	4	5	6
Вероятность (%)	28.5	28.8	13	13	6	3.3	7.5
Таблица 2. Закон распределения количества посетителей

Отклонение от среднего

Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:

График 2. График функции вероятности. Распределение ≈ 100±5

Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы использовать в качестве меры удалённости “разность” между средним и случайными величинами:

(7) x_i – μ

но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц между величинами и средним значением:

(8) (x_i – μ)²

Соответственно, среднее значение удалённости – это математическое ожидание квадратов удалённости:

(9) σ² = E[(X – E(X))²] Поскольку вероятности любой удалённости равносильны – вероятность каждого из них – 1/n, откуда: (10) σ² = E[(X – E(X))²] = ∑[(X_i – μ)²]/n Она же формула центрального момента (6) второй степени

σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ² называется дисперсией. Корень из дисперсии называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:

(11) μ±σ
(12) σ = √(σ²) = √[∑[(X_i – μ)²]/n]

Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:

σ = √(∑(x-μ)²/n) = √{[(90 – 99.95)² + (91 – 99.95)² + (92 – 99.95)² + (93 – 99.95)² + (94 – 99.95)² + (95 – 99.95)² + (96 – 99.95)² + (97 – 99.95)² + (98 – 99.95)² + (99 – 99.95)² + (100 – 99.95)² + (101 – 99.95)² + (102 – 99.95)² + (103 – 99.95)² + (104 – 99.95)² + (105 – 99.95)² + (106 – 99.95)² + (107 – 99.95)² + (108 – 99.95)² + (109 – 99.95)² + (110 – 99.95)²]/21} = 6.06
Итак, для графика 2 мы получили:
X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного “на глаз”

Квантиль

График 3. Функция распределения. Медиана

График 4. Функция распределения. 4-квантиль или квартиль

График 5. Функция распределения. 0.34-квантиль

Для анализа функции распределения ввели понятие квантиль. Квантиль – это случайная величина при заданном уровне вероятности, т.е.: квантиль для уровня вероятности 50% – это случайная величина на графике плотности вероятности, которая имеет вероятность 50%. На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)

• 2-квантиль – медиана
• 4-квантиль – квартиль
• 10-квантиль – дециль
• 100-квантиль – перцентиль

То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям, и для каждого дециля нашли значение случайной величины.

Также, используется обозначение x-квантиль, где х – дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при p = 0.34.

Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.

Построение интервалов

Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например, интерес – случайное число = 98), а для группы событий (например, интерес – случайное число между 96 и 99). Доверительный интервал бывает двух видов: односторонний и двусторонний. Параметр доверительного интервала – уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.

Двусторонний доверительный интервал

Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются “критическая область“

Первый квартиль

Значение квартиля Q1 находится в интервале 68,98 – 71,70, соответствующего частоте fQ1 = 150:4 = 37,5

Третий квартиль

Значение квартиля находится в интервале 68,98 – 71,70, соответствующего частоте fQ3 = (3*150):4 = 112,5

Квартили непрерывного распределения

Если функция распределения F (х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х) =0,25, второй – F(х) =0,5, а третий F(х) =0,75.

Примечание : Подробнее о Функции распределения см. статью Функция распределения и плотность вероятности в MS EXCEL .

Если известна функция плотности вероятности p (х) , то 1-й квартиль можно найти из уравнения:

Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ ² ), получим, что медиана (2-й квартиль ) вычисляется по формуле e ^μ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.

Обратите внимание на точку Функции распределения , для которой F(х)=0,5 (см. картинку выше или файл примера , лист Квартиль-распределение) . Абсцисса этой точки равна 2,718. Это и есть значение 2-го квартиля ( медианы ), что естественно совпадает с ранее вычисленным значением по формуле e ^μ .

Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:

Поэтому, линии квартилей ( х=квартиль ) делят площадь под графиком функции плотности вероятности на 4 равные части.

Квартили в MS EXCEL

Чтобы вычислить в MS EXCEL квартили заданного распределения необходимо использовать соответствующую обратную функцию распределения .

При вычислении квартилей в MS EXCEL используются обратные функции распределения : НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР() , ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .

Например, в MS EXCEL 1-й квартиль для логнормального распределения LnN(1;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,25;1;1) , а 3-й квартиль для стандартного нормального распределения по формуле =НОРМ.СТ.ОБР(0,75) .

Моменты случайной величины

Моменты случайно величины описывают различные аспекты характера и формы нашего распределения.

#1 — первый момент случайной величины — среднее значение данных, которое показывает место распределения.

#2 — второй момент случайной величины — дисперсия, которая показывает разброс распределения. Большие значения имеют больший размах, чем маленькие.

#3 — третий момент случайной величины — коэффициент асимметрии — мера того, насколько неравномерным является распределение. Коэффициент асимметрии положителен, если распределение наклонено влево и левый хвост короче правого. То есть среднее значение находится правее. И наоборот:

#4 — четвертый момент случайной величины — коэффициент эксцесса, который описывает то, насколько толстый хвост и насколько острый пик распределения. Этот коэффициент показывает, насколько вероятно найти точки экстремума в данных. Чем выше значение, тем вероятнее выбросы. Это похоже на разброс (дисперсию), но между ними есть отличия.

Как видно на графике, чем выше значение пики, тем выше коэффициент эксцесса, т.е. у верхней кривой коэффициент эксцесса выше, чем у нижней.

Статистический анализ роста доли дохода в Excel за период

Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.

Вид исходной таблицы:

Определим 3-й по формуле:

Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:

=СЧЁТЕСЛИ(B2:B13;”<“&B15)/СЧЁТ(B2:B13)

Полученные результаты:

Анализ статистики случайно сгенерированных чисел в Excel

Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.

Чтобы сгенерировать случайное число в Excel воспользуемся функцией:

=СЛУЧМЕЖДУ(0;1000)

После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:

Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):

Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:

Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.

Расчет квартилей в R и SAS

Функция quantile в R использует все девять алгоритмов расчета квантилей, в соответствии с нумерацией, предложенной Hyndman and Fan в работе 1996 г. (рис. 15; если вы не знакомы с R, рекомендую начать с Алексей Шипунов. Наглядная статистика. Используем R!). Квантиль при i-м методе расчета:

где i – номер метода, 1 ≤ i ≤ 9, (j–m)/n ≤ p < (j–m+1)/n, х_j – j-ый порядковый элемент упорядоченного ряда, n – размер выборки, γ является функцией двух параметров: j = floor(np + m) и g = np + m – j, где floor – функция возвращающая наибольшее целое, но всё еще меньшее, чем аргумент функции (аналог в Excel – ОКРВНИЗ.МАТ), m – константа, определяемая типом алгоритма расчета квантиля. Если вас интересуют подробности, обратитесь к справочной системе R.

SAS предлгает 5 методов расчета квантилей.

Расчет децилей для дискретного ряда

1. Определяем номер дециля по формуле: ,

2. Если номер дециля – целое число, то значение дециля будет равно величине элемента ряда, которое обладает накопленной частотой равной номеру дециля. Например, если номер дециля равен 20, его значение будет равно значению признака с S =20 (накопленной частотой равной 20).

Если номер дециля – нецелое число, то дециль попадает между двумя наблюдениями. Значением дециля будет сумма, состоящая из значения элемента, для которого накопленная частота равна целому значению номера дециля, и указанной части (нецелая часть номера дециля) разности между значением этого элемента и значением следующего элемента.

Например, если номер дециля равна 20,25, дециль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 разности между значением 20-го и 21-го наблюдений.

Квантили специальных видов

Часто используются Квантили специальных видов:

• процентили x _p/100 , p=1, 2, 3, …, 99
• квартили x _p/4 , p=1, 2, 3
• медиана x _1/2

В качестве примера вычислим медиану (0,5-квантиль) логнормального распределения LnN(0;1) (см. файл примера лист Медиана ).

Это можно сделать с помощью формулы =ЛОГНОРМ.ОБР(0,5; 0; 1)

Квантили стандартного нормального распределения

Необходимость в вычислении квантилей стандартного нормального распределения возникает при проверке статистических гипотез и при построении доверительных интервалов.

Примечание : Про проверку статистических гипотез см. статью Проверка статистических гипотез в MS EXCEL . Про построение доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .

В данных задачах часто используется специальная терминология:

• Нижний квантиль уровня альфа ( α percentage point)
  
• Верхний квантиль уровня альфа (upper α percentage point)
  
• Двусторонние квантили уровня альфа .

Нижний квантиль уровня альфа – это обычный α-квантиль. Чтобы пояснить название « нижний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения (см. файл примера лист Квантили ).

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше α-квантиля . Из определения квантиля эта вероятность равна α . Из графика функции распределения становится понятно, откуда происходит название ” нижний квантиль” – выделенная область расположена в нижней части графика.

Для α=0,05, нижний 0,05-квантиль стандартного нормального распределения равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:

=НОРМ.СТ.ОБР(0,05)

Однако, при проверке гипотез и построении доверительных интервалов чаще используется “верхний” α-квантиль. Покажем почему.

Верхним α – квантилем называют такое значение x _α , для которого вероятность, того что случайная величина X примет значение больше или равное x _α равна альфа: P(X>= x _α )= α . Из определения понятно, что верхний альфа – квантиль любого распределения равен нижнему (1- α) – квантилю. А для распределений, у которых функция плотности распределения является четной функцией, верхний α – квантиль равен нижнему α – квантилю со знаком минус . Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.

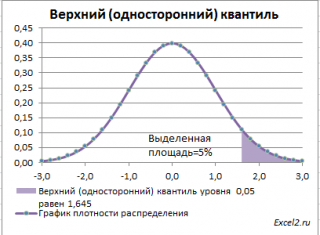
Действительно, для α=0,05, верхний 0,05-квантиль стандартного нормального распределения равен 1,645. Т.к. функция плотности вероятности стандартного нормального распределения является четной функцией, то вычисления в MS EXCEL верхнего квантиля можно сделать по двум формулам:

=НОРМ.СТ.ОБР(1-0,05)

=-НОРМ.СТ.ОБР(0,05)

Почему применяют понятие верхний α – квантиль? Только из соображения удобства, т.к. он при α всегда положительный (в случае стандартного нормального распределения ). А при проверке гипотез α равно уровню значимости , который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре проверки гипотез пришлось бы записывать условие отклонения нулевой гипотезы μ>μ ₀ как Z ₀ >Z _{1- α} , подразумевая, что Z _{1- α} – обычный квантиль порядка 1- α (или как Z ₀ >-Z _α ). C верхнем квантилем эта запись выглядит проще Z ₀ >Z _α .

Примечание : Z ₀ – значение тестовой статистики , вычисленное на основе выборки . Подробнее см. статью Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) .

Чтобы пояснить название « верхний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения для α=0,05.

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше верхнего 0,05-квантиля , т.е. больше значения 1,645. Эта вероятность равна 0,05.

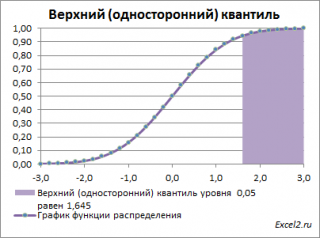
На графике плотности вероятности площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика функции распределения становится понятно, откуда происходит название “верхний” квантиль – выделенная область расположена в верхней части графика. Если Z ₀ больше верхнего квантиля , т.е. попадает в выделенную область, то нулевая гипотеза отклоняется.

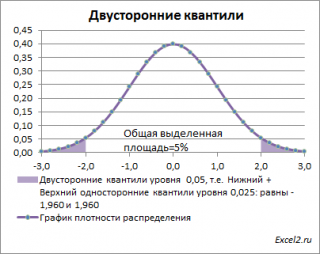
Также при проверке двухсторонних гипотез и построении соответствующих доверительных интервалов иногда используется понятие “двусторонний” α-квантиль. В этом случае условие отклонения нулевой гипотезы звучит как |Z ₀ |>Z _{α /2} , где Z _{α /2} – верхний α/2-квантиль . Чтобы не писать верхний α/2-квантиль , для удобства используют “двусторонний” α-квантиль. Почему двусторонний? Как и в предыдущих случаях, построим график плотности вероятности стандартного нормального распределения и график функции распределения .

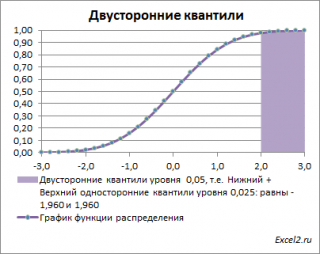
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение между нижним квантилем уровня α /2 и верхним квантилем уровня α /2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z ₀ попадает в одну из выделенных областей, то нулевая гипотеза отклоняется.

Вычислить двусторонний 0,05 – квантиль это можно с помощью формул MS EXCEL: =НОРМ.СТ.ОБР(1-0,05/2) или =-НОРМ.СТ.ОБР(0,05/2)

Другими словами, двусторонние α-квантили задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.

Квантили распределения Стьюдента

Аналогичным образом квантили вычисляются и для распределения Стьюдента . Например, вычислять верхний α/2- квантиль распределения Стьюдента с n -1 степенью свободы требуется, если проводится проверка двухсторонней гипотезы о среднем значении распределения при неизвестной дисперсии ( см. эту статью ).

Для верхних квантилей распределения Стьюдента часто используется запись t _α/2,n-1 . Если такая запись встретилась в статье про проверку гипотез или про построение доверительного интервала , то это именно верхний квантиль .

Примечание : Функция плотности вероятности распределения Стьюдента , как и стандартного нормального распределения , является четной функцией.

Чтобы вычислить в MS EXCEL верхний 0,05/2 – квантиль для t-распределения с 10 степенями свободы (или тоже самое двусторонний 0,05-квантиль ), необходимо записать формулу =СТЬЮДЕНТ.ОБР.2Х(0,05; 10) или =СТЬЮДРАСПОБР(0,05; 10) или =СТЬЮДЕНТ.ОБР(1-0,05/2; 10) или =-СТЬЮДЕНТ.ОБР(0,05/2; 10)

.2X означает 2 хвоста, т.е. двусторонний квантиль .

Квантили распределения ХИ-квадрат

Вычислять квантили распределения ХИ-квадрат с n -1 степенью свободы требуется, если проводится проверка гипотезы о дисперсии нормального распределения (см. статью Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения ).

При проверке таких гипотез также используются верхние квантили. Например, при двухсторонней гипотезе требуется вычислить 2 верхних квантиля распределения ХИ ² : χ ² _α/2,n-1 и χ ² _{1- α/2,n-1} . Почему требуется вычислить два квантиля , не один, как при проверке гипотез о среднем , где используется стандартное нормальное распределение или t-распределение ?

Дело в том, что в отличие от стандартного нормального распределения и распределения Стьюдента , плотность распределения ХИ ² не является четной (симметричной относительно оси х). У него все квантили больше 0, поэтому верхний альфа-квантиль не равен нижнему (1-альфа)-квантилю или по-другому: верхний альфа-квантиль не равен нижнему альфа-квантилю со знаком минус.

Чтобы вычислить верхний 0,05/2 – квантиль для ХИ ² -распределения с числом степеней свободы 10, т.е. χ ² _0,05/2,n-1 , необходимо в MS EXCEL записать формулу =ХИ2.ОБР.ПХ(0,05/2; 10) или =ХИ2.ОБР(1-0,05/2; 10)

Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике функции распределения .

Чтобы вычислить верхний (1-0,05/2)- квантиль при том же числе степеней свободы , т.е. χ ² _1-0,05/2,n-1 и необходимо записать формулу =ХИ2.ОБР.ПХ(1-0,05/2; 10) или =ХИ2.ОБР(0,05/2; 10)

Результат равен 3,25.

Источники

• https://dic.academic.ru/dic.nsf/ruwiki/291015
• https://k-tree.ru/articles/statistika/analiz_dannyh/svoistva_raspredeleniia
• https://univer-nn.ru/zadachi-po-statistike-primeri/kvartili-v-statistike/
• https://excel2.ru/articles/kvartili-i-interkvartilnyy-interval-iqr-v-ms-excel
• https://nuancesprog.ru/p/3307/
• https://exceltable.com/funkcii-excel/primery-funkcii-kvartil
• https://baguzin.ru/wp/kvartil-kakie-formuly-rascheta-ispol/
• https://studfile.net/preview/5316597/page:4/
• https://excel2.ru/articles/kvantili-raspredeleniy-ms-excel

August 27, 2013 by abhid90210

0

According to Wikipedia, for discrete distributions, there is no universally agreed method of calculating a Quantile, however in Excel one can simply use PERCENTILE function to calculate any arbitrary quantile.

e.g.: to calculate 1 to 10th deciles:

1st decile is the 0.1 percentile, hence the C2/10 in the formula at D2.

Similarly 1st Quartile is 0.25 percentile and so on.

Квартиль — одна из статистик, используемая при описании выборок (подробнее о различных статистиках см. Определение среднего значения, вариации и формы распределения. Описательные статистики). В то время как медиана разделяет упорядоченный массив пополам, квартили разбивают набор данных на четыре части. Первый квартиль – это число, разделяющее выборку на две части: 25% элементов меньше, а 75% — больше значения первого квартиля. Третий квартиль — это число, разделяющее выборку также на две части: 75% элементов меньше, а 25% — больше третьего квартиля.

Рис. 1. 5-числовые сводки: М – медиана, Н1 и Н2 – сгибы (они же квартили)

Скачать заметку в формате Word или pdf, примеры в формате Excel (файл содержит код VBA).

Для расчета квартилей в Excel2007 и более ранних версиях использовалась функция КВАРТИЛЬ. Начиная с версии Excel2010 применяются две функции: КВАРТИЛЬ.ВКЛ и КВАРТИЛЬ.ИСКЛ (функция КВАРТИЛЬ оставлена для совмещения с более ранними версиями Excel; эта функция возвращает те же значения, что и КВАРТИЛЬ.ВКЛ). Эти две функции возвращают различные значения, но я нигде не нашел, какой алгоритм они используют при расчетах. Замечу, что для корректной работы функций данные можно не упорядочивать.

Изучение литературы показало, что в отличие от большинства других статистик, единодушия в методике расчета квартилей нет)) Я нашел упоминание о девяти различных подходах…

Начнем с метода Джона Тьюки, описанного им в, уже ставшем классическом, труде Анализ результатов наблюдений. Разведочный анализ, изданном в 1977 г. Он начинает с введения трех сводок, характеризующих выборку: минимальное, максимальное значения и медиана. Далее он продолжает: «Если мы хотим добавить еще два числа, чтобы образовать 5-числовую сводку, то естественно определять их подсчетом до половины расстояния от каждого из концов к медиане. Процесс нахождения медианы, а затем и этих новых значений можно представить себе, как складывание листа бумаги. Поэтому эти новые значения естественно назвать сгибами» (англ. – hinge; рис. 1). Мы их называем квартилями.

Такие рисунки выглядят очень аккуратно, если число элементов выборки N = 4k + 1, например, 9, 13, 17… Но как быть, если в выборке 12 или 19 элементов? Наглядную картину представил Jon Peltier в серии заметок в своем блоге. Упорядочим элементы случайной выборки и разместим их над линейкой (рис. 2; случайная выборка, элементы которой упорядочены называется вариационным рядом). Серые числа под линейкой – индекс ряда (Джон зачем-то в качестве выборки – над линейкой – взял ряд целых чисел; наверное, чтобы запутать нас). Красное число над рядом – значение сводки; если оно дробное, значит полученное значение является интерполяцией между соседними значениями. Мы определяем медиану, как среднее значение набора данных, а первую квартиль – как медиану нижней половины данных.

Рис. 2. Инклюзивные квартили

Когда Джон Тьюки впервые предложил такой подход, он решил, что медиана (если число элементов в выборке нечетное) должна быть включена как в нижнюю (левую на рисунке), так и в верхнюю половинку данных при определении медиан этих половинок, то есть сгибов. Поэтому такой подход и называется инклюзивным (с включением).

Эксклюзивный подход. Некоторым статистикам не нравится, что медиана учитывается дважды. Они решили, что сгибы должны быть определены как медианы верхней и нижней половин набора данных, из которых срединное значение исключено (рис. 3). Такой взгляд отстаивали Moore и McCabe, или кратко M&M. Если набор данных содержит четное количество значений, инклюзивные и эксклюзивные квартили равны, так как нет элемента выборки (соответствующего центральной медиане), который можно было бы включить или исключить из рассмотрения. Для нечетного числа элементов, инклюзивные сгибы всегда ближе к медиане.

Рис. 3. Эксклюзивные квартили

Третий подход – компромисс между Тьюки и М&M – называется Эмпирическая функции распределения или Интегральная функция распределения (английская аббревиатура CDF). В случае нечетного числа значений в наборе данных, следует включить или исключить медиану, ориентируясь на то, чтобы оставшиеся половинки содержали нечетное число элементов. Например, если в выборке 9 элементов, медиану следует включить, а при 11 элементах – исключить. В обоих случаях половинки будут содержать по 5 элементов. Преимущество этого компромисса заключается в том, что в качестве значения квартиля всегда получается один из элементов набора данных (а не среднее значение двух соседних элементов). CDF является методом по умолчанию в статистическом пакете SAS.

Все возможные случаи N. Мы не всегда можем изобразить данные в W-образной форме, как на рис. 1, поэтому удобнее пользоваться линейкой. В общем случае возможны четыре варианта по числу элементов в выборке: N = 4k, N = 4k + 1, N = 4k + 2, N = 4k + 3… и три подхода к расчету квартилей: Тьюки, M&M, CDF (рис. 4–7).

Рис. 4. Число элементов в выборке N = 4k; все три метода дают одинаковые значения квартилей

Рис. 5. Число элементов в выборке N = 4k + 1; M&M дает значения, отстоящие дальше от медианы

Рис. 6. Число элементов в выборке N = 4k + 2; все три метода дают одинаковые значения квартилей

Рис. 7. Число элементов в выборке N = 4k + 3

Методы интерполяции. Помимо трех описанных выше методов, применяют и целый ряд индексных алгоритмов. Мы рассмотрим три из них. Первый индекс во всех методах равен 0, а последний – N–1, N, N + 1. Например, для N=8 индексированные ряды представлены на рис. 8.

Рис. 8. Индексные ряды на основе N–1, N и N + 1 для N = 8

Положение перцентиля р – доля длины индексной линии, или р(N–1), рN, р(N+1), соответственно. р = 0,25 соответствует первому квартилю, а р = 0,75 – третьему. Ниже наглядно представлен расчет квартилей при различном числе элементов в выборке и трех методах интерполяции на основе N–1, N и N + 1 (рис. 9, 11–13). Обратите внимание, что рассчитанные числа (по формулам справа от линеек) являются не значениями квартилей, а значениями индексов квартилей. Над линейками показано значение квартилей для ряда значений {1, 2, 3, 4, 5, 6, 7, 8}.

Рис. 9. Число элементов в выборке N = 4k

Если, например, наша выборка {2, 3, 5, 8, 11, 12, 14, 17}, то расчет квартилей на основе N–1-метода даст индексы 1,75, 3,5 и 5,25, и значения квартилей 4,5, 9,5 и 12,5 (рис. 10).

Рис. 10. От индексов к значениям квартилей для N–1-метода и N = 4k

Рис. 11. Число элементов в выборке N = 4k + 1

Рис. 12. Число элементов в выборке N = 4k + 2

Рис. 13. Число элементов в выборке N = 4k + 3

Какой алгоритм считать стандартным для вычисления квартилей?

В 1996 году Роб Дж. Хиндман и Янан Фан опубликовали статью в American Statistician под названием Квантили выборок в статистических пакетах. В ней они рассматривали различные алгоритмы расчета квантилей (квартили – это частный случай квантилей). Их целью было указать методологию, которая могла бы стать стандартом для поставщиков статистического программного обеспечения, чтобы расчет квартилей не зависел от типа пакета. В статье они описали девять методов для расчета квантилей. Таблица показывает некоторые статистические пакеты и используемые в них алгоритмы (рис. 14; таблица, этот раздел заметки и код VBA ниже базируются на тексте с сайта Bacon Bits). Обратите внимание, что R и Maple применяют весь спектр алгоритмов.

Рис. 14. Алгоритмы, используемые в статистических пакетах

Кстати, Хиндман и Фан в завершении своей статьи рекомендовали метод 8 в качестве стандарта для статистических пакетов. По их мнению, этот метод оценки квантиля не зависит от распределения, что делает его наиболее приемлемым для расчета.

Расчет квартилей в Excel

Функция Excel КВАРТИЛЬ.ИСКЛ использует следующую формулу для расчета квартилей:

где Q_p – p-й квантиль: p = 0 – для минимального значения, 0,25 – для первого квартиля, 0,5 – для медианы, 0,75 – для третьего квартиля, 1 – для максимального значения;

x – индекс квантиля (может быть дробным); x = (n+1)p, где n – число элементов в выборке; обратите внимание на (n+1), поэтому метод и называется N+1-интерполяция;

i – индекс элемента в упорядоченной выборке; самое большое целое всё еще меньшее, чем x;

A₁, A₂, …, A_i, A_i+1, …, A_n – элементы случайной выборки, упорядоченной по возрастанию.

Формула для КВАРТИЛЬ.ВКЛ отличается только методом расчета х: x = (n-1)p+1; обратите внимание на (n–1), поэтому метод называется N–1-интерполяция. Подробнее с работой формул можно ознакомиться в приложенном Excel-файле на листе Формулы.

Расчет квартилей в R и SAS

Функция quantile в R использует все девять алгоритмов расчета квантилей, в соответствии с нумерацией, предложенной Hyndman and Fan в работе 1996 г. (рис. 15; если вы не знакомы с R, рекомендую начать с Алексей Шипунов. Наглядная статистика. Используем R!). Квантиль при i-м методе расчета:

где i – номер метода, 1 ≤ i ≤ 9, (j–m)/n ≤ p < (j–m+1)/n, х_j – j-ый порядковый элемент упорядоченного ряда, n – размер выборки, γ является функцией двух параметров: j = floor(np + m) и g = np + m – j, где floor – функция возвращающая наибольшее целое, но всё еще меньшее, чем аргумент функции (аналог в Excel – ОКРВНИЗ.МАТ), m – константа, определяемая типом алгоритма расчета квантиля. Если вас интересуют подробности, обратитесь к справочной системе R.

SAS предлгает 5 методов расчета квантилей. И вновь за подробностями я отсылаю вас к справочной системе.

Рис. 15. Расчет квартилей в R девятью способами

Расчет квартилей в Excel любым методом с помощью VBA

Ниже представлен код пользовательской функции, которая позволяет воспроизвести любой из шести методов, перечисленных в таблице на рис. 14. Даже если у вас Excel 2007, и вам недоступна функция КВАРТИЛЬ.ИСКЛ, вы сможете рассчитать квартиль шестым методом с помощью этой функции.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

Function Quantile(MyRange As Range, p As Double, Optional m As Variant) ‘Mike Alexander: www.datapigtechnologies.com ‘Based on Code originally posted by Jerry W. Lewis (former Excel MVP) ‘********************************************************************* ‘This function will replicate various quantile calcuations found ‘in statistical software packages. ‘Calculation is determined by the Hyndman—Fan method used. ‘Hyndman-Fan Method 4 Replicates: ‘SAS(PCTLDEF=1), R(type=4), Maple(method=3) ‘Hyndman-Fan Method 5 Replicates: R(type=5), Maple(method=4) ‘Hyndman—Fan Method 6 Replicates: Excel(QUARTILE.EXC), SAS(PCTLDEF=4), ‘R(type=6), Minitab, SPSS, BMDP, JMP, Maple(method=5) ‘Hyndman—Fan Method 7 Replicates: Excel (QUARTILE and QUARTILE.INC), ‘R(type=7), S-Plus, Maxima, Maple(method=6) ‘Hyndman—Fan Method 8 Replicates: R(type=8), Maple(method=7) ‘Hyndman-Fan Method 9 Replicates: R(type=9), Maple(method=8) ‘********************************************************************** ‘Call function from Excel Spreadhseet by entering ‘=Quantile(Range, p, m) ‘Enter p as the fraction of the population ‘(.25 for quartile 1, .75 for quartile 3, etc....) ‘Enter m as the Hyndman-Fan Quantile method number (4, 5, 6, 7, 8 or 9) ‘If m is left blank, the function will use method 6 by default ‘********************************************************************** Dim n As Long Dim i As Long Dim QDef As Double Dim x As Double ‘Identify method and set the interpolation basis used Select Case m     Case Is = 4         QDef = 0     Case Is = 5         QDef = 0.5     Case Is = 6         QDef = p     Case Is = 7         QDef = 1 — p     Case Is = 8         QDef = (p + 1) / 3     Case Is = 9         QDef = (p + 1.5) / 4     Case Else ‘Use Hyndman-Fan 6 by default         QDef = p End Select ‘Count values within MyRange and calculate the required position index n = WorksheetFunction.Count(MyRange) x = n * p + QDef i = WorksheetFunction.Max(WorksheetFunction.Min(Fix(x), n), 1) ‘Perform interpolation and return answer If (x — i) >= 0 And i < n Then     Quantile = (1 — (x — i)) * WorksheetFunction.Small(MyRange, i) + _     (x — i) * WorksheetFunction.Small(MyRange, i + 1) Else     Quantile = WorksheetFunction.Small(MyRange, i) End If End Function

После того, как вставите код в стандартный модуль книги, вы сможете использовать функцию (рис. 16): =Quantile(MyRange; P; M), где MyRange – диапазон, включающий выборку (можно оставить его неупорядоченным); Р – статистика: 0 – минимум, 0,25 – 1-й квартиль, 0,5 – медиана, 0,75 – 3-й квартиль, 1 – максимум; возможно введение иных значений в диапазоне от 0 до 1; М – номер метода из таблицы на рис. 14.

Рис. 16. Синтаксис пользовательской функции Quantile

В таблице (рис. 17) приведен расчет квартилей по всем методам. Обратите внимание, как метод 8 (который Хиндман и Фан рекомендуют в качестве стандарта) вычисляет квартили, которые ложатся между значениями, вычисляемыми по методам 6 и 7. Действительно, метод 8 дает наиболее сбалансированный набор квартилей.

Рис. 17. Значения квартилей, вычисленные различными методами

Сравнение алгоритмов вычисления квартилей

Стандартом де-факто вычисления квартилей в статистических пакетах и Excel является метод 6 на основе N+1-интерполяции. Если вы хотите, чтобы ваши данные были одинаковыми при использовании различных инструментов, используйте именно этот метод. В Excel он лежит в основе работы функции КВАРТИЛЬ.ИСКЛ. К сожалению, этот метод приводит к увеличению межквартильного интервала. Для нашего примера (рис. 17) с 13,0 до 15,5. Если сравнить все пять методов расчета (рис. 18), то видно, что минимальный межквартильный интервал соответствует методу 7, а максимальный – методу 6. На что это влияет мы рассмотрим в заметке Визуализация статистических данных с помощью диаграммы ящик с усами. Если же вы используете только Excel рекомендую метод 7 на основе N–1-интерполяции. Это позволит вам оперировать с самым узким межквартильным интервалом.

Рис. 18. Влияние алгоритма расчета квартилей на межквартильный интервал; цифры от 5 до 9 – номера методов