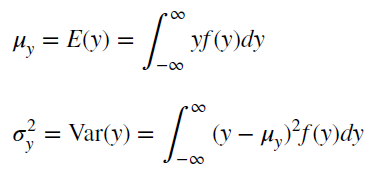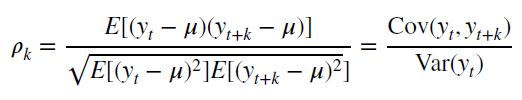Проверка ряда на стационарность в excel

history 4 июля 2021 г.

Группы статей

В

первом разделе статьи

модели для прогнозирования временных рядов сравниваются с моделями, построение которых основано на причинно-следственных закономерностях.

Во

втором разделе

приведен краткий обзор трендов временных рядов (линейный и сезонный тренд, стационарный процесс). Для каждого тренда предложена модель для прогнозирования.

Затем даны ссылки на сайты по теории прогнозирования временных рядов и содержащие базы статистических данных.

Disclaimer:

Напоминаем, что задача сайта excel2.ru (раздел

Временные ряды

) продемонстрировать использование MS EXCEL для решения задач, связанных с прогнозированием временных рядов. Поэтому, статистические термины и определения приводятся лишь для логики изложения и демонстрации идей. Сайт не претендует на математическую строгость изложения статистики. Однако в наших статьях:

•    ПОЛНОСТЬЮ описан встроенный в EXCEL инструментарий по анализу временных рядов (в составе

надстройки Пакет анализа

, различных

типов Диаграмм

(

гистограмма

,

линия тренда

) и формул);

•    созданы файлы примера для построения соответствующих графиков, прогнозов и их интервалов предсказания, вычисления ошибок, генерации рядов (с

трендами

и

сезонностью

) и пр.

Модели временных рядов и модели предметной области

Напомним, что временным рядом (англ. Time Series) называют совокупность наблюдений изучаемой величины, упорядоченную по времени. Наблюдения производятся через одинаковые периоды времени. Другой информацией, кроме наблюдений, исследователь не обладает.

Основной целью исследования временного ряда является его прогнозирование – предсказание будущих значений изучаемой величины. Прогнозирование основывается только на анализе значений ряда в предыдущие периоды, точнее — на идентификации трендов ряда. Затем, после определения трендов, производится моделирование этих трендов и, наконец, с помощью этих моделей — экстраполяция на будущие периоды.

Таким образом, прогнозирование основывается на фактических данных (значениях временного ряда) и модели (

скользящее среднее

,

экспоненциальное сглаживание

,

двойное и тройное экспоненциальное сглаживание

и др.).

Примечание

: Прогнозирование методом Скользящее среднее в MS EXCEL подробно рассмотрено в

одноименной статье

.

В отличие от методов временных рядов,

где зависимости ищутся внутри самого процесса

, в «моделях предметной области» (англ. «Causal Models») кроме самих данных используют еще и законы предметной области.

Примером построения «моделей предметной области» (

моделей строящихся на основе причинно-следственных закономерностей, априорно известных независимо от имеющихся данных

) может быть промышленный процесс изготовления защитной ткани. Пусть в таком процессе известно, что прочность материала ткани зависит от температуры в реакторе, в котором производится процесс полимеризации (температура — контролируемый фактор). Однако, прочность материала является все же случайной величиной, т.к. зависит помимо температуры также и от множества других факторов (качества исходного сырья, температуры окружающей среды, номера смены, умений аппаратчика реактора и пр.). Эти другие факторы в процессе производства стараются держать постоянными (сырье проходит входной контроль и его поставщик не меняется; в помещении, где стоит реактор, поддерживается постоянная температура в течение всего года; аппаратчики проходят обучение и регулярно проводится переаттестация). Задачей статистических методов в этом случае – предсказать значение случайной величины (прочности) при заданном значении изменяемого фактора (температуры).

Обычно для описания таких процессов (зависимость случайной величины от управляемого фактора) являются предметом изучения в разделе статистики «

Регрессионный анализ

», т.к. есть основания сделать гипотезу о существовании причинно-следственной связи между управляемым фактором и прогнозируемой величиной.

Модели, строящиеся на основе причинно-следственных закономерностей, упомянуты в этой статье для того чтобы акцентировать, что их изучение предшествует теме «временные ряды». Так, часть методов, например «Регрессионный анализ» (используется

метод наименьших квадратов — МНК

), используется при анализе временных рядов, но изучаются в моделях предметной области, поэтому неподготовленным «пытливым умам» не стоит игнорировать раздел статистики «

Статистический вывод

», в котором проверяются гипотезы о

равенстве среднего значения

и строятся

доверительные интервалы для оценки среднего

, и упомянутый выше «Регрессионный анализ».

Кратко о типах процессов и моделях для их прогнозирования

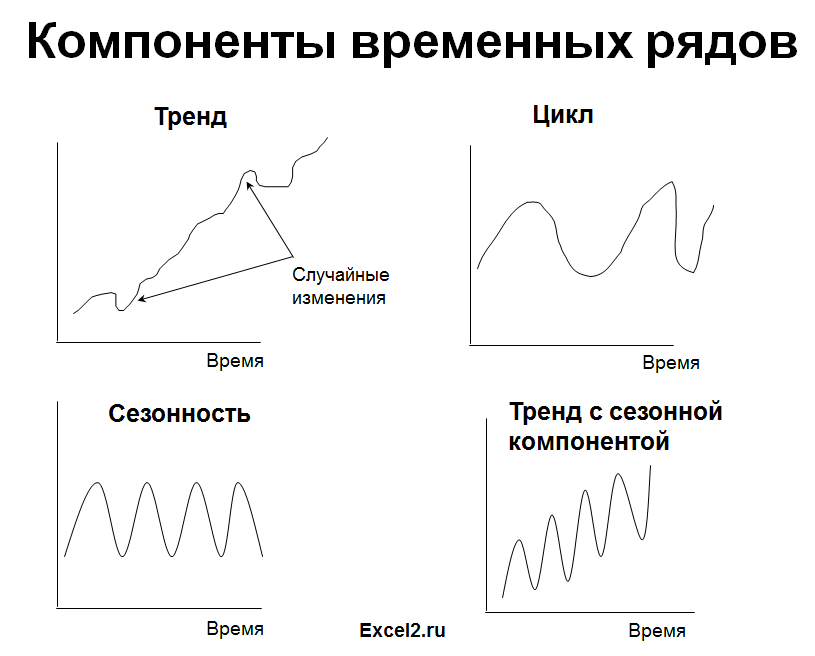
Выбор подходящей модели прогнозирования делается с учетом типа моделируемого процесса (наличие трендов). Рассмотрим основные типы процессов.

1. Стационарный процесс

Стационарный процесс – это случайный процесс чьи характеристики не зависят от времени их наблюдения. Этими характеристиками являются

среднее значение

,

дисперсия

и автоковариация. В стационарном процессе не могут быть выделены предсказуемые паттерны. Соответственно ряды демонстрирующие тренд и сезонность — не стационарны. А вот ряд с цикличностью (апериодической) является стационарным, т.к. на долгосрочном временном интервале появление циклов предсказать невозможно.

Почему стационарный процесс важен? Так как стационарность подразумевает нахождение процесса в состоянии статистической стабильности, то такие временные ряды имеют постоянное среднее значение и дисперсию, которые определяются стандартным образом.

Также для стационарного процесса определяется

функция автокорреляции

– совокупность коэффициентов корреляции значений временного ряда с собственными значениями, сдвинутыми по времени на один или несколько периодов. Сдвиг на несколько временных периодов часто называется лагом (обозначается k).

Функция автокорреляции является важным источником информации о временном ряде.

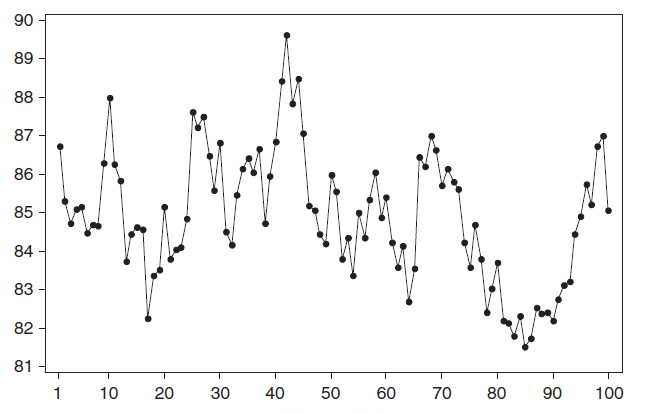
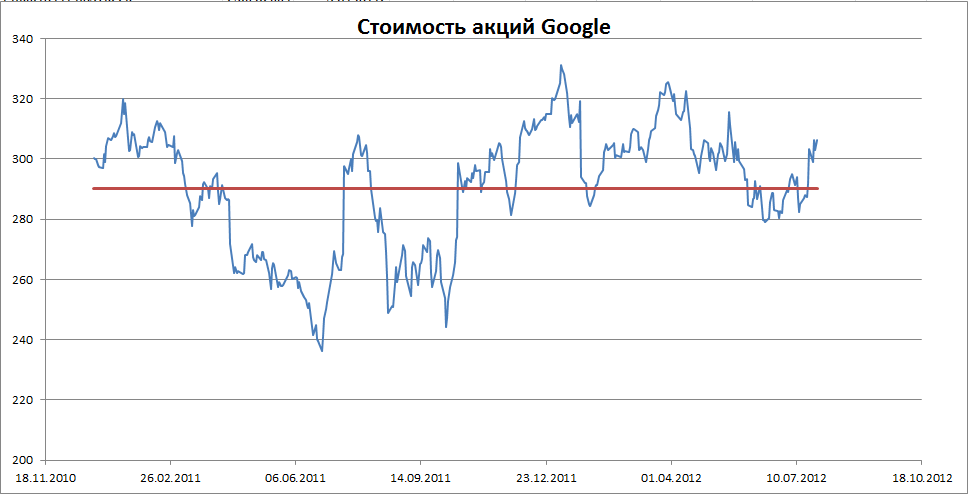
Примером стационарного процесса является колебания биржевого индекса, состоящего из стоимости акций нескольких компаний, около определённого значения (в период стабильности рынка).

Примечание

: график стоимости акций построен на реальных данных, см.

файл примера Google

.

Специальным видом стационарного процесса является белый шум. У этого процесса: среднее значений ряда равно 0, имеется конечная дисперсия и отсутствует корреляция между значениями исходного ряда и рядом сдвинутым на произвольное количество периодов (лагов). В MS EXCEL белый шум можно сгенерировать функцией СЛЧИС().

2. Линейный тренд

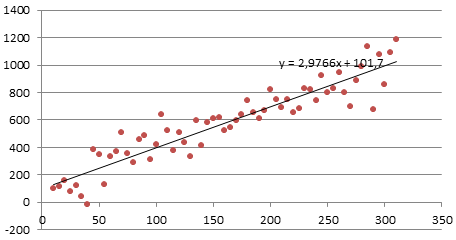
Некоторые процессы генерируют тренд (монотонное изменение значений ряда). Например, линейный тренд y=a*x+b, точнее y=a*t+b, где t – это время. Примером такого (не стационарного) процесса может быть монотонный рост стоимости недвижимости в некотором районе.

Для вычисления прогнозного значения можно воспользоваться методами

Регрессионного анализа

и подобрать параметры тренда: наклон и смещение по вертикали.

Примечание

: Про генерацию случайных значений, демонстрирующих линейный тренд, можно посмотреть в статье

Генерация данных для простой линейной регрессии в EXCEL

.

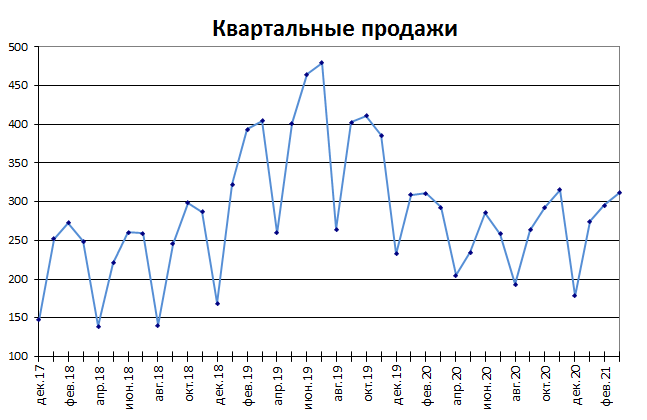
3. Процессы, демонстрирующие сезонность

В сезонном процессе присутствует точно или примерно фиксированный интервал изменений, например, продажи некоторых товаров имеют четко выраженный пик в ноябре-декабре каждого года в связи с праздником.

Для прогнозирования вычисляется индекс сезонности, затем ряд очищается от сезонной компоненты. Если ряд также демонстрирует тренд, то после очистки от сезонности используются методы регрессионного анализа для вычисления тренда.

Примечание

: Про генерацию случайных значений, демонстрирующих сезонность, можно посмотреть в статье Генерация сезонных трендов в EXCEL.

Часто на практике встречаются ряды, являющиеся комбинацией вышеуказанных типов тенденций.

О моделях прогнозирования

В качестве простейшей модели для прогноза можно взять последнее значение индекса. Этой модели соответствует следующий ход мысли исследователя: «Если значение индекса вчера было 306, то и завтра будет 306».

Этой модели соответствует формула Y

_{прогноз(t)}

= Y

_t-1

(прогноз в момент времени t равен значению временного ряда в момент t-1).

Другой моделью является среднее за последние несколько периодов (

скользящее среднее

). Этой модели соответствует другой ход мысли исследователя: «Если среднее значение индекса за последние n периодов было 540, то и завтра будет 540». Этой модели соответствует формула Y

_{прогноз(t)}

=(Y

_t-1

+ Y

_t-2

+…+Y

_t-n

)/n

Обратите внимание, что значения временного ряда берутся с одинаковым весом 1/n, то есть более ранние значения (в момент t-n) влияют на прогноз также как и недавние (в момент t-1). Конечно, в случае, если речь идет о стационарном процессе (без тренда), такая модель может быть приемлема. Чем больше количество периодов усреднения (n), тем меньше влияние каждого индивидуального наблюдения.

Третьей моделью для стационарного процесса может быть

экспоненциальное сглаживание

. В этом случае веса более ранних периодов будут меньше чем веса поздних. При этом учитываются все предыдущие наблюдения. Вес каждого последующего наблюдения больше на 1-α (Фактор затухания), где α (альфа) – это константа сглаживания (от 0 до 1).

Этой модели соответствует формула Y

_{прогноз(t)}

=α*Y

_t-1

+ α*(1-α)*Y

_t-2

+ α*(1-α)2*Y

_t-3

+…)

Формулу можно переписать через предыдущий прогноз Y

_{прогноз(t)}

=α*Y

_t-1

+(1- α)* Y

_{прогноз(t-1)}

= α*(Y

_t-1

— Y

_{прогноз(t-1)}

)+Y

_{прогноз(t-1)}

= α*(ошибка прошлого прогноза)+ прошлый прогноз

При экспоненциальном сглаживании прогнозное значение равно сумме последнего наблюдения с весом альфа и предыдущего прогноза с весом (1-альфа). Этой модели соответствует следующий ход мысли исследователя: «Вчера рано утром я предсказывал, что индекс будет равен 500, но вчера в конце дня значение индекса составило 480 (ошибка составила 20). Поэтому за основу сегодняшнего прогноза я беру вчерашний прогноз и корректирую его на величину ошибки, умноженную на альфа. Параметр альфа (константа) я найду методом экспоненциального сглаживания».

Подробнее о методе прогнозирования на основе экспоненциального сглаживания можно

найти в этой статье

.

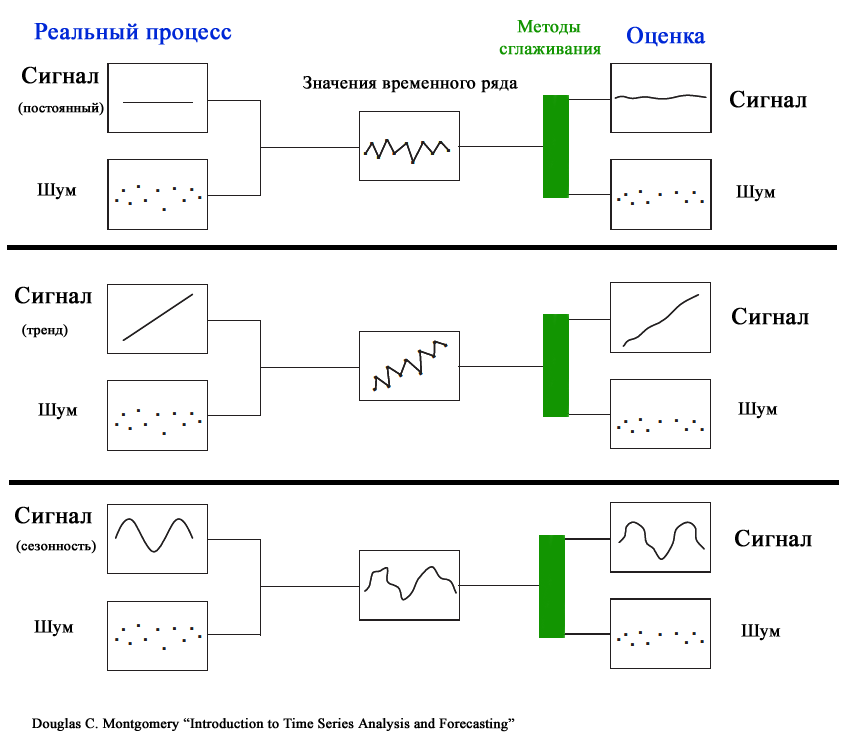
Полезный сигнал и шум

Из-за случайного разброса, присущему временному ряду, временной ряд представляют как комбинацию двух различных компонентов: полезного сигнала и шума (ошибки). Полезный сигнал следует одному из 3-х вышеуказанных типов процессов. Сигнал может быть смоделирован и соответственно спрогнозирован. Шум представляет собой случайные ошибки (со средним значением =0, отсутствием корреляции и с фиксированной

дисперсией

).

Основной задачей моделирования идентификация полезного сигнала, имеющего определенный тренд, от непредсказуемого шума. Для этого как раз и используются Модели сглаживания.

Ссылки на источники статистических данных и обучающие материалы

Все источники англоязычные.

Сайт о применении EXCEL в статистике

Welcome

Национальный Институт Стандартов и технологии

https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm

Using R for Time Series Analysis

https://a-little-book-of-r-for-time-series.readthedocs.io/en/latest/src/timeseries.html#time-series-analysis

Учебник по прогнозированию временных рядов

https://otexts.com/fpp2/

Данные по болезням в Великобритании

https://ms.mcmaster.ca/~bolker/measdata.html

Курсы в Eberly College of Science (есть ссылки на базы данных)

https://online.stat.psu.edu/stat501/lesson/welcome-stat-501

https://online.stat.psu.edu/stat510/

Обнаружение стационарности в данных временных рядов

  Перевод

  Ссылка на автора

Стационарность является важной концепцией в анализе временных рядов. Для краткого (но подробного) введения в тему и причин, которые делают ее важной, взгляните на мой предыдущий пост в блоге на эту тему, Не повторяя слишком много, достаточно сказать, что:

1. Стационарность означает, что статистические свойства временного ряда (или, скорее, процесса, его генерирующего) не изменяются со временем.
2. Стационарность важна, потому что многие полезные аналитические инструменты и статистические тесты и модели полагаются на нее.

Как таковая, способность определять, является ли временной ряд стационарным, важна. Вместо того, чтобы выбирать между двумя строгими вариантами, это обычно означает возможность с высокой вероятностью установить, что серия генерируется стационарным процессом.

В этом кратком посте я расскажу о нескольких способах сделать это.

Зрительные

Самые основные методы обнаружения стационарности основаны на построении графиков данных или их функций и определении визуально, представляют ли они какое-либо известное свойство стационарных (или нестационарных) данных.

Глядя на данные

Попытка определить, был ли временной ряд сгенерирован стационарным процессом, просто взглянув на его график, является сомнительным предприятием. Тем не менее, есть некоторые основные свойства нестационарных данных, которые мы можем искать. Давайте возьмем в качестве примера следующие хорошие сюжеты из [ Hyndman & Athanasopoulos, 2018 ]:

[Hyndman & Athanasopoulos, 2018] приводят несколько эвристик, используемых для исключения стационарности на приведенных выше графиках, соответствующих основной характеристике стационарных процессов (которые мы обсуждали ранее):

• Выдающаяся сезонность может наблюдаться в сериях (d), (h) и (i).
• Заметные тенденции и изменяющиеся уровни можно увидеть в сериях (а), (с), (е), (f) и (i).
• Ряд (i) показывает возрастающую дисперсию.

Авторы также добавляют, что, хотя сильные циклы в ряду (g) могут показаться нестационарными, синхронизация этих циклов делает их непредсказуемыми (из-за лежащей в основе динамической доминирующей популяции рыси, частично обусловленной доступным кормом). Это оставляет ряды (b) и (g) единственными стационарными рядами.

Если, как и я, вы не нашли хотя бы некоторые из этих наблюдений тривиальными, глядя на рисунок выше, вы не единственный. Действительно, это не очень надежный метод обнаружения стационарности, и он обычно используется для получения первоначального представления о данных, а не для того, чтобы делать определенные утверждения.

Рассматривая графики функции автокорреляции (ACF)

автокорреляция является корреляцией сигнала с задержанной копией — или задержкой — самого себя как функция задержки. При построении значения ACF для увеличения лагов (график называется коррелограмма), значения имеют тенденцию быстро уменьшаться до нуля для стационарных временных рядов (см. рисунок 1, справа), тогда как для нестационарных данных ухудшение будет происходить медленнее (см. рисунок 1, слева).

В качестве альтернативы, [ Нильсен, 2006 ] предполагает, что построение коррелограмм на основе как автокорреляций, так и масштабированных автоковариаций и сравнение их обеспечивает лучший способ различения стационарных и нестационарных данных.

Параметрические испытания

Другой, более строгий подход к обнаружению стационарности в данных временных рядов использует статистические тесты, разработанные для обнаруженияконкретные типыстационарности, а именно обусловленные простыми параметрическими моделями порождающего случайного процесса (см. мой предыдущий пост для деталей).

Я представлю здесь самые выдающиеся тесты. Я также назову реализации Python для каждого теста, предполагая, что я их нашел. Для реализации R см. CRAN Task View: анализ временных рядов (также Вот).

Модульные корневые тесты

Тест Дики-Фуллера
Дики-Фуллера test был первым статистическим тестом, разработанным для проверки нулевой гипотезы о том, что единичный корень присутствует в авторегрессионной модели заданного временного ряда и что процесс, таким образом, не является стационарным. Оригинальный тест относится к случаю простой модели AR лаг-1 У теста есть три версии, которые отличаются моделью корневого процесса, для которого они тестируют;

1. Тест для единичного корня: ∆yᵢ = δyᵢ₋₁ + uᵢ
2. Тест для единичного корня со сносом: ∆yᵢ = a₀ + δyᵢ₋₁ + uᵢ
3. Тест для единичного корня с дрейфом и детерминированным временным трендом:
   ∆yᵢ = a₀ + a₁ * t + δyᵢ₋₁ + uᵢ

При выборе используемой версии, которая может существенно повлиять на размер и мощность теста, можно использовать предварительные знания или структурированные стратегии для серии упорядоченных тестов, что позволяет найти наиболее подходящую версию.

Расширения теста были разработаны для размещения более сложных моделей и данных; это включает Дополненный Дики-Фуллер (ADF) (используя AR любого порядкапи поддержку моделирования временных трендов), Тест Филлипса-Перрона (ПП) (добавление устойчивости к неопределенной автокорреляции и гетероскедастичности) и ADF-GLS тест (локально изменяющиеся данные для работы с постоянными и линейными тенденциями).

Реализации Python можно найти в statsmodels а также ARCH пакеты.

Тест КПСС
Другим важным тестом на наличие единичного корня является KPSS тест, [Kwiatkowski et al, 1992] В противоположность семейству тестов Дики-Фуллера нулевая гипотеза предполагает стационарность вокруг среднего или линейного тренда, в то время как альтернативой является наличие единичного корня.

Тест основан на линейной регрессии, разбивая ряд на три части: детерминистический тренд (& beta; t), случайная прогулка (к.т.) и стационарная ошибка (εt), с уравнением регрессии:

и гдеU~ (0, σ²) ин.о.р., Таким образом, нулевая гипотезаH₀: σ² = 0в то время как альтернативаHₐ: σ²> 0, Находит ли стационарность в нулевой гипотезе среднее значение или тренд, определяется установкойβ = 0(в таком случаеИкснеподвижен вокруг среднего значения r₀) илиβ ≠ 0соответственно.

Тест KPSS часто используется для дополнения тестов типа Дики-Фуллера. Я буду касаться того, как интерпретировать такие объединенные результаты в следующем посте.

Реализации Python можно найти в statsmodels а также ARCH пакеты.

Тест Зивота и Эндрюса
Вышеупомянутые тесты не допускают возможности структурный разрыв — резкое изменение, включающее изменение среднего значения или других параметров процесса. Предполагая время разрыва как экзогенное явление, Перрон показал, что способность отклонять единичный корень уменьшается, когда стационарная альтернатива верна и структурный разрыв игнорируется.

[Zivot and Andrews, 1992] предлагают проверку единичного корня, в которой они предполагают, что точное время точки останова неизвестно. После того, как Перрон охарактеризовал форму структурного разрушения, Зивот и Эндрюс приступили к трем моделям для проверки единичного корня:

• Модель A: допускает одноразовое изменение уровня серии.
• Модель B: допускает одноразовое изменение наклона функции тренда.
• Модель C: объединяет одноразовые изменения уровня и наклона функции тренда серии.

Следовательно, для проверки единичного корня по сравнению с альтернативой одноразового структурного разрыва Zivot и Andrews используют следующие уравнения регрессии, соответствующие вышеуказанным трем моделям: [Waheed et al, 2006]

Реализация Python может быть найдена в ARCH пакет и Вот,

Полупараметрические единичные корневые тесты

Тест отношения дисперсии
[Breitung, 2002] предложил непараметрический тест на наличие единичного корня на основе статистики коэффициента дисперсии. Нулевая гипотеза — это процесс I (1) (интегрированный первого порядка), в то время как альтернативой является I (0). Я перечисляю этот тест как полупараметрический, потому что он проверяет конкретное, основанное на модели, понятие стационарности.

Непараметрические тесты

Вслед за ограничениями параметрических тестов и признанием, что они охватывают только узкий подкласс возможных случаев, встречающихся в реальных данных, в литературе по анализу временных рядов появился класс непараметрических тестов на стационарность.

Естественно, что эти тесты открывают многообещающий путь для исследования данных временных рядов: вам больше не нужно предполагать, что очень простые параметрические модели применяются к вашим данным, чтобы выяснить, являются ли они стационарными или нет, или рискуют не обнаружить сложную форму феномен, не охваченный этими моделями.

Реальность этого, однако, более сложна; на данный момент не существует каких-либо широко применяемых непараметрических тестов, которые охватывают все реальные сценарии, генерирующие данные временных рядов. Вместо этого эти тесты ограничиваются определенными типами данных или процессов. Кроме того, я не смог найти реализации ни для одного из следующих тестов

Я упомяну здесь несколько, с которыми я столкнулся:

Непараметрический критерий стационарности в марковских процессах с непрерывным временем

[ Каная, 2011 ] предложить этот непараметрический тест стационарности дляодномерный однородные по времени марковские процессы толькопостроить статистику теста на основе ядра и провести моделирование по методу Монте-Карло для изучения конечного размера выборки и энергетических свойств теста.

Непараметрический критерий стационарности в функциональных временных рядах

[Delft et al, 2017] предлагают непараметрический тест стационарности, ограниченный функциональными временными рядами — данные, полученные путем разделениянепрерывный(в природе) запись времени в естественные последовательные интервалы, например дни. Обратите внимание, что [Delft and Eichler, 2018] предложили тест на локальную стационарность для функциональных временных рядов (см. мой предыдущий пост для некоторых ссылок на локальную стационарность). Кроме того, [Vogt & Dette, 2015] предлагают непараметрический метод для оценки точки плавного изменения в локально стационарной структуре.

Непараметрический критерий стационарности на основе локального анализа Фурье

[ Басу и др., 2009 ] предложить, какой может быть наиболее применимый непараметрический критерий стационарности, представленный здесь, поскольку он применим к любому случайному процессу с дискретным временем с нулевым средним (и я предполагаю, что здесь любая конечная выборка дискретного процесса, которую вы можете иметь, может быть легко преобразована в ноль означает).

Заключительные слова

Это оно. Я надеюсь, что приведенный выше обзор дал вам некоторое представление о том, как подойти к вопросу обнаружения стационарности в ваших данных. Я также надеюсь, что это раскрыло вам сложности этой задачи; из-за отсутствия реализаций для нескольких непараметрических тестов вы будете вынуждены делать серьезные предположения о ваших данных и интерпретировать полученные результаты с необходимым количеством сомнений.

Что касается вопроса о том, что делать, если вы обнаружили какой-то тип стационарности в своих данных, я надеюсь затронуть этот вопрос в следующем посте. Как всегда, я хотел бы услышать о вещах, которые я пропустил или ошибался. Ура!

Ссылки

Академическая литература

• Basu, P., Rudoy, ​​D. & Wolfe, P.J. (2009, апрель). Непараметрический критерий стационарности на основе локального анализа Фурье, В2009 IEEE Международная конференция по акустике, обработке речи и сигналов(стр. 3005–3008). IEEE.
• Breitung, J. (2002). Непараметрические тесты на единичные корни и коинтеграцию,Журнал эконометрики, 108 (2), 343–363.
• Cardinali, A. & Nason, G.P. (2018). Практические мощные вейвлет-пакетные тесты для стационарности второго порядка.Прикладной и вычислительный гармонический анализ,44(3), 558–583.
• Hyndman R.J. & Athanasopoulos G. (2018). Прогнозирование: принципы и практика, OTexts.
• Каная, С. (2011). Непараметрический критерий стационарности в непрерывных и временных марковских процессах,Бумага рынка труда, Оксфордский университет,
• Квятковски Д., Филлипс П.С., Шмидт П. и Шин Ю. (1992). Проверка нулевой гипотезы стационарности против альтернативы единичного корня: насколько мы уверены, что экономические временные ряды имеют единичный корень?,Журнал эконометрики,54(1–3), 159–178.
• Нильсен, Б. (2006). Коррелограммы для нестационарных авторегрессий.Журнал Королевского статистического общества: серия B (статистическая методология),68(4), 707–720.
• Waheed, M., Alam, T. & Ghauri, S.P. (2006). Структурные разрывы и единичный корень: данные из пакистанских макроэкономических временных рядов,Доступный в SSRN 963958,
• van Delft, A., Characteriejus, V. & Dette, H. (2017). Непараметрический критерий стационарности в функциональных временных рядах.Препринт arXiv arXiv: 1708.05248,
• van Delft, A. и Eichler, M. (2018). «Локально стационарные функциональные временные ряды».Электронный журнал статистики12: 107–170.
• Vogt, M. & Dette, H. (2015). Выявление постепенных изменений локально стационарных процессов.Летопись статистики,43(2), 713–740.
• Живот, Э. и Д. Эндрюс, (1992), Еще одно свидетельство большого краха, шок цен на нефть и гипотеза единичного корня,Журнал деловой и экономической статистики,10, 251–270.

Интернет ссылки

• Преобразования данных и модели прогнозирования: что использовать и когда
• Схема прогнозирования
• Документация пакета egcm R
• «Нестационарные временные ряды и единичные корневые тесты» Хейно Бон Нильсен
• Как интерпретировать юнит-тест Zivot & Andrews?

1.2. Распознавание стационарности временного ряда с помощью построения его графика

Существуют различные методы распознавания стационарности временного ряда, однако, пожалуй, самым простым из них является построение графика временного ряда с последующим визуальным определением наличия в нем тренда.

С этой целью мы решили построить график ежемесячных колебаний курса доллара к рублю за период с июня 1992 г. до апреля 2010 г. Читатели, которые не умеют строить диаграммы, могут ознакомиться с представленным ниже алгоритмом действий №1 и № 2

Алгоритм действий № 1 «Как строить диаграммы в Microsoft Excel»

Шаг 1. Поиск данных, их загрузка и первичная обработка в Excel

Во-первых, нужно на сайте Банка России http://www.cbr.ru/ взять необходимые данные по ежедневным курсам доллара за весь интересующий нас период. Во-вторых, после того как мы скопируем рыночную статистику в файл Microsoft Excel, все данные по курсу доллара к рублю с 1 июля 1992 г. по 1 января 1998 г. необходимо разделить на 1000, поскольку на сайте Банка России за этот период они приводятся в неденоминированном виде. В-третьих, для того, чтобы из всего массива данных оставить только необходимые для нас данные, а именно: курс доллара на конец месяца, необходимо их отфильтровать с помощью опций ДАННЫЕ/дополнительно/расширенный фильтр.

Шаг 2. Построение графика в Excel

Выделим с помощью мышки столбец с ежемесячными данными (на конец месяца) по курсу пары рубль — доллар за период с июня 1992 г. (на конец июня из-за отсутствия на сайте Банка России более ранних данных возьмем курс доллара на 1 июля 1992 г.) по апрель 2010 г. и столбец с соответствующими обозначениями месяцев. Далее выбираем в панели инструментов кнопку Вставка (в Excel 2007 г.), либо кнопку Мастер диаграмм (в Excel 1997-2003 гг.), в которой выбираем опцию График (см. рис.1.1).

Рис. 1.1. Опция «График» — ВСТАВКА/МАСТЕР ДИАГРАММ

В результате у нас получился график (см. рис. 1.2), свидетельствующий о том, что динамику колебаний ежемесячного курса доллара нельзя назвать стационарной. Судя по данному графику, можно прийти к выводу, что во временном ряде наблюдается тенденция к росту, а среднее значение курса доллара в разные периоды времени принимает различные значения. В частности, на графике хорошо видно, что во второй половине 1992 г. курс доллара, хотя и систематически рос, но в целом был лишь немного выше нулевой отметки. В то время как к концу 1998 г. он превысил уровень в размере 20 руб., а в 1999 — 2010 гг. курс американской валюты колебался в пределах от 24 руб. до 35 руб.

Рис. 1.2. Ежемесячный курс доллара США, в руб.

Источник: здесь и далее (если особо не оговорено) даются данные Банка России и расчеты автора

Теперь построим аналогичный график в EViews. Однако прежде нам нужно научиться импортировать данные в эту программу из исходного экселевского файла. Умение выполнять эту процедуру потребуется для последующей работы в EViews. С этой целью следует ознакомиться с алгоритмом действий № 2.

Алгоритм действий № 2 «Импорт данных и создание рабочего файла в EViews»

Шаг 1. Подготовка данных в Excel для их последующего импорта в EViews

Прежде чем приступить к созданию диаграммы в EViews нужно сначала импортировать в эту программу из Excel ежемесячные данные по курсу доллара к рублю. При работе в более ранних версиях EViews импортируемые данные необходимо сохранять в формате Excel 5.0/95 поскольку при использовании других экселевских форматов в EViews появится сообщение об ошибке. Однако в последних версиях EViews можно загружать данные из экселевских файлов в любом формате, в том числе и в форматах Excel 2007 и 2010 года.

Причем, импортируемые данные следует размещать в виде столбца в самой верхней строке экселевского листа слева. Например, заголовок первого столбца с данными должен быть помещен в ячейке B1, заголовок второго столбца с данными — в ячейке C1 и так далее, в то время как заголовок с соответствующими датами — в ячейке A1.

Заголовки столбцов следует обозначать латинскими буквами, поскольку англоязычная программа EViews не понимает кириллицу. В частности, столбец с ежемесячными данными по курсу доллара США мы решили обозначить как USDOLLAR (поместили в ячейку B1), а заголовок (в ячейке А1) с названиями месяцев — Month. И последний важный момент: экселевский лист, на котором мы разместим подготовленные к импорту в EViews данные, нужно также переименовать латинскими буквами. В данном случае мы назвали экселевский лист с импортируемыми данными sheet1.

Шаг 2. Создание рабочего файла в EViews

Для того чтобы создать рабочий файл, содержащий данные, с которыми мы собираемся работать, необходимо в главном меню EViews выбрать опции File/New/Workfile. В результате откроется следующее диалоговое мини-окно (см. рис. 1.3.):

Рис. 1.3. Диалоговое окно Workfile create

В этом диалоговом окне необходимо задать соответствующую информацию. Так, в мини-окне Workfile structure type (структура рабочего файла) мы задаем опцию Dated-regular frequency (даты с определенной частотой). Соответственно, в мини-окне Frequency (частота данных) ставим опцию Monthly (ежемесячные данные), в Start date (начальная дата) — 92:06 (июнь 1992 г.), в End date(конечная дата) — 2010:03 (март 2010 г.). Хочу заметить, что в мини-окне End date дату года нужно обязательно давать четырехзначной, в то время как в Start date она может быть двузначной. В результате у нас получится (см. рис.1. 4) неполный рабочий файл (Workfile): в нем будут отсутствовать данные, которые еще предстоит импортировать.

Рис. 1.4. Неполный рабочий файл Workfile

Шаг 3. Импорт данных в EViews

Перед импортом данных экселевский файл нужно обязательно закрыть, поскольку иначе появится сообщение об ошибке. При работе в последних версиях EViews в командной строке этой программы нужно воспользоваться опцией IMPORT/IMPORT FROM FILE. После открытия экселевского файла появится окошко Excel read‑Step 1 of 3 (см. рис. 1.5), в котором следует выбрать одну из двух опций: Predefined range (предопределенный диапазон) или Custom range (обычный диапазон). В случае выбора Predefined range в EViews загружаются уже выбранные программой данные, а если вы воспользуетесь опцией Custom range, то в этом случае можно самому выбрать требуемый диапазон данных, в том числе внести необходимые правки в опции SHEET (лист), START CELL (начальная ячейка), END CELL (конечная ячейка).

Рис. 1.5. Окно Excel 97-2003 Read — Step 1 of 3

Если вы работает в более ранних версиях EViews, то при импорте данных в командной строке нужно выбрать опции File/Import/Read Text-Lotus-Excel. После этого появится новое диалоговое окно Excel Spreadsheet Import (импорт листа Excel). В открывшемся диалоговом окне (см. рис. 1.6) нужно отметить в мини-окне Excel5+sheet name — название листа, которое у нас обозначено как sheet1. В мини-окне Names for series or Number if named in file (название для серии данных или номер серии данных, если у нее есть название в файле) — поставим цифру 1, поскольку мы импортируем лишь одну серию данных, которую уже назвали USDOLLAR. В остальных мини-окнах соответствующие опции в EViews устанавливаются по умолчанию. В частности, в мини-окне UPPER-LEFT DATA CELL (верхняя левая ячейка с данными) — по умолчанию указывается ячейка B2.

Более подробно обо всех нюансах импорта данных из Excel в EViews можно прочитать, например, в книге Турунцевой М.Ю. Анализ временных рядов / МИЭФ ГУ-ВШЭ. — М., 2003 стр. 4-9.

Рис. 1.6. Диалоговое окно Excel Spreadsheet Import (импорт листа Excel)

Поскольку мы уже создали рабочий файл в EViews, то построить график курса доллара, аналогичный экселевскому (см. рис. 1.2), не представляет особого труда. В рабочем файле (Workfile) EViews открываем файл USDOLLAR, после чего используем для построения диаграммы в виде графика (LINE) опции VIEW/GRAPH/LINE (см. рис. 1.7).

Рис. 1.7. Использование опции VIEW/GRAPH/LINE для построения в EViews линейного графика LINE

В результате у нас получилась диаграмма (рис. 1.8), вполне аналогичная (если не считать различный тип форматирования) диаграмме на рис 1.2, построенной в Excel. Для того чтобы сохранить полученную диаграмму в EViews на отдельном листе следует нажать верхнюю кнопку FREEZE (окончательно принять).

Рис 1.8. График курса доллара, полученный в EViews

Таким образом, построив соответствующие графики в EViews и Excel, нам удалось выяснить, что временной ряд, характеризующий динамику ежемесячного курса доллара, является нестационарным, поскольку в нем наблюдается ярко выраженный тренд. Вместе с тем, как мы уже говорили ранее, нестационарный временной ряд содержит не только тренд, но и случайную компоненту. Следовательно, чтобы сделать адекватный прогноз по курсу доллара необходимо учесть как тренд, так и случайную компоненту, поскольку оба эти фактора существенно влияют на динамику валюты.

Схематично, наша дальнейшая работа, которой посвящены последующие главы этой книги, будет заключаться в следующем. Во-первых, нам нужно составить уравнение регрессии, с помощью которого можно будет делать прогнозы с необходимой точностью. Во-вторых, необходимо протестировать данное уравнение регрессии (прогностическую модель) на его адекватность с точки зрения прогностических качеств. В-третьих, надо составить точечные прогнозы по курсу американской валюты, используя полученную математическую модель. В-четвертых, нужно удостовериться в приемлемой точности составленных точечных прогнозов. В-пятых, необходимо убедиться, что получившиеся в результате отклонения фактического курса доллара от его предсказанных (расчетных) значений представляют собой стационарный ряд. В-шестых, надо посмотреть, является ли распределения остатков нормальным, что позволит нам впоследствии составить интервальные прогнозы — с учетом диапазона отклонений точечных прогнозов от фактического курса доллара — с определенным уровнем надежности. В-седьмых, нужно проверить, соответствует ли точность интервальных прогнозов заданному уровню надежности. В-восьмых, научиться применять полученную статистическую модель для составления рекомендуемых цен покупки и продажи валюты, используемых в качестве стоп-приказов при работе на валютном рынке. При этом выполнение всех этих процедур будет сопровождаться подробным рассказом о том, как их можно выполнить в Excel или EViews, что поможет нашим читателям впоследствии самостоятельно решать эти задачи.

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)