17 авг. 2022 г.
читать 2 мин
В статистике проверка гипотезы используется для проверки некоторого предположения о параметре совокупности .
Существует множество различных типов проверки гипотез, которые вы можете выполнять в зависимости от типа данных, с которыми вы работаете, и цели вашего анализа.
В этом руководстве объясняется, как выполнять следующие типы проверок гипотез в Excel:
- Один образец t-критерия
- Два выборочных t-теста
- Парные выборки t-критерий
- Z-тест одной пропорции
- Z-тест с двумя пропорциями
Давайте прыгать!
Пример 1: один образец t-критерия в Excel
Одновыборочный t-критерий используется для проверки того, равно ли среднее значение совокупности некоторому значению.
Например, предположим, что ботаник хочет знать, равна ли средняя высота определенного вида растений 15 дюймам.
Чтобы проверить это, она собирает случайную выборку из 12 растений и записывает их высоту в дюймах.
Она записала бы гипотезы для этого конкретного t-критерия одной выборки следующим образом:
- H 0 : µ = 15
- НА : мк ≠ 15
Обратитесь к этому руководству для пошагового объяснения того, как выполнить эту проверку гипотезы в Excel.
Пример 2. Двухвыборочный t-критерий в Excel
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
Например, предположим, что исследователи хотят знать, имеют ли два разных вида растений одинаковую среднюю высоту.
Чтобы проверить это, они собирают случайную выборку из 20 растений каждого вида и измеряют их высоту.
Исследователи записали бы гипотезы для этого конкретного двухвыборочного t-критерия следующим образом:
- Н 0 : мк 1 = мк 2
- H A : µ 1 ≠ µ 2
Обратитесь к этому руководству для пошагового объяснения того, как выполнить эту проверку гипотезы в Excel.
Пример 3: t-критерий парных выборок в Excel
Стьюдентный критерий для парных выборок используется для сравнения средних значений двух выборок, когда каждое наблюдение в одной выборке может быть сопоставлено с наблюдением в другой выборке.
Например, предположим, что мы хотим знать, значительно ли влияет определенная учебная программа на успеваемость студента на конкретном экзамене.
Чтобы проверить это, у нас есть 20 учеников в классе, которые проходят предварительный тест. Затем каждый из студентов участвует в учебной программе в течение двух недель. Затем учащиеся пересдают пост-тест аналогичной сложности.
Мы бы записали гипотезы для этого конкретного двухвыборочного t-критерия следующим образом:
- H 0 : µ до = µ после
- H A : µ до ≠ µ после
Обратитесь к этому руководству для пошагового объяснения того, как выполнить эту проверку гипотезы в Excel.
Пример 4: Z-тест одной пропорции в Excel
Z-критерий одной пропорции используется для сравнения наблюдаемой пропорции с теоретической.
Например, предположим, что телефонная компания утверждает, что 90% ее клиентов удовлетворены их услугами.
Чтобы проверить это утверждение, независимый исследователь собрал простую случайную выборку из 200 клиентов и спросил их, довольны ли они своим сервисом.
Мы бы записали гипотезы для этого конкретного двухвыборочного t-критерия следующим образом:
- Н 0 : р = 0,90
- НА : р ≠ 0,90
Обратитесь к этому руководству для пошагового объяснения того, как выполнить эту проверку гипотезы в Excel.
Пример 5: Z-тест для двух пропорций в Excel
Z-критерий двух пропорций используется для проверки разницы между двумя пропорциями населения.
Например, предположим, что руководитель школьного округа утверждает, что процент учащихся, предпочитающих шоколадное молоко обычному молоку в школьных столовых, одинаков для школы 1 и школы 2.
Чтобы проверить это утверждение, независимый исследователь получает простую случайную выборку из 100 учеников из каждой школы и опрашивает их об их предпочтениях.
Мы бы записали гипотезы для этого конкретного двухвыборочного t-критерия следующим образом:
- Н 0 : р 1 = р 2
- Н А : п 1 ≠ п 2
Обратитесь к этому руководству для пошагового объяснения того, как выполнить эту проверку гипотезы в Excel.
Рассмотрим использование MS EXCEL при проверке статистических гипотез о дисперсии нормального распределения. Вычислим тестовую статистику χ
2
и Р-значение (Р-
value
).
Первое знакомство с
процедурой проверки гипотез
(Hypothesis testing) для
дисперсии
рекомендуется начать с изучения построения соответствующего
доверительного интервала
(см. статью
Доверительный интервал для оценки дисперсии в MS EXCEL
).
Примечание
:
Перечень статей о
проверке гипотез
приведен в статье
Проверка статистических гипотез в MS EXCEL
.
СОВЕТ
: Для
проверки гипотез
потребуется знание следующих понятий:
-
дисперсия и стандартное отклонение
,
-
доверительный интервал для оценки среднего
,
-
выборочное распределение статистики
,
-
уровень доверия/ уровень значимости
,
-
нормальное распределение
,
распределение χ
2
и ихквантили
.
Формулировка задачи.
Из
генеральной совокупности
имеющей
нормальное распределение
с неизвестным
средним значением
μ (мю) и неизвестной
дисперсией
σ
2
(
сигма
2
) взята
выборка
размера n. Необходимо проверить
двустороннюю статистическую гипотезу
о равенстве неизвестной
дисперсии
σ
2
заданному исследователем значению σ
0
2
(англ. Inference on the variance of a normal population).
Примечание
: Изложенный ниже метод
проверки гипотез
о
дисперсии
,очень чувствителен к выполнению требования о
нормальности распределения
, из которого берется
выборка
. Если это требование не выполняется, то этот метод
проверки гипотез
будет давать неточные значения.
В качестве
точечной оценкой дисперсии распределения,
из которого взята
выборка
, используют
Дисперсию выборки
s
2
.
Перед
процедурой проверки гипотезы
, исследователь устанавливает требуемый
уровень значимости
– это допустимая для данной задачи
ошибка первого рода
, т.е. вероятность отклонить
нулевую гипотезу
, когда она верна (
уровень значимости
обозначают буквой α (альфа) и чаще всего выбирают равным 0,1; 0,05 или 0,01).
Тестовой статистикой
для проверки этой гипотезы является величина:
В статье про
χ
2
-распределение показано
, что
выборочное распределение
этой статистики, имеет
χ
2
-распределение
с n-1 степенью свободы, которое является «
эталонным распределением
» (англ. Reference distribution) для данного теста о равенстве
дисперсии
.
Значение, которое приняла
χ
2
-статистика
обозначим
χ
0
2
.
Нулевая гипотеза
Н
0
о равенстве
дисперсии
значению σ
0
2
отвергается в том случае, если
χ
0
2
>χ
2
α/2,n-1
или
χ
0
2
<χ
2
1-α/2,n-1
где:
χ
2
α/2,n-1
– верхний α/2-квантиль распределения
χ
2
с
n
-1 степенью свободы
(такое значение случайной величины
χ
2
n-1
,
что
P
(
χ
2
n-1
>=
χ
2
α/2,n-1
)=α/2
).
χ
2
1-α/2,n-1
– верхний (1-α/2)-квантиль распределения
χ
2
с
n
-1 степенью свободы
(такое значение случайной величины
χ
2
n-1
,
что
P
(
χ
2
n-1
>=
χ
2
1-α/2,n-1
)
=1-α/2
).
Примечание
: Подробнее про
квантили
распределения можно прочитать в статье
Квантили распределений MS EXCEL
.
В MS EXCEL
верхний α/2-квантиль распределения
χ
2
вычисляется с помощью формулы
=ХИ2.ОБР.ПХ(α/2; n-1)
Верхний
(1-α
/2)-квантиль
вычисляется с помощью аналогичной формулы
=ХИ2.ОБР.ПХ(1-α/2; n-1)
или через равный ему
нижний квантиль
=ХИ2.ОБР(α/2; n-1)
Вычисления приведены в
файле примера
.
В случае
односторонней гипотезы
речь идет об отклонении
дисперсии
только в одну сторону: либо больше либо меньше σ
0
2
. Если
альтернативная гипотеза
звучит как σ
2
> σ
0
2
, то гипотеза Н
0
отвергается в случае
χ
0
2
>
χ
2
α
,n-1
. Если
альтернативная гипотеза
звучит как σ
2
< σ
0
2
, то гипотеза Н
0
отвергается в случае
χ
0
2
<
χ
2
1-α
,n-1
.
СОВЕТ
: О
проверке гипотезы о равенстве дисперсий двух нормальных распределений
(
F-test
) см. статью
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
.
Вычисление Р-значения
При
проверке гипотез
большое распространение также получил еще один эквивалентный подход, основанный на вычислении
p
-значения
(p-value).
СОВЕТ
: Подробно про
p
-значение
написано в статье
Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)
.
Если
p-значение
, вычисленное на основании
выборки
, меньше чем заданный
уровень значимости α
, то
нулевая гипотеза
отвергается и принимается
альтернативная гипотеза
. И наоборот, если
p-значение
больше α, то
нулевая гипотеза
не отвергается.
Формула для вычисления
p-значения
зависит от формулировки
альтернативной гипотезы
:
-
Для
односторонней гипотезы
σ
2
< σ
0
2
p-значение
вычисляется как
=ХИ2.РАСП(
χ
0
2
; n-1;ИСТИНА)
-
Для другой
односторонней гипотезы
σ
2
> σ
0
2
p-значение
вычисляется как
=ХИ2.РАСП.ПХ(
χ
0
2
; n-1)
-
Для
двусторонней гипотезы
p-значение
вычисляется как
=2*МИН(ХИ2.РАСП(
χ
0
2
;n-1;ИСТИНА); ХИ2.РАСП.ПХ(
χ
0
2
;n-1))
Соответственно,
χ
0
2
= (СЧЁТ(
выборка
)-1)* ДИСП.В(
выборка
)/ σ
0
2
, где
выборка
– ссылка на диапазон, содержащий значения
выборки
.
СОВЕТ
: Подробнее про вышеуказанные функции MS EXCEL см.
статью про
χ
2
-распределение
.
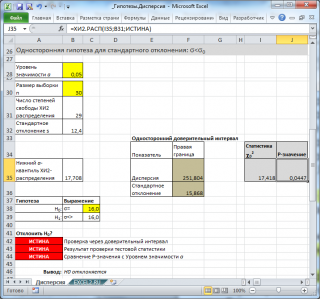
В
файле примера на листе Дисперсия
показано решение задач
проверки двусторонней
и
односторонних гипотез
.
Many statistical tests make the assumption that the values in a dataset are normally distributed.
One of the easiest ways to test this assumption is to perform a Jarque-Bera test, which is a goodness-of-fit test that determines whether or not sample data have skewness and kurtosis that matches a normal distribution.
This test uses the following hypotheses:
H0: The data is normally distributed.
HA: The data is not normally distributed.
The test statistic JB is defined as:
JB =(n/6) * (S2 + (C2/4))
where:
- n: the number of observations in the sample
- S: the sample skewness
- C: the sample kurtosis
Under the null hypothesis of normality, JB ~ X2(2).
If the p-value that corresponds to the test statistic is less than some significance level (e.g. α = .05), then we can reject the null hypothesis and conclude that the data is not normally distributed.
This tutorial provides a step-by-step example of how to perform a Jarque-Bera test for a given dataset in Excel.
Step 1: Create the Data
First, let’s create a fake dataset with 15 values:
Step 2: Calculate the Test Statistic
Next, calculate the JB test statistic. Column E shows the formulas used:
The test statistic turns out to be 1.0175.
Step 3: Calculate the P-Value
Under the null hypothesis of normality, the test statistic JB follows a Chi-Square distribution with 2 degrees of freedom.
So, to find the p-value for the test we will use the following function in Excel: =CHISQ.DIST.RT(JB test statistic, 2)
The p-value of the test is 0.601244. Since this p-value is not less than 0.05, we fail to reject the null hypothesis. We don’t have sufficient evidence to say that the dataset is not normally distributed.
In other words, we can assume that the data is normally distributed.
Additional Resources
How to Create a Q-Q Plot in Excel
How to Perform a Chi-Square Goodness of Fit Test in Excel
Решения задач на проверку статистических гипотез
Проверка статистических гипотез включает в себя большой пласт задач математической статистики. Зная некоторые характеристики выборки (или имея просто выборочные данные), мы можем проверять гипотезы о виде распределении случайной величины или ее параметрах (примеры этих задач на странице Проверка гипотез о параметрах распределения).
Ниже в примерах мы разберем основные учебные задачи на проверку гипотез о виде распределения. Чаще всего для этого используется критерий согласия $chi^2$ Пирсона, а также критерий Колмогорова-Смирнова.
Критерий согласия Пирсона (или критерий $chi^2$ — «хи квадрат») — наиболее часто употребляемый для проверки гипотезы о принадлежности некоторой выборки теоретическому закону распределения (в учебных задачах чаще всего проверяют «нормальность» — распределение по нормальному закону).
В учебных задачах обычно используется следующий алгоритм:
- Выбор теоретического закона распределения (обычно задан заранее, если не задан — анализируем выборку, например с помощью гистограммы относительных частот, которая имитирует плотность распределения).
- Оцениваем параметры распределения по выборке (для этого вычисляется математическое ожидание и дисперсия): $a, sigma$ для нормального, $a,b$ — для равномерного, $lambda$ — для распределения Пуассона и т.д.
- Вычисляются теоретические значения частот (через теоретические вероятности попадания в интервал) и сравниваются с исходными (выборочными).
- Анализируется значение статистики $chi^2$ и делается вывод о соответствии (или нет) теоретическому закону распределения.
Подробные примеры на разные распределения и критерии вы найдете ниже.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
73 Наблюдаемое значение статистики Пирсона попадает в критическую область Кнабл Kkp, поэтому есть основания отвергать основную гипотезу. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Пример . Имеются следующие данные о количестве заявок на автомобили технической помощи по дням. Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Скачать решение
Нормальное распределение (Normal Distribution)
Пример 1. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X по результатам выборки:
X 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
N 7 9 28 27 30 26 21 25 22 9 5
Свойства нормального распределения
Кривая стандартного нормального распределения симметрична относительно Среднего арифметического (Mean), Медианы (Median) и Моды (Mode). Более того, также являются нормальным распределением произведение двух нормальных распределений и их сумма. Магия, не правда ли? Существуют и другие, более сложные закономерности, пока обойдемся самыми понятными.
Вы слышали об эмпирическом правиле? Оно часто используется в статистике и гласит: «68,27% наблюдений случайной Выборки (Sample) лежат в пределах одного Стандартного отклонения (Standard Deviation), 95,45% – в пределах двух, а 99,73 – в пределах трех стандартных отклонений от среднего»:
Это правило позволяет нам идентифицировать Выбросы (Outlier) и очень полезно при Проверке на нормальность (Normality Test).
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Преимущество его заключается в том, что тот же подход можно использовать для сравнения любого распределения, не обязательно только нормального распределения. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Если копнуть глубже, то нормальное распределение можно найти в распределении многих показателях в системах связи (сигналы, шумы, помехи и другие), под нормальное распределение подгоняют многие финансовые показатели. Хотя следует подчеркнуть, что именно подгоняют, поскольку признаки нормальности в этих случаях часто бывают смещены.
Проверка гипотезы о нормальном распределении по критерию Пирсона. Подробный пример решения
Стандартное отклонение (σ), может принимать значения от нуля до плюс бесконечности. При увеличении стандартного отклонения график плотности нормального распределения становится более растянутым вдоль оси Ox, а при уменьшении — наоборот, сжимается. Это показано на графике снизу.
Проверка гипотезы о нормальном распределении
Критерий согласия Пирсона:
| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x — xср|*f | (x — xср) 2 *f | Частота, fi/n |
| 43 — 45.83 | 44.42 | 1 | 44.42 | 1 | 8.88 | 78.91 | 0.0278 |
| 45.83 — 48.66 | 47.25 | 1 | 47.25 | 2 | 6.05 | 36.64 | 0.0278 |
| 48.66 — 51.49 | 50.08 | 6 | 300.45 | 8 | 19.34 | 62.33 | 0.17 |
| 51.49 — 54.32 | 52.91 | 18 | 952.29 | 26 | 7.07 | 2.78 | 0.5 |
| 54.32 — 57.15 | 55.74 | 4 | 222.94 | 30 | 9.75 | 23.75 | 0.11 |
| 57.15 — 59.98 | 58.57 | 6 | 351.39 | 36 | 31.6 | 166.44 | 0.17 |
| 36 | 1918.73 | 82.7 | 370.86 | 1 |
| Интервалы группировки | Наблюдаемая частота ni | x1 = (xi— x )/s | x2 = (xi+1— x )/s | Ф(x1) | Ф(x2) | Вероятность попадания в i-й интервал, pi = Ф(x2) — Ф(x1) | Ожидаемая частота, 36pi | Слагаемые статистики Пирсона, Ki |
| 43 — 45.83 | 1 | -3.16 | -2.29 | -0.5 | -0.49 | 0.01 | 0.36 | 1.14 |
| 45.83 — 48.66 | 1 | -2.29 | -1.42 | -0.49 | -0.42 | 0.0657 | 2.37 | 0.79 |
| 48.66 — 51.49 | 6 | -1.42 | -0.56 | -0.42 | -0.21 | 0.21 | 7.61 | 0.34 |
| 51.49 — 54.32 | 18 | -0.56 | 0.31 | -0.21 | 0.13 | 0.34 | 12.16 | 2.8 |
| 54.32 — 57.15 | 4 | 0.31 | 1.18 | 0.13 | 0.38 | 0.26 | 9.27 | 3 |
| 57.15 — 59.98 | 6 | 1.18 | 2.06 | 0.38 | 0.48 | 0.0973 | 3.5 | 1.78 |
| 36 | 9.84 |
Пример №2 . Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение находим с помощью калькулятора.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x- x )·f | (x- x ) 2 ·f | (x- x ) 3 ·f | Частота, fi/n |
| 5 | 15 | 75 | 15 | 114.45 | 873.25 | -6662.92 | 0.075 |
| 7 | 26 | 182 | 41 | 146.38 | 824.12 | -4639.79 | 0.13 |
| 9 | 25 | 225 | 66 | 90.75 | 329.42 | -1195.8 | 0.13 |
| 11 | 30 | 330 | 96 | 48.9 | 79.71 | -129.92 | 0.15 |
| 13 | 26 | 338 | 122 | 9.62 | 3.56 | 1.32 | 0.13 |
| 15 | 21 | 315 | 143 | 49.77 | 117.95 | 279.55 | 0.11 |
| 17 | 24 | 408 | 167 | 104.88 | 458.33 | 2002.88 | 0.12 |
| 19 | 20 | 380 | 187 | 127.4 | 811.54 | 5169.5 | 0.1 |
| 21 | 13 | 273 | 200 | 108.81 | 910.74 | 7622.89 | 0.065 |
| 200 | 2526 | 800.96 | 4408.62 | 2447.7 | 1 |
Пример 2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение.
Таблица для расчета показателей.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Естественно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он характеризует близость эмпирического и теоретического распределений. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Имеется несколько критериев согласия. Наиболее часто используется критерий согласия К.Пирсона («хи-квадрат»). Здесь мы ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.
Проверка гипотезы о виде распределения онлайн
Если наблюдаемые данные полностью соответствуют нормальному распределению, значение статистики KS будет равно 0. Значение P используется, чтобы решить, достаточно ли велика разница, чтобы отклонить нулевую гипотезу:
| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x — xср|*f | (x — xср) 2 *f | Частота, fi/n |
| 43 — 45.83 | 44.42 | 1 | 44.42 | 1 | 8.88 | 78.91 | 0.0278 |
| 45.83 — 48.66 | 47.25 | 1 | 47.25 | 2 | 6.05 | 36.64 | 0.0278 |
| 48.66 — 51.49 | 50.08 | 6 | 300.45 | 8 | 19.34 | 62.33 | 0.17 |
| 51.49 — 54.32 | 52.91 | 18 | 952.29 | 26 | 7.07 | 2.78 | 0.5 |
| 54.32 — 57.15 | 55.74 | 4 | 222.94 | 30 | 9.75 | 23.75 | 0.11 |
| 57.15 — 59.98 | 58.57 | 6 | 351.39 | 36 | 31.6 | 166.44 | 0.17 |
| 36 | 1918.73 | 82.7 | 370.86 | 1 |
На чтение 4 мин. Просмотров 53 Опубликовано 06.06.2021
Проверка гипотез – одна из основных тем в области логической статистики. Есть несколько шагов для проверки гипотезы, и многие из них требуют статистических расчетов. Статистическое программное обеспечение, такое как Excel, можно использовать для проверки гипотез. Мы увидим, как функция Excel Z.TEST проверяет гипотезы о неизвестном среднем значении совокупности.
Содержание
- Условия и предположения
- Структура проверки гипотез
- Функция Z.TEST
- Примечания и предупреждения
- Пример
Условия и предположения
Начнем формулируя предположения и условия для этого типа проверки гипотез. Для вывода о среднем мы должны иметь следующие простые условия:
- Выборка представляет собой простую случайную выборку.
- Размер выборки невелик по сравнению с генеральной совокупностью. Обычно это означает, что размер генеральной совокупности более чем в 20 раз превышает размер выборки.
- Изучаемая переменная имеет нормальное распределение.
- Стандартное отклонение генеральной совокупности известно .
- Среднее значение для генеральной совокупности неизвестно.
Маловероятно, что все эти условия будут выполнены на практике. Однако эти простые условия и соответствующая проверка гипотезы иногда встречаются на ранних этапах статистического класса. После изучения процесса проверки гипотез эти условия смягчаются, чтобы работать в более реалистичных условиях.
Структура проверки гипотез
Рассматриваемая нами конкретная проверка гипотез имеет следующую форму:
- Сформулируйте нулевую и альтернативную гипотезы.
- Рассчитайте статистику теста, которая представляет собой z -счет.
- Рассчитайте p-значение, используя нормальное распределение. В этом случае p-значение представляет собой вероятность получения не менее экстремальной, чем наблюдаемая статистика теста, при условии, что нулевая гипотеза верна.
- Сравните p-значение с уровнем значимости, чтобы определить отвергать или не отвергать нулевую гипотезу.
Мы видим, что шаги два и три требуют больших вычислительных ресурсов по сравнению с двумя шагами один и четыре. Функция Z.TEST выполнит эти вычисления за нас.
Функция Z.TEST
Функция Z.TEST делает все расчетов из шагов два и три выше. Он выполняет большую часть обработки чисел для нашего теста и возвращает p-значение. В функцию можно ввести три аргумента, каждый из которых отделяется запятой. Ниже объясняются три типа аргументов для этой функции.
- Первый аргумент для этой функции – это массив образцов данных. Мы должны ввести диапазон ячеек, который соответствует расположению выборки данных в нашей электронной таблице.
- Второй аргумент – это значение μ, которое мы проверяем в наших гипотезах. Итак, если наша нулевая гипотеза H 0 : μ = 5, то мы должны ввести 5 для второго аргумента.
- Третий аргумент – это значение известное стандартное отклонение населения. Excel рассматривает это как необязательный аргумент.
Примечания и предупреждения
Следует отметить несколько моментов. об этой функции:
- Значение p, выводимое функцией, одностороннее. Если мы проводим двусторонний тест, то это значение необходимо удвоить.
- Односторонний вывод p-значения из функции предполагает, что выборочное среднее больше, чем значение μ, которое мы тестируем против. Если выборочное среднее меньше значения второго аргумента, то мы должны вычесть выходные данные функции из 1, чтобы получить истинное p-значение нашего теста.
- Последний аргумент для Стандартное отклонение населения не является обязательным. Если он не введен, это значение автоматически заменяется в расчетах Excel на стандартное отклонение выборки. Когда это будет сделано, теоретически следует использовать t-тест.
Пример
Мы предполагаем, что следующие данные взяты из простой случайной выборки нормально распределенной совокупности с неизвестным средним и стандартным отклонением 3:
1, 2, 3, 3, 4 , 4, 8, 10, 12
При уровне значимости 10% мы хотим проверить гипотезу о том, что данные выборки взяты из генеральной совокупности со средним большим чем 5. Более формально мы имеем следующие гипотезы:
- H 0 : μ = 5
- H a : μ> 5
Мы используем Z. ТЕСТ в Excel, чтобы найти значение p для этой проверки гипотезы.
- Введите данные в столбец в Excel. Предположим, это от ячейки A1 до A9.
- В другую ячейку введите = Z.TEST (A1: A9,5,3)
- Результат – 0,41207.
- Поскольку наше значение p превышает 10%, мы не можем отклонить нулевую гипотезу.
Z.TEST Функция может использоваться для тестов с нижним хвостом, а также для двусторонних тестов. Однако результат не такой автоматический, как в этом случае. Другие примеры использования этой функции см. Здесь.