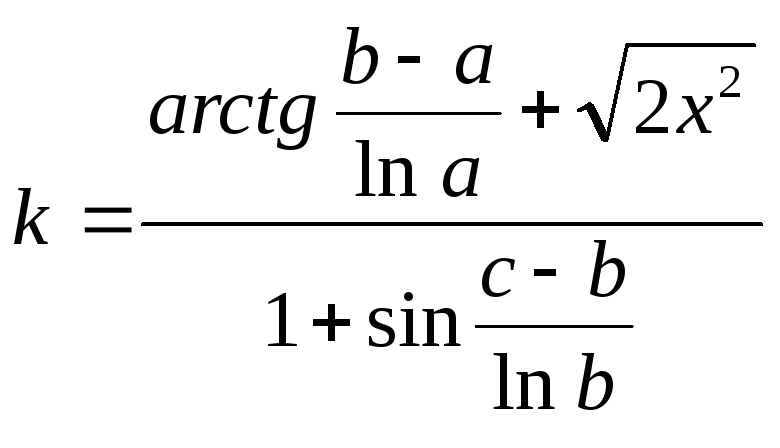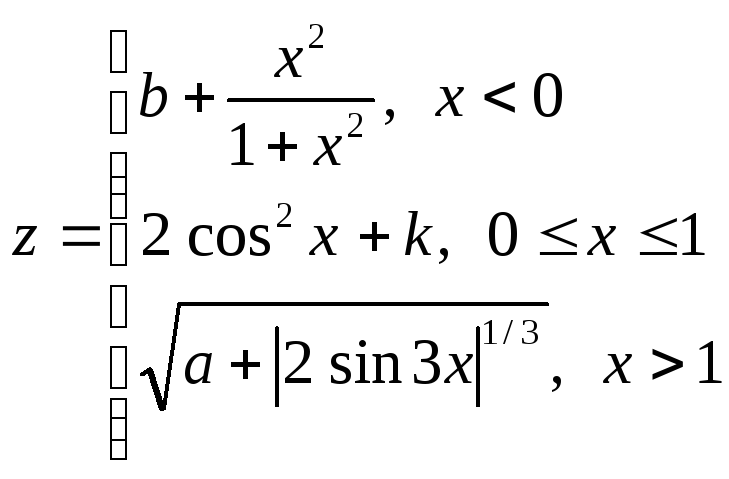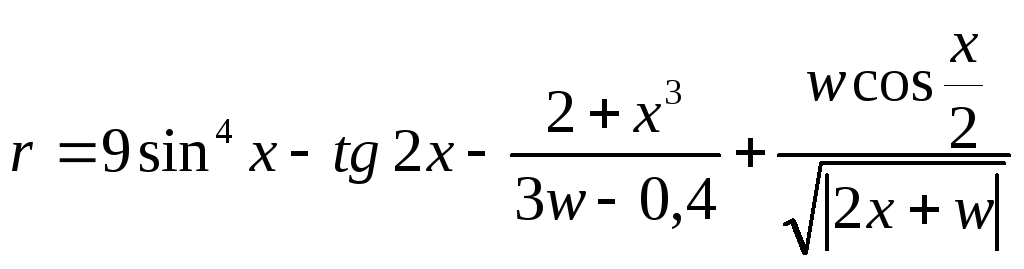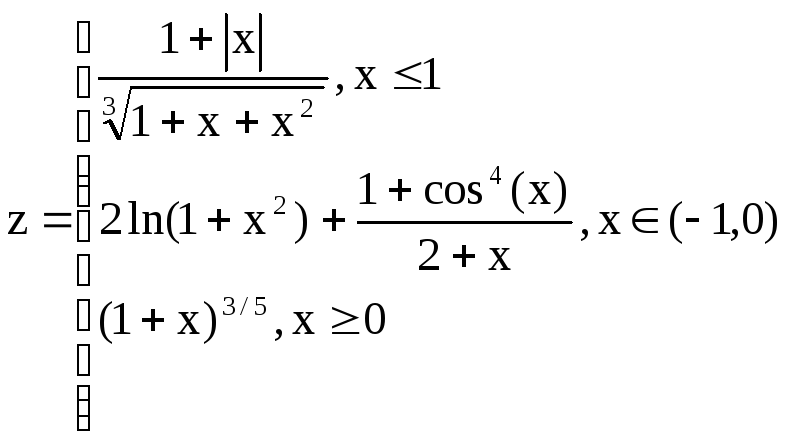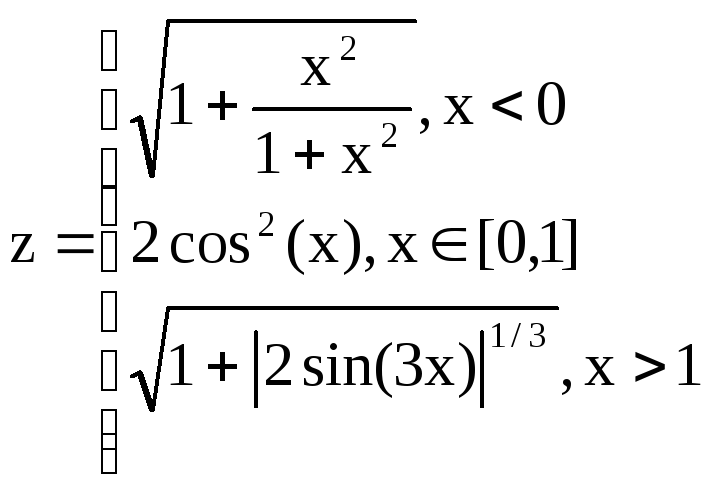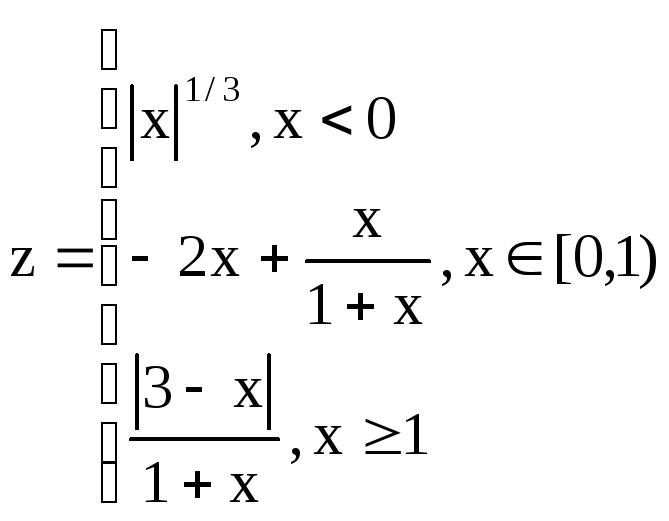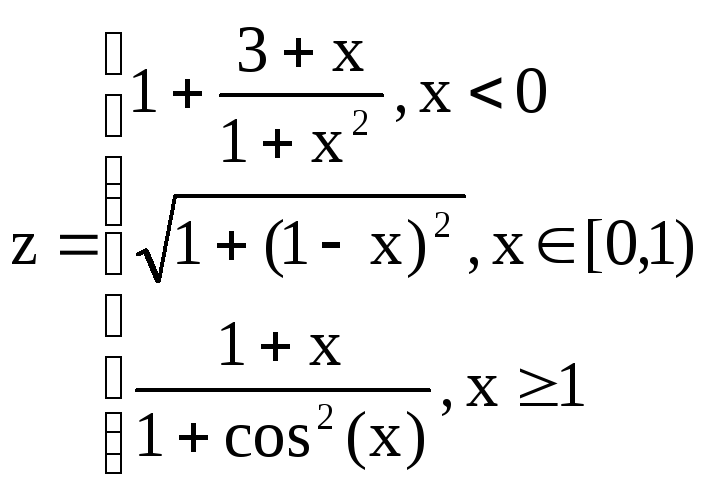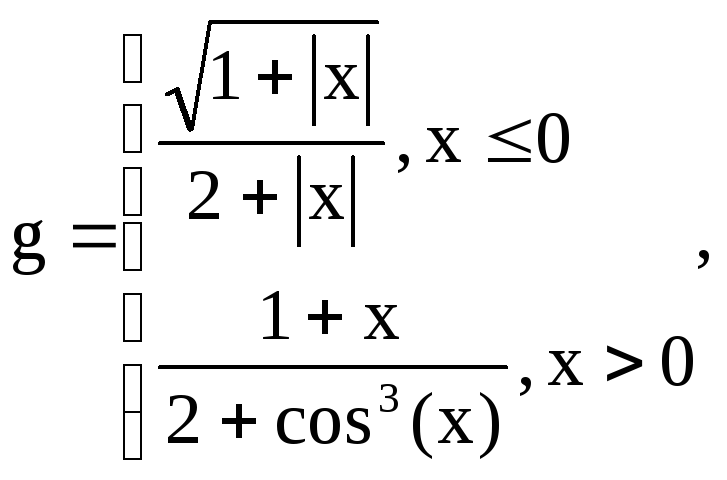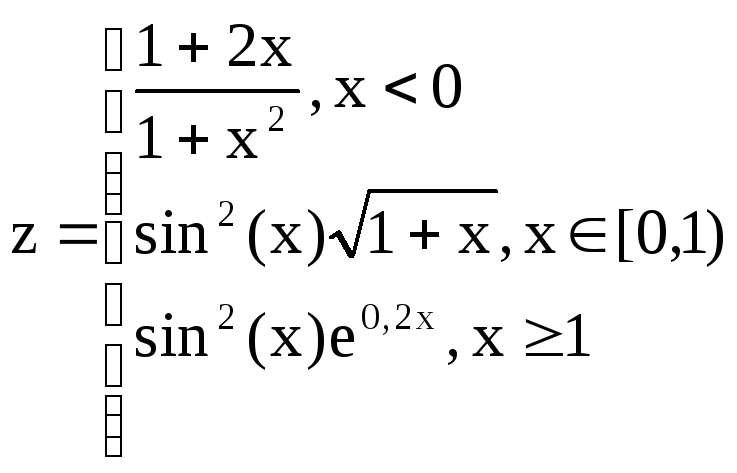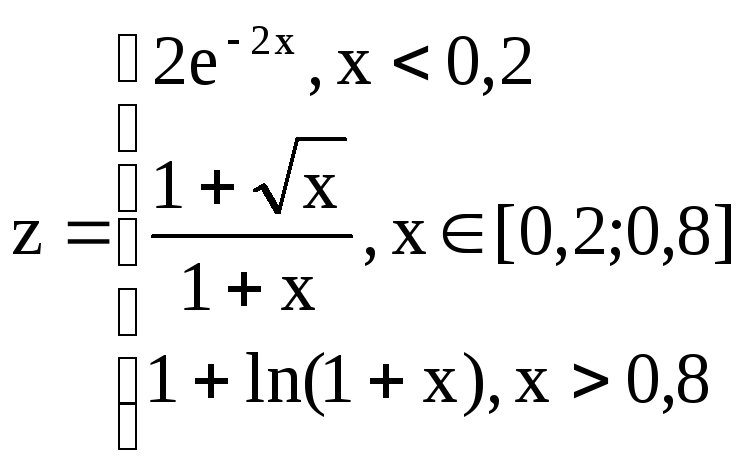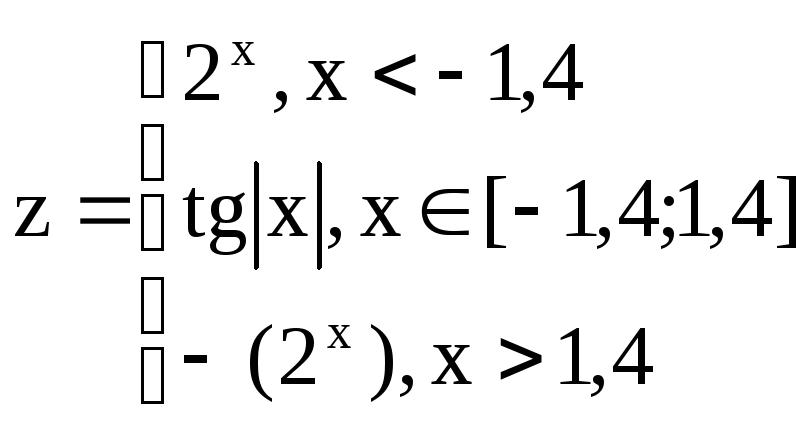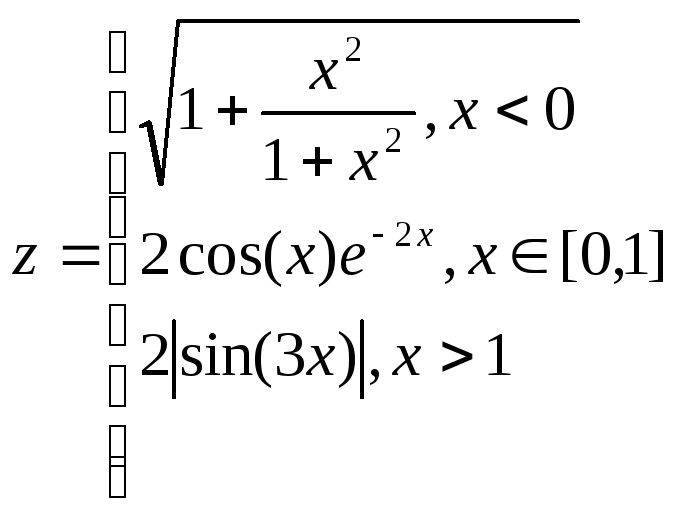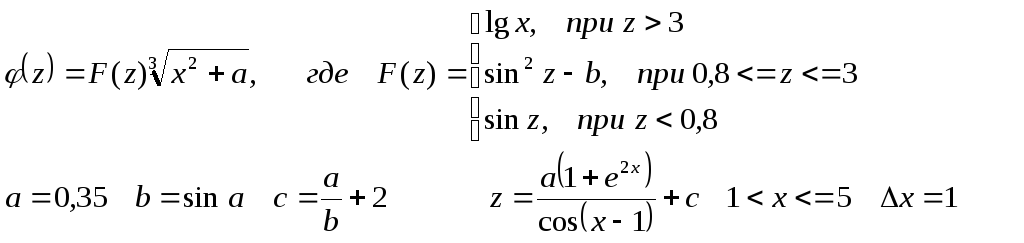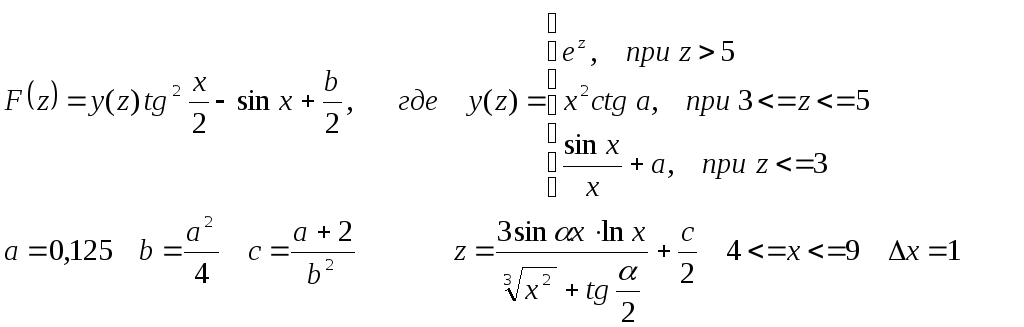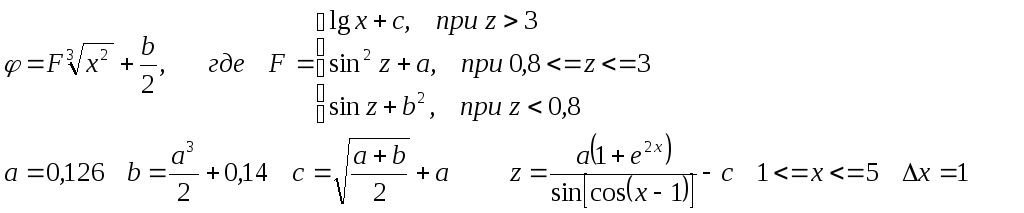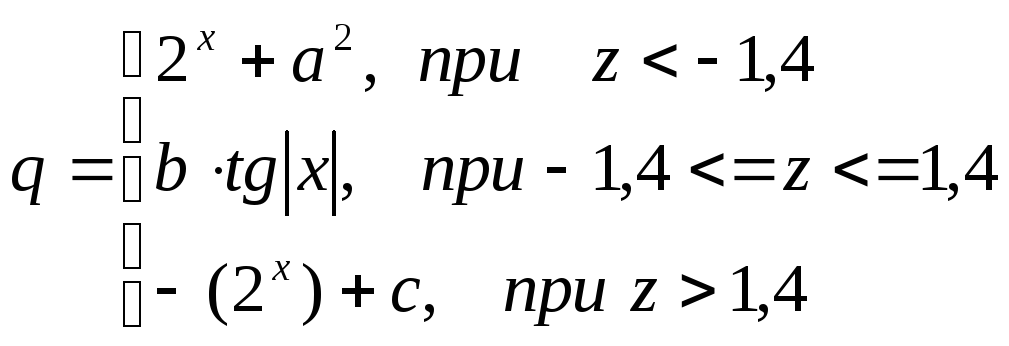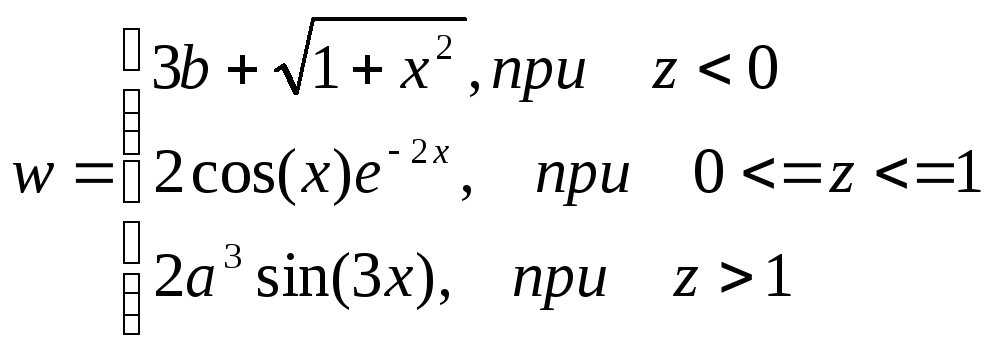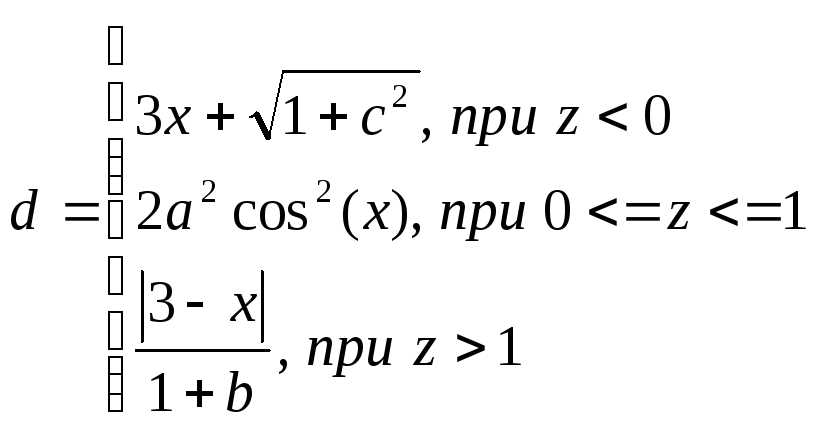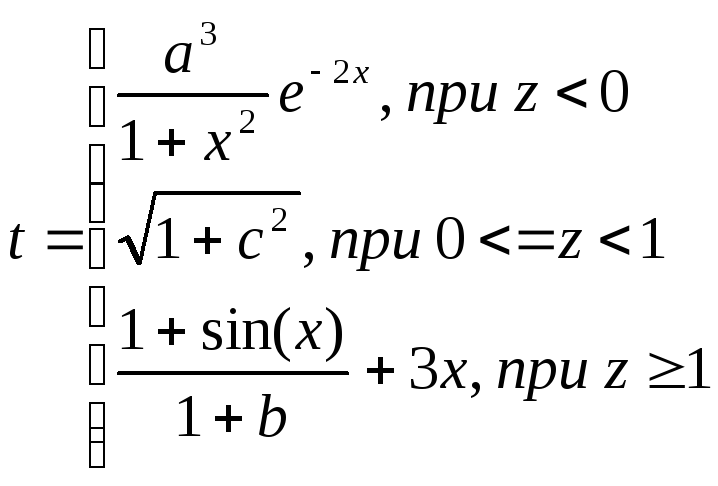Протабулировать функцию в excel это как

Содержание

• Использование табулирования
  • Создание таблицы
  • Построение графика
• Вопросы и ответы

Табулирование функции представляет собой вычисление значения функции для каждого соответствующего аргумента, заданного с определенным шагом, в четко установленных границах. Эта процедура является инструментом для решения целого ряда задач. С её помощью можно локализовать корни уравнения, найти максимумы и минимумы, решать другие задачи. С помощью программы Excel выполнять табулирование намного проще, чем используя бумагу, ручку и калькулятор. Давайте выясним, как это делается в данном приложении.

Использование табулирования

Табулирование применяется путем создания таблицы, в которой в одной колонке будет записано значение аргумента с выбранным шагом, а во второй — соответствующее ему значение функции. Затем на основе расчета можно построить график. Рассмотрим, как это делается на конкретном примере.

Создание таблицы

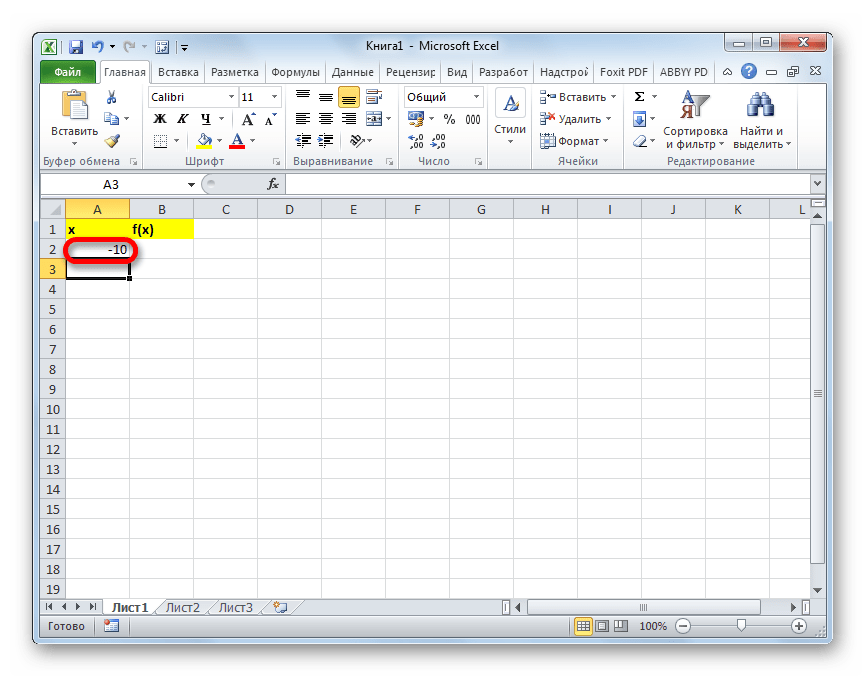
Создаем шапку таблицы с колонками x, в которой будет указано значение аргумента, и f(x), где отобразится соответствующее значение функции. Для примера возьмем функцию f(x)=x^2+2x, хотя для процедуры табулирования может использоваться функция любого вида. Устанавливаем шаг (h) в размере 2. Граница от -10 до 10. Теперь нам нужно заполнить столбец аргументов, придерживаясь шага 2 в заданных границах.

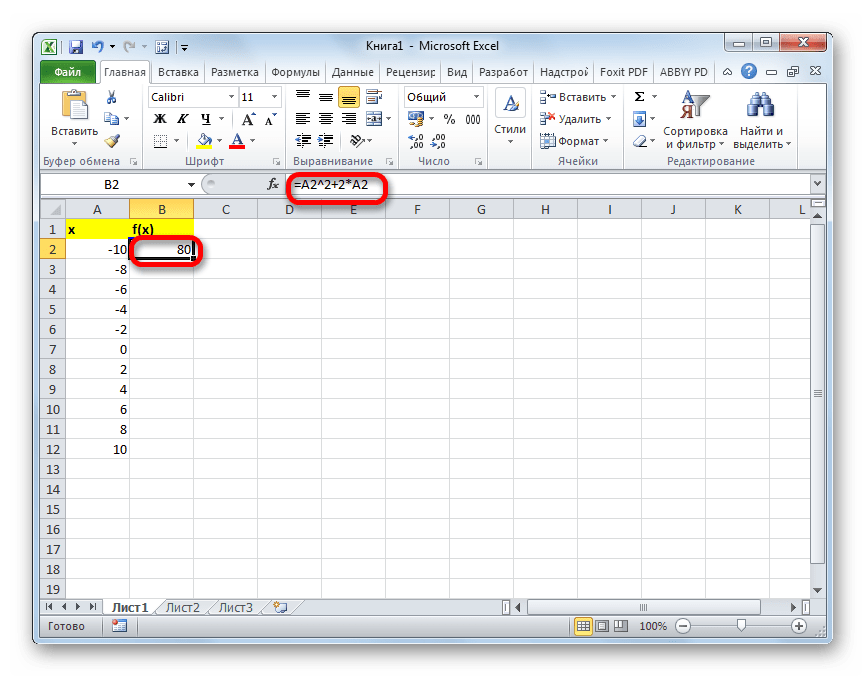
1. В первую ячейку столбца «x» вписываем значение «-10». Сразу после этого жмем на кнопку Enter. Это очень важно, так как если вы попытаетесь произвести манипуляцию мышкой, то значение в ячейке превратится в формулу, а в данном случае это не нужно.



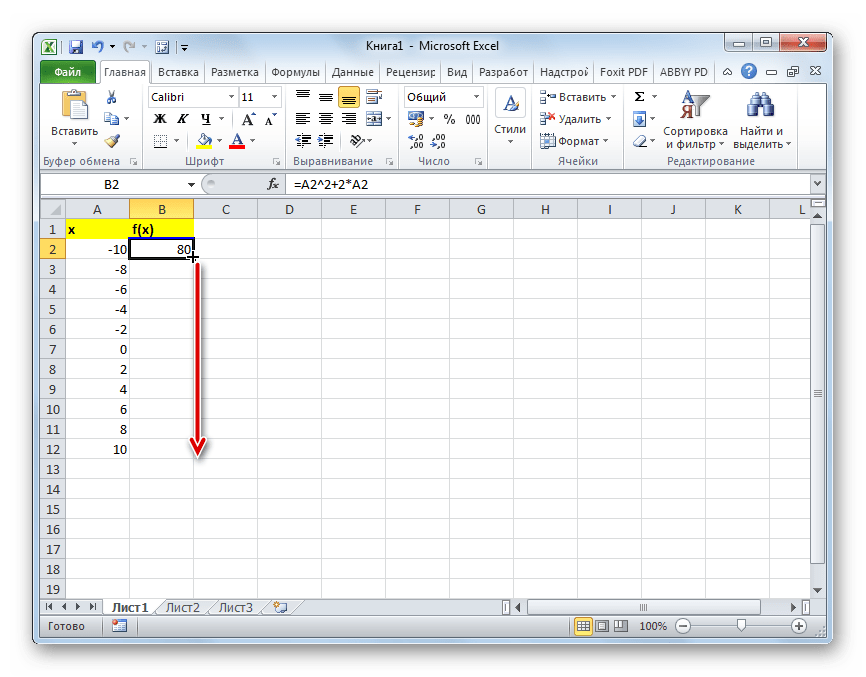
2. Все дальнейшие значения можно заполнить вручную, придерживаясь шага 2, но удобнее это сделать с помощью инструмента автозаполнения. Особенно этот вариант актуален, если диапазон аргументов большой, а шаг — относительно маленький.

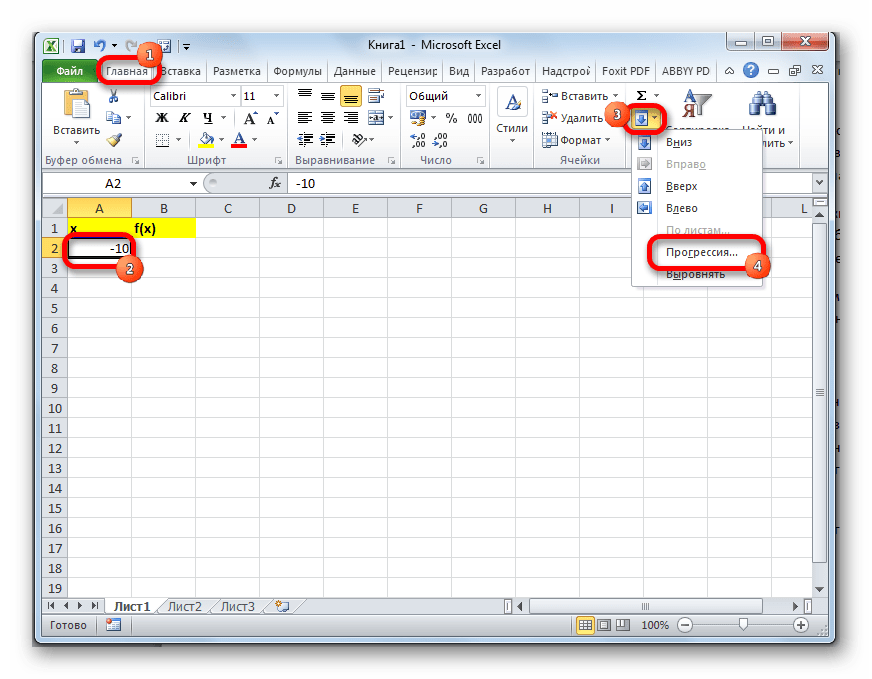
   Выделяем ячейку, в которой содержится значение первого аргумента. Находясь во вкладке «Главная», кликаем по кнопке «Заполнить», которая размещена на ленте в блоке настроек «Редактирование». В появившемся списке действий выбираем пункт «Прогрессия…».



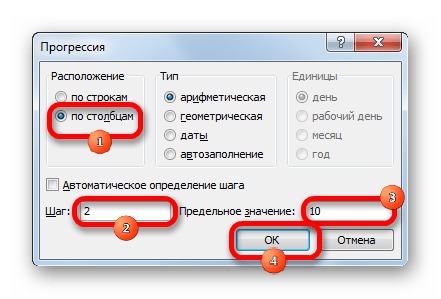
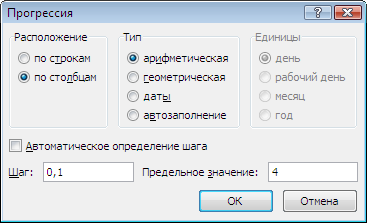
3. Открывается окошко настройки прогрессии. В параметре «Расположение» устанавливаем переключатель в позицию «По столбцам», так как в нашем случае значения аргумента будут размещаться именно в колонке, а не в строке. В поле «Шаг» устанавливаем значение 2. В поле «Предельное значение» вписываем число 10. Для того чтобы запустить прогрессию, жмем на кнопку «OK».



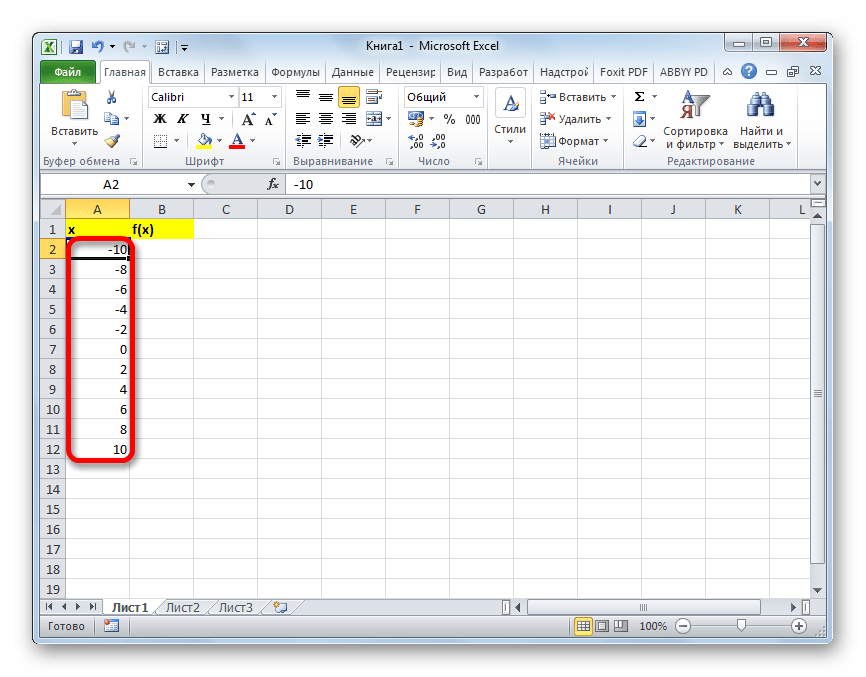
4. Как видим, столбец заполнен значениями с установленными шагом и границами.



5. Теперь нужно заполнить столбец функции f(x)=x^2+2x. Для этого в первую ячейку соответствующей колонки записываем выражение по следующему шаблону:

   =x^2+2*x

   При этом, вместо значения x подставляем координаты первой ячейки из столбца с аргументами. Жмем на кнопку Enter, чтобы вывести результат вычислений на экран.



6. Для того, чтобы произвести вычисление функции и в других строках, снова воспользуемся технологией автозаполнения, но в данном случае применим маркер заполнения. Устанавливаем курсор в нижний правый угол ячейки, в которой уже содержится формула. Появляется маркер заполнения, представленный в виде небольшого по размеру крестика. Зажимаем левую кнопку мыши и протягиваем курсор вдоль всего заполняемого столбца.



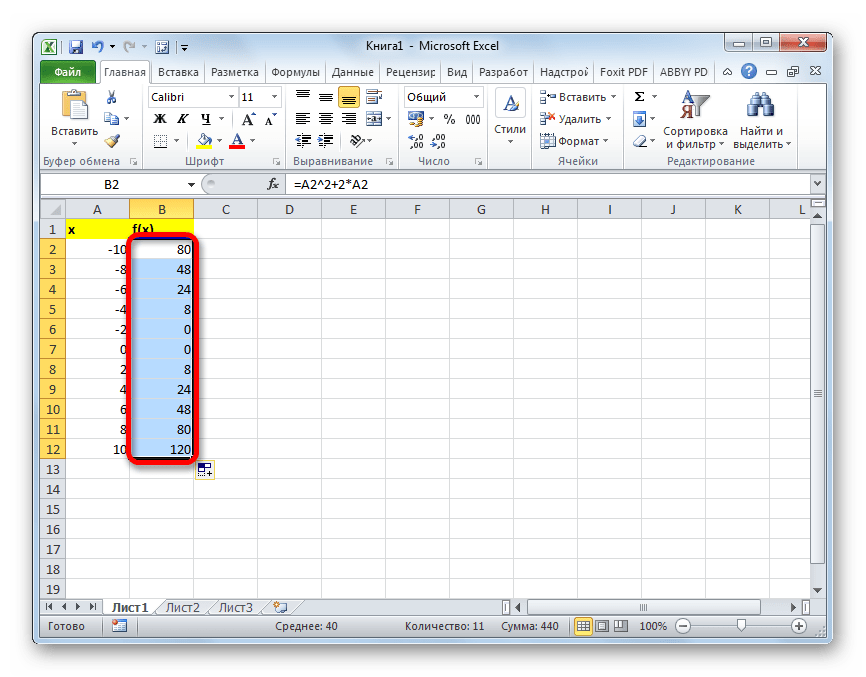
7. После этого действия вся колонка со значениями функции будет автоматически заполнена.

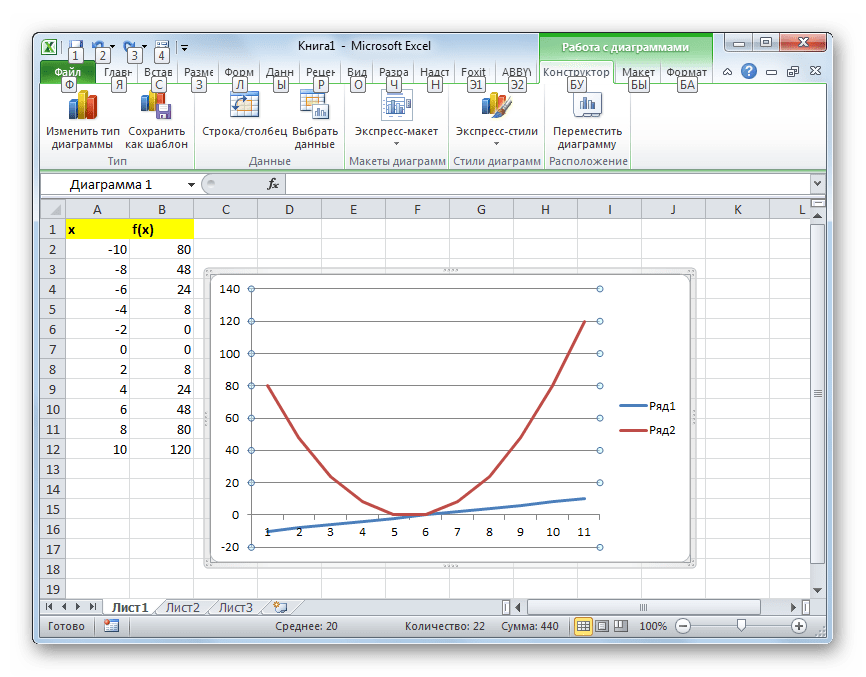
Таким образом, табуляция функции была проведена. На её основе мы можем выяснить, например, что минимум функции (0) достигается при значениях аргумента -2 и 0. Максимум функции в границах вариации аргумента от -10 до 10 достигается в точке, соответствующей аргументу 10, и составляет 120.

Урок: Как сделать автозаполнение в Эксель

Построение графика

На основе произведенной табуляции в таблице можно построить график функции.

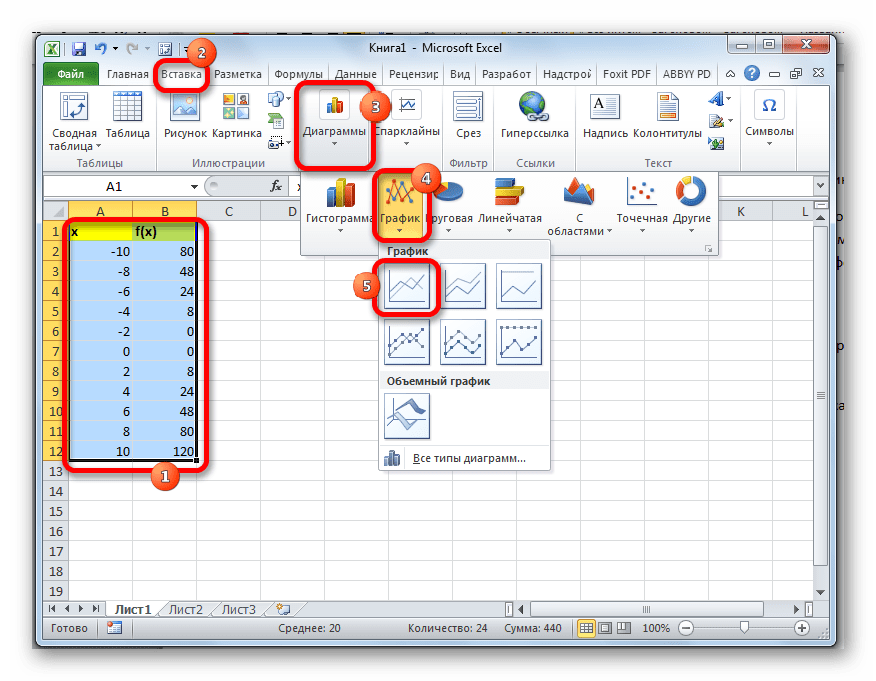
1. Выделяем все значения в таблице курсором с зажатой левой кнопкой мыши. Перейдем во вкладку «Вставка», в блоке инструментов «Диаграммы» на ленте жмем на кнопку «Графики». Открывается список доступных вариантов оформления графика. Выбираем тот вид, который считаем наиболее подходящим. В нашем случае отлично подойдет, например, простой график.



2. После этого на листе программа выполняет процедуру построения графика на основе выделенного табличного диапазона.

Далее по желанию пользователь может отредактировать график так, как считает нужным, используя для этих целей инструменты Excel. Можно добавить названия осей координат и графика в целом, убрать или переименовать легенду, удалить линию аргументов, и т.д.

Урок: Как построить график в Эксель

Как видим, табулирование функции, в общем, процесс несложный. Правда, вычисления могут занять довольно большое время. Особенно, если границы аргументов очень широкие, а шаг маленький. Значительно сэкономить время помогут инструменты автозаполнения Excel. Кроме того, в этой же программе на основе полученного результата можно построить график для наглядного представления.

Еще статьи по данной теме:

Помогла ли Вам статья?

Введение

Табулированием функции является процесс вычисления значений функции для всех аргументов, заданных с некоторым шагом, при назначенных пределах их изменения. Данная операция используется в качестве инструмента при решении задач определённого класса. Она позволяет осуществить локализацию корней уравнения, определять минимумы и максимумы, выполнять решение других задач. При помощи программы Excel осуществлять процесс табулирования значительно проще, чем просто на калькуляторе с записью результатов на бумаге.

Табулирование функции одной переменной средствами MS Excel

Табулирование осуществляется за счёт формирования таблицы, где в одной из колонок записывается значение аргумента с требуемым шагом, а в другой колонке будет располагаться определяемое данным аргументом значение функции. Далее на базе этих расчётов может быть построен график. Приведём конкретный пример. Прежде всего необходимо сформировать шапку таблицы, где есть колонка x, с указанием значений аргумента, и колонка f(x), в которой будет отображаться соответствующее аргументу значение функции.
В качестве примера используем следующую функцию:

f(x)=x^2+2x

Следует отметить, что в операции табулирования в принципе могут использоваться функции любого типа.

Выбираем шаг табулирования h равный двум. Диапазон допустимого изменения аргумента назначим от минус десяти до плюс десяти. Далее следует выполнить заполнение столбца аргументов, с соблюдением заданного шага два при заданных граничных значениях. То есть, необходимо сначала в первую ячейку столбца «х» записать величину минус десять. Непосредственно за этим действием следует нажать клавишу Enter. Это важное замечание, поскольку если попытаться манипулировать мышью, то значение в ячейке преобразуется в формулу, а для рассматриваемого примера это не требуется. Эта процедура показана на рисунке ниже.

«Табулирование функции одной переменной средствами MS Excel» 👇

Можно и дальше заполнять в ручном режиме этот столбец, выдерживая шаг два, однако более удобно эту операцию осуществить при помощи процедуры автоматического заполнения. Использование этого варианта особенно актуально, когда диапазон изменения аргумента значительный, а величина шага незначительная.

Для автоматического заполнения столбца следует выделить ячейку, содержащую величину первого аргумента. Далее на вкладке «Главная, нужно сделать клик по клавише «Заполнить», размещённой на ленте в группе настроек «Редактирование». Затем в представленном списке операций необходимо сделать выбор пункта «Прогрессия…». Появится окно настройки прогрессии. Надо выбрать параметр «Расположение» и там установить режим выбора «По столбцам», поскольку в рассматриваемом примере значения аргумента размещаются не в строчках, а в столбцах. В поле «Шаг», необходимо установить величину два. В поле «Предельное значение» нужно занести верхнюю границу диапазона изменения аргумента, то есть число десять. Для реализации прогрессии нужно нажать клавишу «ОК».

А затем требуется осуществить заполнение столбца функции f(x)=x^2+2x. Чтобы это выполнить, нужно в первую ячейку колонки с функцией записать выражение, используя следующий шаблон.

Следует вместо значения x в формуле подставить значение первой ячейки из столбца, где располагаются аргументы. После этого надо нажать клавишу Enter для вывода итога вычислений на дисплей. Для осуществления вычислений значения функции для других строк, можно также использовать технологию автоматического заполнения, но в этом варианте нужно применять маркер заполнения. Для этого нужно установить курсор в нижний правый угол ячейки, уже содержащей формулу. При этом должен появиться маркер заполнения, который будет представлен как небольшой по размерам крестик. Далее надо нажать левую клавишу мышки и протянуть курсор по всему заполняемому столбцу. Образец выполнения табуляции представлен на рисунке ниже.

На её базе возможно увидеть, к примеру, что минимальное значение функции, а именно нуль, получается, когда величина аргумента равняется минус два. Максимальное значение функции в заданном диапазоне изменения аргумента, то есть, от минус десяти до десяти, получается в точке с аргументом десять, и равняется ста двадцати.

Используя итоговые результаты выполненной табуляции в таблице, можно представить эту функцию в виде графика. Нужно выделить все значения в таблице при помощи курсора, зажав левую клавишу мышки. Далее надо перейти на вкладку «Вставка», в группе инструментов «Диаграммы» на ленте нужно нажать клавишу «Графики». Должен открыться перечень возможных версий формирования графика. Следует выбрать такой вид, который покажется пользователю самым подходящим. Можно сделать выбор, к примеру, простого типа графика. Далее программа на листе исполнит процедуру формирования графика на базе заданного табличного диапазона. Образец сформированного графика показан на рисунке ниже.

Если у пользователя появится желание, то он может осуществить редактирование этого графика таким образом, как ему будет необходимо, применяя для этого инструментальный набор программы Excel. Имеется возможность добавления наименований осей координат и всего графика, а также можно удалить легенду или присвоить ей новое имя, убрать линию аргументов и так далее.

Как видно из приведённого выше примера табулирование функции является достаточно простым процессом. Но следует отметить, что вычислительный процесс может занимать достаточно много времени, в частности, когда диапазон изменения аргументов имеет широкие пределы, а шаг табуляции, при этом, очень небольшой. Существенную экономию времени могут дать инструменты автоматического заполнения Excel. И, как показано выше, эта же программа на базе сформированных результатов позволяет сформировать график функции, дающий более наглядное представление.

Табулирование функций

Задача
1

Протабулировать
функции y, z
и q
на данном диапазоне аргумента x.
Построить графики этих функций в одной
системе координат.

Диапазон
изменения аргумента 1 
x

4 с шагом 0,1;

,

,

1.
Построить таблицу значений функций для
соответствующего аргумента.

1.1.
Заполнить столбецx
автозаполнением с помощью прогрессии.
В ячейку А2 набрать данное начальное
значение x
и нажать кнопку ввода на cтроке
формул. Выбрать команду Главная
/ Редактирование
/ Прогрессия.
В появившемся диалоговом окне отметить

1.2.
В ячейку В2 ввести формулу:

=(1/tan(A2/2)+(A2^2+4)^(1/3))
/ (exp(abs(A2))+4)+cos(A2/3)^2

1.3.
В ячейку С2 ввести формулу:

=B2^2
+ A2^3/2

1.4.
В ячейку D2
ввести формулу: =С2^2 + B2^2

В
итоге получим значения функций y,
z
и q
для x
= 1. Для того, чтобы распространить формулы
на соседние ячейки и найти значения
функций для остальных значений аргумента
x
нужно использовать маркер
заполнения
(черный квадратик в нижнем правом углу
активной ячейки). Установить на него
курсор и протянуть мышкой маркер
заполнения до предельного значения
аргумента.

При
копировании формул маркером вертикально
вниз в относительных адресах будут
автоматически меняться номера строк.
Формулы пересчитываются для соответствующего
значения аргумента.

2.
Построение графиков функций.

В
Excel
имеется возможность графического
представления данных в виде диаграмм.
Диаграммы связаны с данными листа, на
основе которых они были созданы, и
изменяются каждый раз, когда изменяются
данные на листе.

Порядок
работы с мастером диаграмм.

1.
Выделить полученную таблицу.

2.
Выбрать команду Вставка.
На ленте выбрать Диаграммы
/ Точечная
(последний вид).

3.
Настроить шкалу x.
В появившемся графике с помощью правой
клавиши мыши вызвать контекстное меню
шкалы x.
Выбрать команду Формат
оси. В
диалоговом окне в пункте Параметры
оси выбрать
фиксированные значения и ввести данные
в соответствующие строки.

Изменить
ширину линии и цвет можно в этом же окне,
выбрав пункты Тип
линии и Цвет
линии
соответственно.

4.
Линии сетки. При выделенном графике
использовать команду Макет
/ Сетка.
Горизонтальные и вертикальные линии
выбрать основные и промежуточные.

Результат
показан на рисунке 1.

Рис.
1. Табулирование функций

Задача
2

Протабулировать
функции y,
g
и z
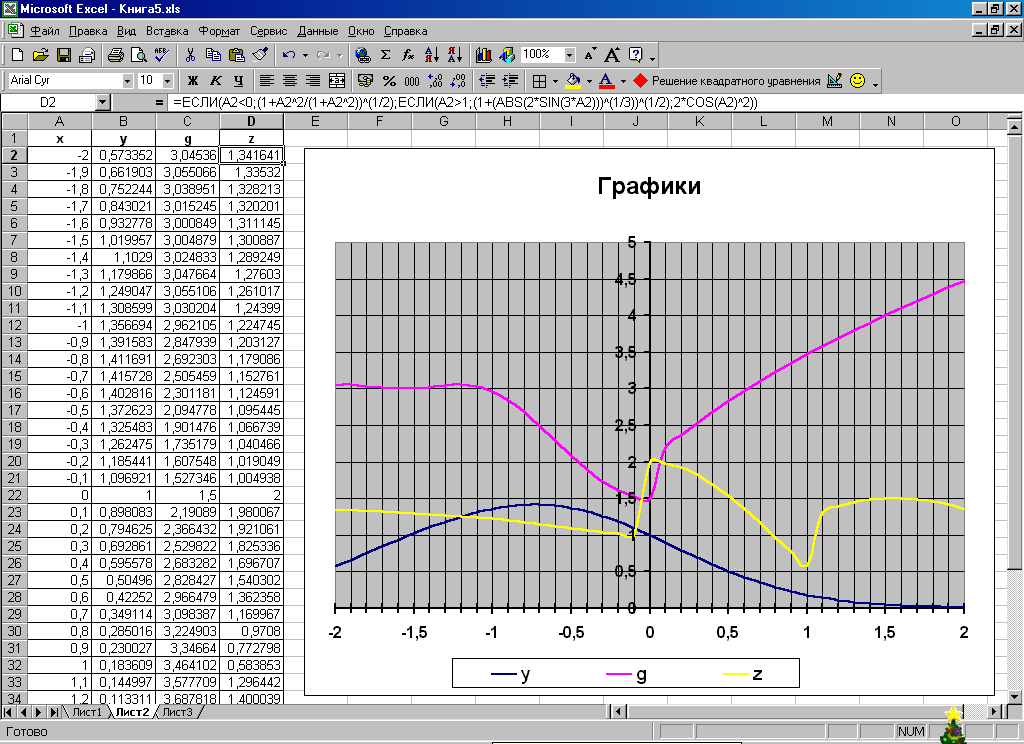
на данном диапазоне аргумента x.
Построить графики этих функций в одной
системе координат.

,

,

При
значениях аргумента -2

х 
2 с шагом 0,1.

1.
Построить таблицу значений функций для
соответствующего аргумента.

Выполнить
п. 1.1. задачи 1.

1.2.
В ячейку В2 ввести формулу:

=(1+cos(A2))
/ (1+exp(2*A2))

1.3.
В ячейку С2 ввести формулу:

=Если
(А2<=0;
(3+sin(2*A2)^2) / (1+cos(A2)^2); 2*(1+2*A2)^(1/2))

1.4.
В ячейку D2
ввести формулу:

=Если
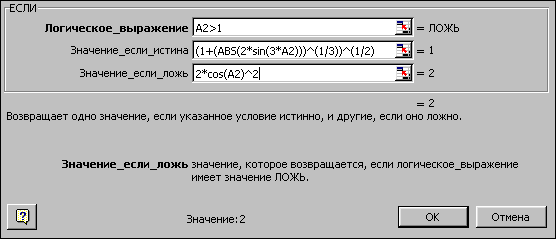
(A2<0; (1+A2^2 / (1+A2^2))^(1/2); Если(A2>1;
(1+(ABS(2*sin(3*A2)))^(1/3))^(1/2); 2*cos(A2)^2)).

Заполнить
остальные ячейки столбца с помощью
маркера заполнения.

Формулы
п. 1.3. и п. 1.4. этой задачи можно вводить
с помощью мастера функций.

Выбрать
команду Формулы
/ Вставить функцию / категория логические
Если. В
появившемся окне заполнить строки
следующим образом:

Рис.
2. Вычисление функция g

Рис.
3а. Вычисление функции z

Установить
курсор в третью строку Значение_если_ложь,
выбрать мышью в строке формул функцию
Если. В появившемся новом окне заполнить
строки следующим образом:

Рис.
3б. Вычисление функции z

2.
Построить график функций см. п.2 задачи
1.

Результат
показан на рисунке 4.

Рис.
4.

Задача
3

Протабулировать
функции k
и z
на данном диапазоне аргумента x.
Построить графики этих функций в одной
системе координат.

При
значениях аргумента -2

х 
2 с шагом 0,1.

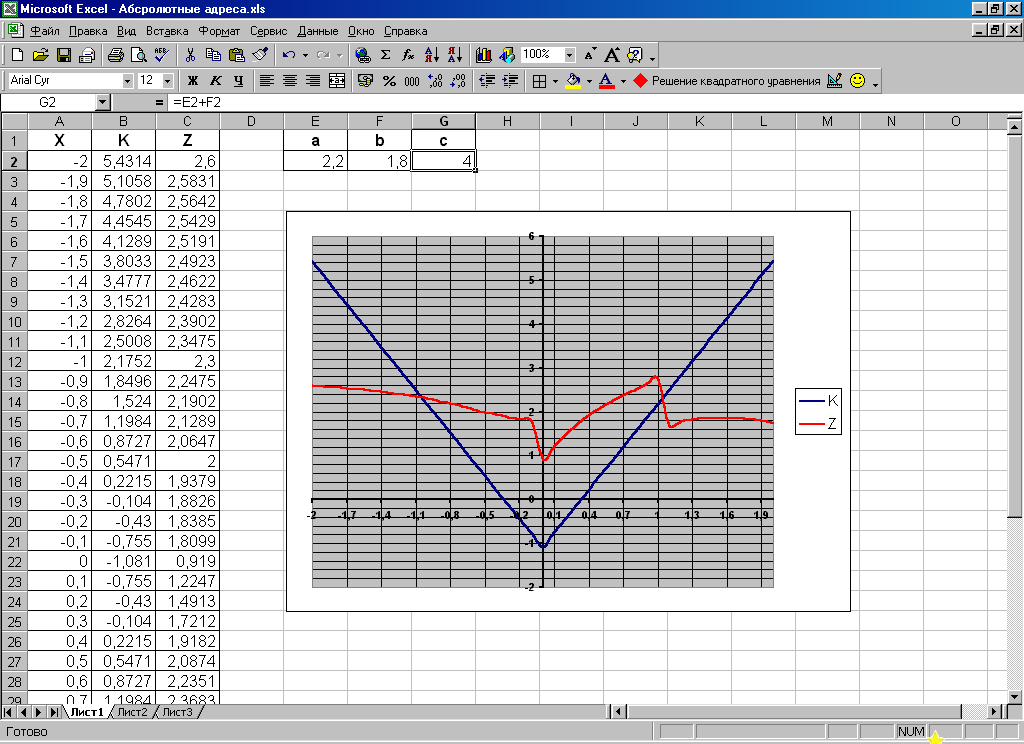
Константы

a
=2,2 b = 1,8 c = a + b

1.
Построить таблицу значений функций для
соответствующего аргумента.

Выполнить
п. 1.1. задачи 1.

1.2.
В ячейку В2 ввести формулу:

=(
atan(($F$2 – $E$2) / ln($E$2)) + (2*A2)^(1/2) ) / ( 1 + sin(($G$2 –
$F$2) / ln($F$2)) )

1.3.
В ячейку С2 ввести формулу:

=Если
(A2<0; $F$2 + A2^2 / (1 + A2^2); Если
(A2>1; ( $E$2 + (abs(2*sin(3*A2)))^(1/3)
)^(1/2); 2*cos(A2)^2 + B2))

Заполнить
остальные ячейки столбца с помощью
маркера заполнения.

2.
Построить график функций см. п.2 задачи
1.

Результат
показан на рисунке 5.

Рис.
5.

Варианты
заданий к задаче 1

Вариант
1

,

Диапазон
изменения аргумента -3 ≤ x
≤ 3 с шагом Δx
= 0,3

Вариант
2

,

Диапазон
изменения аргумента -2 ≤ x
≤ 2 с шагом Δx
= 0,2

Вариант
3

,

,

Диапазон
изменения аргумента 2 ≤ x
≤ 3 с шагом Δx
= 0,1

Вариант
4

,

Диапазон
изменения аргумента -0,3 ≤ x
≤ 3 с шагом Δx
= 0,25

Вариант
5

,

,

Диапазон
изменения аргумента 2 ≤ x
≤ 3 с шагом Δx
= 0,08

Вариант
6

,

,

Диапазон
изменения аргумента 3 ≤ x
≤ 4 с шагом Δx
= 0,05

Вариант
7

,

,

Диапазон
изменения аргумента -2 ≤ x
≤ 4 с шагом Δx
= 0,7

Вариант
8

,

Диапазон
изменения аргумента -1 ≤ x
≤ 3 с шагом Δx
= 0,1

Вариант
9

,

Диапазон
изменения аргумента 2 ≤ x
≤ 9 с шагом Δx
= 0,8

Вариант
10

,

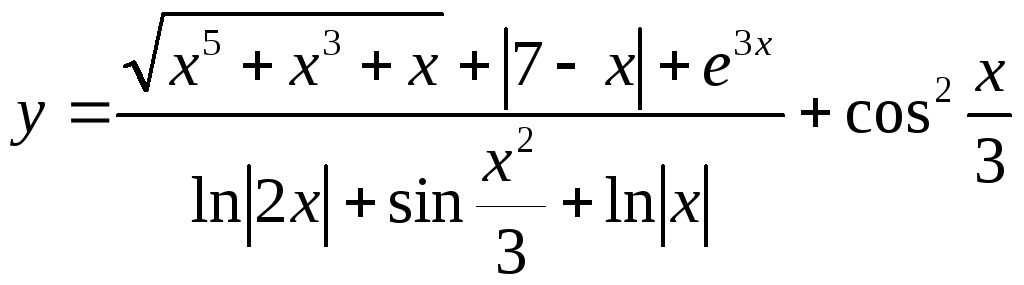
Диапазон
изменения аргумента 2 ≤ x
≤ 4 с шагом Δx
= 0,3

Вариант
11

,

Диапазон
изменения аргумента -2 ≤ x
≤ 5 с шагом Δx
= 0,3

Вариант
12

,

Диапазон
изменения аргумента -7 ≤ x
≤ 2 с шагом Δx
= 0,7

Вариант
13

,

Диапазон
изменения аргумента -5 ≤ x
≤ 6 с шагом Δx
= 0,8

Вариант
14

,

Диапазон
изменения аргумента -4 ≤ x
≤ 3 с шагом Δx
= 0,7

Вариант
15

,

Диапазон
изменения аргумента -4 ≤ x
≤ 4 с шагом Δx
= 0,6

Вариант
16

,

Диапазон
изменения аргумента -2 ≤ x
≤ 4 с шагом Δx
= 0,5

Вариант
17

,

Диапазон
изменения аргумента -2 ≤ x
≤ 2 с шагом Δx
= 0,4

Вариант
18

,

Диапазон
изменения аргумента -2 ≤ x
≤ 2 с шагом Δx
= 0,5

Вариант
19

Диапазон
изменения аргумента -1 ≤ x
≤ 2 с шагом Δx
= 0,3

Вариант
20

Диапазон
изменения аргумента -1 ≤ x
≤ 1 с шагом Δx
= 0,2

Варианты
заданий к задаче 2

Диапазон
изменения аргумента для всех вариантов
-2 ≤ x
≤ 2 с шагом Δx
= 0,1

Вариант
1

,

,

Вариант
2

,

,

Вариант
3

,

,

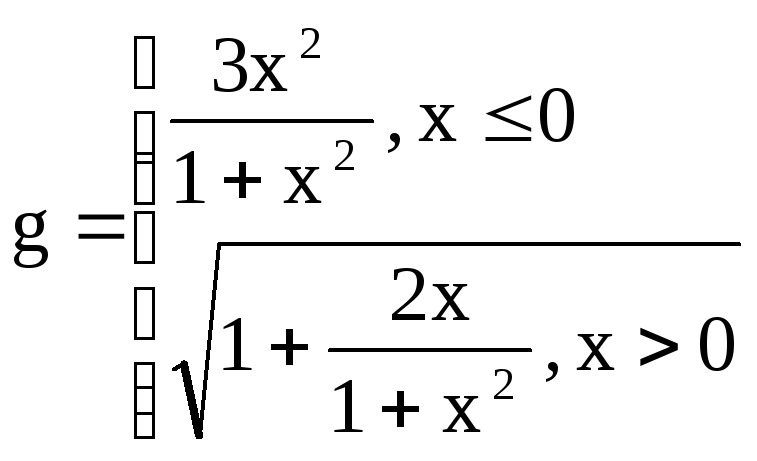
Вариант
4

,

,

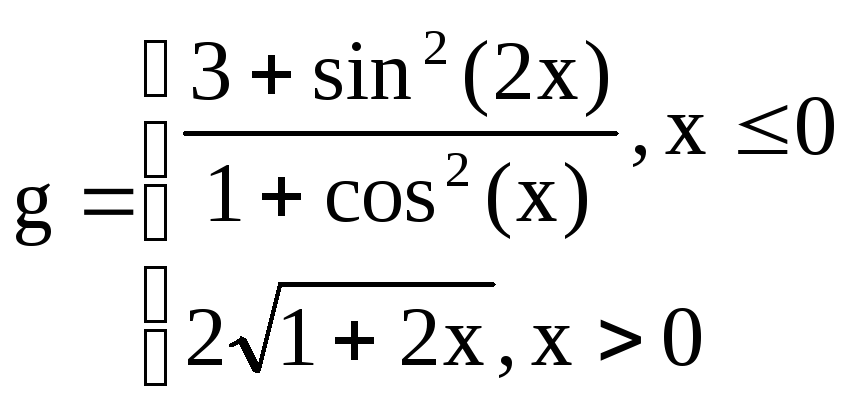
Вариант
5

,

,

Вариант
6

,

,

Вариант
7

,

,

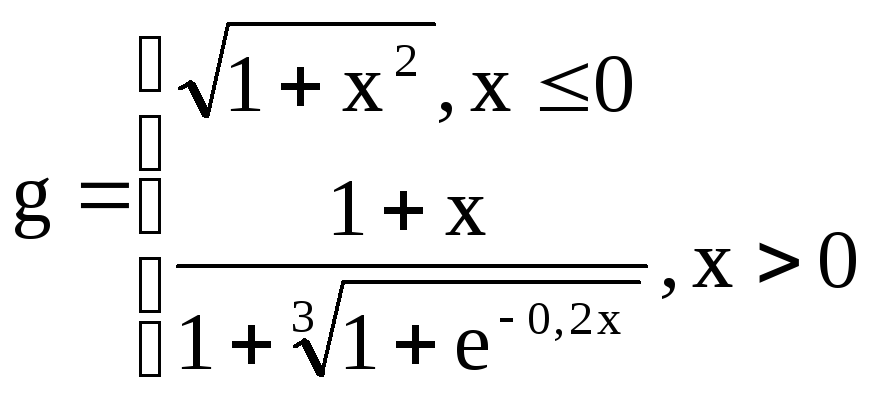
Вариант
8

,

,

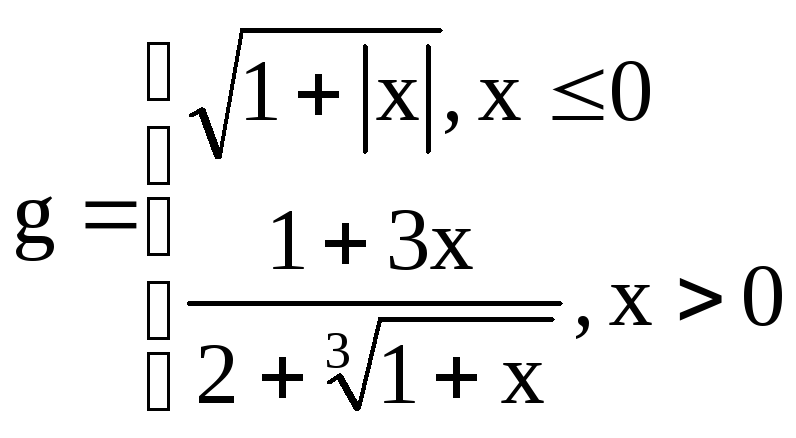
Вариант
9

,

Вариант
10

,

,

Вариант
11

y=cos²(πx),

,

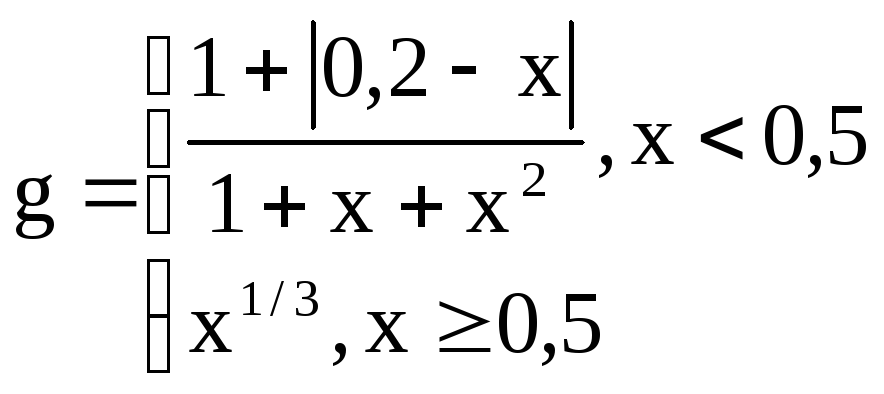
Вариант
12

,

,

Вариант
13

,

,

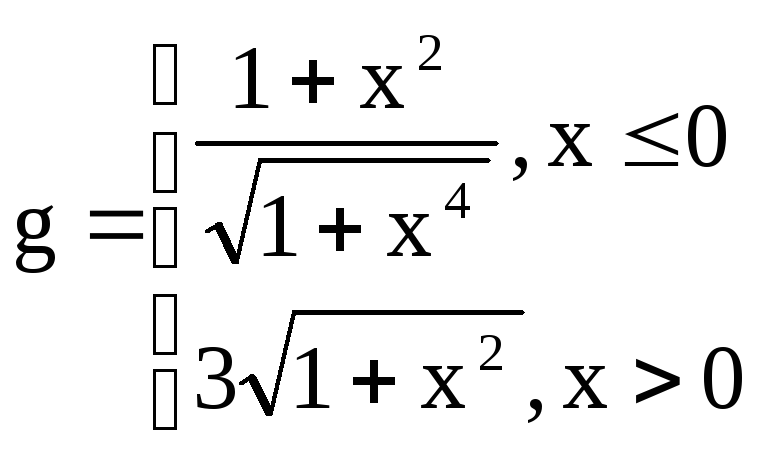
Вариант
14

,

,

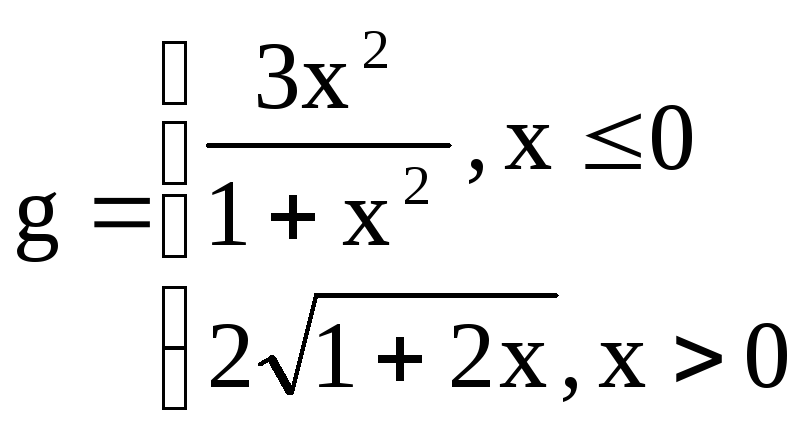
Вариант
15

,

,

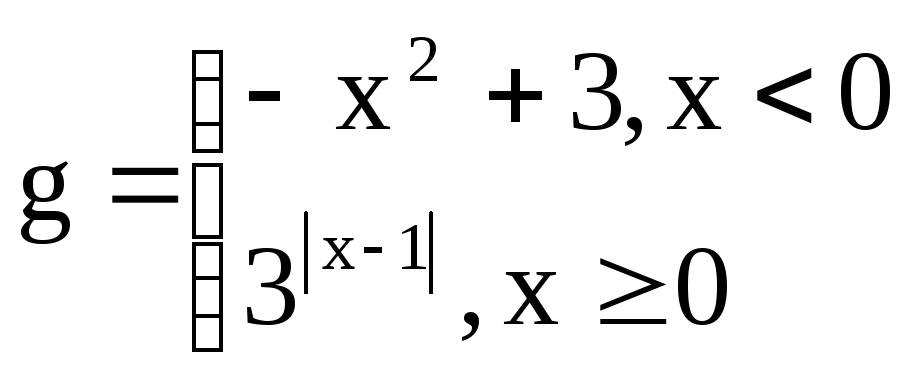
Вариант
16

,

,

Вариант
17

,

,

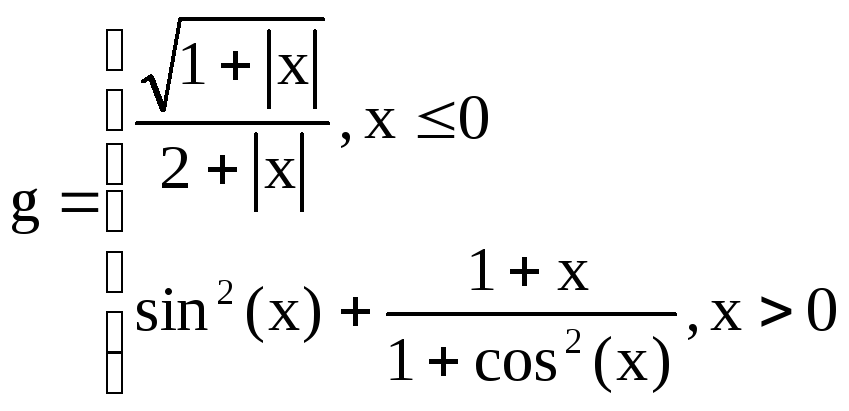
Вариант
18

,

,

Вариант
19

,

,

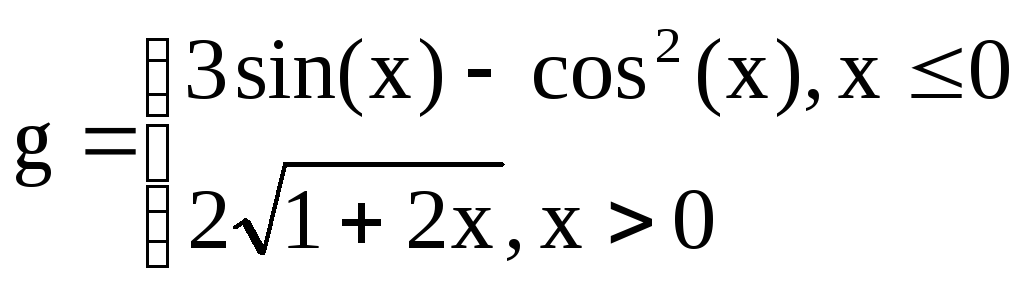
Вариант
20

,

,

Варианты
заданий к задаче 3

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9

Вариант 10

Вариант 11

Вариант 12

Вариант 13

Вариант
14

,
где

1<=
x<=
3 Δx=0,3

Вариант
15

,
где

1<=
x <= 5 Δx
= 0,8

Вариант
16

,
где

-1<=x<=1
Δx=0,2

Вариант
17

,
где

2<=x<=5
Δx=0,4

Вариант
18

,
где

3<=x<=7
Δx=0,5

Вариант
19

,
где

1<=x<=6
Δx=0,2

Вариант
20

,
где

1<=x<=10
Δx=0,5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Табулирование функций с
использованием автозаполнения

Пример.    Создать таблицу значений функции y=x²+3

на отрезке [-3;3]  с шагом 0,5.

АЛГОРИТМ табулирования функции:

1. в ячейку А1 ввести текст Х, а
   в ячейку В1 – текст У.
2. в ячейку А2 ввести начальное значение
   Х, т.е. -3

3.      с помощью автозаполнения ввести следующие значения Х:

Ø  
установить курсор в ячейку А2;

Ø  
выполнить команду Главная —  — Прогрессия…;

Ø  
в диалоговом окне установить:

Расположение – по
столбцам; Тип – арифметическая;     

Шаг:  0,5; Предельное значение: 3;
щелкнуть по кнопке ОК.

1. в ячейку В2 записать формулу  =А2^2+3
2. скопировать формулу из ячейки В2 в
   диапазон В3:В14.

Задания для самостоятельного выполнения

Все задания
выполнить в одном файле на разных листах, результат сохранить под именем Табулирование.

1.     
Протабулировать функцию на
отрезке [-5;5] с шагом 1.

2.     
Протабулировать функцию  на
отрезке [0;2] с шагом 0,2.

3.     
Протабулировать функцию  на
отрезке [2;8] с шагом 0,5.

4.     
Протабулировать функцию  на
отрезке [0;3] с шагом 0,2.

5.     
Протабулировать функцию  на
отрезке [0;2] с шагом 0,1.

6.     
Протабулировать функцию  на
отрезке [1;5] с шагом 0,5.

Табулирование
функций с использованием автозаполнения

Пример.    Создать таблицу значений функции y=x²+3

на отрезке [-3;3]  с шагом 0,5.

АЛГОРИТМ
табулирования функции:

1. в ячейку А1 ввести текст Х, а
   в ячейку В1 – текст У.
2. в ячейку А2 ввести начальное значение
   Х, т.е. -3

3.      с помощью автозаполнения ввести следующие значения Х:

Ø 
установить курсор в ячейку А2;

Ø 
выполнить команду Главная —  — Прогрессия…;

Ø 
в диалоговом окне установить:

Расположение – по
столбцам; Тип – арифметическая;     

Шаг:  0,5; Предельное значение: 3;
щелкнуть по кнопке ОК.

1. в ячейку В2 записать формулу  =А2^2+3
2. скопировать формулу из ячейки В2 в
   диапазон В3:В14.

Задания для самостоятельного выполнения

Все задания
выполнить в одном файле на разных листах, результат сохранить под именем Табулирование.

1.     
Протабулировать функцию на
отрезке [-5;5] с шагом 1.

2.     
Протабулировать функцию  на
отрезке [0;2] с шагом 0,2.

3.     
Протабулировать функцию  на
отрезке [2;8] с шагом 0,5.

4.     
Протабулировать функцию  на
отрезке [0;3] с шагом 0,2.

5.     
Протабулировать функцию  на
отрезке [0;2] с шагом 0,1.

6.     
Протабулировать функцию  на
отрезке [1;5] с шагом 0,5.