Простые ставки в excel

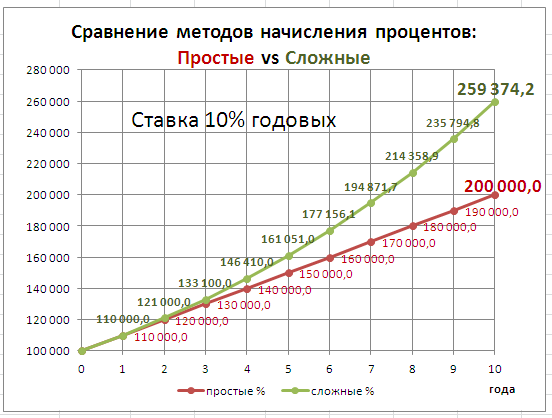
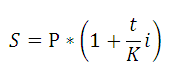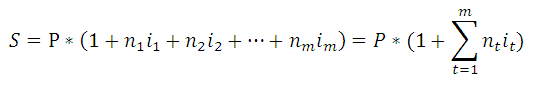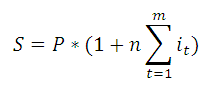Рассмотрим простые проценты — метод начисления, при котором сумма начисленных процентов определяется исходя только из первоначальной величины вклада (или долга). Процент на начисленные проценты не начисляется (проценты не капитализируются).

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по простым процентам и по

сложным процентам

.

Сущность метода начисления по простым процентам сводится к тому, что проценты начисляются в течение всего срока кредита на одну и ту же величину капитала, предоставленного в кредит (или на одну и ту же величину вклада).

В случае известной годовой процентной ставки (i), суммы капитала, предоставленного в кредит (P) и срока ссуды (n, лет), можно рассчитать так называемую

Наращенную сумму S

– сумму первоначального капитала (Р) и начисленных на него процентов (I).

Примечание

.

В случае вклада на определенный срок, S представляет собой

Будущую стоимость

вклада, вычисленную по методу простых процентов.

Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) записывается в следующем виде: S= P+I= P+P*n*i= P*(1+n*i)

Выражение (1+n*i) называется множителем наращения процентов. В формуле предполагается, что процентная ставка (i) не изменяется в течение всего срока предоставления кредита. В

файле примера

приведен расчет наращенной суммы для заданного количества лет, годовой % ставке и заданной величине первоначальной суммы. Также приведен график для сравнения наращенной суммы с использованием простых и

сложных процентов

.

Вычисление наращенной суммы при постоянной процентной ставке

Вышеуказанная формула простых процентов настолько проста, что не понятно, в чем вообще состоит проблема вычислений? Вычислить

Наращенную сумму

S

при известных Р, n, i или вычислить i при известных  Р, n, S можно и на калькуляторе. Однако, все несколько усложняется в случае, когда срок финансовой сделки не равен целому числу лет.

Если срок предоставления кредита определен в месяцах, то формулу для определения наращенной суммы необходимо изменить, разделив годовую ставку i на 12 (12 месяцев в году). Под n теперь будем понимать количество месяцев. S=P*(1+n*i/12) i/12 – это ставка за период (за месяц).

Если срок финансовой сделки определен в кварталах, то под n будем понимать количество кварталов, на который был выдан кредит (или заключен договор срочного вклада). Годовую ставку i нужно разделить на 4 (4 квартала в году). Формула выглядит так: S=P*(1+n*i/4)

По аналогии, можно предположить, что если срок финансовой сделки определен в днях, то под n разумно понимать количество дней, на который был выдан кредит. Однако со ставкой за период не все так просто. Действительно, i нужно делить на 365 (365 дней в году) или на 366 в случае

високосного года

? Поэтому, если срок финансовой сделки определен в днях, то формулу определения наращённой суммы записывают несколько в ином виде:

где t — число дней функционирования сделки (число дней, на которое предоставили кредит); К — временная база (число дней в году).

Временную базу года можно брать число дней в году (365 или 366), или даже 360. Откуда 360? Дело в том, что в ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года

К

принимается равной 360 дням (12*30).

В этой связи различают три метода процентных расчетов, зависимых от выбранного периода начисления.

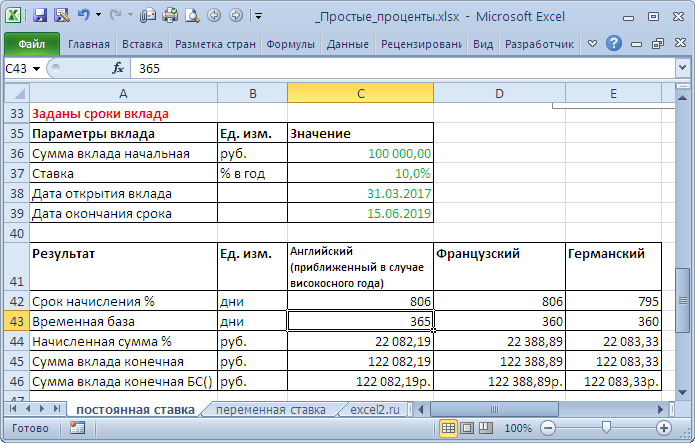
1. Точные проценты с точным числом дней ссуды (английский (британский) метод). При этом методе продолжительность года К принимается равной 365 (или 366) дням и определяется фактическое число дней t между двумя датами (датой получения и погашения кредита), т.е. временная база – календарный год.

Примечание

.

Вычисление по формуле S=P*(1+n*i/365) является лишь приблизительным по английскому методу в случае високосного года (см. ниже).

1. Обыкновенные (обычные) проценты с точным числом дней ссуды (французский метод, банковское правило, гибридный метод). При этом методе величина t рассчитывается, как и в предыдущем методе, а продолжительность года принимается равной К = 360 дням (коммерческий год, обыкновенный год). Это позволяет французским банкирам зарабатывать в 1,01388 раза больше денег, чем английским (365/360= 1,01388) за тот же период.

Примечание

.

Вычисление по французскому методу можно производить по формуле S=P*(1+n*i/360), где i – годовая ставка, n – число дней ссуды.

1. Обыкновенные проценты с приближенным числом дней ссуды (германский метод). При этом методе величина t определяется так:

   количество полных месяцев

   ссуды *умноженное на 30 дней в каждом + точное число дней ссуды в неполных месяцах; продолжительность года К = 360 дней.

В

файле примера

приведен расчет начисления процентов по 3-м методам.

Примечание

.

При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.

Понятно, что вычисления по английской и германской системе могут быть сделаны, только если заданы конкретная дата выдачи кредита и дата окончания его срока. Т.к. чтобы вычислить по английской системе – требуется знать продолжительность конкретного года (високосный или нет), а по немецкой – требуется знать количество полных месяцев и число дней ссуды в неполных месяцах. По французскому методу количество дней ссуды берется фактическое, а временная база всегда =360, поэтому вычисления производить можно и без знания конкретных дат (достаточно знать количество дней ссуды). Еще одно замечание о вычислении наращенной суммы при использовании английского метода. Напомним, что продолжительность года в этом методе принимается равной 365 (или 366) дней, правда, не всегда понятно как проводить вычисления, если срок кредита приходится и на високосный и обычный год (например, кредит выдан 31.10.2016, а должен быть погашен в 15.06.2017, високосный 2016). Т.к. в РФ используется английский метод, то ЦЕНТРАЛЬНЫЙ БАНК РОССИЙСКОЙ ФЕДЕРАЦИИ опубликовал письмо от 27 декабря 1999 г. N 361-Т для разъяснения этой ситуации:

В случае, если дни периода начисления процентов по привлеченным (размещенным) банками денежным средствам приходятся на календарные годы с разным количеством дней (365 и 366 дней соответственно), то начисление процентов за дни, приходящиеся на календарный год с количеством дней 365, производится из расчета 365 календарных дней в году, а за дни, приходящиеся на календарный год с количеством дней 366, производится из расчета 366 календарных дней в году.

В

файле примера

в ячейке

В50

приведена

формула массива

, которая позволяет вычислить наращенную сумму в случае кредита, когда года даты выдачи и даты погашения ссуды не совпадают (например, кредит выдан 31.03.2015, а должен быть погашен в 15.06.2017).

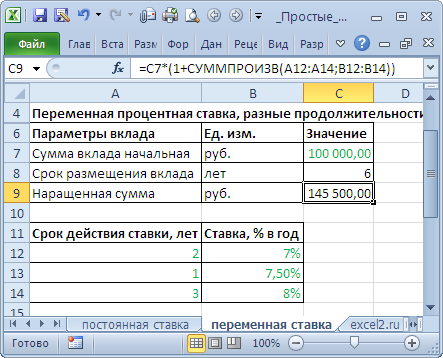
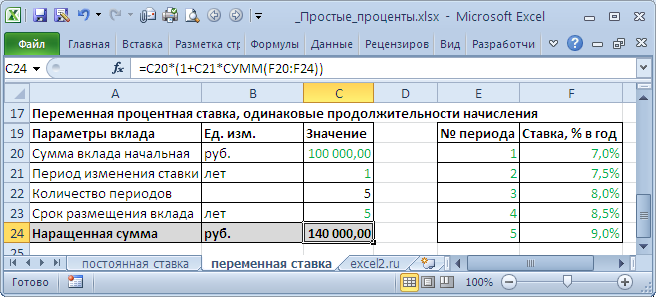
Вычисление наращенной суммы при переменной процентной ставке

При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная ставка определяется по формуле:

В

файле примера

на листе

Переменная ставка

сделаны расчеты по этой формуле: =

C7*(1+СУММПРОИЗВ(A12:A14;B12:B14))

В случае, если процентная ставка изменяется через равные периоды, то вышеуказанную формулу можно несколько упростить.

n – период действия ставки без изменения.

Функция СТАВКА используется для определения процентной ставки по инвестиции либо денежному займу с аннуитетной структурой графика погашения для одного периода выплат (при условии, что будущая стоимость ценных бумаг, обеспечивающих инвестицию либо кредит является известной величиной) и возвращает полученное значение.

Если при заключении сделки процентная ставка не была установлена жестко, функция СТАВКА позволяет определить размер неявной ставки (то есть такой ставки, которая обеспечила бы получение эквивалентного дохода).

Примеры финансовых расчетов по функции СТАВКА в Excel

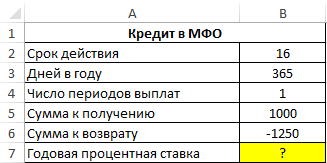
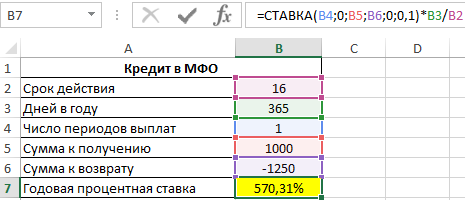
Пример 1. В МФО был взят кредит сроком на 16 дней, сумма которого составляет 1000 долларов. Сумма возврата составляет 1250 долларов. Определить годовую процентную ставку по указанным условиям займа.

Таблица данных:

Для расчета в ячейку B7 введем следующую формулу:

=СТАВКА(B4;0;B5;B6;0;0,1)*B3/B2

Описание аргументов:

• B4 – число периодов выплат (в данном случае – 1);
• 0 – размер фиксированной выплаты (поскольку в данном примере только один период выплат, указано значение 0);
• B5 – тело кредита;
• B6 – сумма на момент погашения долга;
• 0 – характеризует тип выплат, при котором выплата производится в конце периода;
• 0,1 – предполагаемое значение процентной ставки (любое число из диапазона от 0 до 1);
• B3/2 – коэффициент для пересчета полученного значения ставки к годовой процентной ставке.

Результат вычислений:

Пи данных условиях микрокредитования сроком займа на 16 дней процентная ставка составляет 570,31% годовых! Несмотря на это, услуги по микрокредитованию сегодня продолжают набирать популярность.



Анализ пенсионных отчислений с использованием функции СТАВКА в Excel

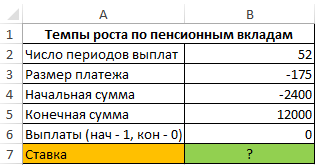
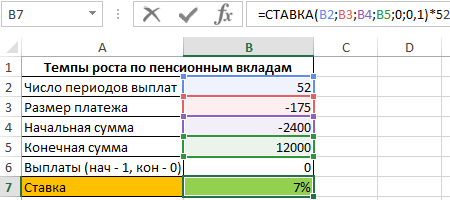
Пример 2. Определить темпы роста пенсионных отчислений (процентную ставку), если баланс средств на конец года составляет 12000 долларов, а в начале года – 2400 долларов. Еженедельные платежи на протяжении года составляли 150 долларов (то есть, количество периодов – 52).

Исходные данные:

Формула для расчета:

=СТАВКА(B2;B3;B4;B5;0;0,1)*52

Описание аргументов:

• B2 – количество периодов выплат;
• B3 – сумма платежа (расходная операция, поэтому отрицательное значение);
• B4 – сумма средств до наступления первого периода выплат;
• B5 – сумма по окончанию последнего периода выплат;
• 0 – выплаты в конце периода;
• 0,1 – произвольное значение из интервала от 0 до 1;
• 52 – количество периода выплат для пересчета размера ставки в годовых.

Результат вычислений:

То есть, пенсионные отчисления выполняются под 7% годовых.

Определение реальной процентной ставки по кредиту

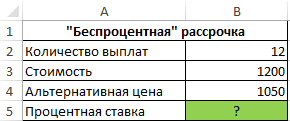
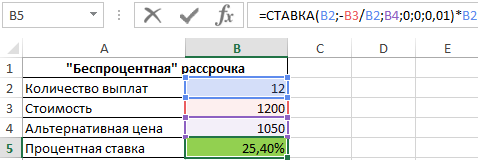
Пример 3. Ноутбук одной и той же модели можно приобрести за 1200 долларов в рассрочку (беспроцентную, судя по рекламе в первом магазине) или за 1050 долларов в другом магазине. Рассрочка выдается на 1 год с 12 периодами выплат. Определить реальный процент «беспроцентной» рассрочки платежей по кредиту.

Исходные данные:

Формула для расчета:

=СТАВКА(B2;-B3/B2;B4;0;0;0,01)*B2

Описание аргументов:

• B2 – число периодов выплат;
• -B3/B2 – выражение для расчета размера ежемесячного платежа;
• B4 – реальная стоимость ноутбука (используется как начальная стоимость финансового инструмента, цена которого повысится до 1200 к окончанию последнего периода выплат);
• 0 – остаток по окончанию последнего периода выплат;
• 0 — выплаты в конце периода;
• 0,01 — произвольное значение предполагаемой ставки.

Результат расчетов:

То есть, фактически в первом магазине клиенту предложили кредит на ноутбук под 25,4% годовых.

Функция СТАВКА в Excel и особенности ее использования

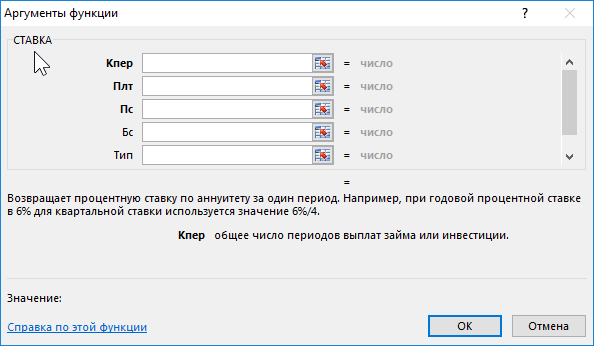
Функция СТАВКА имеет следующий синтаксис:

= СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])

Описание аргументов:

• кпер – обязательный аргумент, характеризующий число периодов выплат по аннуитетной схеме.
• плт – обязательный аргумент, характеризующий фиксированное значение выплаты, производимой в каждый из периодов выплат. Сумма выплаты за каждый период включает две составляющие: тело и проценты без учета прочих комиссий и сборов. Если данный аргумент опущен, следующий аргумент должен быть указан явно.
• пс – обязательный аргумент, характеризующий текущую стоимость задолженности (либо вознаграждения), эквивалентную общей сумме последующих платежей на данный момент. Если значение неизвестно, необходимо явно указать значение 0 (нуль).
• [бс] – необязательный аргумент, характеризующий размер желаемого остатка средств после выполнения последней выплаты согласно графика платежей. Если явно не указан, по умолчанию используется значение 0 (нуль), а аргумент пс становится обязательным для заполнения.
• [прогноз] – необязательный аргумент, характеризующий предполагаемый размер процентной ставки. Если аргумент явно не указан, по умолчанию принимается значение 10%. Если полученное в результате вычислений значение не сходится с указанной прогнозной величиной, величину данного аргумента следует изменить. Рекомендуется выбирать значение для аргумента [прогноз] из диапазона от 0 до 1.
• [тип] – необязательный аргумент, принимающий значения 0 или 1:

1. Если введен 0, считается, что выплата производится в конце периода;
2. Если введен 1, считается, что выплата производится в начале периода.

Примечания:

1. Единицы измерения величин, указанных в качестве аргументов кпер и [прогноз], должны соответствовать друг другу. Например, при расчете ставки по займу, выданному на два года под 16% с ежемесячными выплатами необходимо, в качестве аргумента [прогноз] необходимо использовать значение 16%/12, а кпер – 2*12.
2. Если хотя бы в качестве одного из аргументов функции было передано текстовое значение, результатом выполнения функции будет являться код ошибки #ЗНАЧ!.
3. Аннуитетная схема выплаты вознаграждения либо погашения задолженности предполагает выплаты фиксированной суммы, включающей вознаграждение или тело кредита и дополнительных процентов (в зависимости от установленной процентной ставки) на протяжении установленного количества периодов выплат. В отличие от классической схемы, при которой проценты начисляются на остаток вознаграждения или задолженности, в аннуитетной схеме соотношение тело кредита/проценты является изменяющейся величиной.
4. При выполнении расчетов функция СТАВКА использует итерационный метод. Если после 20 итераций последующие результаты вычислений отличаются друг от друга более, чем на 10-7, результатом вычислений будет являться код ошибки #ЗНАЧ!.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Чтобы рассчитывать доходность банковских вкладов, нужно разобраться с простыми и сложными процентами.

• Простые проценты (P — principal) начисляют на первоначальный вклад в конце отчетного периода. 
• Частота начисления процентов — период времени, в конце которого банк пересчитывает сумму на вкладе.
• Период вложения — время, на которое сделан вклад. При этом за период вложения проценты могут начисляться несколько раз.
• Процентная ставка (r — rate) — собственно величина, на которую умножается сумма на вкладе с определённой частотой.

Например, при начислении процентов раз в год по вкладу в 10 тыс. рублей под 12% годовых в конце мы получим прибыль 10 000 х 0,12 = 1200 рублей. 

Сложные проценты — это когда проценты начисляются не только на основной капитал, но и на полученную в предыдущих периодах прибыль. То есть, с определённой периодичностью сумма вклада пересчитывается и начисляются, в том числе, проценты на проценты. Сумма растёт по экспоненте.

Сложные проценты могут называть по-разному:

• эффективные проценты;
• проценты на проценты;
• композиционный процент;
• норма доходности с учетом капитализации;
• норма доходности с учетом реинвестирования.

Расчёт сложных и простых процентов на реальном примере

Предположим, есть два брата, и у обоих на руках есть первоначальный капитал в размере 10 000 рублей. Они решают сделать вклад на 20 лет. 

Первый брат делает вклад на депозитный счет с простой процентной ставкой 9%, а второй делает вклад на счет со сложной процентной ставкой 8%.

Начисление процентов происходит в конце каждого года. 

Итак имеем:

• P₀ = 10 000 руб.,
• r₁ = 9%,
• r₂ = 8%,
• t = 20 лет.

Формула расчета простых процентов:

Формула расчета сложных процентов:

t — число реинвестиций (капитализаций) в течение одного года. В нашем примере t = 1, поскольку начисление процентов происходит только раз в год.

В Excel рост капитала двух братьев будет выглядеть следующим образом. 

• Период — год от момента открытия вклада. 
• Капитал — сумма, на которую начисляются проценты в конце года. 
• Процент — проценты по вкладу за этот год. В первом случае процент считаем от первоначального капитала, каждый год прибыль одинаковая. Во втором случае процент начисляется на весь капитал, то есть на первоначальную сумму плюс проценты за все прошлые годы — прибыль постоянно реинвестируется.
• Баланс — итого на счёте в конце года.

Если хотите узнать больше о работе в Excel, то рекомендуем записаться на наш обширный онлайн-курс «Академия Excel».

Можно заметить, что первые несколько лет вклад с простыми процентами выгоднее за счёт более высокой процентной ставки. Но затем ситуация меняется, и даже при меньшей ставке второй брат получил через 20 лет 466% от первоначальной суммы, а первый брат — 280%.

На рисунке ниже показан рост капитала при различных видах процента.

Корректировки на ситуацию вокруг

Чтобы получить высокую доходность при сложном проценте, необходимо ждать длительное время. С этим могут быть сложности в реальных условиях российской экономики (например: кризисы 1998 г., 2008 г., 2014 г. и т.д.). 

Кроме того, уровень инфляции постепенно растёт, и прибыль по вкладам, особенно с более низкой ставкой при сложных процентах, может свестись к нулю.

Читайте также: О курсе «Excel Academy»

По норме доходность акции значительно превосходят доходность по банковским вкладам, но это более рискованный инструмент. С другой стороны, многие российские банки получают прибыль как раз за счёт активной деятельности на фондовом рынке — то есть несут те же риски, но прибыль вы получаете меньше. 

Таким образом, банковские вклады могут выступать в роли сохранения первоначальной ценности капитала (с небольшим риском), и никак не являются механизмом получения прибыли. Чтобы капитал рос в имеющихся условиях, целесообразнее самостоятельно заниматься инвестированием в развивающиеся отрасли.

Это тоже интересно:

Правда и вымысел о финансовой безграмотности россиян

Как работать с дублями в Excel?

Что должен уметь финансист будущего: технические навыки и инструменты

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Блог SF Education

MS Office

Мультипликаторы для оценки бизнеса

Содержание статьи Основные методы сравнительного подхода к оценке бизнеса — метод рынка капитала и метод сделок, применение которых предполагают обязательный этап — расчет оценочных мультипликаторов…

Разбор структуры капитала «Райффайзенбанк»

Содержание статьи Капитал банка является обязательным условием образования и функционирования любого коммерческого банка. Капитал формируется из собственных средств акционеров или участников банка. Основной функцией…

В этой статье описаны синтаксис формулы и использование функции СТАВКА в Microsoft Excel.

Описание

Возвращает процентную ставку за период аннуитета. Ставка вычисляется с помощью итерации и может иметь ноль или больше решений. Если последовательные результаты rate не сходятся в пределах 0,00000001 после 20 итерации, то ставка возвращает результат #NUM! значение ошибки #ЗНАЧ!.

Синтаксис

СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])

Примечание: Полное описание аргументов «кпер», «плт», «пс», «бс» и «тип» см. в разделе, посвященном функции ПС.

Аргументы функции СТАВКА описаны ниже.

• Кпер    — обязательный аргумент. Общее количество периодов платежей по аннуитету.

• Плт    Обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.

• Пс    — обязательный аргумент. К настоящему моменту — общая сумма, на которую сейчас стоит ряд будущих платежей.

• Fv    Необязательный. Будущая стоимость или баланс, который вы хотите достичь после последнего платежа. Если значение «ок» опущено, предполагается значение 0 (например, будущая стоимость займа — 0). Если аргумент «пс» опущен, необходимо включить аргумент «pmt».

• Тип    Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.

Тип	Когда нужно платить
0 или опущен	В конце периода
1	В начале периода

• Прогноз    Необязательный. Предполагаемая величина ставки.

  • Если аргумент «прогноз» опущен, предполагается, что его значение равно 10 %.

  • Если функция СТАВКА не сходится, попробуйте изменить значение аргумента «прогноз». Функция СТАВКА обычно сходится, если значение этого аргумента находится между 0 и 1.

Замечания

Убедитесь, что единицы измерения, выбранные для аргументов «прогноз» и «кол_пер» соответствуют друг другу. При ежемесячных выплатах по четырехгодичному займу под 12 процентов годовых используйте значение 12%/12 для аргумента «прогноз» и 4*12 — для аргумента «кол_пер». При ежегодных платежах по тому же займу используйте значение 12% для аргумента «прогноз» и 4 —для аргумента «кол_пер».

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
4	Срок займа в годах
-200	Ежемесячная сумма платежа
8000	Сумма займа
Формула	Описание	Результат
=СТАВКА(A2*12; A3; A4)	Месячная процентная ставка по займу в соответствии с условиями, указанными в диапазоне A2:A4 в качестве аргументов.	1 %
=СТАВКА(A2*12; A3; A4)*12	Годовая процентная ставка по займу в соответствии с теми же условиями.	9,24 %

1. Основные понятия

_{Термин «процент»
происходит от латинского pro centum, что
переводится как «на сотню, или за
сто». При такой трактовке процент
выступает в качестве так называемого
процентного числа, указывающего на
часть целой величины или доли, и широко
используется в социально-экономической
статистике и законодательной практике
регулирования предпринимательской
деятельности (например, при начислении
налогов). В процентных вычислениях важно
понимать, какая величина принята за
100%, т.е. что используется в качестве базы
[2].}

_{В финансово-кредитной
сфере важную роль играет временной
фактор денег, поскольку разумно вложенные
денежные средства должны приносить их
владельцу определенный доход (процент),
зависящий от длительности их использования.}

_{В данном случае
процент — это абсолютная величина дохода
от предоставления денег в долг (кредит)
в любой его форме. Процентная ставка —
относительная величина дохода за
фиксированный интервал времени (период
начисления), измеряемая в процентах
(сотая часть числа) или в виде дроби.}

_{Проценты
различаются по базе начисления, которая
может быть либо постоянной, либо
последовательно изменяющейся
(наращиваемой). В первом случае
рассчитываются простые проценты, к
которым прибегают при выдаче краткосрочных
(до одного года) ссуд или при периодических
выплатах процентов кредитору (когда
проценты не присоединяются к сумме
долга).}

_{Во втором случае
рассчитываются сложные проценты, к
которым обычно прибегают в среднесрочных
и долгосрочных кредитно-финансовых
отношениях, когда проценты не выплачиваются
немедленно после их начисления, а
присоединяются к сумме долга (капитализация
процентов). База для начисления сложных
процентов увеличивается (наращивается)
с каждым периодом начисления процентов.}

1. Наращение по простой процентной ставке

_{Ниже рассмотрены
основные типы моделей финансовых
расчетов на основе простых процентов.
Следует отметить, что в Excel отсутствуют
встроенные финансовые функции для
вычисления простых процентов, но они
могут быть сравнительно легко реализованы
на основе следующих формул [3]:}

I = P • n
• i, (1.1)

S = P +1 =
P+ P • n • i = P • (1 + n • i) (1.2),

где I
— проценты за весь срок, на который
предоставлена ссуда;

P — первоначальная
сумма ссуды (долга);

S — наращенная сумма
в конце срока погашения ссуды;

i — величина
процентной ставки (десятичная дробь);

n — срок погашения
ссуды (обычно в годах).

_{При сроке ссуды,
не кратном периоду начисления, n
рассчитывается по следующей формуле:}

n = t/k
(1.3)

_{где t — количество
дней, составляющих срок ссуды;}

_{k — количество
дней в периоде начисления (при расчете
обыкновенных или коммерческих процентов
принимается: год — 360 дней, месяц — 30 дней;
при расчете точных процентов берутся
фактические значения).}

_{Задача №1.}

_{Вкладчик поместил
вклад в размере 3000 рублей в банк под 7%
годовых (простых). Какая сумма будет на
счете вкладчика:}

_{а) через 3 месяца;}

_{б) через 1 год;}

_{в) через 3 года
5 месяцев?}

_{Решение.}

_{Для расчета
суммы вклада в каждом из трех случаев
используем формулу (1.2) согласно которой}

<sub>а) S = 3000 * (1 + 0,07
* 90 / 360) = 3000 * (1 + 0,0175) = 3000 * 1,0175 = 3052,5 р.</sub>

_{б) S = 3000 * (1 + 0,07)
= 3000 * 1,07 = 3210 р.}

<sub>в) S = 3000 * (1 + 0,07
* ( 3 + 5 * 30 / 360)) =3000 * (1 + 0,239) = 3000 * 1,293 = 3717,5 р.</sub>

_{Задача №2.}

_{Реализовать
приведенные выше расчеты наращенной
суммы в зависимости от первоначального
вклада, процентной ставки и периода
начисления в Excel. Использовать при этом
возможность присвоения содержательных
имен ячейкам таблицы.}

_{Из базовой
формулы (1.2) можно получить ряд соотношений,
часто используемых в финансовой практике.
Например, зная наращенную сумму S,
количество периодов начисления простых
процентов n и величину процентной ставки
i, можно рассчитать вложенную сумму}

P
=
(1.4)

_{Эта операция,
обратная наращению, называется
дисконтированием; она позволяет по
известной будущей стоимости (S) получить
текущую стоимость (P), называемую также
современной капитализированной
стоимостью.}

_{Дисконтный
множитель, равный 1/(1+n*i), показывает,
какую долю составляет первоначальная
величина вклада (займа) в его окончательной
сумме. При этом говорят, что сумма S
дисконтируется или учитывается, а сам
процесс начисления процентов и их
удержания называется учетом; величина
удержанных процентов называется
дисконтом (D) и рассчитывается как}

D = S — P.
(1.5)

_{Задача №3.}

_{Банк выплачивает
7% простых в год. Гражданин Иванов хочет
получить через 2 года и 6 месяцев 10000
рублей. Какую сумму он должен положить
в банк в настоящий момент?}

_{Решение.}

_{Подставляя
данные, приведенные в условии задачи,
в формулу (1.4), получаем ответ}

_{P = 10000 / (1 + 0,07 *
2,5) = 10000 / 1,175 = 8510,64 р.}

_{Задача №4.}

_{Реализовать
приведенный выше расчет первоначального
вклада в зависимости от суммы приращения,
простой процентной ставки и периода
начисления в Excel.}

_{Зная вложенную
сумму P, наращенную сумму S и количество
периодов начисления простых процентов
n, можно рассчитать величину процентной
ставки}

i =
(1.6)

_{Задача №5.}

_{В банке был
размещен вклад в размере 1500 р. Через 1
год и 3 месяца на счете было 1631,25 р. Сколько
простых процентов в год выплачивает
банк? Реализовать расчет простой
процентной ставки в Excel.}

_{Задача №6.}

_{Гражданин Петров
взял в долг у своего приятеля Сидорова
9800 р., выдав последнему вексель (долговую
расписку), по которому обязался выплатить
10000 р. через 3 месяца. Под какой годовой
процент выдан данный вексель? Реализовать
расчет простой процентной ставки в
Excel.}

Соседние файлы в папке практическе работы

• #
• #
• #