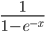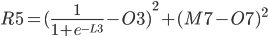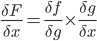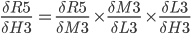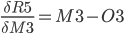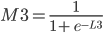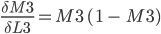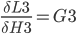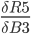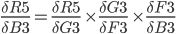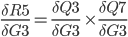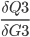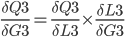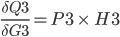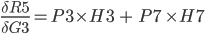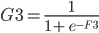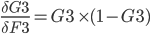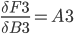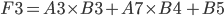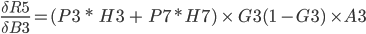Простая нейросеть в excel

В современном мире трудно найти человека, который бы не слышал про нейронные сети. Кажется, их применяют всюду: оживление фотографий, DeepFake, маски для фото в соцсетях и прочее. Но для большинства людей они являются чем-то абстрактным и непонятным.

Однако создать свою нейросеть можно даже не имея знаний о языках программирования, и используя простейший инструмент, знакомый любому офисному сотруднику – MS Excel.

Схематично моя будущая нейросеть выглядит так:

Это упрощенная схема перцептрона. Перцептрон – простейший вид нейронных сетей, в основе которых лежит математическая модель восприятия информации мозгом, состоящая из сенсоров, ассоциативных и реагирующих элементов. На вход подаются значения признаков, которые могут быть равны 0 или 1. Строгая бинарность обусловлена тем, что признаки – это, своего рода, сенсоры, и они могут находиться либо в состоянии покоя (равны 0), либо в состоянии возбуждения (равны 1). Затем эти признаки умножатся на вес и суммируются. После при помощи функции активации (сигмоиды) получаю значения на выходе от 0 до 1. Таким образом, главной задачей является нахождение весов, обеспечивающих наиболее точное прогнозирование.

Представлю, что требуется по определенному набору признаков научить нейросеть определять является ли животное домашней кошкой или нет.

В датасете имеется 9 признаков, если экземпляр им обладает, то ставится 1, если нет, то 0. Целевой столбец назван «Выход»: 1 – значит экземпляр кошка, 0 – не кошка. В идеале нейросеть должна предсказать 1 для всех кошек и 0 для всех не кошек.

Первый шаг – создание таблицы поиска весов для каждого признака:

В диапазоне M3:U2 генерирую случайные величины весов при помощи формулы СЛЧИС().

Далее создаю столбцы для Bias (смещение) и Output (предсказание модели):

Формула в ячейке W3:

=B3*M3+C3*N3+D3*O3+E3*P3+F3*Q3+G3*R3+H3*S3+I3*T3+J3*U3

Протягиваю формулу до ячейки W14.

Bias – нейрон смещения. Простыми словами, это дополнительная информация о природе данных для модели, способ показать модели, «в какую сторону думать».

Формула в ячейке output – функция сигмоиды:

=ЕСЛИ(Bias=0;0;1/(1+(EXP(-Bias))))

Данная функция необходима для интерпретации значения bias. Мне нужно получить значения от 0 до 1. Output – предсказание модели. Если значение меньше 0.5, то экземпляр не является кошкой, если больше, то является.

Создаю таблицу для корректировки весов:

В ячейке Z3 следующая формула:

=($K3-$X3)*B3*$X3*(1-$X3)

Протягиваю её на весь диапазон Z1:AH14

Возвращаюсь в блок с весами: в ячейку М4 прописываю формулу: =M3+Z3

Протягиваю её на диапазон M4:U14:

В диапазоне AJ3:AJ14 пишу формулу: =ЕСЛИ(X3<0,5;0;1) – если значение в столбце Output больше, либо равно 0.5, то модель предполагает, что в строке домашняя кошка.

В диапазоне AK3:AK14 пишу формулу: =ЕСЛИ(K3=1;ЕСЛИ(AJ3=K3;1;0);»») – проверяю правильно ли модель предсказала домашнюю кошку.

В диапазоне AL3:AL14 пишу формулу: =ЕСЛИ(K3=0;ЕСЛИ(AJ3=K3;1;0);»»)– проверяю правильно ли модель предсказала не домашнюю кошку.

В ячейках AK15 и AL15 формулы СРЗНАЧ() для отображения доли правильных ответов.

На рисунке видно, что на данный момент модель считает все записи домашними кошками (цифра 1 в столбце «Предсказание»).

Копирую диапазон M14:U14 и вставляю значения в диапазон M3:U3:

Смотрю результат:

Теперь модель не все записи считает домашними кошками, но результат пока ещё не лучший.

Совершаю ещё несколько итераций. Копирую диапазон M14:U14 и вставляю значения в диапазон M3:U3. В таблице ниже видно, как менялись предсказания после каждого цикла:

В итоге, моя нейросеть после восьми итераций верно предсказала значения для всех строк.

Используя полученные веса из диапазона M14:U14, можно проверять другие комбинации признаков, и модель будет предсказывать является ли представленная строка домашней кошкой или нет.

Видно, что модель неидеальна, так как неверно предсказала рысь. Зато манула она определила верно, несмотря на то, что он больше походит на домашнюю кошку, чем рысь. На самом деле 100%-я точность для нейросетей невозможна, поэтому полученный результат можно считать неплохим. На практике использование MS Excel для задач машинного обучения — не очень хорошая идея, так как он не может работать с большим объемом данных, да и создан совершенно для другого. Однако, используя методы, представленные в посте, можно самостоятельно «поиграть» с данными, что поможет понять базовые принципы работы нейросетей.

  Перевод

  Ссылка на автора

Чтобы упростить концепцию сверточных нейронных сетей, я попытаюсь объяснить, что происходит при разработке модели глубокого обучения. Для получения дополнительной информации, я рекомендую поиск онлайн как есть обильное количество доступной информации (как это видео). Это объяснение получено из fast.ai репозиторий.

Эта картина простой нейронной сети в основном представляет то, что происходит в этом примере.

Входной слой

Эти данные изображения № 7 из MNIST базы данных, и мы предполагаем, что вы используете модель перед поездом для классификации.

Скрытый слой 1

Скрытый слой — это то, что преобразует входные данные, чтобы отличить более сложные элементы от данных для выходного уровня, чтобы сделать более точную оценку.

Два фильтра будут представлять разные формы — первый фильтр предназначен для обнаружения горизонтальных краев, второй фильтр обнаруживает вертикальные края. Этот фильтр 3х3 называется сверточное ядро, Фильтр 1 активируется для горизонтальных ребер на входе. Conv1 показывает активацию обоих после взятия секции 3×3 ввода и умножения ее на сверточное ядро. Следующая картина ниже дает вам лучшую идею.

* Хотя это представлено в 2d массиве, они должны быть сложены как Тензор, Где каждая матрица представляет срез в тензоре. Это все по существу строковые операции (Линейная алгебра), которые происходят.

= SUM (F11: H13 * $ AD $ 11: $ AF $ 13) — это происходящая Свертка.

Эта сумма приведет к числу активации 3 для этого конкретного места 3×3 на входе.

Функция активации

Далее мы используем нашу единицу нелинейности с помощью РЕЛУ как наша функция активации для устранения негативов. Далее мы видим, что негативы исчезают на следующей картинке.

Скрытый слой 2

Далее мы делаем еще одну свертку. Conv2 будет следующим скрытым слоем. Это взвесит обе матрицы в Conv1, взяв их произведение суммы. Ядро свертки здесь будет представлять собой Тензор 2X3X3.

После использования RELU мы создали второй слой.

Макс Пул

Максимальное объединение вдвое уменьшает разрешение по высоте и ширине, принимая только максимум 2х2 в Conv2. В матрице Макспула мы видим только максимальное значение сечения 2×2 в Conv2, которое равно 33. Пул вычисляется быстрее, чем свертки. Кроме того, это дает вам некоторое количество инвариантность перевода,

Выходной слой

Затем мы создаем наш полностью связанный слой, взяв все наши активации в Maxpool и придав им всем вес. Это делается с помощью матричного продукта. В Excel, мы возьмем сумму активаций и весов. Таким образом, вместо синтаксического анализа каждой секции в сверточном слое, как и раньше, полностью подключенный слой (плотный слой) будет выполнять классификацию объектов, которые были извлечены сверточными слоями и подвергнуты понижающей дискретизации слоями с максимальным пулом.

Этот пример представляет только один класс, то есть один номер. Нам еще предстоит классифицировать остальные числа.

Introduction

This article is written for you who is curious of the mathematics behind neural networks, NN. It might also be useful if you are trying to develop your own NN. It is a cell by cell walk through of a three layer NN with two neurons in each layer. Excel is used for the implementation.

• Download neuralnetwork Sigmoid — 1.2
• Download neuralnetwork Leaky ReLu — 1.2

Background

If you are still reading this, we probably have at least one thing in common. We are both curious about Machine Learning and Neural Networks. There are several frameworks and free api:s in this area and it might be smarter to use them than inventing something that is already there. But on the other hand, it does not hurt to know how machine learning works in depth. And it is also a lot more fun to explore things in depth.

My journey into machine learning has perhaps just started. And I started by Googling, reading a lot of great stuff on the internet. I also saw a few good YouTube videos. But I it was hard to gain enough knowledge to start coding my own AI.
Finally, I found this blog post: A Step by Step Backpropagation Example by Matt Mazur. It suited me, and the rest of this text is based on it.

Construction

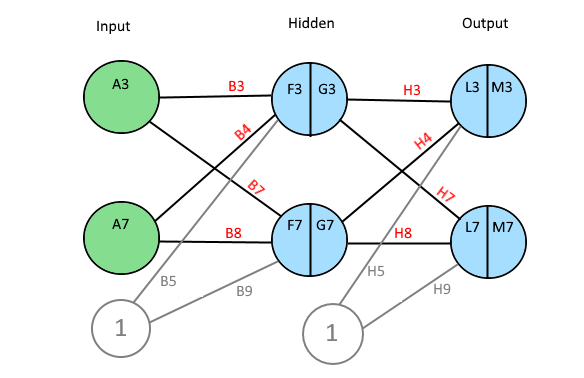
A Neural Network, NN, consists of many layers of neurons. A Neuron has a value and connections with weights to all other neurons in the next layer.

The first layer is the input layer and the last layer is the output layer. Between input and output, there might be one or many hidden layers. The number of neurons in a layer is variable.

If a NN is used to, for example, classify images, the number of neurons in the input layer is of course equal to the number of pixels in the image. Then in the output, each neuron represents a classification of the image. (E.g., a type of animal, a flower or a digit.)

Calculations

Before the calculations, all the weights in the NN have to be initialized with random numbers.

The image below is a print screen of the spread sheet that I refer to in the rest of this article. It might be a good idea to keep an open window of that sheet. That should make it easier to follow along.
A tip: Row 2 is the order of calculations.

Step 1 — 3. Forward Pass

The value of one neuron is calculated by taking the sum of every previous neuron multiplied by its weight.
An extra bias weight which has no neuron is also added:

F3 = A3 * B3 + A7 * B4 + B5

The value is normalized through a activation function. There are several different activation functions used in neural networks.
I have used the logistic function:

G3 = 1 / (1 + EXP(-F3))

Step 4 — 5. Forward Pass

The neurons of the output layer is calculated the same way as hidden layer.

L3 = G3 * H3 + G7 * H4 + H5
and
M3 = 1 / (1 + EXP(-L3))

Step 6 — 7. The Error

The error of each output neuron is calculated using an expected or a target value. When classifying images, it is common to set one neuron close to 1 and the rest of the neurons close to zero.

For the errors in column Q:

Q3 = (M3 — O3)²

and:

Q7 = (M7 — O7)²

The total Error R5 is the average of all errors and should get closer and closer to zero as the network is trained.

R5 = (Q3 + Q7) / 2

Backward Propagation

A Neural Network is trained by passing it lots of train data repeatedly.
Then, for every iteration, errors and deltas are calculated. This is used to make small adjustments to all the weights in such a way that the network becomes better and better.
This is called backpropagation.
Since the total error can be expressed as a mathematical functions of each weight, one can derive those functions to obtain the slopes of the function curves in one point. The slopes indicate the direction towards a minimum for the total error and proportionally how much each weight should be adjusted in order for the total error to approach zero.

A delta value is calculated below for each weight. The deltas are stored in column I and D, for output and hidden layer respectively.

Chain Rule — Friend of Backpropagation

In practice, we want to derive the total error R5 with respect to H3 so we first to express R5 as a function of H3 using substitutions.

Since

R5 = (Q3 + Q7) / 2
R5 = (M3 - O3)² / 2 + (M7 - O7)² / 2

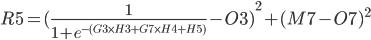
The above function does not look very easy to derive. Is it even possible?
We will instead use the chain rule².
It states that if we have a composition of two or more functions f(g(x)) and let F(x) = f(g(x)), we can derive like this:

F’(x) = f’(g(x)) * g’(x) or in another notation:

In our case, we have the following dependency:

R5(M3(L3(H3))) and we can write:

Step 9. Output layer Deltas

The function for the total error R5 is derived with respect to the first weight H3 of the output layer.

In the above formula, the chain rule is used to make it simpler to derive.

Since:

Proof of derivation of Logistic function found in this article³.

Since 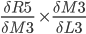will be used later in the backpropagation, it is stored in the cell P3.

P3 = (M3-O3) * M3 * (1 - M3)

The last derivative of the chain of derivatives above is simpler.
Since L3 = G3 * H3 + G7 * H4 + H5

We can now put everything together and store 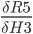into cell I3.

I3 = P3 * G3

The rest of the weights in output layer is calculated the same way and we get:

P7 = (M7-O7) * M7 * (1 - M7)

I4 = G7 * P3
I5 = 1 * P3 (bias neuron)
I7 = G3 * P7
I8 = G7 * P7
I9 = 1 * P7 (bias neuron)

Step 10. Backpropagation in Hidden Layer

In this step, we calculate:

The chain rule from previous steps helps to transform it to something we can use:

First term also must be split up on both errors Q3 and Q7 so:

First look at this:

It can be further split up like this:

First 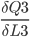is already stored in P3 = (M3-O3) * M3* (1 - M3)

Since L3 = G3 * H3 + G7 * H4 + H5

When we put the above together, we get:

And in the same way as above:

First problem is solved.

Time for

We know that:

And we have previously learned to derive the logistic function.

And now:

Because:

We now put the above together to get one expression for the derivative of the total error with respect to first weight of the hidden layer.

This is stored in cell C3.

The calculations for the above is repeated for all hidden layer weights:

C3 = (P3 * H3 + P7 *H7) * (G3 *(1 - G3)) * A3
C4 = (P3 * H3 + P7 *H7) * (G3 *(1 - G3)) * A7
C5 = (P3 * H3 + P7 *H7) * (G3 *(1 - G3)) * 1
C7 = (P3 * H4 + P7 *H8) * (G7 *(1 - G7)) * A3
C8 = (P3 * H4 + P7 *H8) * (G7 *(1 - G7)) * A7
C9 = (P3 * H4 + P7 *H8) * (G7 *(1 - G7)) * 1

Now it is easy to calculate new weights using a selected learning rate from cell A13.

For example: (new B3)

D3 = B3 - C3 * A13

There is a macro connected to the train button in the Excel document. The macro iterates many times and we can see how the output neurons in column M gets closer and closer to their target values and that the total Error in R5 gets closer and closer to zero.

G3 = IFS(F3 > 0; F3; F3 <= 0; F3/20)
and
P3= (M3-O3) * IFS(M3 > 0;1;M3<=0;1/20)

Final Words

I realize this article might take some time to digest. I tried to explain it as I understood it. Please comment below if you find any errors.

After I sorted out how NNs work in Excel, I wrote a C# program that can interpret hand written digits. It has a Windows Forms user interface which works well. It seems to recognize almost any digit I draw, even ugly once. That was a proof to me that my understanding of Artificial Neural Networks is correct so far.

That article can be found here:

Handwritten digits reader UI⁵

Links

1. A Step by Step Backpropagation Example — Matt Mazur.
2. Chain rule — Wikipedia
3. Logistic function — Wikipedia
4. Rectifier (neural networks) — Wikipedia
5. Handwritten digits reader UI — Kristian Ekman

History

• 1^st January, 2019 — Version 1.0
• 8^th January, 2019 — Version 1.1
  • Replaced Logistic activation function with LeakyReLu
• 11^th January, 2019 — Version 1.2
  • Update of names of biases in diagrams
• 23th Januray, 2019 — Version 1.3
  • Changed du calculation to the total error to the average av errors