Производственная задача в excel пример - Word и Excel - помощь в работе с программами

Начало работы

В данном разделе мы рассмотрим, как можно решить производственную задачу в
программе Microsoft Excel версий 2007, 2010, 2013 или 2016. Если у вас более старая
версия программы Microsoft Excel, то перейдите в другой раздел.

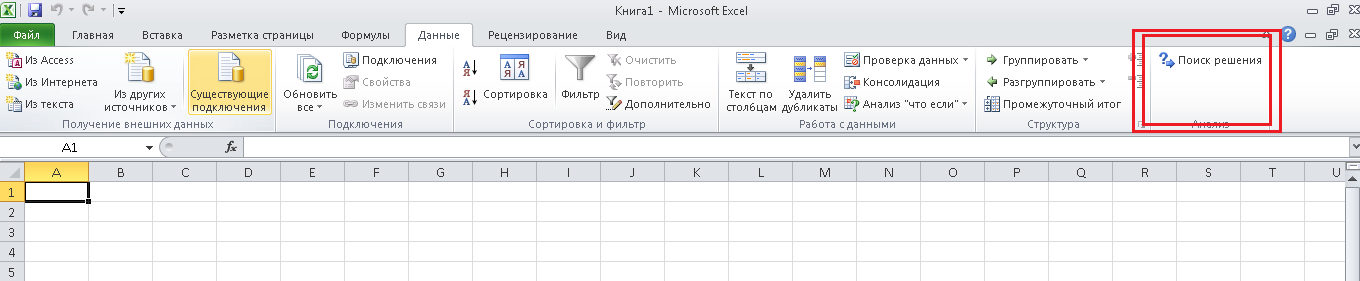
Итак, запустим Microsoft Excel, и перейдем на вкладку «Данные». Справа должна располагаться
кнопка «Поиск решения», как на картинке:

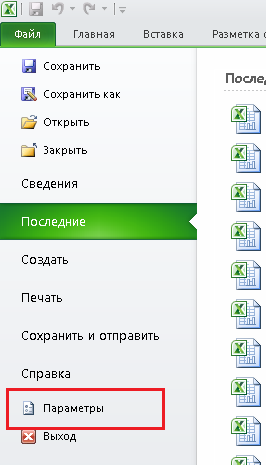
Если же этой кнопки нет, то необходимо включить соответствующую надстройку. Для этого откроем
меню файл, и выберем пункт «Параметры»:

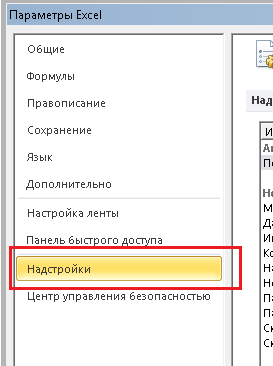
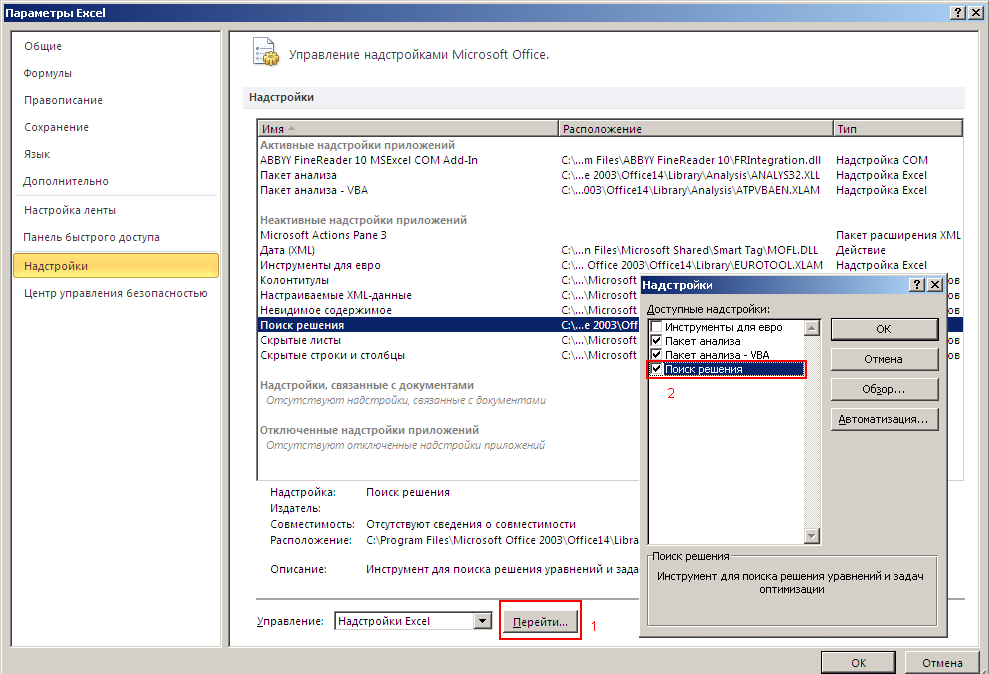
В открывшемся меню необходимо выбрать пункт «Надстройки»:

Затем в правой части, внизу, необходимо выбрать из выпадающего списка «Надстройки Excel», если
они еще не выбраны, и нажать кнопку «Перейти»:

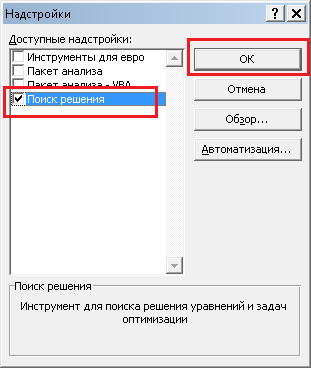
Появится следующее окно, в котором необходимо отметить галочкой необходимую надстройку
(Поиск решения), и нажать кнопку «ОК». После этого на вкладке Данные, в правой части должна
появиться показанная выше кнопка

Понравилось? Добавьте в закладки

Пример решения ЗЛП в Excel 2010

Возьмем ту же задачу, которую мы решали в предыдущем разделе, и попытаемся решить с помощью компьютера:

Ресурс	Изделие A	Изделие B	Изделие C	Сколько ресурса на складах
R1	1	2	3	35
R2	2	3	2	45
R3	3	1	1	40
Прибыль	4	5	6

Как мы помним из предыдущего раздела, наши ограничения и целевая функция выглядят
следующим образом

$$begin{array}{l}
left{ {begin{array}{*{20}{c}}
{{x_A} + 2{x_B} + 3{x_C} le 35}\
{2{x_A} + 3{x_B} + 2{x_C} le 45}\
{3{x_A} + {x_B} + {x_C} le 40}
end{array}} right.\
{x_A},{x_B},{x_C} ge 0\
F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C} to max
end{array}$$

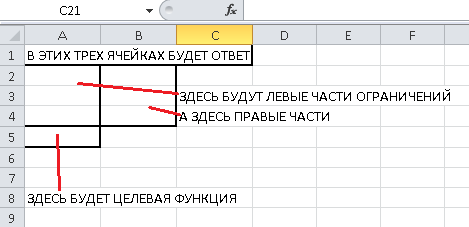
Мы будем заносить данные в следующие ячейки листа Excel:

Итак, начнем заполнение. В верхние три ячейки нужно занести ответ, то есть,
количество производимых изделий A, B и C. Так как ответ мы не знаем (а иначе
зачем бы мы задачу решали), то пока занесем туда три нуля:

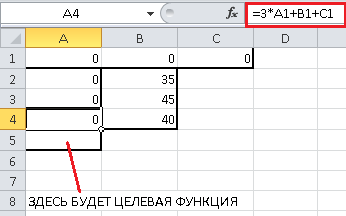
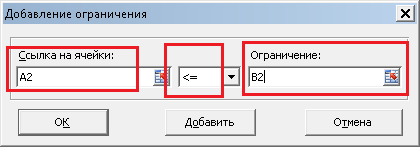
Занесем левые и правые части ограничений в соответствующие ячейки. Например,
для первого ограничения ${x_A} + 2{x_B} + 3{x_C} le 35$ нам нужно занести в ячейку
A2 формулу «=A1+2*B1+3*C1», а в ячейку B2 — правую часть ограничения — 35. Точно
так же занесем и два других ограничения. Не стоит пугаться, что в ячейках A2-A4
пока будут нули — это естественно, так как пока наше «решение» состоит в том,
чтобы не производить ни одного изделия. Должно получиться следующее (красным
цветом выделено значение ячейки A4, то есть, третье ограничение $3{x_A} + {x_B} + {x_C} le 40$):

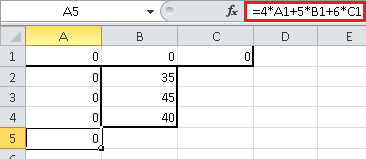
Точно так же, в ячейку A5 занесем формулу для целевой функции $F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C}$ —
в Excel это будет формула «=4*A1+5*B1+6*C1». Точно так же, не обращаем внимания,
что результатом будет 0 — это естественно, ведь целевая функция представляет из
себя прибыль предприятия, а раз мы ничего не производим, то естественно, получаем
нулевую прибыль:

Мы занесли все необходимые данные, теперь необходимо выполнить поиск решения. Для
этого на вкладке «Данные» нажимаем кнопку «Поиск решения». Видим следующее окно:

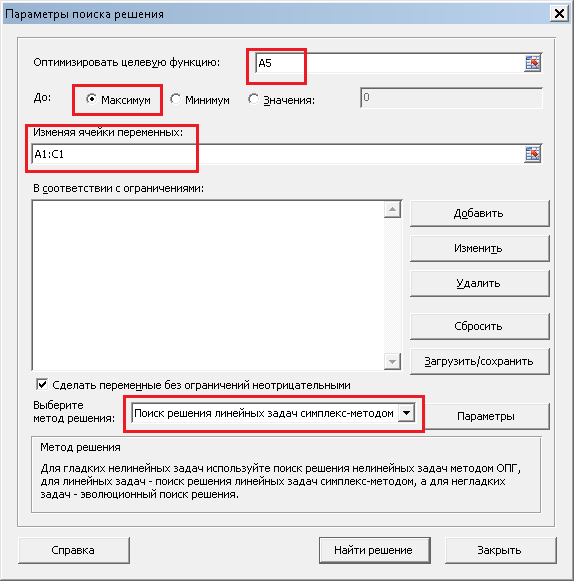
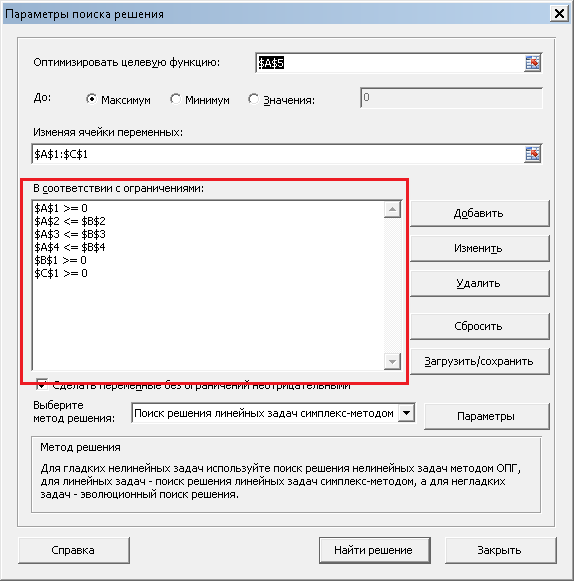
В поле «Оптимизировать целевую функцию» записываем A5, так как именно в ячейке A5
у нас записана целевая функция. На следующей строке выбираем «Максимум», так как нам
необходимо максимизировать целевую функцию, то есть, прибыль. В поле «Изменяя ячейки
переменных» записываем A1:C1, так как в ячейках A1, B1 и C1 у нас количество
производимых товаров, которые необходимо подобрать. В поле «Выберите метод решения»
выбираем «Поиск решения линейных задач симплекс-методом». Теперь необходимо задать
ограничения. Для этого нажимаем на кнопку «Добавить», и пишем (для первого ограничения)
следующее:

То есть, говорим, что значение ячейки A2 (первое ограничение) должно быть «меньше
или равно» значению ячейки B2 (правой части первого ограничения). Нажимаем OK, и
ограничение добавится в список. Таким же образом добавляем два других ограничения,
а также еще три ограничения — что наши переменные должны быть больше или равны
нулю. Должно получиться следующее:

Задача почти решена. Просто нажимаем кнопку «Найти решение», и появляется окно,
в котором нам сообщают, что задача решена (решение найдено), а также спрашивают,
хотим ли мы его сохранить:

Нажимаем OK, и видим решение в ячейках A1, B1, C1:

В ячейке A1 мы видим число 10 — число изделий A, которые необходимо произвести,
в ячейке A2 — число 5 — число изделий B, которые необходимо произвести, а в ячейке
A3 — число 5 — число изделий C, которые необходимо произвести. То есть, мы получили
решение (10;5;5) — такое же, как и в предыдущем разделе. Кроме того, в ячейке A5
мы видим максимальное значение целевой функции — тоже, такое же, как и в предыдущем
разделе. Задача решена верно.

Конечно, мы решили задачу совсем без оформления. Если вам нужно решить такую
задачу для сдачи в университет, то вы можете оформить ее, например, так:

Итоги

Мы научились решать производственную задачу с помощью надстройки Excel под
названием «Поиск решения». В следующем разделе мы рассмотрим решение целочисленной
производственной задачи, то есть задачи ЛП с дополнительным ограничением —
все значения переменных должны быть целыми.

Далее: 2.1.4. Решение ЗЛП в Excel 2003, 2.1.5. Целочисленное решение ЗЛП

Полезное по теме

Примеры решений задач ЛП в Excel
Выполненные контрольные по линейному программированию
Заказать решение своих задач

Источник

Задачи оптимизации в Excel

Пример решения производственной задачи

ЗАДАНИЕ.

Для производства двух
видов изделий А и В предприятие использует три вида сырья. Нормы расхода
каждого вида сырья на изготовление единицы продукции данного вида в таблице 6.
В ней же указаны прибыль от реализации единицы изделия каждого вида и общее
количество сырья данного, которое может быть использовано предприятием.

Вид сырья	Нормы расхода сырья (кг) на одно изделие	Общее количество сырья (кг)
А	В
І	12	4	300
ІІ	4	4	120
ІІІ	3	12	252
Прибыль от реализации изделия одного вида (руб.)	30	40

Требуется такой составить
такой план производства изделий А и В, при котором прибыль от реализации будет
максимальной?

РЕШЕНИЕ.

Пусть
предприятие производит ед. изделия А и ед. изделия В. Тогда

общая прибыль предприятия (целевая
функция) составит: = 30 + 40 .

Требуется найти максимальное значение
целевой функции при следующих

ограничениях:

124+
12+ 4+ 4 ≤ 252≤ 120≤ 300 по ресурсу I

по ресурсу II

по ресурсу III

При этом полагаем, что искомые значения
и могут быть неотрицательными. Получаем задачу линейного программирования:

экономике

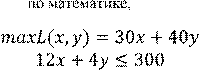
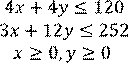
Для использования EXCEL заполняем
страницу в соответствии с математической постановкой двойственной задачи:

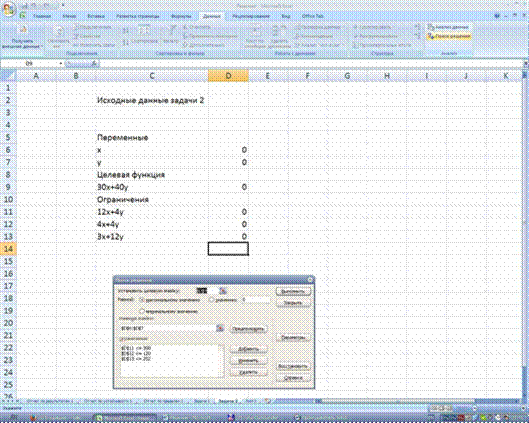
Для решения задачи ЛП в Excel используют
во вкладке Анализ данных надстройку Поиск решения.

Целевая ячейка (Максимум)

Ячейка	Имя	Исходное значение	Результат
$D$9	30x+40y	750	1080

Изменяемые ячейки

Ячейка	Имя	Исходное значение	Результат
$D$6	x	25	12
$D$7	y	0	18

Ограничения

Ячейка	Имя	Значение	Формула	Статус	Разница
$D$11	12x+4y	216	$D$11<=300	не связан.	84
$D$12	4x+4y	120	$D$12<=120	связанное
$D$13	3x+12y	252	$D$13<=252	связанное

Таким образом, максимальная прибыль
составит^о= 12 (_о= 18, ) = 1080

руб.; значения оптимального плана
производства: ед.; ед.

Решение двойственной
задачи 2 с использованием пакета Excel

Степень
дефицитности каждого вида ресурса оценим по двойственным

оценкам
, , , найденнымmin (12)
из=
300+ 4
решения+
4, … ,+ 12+ 3+ 120 ≥ 0двойственной≥
30≥ 40+ 252 задачи: 4

Для использования EXCEL заполняем
страницу в соответствии с математической постановкой двойственной задачи:

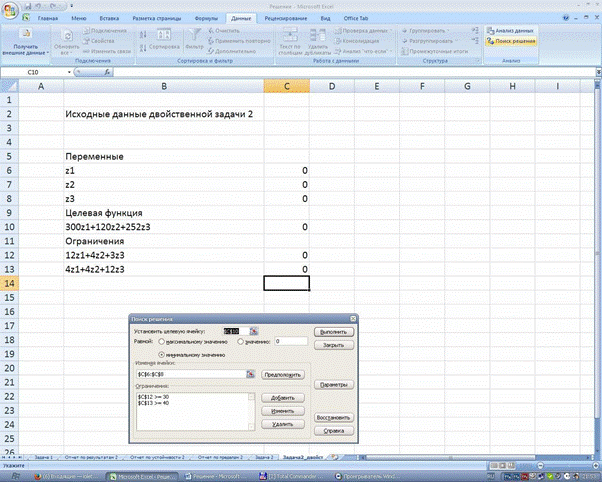
Для решения задачи ЛП в Excel используют
во вкладке Анализ данных надстройку Поиск решения.

Целевая ячейка (Минимум)

Ячейка	Имя	Исходное значение	Результат
$C$10	300z1+120z2+252z3	0	1080

Изменяемые ячейки

Ячейка		Имя	Исходное значение		Результат
$C$6	z1			0
$C$7	z2			0
$C$8	z3			0	1,111111111

Ограничения

Ячейка Имя
Значение Формула Статус Разница

$C$12 12z1+4z2+3z3 30
$C$12>=30 связанное

$C$13 4z1+4z2+12z3 40
$C$13>=40 связанное

плана1080
исходной задачи составят = 0, =
6,67,
=
1,11,
min
( ) = Из
решения задачи следует, что двойственные оценки оптимального

Это
означает, что первый вид ресурса не является дефицитным, и увеличение его
запаса не принесет увеличение целевой функции. Напротив, второй и третий виды
ресурсов являются дефицитными. Увеличение (уменьшение) запаса второго ресурса
на одну единицу приведет к увеличению (или к уменьшению) прибыли на 6,67 руб.
Увеличение (уменьшение) запаса третьего ресурса на одну единицу приведет к
увеличению (или к уменьшению) прибыли на 1,11 руб.

Источник

20.08.2015 Бизнес-планирование, Бюджетирование, Калькуляторы, шаблоны, форматы, Малая автоматизация

Предлагаю вашему вниманию шаблон для определения оптимального плана выпуска продукции в Excel.

Данная классическая задача относиться к задачам линейного программирования и сводиться к нахождению такого плана выпуска продукции, при котором прибыль от ее реализации (целевая функция) является максимальной.

Казалось бы, чем больше выпуск, тем больше прибыль, однако мы интуитивно понимаем, что существуют некие ограничения.

В данном случае это ограничения по объему выпуска связанные с возможностью продать продукцию (или производственной мощностью оборудования) и наличием дефицита ресурсов для производства, например отсутствием на складе нужного материала или отсутствием нужных специалистов в достаточном количестве.

Также мы можем иметь ограничение по минимальному уровню выпуска, например, в производство запускаются партии не меньше 100 единиц продукции.

Таким образом, мы имеем три вида ограничений:

1) По максимально возможному объему выпуска;

2) По минимально возможному объему выпуска;

3) По наличию ресурсов (материальных, трудовых, финансовых и т.д.).

Соответственно, с учетом этих ограничений мы должны так скомбинировать производственную программу, чтобы прибыль была максимальной.

Прибыль у нас будет определяться маржинальной прибылью на единицу продукции, т.е. разницей между ценой реализации единицы продукции и переменными затратами на ее производства.

Этот параметр будем считать постоянным и известным для каждого вида продукции.

Я не буду приводить здесь систему линейных уравнений, по которым решается эта задача, так как мы будем искать решение не на бумаге, а посредством программы Excel. Желающие же смогут легко найти всю теоретическую базу необходимую для решения этой классической задачи.

Для поиска оптимального решения в программе Excel необходимо чтобы была установлена надстройка «Поиск решения«.

Для установки соответствующей надстройки необходимо перейти на вкладку Файл, пункт Параметры и в отрывшемся окне выбрать пункт Надстройки.

В открывшемся диалоговом окне выбрать надстройку Поиск решения (если надстройка еще не активна) и нажать кнопку Перейти (1)

В открывшемся окне установить соответствующую галочку (2) и нажать кнопку Ок.

poisk

Далее для удобства присваиваем диапазонам, в которых находятся наши данные имена.

Так, ячейке, в которой у нас будет находиться целевая функция, дадим имя «Прибыль». Она должна стремиться к максимуму.

Диапазон с данными о маржинальной прибыли на единицу продукции назовем «Маржа».

Диапазон с данными оптимального выпуска назовем «Выпуск». Этот параметр мы и будем оптимизировать.

Соответственно прибыль у нас рассчитается по формуле:

=СУММПРОИЗВ(Маржа;Выпуск)

Диапазону с данными о наличии того или иного ресурса присвоим имя «Наличие».

Ограничение по максимальному выпуску назовем «Максимум» а по минимальному соответственно «Минимум».

В область «Норма расхода ресурсов» шаблона вводим данные о соответствующих нормах расхода того или иного ресурса на производство единицы продукции по каждому виду продукции и ресурса.

Потребность в каждом виде ресурса мы рассчитываем как сумму произведений нормы расхода на объем выпуска по каждому виду продукции.

Например для первого вида ресурса формула будет выглядеть так:

=СУММПРОИЗВ(Выпуск;$C14:$V14),

где диапазон $C14:$V14 содержит данные о норме расхода данного вида ресурса по всем видам продукции.

Соответственно диапазону данных с потребностью в ресурсах на выполнение плана выпуска мы присвоим имя «Потребность».

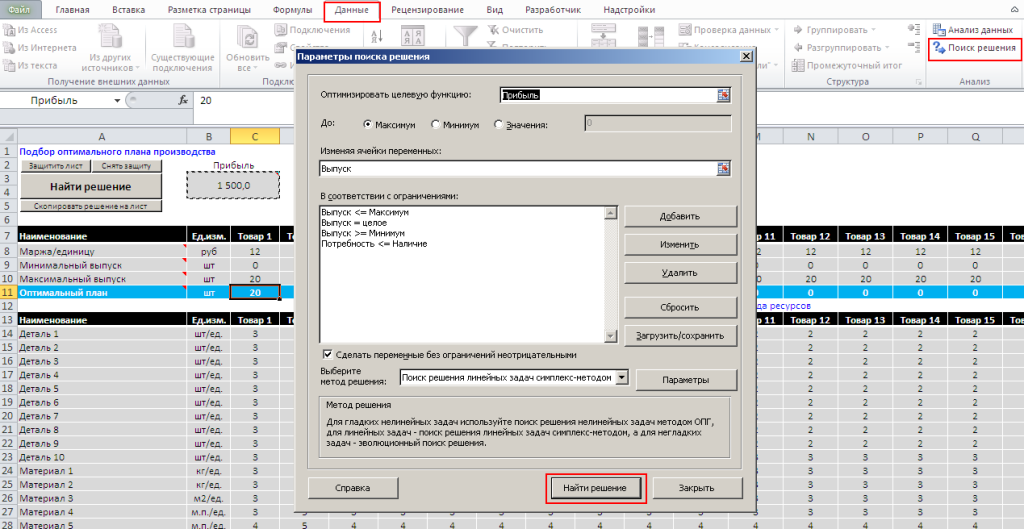
Теперь, когда мы присвоили всем рабочим диапазонам соответствующие имена, мы можем приступать к формированию параметров поиска решения.

Все ограничения теперь интуитивно понятны и выглядят следующим образом:

Выпуск <= Максимум

Выпуск => Минимум

Выпуск = целое (целое число для штучных единиц продукции)

Потребность <= Наличие

Оптимизируем Прибыль до максимального значения.

Теперь, после того как мы сформировали логику поиска решения остается самое простое, внести параметры поиска решения в соответствующую надстройку.

На вкладке Данные вызываем Надстройку Поиск решения и вносим соответствующие параметры и ограничения.

Ограничения вносим используя кнопку Добавить.

Все. Теперь остается Нажать копку Найти решение и в нашем диапазоне «Выпуск» появится оптимальный план выпуска при котором значение прибыли примет максимально возможное для данных условий значение.

Для удобства в шаблоне присутствует макрос, который при нажатии на кнопку «Найти решение» осуществляет запуск надстройки поиска решений.

Чтобы он корректно работал, необходимо в редакторе VBAустановить ссылку на SOLVER.

Как это сделать вы найдете на листе «Справка» в шаблоне.

Для того чтобы увидеть файл в полном размере нажмите «квадратики» в правом нижнем углу.

Источник

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

Завод производит
электронные приборы трех видов (прибор
А, прибор В и прибор С), используя при
сборке микросхемы трех видов (тип 1,
тип2, тип3). Расход микросхем задается
следующей таблицей:

	Прибор А	Прибор В	Прибор С
Микросхема 1	2	5	1
Микросхема 2	2	0	4
Микросхема 3	2	1	1

Стоимость
изготовленных приборов одинакова.
Ежедневно на склад завода поступает
500 микросхем типа 1 и по 400 микросхем
типов 2 и 3. Каково оптимальное соотношение
дневного производства приборов различного
типа, если производственные мощности
завода позволяют использовать запас
поступивших микросхем полностью?

Формальная математическая постановки задачи

Константы

Пусть
m_ij
– расход микросхем i
для прибора j,
где i=1,2,3;
j=1,2,3.

2

5

1

m_ij=

2

0

4

2

1

1
Пусть
Z_i– ежедневный
запас микросхем i
на складе, где i=1,2,3.

Z₁=500;
Z₂=400;
Z₃=400.

Переменные

Обозначим
через x_j
дневное производство приборов j,
j=1,2,3,
то есть
x₁— дневной
выпуск приборов А;

x₂— дневной
выпуск приборов В;

x₃— дневной
выпуск приборов С.
Обозначим
через R_i
расход микросхем i,
где i=1,2,3,
то есть
R₁— расход
микросхем 1-го типа;
R₂
– расход микросхем 2-го типа;
R₃
– расход микросхем 3-го типа.
Обозначим
через N
дневное производство всех видов
приборов.

Решение

1.Зададим
математическую модель расхода микросхем

,
где i=1,2,3.

или

Зададим
математическую модель нахождения
общего количества приборов N=x₁+x₂+x₃.
Его максимизация является целью решения
задачи. Следовательно, целевая функция
будет иметь вид:

Ограничения

Расход
микросхем не
должен превышать
их запас

(для микросхем
1-го типа)

или (для микросхем 2-го типа)

(для микросхем 3-го типа)

Количество
выпускаемых приборов должно быть целым
числом.
Поскольку
x₁,
x₂,
x₃
выражают объем выпускаемых приборов,
то они не могут быть отрицательны, то
есть
x₁≥0;
x₂≥0;
x₃≥0;
x₄≥0

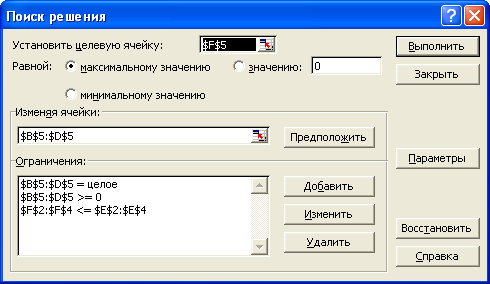
Методика выполнения в Microsoft Excel

1. Запустите
программу Excel
(Пуск
ПрограммыMicrosoft
Excel)
и создайте рабочую книгу.

2. Создайте новый
рабочий лист «Организация
производства 2».

3. В ячейки E2,
E3,
и E4
занесите дневной запас микросхем –
числа 500, 400, и 400 соответственно.

4. В ячейки B5,
C5
и D5
занесите нули – в дальнейшем значения
этих ячеек будут подобраны автоматически.

5. В ячейках диапазона
A1:D4
разместите таблицу расхода комплектующих.

6. В ячейках F2:F4
нужно указать формулы для расчета
расхода микросхем по типам. В ячейке F2
формула будет иметь вид =$B$5*B2+$C$5*C2+$D$5*D2,
а остальные формулы можно получить
методом автозаполнения (обратите
внимание на использование абсолютных
и относительных ссылок).

7. В ячейку F5
занесите формулу, вычисляющую общее
количество произведенных приборов: для
этого выделите диапазон B5:D5
и щелкните на кнопке Автосумма
на стандартной
панели инструментов.

8.
Дайте команду
СервисПоиск
решения – откроется
диалоговое окно
Поиск решения.

9. В поле Установить
целевую укажите
ячейку, содержащую оптимизируемое
значение (F5).
Установите переключатель Равной
максимальному значению (требуется
максимальный объем производства).

10. В поле Изменяя
ячейки задайте
диапазон подбираемых параметров –
B5:D5.

11. Необходимо
добавить ограничения:

Расход
микросхем не
должен превышать
их запас.
Количество
выпускаемых приборов должно быть целым
числом.
Число
производимых приборов неотрицательно

12. Чтобы определить
набор ограничений, щелкните на кнопке
Добавить. В
диалоговом окне Добавление
ограничения в
поле Ссылка
на ячейку укажите
диапазон F2:F4.
В качестве условия задайте <=. В поле
Ограничение
задайте
диапазон E2:E4.
Это условие указывает, что дневной
расход комплектующих не должен
превосходить запасов. Щелкните на кнопке
ОК.

13. Снова щелкните
на кнопке Добавить.
В поле Ссылка
на ячейку укажите
диапазон B5:D5.
В качестве условия задайте >=. В поле
Ограничение
задайте
число 0. Это условие указывает, что число
производимых приборов неотрицательно.
Щелкните на кнопке ОК.

14. Снова щелкните
на кнопке Добавить.
В поле Ссылка на ячейку укажите диапазон
B5:D5.
В качестве условия выберите пункт цел.
Это условие не позволяет производить
доли приборов. Щелкните на кнопке ОК.

15. Щелкните на
кнопке Выполнить.
По завершении
оптимизации откроется диалоговое окно
Результаты
поиска решения.

16. Установите
переключатель Сохранить
найденное решение, после
чего щелкните на кнопке ОК.

17. Проанализируйте
полученное решение. Кажется ли оно
очевидным? Проверьте его оптимальность,
экспериментируя со значениями ячеек
B5:D5.
Чтобы восстановить оптимальные значения,
можно в любой момент повторить операцию
поиска решения.

18. Сохраните рабочую
книгу.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

	2	5	1
m_ij=	2	0	4
	2	1	1