Программы математического моделирования excel - Word и Excel

Цели урока:

Обучающие: Повторить и закрепить навыки
работы в MS Excel; научить применять современное
программное обеспечение в решении
математических задач, строить математические
модели в среде MS Excel.

Развивающие: Развивать: практические и
исследовательские навыки по составлению моделей
в электронных таблицах, научное мировоззрение
через связь информационных технологий с другими
школьными предметами, логическое и
алгоритмическое мышление, аналитические
способности, внимание, память.

Воспитательные: Воспитание общей и
информационной культуры, творческого подхода к
работе, желания экспериментировать,
самостоятельности в учебном труде.

Тип урока: Комплексного применения
знаний, обобщения и систематизации.

Программное и техническое обеспечение
урока:

компьютеры с ОС MS Windows XP;

пакет Microsoft Office;

мультимедийный проектор

Время проведения урока: один из
последних уроков в разделе «Информационное
моделирование».

План урока: (40 минут)

Орг. момент. (1 мин)
Проверка и актуализация знаний. / Тестирование
по теме (4 мин)./ Разминка (5 мин)
Теоретическая часть. (10 мин)
Практическая часть. (10 мин)
Самостоятельная работа. (8 мин)
Подведение итогов. Д/з (2 мин)

Ход урока:

1. Организационный момент.

Приветствие, проверка присутствующих.

С помощью проектора демонстрируется
на экране первый слайд презентации. Приложение 1

Сообщается тема урока: «Математическое
моделирование в среде электронных таблиц MS Excel
«.Озвучить цели и план урока.

2. Актуализация опорных знаний.

Пройденная нами тема «Электронные
таблицы»– одна из наиболее практически
значимых, востребованных, после текстового
редактора Word и его возможностей. Но электронные
таблицы не только позволяют автоматизировать
расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций.
Меняя значения исходных данных, можно проследить
за изменением получаемых результатов и из
множества вариантов решения задачи выбрать
наиболее подходящий.

Перечислите, что вы научились делать,
изучая табличный процессор MS Excel?

– выполнять вычислительные операции
при помощи формул;

– составлять таблицы;

– строить графики и диаграммы.

Тестирование по теме «Электронные
таблицы».

Домашним заданием было повторить весь
изученный материал по теме «Электронные
таблицы». Чтобы проверить домашнее задание, я
предлагаю Вам ответить на вопросы электронного
теста. (Дети уже знакомы с работой системы
дистанционного обучения MyTestServer 1.1) Приложение 2

Перед началом работы учащиеся
прослушивают инструкцию по выполнению теста.

Тест состоит из 5 вопросов. Дается
только одна попытка, будьте внимательны, не
торопитесь. Время на тест 3 минуты.

После завершения тестирования каждому
ученику системой выставляется оценка, которую он
видит на экране своего монитора.

Сегодня на уроке мы будем использовать
электронные таблицы с их мощным вычислительным
потенциалом для решения математических задач –
построим математическую модель в среде MS Excel и
проведем небольшое исследование.

А для этого вспомним основные понятия
по теме “моделирование” (проводим устную разминку).

Вопросы разминки: Приложение 1

Моделирование – метод познания
окружающего мира, состоящий..

Модель – это объект, который
используется в качестве..

Различают ____________и ___________модели.

Натурные модели – это…

Информационные модели – это…

Основными видами информационных
моделей являются:_________ ,_________, __________.

А как вы думаете, математическая
модель к какому виду принадлежит?

Математическая модель – это модель,
построенная с использованием…

Приведите пример знаковой
информационной модели, рассматриваемой на
уроках математики.

Основным языком информационного
моделирования в науке является язык математики.

3. Теоретическая часть.

Какую бы жизненную задачу ни взялся
решать человек, первым делом он строит модель
заданного объекта. Очень часто задачи связаны с
потребностями человека.

Сегодня нам предстоит решить
следующую задачу:

Задача 1: Приложение
1

У маленького Васи есть небольшой
бассейн во дворе. Иногда Вася ходит к речке и
приносит воду в бассейн в небольшой цистерне
цилиндрической формы. Известны ширина ШБ, высота
ВБ, ДБ бассейна и объем цистерны Об Ц. Сколько раз
Васе нужно сходить к речке за водой, чтобы
наполнить бассейн наполовину?

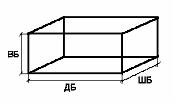
Этот текст можно рассматривать как
словесную модель бассейна.

Постановка задачи: выяснение
условий

Какую форму может иметь бассейн?
(ответы детей).

А какой формы он в нашей задаче?– В
форме куба или параллелепипеда, потому, что даны
его параметры: ширина, высота, длина. А что еще нам
известно?

– объем цистерны.

Давайте попробуем решить задачу:
узнаем сколько раз (N) Васе нужно сходить к речке
за водой, чтобы наполнить бассейн наполовину.

Что для этого нужно знать?

– сколько цистерн воды помещается в
бассейн.

А как это узнать?

– определить объем бассейна (Об Б)

– сравнить половину объема бассейна и
объем цистерны (Об Б / Об Ц / 2).

4. Практическая часть.

Карточка – задание №1 Приложение 3

Задание для практической работы: Скопировать
в свою папку файл – шаблон Excel Приложение 4

Назвать лист номером задачи «Задача
1» (редактирование названия – двойной щелчок
мыши на «Лист 1»).

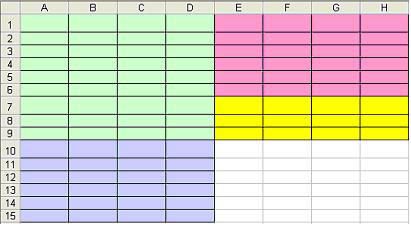
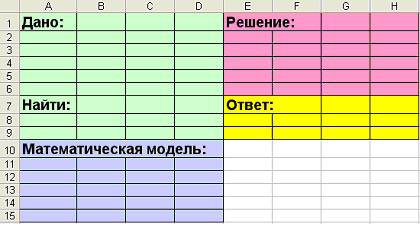
Оформить на листе решения разделы «Дано«,
«Найти«, «Математическая модель«,
«Решение«, «Ответ» (по образцу):

В ячейках А1и А7 напечатать
слова «Дано» и «Найти«.

Объединить ячейки А10, В10 и С10,
ввести текст: «Математическая модель«

Объединить ячейки Е1 и F1,
напечатать слово «Решение«.

В ячейку Е7 – «Ответ«.

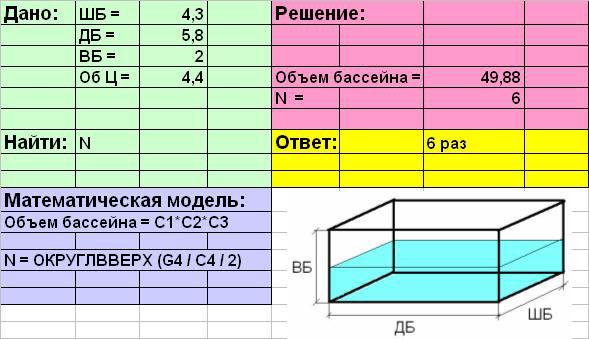
Заполнить таблицу начальными
данными.

В ячейки В1:В4 ввести текст: ШБ=;
ДБ=; ВБ=; Об Ц=.

В ячейки С1:С4; ввести
соответствующие значения параметров: 4,3; 5,8; 2; 4,5.

Для наглядности, если есть
возможность, можно построить графическую модель
(рисунок задаче) в Painte и скопировать ее в
электронную таблицу или нарисовать бассейн
непосредственно в Excel.

Далее заполнить раздел таблицы
«Математическая модель».

Объединить ячейки А11, В11 и С11,
ввести формулы (тип данных – текст) в раздел
(пробел перед знаком «=»). «Объем бассейна
=С1*С2*С3«

Объединить ячейки А13, В13 и С13
и ввести текст «N = ОКРУГЛВВЕРХ(G4 / C4 / 2)«.
(для получения целого числа используем функцию
округления ОКРУГЛВВЕРХ)

В разделе «Решение»
создать сетку вычислений:

– Обозначить искомые и промежуточные
величины.

– Объединить ячейки Е4 и F4,
ввести текст: «Объем бассейна =«. В ячейку
Е5 – «N =«(тип данных – текст).

В ячейки G4 и G5; ввести
соответствующие формулы (тип данных – формулы):
=С1*С2*С3;

Используем функцию округления
дробного числа до целого:

Вставка-функция – математические –
ОКРУГЛВВЕРХ – число разрядов выбираем «0«.

=ОКРУГЛВВЕРХ(G4 / C4 / 2)

В разделе «Ответ» запишем
искомый результат в ячейку G7 (тип данных –
текст).

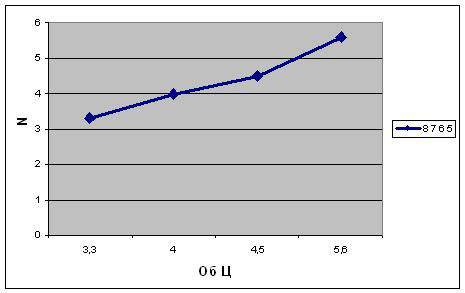
Проведем небольшое исследование:

Вопрос: Сколько раз Васе нужно будет
сходить к речке за водой, если он возьмет
цистерну емкостью 5,6 литров; 4 литра; 3,3
литра?

Меняем в ячейке С4 значение на 5,6
и электронные таблицы автоматически производят
пересчет.

Создадим таблицу значений Об Ц и
будем заносить в нее результаты вычислений N.

Введем в ячейку А20 и В2 текст
«Об Ц» и » N«. Заполним таблицу
данными.

Об Ц	N
3,3	8
4	7
4,5	6
5,6	5

Для графического представления
результатов выделить диапазон А21: В24,
построить график функции, отредактировать его.

Анализ полученных результатов.

5. Самостоятельная работа.

Задание для самостоятельной разработки:

Карточка – задание №2 Приложение
3

Задача 2. Пешеход начал движение из
начала координат со скоростью V=0,6 м/с.
Найдите, какой путь S прошел пешеход за одну
минуту t после начала движения, если он
двигался равномерно.

Постановка задачи: выяснение
условий

Скажите, что мы будем моделировать? –

– движение

Какие виды движения вы знаете? (ответы
детей)

Какое движение рассматривается в
нашей задаче?

– равномерное. Приложение 1

Давайте вспомним формулу расчета
скорости: V=s/t– отсюда s=V*t

Технология моделирования:

Назвать лист номером задачи «Задача 2»
(редактирование названия – двойной щелчок мыши
на «Лист 2»).
Выделить расчетную таблицу на листе «Задача1»
и скопировать ее на лист «Задача 2«.
Заполнить таблицу новыми начальными данными.
Ввести формулу (тип данных – текст) в раздел
«Математическая модель» (пробел перед
знаком «=»).
Ввести фоpмулу (тип данных – формулы) в
раздел «Решение«.
В разделе «Ответ» записать искомый
результат (тип данных – текст).

Создать таблицу значений t и занести в нее
результаты вычислений S. Заполнить таблицу
данными.
Для графического представления результатов
выделить область аргументов и функций, построить
график зависимости пути S от времени при t=40;60;90,
отредактировать график.

6. Итог урока.

Сегодня на уроке мы узнали, как можно
использовать электронные таблицы в решении
математических задач, научились строить
математические модели в. среде MS Excel

Домашним заданием будет: самим
придумать задачу, разработать ее математическую
модель.

У кого есть вопросы по пройденному материалу?

Спасибо за работу. Вы сегодня молодцы. Можете
быть свободны.

Источник

Изучение построения компьютерной математической модели на примере решения квадратного уравнения

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Слайд 1

Проект : «Моделирование математических объектов средствами Microsoft Excel » Цель проекта: Изучение построения компьютерной математической модели на примере решения квадратного уравнения.

Слайд 2

Представление о математической модели Модель-это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Часто исследуемый объект или процесс может быть описан в виде формул, связывающих его количественные параметры. Для описания моделей используется различные системы обозначений, принятые в той или иной науке. Составление математической модели заключается в выводе математических формул, связывающих ее параметры, по которым в дальнейшем будет производиться расчет. Компьютер позволяет на качественно новом уровне перевести мысленную модель в знаковую формулу. Поставленные задачи обычно решают с помощью языков программирования или другими средствами, хотя эти задачи можно легко и эффективно решать средствами Excel.

Слайд 3

Процесс разработки моделей и их исследование на компьютере можно разделить на несколько основных этапов: Информационная модель. Формальная модель. Компьютерная модель. Компьютерный эксперимент и анализ полученных результатов.

Слайд 4

Этапы моделирования проследим на примере решения квадратного уравнения ax 2 +bx+c=0 различными способами. Информационная модель. На этом этапе можно определить некоторые особенности квадратного уравнения : полное оно или неполное, приведенное, с четным вторым коэффициентов и т.д., которые позволяют выбрать тот или иной способ решения.

Слайд 5

2. Формальная модель . Формализовать модель значить преобразовать информационную модель на какой-либо формальный язык. В нашем примере – это язык математики. ax 2 +bx+c=0 D=b 2 — 4ac,

Слайд 6

3 . Компьютерная модель . Компьютерная модель проекта создаём с помощью электронной таблицы Excel. Таблицу можно сформировать примерно вот так:

Слайд 7

Далее средствами Excel формальную модель преобразуем в компьютерную, используя правила записи математических формул, принятых в Excel .

Слайд 8

4. Компьютерный эксперимент и анализ полученных результатов . На последнем этапе проведем компьютерный эксперимент: Введем в соответствующие ячейки значения коэффициентов a, b и c

Слайд 9

В случае, если дискриминант отрицательный ,программа выдаст соответствующий ответ: Построенная модель позволяет решать любые квадратные уравнения и значительно экономит время для их решения.

Слайд 10

Рассмотрим графический способ решения квадратного уравнения, преобразуем уравнение x 2 — 2x-8=0 . x 2 = 2x+8 и построим графики функций y=x 2 и y=2x+8 . Построим таблицу значений x -5 -4 -3 -2 -1 0 1 2 3 4 5 y=x 2 25 16 9 4 1 0 1 4 9 16 25 y=2x+1 -2 0 2 4 6 8 10 12 14 16 18

Слайд 11

Выполним вставку диаграммы Точечная. Точки пересечения графиков и есть решения данного уравнения х 1 =-2; х 2 =4

Слайд 12

Подбор параметра MS Excel позволяет решать различные уравнения с помощью функции Подбор параметра . Рассмотрим квадратное уравнение 3x 2 -5x+10=0 . Левая часть уравнения представляет собой квадратичную функцию y= 3x 2 — 5x+10 . Построим таблицу значений функции, например, на промежутке [- 3 ; 5 ] .

Слайд 13

x -3 -2 -1 0 1 2 3 4 5 y 32 12 -2 -10 -12 -8 2 18 40 Из таблицы видно, что функция меняет свой знак на промежутках [- 2;-1 ] , [ 2 ; 3 ] , значит корни уравнения лежат именно на этих промежутках. Рассмотрим промежуток [- 2;-1 ] . На этом отрезке будем подбирать параметр . В качестве приближения можно взять точки х=-2 или х=-1. М ы взяли х=-2 и соответствующее ему значение y= 12. Для удобства зна чения x 1 =-2 и y 1 =12 поместим в отдельную таблицу.

Слайд 14

Выберем на вкладке Данные Анализ «что если» Подбор параметра. В окне диалога у становим следующие значения: в поле Установить в ячейке выберем ячейку E6 , в поле Значение установим 0, в поле Изменяя значение ячейки – ячейку С6. Щелкнем OK .

Слайд 15

Результат вы видите на экране. Первый корень уравнения найден.

Слайд 16

Аналогично на отрезке [ 2; 3 ] определяется второй корень уравнения.

Слайд 17

Таким образом, мы рассмотрели различные способы решения квадратного уравнения в среде MS Excel 2010 . В последних двух способах представлены только компьютерные модели проекта.

Слайд 18

Над проектом работали: ученики 8 «а» класса Аракелян Ишхан и Ливковский Владислав. ГБПОУ ПК им. Н.Н. Годовикова

Источник

Автор: Андреев Кирилл

Место работы/учебы (аффилиация): Региональный технический колледж в г. Мирном, Республика Саха (Якутия), студент

Цель работы: исследовать возможность моделирования математических функций, при помощи современных компьютерных средств, а именно разработать компьютерную модель для исследования математических функций на основе программы Microsoft Excel.

Методы: математическое моделирование.

Актуальность. Microsoft Excel — многофункциональная программа в пакете MS Office, используемая для создания простых таблиц, построения диаграмм и графиков до решения сложных вычислительных задач и моделирования различных процессов. Данная работа посвящена использованию электронных таблиц Excel в анализе функций. В ней, используя знания и навыки работы с мастером функций и диаграмм Excel, будет проведен анализ функций с проведением расчетов по формулам и с построением графиков.

Практическая значимость: данная работа может быть использована при организации работы на занятиях по информатике и математике, а так же может служить материалом для самоподготовки студентами.

Результаты: в ходе проектно-исследовательской работы были изучены функций, их свойства и графики. Методом математического моделирования были решены примеры по всем изученным функциям в табличном процессоре MS Excel путем оптимизации и моделирования математических задач.

Этапы работы:

Изучить моделирование решения математических задач, на примере построения графиков функций.
Изучить виды функций, их свойства и графики.
Составить алгоритм построения графиков функций.
Изучить моделирование задач на оптимизацию, на примере нахождения корней системы уравнений, вычисление корней функции одной переменной (значения функции в точке и на отрезке, экстремумы функции)
Перевести результат математического решения задачи на решение задачи в MS Excel.

Источник

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

Федеральное
агентство по образованию

ГОУ ВПО «Российский
государственный профессионально–педагогический

университет»

Уральское отделение
Российской академии образования

Академия
профессионального образования

Екатеринбург

2007

УДК

ББК

Городецкая
Н.В.
Математическое моделирование в MS
Excel:
Учеб. пособие. Екатеринбург: Изд-во ГОУ
ВПО «Рос. гос. проф.-пед. ун-т», 2007. 64 с.

Учебное пособие
содержит лабораторные работы,
ориентированные на знакомство с одной
из технологий – математическое
моделирование на основе среды Microsoft
Excel.

Лабораторные
работы включают необходимый теоретический
материал и непосредственные инструкции
по освоению математического моделирования
в среде Microsoft
Excel.

Пособие может быть
использовано для преподавания дисциплины
«Математическое моделирование» у
студентов специальности
050501 Профессиональное обучение
(информатика, вычислительная техника
и компьютерные технологии) (030500.06),
специализации «Компьютерные технологии».

Практикум подготовлен
при финансовой поддержке Российского
гуманитарного научного фонда в рамках
научно–исследовательского проекта
«Психолого–педагогические и
технологические условия применения
адаптивных методических систем в
дистанционных образовательных
технологиях» (№ 06−06−00475а).

Рецензенты: д-р
физ.-мат. наук, проф. В.Е. Третьяков
(ГОУ ВПО «Уральский государственный
университет»); д-р пед. наук, проф. Л.И.
Долинер (ГОУ ВПО «Российский
государственный профессионально-педагогический
университет»)

государственный
профессионально-

педагогический
университет», 2007

Преподавателю: как использовать это пособие

Данная
серия лабораторных работ предназначена
для знакомства обучаемых с технологией
использования математического
моделирования для решения задач. В
качестве конкретного инструментального
средства выбрана среда MicrosoftExcel.

Для
использования данного пособия в обучении
необходимо:

иметь
дискету, прилагаемую к пособию, для
установки рабочих файлов (без них работа
с пособием невозможна);
установить
на компьютере полную версию MicrosoftExcel(с возможностью
осуществлятьПоиск решения);
создать
(в случае отсутствия) в корневом каталоге
одного из дисков папку Учебнаяи
скопировать в папкуУчебнаяпапкуМАТ_МОД, содержащую учебные файлы
с прилагаемой дискеты.

Тому, кто хочет научиться

Если
Вы решили с помощью этого пособия
познакомиться с технологией использования
математического моделирования в среде
MicrosoftExcel,
рекомендуется:

расположиться
перед включенным компьютером с
установленной полной версией MicrosoftExcel;
выполнять
лабораторные работы как можно более
точно, поскольку тексты лабораторных
работ представляют собой в некотором
роде инструкции, соблюдение которых
обеспечит Вам успешную и комфортную
работу;
соблюдать
следует следующие правила:

текст,
который никак не выделен, следует только
читать;
определения,
отмеченные значком
,
необходимо запомнить;
обращать
внимание на текст, помеченный значком
;
практические
задания, отмеченные словом «Задание»,
следует обязательно и в полном объеме
выполнять на компьютере;
контрольные
задания следует также выполнять
самостоятельно; если Вы справитесь с
ними без помощи преподавателя, это
означает, что Вы усвоили материал;
на
контрольные вопросы нужно отвечать
устно – они подготовят Вас к компьютерным
тестовым вопросам;
для
повторения пройденного материала
следует использовать резюме;

делать
краткий конспект — это поможет Вам
ускорить усвоение материала;
отвечать
на все вопросы, приведенные в конце
каждой лабораторной работы;
приглашать
преподавателя тогда, когда это
предлагается сделать в тексте лабораторной
работы;
если
Вы занимаетесь без преподавателя,
выполняйте полностью все задания
лабораторных работ, отвечайте устно
на вопросы.

В книге
приняты следующие обозначения:

—
этот символ используется для выделения
определений;

—
так помечаются важные замечания;

—
резюме;

—
при встрече с таким символом следует
пригласить преподавателя (консультанта)
и показать ему результаты выполнения
заданий. Если Вы работаете самостоятельно,
просто пропустите текст, помеченный
этим символом;

ЛП– линейное программирование; ЦФ–
целевая функция;

РЗ– распределительная задача; ТЗ–
транспортная задача.

Соседние файлы в папке Исслед_опер

#
24.04.201517.92 Кб149lab_3(b).xls
#
24.04.201517.92 Кб88lab_3(а).xls
#
24.04.201527.14 Кб114lab_4(a).xls
#
24.04.201523.04 Кб91lab_4(b).xls
#
24.04.201519.97 Кб143lab_5.xls
#

Источник

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Решение задач оптимизации в Excel

Решение финансовых задач в Excel

Решение эконометрики в Excel

Решение логических задач в Excel

Решение математических задач в Excel

Оглавление

Преподавателю: как использовать это пособие

Тому, кто хочет научиться