Программа статистика для excel - Word и Excel - помощь в работе с программами

Содержание

Использование описательной статистики
- Подключение «Пакета анализа»
- Применение инструмента «Описательная статистика»
Вопросы и ответы

Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

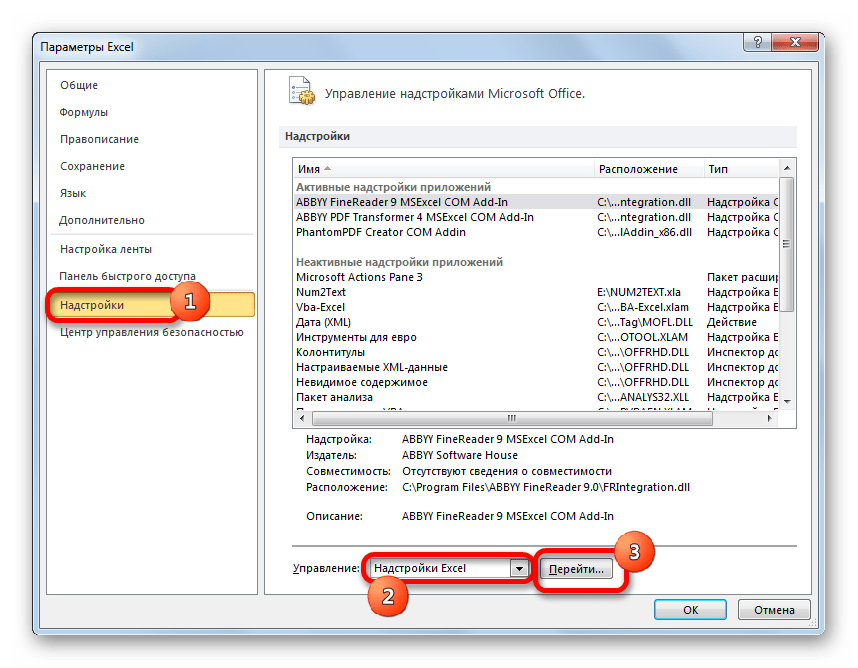
В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

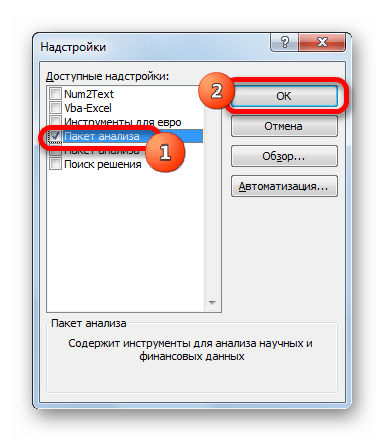
Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.

Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».

Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».

После выполнения данных действий непосредственно запускается окно «Описательная статистика».
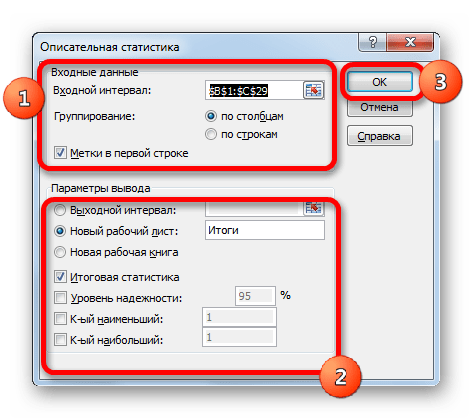
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».

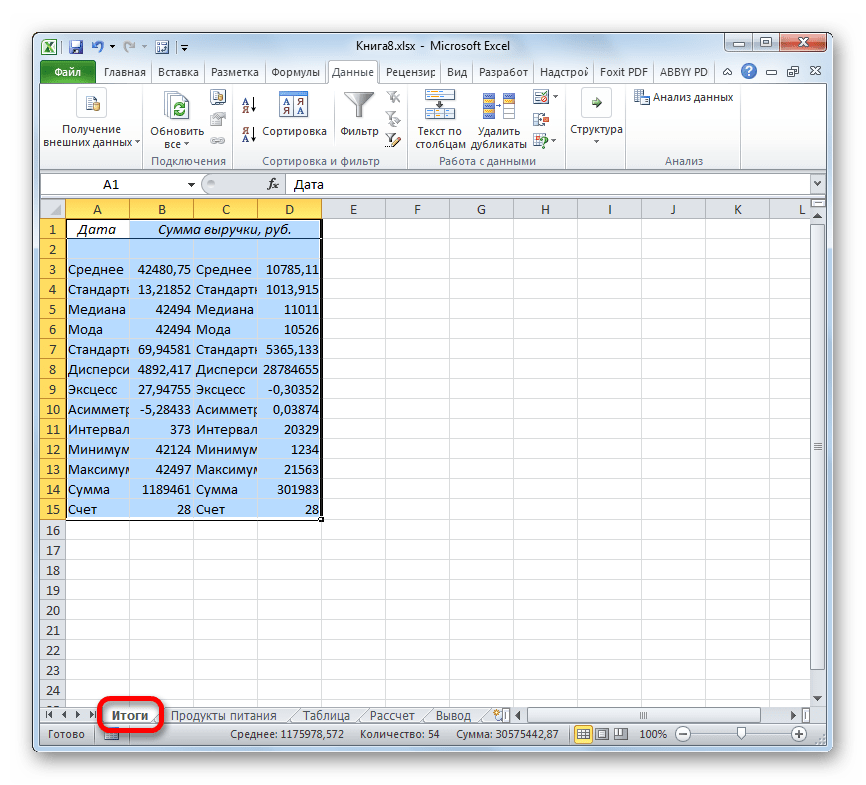
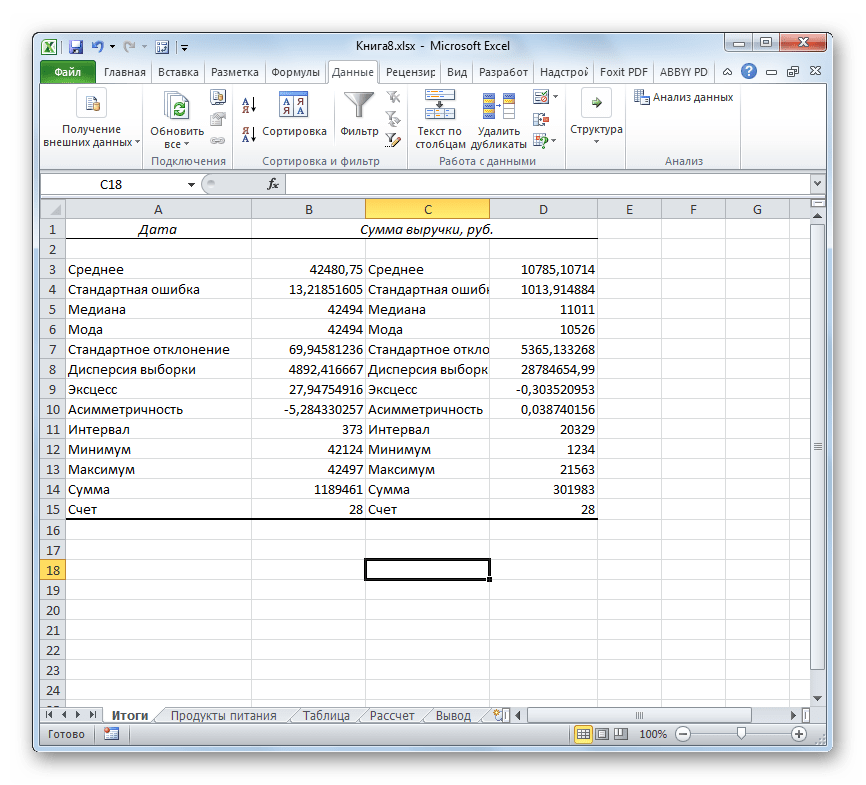
После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.

После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.

Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.

Урок: Статистические функции в Excel

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

XLSTAT — это надстройка для MS Excel для статистики и анализа данных, которая разрабатывается с 1993 года. Она включает более 200 функций общей и специфической направленности. Использование Excel в качестве интерфейса делает XLSTAT удобным и эффективным набором инструментов для статистического и многомерного анализа данных.

В число функций входят регрессия (линейная, нелинейная, логистическая), многомерный анализ данных (метод главных компонент, дискриминантный анализ, анализ соответствий, многомерное шкалирование, иерархическая кластеризация, метод k-средних, метод k-ближайших соседей, деревья решений), корреляционные тесты, параметрические и непараметрические тесты, ANOVA, ANCOVA, смешанные модели и многое другое.

Для решения специфических задач доступны расширенный многомерный анализ (RDA, CCA, MFA), построение карт предпочтений и другие инструменты сенсометрии, статистическое управление процессами, симуляция, анализ временных рядов, построение кривой «доза-эффект», модели выживаемости, сопряженный анализ, метод частичных наименьших квадратов, моделирование структурными уравнениями, анализ OMICS-данных.

Дополнительные модули включают 3D-визуализацию и модели латентных классов. Инструмент статистического анализа XLSTAT совместим со всеми версиями Excel с 2003 по 2016. Кроме того, на сайте XLSTAT доступна версия для Mac, совместимая с Excel 2011 и 2016.

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

Если вам нужно разработать сложный статистический или инженерный анализ, вы можете сэкономить время и этапы с помощью этого средства. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.

Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.

Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».

Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.

Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
- Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
- Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.

Примечание: Чтобы включить Visual Basic для приложений (VBA) для надстройки «Надстройка анализа», вы можете загрузить надстройку VBA так же, как и надстройку «Надстройка анализа». В поле Доступные надстройки выберите «Надстройка анализа — VBA».

Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.

Однофакторный дисперсионный анализ

Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ дает проверку гипотезы о том, что каждая выборка взята из одного и того же распределения вероятности на основе альтернативной гипотезы о том, что для всех выборок распределение вероятности не одно и то же. Если есть только два примера, можно использовать функцию T.ТЕСТ. В более чем двух примерах нет удобного обобщения T.ВМЕСТОэтого можно использовать модель Anova для одного фактора.

Двухфакторный дисперсионный анализ с повторениями

Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:

Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.

Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.

Двухфакторный дисперсионный анализ без повторений

Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).

Функции CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, если для каждой переменной наблюдаемы измерения по каждому из N-объектов. (Любые отсутствующие наблюдения по любой теме вызывают игнорирование в анализе.) Средство анализа корреляции особенно удобно использовать, если для каждого субъекта N имеется более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение CORREL (или PEARSON),примененного к каждой из возможных пар переменных измерения.

Коэффициент корреляции, как и ковариана, — это мера степени, в которой две единицы измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц измерения, выраженных в двух переменных измерения. (Например, если двумя переменными измерения являются вес и высота, то значение коэффициента корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно от -1 до +1 включительно.

Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).

Средства корреляции и коварианс могут использоваться в одном и том же параметре, если у вас есть N различных переменных измерения, наблюдаемые для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, которая показывает коэффициент корреляции или коварианс между каждой парой переменных измерения соответственно. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансы не масштабироваться. Коэффициент корреляции и коварианс — это показатели степени, в которой две переменные «различаются».

Инструмент Ковариана вычисляет значение функции КОВАРИАНА. P для каждой пары переменных измерения. (Прямое использование КОВАРИАНА. P вместо ковариана является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись в диагонали выходной таблицы средства Коварица в строке i, столбце i — коварианс i-й переменной измерения. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕРС.P.

Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).

Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.

Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.

Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.

Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.

Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.

С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости «Альфа». Если f > 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для «Альфа».

Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.

Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.

Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.

Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:

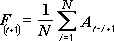
где

N — число предшествующих периодов, входящих в скользящее среднее;
A
j — фактическое значение в момент времени j;
F
j — прогнозируемое значение в момент времени j.

Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.

Средство анализа Ранг и процентиль создает таблицу, которая содержит порядковую и процентную ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая обрабатывает связанные значения как имеющие одинаковый ранг или использует РАНГ.Функция AVG, которая возвращает средний ранг связанных значений.

Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.

В средстве регрессии используется функция LINEST.

Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.

Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.

Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 «P(T <= t) одностороннее» дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 «P(T <= t) одностороннее» делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. «t критическое одностороннее» дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного «t критическое одностороннее» равно «Альфа».

«P(T <= t) двустороннее» дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. «P критическое двустороннее» выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем «P критическое двустороннее», равно «Альфа».

Парный двухвыборочный t-тест для средних

Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.

Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:

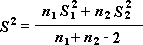
Двухвыборочный t-тест с одинаковыми дисперсиями

Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Его называют гомике t-тестом. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения.

Двухвыборочный t-тест с различными дисперсиями

Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных были полученными из распределения с неравными дисперсиями. Его называют гетероскестическими t-тестами. Как и в предыдущем примере с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения. Этот тест можно использовать, если в двух примерах есть отдельные объекты. Используйте тест Парный, описанный в примере, если существует один набор тем и две выборки представляют измерения по каждой теме до и после обработки.

Для определения тестовой величины t используется следующая формула.

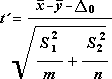
Следующая формула используется для вычисления степеней свободы (df). Так как результат вычисления обычно не является integer, значение df округлится до ближайшего другого, чтобы получить критическое значение из таблицы t. Функция Excel T .Test использует вычисляемую величину df без округлений, так как можно вычислить значение для T.ТЕСТ с неинтегрированной df. Из-за этих разных подходов к определению степеней свободы результаты T.Тест и этот t-тест будут отличаться в случае неравных дисперсий.

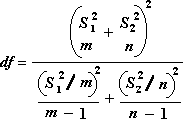
Z-тест. Средство анализа «Две выборки для середины» выполняет два примера z-теста для средств со известными дисперсиями. Этот инструмент используется для проверки гипотезы NULL о том, что между двумя значениями численности населения нет различий между односторонними или двухбокльными альтернативными гипотезами. Если дисперсии не известны, функция Z .Вместо этого следует использовать тест.

При использовании этого инструмента следует внимательно просматривать результат. «P(Z <= z) одностороннее» на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z <= z) двустороннее» на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент «z-тест» можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Создание гистограммы в Excel 2016

Создание диаграммы Парето в Excel 2016

Загрузка средства анализа в Excel

Инженерные функции (справка)

Общие сведения о формулах в Excel

Рекомендации, позволяющие избежать появления неработающих формул

Поиск ошибок в формулах

Сочетания клавиш и горячие клавиши в Excel

Функции Excel (по алфавиту)

Функции Excel (по категориям)

Нужна дополнительная помощь?

Источник

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Если вы ищете работу и она хоть как-то связана с математикой/экономикой/финансами, то вы очень часто будете встречать такие требования к кандидату:
— Отличное знание статистики;
— Знание и умение Python/R, чтобы эту статистику применять.

Но что делать, если никаких знаний по языкам программирования у вас нет, а встречаться со статистическими моделями так или иначе придется? А работу-то найти нужно срочно…

К счастью, в версии Microsoft Excel выше 2010 вшит целый статистический пакет. О нем мало кто знает, а его реально можно использовать, если нет навыков программирования или доступного компилятора под рукой.

Для начала поговорим, где все эти формулы найти. Как обычно, переходим на вкладку «Формулы» на главной панели, выбираем «Другие функции» и пакет «Статистические». Перед Вами полный перечень статистических возможностей Excel.

Список статистических функций

Как вы можете видеть, формул в этом разделе представлено довольно много, как «ходовых», так и «узкоспециализированных». К сожалению, разобрать все в одной статье не получится, поэтому рассмотрим здесь самые часто встречающиеся. Если вы хотите познакомиться с математическими функциями Excel, то рекомендуем скачать наш бесплатный гайд.

На первый взгляд они могут показаться очень простыми. Однако, мы постарались раскрыть те моменты, которые обычно остаются без внимания и могут быть полезными.

СРЗНАЧ() и СРЗНАЧА()

Редко кто задумывался, а ведь вычисление среднего значения – сугубо статистическая процедура: именно поэтому это операция и помещена в статистический пакет.

Наверно, особо не стоит останавливаться на правилах использования формулы: функция СРЗНАЧ() принимает на вход массив аргументов и дает на выходе среднее значение по всем ячейкам, содержащим числа(!). Это очень важный момент, который далеко не все знают. Поясним на примере.

Пусть дан диапазон А1:С2 и мы ищем среднее значение по всем 6 ячейкам диапазона:

Применение функции СРЗНАЧ()

Однако, результат функции СРЗНАЧ(А1:С2) будет не 8,7, а 13. Почему? (4+15+11+22)/6 = 8,7 ведь?

Да, это правильно, но функция СРЗНАЧ() берет в расчет только те ячейки, где «встречает» числа. Текстовая информация и пустые ячейки просто игнорируются. Поэтому в данном примере СРЗНАЧ() усредняет по 4 ячейкам и выдает правильный ответ – 13.

А вот если нужно произвести усреднение по всему диапазону, вне зависимости от типа данных, нужно использовать функцию СРЗНАЧА().

Принцип работы такой же, как и у СРЗНАЧ(), только на вход будут поступать абсолютно все ячейки. Результат в нашем примере будет уже ожидаемый – 8,7.

Применение функции СРЗНАЧА()

Замечание

Выбор той или иной функции происходит в зависимости от задачи. В реальной жизни они могут понадобится в одинаковой мере.

Например, менеджеру нужно узнать среднедневную выручку за месяц на основании продаж за каждый день. Допустим, за несколько дней ячейки оставлены пустыми. Есть два варианта, почему так произошло:

1. В эти дни не было ни одной продажи. Тогда эти дни должны принимать участие в расчете среднего значения и менеджеру нужно использовать СРЗНАЧА() – так он исключит игнорирование пустых ячеек.

2. Эти дни были выходными. Тогда пропуски сами по себе никакой информации не несут и их надо игнорировать: фактически, эти дни не принимают участие в статистической выборке и функция СРЗНАЧ() поможет их пропустить.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

СРЗНАЧЕСЛИ()

Очевидно, что функция СРЗНАЧЕСЛИ() возвращает среднее тех значений, который удовлетворяют каким-то условиям. Помимо этого, условия можно накладывать не только на сами значения, но и на другие ячейки. Проиллюстрируем.

Например, вычислим среднее значение всех ячеек, которые больше нуля:

Применение функции СРЗНАЧЕСЛИ() с условием на аргумент

Мы выделили диапазон А1:С3 и наложили на него условие – «>0». А можно сделать по-другому.

Рассмотрим таблицу, в которую занесены продажи лекарств в городе. Посчитаем среднюю цену Анальгина по всему городу. Для этого наложим условие уже не на саму цену, а на название лекарства.

Формула записывается так:

=СРЗНАЧЕСЛИ(Диапазон_на_который_накладываем_условия; “Условие”; Диапазон_по_которому_считаем_среднее_значение)

В нашем случае это примет вид:

Применение функции СРЗНАЧЕСЛИ() с условием на другой диапазон

Кстати говоря, условия можно комбинировать с помощью функции СРЗНАЧЕСЛИМН().

Предположим, что в аптеке Зеленый Крест продается несколько видов Анальгина и в нашу таблицу они все занесены как Анальгин.

Тогда, чтобы усреднить цену всех Анальгинов в аптеке Зеленый Крест, нужно просто использовать формулу:

=СРЗНАЧЕСЛИМН(С2:С13; A2:A13; “зеленый крест”;B2:B13; “анальгин”)

Обратите внимание: диапазон усреднения указывается в конце только при использовании функции СРЗНАЧЕСЛИ() с дополнительным условием. В остальных случаях диапазон ячеек, по которым вычисляется среднее значение, стоит первым.

МИН()/МАКС() и НАИБОЛЬШИЙ()/НАИМЕНЬШИЙ()

На первый взгляд, разница между этими функциями не особо прослеживается, хотя зачем их используют – очевидно – найти самое большое или маленькое число. Однако, в работе этих функций есть небольшая, но очень полезная разница. Разберем подробней.

Функция МИН() просто принимает массив аргументов и находит самое маленькое число. МАКС() – самое большое. Все просто.

Функция НАИМЕНЬШИЙ() же находит n-ое наименьшее число в массиве. НАИБОЛЬШИЙ(), наоборот, находит n-ое наибольшее число.

Например, нужно найти пятое по величине число. Вводим:

=НАИБОЛЬШИЙ(диапазон; 5).

Фактически, получается, что результат работы НАИБОЛЬШИЙ(массив;1) и МАКС(массив) – одно и то же. Аналогичная ситуация с НАИМЕНЬШИЙ(массив;1) и МИН(массив).

Рекомендуем записаться на наш открытый онлайн-курс «Аналитика в Excel», если вы хотите научиться выполнять рутинную работу быстрее.

МЕДИАНА() и МОДА()

Общеизвестные и достаточно важные статистические характеристики моды и медианы вычисляются по одноименным формулам.

Напомним, что медианой называется «середина» числового множества.

Например, если есть массив чисел от одного до десяти, то медианой будет число 5,5 (хотя оно само в массив не входит). Это из-за того, что количество элементов в массиве – четно и выбрать «центральное» просто невозможно.

Поиск медианы для «четного» массива

Вот если бы выборка начиналась не с единицы, а с двойки, то ответ был бы ровно 6.

Поиск медианы для «нечетного» массива

Теперь перейдем к моде. Мода – самое часто встречающееся число в выборке.

У функции нахождения моды есть целых три модификации в Excel старшее версии 2010 года: МОДА(), МОДА.ОДН() и МОДА.НСК().

Функция МОДА() оставлена для совместимости – ей, в целом, можно пользоваться: она работает совершенно аналогично функции МОДА.ОДН().

«ОДН» в названии функции значит, что, если в выборке несколько самых часто встречающихся элементов, то возвращено в качестве ответа будет только первое.

Применение функций МОДА() и МОДА.ОДН()

Для подсчета всех мод в выборке нужно использовать функцию МОДА.НСК().

Работает МОДА.НСК() следующим образом: выделяем побольше ячеек (если заранее не знаем, сколько мод у нас получится), в строке формул прописываем =МОДА.НСК(диапазон) и нажимаем Ctrl+Shift+Enter. Получили все моды в столбик.

«Слепой» метод применения функции МОДА.НСК()

Значения #Н/Д появляются, просто потому что мод у нас всего 2. Такой метод поиска мод называется «слепым» – мы просто берем побольше ячеек, чтобы наверняка хватило.

Если Вы не любите подобный «мусор» и Вам нравится, когда все красиво, можно сначала оценить: а сколько же у нас вообще будет мод? А потом просто выделить нужное количество ячеек.

Делается это так: сначала применяем функцию СЧЁТ() к нашей МОДА.НСК() – получили количество мод. А теперь выделяем только две ячейки и делаем все также, как написано выше.

Модификация применения МОДА.НСК()

Заключение

Статистический пакет Microsoft Excel содержит в себе еще огромное количество формул: проверку гипотез, принадлежность распределениям, доверительные интервалы, корреляцию и прочие инструменты, которые могут пригодиться при работе со статистикой даже на серьезном уровне.

Как мы и писали ранее, обозреть все в одной статье невозможно. Поэтому, если вы хотите узнать про менее известные, но не менее полезные статистические возможности Excel – пишите в комментариях, что вам было бы интересно и мы подготовим для вас новую статью из этого цикла.

Автор: Андрон Алексанян, СОО “Аптека-Центр”, эксперт SF Education

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Блог SF Education

MS Office

5 примеров экономии времени в Excel

Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…

Как работать с датами в Excel?

Содержание статьи История о том, как я пропустил свидание с очаровательной блондинкой… Вы никогда не попадали впросак из-за того, что неправильно читали дату? «Да…

Источник

Содержание

Использование описательной статистики
Подключение «Пакета анализа»
Размах вариации
Вычисление коэффициента вариации
Шаг 1: расчет стандартного отклонения
Шаг 2: расчет среднего арифметического
Шаг 3: нахождение коэффициента вариации
Простая формула для расчета объема выборки
Пример расчета объема выборки
Задачи о генеральной доле
По части судить о целом
Как рассчитать объем выборки
Как определить статистические выбросы и сделать выборку для их удаления в Excel
Способ 1: применение расширенного автофильтра
Способ 2: применение формулы массива
СРЗНАЧ()
СРЗНАЧЕСЛИ()
МАКС()
МИН()

Использование описательной статистики

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Подключение «Пакета анализа»

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

Размах вариации

Размах вариации – разница между максимальным и минимальным значением:

Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.

С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.

В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Синтаксис данных функций выглядит соответствующим образом:

= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)

Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.

Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».

Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»

В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.

Шаг 2: расчет среднего арифметического

Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.

«Вставить функцию»

В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».

Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».

Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.

Шаг 3: нахождение коэффициента вариации

Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.

«Главная»

«Число»

«Процентный»

Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.

Как видим, результат расчета выведен на экран.

Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.

Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:

Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.

После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.

Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.

Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.

Разделы: Математика

Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

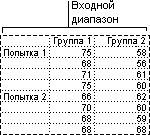
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26
32 33 31 31 25 33 25 29 30 28
23 30 29 24 33 30 30 28 26 25
26 29 27 29 26 28 27 26 29 28
29 30 27 30 28 32 28 26 30 26
31 27 30 27 33 28 26 30 31 29
27 30 30 29 27 26 28 31 29 28
33 27 30 33 26 31 34 28 32 22
29 30 27 29 34 29 32 29 29 30
29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики:

моду
медиану
размах ряда
построить полигон частот
построить столбчатую и круговую диаграммы
раскрыть смысловую сторону каждой характеристики

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i случайной величины меняются от 22 до 36 включительно шагом 1.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Простая формула для расчета объема выборки

где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;

p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = (1 – p);

e – допустимая ошибка, в долях.

Пример расчета объема выборки

Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

Получаем объем выборки n = 96 человек.

Задачи о генеральной доле

На вопрос «Накрывает ли доверительный интервал заданное значение p₀?» — можно ответить, проверив статистическую гипотезу H₀:p=p₀. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p^* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H₀ используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле

Гипотеза	H₀:p=p₀	H₀:p₁=p₂
Предположения	Схема испытаний Бернулли	Схема испытаний Бернулли
Оценки по выборке
Статистика K
Распределение статистики K	Стандартное нормальное N(0,1)	Стандартное нормальное N(0,1)

Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле

Значение u_кр находим по таблице функции Лапласа из соотношения 2Ф(u_кр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.

Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
Ф(2.23) = 0.49, u_кр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.

Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.

Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01

Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H₀:p=p₀=0,97 — неизвестная генеральная доля p равна заданному значению p₀=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H₁:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p₀=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства

По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-K_kp)= (-∞;-2,05). Наблюдаемое значение К_набл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.

Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H₀:p₁=p₂ — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H₀:p₁≠p₂ — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.

Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение K_набл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.

По части судить о целом

О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при

достаточном числе наблюдений

. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:

С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.

Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.

Как рассчитать объем выборки

Достаточный размер выборки зависит от следующих составляющих:

изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)

ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента

Формулы для расчета объема выборки:

Формулы расчета объема выборки

Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.

График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.

Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.

Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.

Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.

Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.

В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.

В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:

Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.

Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.

Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.

Способ 1: применение расширенного автофильтра

Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.

Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».

Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».

После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».

Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».

Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.

Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».

Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.

Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».

Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».

Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.

Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».

Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).

В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».

Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».

Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.

Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».

Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».

При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.

Способ 2: применение формулы массива

Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.

На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.

Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.

Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.

Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Жмем сочетание клавиш Ctrl+Shift+Enter.

Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Опять набираем сочетание клавиш Ctrl+Shift+Enter.

Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.

Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».

В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».

Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».

В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».

В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».

На кнопку с точно таким же названием жмем после возвращения в окно создания условий.

Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.

СРЗНАЧ()

Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.

Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:

Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13

Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).

Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:

СРЗНАЧЕСЛИ()

Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:

В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.

Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:

Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.

МАКС()

Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:

МИН()

Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:

Источники

https://lumpics.ru/descriptive-statistics-in-excel/
https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
http://galyautdinov.ru/post/formula-vyborki-prostaya
https://math.semestr.ru/group/interval-estimation-share.php
https://tidydata.ru/sample-size
https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
https://lumpics.ru/how-to-make-a-sample-in-excel/
https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html

Источник

Введение

Статистика
—
комплекс учебных дисциплин, обеспечивающих
овладение методологией статистического
исследования массовых социально-
экономических явлений и процессов с
целью выявления закономерностей их
развития в конкретных условиях места
и времени.

Отрасли
экономической статистики – статистика
промышленности, сельского хозяйства,
строительства, связи, природных ресурсов,
транспорта и.т.д.

Тема
данной курсовой работы – «Анализ и
прогнозирование технико-экономических
показателей деятельности предприятия».

Результаты
анализа являются основой для принятия
управленческих решений, действенным
средством повышения эффективности
производства. В содержание экономического
анализа входит: изучение экономических
явлений и обусловивших их причин;
достоверная оценка действующих норм и
нормативов; разработка мероприятий по
повышению эффективности производства.

Статистический
анализ используется сегодня каждым
серьезным предприятием для оценки своей
деятельности и планирования деятельности
на перспективу.

Таким
образом, из вышесказанного вытекает,
что выбранная нами тема весьма актуальна.

В
работе кратко описаны статистика, ее
информационная база, значение и задачи
статистики автомобильных перевозок,
Применение
пакета программ «SТАТISTICA».

В
практической части проведена структурная
и аналитическая группировки на транспорте;
определена теснота связи между факторами
и доля влияния факторов на результат
показателей; рассчитаны показатели
вариации (среднее линейное и среднее
квадратическое отклонения, коэффициент
вариации), коэффициент корреляции и
регрессии, основные показатели
динамического ряда; а также проведен
анализ перевозок грузов с помощью
расчета индекса сезонности. [6, с. 9]

Задачей
транспортной отрасли экономической
статистики является разработка и анализ
статистических показателей развития
транспортной отрасли.

Статистика
автомобильного транспорта – отрасль
экономической статистики. Объект ее
изучения – автомобильный транспорт,
т.е. совокупность автотранспортных
предприятий, производственный процесс
которых заключается в перемещении
грузов и пассажиров.

Предмет
изучения статистикb
автомобильного транспорта – массовые
экономические явления и процессы на
АТП, представляющие собой результат
транспортного процесса и условия
(факторы) его осуществления в конкретных
условиях места и времени.

Основная
цель работы анализ и прогнозирование
технико-экономических показателей 20
автотранспортных предприятий.

Общий
объем курсовой работы составляет 44
страниц.

Курсовая
работа содержит 11 рисунков и 18 таблиц.

В
ходе выполнения курсовой работы было
использовано 31 источников литературы.

СТАТИСТИЧЕСИКЕ
МЕТОДЫ В ИССЛЕДОВАНИИ ТЕХНИКО-ЭКОНОМИЧЕСКИХ
ПОКАЗАТЕЛЕЙ ДЕЯТЕЛЬНОСТИ
ПРЕДПРИЯТИ

Статистика
и ее информационная база

Современные
значения термина статистика:

Отрасль
практической деятельности людей по
сбору, обработке и анализу данных,
которая характеризует состояние
экономики и культуры страны.
Общественная
наука, которая занимается разработкой
теоретических положений и методов,
используемых практикой.
Статистические
данные, представляемые в отчетности
предприятия, которые публикуются в
статистических справочниках.

Статистика
как наука представляет собой систему
различных дисциплин:

Теоретическая
статистика – изучает общие методы и
принципы статистических исследований,
это методологическая основа для всех
отраслевых статистик.
Экономическая
статистика – разрабатывает и анализирует
синтетические показатели, включая
макроэкономические показатели.
Социальная
статистика – формирует и анализирует
системы показателей, комплексно
характеризующих различные стороны
социальных условий жизни населения.

Статистика
– это отрасль общественной науки,
которая с помощью обобщающих показателей
изучает количественную сторону
общественных явлений в конкретных
условиях места и времени.

Предметом
статистики
является выявление закономерностей
развития социально-экономических
явлений общества и их взаимосвязи.

Объектом
изучения
статистики являются совокупности
данных,
то есть множество
единиц
варьирующего
признака.

Признаки
по внешнему выражению подразделяются
на:

—
Атрибутивные (качественные, описательные),
их нельзя выразить числами. Например:
подразделение рабочих по специальности,
людей по национальности и.т.п.

—
Количественные – выражаются числами
и подразделяются на дискретные (только
целые числа) и непрерывные (любое
промежуточное значение). Например:
дискретные (численность работающих на
предприятии, количество детей в семье
и.т.д.), непрерывные (стоимость ОПФ, рост,
вес и.т.д.).

Государственная
статистика основана на единой системе
учета и статистики,
которая включает:

1)
оперативно-технический учет: первичный,
детальный, низовой, в основном использует
натурально-вещественные показатели;

2)
бухгалтерский учет: непрерывный сплошной
учет хозяйственных операций предприятия,
использует денежную оценку;

3)
статистический учет: агрегированный
учет, использует результаты вышеперечисленных
учетов и собственных методов получения
информации, например, хронометража,
анкетирования, переписи).

Все
виды учета взаимосвязаны, а их результаты
не должны противоречить друг другу.

Этапы
статистического исследования.
Характеристика
статистического наблюдения

Любое
статистическое исследование включает
в себя следующие этапы:

1)
формулировка целей;

2)
сбор информации (статистическое
наблюдение);

3)
обработка информации (сводка и
группировка);

4)
анализ информации (индексный, дисперсионный,
корреляционно-регрессионный анализ);

5)
выводы.

Статистическое
наблюдение
– один из основных этапов исследования,
обеспечивающий качество исходной
информации. От организации статистического
наблюдения зависят другие этапы
статистического исследования, так как
любая ошибка в статистическом наблюдении
может привести к ошибочным выводам.

Цель
проведения статистического исследования
определяет целесообразность проведения
статистического наблюдения, масштабы,
сроки, методы проведения наблюдения,
объем требуемых ресурсов.

Значение
индексов сезонности. Задачи статистки
АТП.

В
статистике периодические колебания,
которые имеют определенный и постоянный
период, равный годовому промежутку,
называется «сезонные колебания» или
«сезонные волны», а динамический ряд –
сезонным рядом динамики.

Существуют
ряд методов изучения и измерения сезонных
колебаний. Самый простой заключается
в построении специальных показателей,
которые называются индексами сезонности
Is.
Совокупность этих показателей отражают
сезонную волну. Индексами сезонности
являются процентные отношения фактических
внутригрупповых уровней к теоретическим
уровням, выступающие в качестве базы
сравнения.

Среднесуточный
объем перевозок

,
где (1.2.1.)

—
среднемесячный объем перевозок i-го
месяца j-го
года.

—
дни календарные i-го
месяца j-го
года.

Среднесуточный
объем перевозок для каждого месяца по
данным за 3 года.

,
где (1.2.2.)

— объем перевозок i-го
месяца за 1,2,3 год соответственно.

Индексы
сезонности для построения сезонной
волны:

,
где (1.2.3.)

—
общая среднесуточная величина за
исследуемый период, определяется как
средневзвешенная арифметическая из
среднесуточных объемов по месяцам за
3 года.

. (1.2.4.)

Задачи
статистики АТП:

Изучение
перевозок – центральная задача
статистики, т.к. участие транспорта в
общем процессе воспроизводства
непосредственно выражается в перевозках
грузов и пассажиров. Хозяйственное и
социальное развитие страны и отдельных
ее регионов требует слаженной
высокопроизводительной работы всех
видов транспорта, четкого взаимодействия
со всеми отраслями экономики. Этого
можно достигнуть за счет улучшения
организации перевозочного процесса,
совершенствование координации работы
всех видов транспорта, повышения их
конкурентоспособности.

В
настоящее время транспортная система
страны справляется с перевозкой грузов
и пассажиров, обеспечивая платежеспособный
спрос на ее услуги.

Общее
увеличение грузооборота по всем видам
транспорта обусловлено причинами,
связанными с общим состоянием экономики
страны: некоторым увеличением производства
в большинстве отраслей хозяйства;
восстановлением прежних межотраслевых
связей; увеличение объема договорных
обязательств потребителей со
специализированными предприятиями
транспорта.

Главные
виды транспорта при перевозке пассажиров:
автомобильный, железнодорожный и
воздушный. Так, удельный вес автомобильного
транспорта по объему пассажирооборота
в 2009г. составил 32,7%, а по числу привезенных
пассажиров – 49,6%.

Становление
рыночных отношений в экономике привело
к перестройке хозяйственного механизма
и на автомобильном транспорте, что
обусловило снижение государственной
формы собственности, децентрализацию
управления, развитие горизонтальных
договорных отношений между транспортными
предприятиями и потребителями их услуг,
либерализацию тарифов, ликвидацию
безвозмездной государственной поддержки.

Задачи
статистики изучения перевозок грузов
и пассажиров для каждого предприятия
транспорта неотделимы от задач
хозяйственного руководства и планирования.
Рост объема перевозок, снижение
транспортных тарифов, повышение качества
обслуживания достигаются за счет
совершенствования планирования и
организации перевозочного процесса.
Решающее значение в реализации этих
задач имеет статистическая информация
о выполненных перевозках, перспективах
их развития, размере спроса на перевозки
различными видами транспорта и их
конкурентоспособности.

При
изучении перевозок грузов и пассажиров
статистика определяет объемные и
качественные показатели по перевозкам
за отчетный период. Эти показатели
используются при контроле за выполнением
плана, а также для оперативного и
перспективного планирования. Особое
внимание уделяется за выполнением
контроля договорных обязательств. Их
соблюдение является основным критерием
оценки работы предприятия клиентурой.

Рост
объемов перевозок, повышение эффективности
работы предприятия невозможны без
широкого внедрения прогрессивных
методов организации перевозок. К их
числу относятся централизованные
перевозки, контейнерные и пакетные
перевозки грузов. Контроль за выполнением
плана и изучение динамики по этим видам
перевозок – особая задача статистики.

Главная
цель проверки выполнения плана –
своевременно обнаружить и предупредить
возможные диспропорции, выявить
неиспользованные производственные
резервы для перевыполнения плана и
улучшения качества обслуживания
пассажиров и предприятий других отраслей.
Для раскрытия резервов статистика
отражает условия выполнения перевозок
и использование подвижного состава.
Это достигается исчислением
технико-эксплуатационных показателей
работы подвижного состава и последующим
взаимосвязанным их анализом.

Статистические
данные о перевозках необходимы для
составления текущих и перспективных
планов развития предприятия. Обеспечивая
потребности планирования, статистика
устанавливает и анализирует отчетные
данные:

—
о размере пассажиро- и грузопотоков
между отдельными районами;

—
о распределении перевозимых грузов по
родам и отраслям экономики;

—
о дальности перевозок;

—
о скорости доставки грузов и перевозки
пассажиров;

—
о регулярности движения и т.д.

Все
эти сведения должны устанавливаться
не только за год, но и за более короткие
сроки (декаду, месяц). Они необходимы
для планирования и систематического
наблюдения за работой предприятия,
чтобы можно было своевременно принять
меры для устранения выявленных
недостатков.

Статистическое
изучение закономерностей развития
грузовых и пассажирских перевозок, их
сезонной неравномерности и
конкурентоспособности составляет базу
построения прогнозов, необходимых на
стадии разработки планов предприятия.

Отчетные
данные по перевозкам отдельных предприятий
используются для построения транспортных
балансов по регионам и в целом по стране
и исчисления синтетических показателей,
выражающих участие транспорта и отдельных
его видов в создании валового внутреннего
продукта страны.

[6,
с.40-44].

Прикладные
программы предназначены для того, чтобы
обеспечить применение вычислительной
техники в различных сферах деятельности
человека. Поэтому этот класс программ
представляет наибольший интерес для
массового пользователя компьютеров.

В
экономической практике пакеты прикладных
программ используются в бухгалтерском
учете, документационном обеспечении
управления, в налогообложении, управлении
проектами и персоналом, банковском
деле, статистической обработке данных,
финансовом анализе, планировании и
принятии решений, в страховой деятельности
и во многих других областях данной
сферы. Популярны так называемые
интегрированные системы.

Применение
статистических ППП позволяет: улучшить
содержательную часть решаемых задач;
повысить эффективность учебного процесса
за счет сокращения рутинных процедур,
эффективного поиска правильного решения
за счет быстрой, программной реализации
большого количества альтернативных
способов решения.

«Microsoft
Excel»

Основным
средством решения экономических задач
является табличный процессор Excel.
Microsoft Excel — средство для работы с
электронными таблицами, намного
превышающее по своим возможностям
существующие редакторы таблиц, первая
версия данного продукта была разработана
фирмой Microsoft в 1985 году. Табличные
процессоры — удобный инструмент для
экономистов, бухгалтеров, инженеров,
научных работников — всех тех, кому
приходится работать с большими массивами
числовой информации. Эти программы
позволяют создавать таблицы, которые
являются динамическими, т.е. содержат
так называемые вычисляемые поля, значения
которых автоматически пересчитываются
по заданным формулам при изменении
значений исходных данных, содержащихся
в других полях. В дальнейшем ее можно
просматривать, изменять, записывать на
магнитный диск для хранения, печатать
на принтере. Microsoft
Excel
– это программа управления электронных
таблицами общего назначения, которая
используется для вычислений, организации
и анализа деловых данных. Многие фирмы
разработчики программного обеспечения
для ПК создали свои версии табличных
процессоров. Из них наибольшую известность
приобрели Lotus 1-2-3 фирмы Lotus Development,
Supercalc фирмы Computer Associates.

Excel,
как видно из всего сказанного выше очень
мощный инструмент для решения задач
имеющих дело с массивами разнообразных
данных, поэтому область его применения
обширна, начиная от бухгалтерских и
складских задач и заканчивая расчетами
энергетики спутниковых линий. В Excel
удобно решать задачи линейной алгебры,
такие как работа с матрицами и др. Так
же есть все возможности по полноценной
работе (сортировка, выборка, сводные
таблицы, анализ) с базами данных. Благодаря
наличию языка программирования в Excel
возможно создание различных пользовательских
программ, которые автоматизируют
специфические стандартные задачи.

«Statistica»

Рынок
статистических пакетов достаточно
обширен и достигает нескольких тысяч.
Это профессиональные пакеты (SAS, BMDP),
универсальные пакеты (STADIA, OLIMP, STATGRAPHICS,
SPSS, STATISTICA,…), специализированные (BIOSTAT,
MESOSAUR, DATASCOPE,…). Благодаря деятельности
корпорации Софтлайн, являющейся дилером
компании производителя StatSoft (USA), одним
из наиболее известных в России пакетов
для прикладного статистического анализа
данных является пакет STATISTICA.

ППП
STATISTICA — это универсальная интегрированная
система, предназначенная для статистического
анализа и визуализации данных, содержащая
широкий набор процедур анализа для
применения в научных исследованиях
различных направлений, технике, бизнесе,
учебном процессе.

Преимущества
ППП STATISTICA перед другими статистическими
пакетами, подчеркивающие целесообразность
его использования в производственном
процессе следующие:

—
с помощью реализованных в системе
STATISTICA языков программирования (SCL,
STATISTICA BASIC), снабженных специальными
средствами поддержки, легко создаются
законченные пользовательские решения
и встраиваются в различные другие
приложения или вычислительные среды;

—
переведен на русский язык и можно
приобрести лицензионную, русифицированную
версию, издано большое число книг с
подробным описанием системы STATISTICA 5.0;

—
возможно расширение пользователем
библиотеки функций, что позволит решать
большинство задач по теории вероятностей;

—
реализован обмен данными между STATISTICA
и Windows приложениями;

особую
актуальность пакет приобретает при
решении достаточно трудоемких, сложных
с математической точки зрения, и
громоздких в реализации методов
многомерного анализа;

—
любая графическая и текстовая информация
в STATISTICA может быть выведена в файл в
формате RTF (Rich Text Format — расширенный
текстовый формат), который открывается
и редактируется в Microsoft Office Word.

http://xreferat.ru/33/6418-1-primenenie-paketov-prikladnyh-programm-v-ekonomike.html

РАСЧЕТ
И АНАЛИЗ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ,
ХАРАКТЕРИЗУЮЩИХ ТЕХНИКО-ЭКОНОМИЧЕСКИЕ
ПОКАЗАТЕЛИ ДЕЯТЕЛЬНОСТИ АТП

Сводка
и группировка статистических данных

Таблица
1

Средние
данные о численности работников и объеме
перевезенных грузов

по
ряду АТП

№ АТП	Среднеспис. числ, чел	Объем перевезенного груза, тыс.т
1	2152,5	4756,5
2	1768,2	5321,4
3	690,9	1167,6
4	865,2	2984,1
5	1585,5	6594,0
6	1449,0	5533,5
7	1932,0	5621,7
8	1138,2	3767,4
9	1940,4	8633,1
10	1512,0	7408,8
11	1071,0	1980,3
12	2352,0	4116,0
13	898,8	2956,8
14	1724,1	8068,2
15	1005,9	2322,6
16	1732,5	6079,5
17	1558,2	2803,5
18	682,5	2457,0
19	871,5	1917,3
20	1703,1	6163,5

Статистическая
совокупность состоит из АТП.

Признак:
Объем перевезенного груза.

Определяем
количество групп в выборке по формуле
Стерджесса.

_(2.1.1.)

Подсчитываем
величину интервала по формуле:

тыс.т. (2.1.2)

Строим
интервальный ряд распределения

Интервальный
ряд распределения
– ряд распределения, построенный по
непрерывному признаку.

Таблица
2

Группировка
данных по объемам перевезенных грузов

Объем перевез. груза, тыс.т	fi частота	xi середина интервала	wi частость	cum fi накопл. частоты	cum wi накопл. частости
1167,6 – 2660,7	5	1914,15	25	5	25
2660,7 – 4153,8	5	3407,25	25	10	50
4153,8 – 5646,9	4	4900,35	20	14	70
5646,9 – 7140,0	3	6393,45	15	17	85
7140,0 – 8633,1	3	7886,55	15	20	100
Всего	20		100

fi
– частота – численность отдельных
вариантов, т.е. числа, показывающие как
часто встречается в ряду распределения.

xi
– середина интервала

wi
– частость – частоты, выраженные в виде
относительных величин, их сумма равна
1 или 100%.

Находим
по формуле (2.1.3.)

[1
с. 4-6]

Расчет
относительных величин

Относительный
показатель
–
представляет собой числовую меру
соотношения двух сопоставляемых
абсолютных величин.

Основное
условие правильного расчета относительной
величины -сопоставимость сравниваемых
показателей и наличие реальных связей
между изучаемыми явлениями. Относительный
показатель может выражаться в
коэффициентах, процентах, промилле,
продецимилле или быть именованным
числом.

Основные
показатели:

Величина
динамики – рассчитывается как отношение
признака в определенный период времени
к уровню этого же признака в предшествующий
период.

ОПД
= Текущий показатель / Предшествующий
или базовый показатель. (2.2.1.)

Относительная
величина планового задания –
рассчитывается как отношение уровня
запланированного на предстоящий период
к уровню фактически сложившемуся
раннее.

Относительная
величина выполнения планового задания
– отношение уровня фактически достигнутого
в данном периоде к уровню запланированному.

ОПП
= Показатель, планируемый на (i
+
1)-й период / Показатель,

достигнутый
в (i
–
1)-й период; (2.2.2.)

ОПРП
= Показатель, достигнутый в (i
+
1)-й период / Показатель,

планируемый
на (i
+
1)-й период. (2.2.3.)

Таблица
3

Грузооборот
по предприятиям за 2009 – 2010гг.

АТП	2009г. тыс. т-км.	2010г. тыс. т-км.
План	Факт
№1	12	14	13
№2	8	7	9
№3	20	22	25
№4	6	5	4
№5	15	17	20

Результаты
решения сразу сведем в таблицу №4.

Таблица
4

Результаты
расчетов относительных величин

АТП	Относительные показатели
Динамики	Планового задания	Выполнения планового задания
		%		%		%
№1	1,08	108	1,17	117	0,93	93
№2	1,13	113	0,88	88	1,29	129
№3	1,25	125	1,10	110	1,14	114
№4	0,67	67	0,83	83	0,80	80
№5	1,33	133	1,13	113	1,18	118

Вывод:
По данным таблицы 4 видно, что АТП №1 и
№4 недовыполнили план, а АТП №2,3,5
выполнили план грузооборота, отличилось
АТП №2, они перевыполнили план на 29%.

Относительный
показатель структуры (ОПС)
показывает
удельный вес каждой группы в общей
численности совокупности и представляет
собой соотношение структурных частей
изучаемого объекта и их целого. Их
получают путем деления численности
каждой группы, входящей в совокупность,
на численность всей совокупности. [2.]

(2.2.4.)

Таблица
5

Структура
грузооборота за 2010г. год по всем АТП

№	Структура грузооборота	Объем
тыс. т-км.	% к итогу
1	Груз, всего	71	100,0
2	В том числе, гравий	12	16,9
3	щебень	16	22,6
4	мука	3	4,2
5	зерно	2	2,8
6	кирпич	15	21,1
7	сахар	3	4,2
8	бетон	20	28,2

Рисунок
4. Относительный показатель структуры

Вывод:
По данным рисунка видно, что за 2010 год
грузооборот бетона больше всех остальных
грузов 20 тыс. т-км, что составляет 28% от
общего объема грузооборота.

Относительный
показатель координации
(ОПК)
представляет
собой отношение одной части
совокупности к другой части этой же
совокупности. [2.]

_(2.2.5.)

Таблица
6.

Грузооборот
АТП

%	Грузооборот	тыс. т-км.	Показатель
1	гравий	12	0,60
2	щебень	16	0,80
3	мука	3	0,15
4	зерно	2	0,10
5	кирпич	15	0,75
6	сахар	3	0,15
7	бетон	20	—

Рисунок
5. Относительный показатель координации

Вывод:
По данным рисунка видно, что на каждый
т-км грузооборота бетона, приходится
75% грузооборота кирпича и 10% зерна.

Относительный
показатель интенсивности
(ОПИ)
характеризует
степень распространения изучаемого
процесса или явления и представляет
собой отношение исследуемого показателя
к размеру присущей ему среды. [2.]

_(2.2.6.)

Таблица
7

Распределение
всего груза на количество подвижного
состава в АТП

АТП №	Груз тыс.т.	Подвижной состав	Показатель
1	14	47	0,3
2	7	32	0,2
3	22	56	0,4
4	5	25	0,2
5	17	50	0,3

_{Рисунок

6. Относительный показатель интенсивности}

_{Вывод:

По данным рисунка видно, что на все

количество подвижного состава приходится:

в АТП №1 — 30%, в АТП №2 — 20%, в АТП №3 — 40%, в

АТП №4 — 20%, в АТП №5 — 30% всего груза.}

Относительный
показатель сравнения – представляет
собой соотношение одноименных
абсолютных показателей, характеризующих
разные объекты (предприятия, фирмы,
районы, области, страны и т.п.). [2.]

_(2.2.7.)

Таблица
8

Объем
и структура грузооборота предприятий

%	Грузооборот	тыс. т-км.	Показатель
1	гравий	12	1,7
2	щебень	16	1,3
3	мука	3	6,7
4	зерно	2	10,0
5	кирпич	15	1,3
6	сахар	3	6,7
7	бетон	20	—

Рисунок
7. Относительный показатель сравнения

Вывод:
По данным рисунка видно, что грузооборот
бетона в 1,7 раз превысил грузооборот
гравия, в 1,3 раза — щебня, в 6,7 раза – муки,
в 10 раз – зерна, в 1,3 раза – кирпича и в
6,7 раза больше, чем грузооборот сахара.

Расчет
средних величин

Средние
величины
– основные обобщающие показатели,
используемые при анализе статистических
таблиц.

Средние
величины рассчитываются на 3 стадии
экономико-статистического исследования.

Основное
условие использования средних величин:
расчет только для качественно-однородной
совокупности.

Рассчитываем
среднюю арифметическую взвешенную.

Таблица
9 (продолжение табл. 2)

Данные
для расчета средних величин

x_i	f_i	x_i∙f_i
1914,15	5	9570,75
3407,25	5	17036,25
4900,35	4	19601,4
6393,45	3	19180,35
7886,55	3	23659,65
Итого:	20	89048,4

Средняя
арифметическая взвешенная применяется
в случае сгруппированных данных, т.е.
если построен ряд распределения.

_(2.3.1.)

_{Рассчитываем

среднюю арифметическую взвешенную по

данным таблицы 9:}

тыс.т.

Вывод:
Это наиболее типичный объем перевезенного
груза в данной совокупности.

[1
с.4-8]

Средняя
гармоническая взвешенная определяется
по формуле

(2.3.2.)

Известны
данные о перевезенном грузе пяти АТП в
2009г. (табл.10)

Таблица
10

Данные
о перевезенном грузе

№ АТП	Объем перевезенного груза V, тыс.т.	Подвижной состав, х.
1	2	3	4
1	13	10	1,3
2	9	5	1,8
3	25	16	1,6
4	4	2	2
5	20	13	1,5
Итого:	71	46	8,2

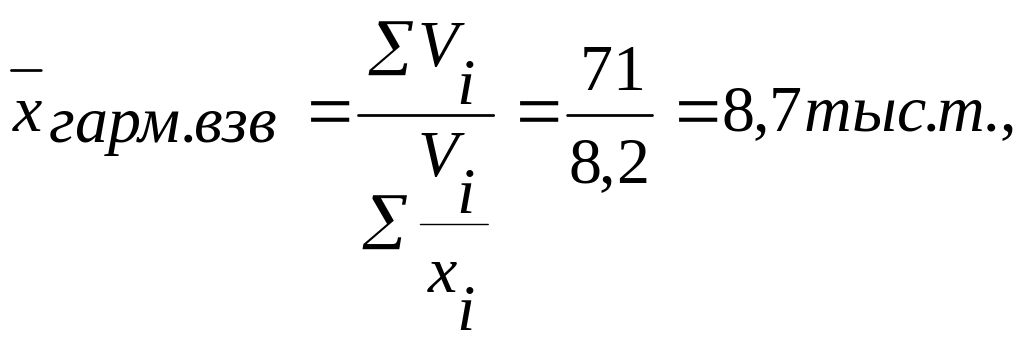
Вывод:
В 2009г. средний объем перевезенного груза
на подвижной состав составил 8,7 тыс.т.
[2 c.49]

Подсчитываем
структурные средние.

Используются
для изучения рядов распределения, т.е.
определяется структура. К ним относятся
мода (Мо) и медиана (Ме).

Мода.

Мода
– наиболее часто встречаемое значение
признака.

Определяется
модальный интервал по столбцу частот,
находим самую большую частоту.

fi=5,
поэтому берем интервал 1167,6 – 4153,8

По
данным таблицы 2 рассчитываем моду по
формуле.

(2.3.3.)

— начало модального интервала;

h
– шаг интервала;

– частота предшествующего модального
интервала;

— частота модального интервала;

— частота последующего интервала.

Решение:

тыс.т.

Для
графического отображения моды строится
гистограмма.

Рисунок
8. Гистограмма

Вывод:
Чаще всего в данной совокупности
встречается перевезенный груз с объемом
3656,1 (тыс.т.).

Источник

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28