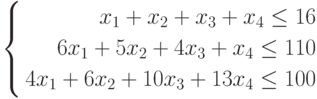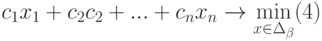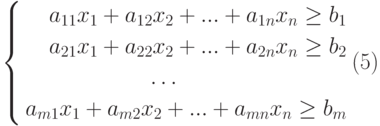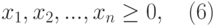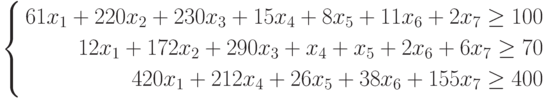В этой статье обсуждается использование надстройки Microsoft Excel «Решение», которая позволяет анализировать «что если» для определения оптимального сочетания продуктов.
Как определить ежемесячный набор продуктов, который позволяет повысить прибыльность?
Компаниям часто требуется определять количество каждого продукта, который будет создаваться ежемесячно. В простейшей форме проблема в наборе продуктов состоит в том, как определить объем каждого продукта, который должен быть произведен в течение месяца, чтобы максимально увеличить прибыль. Сочетание продуктов обычно должно соответствовать следующим ограничениям:
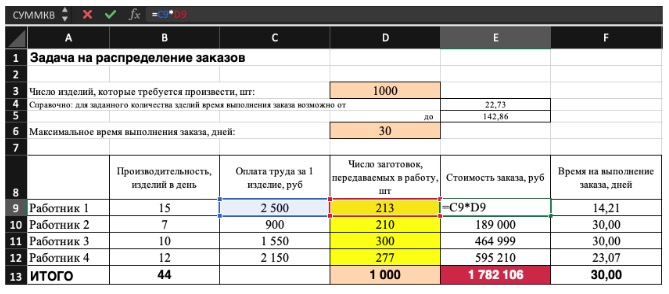
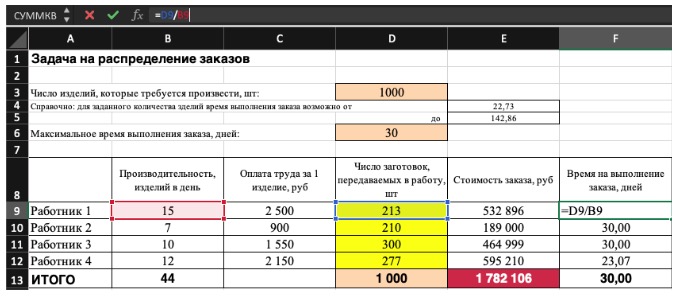
-
Сочетание продуктов не может использовать больше ресурсов, чем доступно.
-
Потребность в каждом продукте ограничена. В течение месяца мы не можем создать больше продукции, чем это диктует потребность в продукции, так как в нее нагребают лишние продукты (например, избежаемый продукт).
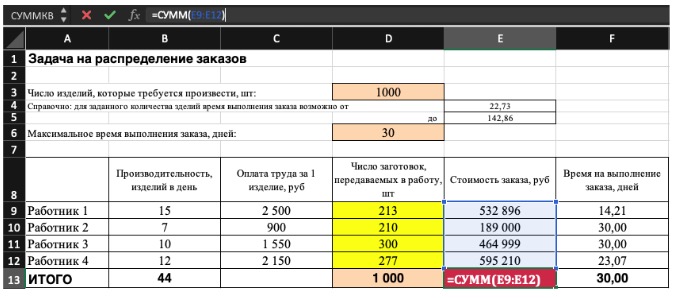
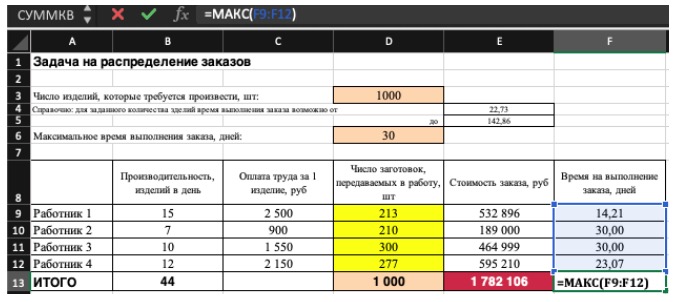
Теперь рассмотрим пример проблемы со сочетанием продуктов. Решение этой проблемы можно найти в файле Prodmix.xlsx, как показано на рисунке 27-1.
Предположим, что мы работаем в компании, которая производит шесть различных продуктов на своем заводе. Для производства каждого продукта требуются трудовые и необработанные материалы. В строке 4 на рисунке 27-1 показано количество часов труда, необходимое для получения фунта каждого товара, а в строке 5 — фунт необработанных материалов, необходимых для получения фунта каждого товара. Например, для получения фунта продукта 1 требуется 6 часов труда и 3,2 фунта неотработанных материалов. Цена за фунт для каждого фунта задается в строке 6, цена за единицу за фунт — в строке 7, а доход за фунт — в строке 9. Например, товар 2 продается по 11,00 долларов США за фунт, за единицу стоит 5,70 долларов США за фунт и вклад в сумму 5,30 долларов США за фунт. Запрос за месяц для каждого подмайки выдается в строке 8. Например, потребность в продукте 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов необработанных материалов. Как эта компания может максимально увеличить ежемесячную прибыль?
Если бы нам не было известно ничего о надстройке Excel «Решение», мы могли бы решить эту проблему, построив на этом листах данные о прибылях и использовании ресурсов, связанных с этим сочетанием продуктов. Затем мы использовали пробные и ошибки, чтобы оптимизировать прибыль, не используя при этом больше ресурсов и необработанных материалов, чем доступно, и не изменяя при этом лишние продукты. Над решением этой процедуры мы используем только пробную стадию с ошибкой. По сути, «Поиск решения» — это механизм оптимизации, который безукоризненно выполняет поиск по пробным версиям и ошибкам.
Ключ к решению этой проблемы — эффективное вычисление использования ресурсов и прибыли, связанных с любым сочетанием продуктов. Для этого важно использовать функцию СУММПРОИDUCT. Функция СУММПРОИCT перемножает соответствующие значения в диапазонах ячеев и возвращает сумму этих значений. Каждый диапазон ячеок, используемый в оценке СУММПРОИДУCT, должен иметь одинаковые размеры, что подразумевает, что можно использовать суммпроидуц с двумя строками или двумя столбцами, но не с одной строкой и столбцом.
В качестве примера использования функции СУММПРОИПР в нашем примере мы постараемся вычислить использование ресурсов. Трудоемкие труды вычисляются по
(Количество трудовых единиц, использованных для одного фунта воды в секунду)*(1 фунт 1, произведено)+
(Трудоемка, используемая для одного фунта валюты 2)*(2 фунта, произведенного) + …
(Трудоемка, используемая для одного фунта валюты 6)*(6 фунтов в секунду)
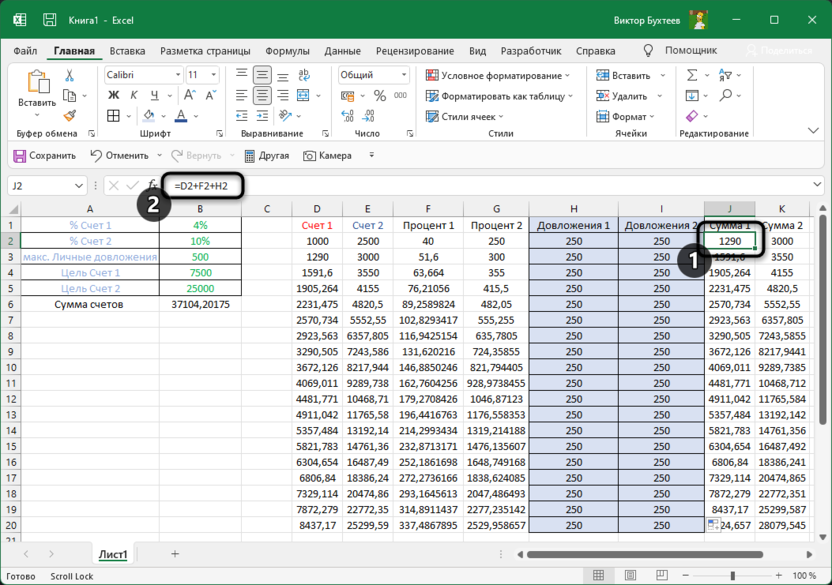
Мы могли бы более утомительным образом вычислять использование труда, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Кроме того, использование необработанных материалов можно вычислять как D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на таблицу для шести продуктов отнимает много времени. Представьте, сколько времени займет работа с компанией, которая производит, например, 50 продуктов на своем заводе. Гораздо проще вычислять трудоемкие и необработанные данные, скопируя из D14 в D15 формулу СУММПРОИДУCT($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш рабочий процесс), но гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, чтобы при копировании формулы все равно записать сочетание продуктов из строки 2. Формула в ячейке D15 вычисляет использование необработанных материалов.
Аналогичным образом прибыль определяется с помощью
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Доход легко вычисляется в ячейке D12 с помощью формулы СУММПРОИКТ(D9:I9;$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для всех продуктов.
-
Целевая ячейка. Наша цель — максимально увеличить прибыль (вычисленную в ячейке D12).
-
Изменяя ячейки. Количество фунта, произведенного каждым продуктом (в диапазоне ячеок D2:I2)
-
Ограничения. В этом примере есть следующие ограничения:
-
Не используйте больше трудовых или необработанных материалов, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
-
Не выполыв при этом больше средств, чем нужно. Это значит, что значения в ячейках D2:I2 (фунта, произведенного для каждого пациента) должны быть меньше или равны требованию для каждого пациента (в ячейках D8:I8).
-
Мы не можем привести к отрицательным последствиям любых проблем с наркотиками.
-
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в «Найти решение». Все, что вам нужно сделать, — это нажать кнопку «Найти решение», чтобы найти набор товаров, который максимально увеличить прибыль!
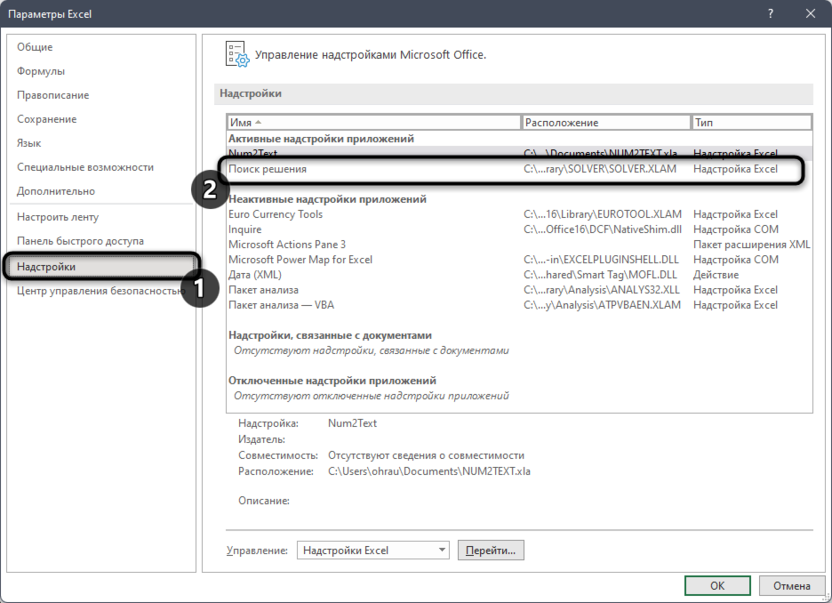
Для начала на вкладке «Данные» в группе «Анализ» нажмите кнопку «Найти решение».
Примечание: Как объяснялось в главе 26 «Введение в оптимизацию с помощью надстройки Excel «Решение», надстройка «Решение» устанавливается с помощью кнопки Microsoft Office, а затем параметров Excel и надстройки. В списке «Управление» щелкните «Надстройки Excel», выберите поле «Найти решение» и нажмите кнопку «ОК».
Появится диалоговое окно «Параметры решения», как показано на рисунке 27–2.
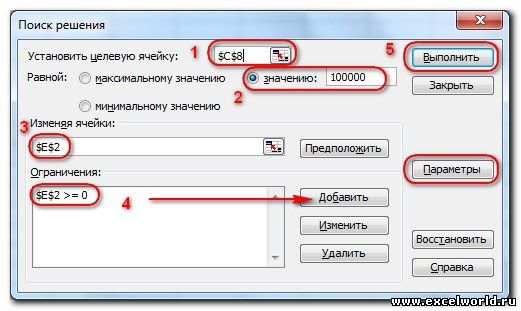
Щелкните поле «Установить целевую ячейку» и выберите ячейку прибыли (ячейка D12). Щелкните поле «Изменяя ячейки», а затем найдите диапазон D2:I2, содержащий количество отсюдоха каждого пациента. Диалоговое окно будет выглядеть как «Рисунок 27-3».
Теперь можно добавить ограничения в модель. Нажмите кнопку «Добавить». На рисунке 27–4 показано диалоговое окно «Добавить ограничение».
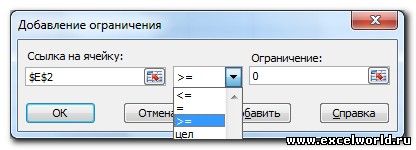
Чтобы добавить ограничения использования ресурсов, щелкните поле «Ссылка на ячейку» и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле ограничения, а затем выберите диапазон ячеев F14:F15. Диалоговое окно «Добавить ограничение» должно выглядеть так: «Рисунок 27-5».
Теперь, когда «Найти решение» пытается использовать другие значения для изменяющихся ячеек, будут учитываться только сочетания, которые удовлетворяют как D14<=F14 (трудоемка меньше или равна доступной работе), так и D15<=F15 (используемый необработаный материал меньше или равен доступному неоцененному). Нажмите кнопку «Добавить», чтобы ввести ограничения по запросу. Заполните поле в диалоговом окне «Добавить ограничение», как показано на рисунке 27–6.
Добавление этих ограничений гарантирует, что при попытках «Найти решение» для изменяемого значения ячейки будут учитываться только сочетания, которые удовлетворяют следующим параметрам:
-
D2<=D8 (количество произведенного средства 1 не превышает потребность в этом средстве)
-
E2<=E8 (количество произведенного средства 2 не превышает или равно запросу на доступ к более 2).
-
F2<=F8 (количество произведенного средства 3 не превышает потребность в этом средстве)
-
G2<=G8 (количество произведенного средства 4 не превышает или равно запросу на доступ к наркотиками 4)
-
H2<=H8 (количество произведенного средства 5 не превышает или равно запросу на доступ к более 5).
-
I2<=I8 (количество произведенного средства 6 не превышает потребность в этом средстве)
В диалоговом окне «Добавить ограничение» нажмите кнопку «ОК». Окно «Решение» должно выглядеть так: «Рисунок 27-7».
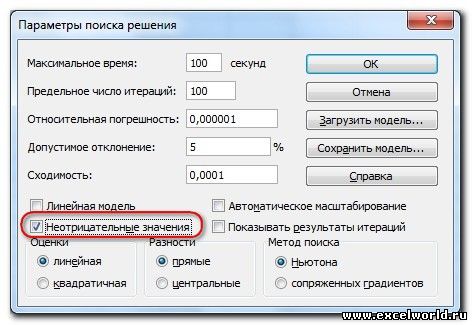
В диалоговом окне «Параметры решения» введите ограничение на то, что изменяющиеся ячейки не должны быть отрицательными. Нажмите кнопку «Параметры» в диалоговом окне «Параметры решения». Проверьте окне «Предполагаемая линейная модель» и «Нео отрицательная», как показано на рисунке 27–8 на следующей странице. Нажмите кнопку «ОК».
При проверке значения «Предположим, неохожим» над решением будут учитываться только сочетания изменяющихся ячеек, в которых каждая из изменяющихся ячеек принимает нео отрицательное значение. Мы проверили поле «Предполагаемая линейная модель», так как проблема с сочетанием продуктов — это особый тип решения, называемый линейной моделью. По сути, модель «Поиск решения» является линейной в следующих условиях:
-
Целевая ячейка вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа).
-
Каждое ограничение соответствует «требованиям к линейной модели». Это означает, что каждое ограничение вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой.
Почему эта проблема «Поиск решения» линейный? Целевая ячейка (прибыль) вычисляется как
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Эта вычисление вычисляется по шаблону, в котором вычисляется значение конечной ячейки путем с суммирования терминов формы (изменяемой ячейки)*(константа).
Наше ограничение на работу вычисляется путем сравнения значения, полученного из (Количество, используемого в фунте по 1)*(1 фунта влияния) + (Количество, используемого для одного фунта в фунте до 2)*(Фунт 2, полученный в качестве 2 фунта)+ (Трудоемкие мыed per pound of Drug 6)*(Pound 6 pound produced) to the labor available.
Следовательно, ограничение трудоемких ресурсов вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой. Ограничение трудоемких ресурсов и ограничение в необработанных материалах отвечают требованиям к линейной модели.
Наши ограничения запроса принимают форму
(От 1 досье 1)<=(Потребность в наркотиками 1)
(От 2 досье 2)<=(Потребность в наркотиками 2)
§
(от 6 досье 6)<=(Потребность в наркотиками 6)
Каждое ограничение запроса также соответствует требованию к линейной модели, поскольку каждое из них вычисляется путем свести вместе условия формы (изменяемая ячейка)*(константа) и сравнить суммы с константой.
Если вы показываете, что модель нашего продукта является линейной, почему это важно?
-
Если модель «Поиск решения» является линейной и выбран вариант «Предположим, линейный режим», «Поиск решения» гарантирован, что будет найдено оптимальное решение для модели «Поиск решения». Если модель «Поиск решения» не линейный, «Поиск решения» может не найти оптимальное решение.
-
Если модель «Поиск решения» является линейной и выбран вариант «Предполагаемая линейная модель», то для поиска оптимального решения модели используется очень эффективный алгоритм (метод простого решения). Если модель «Поиск решения» является линейной и не выбран вариант «Предполагаемая линейная модель», «Поиск решения» использует очень неэффективный алгоритм (метод ОГР2), что может затруднить поиск оптимального решения модели.
После нажатия кнопки «ОК» в диалоговом окне «Параметры решения» вернимся в главное диалоговое окно «Решение», показанное ранее на рисунке 27–7. При нажатии кнопки «Поиск решения» «Поиск решения» вычисляет оптимальное решение (если оно существует) для модели микса продуктов. Как было сказано в главе 26, оптимальным решением для модели набора продуктов является набор изменяемых значений ячеок (фунта, произведенного каждым продуктом), который позволяет максимально увеличить прибыль в наборе всех возможных решений. В этом же, целесообразное решение — это набор изменяющихся значений ячеок, удовлетворяющий всем ограничениям. Изменяющиеся значения ячеок, показанные на рисунке 27–9, являются допустимым решением, поскольку все производственные уровни неоценимы, производственные уровни не превышают потребность, а использование ресурсов не превышает доступных ресурсов.
Изменяемые значения ячеек, показанные на рисунке 27–10 на следующей странице, являются неизменяемым решением по следующим причинам:
-
Мы выпускаем больше 5, чем за него требуются.
-
Мы используем больше трудоемких ресурсов, чем доступно.
-
Мы используем больше необработанных материалов, чем доступно.
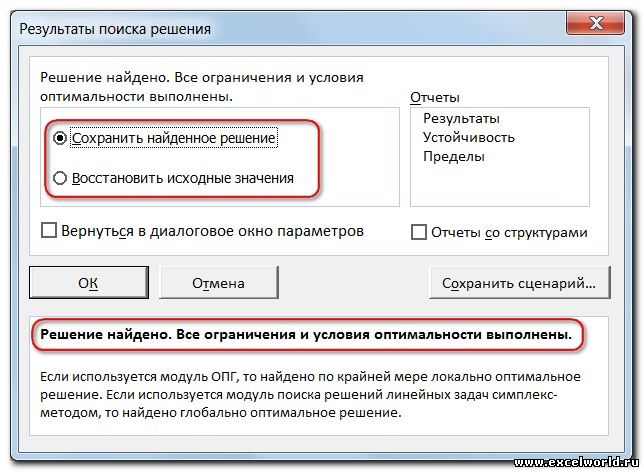
Нажав кнопку «Поиск решения», «Поиск решения» быстро найдет оптимальное решение, показанное на рисунке 27–11. Вам нужно выбрать «Сохранить решение для решения проблемы», чтобы сохранить оптимальные значения решения на работе.
Наша организация, которая занимается наркотиками, может увеличить ежемесячную прибыль в размере 6 625,20 долларов США, выполив 596,67 фунта 4, 1084 фунта для подавлили 5 рублей и ни одного другого фунта! Мы не можем определить, можно ли достичь максимальной прибыли в 6 625,20 долларов США другими способами. Все, что мы можем быть уверены, что из-за ограниченных ресурсов и требований в этом месяце нельзя внести больше 6 627,20 долларов США.
Предположим, что потребность в каждом продукте должна быть выполнены. (См. таблицу «Нет реального решения» в Prodmix.xlsx.) Затем нам нужно изменить ограничения по запросу с D2:I2<=D8:I8 на D2:I2>=D8:I8. Для этого откройте «Решение», выберите ограничение D2:I2<=D8:I8 и нажмите кнопку «Изменить». Появится диалоговое окно «Изменение ограничения», показанное на рисунке 27–12.
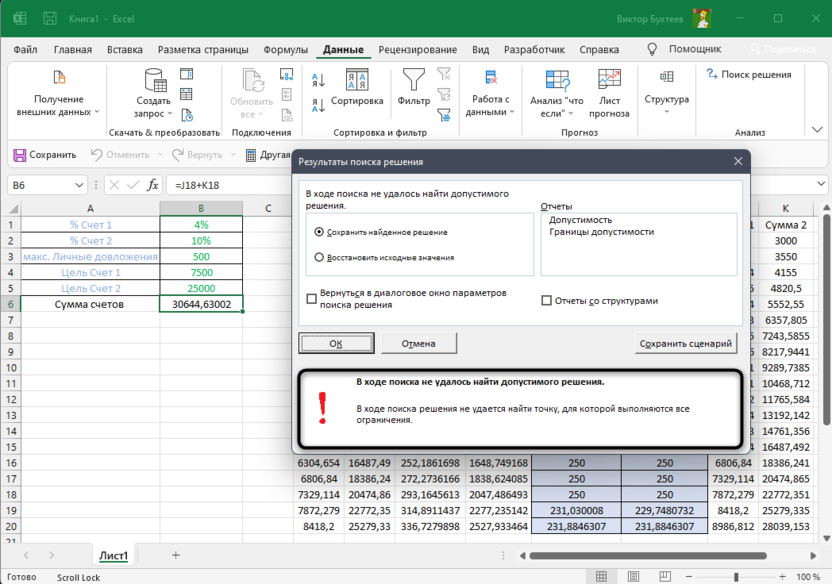
Выберите >=, а затем нажмите кнопку «ОК». Теперь над решением можно изменить только значения ячеок, которые соответствуют всем запросам. При нажатии кнопки «Найти решение» отобразилось сообщение «Поиск решения не удалось найти целесообразное решение». Это сообщение не означает, что мы допустили ошибку в модели, а о том, что из-за ограниченных ресурсов мы не сможем выполнить потребность во всех товарах. Надстройка «Решение» просто сообщает нам, что если мы хотим удовлетворить потребность в каждом продукте, нам нужно добавить больше труда, дополнительных необработанных материалов или и тех, и других.
Давайте посмотрим, что произойдет, если разрешить неограниченную потребность в каждом продукте и разрешить отрицательные количества каждого товара. (Эта проблема возникает в области «Набор значений не сходится» на Prodmix.xlsx.) Чтобы найти оптимальное решение в этой ситуации, откройте «Поиск решения», нажмите кнопку «Параметры» и откроем поле «Неохритимые». В диалоговом окне «Параметры решения» выберите ограничение запроса D2:I2<=D8:I8, а затем нажмите кнопку «Удалить», чтобы удалить это ограничение. При нажатии кнопки «Найти решение» возвращается сообщение «Установить значение ячейки не сходится». Это сообщение означает, что если нужно развернуть целевую ячейку (как в нашем примере), существуют допустимые решения, в том числе и для суммарных значений целевых ячеок. (Если целевая ячейка должна быть свернута, сообщение «Установить значения ячейки не сходятся» означает, что существуют возможные решения с небольших целевых значений, заверяемого в третейском деле.) В нашем случае, разрешив негативное производство в случае злоупотреблений, мы фактически создадим ресурсы, которые можно использовать для вывода в произвольное количество других средств. С учетом нашего неограниченного запроса это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечно. Если вы видите сообщение «Установить значения не сходятся», это означает, что в модели есть ошибка.
-
Предположим, в нашей компании в течение часа можно приобретать до 500 часов работы на 100 рублей больше, чем за текущие трудоемкие расходы. Как максимально увеличить прибыль?
-
На изготовителе микросхем четыре технических специалиста (A, B, C и D) выпускают три продукта («Товары 1», «2» и «3»). В этом месяце изготовитель микросхемы может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Специалист А может делать только продукты 1 и 3. Специалист Б может делать только продукты 1 и 2. Специалист C может сделать только продукт 3. Специалист D может сделать только продукт 2. Для каждого произведенного товара внести следующую прибыль: Товар 1; 600 рублей; Товар 2; 7000 рублей; и товар 3, 1000 рублей. Время (в часах) каждого технических специалиста, необходимое для производства продукта, должно быть следующим:
Продукт
Специалист А
Специалист Б
Специалист C
Специалист Д
1
2
2,5
Не удается сделать
Не удается сделать
2
Не удается сделать
3
Не удается сделать
3,5
3
3
Не удается сделать
4
Не удается сделать
-
Каждый специалист может работать до 120 часов в месяц. Как изготовитель микросхем может максимально увеличить ежемесячную прибыль? Предположим, что можно получить лишь дробное количество единиц.
-
Компьютерный завод производит мыши, клавиатуры и игровые joysticks. Доход за единицу, за единицу трудоемких ресурсов, ежемесячная потребность и за единицу машинного времени даются в следующей таблице:
Мыши
Клавиатуры
Joysticks
Прибыль/единица
8 $
11 $
9 $
Использование трудов и единицы
0,2 часа
0,3 часа
0,24 часа
Машинное время/единица
0,04 ч
0,055 ч.
0,04 ч
Ежемесячный запрос
15 000
27,000
11,000
-
Каждый месяц доступно 13 000 часов труда и 3000 часов машинного времени. Как изготовитель может максимально увеличить ежемесячный взнос в прибыль от растения?
-
Допустим, необходимо устранить проблему с этой проблемой при условии, что должны быть выполнены минимальные требования к 200 единицам для каждого из них.
-
Он делает ромбовидные ромбои, окаймлы и затейные. Он хочет работать не более 160 часов в месяц. У него 800 ромбов. Ниже дается прибыль, время труда и количество ромбов, необходимых для получения каждого товара. Если потребность в каждом продукте не ограничена, как Максим может увеличить прибыль?
Продукт
Прибыль за единицу
Трудоемкие часы на единицу
Ромбы на единицу
Лексема
300р.
.35
1,2
Кулигов
200 ₽
.15
.75
Кулигов
100р.
0,05
.5
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Содержание
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
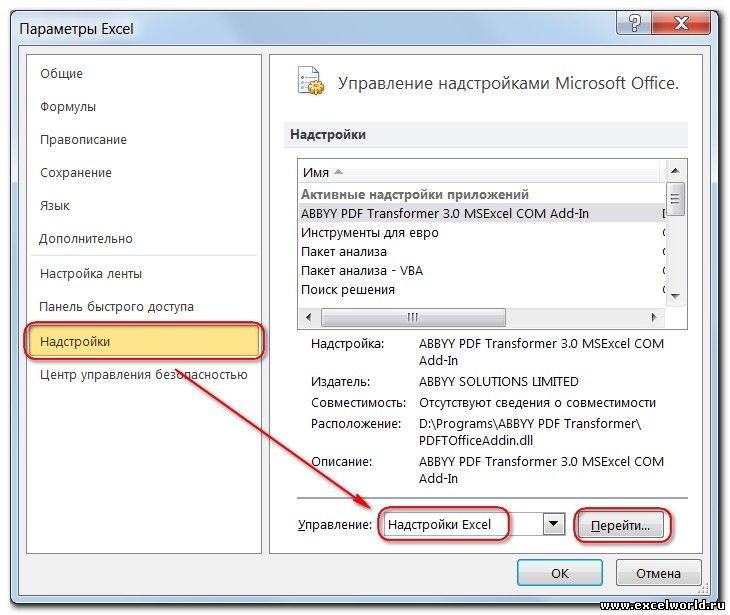
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
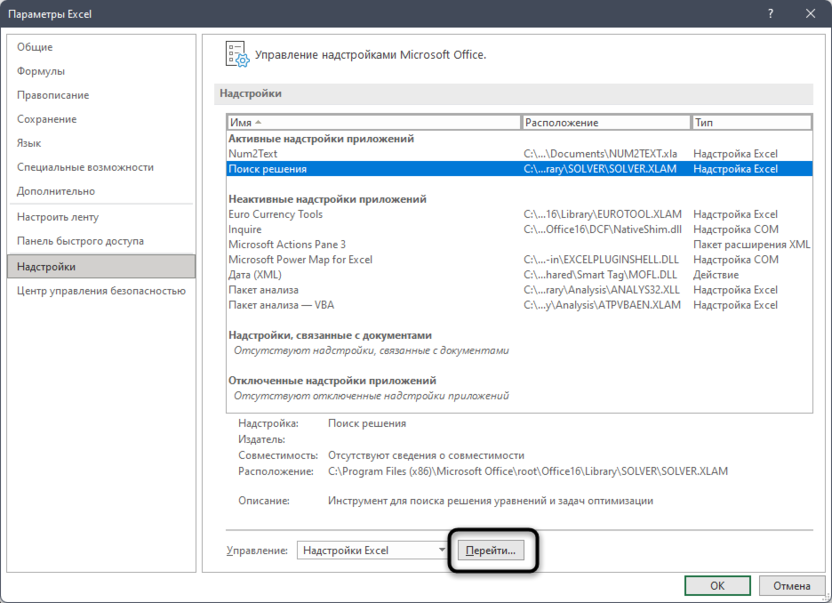
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
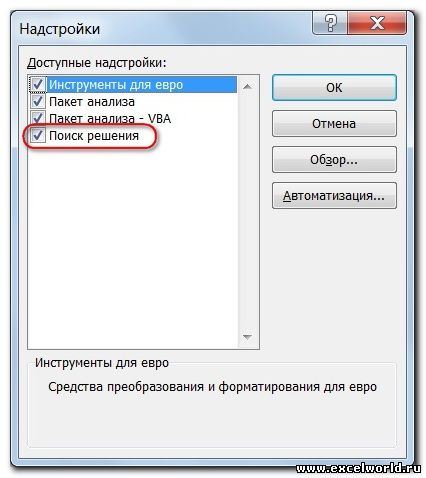
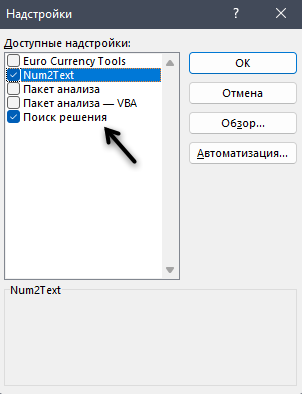
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
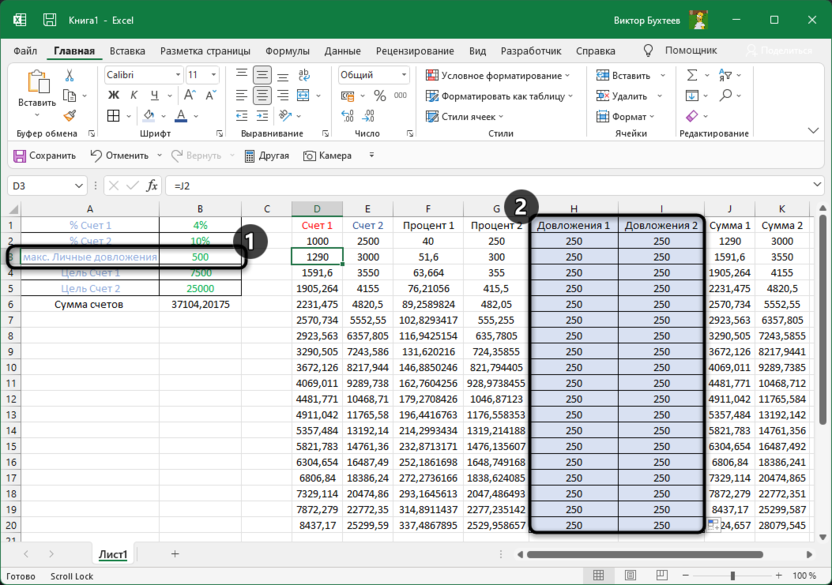
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
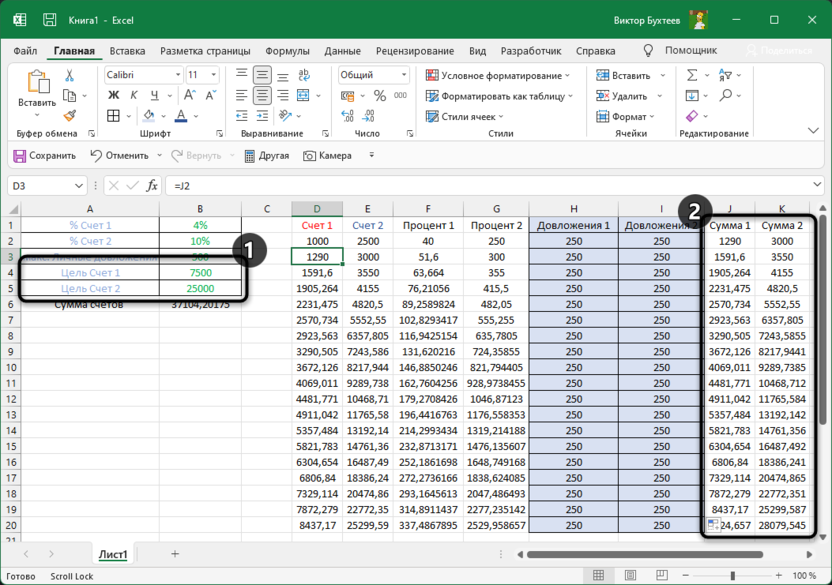
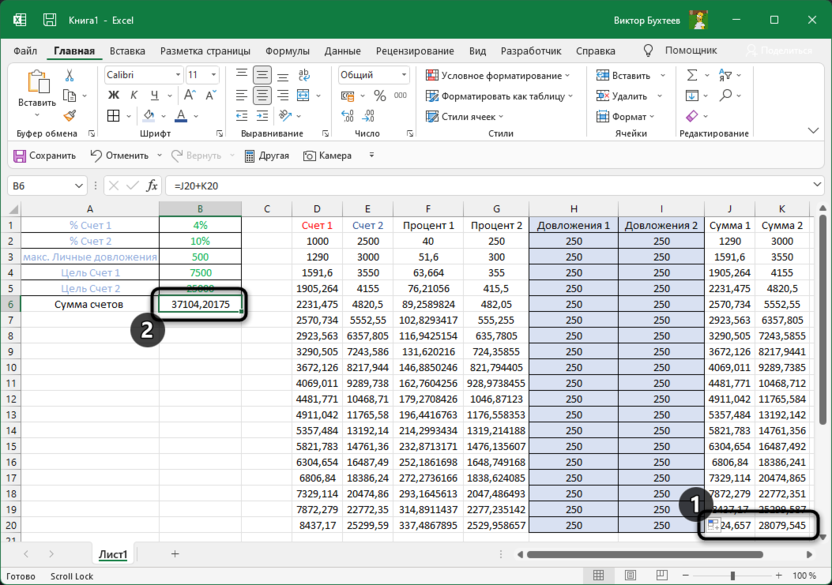
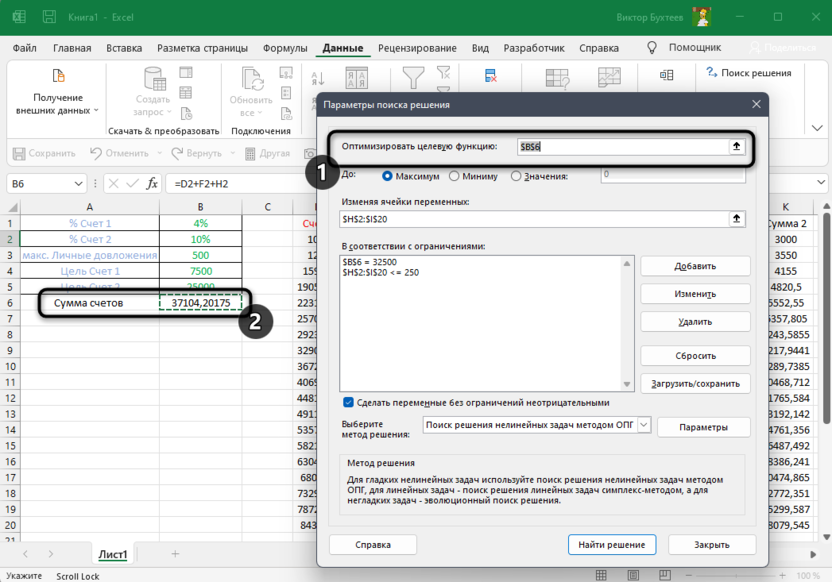
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
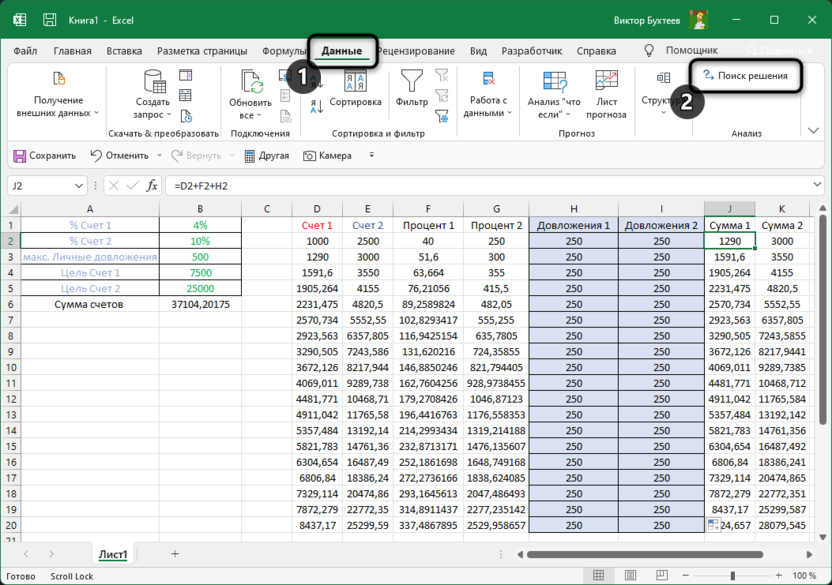
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
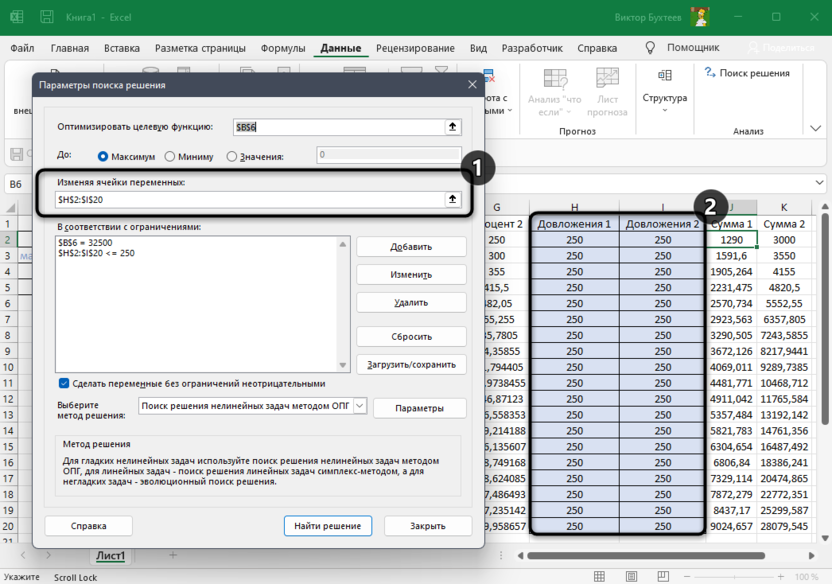
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
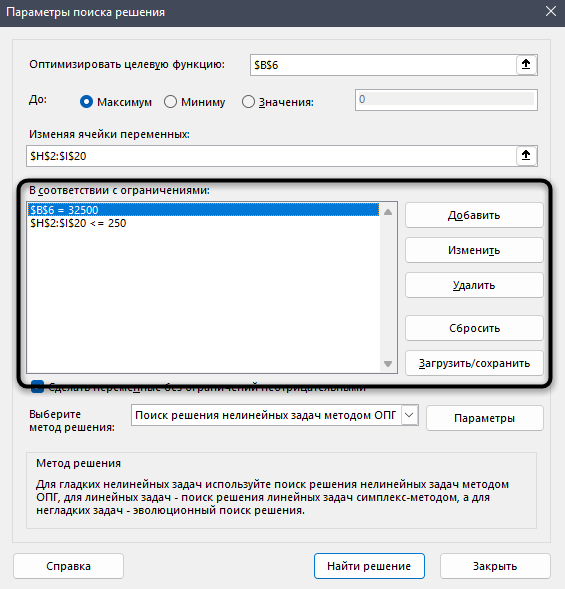
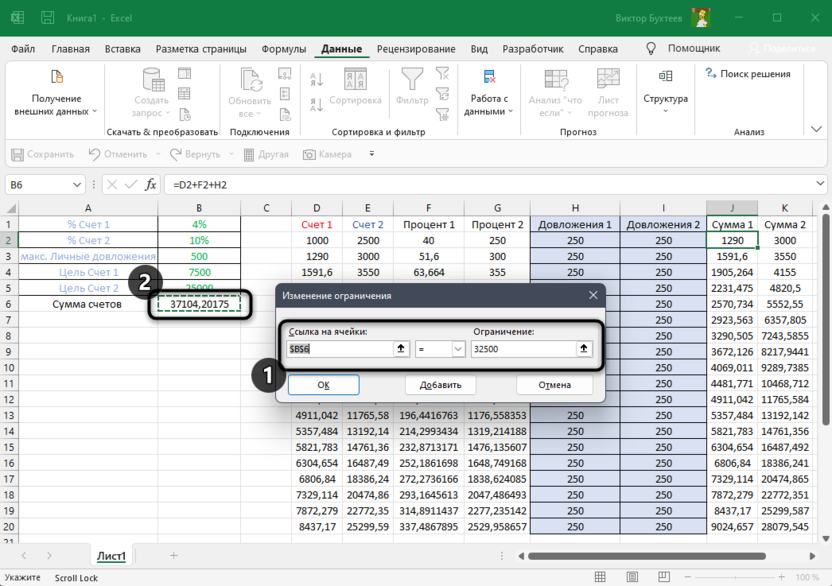
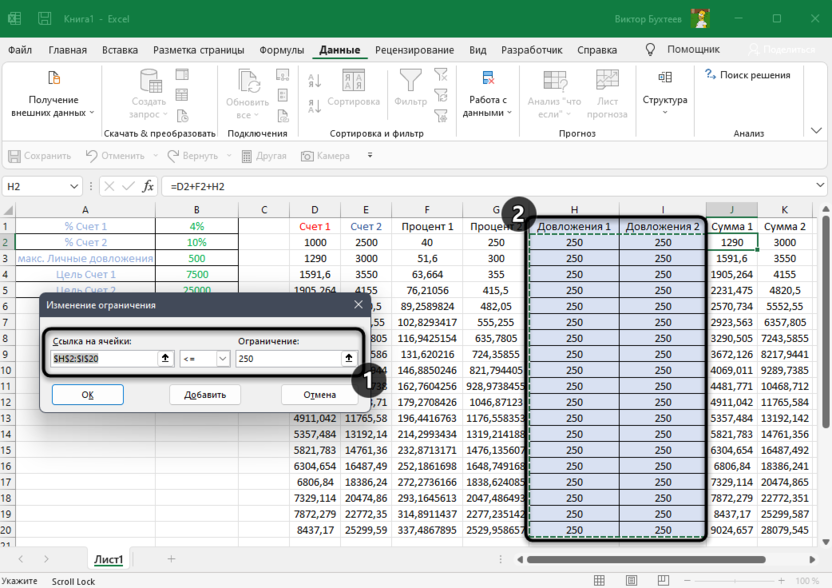
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
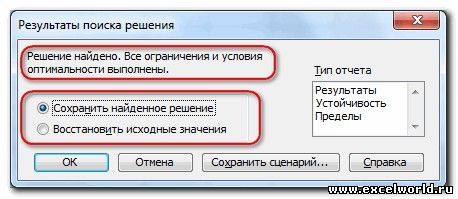
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
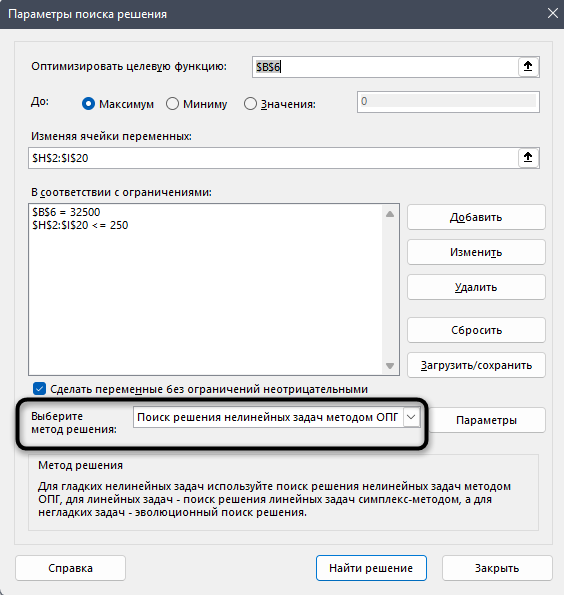
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
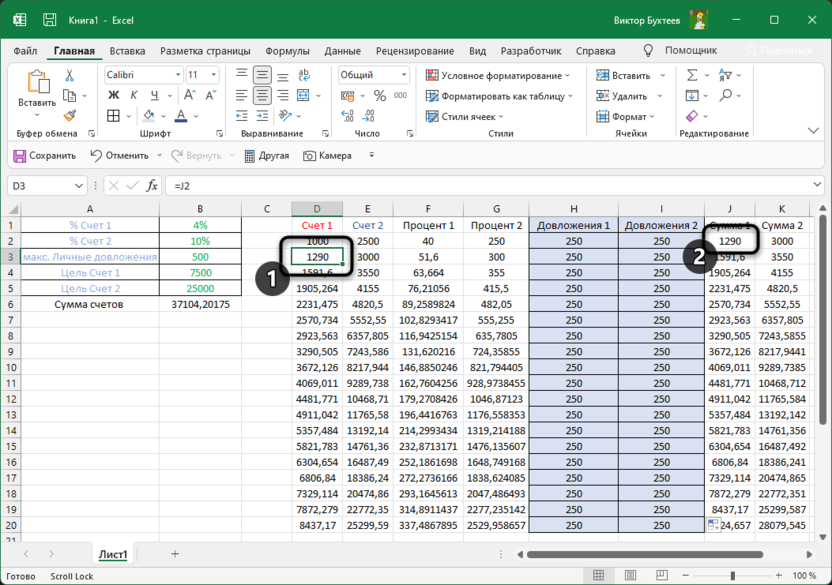
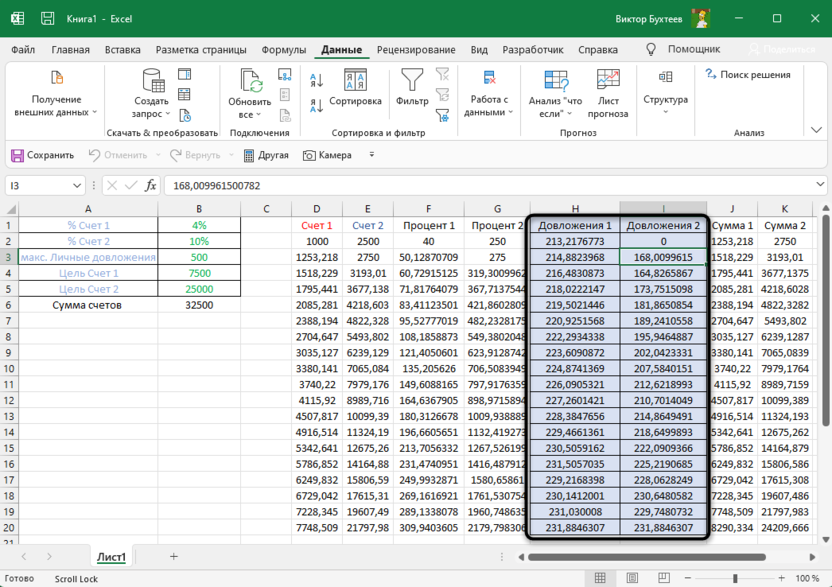
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.
В данной статье рассматривается расчет инструмента Excel «Поиск решений». Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья и штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы.
Зачастую экономисты в своей практике встречаются с вопросами оптимизации расходов.
Рассмотрим пример оптимизации транспортных расходов с помощью инструмента Excel «Поиск решений».
Пример 1
На предприятии X осуществляются транспортные перевозки с помощью четырех компаний до пяти населенных пунктов. Руководство компании решило распределить все количество перевозок между поставщиками транспортных услуг (транспортными компаниями) в определенной пропорции, выраженной в процентном соотношении — удельный вес в общем количестве перевозок. Известны также тарифы транспортных компаний за одну ездку и количество плановых перевозок до каждого населенного пункта в планируемом периоде .
Необходимо оптимально распределить ездки в населенные пункты между транспортными компаниями таким образом, чтобы транспортные расходы были минимальными.
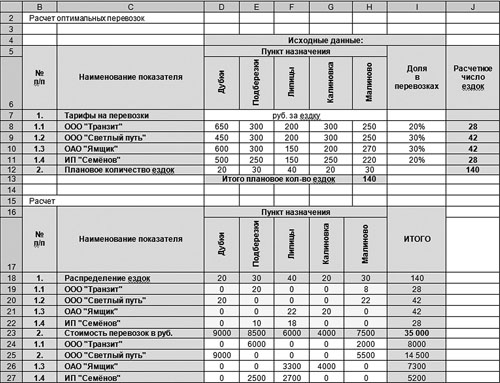
Для успешного решения этой задачи необходимо выбрать минимизируемую ячейку, определить ограничения, а также правильно сформировать таблицы с исходными и расчетными данными (рис. 1).
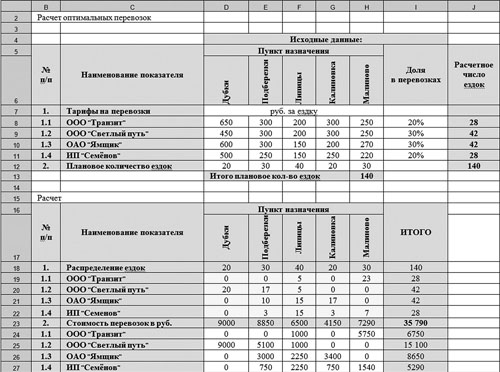
Рис. 1. Расчет оптимальных перевозок
На рис. 1 расположены две таблицы: с исходными данными и расчетными данными. В ячейках D8:H11 расположены тарифы за 1 ездку в разрезе транспортных компаний до пунктов назначения, в ячейках D12:H12 — плановое количество ездок за период до пунктов назначения, в ячейках I8:I11 — удельный вес перевозок каждой транспортной компании в общем количестве планируемых перевозок за период. Эти ячейки для удобства не раскрашены. В ячейках J8:J12 и Н13 рассчитано число ездок по каждой транспортной компании и в целом за период. Формулы в этих ячейках выглядят следующим образом:
Ячейка Н13: =СУММ(D12:H12),
Ячейка J8: =I8*$H$13.
Данную формулу из ячейки J8 протаскиваем (копируем) в ячейки J9, J10, J11.
Ячейка J12: =СУММ(J8:J11).
Следующая таблица на листе посвящена расчету и называется «Расчет». Ячейки D19:Н22 предназначены для распределения количества ездок до пунктов назначения между транспортными компаниями. На рис. 1 в ячейках дано такое распределение, заполненное вручную. В ячейках D23:I27 рассчитаны суммы расходов на транспортные перевозки в разрезе транспортных компаний, оказывающих транспортные услуги, и пунктов назначений, а также итоги.
Приведем формулы, представленные в этих ячейках.
Значения в ячейках D24:Н27 получены перемножением количества ездок (ячейки D19:Н22) на тарифы (ячейки D8:Н12). В ячейку D24 запишем формулу:
=D19*D8.
Протащим (скопируем) формулу в ячейки D25:D27 и E24:Н27.
В ячейках D23:I23 формируются итоговые суммы транспортных услуг в разрезе пунктов назначения. Запишем в ячейку D23 формулу:
=СУММ(D24:D27).
Протащим (скопируем) эту формулу в ячейки Е23:I23.
В ячейках I24:I27 формируются итоговые суммы транспортных услуг в разрезе компаний, оказывающих эти услуги. Запишем в ячейку I24 формулу:
=СУММ(D24:H24).
Протащим (скопируем) ее в ячейки I25:I27.
Таким образом, стоимость транспортных расходов по компании в целом формируется в ячейке I23. В первоначальном расчете, представленном на рис. 1, данная сумма равна 35 790 руб.
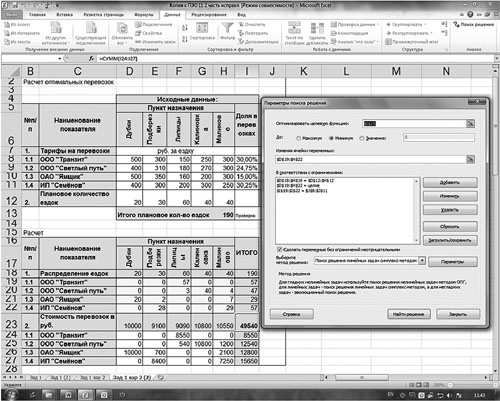
Скопируем данный лист в эту же книгу. Далее необходимо приступить непосредственно к оптимизации. Задача — подобрать в ячейках D19:Н22 такие значения, чтобы в ячейке I23 была рассчитана минимальная сумма расходов на транспорт. Для этого воспользуемся инструментом «Поиск решений».
Для начала надо выбрать оптимизируемую ячейку (I23). Затем вызовем диалоговое окно «Поиск решений», представленное на рис. 2.
Это важно. Надстройку «Поиск решений» не всегда можно обнаружить в меню рабочего стола компьютера, так как она может быть не подключена. Для ее подключения необходимо выполнить ряд действий, которые аналогичны во всех версиях MS Office: «Сервис — Надстройки — Поиск решений (установить флажок)». Теперь данный инструмент можно будет найти на панели инструментов рабочего стола.
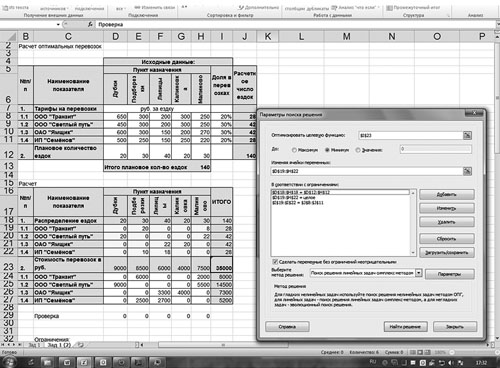
Рис. 2. Использование надстройки «Поиск решений»
В строке «Оптимизировать целевую функцию» будет стоять адрес оптимизируемой ячейки, в данном случае — $I$23. Выберем цель, поставив флажок «Минимум». В строке «Изменяя ячейки переменных» помещаются адреса ячеек, которые необходимо будет подобрать для достижения желаемого результата ($D$19:$Н$22).
В поле запишем ограничения в соответствии с ограничениями. Для этого воспользуемся кнопкой «Добавить», которая откроет окно «Добавить ограничения». Введем одно из ограничений:
$D$19:$H$22 = целое,
$D$12:$H$12 = $D$18:$H$18,
$J$8:$J$11 = $I$19:$I22.
Чтобы добавить следующее ограничение, в этом же окне нажмите на кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, а поля окна «Добавить ограничения» будут очищены для ввода следующего ограничения. После того как введено последнее из ограничений, необходимо нажать на кнопку «ОК».
Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.
В данном примере все ограничения представлены в виде равенств. Но существуют задачи, в которых требуются ввести ограничения в виде неравенств. Например, в транспортных компаниях объем перевозимого груза не может превышать грузоподъемности автомобиля (или время работы автотранспортного средства не может превышать количества часов в сутки за вычетом нормативных простоев).
Очень важно правильно сформулировать ограничения. Для того чтобы не забыть ни одно из ограничений, необходимо правильно поставить задачу и определить ее цели. Не бывает мелочей в постановке задачи. В задаче о поставке деталей необходимо учесть, что количество деталей на складе на начало периода плюс количество поступивших за планируемый период деталей должно равняться сумме их остатка на складе на конец периода плюс количество отгруженных деталей за планируемый период. Или, например, количество деталей на начало планируемого периода должно равняться количеству деталей на конец периода, предшествующему планируемому.
Необходимо также помнить о том, что некоторые показатели могут быть только положительными значениями (например, сумма поступления от покупателя на расчетный счет поставщик). В данном случае в ограничениях целесообразно указать, что эта величина не может быть отрицательной, иначе надстройка «Поиск решений», вполне возможно, предложит в качестве решения отрицательное число.
Далее следует выбрать метод решения. Для этого необходимо определить, является модель линейной или нелинейной. Напомним, что линейной моделью является такая модель, связи в которой между данными для расчета и результирующим показателем можно описать линейными функциями. Линейная функция имеет следующий вид:
F(x) = a1 × x1 + а2 × x2 + … + аn × xn,
где a1, а2, …, аn — константы;
x1, x2, …, xn — переменные.
Данная модель является линейной.
Примером нелинейной модели является оптимизация перевозок с целью минимизации расходов, когда тарифы на перевозки распределены по интервалам:
- от 0 до 10 км — стоимость перевозки 200 руб.;
- от 11 до 20 км — стоимость перевозки 250 руб.;
- от 21 до 50 км — стоимость перевозки 500 руб. и т. д.
Вернемся к диалоговому окну «Параметры поиска решений». Далее нажимаем кнопку «Найти решение», в результате чего появится окно с результатом поиска решения. Так как нам необходимо сохранить найденный результат, то ставим флажок «Сохранить найденное решение», в результате чего на нашем листе сохранится найденное решение. Нажмем кнопку «ОК».
В ячейках $D$19:$Н$22 появляются подобранные системой значения, при которых в ячейке I23 формируется минимальное значение стоимости транспортных услуг — 35 000 руб.
В данном случае отклонения от подобранного нами вручную результата составляют лишь 2,2 %, или 790 руб., но это означает лишь то, что мы вручную удачно подобрали решение.
На рис. 3 представлены полученные при оптимизации данные.
Рис. 3. Результаты оптимизации
Для того чтобы использовать ссылки на ячейки в составе сценария, необходимо сохранить этот сценарий, нажав на кнопку «Сохранить сценарий» в окне «Результат поиска решения», введя имя сценария и нажав кнопку «ОК». При этом исходные данные сохраняются.
Таким образом, предоставлена возможность сохранить все варианты решений при изменении исходных данных. Затем можно создавать отчеты, по которым можно сравнивать влияние изменений исходных данных и ограничений на результат решения.
Существует одна важная деталь: при расчетах количества ездок лучше всего в ячейках J8:J11 использовать функцию округления, чтобы значения были целыми числами.
По этому случаю рассмотрим пример с другими исходными данными.
Пример 2
В ячейках J8:J11 запишем формулу, позволяющую округлить вычисляемые значения до целого числа, которая имеет вид:
Ячейка J8: =ОКРУГЛ(I8*$H$13;0).
Протащим (скопируем) эту формулу в ячейки J9:J11.
Как видим (рис. 4) плановое количество ездок в ячейке Н13 отличается от суммы в ячейках J8:J11, записанной в ячейке J12: значение в ячейке J12, полученное в результате суммирования округленных результатов расчетов числа ездок в ячейках J8:J11, не равно значению в ячейке Н13, полученному суммированием планового числа ездок до пунктов назначения. Это издержки примененной функции округления. Для того чтобы избежать данной ошибки, проделаем следующую процедуру. Для контроля и удобства вычислений введем проверочную ячейку J13. Формула в этой ячейке будет представлять собой разницу полученных значений в ячейках J12 и H13. Ячейка понадобится нам для коррекции вычислений.
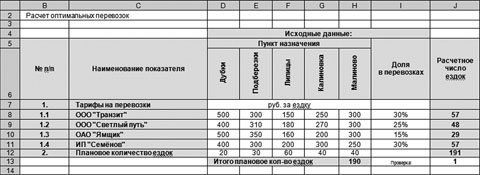
Рис. 4. Пример с функцией округления расчетного числа ездок до целого числа
Используем для коррекции инструмент «Подбор параметра». Процедура подбора иллюстрируется на рис. 5.
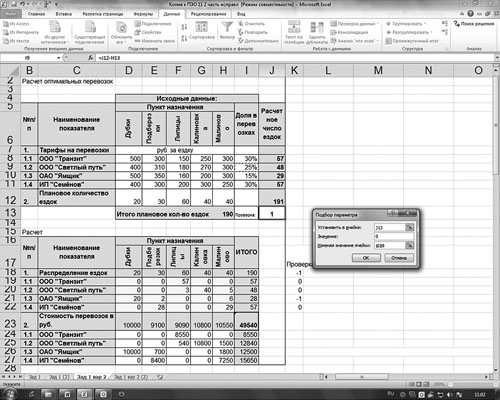
Рис. 5. Использование инструмента «Подбор параметра»
Здесь необходимо применить следующую схему: подобрать в ячейке J13 значение равное 0, изменяя значение в ячейке I9 (доля в перевозках). Предварительно в ячейку I11 целесообразно ввести следующую формулу:
=100 % – I8 – I9 – I10.
Тогда при изменении значения в ячейке I9 в результате применения инструмента «Подбор параметра» автоматически изменится и значение в ячейке I11.
Так как в ячейках I8:I11 применено округление до целого значения, изменения в ячейках I9 и I11 на 0,25 % не обнаруживаются. Эти изменения будут видны, если мы добавим знаки после запятой.
Результат применения инструмента «Подбор параметра» приведен на рис. 6 (на с. …).
Необходимо проделать процедуры, что и в предыдущем примере (см. рис. 1, 2, 3). В ячейках D19:H22 распределим количество ездок для каждой транспортной компании до каждого пункта назначения, используя следующие ограничения:
D19:H22 = целое,
D12:H12 = D18:H18,
J8:J11 = I19:I22.
Сумма транспортных расходов в ячейке I23 на рис. 6 рассчиталась равной 49 540 руб., а наша задача — минимизировать ее.
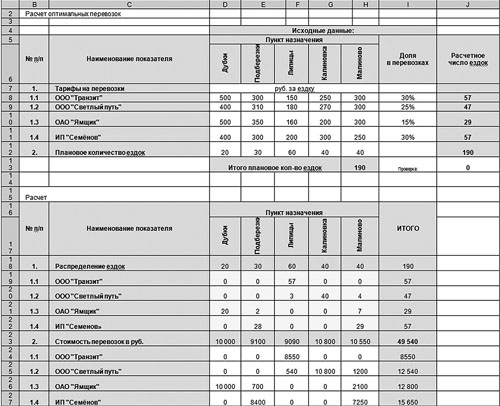
Рис. 6. Скорректированный вариант
На рис. 7 представлена демонстрация использования инструмента «Поиск решений» для оптимизации результата.
Рис. 7. Минимизация значения в ячейке I23 с помощью надстройки «Поиск решения»
На рис. 8 в ячейках D19:Н22 представлены данные, полученные в ходе оптимизации с помощью инструмента «Поиск решений». В результате минимизации в ячейке I23 получено значение 44 990 руб. Отклонения от достигнутого при первоначальном распределении результата составило 9 %, или 4550 руб.
Возможно, имеет право на существование такой вопрос: «Для чего нужна табличная часть со стоимостями перевозок в разрезе транспортных компаний и пунктов назначений?». Ведь можно было бы просто в итоговую ячейку I23 ввести формулу:
=СУММПРОИЗВ(D8:D11;D19:D22)+СУММПРОИЗВ(E8:E11;E19:E22)+СУММПРОИЗВ(F8:F11;F19:F22)+СУММПРОИЗВ(G8:G11;G19:G22)+СУММПРОИЗВ(H8:H11;H19:H22).
Следует помнить следующее:
- строк и столбцов может быть достаточно большое количество. Это значит, что написание самой формулы в ячейках будет слишком трудоемкой задачей;
- потеряется возможность анализа данных по компаниям и пунктам назначения. Значит, целесообразнее использовать вспомогательную таблицу (в нашем примере это ячейки B23:I27), которая содержала бы множество простых формул. Эти формулы записываются всего в два мгновения: запись в одной из ячеек и копирование или протаскивание в остальные ячейки. Такая таблица несет в себе полезную для анализа информацию о стоимости транспортных услуг в разрезе перевозчиков и пунктов назначения.
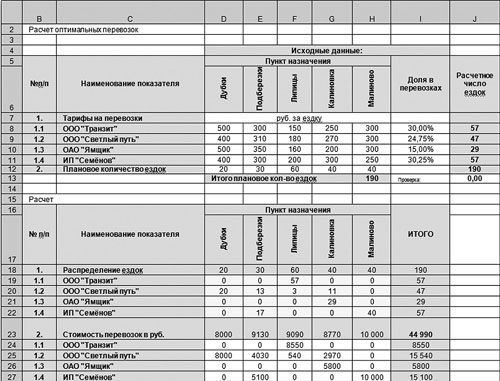
Рис. 8. Результат оптимизации примера с округлением
Заключение
В данной статье рассмотрена простейшая задача, цель статьи — побудить экономистов использовать в расчетах инструмент Excel «Поиск решений», который удобен и прост в применении. Освоив и поняв данный инструмент, можно будет переходить к более сложным задачам.
Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.
Статья опубликована в журнале «Планово-экономический отдел» № 11, 2012.
Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.
Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых «задач оптимизации».
Если Вы раньше не использовали Поиск решения, то Вам потребуется установить соответствующую надстройку.
Сделать это можно так:
для версий старше Excel 2007 через команду меню Сервис —> Надстройки;
начиная с Excel 2007 через диалоговое окно Параметры Excel
Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные.
В версиях до Excel 2007 аналогичная команда появится в меню Сервис
Разберём порядок работы Поиска решения на простом примере.
Пример 1. Распределение премии
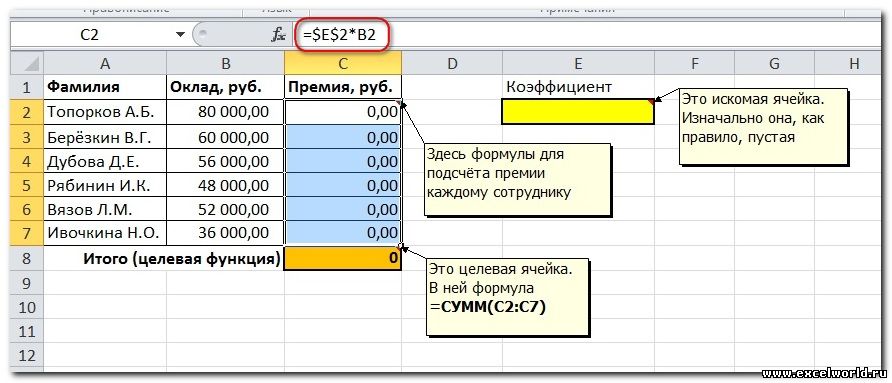
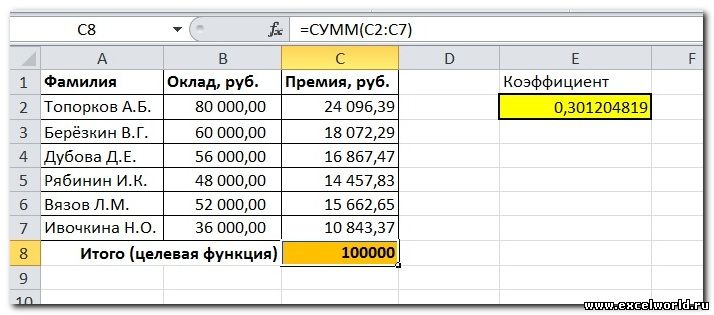
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
Начиная с Excel 2010
До Excel 2010
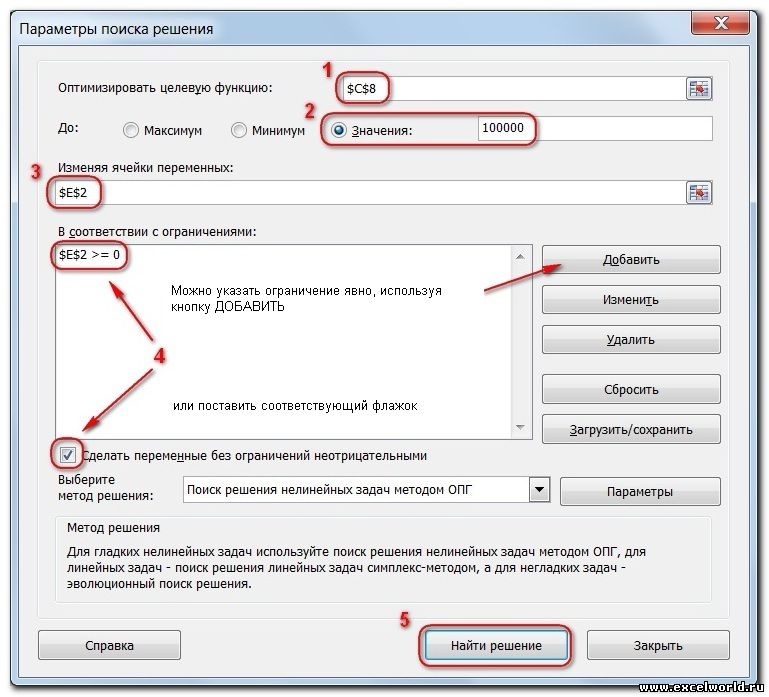
- Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
- Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
- Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
- Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии Excel 2010).
В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
- Кнопка, включающая итеративные вычисления с заданными параметрами.
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
До Excel 2010
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
Разберём еще одну задачу оптимизации (получение максимальной прибыли)
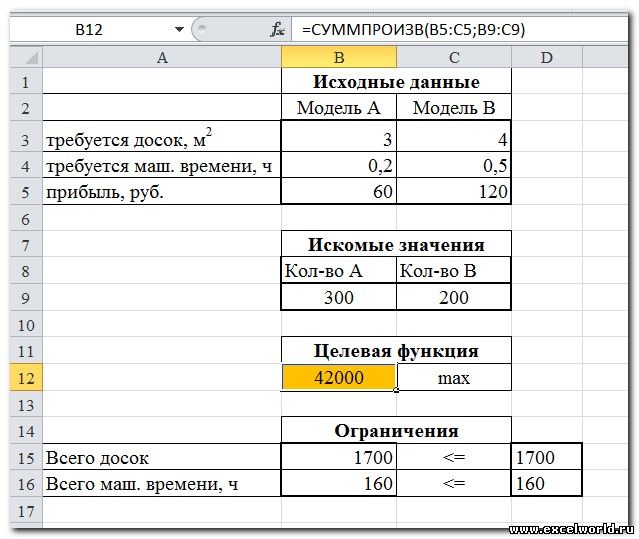
Пример 2. Мебельное производство (максимизация прибыли)
Фирма производит две модели А и В сборных книжных полок.
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.
Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?
Порядок действий нам уже известен.
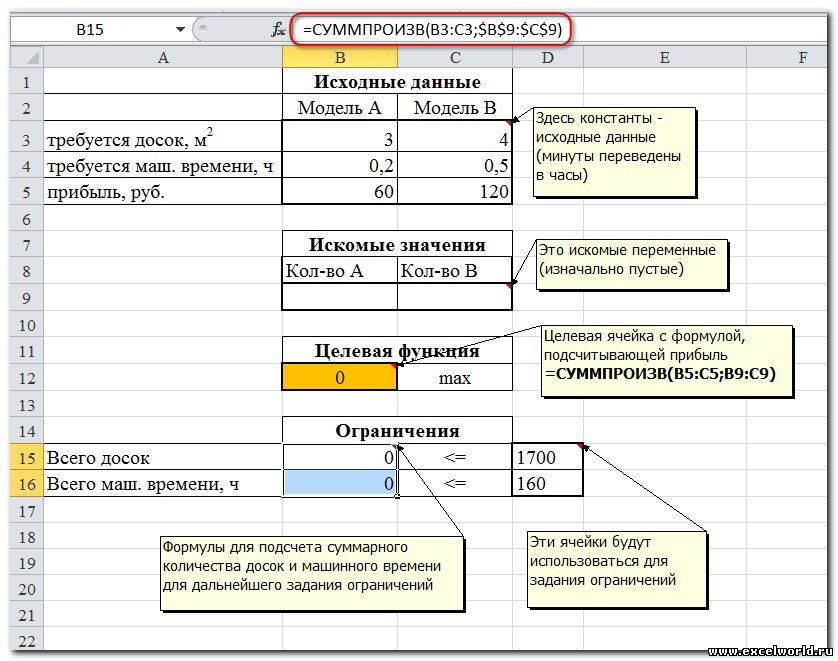
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке
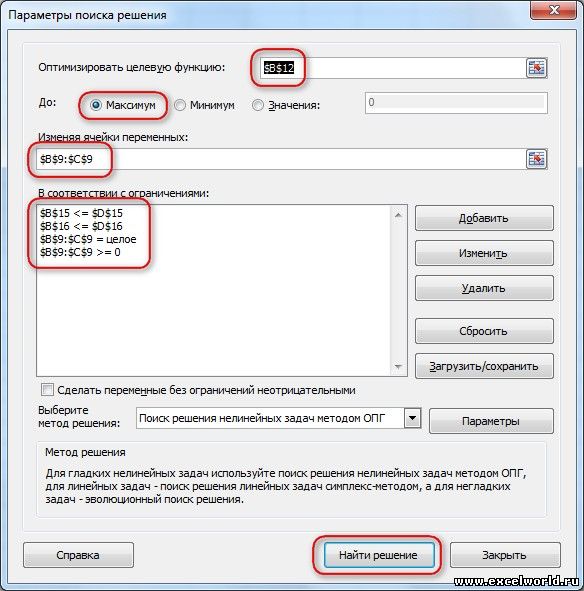
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры
- Целевая ячейка B12 содержит формулу для расчёта прибыли
- Параметр оптимизации — максимум
- Изменяемые ячейки B9:C9
- Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
- Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
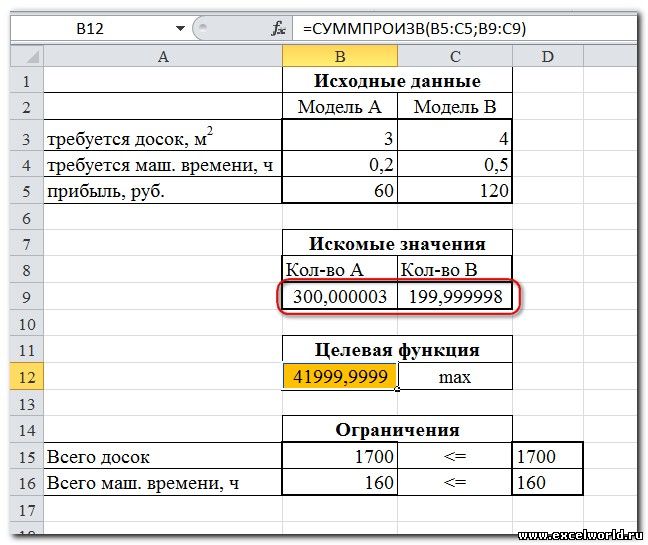
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:
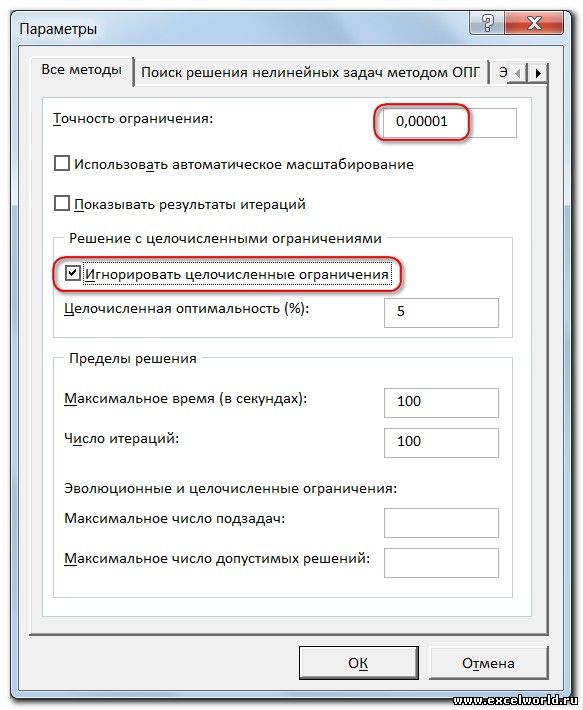
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.
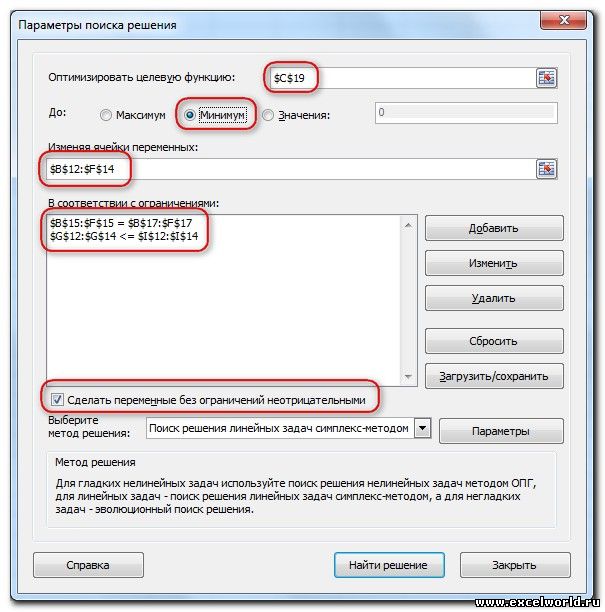
Пример 3. Транспортная задача (минимизация затрат)
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.
Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».
Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.
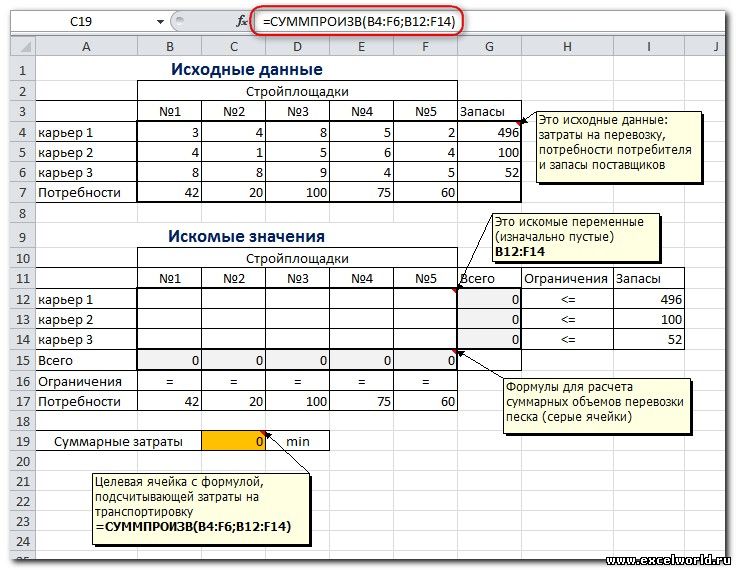
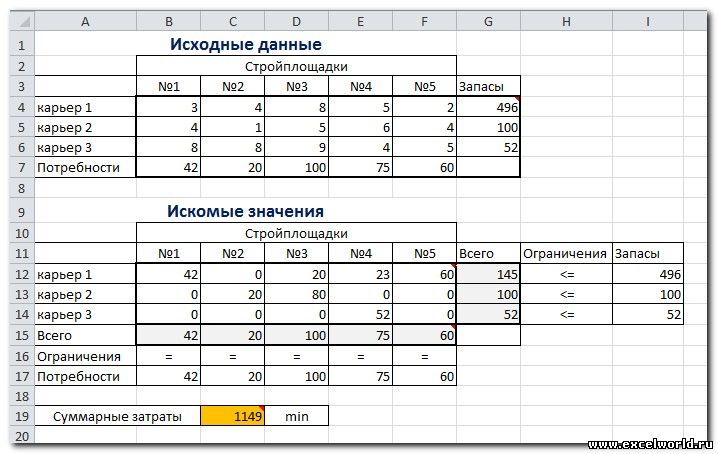
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже
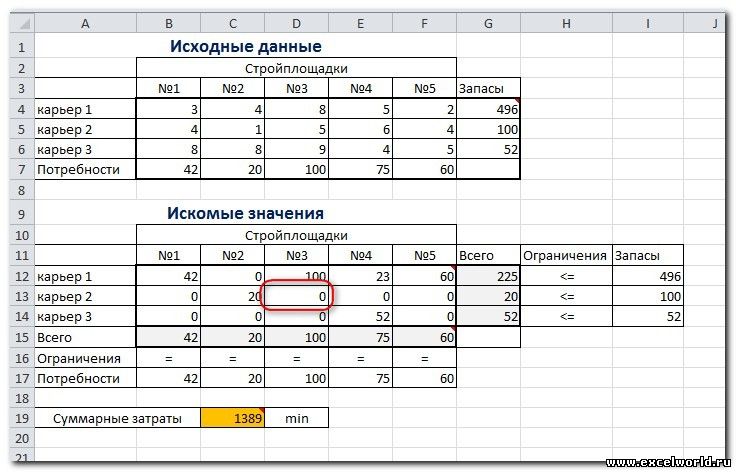
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат
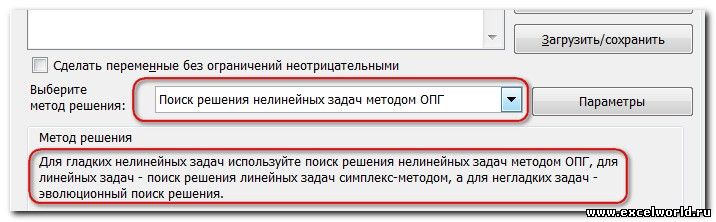
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения
Начиная с Excel 2010
До Excel 2010
В заключение предлагаю попробовать свои силы в применении Поиска решения и решить с его помощью старинную задачу:
Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек. Сколько быков, коров и телят купил крестьянин?
Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:
- В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
- В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.
С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.
Каждый отчет создается на отдельном листе текущей рабочей книги.
Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).
- Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
- Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
- Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.
Рассмотрим применение процессора Excel для решения ЗЛП на примерах.
Задача 1. Планирование производства
Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.
МП выпускает товары х1,х2,х3,х4, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.
| Затраты | х1 | х2 | x3 | х4 | Всего |
|---|---|---|---|---|---|
| Трудовые | 1 | 1 | 1 | 1 | 16 |
| Сырьевые | 6 | 5 | 4 | 1 | 110 |
| Финансы | 4 | 6 | 10 | 13 | 100 |
- Максимум прибыли в зависимости от оптимального распределения затрат.
- Минимум ресурсов, необходимых для получения максимальной прибыли.
Решение задачи средствами Excel состоит из 4 этапов:
- Создание математической модели задачи ЛП.
- Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
- Ввод данных из формы в окно Excel Поиск решения из меню Данные.
- Задание параметров поиска и решение задачи.
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:
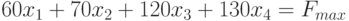
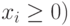
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.
Создание формы
- Составление формы в виде:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | х7 | х2 | x3 | х4 | Формула | Знак | Св.член |
| 2 | Значение | |||||||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | =СУММПРОИЗВ(В$2:Е$2;В3:Е3) | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | =СУММПРОИЗВ(В$2:Е$2;В4:Е4) |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | =СУММПРОИЗВ(В$2:Е$2;В5:Е5) |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | =СУММПРОИЗВ(В$2:Е$2;В6:Е6) |  |
100 |
- Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
- Ввод формул с помощью fx – Мастера функций.
Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций fx на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х1..х4), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).
Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.
Нажать клавишу ОК, в ячейку F3 запишется формула 60х1+70х2+120х3+ 130х4 в виде СУММПРОИЗВ(В2:Е2;В3:Е3).
Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:
После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.
В результате копирования мы увидим следующие формулы:
- в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
- в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
- в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).
Заполнение окна Поиск решения
Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).
Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак «
Аналогично через «Добавить» ввести 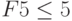
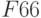
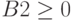
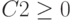
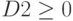
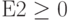
Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.
После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».
Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.
Параметры поиска
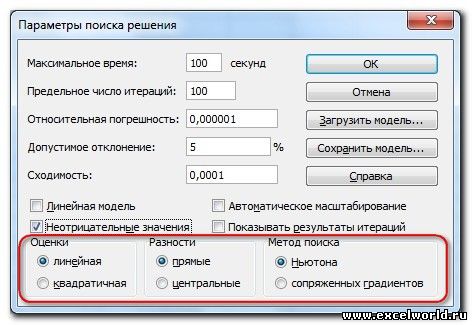
В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).
Результаты поиска решения с таблицей результатов:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | X1 | X2 | X3 | X4 | Формула | Знак | Св.член |
| 2 | Значение | 10 | 0 | 6 | 0 | |||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | 1320 | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | 16 |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | 84 |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | 100 |  |
100 |
Таким образом оптимальный план Х(Х1,Х2,Х3,Х4)=(10,0,6,0) при минимальном использовании ресурсов
- Трудовые – 16 (У1)
- Сырьевые – 84 (У2)
- Финансы – 100 (У3)
даёт максимум прибыли F в 1320 руб.
Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х1 и Х3 в количестве 10 и 6 штук соответственно, товары Х3 и Х4 выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У1) и финансовые (У3) ресурсы используются полностью, по сырьевым ресурсам (У2) есть запас в 110-84=26 ед.
Кроме того, это означает, что изменение трудовых ( y1 ) и финансовых ( y3 ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y2 ) – нет.
Разности между плановыми ресурсами и использованными являются двойственными переменными y1, y2 и y3 сопряжённой задачи линейного программирования. В данном случае y1=y3=0 , а y2=26 ед. Таким образом, ресурс y2 можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.
Задача 2. Задача об оптимальной диете
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.
Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:
где множество допустимых альтернатив 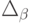
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.
Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).
Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2= 70, в углеводах b3 = 400.
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 61 | 220 | 230 | 15 | 8 | 11 | 6 |
| Жиры | 12 | 172 | 290 | 1 | 1 | 2 | 2 |
| Углеводы | 420 | 0 | 0 | 212 | 26 | 38 | 155 |
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:

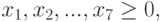
Создание формы
Для решения поставленной задачи выполним следующие подготовительные действия:
- Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
- В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с1 = 2060, с2 = 2430, с3 = 3600, с4 = 890, с5 = 140, с6 = 230, с7 = 650.
- В ячейку I2 введем формулу: =СУММПРОИЗВ( b 2:Н2;B3:H3), которая представляет целевую функцию (4).
- В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.
- В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b 1=100 , жирах b 2= 70 и углеводах b3 = 400.
- В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
- Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
- Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).
Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.
Заполнение окна Поиск решения
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.
После появления диалогового окна Поиск решения следует выполнить следующие действия:
- В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
- Для группы Равной: выбрать вариант поиска решения – минимальному значению.
- В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
- Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
- для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
- в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
- в качестве значения правой части ограничения выбрать ячейку $J$5 ;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
- аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).
Параметры
В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.
Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х1 = 0, х2 = 0,211, 3 = 0,109, х4= 1,887, х5 = 0, х6 = 0, х7 = 0, которым соответствует значение целевой функции: fопт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.
ЗАДАНИЕ
- Составить математическую модель задачи линейного программирования.
- Решить задачу линейного программирования в Excel с помощью Поиска решения.
- Сохранить в виде модели установочные параметры.
Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.
Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

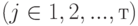
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 66 | 225 | 235 | 20 | 13 | 16 | 11 |
| Жиры | 17 | 177 | 295 | 1 | 1 | 7 | 7 |
| Углеводы | 425 | 0 | 0 | 217 | 31 | 43 | 200 |
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 105, в жирах b 2 = 75, в углеводах b 3 = 405.
Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.
Таблица 1. Расход химических веществ на изготовления клея, их запас на складе
| Вид клея /Химические вещества | Клей № 1 | Клей № 2 | Клей № 3 | Запас на складе |
|---|---|---|---|---|
| Крахмал | 0,4 | 0,3 | 0,2 | 20 |
| Желатин | 0,2 | 0,3 | 0,4 | 35 |
| Квасцы | 0,05 | 0,07 | 0,1 | 7 |
| Мел | 0,01 | 0,05 | 0,15 | 10 |
Стоимость каждого вида клея для оптовых покупателей следующая:с1 = 380 руб/кг,с2 =430 руб/кг,с3 = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.
Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с1 = 470,с2= 380,с3 = 350,с4 = 1460,с5 = 2150,с6 = 2070, с7 = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2 = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).
Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Поиск решения задач в Excel с примерами
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
источники:
http://intuit.ru/studies/courses/3659/901/lecture/32717
http://exceltable.com/vozmojnosti-excel/poisk-resheniya-v-excel
«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.
Основные параметры поиска решений
Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.
Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).
Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.
Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.
Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.
Пример использования поиска решений
Теперь перейдем к самой функции.
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.
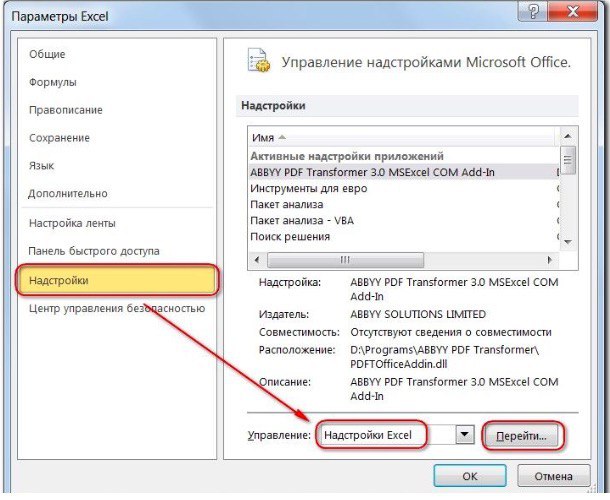
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».
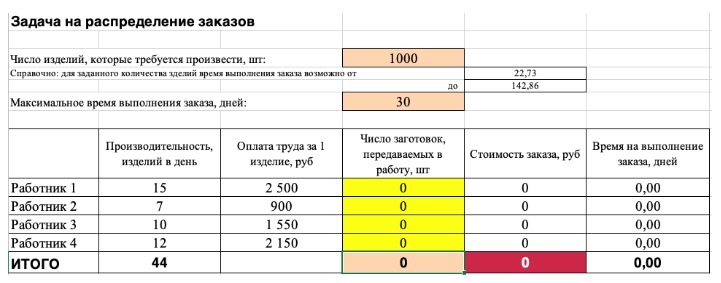
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
- количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).
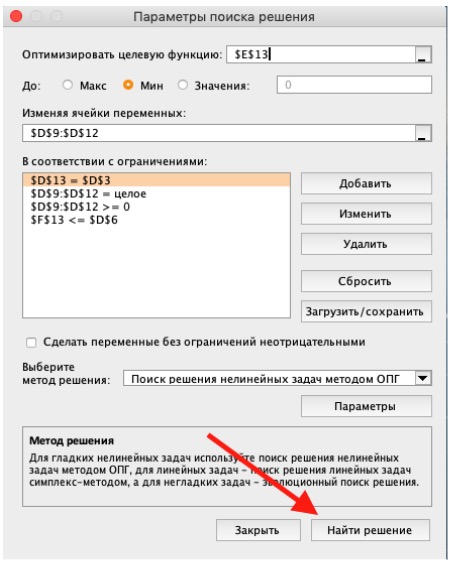
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.
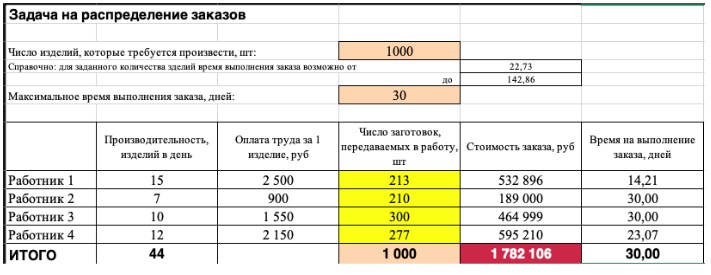
Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!
Для вызова программы
оптимизатора выберите команду меню
Сервис Поиск решения. Если команда Поиск
решения отсутствует в меню Сервис,
то надо установить эту надстройку.
Установка программы
Поиск решения
В меню Сервис
выберите команду Надстройки.
В диалоговом окне
Надстройки установите флажок Поиск
решения. Если диалоговое окно
Надстройки не содержит команду Поиск
решения, нажмите кнопку Обзор и
укажите диск и папку, в которых содержится
файл надстройки Solver.xla (как правило, это
папка LibrarySolver folder), или запустите
программу Setup, если найти файл не удается.
Надстройка,
указанная в диалоговом окне Надстройки,
остается активной до тех пор, пока
она не будет удалена.
Настройка
экономико-математической модели
Для обработки
таблицы Excel оптимизатором необходимо
вызвать его диалоговое окно Поиск
решения (рис. 5.1) и настроить
экономико-математическую модель. Отличие
экономико-математической постановки
задачи оптимизации в табличном процессоре
от традиционой экономико-математической
постановки состоит в том, что в формулах
задаются не символьные обозначения
переменных и параметров, а координаты
ячеек таблицы, в которых хранятся эти
переменные. Excel позволяет писать в
формулы символьные имена ячеек, но
программа Поиск решения в 70 % случаев
имена не воспринимает. Приходится
использовать координатные ссылки на
ячейки.
Поле Установить
целевую ячейку служит для указания
целевой ячейки, значение которой
необходимо максимизировать, минимизировать
или установить равным заданному
числу. Эта ячейка должна содержать
формулу. В нашем примере это ячейка D18
(Прибыль).
Кнопка Равной
служит для выбора варианта оптимизации
значения целевой ячейки (максимизация,
минимизация или подбор заданного числа).
Чтобы установить заданное число, введите
его в поле. В нашем примере для максимизации
прибыли мы нажимаем кнопку максимальному
значению.
Поле Изменяя ячейки
служит для указания ячеек, значения
которых изменяются в процессе поиска
решения до тех пор, пока не будут выполнены
наложенные ограничения и условие
оптимизации значения ячейки, указанной
в поле Установить целевую ячейку. В поле
Изменяя ячейки вводятся имена или адреса
изменяемых ячеек, разделяя их запятыми.
В нашем примере введен диапазон ячеек
D9:F9, содержащий искомые величины плана
производства продукции. Изменяемые
ячейки должны быть прямо или косвенно
связаны с целевой ячейкой. Допускается
установка до 200 изменяемых ячеек.
Поле Предположить
используется для автоматического поиска
ячеек, влияющих на формулу, ссылка на
которую дана в поле Установить целевую
ячейку. Результат поиска отображается
в поле Изменяя ячейки.
Поле Ограничения
служит для отображения списка граничных
условий поставленной задачи. В нашем
примере это величины диапазона расхода
комплектующих С11:С15. Они не должны
превышать запаса на складе В11:В15.
Команда Добавить
служит для отображения диалогового
окна Добавить ограничение.
Команда Изменить
служит для отображения диалогового
окна Изменение ограничения.
Команда Удалить
служит для снятия указанного курсором
ограничения.
Команда Выполнить
служит для запуска поиска решения
поставленной задачи.
Команда Закрыть
служит для выхода из окна диалога без
запуска поиска решения поставленной
задачи. При этом сохраняются установки,
сделанные в окнах диалога, появлявшихся
после нажатий на кнопки Параметры,
Добавить, Изменить или Удалить.
Кнопка Параметры
служит для отображения диалогового
окна Параметры поиска решения, в
котором можно загрузить или сохранить
оптимизируемую модель и указать
предусмотренные варианты поиска решения.
Кнопка Восстановить
служит для очистки полей окна диалога
и восстановления значений параметров
поиска решения, используемых по умолчанию.
Ввод и
редактирование ограничений
Диалоговые окна
изменения и добавления ограничений
одинаковы, рис. 5.2.
Выберите из
раскрывающегося списка условный
оператор, который необходимо разместить
между ссылкой и ее ограничением Это
знаки операторов не более, не менее,
равно и т д
В поле Ограничения
введите число, формулу или имя ячейки
или диапазона, содержащих или
вычисляющих ограничивающие значения.
Чтобы приступить
к набору нового условия, нажмите кнопку
Добавить
Чтобы вернуться
в диалоговое окно Поиск решения, нажмите
кнопку ОК
Условные операторы
целого и двоичного типа можно применять
только при наложении ограничений на
изменяемые ячейки.
Флажок Линейная
модель в диалоговом окне Параметры
поиска решения позволяет задать
любое количество ограничений При решении
нелинейных задач на значения изменяемых
ячеек можно наложить двоичное или
целочисленное ограничение с верхней,
нижней или обеими границами. Верхнюю,
нижнюю или обе границы допустимо наложить
только на 100 других ячеек. Когда не
хватает ячеек для ограничений, приходится
нелинейную модель преобразовывать
в линейную, например как в работе по
оптимальному планированию финансовых
портфелей банков.
Настройка параметров
алгоритма и программы
Настройка параметров
алгоритма и программы производится в
диалоговом окне Параметры поиска
решения, рис. 5.3.

окне устанавливаются ограничения на
время решения задач, выбираются
алгоритмы, задается точность решения,
предоставляется возможность для
сохранения вариантов модели и их
последующей загрузки Значения и состояния
элементов управления, используемые по
умолчанию, подходят для решения
большинства задач
Поле Максимальное
время служит для ограничения времени,
отпускаемого на поиск решения задачи
В поле можно ввести время (в секундах),
не превышающее 32 767; значение 100,
используемое по умолчанию, подходит
для решения большинства лабораторных
работ.
Поле Предельное
число итераций служит для управления
временем решения задачи, путем
ограничения числа промежуточных
вычислений. В поле можно ввести время
(в секундах), не превышающее 32 767; значение
100, используемое по умолчанию, подходит
для решения большинства простых задач.
При достижении
отведенного временного интервала или
при выполнении отведенного числа
итераций на экране появляется диалоговое
окно Текущее состояние поиска решения
Поле Относительная
погрешность служит для задания точности
(допустимой погрешности), с которой
определяется соответствие ячейки
целевому значению или приближение к
указанным границам. Поле должно содержать
число из интервала от
0 до 1. Низкая
точность соответствует введенному
числу, содержащему меньшее количество
десятичных знаков, чем число, используемое
по умолчанию, например 0,0001. Высокая
точность увеличит время, которое
требуется для того, чтобы сошелся процесс
оптимизации. Чем меньше введенное число,
тем выше точность результатов.
Поле Допустимое
отклонение служит для задания допуска
на отклонение от оптимального решения,
если множество значений влияющей ячейки
ограничено множеством целых чисел. При
указании большего допуска поиск
решения заканчивается быстрее.
Поле Сходимость
результатов поиска решения применяется
только к нелинейным задачам. Когда
относительное изменение значения в
целевой ячейке за последние 5 итераций
становится меньше числа, указанного в
поле Сходимость, поиск прекращается.
Условием сходимости служит дробь из
интервала от 0 до 1. Лучшую сходимость
характеризует большее количество
десятичных знаков, например 0,0001 — это
меньшее относительное изменение, чем
0,01. Чем меньше это значение, тем выше
точность результатов. Лучшая сходимость
требует больше времени на поиск
оптимального решения
Флажок Линейная
модель служит для ускорения поиска
решения линейной задачи оптимизации
или линейной аппроксимации нелинейной
задачи
Флажок Неотрицательные
значения позволяет установить нулевую
нижнюю границу для тех влияющих ячеек,
для которых она не была указана в поле
Ограничение диалогового окна Добавить
ограничение.
Флажок Автоматическое
масштабирование служит для включения
автоматической нормализации входных
и выходных значений, качественно
различающихся по величине, например
максимизация прибыли в процентах по
отношению к вложениям, исчисляемым в
миллионах рублей.
Флажок Показывать
результаты итераций служит для
приостановки поиска решения для
просмотра результатов отдельных
итераций.
Кнопки Оценки
служат для указания метода экстраполяции
(линейная или квадратичная), используемого
для получения исходных оценок значений
переменных в каждом одномерном поиске.
Линейная служит
для использования линейной экстраполяции
вдоль касательного вектора.
Квадратичная
служит для использования квадратичной
экстраполяции, которая дает лучшие
результаты при решении нелинейных
задач.
Кнопки Разности
(производные) служат для указания метода
численного дифференцирования (прямые
или центральные производные), который
используется для вычисления частных
производных целевых и ограничивающих
функций.
Прямые используются
для гладких непрерывных функций.
Центральные
используются для функций, имеющих
разрывную производную. Несмотря на
то что данный способ требует больше
вычислений, он может помочь при получении
итогового сообщения о том, что процедура
поиска решения не может улучшить текущий
набор влияющих ячеек.
Кнопки Метод поиска
служат для выбора алгоритма оптимизации
(метод Ньютона или сопряженных
градиентов).
Кнопка Ньютона
служит для реализации квазиньютоновского
метода, в котором запрашивается больше
памяти, но выполняется меньше итераций,
чем в методе сопряженных градиентов.
Здесь вычисляются частные производные
второго порядка.
Кнопка Сопряженных
градиентов служит для реализации метода
сопряженных градиентов, в котором
запрашивается меньше памяти, но
выполняется больше итераций, чем в
методе Ньютона. Данный метод следует
использовать, если задача достаточно
велика и необходимо экономить память,
а также если итерации дают слишком малое
отличие в последовательных приближениях.
Для решения линейных
задач используются алгоритмы симплексного
метода. Для решения целочисленных задач
используется метод ветвей и границ.
Команда Сохранить
модель служит для отображения на экране
диалогового окна Сохранить модель,
в котором можно задать ссылку на область
ячеек, предназначенную для хранения
модели оптимизации. Данный вариант
предусмотрен для хранения на листе
более одной модели оптимизации. Первая
модель сохраняется автоматически.
Команда Загрузить
модель служит для отображения на экране
диалогового окна Загрузить модель,
в котором можно задать ссылку на область
ячеек, содержащих загружаемую модель.
Сохранение и
загрузка модели
Обычно преподаватель
предлагает для лабораторных работ
разные варианты моделей. Работающий
экономист также варьирует модели:
расширяет, усложняет их. Поиск решения
предоставляет возможность сохранения
вариантов моделей и быстрой их загрузки.
Сохранение модели
оптимизации:
В меню Сервис
выберите команду Поиск решения.
Нажмите кнопку
Параметры.
Нажмите кнопку
Сохранить модель. Появляется окно
Сохранить модель, рис. 5.4.
В поле Задайте
область модели введите ссылку на верхнюю
ячейку столбца, в котором хотите
разместить модель оптимизации.
Значения элементов
управления диалоговых окон Поиск решения
и Параметры поиска решения записываются
на лист. Чтобы использовать на листе
несколько моделей оптимизации, нужно
сохранить их в разных диапазонах
(столбцах).
Предлагаемый
диапазон содержит ячейку для каждого
ограничения, а также еще 3 ячейки. Можно
также ввести ссылку только на верхнюю
ячейку столбца, в котором следует
сохранить модель.
Диалоговое окно
Загрузить модель используется для
задания ссылки на область загружаемой
модели оптимизации. Ссылка должна
адресовать область модели целиком,
недостаточно указать только первую
ячейку.
Загрузка модели
оптимизации
Перед тем как
использовать данную процедуру, необходимо
сохранить хотя бы одну модель.
В меню Сервис
выберите команду Поиск решения.
Нажмите кнопку
Параметры.
Нажмите кнопку
Загрузить модель. Появляется окно,
аналогичное окну Сохранить модель.
Введите ссылку на
область модели.
Диалоговое окно
Загрузить модель используется для
задания ссылки на область загружаемой
(ранее сохраненной) модели оптимизации.
Ссылка должна адресовать область модели
целиком, недостаточно указать только
первую ячейку.
Вычисления и
результаты решения задачи
Для запуска
оптимизатора нажмите кнопку Выполнить
в окне Поиск решения.
Программа начинает
работать, в строке сообщений (слева
внизу листа) появляется сообщение
Постановка задачи… Ваша таблица с
моделью и параметрами алгоритма
автоматически приводится к стандартам
постановки задач математического
программирования. Это преимущество
Excel. В других пакетах вам пришлось бы
оторваться от экономической сути задачи
и заниматься формальной математической
постановкой задачи. После этапа постановки
решается задача.
Чтобы прервать
поиск решения, нажмите клавишу Esc.
Microsoft Excel пересчитает лист с учетом
найденных значений влияющих ячеек.
По окончании счета
появляется диалоговое окно Результаты
поиска решения (рис. 5.5).
Нажав соответствующую
кнопку, можно сохранить найденное
решение во влияющих ячейках модели или
восстановить исходные значения.
Поле Тип отчета
служит для указания типа отчета,
размещаемого на отдельном листе
книги.
Отчет Результаты
используется для создания отчета,
состоящего из целевой ячейки и списка
влияющих ячеек модели, их исходных и
конечных значений, а также формул
ограничений и дополнительных сведений
о наложенных ограничениях.
Отчет Устойчивость
используется для создания отчета,
содержащей сведения о чувствительности
решения к малым изменениям в формуле
мо дели или в формулах ограничений.
Такой отчет не создается для моделей
значения в которых ограничены множеством
целых чисел. В случае нелинейных моделей
отчет содержит данные для градиентов
и множителей Лагранжа. В отчет по
нелинейным моделям включаются ограниченные
затраты, фиктивные цены, а также диапазоны
ограничений.
Отчет Пределы
используется для создания отчета,
состоящего из целевой ячейки и списка
влияющих ячеек модели, их значений, а
также нижних и верхних границ. Такой
отчет не создается для моделей, значения
в которых ограничены множеством целых
чисел. Нижним пределом являете наименьшее
значение, которое может содержать
влияющая ячейка, в т время как значения
остальных влияющих ячеек фиксированы
и удовлетворяют наложенным ограничениям.
Соответственно верхним пределом
называется наибольшее значение.
К сожалению, эти
отчеты очень неудобны. Они перегружены
плохо читаемыми абсолютными ссылками
со знаками доллара. Желает лучшего
перевод с английского на русский.
Кнопка Сохранить
сценарий служит для отображения
диалогового окна Сохранение сценария,
в котором можно сохранить сценарий
решения задачи, чтобы использовать его
в дальнейшем с помощью диспетчера
сценарии Microsoft Excel. В поле Название
сценария введите имя сценария. Чтоб
создать сценарий, не сохраняя найденное
решение и не отображая результатов на
листе, сохраните сценарий в диалоговом
окне Результаты поиска решения, а затем
выберите Восстановить исходные значения.
Просмотр промежуточных
результатов поиска решения
Режим пошагового
решения задач используется при отладке
моделей. В лабораторных работах его
полезно использовать, чтобы студенты
почувствовали процесс сходимости
решения к оптимуму.
В диалоговом окне
Поиск решения нажмите кнопку Параметры.
Чтобы получить
возможность просмотра текущих значений
влияющих ячеек каждой итерации, установите
флажок Показывать результаты итераций,
нажмите кнопку ОК, а затем кнопку
Выполнить.
На экране появится
диалоговое окно Текущее состояние
поиска решения (рис. 5.6), а влияющие
ячейки листа изменят свои значения.
Чтобы остановить
поиск решения и вывести на экран
диалоговое окно Результаты поиска
решения, нажмите кнопку Стоп.
Чтобы выполнить
следующую итерацию и просмотреть ее
результаты, нажмите кнопку Продолжить.
Возникающие
проблемы и сообщения процедуры поиска
решения
При моделировании
или отладке моделей не все получается,
как задумано. Нередко студенты
вскрикивают за экраном, получив от
компьютера неожиданное сообщение, что
он не может решить задачу. Студент
теряется. Перечислив некоторые ситуации,
мы поможем студенту.
Оптимальное решение
не найдено.
Поиск решения
может остановиться до достижения
оптимального решения по следующим
причинам:
Пользователь
прервал процесс поиска.
Команда Показывать
результаты итераций в диалоговом окне
Параметры поиска решения выбрана
перед Выполнить.
Пользователь нажал
кнопку Стоп в режиме пошагового выполнения
итераций, по истечении времени, отведенного
на работу процедуры, или после
выполнения заданного числа итераций.
Установлен флажок
Линейная модель в диалоговом окне
Параметры поиска решения, в то время
как решаемая задача нелинейна
Значение, заданное
в поле Установить целевую диалогового
окна Поиск решения, неограниченно
увеличивается или уменьшается. Необходимо
уменьшить значения полей Максимальное
время или Итерации в диалоговом окне
Параметры поиска решения.
В случае задач,
значения в которых ограничены множеством
целых чисел, необходимо уменьшить
значение в поле Допустимое отклонение
диалогового окна Параметры поиска
решения, что позволит найти лучшее
решение.
В случае нелинейных
задач необходимо уменьшить значение в
поле Сходимость диалогового окна
Параметры поиска решения, что позволит
продолжать поиск решения, когда значение
в целевой ячейке изменяется медленно.
Если значения
влияющих ячеек или значения влияющей
и целевой ячеек различаются на
несколько порядков, необходимо установить
флажок Автоматическое масштабирование
в диалоговом окне Параметры поиска
решения. Внесите нужные изменения и
запустите процедуру поиска решения
снова.
Если найденное
решение нелинейной задачи существенно
отличается от ожидаемого результата,
запустите процедуру поиска решения с
другими начальными значениями
влияющих ячеек. Если задать такие
значения влияющих ячеек, которые
близко расположены от экстремальной
точки целевой функции, можно значительно
сократить время поиска решения. Итоговые
сообщения процедуры поиска решения
1. Если поиск решения
успешно завершен, в диалоговом окне
Результаты поиска решения выводится
одно из следующих сообщений:
Решение найдено.
Все ограничения и условия оптимальности
выполнены.
Все ограничения
соблюдены с установленной точностью,
и найдено заданное значение целевой
ячейки.
Поиск свелся к
текущему решению. Все ограничения
выполнены.
Относительное
изменение значения в целевой ячейке за
последние 5 итераций стало меньше
установленного значения параметра
Сходимость в диалоговом окне Параметры
поиска решения. Чтобы найти более точное
решение, установите меньшее значение
параметра Сходимость, но это займет
больше времени.
2. Если поиск не
может найти оптимальное решение, в
диалоговом окне
Результаты поиска
решения выводится одно из следующих
сообщений.
Поиск не может
улучшить текущее решение. Все ограничения
выполнены.
В процессе поиска
решения нельзя найти такой набор значений
влияющих ячеек, который был бы лучше
текущего решения Приблизительное
решение найдено, но либо дальнейшее
уточнение невозможно, либо заданная
погрешность слишком высока. Измените
погрешность на меньшее число и
запустите процедуру поиска решения
снова.
3. Поиск остановлен
(истекло заданное на поиск время).
Время, отпущенное
на решение задачи, исчерпано, но достичь
удовлетворительного решения не
удалось. Чтобы при следующем запуске
процедуры поиска решения не повторять
выполненные вычисления, установите
переключатели Сохранить найденное
решение или Сохранить сценарий.
4. Поиск остановлен
(достигнуто максимальное число итераций).
Произведено
разрешенное число итераций, но достичь
удовлетворительного решения не
удалось. Увеличение числа итераций
может помочь, однако следует рассмотреть
результаты, чтобы понять причины
остановки. Чтобы при следующем запуске
процедуры поиска решения не повторять
выполненные вычисления, установите
переключатель Сохранить найденное
решение или нажмите кнопку Сохранить
сценарий.
5. Значения целевой
ячейки не сходятся.
Значение целевой
ячейки неограниченно увеличивается
(или уменьшается), даже если все
ограничения соблюдены. Возможно, следует
в задаче снять одно ограничение или
сразу несколько или наложить дополнительные
ограничения. Изучите процесс расхождения
решения, проверьте ограничения и
запустите задачу снова. Например, в
задаче об оптимальных портфелях
банков, если не наложить ограничение
на портфель привлечения ресурсов,
банк, как аферист, будет занимать деньги
до бесконечности.
6. Поиск не может
найти подходящего решения.
В процессе поиска
решения нельзя сделать итерацию, которая
удовлетворяла бы всем ограничениям
при заданной точности. Вероятно,
ограничения противоречивы. Исследуйте
лист на предмет возможных ошибок в
формулах ограничений или в выборе
ограничений.
7. Поиск остановлен
по требованию пользователя.
Нажата кнопка Стоп
в диалоговом окне Текущее состояние
поиска решения после прерывания
поиска решения в процессе выполнения
итераций.
8. Условия для
линейной модели не удовлетворяются.
Установлен флажок
Линейная модель, однако итоговый пересчет
порождает такие значения, которые
не согласуются с линейной моделью. Это
означает, что решение недействительно
для данных формул листа. Чтобы проверить
линейность задачи, установите флажок
Автоматическое масштабирование и
повторно запустите задачу. Если это
сообщение опять появится на экране,
снимите флажок Линейная модель и снова
запустите задачу.
9. При поиске решения
обнаружено ошибочное значение в целевой
ячейке или в ячейке ограничения.
При пересчете
значений ячеек обнаружена ошибка в
одной формуле или в нескольких сразу.
Найдите целевую ячейку или ячейку
ограничения, по рождающие ошибку, и
измените их формулы так, чтобы они
возвращали подходящее числовое значение.
Набрано неверное
имя или формула в окнах Добавить
ограничение или Изменить ограничение,
или в поле Ограничение были заданы целое
или двоичное ограничение. Чтобы ограничить
значения ячейки множеством целых чисел,
выберите оператор целого ограничения
в списке условных oneраторов. Чтобы
установить двоичное ограничение,
выберите оператор дл двоичного
ограничения.
10. Мало памяти для
решения задачи.
Система не смогла
выделить память, необходимую для поиска
решение Закройте некоторые файлы или
приложения и попытайтесь снова выполнить
процедуру поиска решения.
Создатель сложной таблицы в Microsoft Excel, в которой требуется найти оптимальное значение для определенного диапазона данных, может вручную перебирать все возможные варианты или использовать вспомогательные формулы для расчетов. Однако это все сложно и часто не нужно, ведь можно обратиться к надстройке «Поиск решения», задать для нее цель, ограничения и указать область с переменными значениями, чтобы программа сама высчитала идеальное решение для вас.
Как раз об этой опции и пойдет речь далее.
Используемый пример для поиска решения
Сначала я хочу остановиться на исходной таблице и разобраться, в каких целях может применяться рассматриваемая надстройка. К тому же описываемый далее шаблон сделает понятным принцип устанавливаемых целей и ограничений, чтобы вы могли использовать его как исходную точку, оптимизировав под себя. Поиск решения поможет вам рассчитать кредитную ставку, узнать, как лучше вкладывать средства для достижения желаемого результата, определить лучшие маршруты для логистики, сбалансировать цены и потребление и многое другое, что требуется для обработки довольно большого массива данных.
В моем примере мы возьмем два депозитных счета, на каждый из которых каждый цикл начисляется фиксированный процент. Это вы видите в обводке на следующем изображении, где двойкой отмечены начальные суммы на каждом счете. Именно от них и отталкиваются следующие расчеты.
Процент каждый раз начисляется одинаковый, поэтому является константой. Его я растягиваю на все допустимые циклы начислений. Не обращайте внимание на то, что какие-то значения уже есть, поскольку сначала нужно заполнить таблицу полностью, подставив любые значения для начислений.
Помимо начисления процентов каждый цикл я буду докладывать на каждый счет до 500 условных единиц. Для удобства разделю их пополам на каждый счет, чтобы каждый цикл поступало не больше 250 на отдельный баланс. В итоге количество этих довложений и будет считаться надстройкой, чтобы сэкономить максимальное количество средств до конца всех циклов.
Теперь нужно решить, к чему мы хотим прийти. Я выставил две отдельные цели для каждого счета, но они будут только примерными, поскольку в итоге я хочу прийти к общему балансу, чтобы он соответствовал моим требованиям.
Для этого я сначала добавляю функцию СУММ для суммы счетов и считаю сумму каждого в последнем цикле.
Если вы собираетесь строить примерно такую же таблицу, как у меня, обращу ваше внимание на то, что в начале каждого следующего цикла сумма на счете будет переноситься автоматически, поэтому нужно самостоятельно ссылаться во втором цикле на конечную сумму счета из первого, чтобы при растяжении таблицы всегда получать корректные результаты.
Сама сумма же формируется из исходного баланса, постоянного процента и суммы довложений, которая будет меняться в зависимости от того, как решит надстройка «Поиск решения».
Возможно, текстом описать принцип работы этой таблицы сложно, но я постарался сделать это максимально доходчиво. В итоге получил таблицу с двумя счетами с разными процентами начислений и разными целями. Общая сумма довложений не должна быть более 500, а цель является общей, поскольку предполагается, что весь баланс с депозитных счетов все равно будет выведен на один. Поэтому далее я сделаю так, чтобы баланс к концу всех циклов получился 32500 (7500 + 25000, это предполагаемые цели первого и второго счета). При этом количество довложений должно быть минимальным, чтобы не тратить личные средства, и, соответственно, не превышать установленное ограничение в 500 условных единиц. Теперь давайте разберемся с тем, как реализовать это при помощи рассматриваемой надстройки.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
Включение надстройки «Поиск решения»
Прежде чем обращаться к самой надстройке, ее необходимо включить, поскольку по умолчанию в Экселе она не отображается на необходимой вкладке с инструментами. Выполните следующий алгоритм действий, чтобы активировать эту функцию.
-
В таблице перейдите на вкладку «Файл».
-
Откройте раздел «Другие».
-
Из появившегося меню выберите пункт «Параметры».
-
Откройте категорию настроек «Надстройки» и отыщите пункт с названием «Поиск решения», после чего выделите его нажатием левой кнопки мыши.
-
Кликните по кнопке «Перейти», находящейся внизу окна.
-
Активируйте галочку возле пункта «Поиск решения» и нажмите «ОК», чтобы выйти из данного окна.
-
Теперь давайте убедимся в том, что надстройка появилась в таблице. Для этого откройте вкладку «Данные» и найдите блок «Анализ», где и должен находиться соответствующий инструмент.
Надстройка включена, поэтому смело переходите к следующему разделу статьи, чтобы справиться с поставленной задачей. Как я уже и сказал, буду использовать таблицу из своего примера, а вы можете менять параметры в зависимости от личных целей.
Настройка «Поиска решений» для таблицы
Давайте каждое действие буду описывать максимально детально, разбирая то, какие значения я выбираю и что это даст в итоге. По сути, принцип действий с параметрами поиска решения заключается в том, что мы должны оптимизировать целевую функцию, изменяя ячейки переменных. Функцией у нас является сумма счетов по окончании цикла, а переменные – довложения в каждый цикл. Соответственно, программа будет искать вариант достижения цели с минимальными количествами довложений.
-
Выбрав пункт «Поиск решения» на панели, о которой говорилось выше, вы будете перенаправлены в окно с параметрами. Сначала выберите «Оптимизировать целевую функцию» и выберите ту ячейку, в которой отображается конечный результат всех циклов.
-
Для «Изменяя ячейки переменных» укажите область данных, куда могут вноситься изменения. В моем случае это будут довложения для каждого счета.
-
Теперь обратите внимание на «В соответствии с ограничениями». У нас есть ограничения, поэтому нужно указать их, чтобы программа понимала, какие значения может использовать и к какому результату ей стремиться. Нажмите «Добавить», чтобы создать первое ограничение.
-
В моем случае первое ограничение – итоговая сумма в функции, которой нужно добавиться. Вы можете указать разные знаки неравенства, если, например, можно выбрать одно значение или меньше. В моем случае я хочу получить точный результат, поэтому указываю знак = и ввожу само ограничение в виде суммы.
-
Вторым ограничением является максимальное количество довложений для каждой ячейки. Оно может равняться или быть меньше 250. Соответственно, в вашем случае это будут совершенно другие значения в зависимости от того, с какими исходными данными вы работаете.
-
Сейчас это были все ограничения, но, если у вас их больше, продолжайте добавление в таком же ключе. По завершении убедитесь в том, что метод решения выбран как ОПГ, после чего запустите «Найти решение».
-
Расчет происходит буквально за несколько секунд, после чего мы видим оптимальное решение. В моем случае каждый цикл на балансы начислялось меньше 250, в один месяц даже 0, а в конце всех циклов получилось достичь нужной суммы с точностью до сотых. «Найти решение» показало, как мне действовать каждый цикл, чтобы вкладывать минимальную сумму, но дойти до нужного результата в конце. У вас решение может быть совершенно другим.
-
Если же программа посчитала все возможные исходы и в итоге не нашла решения, на экране появится информация об ошибке. Сравните полученные значения в таблице, чтобы понять, на каком этапе произошло завершение вычислений, то есть программа уперлась в установленные ограничения. В итоге вам нужно будет увеличить количество циклов или изменить эти самые ограничения.
В этой инструкции я пошел по самому простому пути, поскольку объединил два счета в одну итоговую сумму и проигнорировал минимальные начисления на каждом из них. В итоге на одном счете получилось немного больше средств, на другом меньше, но сумма все равно соответствовала требуемым условиям. Вы можете добавлять больше ограничений и разных значений, чтобы получить более эффективную оптимизацию в соответствии с вашими задачами.
Я ставил цель показать вам, как работает программа «Поиск решения» в Microsoft Excel, чтобы вы узнали, как можно автоматически найти оптимальные значения для большой таблицы, избегая ручной переборки значений. Надеюсь, все объяснения и примеры были вам понятны, и теперь вы освоили еще одну очень удобную функцию, упрощающую взаимодействие с электронными таблицами, созданными в Экселе.

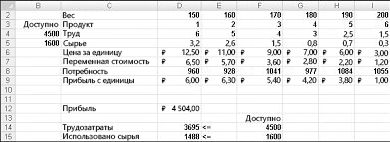
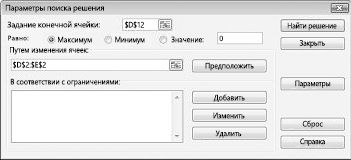
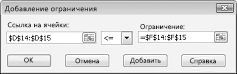
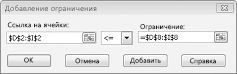
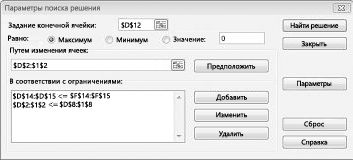
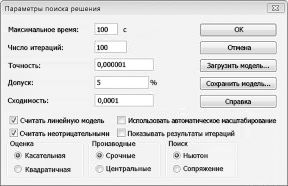
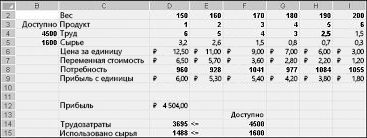
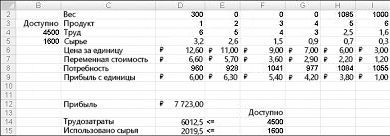

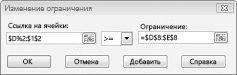

























 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.