Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
В этой статье обсуждается использование надстройки Microsoft Excel «Решение», которая позволяет анализировать «что если» для определения оптимального сочетания продуктов.
Как определить ежемесячный набор продуктов, который позволяет повысить прибыльность?
Компаниям часто требуется определять количество каждого продукта, который будет создаваться ежемесячно. В простейшей форме проблема в наборе продуктов состоит в том, как определить объем каждого продукта, который должен быть произведен в течение месяца, чтобы максимально увеличить прибыль. Сочетание продуктов обычно должно соответствовать следующим ограничениям:
-
Сочетание продуктов не может использовать больше ресурсов, чем доступно.
-
Потребность в каждом продукте ограничена. В течение месяца мы не можем создать больше продукции, чем это диктует потребность в продукции, так как в нее нагребают лишние продукты (например, избежаемый продукт).
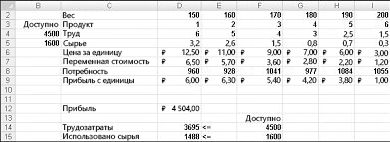
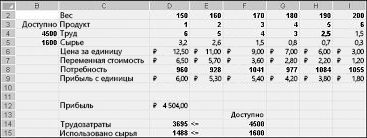
Теперь рассмотрим пример проблемы со сочетанием продуктов. Решение этой проблемы можно найти в файле Prodmix.xlsx, как показано на рисунке 27-1.
Предположим, что мы работаем в компании, которая производит шесть различных продуктов на своем заводе. Для производства каждого продукта требуются трудовые и необработанные материалы. В строке 4 на рисунке 27-1 показано количество часов труда, необходимое для получения фунта каждого товара, а в строке 5 — фунт необработанных материалов, необходимых для получения фунта каждого товара. Например, для получения фунта продукта 1 требуется 6 часов труда и 3,2 фунта неотработанных материалов. Цена за фунт для каждого фунта задается в строке 6, цена за единицу за фунт — в строке 7, а доход за фунт — в строке 9. Например, товар 2 продается по 11,00 долларов США за фунт, за единицу стоит 5,70 долларов США за фунт и вклад в сумму 5,30 долларов США за фунт. Запрос за месяц для каждого подмайки выдается в строке 8. Например, потребность в продукте 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов необработанных материалов. Как эта компания может максимально увеличить ежемесячную прибыль?
Если бы нам не было известно ничего о надстройке Excel «Решение», мы могли бы решить эту проблему, построив на этом листах данные о прибылях и использовании ресурсов, связанных с этим сочетанием продуктов. Затем мы использовали пробные и ошибки, чтобы оптимизировать прибыль, не используя при этом больше ресурсов и необработанных материалов, чем доступно, и не изменяя при этом лишние продукты. Над решением этой процедуры мы используем только пробную стадию с ошибкой. По сути, «Поиск решения» — это механизм оптимизации, который безукоризненно выполняет поиск по пробным версиям и ошибкам.
Ключ к решению этой проблемы — эффективное вычисление использования ресурсов и прибыли, связанных с любым сочетанием продуктов. Для этого важно использовать функцию СУММПРОИDUCT. Функция СУММПРОИCT перемножает соответствующие значения в диапазонах ячеев и возвращает сумму этих значений. Каждый диапазон ячеок, используемый в оценке СУММПРОИДУCT, должен иметь одинаковые размеры, что подразумевает, что можно использовать суммпроидуц с двумя строками или двумя столбцами, но не с одной строкой и столбцом.
В качестве примера использования функции СУММПРОИПР в нашем примере мы постараемся вычислить использование ресурсов. Трудоемкие труды вычисляются по
(Количество трудовых единиц, использованных для одного фунта воды в секунду)*(1 фунт 1, произведено)+
(Трудоемка, используемая для одного фунта валюты 2)*(2 фунта, произведенного) + …
(Трудоемка, используемая для одного фунта валюты 6)*(6 фунтов в секунду)
Мы могли бы более утомительным образом вычислять использование труда, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Кроме того, использование необработанных материалов можно вычислять как D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на таблицу для шести продуктов отнимает много времени. Представьте, сколько времени займет работа с компанией, которая производит, например, 50 продуктов на своем заводе. Гораздо проще вычислять трудоемкие и необработанные данные, скопируя из D14 в D15 формулу СУММПРОИДУCT($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш рабочий процесс), но гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, чтобы при копировании формулы все равно записать сочетание продуктов из строки 2. Формула в ячейке D15 вычисляет использование необработанных материалов.
Аналогичным образом прибыль определяется с помощью
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Доход легко вычисляется в ячейке D12 с помощью формулы СУММПРОИКТ(D9:I9;$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для всех продуктов.
-
Целевая ячейка. Наша цель — максимально увеличить прибыль (вычисленную в ячейке D12).
-
Изменяя ячейки. Количество фунта, произведенного каждым продуктом (в диапазоне ячеок D2:I2)
-
Ограничения. В этом примере есть следующие ограничения:
-
Не используйте больше трудовых или необработанных материалов, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
-
Не выполыв при этом больше средств, чем нужно. Это значит, что значения в ячейках D2:I2 (фунта, произведенного для каждого пациента) должны быть меньше или равны требованию для каждого пациента (в ячейках D8:I8).
-
Мы не можем привести к отрицательным последствиям любых проблем с наркотиками.
-
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в «Найти решение». Все, что вам нужно сделать, — это нажать кнопку «Найти решение», чтобы найти набор товаров, который максимально увеличить прибыль!
Для начала на вкладке «Данные» в группе «Анализ» нажмите кнопку «Найти решение».
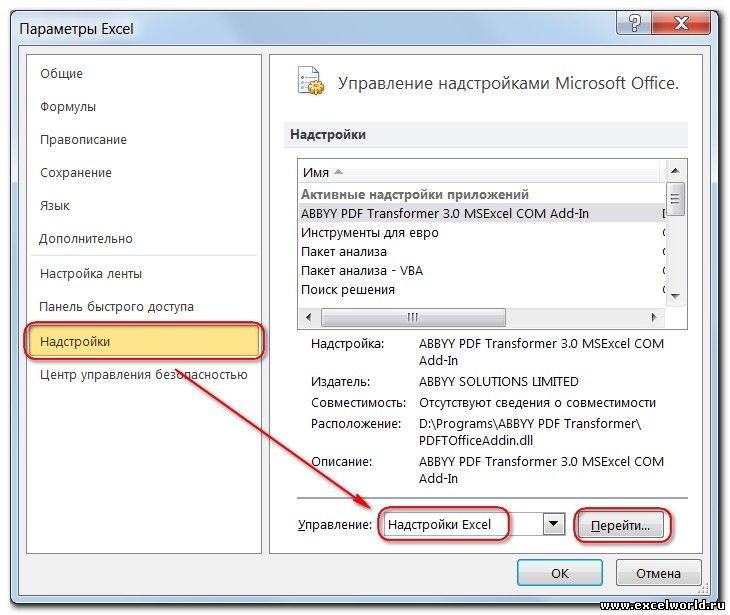
Примечание: Как объяснялось в главе 26 «Введение в оптимизацию с помощью надстройки Excel «Решение», надстройка «Решение» устанавливается с помощью кнопки Microsoft Office, а затем параметров Excel и надстройки. В списке «Управление» щелкните «Надстройки Excel», выберите поле «Найти решение» и нажмите кнопку «ОК».
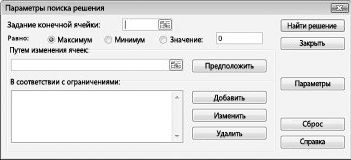
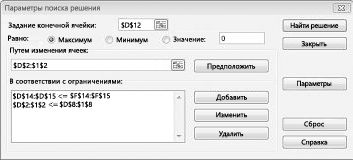
Появится диалоговое окно «Параметры решения», как показано на рисунке 27–2.
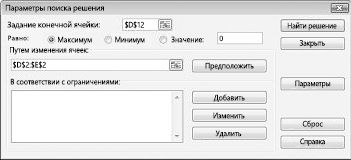
Щелкните поле «Установить целевую ячейку» и выберите ячейку прибыли (ячейка D12). Щелкните поле «Изменяя ячейки», а затем найдите диапазон D2:I2, содержащий количество отсюдоха каждого пациента. Диалоговое окно будет выглядеть как «Рисунок 27-3».
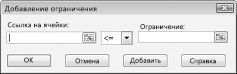
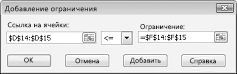
Теперь можно добавить ограничения в модель. Нажмите кнопку «Добавить». На рисунке 27–4 показано диалоговое окно «Добавить ограничение».
Чтобы добавить ограничения использования ресурсов, щелкните поле «Ссылка на ячейку» и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле ограничения, а затем выберите диапазон ячеев F14:F15. Диалоговое окно «Добавить ограничение» должно выглядеть так: «Рисунок 27-5».
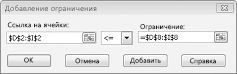
Теперь, когда «Найти решение» пытается использовать другие значения для изменяющихся ячеек, будут учитываться только сочетания, которые удовлетворяют как D14<=F14 (трудоемка меньше или равна доступной работе), так и D15<=F15 (используемый необработаный материал меньше или равен доступному неоцененному). Нажмите кнопку «Добавить», чтобы ввести ограничения по запросу. Заполните поле в диалоговом окне «Добавить ограничение», как показано на рисунке 27–6.
Добавление этих ограничений гарантирует, что при попытках «Найти решение» для изменяемого значения ячейки будут учитываться только сочетания, которые удовлетворяют следующим параметрам:
-
D2<=D8 (количество произведенного средства 1 не превышает потребность в этом средстве)
-
E2<=E8 (количество произведенного средства 2 не превышает или равно запросу на доступ к более 2).
-
F2<=F8 (количество произведенного средства 3 не превышает потребность в этом средстве)
-
G2<=G8 (количество произведенного средства 4 не превышает или равно запросу на доступ к наркотиками 4)
-
H2<=H8 (количество произведенного средства 5 не превышает или равно запросу на доступ к более 5).
-
I2<=I8 (количество произведенного средства 6 не превышает потребность в этом средстве)
В диалоговом окне «Добавить ограничение» нажмите кнопку «ОК». Окно «Решение» должно выглядеть так: «Рисунок 27-7».
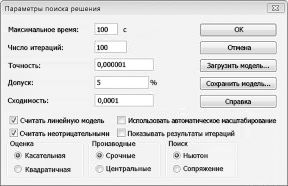
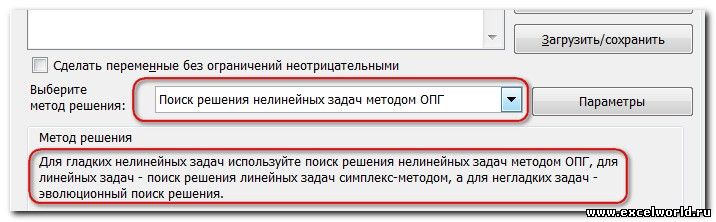
В диалоговом окне «Параметры решения» введите ограничение на то, что изменяющиеся ячейки не должны быть отрицательными. Нажмите кнопку «Параметры» в диалоговом окне «Параметры решения». Проверьте окне «Предполагаемая линейная модель» и «Нео отрицательная», как показано на рисунке 27–8 на следующей странице. Нажмите кнопку «ОК».
При проверке значения «Предположим, неохожим» над решением будут учитываться только сочетания изменяющихся ячеек, в которых каждая из изменяющихся ячеек принимает нео отрицательное значение. Мы проверили поле «Предполагаемая линейная модель», так как проблема с сочетанием продуктов — это особый тип решения, называемый линейной моделью. По сути, модель «Поиск решения» является линейной в следующих условиях:
-
Целевая ячейка вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа).
-
Каждое ограничение соответствует «требованиям к линейной модели». Это означает, что каждое ограничение вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой.
Почему эта проблема «Поиск решения» линейный? Целевая ячейка (прибыль) вычисляется как
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Эта вычисление вычисляется по шаблону, в котором вычисляется значение конечной ячейки путем с суммирования терминов формы (изменяемой ячейки)*(константа).
Наше ограничение на работу вычисляется путем сравнения значения, полученного из (Количество, используемого в фунте по 1)*(1 фунта влияния) + (Количество, используемого для одного фунта в фунте до 2)*(Фунт 2, полученный в качестве 2 фунта)+ (Трудоемкие мыed per pound of Drug 6)*(Pound 6 pound produced) to the labor available.
Следовательно, ограничение трудоемких ресурсов вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой. Ограничение трудоемких ресурсов и ограничение в необработанных материалах отвечают требованиям к линейной модели.
Наши ограничения запроса принимают форму
(От 1 досье 1)<=(Потребность в наркотиками 1)
(От 2 досье 2)<=(Потребность в наркотиками 2)
§
(от 6 досье 6)<=(Потребность в наркотиками 6)
Каждое ограничение запроса также соответствует требованию к линейной модели, поскольку каждое из них вычисляется путем свести вместе условия формы (изменяемая ячейка)*(константа) и сравнить суммы с константой.
Если вы показываете, что модель нашего продукта является линейной, почему это важно?
-
Если модель «Поиск решения» является линейной и выбран вариант «Предположим, линейный режим», «Поиск решения» гарантирован, что будет найдено оптимальное решение для модели «Поиск решения». Если модель «Поиск решения» не линейный, «Поиск решения» может не найти оптимальное решение.
-
Если модель «Поиск решения» является линейной и выбран вариант «Предполагаемая линейная модель», то для поиска оптимального решения модели используется очень эффективный алгоритм (метод простого решения). Если модель «Поиск решения» является линейной и не выбран вариант «Предполагаемая линейная модель», «Поиск решения» использует очень неэффективный алгоритм (метод ОГР2), что может затруднить поиск оптимального решения модели.
После нажатия кнопки «ОК» в диалоговом окне «Параметры решения» вернимся в главное диалоговое окно «Решение», показанное ранее на рисунке 27–7. При нажатии кнопки «Поиск решения» «Поиск решения» вычисляет оптимальное решение (если оно существует) для модели микса продуктов. Как было сказано в главе 26, оптимальным решением для модели набора продуктов является набор изменяемых значений ячеок (фунта, произведенного каждым продуктом), который позволяет максимально увеличить прибыль в наборе всех возможных решений. В этом же, целесообразное решение — это набор изменяющихся значений ячеок, удовлетворяющий всем ограничениям. Изменяющиеся значения ячеок, показанные на рисунке 27–9, являются допустимым решением, поскольку все производственные уровни неоценимы, производственные уровни не превышают потребность, а использование ресурсов не превышает доступных ресурсов.
Изменяемые значения ячеек, показанные на рисунке 27–10 на следующей странице, являются неизменяемым решением по следующим причинам:
-
Мы выпускаем больше 5, чем за него требуются.
-
Мы используем больше трудоемких ресурсов, чем доступно.
-
Мы используем больше необработанных материалов, чем доступно.
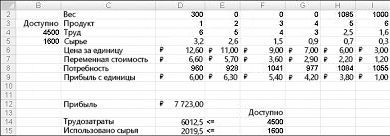
Нажав кнопку «Поиск решения», «Поиск решения» быстро найдет оптимальное решение, показанное на рисунке 27–11. Вам нужно выбрать «Сохранить решение для решения проблемы», чтобы сохранить оптимальные значения решения на работе.
Наша организация, которая занимается наркотиками, может увеличить ежемесячную прибыль в размере 6 625,20 долларов США, выполив 596,67 фунта 4, 1084 фунта для подавлили 5 рублей и ни одного другого фунта! Мы не можем определить, можно ли достичь максимальной прибыли в 6 625,20 долларов США другими способами. Все, что мы можем быть уверены, что из-за ограниченных ресурсов и требований в этом месяце нельзя внести больше 6 627,20 долларов США.
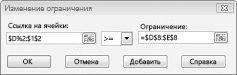
Предположим, что потребность в каждом продукте должна быть выполнены. (См. таблицу «Нет реального решения» в Prodmix.xlsx.) Затем нам нужно изменить ограничения по запросу с D2:I2<=D8:I8 на D2:I2>=D8:I8. Для этого откройте «Решение», выберите ограничение D2:I2<=D8:I8 и нажмите кнопку «Изменить». Появится диалоговое окно «Изменение ограничения», показанное на рисунке 27–12.
Выберите >=, а затем нажмите кнопку «ОК». Теперь над решением можно изменить только значения ячеок, которые соответствуют всем запросам. При нажатии кнопки «Найти решение» отобразилось сообщение «Поиск решения не удалось найти целесообразное решение». Это сообщение не означает, что мы допустили ошибку в модели, а о том, что из-за ограниченных ресурсов мы не сможем выполнить потребность во всех товарах. Надстройка «Решение» просто сообщает нам, что если мы хотим удовлетворить потребность в каждом продукте, нам нужно добавить больше труда, дополнительных необработанных материалов или и тех, и других.
Давайте посмотрим, что произойдет, если разрешить неограниченную потребность в каждом продукте и разрешить отрицательные количества каждого товара. (Эта проблема возникает в области «Набор значений не сходится» на Prodmix.xlsx.) Чтобы найти оптимальное решение в этой ситуации, откройте «Поиск решения», нажмите кнопку «Параметры» и откроем поле «Неохритимые». В диалоговом окне «Параметры решения» выберите ограничение запроса D2:I2<=D8:I8, а затем нажмите кнопку «Удалить», чтобы удалить это ограничение. При нажатии кнопки «Найти решение» возвращается сообщение «Установить значение ячейки не сходится». Это сообщение означает, что если нужно развернуть целевую ячейку (как в нашем примере), существуют допустимые решения, в том числе и для суммарных значений целевых ячеок. (Если целевая ячейка должна быть свернута, сообщение «Установить значения ячейки не сходятся» означает, что существуют возможные решения с небольших целевых значений, заверяемого в третейском деле.) В нашем случае, разрешив негативное производство в случае злоупотреблений, мы фактически создадим ресурсы, которые можно использовать для вывода в произвольное количество других средств. С учетом нашего неограниченного запроса это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечно. Если вы видите сообщение «Установить значения не сходятся», это означает, что в модели есть ошибка.
-
Предположим, в нашей компании в течение часа можно приобретать до 500 часов работы на 100 рублей больше, чем за текущие трудоемкие расходы. Как максимально увеличить прибыль?
-
На изготовителе микросхем четыре технических специалиста (A, B, C и D) выпускают три продукта («Товары 1», «2» и «3»). В этом месяце изготовитель микросхемы может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Специалист А может делать только продукты 1 и 3. Специалист Б может делать только продукты 1 и 2. Специалист C может сделать только продукт 3. Специалист D может сделать только продукт 2. Для каждого произведенного товара внести следующую прибыль: Товар 1; 600 рублей; Товар 2; 7000 рублей; и товар 3, 1000 рублей. Время (в часах) каждого технических специалиста, необходимое для производства продукта, должно быть следующим:
Продукт
Специалист А
Специалист Б
Специалист C
Специалист Д
1
2
2,5
Не удается сделать
Не удается сделать
2
Не удается сделать
3
Не удается сделать
3,5
3
3
Не удается сделать
4
Не удается сделать
-
Каждый специалист может работать до 120 часов в месяц. Как изготовитель микросхем может максимально увеличить ежемесячную прибыль? Предположим, что можно получить лишь дробное количество единиц.
-
Компьютерный завод производит мыши, клавиатуры и игровые joysticks. Доход за единицу, за единицу трудоемких ресурсов, ежемесячная потребность и за единицу машинного времени даются в следующей таблице:
Мыши
Клавиатуры
Joysticks
Прибыль/единица
8 $
11 $
9 $
Использование трудов и единицы
0,2 часа
0,3 часа
0,24 часа
Машинное время/единица
0,04 ч
0,055 ч.
0,04 ч
Ежемесячный запрос
15 000
27,000
11,000
-
Каждый месяц доступно 13 000 часов труда и 3000 часов машинного времени. Как изготовитель может максимально увеличить ежемесячный взнос в прибыль от растения?
-
Допустим, необходимо устранить проблему с этой проблемой при условии, что должны быть выполнены минимальные требования к 200 единицам для каждого из них.
-
Он делает ромбовидные ромбои, окаймлы и затейные. Он хочет работать не более 160 часов в месяц. У него 800 ромбов. Ниже дается прибыль, время труда и количество ромбов, необходимых для получения каждого товара. Если потребность в каждом продукте не ограничена, как Максим может увеличить прибыль?
Продукт
Прибыль за единицу
Трудоемкие часы на единицу
Ромбы на единицу
Лексема
300р.
.35
1,2
Кулигов
200 ₽
.15
.75
Кулигов
100р.
0,05
.5
Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.
Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых «задач оптимизации».
Если Вы раньше не использовали Поиск решения, то Вам потребуется установить соответствующую надстройку.
Сделать это можно так:
для версий старше Excel 2007 через команду меню Сервис —> Надстройки;
начиная с Excel 2007 через диалоговое окно Параметры Excel
Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные.
В версиях до Excel 2007 аналогичная команда появится в меню Сервис
Разберём порядок работы Поиска решения на простом примере.
Пример 1. Распределение премии
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
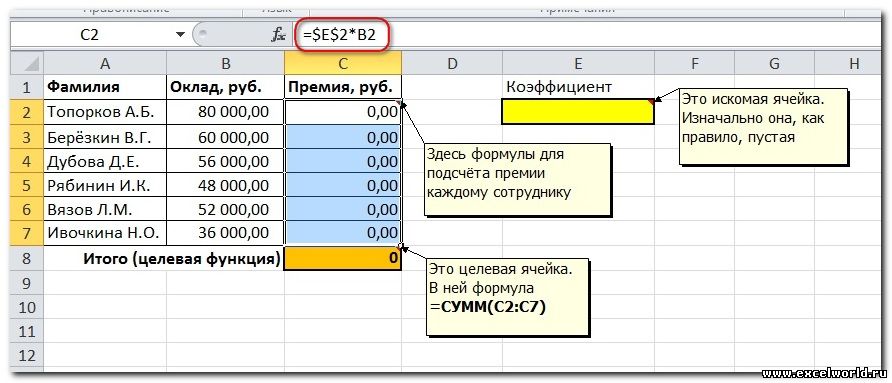
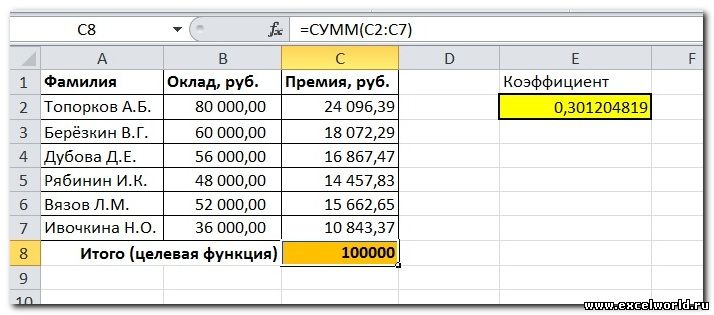
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
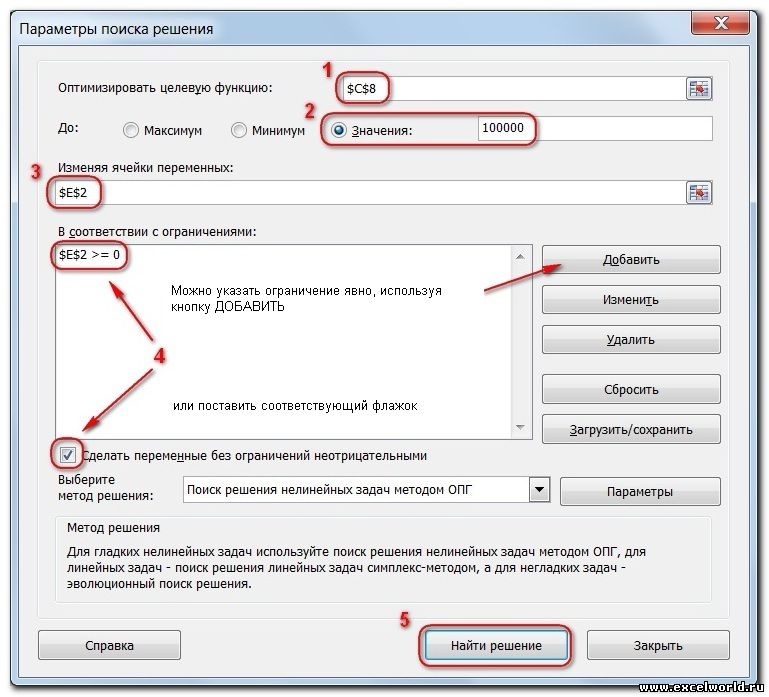
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
Начиная с Excel 2010
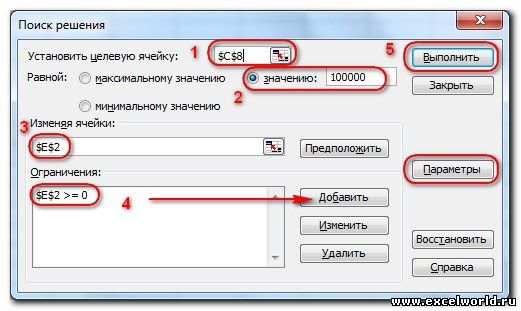
До Excel 2010
- Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
- Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
- Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
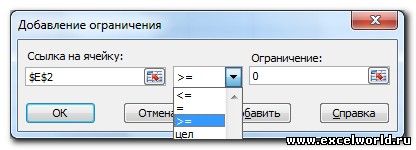
- Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии Excel 2010).
В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
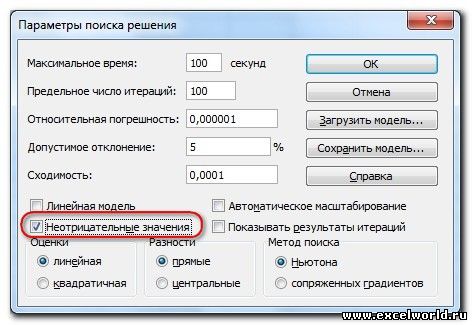
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
- Кнопка, включающая итеративные вычисления с заданными параметрами.
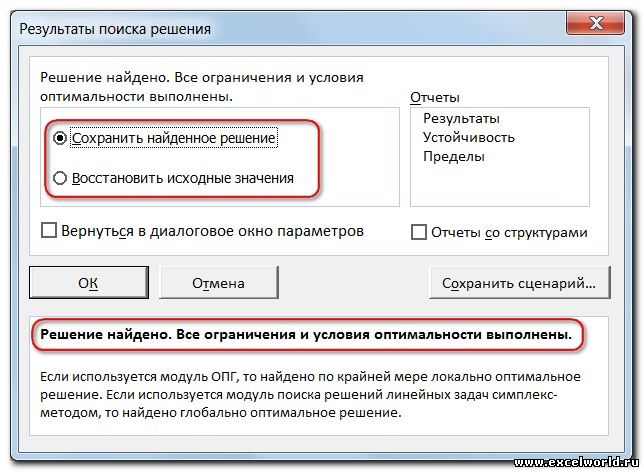
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
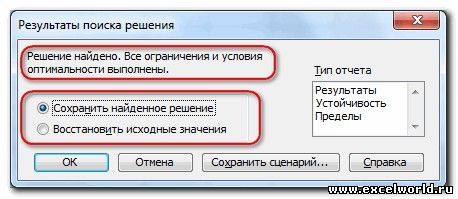
До Excel 2010
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
Разберём еще одну задачу оптимизации (получение максимальной прибыли)
Пример 2. Мебельное производство (максимизация прибыли)
Фирма производит две модели А и В сборных книжных полок.
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.
Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?
Порядок действий нам уже известен.
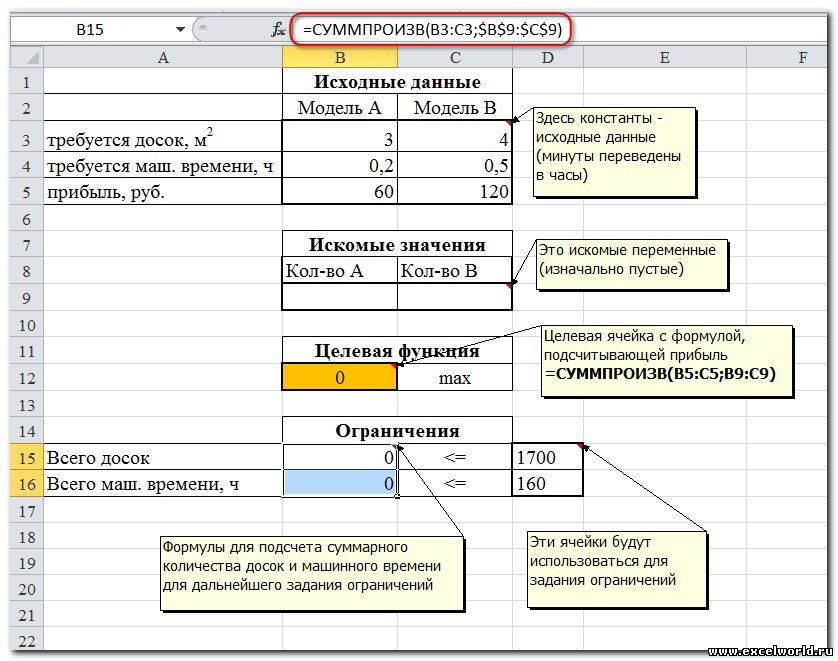
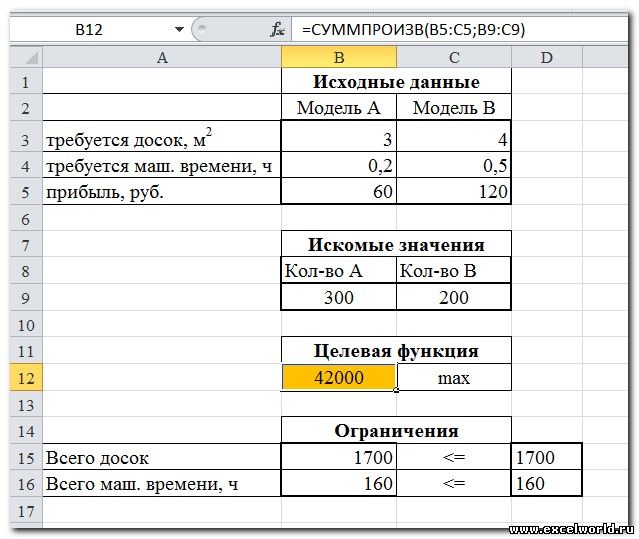
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке
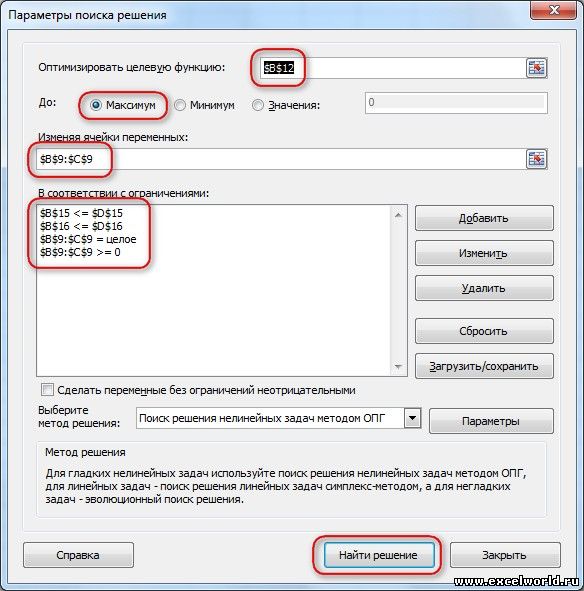
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры
- Целевая ячейка B12 содержит формулу для расчёта прибыли
- Параметр оптимизации — максимум
- Изменяемые ячейки B9:C9
- Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
- Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
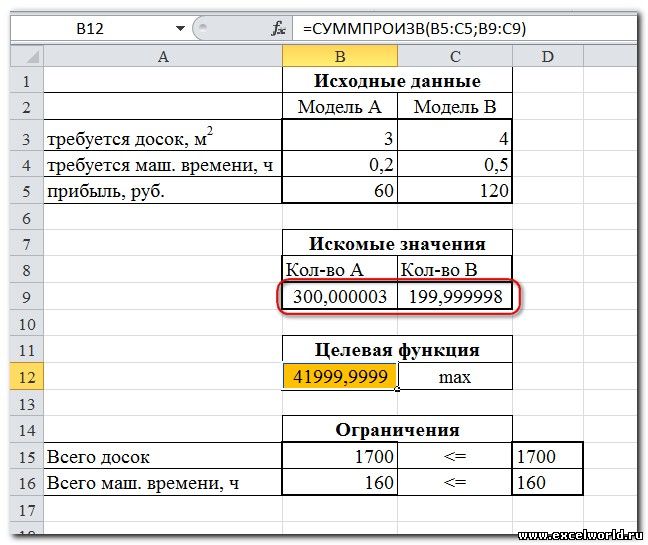
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:
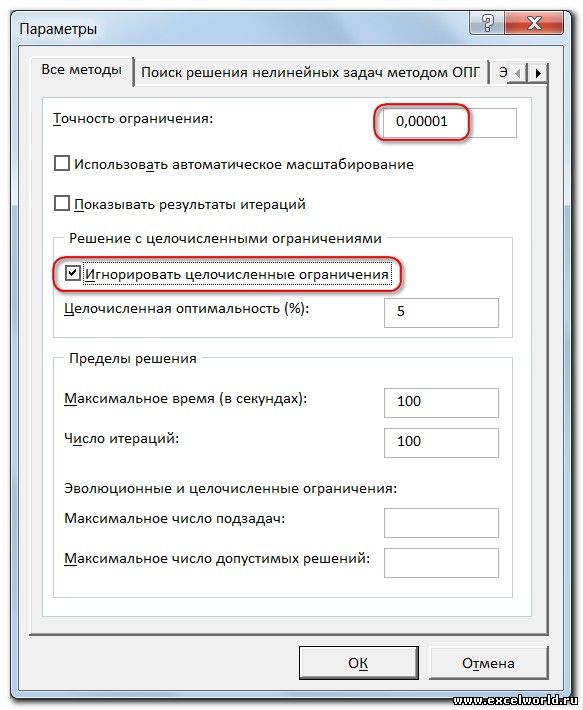
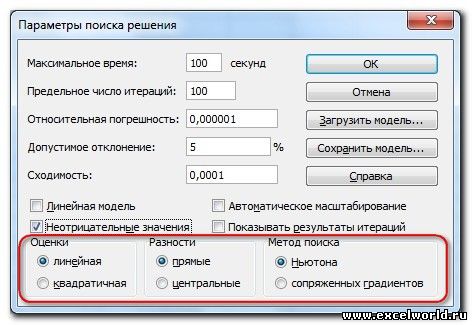
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.
Пример 3. Транспортная задача (минимизация затрат)
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.
Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».
Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.
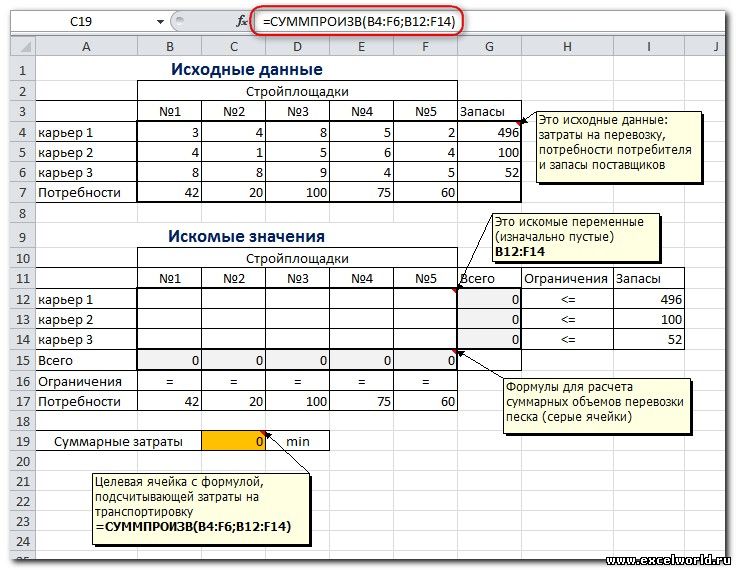
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.
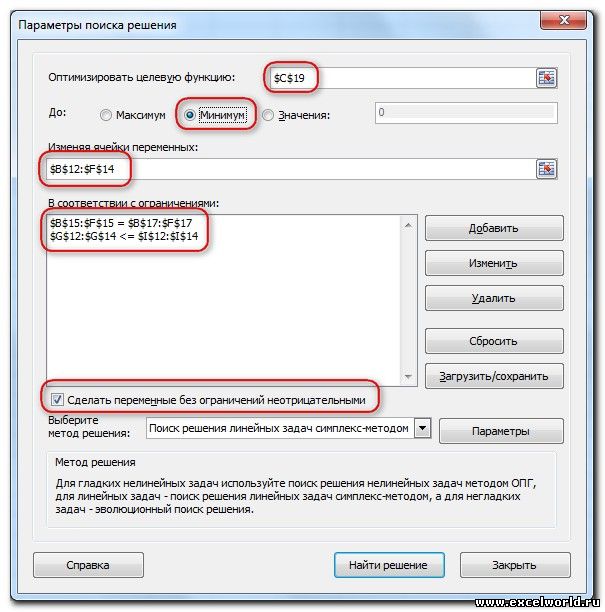
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)
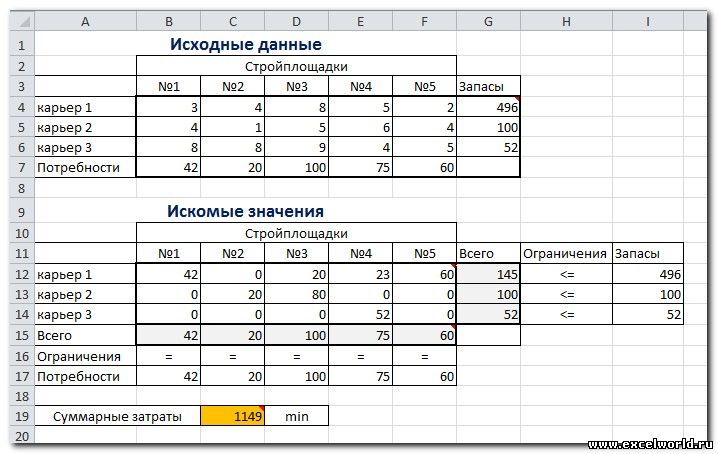
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже
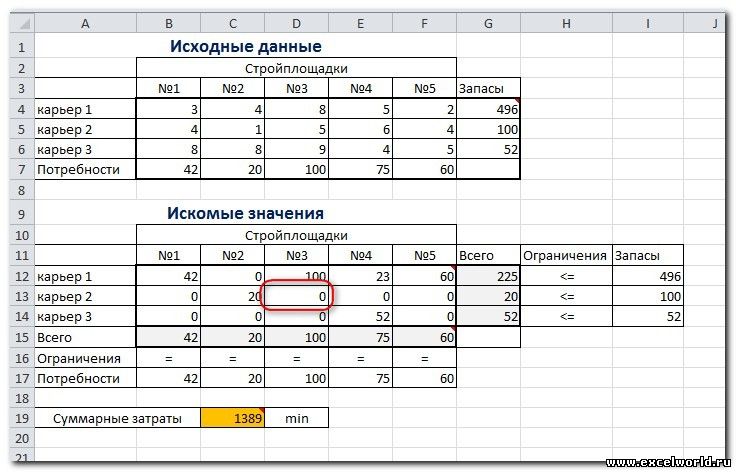
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения
Начиная с Excel 2010
До Excel 2010
В заключение предлагаю попробовать свои силы в применении Поиска решения и решить с его помощью старинную задачу:
Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек. Сколько быков, коров и телят купил крестьянин?
Solver is a Microsoft Excel add-in program you can use for optimization in what-if analysis.
According to O’Brien and Marakas, optimization analysis is a more complex extension of goal-seeking analysis. Instead of setting a specific target value for a variable, the goal is to find the optimum value for one or more target variables, under certain constraints. Then, one or more other variables are changed repeatedly, subject to the specified constraints, until you discover the best values for the target variables.
In Excel, you can use Solver to find an optimal value (maximum or minimum, or a certain value) for a formula in one cell called the objective cell, subject to certain constraints or limits, on the values of other formula cells on the worksheet.
This means that the Solver works with a group of cells called decision variables that are used in computing the formulas in the objective and constraint cells. Solver adjusts the values in the decision variable cells to satisfy the limits on constraint cells and produce the result you want for the objective cell.
You can use Solver to find optimal solutions for diverse problems such as −
-
Determining the monthly product mix for a drug manufacturing unit that maximizes the profitability.
-
Scheduling workforce in an organization.
-
Solving transportation problems.
-
Financial planning and budgeting.
Activating Solver Add-in
Before you proceed with finding solution for a problem with Solver, ensure that the Solver Add-in is activated in Excel as follows −
- Click the DATA tab on the Ribbon. The Solver command should appear in the Analysis group as shown below.
In case you do not find the Solver command, activate it as follows −
- Click the FILE tab.
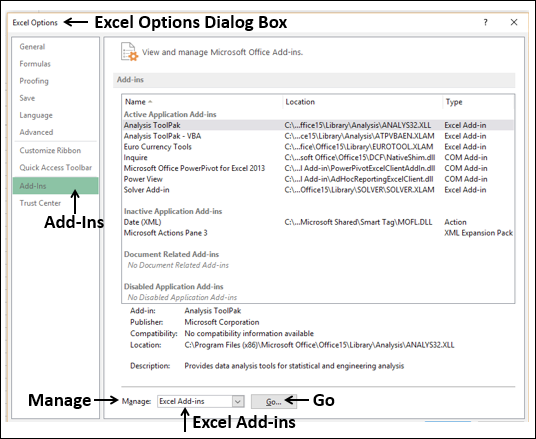
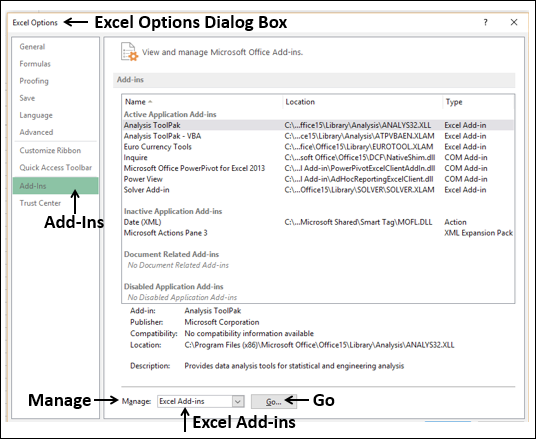
- Click Options in the left pane. Excel Options dialog box appears.
- Click Add-Ins in the left pane.
- Select Excel Add-Ins in the Manage box and click Go.
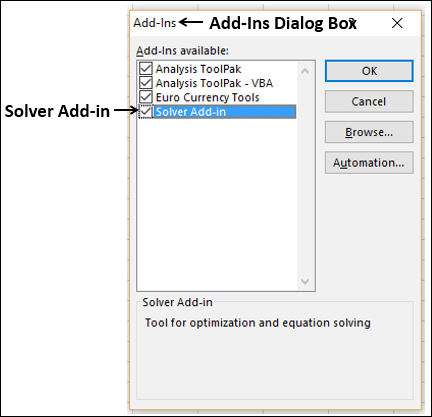
The Add-Ins dialog box appears. Check Solver Add-in and click Ok. Now, you should be able to find the Solver command on the Ribbon under the DATA tab.
Solving Methods used by Solver
You can choose one of the following three solving methods that Excel Solver supports, based on the type of problem −
LP Simplex
Used for linear problems. A Solver model is linear under the following conditions −
-
The target cell is computed by adding together the terms of the (changing cell)*(constant) form.
-
Each constraint satisfies the linear model requirement. This means that each constraint is evaluated by adding together the terms of the (changing cell)*(constant) form and comparing the sums to a constant.
Generalized Reduced Gradient (GRG) Nonlinear
Used for smooth nonlinear problems. If your target cell, any of your constraints, or both contain references to changing cells that are not of the (changing cell)*(constant) form, you have a nonlinear model.
Evolutionary
Used for smooth nonlinear problems. If your target cell, any of your constraints, or both contain references to changing cells that are not of the (changing cell)*(constant) form, you have a nonlinear model.
Understanding Solver Evaluation
The Solver requires the following parameters −
- Decision Variable Cells
- Constraint Cells
- Objective Cells
- Solving Method
Solver evaluation is based on the following −
-
The values in the decision variable cells are restricted by the values in the constraint cells.
-
The calculation of the value in the objective cell includes the values in the decision variable cells.
-
Solver uses the chosen Solving Method to result in the optimal value in the objective cell.
Defining a Problem
Suppose you are analyzing the profits made by a company that manufactures and sells a certain product. You are asked to find the amount that can be spent on advertising in the next two quarters subject to a maximum of 20,000. The level of advertising in each quarter affects the following −
- The number of units sold, indirectly determining the amount of sales revenue.
- The associated expenses, and
- The profit.
You can proceed to define the problem as −
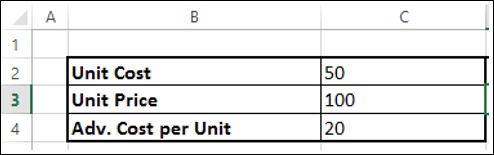
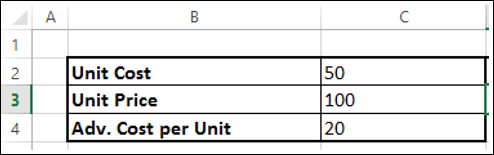
- Find Unit Cost.
- Find the advertising cost per Unit.
- Find Unit Price.
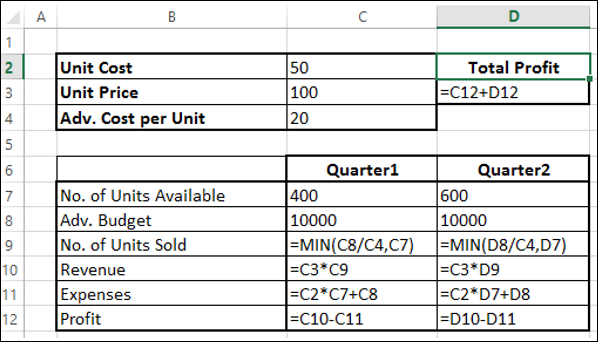
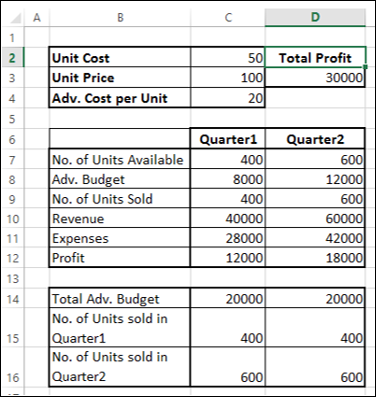
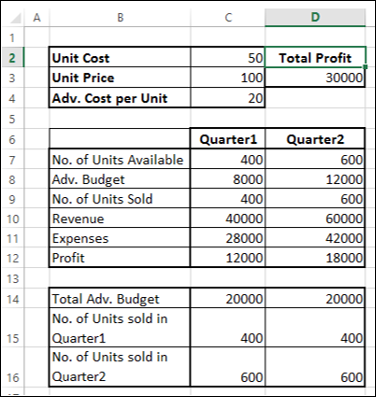
Next, set the cells for the required calculations as given below.
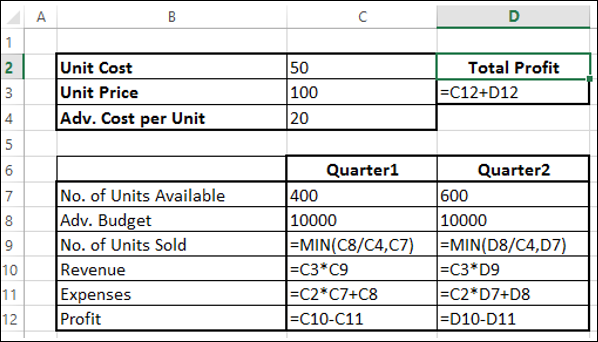
As you can observe, the calculations are done for Quarter1 and Quarter2 that are in consideration are −
-
No. of units available for sale in Quarter1 is 400 and in Quarter2 is 600 (cells – C7 and D7).
-
The initial values for advertising budget are set as 10000 per Quarter (Cells – C8 and D8).
-
No. of units sold is dependent on the advertising cost per unit and hence is budget for the quarter / Adv. Cost per unit. Note that we have used the Min function to take care to see that the no. of units sold in <= no. of units available. (Cells – C9 and D9).
-
Revenue is calculated as Unit Price * No. of Units sold (Cells – C10 and D10).
-
Expenses is calculated as Unit Cost * No. of Units Available + Adv. Cost for that quarter (Cells – C11 and D12).
-
Profit is Revenue – Expenses (Cells C12 and D12).
-
Total Profit is Profit in Quarter1 + Profit in Quarter2 (Cell – D3).
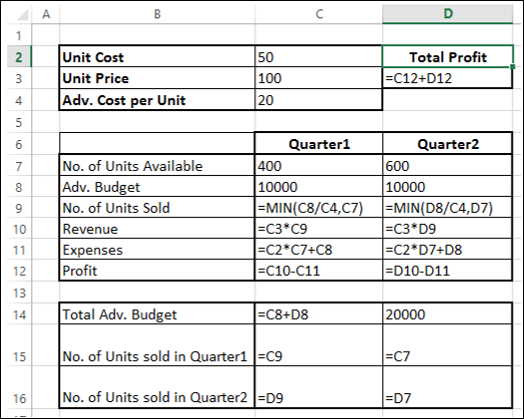
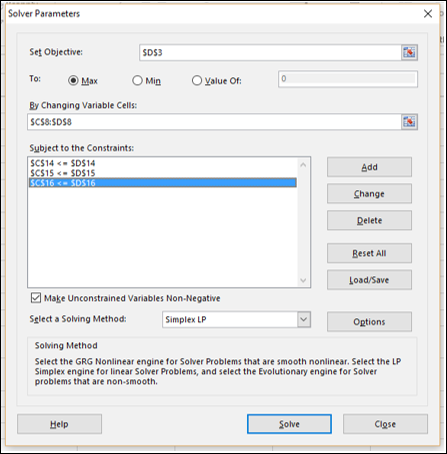
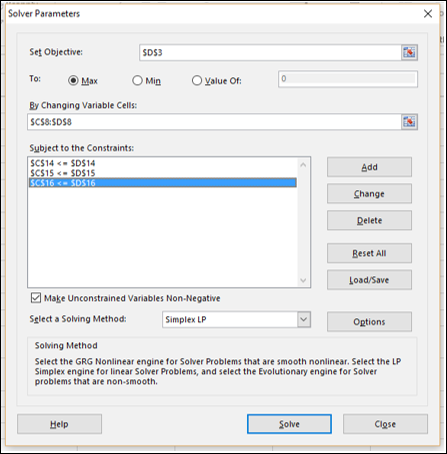
Next, you can set the parameters for Solver as given below −
As you can observe, the parameters for Solver are −
-
Objective cell is D3 that contains Total Profit, which you want to maximize.
-
Decision Variable cells are C8 and D8 that contain the budgets for the two quarters – Quarter1 and Quarter2.
-
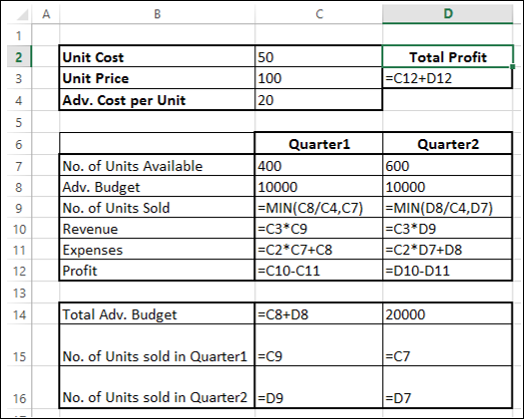
There are three Constraint cells — C14, C15 and C16.
-
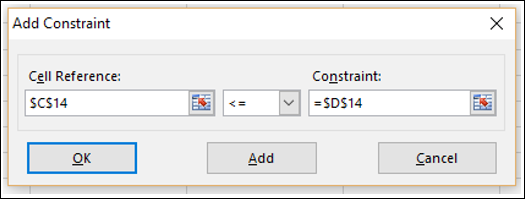
Cell C14 that contains total budget is to set the constraint of 20000 (cell D14).
-
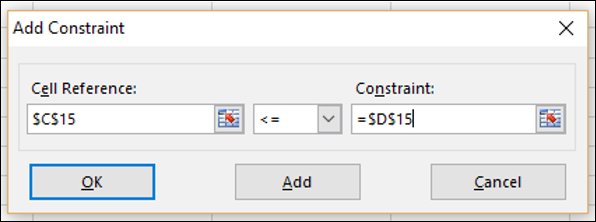
Cell C15 that contains the no. of units sold in Quarter1 is to set the constraint of <= no. of units available in Quarter1 (cell D15).
-
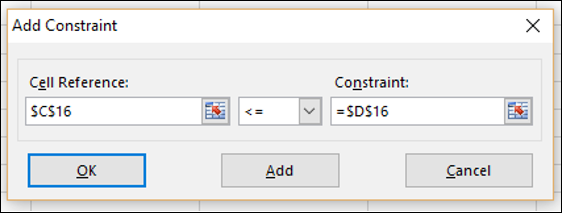
Cell C16 that contains the no. of units sold in Quarter2 is to set the constraint of <= no. of units available in Quarter2 (cell D16).
-
Solving the Problem
The next step is to use Solver to find the solution as follows −
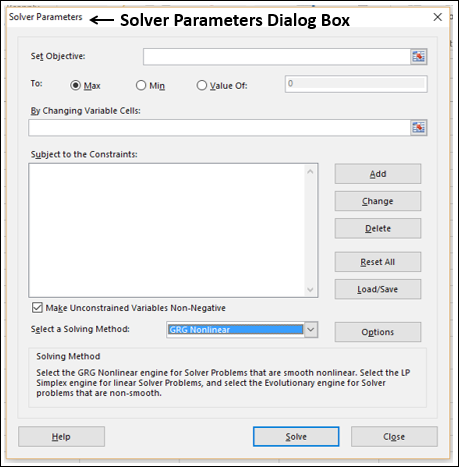
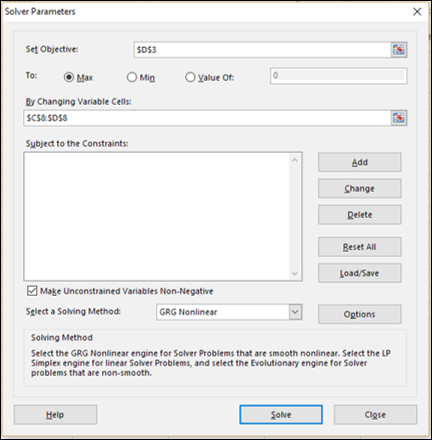
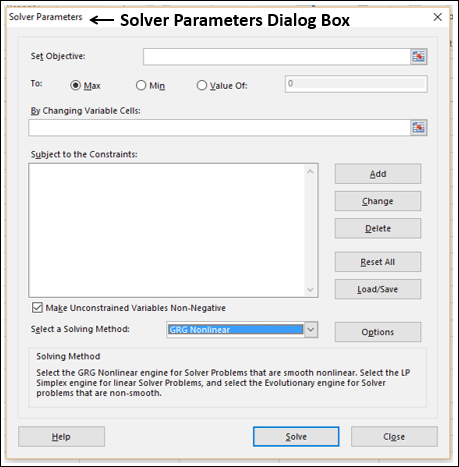
Step 1 − Go to DATA > Analysis > Solver on the Ribbon. The Solver Parameters dialog box appears.
Step 2 − In the Set Objective box, select the cell D3.
Step 3 − Select Max.
Step 4 − Select range C8:D8 in the By Changing Variable Cells box.
Step 5 − Next, click the Add button to add the three constraints that you have identified.
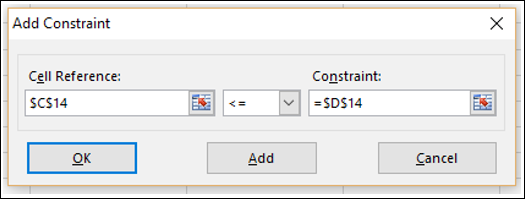
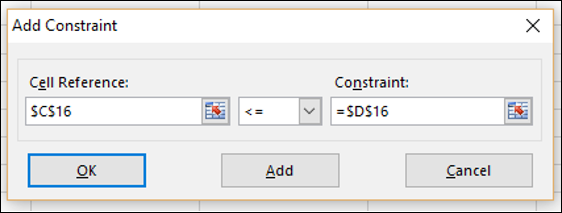
Step 6 − The Add Constraint dialog box appears. Set the constraint for total budget as given below and click Add.
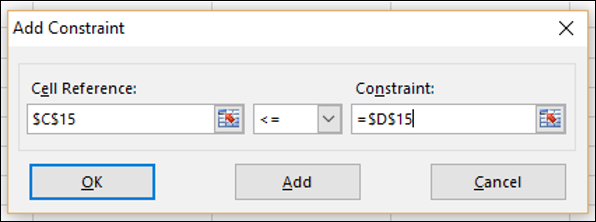
Step 7 − Set the constraint for total no. of units sold in Quarter1 as given below and click Add.
Step 8 − Set the constraint for total no. of units sold in Quarter2 as given below and click OK.
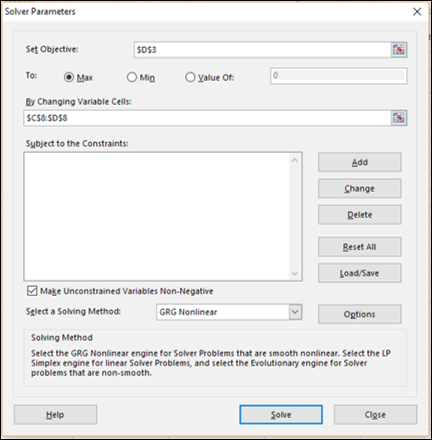
The Solver Parameters dialog box appears with the three constraints added in box –Subject to the Constraints.
Step 9 − In the Select a Solving Method box, select Simplex LP.
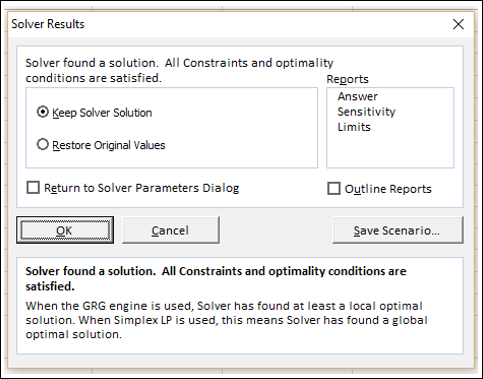
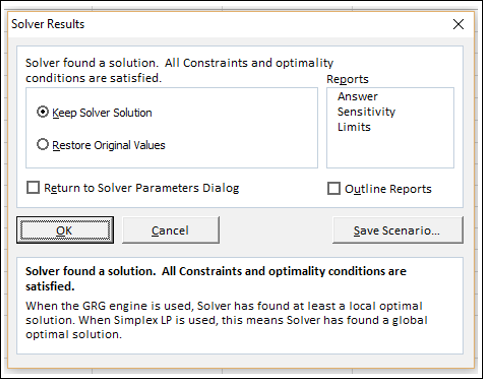
Step 10 − Click the Solve button. The Solver Results dialog box appears. Select Keep Solver Solution and click OK.
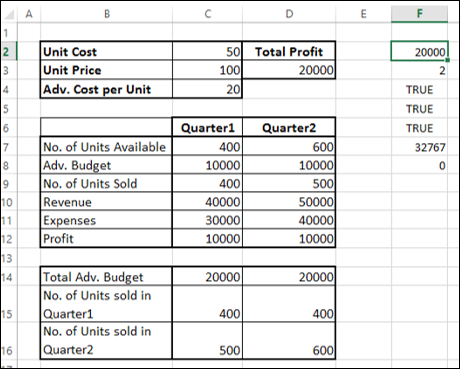
The results will appear in your worksheet.
As you can observe, the optimal solution that produces maximum total profit, subject to the given constraints, is found to be the following −
- Total Profit – 30000.
- Adv. Budget for Quarter1 – 8000.
- Adv. Budget for Quarter2 – 12000.
Stepping through Solver Trial Solutions
You can step through the Solver trial solutions, looking at the iteration results.
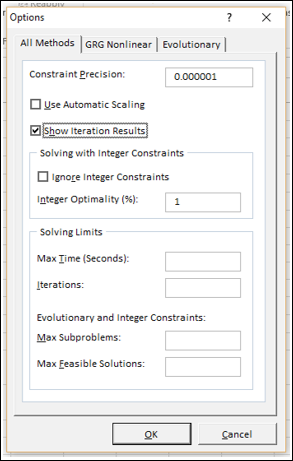
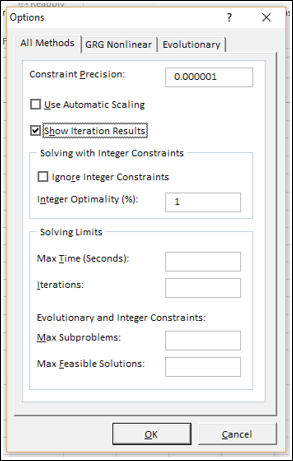
Step 1 − Click the Options button in the Solver Parameters dialog box.
The Options dialog box appears.
Step 2 − Select the Show Iteration Results box and click OK.
Step 3 − The Solver Parameters dialog box appears. Click Solve.
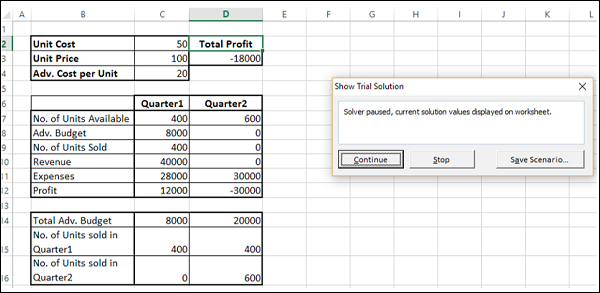
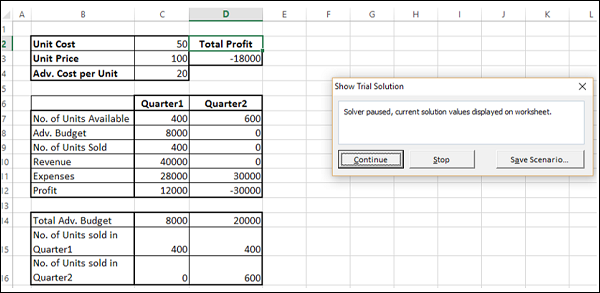
Step 4 − The Show Trial Solution dialog box appears, displaying the message — Solver paused, current solution values displayed on worksheet.
As you can observe, the current iteration values are displayed in your working cells. You can either stop the Solver accepting the current results or continue with the Solver from finding solution in further steps.
Step 5 − Click Continue.
The Show Trial Solution dialog box appears at every step and finally after the optimal solution is found, Solver Results dialog box appears. Your worksheet is updated at every step, finally showing the result values.
Saving Solver Selections
You have the following saving options for the problems that you solve with Solver −
-
You can save the last selections in the Solver Parameters dialog box with a worksheet by saving the workbook.
-
Each worksheet in a workbook can have its own Solver selections, and all of them will be saved when you save the workbook.
-
You can also define more than one problem in a worksheet, each with its own Solver selections. In such a case, you can load and save problems individually with the Load/Save in the Solver Parameters dialog box.
-
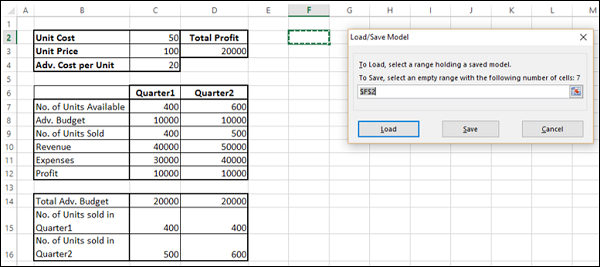
Click the Load/Save button. The Load/Save dialog box appears.
-
To save a problem model, enter the reference for the first cell of a vertical range of empty cells in which you want to place the problem model. Click Save.
-
-
The problem model (the Solver Parameters set) appears starting at the cell that you have given as the reference.
-
To load a problem model, enter the reference for the entire range of cells that contains the problem model. Then, click on the Load button.
Solver – это надстройка Microsoft Excel, которую можно использовать для оптимизации в анализе «что, если».
По мнению О’Брайена и Маракаса, оптимизационный анализ является более сложным расширением целенаправленного анализа. Вместо того, чтобы устанавливать конкретное целевое значение для переменной, цель состоит в том, чтобы найти оптимальное значение для одной или нескольких целевых переменных при определенных ограничениях. Затем одна или несколько других переменных меняются неоднократно, с учетом указанных ограничений, пока вы не найдете лучшие значения для целевых переменных.
В Excel вы можете использовать Solver, чтобы найти оптимальное значение (максимальное или минимальное или определенное значение) для формулы в одной ячейке, называемой целевой ячейкой, при условии соблюдения определенных ограничений или ограничений для значений других ячеек формулы на рабочем листе. ,
Это означает, что Солвер работает с группой ячеек, называемых переменными решения, которые используются при вычислении формул в ячейках цели и ограничения. Солвер корректирует значения в ячейках переменных решения, чтобы удовлетворить ограничения на ячейки ограничений и получить желаемый результат для целевой ячейки.
Вы можете использовать Solver, чтобы найти оптимальные решения для различных проблем, таких как –
-
Определение ежемесячного ассортимента продукции для подразделения по производству лекарств, которое максимизирует прибыльность.
-
Планирование рабочей силы в организации.
-
Решение транспортных проблем.
-
Финансовое планирование и бюджетирование.
Определение ежемесячного ассортимента продукции для подразделения по производству лекарств, которое максимизирует прибыльность.
Планирование рабочей силы в организации.
Решение транспортных проблем.
Финансовое планирование и бюджетирование.
Активация Solver надстройки
Прежде чем приступить к поиску решения проблемы с Solver, убедитесь, что надстройка Solver активирована в Excel следующим образом:
- Нажмите вкладку ДАННЫЕ на ленте. Команда Solver должна появиться в группе «Анализ», как показано ниже.
Если вы не можете найти команду Солвера, активируйте ее следующим образом:
- Нажмите вкладку ФАЙЛ.
- Нажмите Опции на левой панели. Откроется диалоговое окно «Параметры Excel».
- Нажмите Надстройки на левой панели.
- Выберите Надстройки Excel в поле «Управление» и нажмите «Перейти».
Откроется диалоговое окно «Надстройки». Проверьте Надстройку Solver и нажмите Ok. Теперь вы можете найти команду Solver на ленте под вкладкой DATA.
Методы решения, используемые Solver
Вы можете выбрать один из следующих трех методов решения, которые поддерживает Excel Solver, в зависимости от типа проблемы:
LP Simplex
Используется для линейных задач. Модель Солвера является линейной при следующих условиях:
-
Целевая ячейка вычисляется путем сложения членов формы (изменяющаяся ячейка) * (постоянная).
-
Каждое ограничение удовлетворяет требованию линейной модели. Это означает, что каждое ограничение оценивается путем сложения членов формы (изменяющейся ячейки) * (константы) и сравнения сумм с константой.
Целевая ячейка вычисляется путем сложения членов формы (изменяющаяся ячейка) * (постоянная).
Каждое ограничение удовлетворяет требованию линейной модели. Это означает, что каждое ограничение оценивается путем сложения членов формы (изменяющейся ячейки) * (константы) и сравнения сумм с константой.
Обобщенный редуцированный градиент (GRG) нелинейный
Используется для гладких нелинейных задач. Если ваша целевая ячейка, любое из ваших ограничений или оба содержат ссылки на изменяющиеся ячейки, которые не имеют (изменяющейся ячейки) * (постоянной) формы, у вас есть нелинейная модель.
эволюционный
Используется для гладких нелинейных задач. Если ваша целевая ячейка, любое из ваших ограничений или оба содержат ссылки на изменяющиеся ячейки, которые не имеют (изменяющейся ячейки) * (постоянной) формы, у вас есть нелинейная модель.
Понимание оценки Солвера
Для Солвера требуются следующие параметры –
- Ячейки с переменными решениями
- Клетки ограничения
- Объективные Клетки
- Метод решения
Оценка решателя основана на следующем:
-
Значения в ячейках переменных решения ограничены значениями в ячейках ограничений.
-
Вычисление значения в целевой ячейке включает значения в ячейках переменных решения.
-
Солвер использует выбранный метод решения, чтобы получить оптимальное значение в целевой ячейке.
Значения в ячейках переменных решения ограничены значениями в ячейках ограничений.
Вычисление значения в целевой ячейке включает значения в ячейках переменных решения.
Солвер использует выбранный метод решения, чтобы получить оптимальное значение в целевой ячейке.
Определение проблемы
Предположим, вы анализируете прибыль, полученную компанией, которая производит и продает определенный продукт. Вас просят найти сумму, которая может быть потрачена на рекламу в следующие два квартала, но не более 20 000. Уровень рекламы в каждом квартале влияет на следующее –
- Количество проданных единиц, косвенно определяющих сумму выручки от продаж.
- Сопутствующие расходы и
- Прибыль
Вы можете приступить к определению проблемы как –
- Найти стоимость единицы.
- Найти стоимость рекламы на единицу.
- Найти цену за единицу.
Затем установите ячейки для необходимых расчетов, как указано ниже.
Как вы можете заметить, расчеты сделаны для квартала 1 и квартала 2, которые рассматриваются:
-
Количество единиц, доступных для продажи в квартале 1, составляет 400, а в квартале 2 – 600 (ячейки – C7 и D7).
-
Начальные значения для рекламного бюджета установлены как 10000 за квартал (ячейки – C8 и D8).
-
Количество проданных единиц зависит от стоимости рекламы на единицу и, следовательно, является бюджетом на квартал / Adv. Стоимость за единицу. Обратите внимание, что мы использовали функцию Min, чтобы убедиться, что нет. единиц, проданных в <= нет. из доступных единиц. (Клетки – C9 и D9).
-
Выручка рассчитывается как цена за единицу * Количество проданных единиц (ячейки – C10 и D10).
-
Расходы рассчитываются как стоимость единицы * Количество доступных единиц + Adv. Стоимость за этот квартал (Клетки – C11 и D12).
-
Прибыль – это доход – расходы (ячейки C12 и D12).
-
Общая прибыль – это прибыль за квартал 1 + прибыль за квартал 2 (ячейка – D3).
Количество единиц, доступных для продажи в квартале 1, составляет 400, а в квартале 2 – 600 (ячейки – C7 и D7).
Начальные значения для рекламного бюджета установлены как 10000 за квартал (ячейки – C8 и D8).
Количество проданных единиц зависит от стоимости рекламы на единицу и, следовательно, является бюджетом на квартал / Adv. Стоимость за единицу. Обратите внимание, что мы использовали функцию Min, чтобы убедиться, что нет. единиц, проданных в <= нет. из доступных единиц. (Клетки – C9 и D9).
Выручка рассчитывается как цена за единицу * Количество проданных единиц (ячейки – C10 и D10).
Расходы рассчитываются как стоимость единицы * Количество доступных единиц + Adv. Стоимость за этот квартал (Клетки – C11 и D12).
Прибыль – это доход – расходы (ячейки C12 и D12).
Общая прибыль – это прибыль за квартал 1 + прибыль за квартал 2 (ячейка – D3).
Далее вы можете установить параметры для Солвера, как указано ниже –
Как вы можете заметить, параметры Солвера –
-
Объективная ячейка – D3, в которой содержится общая прибыль, которую вы хотите максимизировать.
-
Ячейки с переменными решениями – это C8 и D8, которые содержат бюджеты на два квартала – квартал 1 и квартал 2.
-
Есть три ячейки ограничения – C14, C15 и C16.
-
Ячейка C14, которая содержит общий бюджет, должна установить ограничение 20000 (ячейка D14).
-
Ячейка C15, которая содержит номер единиц, проданных в первом квартале, – установить ограничение <= нет. единиц, доступных в Quarter1 (ячейка D15).
-
Ячейка C16, которая содержит номер единиц, проданных в Quarter2, это установить ограничение <= нет. единиц, доступных в квартале 2 (ячейка D16).
-
Объективная ячейка – D3, в которой содержится общая прибыль, которую вы хотите максимизировать.
Ячейки с переменными решениями – это C8 и D8, которые содержат бюджеты на два квартала – квартал 1 и квартал 2.
Есть три ячейки ограничения – C14, C15 и C16.
Ячейка C14, которая содержит общий бюджет, должна установить ограничение 20000 (ячейка D14).
Ячейка C15, которая содержит номер единиц, проданных в первом квартале, – установить ограничение <= нет. единиц, доступных в Quarter1 (ячейка D15).
Ячейка C16, которая содержит номер единиц, проданных в Quarter2, это установить ограничение <= нет. единиц, доступных в квартале 2 (ячейка D16).
Решение проблемы
Следующим шагом является использование Солвера, чтобы найти решение следующим образом:
Шаг 1 – Перейдите в ДАННЫЕ> Анализ> Решатель на ленте. Откроется диалоговое окно «Параметры решателя».
Шаг 2 – В поле «Установить цель» выберите ячейку D3.
Шаг 3 – Выберите Макс.
Шаг 4 – Выберите диапазон C8: D8 в поле « Изменение переменных ячеек» .
Шаг 5 – Затем нажмите кнопку Добавить, чтобы добавить три ограничения, которые вы определили.
Шаг 6 – Откроется диалоговое окно Add Constraint. Установите ограничение для общего бюджета, как указано ниже, и нажмите «Добавить».
Шаг 7 – Установите ограничение для общего номера. единиц, проданных в квартале 1, как указано ниже, и нажмите кнопку Добавить.
Шаг 8 – Установите ограничение для общего номера. единиц, проданных в квартале 2, как указано ниже, и нажмите кнопку ОК.
Появится диалоговое окно «Параметры решателя» с тремя ограничениями, добавленными в поле «Подчинить ограничениям».
Шаг 9 – В поле « Выбрать метод решения» выберите Simplex LP.
Шаг 10 – Нажмите кнопку Решить. Откроется диалоговое окно «Результаты решателя». Выберите Keep Solver Solution и нажмите ОК.
Результаты появятся в вашем рабочем листе.
Как вы можете заметить, оптимальное решение, которое дает максимальную общую прибыль с учетом данных ограничений, оказывается следующим:
- Общая прибыль – 30000.
- Adv. Бюджет на 1 квартал – 8000.
- Adv. Бюджет на Квартал2 – 12000.
Пошаговое решение Solver Trial Solutions
Вы можете просмотреть пробные решения Solver, посмотрев результаты итерации.
Шаг 1 – Нажмите кнопку «Параметры» в диалоговом окне «Параметры решателя».
Откроется диалоговое окно « Параметры ».
Шаг 2 – Установите флажок «Показать результаты итерации» и нажмите «ОК».
Шаг 3 – Откроется диалоговое окно « Параметры решателя». Нажмите Решить .
Шаг 4 – Появится диалоговое окно « Показать пробное решение », в котором будет отображено сообщение « Солвер остановлен», а текущие значения решения будут отображены на листе .
Как вы можете видеть, текущие значения итерации отображаются в ваших рабочих ячейках. Вы можете либо остановить Солвер, принимая текущие результаты, либо продолжить, пока Солвер не найдет решение на следующих шагах.
Шаг 5 – Нажмите Продолжить.
Диалоговое окно « Показать пробное решение » появляется на каждом этапе, и, наконец, после нахождения оптимального решения открывается диалоговое окно «Результаты решения». Ваш рабочий лист обновляется на каждом шаге, и, наконец, отображаются значения результатов.
Сохранение выбора Солвера
У вас есть следующие варианты сохранения для задач, которые вы решаете с помощью Солвера –
Вы можете сохранить последние выбранные значения в диалоговом окне «Параметры решателя» вместе с рабочим листом, сохранив рабочую книгу.
Каждый лист в книге может иметь свои собственные варианты Солвера, и все они будут сохранены при сохранении книги.
Вы также можете определить более одной проблемы на рабочем листе, каждый из которых имеет свой собственный выбор Солвера. В таком случае вы можете загружать и сохранять проблемы по отдельности с помощью диалогового окна «Параметры решателя» «Загрузить / сохранить».
Нажмите кнопку Загрузить / Сохранить . Откроется диалоговое окно загрузки / сохранения.
Чтобы сохранить модель проблемы, введите ссылку для первой ячейки вертикального диапазона пустых ячеек, в который вы хотите поместить модель проблемы. Нажмите Сохранить.
Модель проблемы (набор параметров решателя) появляется начиная с ячейки, которую вы указали в качестве справочной.
Чтобы загрузить модель проблемы, введите ссылку для всего диапазона ячеек, которые содержат модель проблемы. Затем нажмите на кнопку «Загрузить».