Проектирование нейронных сетей в ms excel - Word и Excel

Ты
узнаешь:

·
крытые
слои нейрона;

·
математическую
запись функции единичного скачка;

·
формулу
среднеквадратичной ошибки.

Ты
научишься:

·
проектировать
искусственный нейрон в электронной таблице;

·
вычислять
функцию единичного скачка и среднеквадратичную ошибку.

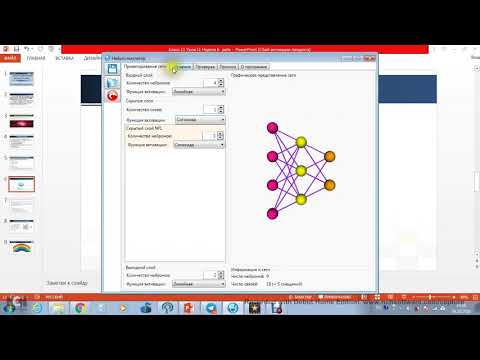
В
случае, когда нейросеть состоит из большого количества нейронов, вводят
термин «слой». Слои делятся на три основных типа: входной
(синий), скрытый (фиолетовый) и выходной (зеленый). Соответственно, есть
входной слой, который получает информацию, n скрытых слоев, которые ее
обрабатывают, и выходной слой, который выводит результат.

Нейроны
оперируют числами в диапазоне [0, 1] или [–1, 1]. Продемонстрируем
расчет результата нейронной сети с использованием логистической функции и ее
ошибку, используя среднеквадратичную ошибку.

Тренировочный
сет, или обучающая выборка (датасет), – набор
данных, на которых нейронная сеть будет обучаться. В нашем случае
исключающего или (xor) у нас всего 4 разных исхода, то есть у нас
будет 4 тренировочных сета: 0xor0 = 0, 0xor1 =
1, 1xor0 = 1,1xor1 = 0.

Итерация –
это своеобразный счетчик, который увеличивается каждый раз, когда нейронная
сеть проходит один набор данных.

Важно не
путать итерацию с эпохой и понимать последовательность их инкремента.
Сначала n раз увеличивается итерация, а потом уже эпоха, и
никак не наоборот.

Эпоха –
при инициализации нейронной сети эта величина устанавливается в 0 и
имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована
сеть, и тем лучше ее результат. Эпоха увеличивается каждый раз, когда мы
проходим весь набор обучающих выборок, в нашем случае 4 сета,
или 4 итерации.

Ошибка –
формируется каждую эпоху и должна идти на спад. Если этого не происходит,
значит, вы что-то делаете не так. Ошибку можно вычислить разными способами,
но мы рассмотрим два: среднеквадратичную ошибку и среднеквадратичное
отклонение.

Формула
вычисления среднеквадратичной ошибки:

Cреднеквадратичное
отклонение вычисляется по формуле:

O₁, O₂,
…, O_n – фактический сигнал, полученный на выходе
(входе);

A₁, A₂,
…, A_n – идеальный сигнал, который должен быть
получен на выходе (входе);

n –
количество датасетов.

I₁, I₂ –
входные нейроны;

H₁, H₂ –
скрытые нейроны;

O₁ –
выходной нейрон.

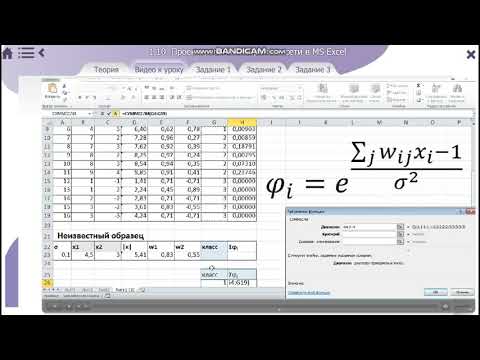
Запишем
значения параметров в Excel:

Вычисляем
взвешенную сумму для первого входа:

Взвешенная
сумма первого входа: H1input = 0 ⋅ 0,13
+ 1 ⋅
(–0,58) = –0,58.

Используем
сигмоидную функцию активации для первого входа. В этом нам поможет встроенная
функция экспоненты (EXP) в MS Excel: H1output = sigmoid(–0,58) =
0,36.

Вычисляем
взвешенную сумму для второго входа:

Взвешенная
сумма второго входа: H2input = 0 ⋅ 0,52
+ 1 ⋅ 0,63
= 0,63.

Используем
сигмоидную функцию активации для второго входа: H2output = sigmoid(0,63) =
0,65.

Вычисляем
взвешенную сумму для выхода:

O1input =
0,36 ⋅ 2,5
+ 0,65 ⋅
(–0,3) = 0,7.

Используем
сигмоидную функцию активации для выхода.

O1output = sigmoid(0,7) =
0,67.

Вычисляем
ошибку по формуле, используя встроенная функцию СТЕПЕНЬ в MS Excel:

Среднеквадратичная
ошибка O1ideal = 1 (0xor1 = 1).

Error = ((1 – 0,67)²)/1
= 0,11.

Результат
на выходе нейрона будет равен 0,67, а среднеквадратичная ошибка будет
равна 11 %.

Кроме
сигмоидной функции, существует ряд и других фукнции активации, которые
используются при обучении искусственной нейронной сети. Функция
единичного скачка – это простой вид функции активации, где выход
нейрона может быть равен только 0 или 1.

Графически
эту функцию можно изобразить следующим образом:

Математическая
запись функции единичного скачка выгдядит так:

Если
взвешенная сумма больше определенного порога b, то выход нейрона
равен 1.

Как ее
можно использовать? Предположим, что мы поедем на море только тогда, когда
взвешенная сумма больше или равна 5. Если взвешенная сумма = 2,
выход нейрона = 0, то мы никуда не едем. Если взвешенная сумма = 7,
значит, выходной сигнал нашего нейрона равен 1, и мы едем на море.
Нейрон зависит от взвешенной суммы, и если она получается больше его порога,
то нейрон выдает выходной сигнал, равный 1.

Источник

Опубликовано: 14.01.2021,
Автор: Elvira_198401 334

Ты узнаешь:

крытые слои нейрона;
математическую запись функции единичного скачка;
формулу среднеквадратичной ошибки.

Ты научишься:

проектировать искусственный нейрон в электронной таблице;
вычислять функцию единичного скачка и среднеквадратичную ошибку.

В случае, когда нейросеть состоит из большого количества нейронов, вводят термин «слой». Слои делятся на три основных типа: входной (синий), скрытый (фиолетовый) и выходной (зеленый). Соответственно, есть входной слой, который получает информацию, n скрытых слоев, которые ее обрабатывают, и выходной слой, который выводит результат.

Источник

Обновлено: 15.04.2023

Вы могли уже видеть мой рассказ на тему того, почему в нейронных сетях так часто используют Сигмоиды для всевозможных преобразований. А сейчас я хочу привести пример простой нейронной сети, которая обучается и прекрасно аппроксимирует произвольные монотонные зависимости с помощью единственной универсальной функции. Ну и делать мы будем это снова в Excel, чтобы это мог повторить любой офисный работник без установки чего-либо к себе на комп.

Для начала нам придётся открыть Excel и как в прошлый раз нажать Alt+F11. В открывшемся окне создадим новый модуль для класса (правый клик где-нибудь слева => insert => Class Module) . И в него будем последовательно вставлять весь тот код, что будет ниже. Его я буду сопровождать своими комментариями.

Dim c(0 To 3) As Double ‘Коэффициенты
Dim tc(0 To 3) As Double ‘Пробные коэффициенты
Dim dc(0 To 3) As Double ‘Пробные изменения
Dim dy(0 To 3) As Double ‘Результаты изменения коэффициентов
Const st = 0.2 ‘Скорость обучения

Здесь мы просто определяем все переменные, которые будут использоваться в рамках конкретного нейрона.

Sub init() ‘Инициализация случайных значений коэффициентов сигмоиды
For i = 0 To 3
c(i) = Rnd() * 2 — 1
Next i
End Sub

Сигмоида у нас задаётся четырьмя параметрами. Первый коэффициент стоит, как множитель ко всей функции в целом. Второй коэффициент — перед иксом. Третий — прибавляется к иксу. Четвёртый — прибавляется ко всей функции в целом. И все эти коэффициенты задаются случайным образом от минус единицы до плюс единицы. F(x)=c1/e^(-c2*(x+c3))+c4

Таким подходом мы задаём всё многообразие сигмоид.

Sub NewC(De As Double, n As Integer) ‘Генерируем новый тестовый вес
For i = 0 To 3
If n = i Then
dc(i) = De * st
End If
tc(i) = c(i) + IIf(n = i, dc(i), 0)
Next i
End Sub

Передаём значение, на которое ошиблась наша функция и номер коэффициента, который хотим изменить. Изменяем этот коэффициент с учётом скорости обучения и нашей ошибки.

Sub SaveC(d As Worksheet, r As Integer) ‘Сохраняем веса
For i = 0 To 3
d.Cells(r, 8 + i) = c(i)
Next i
End Sub

Sub LoadC(d As Worksheet, r As Integer) ‘Загружаем веса
For i = 0 To 3
c(i) = d.Cells(r, 8 + i)
Next i
End Sub

Простые функции сохранения и загрузки коэффициентов, чтобы можно было продолжать работать с того места, где остановились.

Sub FixC() ‘Сохраняем тестовые веса
Dim my As Double
Dim j As Integer
j = 1
my = dy(0)
For i = 1 To 3 ‘Определяем максимальное изменение y
If dy(i) > my Then
my = dy(i)
j = i
End If
Next i
For i = 0 To 3 ‘Для максимального изменения y вес меняем полностью, для остальных в зависимости от величины изменения
c(i) = c(i) + dy(i) / my * dc(i)
Next i
End Sub

Сохраняем веса так, чтобы наиболее эффективное изменение веса с точки зрения устранения ошибки применялось полностью, а остальные — в соответствии с их вкладом в минимизацию ошибки.

Function res(x As Double, T As Boolean) As Double ‘Расчёт значения функции
c1 = IIf(T, tc(0), c(0))
c2 = IIf(T, tc(1), c(1))
c3 = IIf(T, tc(2), c(2))
c4 = IIf(T, tc(3), c(3))
ie = -c2 * (x + c3)
If ie > 40 Then ‘Если число в знаменателе очень большое, можно считать значение нулём
res = c4
ElseIf ie Then ‘Если число очень маленькое — единицей
res = c1 + c4
Else ‘В остальных случаях считаем честно
res = c1 / (1 + Exp(ie)) + c4
End If
End Function

Функция расчёта значения нашей сигмоиды. Чтобы не было деления на ноль и прочих проблем, для больших значений экспоненты ставим известные значения. Параметр Т отвечает за то, используем мы тестовые коэффициенты или боевые.

Sub TryC(x As Double, y As Double, n As Integer) ‘Пробуем изменить конкретный вес. Если стало лучше, фиксируем это
Dim De As Double
De = Abs(y — res(x, False))
Call NewC(De, n)
Dim NDe As Double
NDe = Abs(y — res(x, True))
If NDe >= De Then
Call NewC(-De, n)
NDe = Abs(y — res(x, True))
End If
If NDe Then
dy(n) = De — NDe
End If
End Sub

Пробуем изменить тестовые коэффициенты. Если ошибка уменьшилась, фиксируем это, чтобы в будущем изменить уже боевые коэффициенты.

Public Function MakeRnd(n As Integer) As String ‘Формируем случайный перебор значений от нуля до n-1
Randomize
Dim i As Integer
MakeRnd = «,»
Dim S As String
NewS:
S = Val(Rnd() * n)
If MakeRnd Like «*,» & S & «,*» Then GoTo NewS
If S >= n Then GoTo NewS
MakeRnd = MakeRnd & S & «,»
i = i + 1
If i Then GoTo NewS
MakeRnd = Left(MakeRnd, Len(MakeRnd) — 1)
MakeRnd = Right(MakeRnd, Len(MakeRnd) — 1)
End Function

Это простая функция, которая генерирует случайную по порядку последовательность от нуля до n-1. Мы её будем использовать, чтобы случайно перебирать коэффициенты не по порядку. В некоторых ситуациях это может иметь значение и делать расчёт сети предвзятым.

Sub Chng(x As Double, y As Double)
For i = 0 To 3 ‘Обнуляем значения
dy(i) = 0
dc(i) = 0
Next i
Dim tw() As String
tw = Split(MakeRnd(4), «,»)
For i = 0 To UBound(tw)
Call TryC(x, y, Val(tw(i)))
Next i
Call FixC
End Sub

Эта процедура просто отражает логику использования функций. Сначала обнуляем все значения, затем формируем последовательность, для перебора весов. Затем вычисляем эффективность изменения веса при устранении ошибки. Затем сохраняем новые веса.

Теперь заполним какими-нибудь данными нашу функцию. Я в первом столбце перечислил значения аргументов, в третьем — значение целевой функции. А четвёртый столбец остаётся для занесения результатов расчёта сети, чтобы сравнить с целевой функцией. Ну и отдельно посчитал среднюю квадратичную ошибку. Вышло примерно так:

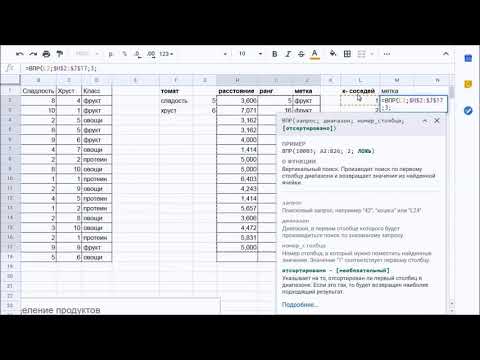
Разработка алгоритма распознавания чисел с эмуляцией нейронной сети на основе использования стандартных функций табличного процессора MS Excel. Распознавание образов знаков десятичной системы, построенной с помощью горизонтальных и вертикальных штрихов.

Рубрика Программирование, компьютеры и кибернетика

Вид статья

Язык русский

Дата добавления 29.01.2020

Размер файла 153,7 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Омская гуманитарная академия

ПРОЕКТИРОВАНИЕ НЕЙРОННОЙ СЕТИ В ТАБЛИЧНОМ ПРОЦЕССОРЕ MS EXCEL

Д.П. Денисов, О.К. Касымова

Разработан алгоритм распознавания чисел с эмуляцией нейронной сети на основе использования стандартных функций табличного процессора MS Excel. Информация может быть полезной для специалиста и слушателя в плане изучения проблем нейронной сети.

Ключевые слова: нейронная сеть, алгоритм распознавания чисел.

Нейронные сети широко используются в распознавании образов, идентификации объектов и прогнозировании экономических процессов.

Под образом понимается структурированное описание изучаемого объекта, процесса или явления, представленное вектором признаков, выражаемых количественно. В результате идентификации объектов осуществляется их классификация, позволяющая выявлять закономерности и выполнять прогнозы [1].

С целью наглядного отражения принципа работы нейронной сети спроектирован алгоритм распознавания знаков с использованием стандартных функций табличного процессора MS Excel. Решение компактно размещается на одной странице электронной книги (рисунок), обозримо без применения скроллинга [2] и позволяет ознакомиться с основными элементами и режимами работы нейронной сети в интерактивном режиме.

Системе предлагается распознать образы знаков десятичной системы (0, 1, 2, …, 9), построенные с помощью горизонтальных, вертикальных и наклонных штрихов (коротких линий):

Чтобы упростить концепцию сверточных нейронных сетей, я попытаюсь объяснить, что происходит при разработке модели глубокого обучения. Для получения дополнительной информации, я рекомендую поисконлайнкак есть обильное количество доступной информации (как этовидео). Это объяснение получено изfast.aiрепозиторий.

Эта картина простой нейронной сети в основном представляет то, что происходит в этом примере.

Эти данные изображения № 7 изMNISTбазы данных, и мы предполагаем, что вы используетемодель перед поездомдля классификации.

Скрытый слой 1

Скрытый слой — это то, что преобразует входные данные, чтобы отличить более сложные элементы от данных для выходного уровня, чтобы сделать более точную оценку.

Два фильтра будут представлять разные формы — первый фильтр предназначен для обнаружения горизонтальных краев, второй фильтр обнаруживает вертикальные края. Этот фильтр 3х3 называетсясверточное ядро, Фильтр 1 активируется для горизонтальных ребер на входе. Conv1 показывает активацию обоих после взятия секции 3×3 ввода и умножения ее на сверточное ядро. Следующая картина ниже дает вам лучшую идею.

* Хотя это представлено в 2d массиве, они должны быть сложены какТензор, Где каждая матрица представляет срез в тензоре. Это все по существу строковые операции (Линейная алгебра), которые происходят.

= SUM (F11: H13 * $ AD $ 11: $ AF $ 13) — это происходящая Свертка.

Эта сумма приведет к числу активации 3 для этого конкретного места 3×3 на входе.

Функция активации

Далее мы используем нашу единицу нелинейности с помощьюРЕЛУкак наша функция активации для устранения негативов. Далее мы видим, что негативы исчезают на следующей картинке.

Скрытый слой 2

Далее мы делаем еще одну свертку. Conv2 будет следующим скрытым слоем. Это взвесит обе матрицы в Conv1, взяв их произведение суммы. Ядро свертки здесь будет представлять собой Тензор 2X3X3.

После использования RELU мы создали второй слой.

Макс Пул

Максимальное объединение вдвое уменьшает разрешение по высоте и ширине, принимая только максимум 2х2 в Conv2. В матрице Макспула мы видим только максимальное значение сечения 2×2 в Conv2, которое равно 33. Пул вычисляется быстрее, чем свертки. Кроме того, это дает вам некоторое количествоинвариантность перевода,

Выходной слой

Затем мы создаем наш полностью связанный слой, взяв все наши активации в Maxpool и придав им всем вес. Это делается с помощью матричного продукта. В Excel, мы возьмем сумму активаций и весов. Таким образом, вместо синтаксического анализа каждой секции в сверточном слое, как и раньше, полностью подключенный слой (плотный слой) будет выполнять классификацию объектов, которые были извлечены сверточными слоями и подвергнуты понижающей дискретизации слоями с максимальным пулом.

Этот пример представляет только один класс, то есть один номер. Нам еще предстоит классифицировать остальные числа.

вычислять функцию единичного скачка и среднеквадратичную ошибку.

1) Нужно зарегистрироваться/авторизоваться на сайте.
2) Добавить материал (публикацию) на сайт. ссылка на добавление материала.
В топе показаны авторы, у которых самое большое количество публикаций. Подробная инструкция для публикации материала

Читайте также:



Конспект занятия путешествие в осенний лес



Конспект занятия по логоритмике новый год



Открытка с лилией технология 2 класс конспект



Конспект урока по немецкому языку в 9 классе по теме сми



Цепочки калькулятор конспект урока 2 класс петерсон презентация

Источник

В современном мире трудно найти человека, который бы не слышал про нейронные сети. Кажется, их применяют всюду: оживление фотографий, DeepFake, маски для фото в соцсетях и прочее. Но для большинства людей они являются чем-то абстрактным и непонятным.

Однако создать свою нейросеть можно даже не имея знаний о языках программирования, и используя простейший инструмент, знакомый любому офисному сотруднику – MS Excel.

Схематично моя будущая нейросеть выглядит так:

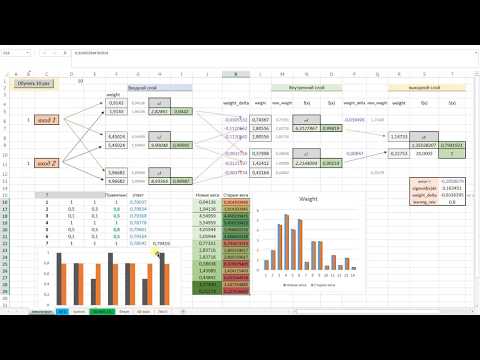
Это упрощенная схема перцептрона. Перцептрон – простейший вид нейронных сетей, в основе которых лежит математическая модель восприятия информации мозгом, состоящая из сенсоров, ассоциативных и реагирующих элементов. На вход подаются значения признаков, которые могут быть равны 0 или 1. Строгая бинарность обусловлена тем, что признаки – это, своего рода, сенсоры, и они могут находиться либо в состоянии покоя (равны 0), либо в состоянии возбуждения (равны 1). Затем эти признаки умножатся на вес и суммируются. После при помощи функции активации (сигмоиды) получаю значения на выходе от 0 до 1. Таким образом, главной задачей является нахождение весов, обеспечивающих наиболее точное прогнозирование.

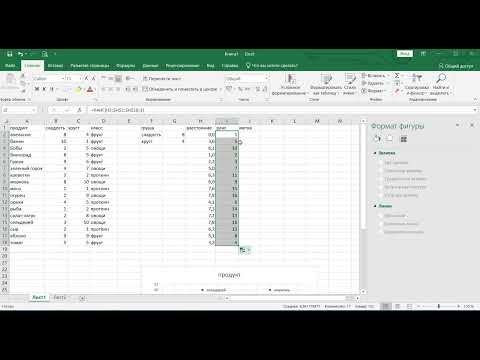
Представлю, что требуется по определенному набору признаков научить нейросеть определять является ли животное домашней кошкой или нет.

В датасете имеется 9 признаков, если экземпляр им обладает, то ставится 1, если нет, то 0. Целевой столбец назван «Выход»: 1 – значит экземпляр кошка, 0 – не кошка. В идеале нейросеть должна предсказать 1 для всех кошек и 0 для всех не кошек.

Первый шаг – создание таблицы поиска весов для каждого признака:

В диапазоне M3:U2 генерирую случайные величины весов при помощи формулы СЛЧИС().

Далее создаю столбцы для Bias (смещение) и Output (предсказание модели):

Формула в ячейке W3:

=B3*M3+C3*N3+D3*O3+E3*P3+F3*Q3+G3*R3+H3*S3+I3*T3+J3*U3

Протягиваю формулу до ячейки W14.

Bias – нейрон смещения. Простыми словами, это дополнительная информация о природе данных для модели, способ показать модели, «в какую сторону думать».

Формула в ячейке output – функция сигмоиды:

=ЕСЛИ(Bias=0;0;1/(1+(EXP(-Bias))))

Данная функция необходима для интерпретации значения bias. Мне нужно получить значения от 0 до 1. Output – предсказание модели. Если значение меньше 0.5, то экземпляр не является кошкой, если больше, то является.

Создаю таблицу для корректировки весов:

В ячейке Z3 следующая формула:

=($K3-$X3)*B3*$X3*(1-$X3)

Протягиваю её на весь диапазон Z1:AH14

Возвращаюсь в блок с весами: в ячейку М4 прописываю формулу: =M3+Z3

Протягиваю её на диапазон M4:U14:

В диапазоне AJ3:AJ14 пишу формулу: =ЕСЛИ(X3<0,5;0;1) – если значение в столбце Output больше, либо равно 0.5, то модель предполагает, что в строке домашняя кошка.

В диапазоне AK3:AK14 пишу формулу: =ЕСЛИ(K3=1;ЕСЛИ(AJ3=K3;1;0);»») – проверяю правильно ли модель предсказала домашнюю кошку.

В диапазоне AL3:AL14 пишу формулу: =ЕСЛИ(K3=0;ЕСЛИ(AJ3=K3;1;0);»»)– проверяю правильно ли модель предсказала не домашнюю кошку.

В ячейках AK15 и AL15 формулы СРЗНАЧ() для отображения доли правильных ответов.

На рисунке видно, что на данный момент модель считает все записи домашними кошками (цифра 1 в столбце «Предсказание»).

Копирую диапазон M14:U14 и вставляю значения в диапазон M3:U3:

Смотрю результат:

Теперь модель не все записи считает домашними кошками, но результат пока ещё не лучший.

Совершаю ещё несколько итераций. Копирую диапазон M14:U14 и вставляю значения в диапазон M3:U3. В таблице ниже видно, как менялись предсказания после каждого цикла:

В итоге, моя нейросеть после восьми итераций верно предсказала значения для всех строк.

Используя полученные веса из диапазона M14:U14, можно проверять другие комбинации признаков, и модель будет предсказывать является ли представленная строка домашней кошкой или нет.

Видно, что модель неидеальна, так как неверно предсказала рысь. Зато манула она определила верно, несмотря на то, что он больше походит на домашнюю кошку, чем рысь. На самом деле 100%-я точность для нейросетей невозможна, поэтому полученный результат можно считать неплохим. На практике использование MS Excel для задач машинного обучения — не очень хорошая идея, так как он не может работать с большим объемом данных, да и создан совершенно для другого. Однако, используя методы, представленные в посте, можно самостоятельно «поиграть» с данными, что поможет понять базовые принципы работы нейросетей.

Источник

Перевод

Ссылка на автора

Чтобы упростить концепцию сверточных нейронных сетей, я попытаюсь объяснить, что происходит при разработке модели глубокого обучения. Для получения дополнительной информации, я рекомендую поиск онлайн как есть обильное количество доступной информации (как это видео). Это объяснение получено из fast.ai репозиторий.

Эта картина простой нейронной сети в основном представляет то, что происходит в этом примере.

Простая нейронная сеть

Входной слой

Эти данные изображения № 7 из MNIST базы данных, и мы предполагаем, что вы используете модель перед поездом для классификации.

Вы можете увидеть 7 по большим числам в данных

Скрытый слой 1

Скрытый слой — это то, что преобразует входные данные, чтобы отличить более сложные элементы от данных для выходного уровня, чтобы сделать более точную оценку.

Два фильтра будут представлять разные формы — первый фильтр предназначен для обнаружения горизонтальных краев, второй фильтр обнаруживает вертикальные края. Этот фильтр 3х3 называется сверточное ядро, Фильтр 1 активируется для горизонтальных ребер на входе. Conv1 показывает активацию обоих после взятия секции 3×3 ввода и умножения ее на сверточное ядро. Следующая картина ниже дает вам лучшую идею.

* Хотя это представлено в 2d массиве, они должны быть сложены как Тензор, Где каждая матрица представляет срез в тензоре. Это все по существу строковые операции (Линейная алгебра), которые происходят.

= SUM (F11: H13 * $ AD $ 11: $ AF $ 13) — это происходящая Свертка.

Эта сумма приведет к числу активации 3 для этого конкретного места 3×3 на входе.

Это это будет представлять один слой.

Функция активации

Далее мы используем нашу единицу нелинейности с помощью РЕЛУ как наша функция активации для устранения негативов. Далее мы видим, что негативы исчезают на следующей картинке.

Скрытый слой 2

Далее мы делаем еще одну свертку. Conv2 будет следующим скрытым слоем. Это взвесит обе матрицы в Conv1, взяв их произведение суммы. Ядро свертки здесь будет представлять собой Тензор 2X3X3.

После использования RELU мы создали второй слой.

Слой 1 и 2

Макс Пул

Максимальное объединение вдвое уменьшает разрешение по высоте и ширине, принимая только максимум 2х2 в Conv2. В матрице Макспула мы видим только максимальное значение сечения 2×2 в Conv2, которое равно 33. Пул вычисляется быстрее, чем свертки. Кроме того, это дает вам некоторое количество инвариантность перевода,

Выходной слой

Затем мы создаем наш полностью связанный слой, взяв все наши активации в Maxpool и придав им всем вес. Это делается с помощью матричного продукта. В Excel, мы возьмем сумму активаций и весов. Таким образом, вместо синтаксического анализа каждой секции в сверточном слое, как и раньше, полностью подключенный слой (плотный слой) будет выполнять классификацию объектов, которые были извлечены сверточными слоями и подвергнуты понижающей дискретизации слоями с максимальным пулом.

Этот пример представляет только один класс, то есть один номер. Нам еще предстоит классифицировать остальные числа.

Источник

В этой статье вы получите ряд разъяснений и рекомендаций, которые пригодятся вам при создании нейронной сети. Также будут предоставлены полезные ссылки для самостоятельного изучения. Что же, не будем терять времени!

Шаг 1. Поговорим о нейронах и методах прямого распространения

Прежде чем начать разговор о нейронных сетях, нужно сначала разобраться с тем, что такое один нейрон. Здесь всё достаточно просто: нейрон принимает несколько значений, а возвращает только одно, стало быть, он похож на функцию.

Для наилучшего понимания давайте посмотрим на картинку ниже. Круг — это искусственный нейрон. Он получает 5, а возвращает 1. Под вводом понимается сумма трёх синапсов, соединённых с нейроном (это три стрелки слева).

При этом входные данные могут быть численными представлениями 2-х различных свойств. К примеру, когда создаёшь спам-фильтр, они могут означать наличие больше чем одного слова, написанного прописными буквами, и наличие слова «Виагра».

Также следует понимать, что входные значения умножаются на собственные так называемые «веса» — в нашем случае это 7 и 3 (выделены синим).

Далее полученные значения складываются со смещением, и получается число 5, которое у нас выделено красным. Это и есть ввод искусственного нейрона.

Идём дальше. Нейрон выполняет вычисление, выдавая выходное значение. Мы получили 1, так как именно единице равно округлённое значение сигмоиды в точке 5. Если, опять же, вспомнить про спам-фильтр, то факт вывода единицы означал бы, что текст был помечен нейроном в качестве спама.

Объединив эти нейроны, вы получите в итоге прямо распространяющуюся нейронную сеть. В ней процесс идёт от ввода к выводу и через нейроны, которые соединены синапсами.

Для наилучшего понимания этого процесса посмотрите серию видео на английском, от Welch Labs.

Шаг 2. Сигмоида

Прежде чем приступить к следующему шагу, было бы неплохо ознакомиться с 4-й неделей курса по Machine Learning от Coursera — она как раз посвящена нейронным сетям и помогла бы вам разобраться в особенностях и принципах их работы. Да, этот курс слишком сильно углубляется в математику, плюс основан на Octave, хотя многие предпочитают Python. Но тем не менее там можно почерпнуть много полезных знаний.

Итак, вернёмся к нашей сигмоиде. Дело в том, что она фигурирует во многих аспектах нейронных сетей. Её описание вы можете посмотреть, например, здесь. Но на одной теории, сами понимаете, далеко не уедешь. Именно поэтому для наилучшего понимания следует закодить её самостоятельно. Чтобы это сделать, следует написать реализацию алгоритма логистической регрессии, использующего сигмоиду.

Если честно, это может занять целый день, причём результат будет далёк от идеального. Вот, к примеру, как с этим справился Per Harald Borgen, англоязычная статья которого стала основой материала, который вы сейчас читаете. Но главное здесь не в том, чтобы сделать всё идеально, а в том, чтобы разобраться, как всё работает. И понять, как устроена сигмоида.

Шаг 3. О методе обратного распространения ошибки

Понимание принципа работы нейронной сети, начиная от ввода, заканчивая выводом, вряд ли вызовет у вас затруднения. Намного тяжелее понять, каким образом нейронная сеть обучается, используя для этого наборы данных. Один из применяемых принципов называют методом обратного распространения ошибки.

Если говорить коротко, то вы оцениваете, насколько сильно ошиблась сеть, а потом изменяете вес входных значений (на первой картинке это синие числа).

Собственно говоря, процесс движется от конца к началу, ведь мы начинаем с конца сети и смотрим, как сильно догадка сети отклоняется от истины.

При этом двигаемся назад, изменяя веса, и так до тех пор, пока не дойдём до ввода. А для вычисления всего этого вручную вам потребуется знание математического анализа.

Однако вы можете на заморачиваться и использовать библиотеки, которые всё посчитают за вас.

Если вас интересуют англоязычные источники, которые помогут разобраться в данном методе, то держите:
• A Step by Step Backpropagation Example;
• Hacker’s guide to Neural Networks;
• Using neural nets to recognize handwritten digits.

Однако учтите, что читая первые 2 статьи, вам обязательно придётся кодить самому, что поможет в дальнейшем. Избегать этого не рекомендуется, ведь в нейронных сетях невозможно разобраться, не практикуя.

Что касается 3-й статьи, то это материал размером с книгу, больше напоминающую энциклопедию. Зато в ней даны подробные разъяснения важнейших принципов работы нейронных сетей.

В частности, вы изучите функцию стоимости, градиентный спуск и т. д.

Шаг 4. Создание своей нейросети

Читая разные статьи и руководства, вы так или иначе будете создавать небольшие нейросети. И это очень эффективно для обучения в целом.

Пример очень полезной информации можно найти здесь. В этом материале удивительное количество знаний сжато до 11 строк кода.

Что ещё? Ну, при реализации многих примеров используются векторные вычисления, поэтому понимание линейной алгебры тоже потребуется. Если же интересуют нейронные сети посложнее, то вот вам очередное руководство.

Кстати, если интересуют хорошие наборы данных, вы можете посетить этот сайт.

Чем раньше вы начнёте свои эксперименты, тем лучше. Будет кстати и изучение Python-библиотек для программирования нейронных сетей: Theano, Lasagne, Nolearn. А ещё лучше — записаться на курс «Нейронные сети на Python» в OTUS. С его помощью вы освоите архитектуру нейронных сетей, узнаете методы их обучения и особенности реализации.

Источник: https://otus.ru/nest/post/725/

Neural Excel — Лаборатория нейросетевых технологий

Neural Excel — это аналитическая надстройка для Microsoft Excel, позволяющая работать с нейронными сетями. Простая в использовании надстройка позволяет быстро сконфигурировать и обучить нейронную сеть прямо в среде Microsoft Excel.

Инструмент ориентирован на людей, которые хотят быстро получить отдачу от использования нейронных сетей и при этом не сильно углубляться в теорию. Надстройка позволяет использовать обученные сети как непосредственно в Microsoft Excel, так и интегрировать их в свои собственные приложения.

Простота использования, минимум настроек и демократичная цена делают это приложение отличным выбором для студентов и начинающих специалистов в области нейронных сетей.

Области применения

Финансовые операции:

Прогнозирование поведения клиента
Прогнозирование и оценка риска предстоящей сделки
Прогнозирование возможных мошеннических действий
Прогнозирование остатков средств на корреспондентских счетах банка
Прогнозирование движения наличности, объемов оборотных средств
Прогнозирование экономических параметров и фондовых индексов

Планирование работы предприятия:

Прогнозирование объемов продаж
Прогнозирование загрузки производственных мощностей
Прогнозирование спроса на новую продукцию

Бизнес-аналитика и поддержка принятия решений:

Выявление тенденций, корреляций, типовых образцов и исключений в больших объемах данных
Анализ работы филиалов компании
Сравнительный анализ конкурирующих фирм

Другие приложения:

Оценка стоимости недвижимости
Контроль качества выпускаемой продукции
Системы слежения за состоянием оборудования
Проектирование и оптимизация сетей связи, сетей электроснабжения
Прогнозирование потребления энергии

Функциональные возможности программы

Neural Excel выполнена в виде обычной (не COM!) надстройки, что дает возможность очень простой установки. Программа позволяет конфигурировать и обучать многослойные нейронные сети непосредственно в Microsoft Excel, начиная с 2007 версии.

Конфигурация сети может быть задана как пользователем, так и получена автоматически в процессе обучения.

Обученные нейронные сети могут быть сохранены непосредственно в книге Microsoft Excel в виде формул (функция поддерживается на версиях Microsoft Excel, начиная с 2010). Кроме того, использование сетей в виде формул позволяет автоматически пересчитывать выходные данные при изменении входных параметров.

Обученные нейронные сети могут быть также сохранены в файл, а учитывая, что в комплекте с программой поставляются компоненты Delphi (а в ближайшее время будут добавлены и компоненты для Visual Studio) с исходными кодами, то пользователь имеет возможность интегрировать сети в свои собственные приложения буквально несколькими строчками кода.

Опционально можно задавать генерацию листов с итоговой статистикой, копией обучающего множества и лист с шаблоном тестового множества.
Используемые входные или выходные параметры для разных наборов данных (обучение, дообучение, тестирование или прогнозирование) могут быть представлены в разном порядке, а, кроме того, наборы данных могут быть дополнены дополнительными полями.

Условия использования

Neural Excel является платной программой для использования в коммерческих целях. Для учебных и научных задач эта программа бесплатна, при этом ссылка на программу в своих работах является обязательной. Приобрести лицензии можно по запросу.

Презентация программы

Источник: http://www.neurotechlab.ru/software/neural-excel

Пишем вместе с нуля простейшую Нейронную Сеть с Сигмоидой в Excel #94

Вы могли уже видеть мой рассказ на тему того, почему в нейронных сетях так часто используют Сигмоиды для всевозможных преобразований.

А сейчас я хочу привести пример простой нейронной сети, которая обучается и прекрасно аппроксимирует произвольные монотонные зависимости с помощью единственной универсальной функции.

Ну и делать мы будем это снова в Excel, чтобы это мог повторить любой офисный работник без установки чего-либо к себе на комп.

Иллюстрация на тему «Офисный работник»

Для начала нам придётся открыть Excel и как в прошлый раз нажать Alt+F11. В открывшемся окне создадим новый модуль для класса (правый клик где-нибудь слева => insert => Class Module). И в него будем последовательно вставлять весь тот код, что будет ниже. Его я буду сопровождать своими ми.

Dim c(0 To 3) As Double ‘КоэффициентыDim tc(0 To 3) As Double ‘Пробные коэффициентыDim dc(0 To 3) As Double ‘Пробные измененияDim dy(0 To 3) As Double ‘Результаты изменения коэффициентовConst st = 0.2 ‘Скорость обучения

Здесь мы просто определяем все переменные, которые будут использоваться в рамках конкретного нейрона.

Sub init() ‘Инициализация случайных значений коэффициентов сигмоидыFor i = 0 To 3 c(i) = Rnd() * 2 — 1Next iEnd Sub

Таким подходом мы задаём всё многообразие сигмоид.

Sub NewC(De As Double, n As Integer) ‘Генерируем новый тестовый весFor i = 0 To 3If n = i ThenEnd If tc(i) = c(i) + IIf(n = i, dc(i), 0)Next iEnd Sub

Sub SaveC(d As Worksheet, r As Integer) ‘Сохраняем весаFor i = 0 To 3 d.Cells(r, 8 + i) = c(i)Next iEnd SubSub LoadC(d As Worksheet, r As Integer) ‘Загружаем весаFor i = 0 To 3 c(i) = d.Cells(r, 8 + i)Next iEnd Sub

Sub FixC() ‘Сохраняем тестовые весаDim my As DoubleDim j As Integer j = 1 my = dy(0)For i = 1 To 3 ‘Определяем максимальное изменение yIf dy(i) > my ThenEnd IfNext iFor i = 0 To 3 ‘Для максимального изменения y вес меняем полностью, для остальных в зависимости от величины изменения c(i) = c(i) + dy(i) / my * dc(i)Next iEnd Sub

Function res(x As Double, T As Boolean) As Double ‘Расчёт значения функции c1 = IIf(T, tc(0), c(0)) c2 = IIf(T, tc(1), c(1)) c3 = IIf(T, tc(2), c(2)) c4 = IIf(T, tc(3), c(3)) ie = -c2 * (x + c3)If ie > 40 Then ‘Если число в знаменателе очень большое, можно считать значение нулём res = c4ElseIf ie < -40 Then ‘Если число очень маленькое — единицей res = c1 + c4Else ‘В остальных случаях считаем честно res = c1 / (1 + Exp(ie)) + c4End If End Function

Sub TryC(x As Double, y As Double, n As Integer) ‘Пробуем изменить конкретный вес. Если стало лучше, фиксируем этоDim De As Double De = Abs(y — res(x, False)) Call NewC(De, n)Dim NDe As Double NDe = Abs(y — res(x, True))If NDe >= De Then Call NewC(-De, n) NDe = Abs(y — res(x, True))End IfIf NDe < De ThenEnd IfEnd Sub

Пробуем изменить тестовые коэффициенты. Если ошибка уменьшилась, фиксируем это, чтобы в будущем изменить уже боевые коэффициенты.

Public Function MakeRnd(n As Integer) As String

Источник: https://zen.yandex.ru/media/id/5b6e17c6458d1300a9eb8fd2/5c6edcd1ddad6b00af0d6b7c

Создаем нейронную сеть для прогнозирования временного ряда

Анализируя посещаемость нашего сайта, мы видим колоссальный интерес читателей к нейронным сетям. Данный инструментарий может решать целый набор задач, в том числе, прогнозировать временные ряды весьма эффективно. В частности, в своей диссертации я пишу следующим образом.

— В ряде работ [2],[36],[37] указано, что на сегодняшний день наиболее распространенными моделями прогнозирования являются авторегрессионные модели (ARIMAX), а также нейросетевые модели (ANN).

В статье [3], в частности, утверждается: «Without a doubt ARIMA(X) and GRACH modeling methodologies are the most popular methodologies for forecasting time series.

Neural networks are now the biggest challengers to conventional time series forecasting methods».

— Без сомнений модели ARIMA(X) и GARCH являются самыми популярными для прогнозирования временных рядов. В настоящее время главную конкуренцию данным моделям составляют модели на основе ANN.

У нас на сайте пока опубликован только один материал, посвященный нейронным сетям, в котором я давала советы по созданию сети.

Интерес со стороны читателей заставляет меня более активно заниматься нейросетевым прогнозированием.

Давайте попробуем шаг за шагом проделать работу по созданию, эффективному обучению и адаптации нейронной сети с тем, чтобы разобраться в нюансах нейросетевых моделей прогнозирования.

Первая нейронная сеть

Не стоит изобретать велосипед, а стоит взять готовый пример из книги Хайкина. Сама задача и ее решение подробно описаны в разделе 4.8 данной книги. Полный архив примеров для книги выложен у нас на форуме. Отдельно взятый рабочий пример можно скачать в архиве. Главный файл называется Create_ANN_step_0.m.

Приведенная программа решает задачу классификации. Прокомментирую текст основного файла.

% 1. Формирование исходного массива данных
P=mk_data(500);

% 2. Обучение нейронной сети по методу
% Back Propagation Error (обратное распространение ошибки)
[W1, b1, W2, b2, ep_err, a, end_ep]=… bpm_train(P, 4, 2, 2, .1, .5, 500, 0,0,0,0,0);

% 3. Проверка граничных значений
bpm_dec_bnds(W1, b1, W2, b2, .1);

% 4. Формирование тестового массива
T=mk_data(10000);

% 5. Проверка созданной сети на тестовом массиве
[cor, uncor]=bpm_test(W1,b1,W2,b2,T);

% 6. Построение графика
c=pl_circ([-2/3 0], 2.34, .01, 1);

Прогнозирование с помощью нейронной сети

Я взяла данный пример реализации нейронной сети, просмотрела внимательно содержание его функций и сделала свою нейронную сеть, которая прогнозирует торговый график по европейской территории РФ (далее ТГ) на 24 значения вперед. В архиве вы можете скачать, как полученный мною пример, так и исходные данные к нему. Основной файл называется Create_ANN_step_1.m

Шаг 1. Инициализация и исходные данные

Исходные данные по торговому графику содержатся в файле VOLUMES_EUR.mat

Источник: https://www.mbureau.ru/blog/sozdaem-neyronnuyu-set-dlya-prognozirovaniya-vremennogo-ryada

Изучаем нейронные сети за четыре шага

Перевод статьи «Learning How To Code Neural Networks»

Рассказывает Per Harald Borgen

В этот раз я решил изучить нейронные сети. Базовые навыки в этом вопросе я смог получить за лето и осень 2015 года. Под базовыми навыками я имею в виду, что могу сам создать простую нейронную сеть с нуля. Примеры можете найти в моих репозиториях на GitHub. В этой статье я дам несколько разъяснений и поделюсь ресурсами, которые могут пригодиться вам для изучения.

Шаг 1. Нейроны и метод прямого распространения

Так что же такое «нейронная сеть»? Давайте подождём с этим и сперва разберёмся с одним нейроном.

Нейрон похож на функцию: он принимает на вход несколько значений и возвращает одно.

Круг ниже обозначает искусственный нейрон. Он получает 5 и возвращает 1. Ввод — это сумма трёх соединённых с нейроном синапсов (три стрелки слева).

В левой части картинки мы видим 2 входных значения (зелёного цвета) и смещение (выделено коричневым цветом).

Входные данные могут быть численными представлениями двух разных свойств. Например, при создании спам-фильтра они могли бы означать наличие более чем одного слова, написанного ЗАГЛАВНЫМИ БУКВАМИ, и наличие слова «виагра».

Входные значения умножаются на свои так называемые «веса», 7 и 3 (выделено синим).

Теперь мы складываем полученные значения со смещением и получаем число, в нашем случае 5 (выделено красным). Это — ввод нашего искусственного нейрона.

Потом нейрон производит какое-то вычисление и выдает выходное значение. Мы получили 1, т.к. округлённое значение сигмоиды в точке 5 равно 1 (более подробно об этой функции поговорим позже).

Если бы это был спам-фильтр, факт вывода 1 означал бы то, что текст был помечен нейроном как спам.

Иллюстрация нейронной сети с Википедии.

Если вы объедините эти нейроны, то получите прямо распространяющуюся нейронную сеть — процесс идёт от ввода к выводу, через нейроны, соединённые синапсами, как на картинке слева.

Я очень рекомендую посмотреть серию видео от Welch Labs для улучшения понимания процесса.

Шаг 2. Сигмоида

После того, как вы посмотрели уроки от Welch Labs, хорошей идеей было бы ознакомиться с четвертой неделей курса по машинному обучению от Coursera, посвящённой нейронным сетям — она поможет разобраться в принципах их работы. Курс сильно углубляется в математику и основан на Octave, а я предпочитаю Python. Из-за этого я пропустил упражнения и почерпнул все необходимые знания из видео.

Сигмоида просто-напросто отображает ваше значение (по горизонтальной оси) на отрезок от 0 до 1.

Первоочередной задачей для меня стало изучение сигмоиды, так как она фигурировала во многих аспектах нейронных сетей. Что-то о ней я уже знал из третьей недели вышеупомянутого курса, поэтому я пересмотрел видео оттуда.

Но на одних видео далеко не уедешь. Для полного понимания я решил закодить её самостоятельно. Поэтому я начал писать реализацию алгоритма логистической регрессии (который использует сигмоиду).

Это заняло целый день, и вряд ли результат получился удовлетворительным. Но это неважно, ведь я разобрался, как всё работает. Код можно увидеть здесь.

Вам необязательно делать это самим, поскольку тут требуются специальные знания — главное, чтобы вы поняли, как устроена сигмоида.

Шаг 3. Метод обратного распространения ошибки

Понять принцип работы нейронной сети от ввода до вывода не так уж и сложно. Гораздо сложнее понять, как нейронная сеть обучается на наборах данных. Использованный мной принцип называется методом обратного распространения ошибки.

Вкратце: вы оцениваете, насколько сеть ошиблась, и изменяете вес входных значений (синие числа на первой картинке).

Процесс идёт от конца к началу, так как мы начинаем с конца сети (смотрим, насколько отклоняется от истины догадка сети) и двигаемся назад, изменяя по пути веса, пока не дойдём до ввода.

Для вычисления всего этого вручную потребуются знания матанализа. Khan Academy предоставляет хорошие курсы по матанализу, но я изучал его в университете.

Также можно не заморачиваться и воспользоваться библиотеками, которые посчитают весь матан за вас.

Скриншот из руководства Мэтта Мазура по методу обратного распространения ошибки.

Вот три источника, которые помогли мне разобраться в этом методе:

В процессе прочтения первых двух статей вам обязательно нужно кодить самим, это поможет вам в дальнейшем. Да и вообще, в нейронных сетях нельзя как следует разобраться, если пренебречь практикой.

Третья статья тоже классная, но это скорее энциклопедия, поскольку она размером с целую книгу. Она содержит подробные объяснения всех важных принципов работы нейронных сетей.

Эти статьи также помогут вам изучить такие понятия, как функция стоимости и градиентный спуск.

Шаг 4. Создание своей нейронной сети

При прочтении различных статей и руководств вы так или иначе будете писать маленькие нейронные сети. Рекомендую именно так и делать, поскольку это — очень эффективный метод обучения.

Ещё одной полезной статьёй оказалась A Neural Network in 11 lines of Python от IAmTrask. В ней содержится удивительное количество знаний, сжатых до 11 строк кода.

Скриншот руководства от IAmTrask

После прочтения этой статьи вам следует написать реализацию всех примеров самостоятельно. Это поможет вам закрыть дыры в знаниях, а когда у вас получится, вы почувствуете, будто обрели суперсилу.

Поскольку в примерах частенько встречаются реализации, использующие векторные вычисления, я рекомендую пройти курс по линейной алгебре от Coursera.

После этого можно ознакомиться с руководством Wild ML от Denny Britz, в котором разбираются нейронные сети посложнее.

Скриншот из руководства WildML

Теперь вы можете попробовать написать свою собственную нейронную сеть или поэкспериментировать с уже написанными. Очень забавно найти интересующий вас набор данных и проверить различные предположения при помощи ваших сетей.

Для поиска хороших наборов данных можете посетить мой сайт Datasets.co и выбрать там подходящий.

Так или иначе, теперь вам лучше начать свои эксперименты, чем слушать мои советы. Лично я сейчас изучаю Python-библиотеки для программирования нейронных сетей, такие как Theano, Lasagne и nolearn.

Удачи!

Не смешно? А здесь смешно: @ithumor

Источник: https://tproger.ru/translations/learning-neural-networks/

Как создать нейронную сеть в excel — Нейронные сети — 2 ответа

Ответ от Наталья[гуру]Иску́сственные нейро́нные се́ти (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.

Это понятие возникло при изучении процессов, протекающих в мозге при мышлении, и при попытке смоделировать эти процессы. Первой такой моделью мозга был перцептрон. Впоследствии эти модели стали использовать в практических целях, как правило в задачах прогнозирования.

С точки зрения машинного обучения, нейронная сеть представляет собой частный случай методов распознавания образов, дискриминантного анализа, методов кластеризации и т. п. С математической точки зрения обучение нейронных сетей, это многопараметрическая задача нелинейной оптимизации.

С точки зрения кибернетики, нейронная сеть используется в задачах адаптивного управления и как алгоритмы для робототехники. С точки зрения развития вычислительной техники и программирования, нейронная сеть — способ решения проблемы эффективного параллелизма.

А с точки зрения искусственного интеллекта, ИНС является основой философского течения коннективизма и основным направлением в структурном подходе по изучению возможности построения (моделирования) естественного интеллекта с помощью компьютерных алгоритмов.ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов).

Такие процессоры обычно довольно просты, особенно в сравнении с процессорами, используемыми в персональных компьютерах. Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые процессоры вместе способны выполнять довольно сложные задачи.

Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами.

В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что, в случае успешного обучения, сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке.

Ответ от 2 ответа[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Нейронные сетиОтвет от FUCKyou™[гуру]Юзай википедию=) Вот это оттуда

Иску́сственные нейро́нные се́ти (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге при мышлении, и при попытке смоделировать эти процессы. Первой такой моделью мозга был перцептрон. Впоследствии эти модели стали использовать в практических целях, как правило в задачах прогнозирования.

Ответ от Ѕороший Человек[гуру]В мозгах нейроны связаны для передачи электрических импульсов. Есть такие нейро-компьютеры уже, по принципу строения головного мозга, вероятно сети именно к ним относят.

Ответ от Евгений[гуру]я помню читал в каком-то компьютерном журнале о эксперементальной разработке нейрокомпьютеров на основе живой нервной ткани пиявки и на нем получилось произвести простейшие матаматические операции на очень маленькой скорости .

конечно использовать его сейчас не реально но факт остается фактом.

Источник: https://2oa.ru/kak-sozdat-neironnuiu-set-v-excel/

Источник

Проектирование RBF-нейронной сети в Microsoft ExcelПодробнее

проектирование нейронных сетей в ms excel 11 классПодробнее

Пример работы с Neural Excel (2 часть)Подробнее

Проектирование нейронных сетей в Google Таблицах 2ч. Классификация продукта по обучающей выборке.Подробнее

Проектирование нейронной сети в электронных таблицахПодробнее

Проектирование нейронной сети в Google Таблице 1чПодробнее

Машинное обучение в Excel с функцией МУМНОЖ (MMULT)Подробнее

К- ближайших соседей в Excel моделирование машинное обучениеПодробнее

Урок 10 Класс 11. Проектирование нейронной сетиПодробнее

Урок 11 Класс 11 Проектирование нейронной сетиПодробнее

MS Excel. Flash Fill. Искусственный интеллект Excel в действии.Подробнее

KNN Machine Learning Algorithm Excel | KNN with Excel Euclidean Distance | KNN Using Microsoft ExcelПодробнее

Нейросеть в Excel с оптимизацией Adaptive moment estimation (Adam)Подробнее

Нейронная сеть в excel — Метод обратного распространения ошибкиПодробнее

Используем ChatGPT при работе в ExcelПодробнее

События

Источник

Рубрика	Программирование, компьютеры и кибернетика
Вид	статья
Язык	русский
Дата добавления	29.01.2020
Размер файла	153,7 K