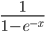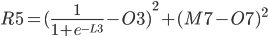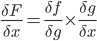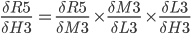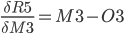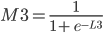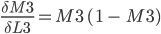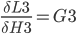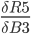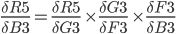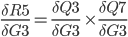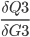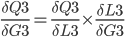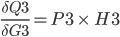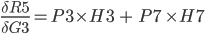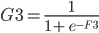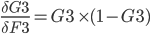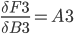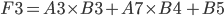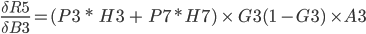Проектирование нейронной сети в excel

Ты
узнаешь:

·       
крытые
слои нейрона;

·       
математическую
запись функции единичного скачка;

·       
формулу
среднеквадратичной ошибки.

Ты
научишься:

·       
проектировать
искусственный нейрон в электронной таблице;

·       
вычислять
функцию единичного скачка и среднеквадратичную ошибку.

В
случае, когда нейросеть состоит из большого количества нейронов, вводят
термин «слой». Слои делятся на три основных типа: входной
(синий), скрытый (фиолетовый) и выходной (зеленый). Соответственно, есть
входной слой, который получает информацию, n скрытых слоев, которые ее
обрабатывают, и выходной слой, который выводит результат.

Нейроны
оперируют числами в диапазоне [0, 1] или [–1, 1]. Продемонстрируем
расчет результата нейронной сети с использованием логистической функции и ее
ошибку, используя среднеквадратичную ошибку.

Тренировочный
сет, или обучающая выборка (датасет), – набор
данных, на которых нейронная сеть будет обучаться. В нашем случае
исключающего или (xor) у нас всего 4 разных исхода, то есть у нас
будет 4 тренировочных сета: 0xor0 = 0, 0xor1 =
1, 1xor0 = 1,1xor1 = 0.

Итерация –
это своеобразный счетчик, который увеличивается каждый раз, когда нейронная
сеть проходит один набор данных.

Важно не
путать итерацию с эпохой и понимать последовательность их инкремента.
Сначала n раз увеличивается итерация, а потом уже эпоха, и
никак не наоборот.

Эпоха –
при инициализации нейронной сети эта величина устанавливается в 0 и
имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована
сеть, и тем лучше ее результат. Эпоха увеличивается каждый раз, когда мы
проходим весь набор обучающих выборок, в нашем случае 4 сета,
или 4 итерации.

Ошибка –
формируется каждую эпоху и должна идти на спад. Если этого не происходит,
значит, вы что-то делаете не так. Ошибку можно вычислить разными способами,
но мы рассмотрим два: среднеквадратичную ошибку и среднеквадратичное
отклонение.

Формула
вычисления среднеквадратичной ошибки:

Cреднеквадратичное
отклонение вычисляется по формуле:

O₁, O₂,
…, O_n – фактический сигнал, полученный на выходе
(входе);

A₁, A₂,
…, A_n – идеальный сигнал, который должен быть
получен на выходе (входе);

n –
количество датасетов.

I₁, I₂ –
входные нейроны;

H₁, H₂ –
скрытые нейроны;

O₁ –
выходной нейрон.

Запишем
значения параметров в Excel:

Вычисляем
взвешенную сумму для первого входа:

Взвешенная
сумма первого входа: H1input = 0 ⋅ 0,13
+ 1 ⋅
(–0,58) = –0,58.

Используем
сигмоидную функцию активации для первого входа. В этом нам поможет встроенная
функция экспоненты (EXP) в MS Excel: H1output = sigmoid(–0,58) =
0,36.

Вычисляем
взвешенную сумму для второго входа:

Взвешенная
сумма второго входа: H2input = 0 ⋅ 0,52
+ 1 ⋅ 0,63
= 0,63.

Используем
сигмоидную функцию активации для второго входа: H2output = sigmoid(0,63) =
0,65.

Вычисляем
взвешенную сумму для выхода:

O1input =
0,36 ⋅ 2,5
+ 0,65 ⋅
(–0,3) = 0,7.

Используем
сигмоидную функцию активации для выхода.

O1output = sigmoid(0,7) =
0,67.

Вычисляем
ошибку по формуле, используя встроенная функцию СТЕПЕНЬ в MS Excel:

Среднеквадратичная
ошибка O1ideal = 1 (0xor1 = 1).

Error = ((1 – 0,67)²)/1
= 0,11.

Результат
на выходе нейрона будет равен 0,67, а среднеквадратичная ошибка будет
равна 11 %.

Кроме
сигмоидной функции, существует ряд и других фукнции активации, которые
используются при обучении искусственной нейронной сети. Функция
единичного скачка – это простой вид функции активации, где выход
нейрона может быть равен только 0 или 1.

Графически
эту функцию можно изобразить следующим образом:

Математическая
запись функции единичного скачка выгдядит так:

Если
взвешенная сумма больше определенного порога b, то выход нейрона
равен 1.

Как ее
можно использовать? Предположим, что мы поедем на море только тогда, когда
взвешенная сумма больше или равна 5. Если взвешенная сумма = 2,
выход нейрона = 0, то мы никуда не едем. Если взвешенная сумма = 7,
значит, выходной сигнал нашего нейрона равен 1, и мы едем на море.
Нейрон зависит от взвешенной суммы, и если она получается больше его порога,
то нейрон выдает выходной сигнал, равный 1.

В современном мире трудно найти человека, который бы не слышал про нейронные сети. Кажется, их применяют всюду: оживление фотографий, DeepFake, маски для фото в соцсетях и прочее. Но для большинства людей они являются чем-то абстрактным и непонятным.

Однако создать свою нейросеть можно даже не имея знаний о языках программирования, и используя простейший инструмент, знакомый любому офисному сотруднику – MS Excel.

Схематично моя будущая нейросеть выглядит так:

Это упрощенная схема перцептрона. Перцептрон – простейший вид нейронных сетей, в основе которых лежит математическая модель восприятия информации мозгом, состоящая из сенсоров, ассоциативных и реагирующих элементов. На вход подаются значения признаков, которые могут быть равны 0 или 1. Строгая бинарность обусловлена тем, что признаки – это, своего рода, сенсоры, и они могут находиться либо в состоянии покоя (равны 0), либо в состоянии возбуждения (равны 1). Затем эти признаки умножатся на вес и суммируются. После при помощи функции активации (сигмоиды) получаю значения на выходе от 0 до 1. Таким образом, главной задачей является нахождение весов, обеспечивающих наиболее точное прогнозирование.

Представлю, что требуется по определенному набору признаков научить нейросеть определять является ли животное домашней кошкой или нет.

В датасете имеется 9 признаков, если экземпляр им обладает, то ставится 1, если нет, то 0. Целевой столбец назван «Выход»: 1 – значит экземпляр кошка, 0 – не кошка. В идеале нейросеть должна предсказать 1 для всех кошек и 0 для всех не кошек.

Первый шаг – создание таблицы поиска весов для каждого признака:

В диапазоне M3:U2 генерирую случайные величины весов при помощи формулы СЛЧИС().

Далее создаю столбцы для Bias (смещение) и Output (предсказание модели):

Формула в ячейке W3:

=B3*M3+C3*N3+D3*O3+E3*P3+F3*Q3+G3*R3+H3*S3+I3*T3+J3*U3

Протягиваю формулу до ячейки W14.

Bias – нейрон смещения. Простыми словами, это дополнительная информация о природе данных для модели, способ показать модели, «в какую сторону думать».

Формула в ячейке output – функция сигмоиды:

=ЕСЛИ(Bias=0;0;1/(1+(EXP(-Bias))))

Данная функция необходима для интерпретации значения bias. Мне нужно получить значения от 0 до 1. Output – предсказание модели. Если значение меньше 0.5, то экземпляр не является кошкой, если больше, то является.

Создаю таблицу для корректировки весов:

В ячейке Z3 следующая формула:

=($K3-$X3)*B3*$X3*(1-$X3)

Протягиваю её на весь диапазон Z1:AH14

Возвращаюсь в блок с весами: в ячейку М4 прописываю формулу: =M3+Z3

Протягиваю её на диапазон M4:U14:

В диапазоне AJ3:AJ14 пишу формулу: =ЕСЛИ(X3<0,5;0;1) – если значение в столбце Output больше, либо равно 0.5, то модель предполагает, что в строке домашняя кошка.

В диапазоне AK3:AK14 пишу формулу: =ЕСЛИ(K3=1;ЕСЛИ(AJ3=K3;1;0);»») – проверяю правильно ли модель предсказала домашнюю кошку.

В диапазоне AL3:AL14 пишу формулу: =ЕСЛИ(K3=0;ЕСЛИ(AJ3=K3;1;0);»»)– проверяю правильно ли модель предсказала не домашнюю кошку.

В ячейках AK15 и AL15 формулы СРЗНАЧ() для отображения доли правильных ответов.

На рисунке видно, что на данный момент модель считает все записи домашними кошками (цифра 1 в столбце «Предсказание»).

Копирую диапазон M14:U14 и вставляю значения в диапазон M3:U3:

Смотрю результат:

Теперь модель не все записи считает домашними кошками, но результат пока ещё не лучший.

Совершаю ещё несколько итераций. Копирую диапазон M14:U14 и вставляю значения в диапазон M3:U3. В таблице ниже видно, как менялись предсказания после каждого цикла:

В итоге, моя нейросеть после восьми итераций верно предсказала значения для всех строк.

Используя полученные веса из диапазона M14:U14, можно проверять другие комбинации признаков, и модель будет предсказывать является ли представленная строка домашней кошкой или нет.

Видно, что модель неидеальна, так как неверно предсказала рысь. Зато манула она определила верно, несмотря на то, что он больше походит на домашнюю кошку, чем рысь. На самом деле 100%-я точность для нейросетей невозможна, поэтому полученный результат можно считать неплохим. На практике использование MS Excel для задач машинного обучения — не очень хорошая идея, так как он не может работать с большим объемом данных, да и создан совершенно для другого. Однако, используя методы, представленные в посте, можно самостоятельно «поиграть» с данными, что поможет понять базовые принципы работы нейросетей.

  Перевод

  Ссылка на автора

Чтобы упростить концепцию сверточных нейронных сетей, я попытаюсь объяснить, что происходит при разработке модели глубокого обучения. Для получения дополнительной информации, я рекомендую поиск онлайн как есть обильное количество доступной информации (как это видео). Это объяснение получено из fast.ai репозиторий.

Эта картина простой нейронной сети в основном представляет то, что происходит в этом примере.

Входной слой

Эти данные изображения № 7 из MNIST базы данных, и мы предполагаем, что вы используете модель перед поездом для классификации.

Скрытый слой 1

Скрытый слой — это то, что преобразует входные данные, чтобы отличить более сложные элементы от данных для выходного уровня, чтобы сделать более точную оценку.

Два фильтра будут представлять разные формы — первый фильтр предназначен для обнаружения горизонтальных краев, второй фильтр обнаруживает вертикальные края. Этот фильтр 3х3 называется сверточное ядро, Фильтр 1 активируется для горизонтальных ребер на входе. Conv1 показывает активацию обоих после взятия секции 3×3 ввода и умножения ее на сверточное ядро. Следующая картина ниже дает вам лучшую идею.

* Хотя это представлено в 2d массиве, они должны быть сложены как Тензор, Где каждая матрица представляет срез в тензоре. Это все по существу строковые операции (Линейная алгебра), которые происходят.

= SUM (F11: H13 * $ AD $ 11: $ AF $ 13) — это происходящая Свертка.

Эта сумма приведет к числу активации 3 для этого конкретного места 3×3 на входе.

Функция активации

Далее мы используем нашу единицу нелинейности с помощью РЕЛУ как наша функция активации для устранения негативов. Далее мы видим, что негативы исчезают на следующей картинке.

Скрытый слой 2

Далее мы делаем еще одну свертку. Conv2 будет следующим скрытым слоем. Это взвесит обе матрицы в Conv1, взяв их произведение суммы. Ядро свертки здесь будет представлять собой Тензор 2X3X3.

После использования RELU мы создали второй слой.

Макс Пул

Максимальное объединение вдвое уменьшает разрешение по высоте и ширине, принимая только максимум 2х2 в Conv2. В матрице Макспула мы видим только максимальное значение сечения 2×2 в Conv2, которое равно 33. Пул вычисляется быстрее, чем свертки. Кроме того, это дает вам некоторое количество инвариантность перевода,

Выходной слой

Затем мы создаем наш полностью связанный слой, взяв все наши активации в Maxpool и придав им всем вес. Это делается с помощью матричного продукта. В Excel, мы возьмем сумму активаций и весов. Таким образом, вместо синтаксического анализа каждой секции в сверточном слое, как и раньше, полностью подключенный слой (плотный слой) будет выполнять классификацию объектов, которые были извлечены сверточными слоями и подвергнуты понижающей дискретизации слоями с максимальным пулом.

Этот пример представляет только один класс, то есть один номер. Нам еще предстоит классифицировать остальные числа.

Introduction

This article is written for you who is curious of the mathematics behind neural networks, NN. It might also be useful if you are trying to develop your own NN. It is a cell by cell walk through of a three layer NN with two neurons in each layer. Excel is used for the implementation.

• Download neuralnetwork Sigmoid — 1.2
• Download neuralnetwork Leaky ReLu — 1.2

Background

If you are still reading this, we probably have at least one thing in common. We are both curious about Machine Learning and Neural Networks. There are several frameworks and free api:s in this area and it might be smarter to use them than inventing something that is already there. But on the other hand, it does not hurt to know how machine learning works in depth. And it is also a lot more fun to explore things in depth.

My journey into machine learning has perhaps just started. And I started by Googling, reading a lot of great stuff on the internet. I also saw a few good YouTube videos. But I it was hard to gain enough knowledge to start coding my own AI.
Finally, I found this blog post: A Step by Step Backpropagation Example by Matt Mazur. It suited me, and the rest of this text is based on it.

Construction

A Neural Network, NN, consists of many layers of neurons. A Neuron has a value and connections with weights to all other neurons in the next layer.

The first layer is the input layer and the last layer is the output layer. Between input and output, there might be one or many hidden layers. The number of neurons in a layer is variable.

If a NN is used to, for example, classify images, the number of neurons in the input layer is of course equal to the number of pixels in the image. Then in the output, each neuron represents a classification of the image. (E.g., a type of animal, a flower or a digit.)

Calculations

Before the calculations, all the weights in the NN have to be initialized with random numbers.

The image below is a print screen of the spread sheet that I refer to in the rest of this article. It might be a good idea to keep an open window of that sheet. That should make it easier to follow along.
A tip: Row 2 is the order of calculations.

Step 1 — 3. Forward Pass

The value of one neuron is calculated by taking the sum of every previous neuron multiplied by its weight.
An extra bias weight which has no neuron is also added:

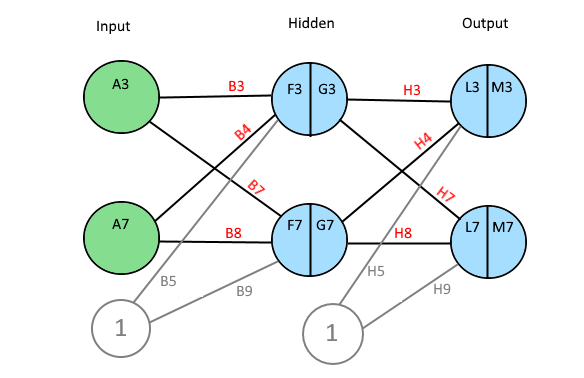
F3 = A3 * B3 + A7 * B4 + B5

The value is normalized through a activation function. There are several different activation functions used in neural networks.
I have used the logistic function:

G3 = 1 / (1 + EXP(-F3))

Step 4 — 5. Forward Pass

The neurons of the output layer is calculated the same way as hidden layer.

L3 = G3 * H3 + G7 * H4 + H5
and
M3 = 1 / (1 + EXP(-L3))

Step 6 — 7. The Error

The error of each output neuron is calculated using an expected or a target value. When classifying images, it is common to set one neuron close to 1 and the rest of the neurons close to zero.

For the errors in column Q:

Q3 = (M3 — O3)²

and:

Q7 = (M7 — O7)²

The total Error R5 is the average of all errors and should get closer and closer to zero as the network is trained.

R5 = (Q3 + Q7) / 2

Backward Propagation

A Neural Network is trained by passing it lots of train data repeatedly.
Then, for every iteration, errors and deltas are calculated. This is used to make small adjustments to all the weights in such a way that the network becomes better and better.
This is called backpropagation.
Since the total error can be expressed as a mathematical functions of each weight, one can derive those functions to obtain the slopes of the function curves in one point. The slopes indicate the direction towards a minimum for the total error and proportionally how much each weight should be adjusted in order for the total error to approach zero.

A delta value is calculated below for each weight. The deltas are stored in column I and D, for output and hidden layer respectively.

Chain Rule — Friend of Backpropagation

In practice, we want to derive the total error R5 with respect to H3 so we first to express R5 as a function of H3 using substitutions.

Since

R5 = (Q3 + Q7) / 2
R5 = (M3 - O3)² / 2 + (M7 - O7)² / 2

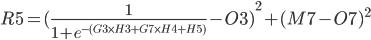
The above function does not look very easy to derive. Is it even possible?
We will instead use the chain rule².
It states that if we have a composition of two or more functions f(g(x)) and let F(x) = f(g(x)), we can derive like this:

F’(x) = f’(g(x)) * g’(x) or in another notation:

In our case, we have the following dependency:

R5(M3(L3(H3))) and we can write:

Step 9. Output layer Deltas

The function for the total error R5 is derived with respect to the first weight H3 of the output layer.

In the above formula, the chain rule is used to make it simpler to derive.

Since:

Proof of derivation of Logistic function found in this article³.

Since 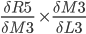will be used later in the backpropagation, it is stored in the cell P3.

P3 = (M3-O3) * M3 * (1 - M3)

The last derivative of the chain of derivatives above is simpler.
Since L3 = G3 * H3 + G7 * H4 + H5

We can now put everything together and store 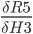into cell I3.

I3 = P3 * G3

The rest of the weights in output layer is calculated the same way and we get:

P7 = (M7-O7) * M7 * (1 - M7)

I4 = G7 * P3
I5 = 1 * P3 (bias neuron)
I7 = G3 * P7
I8 = G7 * P7
I9 = 1 * P7 (bias neuron)

Step 10. Backpropagation in Hidden Layer

In this step, we calculate:

The chain rule from previous steps helps to transform it to something we can use:

First term also must be split up on both errors Q3 and Q7 so:

First look at this:

It can be further split up like this:

First 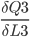is already stored in P3 = (M3-O3) * M3* (1 - M3)

Since L3 = G3 * H3 + G7 * H4 + H5

When we put the above together, we get:

And in the same way as above:

First problem is solved.

Time for

We know that:

And we have previously learned to derive the logistic function.

And now:

Because:

We now put the above together to get one expression for the derivative of the total error with respect to first weight of the hidden layer.

This is stored in cell C3.

The calculations for the above is repeated for all hidden layer weights:

C3 = (P3 * H3 + P7 *H7) * (G3 *(1 - G3)) * A3
C4 = (P3 * H3 + P7 *H7) * (G3 *(1 - G3)) * A7
C5 = (P3 * H3 + P7 *H7) * (G3 *(1 - G3)) * 1
C7 = (P3 * H4 + P7 *H8) * (G7 *(1 - G7)) * A3
C8 = (P3 * H4 + P7 *H8) * (G7 *(1 - G7)) * A7
C9 = (P3 * H4 + P7 *H8) * (G7 *(1 - G7)) * 1

Now it is easy to calculate new weights using a selected learning rate from cell A13.

For example: (new B3)

D3 = B3 - C3 * A13

There is a macro connected to the train button in the Excel document. The macro iterates many times and we can see how the output neurons in column M gets closer and closer to their target values and that the total Error in R5 gets closer and closer to zero.

G3 = IFS(F3 > 0; F3; F3 <= 0; F3/20)
and
P3= (M3-O3) * IFS(M3 > 0;1;M3<=0;1/20)

Final Words

I realize this article might take some time to digest. I tried to explain it as I understood it. Please comment below if you find any errors.

After I sorted out how NNs work in Excel, I wrote a C# program that can interpret hand written digits. It has a Windows Forms user interface which works well. It seems to recognize almost any digit I draw, even ugly once. That was a proof to me that my understanding of Artificial Neural Networks is correct so far.

That article can be found here:

Handwritten digits reader UI⁵

Links

1. A Step by Step Backpropagation Example — Matt Mazur.
2. Chain rule — Wikipedia
3. Logistic function — Wikipedia
4. Rectifier (neural networks) — Wikipedia
5. Handwritten digits reader UI — Kristian Ekman

History

• 1^st January, 2019 — Version 1.0
• 8^th January, 2019 — Version 1.1
  • Replaced Logistic activation function with LeakyReLu
• 11^th January, 2019 — Version 1.2
  • Update of names of biases in diagrams
• 23th Januray, 2019 — Version 1.3
  • Changed du calculation to the total error to the average av errors

Опубликовано: 14.01.2021, 
Автор: Elvira_198401 334

Ты узнаешь:

• крытые слои нейрона;

• математическую запись функции единичного скачка;

• формулу среднеквадратичной ошибки.

Ты научишься:

• проектировать искусственный нейрон в электронной таблице;

• вычислять функцию единичного скачка и среднеквадратичную ошибку.

В случае, когда нейросеть состоит из большого количества нейронов, вводят термин «слой». Слои делятся на три основных типа: входной (синий), скрытый (фиолетовый) и выходной (зеленый). Соответственно, есть входной слой, который получает информацию, n скрытых слоев, которые ее обрабатывают, и выходной слой, который выводит результат.

Время на прочтение
9 мин

Количество просмотров 12K

К старту курса о машинном и глубоком обучении делимся переводом статьи, автор которой показывает на практике, как модель машинного обучения может использоваться через Excel. Зачем это нужно? Компании больше и больше вкладывают в исследования и разработку моделей прогнозов; по мнению автора оригинала статьи, разработчика и основателя компании PyXLL доступ к ML-моделям через Excel открывает новые горизонты. Вы сможете показать модель пользователям Excel, у которых нет опыта программирования или широких знаний в области статистики. При желании можно создавать инструменты разработки и тренировки моделей полностью в Excel, например строить графы в TensorFlow. Весь исходный код из статьи доступен на GitHub.

Надстройка Excel PyXLL встраивает Python в Excel и позволяет расширять возможности Excel через Python. С помощью этой надстройки мы можем добавлять новые функции, макросы, меню и в целом перенести преимущества экосистемы Python и машинное обучение прямо в Excel. К концу статьи мы построим модель классификации животных.

Python для Machine Learning

Python хорошо подходит для машинного обучения, у него большой массив поддерживаемых пакетов, упрощающих программирование и сокращающих время разработки. ML и DL очень хорошо поддерживаются несколькими пакетами, поэтому Python — идеальный выбор. Посмотрим на распространённые пакеты для ML на Python.

Scikit-Learn

Пакет scikit-learn — это лаконичный и последовательный интерфейс к общим алгоритмам ML, упрощая введение ML в производственные системы. Библиотека сочетает высокую производительность, де-факто она отраслевой стандарт машинного обучения на Python. В статье мы будем работать именно с ней.

TensorFlow

TensorFlow от Google. Эта библиотека с открытым исходным кодом для расчёта графов потоков данных оптимизирована для целей ML. Она была разработана, чтобы удовлетворять высоким требованиям обучения нейронных сетей в среде Google и является преемницей DistBelief — основанной на нейронных сетях системы глубокого обучения, применяется в пограничных областях исследований Google.

Впрочем, TensorFlow не строго научна и достаточно обобщена, чтобы применяться в различных прикладных задачах. Ключевая особенность TensorFlow — многослойная система узлов, которая быстро тренирует сети искусственного интеллекта на больших наборах данных. В Google это даёт возможность распознавать голос и находить объекты на изображениях.

Keras

Keras — написанная на Python Open Source библиотека для нейронных сетей. Она способна работать поверх TensorFlow, Microsoft Cognitive Toolkit или Theano и имеет архитектуру, которая позволяет быстро проводить эксперименты с глубоким обучением и сосредоточена на модульности, расширяемости и удобстве пользователя. Из документации следует, что работать с Keras можно, когда вам нужна библиотека глубокого обучения, которая:

• Обладая перечисленными выше преимуществами, позволяет просто и быстро прототипировать решения.

• Поддерживает свёрточные и рекуррентные нейронные сети, а также их комбинирование.

• Без проблем работает на CPU и GPU.

PyTorch

PyTorch — это научный вычислительный пакет на Python, он работает в двух направлениях:

• Как замена NumPy с возможностью задействовать графические процессоры.

• Как платформа исследования Deep Learning с максимумом гибкости и скорости.

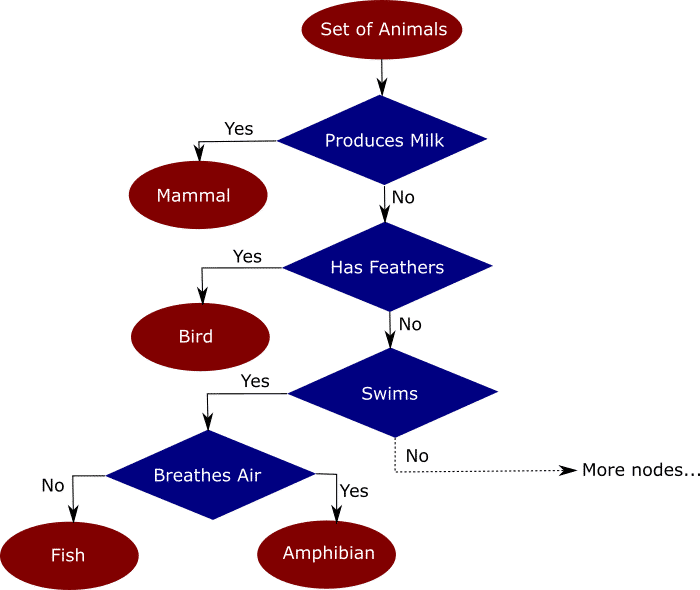
Деревья решений

Деревья решений — техника машинного обучения для решения задач регрессии и классификации. Дерево делит набор данных на множество наборов по признакам так, что одно дерево владеет одним подмножеством данных. Конечные узлы дерева — листья — содержат прогнозы и используются в новых запросах к натренированной модели. Пример ниже поможет понять, как это работает. Предположим, мы имеем набор данных со множеством признаков животных: млекопитающих, птиц, рептилий, насекомых, моллюсков и амфибий. Интуитивно разделить этот набор можно так:

Распределение данных по деревьям на основе признака упрощает классификацию новых данных, точность которой зависит от того, насколько точно деревья отражают действительность. В незаконченное дерево на рисунке выше я заложил мои знания и интуитивные представления о животных. Модель выясняет, как распределить признаки по новым данным — это и называется машинным обучением.

Алгоритм быстро анализирует большой объём данных, чего вручную сделать невозможно. В работе деревьев решений множество аспектов, от математики до логики их построения. Мы не будем касаться этих деталей, но построим модель и я покажу, как работать с ней в Excel.

Тренировка модели

Натренируем модель классифицировать животных при помощи деревьев решений. Воспользуемся для этого набором данных UCI Zoo Data Set из 101 животного, в наборе 17 логических признаков и один признак, который мы будем прогнозировать.

Для загрузки данных воспользуемся pandas, а для построения дерева — scikit-learn. Загрузим данные во фрейм Pandas, разделим на признаки и целевой класс, то есть класс животного. Затем разделим данные на тренировочный и тестовый наборы. Scikit-Learn использует тренировочный набор для обучения деревьев, а тестовый резервируется для проверки точности модели.

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import pandas as pd

# Read the input csv file
dataset = pd.read_csv("zoo.csv")

# Drop the animal names since this is not a good feature to split the data on
dataset = dataset.drop("animal_name", axis=1)

# Split the data into features and target
features = dataset.drop("class", axis=1)
targets = dataset["class"]

# Split the data into a training and a testing set
train_features, test_features, train_targets, test_targets = 
        train_test_split(features, targets, train_size=0.75)

Начинается самое интересное: при помощи классификатора дерева решений в scikit-learn обучим модель на тренировочных данных. Чтобы модель не переобучилась и могла работать, настроим несколько параметров. Максимальная глубина дерева будет равна 5. Поэкспериментируйте со значениями, чтобы увидеть влияние глубины на результаты.

# Train the model
tree = DecisionTreeClassifier(criterion="entropy", max_depth=5)
tree = tree.fit(train_features, train_targets)

Эти две строки строят и обучают модель. Чтобы проверить её точность, подадим на вход данные, которых она не видела.

# Predict the classes of new, unseen data
prediction = tree.predict(test_features)

# Check the accuracy
score = tree.score(test_features, test_targets)
print("The prediction accuracy is: {:0.2f}%".format(score * 100))

Воспользуемся моделью и выполним прогноз на новых данных:

# Try predicting based on some features
features = {
    "hair": 0,
    "feathers": 1,
    "eggs": 1,
    "milk": 0,
    "airbone": 1,
    "aquatic": 0,
    "predator": 0,
    "toothed": 1,
    "backbone": 1,
    "breathes": 1,
    "venomous": 0,
    "fins": 0,
    "legs": 1,
    "tail": 1,
    "domestic": 0,
    "catsize": 0
}

features = pd.DataFrame([features], columns=train_features.columns)
prediction = tree.predict(features)[0]
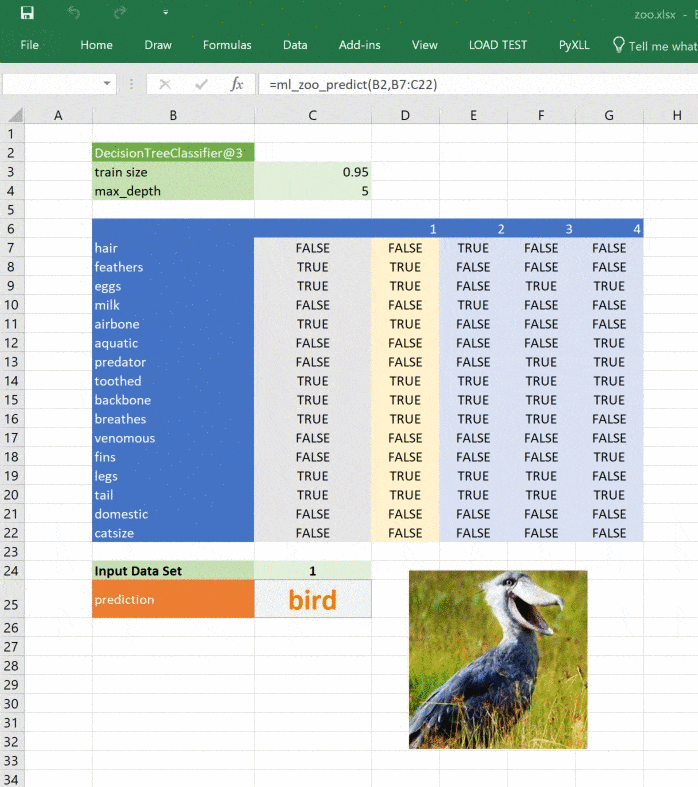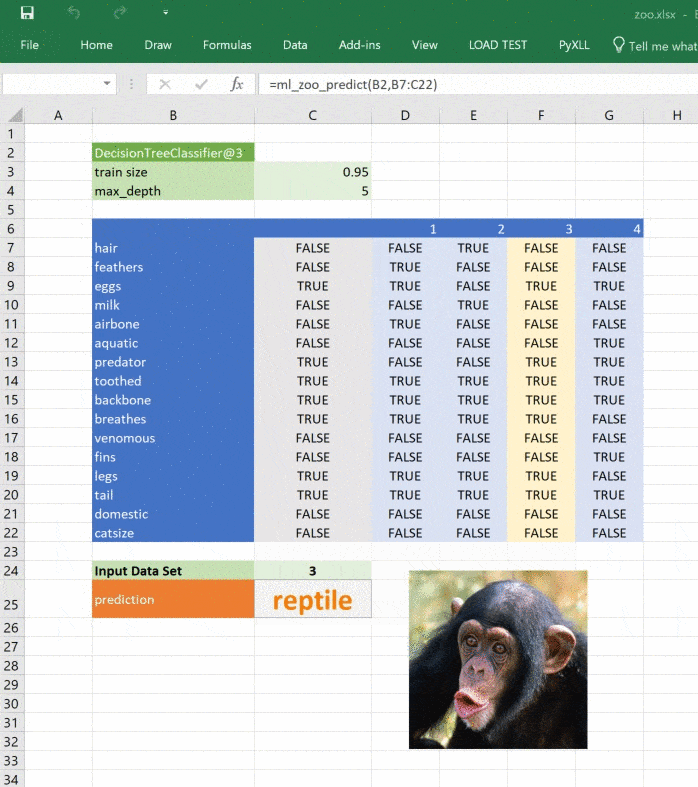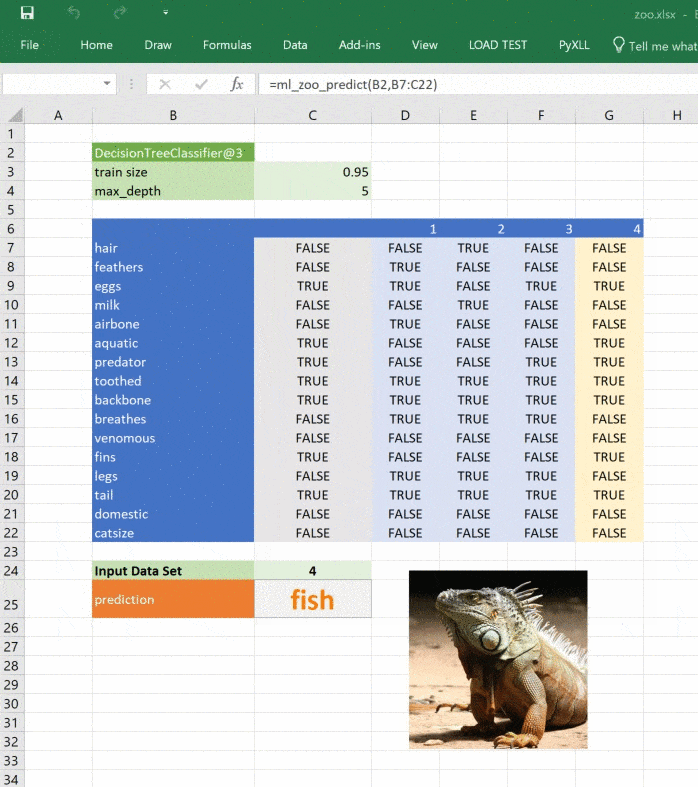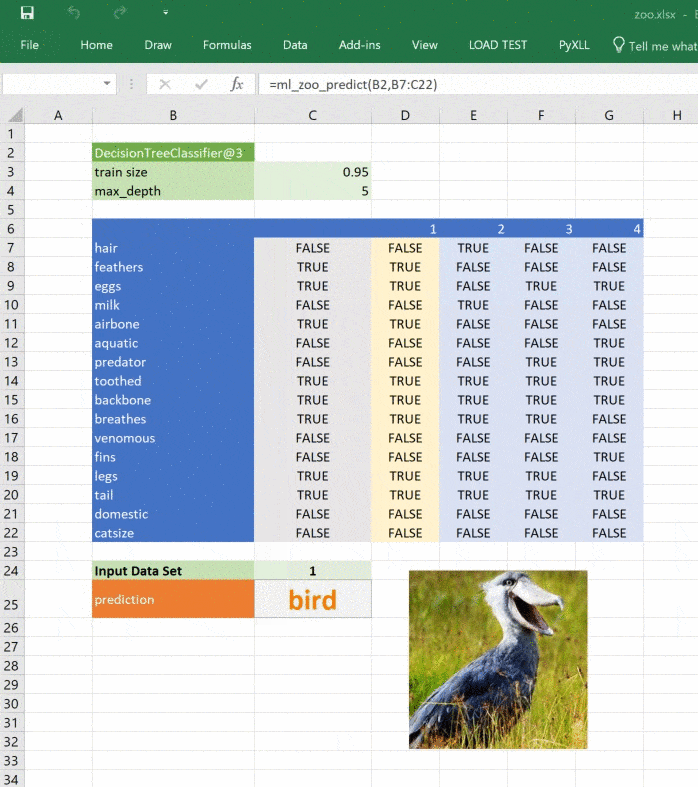
print("Best guess is {}".format(prediction])

Вызовем модель из Excel

Теперь загрузим модель в Excel, который хорошо подходит для интерактивных данных. Он работает почти везде, вы сможете показать модель незнакомым с разработкой людям, это даёт массу преимуществ в бизнесе, особенно когда модель применяется как часть пакетной системы или системы реального времени. Возможность вызывать модель интерактивно может оказаться по-настоящему полезной, когда нужно понять поведение системы.

К счастью, наша модель написана на Python и перенести её в Excel просто. В PyXLL есть всё необходимое, чтобы писать на Python в Excel. Нужно только добавить несколько декораторов @xl_func из модуля pyxll и настроить надстройку PyXLL для загрузки модуля с моделью. Если вы не знакомы с PyXLL, посмотрите введение в PyXLL в руководстве пользователя.

Построим дерево решений

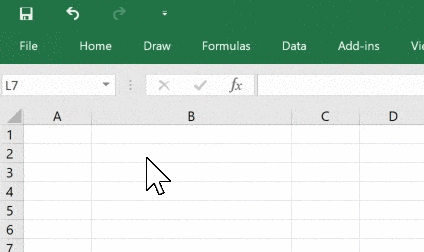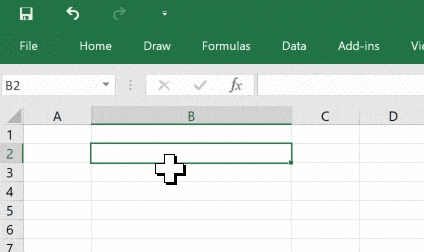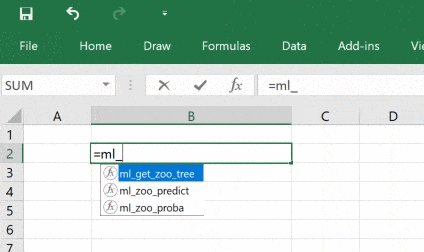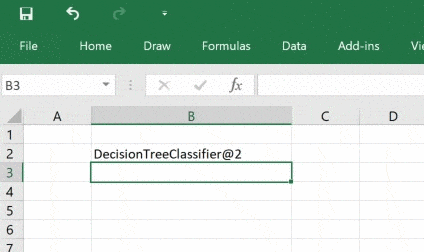
Начнём с функции. Пользователь вызовет её, чтобы получить объект дерева, а затем этот объект для прогнозирования пройдёт через последовательность функций. Снова построим дерево, но пример будет сложнее: сохраним натренированную при помощи pickle и затем вместо того, чтобы каждый раз её создавать, загрузим её в Excel и настроим параметры, это будет интересно!

from pyxll import xl_func
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import pandas as pd
import os

@xl_func("float, int, int: object")
def ml_get_zoo_tree(train_size=0.75, max_depth=5, random_state=245245):
    # Load the zoo data
    dataset = pd.read_csv(os.path.join(os.path.dirname(__file__), "zoo.csv"))

    # Drop the animal names since this is not a good feature to split the data on
    dataset = dataset.drop("animal_name", axis=1)

    # Split the data into a training and a testing set
    features = dataset.drop("class", axis=1)
    targets = dataset["class"]

    train_features, test_features, train_targets, test_targets = 
        train_test_split(features, targets, train_size=train_size, random_state=random_state)

    # Train the model
    tree = DecisionTreeClassifier(criterion="entropy", max_depth=max_depth)
    tree = tree.fit(train_features, train_targets)

    # Add the feature names to the tree for use in predict function
    tree._feature_names = features.columns

    return tree

Код выше совпадает с кодом, который мы видели ранее, за исключением декоратора @xl_func, который сообщает дополнению PyXLL о том, какая функция Python должна стать пользовательской функцией Excel.

Строка float, int, int: object — это сигнатура функции. Она необязательна, но без этой сигнатуры пользователь сможет передавать в функцию свои типы, например, строки и это может привести к сбою. Возвращаемый тип object означает, что классификатор идёт через Excel как объект Python, функция возвращает дескриптор, который возможно передать другим функциям Python.

Код нужно добавить в список модулей конфигурационного файла pyxll.cfg, также необходима надстройка PyXLL, если вы не установили её.

Все аргументы функции имеют значение по умолчанию, поэтому необязательны, но при желании со входными данными можно экспериментировать.

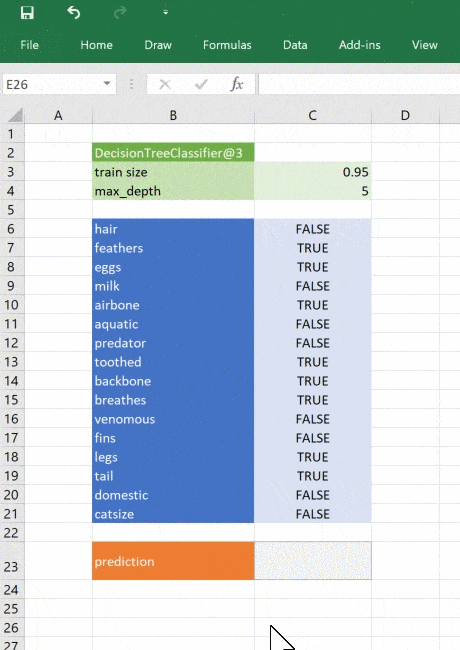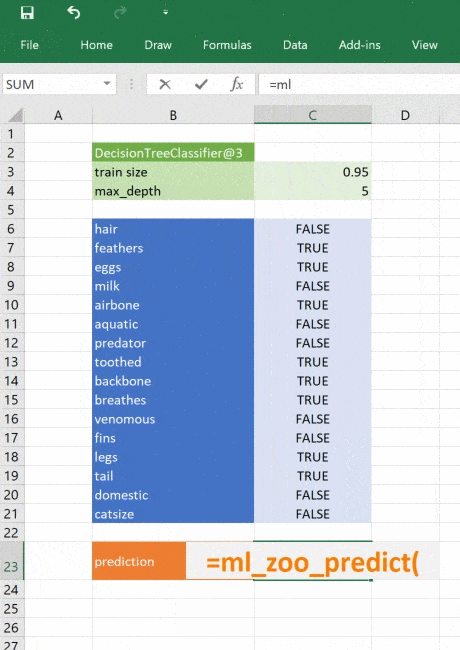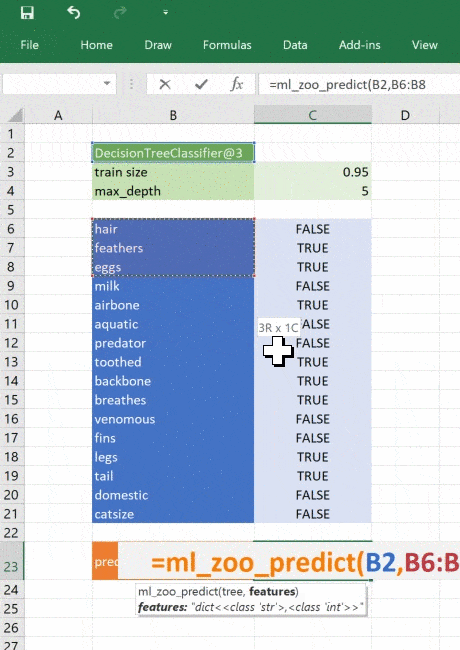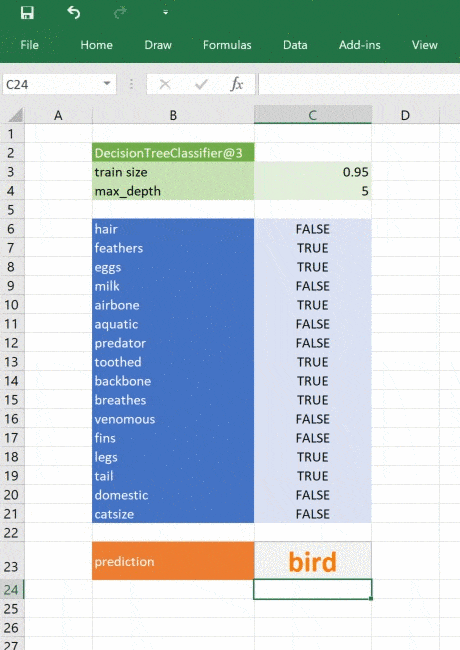
Прогнозируем класс животного

Теперь всё, что нужно для работы с моделью — ещё одна функция для передачи входных данных и получения прогноза. Используем тот же код, что и раньше, но обернём его декоратором @xl_func.

_zoo_classifications = {
    1: "mammal",
    2: "bird",
    3: "reptile",
    4: "fish",
    5: "amphibian",
    6: "insect",
    7: "mollusc"
}

@xl_func("object tree, dict features: var")
def ml_zoo_predict(tree, features):
    # Convert the features dictionary into a DataFrame with a single row
    features = pd.DataFrame([features], columns=tree._feature_names)
    # Get the prediction from the model
    prediction = tree.predict(features)[0]
    return _zoo_classifications[prediction]

Модель возвращает целое число — спрогнозированный класс. Словарь _zoo_classifications содержит эти числа и понятные человеку названия классов.

Эта функция берёт объект дерева из ml_get_zoo_tree и список пар ключ-значение, переданных в неё как словарь. В словаре сопоставлены имена признаков, с которыми мы работали при конструировании дерева, и входные признаки. Их сопоставление таково, что при вызове tree.predict признаки упорядочены правильно.

Это простой пример, натренированный на минимуме данных, но принцип применим к любой сложной модели. При помощи Python вы можете исследовать, разрабатывать и строить модель, чтобы получить ценные инсайты и быстрые прогнозы на реальных данных.

Небольшое дополнение

Чёрно-белые листы с цифрами нравятся всем, но иногда мне нравится добавлять небольшие детали ради привлекательности таблицы. PyXLL позволяет получить доступ к объектной модели Excel с помощью функции xl_app. Объектная модель Excel точно совпадает с той, что применяется в VBA. Функция ниже создаёт на листе объект изображения и загружает его.

from pyxll import xl_app

def show_image_in_excel(classification, figname="prediction_image"):
    """Plot a figure in Excel"""
    # Show the figure in Excel as a Picture object on the same sheet
    # the function is being called from.
    xl = xl_app()
    sheet = xl.ActiveSheet

    # if a picture with the same figname already exists then get the position
    # and size from the old picture and delete it.
    for old_picture in sheet.Pictures():
        if old_picture.Name == figname:
            height = old_picture.Height
            width = old_picture.Width
            top = old_picture.Top
            left = old_picture.Left
            old_picture.Delete()
            break
    else:
        # otherwise create a new image
        top_left = sheet.Cells(1, 1)
        top = top_left.Top
        left = top_left.Left
        width, height = 100, 100

    # insert the picture
    filename = os.path.join(os.path.dirname(__file__), "images", _zoo_classifications[classification] + ".jpg")
    picture = sheet.Shapes.AddPicture(Filename=filename,
                                      LinkToFile=0,  # msoFalse
                                      SaveWithDocument=-1,  # msoTrue
                                      Left=left,
                                      Top=top,
                                      Width=width,
                                      Height=height)

    # set the name of the new picture so we can find it next time
    picture.Name = figname

Вызов ml_zoo_predict обновляет изображение в Excel при каждом изменении прогноза. Функция обновляет Excel, поэтому вызывать её нужно после вычислений, именно этим занимается async_call из pyxll, а ниже вы видите новую версию ml_zoo_predict:

from pyxll import xl_func, async_call

@xl_func("object tree, dict features: var")
def ml_zoo_predict(tree, features):
    # Convert the features dictionary into a DataFrame with a single row
    features = pd.DataFrame([features], columns=tree._feature_names)

    # Get the prediction from the model
    prediction = tree.predict(features)[0]

    # Update the image in Excel
    async_call(show_image_in_excel, prediction)

    return _zoo_classifications[prediction]

Изображение обновляется при изменении прогноза:

Этот материал — яркое напоминание о том, что Excel может справляться с задачами машинного обучения, а область ML сложна, но её сложность преодолима и если вы хотите изменить карьеру или вывести ваши навыки на новый уровень, то можете обратить внимание на наши курсы по Machine Learning, аналитике данных или присмотреться к флагманскому курсу Data Science. Также вы можете узнать, как начать или продолжить развитие в других направлениях:

Data Science и Machine Learning

• Профессия Data Scientist

• Профессия Data Analyst

• Курс «Математика для Data Science»

• Курс «Математика и Machine Learning для Data Science»

• Курс по Data Engineering

• Курс «Machine Learning и Deep Learning»

• Курс по Machine Learning

Python, веб-разработка

• Профессия Fullstack-разработчик на Python

• Курс «Python для веб-разработки»

• Профессия Frontend-разработчик

• Профессия Веб-разработчик

Мобильная разработка

• Профессия iOS-разработчик

• Профессия Android-разработчик

Java и C#

• Профессия Java-разработчик

• Профессия QA-инженер на JAVA

• Профессия C#-разработчик

• Профессия Разработчик игр на Unity

От основ — в глубину

• Курс «Алгоритмы и структуры данных»

• Профессия C++ разработчик

• Профессия Этичный хакер

А также:

• Курс по DevOps