Муниципальное казенное общеобразовательное учреждение «Гимназия №1 г. Майского»
Проект
«Решение практических задач с помощью электронных таблиц»
Выполнили ученики 9 А класса:
Тимошев Рифат
Тимошев Далил
Отрощенко Антон
Руководитель: Ятлова Т.А,
учитель информатики
Майский, 2019 год
Оглавление
Введение 3
Основная часть. 4
Что такое электронная таблица? 4
Типы данных 4
Абсолютные и относительные ссылки 5
Функции 5
Построение диаграмм и графиков 8
Практическая часть 9
Задпние_1 9
Задание_2 9
Заключение 11
Введение
Тема нашего проекта «Решение практических задач с помощью электронных таблиц».
В нашей жизни мы постоянно решаем какие-то задачи. Посещая «Магнит», мы с интересом наблюдаем, как кассиры считывают информацию в виде штрих кода, взвешивают продукт, или подсчитывают количество, и программа сама выдает сумму к оплате. При изучении информатики мы проходили тему «Электронные таблицы». Мы задумались о том, что с помощью этой программы можно решать многие жизненно важные задачи, имеющие практическое применение. Эти вычисления можно выполнять с помощью программы Microsoft Excel.
Мы выбрали эту тему, потому что нам нравится .работать в Excel и для выполнения этой работы требуют наличия хороших знаний по работе в электронных таблицах.
Цель нашей работы – отработка навыка решения задач на компьютере в электронных таблицах.
Для выполнения поставленной цели наметили выполнить следующие задачи:
- Уточнить понятие «электронные таблицы».
- Определить назначение абсолютных и относительных ссылок.
- Выделить категории функций.
- Выявить связь и отличие функций в Microsoft Excel и Open Office Calc.
- Найти применение функций для решения задач.
- Решить задания_19
Проектный продукт: письменная работа и презентация.
Методы работы:
1)анализ литературы по вопросу;
2) поиск информации в книгах и сети Интернет;
3) наблюдение;
Основная часть.
Что такое электронная таблица?
Электронная таблица — это программа обработки числовых данных, хранящая и обрабатывающая данные в прямоугольных таблицах.
Типы данных
Электронные таблицы позволяют работать с тремя основными типами данных: число, текст и формула.
Числа в электронных таблицах Excel могут быть записаны в обычном числовом или экспоненциальном формате, например: 195,2 или 1.952E + 02.
Текстом в электронных таблицах Excel является последовательность символов, состоящая из букв, цифр и пробелов, например, запись «32 Мбайт» является текстовой.
Формулы
Формула должна начинаться со знака равенства и может включать в себя числа, имена ячеек, функции (математические, статистические, финансовые, дата и время и т.д.) и знаки математических операций.
Например, формула «=А1+В2» обеспечивает сложение чисел, хранящихся в ячейках А1 и В2, а формула «=А1*5» — умножение числа, хранящегося в ячейке А1, на 5.
При вводе формулы в ячейке отображается не сама формула, а результат вычислений по этой формуле. При изменении исходных значений, входящих в формулу, результат пересчитывается немедленно.
Абсолютные и относительные ссылки
Существуют два основных типа ссылок: относительные и абсолютные.
Относительная ссылка в формуле используется для указания адреса ячейки, вычисляемого относительно ячейки, в которой находится формула.
Относительные ссылки имеют следующий вид: А1, ВЗ.
Абсолютная адресация: в некоторых случаях оказывается необходимым отменить действие относительной адресации для того, чтобы при переносе формулы адрес ячейки не изменялся (т.е. был бы не относительным, а абсолютным). В таком случае применяется прием, который называется замораживанием адреса. Для этой цели в имени ячейки употребляется символ «$». Для замораживания всего адреса значок $ ставится дважды. Например: $B$2. можно заморозить только столбец ($B2) или только строку (B$2). Тогда часть адреса будет изменяться при переносе формулы, а часть – нет.
В электронных таблицах возможен поиск данных в соответствии с указанными условиями — фильтрами.
Фильтры определяются с помощью условий поиска (больше, меньше, равно и т. д.) и значений (100, 10 и т. д.).
Например, больше 100. В результате поиска будут найдены те ячейки, в которых содержатся данные, удовлетворяющие заданному фильтру.
Функции
Функции могут быть настолько сложными, насколько это необходимо, и могут содержать в качестве аргументов формулы и другие функции. Можно использовать до семи уровней вложенности функций. Если этот предел превысить, Excel выдаст ошибку и такую функцию вычислять не будет.
Ниже рассмотрены наиболее часто встречающиеся функции и их смысл.
Таблица: Наиболее часто используемые функции
|
русский |
англ. |
действие |
синтаксис |
|
СУММ |
SUM |
Суммирует все числа в интервале ячеек |
СУММ(число1:число2) |
|
Пример: |
|||
|
=СУММ(A2:A4) |
|||
|
СЧЁТ |
COUNT |
Подсчитывает количество всех непустых значений указанных ячеек |
СЧЁТ(значение1: [значение2],…) |
|
Пример: |
|||
|
=СЧЁТ(A5:A8) |
|||
|
СРЗНАЧ |
AVERAGE |
Возвращает среднее значение всех непустых значений указанных ячеек |
СРЕДНЕЕ(число1:[число2] ) |
|
Пример: |
|||
|
=СРЗНАЧ(A2:A6) |
|||
|
МАКС |
MAX |
Возвращает наибольшее значение из набора значений |
МАКС(число1;число2; …) |
|
Пример: |
|||
|
=МАКС(A2:A6) |
|||
|
МИН |
MIN |
Возвращает наименьшее значение из набора значений |
МИН(число1;число2; …) |
|
Пример: |
|||
|
=МИН(A2:A6) |
|||
|
ЕСЛИ |
IF |
Проверка условия. Функция с тремя аргументами: первый аргумент — логическое выражение; если значение первого аргумента — истина, то результатом выполнения функции является второй аргумент. Если ложно — третий аргумент. |
ЕСЛИ(лог_выражение; |
|
Пример: |
|||
|
=ЕСЛИ(A2>B2;»Превышение»;»ОК») |
|||
|
СЧЁТЕСЛИ |
COUNTIF |
Количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. |
СЧЁТЕСЛИ(диапазон, критерий) |
|
Пример: |
|||
|
=СЧЁТЕСЛИ(A2:A5;»яблоки») |
|||
|
СУММЕСЛИ |
SUMIF |
Сумма непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. |
СУММЕСЛИ |
|
Пример: |
|||
|
=СУММЕСЛИ(B2:B25;»>5″) |
Построение диаграмм и графиков
Электронные таблицы позволяют представлять числовые данные в виде диаграмм или графиков. Диаграммы бывают различных типов (столбчатые, круговые и т. д.); выбор типа диаграммы зависит от характера данных.
|
|
|
Практическая часть
Задпние_1. Составить таблицу Оплаты электроэнергии за год.
|
Исходная таблица |
Результат |
|
|
|
Задание_2
В электронную таблицу занесли данные о тестировании учеников. Ниже приведены первые десять строк таблицы:В столбце А записан округ, в котором учится ученик; в столбце В — фамилия; в столбце С — любимый предмет; в столбце D — тестовый балл. Всего в электронную таблицу были занесены данные по 1000 ученикам.
Выполните задание.
1. Сколько учеников в Восточном округе (В) выбрали в качестве любимого предмета информатику? Ответ на этот вопрос запишите в ячейку Н2 таблицы.
2. Каков средний тестовый балл у учеников Северного округа (С)? Ответ на этот вопрос запишите в ячейку НЗ таблицы с точностью не менее двух знаков после запятой.
1. Запишем в ячейку E2 следующую формулу =ЕСЛИ(A2=»В»;C2;0) и скопируем ее в диапазон E3:E1001. В ячейку столбца E будет записываться название предмета, если ученик из Восточного округа и «0», если это не так. Применив операцию =ЕСЛИ(E2=»информатика»;1;0), получим столбец (F): с единицами и нулями. Далее, используем операцию =СУММ(F2:F1001). Получим количество учеников, которые считают своим любимым предметом информатику. Таких 10 человек.
2. Для ответа на второй вопрос используем операцию «ЕСЛИ». Запишем в ячейку G2 следующее выражение: =ЕСЛИ(A2=»С»;D2;0), в результате применения данной операции к диапазону ячеек G2:G1001, получим столбец, в котором записаны баллы только учеников Северного округа. Сложив значения в ячейках, получим сумму баллов учеников: 56 737. Найдём количество учеников Северного округа с помощью команды =СЧЁТЕСЛИ(A2:A1001;»С»), получим 105. Разделив сумму баллов на количество учеников, получим: 540,352 — искомый средний балл.
Ответ: 1) 10; 2) 540,35.
Заключение
В этом проекте мы научились работать с электронными таблицами, а также применять их на практике. Мы выяснили, что они используются везде, даже в повседневной жизни. Поэтому знать, и пользоваться нужно уметь каждому!
Содержание
- Поиск решения задач в Excel с примерами
- Решение задач оптимизации в Excel
- Решение финансовых задач в Excel
- Решение эконометрики в Excel
- Решение логических задач в Excel
- Решение математических задач в Excel
- Проект «Решение задач при помощи электронных таблиц»
- Реализация межпредметных связей при обучении математике в системе основного и среднего общего образования
- Организация учебно-исследовательской деятельности учащихся как средство развития познавательной активности при обучении математике в условиях реализации ФГОС ООО и ФГОС СОО
- Ментальная арифметика: отрицательные числа, дроби, возведение в квадрат, извлечение квадратного корня
- Обучение школьников 5-9 классов решению текстовых задач по математике различными способами
- Описание презентации по отдельным слайдам:
- Опытные онлайн-репетиторы
- IV Международный практический «Инфофорум» для педагогов
- 2023 год педагога и наставника: вызовы и решения
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Онлайн-занятия с репетиторами
- Подарочные сертификаты
Поиск решения задач в Excel с примерами
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
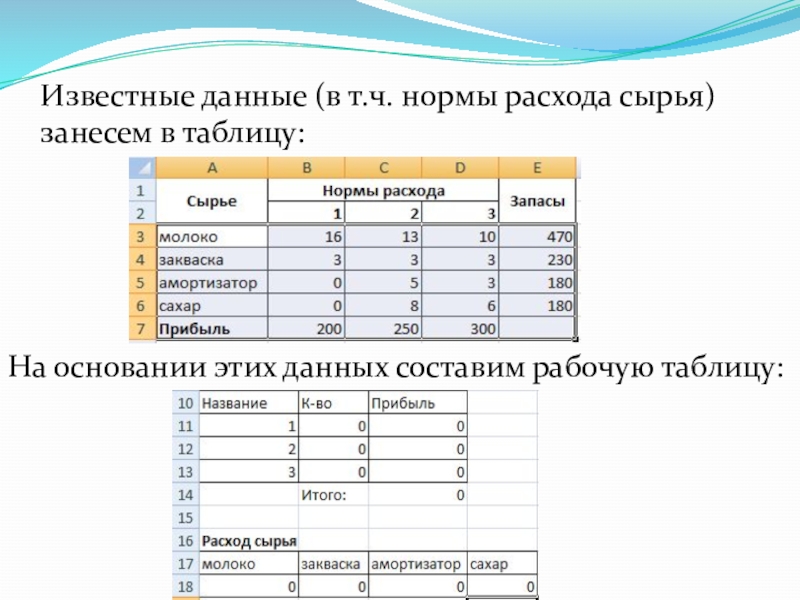
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
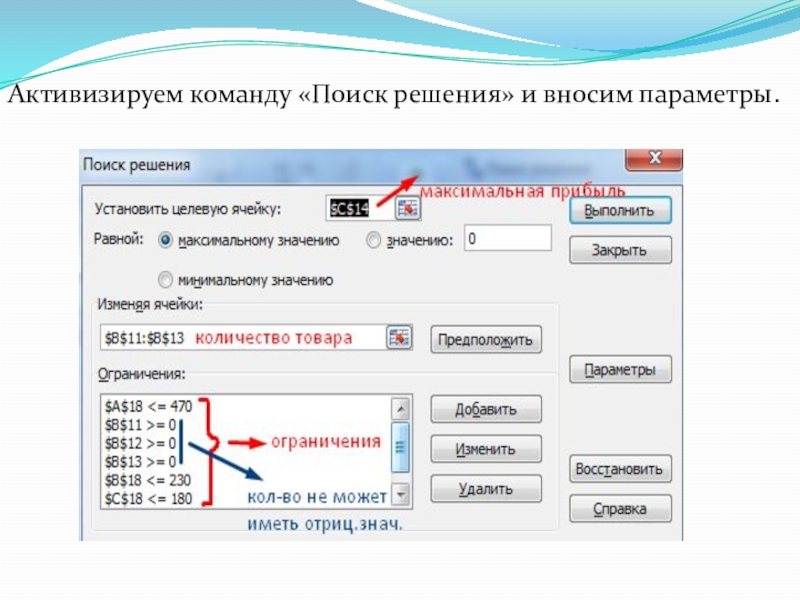
Активизируем команду «Поиск решения» и вносим параметры.
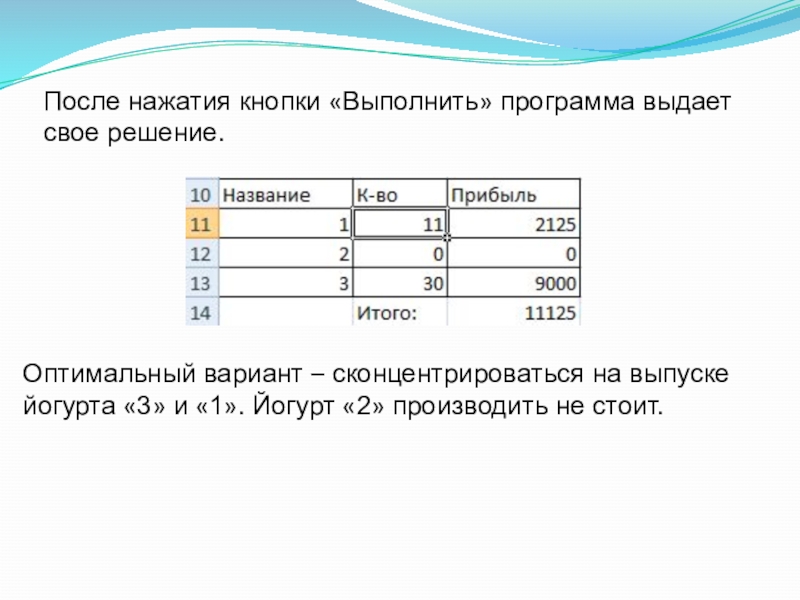
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
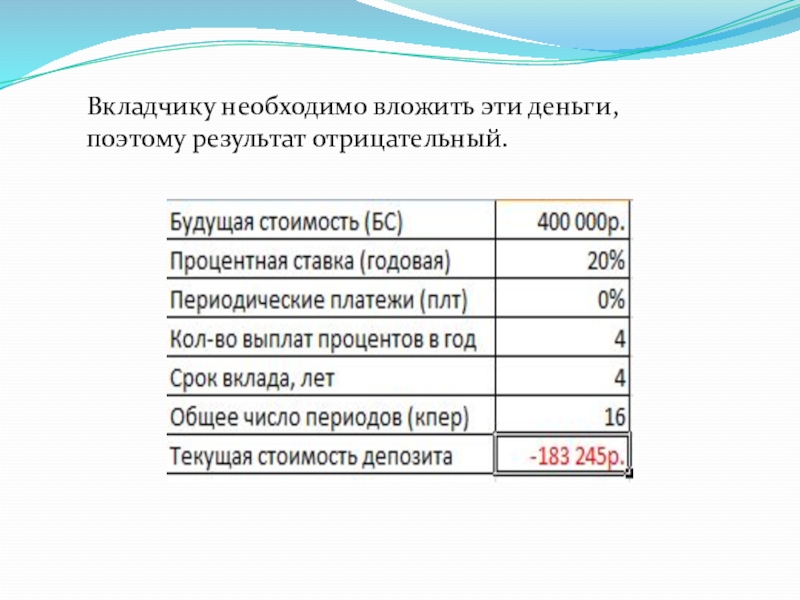
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Источник
Проект «Решение задач при помощи электронных таблиц»

Курс повышения квалификации
Реализация межпредметных связей при обучении математике в системе основного и среднего общего образования
- Сейчас обучается 21 человек из 13 регионов

Курс повышения квалификации
Организация учебно-исследовательской деятельности учащихся как средство развития познавательной активности при обучении математике в условиях реализации ФГОС ООО и ФГОС СОО
- Сейчас обучается 22 человека из 14 регионов

Курс повышения квалификации
Ментальная арифметика: отрицательные числа, дроби, возведение в квадрат, извлечение квадратного корня
- Сейчас обучается 92 человека из 37 регионов

Обучение школьников 5-9 классов решению текстовых задач по математике различными способами
Описание презентации по отдельным слайдам:
Решение задач при помощи электронных таблиц
Автор: Коротков Павел, 8 класс
Руководитель: Гончарук А.В.
МОУ Непецинская СОШ
Целью моей работы было рассмотреть задачи, решаемых при помощи электронных таблиц. Определить роль Excel в различных сферах деятельности, ведь знание Microsoft Excel стало обязательным требованием для офисных рабочих.
Для чего нужен EXCEL?
Во первых excel это самая популярная программа для быстрого и эффективного решения самых разных задач.
Программа способна создавать графики, решать самые различные рода задач: финансовые, экономические, математические, логические, оптимизационные и многие другие.
Например: если получать кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ПОДБОРА ПАРАМЕТРОВ EXCEL
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
4. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В EXCEL
Подбор параметров («Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра») – находит значения, которые обеспечат нужный результат.
Поиск решения (надстройка Microsoft Excel; «Данные» — «Анализ») – рассчитывает оптимальную величину, учитывая переменные и ограничения. Диспетчер сценариев («Данные» — «Работа с данными» — «Анализ «что-если»» — «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске
йогурта «3» и «1». Йогурт «2» производить не стоит.
РЕШЕНИЕ ФИНАНСОВЫХ ЗАДАЧ В EXCEL
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
ПОСТРОЕНИЕ ГРАФИКОВ В EXCEL ПО ДАННЫМ ТАБЛИЦЫ
Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
ЗАКЛЮЧЕНИЕ
Excel – это самое полезное, универсальное и многофункциональное программное средство из пакета Office. Основное назначение Excel – хранение, анализ и визуализация данных, создание отчетов и проведение сложных расчетов.
СПАСИБО ЗА ВНИМАНИЕ!

Лучшее для учеников, педагогов и родителей
Опытные
онлайн-репетиторы
- По любым предметам 1-11 классов
- Подготовка к ЕГЭ и ОГЭ
Рабочие листы и материалы для учителей и воспитателей
Более 7 500 дидактических материалов для школьного и домашнего обучения
IV Международный практический «Инфофорум» для педагогов
2023 год педагога и наставника: вызовы и решения
Ценности гуманной педагогики
Открытая сессия для учителей и руководителей образовательных организаций
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 168 730 материалов в базе
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 31.05.2018 3940
- PPTX 407.4 кбайт
- 65 скачиваний
- Рейтинг: 1 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Гончарук Анастасия Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 9133
- Всего материалов: 7
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 490 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Онлайн-занятия с репетиторами
для весеннего интерьера
Как преуспеть в роли репетитора: запланируйте неудачу, чтобы проект получился удачным
Методическое сопровождение образовательного процесса
Оказание первой помощи при наружных кровотечениях и травмах
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
Разработка проекта «Решение оптимизационных задач средствами Excel»
Место темы в учебном курсе: уроки в 10-м классе
План работы над проектом
|
Стадия работы |
Результат работы |
Домашнее задание |
|
Урок 1. Знакомство с программой «Поиск решения» в Excel на примере задачи из учебника [2] |
Учащиеся решают совместно в программе Excel предложенную задачу |
Найти информацию о Леониде Канторовиче |
|
Урок 2. Оформление презентации по этапам решения задачи |
Учащиеся готовят презентацию по решенной задаче из 7 слайдов
|
Выбор индивидуальной задачи, создание математической модели, проект электронной таблицы с данными |
|
Урок 3. Решение индивидуальной задачи |
Учащиеся решают свою задачу |
Подготовка текста главы проекта Введение |
|
Урок 4. Знакомство с требованиями оформления работы |
В программе WORD учащиеся оформляют свой проект |
Требования по оформлению рефератов |
|
Урок 5. Знакомство с требованиями оформления работы |
В программе WORD учащиеся оформляют свой проект |
Требования по оформлению рефератов |
|
Урок 6. Выполнение итогового теста |
Учащиеся выполняют итоговый тест и сдают папку с законченным проектом |
Урок 1. Знакомство с программой «Поиск решения» в Excel
Построить математическую модель задачи и решить её средствами Excel.
Задача. Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
|
Ресурсы |
Нормы расхода ресурсов на одно изделие |
Общее количество ресурсов |
|
|
стол |
шкаф |
||
|
Древесина 1 вида |
0,2 |
0,1 |
40 |
|
Древесина 2 вида |
0,1 |
0,3 |
60 |
|
Трудоемкость |
1,2 |
1,5 |
371,1 |
|
Прибыль от реализации одного изделия |
6 |
9 |
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.
РЕШЕНИЕ.
Составим математическую модель задачи. Пусть фабрика изготавливает x1 столов и x2 шкафов. По смыслу задачи эти переменные неотрицательны, x x1, 2 ≥ 0 . Прибыль от реализации такого количества шкафов и столов составит F = 6x1 +9x2 рублей, ее нужно максимизировать:
F = 6x1 +9x2 → max .
Теперь составим ограничения задачи.
Для изготовления x1 столов и x2 шкафов потребуется 0,2x1 +0,1x2 древесины первого вида, запасы которой составляют 40 куб.м., поэтому 0,2x1 +0,1x2 ≤ 40 , или 2x1 + x2 ≤ 400. Для изготовления x1 столов и x2 шкафов потребуется 0,1x1 +0,3x2 древесины второго вида, запасы которой составляют 60 куб.м., поэтому 0,1x1 +0,3x2 ≤ 60 , x1 +3x2 ≤ 600.
Для изготовления x1 столов и x2 шкафов потребуется 1,2x1 +1,5x2 древесины третьего вида, запасы которой составляют 371,1 куб.м., поэтому 1,2x1 +1,5x2 ≤ 371,1, 12x1 +15x2 ≤ 3711,
4x1 +5x2 ≤ 1237
Получаем задачу линейного программирования:
F = 6x1 +9x2 → max,
2x1 + x2 ≤ 400,
x1 +3x2 ≤ 600,
4x1 +5x2 ≤1237,
x1, 2 ≥ 0.
Решим задачу средствами Excel. Заполним ячейки исходными данными (в виде таблицы) и формулами математической модели. Вычисляемые ячейки пометим цветом.
Таблице в режиме чисел:
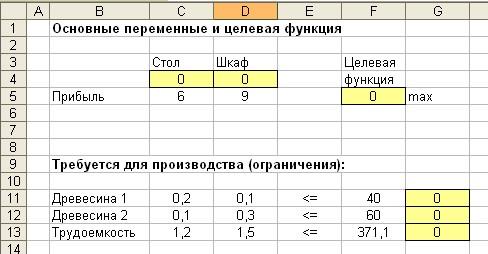
Таблица в режиме формул: (для отображения формул можно перед знаком равно поставить пробел)

Вызываем надстройку «Поиск решения» и заполняем параметры: (для активирования данной функции необходимо выполнить команду СЕРВИС, НАДСТРОЙКА и установить галочку против программы Поиск решения)
Вносим целевую функцию и ограничения.
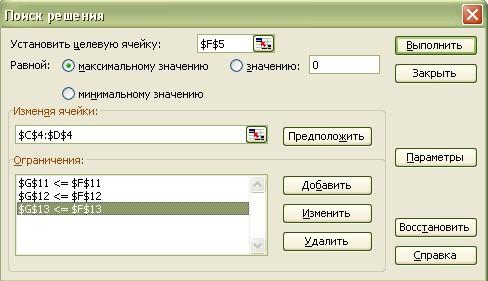
Запускаем решение:

Получаем решение:
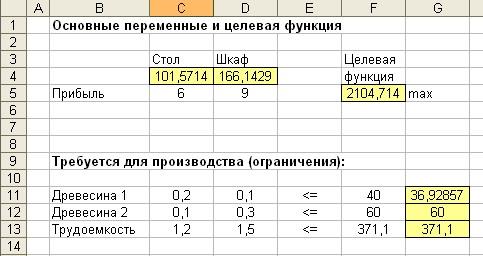
Получили нецелочисленное решение – 101,571 столов и 166,143 стульев. Чтобы получить более «реальное» в экономическом смысле решение, добавим ограничение целочисленности переменных, тогда получим:
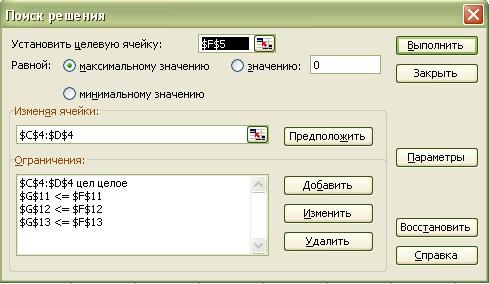
Искомое решение:
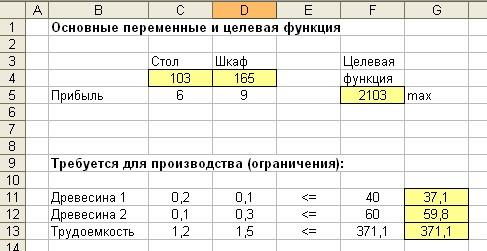
Таким образом, следует производить 103 стула и 165 шкафов, при этом прибыль от реализации будет максимальна и составит 2103 рубля. В процессе производства будут остатки древесины первого и второго типа: 2,9 и 0,2 кубометра соответственно. Трудоемкость будет «использована» в полном размере.
Урок 3. Индивидуальные задания для учащихся
Задача 1. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки? Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5?
Задача 2. Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?
Задача 3. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить 11 кг сырья первого типа, 21 кг сырья второго типа, 31 кг сырья третьего типа. На изготовление единицы Изделия 2 требуется затратить 12 кг сырья первого типа, 22 кг сырья второго типа, 32 кг сырья третьего типа. Производство обеспечено сырьем каждого типа в количестве 100 кг, 150 кг, 180 кг соответственно. Рыночная цена единицы Изделия 1 составляет 3 тыс. руб., а единицы Изделия 2 — 4 тыс.руб. Требуется составить план производства изделий, обеспечивающий максимальную выручку от их реализации.
Задача 4. Для производства двух видов продукции А и В предприятие использует четыре группы оборудования 1, 2, 3, 4. На производство одной штуки продукции А требуется занять в течение одной единицы времени 1, 0, 5, 2 единиц соответственно 1, 2, 3, 4 оборудования. На производство одной штуки продукции В требуется 1, 1, 0, 2 единиц оборудования 1, 2, 3, 4. Имеется оборудования по группам 1-10, 2-12, 3-24, 4-20 единиц. Предприятие получает с одной штуки продукции А доход 4 тыс. рублей, а продукции – 6 тыс. руб.
Сколько штук продукции каждого вида должно производить предприятие, чтобы получить максимальную прибыль?
Задача 5. В мастерской промартели освоили производство столов и тумбочек для торговой сети. Для их изготовления имеется два вида древесины 1- 72м3 и 2-56 м3.
На каждое изделие требуется древесина м3 каждого вида
|
Изделия |
1 |
2 |
|
Стол |
0,18 |
0,08 |
|
Тумбочка |
0,09 |
0,28 |
От производства одного стола промартель получает чистого дохода 1,1 тыс. руб. и от производства тумбочки 700 руб. Определить, сколько столов и тумбочек должна производить промартель, чтобы получить максимальную прибыль?
Задача 6. Цех выпускает трансформаторы двух видов. На один трансформатор первого вида расходуется 3 кг. Проволоки и 5 кг. Железа, а на один трансформатор второго вида требуется 3 кг железа и 2 кг. Проволоки. От реализации одного трансформатора первого вида цех получает прибыль в 1,2 тыс. руб., а от реализации одного трансформатора второго вида 1 тыс. руб. Сколько трансформаторов каждого вида должен производить цех, чтобы получить максимальную прибыль, если цех располагает 480 кг. Железа и 300 кг. Проволоки?
Задача 7. Для откорма животных на ферме в их ежедневный рацион необходимо включить не менее 33 единиц вещества А, 23 единицы питательного вещества В. Для откорма используется два вида кормов. Данные о содержании питательных веществ и стоимости весовой единицы представлены в таблице.
|
В одной весовой единице |
А |
В |
Стоимость одной весовой единицы |
|
Корм 1 Корм 2 |
4 3 |
3 2 |
20 руб 20 руб |
Составьте наиболее дешевый рацион, при котором каждое животное получило бы необходимое количество питательных веществ А и В?
Задача 8. Имеется три вида сырья А, В, С, которые используются для производства двух видов продуктов 1 и 2. В распоряжении находится 500 единиц сырья А, 750 единиц сырья В и 200 единиц сырья С. Продукт 1 состоит из 1 единицы сырья А и двух единиц сырья В. Продукт 2 состоит из двух единиц сырья А, одной единицы сырья В и одной единицы сырья С. Доход от производства одной единицы продукта 1 составляет 4 тыс. руб, а от одной единицы продукта 2 – 3 тыс. руб. Сколько единиц каждого вида продукции производить, чтобы получить максимальную прибыль?
Задача 9. Имеется два вида сырья для производства двух видов продуктов 1 и 2. Продукт 1 состоит из двух единиц сырья А и пяти единиц сырья В. Продукт 2 состоит из трех единиц сырья А и четырех единиц сырья В. Доход от производства одной единицы продукта 1 составляет 4 тыс. руб., а от одной единицы продукта 2 – 5 тыс. руб. Сколько единиц каждого вида продукта нужно производить, чтобы максимизировать прибыль, если в распоряжении имеется 500 единиц сырья А и 750 единиц сырья В?
Задача 10. Фирма производит два вида продукции А и В. Для выпуска каждого вида продукции требуется определенное время обработки на всех устройствах I, II, III:

Пусть время работы на устройствах соответственно 40, 36, 36 часов в неделю. Прибыль от изделий А и В соответственно составляет 5$ и 3$. Определите недельные нормы выпуска изделий для максимизации прибыли. (Рынок сбыта для каждого продукта неограничен.)
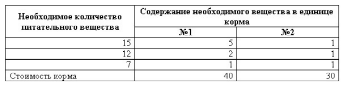
Задача 11. В рационе животных используется два вида кормов. Животные должны получать три вида веществ. Составить рацион кормления, обеспечивающий минимальные затраты. Исходные данные сведены в таблицу.
Задача 12. В рационе лошадей используется два вида кормов (сено и рожь). Лошади должны получать три вида веществ. Составить рацион кормления, обеспечивающий минимальные затраты. Исходные данные сведены в таблицу.

Задача 13. Фирма производит три вида продукции: А, В и С. Для выпуска каждого вида продукции требуется определенное время обработки на всех устройствах I, II, III, IV:
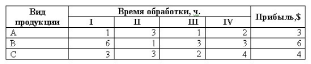
Пусть время работы на устройствах соответственно 84, 42, 21, 42 часа. Определите, какую продукцию и в каких количествах стоит производить для максимизации прибыли. Рынок сбыта для каждого продукта неограничен.
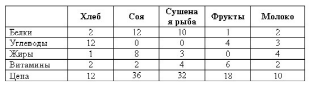
Задача 14. Фирма занимается составлением диеты, содержащей, по крайней мере, 20 ед. белков, 30 ед. углеводов, 10 ед. жиров и 40 ед. витаминов. Как дешевле всего достичь этого при указанных ценах в рублях на 1 кг (1 литр) пяти имеющихся продуктов?
Задача 15. Фирма производит два набора удобрений для газонов: обычный и улучшенный. В обычный входят 3 фунта азотных, 4 фунта фосфорных и один фунт калийных удобрений, а в улучшенный — 2 фунта азотных, 6 фунтов фосфорных и 2 фунта калийных удобрений. Известно, что для некоторых газонов требуется, по меньшей мере, 10 фунтов азотных, 20 фунтов фосфорных и 7 фунтов калийных удобрений. Обычный набор стоит 3$, а улучшенный — 4$. Сколько (целое число) и каких наборов удобрений надо купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Задача 16. Производятся изделия А и В, при изготовлении которых используется два типа технологического оборудования 1 и 2. На производство единицы изделия А оборудование 1 используется 2 часа, а оборудование 2 1 час. На производство единицы изделия В оборудование 1 используется 1 час, а оборудование 2 – 2 часа. Администрация на изготовление изделий может выделить оборудование 1 – на 10 часов, а оборудование 2 – на 8 часов. Спланировать производство изделий А и В так, чтобы общая прибыль была наибольшей, если от реализации единицы изделия А прибыль 5 тыс руб, В – 2 тыс. руб
Задача 17. Цех двойного суперфосфата выпускает два вида минеральных удобрений А и В. На производство 1 кг удобрений А используют 5 кг питательных веществ 1 и 4 кг. Питательного вещества 2. На производство 1 кг удобрений В используют 3 кг питательных веществ 1 и 2 кг. Питательного вещества 2. От реализации 1 кг А цех получает прибыль 40 руб., а от реализации 1 кг В – 35 руб.
Какое количество удобрений должен производить цех, чтобы получить максимальную прибыль, если цех имеет всего 450 кг питательного вещества 1 и 400 кг питательного вещества 2?
Урок 4. План работы над проектом
-
Создать папку «Проект учащегося ФИО», в которую перенести файл с решенной задачей и создать текстовый документ.
-
Содержание работы:
-
Титульный лист
-
Оглавление
-
Теоретическая часть содержит информацию о линейном программировании и людях, которые этим занимались.
-
Практическая часть состоит из технологии решения вашей задачи.
-
Используемые источники
-
Параметры оформления документа
-
Лист книжный
-
Отступы 1,5 см со всех сторон
-
Шрифт Times New Roman для основного текста, размер 12
-
Шрифт Arial для заголовков, размер 14, начертание Ж
-
Номер в правом нижнем углу и без номера на титульном листе
-
Каждый раздел документа располагается с нового листа.
-
Оформление проекта
1. Набрать текст
2. Разделить документ на страницы: титульный лист, оглавление, введение, теоретическая часть, практическая часть, список литературы. Установить курсор в начало новой страницы, выполнить ВСТАВКА/РАЗРЫВ/НОВАЯ СТРАНИЦА
Обратите внимание, что страница ОГЛАВЛЕНИЕ пока пустая.
3. Заполните титульный лист, предмет, свою фамилию. Выровняйте текст, кроме таблицы, по центру.
4. Выделите все заголовки и присвойте им стиль ЗАГОЛОВОК 1.
5. Вставить нумерацию в правом нижнем углу. ВСТАВКА/НОМЕРА СТРАНИЦ/ справа внизу и без номера на первой странице.
6. Перейти на страницу ОГЛАВЛЕНИЕ, вставить оглавление. ВСТАВКА/ССЫЛКА/ОГЛАВЛЕНИЕ И УКАЗАТЕЛИ/ Выбрать выкладку ОГЛАВЛЕНИЕ, задать УРОВНИ -1, убрать отметку о гиперссылках, но задать отметки
-
ПОКАЗАТЬ НОМЕРА СТРАНИЦ
-
НОМЕРА СТРАНИЦ ПО ПРАВОМУ КРАЮ.
Урок 5. Образец выполненного проекта
Урок 6. Вопросы итогового теста
-
Какую опцию главного меню необходимо открыть для выбора функции ПОИСК РЕШЕНИЯ?
-
Задача. Комплект мебели (парта и два стула) стоит 8500 рублей. Известно, что производитель М продает мебель упаковками по 6 комплектов в упаковке, а производитель N — по 4 комплекта в упаковке. Какое максимальное количество можно купить на 150 тыс. рублей? В ответе запишите два целых числа через пробел: количество комплектов и потраченную сумму в рублях. Решение
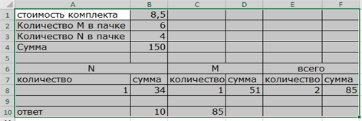
Какая ячейка оптимизируется?
-
Как оптимизируется ячейка? (варианты минимум, максимум, значение и т.д.)
-
Какие ячейки изменяются при оптимизации?
-
На какие ячейки накладываются ограничения при оптимизации?
-
Необходимое условие для автоматического собирания оглавления
-
Для нумерации страниц в работе необходимо выполнить
-
Расставьте по порядку основные разделы документа «Проект»
-
Выберите советского ученого, лауреата Нобелевской премии в области экономики (дан список имен)
-
Выберите верное утверждение (Предлагаются варианты размещения нумерации)
Источники информации
-
Практикум по вычислительной математике: Метод. Разработка/ Сост. Н.Л.Грохульская, С.Г.Ершова, А.Н.Новогрудская; Свердловский педагогический институт. Свердловск, 1990, 215 с, с.111-122
-
Культура информационной деятельности: Учебное пособие для основной школы (9 класс)./ В.В.Мочульский, А.Г.Гейн, В.И.Жильцова, В.И.Кадочникова, Т.В.Шпота, Е.А.Гвоздева, В.Г.Мещеряков, А.Г.Мачульская.- Екатеринбург: Центр «Учебная книга»; Смоленск; Издательство «Ассоциация XXIвек», 2006. – 432 с, с.176-180
-
https://www.matburo.ru/Examples/Files/LP_Excel1.pdf
-
https://inecon.org/docs/Kantorovich_1.pdf
Приложение. Образец выполненного проекта
Министерство образования и молодежной политики Свердловской области
Управление образования администрации Чкаловского района
Образовательная область: технология
Предмет: технология
Проект
Решение оптимизационных задач средствами Excel
|
Исполнитель: Руководитель: |
Ученик 10 класса Фамилия Имя Преподаватель технологии Иванова З.И. |
Екатеринбург
2020 г.
Оглавление
Введение 3
Линейное программирование, оптимизационные задачи 4
Практическая часть 5
Источники информации 8
Введение
Информатизация общества, развитие информационных технологий ставят перед каждым человеком вопрос о необходимости постоянного повышения квалификации, а в некоторых случаях и о неоднократной смене профессиональной деятельности в течение жизни.
Общеобразовательная школа должна формировать новую систему универсальных знаний, умений, навыков, опыт самостоятельной деятельности и личной ответственности обучающихся за сохранение окружающей среды, за разумное использование сырья, то есть современные ключевые компетенции.
Парадокс компетентности состоит в том, что она обнаруживает себя за пределами учебных ситуаций, в задачах, не похожих на те, где знания и умения приобретались.
Старые методики обучения требуют переосмысления и развития по мере появления новых информационных технологий.
Разрешение приведенных противоречий обуславливает актуальность настоящей работы и определяет ее проблему: какие средства могут быть использованы для формирования ИКТ-компетентности у учащихся средней школы?
Этот анализ определил следующий выбор темы проекта: «Методика решения оптимизационных задач средствами Excel».
Объект исследования: формирование ИКТ-компетентности.
Предмет исследования: использование разработки методики решения оптимизационной задачи средствами Excel для формирования ИКТ-компетентности.
Цель исследования: формирование ИКТ-компетентности средствами решения оптимизационной задачи в Excel.
При достижении поставленной цели мы руководствовались следующей гипотезой: разработка проекта будут способствовать формированию ИКТ—компетентности, если будет построена модель методики решения оптимизационных задач средствами Excel.
На основании цели исследования и рабочей гипотезы была сформулирована следующая задача исследования: разработать методику решения оптимизационной задачи средствами Excel для формирования ИКТ-компетентности.
Теоретическую основу исследования составили работы по линейному программированию:
-
https://www.matburo.ru/Examples/Files/LP_Excel1.pdf
-
https://inecon.org/docs/Kantorovich_1.pdf
Теоретическая значимость исследования заключается в следующем: описана последовательность решения оптимизационных задач средствами Excel.
Практическая значимость исследования состоит в том, что теоретические результаты доведены до уровня практического применения: решена конкретная задача.
Линейное программирование, оптимизационные задачи
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась ещё в XIX веке.
Развитие экономики потребовало количественных показателей, и в начале XX века были созданы и исследованы математические модели, которые повлияли на работы экономиста и статистика Василия Васильевича Леонтьева. Он разработал межотраслевую модель производства и распределения продукции.
В 1938 году Леонид Витальевич Канторович в порядке научной консультации приступил к изучению чисто практической задачи по составлению наилучшего плана загрузки лущильных станков (фанерный трест). Эта задача не поддавалась обычным методам. Стало ясно, что задача не случайная. В 1939 году Леонид Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования. Изучение подобных задач привело к созданию новой научной дисциплины линейного программирования и открыло новый этап в развитии экономико-математических методов. В 1975 году он стал лауреатом Нобелевской премии по экономике совместно с Тьяллингом Купмансом за вклад в теорию оптимального распределения ресурсов»).
Общей (стандартной) задачей линейного программирования называется задача нахождения минимума (максимума) линейной целевой функции (линейной формы). Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП).
Примеры задач:
-
транспортная задача;
-
максимальный поток;
-
задача экономного использования сырья.
Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод.
Практическая часть
Задание. Фирма производит два вида продукции A и В. Для выпуска каждого вида продукции требуется определенное время обработки на всех устройствах I, II, III:
Пусть время работы на устройствах соответственно 40, 36, 36 часов в неделю. Прибыль от изделий А и В соответственно составляет 5$ и 3$. Определите недельные нормы выпуска изделий для максимизации прибыли. (Рынок сбыта для каждого продукта неограничен.)
Решение.
Составим математическую модель задачи. Пусть фабрика изготовит х изделий А и у изделий В. По смыслу задачи эти переменные неотрицательные, х,у=0.
Прибыль от реализации такого количества продукции составит F=5*x+3*y.
Эту функцию надо максимизировать
Теперь составим ограничения задачи.
Для изготовления х изделий А и у изделий В потребуется:
0,5*х+0,25*у времени работы I устройства;
0,4*х+0,3*у времени работы II устройства;
0,2*х+0,4*у времени работы III устройства;
Но время работы I устройства ограничено 40 часами, т.е.
0,5*х+0,25*у
время работы II устройства ограничено 36 часами, т.е.
0,4*х+0,3*у
время работы III устройства ограничено 36 часами, т.е.
0,2*х+0,4*у
Получаем задачу линейного программирования:
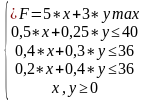
Решаем задачу средствами Excel. Заполняем ячейки исходными данными (в виде таблицы) и формулами математической модели.
Таблица в режиме чисел
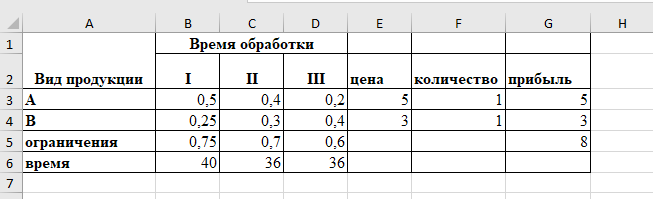
Таблица в режиме формул:
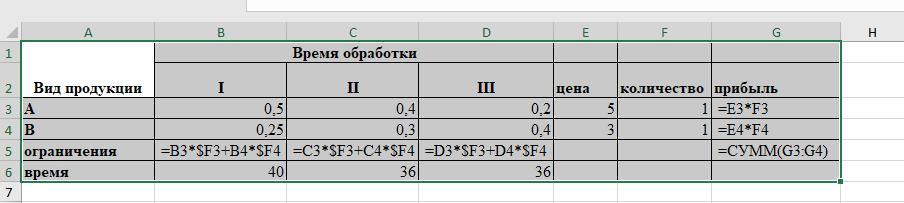
Вызываем надстройку «Данные / Поиск решения» и заполняем параметры:
Вносим целевую функцию и ограничения.
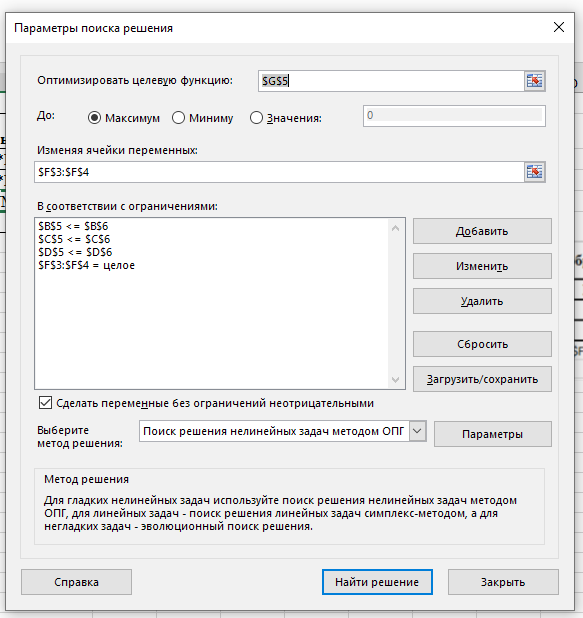
Получаем решение
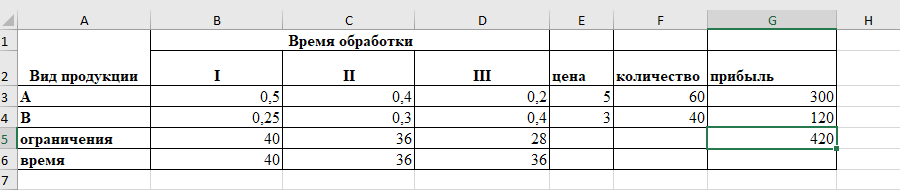
Получили следующий результат:
При заданных ограничениях предприятие может получить максимальную прибыль
420 единиц, изготовляя 60 единиц изделия А и 40 единиц изделия В.
Источники информации
-
Симоненко В.Д. Технология: базовый уровень: 10-11 классы: учебник для учащихся общеобразовательных учреждений / В.Д. Симоненко, О.П.Очинин, Н.В.Матяш: под ред. В.Д.Симоненко. – М.: Вентана-Граф., 2010. – 224 с, : ил.
-
http://www.apmath.spbu.ru/ru/staff/kuzyutin.d/files/vved_v_lp_lekciya.pdf
-
https://math.semestr.ru/simplex/simplex_lectures.php
Слайд 1Решение задач при помощи электронных таблиц
Автор: Коротков Павел, 8 класс
Руководитель: Гончарук

Слайд 2Целью моей работы было рассмотреть задачи, решаемых при помощи электронных таблиц.
Определить роль Excel в различных сферах деятельности, ведь знание Microsoft Excel стало обязательным требованием для офисных рабочих.

Слайд 3 Для чего нужен EXCEL?
Во первых excel это
самая популярная программа для быстрого и эффективного решения самых разных задач.
Программа способна создавать графики, решать самые различные рода задач: финансовые, экономические, математические, логические, оптимизационные и многие другие.
Например: если получать кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?

Слайд 4РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ПОДБОРА ПАРАМЕТРОВ EXCEL
Инструмент «Подбор параметра» применяется в ситуации,
когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Слайд 5Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 =
0. Порядок нахождения корня средствами Excel:
1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.

Слайд 62. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку»
— ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.

Слайд 73. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку»
— ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.

Слайд 84. После нажатия ОК отобразится результат подбора. Если нужно его сохранить,
вновь нажимаем ОК. В противном случае – «Отмена».

Слайд 9РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В EXCEL
Подбор параметров («Данные» — «Работа с данными»
— «Анализ «что-если»» — «Подбор параметра») – находит значения, которые обеспечат нужный результат.
Слайд 10Поиск решения (надстройка Microsoft Excel; «Данные» — «Анализ») – рассчитывает оптимальную
величину, учитывая переменные и ограничения. Диспетчер сценариев («Данные» — «Работа с данными» — «Анализ «что-если»» — «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.
Слайд 11Для решения простейших задач применяется команда «Подбор параметра». Самых сложных –
«Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Слайд 12Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и
«3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Слайд 13Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании
этих данных составим рабочую таблицу:
Слайд 14Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы:
=200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Слайд 15Активизируем команду «Поиск решения» и вносим параметры.
Слайд 16После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться
на выпуске
йогурта «3» и «1». Йогурт «2» производить не стоит.
Слайд 17РЕШЕНИЕ ФИНАНСОВЫХ ЗАДАЧ В EXCEL
Чаще всего для этой цели применяются финансовые
функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:

Слайд 18Так как процентная ставка не меняется в течение всего периода, используем
функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Слайд 20Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Слайд 21ПОСТРОЕНИЕ ГРАФИКОВ В EXCEL ПО ДАННЫМ ТАБЛИЦЫ
Рассмотрим пример построения графика линейной
функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

Слайд 22В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую
ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:

Слайд 23Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ ->
ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)

Слайд 24Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ

Слайд 25 Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у).
В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:

Слайд 26ЗАКЛЮЧЕНИЕ
Excel – это самое полезное, универсальное и многофункциональное программное средство из
пакета Office. Основное назначение Excel – хранение, анализ и визуализация данных, создание отчетов и проведение сложных расчетов.

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.




















