Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Полезная страница? Сохрани или расскажи друзьям
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k}=C_n^k cdot p^k cdot q^{n-k}. qquad(1)
$$
Здесь $C_n^k$ — число сочетаний из $n$ по $k$.
Еще: онлайн калькуляторы для формулы Бернулли.
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП(), выдающая определенную вероятность биномиального распределения.
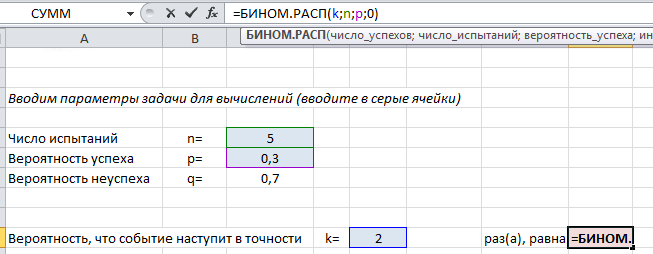
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0).
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^{n-k}$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_{i=k_1}^{k_2} C_n^i cdot p^i cdot q^{n-i}$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_{i=0}^{k_3} C_n^i cdot p^i cdot q^{n-i}$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_{i=k_4}^{n} C_n^i cdot p^i cdot q^{n-i}$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^{n}$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Полезное: расчетный файл по формуле Бернулли
Нужна помощь в решении задач по теории вероятностей?
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$
P_7(5)=C_{7}^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146.
$$
Для вероятности 6 или 7 попаданий суммируем:
$$
P_7(6)+P_7(7)=C_{7}^6 cdot 0,75^6 cdot 0,25^1+C_{7}^7 cdot 0,75^7 cdot 0,25^0= \
= 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495.
$$
А вот это решение в файле эксель:
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_{10}(k)=C_{10}^k cdot 0,5^kcdot 0,5^{10-k}=C_{10}^k cdot 0,5^{10}$$
Приступим к вычислениям:
$$1. P_{10}(2)=C_{10}^2 cdot 0,5^{10} = frac{10!}{2!8!}cdot 0,5^{10} approx 0,044.$$
$$2. P_{10}(4)+P_{10}(5)=C_{10}^4 cdot 0,5^{10} + C_{10}^5 cdot 0,5^{10}=left( frac{10!}{4!6!} + frac{10!}{5!5!} right)cdot 0,5^{10} approx 0,451.$$
$$3. P_{10}(0)+P_{10}(1)+P_{10}(2)=C_{10}^0 cdot 0,5^{10} + C_{10}^1 cdot 0,5^{10}+ C_{10}^2 cdot 0,5^{10}=left( 1+10+ frac{10!}{2!8!} right)cdot 0,5^{10} approx 0,055.$$
$$4. P_{10}(7)+P_{10}(8)+P_{10}(9)+P_{10}(10)=\ = C_{10}^7 cdot 0,5^{10} + C_{10}^8 cdot 0,5^{10}+ C_{10}^9 cdot 0,5^{10}+ C_{10}^10 cdot 0,5^{10} =\=left(frac{10!}{3!7!}+ frac{10!}{2!8!} + 10 +1right)cdot 0,5^{10} approx 0,172.$$
$$5. P_{10}(ge 1)=1-P_{10}(0)=1-C_{10}^0 cdot 0,5^{10} = 1- 0,5^{10} approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$
10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \
4,5 le m le 5,5,\
m=5.
$$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
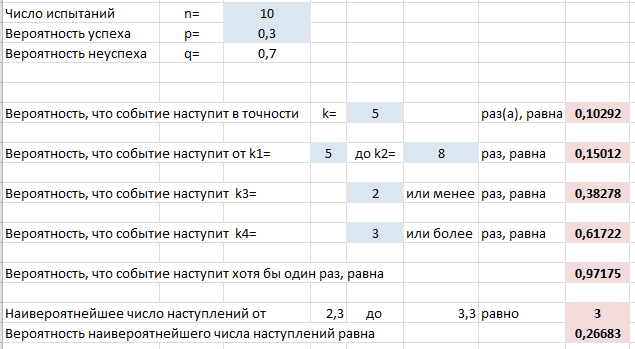
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:
Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.
Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Понравилось? Добавьте в закладки
Полезные ссылки
Расчетный файл эксель для расчетов по формуле Бернулли
|
|
Решебник задач по вероятности
Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
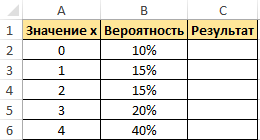
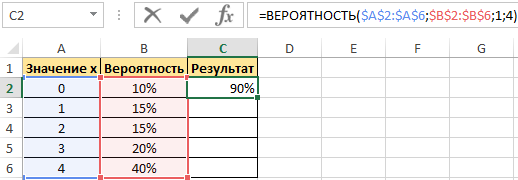
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
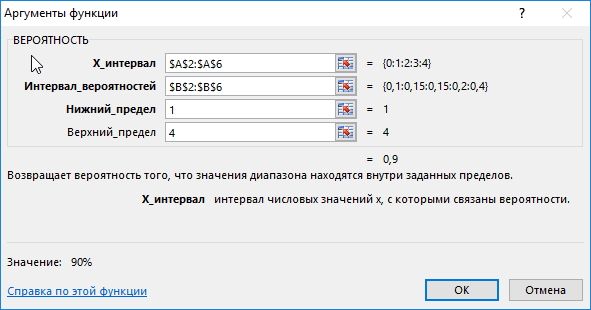
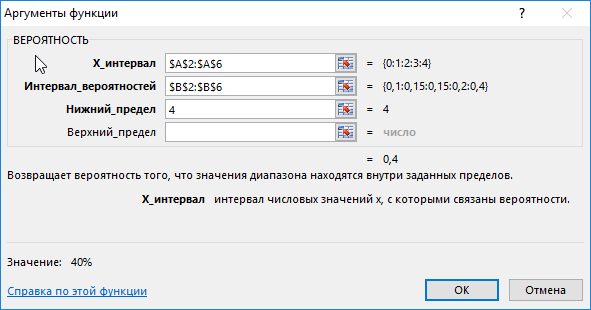
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
В результате выполненных вычислений получим:
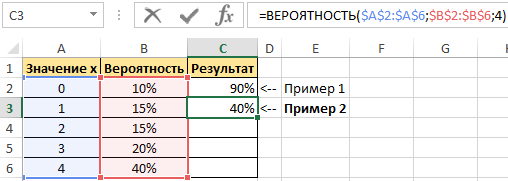
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
Пример 1: Вероятность игры в кости
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:
Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:
Вероятность оказывается равной 0,5 .
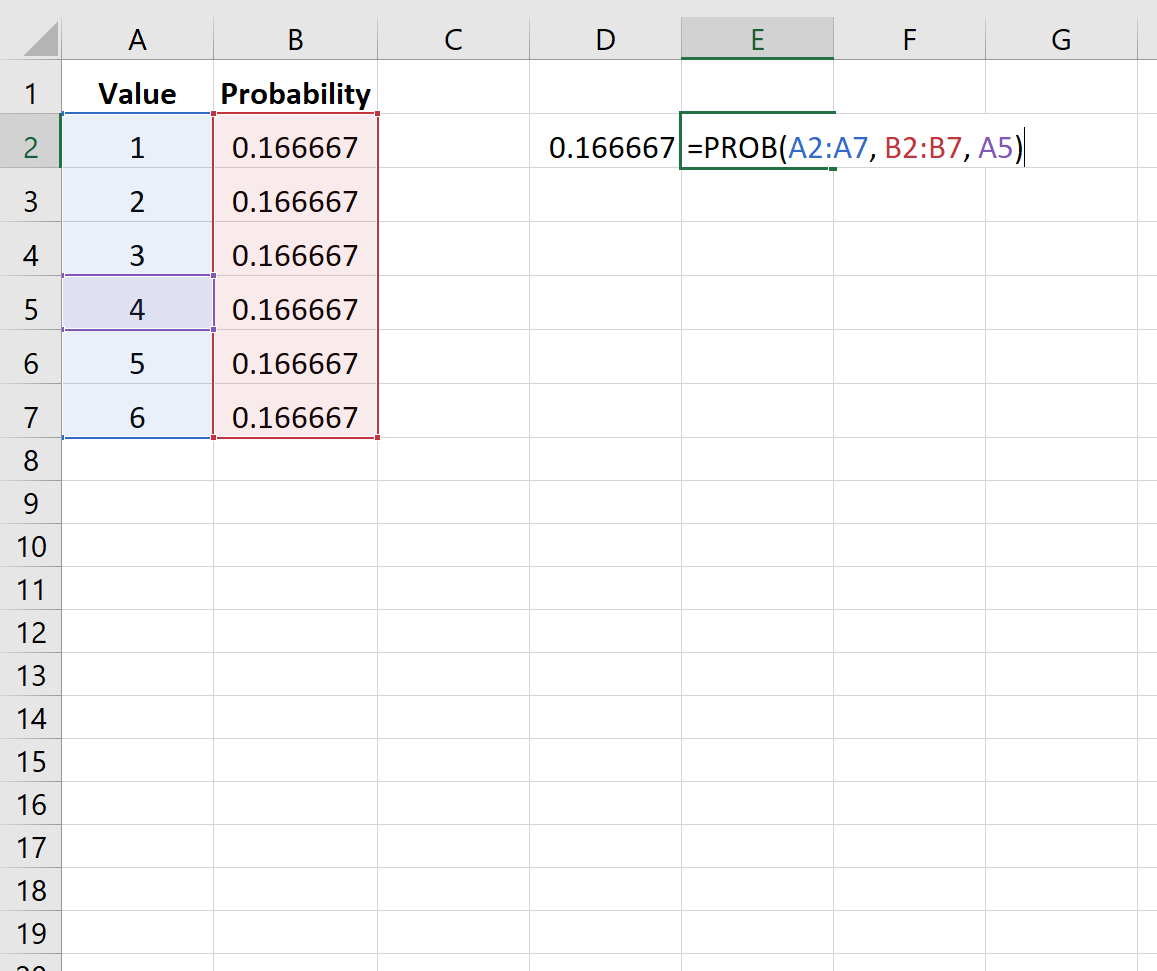
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
Вероятность оказывается равной 0,166667 .
Пример 2: Вероятность продаж
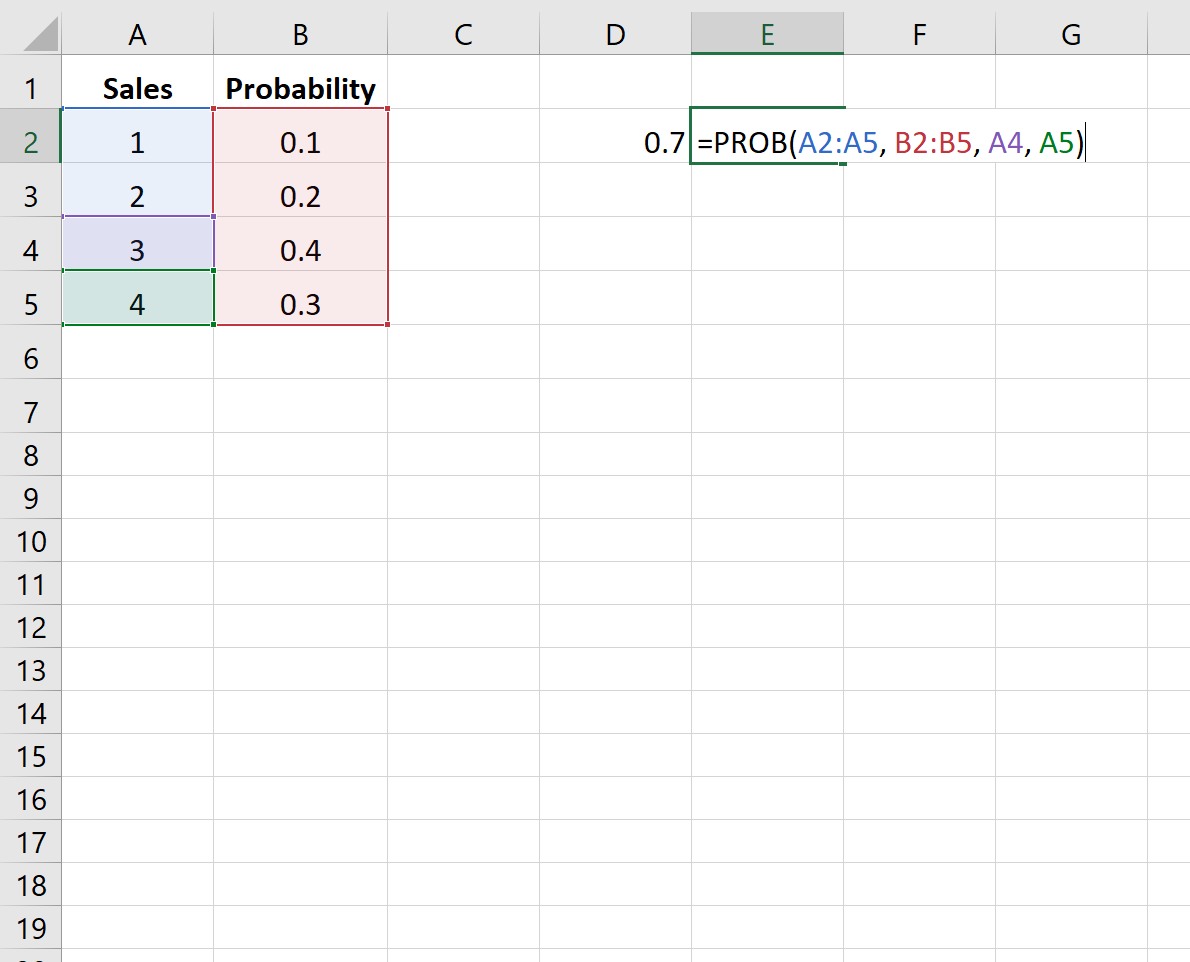
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Цели и задачи:
Образовательные: закрепить такие
понятия теории вероятности как: среднее
арифметическое, размах, мода и медиана рядов
чисел; систематизировать знания по пройденной
теме, формировать умение учащихся применять
знания к решению практических задач, контроль,
оценка и проверка знаний учащихся, закрепить
знание способов ввода данных в ячейки и порядок
создания формул с использованием встроенных
функций в табличном процессоре MS Excel. Показать
важность межпредметных связей
Развивающие: развитие
познавательной активности, творческих
способностей учащихся, умения сопоставлять,
анализировать, развить навыки ввода данных в
ячейки с использованием автозаполнения и
вычисления итоговых значений с помощью
статистических функций табличного процессора MS
Excel;
Воспитательные: способствовать
воспитанию у учащихся аккуратности, усидчивости,
навыков учебного труда, интереса к предмету.
Ход урока
-
Организационный момент.
-
Актуализация опорных знаний. Опрос.
- Как определить среднее арифметическое ряда?
- Что называется модой ряда?
- Как определить размах ряда?
- Что называется медианой ряда?
- Что такое адрес ячейки и из чего он состоит?
- Чем абсолютный адрес отличается от
относительного? - Что такое автозаполнение и как им пользоваться?
- Что такое функция Excel?
-
Решить задачу:
- Администрация школы решила проверить
математическую подготовку учащихся 8 класса. С
этой целью был составлен тест, содержащий 9
заданий. Работу выполняли 40 учащихся школы. При
проверке каждой работы учитель отмечал число
верно выполненных заданий. В результате был
составлен такой ряд чисел:
- Определить сколько заданий в среднем выполнил
каждый ученик верно? - Найти разницу в числе верно выполненных заданий
между учащимися. - Чему равна мода и медиана данного ряда?
-
Закрепление материала
6,5,4,0,4,5,7,9,1,6,8,7,9,5,8,6,7,2,5,7,6,3,4,4,5,6,8,6.7,7,4,3.5,9,6,7,8,6,9,8.
Задача разбирается вместе с учителем
для постановки проблемной ситуации, в разрешении
которой помогает использование электронных
таблиц.
Чтобы ответить на вопросы задачи
необходимо упорядочить ряд данных, а при
нахождении статистических характеристик ряда
нам помогут на доске записанные статистические
функции Excel, которые используются для нахождения
среднего арифметического, размаха, моды и
медианы рядов чисел:
=МЕДИАНА(аргументы) – медиана
ряда;
=СРЗНАЧ(аргументы) – среднее
арифметическое ряда;
=МОДА(аргументы) – мода ряда;
=МАКС(аргументы)-МИН(аргументы)
– размах ряда.
Учащиеся получают листки с задачами,
рассаживаются за компьютеры и решают их с
помощью Excel. Для решения задач необходим файл
(Приложение1)
Задачи для закрепления
- Найдите среднее арифметическое, размах, моду и
медиану рядов чисел; - За четверть Люда получила по алгебре пять двоек,
четыре четверки и две пятерки. Ее мама считает,
что за четверть Люде надо ставить двойку, папа
считает, что надо ставить тройку, а сама Люда
считает, что надо ставить четверку. Попробуйте
привести аргументы в пользу каждой точки зрения
(какие статистические характеристики вычисляет
каждый член семьи?). Какую бы оценку вы поставили
Люде? - В таблице представлены результаты опроса 100
человек. - Света, Люда и Женя договорились в течение трех
дней по-очереди поливать в классе цветы. Сколько
у них есть способов установить порядок
дежурства? - 8 детей делят пирожки. Все пирожки имеют разную
начинку. Один из них с морковью. Сколько
существует способов разделить пирожки (каждому
по штуке) так, чтобы пирожок с морковью не
достался ребенку, который не любит такую начинку?
| Количество опрошенных | Зарплата |
| 10 | 500 |
| 30 | 1000 |
| 50 | 1500 |
| 10 | 3000 |
а) сколько денег, в среднем, получает один
человек из этой группы (найдите среднее
арифметическое ряда данных)?
б) сколько денег получает ежемесячно
“средний” человек из этой группы (найдите
медиану этих данных)?
в) какой заработок наиболее распространен у
членов этой группы (найдите моду этих данных)?
-
Подведение итогов (выставление оценок)
Приложение
Probability describes the likelihood that some event occurs.
We can calculate probabilities in Excel by using the PROB function, which uses the following syntax:
PROB(x_range, prob_range, lower_limit, [upper_limit])
where:
- x_range: The range of numeric x values.
- prob_range: The range of probabilities associated with each x value.
- lower_limit: The lower limit on the value for which you want a probability.
- upper_limit: The upper limit on the value for which you want a probability. Optional.
This tutorial provides several examples of how to use this function in practice.
Example 1: Dice Probabilities
The following image shows the probability of a dice landing on a certain value on a given roll:
Since the dice is equally likely to land on each value, the probability is the same for each value.
The following image shows how to find the probability that the dice lands on a number between 3 and 6:
The probability turns out to be 0.5.
Note that the upper limit argument is optional. So, we could use the following syntax to find the probability that the dice lands on just 4:
The probability turns out to be 0.166667.
Example 2: Sales Probabilities
The following image shows the probability of a company selling a certain number of products in the upcoming quarter:
The following image shows how to find the probability that the company makes either 3 or 4 sales:
The probability turns out to be 0.7.
Additional Resources
How to Calculate Relative Frequency in Excel
How to Calculate Cumulative Frequency in Excel
How to Create a Frequency Distribution in Excel
Элементы
теории вероятностей
Цели
задания:
-
Повторение
основных приемов создания и форматирования
таблиц средствами MS
Excel. -
Изучение
новых математических функций, входящих
в MS
Excel. -
Решение
задач по теме «Элементы теории
вероятностей. Классическое определение
вероятности».
Подготовка
к заданию:
-
Повторить
тему «Элементы
теории вероятностей»
по электронному конспекту, расположенному
на сервере по адресу «F:Методические
материалы Информационные технологии
Математика и информатика для юристов». -
Познакомиться
с помощью справочной системы MS Excel с
математическими функциями ФАКТР
и ЧИСЛОКОМБ.
Состав
задания:
-
Решить
задачи по теории вероятностей и оформить
их решение средствами MS Excel
в виде таблиц в соответствии с
предложенными ниже образцами. Для
вычисления числа вариантов по формулам
комбинаторики использовать соответствующие
математические функции MS
Excel.
Задачи:
-
Назовём
игральной костью кубик из однородного
материала с гранями, занумерованными
цифрами от 1 до 6. Бросаются 2 игральных
кости. Какова вероятность того, что
сумма очков, выпавших на 2 костях,
окажется равной 8?
-
Юная
студентка юрфака наивно верит, что
если она соберет 20 разных крышек от
«Pepsi» и отошлет их по указанному адресу,
то добрые дяди и тети предоставят ей
путевку в «DisneyLand».
Какова вероятность того, что удастся
собрать 20 разных крышек, купив 20
бутылок?
-
В
соревнованиях по стрельбе на огневом
рубеже размещаются 8 стрелков. Какова
вероятность того, что два определенных
участника окажутся рядом?
-
Колода
карт содержит 36 различных карт (9 карт
пиковой масти, 9 треф, 9 бубен и 9 червей).
Сдача карт одному игроку состоит из 6
карт, порядок которых не важен. Какова
вероятность того, что:
-
в
сдаче все карты будут трефовой масти? -
в
сдаче все карты будут одной масти? -
в
сдаче будет 4 туза? -
в
сдаче будет точно 2 дамы?
-
В
урне 5 белых и 7 черных шаров. Из урны
одновременно вынимают два шара. Какова
вероятность, что оба шара белые?
Образцы
решения и оформления задач:
Задача
1.
Из урны, в которой находятся 8 синих,
3 красных,
6 чёрных
и 7 белых
шаров, наудачу вынимается один. Какова
вероятность того, что вынутый шар
окажется а)
белым;
б) зеленым?
Решение.
Это испытание имеет 24 равновозможных
исхода. Каждый исход означает выбор
одного шара. Пусть событие А означает
выбор
белого шара,
а событие В – выбор
зеленого шара.
Число исходов, благоприятных событию
А , равно 7, а исходов, благоприятных
событию В, нет (оно является невозможным).
Оформление
этой задачи в среде MS
Excel
приведено ниже.
Задача
2.
На зачёте по Истории студенту предлагается
ответить на 2 вопроса из 36. Студент
подготовил ответы на 19 вопросов. Какова
вероятность, что на зачёте ему предложат
два вопроса, на которые он подготовил
ответ?
Решение.
Рассмотрим
испытание, состоящее в выборе двух из
36 вопросов. Исходом испытания является
пара вопросов. Поскольку порядок выбора
вопросов несущественен,
то число всех n
исходов
равно числу
сочетаний из 36 по 2.
Для определения числа сочетаний
воспользуемся функцией ЧИСЛОКОМБ(36;2).
Пусть
событие А состоит в том, что студенту
достаются два подготовленных вопроса.
Число исходов, благоприятных этому
событию определяется как число сочетаний
из 19 по 2. Применим вышеуказанную функцию
ЧИСЛОКОМБ(19;2).
Оформление
решения задачи в среде MS
Excel
приведено ниже
Задача
3.
Десять
различных книг расставлены наудачу на
одной полке. Найти вероятность того,
что три определенные книги окажутся
поставлены рядом.
Решение.
Условимся,
что три определенные книги как бы
находятся в одной упаковке. Тогда число
возможных способов расположения книг
на полке равно числу
перестановок из 8
элементов (одна упаковка плюс остальные
7 книг), т. е. Р8=8!.
Внутри упаковки три книги можно
переставить Р3=3!
способами. По правилу умножения m(A)=
Р8
х Р3.
Число возможных вариантов расстановки
10 книг n=Р10=10!.
Для вычисления факториалов чисел
воспользуемся функцией ФАКТР.
Оформление
решения задачи в среде MS
Excel
приведено ниже
Соседние файлы в папке MS Excel
- #
- #
- #