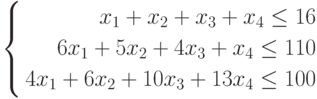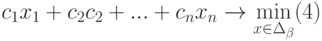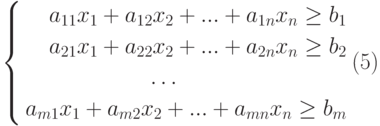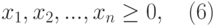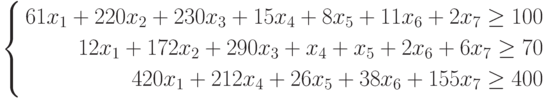Примеры сложных задач в excel - Word и Excel - помощь в работе с программами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

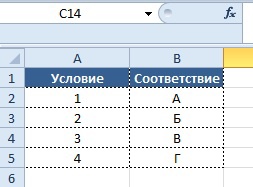
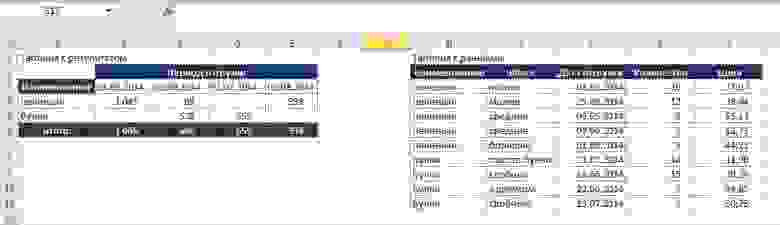
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

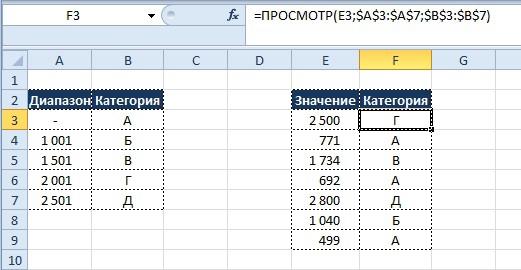
Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

во втором поле выбрать оператор ограничения (>, Поиск решения).

Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:

В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.

С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.

Каждый отчет создается на отдельном листе текущей рабочей книги.

Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).

Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.

Рассмотрим применение процессора Excel для решения ЗЛП на примерах.

Задача 1. Планирование производства

Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.

МП выпускает товары х₁,х₂,х₃,х₄, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.

Затраты	х₁	х₂	x₃	х₄	Всего
Трудовые	1	1	1	1	16
Сырьевые	6	5	4	1	110
Финансы	4	6	10	13	100

Максимум прибыли в зависимости от оптимального распределения затрат.
Минимум ресурсов, необходимых для получения максимальной прибыли.

Решение задачи средствами Excel состоит из 4 этапов:

Создание математической модели задачи ЛП.
Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
Ввод данных из формы в окно Excel Поиск решения из меню Данные.
Задание параметров поиска и решение задачи.

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

— целевая функция прибыли.

— граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.

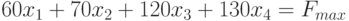
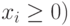
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.

Создание формы

Составление формы в виде:

A	B	C	D	E	F	G	H
1	Переменная	х₇	х₂	x₃	х₄	Формула	Знак	Св.член
2	Значение
3	Коэф. ЦФ	60	70	120	130	=СУММПРОИЗВ(В$2:Е$2;В3:Е3)	Max
4	Трудовые	1	1	1	1	=СУММПРОИЗВ(В$2:Е$2;В4:Е4)		16
5	Сырьевые	6	5	4	1	=СУММПРОИЗВ(В$2:Е$2;В5:Е5)		110
6	Финансы	4	6	10	13	=СУММПРОИЗВ(В$2:Е$2;В6:Е6)		100

Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
Ввод формул с помощью f_x – Мастера функций.

Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций f_x на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х₁..х₄), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).

Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.

Нажать клавишу ОК, в ячейку F3 запишется формула 60х₁+70х₂+120х₃+ 130х₄ в виде СУММПРОИЗВ(В2:Е2;В3:Е3).

Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:

После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.

В результате копирования мы увидим следующие формулы:

в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).

Заполнение окна Поиск решения

Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).

Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак ««, в поле справа ввести Н4 (рис. 12. рис. 12.2).

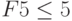
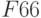
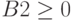
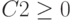
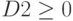
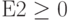
Аналогично через «Добавить» ввести , для системы ограничений (2), а также , , и .

Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.

После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».

Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.

Параметры поиска

В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).

Результаты поиска решения с таблицей результатов:

A	B	C	D	E	F	G	H
1	Переменная	X1	X₂	X₃	X₄	Формула	Знак	Св.член
2	Значение	10	0	6	0
3	Коэф. ЦФ	60	70	120	130	1320	Max
4	Трудовые	1	1	1	1	16		16
5	Сырьевые	6	5	4	1	84		110
6	Финансы	4	6	10	13	100		100

Таким образом оптимальный план Х(Х₁,Х₂,Х₃,Х₄)=(10,0,6,0) при минимальном использовании ресурсов

Трудовые – 16 (У₁)
Сырьевые – 84 (У₂)
Финансы – 100 (У₃)

даёт максимум прибыли F в 1320 руб.

_Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х₁ и Х₃ в количестве 10 и 6 штук соответственно, товары Х₃ и Х₄ выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У₁) и финансовые (У₃) ресурсы используются полностью, по сырьевым ресурсам (У₂) есть запас в 110-84=26 ед.

Кроме того, это означает, что изменение трудовых ( y₁ ) и финансовых ( y₃ ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y₂ ) – нет.

Разности между плановыми ресурсами и использованными являются двойственными переменными y₁, y₂ и y₃ сопряжённой задачи линейного программирования. В данном случае y₁=y₃=0 , а y₂=26 ед. Таким образом, ресурс y₂ можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.

Задача 2. Задача об оптимальной диете

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.

Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:

где множество допустимых альтернатив 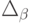формируется следующей системой ограничений типа неравенств:

Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.

Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).

Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂= 70, в углеводах b3 = 400.

Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	61	220	230	15	8	11	6
Жиры	12	172	290	1	1	2	2
Углеводы	420	0	0	212	26	38	155

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

– целевая функция (суммарная калорийность продуктов).

– граничные условия

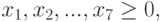
Создание формы

Для решения поставленной задачи выполним следующие подготовительные действия:

Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с₁ = 2060, с₂ = 2430, с₃ = 3600, с₄ = 890, с₅ = 140, с₆ = 230, с₇ = 650.
В ячейку I2 введем формулу: =СУММПРОИЗВ( b ₂:Н2;B3:H3), которая представляет целевую функцию (4).
В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.

В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b ₁=100 , жирах b ₂= 70 и углеводах b3 = 400.
В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).

Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.

Заполнение окна Поиск решения

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
Для группы Равной: выбрать вариант поиска решения – минимальному значению.
В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
- для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
- в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
- в качестве значения правой части ограничения выбрать ячейку $J$5 ;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
- аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).

Параметры

В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.

Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х₁ = 0, х₂ = 0,211, 3 = 0,109, х₄= 1,887, х₅ = 0, х₆ = 0, х₇ = 0, которым соответствует значение целевой функции: f_опт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.

Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.

ЗАДАНИЕ

Составить математическую модель задачи линейного программирования.
Решить задачу линейного программирования в Excel с помощью Поиска решения.
Сохранить в виде модели установочные параметры.

Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.

Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

не менее 0.8%, но не более 1.2% кальция;
не менее 22% белка;
не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n >). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

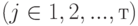
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	66	225	235	20	13	16	11
Жиры	17	177	295	1	1	7	7
Углеводы	425	0	0	217	31	43	200

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 105, в жирах b ₂ = 75, в углеводах b ₃ = 405.

Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.

Таблица 1. Расход химических веществ на изготовления клея, их запас на складе

Вид клея /Химические вещества	Клей № 1	Клей № 2	Клей № 3	Запас на складе
Крахмал	0,4	0,3	0,2	20
Желатин	0,2	0,3	0,4	35
Квасцы	0,05	0,07	0,1	7
Мел	0,01	0,05	0,15	10

Стоимость каждого вида клея для оптовых покупателей следующая:с₁ = 380 руб/кг,с₂ =430 руб/кг,с₃ = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.

Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Смесь должна содержать:

не менее 0.8%, но не более 1.2% кальция;
не менее 22% белка;
не более 5% клетчатки.

Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с₁ = 470,с₂= 380,с₃ = 350,с₄ = 1460,с₅ = 2150,с₆ = 2070, с₇ = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂ = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).

Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Поиск решения задач в Excel с примерами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Решение задач оптимизации в Excel

В Excel для решения задач оптимизации используются следующие команды:

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Оформим исходные данные в виде таблицы:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Дано 2 диапазона значений:

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

источники:

http://intuit.ru/studies/courses/3659/901/lecture/32717

http://exceltable.com/vozmojnosti-excel/poisk-resheniya-v-excel

Источник

Создание сложных формул с помощью встроенных логических функций Excel

Логические выражения в Excel используются для записи условий, в которых сравниваются числа, функции, формулы, текстовые или логические значения. Любое логическое выражение должно содержать, по крайней мере, один оператор сравнения, который определяет отношение между элементами логического выражения.

Ниже представлен список операторов сравнения Excel:

Больше или равно

Результатом логического выражения является логическое значение ИСТИНА (1) или логическое значение ЛОЖЬ (0).

Функция ЕСЛИ – это функция, которая позволяет вывести в ячейку одно значение, если заданное пользователем условие выполняется и другое – если условие не выполняется.

ЕСЛИ(лог_выраж.; знач._если_истина; знач._если_ложь)

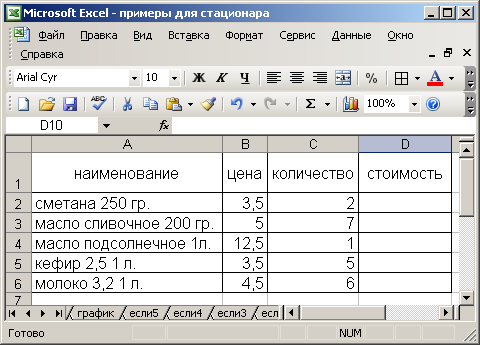
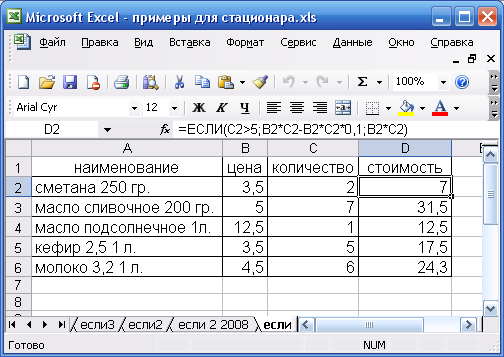
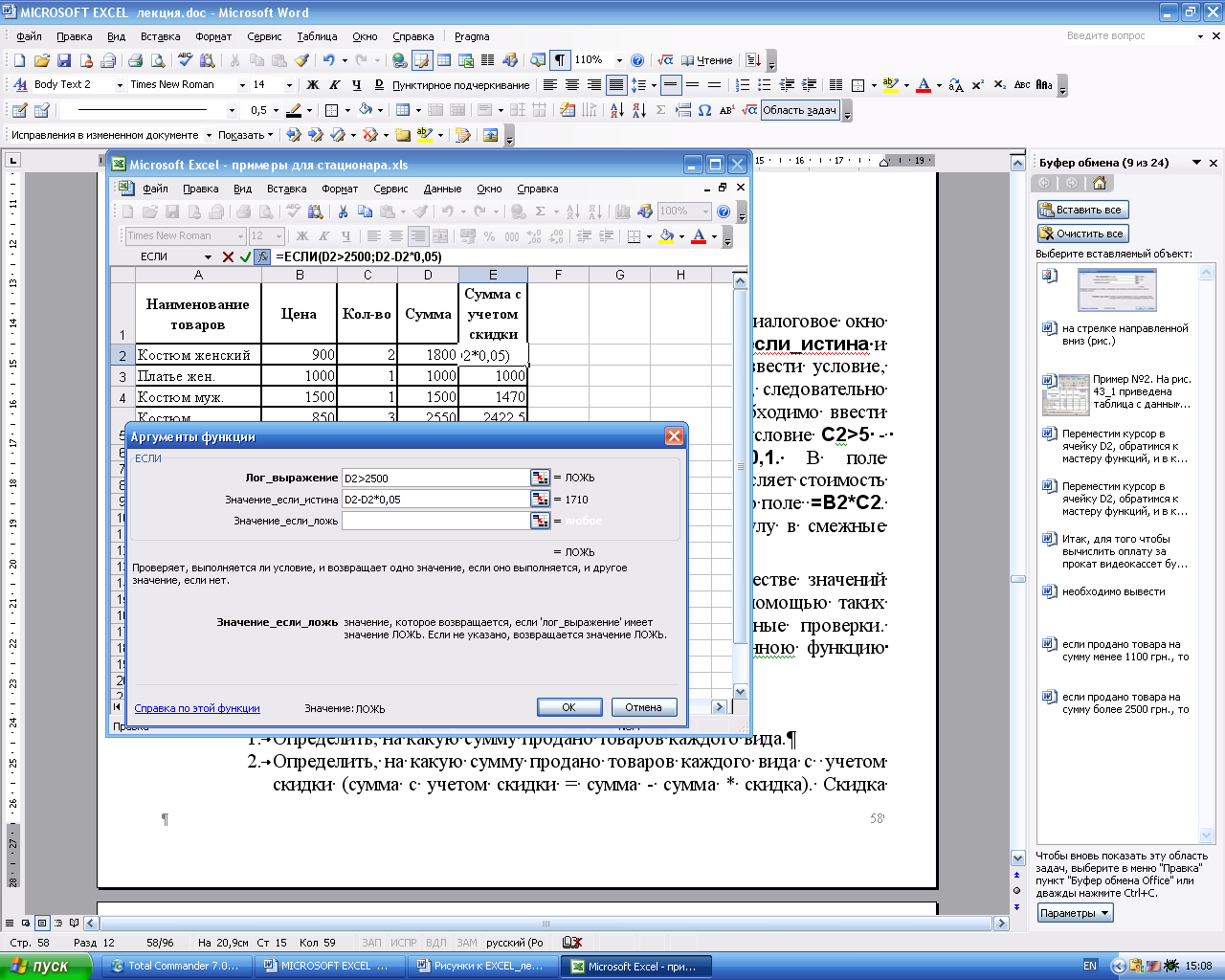
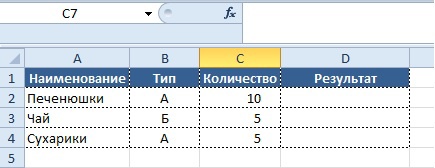
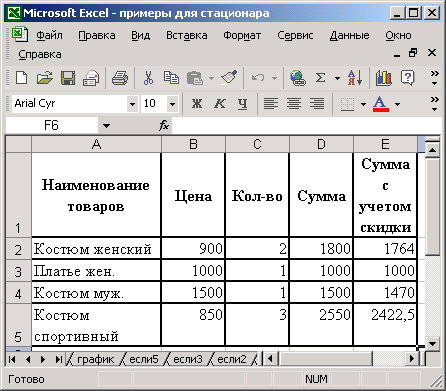
Рассчитать стоимость товара с учетом того, что если количество превысило 5 шт., то магазин дает скидку 10%. Исходные данные приведены на рис. 26.

Для того чтобы рассчитать стоимость товара с учетом скидки необходимо:

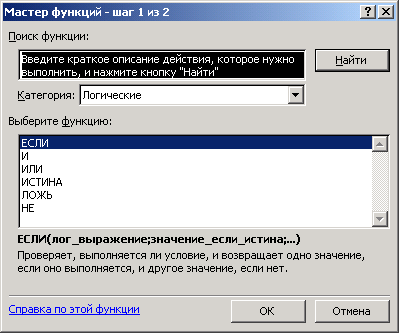
Переместить курсор в ячейку D2. С помощью мастера функций выбрать из категории Логические функцию ЕСЛИ (рис. 27), а затем щелкнуть на кнопке ОК.

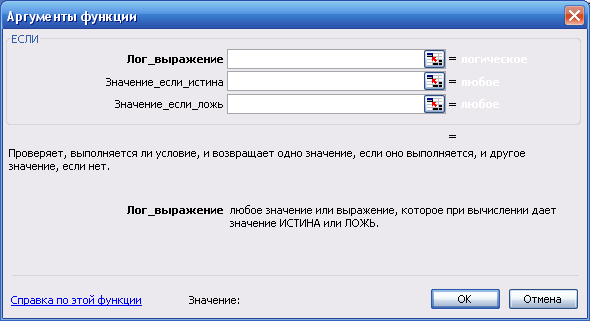
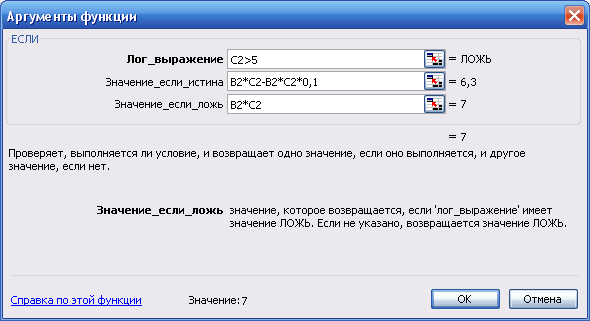
Диалоговое окно Аргументы функции (рис. 28) содержит три поля ввода. В поле Лог_выражение необходимо ввести условие, которое определяет, превышает ли проданное кол-во товара 5 шт., следовательно введем в это поле С2>5. В поле Значение_если_истина необходимо ввести формулу, которая вычисляет стоимость товара с учетом скидки, тогда введем в это поле B2*C2-B2*C2*0,1. В поле Значение_если_ложь необходимо ввести формулу, которая вычисляет стоимость товара без учета скидки (условие С2>5 — Ложь), в тогда введем в это поле B2*C2 (см. рис. 29). Теперь щелкнем на кнопке OK.

Скопировать полученную формулу в смежные ячейки. Результаты вычислений формул приведены на рис. 30.

Функции ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина и значение_если_ложь. С помощью таких вложенных функций Если можно конструировать более сложные проверки. Рассмотрим на примерах, как необходимо использовать вложенной функцией ЕСЛИ.

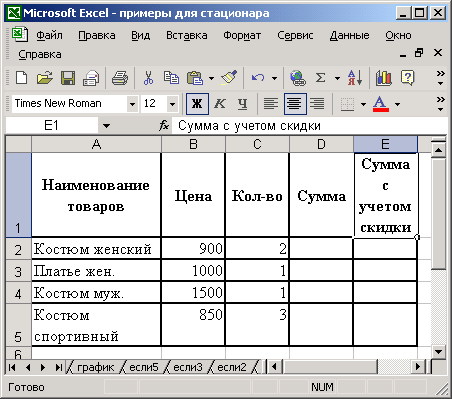
На рис. 31 приведена таблица с данными. Необходимо:

Определить, на какую сумму продано товаров каждого вида.

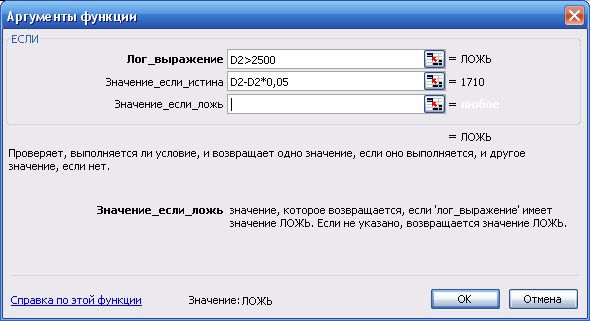
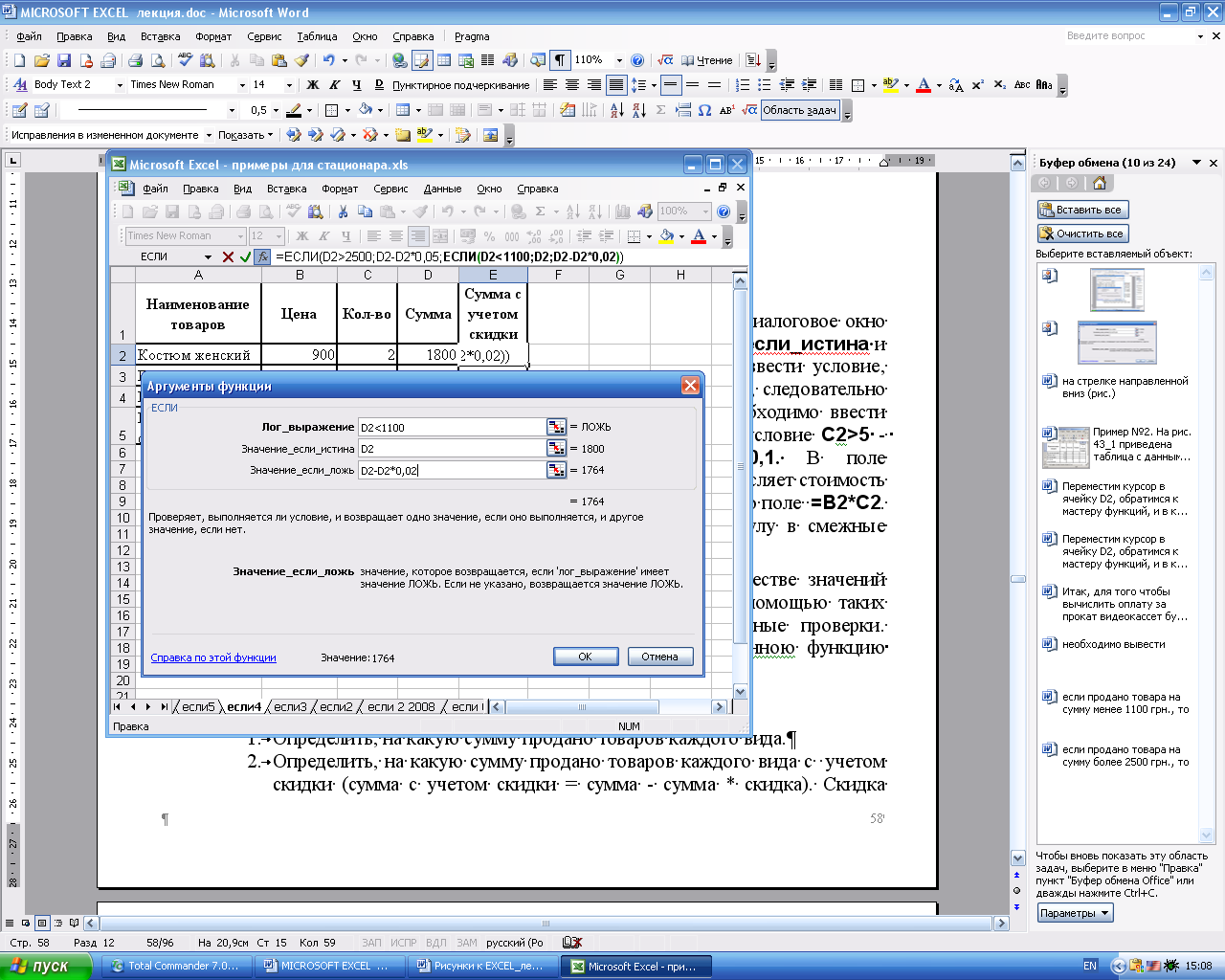
Определить, на какую сумму продано товаров каждого вида с учетом скидки (сумма с учетом скидки = сумма — сумма * скидка). Скидка начисляется по следующему принципу: если продано товара на сумму более 2500 грн., то скидка составит 5%, если продано товара на сумму менее 1100 грн., то скидка составит 0%, в остальных случаях скидка составит 2%.

Для того чтобы выполнить первый пункт задания необходимо в ячейку D2 ввести формулу =C2*B2.

Для того чтобы вычислить сумму со скидкой будем использовать вложенную функцию ЕСЛИ, так как существует три варианта начисления скидки.

Переместим курсор в ячейку E2 и с помощью мастера функций введем следующую формулу (рис. 33 – 34). Результаты решения приведены на рис. 35.

Рис. 35

Функции ИЛИ, И

Функции И и функция ИЛИ из категории Логические способны заметно улучшить наглядность и понятность сложных логических проверок. Функция ИЛИ и функция И позволяют задавать в формуле одновременно несколько условий, т.е. дают возможность создавать сложные логические выражения. Эти функции работают в сочетании с простыми операторами сравнения. Функции И и ИЛИ могут иметь до 30 логических аргументов и имеют синтаксис:

Аргументы функций И, ИЛИ могут быть логическими выражениями, массивами или ссылками на ячейки, содержащие логические значения.

Функция ИЛИ возвращает логическое значение ИСТИНА, если хотя бы одно из логических выражений истинно, а функция И возвращает логическое значение ИСТИНА, только если все логические выражения истинны.

Предположим, что нужно вывести сообщение «Светофор», если содержимое ячейки B4 или «красный», или «зеленый», или «желтый». Если же она содержит любую другую информацию, то необходимо вывести сообщение «Это не светофор. ».

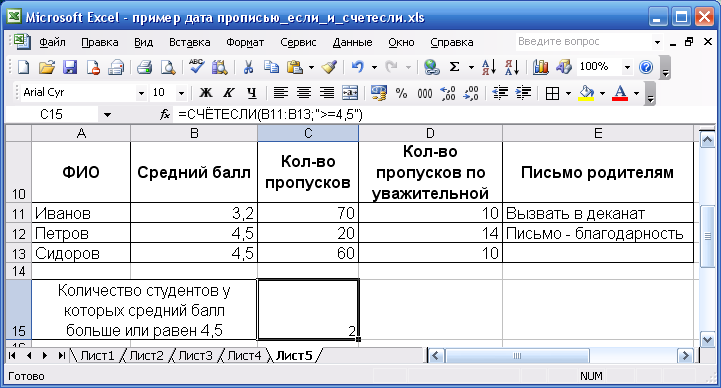
Предположим, что нужно вывести на экран содержимое ячейки B4, если она содержит число строго между 1 и 100 (1 =1; B4 =4.5.

Тогда в ячейку С15 необходимо ввести формулу: =СЧЁТЕСЛИ(B11:B13;»>=4,5″). Результат приведен на рис. 40

СУММЕСЛИ (диапазон; критерий; диапазон_суммирования)

диапазон — диапазон ячеек проверяемых на критерий (условие).

критерий — критерий (условие) в форме числа, выражения или текста, определяющего суммируемые ячейки.

диапазон_суммирования — фактические ячейки для суммирования.

Функция СУММЕСЛИ работает следующим образом: ячейки из «диапазон_суммирования» суммируются, только если соответствующие им ячейки в аргументе «диапазон» удовлетворяют условию (критерию). В тех случаях, когда диапазон вычисляемых ячеек (где проверяется условие) и диапазон фактических ячеек для суммирования совпадают, аргумент «диапазон_суммирования» можно не указывать.

В таблице на рис. 41 приведены объемы партий товара, полученные магазином. Необходимо просуммировать только объемы тех партий, значения которых превышают 20. Решение на рис. 42

Логические функции в excel с примерами их использования

Логические функции в Excel проверяют данные и возвращают результат «ИСТИНА», если условие выполняется, и «ЛОЖЬ», если нет.

Рассмотрим синтаксис логических функций и примеры применения их в процессе работы с программой Excel.

Использование логических функций в Excel

Логические функции в Excel и примеры решения задач

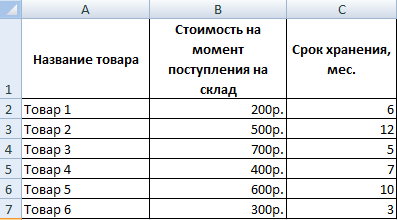
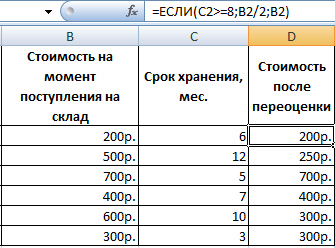
Задача 1. Необходимо переоценить товарные остатки. Если продукт хранится на складе дольше 8 месяцев, уменьшить его цену в 2 раза.

Сформируем таблицу с исходными параметрами:

Чтобы решить поставленную задачу, воспользуемся логической функцией ЕСЛИ. Формула будет выглядеть так: =ЕСЛИ(C2>=8;B2/2;B2).

Логическое выражение «С2>=8» построено с помощью операторов отношения «>» и «=». Результат его вычисления – логическая величина «ИСТИНА» или «ЛОЖЬ». В первом случае функция возвращает значение «В2/2». Во втором – «В2».

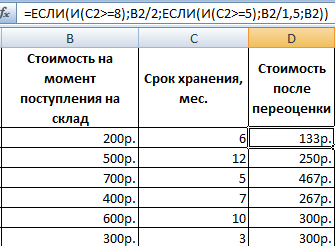
Усложним задачу – задействуем логическую функцию И. Теперь условие такое: если товар хранится дольше 8 месяцев, то его стоимость уменьшается в 2 раза. Если дольше 5 месяцев, но меньше 8 – в 1,5 раза.

Формула приобретает следующий вид: =8);B2/2;ЕСЛИ(И(C2>=5);B2/1,5;B2))’ class=’formula’>.

В функции ЕСЛИ можно использовать в качестве аргументов текстовые значения.

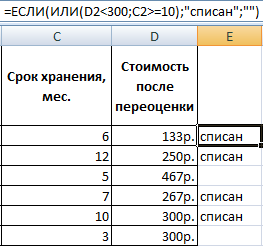
Задача 2. Если стоимость товара на складе после уценки стала меньше 300 р. или продукт хранится дольше 10 месяцев, его списывают.

Для решения используем логические функции ЕСЛИ и ИЛИ: =10);»списан»;»»)’ class=’formula’>. Условие, записанное с помощью логической операции ИЛИ, расшифровывается так: товар списывается, если число в ячейке D2 = 10.

При невыполнении условия функция ЕСЛИ возвращает пустую ячейку.

В качестве аргументов можно использовать другие функции. К примеру, математические.

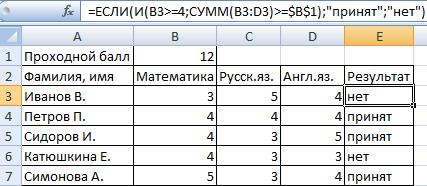
Задача 3. Ученики перед поступлением в гимназию сдают математику, русский и английский языки. Проходной балл – 12. По математике для поступления нужно получить не менее 4 баллов. Составить отчет о поступлении.

Составим таблицу с исходными данными:

Нужно общее количество баллов сравнить с проходным баллом. И проверить, чтобы по математике оценка была не ниже «4». В графе «Результат» поставить «принят» или «нет».

Введем формулу вида: =4;СУММ(B3:D3)>=$B$1);»принят»;»нет»)’ class=’formula’>. Логический оператор «И» заставляет функцию проверять истинность двух условий. Математическая функция «СУММ» используется для подсчета итогового балла.

Функция ЕСЛИ позволяет решать многочисленные задачи, поэтому используется чаще всего.

Статистические и логические функции в Excel

Задача 1. Проанализировать стоимость товарных остатков после уценки. Если цена продукта после переоценки ниже средних значений, то списать со склада этот продукт.

Работаем с таблицей из предыдущего раздела:

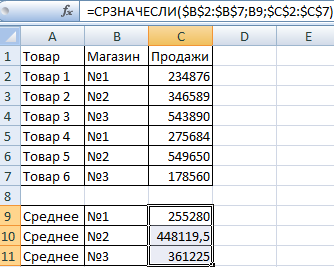
Для решения задачи используем формулу вида: . В логическом выражении «D2 . Первый аргумент – $B$2:$B$7 – диапазон ячеек для проверки. Второй аргумент – В9 – условие. Третий аргумент – $C$2:$C$7 – диапазон усреднения; числовые значения, которые берутся для расчета среднего арифметического.

Функция СРЗНАЧЕСЛИ сопоставляет значение ячейки В9 (№1) со значениями в диапазоне В2:В7 (номера магазинов в таблице продаж). Для совпадающих данных считает среднее арифметическое, используя числа из диапазона С2:С7.

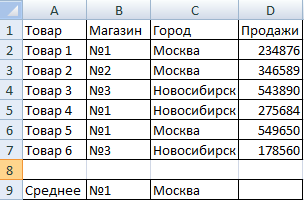
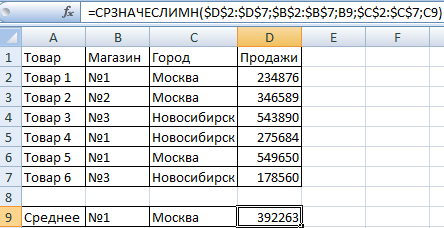
Задача 3. Найти средние продажи в магазине №1 г. Москва.

Видоизменим таблицу из предыдущего примера:

Нужно выполнить два условия – воспользуемся функцией вида: .

Функция СРЗНАЧЕСЛИМН позволяет применять более одного условия. Первый аргумент – $D$2:$D$7 – диапазон усреднения (откуда берутся цифры для нахождения среднего арифметического). Второй аргумент – $B$2:$B$7 – диапазон для проверки первого условия.

Третий аргумент – В9 – первое условие. Четвертый и пятый аргумент – диапазон для проверки и второе условие, соответственно.

Функция учитывает только те значения, которые соответствуют всем заданным условиям.

БЛОГ

Только качественные посты

Практический справочник функций Microsoft Excel с примерами их использования

На сегодняшний день программа Microsoft Excel является самой популярной программой в бизнесе, которая позволяет решать различные задачи — от анализа до учета данных. Самым популярным инструментом в Excel являются встроенные функции, количество которых приближается к 1000 штук.

Отсюда вытекает вопрос: Сколько нужно знать функций Excel, чтобы решать практически любую задачу в Excel?

Могу с уверенностью, опираясь на свой 17 летний профессиональный опыт работы в Excel, сказать, что достаточно освоить всего около 100 функций…

Представляю Вам ТОП-50 самых главных функций в Microsoft Excel с примерами их использования

– изучив данные Excel функции, у Вас будет достаточно теоретических знаний, чтобы решать практически любую задачу в Excel

( Для перехода к примерам нажмите на название функции. Все примеры — это ссылки на лучшие статьи уважаемых специалистов по Excel и наших партнеров)

1. СУММ / СРЗНАЧ / СЧЁТ / МАКС / МИН (SUM / AVERAGE / COUNT / MAX / MIN) — [Базовые формулы Excel]
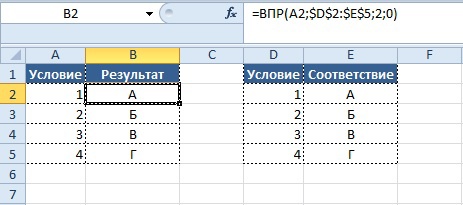
2. ВПР (VLOOKUP) — [Ищет значение в первом столбце массива и выдает значение из ячейки в найденной строке и указанном столбце]
3. ИНДЕКС (INDEX) — [По индексу получает значение из ссылки или массива]
4. ПОИСКПОЗ (MATCH) — [Ищет значения в ссылке или массиве]
5. СУММПРОИЗВ (SUMPRODUCT) — [Вычисляет сумму произведений соответствующих элементов массивов (позволяет работать с массивами без формул массива)]
6. АГРЕГАТ / ПРОМЕЖУТОЧНЫЕ.ИТОГИ (AGGREGATE / SUBTOTALS) — [Возвращает общий итог или промежуточный итог в списке или базе данных с учетом фильтров или без учета фильтров]
7. ЕСЛИ (IF) — [Выполняет проверку условия]
8. И / ИЛИ / НЕ (AND / OR / NOT) — [Логические условия, как правило для функции ЕСЛИ]
9. ЕСЛИОШИБКА (IFERROR) — [Если формула возвращает ошибку то что]
10. СУММЕСЛИМН (SUMIFS) — [Суммирует ячейки, удовлетворяющие заданным критериям. Допускается указывать более одного условия]
11. СРЗНАЧЕСЛИМН (AVERAGEIFS) — [Возвращает среднее арифметическое значение всех ячеек, которые соответствуют нескольким условиям]
12. СЧЁТЕСЛИМН (COUNTIFS) — [Подсчитывает количество ячеек, которые соответствуют нескольким условиям]
13. МИНЕСЛИ / МАКСЕСЛИ (MINIFS / MAXIFS) — [Возвращает минимальное/максимальное значение всех ячеек, которые соответствуют нескольким условиям]
14. НАИБОЛЬШИЙ / НАИМЕНЬШИЙ (LARGE / SMALL) — [Возвращает k-ое наибольшее/наименьшее значение в множестве данных]
15. ДВССЫЛ (INDIRECT) — [Определяет ссылку, заданную текстовым значением]
16. ВЫБОР (CHOOSE) — [Выбирает значение из списка значений по индексу]
17. ПРОСМОТР (LOOKUP) — [Ищет значения в массиве]
18. СМЕЩ (OFFSET) — [Определяет смещение ссылки относительно заданной ссылки]
19. СТРОКА / СТОЛБЕЦ (ROW / COLUMN) — [Возвращает номер строки/столбца, на который указывает ссылка]
20. ЧИСЛСТОЛБ / ЧСТРОК (COLUMNS / ROWS) — [Возвращает количество столбцов/строк в ссылке]
21. ОКРУГЛ / ОКРУГЛТ / ОКРУГЛВНИЗ / ОКРУГЛВВЕРХ (ROUND / MROUND / ROUNDDOWN / ROUNDUP) — [Округляет число до указанного количества десятичных разрядов]
22. СЛЧИС / СЛУЧМЕЖДУ / РАНГ (RAND / RANDBETWEEN / RANK) — [Возвращает случайное число]
23. Ч (N) — [Возвращает значение, преобразованное в число]
24. ЧАСТОТА (FREQUENCY) — [Находит распределение частот в виде вертикального массива]
25. СЦЕПИТЬ / СЦЕП / ОБЪЕДИНИТЬ / & (CONCATENATE / CONCAT / TEXTJOIN / &) — [Объединения двух или нескольких текстовых строк в одну]
26. ПСТР (MID) — [Выдает определенное число знаков из строки текста, начиная с указанной позиции]
27. ЛЕВСИМВ / ПРАВСИМВ (LEFT / RIGHT) — [Возвращает заданное количество символов текстовой строки слева / права]
28. ДЛСТР (LEN) — [Определяет количество знаков в текстовой строке]
29. НАЙТИ / ПОИСК (FIND / SEARCH) — [Поиск текста в ячейке с учетом / без учета регистр]
30. ПОДСТАВИТЬ / ЗАМЕНИТЬ (SUBSTITUTE / REPLACE) — [Заменяет в текстовой строке старый текст новым]
31. СТРОЧН / ПРОПИСН / ПРОПНАЧ (LOWER / UPPER) — [Преобразует все буквы текста в строчные/прописные/ или первую букву в каждом слове текста в прописную]
32. ГИПЕРССЫЛКА (HYPERLINK) — [Создает ссылку, открывающую документ, находящийся на жестком диске, сервере сети или в Интернете]
33. СЖПРОБЕЛЫ (TRIM) — [Удаляет из текста все пробелы, за исключением одиночных пробелов между словами]
34. ПЕЧСИМВ (CLEAN) — [Удаляет все непечатаемые знаки из текста]
35. СОВПАД (EXACT) — [Проверяет идентичность двух текстов]
36. СИМВОЛ / ПОВТОР (CHAR / REPT) — [Возвращает знак с заданным кодом/Повторяет текст заданное число раз]
37. СЕГОДНЯ / ТДАТА (TODAY / NOW) — [Возвращает текущую дату в числовом формате / Возвращает текущую дату и время в числовом формате]
38. МЕСЯЦ / ГОД (MONTH / YEAR) — [Вычисляет год / месяц от заданной даты]
39. НОМНЕДЕЛИ (WEEKNUM) — [Преобразует дату в числовом формате в число, которое указывает, на какую неделю года приходится дата]
40. ДАТАЗНАЧ (DATEVALUE) — [Преобразует дату из текстового формата в числовой]
41. РАЗНДАТ (DATEDIF) — [Вычисляет количество дней, месяцев или лет между двумя датами]
42. РАБДЕНЬ (WORKDAY) — [Возвращает дату в числовом формате, отстоящую вперед или назад на заданное количество рабочих дней]
43. ЯЧЕЙКА (CELL) — [Возвращает сведения о формате, расположении или содержимом ячейки]
44. ТРАНСП (TRANSPOSE) — [Выдает транспонированный массив]
45. ПРЕОБР (CONVERT) — [Преобразует число из одной системы мер в другую]
46. ПРЕДСКАЗ (FORECAST) — [Вычисляет или предсказывает будущее значение по существующим значениям линейным трендом]
47. ТИП.ОШИБКИ (ERROR.TYPE) — [Возвращает числовой код, соответствующий типу ошибки]
48. ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GETPIVOTDATA) — [Возвращает данные, хранящиеся в сводной таблице]
49. БДСУММ (DSUM) — [Суммирует числа в поле (столбце) записей списка или базы данных, которые удовлетворяют заданным условиям]
50. В качестве бонуса рекомендую изучить Пользовательские форматы в Excel.

После освоения данных функций, следующим этапом рекомендую осваивать инструменты Бизнес- аналитики Business Intelligence (BI)

В Excel к инструментам бизнес-аналитики уровня Self-Service BI относятся бесплатные надстройки «Power»:

Power Query — это технология подключения к данным, с помощью которой можно обнаруживать, подключать, объединять и уточнять данные из различных источников для последующего анализа.
Power Pivot — это технология моделирования данных, которая позволяет создавать аналитические модели данных, устанавливать отношения и добавлять аналитические вычисления.
Power View — это технология визуализации данных, с помощью которой можно создавать интерактивные диаграммы, графики, карты и другие наглядные элементы, позволяющие визуализировать различную информацию.

Ну и если Вы со временем поймете, что возможностей Excel для решения ваших аналитических задач недостаточно, то вам пора переходить к изучению промышленных решений уровня Business Intelligence (BI)

6 малоизвестных, но очень полезных функций Excel

Microsoft Excel на сегодняшний день просто незаменим, особенно когда дело касается обработки больших объемов данных. Однако у этой программы столько функций, что непросто разобраться, какие их них действительно нужные и полезные.

И поэтому сегодня AdMe.ru расскажет, какими способами можно эффективно систематизировать информацию и разложить все по полочкам.

Сводные таблицы

С помощью сводных таблиц очень удобно сортировать, рассчитывать сумму или получать среднее значение из данных электронной таблицы, при этом никакие формулы выводить не нужно.

Как применять:

Выберите Вставка > Рекомендуемые сводные таблицы.
В диалоговом окне Рекомендуемые сводные таблицы щелкните любой макет сводной таблицы, чтобы увидеть его в режиме предварительного просмотра, а затем выберите тот из них, в котором данные отображаются нужным вам образом. Нажмите кнопку ОК.
Excel добавит сводную таблицу на новый лист и отобразит список полей, с помощью которого можно упорядочить данные в таблице.

Подбор параметра

Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров.

Как применять:

Выберите Данные > Работа с данными > Анализ «что если» > Подбор параметра.
В поле Установить в ячейке введите ссылку на ячейку, в которой находится нужная формула.
В поле Значение введите нужный результат формулы.
В поле Изменяя значениеячейки введите ссылку на ячейку, в которой находится корректируемое значение, и нажмите кнопку ОК.

Условное форматирование

Условное форматирование позволяет быстро выделить на листе важные сведения.

Как применять:

На вкладке Главная в группе Стили щелкните стрелку рядом с кнопкой Условное форматирование и выберите формулу, которая вам понадобится.

Например, если вам нужно выделить все значения меньше 100, выберите Правила выделения ячеек > Меньше, а затем наберите 100. Перед тем как нажать ОК, можно выбрать формат, который будет применяться для подходящих значений.

ИНДЕКС и ПОИСКПОЗ

Если ВПР помогает находить нужные данные только в первом столбце, то, благодаря функциям ИНДЕКС и ПОИСКПОЗ, можно искать информацию внутри таблицы.

Как применять:

Убедитесь, что ячейки с данными образуют сетку, где есть заголовки и названия строк.
Используйте функцию ПОИСКПОЗ: сначала, чтобы найти столбец, в котором расположен искомый элемент, и затем еще раз, чтобы перейти к строке с ответом.
Вставьте ответы в ИНДЕКС, и Excel сможет указать на ячейку, где эти значения пересекаются.

Например: ИНДЕКС (array, ПОИСКПОЗ (lookup_value, lookup_array, 0), ПОИСКПОЗ (lookup_value, lookup_array, 0)).

Диаграмма «водопад»

Это одна из форм визуализации данных, которая позволяет увидеть, в какую сторону менялись показатели в течение определенного периода. Очень полезная штука для тех, чья работа связана с финансами или статистикой.

Как применять:

В версии Excel 2016 необходимо выделить нужные данные и выбрать Вставка > Водопад или Диаграмма > Водопад.

Данная функция позволяет вычислять и предсказывать будущие значения на основе уже имеющихся данных.

Использование логических функций в Excel

Табличный редактор Эксель – очень гибкий и мощный инструмент для структурированной работы с данными. Среди большого количества его эффективных инструментов стоит отдельно выделить логические операторы, в основе использования которых лежит признание выражения истинным или ложным. Эти функции эффективно встроены в инструментарий формул и позволяют создавать гибкие условия для различных вычислений или заполнения ячеек на основе логических выражений. В данной статье будут описаны основные используемые функции, а также приведен практический пример использования логических операторов в Excel.

Основные логические функции, используемые в Эксель

Перечень наиболее часто используемых логических операторов можно ограничить следующим набором:

В большинстве случаев их достаточно для построения сложных логических конструкций и задания условий.

Для каждого из указанных выше операторов существуют аргументы (за исключением функций ИСТИНА и ЛОЖЬ) – это могут быть как цифровые или текстовые значения, так и ссылки на данные, содержащиеся в других ячейках.

Операторы ИСТИНА и ЛОЖЬ

Функция ИСТИНА не имеет собственных аргументов и практически всегда используется, как структурный компонент для других логических выражений, так как принимает одно конкретно заданное значение.

Функция ЛОЖЬ, напротив, может принимать любые значения, не являющиеся истинными. Как и ИСТИНА, практически всегда используется, как структурный компонент для других сложных выражений.

Операторы И и ИЛИ

Синтаксис оператора И выглядит следующим образом:

=И(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.

Оператор И используется в качестве элемента-связки для нескольких условий логического выражения. Важно, чтобы все аргументы оператора имели значение ИСТИНА (если в выражении их несколько), в противном случае вся логическая цепочка будет возвращать значение ЛОЖЬ.

Синтаксис оператора ИЛИ:

=ИЛИ(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.

В отличие от И, функция ИЛИ будет возвращать значение ИСТИНА даже в случае, когда хотя бы один из используемых аргументов ему соответствует, а все остальные – ложные.

Оператор НЕ

Синтаксис функции НЕ: =НЕ(лог_значение).

Количество аргументов оператора НЕ – всегда один. Соответственно, результат функции (ИСТИНА/ЛОЖЬ) полностью зависит только от значения аргумента.

Операторы ЕСЛИ и ЕСЛИОШИБКА

Общий синтаксис функции ЕСЛИ представляет собой конструкцию:

=ЕСЛИ(логическое_выражение;значение_если_истина;значение_если-ложь).

Оператор ЕСЛИ используется для построения сложных развернутых логических цепочек. Суть функции – в проверке внесенного в качестве логического выражения условия. Если условие выполняется, и оно истинно, то в качестве результата функции возвращается одно выражение, если же логическое выражение ложно, то в качестве результата функции возвращается другое условие.

Синтаксис оператора ЕСЛИОШИБКА имеет вид:

=ЕСЛИОШИБКА(значение;значение_если_ошибка).

Функция проверяет истинность логического выражения для первого аргумента, и если он соблюдается, то возвращает в качестве результата его значение. Если же выражение ложно, то в качестве результата выдается значение второго аргумента, указанное в функции.

Операторы ЕОШИБКА и ЕПУСТО

Оператор ЕОШИБКА имеет следующую структуру:

=ЕОШИБКА(значение)

Он позволяет осуществить проверку корректности уже заполненных ячеек (одной или диапазона), и, если ячейка некорректно заполнена, возвращает результат ИСТИНА, в противном случае – ЛОЖЬ.

Примеры значений в некорректно заполненных ячейках:

Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.

Формула функции ЕПУСТО выглядит следующим образом:

=ЕПУСТО(значение)

Функционал оператора проверяет ячейку или диапазон ячеек и возвращает ИСТИНА, если в ячейке/диапазоне ячеек нет данных, и ЛОЖЬ, если в ячейке/диапазоне ячеек присутствуют данные. Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.

Практический пример использования логических функций

В примере ниже попробуем частично использовать описанные выше функции для решения задачи, приближенной к реальной ситуации с расчетом премии, зависящей от определенных условий.

В качестве исходных данных – таблица со сведениями о работниках, в которой указан их пол и возраст.

Нам необходимо произвести расчет премии. Ключевые условия, от которых зависит размер премии:

величина обычной премии, которую получат все сотрудники без исключения – 3 000 руб.;
сотрудницам женского пола положена повышенная премия – 7 000 руб.;
молодым сотрудникам (младше 1984 г. рождения) положена повышенная премия – 7 000 руб.;

Выполним необходимые расчеты, используя логические функции.

Встаем в первую ячейку столбца, в которой хотим посчитать размеры премий и щелкаем кнопку “Вставить функцию” (слева от сроки формул).
В открывшемся Мастере функций выбираем категорию “Логические”, затем в предложенном перечне операторов кликаем по строке “ЕСЛИ” и жмем OK.
Теперь нам нужно задать аргументы функции. Так как у нас не одно, а два условия получения повышенной премии, причем нужно, чтобы выполнялось хотя бы одно из них, чтобы задать логическое выражение, воспользуемся функцией ИЛИ. Находясь в поле для ввода значения аргумента “Лог_выражение” кликаем в основной рабочей области книги на небольшую стрелку вниз, расположенную в левой верхней части окна программы, где обычно отображается адрес ячейки. В открывшемся списке функций выбираем оператор ИЛИ, если он представлен в перечне (или можно кликнуть на пункт “Другие функции” и выбрать его в новом окне Мастера функций, как мы изначально сделали для выбора оператора ЕСЛИ).
Мы переключимся в окно аргументов функци ИЛИ. Здесь задаем наши условия получения премии в 7000 руб.:
- год рождения позже 1984 года;
- пол – женский;
Теперь обращаем внимание на строку формул. Кликаем в ней на название первоначального оператора ЕСЛИ, чтобы переключиться в аргументы этой функции.
Заполняем аргументы функции и щелкаем OK:
- в значении “Истина” пишем цифру 7000;
- в значении “Ложь” указываем цифру 3000;
Результат работы логических операторов отобразится в первой ячейке столбца, которую мы выбрали. Как мы можем видеть, окончательный вид формулы выглядит следующим образом:
=ЕСЛИ(ИЛИ(C2>1984;D2=»жен.»);7000;3000) .
Кстати, вместо использования Мастера функций можно было вручную составить и прописать данную формулу в требуемой ячейке.
Чтобы рассчитать премию для всех сотрудников, воспользуемся Маркером заполнения. Наведем курсор на правый нижний угол ячейки с формулой. После того, как курсор примет форму черного крестика (это и есть Маркер заполнения), зажимаем левую кнопку мыши и протягиваем выделение вниз, до последней ячейки столбца.
Все готово. Благодаря логическим операторам мы получили заполненные данные для столбца с премиями.

Заключение

Логические операторы используются практически во всех сложных формулах, в которых значение в ячейке зависит от соблюдения одного или нескольких условий и позволяют строить гибкие конструкции, объединяя простые функции и расчеты в одной ячейке. Это дает возможность значительно сократить время на обработку данных и повысить эффективность работы, так как снимает большое количество промежуточных шагов в расчетах и вычислениях.

Источник

Вычислительные функции — это сердцевина Excel и то, что, по-сути, отличает программу от обычного калькулятора. Функций в программе довольно много — более 400. Часть из них дублируется, но тем не менее, возможности для экономических расчетов в программе огромные.
С помощью формул можно безошибочно рассчитать себестоимость товара, подготовить аналитические отчеты, свести планы. Решить как простые экономические задачи учета, так и составить полный баланс предприятия. Подборку инструментов Excel для бухгалтера мы уже делали. Настал черед рассмотреть основные функции Excel для экономиста, которые упростят работу с данными и большими таблицами.

Что такое функции Excel и где они находятся

Функции в Excel — это команды, которые помогают в считанные минуты откорректировать данные в ячейках, рассчитать значения по определенным критериям, изъять нужную информацию из огромного массива. Функции часто используют в формулах, чтобы их упростить и сделать более гибкими.

Как мы уже говорили, в программе функций много — около 10 категорий: есть математические, логические, текстовые. И специальные функции — финансовые, статистические и пр. Все функции лежат во вкладке «Формулы». Перейдя в нее, нужно нажать на кнопку «Вставить функцию» на панели инструментов, после чего запустится «Мастер функций».

Останется выбрать в «Категориях» нужную функцию для вычислений и заполнить данные по структуре в выпадающем окошке.

Если вы знаете, какая функция вам нужна, просто введите ее в строке формул, начиная со знака «=». Как только ввели, нажмите «Enter» для вычисления.

Запоминать, что делает каждая функция не нужно. В Excel есть удобные подсказки, зачем нужна та или иная формула, и как ее использовать.

Ниже рассмотрим основные и часто используемые формулы в Excel для экономистов: ЕСЛИ, СУММЕСЛИ, ВПР, СУММПРОИЗВ, СЧЁТ, СРЗНАЧ и МАКС/МИН.

Функция ЕСЛИ для сравнения данных

Самая популярная логическая функция, которая полезна экономистам, бухгалтерам. С ее помощью можно сравнить числовые и текстовые значения по определенным критериям. Например, рассчитать амортизацию, скидки, наценку или убрать ошибки из расчетов. Иногда используется встроенная функция ЕСЛИ в статистических, текстовых и математических формулах, что наделяет их способностью «принимать решения».

Функция ЕСЛИ помогает точно сравнить значения и получить результат, в зависимости от того, истинно сравнение или нет.

Так выглядит формула:
=ЕСЛИ(лог_выражение;[значение_если_истина];[значение_если_ложь])

Лог_выражение — это то, что нужно проверить или сравнить (числовые или текстовые данные в ячейках)
Значение_если_истина — это то, что появится в ячейке, если сравнение будет верным.
Значение_если_ложь — то, что появится в ячейке при неверном сравнении.

Например, магазин торгует аксессуарами для мужчин и женщин. В текущем месяце на все женские товары скидка 20%. Отсортировать акционные позиции можно с помощью функции ЕСЛИ для текстовых значений.

Пропишем формулу в столбце «Скидка» так:
=ЕСЛИ(B2=»женский»;20%;0)
И применим ко всем строкам. В ячейках, где равенство выполняется, увидим товары по скидке.

Так применяется функция ЕСЛИ для текстовых значений с одним условием

Функции СУММЕСЛИ и СУММЕСЛИМН

Еще одна полезная функция СУММЕСЛИ, которая позволяет просуммировать несколько числовых данных по определенному критерию. Состоит формула из 2-х частей:

СУММ — математическая функция сложения числовых значений. Записывается как =СУММ(ячейка/диапазон 1; ячейка/диапазон 2; …).
и функция ЕСЛИ, которую рассмотрели выше.

Например, вам нужно просчитать общую сумму начисленной заработной платы менеджерам, а в отчете указаны данные по всем сотрудникам предприятия.

В формуле нужно прописать такие аргументы:

Выделить диапазон всех должностей сотрудников — в нашем случае B2:B10.
Прописываем критерий выбора через точку с запятой — “менеджер”.
Диапазон суммирования — это заработные платы. Указываем C2:C10.

И получаем в один клик общую сумму заработной платы менеджеров:

С помощью СУММЕСЛИ можно просуммировать ячейки, которые соответствуют определенному критерию

Важно! Функция СУММЕСЛИ чувствительна к правильности и точности написания критериев. Малейшая опечатка может дать неправильный результат. Это также касается названий ячеек. Формула выдаст ошибку, если написать диапазон ячеек кириллицей, а не латиницей.

Более сложный вариант этой формулы — функция СУММЕСЛИМН. По-сути, это выборочное суммирование данных, отобранных по нескольким критериям. В отличие от СУММЕСЛИ, можно использовать до 127 критериев отбора данных. Например, с помощью этой формулы легко рассчитать суммарную прибыль от поставок разных товаров сразу в несколько стран.

В функции СУММЕСЛИМН можно работать с подстановочными символами, использовать операторы для вычислений типа «больше», «меньше» и «равно». Для удобства работы с функцией лучше применять абсолютные ссылки в Excel — они не меняются при копировании и позволяют автоматически пересчитать формулу, если данные в ячейке изменились.

Функции ВПР и ГПР — поиск данных в большом диапазоне

Экономистам часто приходится обрабатывать огромные таблицы, чтобы получить необходимые данные для анализа. Или сводить две таблицы в одну, что тоже не редкость. Функция ВПР или, как ее еще называют, вертикальный просмотр (англ. вариант VLOOKUP) позволяет быстро найти и извлечь нужные данные в столбцах. Либо перенести данные из одной таблицы в соответствующие ячейки другой.

Синтаксис самой простой функции ВПР выглядит так:
= ВПР(искомое_значение; таблица; номер_столбца; [интервальный просмотр]).

Например, вам нужно быстро извлечь наименование товара по номеру в списке. С помощью функции ВПР это сделать очень просто:

Функция ВПР позволяет быстро найти нужные данные и перенести их в выделенную ячейку.

В ячейке С1 мы указали номер товара. Потом выделили диапазон ячеек, где его искать (A1:B10) и написали номер столбца «2», в котором нужно взять данные. Нажали Enter и получили нужный товар в выделенной ячейке.

Есть менее популярная функция ГПР. Она работает также, как ВПР, но ищет данные в горизонтальных списках.

Важно! Чтобы увеличить область применения этой функции, можно задать данные с помощью подстановочных знаков.

Одна из задач этой функции — упростить подготовку исходных данных для аналитических и сводных таблиц. Как подготовить такую таблицу можете почитать бесплатно в книге Сводные таблицы в Excel.

Функция СУММПРОИЗВ в Excel

Четвертая функция нашего списка — СУММПРОИЗВ или суммирование произведений. Поможет быстро справиться с любой экономической задачей, где есть массивы. Включает в себя возможности предыдущих формул ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, а также позволяет провести расчеты в 255 массивах. Ее любят бухгалтеры и часто используют при расчетах заработной платы и других расходов.

Что в данном случае может быть произведениями? Как заданные диапазоны, так и целые массивы данных. Чтобы задать количество массивов, их нужно перечислить через точку с запятой, потом перемножить, а затем просуммировать. При этом, есть одно условие — массивы должны быть одинаковые по типу и длине.

Например, у вас есть месячный отчет по продажам в магазине, из которого нужно узнать, на какую сумму продали футболок размера «М».

Для этого используем функцию СУММПРОИЗВ и указываем 2 условия. Каждое из них берем в скобки, а между ними ставим «звездочку», которая в Excel читается как союз «и».

Запишем команду так: =СУММПРОИЗВ((A5:A11=A13)*(B5:B11=B13)*C5:C11), где

первое условие A5:A11=A13— диапазон поиска и наименование нужного товара
второе условие B5:B11=B13 — диапазон поиска и размер
C5:C11 — массив, из которого берется итоговая сумма

С помощью функции СУММПРОИЗВ мы узнали за пару минут, что в магазине за месяц продали футболок М-размера на 100 у.е.

Чтобы узнать продажи по другому товару и размеру, нужно просто заменить данные в ячейках A13 и B13.

Данный пример слишком прост, по сравнению с тем, с какими объемами данных приходится работать экономистам. Но зная, что умеет данная формула, уже не так страшны таблицы в миллионы строк и сотни столбцов, а нужные данные находятся за считанные минуты.

Как применить МАКС, ВПР и ПОИСКПОЗ для решения задач

Функции МИН и МАКС помогают найти наименьшее или наибольшее значение данных. Функция ПОИСКПОЗ помогает найти номер указанного элемента в выделенном диапазоне. А формула ВПР, напомним, позволяет извлечь нужные данные из столбцов в указанные ячейки.

Рассмотрим комбинацию этих функций на примере решения задачи в Excel для экономистов. Составим комбинированную формулу, чтобы найти компанию с наибольшей суммой задолженности.

Для начала составим список должников, укажем сумму их задолженности и выставим дату окончания кредитного договора.

Для решения задачи, можно применить функции последовательно:

Найти самый крупный долг поможет функция МАКС (=МАКС(B2:B10)), где B2:B10 — столбец с данными по задолженности.

Чтобы найти номер компании-должника в списке, нужно в таблицу добавить столбец с нумерацией. Так как функция ПОИСКПОЗ ищет данные только в крайнем левом столбце выделенного диапазона.

Составляем функцию по формуле:
ПОИСКПОЗ(искомое_значение;просматриваемый_массив;[тип_сопоставления])

В нашем случае это будет =ПОИСКПОЗ(14569;C2:C10;0), где искомое — максимальная сумма долга. Тип сопоставления будет “0”, потому что к столбцу с долгами мы не применяли сортировку.

Чтобы узнать название компании-должника, применим знакомую функцию ВПР.

Выглядеть она будет так =ВПР(D14;A2:B10;2), где D4 — искомое, A2:B10 — таблица или выделенный диапазон с названиями компаний и нумерацией, а “2” — номер столбца с должниками.

Этот же результат можно было получить, собрав одну формулу из 3-х:

=ВПР (ПОИСКПОЗ (МАКС (C2:C10); C2:C10;0); A2:B10;2).

В экономических расчетах функция ВПР помогает быстро извлечь нужное значение из огромного диапазона данных. Причем значение можно найти по разным критериям отбора. Например, цену товара можно извлечь по идентификатору, налоговую ставку — по уровню дохода и пр.
Кроме вышеупомянутых функций, экономисты часто используют формулу СРЗНАЧ, например, для расчета средней заработной платы. Функцию СЧЁТ, когда нужно рассчитать количество отгрузок в разрезе клиентов или стоимости товара за определенный период. Кстати, на примере отгрузок, формула МИН/МАКС поможет отследить диапазон, в котором изменялась стоимость товара.

Существует еще сотня математических и финансовых функций в Ехсеl, с помощью которых можно решить экономические задачи разной сложности. Например, обрабатывать заказы, планировать загрузку производства, рассчитывать налоги, вести кадровый учет и управлять сбытом. Но для решения подобных задач, подсказок в Excel будет уже недостаточно. Тут необходимо глубже погружаться в программу и учиться работать с разными ее инструментами: от функций и сводных таблиц, до диаграмм и макросов.

Цветные диаграммы лучше покажут вашу работу с данными, чем сетка Excel!
Освойте программу Power BI, создавайте визуальные отчеты в пару кликов после курса «ACPM: Бизнес-анализ данных в финансах»!

Насколько уверенно вы владеете Excel?

Источник

Время на прочтение
16 мин

Количество просмотров 236K

Добрый день, уважаемые хаброжители!

Время от времени некоторым (а может и более, чем некоторым) из нас приходится сталкиваться с задачами по обработке небольших массивов данных, начиная от составления и анализа домашнего бюджета и заканчивая какими-либо расчетами по работе, учебе и т.д. Пожалуй, наиболее подходящим инструментом для этого является Microsoft Excel (или возможно иные его аналоги, но они менее распространены).

Поиск выдал мне всего одну статью на Хабре по схожей тематике — «Талмуд по формулам в Google SpreadSheet». В ней дано хорошее описание базовых вещей для работы в excel (хотя он и не 100% про сам excel).

Таким образом, накопив определенный пул запросов/задач, появилась идея их типизировать и предложить возможные решения (пусть не все возможные, но быстро дающие результат).

Речь пойдет о решении наиболее распространенных задач, с которыми сталкиваются пользователи.

Описание решений построено следующим образом – дается кейс, содержащий исходное задание, которое постепенно усложняется, к каждому шагу дано развернутое решение с пояснениями. Наименования функций будут даваться на русском языке, но в скобках при первом упоминании будет приводиться оригинальное наименование на английском языке (т.к. по опыту у подавляющего большинства пользователей установлена русскоязычная версия).

Кейс_1: Логические функции и функции поиска совпадений
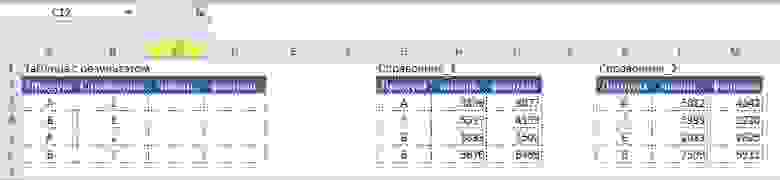
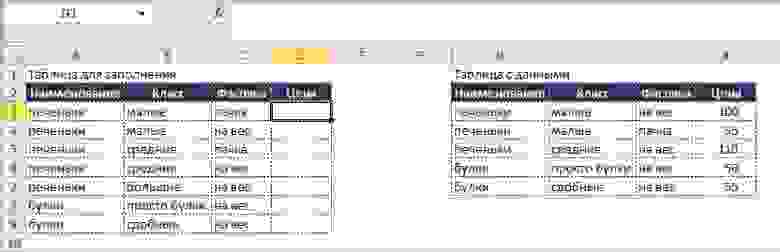
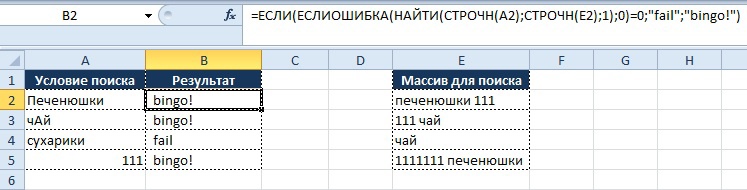
«У меня есть набор значений в табличке и необходимо что бы при выполнении определенного условия/набора условий выводилось определенное значение» (с) Пользователь

Данные, как правило, представлены в табличной форме:

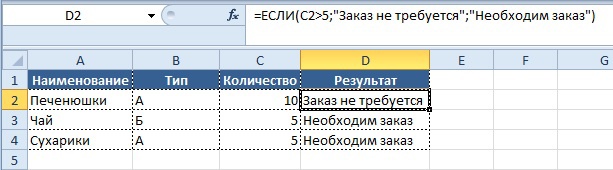
Условие:

если значение в столбце «Количество» больше 5,
то нужно вывести в колонке «Результат» значение «Заказ не требуется»,

В этом нам поможет формула «ЕСЛИ» (IF), которая относится к логическим формулам и может выдавать в решении любые значения, которые мы заранее записываем в формуле. Обращаю внимание, что любые текстовые значения записываются, используя кавычки.

Синтаксис формулы следующий:
ЕСЛИ(лог_выражение, [значение_если_истина], [значение_если_ложь])

Лог_выражение — выражение, дающее в результате значение ИСТИНА или ЛОЖЬ.
Значение_если_истина — значение, которое выводится, если логическое выражение истинно
Значение_если_ложь — значение, которое выводится, если логическое выражение ложно

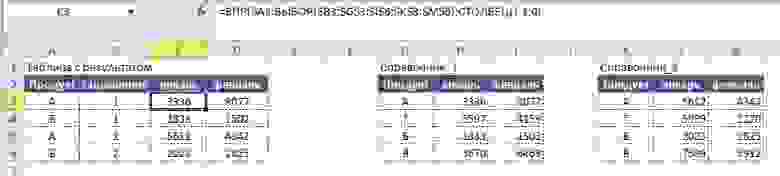
Синтаксис формулы для решения:
Вывод результата в ячейку D2:

=ЕСЛИ(C5>5;«Заказ не требуется»;«Необходим заказ»)

На выходе получаем результат:

Бывает, что условие носит более сложный характер, например выполнение 2-х и более условий:

если значение в столбце «Количество» больше 5, а значение в колонке «Тип» равно «А»
то нужно вывести в колонке «Результат» значение «1», в обратном случае «0».

В данном случае мы уже не можем ограничиться использованием одной только формулы «ЕСЛИ», необходимо добавить в ее синтаксис другую формулу. И это будет еще одна логическая формула «И» (AND).
Синтаксис формулы следующий:
И(логическое_значение1, [логическое_значение2], …)

Логическое_значение1-2 и т.д. — проверяемое условие, вычисление которого дает значение ИСТИНА или ЛОЖЬ

Синтаксис решения будет следующим:
Вывод результата в ячейку D2:

=ЕСЛИ(И(C2>5;B2=«А»);1;0)

Таким образом, используя сочетание 2-х формул, мы находим решение нашей задачи и получаем результат:

Попробуем усложнить задачу – новое условие:

если значение в столбце «Количество» равно 10, а значение в колонке «Тип» равно «А»
или же значение в столбце «Количество» больше или равно 5, а значение «Тип» равен «Б»
то нужно вывести в колонке «Результат» значение «1», в обратном случае «0».

Синтаксис решения будет следующим:
Вывод результата в ячейку D2:

=ЕСЛИ(ИЛИ(И(C2=10;B2=«А»); И(C2>=5;B2=«Б»));1;0)

Как видно из записи, в формулу «ЕСЛИ» включено одно условие «ИЛИ» (OR) и два условия с использованием формулы «И», включенных в него. Если хотя бы одно из условий 2-го уровня имеет значение «ИСТИНА», то в колонку «Результат» будет выведен результат «1», в противном случае будет «0».
Результат:

Теперь перейдем к следующей ситуации:
Представим, что в зависимости от значения в столбце «Условие» должно выводиться определенное условие в столбце «Результат», ниже приведено соответствие значений и результата.
Условие:

1 = А
2 = Б
3 = В
4 = Г

При решении задачи с помощью функции «ЕСЛИ», синтаксис будет следующим:
Вывод результата в ячейку B2:

=ЕСЛИ(A2=1;«А»; ЕСЛИ(A2=2;«Б»; ЕСЛИ(A2=3;«В»; ЕСЛИ(A2=4;«Г»;0))))

Результат:

Как видно, написание подобной формулы не только не очень удобно и громоздко, но и может занять некоторое время на ее редактирование у неопытного пользователя в случае ошибки.
Минус подобного подхода в том, что он применим для небольшого количества условий, ведь, все их придется набирать вручную и «раздувать» нашу формулу до больших размеров, однако подход отличает полная «всеядность» к значениям и универсальность использования.

Альтернативное решение_1:
Использование формулы «ВЫБОР» (CHOOSE),
Синтаксис функции:
ВЫБОР(номер_индекса, значение1, [значение2], …)

Номер_индекса — номер выбираемого аргумента-значения. Номер индекса должен быть числом от 1 до 254, формулой или ссылкой на ячейку, содержащую число в диапазоне от 1 до 254.
Значение1, значение2,… — значение от 1 до 254 аргументов-значений, из которых функция «ВЫБОР», используя номер индекса, выбирает значение или выполняемое действие. Аргументы могут быть числами, ссылками на ячейки, определенными именами, формулами, функциями или текстом.

При ее использовании, мы сразу заносим результаты условий в зависимости от указанных значений.
Условие:

1 = А
2 = Б
3 = В
4 = Г

Синтаксис формулы:

=ВЫБОР(A2;«А»;«Б»;«В»;«Г»)

Результат аналогичен решению с цепочкой функций «ЕСЛИ» выше.
При применении этой формулы существуют следующие ограничения:
В ячейку «А2» (номер индекса) могут быть указаны только цифры, а значения результата будут выводиться в порядке возрастания от 1 до 254 значений.
Иными словами, функция будет работать только если в ячейке «А2» указаны цифры от 1 до 254 в порядке возрастания и это накладывает определенные ограничения при использовании этой формулы.
Т.е. если мы захотим, что бы значение «Г» выводилось при указании числа 5,

1 = А
2 = Б
3 = В
5 = Г

то формула будет иметь следующий синтаксис:
Вывод результата в ячейку B2:

=ВЫБОР(A31;«А»;«Б»;«В»;;«Г»)

Как видно, значение «4» в формуле нам приходится оставить пустым и перенести результат «Г» на порядковый номер «5».

Альтернативное решение_2:
Вот мы и подошли к одной из самых популярных функций Excel, овладение которой автоматически превращает любого офисного работника в «опытного пользователя excel» /sarcasm/.
Синтаксис формулы:
ВПР(искомое_значение, таблица, номер_столбца, [интервальный_просмотр])

Искомое_значение – значение, поиск которого осуществляется функцией.
Таблица – диапазон ячеек, содержащий данные. Именно в этих ячейках будет происходить поиск. Значения могут быть текстовыми, числовыми или логическими.
Номер_столбца — номер столбца в аргументе «Таблица», из которого будет выводиться значение в случае совпадения. Важно понимать, что отсчет столбцов происходит не по общей сетке листа (A.B,C,D и т.д.), а внутри массива, указанного в аргументе «Таблица».
Интервальный_просмотр — определяет, какое совпадение должна найти функция — точное или приблизительное.

Важно: функция «ВПР» ищет совпадение только по первой уникальной записи, если искомое_значение присутствует в аргументе «Таблица» несколько раз и имеет разные значения, то функция «ВПР» найдет только самое ПЕРВОЕ совпадение, результаты по всем остальным совпадениям показаны не будутИспользование формулы «ВПР» (VLOOKUP) связано с еще одним подходом в работе с данными, а именно с формированием «справочников».
Суть подхода в создании «справочника» соответствия аргумента «Искомое_значение» определенному результату, отдельно от основного массива, в котором прописываются условия и соответствующие им значения:

Затем в рабочей части таблицы уже прописывается формула со ссылкой на справочник, заполненный ранее. Т.е. в справочнике в столбце «D» происходит поиск значения из столбца «А» и при нахождении соответствия выводится значение из столбца «Е» в столбец «В».
Синтаксис формулы:
Вывод результата в ячейку B2:

=ВПР(A2;$D$2:$E$5;2;0)

Результат:

Теперь представим ситуацию, когда необходимо подтянуть данные в одну таблицу из другой, при этом таблицы не идентичны. См. пример ниже

Видно, что строки в столбцах «Продукт» обеих таблиц не совпадают, однако, это не является препятствием для использования функции «ВПР».
Вывод результата в ячейку B2:

=ВПР($A3;$H$3:$M$6;2;0)

Но при решении сталкиваемся с новой проблемой – при «протягивании» написанной нами формулы вправо от столбца «В» до столбца «Е», нам придется вручную заменять аргумент «номер_столбца». Дело это трудоемкое и неблагодарное, потому, на помощь нам приходит другая функция — «СТОЛБЕЦ» (COLUMN).
Синтаксис функции:
СТОЛБЕЦ([ссылка])

Ссылка — ячейка или диапазон ячеек, для которых требуется возвратить номер столбца.

Если использовать запись типа:

=СТОЛБЕЦ()

то функция выведет номер текущего столбца (в ячейке которого написана формула).
В результате получается число, которое можно использовать в функции «ВПР», чем мы и воспользуемся и получаем следующую запись формулы:
Вывод результата в ячейку B2:

=ВПР($A3;$H$3:$M$6; СТОЛБЕЦ();0)

Функция «СТОЛБЕЦ» определит номер текущего столбца, который будет использоваться аргументом «Номер_столбца» для определения номера столбца поиска в справочнике.
Кроме того, можно использовать конструкцию:

=СТОЛБЕЦ()-1

Вместо числа «1» можно использовать любое число (а также не только вычитать его, но и прибавлять к полученному значению), для получения желаемого результата, если нет желания ссылаться на определенную ячейку в столбце с нужным нам номером.
Получившийся результат:

Продолжаем развивать тему и усложняем условие: представим, что у нас есть два справочника с разными данными по продуктам и необходимо вывести в таблицу с результатом значения в зависимости от того, какой тип справочника указан в колонке «Справочник»
Условие:

Если в столбце «Справочник» указано число 1, данные должны тянуться из таблицы «Справочник_1», если число 2, то из таблицы «Справочник_2» в соответствии с указанным месяцем

Вариант решения, который сразу приходит на ум, следующий:
Вывод результата в ячейку C3:

=ЕСЛИ($B3=1; ВПР($A3;$G$3:$I$6; СТОЛБЕЦ()-1;0); ВПР($A3;$K$3:$M$6; СТОЛБЕЦ()-1;0))

Плюсы: наименование справочника может быть любым (текст, цифры и их сочетание), минусы – плохо подходит, если вариантов более 3-х.
Если же номера справочников всегда представляют собой числа, имеет смысл использовать следующее решение:
Вывод результата в ячейку C3:

=ВПР($A3; ВЫБОР($B3;$G$3:$I$6;$K$3:$M$6); СТОЛБЕЦ()-1;0)

Плюсы: формула может включать до 254 наименований справочников, минусы – их наименование должно быть строго числовым.
Результат для формулы с использованием функции «ВЫБОР»:

Бонус: ВПР по двум и более признакам в аргументе «искомое_значение».
Условие:

Представим, что у нас как всегда есть массив данных в табличной форме (если нет, то мы к нему приводим данные), из массива по определенным признакам необходимо получить значения и поместить их в другую табличную форму.

Обе таблицы приведены ниже:

Как видно из табличных форм, каждая позиция имеет не только наименование (которое не является уникальным), но также и относится к определенному классу и имеет свой вариант фасовки.
Используя сочетание имени и класса и фасовки, мы можем создать новый признак, для этого в таблице с данными создаем дополнительный столбец «Доп.признак», который заполняем при помощи следующей формулы:

=H3&»_»&I3&»_»&J3

Используя символ «&», объединяем три признака в один (разделитель между словами может быть любым, как и не быть вовсе, главное использовать аналогичное правило и для поиска)
Аналогом формулы может быть функция «СЦЕПИТЬ» (CONCATENATE), в этом случае она будет выглядеть следующим образом:

=СЦЕПИТЬ(H3;»_»;I3;»_»;J3)

После того, как дополнительный признак создан для каждой записи в таблице с данными, приступаем к написанию функции поиска по этому признаку, которая будет иметь вид:
Вывод результата в ячейку D3:

=ЕСЛИОШИБКА(ВПР(A2&»_»&B2&»_»&C2;$G$2:$K$6;5;0);0)

В функции «ВПР» в качестве аргумента «искомое_значение» используем все ту же связку трех признаков (наименование_класс_фасовка), но берем ее уже в таблице для заполнения и заносим непосредственно в аргумент (как вариант, можно было бы выделить значение для аргумента в дополнительный столбец в таблице для заполнения, но это действие будет излишним).
Напоминаю, что использование функции «ЕСЛИОШИБКА» (IFERROR) необходимо, если искомое значение так и не будет найдено, и функция «ВПР» выведет нам значение «#Н/Д» (об этом ниже).
Результат на картинке ниже:

Данный прием можно использовать и для большего количества признаков, единственное условие – уникальность получаемых комбинаций, если она не соблюдается, то результат будет некорректным.

Кейс_3 Поиск значения в массиве, или когда ВПР не в силах нам помочь

Рассмотрим ситуацию, когда необходимо понять, есть ли в массиве ячеек нужные нам значения.
Задача:

в столбце «Условие поиска» указано значение и необходимо определить, присутствует ли оно в столбце «Массив для поиска»

Визуально все выглядит в следующем виде:

Как мы видим, функция «ВПР» тут бессильна, т.к. мы ищем не точное совпадение, а именно наличие в ячейке нужного нам значения.
Для решения задачи необходимо использовать комбинацию нескольких функций, а именно:
«ЕСЛИ»
«ЕСЛИОШИБКА»
«СТРОЧН»
«НАЙТИ»

По порядку обо всех, «ЕСЛИ» мы уже разобрали ранее, потому перейдем к функции «ЕСЛИОШИБКА» (IFERROR)

ЕСЛИОШИБКА(значение, значение_при_ошибке)

Значение — аргумент, проверяемый на возникновение ошибок.
Значение_при_ошибке — значение, возвращаемое при ошибке при вычислении по формуле. Возможны следующие типы ошибок: #Н/Д, #ЗНАЧ!, #ССЫЛКА!, #ДЕЛ/0!, #ЧИСЛО!, #ИМЯ? и #ПУСТО!.

Важно: данная формула практически всегда обязательна при работе с массивами информации и справочниками, т.к. зачастую бывает, что искомое значение не находится в справочнике и в этом случае функция возвращает ошибку. Если же в ячейке выводится ошибка и ячейка участвует, например, в вычислении, то оно так же произойдет с ошибкой. Плюс ко всему, ячейкам, где формула возвратила ошибку можно присваивать различные значения, которые облегчают их статистическую обработку. Также, в случае ошибки можно выполнять другие функции, что очень удобно при работе с массивами и позволяет строить формулы с учетом довольно разветвленных условий.

«СТРОЧН» (LOWER)

СТРОЧН(текст)

Текст — текст, преобразуемый в нижний регистр.

Важно: функция «СТРОЧН» не заменяет знаки, не являющиеся буквами.
Роль в формуле: поскольку функция «НАЙТИ» (FIND) осуществляет поиск и учетом регистра текста, то необходимо привести весь текст к одному регистру, в противном случае «чАй» будет не равно «чай» и т.д. Это актуально, если значение регистра не является условием поиска и отбора значений, в противном случае формулу «СТРОЧН» можно не использовать, так поиск будет более точным.

Теперь подробнее о синтаксисе функции «НАЙТИ» (FIND).

НАЙТИ(искомый_текст, просматриваемый_текст, [нач_позиция])

Искомый_текст — текст, который необходимо найти.
Просматриваемый_текст — текст, в котором нужно найти искомый текст.
Нач_позиция — знак, с которого нужно начать поиск. Первый знак в тексте «просматриваемый_текст» имеет номер 1. Если номер не указан, он по умолчанию считается равным 1.

Синтаксис формулы-решения будет иметь вид:
Вывод результата в ячейку B2:

=ЕСЛИ(ЕСЛИОШИБКА(НАЙТИ(СТРОЧН(A2); СТРОЧН(E2);1);0)=0;«fail»;«bingo!»)

Разберем логику формулы по действиям:

СТРОЧН(A2) – преобразует аргумент «Искомый_текст» в ячейке в А2 в текст с нижним регистром
Функция «НАЙТИ» начинает поиск преобразованного аргумента «Искомый_текст» в массиве «Просматриваемый_текст», который преобразовывается функцией «СТРОЧН(E2)», также в текст с нижним регистром.
В случае если, функция находит совпадение, т.е. возвращает порядковый номер первого символа совпадающего слова/значения, срабатывает условие ИСТИНА в формуле «ЕСЛИ», т.к. полученное значение не равно нулю. Как результат, в столбце «Результат» будет выведено значение «Bingo!»
Если же, функция не находит совпадение т.е. порядковый номер первого символа совпадающего слова/значения не указывается и вместо значения возвращается ошибка, срабатывает условие, заложенное в формулу «ЕСЛИОШИБКА» и возвращается значение равное «0», что соответствует условию ЛОЖЬ в формуле «ЕСЛИ», т.к. полученное значение равно «0». Как результат, в столбце «Результат» будет выведено значение «fail».

Как видно из рисунка выше, благодаря функциям «СТРОЧН» и «НАЙТИ» мы находим искомые значения вне зависимости от регистра символов, и места нахождения в ячейке, но необходимо обратить внимание на строку 5.
Условие поиска задано как «111», но в массиве поиска указано значение «1111111 печенюшки», однако формула выдает результат «Bingo!». Это происходит потому, что значение «111» входит в ряд значений «1111111», как следствие находится совпадение. В обратном случае данное условие не сработает.

Кейс_4 Поиск значения в массиве по нескольким условиям, или когда ВПР тем более не в силах нам помочь

Представим ситуацию, когда необходимо найти значение из «Таблица с результатом» в двумерном массиве «Справочник» по нескольким условиям, а именно по значению «Наименование» и «Месяц».
Табличная форма задания будет иметь следующий вид:

Условие:

В таблицу с результатом необходимо подтянуть данные в соответствии с совпадением условий «Наименование» и «Месяц».

Для решения подобной задачи подойдет комбинация функций «ИНДЕКС» и «ПОИСКПОЗ»

Синтаксис функции «ИНДЕКС» (INDEX)

ИНДЕКС(массив, номер_строки, [номер_столбца])

Массив — диапазон ячеек, из которого будут показываться значения в случае совпадения условий их поиска.
Если массив содержит только одну строку или один столбец, аргумент «номер_строки» или «номер_столбца» соответственно не является обязательным.
Если массив занимает больше одной строки и одного столбца, а из аргументов «номер_строки» и «номер_столбца» задан только один, то функция «ИНДЕКС» возвращает массив, состоящий из целой строки или целого столбца аргумента «массив».
Номер_строки — номер строки в массиве, из которой требуется возвратить значение.
Номер_столбца — номер столбца в массиве, из которого требуется возвратить значение.

Иными словами функция возвращает из указанного массива в аргументе «Массив» значение, которое находится на пересечении координат, указанных в аргументах «Номер_строки» и «Номер_столбца».

Синтаксис функции «ПОИСКПОЗ» (MATCH)

ПОИСКПОЗ(искомое_значение, просматриваемый_массив, [тип_сопоставления])

Искомое_значение — значение, которое сопоставляется со значениями в аргументе просматриваемый_массив. Аргумент искомое_значение может быть значением (числом, текстом или логическим значением) или ссылкой на ячейку, содержащую такое значение.
Просматриваемый_массив — диапазон ячеек, в которых производится поиск.
Тип_сопоставления — необязательный аргумент. Число -1, 0 или 1.

Функция ПОИСКПОЗ выполняет поиск указанного элемента в диапазоне ячеек и возвращает относительную позицию этого элемента в диапазоне.
Суть использования комбинации функций «ИНДЕКС» и «ПОИСКПОЗ» в том, то мы производим поиск координат значений по их наименованию по «осям координат».
Осью Y будет столбец «Наименование», а осью X – строка «Месяцы».

часть формулы:

ПОИСКПОЗ($A4;$I$4:$I$7;0)

возвращает число по оси Y, в данном случае оно будет равно 1, т.к. значение «А» присутствует в искомом диапазоне и имеет относительную позицию «1» в этом диапазоне.
часть формулы:

ПОИСКПОЗ(B$3;$J$3:$L$3;0)

возвращает значение #Н/Д, т.к. значение «1» отсутствует в просматриваемом диапазоне.

Таким образом, мы получили координаты точки (1; #Н/Д) которые функция «ИНДЕКС» использует для поиска в аргументе «Массив».
Полностью написанная функция для ячейки B4 будет иметь следующий вид:

=ИНДЕКС($J$4:$L$7; ПОИСКПОЗ($A4;$I$4:$I$7;0); ПОИСКПОЗ(B$3;$J$3:$L$3;0))

По сути, если бы мы знали координаты нужного нам значения, функция выглядела бы следующим образом:

=ИНДЕКС($J$4:$L$7;1;#Н/Д))

Поскольку, аргумент «Номер_столбца» имеет значение «#Н/Д», то результат для ячейки «B4» будет соответствующий.
Как видно из получившегося результата не все значения в таблице с результатом находят совпадение со справочником и в итоге мы видим, что часть значений в таблице выводится в виде «#Н/Д», что затрудняет использование данных для дальнейших расчетов.
Результат:

Что бы нейтрализовать этот негативный эффект используем функцию «ЕСЛИОШИБКА», о которой мы читали ранее, и заменяем значение, возвращающееся при ошибке на «0», тогда формула будет иметь вид:
Вывод результата в ячейку B4:

=ЕСЛИОШИБКА(ИНДЕКС($J$4:$L$7; ПОИСКПОЗ($A4;$I$4:$I$7;0); ПОИСКПОЗ(B$3;$J$3:$L$3;0));0)

Демонстрация результата:

Как видно на картинке, значения «#Н/Д» более не мешают нам в последующих вычислениях с использованием значений в таблице с результатом.

Кейс_5 Поиск значения в диапазоне чисел

Представим, что нам необходимо дать определенный признак числам, входящим в определенный диапазон.
Условие:
В зависимости от стоимости продукта ему должна присваиваться определенная категория
Если значение находится в диапазоне

От 0 до 1000 = А
От 1001 до 1500 = Б
От 1501 до 2000 = В
От 2001 до 2500 = Г
Более 2501 = Д

Функция ПРОСМОТР (LOOKUP) возвращает значение из строки, столбца или массива. Функция имеет две синтаксических формы: векторную и форму массива.

ПРОСМОТР(искомое_значение; просматриваемый_вектор; [вектор_результатов])

Искомое_значение — значение, которое функция ПРОСМОТР ищет в первом векторе. Искомое_значение может быть числом, текстом, логическим значением, именем или ссылкой на значение.
Просматриваемый_вектор — диапазон, состоящий из одной строки или одного столбца. Значения в аргументе просматриваемый_вектор могут быть текстом, числами или логическими значениями.
Значения в аргументе просматриваемый_вектор должны быть расположены в порядке возрастания: …, -2, -1, 0, 1, 2, …, A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ПРОСМОТР может возвратить неправильный результат. Текст в нижнем и верхнем регистрах считается эквивалентным.
Вектор_результатов — диапазон, состоящий из одной строки или столбца. Вектор_результатов должен иметь тот же размер, что и просматриваемый_вектор.

Вывод результата в ячейку B3:

=ПРОСМОТР(E3;$A$3:$A$7;$B$3:$B$7)

Аргументы «Просматриваемый_вектор» и «Вектор_результата» можно записать в форме массива – в этом случае не придется выводить их в отдельную таблицу на листе Excel.
В этом случае функция будет выглядеть следующим образом:
Вывод результата в ячейку B3:
=ПРОСМОТР(E3;{0;1001;1501;2001;2501};{«А»;«Б»;«В»;«Г»;«Д»})

Кейс_6 Суммирование чисел по признакам

Для суммирования чисел по определенным признакам можно использовать три разных функции:
СУММЕСЛИ (SUMIF) – суммирует только по одному признаку
СУММЕСЛИМН (SUMIFS) – суммирует по множеству признаков
СУММПРОИЗВ (SUMPRODUCT) – суммирует по множеству признаков
Существует также вариант с использованием «СУММ» (SUM) и функции формулы массивов, когда формула «СУММ» возводится в массив:
({=СУММ(()*())}
но такой подход довольно неудобен и полностью перекрывается по функционалу формулой «СУММПРОИЗВ»
Теперь подробнее по синтаксису «СУММПРОИЗВ»:

СУММПРОИЗВ(массив1, [массив2], [массив3],…)

Массив1 — первый массив, компоненты которого нужно перемножить, а затем сложить результаты.
Массив2, массив3… — от 2 до 255 массивов, компоненты которых нужно перемножить, а затем сложить результаты.

Условие:

Найти общую сумму по стоимости отгрузок по каждому из продуктов за определенный период:

Как видно из таблицы с данными, что бы посчитать стоимость необходимо цену умножить на количество, а полученное значение, применив условия отбора переносить в таблица с результатом.
Однако, формула «СУММПРОИЗ» позволяет проводить такие расчеты внутри формулы.
Вывод результата в ячейку B4:

=СУММПРОИЗВ(($A4=$H$3:$H$11)*($K$3:$K$11>=B$3)*($K$3:$K$11<C$3);($M$3:$M$11)*($L$3:$L$11))

Разберем формулу по частям:

($A4=$H$3:$H$11)

– задаем условие по отбору в столбце «Наименование» таблицы с данными по столбцу «Наименование» в таблице с результатом

($K$3:$K$11>=B$3)*($K$3:$K$11<C$3)

– задаем условие по временным рамкам, дата больше или равна первого числа текущего месяца, но меньше первого числа месяца следующего. Аналогично – условие в таблице с результатом, массив – в таблице с данными.

($M$3:$M$11)*($L$3:$L$11)

– перемножаем столбцы «Количество» и «Цена» в таблице с данными.
Несомненным плюсом данной функции является свободный порядок записи условий, их можно записывать в любом порядке, на результат это не повлияет.
Результат:

Теперь усложним условие и добавим требование, что бы отбор по наименованию «печеньки» происходил только по классам «малые» и «большие», а по наименованию «булки» все, кроме по классу «с джемом»:

Вывод результата в ячейку B4:

=СУММПРОИЗВ(($A4=$H$3:$H$11)*($J$3:$J$11>=B$3)*($J$3:$J$11<C$3)*(($I$3:$I$11=«малые»)+($I$3:$I$11=«большие»));($L$3:$L$11*$K$3:$K$11))

В формуле для отбора по печенькам добавилось новое условие:

(($I$3:$I$11=«малые»)+($I$3:$I$11=«большие»))

– как видно, два или более условия по одному столбцу выделяются в отдельную группу при помощи символа «+» и заключения условий в дополнительные скобки.
В формуле для отбора по булкам также добавилось новое условие:

=СУММПРОИЗВ(($A5=$H$3:$H$11)*($J$3:$J$11>=B$3)*($J$3:$J$11<C$3)*($I$3:$I$11<>«с джемом»);($L$3:$L$11)*($K$3:$K$11))

это:

($I$3:$I$11<>«с джемом»)

– на самом деле, в данной формуле можно было написать условие отбора также как и при отборе по печенькам, но тогда, пришлось бы перечислять три условия в формуле, в данном случае, проще написать исключение – не равно «с джемом» для этого используем значение «<>».
Вообще, если группы признаков/классов заранее известны, то лучше объединять их в эти группы, создавая справочники, чем записывать все условия в функцию, раздувая ее.
Результат:

Что ж, вот мы и подошли к концу нашего краткого мануала, который на самом деле мог бы быть намного больше, но целью было все-таки дать решение наиболее встречающихся ситуаций, а не описывать решение частных (но гораздо более интересных случаев).
Надеюсь, что мануал поможет кому-нибудь в решении задач при помощи Excel, ведь это будет значить, что мой труд не пропал зря!

Спасибо за уделенное время!

Источник