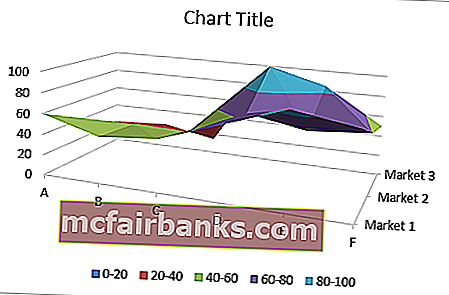
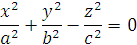Примеры поверхностей в excel - Word и Excel - помощь в работе с программами

Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.

Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.

Построение поверхностной диаграммы в Excel

Практический пример применения и создания поверхностной диаграммы в Excel.

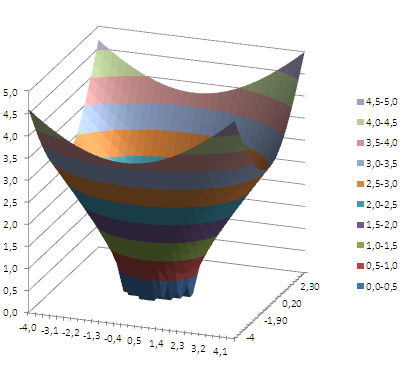
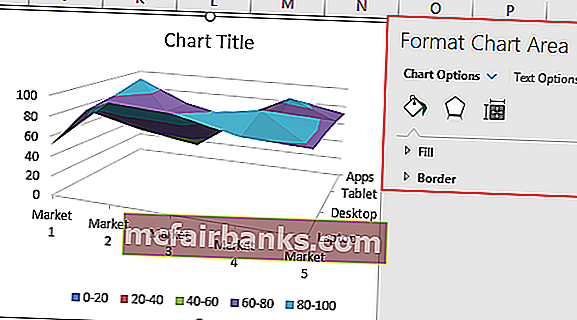
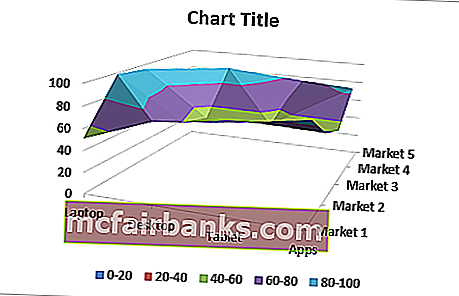
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y]². Начало осей координат расположено центру комнаты.

Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.

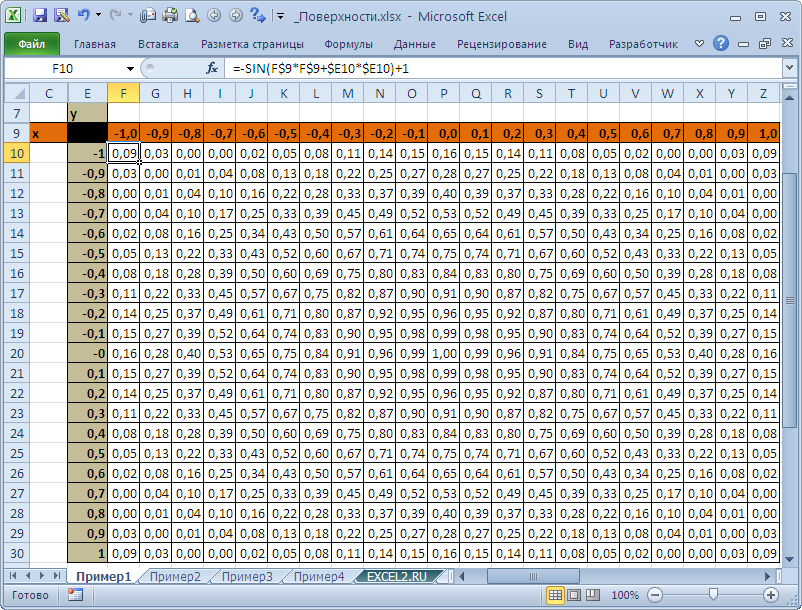
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.

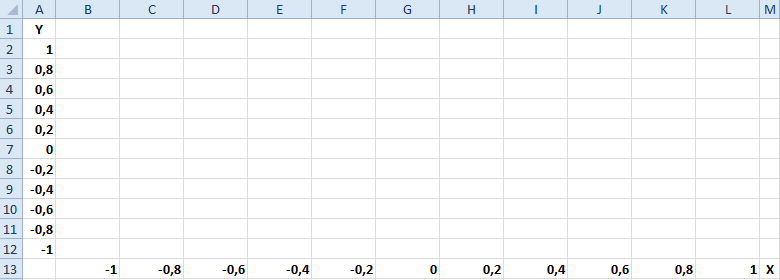
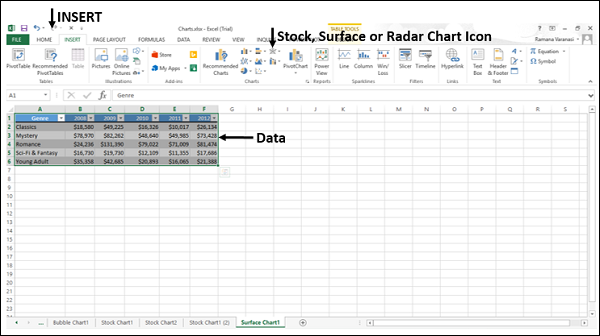
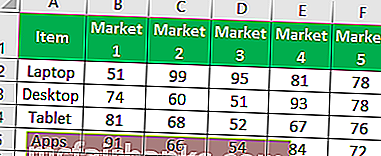
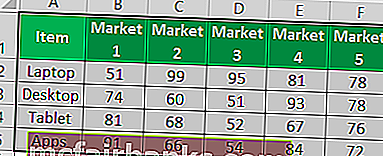
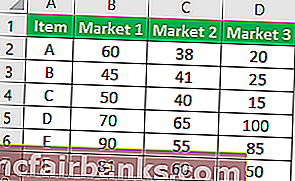
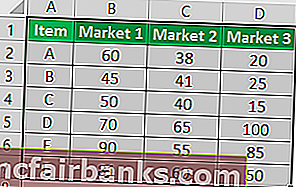
Заполните таблицу как указано на рисунке.

Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
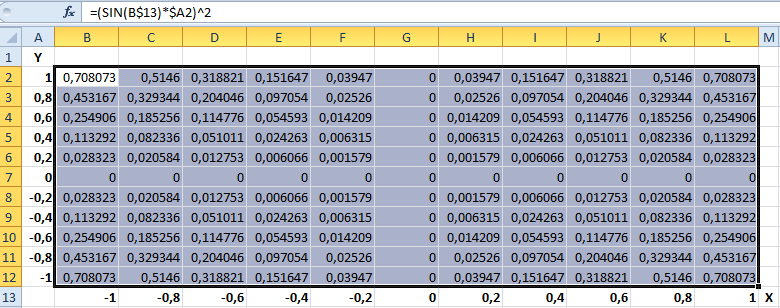
Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.

Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
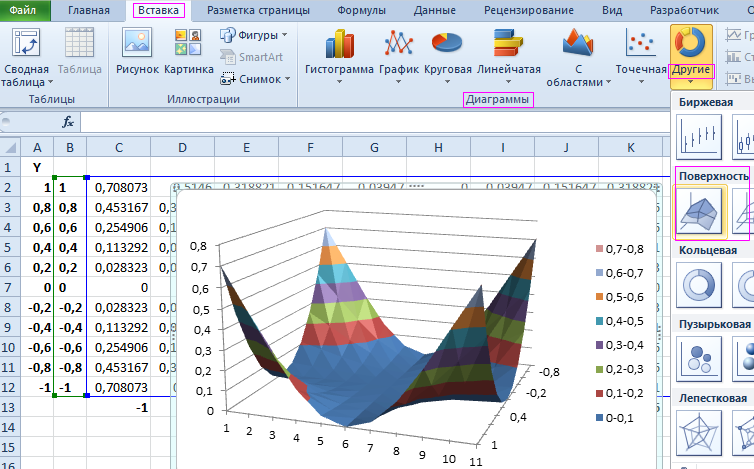
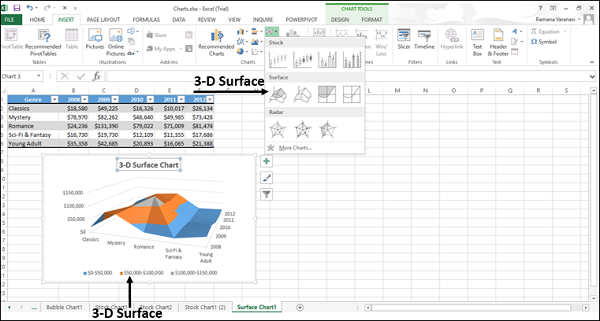
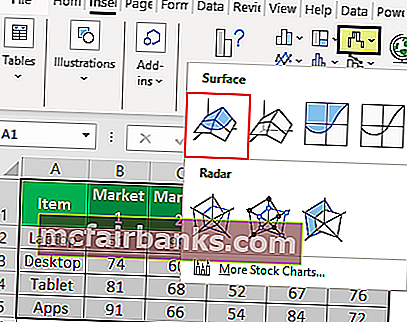
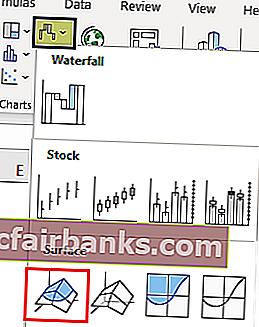
Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».

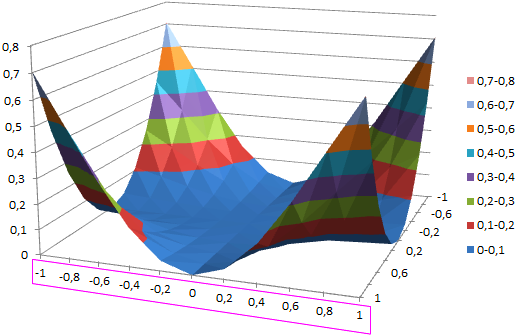
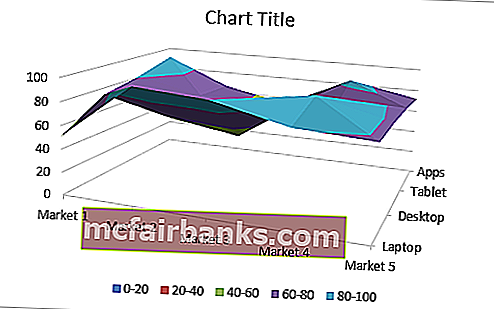
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.

Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».

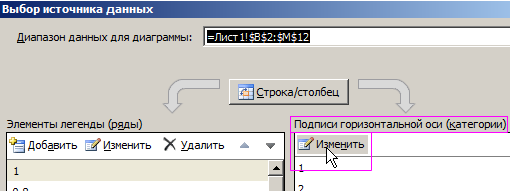
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».

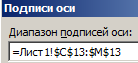
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.

Краткое описание примера

Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.

Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.

Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.

Источник

Трехмерные диаграммы (поверхности и изолинии) в EXCEL

history 16 мая 2015 г.

Диаграммы и графики

Рассмотрим трехмерные диаграммы в MS EXCEL 2010. С помощью трехмерных диаграмм отображают поверхности объемных фигур (гиперболоид, эллипсоид и др.) и изолинии.

Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .

При попытке построить диаграмму типа Поверхность на основе одного ряда данных, MS EXCEL может сказать, что ему требуется как минимум 2 ряда. На самом деле, для более или менее наглядной поверхности потребуется как минимум 10 рядов (лучше 20 – для сложных поверхностей). К счастью, ряды не нужно создавать в ручную – достаточно правильно сформировать таблицу с исходными данными.

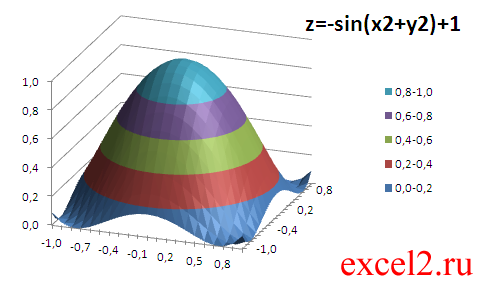
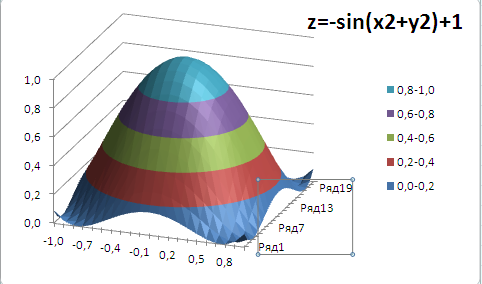
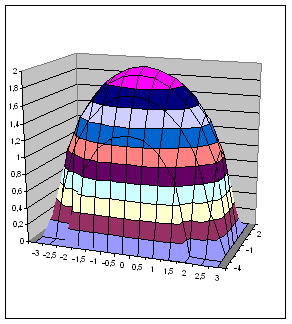
Построим график функции z=-sin(x*х+y*y)+1 (см. файл примера ).

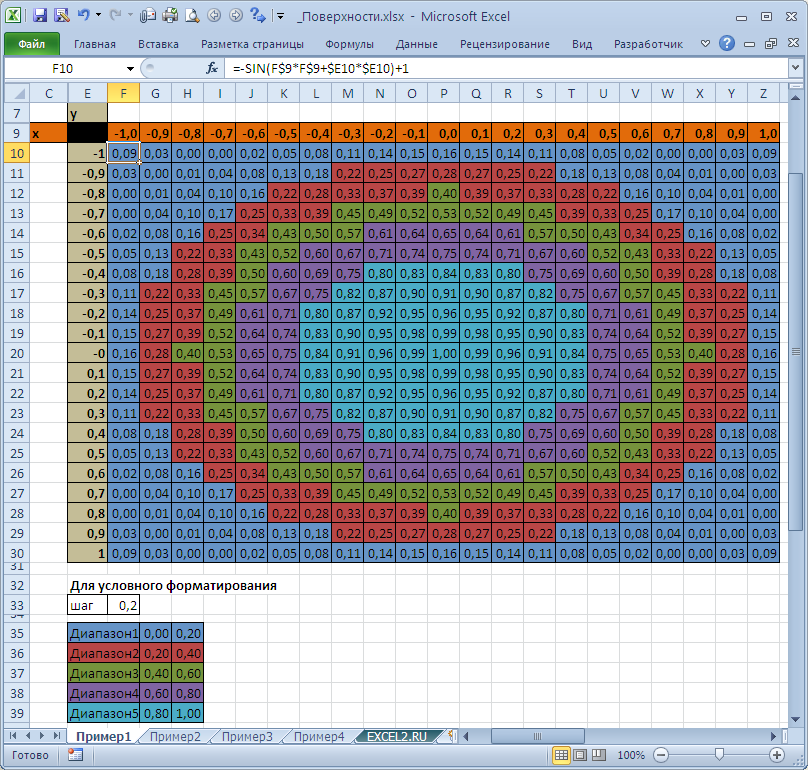
В качестве источника данных используем таблицу, в которой в верхней строке указаны значения Х, а в левом столбце Y. В остальных ячейках – значения Z для всех пар (Х,Y)

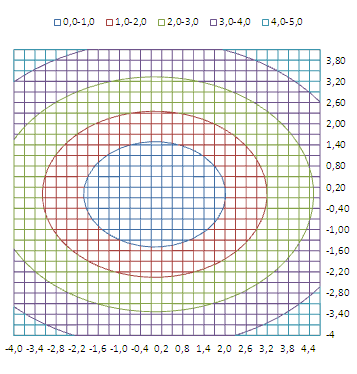
Чтобы значения Z были более информативны — можно использовать Условное форматирование .

Условное форматирование показывает некий вариант изолиний (см. ниже): близкие значения Z выделены одним цветом. Это также позволяет предварительно оценить вид создаваемой диаграммы.

Теперь выделите любую ячейку таблицы и постройте диаграмму типа Поверхность (вкладка Вставка , группа Диаграммы , Кнопка Другие ).

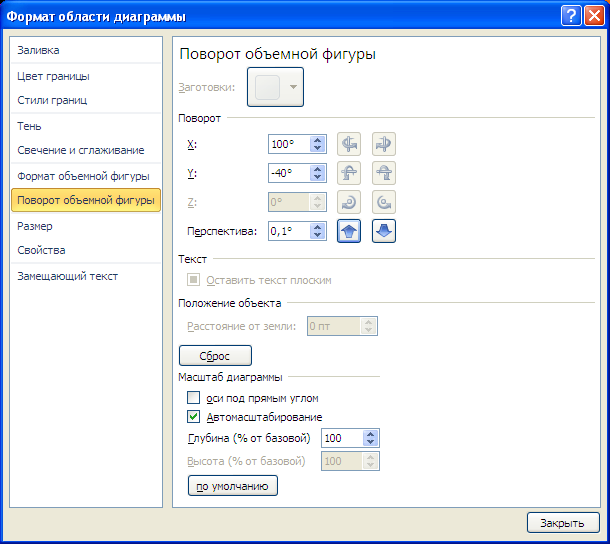
Полученную фигуру можно повращать (кнопка Поворот объемной фигуры на вкладке Макет ).

Для построения диаграммы используется 3 оси: горизонтальная ось (категорий), вертикальная ось (значений), ось Z (рядов значений). Все 3 названия осей требуют пояснения.

Во-первых, ось Z на самом деле является нашей осью Х и отображает имена рядов. Если имена рядов убрать, то изменятся и подписи оси (убрать имена рядов можно нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор ).

Этот факт роднит диаграмму Поверхность с Диаграммой График , где по Х отображаются лишь подписи. Т.е. при попытке построить поверхность с неравномерным шагом по Х (например, 1, 2, 5, 9, 77, 103, ..) получим искажения масштаба: значения по Х будут откладываться последовательно 1, 2, 3, … (конечно, Z будет рассчитаны правильно). Интересно, что формат подписей по оси Z можно настроить только изменяя формат ячеек, на которые ссылаются имена рядов (изменение формата на вкладке Число (в окне Формат Оси) ни к чему не приводит).

Во-вторых, по вертикальной оси (значений) на самом деле откладываются значения Z (это очевидно из рисунка).

И, наконец, в-третьих, горизонтальная ось (категорий) – это значения Y (на самом деле опять только подписи). Подписи, как и для Графика можно удалить или изменить нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор (на этот раз нужно нажать кнопку расположенную справа).

Так как диаграмма Поверхность – это по сути трехмерный График , в котором одному Х соответствует один Y, то некоторые объемные фигуры отобразить на диаграмме Поверхность не удастся. Например, не удастся отобразить гиперболоид, т.к. каждой паре (Х;Y) на диаграмме Поверхность соответствует только один Z, а для гиперболоида это не так (каждой паре соответствует 2 значения Z). Поэтому, в MS EXCEL придется довольствоваться только половиной гиперболоида.

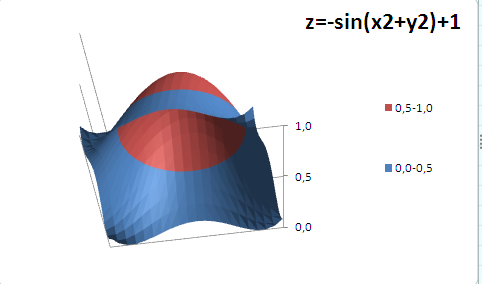
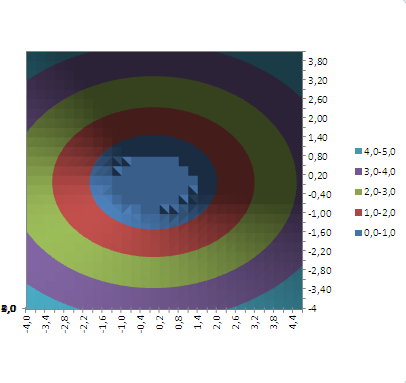
Как видно из диаграммы, близкие значения Z выделены одним цветом, которые указаны в Легенде. К сожалению, в MS EXCEL невозможно управлять этими уровнями (даже при повороте фигуры количество уровней и диапазоны значений существенно изменяются). Это приводит к тому, что построение изолиний ( линии уровня, контурный график, англ. Contour plot ) реализовано в MS EXCEL в достаточно ограниченном виде: невозможно указать на диаграмме значение изолинии (диапазоны цветов указаны на Легенде), разбиение на диапазоны по Z производится MS EXCEL автоматически и нет возможности на это повлиять. Ниже приведены изолинии для упомянутого выше гиперболоида. Это особый вид диаграммы – Проволочная контурная .

Практически такой же картинки можно добиться простым поворотом фигуры на диаграмме Поверхность .

Построение поверхностей второго порядка в excel

Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.

Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.

В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.

Плоскость

Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.

называется общим уравнением плоскости.

Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение

определяет плоскость, проходящую через начало координат.

Если А=О, то уравнение

определяет плоскость, параллельную оси Ох; если А=D =, то уравнение

определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение

определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение

Cz = 0 (или z = 0) определяет координатную плоскость Оху.

Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:

1. Уравнение плоскости в отрезках:

где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.

2. Уравнение плоскости, проходящей через заданную точку :

3. .Уравнение плоскости, проходящей через три точки

В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.

Пример1. Рассмотрим построение плоскости в Excel на примере уравнения . Пусть необходимо построить часть плоскости, лежащей в I квадранте (х Î [0; 6] с шагом = 0,5, у Î [0; 6] с шагом = 1).

Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.

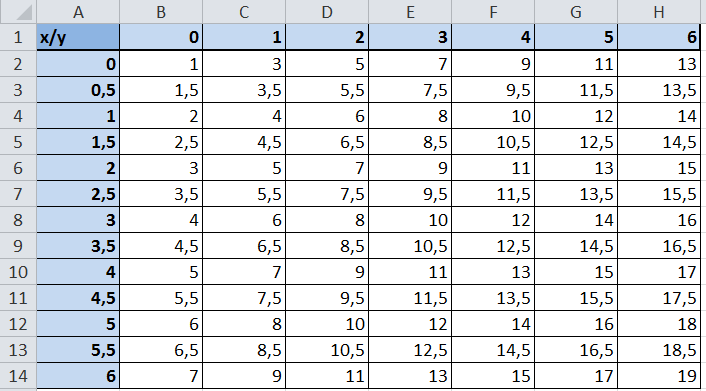
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).

Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).

Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).

В результате должна быть получена следующая таблица (рис. 1).

Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.

Приведите вид получившейся диаграммы как показано на рисунке:

Упражнения

1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.

2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.

3. Построить плоскость, проходящую через точки М(3,3,1), М₂(2,3,2), М₃(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.

Поверхности второго порядка в пространстве

Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:

Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.

Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.

Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.

Эллипсоид

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:

Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).

Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:

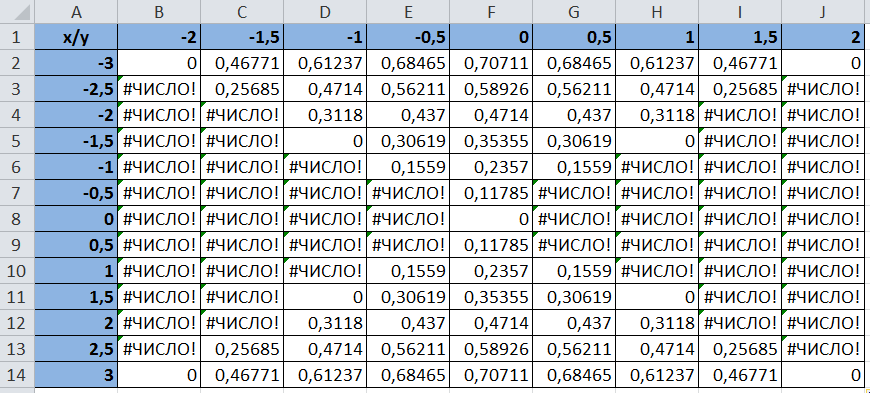
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере

Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):

Приведем вид получившейся диаграммы как показано на рисунке:

Гиперболоид

Существует два вида гиперболоидов: однополостные и двухполостные.

Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.

Двухполостным гиперболоидом называется поверхность, определяемая уравнением

Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).

Пример3. Рассмотрим построение двухполостного гиперболоида вида

Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.

Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере

Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):

Приведем вид получившейся диаграммы как показано на рисунке:

Параболоид

Существует два вида параболоидов: эллиптические и гиперболические.

Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.

Гиперболическим параболоидом называется поверхность, определяемая уравнением

Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.

Пример 4. Рассмотрим построение гиперболического параболоида вида

Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.

Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере

Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):

Приведем вид получившейся диаграммы как показано на рисунке:

Конус второго порядка

Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.

В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.

Упражнения

1. Построить верхнюю часть эллипсоида:

Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.

2. Построить верхнюю часть однополостного гиперболоида:

Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.

3. Построить эллиптический параболоид:

Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.

4. Построить верхнюю часть конуса

Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.

\|	следующая лекция ==>
\|	Решите задачи с использованием диаграммы Эйлера-Венна.

Дата добавления: 2017-02-25 ; просмотров: 2062 | Нарушение авторских прав

Построение поверхностной диаграммы в Excel

Практический пример применения и создания поверхностной диаграммы в Excel.

Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.

Заполните таблицу как указано на рисунке.
Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».

Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.

В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.

Краткое описание примера

by Ирина Кяршис

ГЛАВА 1. Возможности табличного процессора Microsoft Excel

1.1.Ввод данных в Excel

Электронная таблица – это программа, позволяющая автоматизировать табличные расчеты. Документ Microsoft Ехсел является рабочей книгой, состоящей из листов. Таблица состоит из 65536 строк и 256 столбцов. Строки нумеруются числами, столбцы – буквами латинского алфавита (А, В …, Z, АА, АВ …). На пересечении строки и столбца расположена ячейка, которая имеет адрес, состоящий из имени столбца и номера строки (А4). Одна из ячеек всегда является активной.

Прямоугольная группа смежных ячеек называется диапазоном ячеек. Примеры диапазонов – А2: С4, В2: К40.

Ячейки могут содержать данные трех типов:

1) Текстовые данные – это строка текста произвольной длины.

2) Числовые данные – это отдельное число. Может быть целым, дробным (зап.). Если ширина ячейки мала, то число записывается в экспоненциальной форме, например 125 000 000 → 1,25Е + 8 или вместо числа ставятся символы ###. При этом число сохраняется.

3) Формула – это арифметическое выражение. Он представляет собой последовательность чисел, ссылок на ячейки и функций, объединенных знаками арифметических операций: +, -, /, *. Excel предлагает несколько сотен встроенных функций, которые разделены на категории.

Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.

Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.

Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).

1.2.Типы диаграмм

В зависимости от типа диаграммы данные отображаются на ней разным способом.

Можно отметить несколько стандартных типов:

1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.

2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.

3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.

4. С областями . Диаграмма с областями похожа на график.

5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.

Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.

6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)

7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.

8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.

Подробнее о типах диаграмм здесь

1.3 Основы построения диаграмм в Excel

Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.

Совокупность этих элементов определяет макет диаграммы.

Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).

Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.

Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.

6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.

Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).

Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.

ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

2.1 Уравнения поверхностей второго порядка и их графики

Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.

Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.

Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.

Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=1, где a и b – действительные полуоси, с – мнимая полуось.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=-1,где с – действительная полуось, a и b – мнимые полуоси.

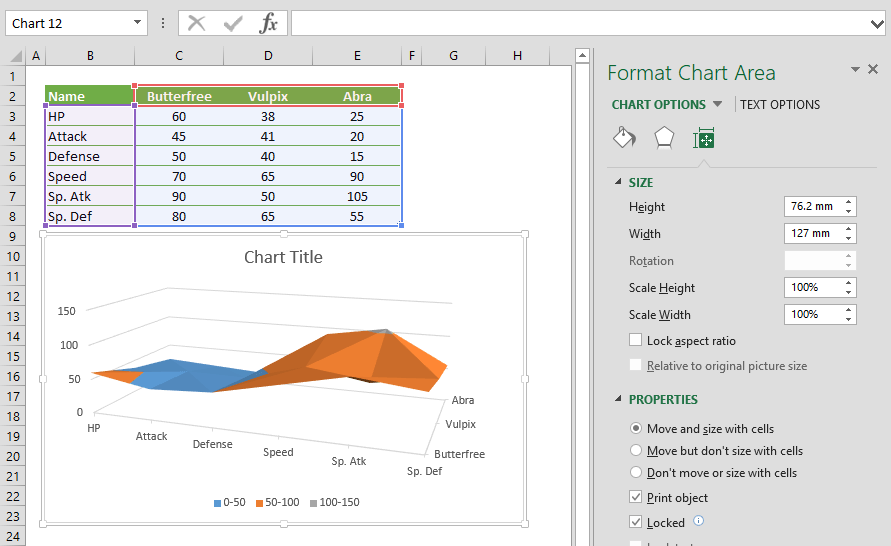
Поверхностная диаграмма в Excel и пример ее построения

Построение поверхностной диаграммы в Excel

Практический пример применения и создания поверхностной диаграммы в Excel.

Заполните таблицу как указано на рисунке.
Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».

Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.

В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.

Краткое описание примера

источники:

http://4systems.ru/inf/postroenie-poverhnostej-vtorogo-porjadka-v-excel/

http://exceltable.com/grafiki/poverhnostnaya-diagramma

Источник

Построение поверхностной диаграммы в Excel

Практический пример применения и создания поверхностной диаграммы в Excel.

Заполните таблицу как указано на рисунке.
Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».

Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.

В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.

Краткое описание примера

Диаграммы Excel – Поверхностная диаграмма

Поверхностные диаграммы полезны, когда вы хотите найти оптимальные комбинации между двумя наборами данных. Как и на топографической карте, цвета и узоры указывают области, которые находятся в одном диапазоне значений.

Чтобы создать диаграмму поверхности, убедитесь, что категории и серии данных являются числовыми значениями.

Шаг 1 – Расположите данные в столбцах или строках на листе.

Шаг 2 – Выберите данные.

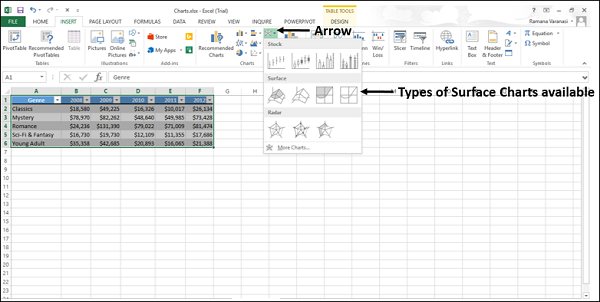
Шаг 3 – На вкладке ВСТАВИТЬ в группе Диаграммы щелкните значок Лента, Поверхность или Радар на ленте.

Вы увидите различные типы доступных карт поверхностей.

Диаграмма поверхности имеет следующие подтипы –

3-D поверхность
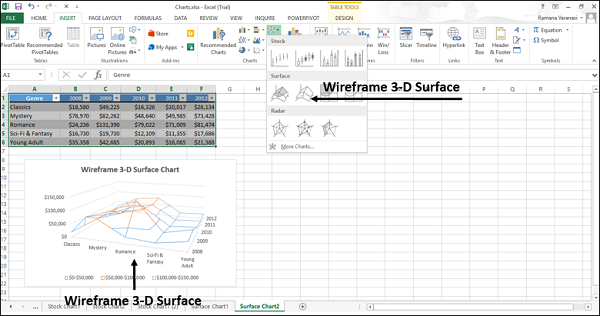
Каркас 3-D Поверхность
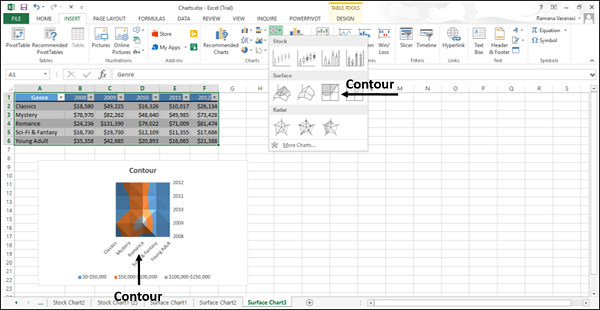
контур
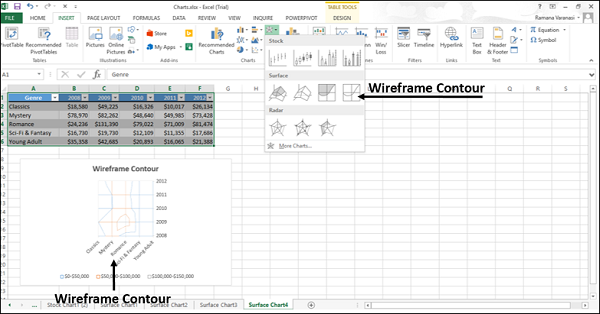
Контур каркаса

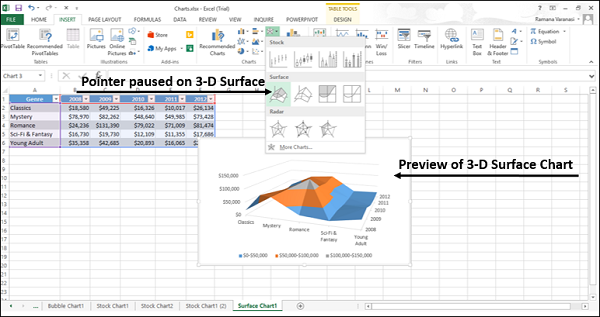
Шаг 4 – Наведите указатель мыши на каждый из значков. Предварительный просмотр этого типа диаграммы будет показан на листе.

Шаг 5 – Дважды щелкните тип диаграммы, который соответствует вашим данным.

В этой главе вы поймете, когда каждый из типов диаграмм Surface полезен.

3-D поверхность

Трехмерная диаграмма поверхности показывает трехмерное представление данных, которое можно представить в виде резинового листа, натянутого на трехмерную диаграмму столбца. Обычно он используется для отображения взаимосвязей между большими объемами данных, которые в противном случае может быть трудно увидеть.

Цветные полосы в диаграмме поверхности –

Не представляйте ряд данных

Укажите разницу между значениями

Не представляйте ряд данных

Укажите разницу между значениями

Вы можете использовать трехмерную диаграмму поверхности –

Когда категории и серии имеют числовые значения.

Показать тренды значений в двух измерениях в виде непрерывной кривой.

Когда категории и серии имеют числовые значения.

Показать тренды значений в двух измерениях в виде непрерывной кривой.

Каркас 3-D Поверхность

Каркасная трехмерная диаграмма поверхности – это трехмерная диаграмма поверхности, отображаемая без цвета на поверхности. Эта диаграмма показывает только линии. Каркасную трехмерную диаграмму поверхности нелегко прочитать, но она может отображать большие наборы данных намного быстрее, чем трехмерная диаграмма поверхности.

Вы можете использовать каркасную трехмерную диаграмму поверхности –

Показать тренды значений в двух измерениях в виде непрерывной кривой.

Когда категории и серии имеют числовые значения.

Когда данные кривые позади себя.

Показать тренды значений в двух измерениях в виде непрерывной кривой.

Когда категории и серии имеют числовые значения.

Когда данные кривые позади себя.

контур

Контурные карты – это поверхностные карты, видимые сверху, аналогичные 2-D топографическим картам.

На контурной диаграмме

Цветные полосы представляют определенные диапазоны значений.

Линии соединяют интерполированные точки одинакового значения.

Цветные полосы представляют определенные диапазоны значений.

Линии соединяют интерполированные точки одинакового значения.

Использовать контурную диаграмму –

Показать двумерный вид сверху трехмерной диаграммы поверхности.

Для представления диапазонов значений используется цвет.

Когда обе категории и серии являются числовыми.

Показать двумерный вид сверху трехмерной диаграммы поверхности.

Для представления диапазонов значений используется цвет.

Когда обе категории и серии являются числовыми.

Контур каркаса

Каркасные контурные диаграммы также являются поверхностными диаграммами, если смотреть сверху. Каркасная диаграмма показывает только линии без цветных полос на поверхности. Каркасные контурные диаграммы нелегко читать. Вместо этого вы можете использовать трехмерную диаграмму поверхности.

Использовать контурную диаграмму каркаса

Отображение двумерного вида сверху трехмерной диаграммы поверхности только с линиями.

Обе категории и серии являются числовыми.

Отображение двумерного вида сверху трехмерной диаграммы поверхности только с линиями.

Обе категории и серии являются числовыми.

Попробуйте вместо этого использовать контурную диаграмму, поскольку цвета добавляют детали к этому типу диаграммы.

Диаграмма поверхности в Excel

Поверхностная диаграмма — это трехмерная диаграмма Excel, на которой точки данных отображаются в трех измерениях. Вы можете видеть сетку поверхности, которая помогает нам найти оптимальную комбинацию между двумя типами точек данных. Типичная поверхностная диаграмма состоит из трех переменных точек данных, назовем их «X, Y и Z». Из этих трех доступных переменных мы можем разделить их на два набора, то есть независимые и зависимые переменные. Две переменные будут независимыми переменными, а одна — зависимой переменной.

Таким образом, диаграмма поверхности показывает взаимосвязь между точками данных через поверхность сетки.

Примеры создания диаграммы поверхности (графика) в Excel

Пример # 1

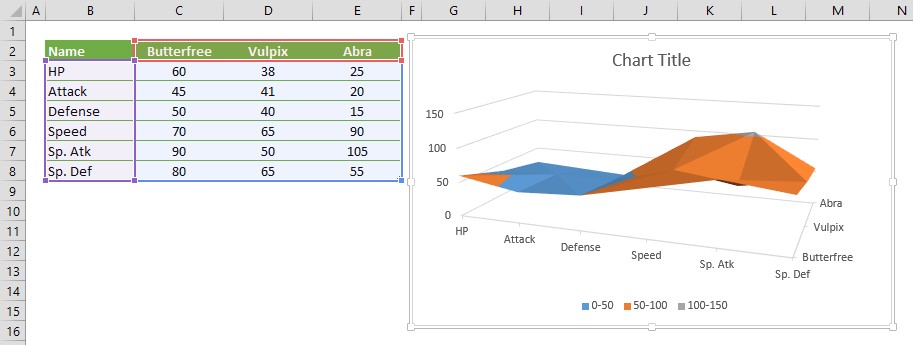
Рассмотрите приведенные ниже данные, чтобы создать свою первую диаграмму поверхности в Excel.

Выполните следующие шаги, чтобы создать поверхностную диаграмму в Excel.

Шаг 1: Сначала откройте электронную таблицу Excel.

Шаг 2: Скопируйте приведенную выше таблицу данных на один из рабочих листов. И выберите диапазон данных.

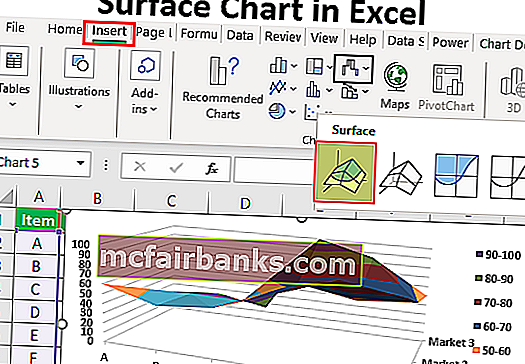
Шаг 3: Теперь на вкладке ленты выберите опцию «ВСТАВИТЬ».

Шаг 4: На вкладке INSERT вы можете увидеть раздел «Диаграмма». В этом разделе в Excel выберите Stock, Surface или Radar Chart. В этой категории диаграмм выберите «3D-поверхность» диаграмма.

Шаг 5: Как только вы нажмете на «3D-диаграмму поверхности», вы увидите приведенную ниже диаграмму поверхности по умолчанию на своем рабочем листе.

Шаг 6: Это не окончательная поверхностная диаграмма конечного пользователя. Нам нужно настроить диаграмму, чтобы это было лучше видно.

Выберите диаграмму и нажмите комбинацию клавиш Ctrl + 1 , чтобы открыть ОБЛАСТЬ ФОРМАТИРОВАНИЯ ДИАГРАММЫ справа от электронной таблицы Excel (Excel 2013 и далее).

Шаг 7: В этой ОБЛАСТИ ФОРМАТИРОВАНИЯ ДИАГРАММЫ вы можете изменить цвет сетки, настройку горизонтальной и вертикальной оси, а также многое другое.

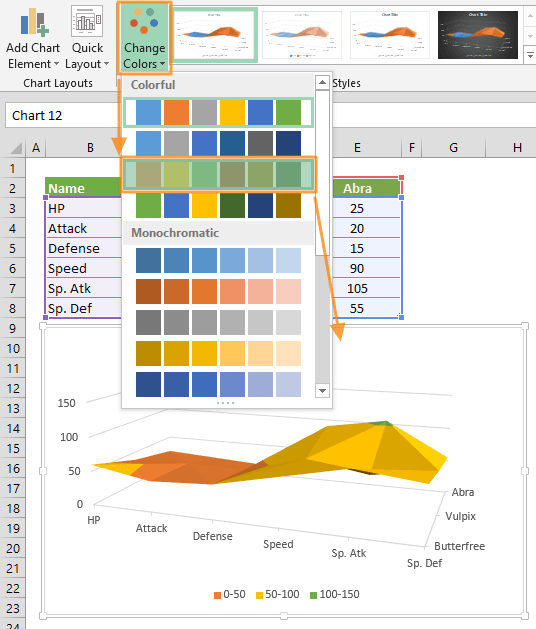
Чтобы изменить цвет сетки, вы можете сделать это на самой вкладке ДИЗАЙН. Выбрав диаграмму, вы увидите две вкладки «Работа с диаграммами», то есть «Дизайн и формат».

Выберите вкладку «Дизайн», перейдите в «Изменить цвет» и выберите цвет по своему усмотрению.

Как видите, я выбрал четвертый, и я вижу предварительный просмотр моей диаграммы с правой стороны. Как и в этом месте, курсор на каждом из разных наборов цветов для предварительного просмотра диаграммы перед окончательной комбинацией цветов.

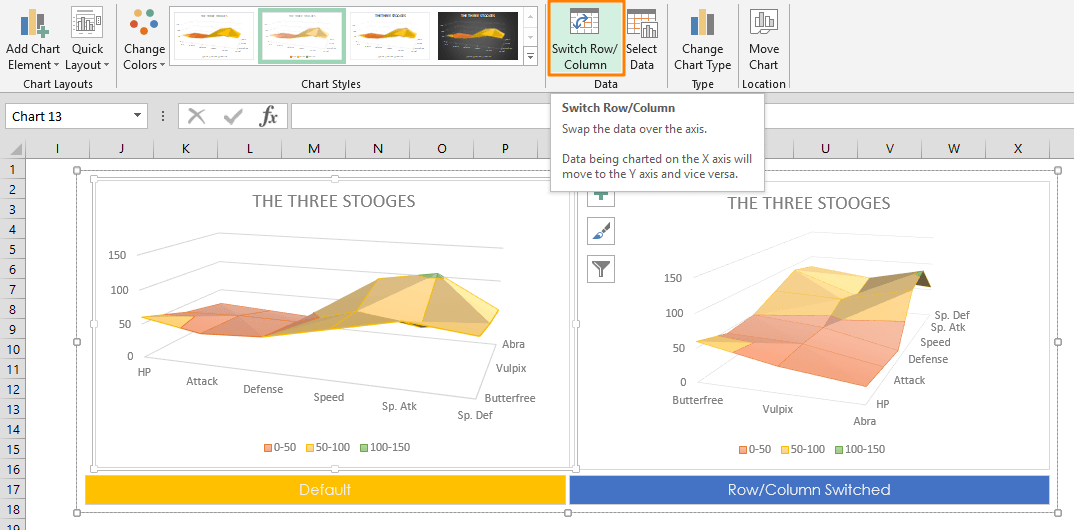
Шаг 8: Следующее, что нам нужно сделать, это «Переключить строку / столбец». Поскольку во время вставки диаграммы Excel предполагает, что горизонтальные объекты — это ряды данных, а вертикальные — категории.

Поэтому нам нужно изменить строку / столбец на вкладке «Дизайн».

Как только вы выберете эту опцию, наша диаграмма изменится автоматически, и теперь она выглядит так, как показано ниже.

Пример # 2

Теперь давайте посмотрим еще на один пример Surface Chart. Для этого рассмотрим набор данных ниже.

Скопируйте данные на рабочий лист.

Выбрав данные, выберите опцию вставки диаграммы.

Теперь мы можем видеть диаграмму ниже.

Теперь на вкладке «Дизайн» выберите «Быстрый макет» и выберите «Макет 5».

Источник

Изучим графические
возможности пакета Excel по построению
графиков функций в трехмерном пространстве.

Пример 1. Построить
верхнюю часть эллипсоида:

Для построения
поверхности необходимо разрешить
заданное уравнение относительно
переменной z.

Так как в условии речь
идет о верхней части эллипсоида, то
рассмотрим ОДЗ положительной части
уравнения:

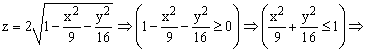
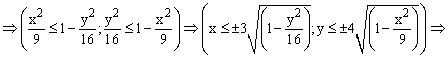
Приступим к построению
поверхности. В диапазон B1:J1 введем
последовательность значений переменной
y: -4, -3, …,4, а в диапазон ячеек А2:А14
последовательность значений переменой
x: -3, -2,5,…3.

В ячейку В2 введем
формулу = 2*(1-($A2^2)/9-(B$1^2)/16)^0,5.

Знак $, стоящий
перед буквой в имени ячейки, дает
абсолютную ссылку на столбец с данным
именем, а знак $, стоящий перед цифрой
— абсолютную ссылку на строку с этим
именем. Поэтому при копировании формулы
из ячейки В2 в ячейки диапазона
B2:J14 в них будет найдено значение z
при соответствующих значениях x, y.
Т.о. создается таблица значений z.

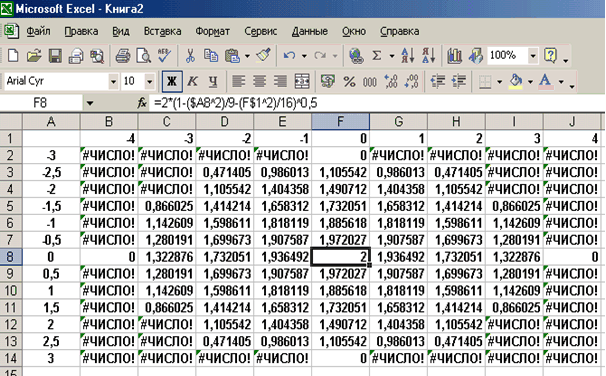
Рис. 2.19. Образцы
заполнения таблицы для построения
поверхности

Перейдем к построению
поверхности. Выделим диапазон ячеек
A1:J14, содержащий таблицу значений
функции и ее аргументов, вызовем Мастер
диаграмм и тип диаграммы Поверхность,
далее заполним диалоговые окна так как
было описано в лабораторной работе по
построению графиков функций. После
нажатия кнопки Готово получим
изображение заданной поверхности.

Рис. 2.20. Образцы
построения поверхностей

Пример
2. Построить поверхность z = x²-y²
при x, y [-1;1].

В диапазон B1:L1
введем последовательность значений
переменной x: -1, -0.8, …,1, а в диапазон
ячеек А2:А12 последовательность
значений переменой y. В ячейку В2
введем формулу = $A2^2-B$1^2 и скопируем
ее в ячейки диапазона B2:L12. На рисунке
2 изображена заданная поверхность.

Самостоятельная
работа

Задание 1. Построить
верхнюю (четные варианты) или нижнюю
(нечетные варианты) часть эллипсоида,
заданного уравнением:

Таблица 2.20

Варианты для самостоятельного выполнения

№	a	b	c	№	a	b	c
1	1	2	3	18	1.5	1.25	1.95
2	2	0.9	1.1	19	4	5	6
3	2	1	3	20	6	5	4
4	0.71	0.75	1.21	21	4	6	5
5	1.72	2.9	3.1	22	1	5	6
6	2	3	5	23	5	6	1
7	3	5	4	24	5	1	6
8	5	3	4	25	7.1	7.5	4.21
9	5	4	3	26	7.2	8.9	1
10	5.71	4.75	4.21	27	1	3	7
11	2.72	3.9	5.1	28	7	3	1
12	2	3	7	29	1	1	2
13	7	4	2	30	1.5	2.78	3.45
14	7	2	4	31	5.1	7.1	1.2
15	1.5	0.78	1.45	32	6.1	3.1	2.2
16	3.1	3.2	5.3	33	5	3	1.1
17	1.25	1.95	1.5	34	2.5	2.78	4.5

Задание
2. Построить однополостный (четные
варианты) или двуполостный (нечетные
варианты) гиперболоид, заданный
уравнением:

Таблица 2.21

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Для начинающих пользователей EXCEL советуем прочитать статью

Основы построения диаграмм в MS EXCEL

, в которой рассказывается о базовых настройках диаграмм, а также

статью об основных типах диаграмм

При попытке построить диаграмму типа

Поверхность

на основе одного ряда данных, MS EXCEL может сказать, что ему требуется как минимум 2 ряда. На самом деле, для более или менее наглядной поверхности потребуется как минимум 10 рядов (лучше 20 – для сложных поверхностей). К счастью, ряды не нужно создавать в ручную – достаточно правильно сформировать таблицу с исходными данными.

Построим график функции z=-sin(x*х+y*y)+1 (см.

файл примера

).

Чтобы значения Z были более информативны — можно использовать

Условное форматирование

Условное форматирование

показывает некий вариант изолиний (см. ниже): близкие значения Z выделены одним цветом. Это также позволяет предварительно оценить вид создаваемой диаграммы.

Теперь выделите любую ячейку таблицы и постройте диаграмму типа

Поверхность

(вкладка

Вставка

, группа

Диаграммы

, Кнопка

Другие

).

Полученную фигуру можно повращать (кнопка

Поворот объемной фигуры

на вкладке

Макет

).

Во-первых, ось Z на самом деле является нашей осью Х и отображает имена рядов. Если имена рядов убрать, то изменятся и подписи оси (убрать имена рядов можно нажав кнопку

Изменить

в окне

Выбор источника данных

, которое доступно через вкладку

Конструктор

).

Этот факт роднит диаграмму

Поверхность

с Диаграммой

График

, где по Х отображаются лишь подписи. Т.е. при попытке построить поверхность с неравномерным шагом по Х (например, 1, 2, 5, 9, 77, 103, ..) получим искажения масштаба: значения по Х будут откладываться последовательно 1, 2, 3, … (конечно, Z будет рассчитаны правильно). Интересно, что формат подписей по оси Z можно настроить только изменяя формат ячеек, на которые ссылаются имена рядов (изменение формата на вкладке Число (в окне Формат Оси) ни к чему не приводит).

Во-вторых, по вертикальной оси (значений) на самом деле откладываются значения Z (это очевидно из рисунка).

И, наконец, в-третьих, горизонтальная ось (категорий) – это значения Y (на самом деле опять только подписи). Подписи, как и для

Графика

можно удалить или изменить нажав кнопку

Изменить

в окне

Выбор источника данных

, которое доступно через вкладку

Конструктор

(на этот раз нужно нажать кнопку расположенную справа).

Так как диаграмма

Поверхность

– это по сути трехмерный

График

, в котором одному Х соответствует один Y, то некоторые объемные фигуры отобразить на диаграмме

Поверхность

не удастся. Например, не удастся отобразить гиперболоид, т.к. каждой паре (Х;Y) на диаграмме

Поверхность

соответствует только один Z, а для гиперболоида это не так (каждой паре соответствует 2 значения Z). Поэтому, в MS EXCEL придется довольствоваться только половиной гиперболоида.

Как видно из диаграммы, близкие значения Z выделены одним цветом, которые указаны в Легенде. К сожалению, в MS EXCEL невозможно управлять этими уровнями (даже при повороте фигуры количество уровней и диапазоны значений существенно изменяются). Это приводит к тому, что построение изолиний (

линии уровня, контурный график, англ. Contour plot

) реализовано в MS EXCEL в достаточно ограниченном виде: невозможно указать на диаграмме значение изолинии (диапазоны цветов указаны на Легенде), разбиение на диапазоны по Z производится MS EXCEL автоматически и нет возможности на это повлиять. Ниже приведены изолинии для упомянутого выше гиперболоида. Это особый вид диаграммы –

Проволочная контурная

.

Практически такой же картинки можно добиться простым поворотом фигуры на диаграмме

Поверхность

.

Источник

A surface chart plots data on a three-dimensional surface, in a similar way that topographic maps visualize elevation. The colors and patterns represent values within the same range. This chart type is especially useful for finding the optimum results when comparing two or more sets of data.

Surface Chart Basics

Sections

A surface chart mainly consists of 6 sections:

Plot Area: This is where the visual representation of data takes place.
Chart Title: The title of the chart. Giving your chart a descriptive name will help your users easily understand the visualization.
Legend: The legend is an indicator that helps distinguish the data series. Unlike in traditional charts, the legend in a surface chart displays the colors or patterns for the areas that share the same range of values.
Horizontal axis: The axis that includes the categories of the data, also known as the x-axis.
Vertical axis: The axis that represents the measured values, also known as the y-axis.
Depth axis: The axis that represents the series of the data, also known as the z-axis.

Types

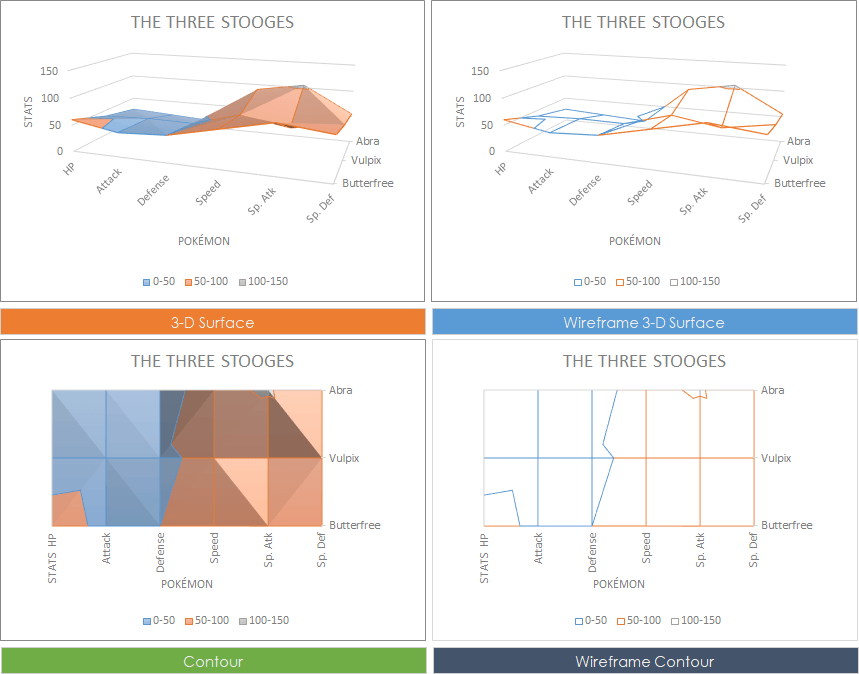
There are 4 commonly used types of surface charts.

3-D Surface: The default surface chart type where data is displayed from a 3-D perspective. This chart type resembles a 3-D column chart.
Wireframe 3-D Surface: This type uses lines instead of filled areas to connect data points.
Contour: This is the 2-D version of surface charts. This type represents a “view from above” perspective.
Wireframe Contour: The version of the Contour type that uses lines instead.

Inserting a Surface Chart in Excel

Begin by selecting your data in Excel. If you include data labels in your selection, Excel will automatically assign them to each column and generate the chart.

Go to the INSERT tab in the Ribbon and click on the Radar, Surface and Stock Chart icon to see the surface chart types. Click on the desired chart type to insert in section named Surface. In this example, we’re going to be using 3-D Surface.

Once you make a selection, Excel will create the default version of the chart. Now, let’s take a look at customization options.

Customizing the Chart

You can customize pretty much every chart element and there are a few ways you can do this. Let’s look at each method.

Double-Clicking

Double-clicking on any item in the chart area pops up the side panel where you can find options for the selected element. Please keep in mind that you don’t need to double click another element to edit it once the side panel is open, the side menu will switch to the element. The side panel contains element specific options, as well as other generic options like coloring and effects.

Right-Click (Context) Menu

Right-clicking an element will display the contextual menu, where you can modify basic element styling like colors, or you can activate the side panel for more options. To display the side panel, choose the option that starts with Format. For example, this option is labeled as Format Data Series… in the following image.

Chart Shortcut (Plus Button)

In Excel 2013 and newer versions, charts also support shortcuts. You can add/remove elements, apply predefined styles and color sets and filter values very quickly.

With shortcuts, you can also see the effects of options on the fly before applying them. In the following image, the mouse is on the Data Labels item and the labels are visible on the chart.

Ribbon (Chart Tools)

Whenever you activate a special object, Excel adds a new tab(s) to the Ribbon. You can see these chart specific tabs under CHART TOOLS. There are 2 tabs — DESIGN and FORMAT. While the DESIGN tab contains options to add elements, apply styles, modify data and modify the chart itself, the FORMAT tab provides more generic options that are common with other objects.

Customization Tips

Preset Layouts and Styles

Try preset layouts or styles to improve visualization of your chart. Instead of dealing with all elements by yourself give a chance to Excel.

You can find styling options in the DESIGN tab under CHART TOOLS or in brush icon of Chart Shortcuts. Below are some examples.

Applying a Quick Layout:

Changing colors:

Update Chart Style:

Changing chart type

You can change the type of your chart any time from the Change Chart Type dialog. Select one of the datasets (series) on the chart, and click on Change Chart Type in the Right-Click (Context) Menu, or from the DESIGN tab. Alternatively, you can change the chart types for all datasets by right-clicking on an empty chart area.

The Change Chart Type menu contains the same options as the Insert Chart dialog. You can find Wireframe or Contour versions here.

Switch Row/Column

By default, Excel assumes that vertical labels of your data are the categories, and the horizontal ones are the data series. If your data is reversed, click Switch Row/Column button in the DESIGN tab, when your chart is selected.

Move a chart to another worksheet

By default, charts are created inside the same worksheet as the selected data. If you need to move your chart into another worksheet, use the Move Chart dialog. Begin by clicking the Move Chart icon under the DESIGN tab or from the right-click menu of the chart itself. Please keep in mind you need to right-click in an empty place in chart area to see this option.

In the Move Chart menu, you have 2 options:

New sheet: Select this option and enter a name to create a new sheet under the specified name and move your chart there.
Object in: Select this option and select the name of an existing sheet from the dropdown input to move your chart to that sheet.

Источник

ОПИСАНИЕ РАБОТЫ

1. Название работы: построение поверхностей в MS
Excel.

2.
Номинация: сценарий
медиаурока с компьютером.

3.
Предмет: информатика +
математика + воображение.

4.
Участники: ученики 9-11
классов.

5. Цели и задачи: раскрыть графические
возможности MS Excel при построении поверхностей, удивить
их многообразием этих возможностей и научить строить их, обратить внимание
учеников на красоту этих поверхностей.

Задачи:

— обучающие: повторение
синтаксиса формулы логического условия, повторить понятие смешанной адресации,
тюнинг поверхностей;

— развивающие: сформировать у учащихся ассоциации
между графическими объектами и объектами окружающего мира;

— воспитательные: научить учащихся удивляться
красоте поверхностей, находить «схожесть» с реальными объектами, развивать
фантазию и воображение.

6.
Аннотация.

Данная разработка урока имеет своей целью раскрыть графические
возможности табличного процессора MS Excel, которые в
большинстве справочной и учебной литературы игнорируются или освещаются очень
бедно.

Все эти возможности очень ярко проявляются при построении
поверхностей.

Сформулируем предположение (гипотезу, догадку): используя
богатый арсенал математических и логических функций, имеющихся в MS Excel, можно построить огромное количество поверхностей, которые являются
моделями реальных объектов (явлений) окружающего мира. Этот урок является
попыткой совместить несовместимое. С одной стороны, мы имеем строгие математические
формулы, а с другой — изящные поверхности, которые и являются графическими
интерпретациями этих формул.

При построении этих поверхностей не покидает чувство: неужели
всё это возможно сделать в обычном и привычном табличном процессоре? Ничего
подобного нигде не встречается. Самое первое чувство, которое испытываешь при
работе над этой темой, это удивление. Учеников надо удивить многообразием самых
фантастических форм. Вы словно открываете ящик Пандоры. Конечно, это эмоции.
Но, зная, что за этой красотой и изяществом форм скрываются обычные
математические формулы, ученики должны понять, что окружающий нас мир можно
описать не только поэтическим языком, но и сухим языком формул.

Кому может пригодиться данная разработка? Наверное,
творческим учителям, будущим художникам и дизайнерам, программистам. Всем тем,
у

кого
богатое воображение и абстрактное мышление тесно переплетены. Данная тема может
стать основой для научно-исследовательской работы.

7. Автор: Никифоров Юрий Васильевич, педагог
дополн. образования

8. Место работы: Пермский край, г. Губаха, Муниципальное
автономное общеобразовательное учреждение «Начальная общеобразовательная школа
№ 1» (МАОУ «НОШ № 1»).

СТРУКТУРА И ХОД УРОКА

№	Этап урока	Название используемых ЭОР	Деятельность учителя	Деятельность ученика	Время (мин.)
1	Организаци- онный		Приветствие, проверка наличия учеников (по классному журналу).	Ученики размещаются по одному за один компьютер.	1 мин.
2	Объявление темы и цели урока		Объявление темы и цели урока.	Находят на рабочем столе значки «Шаблон.xlsx» и «Формулы.xlsx»..	1 мин.
3	Увертюра	Презентация «Ассоциации.pptx»	Демонстрирует презентацию «Ассоциации.pptx»	Просмотр презентации.	5 мин.
4	Объяснение нового материала	Презентация «Surf.pptx»	Учитель объясняет понятие смешанной адресации и алгоритм постр-ния поверхности.	Просмотр презентации.	10 мин.
5	Практическая работа	«Шаблон.xlsx», «Формулы.xlsx»	Индивидуальная работа с каждым учеником.	Учащиеся выбирают из файла «Формулы.xlsx» (без гиперссылок) любую формулу и заполняют таблицу из файла «Шаблон.xlsx».	20 мин.
6	Интрига (момент истины).	Любой файл из папки «Заготовки»	«Как имеющимися средствами MS Excel сделать эту поверхность красивой?»	Ученики используют цветовые схемы и стили из «Разметки страницы».	5 мин.
7	Вывод. (Эпилог)	Файл «Работа.docx», стр.11., файл «Библиотека.docx»	Выводит на экран коллекцию поверхностей и делает выводы.		2 мин.
8	Выставление оценок.				1 мин.

Примечание. Данный урок был проведён в
феврале 2012 года в 9-б классе в обеих группах. Но по времени мы не уложились в
план (около 5 минут).

Объяснение темы урока основано на рассмотрении конкретных
примеров. Учитель вправе выбирать из этих примеров любые. Можно из презентации «Surf.pptx» удалить некоторые примеры (или
добавить свои). На каком-либо примере при объяснении материала учителю можно
остановиться более подробно.

Пример 1.

Рассмотрим пример с функцией z=sin(x)cos(y).
Выясним, как меняется качество прорисовки поверхности от шага изменения
переменных.

На рисунках 1 и 2 видно: как отличаются поверхности с
разными шагами. На первом рисунке (Рис.1) диапазон изменения переменных [-5;5] с
шагом 0,5.

	-5	-5	-4	-4	-3	-3	-2	-2	-1	-1	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5
-5	0,3	0,3	0,2	0,1	-0	-0	-0	-0	-0	-0	0,1	0,2	0,3	0,3	0,2	0	-0	-0	-0	-0
-4,5	-0	-0	-0	-0	0	0,1	0,2	0,2	0,2	0,1	-0	-0	-0	-0	-0	-0	0,1	0,2	0,2	0,2
-4	-1	-1	-0	-0		0,4	0,6	0,7	0,6	0,3	-0	-1	-1	-1	-0	-0	0,2	0,5	0,6	0,6
-3,5	-1	-1	-1	-0	0,1	0,6	0,9	0,9	0,8	0,4	-0	-1	-1	-1	-1	-0	0,3	0,7	0,9	0,9
-3	-1	-1	-1	-0	0,1	0,6	0,9	1	0,8	0,5	-0	-1	-1	-1	-1	-0	0,3	0,7	1	0,9
-2,5	-1	-1	-1	-0	0,1	0,5	0,7	0,8	0,7	0,4	-0	-1	-1	-1	-0	-0	0,3	0,6	0,8	0,8
-2	-0	-0	-0	-0	0,1	0,2	0,4	0,4	0,4	0,2	-0	-0	-0	-0	-0	-0	0,1	0,3	0,4	0,4
-1,5	0,1	0,1	0,1	0	-0	-0	-0	-0	-0	-0	0	0,1	0,1	0,1	0	0	-0	-0	-0	-0
-1	0,5	0,5	0,4	0,2	-0	-0	-0	-1	-0	-0	0,3	0,5	0,5	0,5	0,3	0,1	-0	-0	-1	-1
-0,5	0,8	0,9	0,7	0,3	-0	-1	-1	-1	-1	-0	0,4	0,7	0,9	0,8	0,5	0,1	-0	-1	-1	-1
0	1	1	0,8	0,4	-0	-1	-1	-1	-1	-0	0,5	0,8	1	0,9	0,6	0,1	-0	-1	-1	-1
0,5	0,8	0,9	0,7	0,3	-0	-1	-1	-1	-1	-0	0,4	0,7	0,9	0,8	0,5	0,1	-0	-1	-1	-1
1	0,5	0,5	0,4	0,2	-0	-0	-0	-1	-0	-0	0,3	0,5	0,5	0,5	0,3	0,1	-0	-0	-1	-1

Рис.1

А на Рис.2 эта же самая формула,
но диапазон [-10;10] и шаг равен 0,1. Разница видна сразу. Конечно, таблица
становится большой, но качество прорисовки поверхности гораздо лучше. Кроме
того, благодаря дополнительным настройкам, мы можем менять и цветовую гамму и
стили. Всё это придаёт поверхности естественный вид, и она может быть
сохранена в одном из форматов: .png, .jpg, .gif. Для вставки в презентацию лучше подойдёт
формат .gif или .jpg, так как объём
файла при этих форматах будет в несколько раз меньше и качество рисунка не
ухудшится.

Пример 2.

На следующем этапе станем применять параметры, которые
кардинально могут изменить поверхность. На рисунках 3 и 4 задаются разные
параметры для одной и той же поверхности (формула не меняется). Ячейки, в
которых находятся эти параметры, имеют абсолютную адресацию и их количество
может меняться.

Рис.3 Рис.4

На рисунках видно, что с разными параметрами мы имеем
разные поверхности. А если эти параметры задать через генератор случайной
величины (по формуле =случмежду(m;n)),
то при каждом прерывании мы получим множество различных поверхностей. Для этого
достаточно поставить курсор на границе обозначений строк (столбцов) и один раз
«кликнуть» левой клавишей.

Пример 3.

Существует заблуждение, что стандартными средствами MS
Excel невозможно построить полную сферу. Даже на официальном
сайте программистов (http://www.programmersforum.ru), на форуме любителей MS Excel (http://www.forum.planetaexcel.ru) об этом говорится в категоричной форме. Но есть
способ, который опровергает это мнение. Дело в том, что обычным способом это, действительно,
невозможно. Построить полусферу не составит особого труда, а полную… (?). Рассмотрим
этот способ на примере простейшей сферы с радиусом 1 и с центром в начале
координат.

Уравнение этой сферы: x² + y² + z² = 1 => .
Так как мы имеем арифметический корень, то данное уравнение описывает только
верхнюю часть сферы (полусферу). Для построения нижней части сферы требуется
уравнение . Но в MS Excel невозможно построить в одной системе координат сразу две поверхности.
Но можно сделать так:

1.
построить последовательно две одинаковые
поверхности ; у второй поверхности изменить
порядок оси Z на обратный (это можно сделать с помощью
конструктора или макета);

2.
удалить в обоих чертежах всё лишнее (легенду, оси,
стенки, основание, заливку);

3.
обычным перемещением вторую поверхность совместить
с первой так, чтобы плоскости X0Y совпали;

4.
выделив оба чертежа, сгруппировать стандартным
инструментом.

Данный алгоритм схематически
изображён на рисунках 5 – 6.

Рис. 5
Рис. 6

Рис.
5 Рис. 6

Аналогичным способом можно построить двуполостный
параболоид, тор, и другие поверхности, где переменная Z принимает
противоположные значения.

Пример 4.

Есть ещё один приём, который позволяет
«разрезать» любые поверхности. Это можно связать с такой операцией, как
построение сечений. На рисунке 7 обычная сфера «разрезана» на части. Это
достигается обычным удалением (или вставкой) одной или нескольких строк (или
колонок) таблицы. Данный приём можно применять при моделировании, конструировании
сложных объектов на

уроках
черчения.

Рис. 7 Рис. 8
Рис. 9

Более того, каждую полученную часть можно перемещать. На
рисунке 8 одна из частей перемещена. Это достигается путём перемещения части
таблицы (например, вправо). Более того, можно вырезать часть таблицы и это
сразу отразится на поверхности. Конфигурация такой «вырезки» может быть
произвольной. На рисунке 9 видно, что вырезан фрагмент поверхности,
стилизованный под букву «Е».

Пример 5.

Следующим шагом настроим оси. Дело в том, что в стандартных
настройках каждую ось можно фиксировать минимальным и максимальным значениями.
Тогда любую поверхность можно «обрезать» плоскостью. Такой же результат можно
получить путём подбора параметров. На рисунках 10 и 11 видны результаты такого
«обрезания».

Рис.
10 Рис. 11

На рисунке 10 поверхность ограничена по оси Z, а на рисунке 11 «обрезка» сделана по осям X и Y.

Во всех построенных поверхностях используются стандартные
математические функции, которые «зашиты» в MS Excel.
Следующий приём, который можно использовать в построении поверхностей, не
поддаётся обычной логике. Скорее всего, это на 90% — интуиция. Приведём два
примера.

Пример 6.

Обычный однополостный параболоид строится по формулеЕсли в эту формулу добавить
какую-либо тригонометрическую функцию, то свойство периодичности «проявит» себя
во внешнем виде всей поверхности. Допустим так:

Рис. 13 Рис.
14 Рис. 15

     Рис. 16                                   Рис.
17                                     Рис. 18

На рисунках 13 — 18 видно, как это свойство
(периодичность) меняет внешний вид поверхности. Заметим, что основная форма
(тренд) остаётся прежней (параболоид), но поверхность покрывается «рябью». В
данном случае мы «скрещиваем» данные поверхности.

Пример 7.

В этом примере другой подход. Допустим, необходимо создать
поверхность, напоминающую цветок розы. За основную возьмём поверхность с
концентрическими волнами: Это рисунок 19. Чтобы «гребни»
этих концентрических волн разбить на «лепестки», добавим в формулу в виде
множителя выражение . Причём, параметры m
и n желательно выбирать кратными. А чтобы
изображение не «проваливалось» в отрицательную область, всё выражение надо
сделать абсолютным по величине. Тогда формула примет вид: . На рисунке 20 видна полученная
поверхность.

Рис.
19 Рис. 20

В этом примере мы видим наложение одних волн на другие. В физике
это явление называется интерференцией. Мы
смоделировали это явление с помощью поверхностей. На рисунке 21 изображены
схематически концентрические и гиперболические волны. Пересекаясь, они либо
резонируют, либо подавляют друг друга, тем
самым создавая определённый рисунок. Этот пример открывает отдельное
направление исследования волновых процессов.

Пример 9.

В примере 2 написано о том, что параметров, которые входят
в написание формулы, может быть много. В этом примере их пять. И каждый из них является
случайным числом, так как определяется формулой =случмежду(m;n). Поэтому при каждом прерывании они случайные и
разные. Поэтому и поверхности будут получаться всегда разными. На рисунке 22 мы
видим одну из 2359296 поверхностей. Столько вариантов может быть получено из
одной формулы!

На этом рисунке можно увидеть такие элементы, которые присущи только графическим
3D-редакторам. Это световые блики и тень.

Во вкладке
«Разметка страницы» мы можем подобрать любой стиль и цветовую гамму. Причём
цветовую гамму мы можем создать сами.

Рис. 22

Пример 10.

Для каждой поверхности, заданной формулой z = f(x,y), можно выполнить такое
преобразование, которое задаёт «эффект лесенки». Это можно сделать с помощью
стандартных функций. Например, так: z₁ = целое(f(x,y)). На рисунках 23 и 24 видно, — как изменяется поверхность.

Пример 11.

Если использовать логическую функцию <ЕСЛИ>, то в одной
системе координат можно строить несколько поверхностей. Само условие можно
также задавать какой-либо функцией. В общем виде это будет выглядеть так:
=если(f>m;f1;f2). На Рис.25 функция f задаёт область построения поверхности
f1(если условие выполняется). Тогда в области, где
условие не выполняется, будет строиться поверхность f2.

Пример 12.

При выборе функции условия можно
использовать логическую функцию <И>. Тогда при определении области
построения поверхности мы можем получить более богатые возможности для создания
ещё более сложных поверхностей. На рисунках 27 – 29 приведены примеры таких
поверхностей.

Рис.27
Рис.28 Рис.29

При рассмотрении этих примеров видно,
что данная тема открывает новые возможности, которые раньше нигде не
использовались.

ВЫВОДЫ

Из
рассмотренных примеров можно сделать следующие выводы:

1. графические возможности MS Excel сравнимы с
возможностями графических редакторов;

2. используя графические возможности MS Excel, можно
смоделировать различные явления и объекты;

3. какой бы ни была формула, найдётся объект (или явление) в окружающем
мире, которое имеет соответствующую геометрию;

4. данная разработка урока открывает ученикам несколько новых
перспективных направлений в изучении и применении MS Excel:

— изучение графических возможностей MS Excel;

— построение сечений графических объектов;

— моделирование волновых процессов (интерференция);

— создание «конструктора» поверхностей.

Каждое из этих направлений может стать темой для отдельного
элективного курса. Целью данной разработки является не только раскрытие новых
богатых возможностей табличного процессора MS Excel, но и
мощная эстетическая составляющая (см. папку «Библиотека»). В аннотации было
написано, что данная тема открывает ящик Пандоры. Это не так. Скорее всего, ученики
почувствуют, что открывается настоящий клондайк новых
возможностей.

Результат

Ученица 9 класса Мишталь Екатерина представила эту тему в
своей научно-исследовательской работе («Построение поверхностей в MS Excel») на XXXII региональном конкурсе
исследовательских работ учащихся в области социально-гуманитарных и
естественно-математических наук и стала победителем (I место).
Секция: информатика и ИКТ.

ГБОУ ДОД «Пермский центр «Муравейник», Пермская
региональная детская общественная организация «Муравей», г. Пермь, 14 апреля
2012 г.

Источник

Диаграмма поверхности Excel (график)

Поверхностная диаграмма — это трехмерная диаграмма Excel, на которой точки данных отображаются в трех измерениях. Вы можете видеть сетку поверхности, которая помогает нам найти оптимальную комбинацию между двумя типами точек данных. Типичная поверхностная диаграмма состоит из трех переменных точек данных, назовем их «X, Y и Z». Из этих трех доступных переменных мы можем разделить их на два набора, то есть независимые и зависимые переменные. Две переменные будут независимыми переменными, а одна — зависимой переменной.

Таким образом, диаграмма поверхности показывает взаимосвязь между точками данных через поверхность сетки.

Примеры создания диаграммы поверхности (графика) в Excel

Вы можете скачать этот шаблон Excel Surface Chart здесь — Шаблон Surface Chart Excel

Пример # 1

Рассмотрите приведенные ниже данные, чтобы создать свою первую диаграмму поверхности в Excel.

Выполните следующие шаги, чтобы создать поверхностную диаграмму в Excel.

Шаг 1. Сначала откройте таблицу Excel.

Шаг 2: Скопируйте приведенную выше таблицу данных на один из рабочих листов. И выберите диапазон данных.

Шаг 3: Теперь на вкладке ленты выберите опцию «ВСТАВИТЬ».

Шаг 4: На вкладке ВСТАВИТЬ вы увидите раздел «Диаграмма». В этом разделе выберите Stock, Surface или Radar Chart в excel. В этой категории диаграмм выберите диаграмму «3D Surface» .

Шаг 5: Как только вы нажмете на «Трехмерную диаграмму поверхности», вы увидите приведенную ниже диаграмму поверхности по умолчанию на своем рабочем листе.

Выберите диаграмму и нажмите сочетание клавиш Ctrl + 1, чтобы открыть ОБЛАСТЬ ФОРМАТИРОВАНИЯ ДИАГРАММЫ справа от электронной таблицы Excel (Excel 2013 и далее).

Шаг 7: В этой ОБЛАСТИ ФОРМАТИЧЕСКОЙ ДИАГРАММЫ вы можете изменить цвет сетки, настройку горизонтальной и вертикальной оси и многое другое.

Чтобы изменить цвет сетки, вы можете сделать это на самой вкладке ДИЗАЙН. Выбрав диаграмму, вы увидите две вкладки «Инструменты диаграммы», то есть «Дизайн и формат».

Выберите вкладку «Дизайн», перейдите в «Изменить цвет» и выберите цвет по своему усмотрению.

Как видите, я выбрал четвертый, и я могу видеть предварительный просмотр моей диаграммы справа. Как и в этом месте, курсор на каждом из разных наборов цветов для предварительного просмотра диаграммы перед окончательной комбинацией цветов.

Шаг 8: Следующее, что нам нужно сделать, это «переключить строку / столбец» . Поскольку во время вставки диаграммы Excel предполагает, что горизонтальные объекты — это ряды данных, а вертикальные — категории.

Поэтому нам нужно изменить строку / столбец на вкладке «Дизайн».

Как только вы выберете эту опцию, наша диаграмма автоматически изменится и теперь выглядит так, как показано ниже.

Пример # 2

А теперь посмотрим еще на один пример Surface Chart. Для этого рассмотрим набор данных ниже.

Скопируйте данные на рабочий лист.

Выбрав данные, выберите опцию вставки диаграммы.

Теперь мы можем видеть диаграмму ниже.

Теперь на вкладке дизайна выберите «Quick Layout» и выберите «Layout 5».

Теперь наша диаграмма выглядит так.

Таким образом, мы можем создать сетчатую диаграмму поверхности в Excel.

То, что нужно запомнить

Поверхностная диаграмма не является наиболее часто используемой диаграммой в практическом мире, поэтому вы не найдете так много ресурсов для работы с ней.
Всегда выбирайте другую цветовую комбинацию для создания визуальных эффектов.

Источник