Пример имитационной модели
NOTE:
To change the image on this slide, select the picture and delete it. Then click the Pictures icon in the placeholder to insert your own image.
§26
Информатика, 8 класс
Учитель информатики
Дворецкая Ю.Ю,
1
Основные темы параграфа
- Что такое имитационная модель
- Пример имитационного моделирования в электронной таблице
ОПРЕДЕЛЕНИЕ
ИМИТАЦИОННАЯ МОДЕЛЬ – это логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.
Имитационная модель имеет определенную минимальную опорную структуру, которую пользователь может дополнить и расширить с учетом специфики решаемых задач и базовых методов обработки.
ОПРЕДЕЛЕНИЕ
- ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе.
Отличие от математического моделирования
- имитационное моделирование исследует математические модели в виде алгоритмов , воспроизводящих функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций .
- в имитационных моделях для получения необходимой информации или результатов необходимо осуществлять их «прогон» в отличие от аналитических моделей, которые необходимо «решать».
- имитационные модели неспособны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.
Имитационные модели
В общем виде структуру имитационной модели в математической форме можно представляет следующим образом: ,
где E – результат действия системы;
x i – переменные и параметры, которыми мы можем управлять;
y i – переменные и параметры, которыми мы управлять не можем;
f – функциональная зависимость между x i и y i , которая определяет величину E .
Имитационные модели
Имитационная модель представляет собой комбинацию таких составляющих, как:
- компоненты;
- переменные;
- параметры;
- функциональные зависимости;
- ограничения;
- целевые функции.
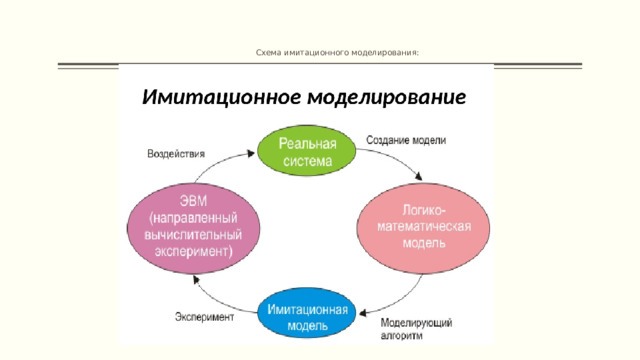
Схема имитационного моделирования:
НЕДОСТАТКИ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ:
- разработка имитационных моделей требует больших затрат, времени и сил;
- любая имитационная модель сложной системы менее объективна, чем аналитическая модель;
- результаты имитационного моделирования носят как правило частный характер, поэтому для предоставления обоснованных выводов необходимо провести серии модельных экспериментов.
Пример имитационного моделирования на компьютере
Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.
Модель – эволюция популяций
- Пусть на определенном пространстве случайным образом расселяются живые организмы.
- В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает.
- Эти процессы протекают в соответствии с законами эволюции (формальными правилами).
Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.
Имитационные модели
Законы эволюции:
- В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет.
- В живой ячейке жизнь может либо сохраниться, либо исчезнуть
- На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа.
- Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения).
- Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.
Модельное описание процесса эволюции популяции
- Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других.
- У ячейки номер 2 соседи: 1, 3 и 4.
- Но ячейка 1 всегда пустая.
- У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5).
- Аналогичная ситуация у крайних правых ячеек.
Кодирование
- Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц.
- Ноль обозначает пустую ячейку , единица — живую .
- Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:
00001001000100000000
Имитационные модели
Введем обозначения:
n — номер ячейки,
R (n) — значение двоичного числа, соответствующего этой ячейке в текущем поколении.
В рассматриваемом примере R (5) = R (8) = R (12) = 1 .
Все остальные значения ячеек равны нулю.
Значения кода в n -й ячейке для следующего поколения будем обозначать S ( n ) .
Проанализировав правила эволюции, приходим к следующей формуле:
Если 1 R ( n — 2) + R ( n — 1) + R ( n ) + R ( n + 1) + R ( n + 2) 3, то S ( n ) = 1, иначе S ( n ) = 0.
Имитационные модели
Эта формула работает для значений n от 3 до 18 .
Всегда: S (1) = S (20) = 0 .
Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе: для этого к отрезку добавим по одной фиктивной ячейке справа и слева.
Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для n от 2 до 19.
Итак, модель построена и формализована.
Имитационные модели
Для реализации применим табличный процессо р.
Моделью жизненного пространства будет строка электронной таблицы.
Первая строка — первое поколение,
вторая строка — второе поколение и т. д.
Тогда номера ячеек будут идентифицироваться именами столбцов таблицы.
Ячейка номер 0 — столбец А,
ячейка 1 — столбец В и т. д.,
ячейка 21 — столбец F.

- В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1 . Незаполненные ячейки по умолчанию приравниваются к нулю.
- Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:
ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 =1; А1 + В1 + С1 + D1 + Е1
- Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.
- Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.
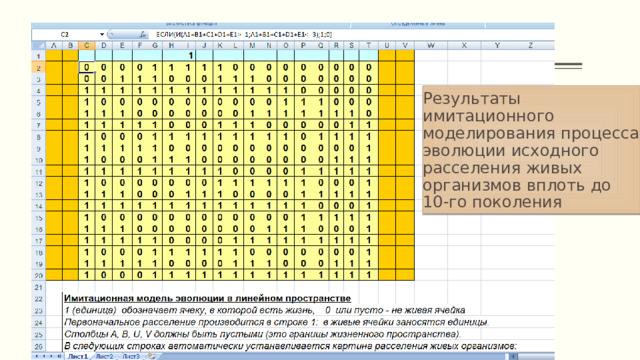
Результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения
Модель Дж. Конуэя «Жизнь»
В этой модели эволюция популяции живых организмов происходит в двумерном пространстве.
Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток.
Но теперь правила эволюции такие:
- если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения;
- если же живых соседей меньше двух, то она погибает от одиночества.
- в пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.
Домашнее задание
§26 конспект
Дмитрий Михайлович Беляев
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Моделирование — это изучение какого-либо явления, процесса или системы объектов посредством формирования и исследования их моделей.
Введение
В системах, связанных с экономикой, руководящим работникам необходимо постоянно принимать решения следующих категорий:
- Стратегические решения.
- Тактические решения.
- Оперативные решения.
Если принимаемые решения обладают низким интеллектуальным уровнем, то простота представления реальных ситуаций обычно ведёт к неточностям при выработке прогнозов, а, кроме того, к убыткам и добавочным финансовым потерям. Чтобы избежать возникновения подобных ситуаций и обеспечить устойчивое экономическое положение, существуют разнообразные системы поддержки выработки решений, усовершенствование которых превращается в наиболее актуальную проблему при наличии жёсткой конкуренции.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Существенным условием для таких программ считается возможность имитации вырабатываемых решений, апробации вероятных коррекций в экономической системе, появляющихся в результате влияния разных факторов, то есть нахождение ответа на вопрос типа, «что случится, если…». Это позволит существенно сократить риски от осуществления решений и сэкономить ресурсы, чтобы достичь поставленной цели.
Такие возможности предоставляют имитационные модели, которые обладают следующим набором качеств:
- Возможность регулировать уровень сложности модели.
- Присутствие случайных факторов.
- Возможность описать процесс, развивающийся по времени.
- Обязательное использование электронной вычислительной машины.
Имитационные модели предназначаются для того, чтобы оценить варианты намечаемых коррекций, обладать игровой формой для обучения работников, визуально отобразить работу исследуемого объекта во времени и так далее. Реализовать модели можно при помощи универсальных языков программирования, к примеру,Pascal, Basic, пакетов прикладных программ, таких как,Excel, MathCAD, и так далее. Выбор конкретного метода моделирования определяется сложностью задачи, наличием необходимых ресурсов и так далее.
«Моделирование в Excel» 👇
Однако имитационное моделирование применяется экономистами и другими специалистами только в малом проценте случаев, в которых можно было бы при помощи моделей поиметь важную для выработки решений информацию.Причина этого явления кроется в отсутствии инструкций по проведению имитационного моделирования при помощи общеизвестного и доступного инструментария, а именно, пакетов прикладного программного обеспечения, такого как Excel и MathCAD, которые могут обеспечить простую платформу для моделирования.Поэтому примеры формирования имитационных моделей при помощи, например, приложения Excel, помогают их широкому распространению в кругу работников, не владеющих языками моделирования и методиками, имеющимися в средах моделирования.
Электронные таблицы Excel как инструмент формирования имитационных моделей
Имитационное моделирование при помощи табличного процессора является отдельным направлением, имеющем свои особенности. Применение таких систем позволяет лучше понять происходящие процессы, в сравнении с использованием специализированных программ, обладающих высокой стоимостью и требующих много времени для их освоения, а также не позволяющих увидеть применяемые механизмы. Например, специалисты полагают, что имитация при помощи таблиц Excel позволяет лучше представить работу систем массового обслуживания, чем даже теория очередей, а также помогает в развитии интуиции, предоставляет даже не знающим программирования пользователям опыт формирования разных моделей. Специалисты предлагают следующие этапы обучения моделированию в Excel:
- Базовые понятия.
- Введение в теорию вероятности и статистику.
- Процесс имитационного моделирования в ручном режиме.
- Имитационное моделирование при помощи электронных таблиц.
- Генерирование случайных чисел.
- Осуществление анализа исходных данных.
- Осуществление анализа итогов моделирования.
При формировании моделей в Excelприменяются следующие главные подходы к осуществлению имитации:
- Подход, который ориентирован на события.
- Подход, имеющий ориентацию на процессы.
- Подход, направленный на сканирование активностей.
Первый подход служит для описания изменений в системе, которые происходят при совершении любого случайного события, например, получение заявки, завершение обслуживания. При его формировании при помощи электронных таблиц обычно применяется одна строчка для каждого события.
Если используется подход, ориентированный на процесс, то выполняется моделирование очерёдности событий для каждой заявки, и чтобы его реализовать, применяется одна строчка для каждого требования (используется при моделировании систем массового обслуживания).
Сканирование активностей состоит в описании действий, возникающих в системе за фиксированный временной интервал (день, неделя, месяц, год), и при его осуществлении, как правило, применяется одна строчка для каждого отрезка времени. К примеру, это может быть моделирование системы управления запасами.
Использование программного пакета MSExcelобладает следующими преимуществами:
- В составе пакета Excelесть значительное число встроенных функций из области математики, статистики и других областей, включая возможность генерации случайных значений.
- Excelдаёт возможность сохранять информацию и иметь к ней доступ.
- Программный пакетExcelпозволяет строить графики и диаграммы.
- Программный пакет Excel обладает встроенным языкомVBA (VisualBasicforApplication).
- Программный пакет Excelшироко распространён среди специалистов, то есть имеется на компьютере практически у всех.
- Наличие возможности экспорта информационных данных в иные программные приложения.
Помимо этих достоинств, возможен просмотр любой формулы, занесённой в ячейку таблицы, что увеличивает уровень доверия к итогам моделирования.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Татарникова Виктория Викторовна1, Гусева Елена Николаевна2
1Магнитогорский государственный технический университет им. Г.И.Носова, студент группы ФЭУПОб-12 института экономики и управления
2Магнитогорский государственный технический университет им. Г.И.Носова, кандидат педагогических наук, доцент кафедры бизнес-информатики и информационных технологий
Аннотация
В статье рассматривается применение компьютерного моделирования в решении задач систем массового обслуживания в Microsoft Excel на примере задачи о сортировочной станции. Акцентируется внимание на удобстве расчетов, рассмотрении различных вариантов решения поставленной задачи и анализируется эффективность работы СМО.
Tatarnikova Victoria Victorovna1, Guseva Elena Nikolaevna2
1Nosov Magnitogorsk State Technical University, student group FEUPOb-12 Institute of Economics and Management
2Nosov Magnitogorsk State Technical University, Associate Professor, Department of Business Informatics and Information Technologies
Abstract
The article deals with the use of computer modeling in solving the problems of queuing systems in Microsoft Excel as an example the problem of the yard. The attention is focused on the convenience of calculation, considering various options for solving the problem and analyze the effectiveness of the CFR.
Библиографическая ссылка на статью:
Татарникова В.В., Гусева Е.Н. Использование компьютерного моделирования в решении задач о системах массового обслуживания // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2016/06/69373 (дата обращения: 07.04.2023).
Одно из важных направлений прикладной математики связано с исследованием систем мaссового обслуживания (СМО). СМО – это системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. Примерами СМО являются магазины, телефонные станции, кассы, ремонтные мастерские, автозаправочные станции, ЭВМ, обрабатывающая запросы от удаленных терминалов [1,7, 9].
При изучении СМО используются методы имитационного моделирования и статистических испытаний (или метод Монте-Карло). При этом создается компьютерная модель, имитирующая поведение системы, с помощью ее производят большое количество реализаций анализируемого процесса и сохраняют получающиеся значения выходных величин. Получающиеся результаты приобретают статистическую устойчивость и после соответствующей математической обработки могут рассматриваться как характеристики изучаемой системы [3,8,12,13]. Имитационные модели используются при изучении социологических, экономических процессов функционирования сложных технических систем (например, ядерного реактора), а также в процессе обучения.
Каждая из систем массового обслуживания состоит из каналов (или приборов) обслуживания, на которые в случайные моменты времени поступает поток заявок или требований. После приема заявки канал оказывается занят на некоторое время обслуживания , после чего он освобождается и ожидает следующей заявки. На входе СМО может накапливаться несколько заявок, они либо становятся в очередь, либо покидают СМО необслуженными [3,5].
Последовательность событий, происходящих друг за другом в случайные моменты времени, называется потоком событий. Если поток событий задается только моментами времени наступления этих событий, то он называется однородным. Поток неоднородных событий характеризуется:
- совокупностью вызывающих моментов времени ,;
- набором признаков событий, к которым относятся принадлежность заявки к тому или иному источнику, приоритет заявки, возможность обслуживания тем или иным каналом и т.д.
Интенсивность потока рассчитывается как отношение числа событий ко времени наблюдения: . В случае, когда вероятность появления заданного числа событий в течение интервала ∆τ зависит исключительно от продолжительности интервала ∆τ и не зависит от времени τ, прошедшего с начала запуска системы, поток событий называется стационарным [10,13].
Любая СМО состоит из приборов обслуживания , каждый из которых имеет накопитель заявок и канала обслуживания заявок . В накопители заявок может одновременно находится заявок, где –емкость i-ого накопителя. В накопитель поступает поток заявок , а в канал – поток обслуживаний . При изучение сложных систем массового обслуживания рассматривают специальные Q-схемы, образующие многоканальные и многофазные сети массового обслуживания. Связи между элементами таких СМО изображают в виде стрелок, которые показывают направления движения заявок. В некоторых случаях говорят о замкнутых СМО, имеющих обратную связь, по которой выходной поток обслуженных заявок снова поступает на вход того или иного прибора обслуживания. В общем случае процесс функционирования СМО любой сложности можно однозначно задать с помощью Q-схемы, учитывающей:
- множество входящих потоков W;
- множество потоков обслуживания U;
- правила R сопряжения элементов СМО;
- множество собственных параметров H;
- оператор алгоритмов обслуживания заявок A;
- вектором состояния Z, элементов которого характеризуют состояния всех приборов обслуживания и их накопителей.
Для изучения функционирования СМО методом статистических испытаний (методом Монте-Карло) стоится имитационная модель процесса и с помощью генератора случайных чисел производится «розыгрыш» случайных событий (входных сигналов и внешних воздействий) в соответствии с заданными законами распределения. Компьютер моделирует более 1000 реализаций исследуемого процесса, выходные сигналы и подвергаются статистической обработке.
Рассмотрим пример решения задачи о грузовой сортировочной станции в Arena и сравним с получившимися данными в Microsoft Excel.
На грузовой станции имеется два выгрузочных фронта. Интенсивность подхода составов под выгрузку составляет 0,4 состава в сутки. Среднее время разгрузки одного состава – 2 суток. Приходящий поезд отправляется на другую станцию, если в очереди на разгрузку стоят более трёх составов.
Оценить эффективность работы выгрузочных фронтов грузовой станции: вероятность, что выгрузочные фронты свободны, вероятность, что состав останется без разгрузки, относительную пропускную способность, абсолютную пропускную способность, среднее число поездов, ожидающих разгрузки, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе. Как изменятся данные показатели, если интенсивность подхода составов увеличится до 0,5?
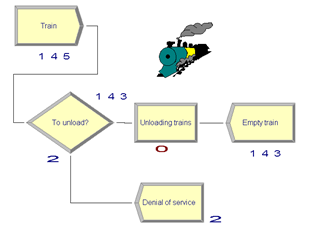
Решение таких задач, не смотря на разработанный математический аппарат, не очень удобно производить вручную. Для наиболее быстрого и эффективного решения, можно использовать различные программные средства: табличный процессор Microsoft Excel и среду имитационного моделирования Arena Rockwell Software. Табличный процессор при решении таких задач может помочь в вычислении приблизительных характеристик исследуемой СМО. Эти значения дают общее представление об эффективности работы системы и конечно не могут учесть массу случайных факторов, влияющих на ее работу. Кроме того, для многих подобных задач не менее важно представить логику работы системы, очереди, увидеть и понять какое количество поступивших составов получают отказ в обслуживании [5,6,8]. Эти вещи позволяет реализовать Arena (рис.1). Для решения задачи был выбран период моделирования равный 12 месяцам, что позволило получить представление о длительном периоде работы системы и наиболее приближенных к реальности показателях системы.
Рисунок 1. Логика задачи в Arena
По условию задачи n = 2, m = 3, т. е. грузовая станция представляет собой многоканальную систему с ограниченной очередью. Интенсивность потока обслуживаний равна μ =1/2 = 0,5. Интенсивность нагрузки канала (трафик) равна ρ = 0,4 ∙ 2 = 0,8. Теперь рассчитаем характеристики для интенсивности подхода составов, равной 0,4: вероятность того, что выгрузочный фронт свободен; вероятность того, что состав будет отправлен на другую станцию; относительную пропускную способность; абсолютную пропускную способность; среднее число составов, ожидающих разгрузки; среднее время ожидания разгрузки; среднее число занятых фронтов (среднее число заявок под обслуживанием); среднее число составов, находящихся у разгрузочного фронта; среднее время пребывания состава у разгрузочного фронта.
Произведем вычисления для интенсивности подхода составов, равной 0,4. Решение проиллюстрировано в таблице 1. Аналогично произведем вычисления для характеристик системы массового обслуживания с интенсивностью прихода составов равной 0,5.
Таблица 1 – Расчет характеристик для грузовой станции в Microsoft Excel
|
Характеристики многоканальной СМО с отказами |
||||
| Число каналов обслуживания | n |
2 |
2 |
|
| Максимальное число составов в очереди | m |
3 |
3 |
|
| Интенсивность прихода составов | λ |
0,4 |
0,5 |
|
| Время разгрузки 1 состава | tоб |
2 |
2 |
|
| Интенсивность разгрузки составов | μ |
0,5 |
0,5 |
|
| Приведенная интенсивность | ρ |
0,8 |
1 |
|
| Вероятность, того что канал свободен | P0 |
0,47 |
0,39 |
|
| Вероятность отказа в разгрузке | Pотк |
0,010 |
0,02 |
|
| Относительная пропускная способность | Q |
0,99 |
0,98 |
|
| Абсолютная пропускная способность | A |
0,40 |
0,49 |
|
| Длина очереди | Nоч |
0,14 |
0,29 |
|
| Среднее время в очереди | Tоч |
0,06 |
0,15 |
|
| Среднее число занятых каналов | k |
0,79 |
0,98 |
|
| Среднее время нахождения состава в системе | Nсист |
0,93 |
1,27 |
|
| Среднее число составов в системе | Tсист |
2,33 |
2,54 |
Сравнивая получившиеся результаты, можно сказать, что вероятность того, что состав будет отправлен на другую станцию при интенсивности подхода составов равной 0,5 больше, чем при интенсивности, равной 0,4.
Исходя из данных, приведённых данных в таблице 1 и получившихся результатах имитационного моделирования (в отчетах среднее время ожидания разгрузки — 9,5ч, а вероятность отказа 1,3%) можно сделать вывод о том, что среднее время пребывания состава в ожидании разгрузки на другой станции невелико, что говорит о нормальной работе разгрузочного узла. При увеличении интенсивности похода составов выгрузочный узел продолжает работать эффективно.
Используя данные программы, можно с легкостью обрабатывать большой массив данных, производить расчеты, наблюдать за многоканальной системой обслуживания в динамике, анализируя все ее слабые и сильные стороны. Помимо этого анимация процессов в программе Arena и обширные статистические данные, собранные в отчетах, помогут опытному пользователю быстро разобраться с причинами возникающих проблем в системе.
Библиографический список
- Акопов А.С. Имитационное моделирование: учебник и практикум. – Москва: Юрайт, 2015.–390 с.
- Баженов Р.И., Лопатин Д.К. Об имитационном моделировании экономических процессов средствами специализированной программной среды // Молодой ученый. 2014. № 4. С. 88-92.
- Гусева Е. Н. Математика и информатика: [электронный ресурс] учеб. пособие/ Е. Н. Гусева, И.Ю. Ефимова, И.Н. Мовчан, Л.А. Савельева. – 3-е изд., стереотип. –М.: Флинта, 2015– 400 с. –Режим доступа: lf5.com/Knigi/Nauka-Obrazovanie/Matematika/Matematika-i-informatika-148-103807
- Гусева Е.Н. Математические основы информатики/ Е.Н. Гусева, И.И. Боброва, И.Ю. Ефимова, И.Н. Мовчан, С.А. Повитухин, Л.А. Савельева. – Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016.- 234 с.
- Гусева Е. Н. Теория вероятностей и математическая статистика: учеб. пособие – 5-е изд., доп. и перераб.: [электронный ресурс]/ Е. Н. Гусева. –М.: Флинта, 2011.– 220 с. – Режим доступа: http://www.knigafund.ru/books/116083/read
- Гусева Е.Н. Имитационное моделирование экономических процессов в среде «Arena»: учеб. пособие: [электронный ресурс]. М.: Флинта, 2011. – 132 с. – Режим доступа: http://www.knigafund.ru/books/114189
- Гусева Е.Н. Имитационное моделирование социально-экономических процессов. – Магнитогорск: изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2015. – 25с.
- Гусева Е.Н. Моделирование макроэкономических процессов: учеб. пособ.: [электронный ресурс]/ Е. Н. Гусева. – М.: Флинта, 2014.–214с.– Режим доступа: http://www.ozon.ru/context/detail/id/28975354/
- Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2007. – 140с.
- Кийкова Е.В. Управление системой закупок товаров, работ и услуг для нужд бюджетного образовательного учреждения на основе имитационного моделирования // Современные проблемы науки и образования. –2013. № 1. С. 302.
- Кийкова Е.В., Лаврушина Е.Г. Значение изучения имитационного моделирования студентами вуза различных уровней подготовки // Современные проблемы науки и образования. –2014. № 3. С. 388.
- Лебединский Б.П., Желекова Е.Э. Имитационное моделирование систем массового обслуживания в программном продукте GPSS // Вестник Курганского государственного университета. Серия: Технические науки. – 2012. № 24. С. 66-69.
- Самаров К. Л. Элементы теории массового обслуживания Учебное пособие для студентов [Электронный ресурс]. – URL: http://www.resolventa.ru/data/metodstud/servtheory.pdf (дата обращения: 19.06.2016).
Количество просмотров публикации: Please wait
Все статьи автора «Татарникова Виктория Викторовна»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Томский государственный университет систем управления и
радиоэлектроники
(ТУСУР)
Кафедра автоматизированных систем (АСУ)
А.А. Мицель Е.Б. Грибанова
ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ В EXCEL
ТОМСК – 2016
Мицель А.А., Грибанова Е.Б.,
Имитационное моделирование экономических процессов в Excel Томск: Изд-во ТУСУР, 2016. –115 с.
В пособии рассматривается технология имитационного моделирования в среде Excel. Приводятся существующие работы по моделированию экономических объектов с помощью данного пакета (одноканальной системы массового обслуживания с неограниченным ограниченным ожиданием; системы управления запасами с пороговой и периодическими стратегиями подачи заявок, с учетом и без учета отложенного спроса и т.д.), а также имитационные модели и шаблоны, разработанные авторами для имитации финансовых механизмов (аукционов, конкурсов), управления производственными запасами, массового обслуживания (с групповым поступлением и обслуживанием заявок), а также различных игр и др. Рассмотрена реализация более 30 моделей. Пособие включает следующие разделы: имитационное моделирование систем массового обслуживания, имитационное моделирование инвестиционных рисков, имитационное моделирование систем управления запасами, имитационное моделирование аукционов и конкурсных механизмов, имитационное моделирование игр. К каждому разделу дана краткая теория, включающая основные понятия и описание существующих в данной области решений, а также задачи для самостоятельного выполнения, связанные с моделированием какого-либо экономического объекта. В приложениях содержится справочная информация, которая может быть полезна при проведении моделирования в среде Excel: основные приемы работы с данным пакетом, способы генерирования с его помощью случайных чисел и событий, а также описание основных функций, этапов построение диаграмм, проведения экспериментов «что будет, если…».
Учебное пособие предназначено для студентов направления 09.03.03 – прикладная информатика (профиль – прикладная информатика в экономике). Кроме того, это пособие может быть использовано студентами других смежных экономических специальностей.
|
СОДЕРЖАНИЕ |
||
|
Введение………………………………………………………………………………………………………… |
4 |
|
|
1. Электронные таблицы Excel как средство реализации имитационных моделей.7 |
||
|
2. Имитационное моделирование систем массового обслуживания………………….. |
10 |
|
|
2.1 |
Одноканальная система массового обслуживания………………………………….. |
12 |
|
2.2 |
Двухканальная система массового обслуживания…………………………………… |
17 |
|
2.3 |
Система массового обслуживания с ограниченным по времени ожиданием19 |
|
|
2.4 |
Система массового обслуживания с очередью……………………………………….. |
23 |
|
2.5 |
Система с групповым обслуживанием заявок …………………………………………. |
26 |
|
2.6 |
Система массового обслуживания с групповым поступлением заявок ……… |
28 |
|
3. Имитационное моделирование инвестиционных рисков ………………………………. |
31 |
|
|
3.1 |
Общая модель оценки рисков………………………………………………………………… |
33 |
|
3.2 |
Модель инвестиционного проекта по производству продукта…………………… |
36 |
|
4. Имитационное моделирование систем управления запасами ………………………. |
40 |
|
|
4.1 |
Однопериодная модель со случайным спросом ……………………………………… |
43 |
|
4.2 |
Производственная модель управления запасами……………………………………. |
46 |
|
4.3 |
Модель с периодической стратегией подачи заявок………………………………… |
50 |
|
4.4 |
Модель с пороговой стратегией подачи заявок……………………………………….. |
52 |
|
5. Имитационное моделирование торгов и конкурсных механизмов …………………. |
56 |
|
|
5.1 |
Обратный аукцион ………………………………………………………………………………… |
59 |
|
5.2 |
Голландский аукцион…………………………………………………………………………….. |
61 |
|
5.3 |
Английский аукцион ………………………………………………………………………………. |
63 |
|
5.4 |
Аукционы Vickery и FPSB ………………………………………………………………………. |
66 |
|
5.5 |
Японский аукцион………………………………………………………………………………….. |
67 |
|
5.6 |
Аукцион с резервированной ценой…………………………………………………………. |
69 |
|
5.7 |
Аукцион с фиксированной ценой ……………………………………………………………. |
71 |
|
5.8 |
Китайский аукцион ………………………………………………………………………………… |
73 |
|
5.9 |
Конкурсное распределение средств……………………………………………………….. |
74 |
|
6. Имитационное моделирование игр……………………………………………………………… |
77 |
|
|
6.1 |
Игра «Найдите слово»…………………………………………………………………………… |
77 |
|
6.2 |
Игра «Эксперты»…………………………………………………………………………………… |
80 |
|
6.3 |
Игра «Выиграй миллион» ………………………………………………………………………. |
82 |
|
6.4 |
Игра «Акция»………………………………………………………………………………………… |
85 |
|
ЛИТЕРАТУРА………………………………………………………………………………………………… |
88 |
|
|
Приложение 1. Основные приемы работы с пакетом Excel ………………………………. |
90 |
|
|
Приложение 2. Моделирование случайных чисел и событий в Excel ………………… |
93 |
|
|
Приложение 3. Основные используемые функции Excel ………………………………….. |
99 |
|
|
Приложение 4. Построение диаграмм в Excel………………………………………………… |
102 |
|
|
Приложение 5. Проведение экспериментов «что будет, если…» в Excel…………. |
113 |
Введение
В экономических системах руководители сталкиваются с необходимостью принятия различных решений: стратегических, тактических, оперативных. При этом низкий интеллектуальный уровень принимаемых решений, упрощения реальной ситуации может привести к погрешностям при составлении прогноза, а также убыткам и дополнительным затратам. Во избежание данных ситуаций для обеспечения устойчивого экономического положения создаются различные системы поддержки принятия решений, совершенствование которых становится все более важной и актуальной задачей в условиях жесткой конкурентной борьбы.
Немаловажным для подобных программ является возможность имитации принимаемых решений, проверки возможных изменений в экономической системе, возникающих в результате действия различных факторов, т. е. предоставление ответа на вопрос «что будет, если…». Это позволяет значительно уменьшить риск от реализации решений, экономить средства для достижения той или иной цели.
Данные возможности могут быть реализованы с помощью имитационных моделей, обладающих качествами из следующего набора: «сложность модели», наличие в ней случайных факторов, описание процесса, развивающего по времени, невозможность получения результатов без ЭВМ. Имитационные модели могут быть предназначены для оценки вариантов предполагаемых изменений, иметь форму игры для обучения сотрудников, визуально представлять функционирование рассматриваемого объекта во времени и т.д. Их реализация может быть выполнена с помощью универсальных языков программирования (Pascal, Basic), пакетов прикладных программ (Excel, MathCAD), языков моделирования (SIMULA, GPSS), сред имитационного моделирования (Anylogic, Arena). Выбор того или иного средства зависит от сложности задачи, денежных, временных, ресурсов разработчика и т.д.
Тем не менее, имитационное моделирование используется экономистами, менеджерами и др. специалистами лишь в небольшом проценте случаев, где они могли бы с помощью имитации получить полезную информацию для принятия решений. Некоторые авторы причину этого видят в отсутствии (либо недостаточной распространенности) описания проведения имитации с помощью известных и доступных специалистам инструментов: пакетов прикладных программ (особенно Excel и MathCAD), обеспечивающих легко-используемую платформу, которая уже имеется на столах аналитиков, менеджеров, инженеров.
Поэтому описание разработки имитационных моделей экономических систем с помощью данного средства может способствовать их большему распространению среди специалистов, незнакомых с языками моделирования и подходами, заложенными в средах моделирования, но которые могли бы использовать рассматриваемый метод при решении простых прикладных задач.
Другая причина заключается в том, что людям, получающим экономическое образование (и после устройства на работу принимающим различные решения в области экономики и т.д.), и не так хорошо владеющих программированием понять метод имитационного моделирования сложнее, чем студентам инженерных специальностей. Поэтому на практике ими чаще используются статические модели.
Внашей стране большинство работ посвящено имитационному моделированию с помощью различных сред и языков моделирования: GPSS, Anylogic и т.д. Имитационное моделирование в Excel рассматривается в виде отдельных примеров в изданиях по моделированию менеджмента: Горшков и др.
[1]описывают модель управления запасами с пороговой и периодической стратегией подачи заявок с учетом и без учета отложенного спроса при дефиците, Лукасевич [2] рассматривал технологию моделирования инвестиционных рисков, связанных с производством продукта. Среди зарубежных сторонников данного направления можно назвать Seila, Grossman, Ingolfsson [3-5], которые основное внимание в своих работах уделяют системам массового обслуживания (на сайтах [6-7] расположены файлы с программами моделирования систем массового обслуживания с неограниченным, ограниченным по времени и длине очереди ожиданием).
Цель представленного пособия заключается в выработки практических навыков имитации с помощью пакета Excel и решения с ее помощью различных экономических задач.
Впособии рассмотрены экономических задачи, встречающиеся в реальной жизни: управление материальными запасами на складе, определение характеристик систем массового обслуживания, учет неопределенности при планировании денежных средств, оценка риска инвестиционных проектов, прогнозирование результатов аукционов по продаже товаров и т.д. Данное пособие является обобщением существующих работ в этой области и содержит некоторые известные задачи, используемые для обучения и в производстве (названных выше авторов), а также разработки авторов, включающие
имитационные модели (и шаблоны): аукционов (Английского, Голландского, Китайского, Японского и т.д.) и конкурсных механизмов, массового обслуживания (с групповым поступлением и обслуживанием заявок), управления производственными запасами (с периодическим производством, отложенным спросом и т.д.), различных игр («Найдите слово», «Стань миллионером» и др.). Рассмотрена их реализация с подробными пояснениями и иллюстрациями. К каждой модели даны задачи для самостоятельного выполнения. Таким образом, пособие включает следующие разделы: имитационное моделирование систем массового обслуживания, имитационное моделирование инвестиционных рисков, имитационное моделирование систем управления запасами, имитационное моделирование аукционов и конкурсных механизмов, имитационное моделирование игр.
Впособии рассмотрены модели различных типов: динамические имитационные модели и Монте-Карло. Первый тип моделей описывает динамику системы и поведение ее взаимодействующих элементов [8]. Эти модели управляются изменениями, происходящими в системе по прошествии некоторого времени (например, будет рассмотрено моделирование системы массового обслуживания). Модели Монте-Карло независимы от времени либо используют подход сканирования активностей (см. главу 1). Они вызывают такие операции, как многократное извлечение выборки случайных чисел из вероятностных распределений для оценки характеристик выходов модели и рисков (к таким моделям относятся, например, модели рисков, управления запасами).
Вприложениях содержится справочная информация, включающая общие сведения о среде Excel, описание способов проведения экспериментов «что будет, если…», а также рассмотрены используемые при моделировании функций
иприемы генерирование случайных чисел и событий в данном пакете. Кроме того, в приложениях приведены этапы построения диаграмм, в том числе Диаграмм заявок и устройств обслуживания, наглядно показывающих функционирование систем массового обслуживания во времени.
1. Электронные таблицы Excel как средство реализации имитационных моделей
Имитация с помощью табличных процессоров (spreadsheet simulation) представляет собой отдельное направление со своими особенностями. Его сторонники утверждают, что использование данных систем улучшает понимание происходящих процессов гораздо лучше, чем применение специализированного программного обеспечения, имеющего высокую стоимость и требующего время для изучения, а также скрывающего используемые механизмы (хотя такие среды довольно широко используются, особенно GPSS, поскольку предоставляют больше возможностей и позволяют моделировать сложные системы). Так, Grossman в своей публикации «Spreadsheet Modeling and Simulation Improves Understanding of Queues» утверждал, что имитация с помощью таблиц Excel гораздо лучше дает представление о системах массового обслуживания, чем теория очередей, и также развивает интуицию, дает даже незнакомым с программированием специалистам опыт реализации различных моделей. Однако эти подходы (реализация с помощью Excel и сред моделирования) не являются взаимоисключающими, а скорее дополняют друг друга. Так, David Goldsman [9] предлагал следующие этапы обучения, каждый из которых, по его мнению, должен сопровождаться интересными примерами из реальной жизни:
1.основные понятия;
2.введение в вероятность и статистику;
3.ручная имитация;
4.имитация с помощью электронной таблицы;
5.генерация случайных чисел;
6.анализ входной информации;
7.анализ результатов моделирования;
8.имитация с использованием языка (пакета) моделирования.
Им также было отмечено, что в случае, когда курс рассчитан на небольшое число часов, лучше всего ознакомить студентов с основами моделирования и ручной имитацией, которая может быть выполнена с помощью Excel, чем предоставить ему симулятор — «черный ящик» со сложными механизмами имитации.
При реализации моделей в Excel используют три основных подхода к проведению имитации: ориентированный на события, ориентированный процессы, сканирования активностей (рис.1). Первый подход описывает
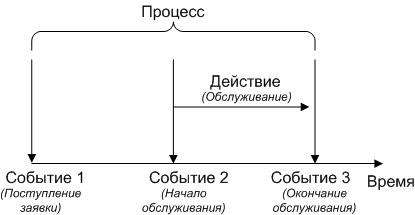
изменения в системе, происходящие в момент совершения каждого случайного события (прибытие заявки, завершение обслуживания), и при его реализации с помощью электронных таблиц, как правило, используется одна строка для каждого события. При использовании процессно-ориентированного подхода происходит моделирование последовательности событий для каждой заявки, и для его реализации обычно используется одна строка для каждого требования (применяется при моделировании систем массового обслуживания). Подход сканирования активностей описывает действия, возникающие в системе в течение фиксированного интервала времени (например, в день, неделю, месяц, год), и при его реализации обычно используется одна строка для каждого временного интервала (например, моделирование систем управления запасами).
Рис. – Связь событий, действий и процесса
Рассмотрим плюсы и минусы использования пакета Excel. В качестве преимуществ можно отметить следующие аргументы:
1.Excel имеет большое количество математических, финансовых, статистических и других видов встроенных функций, в том числе для генерирования случайных величин;
2.программа позволяет хранить данные и осуществлять доступ к ним;
3.пакет обеспечивает построение графиков и диаграмм;
4.имеется встроенный язык VBA;
5.данное программное обеспечение является распространенными и есть практически у каждого специалиста;
6.возможен экспорт в другие программные продукты.
Кроме того, возможность просмотра всех формул, занесенных в ячейки таблицы, повышает доверие к результатам моделирования, а с реализованной моделью пользователь может экспериментировать и оценивать результаты без
привлечения специалистов по имитационному моделированию. По мнению автора [3] экономика – это главная область, где можно встретить такие задачи, которые могут быть эффективно решены с помощью имитационного моделирования и пакета Excel.
Тем не менее, ограничения использования данной программы для имитационного моделирования имеются, и среди них можно назвать:
1.С помощью электронных таблиц можно реализовывать лишь данные с простой структурой. Excel включает группы страниц, состоящих из строк и столбцов. Каждая ячейка может содержать информацию или формулу. Однако в некоторых имитационных моделях имеется более сложная структура данных, например, деревья или списки.
2.Трудно реализовать сложные алгоритмы. Электронные таблицы не имеют удобных средств для выполнения циклов «While» и «Do». (Язык VBA может быть использован для реализации более сложной логики, но он редко применяется пользователями электронных таблиц).
3.Электронные таблицы работают медленнее, чем многие другие инструменты.
4.Объем хранимых данных в таблице ограничен максимальным количеством столбцов.
Существуют различные пакеты: @RISK, Crystal Ball (коммерческие), PopTools (бесплатный, расположен на сайте <http://www.cse.csiro.au/poptools/>) и т.д., обеспечивающие следующие дополнительные возможности Excel: генерация случайных чисел, автоматизация запуска экспериментов, анализ и представление выходной информации и т.д. Генерация случайных чисел может быть также выполнена с помощью надстройки Excel, называемой «Пакет анализа данных».
Наконец, отметим, что в связи с продолжением развития данного программного обеспечения, возможно, будущие версии будут предоставлять больше возможностей и обеспечивать более эффективную имитацию.
2. Имитационное моделирование систем массового обслуживания
В разных областях техники, в организации производства, в экономике и медицине, в социальной сфере, в военном деле и во многих других сферах человеческой деятельности постоянно возникает необходимость решения вероятностных задач, связанных с работой систем массового обслуживания (СМО). Многообразие приложений теории массового обслуживания определяет постоянно растущий интерес к ней, а сложность возникающих задач не позволяет получить исчерпывающие решения на базе аналитических методов. В таких ситуациях часто прибегают к имитационному моделированию. Для имитации подобных систем предназначен язык моделирования GPSS, а также создаются сложные программные системы (ObjectSim, Pigrim [10]), позволяющие реализовать модели систем массового обслуживания с помощью развитой CASEоболочки путем выбора и связи различных строительных блоков. Среди работ, описывающих моделирование СМО с помощью электронных таблиц можно привести следующие — [3-7]. Авторы рассматривают моделирование систем с неограниченным, ограниченным по времени и/или длине очереди ожиданием, которые располагают от 1 до 12 обслуживающими устройствами [7]. При этом различают два основных подхода к моделированию СМО: ориентированный на события и ориентированный на процессы. Событийный подход имеет преимущества в отношении гибкости и эффективности вычислений, однако менее подходит для обучения, поскольку скрывает «жизненный цикл» заявок и является менее понятным на интуитивном уровне. Кроме того, для его реализации требуется управляющая событиями подпрограмма, что приводит к необходимости использования внутреннего языка VBA [11]. Рассмотренные ниже модели будут реализованы с использованием процессно-ориентированного подхода.
Рассмотрим структуру СМО. Каждая СМО состоит из определенного числа обслуживающих единиц, которые называются каналами обслуживания. На вход СМО поступает поток требований (заявок). Таким образом, различают следующие элементы СМО:
1.входной поток заявок;
2.очередь;
3.узел обслуживания;
4.выходной поток.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #