Примеры игр в excel

У нас появилось свободное время.. значит можно поиграть! В этой рубрике мы будем выкладывать простенькие игры в Excel. Да, в Excel тоже можно писать игры, ведь в нем встроен язык программирования VBA. После того как вы скачаете игру (по ссылкам ниже), необходимо будет только включить макросы (как это сделать описано тут). Во многих Ирах в Excel (в макросах) есть много интересных находок. Кто знает, может игра в Excel поможет вам не только скоротать время, но и научиться чему-то новому. Играйте в Excel и пишите игры сами!

Игра в Excel «Морской бой»:

Battleships

Игра в Excel «Змейка»:

snaked

Игра в Excel «Вертолет»:

gmexcopter

Игра в Excel «Квадрат»

Squares

Игра в Excel «Лягушка»

frog_leap

Игра в Excel «Темница»

dungeon

Если у вас есть чем поделиться — присылайте!

Спасибо за внимание.

Время на прочтение
1 мин

Количество просмотров 190K

Бухгалтер из Торонто по имени Кэри Уолкин (Cary Walkin) никогда не занимался разработкой компьютерных игр, но в совершенстве освоил Excel. Этого оказалось достаточно для создания RPG-игры, которая работает на макросах VBA, встроенного языка программирования Excel.

Игру Arena.Xlsm версии 1.0 можно скачать здесь:

v1-0-arena.xlsm (работает в Excel 2007 и Excel 2010 под Windows)

Ключевые особенности:

• Увлекательный сюжет с четырьмя различными концовками, в зависимости от прохождения игры
• Более 2000 врагов с различным уровнем ИИ
• 39 модификаторов вещей означает более 1000 возможных комбинаций и свойств предметов
• 8 схваток с боссами, для победы над каждым из них нужна особая тактика
• 4 предварительно подготовленных игровых пространства
• 31 заклинание, есть много разных стратегий для успеха
• 15 уникальных артефактов
• 36 наград (достижений)
• Вся игра от начала до конца проходит внутри рабочей книги Excel

Официальная wiki-страница для помощи по игре, там же информация о базовых стратегиях.

Так что если увидите бухгалтера в офисе, который целыми сутками сидит в программе Excel, присмотритесь к нему повнимательнее. Кто знает, какие заклинания он сейчас подбирает для босса на шестом уровне.

Теги:

• Arena.Xlsm
• Excel
• RPG
• рабочая книга Excel
• макрос
• VBA

Хабы:

• Ненормальное программирование
• Разработка игр
• Visual Basic for Applications

Программа Microsoft Excel может пригодиться во многих ситуациях. Формулы, функции, справочники и учебные пособия, обработка бизнес-информации — всё это может делать Excel. Однако, что если вы хотите просто расслабиться? Excel может помочь и в этом.

В этой статье мы рассмотрим 8 игр, которые запускаются в Microsoft Excel.

2048

Однопользовательская головоломка популярна на Android и iOS. Данная игра создана на основе предыдущих, таких как Threes и 1024. Всего за одну неделю её создал 19-летний Габриэль Сирулли. Не желая зарабатывать на том, что он не изобретал, Сирулли загрузил бесплатные версии игры 2048 на Android и iOS.

Есть версия игры для Excel, позволяющая играть в таблицах. Предлагается режим просмотра 2D и 3D, звуковые эффекты, отслеживание движений и история, некоторые другие трюки.

Скачать: 2048 для Microsoft Excel (бесплатная)

2048 Stealth Mode в Excel

Если нежелательно, чтобы на работе вас увидели играющим, можно запустить незаметную версию с продвинутым механизмом сокрытия. Со стороны будет казаться, что вы работаете с таблицами.

Scrabble

Продолжая разговор о головоломках, поговорим о Scrabble. Tom_Jobim с Reddit создал игру, которая открывает отдельное окно в Excel, так что она не совсем в таблице. Применяется язык VBA.

Реализация игры на высоком уровне. Вы противостоите искусственному интеллекту с различными уровнями навыка, от 1 до 100. Имеется инструмент анаграмм, встроенный словарь, разные тематические планы, таймеры и многое другое.

Скачать: Scrabble для Microsoft Excel (бесплатная)

Arena.Xlsm

Не хотите головоломки? Arena.Xlsm даст вам возможность противостоять более 2000 потенциальных противников с искусственным интеллектом. Когда они появляются на экране, вы должны сразить их.

Имеется 8 боссов, 12 запрограммированных боевых арен, более 30 заклинаний, 20 уникальных предметов и даже системы достижений.

Arena.Xlsm также доступна на Itch.io, если вы предпочитаете отслеживать игры на определённых платформах.

Скачать: Arena.Xlsm для Microsoft Excel (бесплатная)

Candy Crunch Number Saga

Вы берёте контроль над фондовым рынком, в том числе влияя на рыночную стоимость разработчика этой игры King.com.

Эта сатирическая игра происходит в недалёком будущем, где King.com (KING) провела успешное размещение акций (IPO) и их курс взлетел до небес.

Candy Number Crunch Saga предлагает более 35 новостных событий, которые влияют на стоимость акций. Отображается курс акций в реальном времени. Игра стала результатом четырёх дней работы канадского бухгалтера Кари Уолкина. Он же является автором Arena.Xlsm. Игра также доступна на Itch.io.

Скачать: Candy Crunch Number Saga для Microsoft Excel (бесплатная)

Championship Manager For Microsoft Excel

Одна из наиболее сильно вызывающих привыкание игр есть и на Excel. Это неудивительно, поскольку серия футбольных менеджеров больше других игр похожа на таблицы.

Можно играть в четырёх английских лигах, есть кубок Англии, кубок Лиги, Лига Чемпионов. Для трансферов доступно около 3000 футболистов.

Имеются дисквалификации и травмы, которые можно компенсировать молодёжным составом. Кому-то понравится еженедельная таблица результатов в старом стиле.

Нужно иметь ввиду, что вы не сможете получить лучших футболистов Премьер-лиги из реального мира. Все имена созданы случайным образом, чтобы не нарушать авторские права.

Скачать: Championship Manager для Microsoft Excel (бесплатная)

CellSweeper

CellSweeper представляет собой РПГ с подземельями в жанре Roguelike. Игра основана на Сапёре из старых версий Windows.

Она создана при помощи Excel и содержит шесть классов персонажей, быстрый игровой процесс и возможность поменять уровень сложности. CellSweeper может оказаться более привлекательной, чем кажется, поэтому время пролетит незаметно.

Скачать: CellSweeper для Microsoft Excel (бесплатная)

Tetris

Раз на Excel так много головоломок, невозможно обойтись и без Tetris. Здесь данная игра представлена в довольно простом варианте, но это не делает её менее увлекательной.

Скачать: Tetris для Microsoft Excel (бесплатная)

Yahtzee

Yahtzee представляет собой отличную игру в кости для одного или нескольких человек. Вы пытаетесь сделать покер при помощи набора кубиков, игровой процесс простой и за счёт этого увлекательный.

Играть можно вдвоём или против искусственного интеллекта. Есть инструкции по игре и подсчёту очков.

Скачать: Yahtzee  для Microsoft Excel (бесплатная)

Бонус: Fraqcel

Это не совсем игра, а скорее психоделический опыт. Или хотя бы попытка предложить его.

Fraqcel генерирует разнообразные геометрические фигуры, которые вы можете увеличивать в сотни раз. Есть четыре типа фракталов, возможность экспортировать изображения, глубокий зум и настраиваемые цветовые палитры.

Чем глубже вы погружаетесь, тем более невероятным становится дизайн. Вы можете использовать меню для изменения настроек, смены цветов и т.д.

Скачать: Fraqcel для Microsoft Excel (бесплатная)

Заключение

Игры для Excel являются довольно нишевым продуктом. Чаще всего их создают изучающие язык VBA люди в качестве практики. Почти все такие игры используют сочетание VBA и вручную созданных макросов. Excel также играет роль во многих Flash-играх. В последних сложнее сделать вид, что вы работаете.

Эти игры демонстрируют разнообразие возможностей Excel. Если вас увидят играющим, вы сможете сказать, что улучшаете ваши навыки работы с Excel.

Создание логических игр на языке VBA в среде Microsoft Excel

Содержание

Введение §1. Жанры компьютерных игр §2. Примеры компьютерных логических игр §3. Создание логических игр на языке VBA 3.1 Игра «Быки и коровы» 3.2 Игра «Угадай число» 3.3 Игра «Пятнашки» Заключение Литература

3 4 9 10 11 15 16 21 22

Введение

Научно-технический прогресс, набравший к концу XX века головокружительную скорость, послужил причиной появления такого чуда современности как компьютер и компьютерные технологии. Вместе с появлением компьютеров появились компьютерные игры, которые сразу же нашли массу поклонников. С совершенствованием компьютеров совершенствовались и игры, привлекая всё больше и больше людей.

Ученые считают, что потребность в игре как таковой, свойственна человеку на протяжении всей его жизни. В процессе игры удовлетворяется неосознаваемая познавательная потребность, вследствие чего человек получает удовольствие. Важное место в ряду компьютерных игр занимают логические игры.

Цель данного исследования – разработать и создать логические игры на языке VBA в среде Microsoft Excel.

Объект исследования – язык VBA в среде Microsoft Excel.

Предмет исследования – программирование логических игр.

Гипотеза исследования: язык VBA является удобной средой для создания логических игр в среде Microsoft Excel.

§1. Жанры компьютерных игр

Игру можно назвать восьмым чудом света, так как в ней заложены огромные воспитательные и образовательные возможности. Игра развивает наблюдательность и способность определять свойства предметов, выявлять их существенные признаки. Таким образом, игры оказывают большое влияние на умственное развитие, совершенствуя мышление, внимание, творческое воображение.

Известный французский ученый Луи де Броль утверждал, что все игры (даже самые простые) имеют много общего с работой ученого. В игре привлекает поставленная задача и трудность, которую можно преодолеть, а затем радость открытия и ощущение преодоленного препятствия.

Как правило, в компьютерных играх от игрока требуется:

• владение средствами управления, быстрота и точность манипуляций;

• быстрая и правильная реакция на происходящие события;

• чувство времени, умение выдерживать заданные временные интервалы;

• способность следить за несколькими объектами одновременно;

• знание географии игрового поля, законов игрового мира;

• знание конкретной предметной области, которая моделируется в игре;

• умение искать закономерности;

• умение предугадывать действия противника;

• знание алгоритма и стратегии выигрыша;

• способность к быстрому и максимально полному перебору основных вариантов;

• память на текущие события;

• использование прошлого опыта, что происходило в предыдущих сеансах игры;

• способность интенсивно работать в течение всего сеанса игры.

Компьютерные игры, как и любые другие можно разделить на несколько жанров, в зависимости от их содержания.

Аркадные

Arcade – это крытая галерея магазинов, где традиционно размещали игровые автоматы, которые назывались аркадными. Если компьютерная игра схожа по концепции с играми для автоматов – она называется «аркадой». Аркадные игры представляют собой различные виды единоборств с оружием или без него. В этих играх все сделано так, чтобы не дать игроку расслабиться ни на секунду. Он должен уметь все делать быстро, точно и расчетливо. «Аркада» всегда имеет развитую системой бонусов — это начисление очков, открываемые различные элементы и пр. В последние годы с развитием компьютерной техники появились новые направления аркадных игр: боевые единоборства, варианты компьютерных бильярдов (пинболы), трехмерные боевики (3D Action).

Адвентюрные

Приключенческие игры. Эти игры представляют собой некое путешествие, в которое предлагается вступить играющему, где ему придется решать различные задачи и препятствия. Игры построены на сюжетах сказок, мифов, литературных произведений или известных мультфильмов. Как правило, в каждом эпизоде герою необходимо добыть какой-либо полезный предмет (волшебное средство), который пригодится ему на каком-либо последующем этапе. Целью игры являются различные варианты борьбы против злых сил, выполнение королевского поручения, освобождение принцессы, освобождение от зла какого-либо города).

Ролевые

Специфика ролевых игр заключается в овладении той роли, которую вы выбрали для себя, умелом управлении ролями персонажей вашего отряда, в улучшении личностных качеств персонажей своего отряда.

Стратегические

В стратегических играх от играющего требуется не только оперативная реакция на изменение окружающей обстановки, но и долговременное планирование. В качестве принимаемой роли здесь можно почувствовать себя генералом победоносной армии, руководителем процветающего государства или вождем межзвездной империи. Стратегические игры бывают пошаговые, где игроки поочерёдно делают ходы и каждому игроку отводится неограниченное или ограниченное время на свой ход и в реальном времени, в которых все игроки выполняют свои действия одновременно и ход времени не прерывается.

Игры-симуляторы

Например, симулятор поезда — это жанр компьютерных игр, в котором игроку предоставлена возможность управления железнодорожным составом. Эти игры имеют хорошую физическую модель и неплохую графику. Симулятор свиданий — это жанр компьютерных игр, который тесно связан с романтическими аниме. Сюжет и цель в играх этого жанра — добиться успеха в романтических отношениях с противоположным полом. Игроку предоставляется для выбора большой круг лиц противоположного пола, с которыми можно завязать отношения. Гоночные симуляторы ( Need for Speed). Спортивные имитаторы — от футбола или хоккея до баскетбола и бейсбола.

Логические

Логическая игра — это игра, имеющая четко определенные правила, суть которой состоит в достижении победы путем выполнения последовательности действий, основанных лишь на логических умозаключениях игрока и не зависящая от других его способностей. Логические игры возникли в числе первых. Реализованные в пошаговом режиме, они не требовали особых аппаратных ресурсов и под них использовали даже самые слабые ПК. Ну а то, что, пока компьютер «думал» над очередным ходом, люди успевали выкурить сигарету, считалось нормой. Позже, с появлением графических мониторов, был придуман знаменитый TETRIS, ознаменовав собой возникновение игр-головоломок, или, как их еще называют за рубежом, Puzzle game.

Традиционные

Компьютерные реализации традиционных и настольных игр.

Вывод

В каждом жанре существуют свои разновидности, так что всего разных видов компьютерных игр можно насчитать несколько десятков. Почти ежемесячно появляются новые, а некоторые игры сочетают в себе несколько жанров.

§2. Примеры компьютерных логических игр

Предтечею жанра являлись настольные, графические и механические головоломки — от кроссвордов до кубика Рубика, увидевшего свет в середине 1970-х. Эти головоломки требовали от игрока логики и ловкости в решении, которые также стали играть важную роль в прототипах жанра как Q*bert, Boulder Dash и Marble Madness. Эталоном же жанра стала игра Тетрис, появившаяся в 1985 году и сочетавшая в себе простой и захватывающий игровой процесс.

В начале 1990-х годов такие игры как Lemmings и The Lost Vikings оживили жанр головоломок.

Появление трёхмерной графики поспособствовало развитию головоломок на игровых приставках. Относительно дешёвые для производства игры нашли свою нишу на портативных игровых системах.

В 2000 году игры Pikmin, Meteos, Polarium, LocoRoco и Lumines вновь возродили принципы жанра. В Японии серия игр Brain Training (развивающие логические игры) — один из наиболее крупных успехов индустрии компьютерных игр за 2005 год.

§3. Создание логических игр на языке VBA

VBA (Visual Basic for Applications — Visual Basic для приложений) — немного упрощённая реализация языка программирования Visual Basic, встроенная в линейку продуктов Microsoft Office (включая версии для Mac OS), а также во многие другие программные пакеты, такие как AutoCAD, SolidWorks, CorelDRAW, WordPerfect и ESRI ArcGIS. VBA покрывает и расширяет функциональность ранее использовавшихся специализированных макро-языков, таких как WordBasic.

К достоинствам языка можно отнести сравнительную лёгкость освоения, благодаря которой приложения могут создавать даже пользователи, не программирующие профессионально.

3.1 Игра «Быки и коровы»

Быки и коровы — логическая игра для двоих игроков. Для игры достаточно иметь бумагу, ручку и уметь считать. Также игра может называться «Цифры».

Правила игры

Играют двое. Каждый задумывает и записывает тайное 4-хзначное число с неповторяющимися цифрами. Игрок, который начинает игру по жребию, делает попытку отгадать число. Попытка — это 4-хзначное число с неповторяющимися цифрами, сообщаемое противнику. Противник сообщает в ответ, сколько цифр угадано без совпадения с их позициями в тайном числе и сколько угадано вплоть до позиции в тайном числе. Например:

Задумано тайное число «3219».

Попытка: «2310».

Результат две «коровы» (две цифры: 2 и 3 — угаданы на неверных позициях) и один «бык» (одна цифра 1 угадана вплоть до позиции).

Игроки делают попытки угадать по очереди. Побеждает тот, кто угадает первым.

Вариации игры

В упрощенном английском варианте игры Mastermind (приблизительный перевод гениальный отгадчик) задумываются цифры от 1 до 6, причём цифры могут повторяться.

В усложнённом варианте может использоваться 5-, 6- и более- значное число. В настольном варианте игры вместо чисел загадывается один из шести цветов или шести предметов.

Существует вариант игры со словами. То есть игрок загадывает слово, обычно из 5 букв (в именительном падеже единственном числе по правилам игры балда) и задача противника угадать его используя в качестве попыток такие же корректные слова из словаря русского языка. Известное слово из 4 букв для «подлавливания» новичков — «эльф»; в нём три буквы из четырёх крайне редкие, и неопытный игрок может сделать много ходов, прежде чем добьётся хотя бы «коровы».

Алгоритм

В общем случае количество вариантов для k-значного числа в N-ричной системе счисления без повторений, будет равно числу размещений

В случае варианта с повторениями количество вариантов будет равно N^k.

Большинство известных алгоритмов суть вариации алгоритма полного перебора с определённой эвристикой. В связи с тем что количество вариантов не столь велико и схема прямого перебора элементарно реализуется компьютер играет в «быки и коровы» намного сильнее человека. Чем больше знаков в числе тем больше разница в силе игры человека и компьютера.

Как показал Дональд Кнут для игры Mastermind (64 вариантов) при предложенной им стратегии нужно не более 5 попыток чтобы отгадать любую комбинацию и в среднем 4.34 попыток для отгадывания.

Существует множество вариантов компьютерной реализации. В настоящее время существует большое количество программ играющих в различные вариации в том числе и для мобильных телефонов и мобильных компьютеров.

Создадим игру Быки-Коровы на языке VBA в среде Microsoft Excel

Создадим в Microsoft Excel кнопку «Новая игра», запишем для неё следующий командный код

Option Explicit

Dim comp(1 To 4), n, com As Integer

Dim a, b, c, d As Byte

Dim ot(1 To 4), otv, bik, kor, i, j As Integer

Private Sub CommandButton1_Click()

TextBox1.Text = «»

Cells(11, 5) = «»

Randomize

Do

com = 1000 + Rnd * 8999

comp(1) = com 1000

comp(2) = (com 100) Mod 10

comp(3) = (com 10) Mod 10

comp(4) = com Mod 10

Loop Until comp(1) comp(2) And comp(1) comp(3) And comp(1) comp(4) And comp(2) comp(3) And comp(2) comp(4) And comp(3) comp(4)

n = 0

End Sub

Запись Option Explicit предусматривает, что все использованные переменные величины должны быть объявлены (описаны) перед их использованием.

Функция STR$ используется для преобразования числового значения в строковую величину.

Символ означает целочисленное деление, т.е. остаток при делении одного целого числа на другое отбрасывается. Например, 70 20 = 3.

Mod дает остаток от деления одного целого числа на другое,

Для текстового окна выберите Key Down, чтобы при нажатии клавиши Enter выполнялся программный код:

Private Sub TextBox1_KeyDown(ByVal KeyCode As MSForms.ReturnInteger, ByVal Shift As Integer)

If KeyCode = vbKeyReturn Then

n = n + 1

otv = Val(TextBox1.Text)

If otv = com Then

MsgBox («Правильно! Число попыток = » & Str$(n))

Else

If otv = 0 Then

MsgBox («Вы сдались!»)

Else

ot(1) = otv 1000

ot(2) = (otv 100) Mod 10

ot(3) = (otv 10) Mod 10

ot(4) = otv Mod 10

For i = 1 To 4

If ot(i) = comp(i) Then

bik = bik + 1

End If

Next i

For i = 1 To 4

For j = 1 To 4

If ot(i) = comp(j) And i j Then

kor = kor + 1

End If

Next j

Next i

MsgBox («Число быков = » & Str$(bik) & » Число коров = » & Str$(kor))

End If

End If

kor = 0

bik = 0

TextBox1.Text = «»

Cells(11, 5) = n

End If

End Sub

После этого в ячейке D9 напишем текст «Введите число», а в ячейке D13 «Количество попыток» и оформим остальную часть по своему желанию, например, выбрав единый цвет заливки оставшихся ячеек и скрыв границы.

В конце концов мы должны прийти к такому результату:

Чтобы запустить игру, необходимо нажать на кнопку «Новая игра».

3.2 Игра «Угадай число»

Оформим область игры следующим образом:

Для кнопки Старт необходимо написать следующий программный код:

Dim comp As Integer

Dim n As Integer

Dim a As Integer

Private Sub CommandButton1_Click()

Randomize

comp = Fix(Rnd * 100)

n = 0

TextBox1.Text = «»

End Sub

Для текстового окна программный код выглядит так:

Private Sub TextBox1_KeyDown(ByVal KeyCode As MSForms.ReturnInteger, ByVal Shift As Integer)

a = Val(TextBox1.Text)

n = n + 1

If KeyCode = vbKeyReturn Then

If a = comp Then

MsgBox «Угадано за » & n & » раз !»

End If

If a

MsgBox «Больше!»

TextBox1.Text = «»

End If

If a comp Then

MsgBox «Меньше!»

TextBox1.Text = «»

End If

End If

End Sub

Для запуска новой игры необходимо нажать кнопку Старт.

3.3 Игра «Пятнашки»

Пятна́шки — популярная головоломка, придуманная в 1878 году Ноем Чепмэном. Представляет собой набор одинаковых квадратных костяшек с нанесёнными числами, заключённых в квадратную коробку. Длина стороны коробки в четыре раза больше длины стороны костяшек для набора из 15 элементов (и в три раза больше для набора в 8 элементов), соответственно в коробке остаётся незаполненным одно квадратное поле. Цель игры — перемещая костяшки по коробке добиться упорядочивания их по номерам, желательно сделав как можно меньше перемещений.

История создания

С 1891 года до самой смерти Сэмюэл Лойд считал, что изобрёл головоломку именно он. Однако существуют доказательства того, что он был непричастен к созданию «пятнашек». Настоящим изобретателем был Ной Палмер Чепмэн, почтмейстер из Канастоты, который ещё в 1874 году показывал друзьям головоломку, состоящую из шестнадцати пронумерованных квадратиков, которые надо было сложить в ряды по четыре штуки так, чтобы сумма чисел в каждом ряду была равна 34. Затем сын Ноя Чепмэна, Фрэнк Чепмэн привёз доработанные головоломки в Сиракузы (штат Нью-Йорк), а затем в Хартфорд (Коннектикут), где слушатели Американской школы для слабослышащих начали производство головоломки. К 1879 году она уже продавалась не только в Хартфорде, но и в Бостоне. Тогда о «пятнашках» узнал художник по дереву Маттиас Райс. В декабре 1879 года он начал бизнес по производству новой головоломки под названием «Драгоценная головоломка» (англ. Gem Puzzle). В начале 1880 года некий Чарльз Певи, дантист из Вустера, привлёк внимание общественности, предложил денежное вознаграждение за решение задачи собирания головоломки, что добавило популярности новой забаве. Весной того же года игра достигла Европы. 21 февраля 1880 года Ной Чепмэн попытался оформить патент на своё изобретение (патент назывался «Головоломка из бриллиантовых блоков», «Block Solitaire Puzzle»), однако заявка на патент была отклонена, так как мало отличалась от уже оформленного тремя годами ранее патента «Хитрые блоки», «Puzzle-Blocks».

Математическое описание

Пятнашки представляют собой классическую задачу для моделирования эвристических алгоритмов. Обычно задачу решают через количество перемещений и поиск манхеттенского расстояния между каждой костяшкой и её позицией в собранной головоломке. Для решения используются алгоритмы наподобие алгоритма A*.

Нерешаемая комбинация, предложенная Ноем Чепменом

Можно показать, что ровно половину из всех возможных 1 307 674 368 000 (=15!) начальных положений пятнашек невозможно привести к собранному виду: пусть квадратик с числом i расположен до (если считать слева направо и сверху вниз) k квадратиков с числами меньшими i. Будем считать ni = k, то есть если после костяшки с i-м числом нет чисел, меньших i, то k = 0. Также введем число e — номер ряда пустой клетки (считая с 1). Если сумма является нечётной, то решения головоломки не существует.

Для обобщённых пятнашек (с бо́льшим, чем 15, количеством костяшек) задача поиска кратчайшего решения является NP-полной.

Если допустить поворот коробки на 90 градусов, при котором изображения цифр окажутся лежащими на боку, то можно перевести неразрешимые комбинации в разрешимые (и наоборот). Таким образом, если вместо цифр на костяшки нанести точки и не фиксировать положение коробки, то неразрешимых комбинаций вообще не окажется.

Создадим программу на языке VBA. Для начала откроем Excel и запустим Visual Basic.

Создадим кнопку «Сначала», для которой напишем следующий программный код:

Private Sub CommandButton1_Click()

Randomize

For x = 0 To 3: For y = 0 To 3

Cells(y + 8, x + 6) = «»

Next y, x

For i = 1 To 15

x = Int(Rnd * 4): y = Int(Rnd * 4)

While Cells(y + 8, x + 6) «»: x = Int(Rnd * 4): y = Int(Rnd * 4): Wend

Cells(y + 8, x + 6) = i

Next i

End Sub

Эта процедура расставляет числа в случайном порядке, используя команду Rnd.

Теперь необходимо составить процедуру, которая находила бы свободную ячейку рядом с активной и меняла бы их значения местами.

После процедуры CommandButton1_Click() вставляем следующий код:

Private Sub Worksheet_SelectionChange(ByVal Target As Range)

x = ActiveCell.Column: y = ActiveCell.Row

If x = 6 And x = 8 And y

If x 6 And Cells(y, x — 1) = «» Then

Cells(y, x — 1) = Cells(y, x): Cells(y, x) = «»

ElseIf x

Cells(y, x + 1) = Cells(y, x): Cells(y, x) = «»

ElseIf y 8 And Cells(y — 1, x) = «» Then

Cells(y — 1, x) = Cells(y, x): Cells(y, x) = «»

ElseIf y

Cells(y + 1, x) = Cells(y, x): Cells(y, x) = «»

End If

If test Then MsgBox («Победа!»)

End If

End Sub

Обратите внимание, что в конце имеется строчка выводящая сообщение «Победа» при выполнении условия test. Использование функции предполагает ее объявление в начале программы. Значит, следует добавить ее следующий текст в самое начало кода:

Function test()

c = 0

For x = 0 To 3: For y = 0 To 3

If Cells(y + 8, x + 6) = Cells(x + 3, x + 1) Then c = c + 1

Next y, x

If c = 16 Then test = True Else test = False

End Function

Private Sub CommandButton1_Click()

Randomize

For x = 0 To 3: For y = 0 To 3

Cells(y + 8, x + 6) = «»

Next y, x

For i = 1 To 15

x = Int(Rnd * 4): y = Int(Rnd * 4)

While Cells(y + 8, x + 6) «»: x = Int(Rnd * 4): y = Int(Rnd * 4): Wend

Cells(y + 8, x + 6) = i

Next i

End Sub

Данная функция просто сравнивает сумму столбцов и рядов игрока с той, которая должна получиться при правильной расстановке всех ячеек.

Теперь можно попробовать решить знаменитую головоломку.

Заключение

За последних шестьдесят пять лет область компьютерных игр успела не просто родиться, но и получить всемирную популярность. Компьютерные игры так прочно вошли в нашу жизнь, что теперь практически невозможно представить персональный компьютер, на котором не было бы хоть одной из них. С компьютерными играми приятно проводить время, отдыхать после трудового дня. Любители игр давно пользуются возможностью скачать игры из Интернета. Но как приятно самому создать компьютерную игру, продумать дизайн, написать программу, похвастаться перед друзьями!

В процессе выполнения исследования по теме «Создание логических игр на языке VBA в среде Microsoft Excel» была проанализирована литература и интернет-источники по данному вопросу, в среде Microsoft Excel на языке VBA написаны 3 логических игры: «Быки и коровы», «Угадай число», «Пятнашки».

В дальнейшем хотелось бы продолжить работу по созданию игр на других языках программирования.

Литература

1. Ананьев А., Федоров А. Самоучитель Visual Basic 6.0. — С.-Петербург, Дюссельдороф, Киев, Москва, «Cbhv», 2002. -624с.

2. Волчёнков Н.Г. Программирование на Visual Basic 6. Часть 1. — М.: «ИНФРА-М», 2000. — 288с.

3. Информационная культура: Учебное пособие для средней школы. Часть 1/ Т.А.Матвеева, А.Г.Гейн, В.В. Мачульский, т.В.Шпота, В.И.Кадочникова, В.И.Жильцова, А.С.Щербинин — Екатеринбург: Центр «Учебная книга»; Смоленск: Издательство «Ассоциация XXI век», 2006.-392 с.

4. Могилёв, А.В. Информатика [Текст] // А.В.Могилев, Н.И.Пак, Е.К.Хённер. -М.,ACADEMA, 2007.

5. Моделирование простейших игр в Microsoft Excel. / «Информатика» № 20, 2005.

6. Симонович С.В., Евсеев Г.А. Занимательный компьютер. Книга для детей, учителей и родителей. – М.: АСТ-ПРЕСС КНИГА, Инфорком-Пресс, 2002.

7. http://www.games.ru

8. http://images.yandex.ru/

9. http://ru.wikipedia.org/wiki/Жанры_видеоигр

0

Развлекая — поучай.
(Гораций)

Если вы уже имели какой-то опыт программирования в прошлой жизни (привет, Basic, Pascal и т.д.), то, скорее всего, уже прошли этап «игрописательства». Однако, тряхнуть стариной и размять мозги вполне можно. Если же вы никогда не программировали игр, то никогда не поздно начать этот весьма увлекательный процесс. Всё, что нам потребуется — это Excel (любой версии) и 15-20 минут времени для начала.

Тренироваться будем на известной в узких кругах программистов игре «Жизнь» (Life). Её придумал британский математик Джон Конвей еще в 1970 году на основе работ легендарного Джона фон Неймана — прадедушки всех современных компьютеров. Если вы не сталкивались с ней раньше — не проблема, правила можно объяснить за полминуты:

• Игра идет на большом (иногда даже бесконечном) поле в клеточку («вселенной»). Как вы понимаете, Excel для такого подходит идеально

• В один момент времени каждая клетка может быть в двух состояниях — живой (обозначим её каким-нибудь значком или просто единичкой) или же мертвой (пустой). Начальное состояние всех клеток в игре называют первым поколением.

• Если брать блок клеток 3х3 с текущей клеткой в середине, то вокруг неё оказывается 8 клеток-соседей. Дальнейшая судьба клетки зависит от того, сколько именно живых клеток (N) окажется в этой окружающей области. Вариантов несколько:

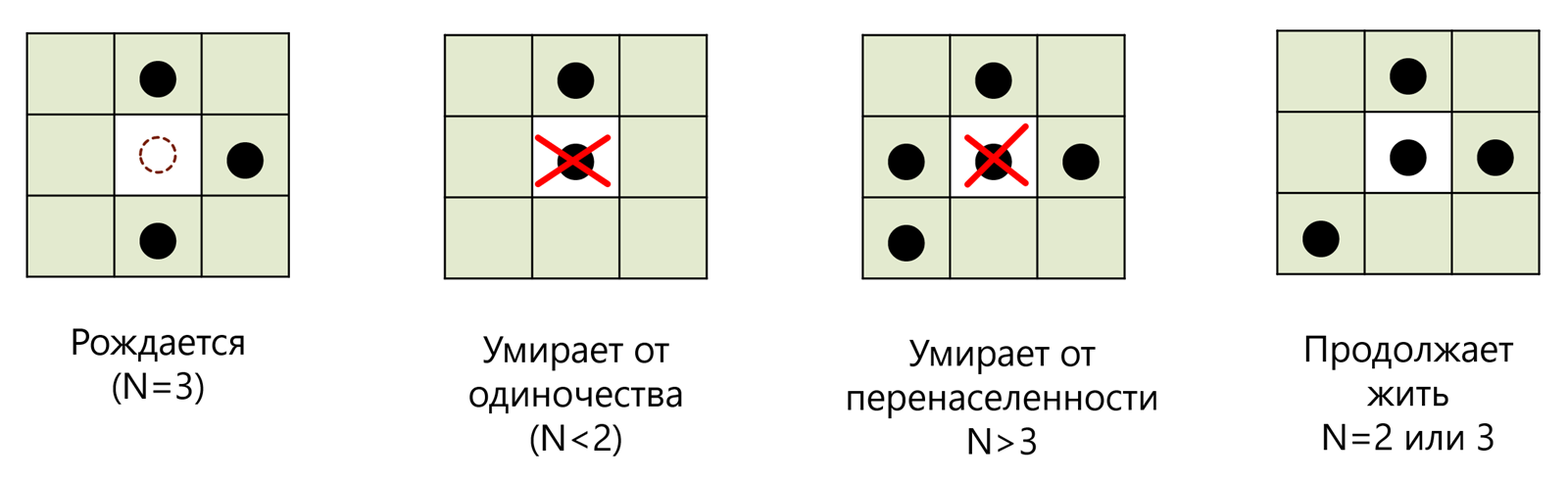
• Если клетка была пустая (мертвая), но у нее есть ровно 3 живых соседа, то в ней зарождается жизнь.
• Если клетка живая, но у неё меньше 2 соседей, то она умирает от одиночества.
• Если клетка живая, но у неё больше 3 соседей, то она умирает от перенаселения.
• Если клетка живая и у нее 2-3 соседа, то клетка продолжает жить.

Вот, собственно, и все правила. Можно даже сказать, что всё это неправильно называть игрой, т.к. здесь нет соперников в привычном понимании. Вы расставляете первое поколение, запускаете процесс и затем просто наблюдаете за развитием вашей «колонии» на протяжении нескольких поколений.

Однако, не стоит недооценивать обманчивую простоту этой логики — количество комбинаций, сценариев игры и многообразие фигур в такой игровой вселенной поражает своим разнообразием и поистине бесконечно. В математике подобные модели называют клеточными автоматами. А самое интересное, что реализовать подобную модель можно в любой версии Excel буквально на 20 строчках кода.

Поехали.

Шаг 1. Готовим игровое пространство

Создадим в новой книге три листа:

• game — это будет основной листы игры, где мы будем наблюдать за развитием нашей «колонии»
• next — этот лист будет формировать следующее поколение, которое затем придет на смену текущему
• start — на этом листе мы будем задавать начальную конфигурацию, т.е. первое поколение в нашей игре

На каждом листе (можно выделить их заранее, удерживая клавишу Shift или Ctrl, чтобы не повторять трижды одни и те же действия), разметим игровое поле размером, допустим, 30 на 30 ячеек. Впоследствии размер поля можно будет подправить в соответствии с вашими аппетитами и мощью вашего ПК:

На листе start разметим с помощью единичек первое поколение любым желаемым образом:

Шаг 2. Пишем макрос

Теперь пришла пора расчехлить наш VBA и написать макрос, который и будет делать всю работу, а именно:

1. Копировать первое поколение с листа start на лист game.
2. Проходить по ячейкам игрового поля на листе game и проверять окружающих соседей (блок 3х3) для каждой из них.
3. В зависимости от результатов проверки помечать на листе следующего поколения next ту же ячейку как живую (1) или мертвую (пусто).
4. Копировать получившееся новое поколение с листа next вместо текущего на листы игры game.
5. Повторять пункты 2-4 несколько раз, сменяя одно поколение другим и отображая на экране изменения в нашей «колонии».

Для начала откроем редактор Visual Basic на вкладке Разработчик (Developer). Если такой вкладки не видно, то её нужно будет сначала отобразить через Файл — Параметры — Настройка ленты (File — Options — Customize Ribbon), включив соответствующий флажок.

В открывшемся окне редактора создадим новый модуль с помощью команды меню Insert — Module, а затем скопируем и вставим туда код нашего макроса:

Sub Life()
    Dim cell As Range, n As Integer, i As Integer
    
    Set rGame = Worksheets("Game").Range("B2:AE31")
    Set rStart = Worksheets("Start").Range("B2:AE31")
    Set rNext = Worksheets("Next").Range("B2:AE31")
    Set wNext = Worksheets("Next")

    rStart.Copy Destination:=rGame
    
    For i = 1 To 50
        rNext.ClearContents
        For Each cell In rGame.Cells
            n = WorksheetFunction.CountA(cell.Offset(-1, -1).Resize(3, 3)) - cell.value
            If cell = "" And n = 3 Then wNext.Cells(cell.Row, cell.Column) = 1
            If cell = 1 And (n = 2 Or n = 3) Then wNext.Cells(cell.Row, cell.Column) = 1
            If cell = 1 And (n < 2 Or n > 3) Then wNext.Cells(cell.Row, cell.Column) = ""
        Next cell
        rNext.Copy Destination:=rGame
    Next i
End Sub

Теперь давайте разберем его построчно для понятности:

Поскольку в коде нам придется несколько раз ссылаться и много раз работать с диапазонами игрового пространства (B2:AE31) на каждом из трёх листов книги, то имеет смысл сразу оформить их как переменные. Это делается в блоке:

Set rGame = Worksheets("Game").Range("B2:AE31")
Set rStart = Worksheets("Start").Range("B2:AE31")
Set rNext = Worksheets("Next").Range("B2:AE31")

Заодно мы создаем ещё и переменную wNext, которая ссылается на весь лист next целиком — это нам тоже пригодится в будущем:

Set wNext = Worksheets("Next")

Затем, перед началом игры, мы должны перенести первое поколение с листа start на лист game. Это выполяется командой прямого копирования с использованием уже созданных переменных:

rStart.Copy Destination:=rGame

Поскольку мы хотим прокрутить в нашей игре не одно, а несколько (например, 50 для начала) поколений, то дальнейшие действия заключены в цикл:

For i = 1 to 50
...
Next i

А внутри этого цикла мы, во-первых, сначала очищаем рабочее пространство на листе next для формирования следующего поколения:

rNext.ClearContents

А, во-вторых, запускаем вложенный цикл прохода по всем ячейкам игровой вселенной на листе game, чтобы проверить каждую из них — это реализовано циклом прохода по коллекции:

For Each cell in rGame.Cells
...
Next cell

Ссылка на очередную проверяемую ячейку будет храниться в переменной cell. Для этой ячейки нам нужно сначала построить окрестность 3х3 с ней в середине. Это выполняется с помощью конструкции:

cell.Offset(-1, -1).Resize(3, 3)

Здесь метод Offset(-1,-1) виртуально сдвигает текущую проверяемую ячейку на одну строку вверх и на один столбец влево, а потом метод Resize(3,3) опять же виртуально растягивает эту одну ячейку до новых размеров 3 на 3:

Чтобы посчитать количество заполненных ячеек в полученной окрестности применяется функция рабочего листа СЧЁТЗ (COUNTA), которую в VBA можно вызвать с помощью объекта WorksheetFunction. Таким образом количество живых соседей в окружающей текущую ячейку области 3 на 3 мы получаем выражением (не забыв вычесть из полученного количества текущую ячейку):

n = WorksheetFunction.CountA(cell.Offset(-1, -1).Resize(3, 3)) - WorksheetFunction.CountA(cell)

Дальше нам нужно проверить полученное количество соседей и пометить на листе следующего поколения текущую ячейку как живую или мертвую, согласно правилам игры. Это выполняет блок из трёх проверок:

If cell = "" And n = 3 Then wNext.Cells(cell.Row, cell.Column) = 1
If cell = 1 And (n = 2 Or n = 3) Then wNext.Cells(cell.Row, cell.Column) = 1
If cell = 1 And (n < 2 Or n > 3) Then wNext.Cells(cell.Row, cell.Column) = ""

Когда цикл прохода по ячейкам будет завершен, то сформированное следующее поколение с листа next нужно скопировать на место текущего на листе game — делаем это уже знакомой конструкцией:

rNext.Copy Destination:=rGame

Вот, собственно, и вся логика.

Осталось вернуться в Excel на лист game, запустить нашу игру через вкладку Разработчик — Макросы (Developer — Macro) и насладиться процессом развития нашей колонии:

Ссылки по теме

• Что такое макросы и как их программировать в Microsoft Excel
• Справочник по игре «Жизнь» — сайт LifeWiki

Вступление

Все мы знакомы с Excel. Вот и я, душный банковский служащий, что-то да слышал об этом инструменте.

Одни люди умеют лишь форматировать ячейки, другие создают клоны Doom, используя встроенный в Microsoft Office язык программирования.

Я не претендую на второй тип, но и к первым себя не отношу. Для меня Visual Basic for Applications, или VBA, стал тем первым ЯП, который заинтересовал и позволил уверовать в свои силы. Путешествие в этот интересный мир началось с автоматической записи макросов и разбора созданного программой кода.

Как начинающему программисту-самоучке, мне приходилось активно шерстить интернет в поисках решения возникающих проблем. Огромное коммьюнити, большое количество тематических сайтов и, на крайний случай, справка Microsoft помогали в решении практически любой проблемы.

Однако наступил такой момент, когда все рабочие задачи оказались решены и автоматизированы, а внутреннему программисту (ха-ха) все ещё хотелось чего-то большего.

Эта серия статей не была задумана как обучающая (ведь я сам ещё учусь), но если что-нибудь изложенное будет полезно начинающим программистам, которые только погружаются в мир Visual Basic, то считайте, что я пополнил интернет одной полезной ссылкой.

Вторая цель создания цикла заключается в самообразовании и развитии навыков. Я буду ставить себе определенную цель, а потом исполнять ее наиболее приближенной к задумке.

К тому же где, как не в комментариях, мне доходчиво и культурным языком укажут на допущенные ошибки?

Я постараюсь объяснять все подробно, но без углубления в простейшие истины. Не буду рассказывать, что такое переменные, циклы или массивы. Всю эту информацию, изложенную доступным языком, можно найти в интернете.

В этих статьях я буду описывать процесс создания игр в Excel, начиная с простейших пятнашек и заканчивая глобальной RPG. Это позволит мне больше углубиться в тему, а вам поглумиться над неумехой-программистом. Или, в лучшем случае, забрать готовое решение на работу и скрывать безделье за мнимой подготовкой отчета. Ссылки на все исходные материалы будут в свободном доступе.

Темы первых статей цикла уже определены. В этой статье я расскажу, как сделать пятнашки в Excel. В следующий раз разберу создание игры в стиле Toon Blast.

Если вам, к моему удивлению, будет интересен такой формат, то пишите в комментариях, какого типа игры вы бы хотели, чтобы я реализовал на базе Excel.

Итак, хватит грофомании! ПЯТНАШКИ.

Первым делом…

Необходимо определиться с игровым полем. В данном случае все просто. Что есть пятнашки? Диапазон размером 4 на 4 ячейки, что в сумме даёт 16 ячеек. Переименовываем первый лист (по желанию), приводим нужные ячейки к квадратной форме и декорируем, как душе угодно. Получается примерно следующее:

Формирование игрового поля

На этом этапе необходимо в случайном порядке расположить числа от 1 до 15, а также пустое поле на выбранном диапазоне. Для этого открываем окно редактирования кода (Alt + F11), добавляем простой модуль (при желании и его можно переименовать для красоты).

Создаем публичную переменную rngPlayField, которая будет хранить координаты нашего игрового поля, и в методе initializeField() пишем следующий код:

Сперва метод создаёт коллекцию чисел от 1 до 16.

Я заметил особенность, что в VBA в большинстве случаев удобнее пользоваться коллекциями элементов, чем одномерными массивами. В моей практике были и такие случаи, когда приходилось использовать коллекции массивов (возможно, из-за моей некомпетентности).

InitializeField() запускает цикл For Each, который распространяется на каждую ячейку нашего диапазона. На первом этапе цикла программа рассчитывает случайное число от 1 до значения размера нашей коллекции (в настоящий момент 16) и помещает в первую ячейку диапазона число, хранящееся в коллекции под полученным случайным индексом.

Далее цикл удаляет из коллекции использованное число и переходит к следующей ячейке.

На последующих этапах происходит то же самое, за тем исключением, что размер коллекции постепенно уменьшается, пока в ней не останется ни одного числа, а все ячейки окажутся заполненными.

UPD. Уже в процессе написания статьи я выяснил, что не все комбинации, полученные таким образом, изначально решаемы. Тогда мной в ускоренном темпе был написан код, который сперва формирует правильное поле от 1 до 16, а затем в стиле песков времени разбирает пятнашки в течении 300 ходов (что мы собственно и делаем в реальной жизни, когда хотим «рестартнуть» игру). Направление движения «костяшки» рассчитывается случайным образом.

Имитация движения «костяшек» по игровому полю

Сперва создаём обработчик события нажатия на определенную ячейку. Для этого в модуле листа, на котором расположено игровое поле, формируем метод Worksheet_SelectionChange и пишем в нем следующий код. Переменная Target при этом содержит адрес выбранной ячейки.

При выборе диапазона ячеек (больше одной), а также если выбранная ячейка не относится к игровому полю, программа завершает работу.

В ином случае запускается метод имитации движения цифр, принимающий адрес выбранной ячейки в качестве аргумента.

В основном модуле в методе moveCells(byVal rngCell as range) пишем следующее:

Цикл проверяет, есть ли слева, справа, снизу или сверху от нажатой ячейки пустое поле (его имитирует число 16) и считывает вхождение смещенной ячейки в диапазон игрового поля. Если условия выполнены, то программа просто меняет числа местами.

Декорирование игрового поля и проверка победы в методе decorateField()

Создаём в рабочей книге второй лист и размещаем на нем победный вариант. Пример:

Далее пишем следующий код:

Данная программа с помощью цикла проверяет значение каждой ячейки игрового поля на соответствие аналогичной ячейке поля с победной расстановкой значений и закрашивает правильные варианты в зелёный цвет. И наоборот. Далее метод проверяет поле на наличие числа 16 (которое имитирует пустую «костяшку», не забываем) и устанавливает для шрифта белый цвет. Последний момент: проверка победы. При каждом совпадении каких-либо чисел с правильной позицией увеличивается переменная countRight, и когда ее значение станет равно 15, игра сообщит о победе.

ЭПИЛОГ

В итоге должно получиться примерно следующее:

Вот таким нехитрым образом можно создать себе развлечение на случай скучных рабочих дней. А тем временем на ум приходит следующая картинка:

При желании в игру можно добавить подсчет ходов, рейтинговую таблицу или график динамики побед.

Сейчас же я считаю, что на этом можно остановиться.

Следующая статья выйдет When it’s done. Скорее всего в течение недели.

Математика, Разработка игр, Дизайн игр

---

Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе — https://katalog-kursov.ru/

В этой части мы решим задачи об оптимальном размещении оружия на танке, пространственном расположении телепортов в MMORPG и сбалансируем бои четырёх классов персонажей RPG.

Задачи о размещении объектов

Электронные таблицы для этой части можно скачать здесь: (SuperTank) (телепорты, часть 1) (телепорты, часть 2)

SuperTank: задача решена!

В первой статье серии мы рассказали о примере задачи для игры под названием SuperTank. Во второй её части, мы познакомились с основными концепциями моделирования решений и я рассказал о решении простого примера с помощью инструмента «Поиск решений» в Excel.

Теперь мы можем применить полученные во второй части знания к задаче SuperTank, и доказать, что с их помощью можно решить эту задачу легко и быстро. Освежу вашу память: SuperTank — это игра, в которой вы можете сражаться на настраиваемом танке. Супертанк выглядит примерно так:

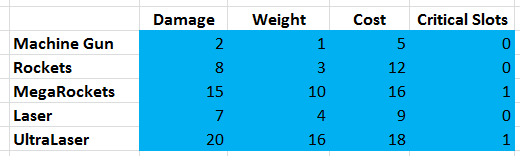
У каждого супертанка может быть любое количество орудий пяти различных типов:

На супертанк может поместиться 50 тонн оружия, а игрок может потратить 100 кредитов. Также у супертанка есть 3 «критических слота», в которые помещаются такие специальные пушки, как MegaRocket и UltraLaser.

Электронную таблицу для этого примера можно скачать здесь.

Цель заключается в том, чтобы подобрать вооружение, максимизирующее наносимый супертанком урон, не выходя при этом за ограничения в 50 тонн, 100 кредитов и 3 критических слота. Также мы предполагаем, что в этой таблице находится вся необходимая информация, и что такие факторы, как дальность, частота и точность стрельбы к делу не относятся или уже учтены в параметре Damage соответствующего оружия.

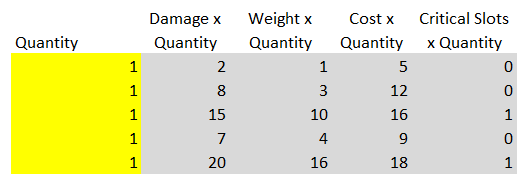
Чтобы оптимизировать эту схему, мы сначала внесём эти данные в электронную таблицу. Сразу под ней мы добавим ещё одну таблицу, в которых будет набор из 5 «количественных» ячеек для указания количества каждого из 5 типов оружия.

Пока мы введём в эти ячейки значение 1, просто чтобы протестировать их работу, но это будут наши ячейки решений — мы попросим инструмент «Поиск решений» (Solver) найти правильные значения этих ячеек. Понять, что это ячейки решений, можно по жёлтой окраске, потому что мы продолжаем следовать правилам форматирования, изложенным во второй части. Справа от «количественных» ячеек мы добавим ячейки вычислений, которые будут умножать значения количества в ячейках решений на значения Damage, Weight, Cost и Critical Slots из таблицы выше. Таким образом, каждая строка этой таблицы будет верно отображать урон, вес, цену и критические слоты, требующиеся для всех использованных пушек во всех категориях вооружений.

Также мы создадим ниже раздел, в котором будут суммироваться все значения количества, веса, стоимости и критических слотов из таблицы выше, и сравниваться с максимальными значениями веса, стоимости и критических слотов, указанных в условиях задачи (соответственно 50, 100 и 3).

В соответствии с правилами форматирования из второй части статьи, синие ячейки наверху являются критериями из условий задачи. Серые ячейки — это ячейки вычислений, представляющие общие значения веса, стоимости и критических слотов на основании суммирования из таблицы количества (т.е. общих значений столбцов Weight x Quantity, Cost x Quantity, и Critical Slots x Quantity). Наконец, оранжевая ячейка представляет общий урон нашего супертанка, полученный на основании общего урона столбца Damage x Quantity из таблицы выше.

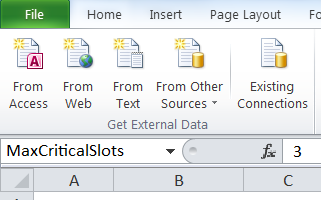
Прежде чем мы приступим к решению, давайте сделаем нашу электронную таблицу более дружелюбной к пользователю. Мы воспользуемся возможностью Excel присваивать каждой ячейке название и дадим понятные названия семи ячейкам в последней таблице вычислений. Это необязательно, но в дальней перспективе это позволит электронной таблице выглядеть гораздо понятнее (например, если вместо $F$21 ячейка будет называться MaxCriticalSlots). Для этого мы просто выбираем ячейку и переходим в поле ввода названия слева от поля формул, и вводим новое название.

Теперь наконец-то давайте перейдём в Excel Solver и найдём решение (перейдите в правую часть вкладки Data («Данные») и выберите Solver («Поиск решений»). Если вы её не видите, то зайдите в Options («Параметры») Excel, выберите категорию Add-Ins («Надстройки»), убедитесь, что в раскрывающемся списке Manage («Управление») выбрано Excel Add-Ins («Надстройки Excel»), нажмите Go («Перейти…») и убедитесь, что поставлен флажок Solver Add-in («Поиск решения»).

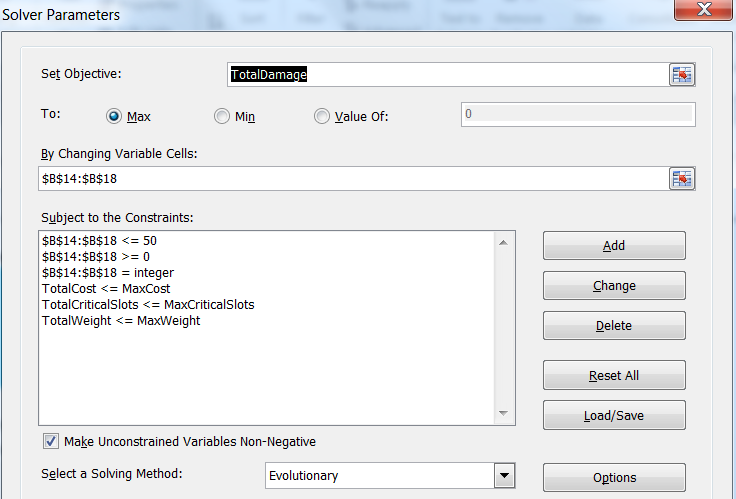
В поле Set Objective («Оптимизировать целевую функцию») мы выберем оранжевую ячейку цели, а ниже нажмём на радиокнопку Max («Максимум»). В поле By Changing Variable Cells («Изменяя ячейки переменных») выберем ячейки решений (жёлтые ячейки в столбце Quantity второй таблицы). Ниже нажмём на кнопку Add («Добавить»), чтобы добавить следующие ограничения:

• Значения ячеек решений должны находиться в интервале от 0 до какого-то разумного максимума (мы выбрали 50, даже несмотря на то, что это вероятно намного большее предельное значение, чем нужно). Также необходимо задать каждой ячейке решения ограничение «= integer» («цел»), потому что у нас не может быть дробной части вооружения, а Excel Solver считает по умолчанию каждую переменную вещественным числом, если не указать обратное.

• Также нам нужно ограничить значения общей стоимости, общего веса и общего количества критических слотов значениями из условий задачи. На изображении диалогового окна видно, что теперь у них есть удобные названия, которые мы добавили в нижнюю таблицу, благодаря чему диалоговое окно читается проще.

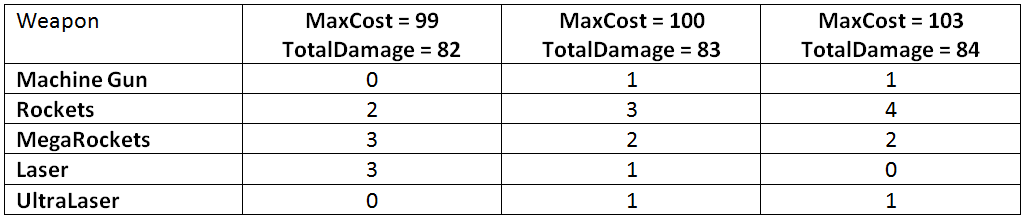
Теперь мы нажмём на кнопку Solve («Найти решение») и после краткого ожидания Solver заполнит значения Quantity, что даст нам следующее:

• 1 Machine Gun
• 3 Rockets
• 2 MegaRockets
• 1 Laser
• 1 UltraLaser

Всё это даёт нам общий урон в 83 единиц и занимает ровно 50 тонн, 100 кредитов и 3 критических слота. Можно увидеть, что наилучшее решение не меняется от времени выполнения Solver. Если сбросить эти значения и выполнить повторную оптимизацию, или перейти в Options и изменить seed, то мы всё равно получим те же значения. Мы не можем быть уверенными на 100%, что это решение оптимально, но с учётом того, что у Solver не получилось усовершенствовать его после нескольких проходов оптимизации, то с большой вероятностью он и является реальным оптимумом, а не просто локальным максимумом.

Задача решена!

Дополнительные способы использования

Здорово здесь то, что мы не только решили задачу гораздо быстрее, чем справились бы вручную, но и настроили её таким образом, что она позволит протестировать, какое оружие в игре SuperTank будет наиболее полезно с разными параметрами (вес, стоимость, критические слоты). Это значит, что мы сможем относительно просто изменить влияние различных изменений этих параметров на игру SuperTank, и если мы захотим добавить новую альтернативную модель супертанка, который будет легче, тяжелее или иметь другое количество критических слотов, то это можно будет сделать очень просто.

Изменяя все эти параметры, мы сможем также получить понимание относительной полезности каждого из этих вооружений, и быстро определять, какое из них слишком полезно, недостаточно полезно, имеет цену, неподходящую к её весу и урону, и так далее.

Повторюсь, смысл в том, что подобный инструмент позволяет нам выполнять поиск по пространству дизайна гораздо быстрее, чем мы бы смогли вручную. Он обеспечивает нам удобную возможность оценить эффект подобных изменений при любом инкрементном дизайнерском решении, которое мы можем придумать, будь то изменение параметров оружия или самого супертанка, добавление нового вооружения или моделей супертанков, а также добавление новых параметров (допустим ограничение размера в кубических метрах).

Чтобы понять, что я имею в виду, перейдите к синей ячейке «Max Cost» и измените её значение с 100 на 99. Теперь запустите Solver заново, и вы получите совершенно другую схему размещения оружия:

• 0 Machine Guns
• 2 Rockets
• 3 MegaRockets
• 3 Lasers
• 0 UltraLasers

Такая схема даёт чуть меньший показатель урона (82 вместо 83), но она радикально отличается от предыдущей.

Если присвоить Max Cost значение 101 или 102, и выполнить расчёт заново, то есть вероятность, что мы получим конфигурацию, похожую первой или совпадающую с ней; как бы то ни было, урон останется равным 83 (схемы могут меняться, потому что в таких случаях есть несколько оптимальных схем). Однако если присвоить Max Cost значение 103, то вы должны получить следующее:

• 1 Machine Gun
• 4 Rockets
• 2 MegaRockets
• 0 Lasers
• 1 UltraLaser

Что увеличивает общий урон до 84.

Это интересно: такая схема размещения оружия очень отличается от первых двух.

Как вы видите, мы получаем неожиданный результат: оптимальный выбор оружия в нашей схеме сильно зависит от параметров супертанка и может значительно меняться даже при небольших изменениях в этих параметрах. Кроме того, это даёт нам всевозможную полезную информацию: все пять типов оружия полезны по крайней мере в двух из трёх настройках супертанка, а Rockets и MegaRockets очевидно полезны во всех трёх. Похоже, это говорит нам, что все пять видов оружия хорошо сбалансированы, то есть полезны относительно друг друга, и в то же время они остаются уникальными.

И как можно также заметить, подобные моделирование и оптимизация решений предоставляют нам отличную возможность быстро выполнять поиск в локальной окрестности и повторную оптимизацию. При некоторых типах задач оно позволит нам обнаружить доминирующие стратегии и эксплойты игроков, которые трудно или невозможно найти любым другим способом.

Телепорты-«червоточины»

Посмотрев на последние два примера (пример с налоговыми ставками в стратегической игре и SuperTank), вы можете подумать, что такие техники применимы только в случаях, когда пользователи имеют дело с числами. Но вы будете абсолютно не правы! Как мы увидим, существует множество примеров того, что можно получить преимущества от оптимизации элементов дизайна, которые не только не выглядят для пользователей числами, но и вообще не похожи на них!

Также вы можете думать, что моделирование решений применимо только к решениям, которые могут принимать в играх игроки. Это тоже неверно: в некоторых случаях их можно использовать для моделирования, чтобы оптимизировать собственные решения как дизайнера.

Допустим, вы работаете над космической MMORPG. Однажды ваш ведущий дизайнер подходит к вам с видимой тревогой на лице. «Мы завершаем редизайн сектора Омега», — говорит он. «И у нас возникла проблема. Мы планируем добавить несколько телепортов-»червоточин» в этом сегменте мира, но не можем договориться, где их размещать».

«Сколько телепортов?», — спрашиваете вы.

«Мы пока не знаем. Вероятно, три, но их может быть от двух до четырёх. Мы ещё не уверены». Потом он показывает вам карту, которая выглядит вот так:

«Что это?», — спрашиваете вы.

«Это карта сектора Омега. Или, по крайней мере, звёздные системы, которые игрок может посетить в этом квадранте. Нам нужно определить, в каких клетках должны быть „червоточины“».

«Ну ладно, а по каким правилам они размещаются? Можно ли размещать „червоточину“ в одном квадранте со звёздной системой?»

«Мы хотим, чтобы ты разместил „червоточины“ таким образом, чтобы минимизировать расстояние от любой звёздной системы до ближайшей „червоточины“. И да, можно помещать их в тот же квадрант, что и звёздная система; это просто небольшие телепорты, висящие в космосе, поэтому их можно помещать где угодно. И помни, что мы ещё не решили, сколько их должно быть, так что дай мне решения для 2, 3 и 4 „червоточин“».

Как сформулировать эту задачу, и как её решить?

Оптимизируем телепорты!

Давайте начнём с подготовки ячеек решений. Обозначим четыре телепорта как A, B, C и D. Мы знаем, что каждый телепорт по сути является не чем иным, как координатами (x,y) на звёздной карте сектора Омега. Также мы знаем, что нам понадобится какой-то способ указания количества активных телепортов, поэтому мы добавим ячейку, позволяющую задать количество телепортов. Телепорт D мы используем только в случае, когда используются 4 «червоточины», а C — только когда у нас есть 3 или больше.

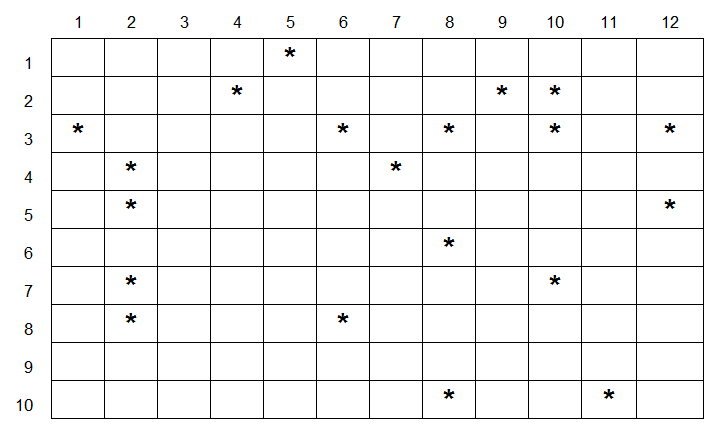
Ниже мы подготовим таблицу для вычисления расстояния от каждой звёздной системы до ближайшего телепорта. Эта таблица выглядит так:

Слева синим показаны координаты каждой звёздной системы на карте. Каждая строка — это одна звёздная система. Мы просто перенесли их из карты сектора Омега, которую нам дал ведущий дизайнер.

Справа мы вычисляем расстояние до каждого из четырёх телепортов. Это просто теорема Пифагора. Расстояние вычисляется как квадратный корень из горизонтального и вертикального расстояния между звёздной системой и телепортом:

=SQRT(($B14-Ax)^2+($C14-Ay)^2)

(Не волнуйтесь — я обещаю, что это самая сложная математика, которая нам встретится в серии!)

Мы берём координаты X и Y каждой звёздной системы из синих ячеек таблицы выше, а координаты X и Y каждого телепорта (ячейки с названиями Ax и Ay для телепорта A в показанной выше функции SQRT()) — из жёлтых ячеек решений сверху.

Наконец, мы берём минимум из этих четырёх значений в столбце Dist to Closest, то есть просто используем функцию MIN() для определения минимума четырёх значений слева. Затем мы внизу суммируем весь столбец; сумма и является ячейкой цели.

Вы могли заметить, что на скриншоте выше все ячейки имеют значение Dist to D. Причина в том, что мы используем ячейку «Number of Teleporters?» в верхнем разделе модели решений, позволяющую настроить количество учитываемых телепортов. Если количество телепортов равно 2, то мы используем значение 99 и в Dist to C, и в Dist to D, а если оно равно 3, то значение 99 используется только в столбце Dist to D. Благодаря этому каждая звёздная система будет игнорировать все лишние телепорты при вычислении расстояния до ближайшего телепорта в случае 2 или 3 телепортов.

Теперь мы запустим Solver:

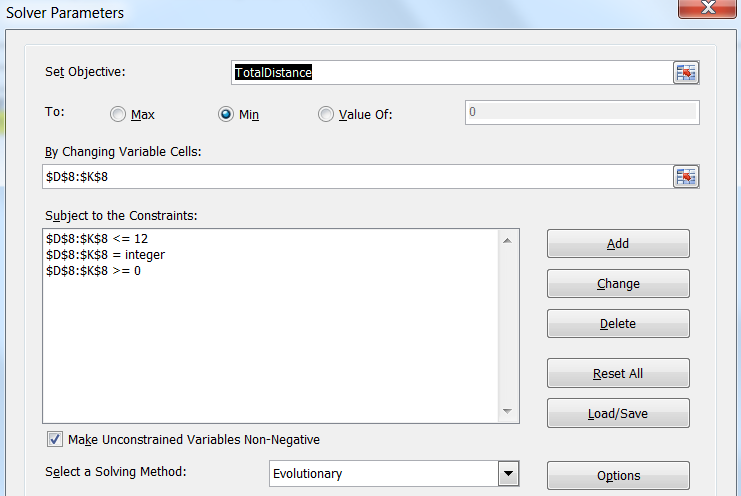
Ячейка цели — это сумма внизу столбца Dist to Closest. Заметьте, что в отличие от других примеров, здесь мы хотим использовать радиокнопку «To: Min» («До: Минимум»), потому что нам нужно минимальное расстояние между всеми звёздными системами и телепортами, а не максимум.

Ниже мы укажем в качестве ячеек решений («By Changing Variable Cells») восемь жёлтых ячеек решений координат X и Y «червоточин» A, B, C и D. В разделе ограничений мы ограничим каждую из координат как целочисленное значение в интервале от 0 до 12. Заметьте, что мы используем для этих ячеек решений целочисленное ограничение, потому что подразумеваем, что ведущий дизайнер просто хочет знать, в какой ячейке будет каждый телепорт, но мы можем запросто пропустить это ограничение, если бы дизайнеру понадобились вещественные координаты.

Если мы зададим для «Number of Teleporters?» значения 2, 3 и 4, и последовательно будем запускать Solver при каждом значении, то получим следующие конфигурации:

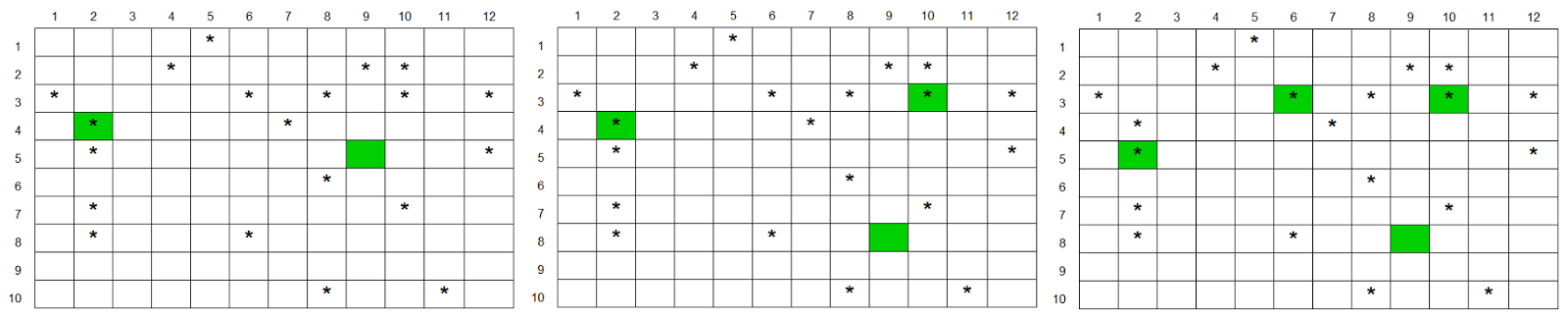
Имея эту информацию, мы можем подойти к ведущему дизайнеру и показать ему оптимальные места для расположения любого количества телепортов в интервале от 2 до 4. Вот как оптимальные расположения «червоточин» для 2, 3 и 4 телепортов выглядят на карте (показаны зелёным).

Электронную таблицу для этого примера можно скачать отсюда.

Я говорил о ниндзя?

«Потрясающе», — говорит ведущий дизайнер, но на лице его вы видите страдание. «Эээ, но я забыл сказать тебе, что некоторые из этих систем населены космическими ниндзя. И мы хотим, чтобы системы с ниндзя были дальше от „червоточин“, чтобы игроки не ощущали чрезмерной угрозы».

«Ого. Это полностью меняет дело».

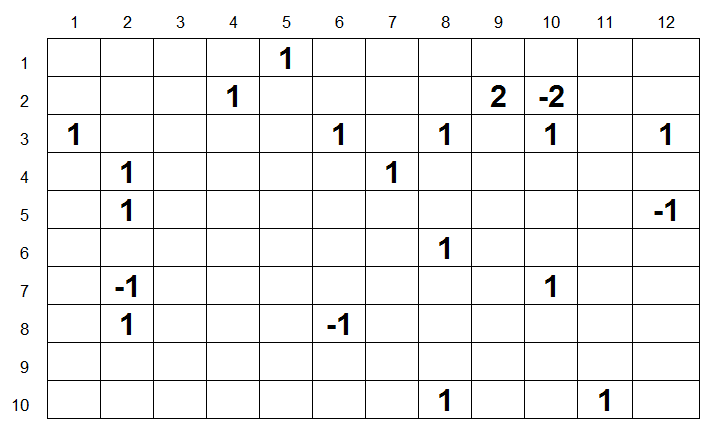
«Точно. Кроме того, в некоторых звёздных системах есть не одна, а две колонии, то есть им вдвое важнее находиться близко к телепортам. Или вдвое важнее находиться дальше, если это система с двумя колониями космических ниндзя. Вот, как выглядит карта теперь:»

Он продолжает: «Каждое отрицательное число — это колония космических ниндзя. Система с числом 2 содержит две человеческие колонии, а с числом -2 — две колонии ниндзя. Можешь сказать, где разместить телепорты в этом случае?»

«Скажи, ну вы хотя бы решили уже, сколько будет телепортов: 2, 3 или 4?», — спрашиваете вы язвительно.

«Боюсь, что пока нет».

Решаем с учётом ниндзя

Чтобы решить эту задачу, нам нужно добавить в таблицу новый столбец, обозначающий веса таблицы. Мы назовём его «множителем» (multiplier). Мы просто будем умножать это значение на значение в столбце «Dist to Closest».

Когда мы это делаем, Dist to Closest слегка изменяет свой смысл. Теперь это не расстояние до ближайшей звёздной системы, потому что для звёздных систем ниндзя значение меняется в -1 раз. Оно больше напоминает обобщённые «очки» (score), поэтому давайте так их и назовём.

Таким образом, очки теперь обозначают совокупное значение. Минимизируя его, мы делаем так, чтобы Solver стремился быть как можно ближе к системам с человеческими колониями и одновременно как можно дальше от населённых ниндзя систем.

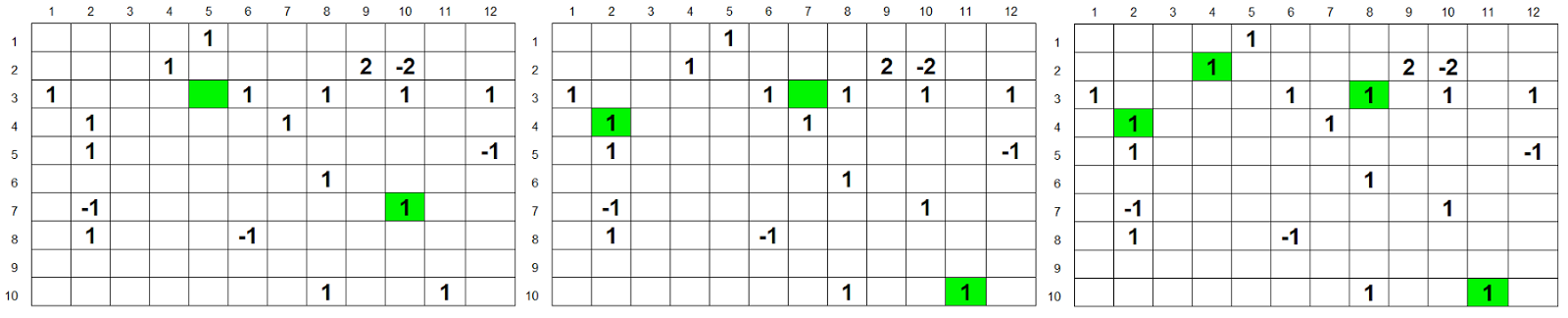
Теперь мы получаем следующие результаты:

Как видите, это даёт нам конфигурацию телепортов, в каждом случае сильно отличающуюся от более простых версий без ниндзя.

Электронную таблицу для этой расширенной версии примера с телепортами можно скачать отсюда.

Как видите, наша модель решений смогла очень быстро решить эту нетривиальную задачу, и мы можем адаптировать её к меняющимся требованиям.

Эта задача относится к классу задач, называемых «задачами о размещении объектов», которые очень хорошо изучены в области оперативного управления. Но как видите, потенциально их можно применять и в гейм-дизайне, а также в дизайне уровней, а решение просто (если не тривиально) находится в Excel.

Балансировка классов для боёв Player-vs-Player

Электронную таблицу для этой части можно скачать отсюда: ссылка

Электронные таблицы и симуляции

В предыдущих трёх частях этой серии статей мы познакомились с концепцией моделирования и оптимизации решений, а также с инструментом «Поиск решений» (Solver) пакета Excel. Мы показали, как их можно использовать для вычисления оптимальных налоговых ставок города в 4X-стратегии, для определения оптимального размещения телепортов в космической игре и для выбора оптимальной схемы расположения оружия для задачи с супертанком, описанной в первой части.

Возникает естественный вопрос: а как насчёт балансировки игры? Можно ли применять подобные техники к всевозможным видам задач сложной балансировки, которые встречаются во множестве разных типов игр, в частности, в стратегиях, RPG и MMORPG?

Ответ на этот вопрос: да, разумеется, но со множеством оговорок. Электронные таблицы в особенности имеют множество ограничений, потому что в большинстве нетривиальных случаев они не точно описывают игру. Поэтому нам сложно будет выполнять надёжную балансировку с помощью техник оптимизации; реальные задачи балансировки подавляющего большинства игр будут далеко за пределами того, что мы можем смоделировать в электронной таблице. Сама по себе симуляция игры обычно бывает слишком сложной, имеет очень много «подвижных частей» и часто выполняется в реальном времени, при попытке дискретной симуляции мы можем столкнуться со всевозможными проблемами.

Поэтому если бы мы хотели использовать подобные техники для балансировки классов в таких MMORPG, как WildStar или в стратегических играх наподобие Planetary Annihilation, то для обеспечения хотя бы какой-то точности и полезности нам бы пришлось интегрировать их в саму симуляцию игры.

Кроме того, истина заключается в том, что некоторые аспекты балансировки невозможно автоматизировать; как мы объяснили в первой части статьи, ощущения от игры автоматически настраивать невозможно.

Поэтому лучшее, на что нам стоит надеяться — это демонстрация простого примера, иллюстрирующего общий подход к задачам такого типа: на простом примере в Excel мы узнаем, как подходить к формулировке такого типа задач балансировки и оптимизировать их. Мы покажем, что по крайней мере для примера простого боя Solver может хорошо выполнять балансировку нескольких RPG-классов относительно друг друга. Потом вы сможете использовать эту базовую структуру как основу для решения подобных задач оптимизации с более сложной схемой и глубже интегрированных в симуляцию игры.

Мы надеемся, что вместе с нами вы изучите все хитрости и увидите, что нам может дать этот простой пример.

Балансировка не определена

Не существует единого, общепринятого определения слова «балансировка». Оно имеет множество значений, и истинное обычно зависит от контекста рассматриваемой игры. В разных условиях балансировка может быть связана с настройкой нескольких классов персонажей с целью равенства их возможностей в ролевой игре, с количеством сил противников, сражающихся друг против друга в стратегической игре или с подгонкой стоимости различных юнитов или ресурсов в соответствии с их полезностью.

Наилучшее определение «балансировки» обычно зависит от целей дизайна рассматриваемой игры, но так как эти цели могут быть любыми, то невозможно априори определить, что балансировка на самом деле означает для игр в целом.

Некоторые игроки склонны считать, что балансировка в бою означает равный урон. Это особенно относится к MMORPG, в которых игроки часто жалуются, что величина урона в секунду (damage per second, DPS) одного класса слишком мала или слишком велика относительно других.

Разумеется, классы невозможно балансировать только по DPS; вполне допустимо, чтобы один класс имел больший DPS, чем другой, но это должно компенсироваться другими факторами, ограничивающими общую полезность класса, например, пониженная выживаемость или меньший долговременный DPS по сравнению с кратковременным DPS.

Крошечная MMO

Представьте, что мы создаём новый проект, очень упрощённую многопользовательскую массовую онлайновую ролевую игру под названием «Tiny MMO». В рамках разработки дизайна мы стремимся сбалансировать четыре класса для боёв «игрок против игрока» (PVP) таким образом, чтобы все четыре класса были относительно равными в бою друг против друга, и чтобы не было явного «лучшего» или «худшего» класса, которым можно сражаться против других классов.

Хоть «Tiny MMO» и является игрой реального времени, действие каждого игрока длится ровно 3 секунды, поэтому мы можем дискретизировать её, представив в виде пошаговой игры, в которой каждый ход является трёхсекундной долей геймплея.

Игроки в этой игре могут выбрать один из четырёх классов персонажей:

• Warrior (Воин) наносит наибольший урон
• Mage (Маг) кастует заклинания на расстоянии и имеет набольшую дальность атаки из всех четырёх классов
• Healer (Хилер) автоматически лечится, восстанавливая за каждый ход определённую часть своего здоровья
• Barbarian (Варвар) имеет больше всего здоровья

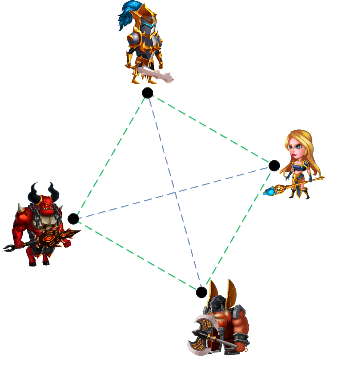
Это всё, что мы знаем об этих четырёх классах, и нам нужно задать изначальные параметры здоровья (HP), урона, лечения и дальности атак для всех четырёх классов. Нам нужно сбалансировать их таким образом, чтобы каждый класс был уникальным и его характеристики значительно отличались от всех других классов, но чтобы в результате каждый класс оказался как можно более «сбалансированным» относительно трёх остальных.

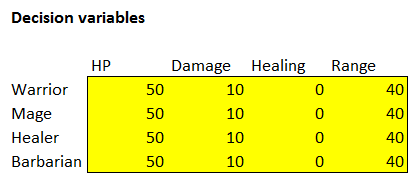
Другими словами, мы стремимся оптимизировать следующую таблицу:

Пока мы используем временные значения и предполагаем, что каждый класс начинает с 50 HP, наносит при атаке 10 единиц урона за ход, излечивает 0 HP за ход и имеет дальность атаки 40 метров. Каждый персонаж движется со скоростью 10 метров за ход. Так как в дизайне указано, что все четыре класса персонажей могут двигаться с одной скоростью, то мы будем считать это значение постоянным, и не станем вносить скорость движения в таблицу переменных решений.

Очевидно, что это учебный пример с очень упрощённой моделью урона. Это непрерывное усреднённое значение урона в секунду, которое игнорирует отличия импульсного урона от длительного урона, а также ману и другие механики, модифицирующие атакующие способности классов. У нас будет только один тип урона, что довольно нереалистично, потому что у большинства классов есть десятки типов урона, и нам нужно будет реализовывать систему ИИ, выбирающую атаку в каждом ходу. Кроме того, в большинстве игр урон имеет элемент случайности, но мы пока это опустим и предположим, что вариативность урона не так велика, чтобы значительно влиять на результат боя между двумя классами.

Разумеется, любая балансировка, выполняемая в Excel, вряд ли будет идеальной или соответствующей окончательному балансу игры; она должна будет пройти множество итераций плейтестинга. Но если мы уделим один-два часа на получение хорошего первого варианта для нашей игры в Excel, то по крайней мере мы с гораздо большей вероятностью приблизимся к качественным параметрам первоначального баланса, что сильнее приблизит нас к тому конечному балансу, который мы хотим получить.

Таблица побед

Нам нужно сбалансировать четыре класса с каждым другим в бою один на один. Так как у нас только 4 класса (Warrior, Mage, Healer и Barbarian), то всего есть 6 возможных комбинаций разных классов:

• Warrior — Mage
• Warrior — Healer
• Warrior — Barbarian
• Mage — Healer
• Mage — Barbarian
• Healer — Barbarian

Подобная балансировка может быть достаточно сложной. Даже в нашем довольно простом случае с четырьмя классами у нас получились шесть междуклассовых соотношений, так же, как мы можем провести шесть прямых между четырьмя точками квадрата.

Каждый раз, когда мы захотим внести даже небольшое изменение в один из параметров любого из классов, то это изменение также повлияет на балансировку PvP между этой парой классов и другими двумя классами. Эта степенная взаимосвязанность при увеличении количества классов будет только расти, и решения о балансировке PvP между любой парой классов, принимаемые «в вакууме», без учёта всех других взаимодействий, могут стать очень опасными.

В идеале нам хотелось бы создать некую таблицу побед наподобие показанной ниже. Если мы сможем смоделировать в электронной таблице бой между каждой из этих 6 пар, то у нас получится сгенерировать некую переменную «очков» для каждой из 6 пар. Чем больше очков, тем лучше, поэтому мы сможем скомбинировать все эти шесть значений очков, чтобы сгенерировать функцию цели.

Заметьте, что в показанной выше таблице ячейки вдоль диагоналей равны нулю, потому что они обозначают пары одного и того же класса, которые будут сбалансированными по определению. Кроме того, ячейки в правом верхнем углу тоже равны нулю, потому что они обозначают точно такие же пары, что и в ячейках внизу слева.

Теперь давайте подготовим модель для боя между двумя разными классами.

«Симулятор боя»

Расположим каждую пару классов на расстоянии 100 метров друг от друга. Каждый персонаж имеет 3 секунды на атаку, поэтому мы можем представить это как пошаговую симуляцию, в которой каждый «ход» обозначает 3 секунды. На каждом «ходу» каждый персонаж или атакует другого, если он находится в пределах дальности атаки, или продолжает двигаться, чтобы сократить расстояние.

Симуляция выглядит так:

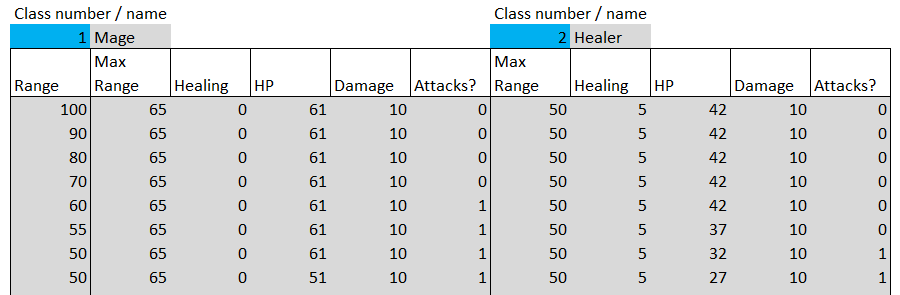
Наверху показана пара персонажей, вступивших в бой: в данном случае это Mage (класс 1) и Healer (класс 2). В левом столбце показано текущее расстояние между двумя симулируемыми персонажами.

Для каждого персонажа столбцы будут такими:

• Max Range: это максимальное расстояние, на котором персонаж может атаковать. Оно берётся непосредственно из жёлтых переменных решений в таблице переменных решений.
• Healing: это величина лечения персонажа за ход, получаемая непосредственно из таблицы переменных решений.
• HP: это здоровье персонажа в каждом ходе. Изначально оно равно соответствующему значению HP из таблицы переменных решений, но со временем при атаках другого персонажа уменьшается. Также оно увеличивается в каждом ходе на величину лечения, которую персонаж может применить к себе в каждом ходе.
• Damage: величина урона, наносимого персонажем врагу, когда тот находится в пределах дальности атаки. Когда персонаж умирает, это значение снижается до 0.
• Attacks?: этот столбец проверяет, находится ли персонаж в пределах дальности атаки. Если да, то это будет означать, что в текущем ходе персонаж атакует; если нет, то персонаж перемещается ближе, чтобы дойти до другого персонажа.

Таким образом, оба персонажа начинают двигаться друг к другу, а затем атакуют, пока один из них или оба не умрут. Каждый персонаж перемещается за каждые 3 секунды на 5 метров (5 метров за «ход»). Когда оба персонажа движутся друг к другу, то Range будет изменяться в каждом ходу на 10 единиц, и на 5 единиц, если движется только один из них. Сама игра структурирована так, что оба персонажа могут начать двигаться одновременно, после чего ход разрешается одновременно, поэтому вполне возможно, что оба персонажа могут умереть одновременно.

Далее нам нужно настроить подсчёт очков для этой таблицы и сгенерировать численное значение, обозначающее, насколько «хорошим» был бой; другими словами, насколько близко мы оказались к достижению наших дизайнерских целей.

Очевидно, что мы хотим, чтобы к концу боя оба персонажа были мертвы, или, по крайней мере, были как можно ближе к смерти. Если бой сбалансирован, то оба из сражающихся классов должны максимально снизить здоровье противника в конце боя.

Однако самого по себе этого недостаточно. Если мы организуем подсчёт очков таким образом, то оптимизатор просто максимально увеличит значения урона, чтобы оба персонажа мгновенно убили друг друга! (Если вам любопытно, то попробуйте изменить приложенную к статье электронную таблицу, чтобы убедиться в этом самостоятельно). Очевидно, что мы стремимся не к мгновенной смерти: нам нужно, чтобы к концу боя оба персонажа были мертвы или почти мертвы, но в то же время мы хотим, чтобы бой длился разумное количество времени.

Другими словами, мы не только стремимся обеспечить относительно равную балансировку всех классов против друг друга; мы ещё и хотим сделать так, чтобы баланс был интересным, в том числе и чтобы бои длились подходящее количество времени.

Чтобы сгенерировать такую оценку баланса, нам нужно создать несколько ячеек справа от каждой таблицы. Duration обозначает длительность боя; она подсчитывает количество строк таблицы, в которых оба персонажа пока живы. Total HP подсчитывает общую сумму хитпоинтов двух выживших персонажей. В идеале она должна быть равна 0, то есть к моменту завершения боя оба персонажа умирают.

И. наконец, Score комбинирует длительность и общую сумму хитпоинтов в виде ( Duration / ( 1 + Total HP ) ). Заметьте, что мы прибавили к делителю 1, потому что Total HP может быть равно 0, и в таком случае мы бы получили ошибку деления на ноль. Таким образом мы можем гарантировать, что вознаграждаем оптимизатор за нахождение максимальной длительности боя и минимального значения суммы хитпоинтов.

(Заметьте, что поскольку в каждой «симуляции» боя класса против класса у нас есть 17 строк. Это значит, что мы по сути приняли дизайнерское решение о том, что бой должен длиться примерно 17 раундов. Если мы хотим, чтобы бой был короче или дольше, то можно изменить количество строк, соответствующим образом отредактировать формулы подсчёта оценки и выполнить повторную оптимизацию.)

Наконец, мы берём эти шесть значений Score (по одному для каждой таблицы) и используем их в представленной выше «Таблице побед», чтобы показать результаты боя между каждой из пар классов.

Можно просто суммировать эти шесть значений оценок и использовать результат как финальное значение Score. Однако, если мы это сделаем, то Solver с большой вероятностью не сможет найти хорошего баланса между наибольшей и наименьшей оценкой для отдельных боёв, а также получит очень высокие оценки для некоторых пар классов и низкие оценки для других. Мы хотим не этого: нам нужно чтобы все оценки были высокими и мы стремимся повышать их все. Чтобы исправить это, мы умножим сумму оценок на наименьшую оценку в группе (с помощью функции Excel MIN()), чтобы заставить Solver сосредоточиться на оценках с наименьшим значением.

Добавляем ограничения

Мы пока не закончили. Если оптимизировать модель решений с текущими параметрами, то, скорее всего, классы будут настроены неправильно — на самом деле, высока вероятность, что модель запишет в таблицу переменных решений одинаковые значения HP, Damage, Healing и Range.

А мы, разумеется, хотим, чтобы у каждого класса была собственная индивидуальность. Нам нужно, чтобы Warrior наносил наибольший урон, Mage имел самый большой Range, Healer имел максимальное значение Healing, а Barbarian обладал наибольшим HP. Также мы хотим, чтобы эти различия не были слишком маленькими — нам нужно чтобы, эти классы сильно отличались друг от друга.

Для этого мы создадим небольшую таблицу ограничений. Эта таблица гарантирует, что каждый из четырёх классов будет иметь соответствующий атрибут, после чего давать оценку 0 или 1, в зависимости от того, удовлетворено ли условие ограничения.

В таблице Min difference справа указана минимальная разность каждого атрибута класса относительно всех других классов. Другими словами, Warrior должен иметь по крайней мере на 4 HP больше урона, чем все другие классы, Mage должен иметь дальность атаки по крайней мере на 10 больше, и так далее.

Теперь, когда мы добавили эти особые ограничения, настало время оптимизировать!

Поиск решений

Теперь мы можем запустить встроенный в Excel инструмент Solver («Поиск решений»), чтобы попытаться оптимизировать исходные параметры. В качестве ячейки цели мы выберем ячейку Score, которая комбинирует результаты всех шести турниров. Мы задаём переменные решений так, чтобы включить в них все 16 ячеек в жёлтой таблице Decision variables, которую мы создали в начале.

Также мы задаём ограничения (в поле Subject to the Constraints) следующим образом:

• Все ячейки решений должны быть целочисленными с минимальным значением 0.
• Все ячейки в столбце HP должны иметь максимальное значение 200 и минимальное 30.
• Все ячейки в столбце Damage имеют максимальное значение 20.
• Все ячейки в столбце Healing имеют максимальное значение 15.
• Все ячейки в столбце Range имеют максимальное значение 100.
• Кроме того, все четыре ячейки в особом разделе Constraints должны иметь значение 1, чтобы удовлетворялись их особые условия.

Наконец, выберем в качестве Solving Method значение Evolutionary и запустим Solver. Учтите, так как это эволюционный алгоритм, существует вероятность улучшения найденного решения при втором или третьем прогоне Solver, или после настройки параметров (кнопка Options) для эволюционной оптимизации.

В результате у нас должно получиться нечто подобное:

… и как по волшебству Solver дал нам хорошую исходную конфигурацию баланса.

Как видите, Warrior теперь наносит наибольший урон, Mage имеет наибольшую дальность, Healer лучше всех лечит, а у Barbarian больше всех HP. Кроме того, можно опуститься к результатам отдельных турниров «класс против класса» и увидеть, как классы проявили себя в бою друг с другом; как видно, большинство из них сбалансировано очень равномерно — к концу боя оба класса умирают, или один из них едва выживает. К тому же все турниры длятся достаточно долго, ни один из классов не может «ваншотнуть» другой.

Неплохо для нескольких часов работы, правда?

Заключение

В этом примере мы создали простую задачу балансировки и продемонстрировали, что на самом деле мы можем решить её с помощью симуляции и оптимизации. Хоть и очевидно, что это простой пример, он показывает нам мощь техник моделирования и оптимизации решений. К тому же он может стать источником вдохновения, который можно использовать в более сложных инструментах балансировки, тесно интегрированных в симуляцию игры. Надеемся, что вы сможете использовать этот пример как руководство к формулировке подобных задач на практике.

В следующих двух частях серии мы погрузимся в область задач о назначениях, которая связана с выбором оптимальных назначений из двух и более множеств сущностей. Мы покажем, как решать такие типы задач и продемонстрируем, как использовали этот подход для создания дизайна башен в нашей стратегической игре для iOS/Android City Conquest.