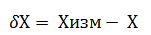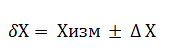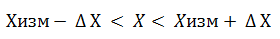Примеры эксперимента в excel

---

Статьи
Карта сайта
Главная страница

 

Ввод текста помогает оформлять заголовки таблиц, записывать
определенные пояснения. Допустим, нам надо рассчитать объем раствора по его
массе 10 г и плотности 1,25 г/мл, используя простейшую формулу V=m/d. Введем
в ячейки В5, С5, D5 заголовки столбцов будущей таблицы,
обозначения величин m, d и V, и приступим к вводу чисел. В
ячейку В6 введем численное значение массы 10. Заканчиваем ввод, нажимая Enter, и убеждаемся, что тест в ячейке, как правило, смещен к правой границе, а число к левой. Это удобно, так как позволяет замечать ошибки
ввода. В ячейку С6 введем дробное число 1,25. Здесь надо учесть, что в
зависимости от настройки конкретного компьютера для разделения целой и дробной
части числа может использоваться или запятая, или точка. При неправильном вводе
наши символы будут восприниматься как текст,  или даже как дата (янв.25).

Наконец, в ячейке D6 введем формулу, по
которой Excel будет проводить вычисления. Ввод формулы начинается со знака
равенства (=). Затем надо показать программе, где находится первое число в
нашей формуле, масса раствора, дать адрес этой ячейки  — В6. Конечно, можно
набрать этот адрес с клавиатуры, надо только учитывать, что В – это символ
английского алфавита. Поэтому, гораздо проще просто щелкнуть по нужной ячейке и
ее адрес будет введен автоматически (=В6). Далее надо ввести знак
арифметического действия. Эти знаки удобно вводить с правой части клавиатуры,
напоминающей клавиатуру калькулятора. Здесь есть клавиши со знаком сложения
(+), вычитания (-), умножения (*) и деления (/). И, наконец, надо показать
компьютеру, где находится делитель – щелкаем мышкой по ячейке С6 и получаем
окончательный вид формулы (=В6/С6). Нажимаем Enter, и,
если все было набрано правильно, получаем в ячейке D6 результат
(8). Таким образом, формулы возвращают в ячейку результат вычислений, число. Но
если щелкнуть по ячейке и посмотреть на строку формул, мы увидим, что на самом
деле находится в ней.

Иногда формула может возвращать и сообщение об ошибке. Щелкнем
по ячейке В6 и введем вместо числа 10 символы «10 г». В ячейке D6
тут же окажется сообщение #ЗНАЧ!, которое говорит о
неверном значении в одной из ячеек. Действительно, запись «10 г» воспринимается
уже как текст. Чтобы исправить ошибку надо снова вместо «10 г»  ввести число
10. (Для исправления неверных действий можно использовать и кнопку «Отменить»
на панели инструментов). Щелкнем теперь по ячейке С6 и нажмем клавишу “Del”. Этим мы удалим содержимое ячейки, и в соседней ячейке
тут же получим сообщение #ДЕЛ/0! (ошибка деления на 0). Действительно,
на ноль делить нельзя и ошибку надо исправить.

Итак, мы научились вводить числа и формулы, а значит и проводить
простейшие вычисления в Excel. Но как упростить эту процедуру, если таких
вычислений много? Здесь помогают приемы копирования, и автоматического
заполнения ячеек методом «протягивания». Пусть у нас 10 порций раствора массой 10 г, и в ячейки В6, В7 …, В16 надо ввести 10, 10, … и т.д. Щелкнем по ячейке В6, где число 10 уже
введено. В черной рамке выделенной ячейки, внизу справа, есть маленький черный
квадратик. При наведении на него указателя мышки, последний меняет форму. Если
в этот момент «взяться» (нажать левую кнопку мыши) и потянуть вниз, до ячейки
В16, то все десять ячеек окажутся автоматически заполнены нужным числом. Не
труднее заполнить и 100 ячеек!

А если массы растворов отличаются на некоторую постоянную
величину, например 10, 12,5, 15 г и т.д.? В этом случае достаточно ввести два
значения: число 10 в ячейку В6 и число 12,5 в ячейку В7. Теперь надо выделить
эти две ячейки. Для этого щелкаем по первой ячейке и, не отпуская кнопки, ведем
до второй. Теперь обе ячейки обведены жирной рамкой. Снова беремся за черный
квадратик и тянем вниз. Получаем ряд значений от 10 до 35.

Поскольку предполагается, что раствор у нас один и тот же,
оставим колонку С в покое и попробуем методом протягивания скопировать формулу,
которая у нас набрана в ячейке D6. Проделываем уже
описанную операцию: выделяем ячейку, беремся, протягиваем… и получаем во всех
ячейках, кроме первой, ошибку! Разберемся, почему это произошло, для чего
щелкнем по ячейке D7 и посмотрим на строку формул. В
ячейке D6 было написано «=В6/С6», а в ячейке D7 уже «=В7/С7»! То есть, при копировании формул Excel
автоматически меняет адреса ячеек, откуда он берет данные для расчетов. И это
совершенно правильно, когда речь идет о массе раствора. Но плотность раствора у
нас постоянная, как показать программе, что адрес этой ячейки менять не надо?

Для этого мы должны познакомиться с такими понятиями, как
относительный и абсолютный адрес. Те адреса, которые мы использовали,
называются относительными и меняются при копировании. Адрес в абсолютной форме
сопровождается знаками доллара и выглядит так: $C$6. Вот
эту поправку нам и надо внести в формулу в ячейке D6.

Исправлять записи в ячейках удобнее в строке формул. Щелкнем
сначала по ячейке D6, (формула появится в строке
формул), затем в нужном месте строки формул – там появится курсор. Конечно
знаки доллара можно ввести с клавиатуры, но проще, установив курсор на адресе
С6, нажать на клавиатуре клавишу F4. Понажимайте ее
несколько раз и посмотрите, как будет меняться адрес. Он может быть полностью
абсолютным, абсолютным по строчке, по колонке, и полностью относительным.
Добейтесь нужного вида и нажмите Enter. Формула
исправлена, теперь ее снова можно протянуть до ячейки D16.
Если все сделано правильно, вы получите ряд значений от 8 до 28 мл.

Итак, если Вы не только прочитали, но и проделали все, о чем шла
речь выше,  Вы научились многому. Вы умеете вводить текст, числа и формулы,
вносить исправления, устранять ошибки, копировать и заполнять ячейки рядами
данных. Не мешает сохранить результаты своей работы. Процедуры сохранения файла
и его открытия полностью совпадают с работой в Worde и не должны вызвать у Вас затруднений.

Формулы с
функциями.

Но в наших расчетах использовались только простейшие
арифметические действия. Для более сложных расчетов нужно научиться
использовать функции. Этим мы займемся на втором листе нашей книги.

Для перехода на нужный лист достаточно щелкнуть по его ярлычку.
Начнем работу с краткого повторения пройденного: дадим листу 2 имя «Ошибки», в
ячейку А3 введем текст «Данные эксперимента», в ячейки А5 и В5 — заголовки
новой таблицы «№» и «Х». Предполагается что мы проделали серию из 10 опытов,
измеряя некоторую величину Х (здесь не важно, что это, длина побега или объем
раствора). Номера опытов от 1 до 10 легко ввести протягиванием, а вот численные
значения Х надо последовательно ввести (табл.1).

Таблица 1. Примерный вид листа
«Ошибки»

Записи в колонках D и
Е – это подсказки, которые помогут разобраться с тем, какие характеристики мы
будем рассчитывать. Колонка F у
Вас должна быть пока пустой, в нее будем помещать наши формулы.

Обработку результатов начнем с расчета числа опытов n. Казалось бы это очевидное число, но в ходе работы, какой-то
результат мы можем отбросить, или провести еще пару опытов. Желательно, чтобы
нам не пришлось при этом переделывать все формулы. Для определения числа
значений используется специальная функция, которая называется СЧЕТ. Для ввода
формулы с функциями используется Мастер функций, который запускается командой
«Вставка функции» через меню «Вставка» – «Функция» или кнопкой на панели
инструментов с обозначением   f_x. Щелкнем мышкой по ячейке F6,
где должен находиться результат и запустим Мастер функций.

Первый шаг работы (рисунок 1) служит
для выбора нужной функции. Все функции разделены, в зависимости от своего
назначения на несколько категорий (математические, логические и др.). Для
обработки данных эксперимента используются в основном статистические функции.
Поэтому, прежде всего в списке категорий выбираем категорию «Статистические».
Во втором окне появляется список статистических функций. Если щелкнуть по любой
из них, внизу появляется краткое описание функции. Специальной ссылкой можно
вызвать систему помощи Excel, в которой данная функция будет разобрана
подробно, с примерами. Список функций упорядочен по алфавиту, что позволяет без
труда нужную нам функцию СЧЕТ («Подсчитывает количество чисел в списке
аргументов»). Выделив щелчком эту функцию, нажимаем кнопку Ok и переходим к шагу 2.

Второй шаг (рисунок 2) служит для задания аргументов функции. 
Функции СЧЕТ надо указать, какие числа ей надо пересчитывать, или в каких
ячейках находятся эти числа. Диапазон ячеек указывается адресами первой и
последней ячейки, записанными через двоеточие, в нашем случае данные находятся
в ячейках В6:В15. Как и в других случаях эти адреса лучше не вводить, а показать
мышкой. Для этого устанавливаем указатель мышки на первую ячейку, нажимаем
левую кнопку и ведем до последней. Обратите внимание, что окно аргументов можно
перемещать, если оно заслоняет нужную часть экрана. Кроме того, рядом с полем
для ввода есть маленькая кнопка с красной стрелочкой. При щелчке по ней окно
аргументов сворачивается до узкой полоски. Когда мы показываем в основном окне
диапазон ячеек, в окне аргументов появляется запись диапазона адресов, а рядом
с ним – значения чисел из первых ячеек. Предварительное значение функции тоже
показывается после ввода ее аргументов. Это помогает избегать ошибок. Помогает
работе с мастером функций и подсказка под полем для ввода аргументов, в которой
разъясняется их смысл и возможные значения. Заканчивается работа с мастером
функций нажатием кнопки “Ok” или клавиши “Enter”. Если все сделано правильно, в ячейке F6 появится нужное значение “10”.

Следующие два этапа обработки серии опытов проводятся
аналогично. В ячейке F7 c
помощью функции СРЗНАЧ рассчитывается
среднее значение выборки, в ячейке F8 – стандартное
отклонение выборки, с помощью функции СТАНДОТКЛОН.
. Будьте аккуратны при выборе функций
– среди них есть очень похожие по названию. Аргументами этих функций служит все
тот же диапазон ячеек.

Следующая формула сложная, частично она набирается как обычная
формула, начиная с символа ”=”. Указав, где находится делимое S и набрав знак операции (=F8/), вызываем
мастер функций. Функция КОРЕНЬ – математическая, поэтому на первом шаге
выбираем категорию математических функций. Аргументом этой функции служит число
опытов, которое мы рассчитали в ячейке F6. Окончательный
вид формулы “=F8/ КОРЕНЬ(F6)”.

Для расчета доверительного интервала необходимо определить
коэффициент Стьюдента. Он зависит от вероятности ошибки (при обычно задаваемой
надежности 95% вероятность ошибки составляет 5%), и от числа степеней свободы n-1). Для нахождения коэффициента Стьюдента используется
статистическая функция Excel СТЬЮДРАСПОБР (“Стьюдента распределение обратное“).
Особенностью этой функции является то, что первый аргумент, число 5% (или 0,05)
вводится в соответствующее окно с клавиатуры. Для второго указываем адрес
ячейки, где находится значение n,
затем дописываем в окне “-1”. Получаем запись “F6-1”.

Для нахождения
доверительного интервала используется обычная формула умножения. Конечно,
вместо букв там должны стоять адреса ячеек, где находятся коэффициент Стьюдента
и стандартное отклонение среднего. Как правило, значение доверительного
интервала округляется до одной значащей цифры, такой же порядок окружения
должен быть и у среднего. Поэтому окончательный результат можно записать так: с
95%-ной надежностью Х = 14,80±0,05. В заключение посчитаем относительную ошибку определения Х: d = ДИ / Х_ср (формула: “=F11/F7”).
Значение относительной ошибки обычно выражают в процентах, у нас 0,3%.

Если Вы впервые
работаете в Excel, описанная процедура обработки данных эксперимента может
показаться очень сложной.  Но на практике, вводить формулы, с помощью мастера
функций, ничуть не сложнее, чем обычные арифметические. К тому же, один раз
подготовив лист Excel для обработки данных, можно скопировать его, и ввести
результаты новой серии опытов в колонку В. Результаты будут тут же рассчитаны
автоматически.

Изучение
зависимостей.

Часто в исследованиях изучается зависимость некоторой величины
от другой. Характер этих зависимостей стремятся выразить математическими
формулами, коэффициенты которой могут иметь определенный физический смысл.
Наиболее употребительна и проста в обработке линейная зависимость, которую
можно выразить уравнением прямой у = kx + b. При этом коэффициент k показывает
степень влияния х на у, а b – некоторое
начальное значение у. Поскольку значения, полученные в ходе эксперимента,
всегда включают некоторую ошибку,  экспериментальные точки не лежат строго на
прямой. Как же провести по этим разбросанным точкам наилучшую линию. Для этого
используется статистический метод «наименьших квадратов» предлагающий
достаточно сложные функции для нахождения коэффициентов k и b, а также для оценки их
достоверности.

В Excel эта
задача решается при помощи статистических функций НАКЛОН (наклон прямой
относительно оси Х, коэффициент k) и ОТРЕЗОК  (отрезок
отсекаемый прямой на оси Y, коэффициент b). Кроме того, Excel позволяет
построить график зависимости, саму прямую, которая называется линией тренда, а
также вывести уравнение прямой на график.

Для знакомства с этим возможностями перейдем на Лист 3 нашей
книги, назовем его «Зависимость» и введем необходимые исходные данные (таблица
2).

Таблица 2. Примерный вид листа
«Зависимость»

В колонках В и С вводятся данные эксперимента по измерению
величин Х и У, записи в колонке Е играют роль подсказок, колонка F заполняется по мере обработки.
Начнем с ячейки F3.

Ввод формул проводится с помощью мастера функций так, как это
описывалось ранее. Маленькое отличие заключается в том, что у функций НАКЛОН и ОТРЕЗОК два
аргумента: диапазон ячеек со значениями Y и диапазон ячеек со значениями Х.
Щелкаем мышкой сначала по полю для ввода первого аргумента, показываем нужный
диапазон (С3:С13). Затем щелкаем по второму поля и повторяем ввод (В3:В13).
Также рассчитывается и значение функции ОТРЕЗОК в ячейке F4.

Для оценки достоверности можно использовать квадрат коэффициента
корреляции Пирсона (R²). Если он равен 1, то
имеет место полная корреляция с моделью, т.е. точки лежат строго на прямой. В
противоположном случае, если коэффициент  равен 0, то уравнение линейной
зависимости полностью неудачно. Для его нахождения используется статистическая
функция КВПИРСОН. Таким образом, данные
нашего эксперимента с достоверностью 0,98 описываются уравнением у = 1,42х+0,905.

Рассмотрим теперь второй метод обработки и представления
результатов эксперимента в виде графика. Для построения графиков и диаграмм в Excel’e используется
Мастер диаграмм, который можно запустить, используя меню Вставка – Диаграмма,
или кнопки на панели инструментов с условным изображением диаграммы.
Предварительно щелкнем мышкой по любой свободной ячейке нашего листа.

Рисунок 3. 

На первом шаге (рисунок 3) выбирается тип и вид диаграммы. Для
построения графика зависимости одной величины от другой используются точечные
диаграммы, причем лучше (из-за разброса точек) выбирать вид «Точки не
соединенные линиями». Заканчиваем выбор, щелкая по кнопке «Далее».

На втором шаге необходимо указать, где у нас находится
независимая величина Х и зависящая от нее Y (рисунок 4).
Для этого щелкаем по ярлычку вкладки «Ряд» и затем по кнопке «Добавить».

Рисунок 4.

Открываются поля для указания Х и Y. Ввод
значений адресов в эти поля не отличаются от работы с Мастером функций (только
при вводе Y предварительно
сотрите условное значение “={1}”. Если Вы правильно выполните эту часть работы,
на поле вверху уже появится примерный вид графика.

Следующие два шага имеют отношение к оформлению и размещению
графика. На первый раз можно, ничего не меняя, просто нажимать кнопки «Далее» и
«Готово». Полученный черновой вариант графика всегда можно редактировать,
изменять или удалять его отдельные элементы. Обычно для этого щелкают по
нужному элементу графика правой (!) кнопкой мышки. При этом открывается
контекстное меню, в котором выбирают подходящую команду.

Если правой кнопкой мышки щелкнуть по одной из точек графика, то
в контекстном меню можно увидеть команду «Добавить линию тренда». Это и есть
необходимая нам линия. Добавляется она тоже в два шага. На первом выбирается
тип (линейный), на втором – параметры. На вкладке Параметры нам важно поставить
галочки против слов: «показывать уравнение» и «поместить величину
достоверности». Если из теоретических предпосылок понятно, что прямая должна
проходить через начало координат (при нулевой концентрации скорость реакции,
очевидно, равна нулю) поставим галочку и в данном пункте. Примерный вид графика
после добавления линии тренда представлен на рисунке 5. Выведенное уравнение
прямой и величины достоверности совпадает с рассчитанными ранее.

Рисунок 5.

Итак, мы рассмотрели важнейшие приемы работы в Microsoft Excel, необходимые для качественной
обработки данных эксперимента. Разумеется эти приемы не исчерпывают всех
возможностей Excel, и могут развиваться в ходе работы.
Автор статьи с удовольствием ответит на все вопросы, связанные с работой в
данной программе. Желаю успеха!

Задать вопрос.

---

Формула Бернулли в Excel

В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!

Схема независимых испытаний

В общем виде схема повторных независимых испытаний записывается в виде задачи:

Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.

Эта вероятность вычисляется по формуле Бернулли:

$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k}=C_n^k cdot p^k cdot q^{n-k}. qquad(1)
$$

Здесь $C_n^k$ — число сочетаний из $n$ по $k$.

Еще: онлайн калькуляторы для формулы Бернулли.

Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:

• Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
• Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
• События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.

Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.

Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.

Формула Бернулли в Эксель

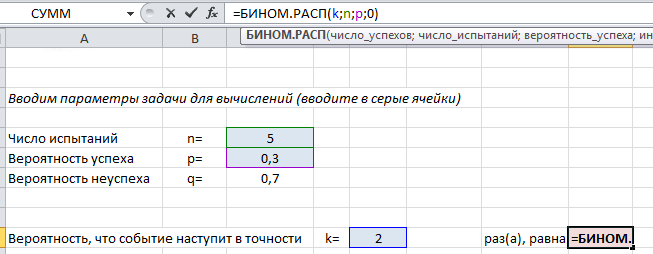
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП(), выдающая определенную вероятность биномиального распределения.

Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0).

Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).

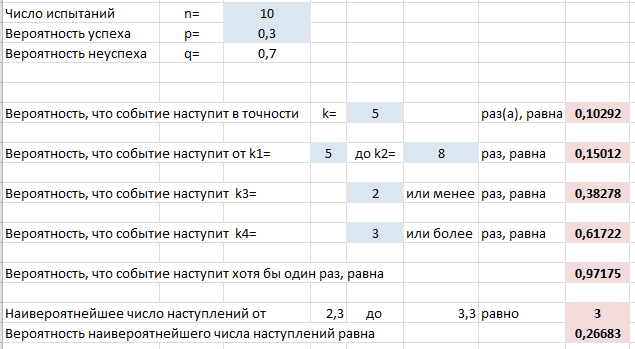
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:

Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):

• Событие произойдет в точности $k$ раз из $n$:
  =БИНОМ.РАСП(k;n;p;0)
  $$P_n(k)=C_n^k cdot p^k cdot q^{n-k}$$
• Событие произойдет от $k_1$ до $k_2$ раз:
  =БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
  $$P_n(k_1le X le k_2)=sum_{i=k_1}^{k_2} C_n^i cdot p^i cdot q^{n-i}$$
• Событие произойдет не более $k_3$ раз:
  =БИНОМ.РАСП(k_3;n;p;1)
  $$P_n(0le X le k_3)=sum_{i=0}^{k_3} C_n^i cdot p^i cdot q^{n-i}$$
• Событие произойдет не менее $k_4$ раз:
  =1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
  $$P_n(k_4le X le n)=sum_{i=k_4}^{n} C_n^i cdot p^i cdot q^{n-i}$$
• Событие произойдет хотя бы один раз:
  =1-БИНОМ.РАСП(0;n;p;0)
  $$P_n( X ge 1)=1-P_n(0)=1-q^{n}$$
• Наивероятнейшее число наступлений события $m$:
  =ОКРУГЛВВЕРХ(n*p-q;0)
  $$np-q le m le np+p$$

Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.

Полезное: расчетный файл по формуле Бернулли

Примеры решений задач

Рассмотрим решение типовых задач.

Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.

Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:

$$
P_7(5)=C_{7}^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146.
$$

Для вероятности 6 или 7 попаданий суммируем:

$$
P_7(6)+P_7(7)=C_{7}^6 cdot 0,75^6 cdot 0,25^1+C_{7}^7 cdot 0,75^7 cdot 0,25^0= \
= 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495.
$$

А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?

Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_{10}(k)=C_{10}^k cdot 0,5^kcdot 0,5^{10-k}=C_{10}^k cdot 0,5^{10}$$
Приступим к вычислениям:

$$1. P_{10}(2)=C_{10}^2 cdot 0,5^{10} = frac{10!}{2!8!}cdot 0,5^{10} approx 0,044.$$

$$2. P_{10}(4)+P_{10}(5)=C_{10}^4 cdot 0,5^{10} + C_{10}^5 cdot 0,5^{10}=left( frac{10!}{4!6!} + frac{10!}{5!5!} right)cdot 0,5^{10} approx 0,451.$$

$$3. P_{10}(0)+P_{10}(1)+P_{10}(2)=C_{10}^0 cdot 0,5^{10} + C_{10}^1 cdot 0,5^{10}+ C_{10}^2 cdot 0,5^{10}=left( 1+10+ frac{10!}{2!8!} right)cdot 0,5^{10} approx 0,055.$$

$$4. P_{10}(7)+P_{10}(8)+P_{10}(9)+P_{10}(10)=\ = C_{10}^7 cdot 0,5^{10} + C_{10}^8 cdot 0,5^{10}+ C_{10}^9 cdot 0,5^{10}+ C_{10}^10 cdot 0,5^{10} =\=left(frac{10!}{3!7!}+ frac{10!}{2!8!} + 10 +1right)cdot 0,5^{10} approx 0,172.$$

$$5. P_{10}(ge 1)=1-P_{10}(0)=1-C_{10}^0 cdot 0,5^{10} = 1- 0,5^{10} approx 0,999.$$

Наивероятнейшее число мальчиков найдем из неравенства:

$$
10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \
4,5 le m le 5,5,\
m=5.
$$

Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).

Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.

Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?

Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!

Полезные ссылки

Расчетный файл эксель для расчетов по формуле Бернулли

Калькуляторы на формулу Бернулли Примеры решений задач

Как решать задачи по теории вероятностей? Решение заданий на заказ

Решебник задач по вероятности

Преподавание физики наряду с изучением теории предполагает исследование реальных объектов, проведение экспериментов и опытов, обработку результатов, установление взаимосвязей. В ходе выполнения лабораторных работ по физике наиболее сложным и трудоемким этапом является обработка результатов экспериментов, требующая многочисленных вычислений. Применение информационных технологий в образовательном процессе позволяет использовать прикладные пакеты программ для обработки результатов физических экспериментов, создания таблиц для выведения результатов, разработки тестов на усвоение материала или определения уровня подготовки. Использование специальных пакетов программ дает возможность упростить расчеты, сократить время на проведение вычислительных операций, рассчитать погрешность, установить зависимости и освободить участников эксперимента от проведения многочисленных рутинных операций. Также использование компьютерных технологий позволяет в более наглядной форме представить результаты эксперимента, создавая графики, таблицы, схемы. Осваивая прикладные программы, обучающиеся могут использовать собственные знания из области информатики, самостоятельно изучать возможности прикладных программ. Использование таких программ существенно повышает интерес к объекту изучения, активизирует самостоятельность в поиске, анализе и выборе методов и средств исследований, формирует умение применять различные программные средства, что задает положительную динамику развития информационной и научно-исследовательской компетенции. Использование компьютерных технологий в ходе лабораторной работы позволит сократить время для вычислений и позволит отвести больше времени для проведения анализа результатов эксперимента и формирования умений делать выводы.

Для предварительной математической обработки и анализа результатов физических экспериментов используют стандартные пакеты прикладных программ, такие как Microsoft Office Excel с дополнительной надстройкой «Пакет анализа». В сравнении со специализированными статистическими программами (Stastistica, Origin), используемыми чаще всего в научной практике, MS Excel обычно не вызывает сложностей у обучающихся. Если встроенных статистических функций не хватает, есть возможность использовать надстройку «Пакет анализа», который предоставляет следующие возможности:

• построение гистограмм,
• извлечение случайных или периодических выборок из набора данных,
• ранжирование данных,
• получение основных статистических характеристик выборки,
• генерации случайных чисел с различным распределением,
• осуществление регрессионного анализа (статистический метод, позволяющий найти уравнение, наилучшим образом описывающее совокупность данных).

Воспользоваться надстройкой Пакет анализа можно, выполнив следующую команду: Сервис — Анализ данных.

Наиболее часто используемыми инструментами в данном пакете являются:

1. Инструмент Гистограмма позволяет построить диаграмму (обычно столбчатую), где для исходного множества значений определяется и отображается число значений, попадающих в интервалы разбиения. Инструмент Гистограмма имеет три аргумента: место расположения данных, место расположение границ интервалов разбиения и верхнюю левую ячейку выходного диапазона, в котором выводятся результаты. Инструмент Гистограмма может создавать отсортированные гистограммы (Парето), выводить накопленные проценты и генерировать диаграммы.
2. Описательная статистика позволяет создавать таблицу основных статистических характеристик для одного или нескольких множеств входных значений. Выходной диапазон этого инструмента содержит таблицу со статистическими характеристиками для каждой переменной из входного диапазона (среднее, стандартная ошибка, медиана, мода, стандартное отклонение, дисперсия выборки, коэффициент эксцесса, коэффициент ассиметрии, размах и др.)

Измерение физической величины происходит в процессе опыта с использованием специальных технических средств для определения её численного отношения к однородной ей величине, которая будет принята за единицу.

На практике не существует абсолютно точных средств и приборов измерений, поэтому результаты проводимых опытов будут в той или иной мере отличатся от истинного значения измеряемой величины. Абсолютную погрешность (либо ошибку) измерения можно определить как разность между измеренным и истинным значениями физической величины:

(1)

В процессе измерения также важно провести оценку погрешности, без которой нельзя говорить о достоверности полученных результатов. Истинное значение измеряемой величины в большинстве физических опытов неизвестно, соответственно вычислить погрешность по формуле 1 не представляется возможным. В связи с этим погрешность измерений определяют по показателям точности измерительных приборов, методики измерений, разбросу экспериментальных данных и т.д. На выходе получают не саму величину , а её приблизительное значение. Результат измерений может быть представлен в следующем виде:

(2)

Такой способ измерения абсолютной погрешности означает, что истинное значение измеряемой величины с высокой вероятностью может находиться в интервале, который именуется доверительным:

(3)

Без определения погрешности результаты измерений представляют собой малую ценность, так как сложно говорить об их достоверности. Согласно целям измерений должна быть определена и точность, с которой необходимо осуществлять измерения.

Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти, например, выпадение решки при подбрасывании монеты или попадание в некоторый объект при стрельбе. В таких ситуациях предсказание точного исхода невозможно, однако можно говорить о вероятности получения того или иного результата.

Случайная погрешность – это составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Наличие случайных погрешностей выявляется при проведении ряда измерений постоянной физической величины, когда оказывается, что результаты измерений не совпадают друг с другом. Случайные погрешности измерений подчиняются статистическим закономерностям и изучаются математической теорией погрешностей.

Представить более наглядным образом изучение закономерностей, которым подчиняются случайные погрешности, можно с помощью построения диаграммы, которая отобразит частоту получения тех либо иных результатов измерений. Данная диаграмма называется гистограммой распределения результатов измерения.

Гистограммы, или линейчатые диаграммы – это удобный и понятный способ обработки и отображения результатов измерений физических величин. Область значений измеряемой величины разделяется на несколько интервалов, которые именуются также карманами, где в виде столбцов отражается количество попавших в такой интервал измерений, называемое частотой. Карманы могут быть не равны между собой, но они должны быть распределены по возрастанию границ. MS Excel позволяет оставлять поле Интервал карманов пустым, в таком случае равномерно распределяя карманы в промежутке от минимального до максимального значения вводимых данных. Число карманов при этом будет равно квадратному корню из количества исходных значений.

Пакет анализа MS Excel позволяет выполнять три типа анализа:

1. Вывод графика.
2. Интегральный процент.
3. Парето (отсортированная гистограмма).

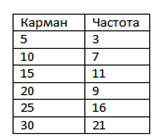
Использование инструмента Гистограмма предполагает введение числа исходных значений в столбце Частота, которые больше или равны левой границе кармана, но меньше левой границы следующего кармана. Пример отображен на рисунке 1.

Рисунок 1. Пример ввода исходных данных для построения гистограммы.

Последним значением столбца является число исходных значений, больших или равных левой границе последнего кармана. Столбец интервалов для карманов копируется в столбец Карман для удобства в случае, когда выходной интервал для результатов анализа задан не рядом с интервалом карманов.

Если установить флажок Интегральный процент в заданной таблице появится столбец с накопляемым процентным вкладом каждого кластера. При выборе вида анализа Парето выходная таблиц будет отсортирована по убыванию частоты. Инструмент Гистограмма создает таблицу числовых констант. При необходимости связи с исходными значениями можно использовать формулы с функцией ЧАСТОТА (например, массив данных, массив карманов).

В качестве примера рассмотрено построение выборочного распределения по данным эксперимента определения периода колебаний. Для этого необходимо указать диапазон карманов – граничных значений, при которых данные будут разделены на группы в интервалы от 0 до 1, от 1 до 1,2, от 1,2 до 1,3 и т.д. При этом следует помнить, что в карман включаются значения по правой границе и не включаются значения по левой границе.

Для построения гистограммы следует выполнить следующий алгоритм действий:

1. Создать таблицу в MS Excel на основе данных проводимого физического эксперимента.
2. Выполнить команду Данные – Анализ данных – Гистограмма.
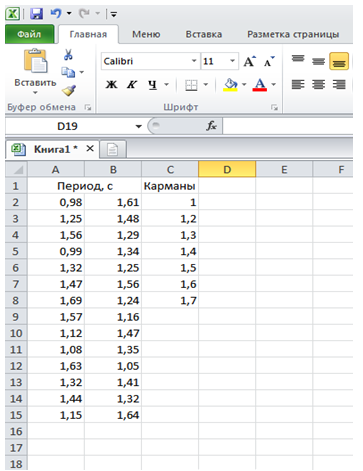
3. Заполнить параметры инструмента Гистограмма в диалоговом окне. Пример ввода данных для построения гистограммы приведен на рисунке 2.

Рисунок 2. Пример ввода данных для построения гистограммы.

1. Осуществить формирование входного интервала на основе диапазона исследуемых данных, в приведенном примере это будут ячейки А2:В15.
2. Заполнить поле Интервал карманов, которое представляет собой границы группировки входных данных, в рассматриваемом примере это ячейки С2:С8. Значения Интервала карманов будут скопированы при построении гистограммы, поэтому для удобства их лучше заполнить числовыми константами, а не формулами. В случае необходимости ввода именно формул, следует использовать абсолютные ссылки, так как в ином случае результаты копирования могут оказаться неверны.
3. Установить Выходной интервал, который является ячейкой для отображения результата, также для вывода гистограммы при необходимости можно использовать новый рабочий лист.
4. Установить флажок Вывод графика для отображения гистограммы. Флажок Интегральный процент используют при вычислении процентов частот с накоплением и для вывода графика интегральных процентов.

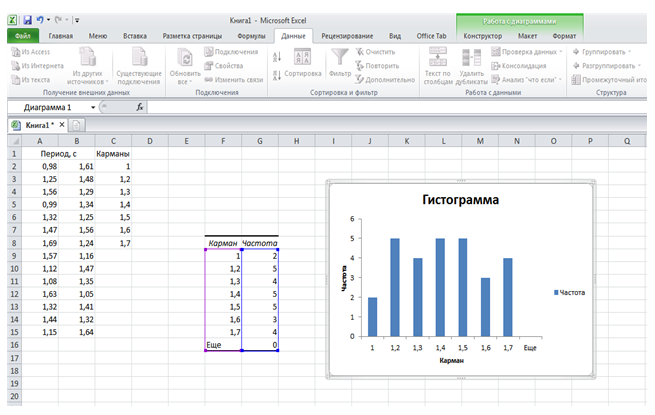
Результат использования инструмента Гистограмма отображен на рисунке 3.

Рисунок 3. Результат применения инструмента Гистограмма

при вычислении статистических характеристик данных физического эксперимента.

Инструмент Описательная статистика является одним из наиболее часто применяемых средств Пакета анализа MS Excel, так как обладает быстротой и простотой вычисления статистических характеристик одномерных выборок.

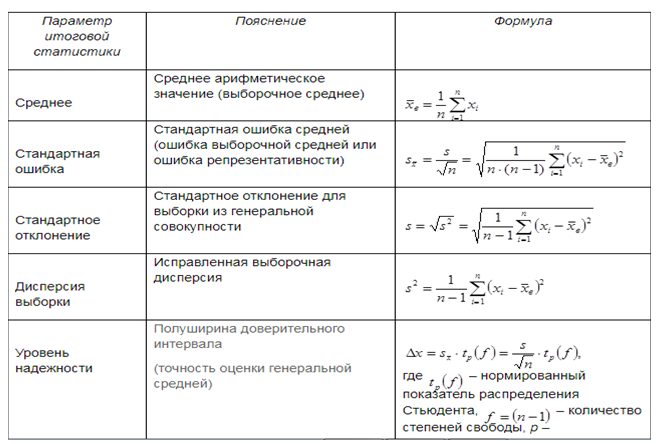
В случае обработки данных случайных выборок первостепенную значимость имеет вычисление их числовых параметров, описывающих тенденции, разброс и изменчивость данных. Для этого используют инструмент Описательная статистика из Пакета анализа, который предоставляет возможность вывода единого статистического отчета по всем характеристикам исследуемых данных. Данный инструмент позволяет создать таблицу параметров описательной статистики для исследуемых данных. В выходном интервале будет отображена таблица, содержащая следующие данные: Среднее, Стандартная ошибка, Медиана, Мода, Стандартное отклонение, Дисперсия выборки, Эксцесс, Асимметричность, Интервал, Минимум, Максимум, Сумма, Счет, Наибольший (k), Наименьший (k) (для любого заданного k) и Уровень надежности (доверительный интервал). На рисунке 4 приведены некоторые из параметров итоговой статистики и формулы для их расчета.

Рисунок 4. Параметры итоговой статистики

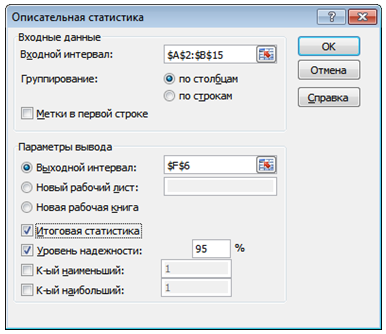
Поле Входной интервал должно содержать ссылку на исследуемый диапазон данных. Для уточнения размещения данных можно использовать переключатель Группирование: по столбцам или по строкам. В случае, когда столбцы или строки данных имеют метки и при установке флажка Метки в первой строке/столбце, они будут использованы в качестве заголовков столбцов статистических параметров в итоговой таблице. Для этой таблицы в поле Выходной интервал следует задать адрес верхней левой ячейки. Если установить флажок Итоговая статистика, будет создана подробная выходная таблица, в которую также можно добавить дополнительные данные, установив соответствующие флажки в диалоговом окне.

Для получения статистических данных с помощью инструмента Описательная статистика используется следующий алгоритм:

1. Данные – Анализ данных – Описательная статистика.
2. Входной интервал представляет собой диапазон исследуемых данных. В приведенном примере это ячейки А2:В15, данные выборки расположены по столбцам, соответственно в поле Группирование установлена метка По столбцам. Пример ввода данных в диалоговое окно Описательная статистика отображен на рисунке 5.

Рисунок 5. Пример заполнения диалогового окна инструмента Описательная статистика

1. Выходной интервал является ячейкой, в которой будет отображена итоговая таблица.
2. В поле Уровень надежности можно выбрать необходимый уровень доверительной вероятности. В большинстве случаев данный показатель равен 95%, соответственно уровень значимости 0,05. Уровень надежности х% – граница доверительного интервала для неизвестного математического ожидания с доверительным уровнем х%, доверительный интервал при этом строится как выборочное среднее плюс-минус данное значение.
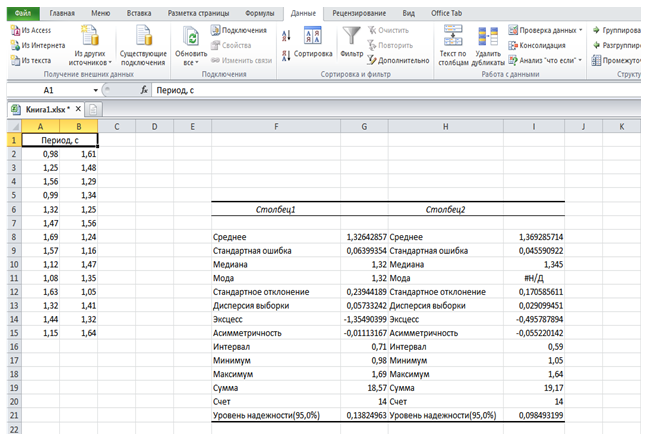
3. Установив флажок Итоговая таблица, в выходном интервале отобразится совокупность статистических показателей исследуемых данных. Результаты использования инструмента Описательная статистика отображен на рисунке 6.

Рисунок 6. Результат применения инструмента Описательная статистикапри вычислении статистических характеристик данных физического эксперимента

На основе полученных статистических характеристик, рассчитанных с помощью Пакета анализа MS Excel, результат измерения периода колебаний рассмотренного примера будет равен для первой и второй совокупности исследуемых данных соответственно Т1 = 1,326 ± 0,138 и Т2 = 1,369 ± 0,0984 при уровне надежности 95%.

Обработка результатов физического эксперимента может осуществляться с помощью различных специальных методов, среди которых Пакет анализа MS Excel является одним из наиболее часто применяемых.

Следует обратить внимание, что расчет параметров в режиме Описательная статистика имеет ряд особенностей:

• не требуется предварительное ранжирование исходных данных (при вычислении показателей ранжирование выделяется автоматически;
• появление в ячейке Мода индикатора ошибки #H/Д указывает, что в анализируемых данных нет одинаковых значений признака;
• индикатор ошибки #ДЕЛ/0! в ячейке Эксцесс и/или Асимметричность означает, что в таблице результатов стандартное отклонение является нулевым или заданный исходный диапазон содержит менее четырех элементов данных.

Создание электронных таблиц на сегодняшний день является простым и естественным способом интерпретации результатов исследований не только при обработке данных физических экспериментов, но и в других сферах деятельности человека. Применения Пакета анализа статистическая обработка данных не занимает большое количество времени, освобождая резервы времени и сил для проведения других экспериментов. Освоив достаточно простой в использовании инструмент MS Excel, можно обрабатывать большие объёмы данных, отображая результаты в наглядной и удобной форме представления. Таким образом, Пакет анализа MS Excel предоставляет огромные возможности для обработки данных физического эксперимента, оптимизируя работу педагогов.

Список литературы:

1. Андрусенко Н.Е., Использование стандартных функций Excel для поиска и связи данных в таблице//информатика и образование.-2003.-№11.-с.7-12.
2. Ивинская Н.Л., решение прикладных задач в Excel//информатика и образование.-2003.-№6.-с.62-64.
3. Леонтьева Н. В. Применение ИКТ в эксперименте лабораторного практикума по физике // Молодой ученый. — 2013. — №6. — С. 700-703.
4. Сидоров М.Г., Обработка данных в Excel //информатика и образование. 2000.-№6.-с. 25-36.
5. Симонович С. В., Информатика: Базовый курс: учеб. / под ред. С. В. Симоновича. – СПб.:Питер, 2005. – 640 с.
6. Романова Ю. Д., Информатика и информационные технологии : учеб. пособие / под ред. Романовой Ю. Д. – М.: Изд-во Эксмо, 2005. – 544 с.
7. Рудикова, Л. В. Microsoft Excel для студента. – СПб.: БВХ-Петербург, 2006. – 386 с.
8. Шрамкова, И. Г. Основы компьютерных технологий: сборник лабораторных работ / И. Г. Шрамкова, Ю. Г. Крат. – Хабаровск: Изд-во ДВГУПС, 2010. – 167 с.