Содержание
- Выполнение аппроксимации
- Способ 1: линейное сглаживание
- Способ 2: экспоненциальная аппроксимация
- Способ 3: логарифмическое сглаживание
- Способ 4: полиномиальное сглаживание
- Способ 5: степенное сглаживание
- Вопросы и ответы
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Урок: Как построить линию тренда в Excel
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
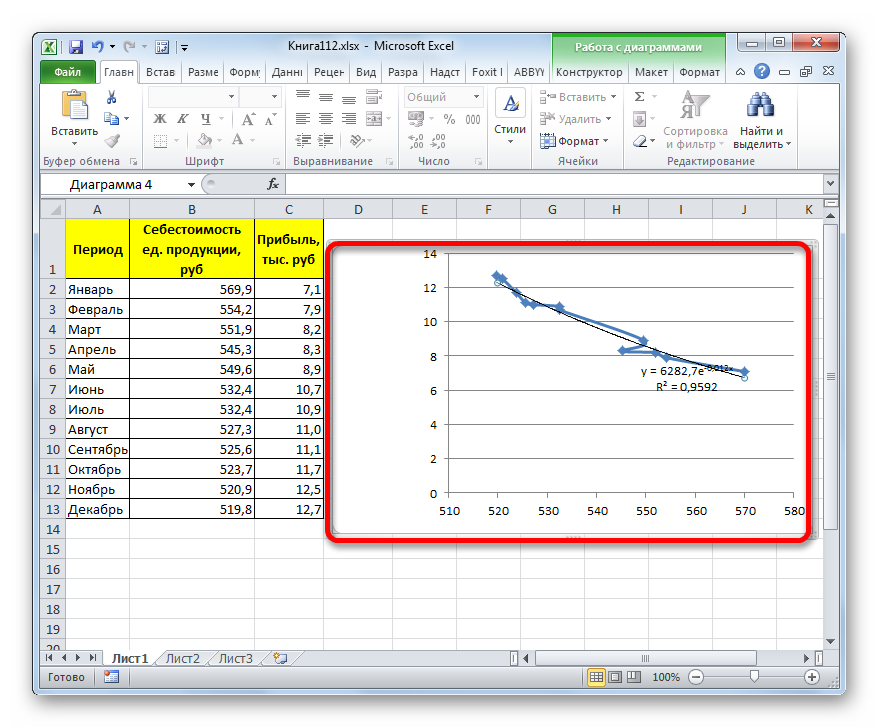
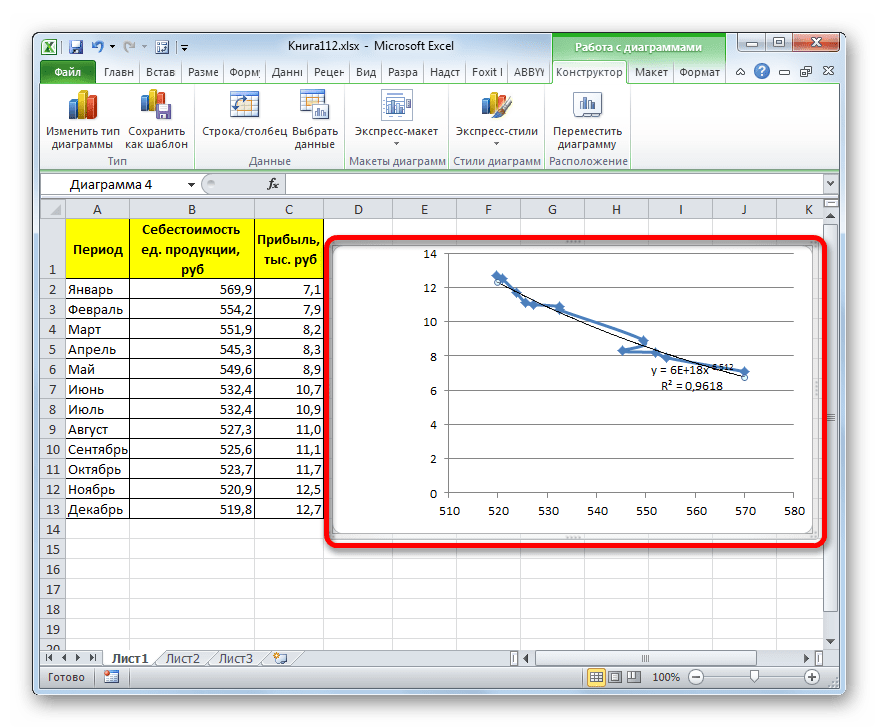
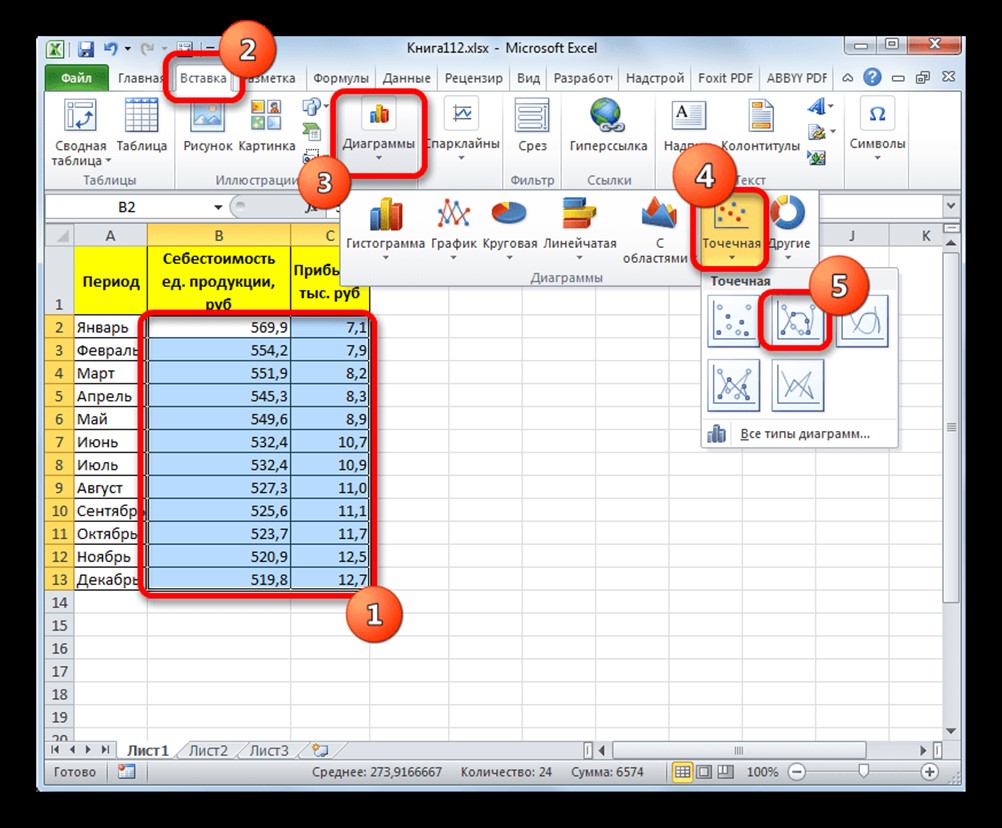
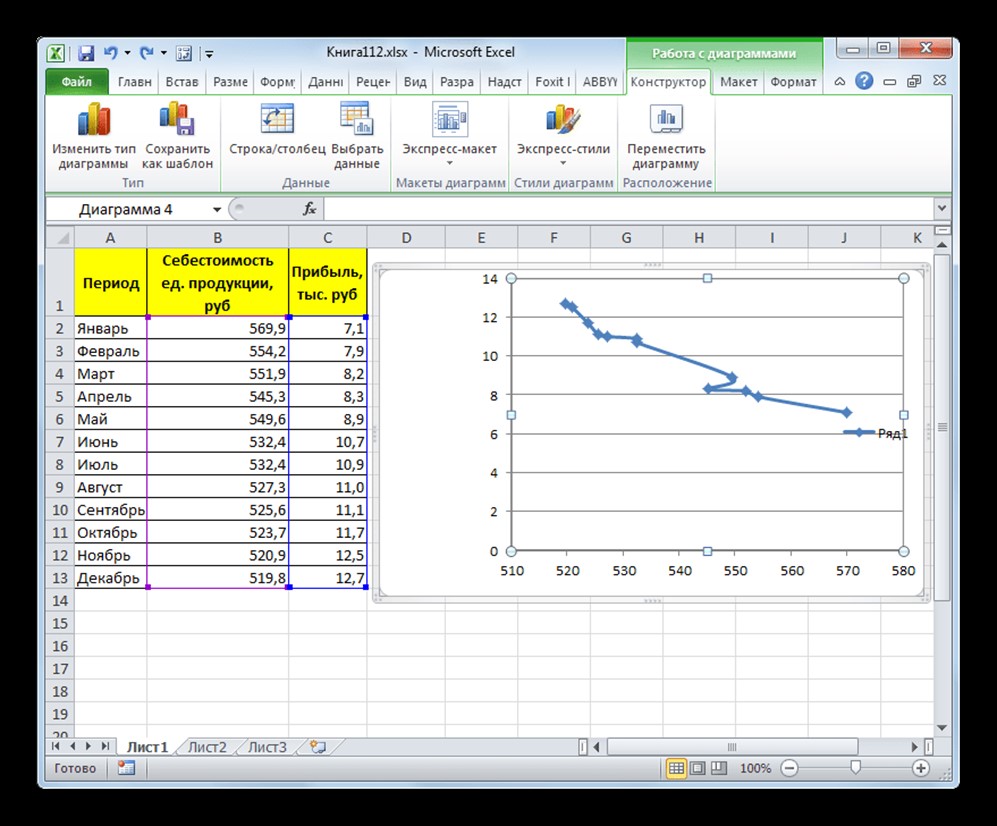
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
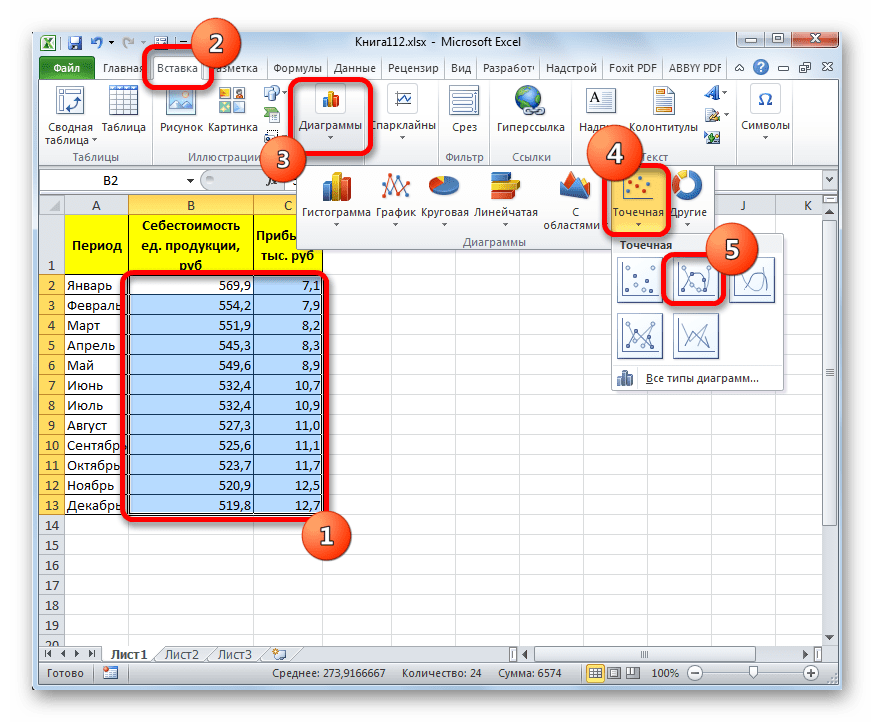
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
- График построен.
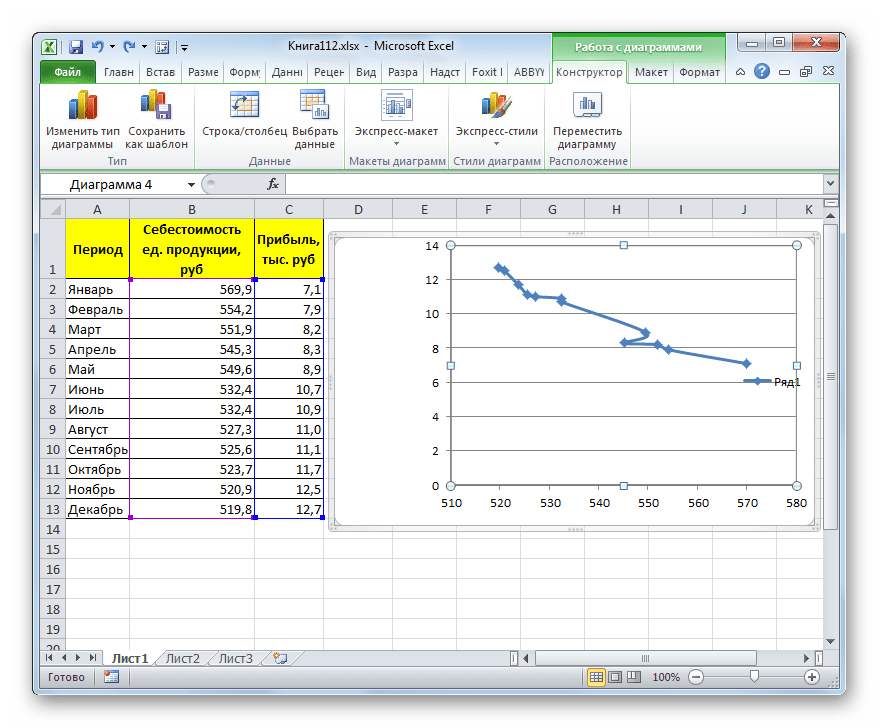
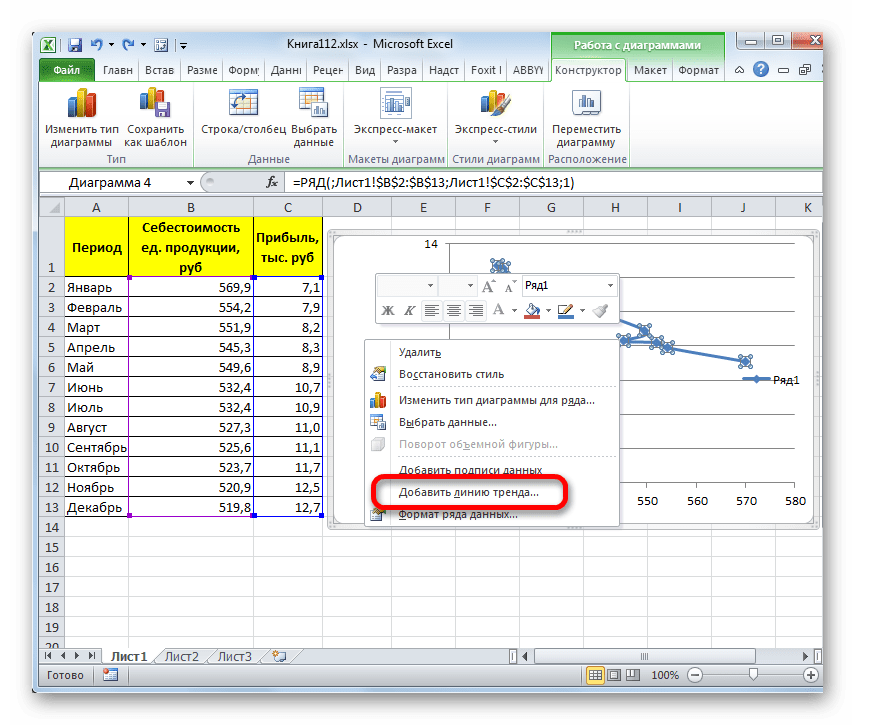
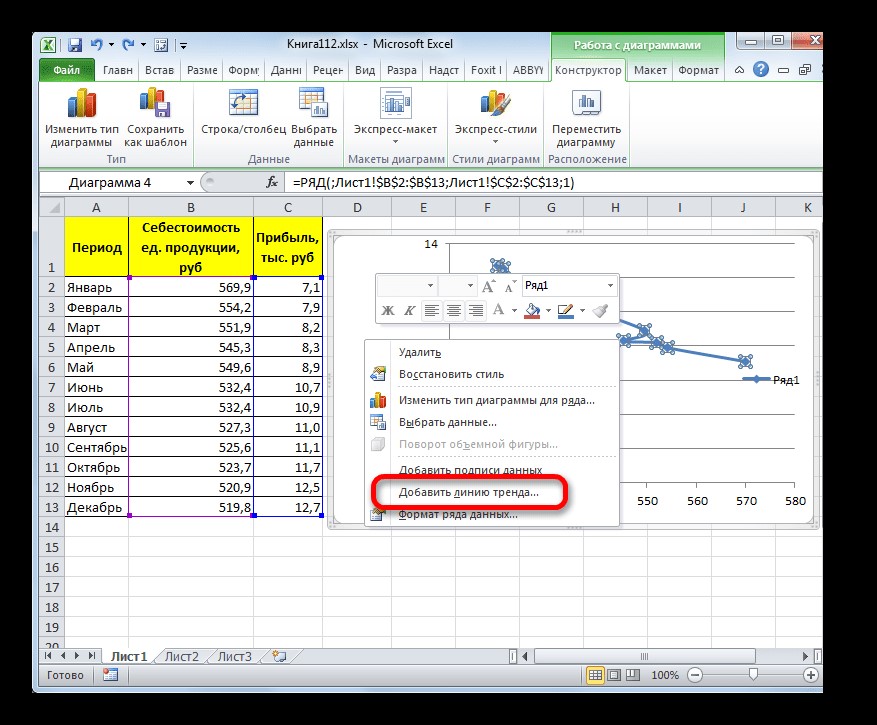
- Для добавления линии тренда выделяем его кликом правой кнопки мыши. Появляется контекстное меню. Выбираем в нем пункт «Добавить линию тренда…».
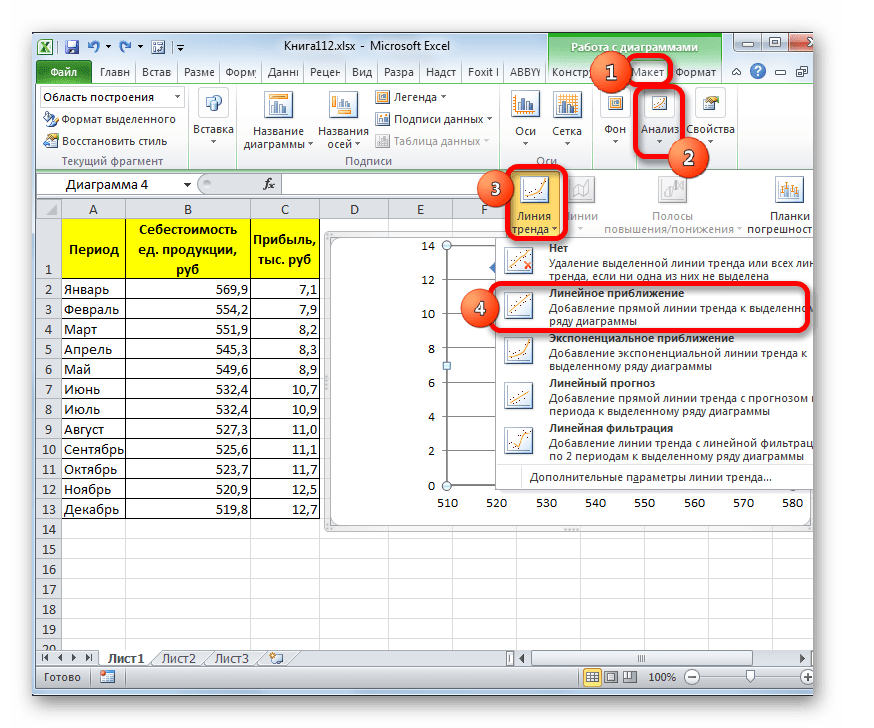
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
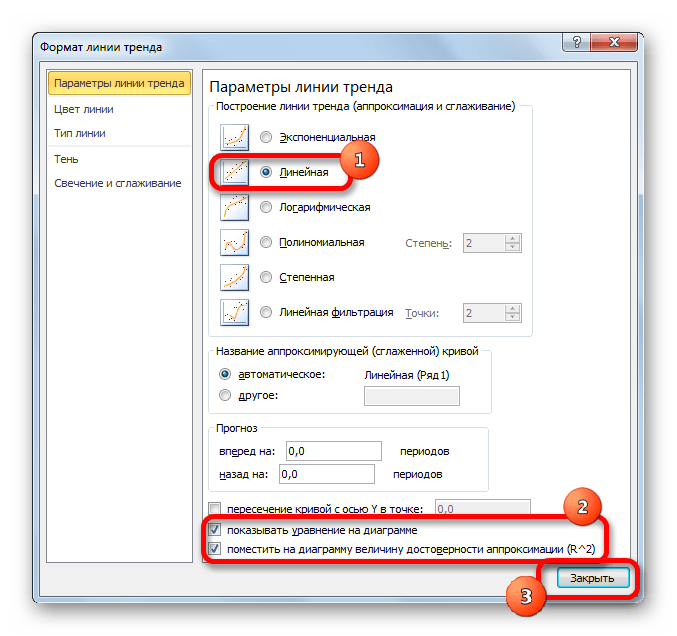
- Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
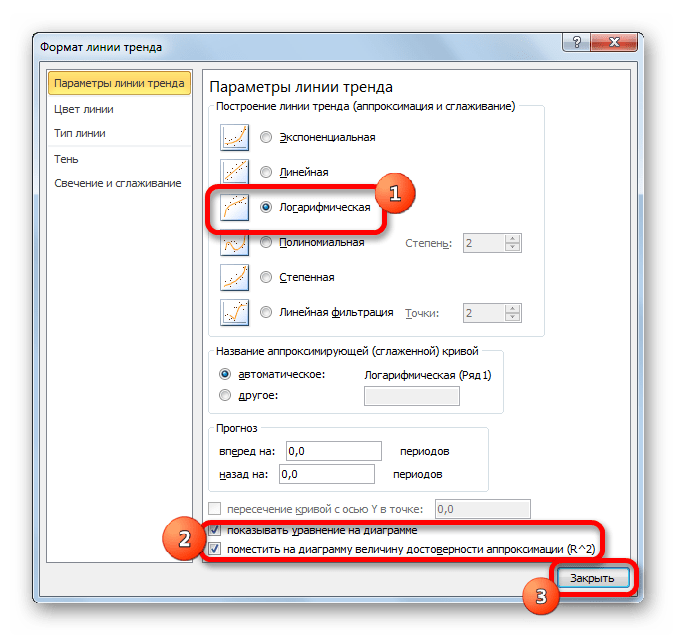
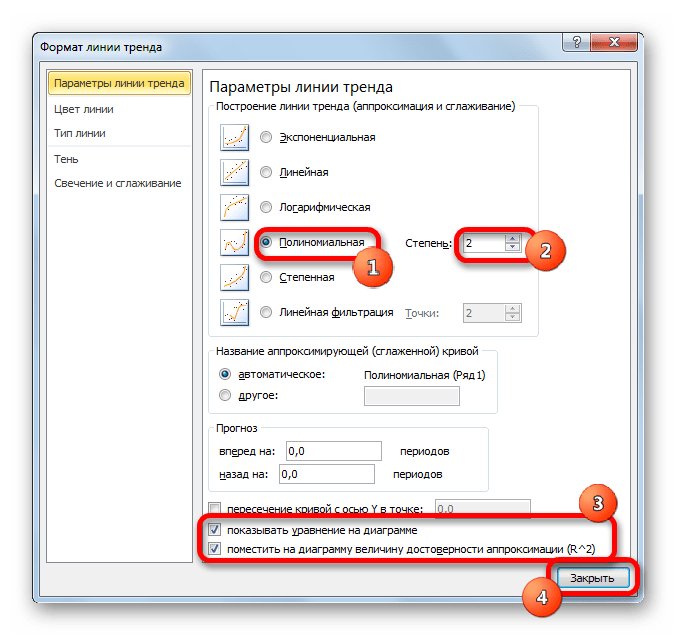
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
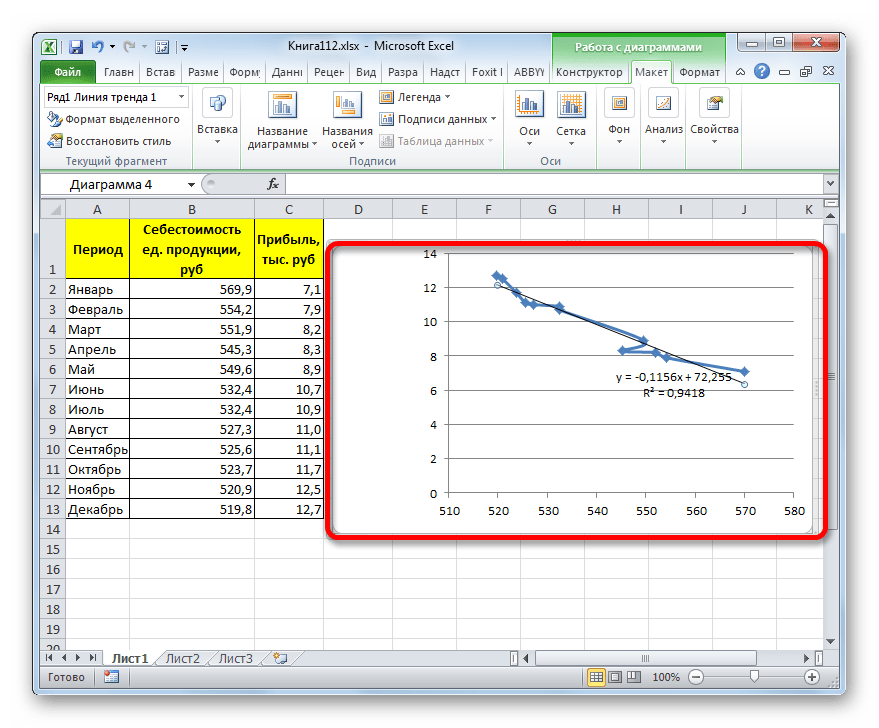
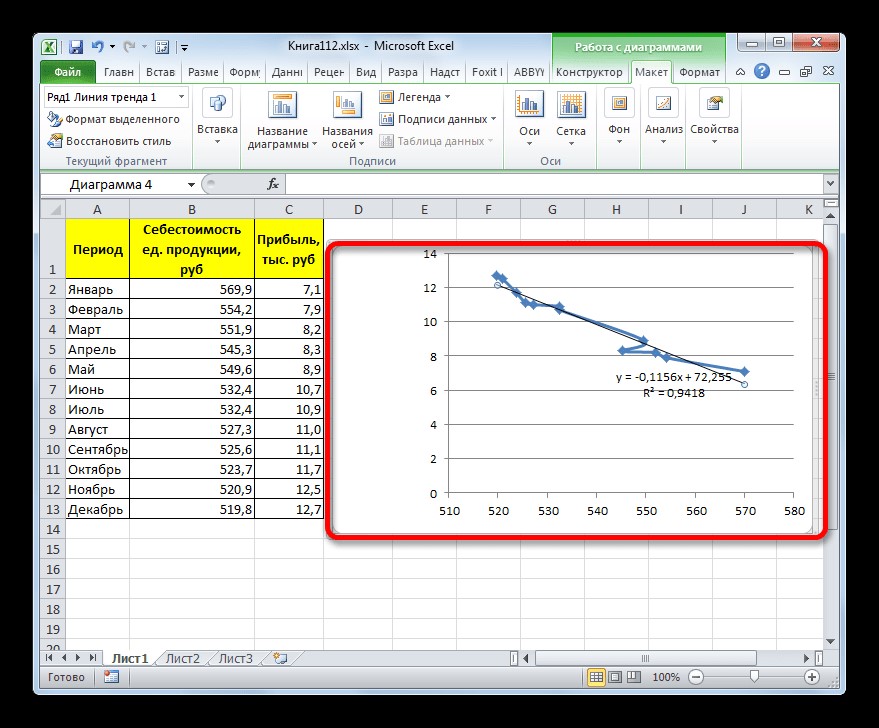
- Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
y=ax+b
В конкретно нашем случае формула принимает такой вид:
y=-0,1156x+72,255
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
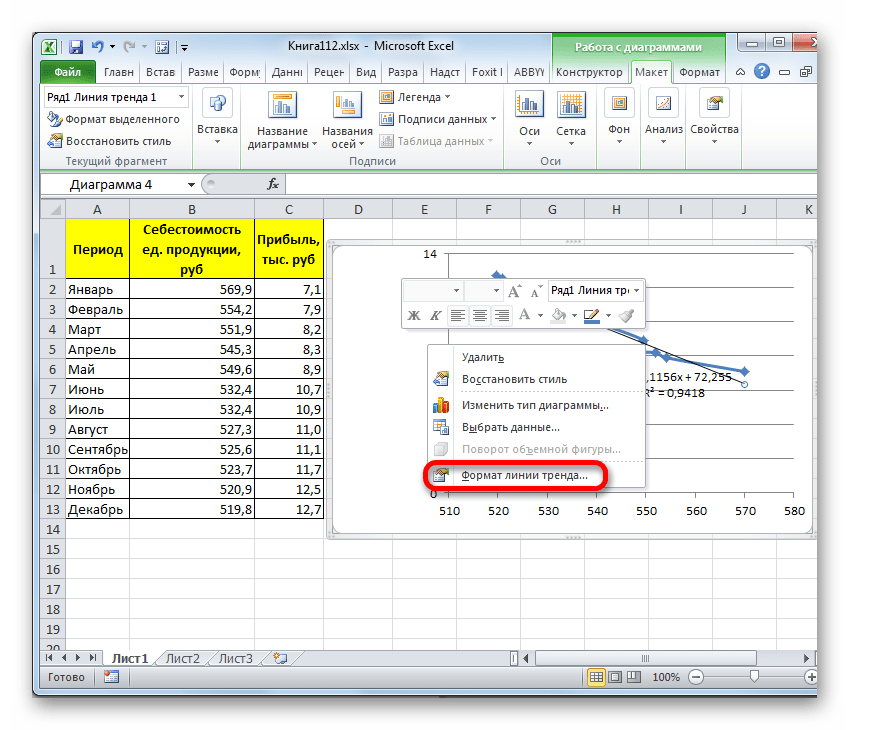
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
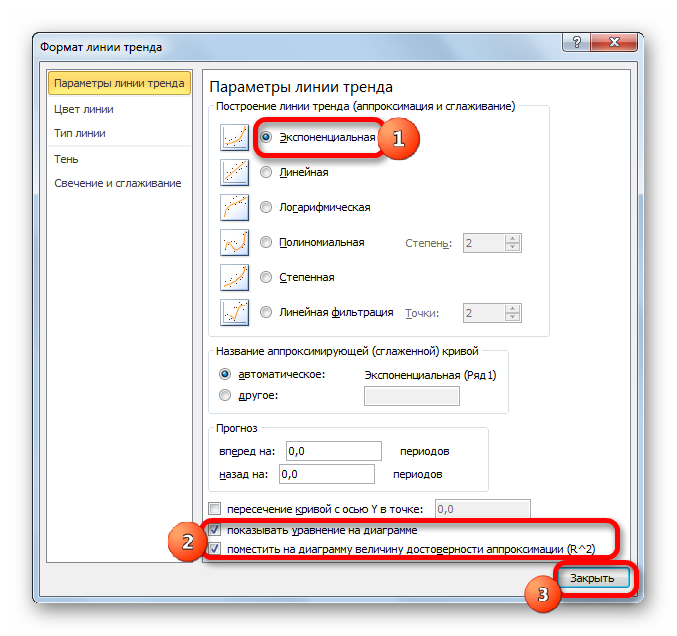
- После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
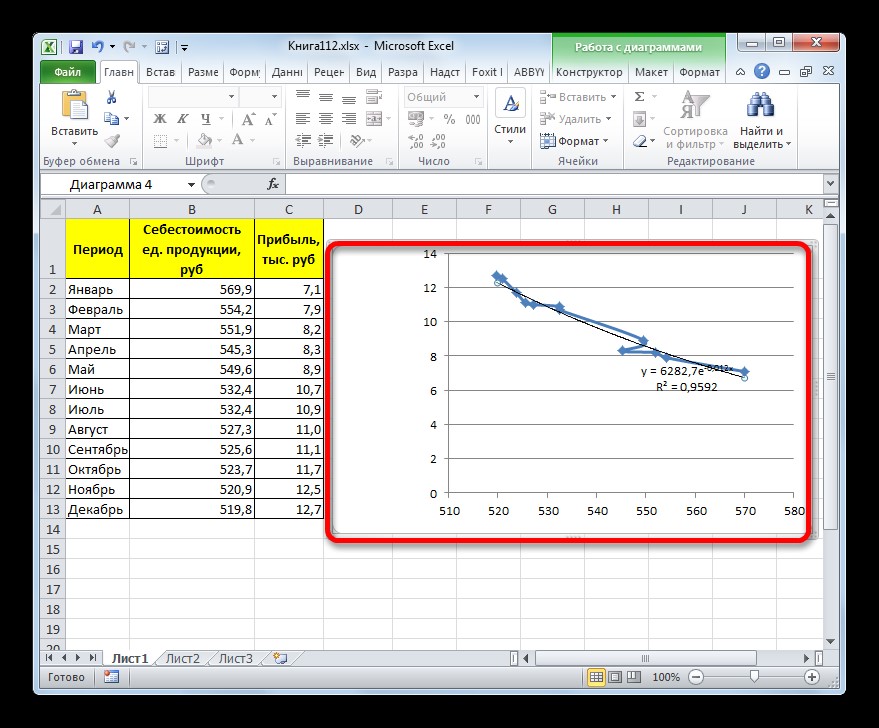
- После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.
Общий вид функции сглаживания при этом такой:
y=be^x
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
y=6282,7*e^(-0,012*x)
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
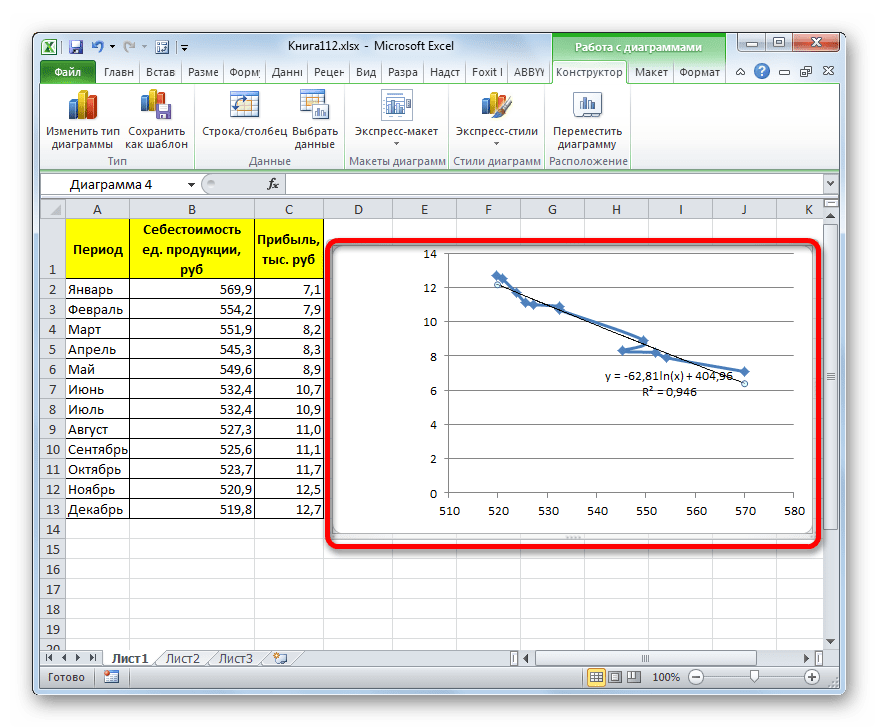
- Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.
В общем виде формула сглаживания выглядит так:
y=a*ln(x)+b
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
y=-62,81ln(x)+404,96
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
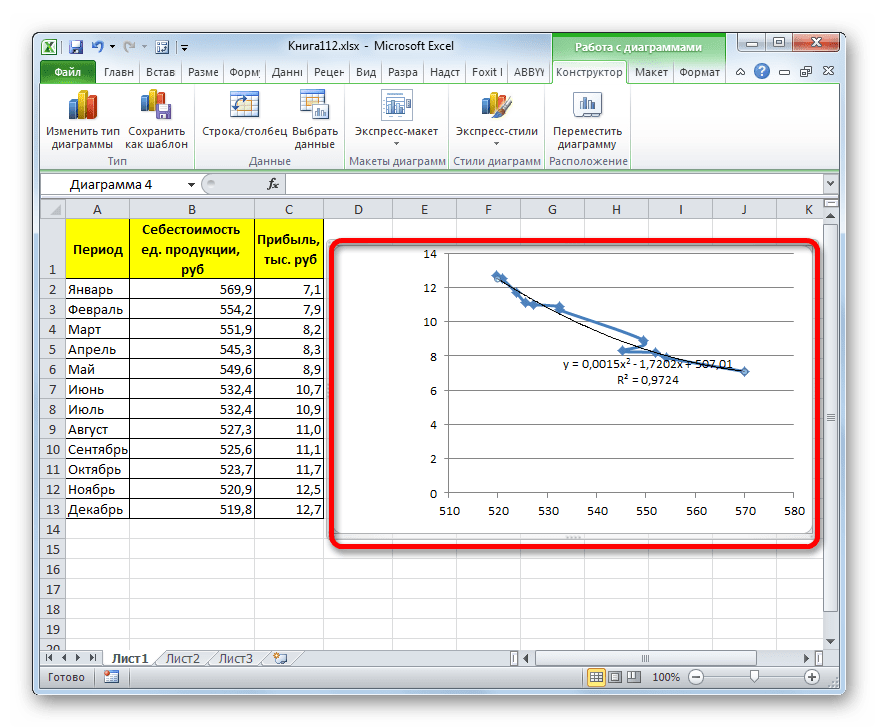
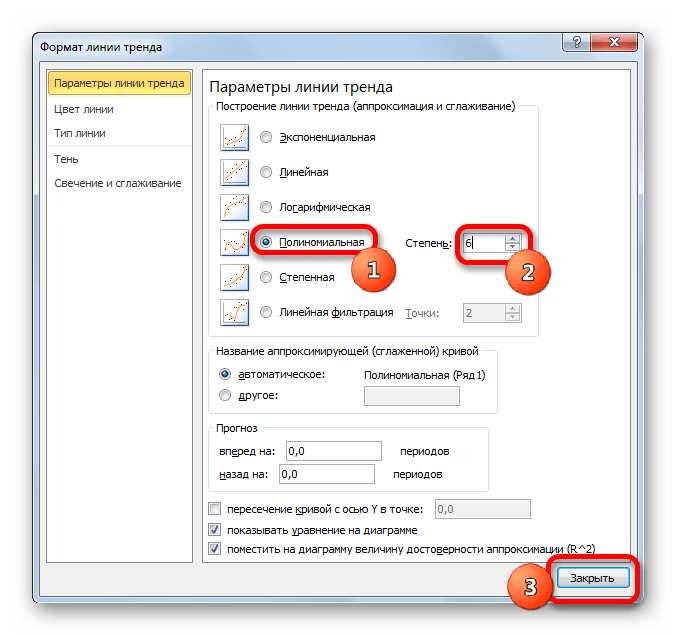
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
- Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
y=a1+a1*x+a2*x^2+…+an*x^nВ нашем случае формула приняла такой вид:
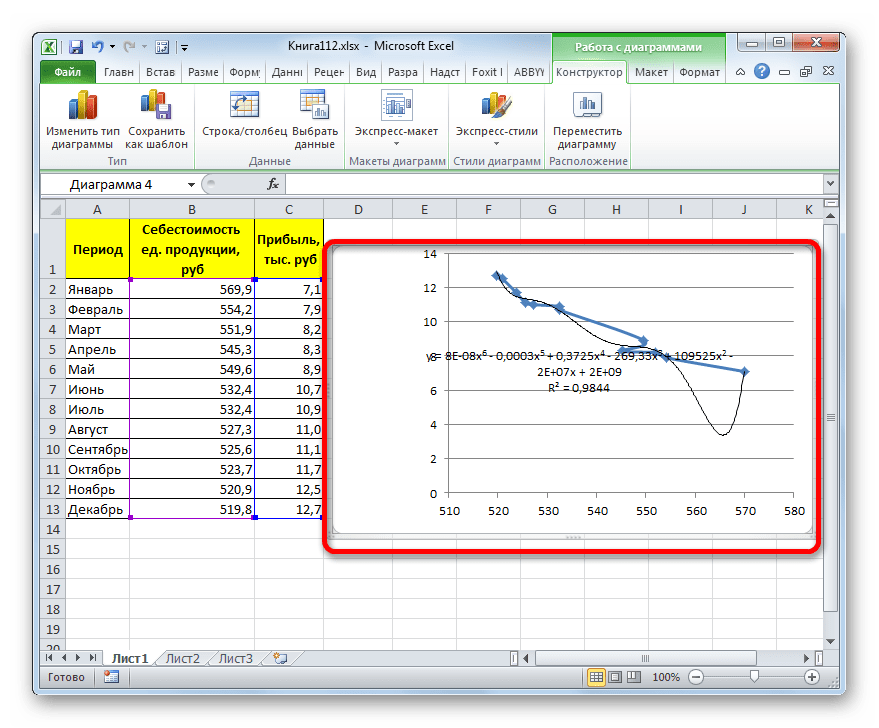
y=0,0015*x^2-1,7202*x+507,01 - Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
- Как видим, после этого наша линия тренда приняла форму ярко выраженной кривой, у которой число максимумов равно шести. Уровень достоверности повысился ещё больше, составив 0,9844.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
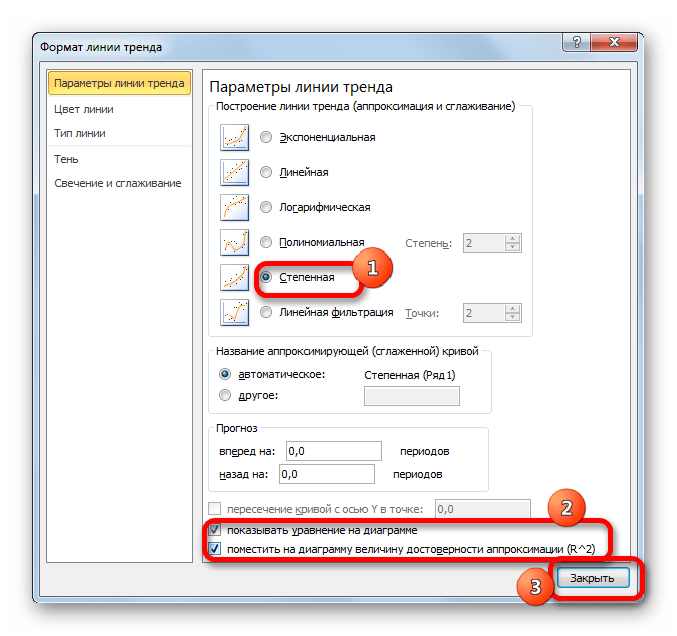
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
- Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
y=bx^n
В конкретно нашем случае она выглядит так:
y = 6E+18x^(-6,512)
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Метод аппроксимации в Microsoft Excel
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
-
Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.
Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
-
Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
-
Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
-
Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
В нашем случае формула приняла такой вид:
y=0,0015*x^2-1,7202*x+507,01
Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
-
Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Помимо этой статьи, на сайте еще 12701 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Аппроксимация в Excel

Учет и контроль! Те, кому за 40 должны хорошо помнить этот лозунг из эпохи построения социализма и коммунизма в нашей стране.
Но без хорошо налаженного учета невозможно эффективное функционирование ни страны, ни области, ни предприятия, ни домашнего хозяйства при любой общественно-экономической формации общества! Для составления прогнозов и планов деятельности и развития необходимы исходные данные. Где их брать? Только один достоверный источник – это ваши статистические учетные данные предыдущих периодов времени.
Учитывать результаты своей деятельности, собирать и записывать информацию, обрабатывать и анализировать данные, применять результаты анализа для принятия правильных решений в будущем должен, в моем понимании, каждый здравомыслящий человек. Это есть ничто иное, как накопление и рациональное использование своего жизненного опыта. Если не вести учет важных данных, то вы через определенный период времени их забудете и, начав заниматься этими вопросами вновь, вы опять наделаете те же ошибки, что делали, когда впервые этим занимались.
«Мы, помню, 5 лет назад изготавливали до 1000 штук таких изделий в месяц, а сейчас и 700 еле-еле собираем!». Открываем статистику и видим, что 5 лет назад и 500 штук не изготавливали…
«Во сколько обходится километр пробега твоего автомобиля с учетом всех затрат?» Открываем статистику – 6 руб./км. Поездка на работу – 107 рублей. Дешевле, чем на такси (180 рублей) более чем в полтора раза. А бывали времена, когда на такси было дешевле…
«Сколько времени требуется для изготовления металлоконструкций уголковой башни связи высотой 50 м?» Открываем статистику – и через 5 минут готов ответ…
«Сколько будет стоить ремонт комнаты в квартире?» Поднимаем старые записи, делаем поправку на инфляцию за прошедшие годы, учитываем, что в прошлый раз купили материалы на 10% дешевле рыночной цены и – ориентировочную стоимость мы уже знаем…
Ведя учет своей профессиональной деятельности, вы всегда будете готовы ответить на вопрос начальника: «Когда. ». Ведя учет домашнего хозяйства, легче спланировать расходы на крупные покупки, отдых и прочие расходы в будущем, приняв соответствующие меры по дополнительному заработку или по сокращению необязательных расходов сегодня.
В этой статье я на простом примере покажу, как можно обрабатывать собранные статистические данные в Excel для возможности дальнейшего использования при прогнозировании будущих периодов.
Аппроксимация в Excel статистических данных аналитической функцией.
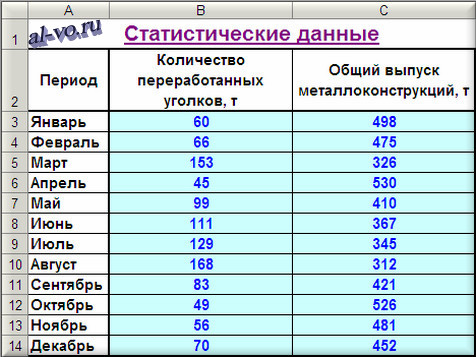
Производственный участок изготавливает строительные металлоконструкции из листового и профильного металлопроката. Участок работает стабильно, заказы однотипные, численность рабочих колеблется незначительно. Есть данные о выпуске продукции за предыдущие 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. После предварительного анализа исходных данных возникло предположение, что суммарный месячный выпуск металлоконструкций существенно зависит от количества уголков в заказах. Проверим это предположение.
Прежде всего, несколько слов об аппроксимации. Мы будем искать закон – аналитическую функцию, то есть функцию, заданную уравнением, которое лучше других описывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а найденное уравнение называется аппроксимирующей функцией для исходной функции, заданной в виде таблицы.
1. Включаем Excel и помещаем на лист таблицу с данными статистики.
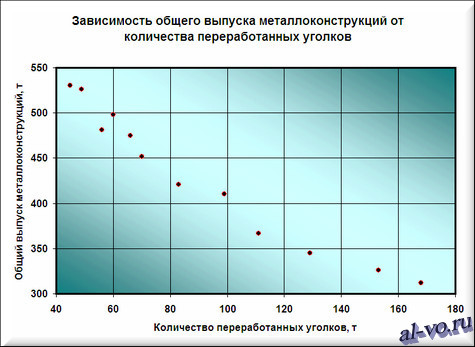
2. Далее строим и форматируем точечную диаграмму, в которой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения исходной функции – общий выпуск металлоконструкций в месяц, заданные таблицей.
О том, как построить подобную диаграмму, подробно рассказано в статье «Как строить графики в Excel?».
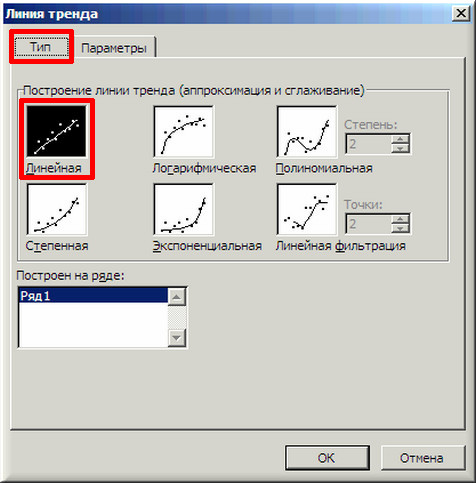
3. «Наводим» мышь на любую из точек на графике и щелчком правой кнопки вызываем контекстное меню (как говорит один мой хороший товарищ — работая в незнакомой программе, когда не знаешь, что делать, чаще щелкай правой кнопкой мыши…). В выпавшем меню выбираем «Добавить линию тренда…».
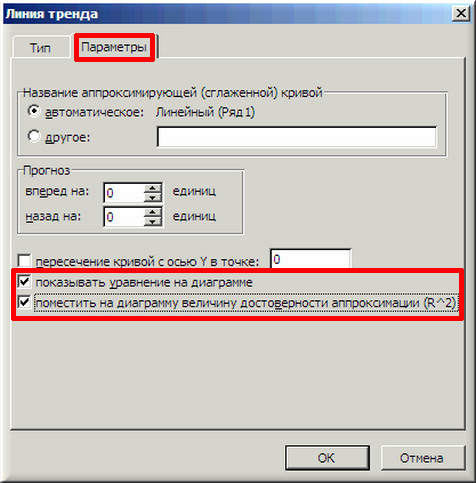
4. В появившемся окне «Линия тренда» на вкладке «Тип» выбираем «Линейная».
5. Далее на вкладке «Параметры» ставим 2 галочки и нажимаем «ОК».
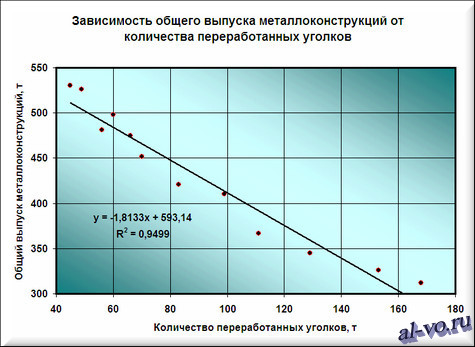
6. На графике появилась прямая линия, аппроксимирующая нашу табличную зависимость.
Мы видим кроме самой линии уравнение этой линии и, главное, мы видим значение параметра R 2 – величины достоверности аппроксимации! Чем ближе его значение к 1, тем наиболее точно выбранная функция аппроксимирует табличные данные!
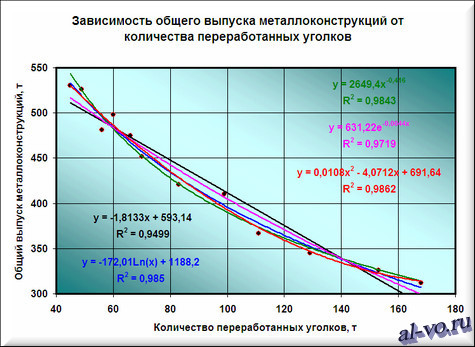
7. Строим линии тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.
Лучше всех из выбранных функций аппроксимирует наши данные полином второй степени, у него максимальный коэффициент достоверности R 2 .
Однако хочу вас предостеречь! Если вы возьмете полиномы более высоких степеней, то, возможно, получите еще лучшие результаты, но кривые будут иметь замысловатый вид…. Здесь важно понимать, что мы ищем функцию, которая имеет физический смысл. Что это означает? Это означает, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только внутри рассматриваемого диапазона значений X, но и за его пределами, то есть ответит на вопрос: «Какой будет выпуск металлоконструкций при количестве переработанных за месяц уголков меньше 45 и больше 168 тонн!» Поэтому я не рекомендую увлекаться полиномами высоких степеней, да и параболу (полином второй степени) выбирать осторожно!
Итак, нам необходимо выбрать функцию, которая не только хорошо интерполирует табличные данные в пределах диапазона значений X=45…168, но и допускает адекватную экстраполяцию за пределами этого диапазона. Я выбираю в данном случае логарифмическую функцию, хотя можно выбрать и линейную, как наиболее простую. В рассматриваемом примере при выборе линейной аппроксимации в excel ошибки будут больше, чем при выборе логарифмической, но не на много.
8. Удаляем все линии тренда с поля диаграммы, кроме логарифмической функции. Для этого щелкаем правой кнопкой мыши по ненужным линиям и в выпавшем контекстном меню выбираем «Очистить».
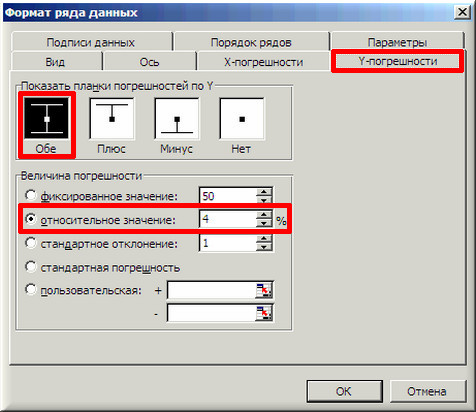
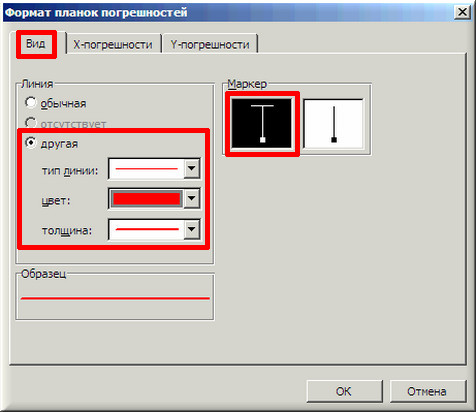
9. В завершении добавим к точкам табличных данных планки погрешностей. Для этого правой кнопкой мыши щелкаем на любой из точек на графике и в контекстном меню выбираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.
10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.
Аналогичным образом форматируются любые другие объекты диаграммы в Excel!
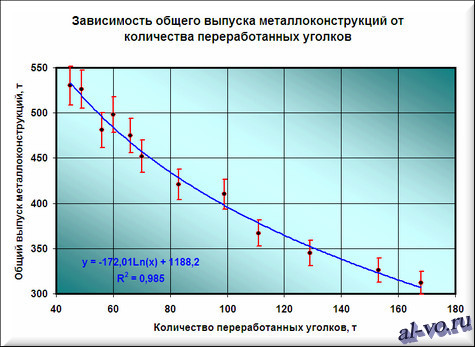
Окончательный результат диаграммы представлен на следующем снимке экрана.
Итоги.
Результатом всех предыдущих действий стала полученная формула аппроксимирующей функции y=-172,01*ln (x)+1188,2. Зная ее, и количество уголков в месячном наборе работ, можно с высокой степенью вероятности (±4% — смотри планки погрешностей) спрогнозировать общий выпуск металлоконструкций за месяц! Например, если в плане на месяц 140 тонн уголков, то общий выпуск, скорее всего, при прочих равных составит 338±14 тонн.
Для повышения достоверности аппроксимации статистических данных должно быть много. Двенадцать пар значений – это маловато.
Из практики скажу, что хорошим результатом следует считать нахождение аппроксимирующей функции с коэффициентом достоверности R 2 >0,87. Отличный результат – при R 2 >0,94.
На практике бывает трудно выделить один самый главный определяющий фактор (в нашем примере – масса переработанных за месяц уголков), но если постараться, то в каждой конкретной задаче его всегда можно найти! Конечно, общий выпуск продукции за месяц реально зависит от сотни факторов, для учета которых необходимы существенные трудозатраты нормировщиков и других специалистов. Только результат все равно будет приблизительным! Так стоит ли нести затраты, если есть гораздо более дешевое математическое моделирование!
В этой статье я лишь прикоснулся к верхушке айсберга под названием сбор, обработка и практическое использование статистических данных. О том удалось, или нет, мне расшевелить ваш интерес к этой теме, надеюсь узнать из комментариев и рейтинга статьи в поисковиках.
Затронутый вопрос аппроксимации функции одной переменной имеет широкое практическое применение в разных сферах жизни. Но гораздо большее применение имеет решение задачи аппроксимации функции нескольких независимых переменных…. Об этом и не только читайте в следующих статьях на блоге.
Подписывайтесь на анонсы статей в окне, расположенном в конце каждой статьи или в окне вверху страницы.
Не забывайте подтверждать подписку кликом по ссылке в письме, которое придет к вам на указанную почту (может прийти в папку «Спам»).
С интересом прочту Ваши комментарии, уважаемые читатели! Пишите!
P.S. (04.06.2017)
Высокоточная красивая замена табличных данных простым уравнением.
Вас не устраивают полученные точность аппроксимации (R 2 2 =0,9963.
Функция ЛГРФПРИБЛ для аппроксимации данных таблиц в Excel
Функция ЛГРФПРИБЛ в Excel предназначена для определения значений, на основе которых может быть построена экспоненциальная кривая, аппроксимирующая имеющиеся числовые данные, и возвращает массив значений. Для корректной работы рассматриваемой функции ее следует вводить как формулу массива.
Методы аппроксимации табличных данных в Excel
Функция ЛГРФПРИБЛ возвращает данные, необходимые для построения кривой, описываемой следующим уравнением:
Если имеется две и более переменных, это уравнение переписывается следующим образом:
Возвращаемые рассматриваемой функцией данные представляют собой следующий массив:
То есть, имеем массив оснований, возводимых в степени (известные значения переменных x), и коэффициент b.
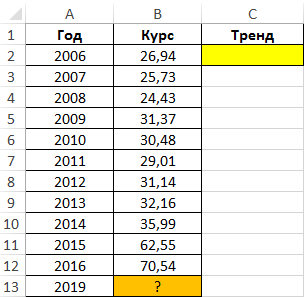
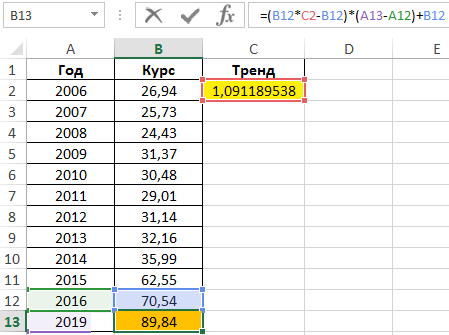
Пример 1. В таблице приведены данные, характеризующие динамику курса доллара на протяжении 10 лет (с 2006 по 2016 год). Необходимо спрогнозировать курс доллара на 2019 год на основании имеющихся данных.
Вид таблицы данных:
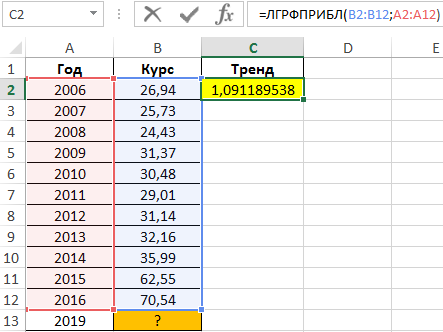
Для расчета тренда (коэффициент, используемый для предсказания последующих значений курса) используем функцию:
- B2:B12 – известные данные зависимой переменной (значения курса);
- A2:A12 – известные данные независимой переменной (года).
Для предсказания курса на 2019 год используем формулу:
Как видно, полученное значение имеет небольшую степень достоверности. Использование данного типа аппроксимации для предсказания курса валют нерационально.
Прогнозирование финансовых результатов методом аппроксимации в Excel
Пример 2. В таблице имеются данные о зарплатах за прошедший год (помесячно). Определить оптимальный способ предсказания размеров зарплат для последующих периодов.
Вид таблицы данных:
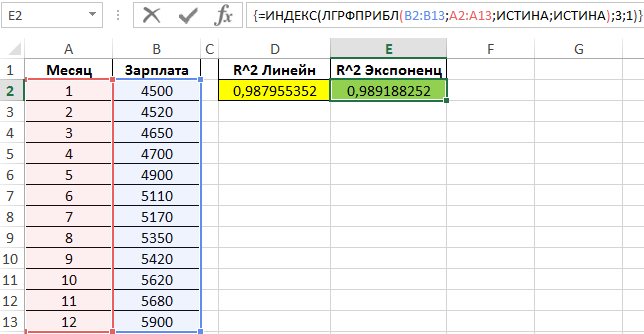
Определим коэффициенты достоверности аппроксимации для линейной и экспоненциальной функций с помощью следующих функций (вводить как формулы массива CTRL+SHIFT+Enter):
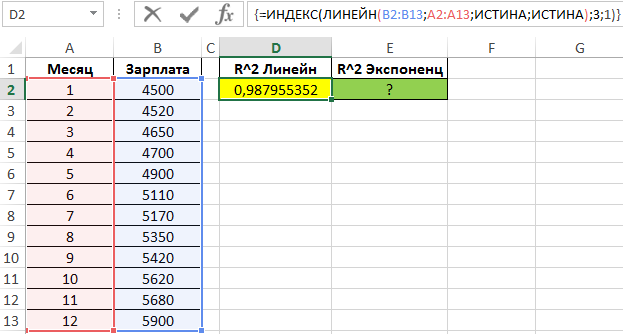
Поскольку обе функции возвращают результат в виде массива данных, в котором в третьей строке первого столбца содержится искомое значение R^2, используем функцию ИНДЕКС для возврата желаемого результата.
Чем ближе значение R^2 к 1, тем выше точность аппроксимации. Как видно, наибольшую точность обеспечивает экспоненциальная функция. Однако разница не является существенной, поэтому использование функции ЛИНЕЙН является допустимым в данном случае.
Правила метода аппроксимации по функции ЛГРФПРИБЛ в Excel
Функция имеет следующую синтаксическую запись:
=ЛГРФПРИБЛ( известные_значения_y; [известные_значения_x];[конст];[статистика])
- известные_значения_y – обязательный, принимает ссылку на диапазон ячеек или массив данных — числовые значения, которые характеризуют состояние зависимой переменной y из указанного выше уравнения;
- [известные_значения_x] – необязательный, принимает ссылку на диапазон ячеек или массив чисел, которые являются уже известными значениями независимой переменной x. Если явно не указан, по умолчанию принимается массив значений <1;2;…N>, где N – количество элементов в массиве, характеризующем известные_значения_y ;
- [конст] – необязательный, принимает данные логического типа, интерпретируемые следующим образом: ИСТИНА или явно не указан – функция вычисляет значение коэффициента b из приведенного выше уравнения, ЛОЖЬ – значение данного коэффициента принимается равным 1;
- [статистика] – необязательный, принимает логические значения ИСТИНА (функция возвращает дополнительные данные на основе проведенного регрессионного анализа) или ЛОЖЬ (значение по умолчанию) – функция возвращает только значения коэффициентов m и b.
- Точность вычислений рассматриваемой функцией зависит от степени близости графика, построенного на основе имеющихся значений, к экспоненциальной кривой.
- В качестве первого или второго аргументов могут быть введены константы массивов, при этом необходимо соблюдать требования к размерностям.
- Если аргумент известные_значения_y указан в виде ссылки на диапазон ячеек, формирующих строку или столбец, каждая строка или столбец соответственно будут интерпретированы как отдельная переменная.
- Если данная функция используется для расчетов с указанием только одной переменной x, первый и второй аргументы могут быть указаны в виде ссылок на диапазоны любой формы. Если по условию имеются две и более переменных x, первый и второй аргументы должны быть указаны в виде векторов данных. Размеры массивов должны совпадать в любом случае.
- Если требуется определить будущие значения переменных (предсказать), можно использовать функцию РОСТ.
источники:
http://al-vo.ru/spravochnik-excel/approksimaciya-v-excel.html
http://exceltable.com/funkcii-excel/approksimaciya-dannyh-lgrfpribl
Функция ЛГРФПРИБЛ в Excel предназначена для определения значений, на основе которых может быть построена экспоненциальная кривая, аппроксимирующая имеющиеся числовые данные, и возвращает массив значений. Для корректной работы рассматриваемой функции ее следует вводить как формулу массива.
Методы аппроксимации табличных данных в Excel
Функция ЛГРФПРИБЛ возвращает данные, необходимые для построения кривой, описываемой следующим уравнением:
F(x) = b*СТЕПЕНЬ(m;x)
Если имеется две и более переменных, это уравнение переписывается следующим образом:
F(x1,x2,…xn)=b*СТЕПЕНЬ(m1;x1)*СТЕПЕНЬ(m2;x2)*…*СТЕПЕНЬ(mn;xn)
Возвращаемые рассматриваемой функцией данные представляют собой следующий массив:
{mn;mn-1;…;m1;b}
То есть, имеем массив оснований, возводимых в степени (известные значения переменных x), и коэффициент b.
Пример 1. В таблице приведены данные, характеризующие динамику курса доллара на протяжении 10 лет (с 2006 по 2016 год). Необходимо спрогнозировать курс доллара на 2019 год на основании имеющихся данных.
Вид таблицы данных:
Для расчета тренда (коэффициент, используемый для предсказания последующих значений курса) используем функцию:
=ЛГРФПРИБЛ(B2:B12;A2:A12)
Описание аргументов:
- B2:B12 – известные данные зависимой переменной (значения курса);
- A2:A12 – известные данные независимой переменной (года).
Результат расчетов:
Для предсказания курса на 2019 год используем формулу:
Результат вычислений:
Как видно, полученное значение имеет небольшую степень достоверности. Использование данного типа аппроксимации для предсказания курса валют нерационально.
Прогнозирование финансовых результатов методом аппроксимации в Excel
Пример 2. В таблице имеются данные о зарплатах за прошедший год (помесячно). Определить оптимальный способ предсказания размеров зарплат для последующих периодов.
Вид таблицы данных:
Определим коэффициенты достоверности аппроксимации для линейной и экспоненциальной функций с помощью следующих функций (вводить как формулы массива CTRL+SHIFT+Enter):
Поскольку обе функции возвращают результат в виде массива данных, в котором в третьей строке первого столбца содержится искомое значение R^2, используем функцию ИНДЕКС для возврата желаемого результата.
Чем ближе значение R^2 к 1, тем выше точность аппроксимации. Как видно, наибольшую точность обеспечивает экспоненциальная функция. Однако разница не является существенной, поэтому использование функции ЛИНЕЙН является допустимым в данном случае.
Правила метода аппроксимации по функции ЛГРФПРИБЛ в Excel
Функция имеет следующую синтаксическую запись:
=ЛГРФПРИБЛ(известные_значения_y;[известные_значения_x];[конст];[статистика])
Описание аргументов:
- известные_значения_y – обязательный, принимает ссылку на диапазон ячеек или массив данных — числовые значения, которые характеризуют состояние зависимой переменной y из указанного выше уравнения;
- [известные_значения_x] – необязательный, принимает ссылку на диапазон ячеек или массив чисел, которые являются уже известными значениями независимой переменной x. Если явно не указан, по умолчанию принимается массив значений {1;2;…N}, где N – количество элементов в массиве, характеризующем известные_значения_y;
- [конст] – необязательный, принимает данные логического типа, интерпретируемые следующим образом: ИСТИНА или явно не указан – функция вычисляет значение коэффициента b из приведенного выше уравнения, ЛОЖЬ – значение данного коэффициента принимается равным 1;
- [статистика] – необязательный, принимает логические значения ИСТИНА (функция возвращает дополнительные данные на основе проведенного регрессионного анализа) или ЛОЖЬ (значение по умолчанию) – функция возвращает только значения коэффициентов m и b.
Примечания:
- Точность вычислений рассматриваемой функцией зависит от степени близости графика, построенного на основе имеющихся значений, к экспоненциальной кривой.
- В качестве первого или второго аргументов могут быть введены константы массивов, при этом необходимо соблюдать требования к размерностям.
- Если аргумент известные_значения_y указан в виде ссылки на диапазон ячеек, формирующих строку или столбец, каждая строка или столбец соответственно будут интерпретированы как отдельная переменная.
- Если данная функция используется для расчетов с указанием только одной переменной x, первый и второй аргументы могут быть указаны в виде ссылок на диапазоны любой формы. Если по условию имеются две и более переменных x, первый и второй аргументы должны быть указаны в виде векторов данных. Размеры массивов должны совпадать в любом случае.
- Если требуется определить будущие значения переменных (предсказать), можно использовать функцию РОСТ.
Решение задач аппроксимации средствами Excel
доктор физ.– мат. наук, профессор Гавриленко В.В. ассистент Парохненко Л.М.
(Национальный транспортный университет)
Теоретическая справка. На практике при моделировании различных про-
цессов, в частности, экономических, физических, технических, социальных,
широко используются те или иные способы вычисления приближенных значе-
ний функций по известным их значениям в некоторых фиксированных точках.
Такого рода задачи приближения функций часто возникают:
∙при построении приближенных формул для вычисления значений характер-
ных величин исследуемого процесса по данным таблиц, полученным в ре-
зультате физического или вычислительного эксперимента;
∙при численном интегрировании, численном дифференцировании, числен-
ном решении дифференциальных уравнений и т.д.;
∙при необходимости вычисления значений функций в промежуточных точ-
ках рассматриваемого интервала;
∙при определении значений характерных величин процесса за пределами рас-
сматриваемого интервала, в частности, при необходимости заглянуть в
“ прошлое”), то есть при определении значений показателей процесса до на-
чала наблюдения;
∙в прогнозировании, то есть при получении предварительных оценок буду-
щих значений интересуемых показателей процесса (возможность заглянуть
в“ будущее”).
Если для моделирования некоторого процесса, заданного таблицей, по-
строить приближенно описывающую данный процесс функцию на основе ме-
тода наименьших квадратов, то она называется аппроксимирующей функцией
(регрессией), а сама задача построения аппроксимирующих функций называет-
ся задачей аппроксимации.
В данной статье рассмотрены возможности пакета Excel [1–3] при реше-
нии задач аппроксимации, а именно, приведены методы и приемы построения
(создания) регрессий для таблично заданных функций, что является основой регрессионного анализа.
ВExcel для построения регрессий имеются такие возможности, как:
1)добавление выбранных регрессий (линий тренда) в диаграмму, построенную на основе таблицы данных для исследуемой характеристики процесса (этим инструментом можно воспользоваться лишь при наличии построенной диа-
граммы);
2)использование встроенных статистических функций рабочего листа Excel,
позволяющих получать регрессии (линии тренда) на основе таблицы исход-
ных данных (использование данного инструмента предварительно не связы-
вается с наличием соответствующей диаграммы).
Добавление линий тренда в диаграмму
Для таблицы данных, описывающих некоторый процесс и представленных диаграммой, в Excel имеется эффективный инструмент регрессионного анали-
за, позволяющий:
∙ строить на основе метода наименьших квадратов и добавлять в диаграмму пять типов регрессий (линий тренда), которые с той или иной степенью точно-
сти моделируют исследуемый процесс;
∙добавлять к диаграмме уравнение построенной регрессии;
∙определять степень соответствия выбранной регрессии отображаемым на диаграмме данным.
Построенные модели процесса – линии тренда (trendlines) показывают
тенденцию изменения данных, дают возможность определять значения иссле-
дуемой характеристики в промежуточных точках, прогнозировать поведение данного процесса в будущем (задача экстраполяции), а также заглянуть в его прошлое.
На основе данных диаграммы Excel позволяет получать такие типы регрес-
сий или линий тренда, как линейный, полиномиальный, логарифмический, сте-
пенной, экспоненциальный, которые задаются уравнением y = y(x) , где x – неза-
висимая переменная, которая часто принимает значения последовательности натурального ряда чисел (1; 2; 3; …) и производит, например, отсчет времени протекания исследуемого процесса.
1. Линейная регрессия хороша при моделировании характеристик, значения которых увеличиваются или убывают с постоянной скоростью. Это наиболее простая в построении, но наименее точная модель исследуемого процесса.
Строится в соответствии с уравнением
y = m x + b ,
где m – угол наклона линейной регрессии к оси абсцисс; b – координата точки пересечения линейной регрессии с осью ординат.
2. Полиномиальная линия тренда полезна для описания характеристик,
имеющих несколько ярко выраженных экстремумов (максимумов и миниму-
мов). Выбор степени полиномиальной линии тренда (полинома) определяется количеством экстремумов исследуемой характеристики. Так, полином второй степени может хорошо описать характеристику, имеющую только один макси-
мум или минимум; полином третьей степени – не более двух экстремумов; по-
лином четвертой степени – не более трех экстремумов и т.д.
Строится в соответствии с уравнением
y = c0 + c1 x + c2 x2 + c3 x3 + c4 x4 + c5 x5 + c6 x6 ,
где коэффициенты c0 , c1, c2 ,…c6 – константы.
3. Логарифмическая линия тренда с успехом применяется при моделирова-
нии характеристик, значения которых вначале быстро растут или убывают по величине, а затем постепенно стабилизируются.
Строится в соответствии с уравнением
y = c × ln(x) + b ,
где коэффициенты b, с – константы.
4. Степенная линия тренда дает хорошие результаты, если значения иссле-
дуемой зависимости характеризуются постоянным изменением скорости роста.
Примером такой зависимости может служить график равноускоренного движе-
ния автомобиля. При наличии в данных нулевых или отрицательных значений использовать степенную линию тренда нельзя.
Строится в соответствии с уравнением
y = c × x b ,
где коэффициенты b, с – константы.
5. Экспоненциальная линия тренда следует использовать в том случае, если скорость изменения данных непрерывно возрастает. Для данных, содержащих нулевые или отрицательные значения, этот вид приближения неприменим.
Строится в соответствии с уравнением
y = c × eb×x ,
где коэффициенты b, с – константы.
При подборе линии тренда Excel автоматически рассчитывает значение величины R2, которая характеризует достоверность аппроксимации: чем ближе значение R2 к единице, тем надежнее линия тренда аппроксимирует исследуе-
мый процесс. При необходимости значение R2 всегда можно отобразить на
диаграмме.
Определяется по формуле
|
R 2 = 1 — |
Σ1 |
Σ1 = ∑(y j − Yj )2 |
S2 = ∑Yj2 — |
1 |
× (∑Yj )2 |
||||
|
S2 |
, где |
; |
. |
||||||
|
j |
j |
n j |
Для добавления линии тренда к ряду данных следует:
1. Активизировать построенную на основе ряда данных диаграмму, т.е. щелк-
нуть в пределах области диаграммы. В главном меню появится пункт Диа—
грамма.
2. После щелчка на этом пункте на экране появится меню, в котором следует выбрать команду Добавить линию тренда.
Пункты 1–2 легко реализуются также следующим приемом: направить ука-
затель мыши к графику, построенного на ряде данных, и щелкнуть правой кла-
вишей мыши, и в появившемся контекстном меню выбрать команду Добавить
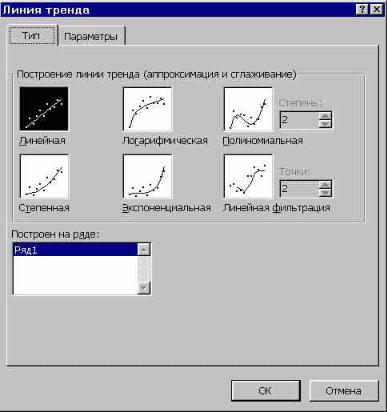
линию тренда. На экране появится диалоговое окно Линия тренда с раскры-
той вкладкой Тип (рис.1).
Рис.1. Вкладка Тип диалогового окна Формат линии тренда
3. Выбрать на вкладке Тип необходимый тип линии тренда (по умолчанию выбирается тип Линейный). Для типа Полиномиальная в поле Степень сле-
дует задать степень выбранного полинома.
4. В поле Построен на ряде перечислены все ряды данных рассматриваемой диаграммы. Для добавления линии тренда к конкретному ряду данных следует в поле Построен на ряде выбрать его имя.
5. При необходимости, перейдя на вкладку Параметры (рис.2), можно для ли-
нии тренда задать следующие параметры:
∙ Изменить название линии тренда в поле Название аппроксимирующей
(сглаженной) кривой;
∙ Задать количество периодов (вперед или назад) для прогноза в поле Про—
гноз.
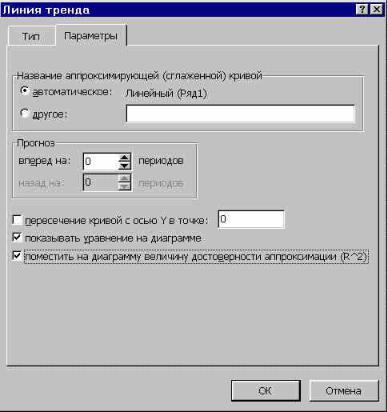
∙ Вывести в область диаграммы уравнение линии тренда, для чего следует ус-
тановить флажок для опции «показать уравнение на диаграмме».
∙ Вывести в область диаграммы значение достоверности аппроксимации R2,
для чего следует установить флажок для опции «поместить на диаграмму ве—
личину достоверности аппроксимации (R^2)».
∙ Задать точку пересечения линии тренда с осью Y, для чего следует устано-
вить флажок для опции «пересечение кривой с осью Y в точке:». 6. Нажать клавишу OK.
Рис.2. Вкладка Параметры диалогового окна Линия тренда
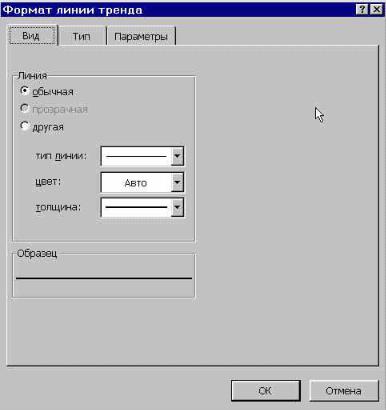
Для редактирования уже построенной линии тренда следует:
1. Щелкнуть левой клавишей мыши по той линии тренда, которую требуется
изменить.
2. Нажать в главном меню клавишу Формат, а появившемся контекстном ме-
ню выбрать команду Выделенная линия тренда.
Пункты 1–2 легко реализуются также следующим приемом: направить ука-
затель мыши к графику линии тренда, щелкнуть правой клавишей мыши, и в появившемся контекстном меню выбрать команду Формат линии тренда.
Еще легче реализуются пункты 1–2: двойным щелчком левой клавишей мыши по графику линии тренда.
3. На экране появится диалоговое окно Формат линии тренда (рис.3), содер-
жащее три вкладки: Вид, Тип, Параметры, причем содержимое вкладок Тип,
Параметры полностью совпадает с аналогичными вкладками диалогового ок-
на Линия тренда (рис.1–2).
4.При необходимости, перейдя на вкладку Вид (рис.3), можно для линии тренда задать тип линии, ее цвет и толщину.
5.Нажать клавишу OK.
Для удаления уже построенной линии тренда следует выбрать удаляемую линию тренда и нажать клавишу Delete.
Достоинствами этого инструмента регрессионного анализа являются:
∙ относительная легкость построения на диаграммах линии тренда без созда-
ния для нее таблицы данных;
∙достаточно широкий перечень типов предложенных линий трендов, причем в этот перечень входят наиболее часто используемые регрессии;
∙возможность прогнозирования поведения исследуемого процесса на произ-
вольное (в пределах здравого смысла) количество шагов вперед, а также назад;
∙возможность получения уравнения линии тренда в аналитическом виде;
∙возможность, при необходимости, получения оценки достоверности прове-
денной аппроксимации.
Кнедостаткам можно отнести следующие моменты:
∙построение линии тренда осуществляется лишь при наличии построенной на ряде данных диаграммы;
∙несколько загроможден процесс формирования рядов данных для исследуе-
мой характеристики на основании полученных для нее уравнений линий трен-
да, так как коэффициенты этих уравнений при каждом изменении значений ря-
да данных пересчитываются, но лишь в пределах области диаграммы;
∙ в отчетах сводных диаграмм при изменении представления диаграммы или связанного отчета сводной таблицы имеющиеся линии тренда не сохраняются,
то есть до проведения линий тренда или другого форматирования отчета свод-
ных диаграмм следует убедиться, что макет отчета удовлетворяет необходи-
мым требованиям.
Рис.3. Вкладка Вид диалогового окна Формат линии тренда
Линиями тренда можно дополнить ряды данных, представленные на гра-
фиках, гистограммах, плоских ненормированных диаграммах с областями, ли-
нейчатых, точечных, пузырьковых и биржевых диаграммах.
Нельзя дополнить линиями тренда ряды данных на объемных, нормиро-
ванных, лепестковых, круговых и кольцевых диаграммах. При замене типа диа-
граммы на один из вышеперечисленных, а также при изменении представления отчета сводной диаграммы или связанного отчета сводной таблицы соответст-
вующие данным линии тренда будут утеряны.
Использование встроенных функций Excel
ВExcel имеется также инструмент регрессионного анализа для построения линий тренда вне области диаграммы. Для этой цели можно использовать ряд статистических функций рабочего листа, однако все они позволяют строить лишь линейные или экспоненциальные регрессии.
ВExcel имеется несколько вариантов построения линейной регрессии (ли-
нейного тренда), в частности:
∙с помощью функции ТЕНДЕНЦИЯ;
∙с помощью функции ЛИНЕЙН;
∙с помощью функций НАКЛОН и ОТРЕЗОК.
ВExcel имеется также несколько вариантов построения экспоненциальной линии тренда, в частности:
∙с помощью функции РОСТ;
∙с помощью функции ЛГРФПРИБЛ.
Следует отметить, что приемы построения регрессий с помощью функций
ТЕНДЕНЦИЯ и РОСТ практически совпадают. То же самое можно сказать и о паре функций ЛИНЕЙН и ЛГРФПРИБЛ. Для всех этих четырех функций при создании таблицы значений используются такие возможности Excel, как формулы массивов, что несколько загромождает процесс построения регрес-
сий. Заметим также, что построение (создание) линейной регрессии, на наш взгляд, легче всего осуществить с помощью функций НАКЛОН и ОТРЕЗОК,
где первая из них определяет угловой коэффициент линейной регрессии, а вто-
рая – отрезок, отсекаемый регрессией на оси ординат.
Достоинствами данного инструмента регрессионного анализа являются:
∙ достаточно простой однотипный процесс формирования рядов данных ис-
следуемой характеристики для всех встроенных статистических функций, за-
дающих линии тренда;
∙ стандартная методика построения линий тренда на основе сформированных рядов данных;
∙ возможность прогнозирования поведения исследуемого процесса на необ-
ходимое количество шагов вперед или назад.
К недостаткам данного инструмента можно отнести то, что в Excel нет встроенных функций для создания других (кроме линейного и экспоненциаль-
ного) типов линий тренда. Это обстоятельство часто не позволяет подобрать с помощью выше перечисленных встроенных функций достаточно точную мо-
дель исследуемого процесса, а также получать близкие к реальности прогнозы.
Кроме того, при использовании функций ТЕНДЕНЦИЯ и РОСТ не известны уравнения линий тренда.
Следует отметить, что в этой статье авторы не ставили целью излагать курс регрессионного анализа с той или иной степенью полноты. Основная цель ста-
тьи – на конкретных примерах показать возможности пакета Excel при реше-
нии задач аппроксимации; продемонстрировать, каким эффективными инстру-
ментами для построения регрессий и прогнозирования обладает Excel; проил-
люстрировать, как относительно легко такие задачи могут быть решены даже пользователем, не владеющим глубокими знаниями регрессионного анализа.
Предложенная в статье методика по овладению навыков решения средства-
ми Excel такого рода задач (см. также [4 – 7], где приведены методики решения в Excel систем линейных алгебраических уравнений, нелинейных уравнений,
задач оптимизации, транспортных задач) может быть полезна и интересна пользователям. Это связано с тем, что пакет Excel установлен практически на каждом современном компьютере, в то время как такие известные специализи-
рованные математические пакеты, как Mathematica, Maple, Matlab, Mathcad,
обладающие более мощными возможностями для построения регрессий и про-
гнозирования, используются значительно меньшей пользовательской аудито-
рией.
Ниже приводятся решения конкретных задач с помощью перечисленных инструментов пакета Excel.
Задача 1. Для таблицы данных о прибыли автотранспортного предприятия за 1995–2002 г.г. необходимо выполнить следующие действия:
Михаил Витер
Эксперт по предмету «Информационные технологии»
Задать вопрос автору статьи
Определение 1
Аппроксимация табличных функций в Excel — это определение аппроксимирующей функции, которая является близкой к заданной.
Понятие аппроксимации
Среди разных методик прогнозирования следует отдельно выделить метод аппроксимации. С его помощью имеется возможность осуществления приблизительных подсчетов и вычисления планируемых показателей, за счёт подмены исходных объектов на более простые. В Excel также присутствует возможность применения этого метода с целью выполнения прогнозов и анализа.
Название этого метода произошло от латинского слова “proxima”, то есть, «ближайшая». Как раз приближение за счет упрощения и сглаживания некоторых показателей, формирование из них тенденции и считается его основой. Но эту методику можно применять не только для прогнозирования, но и для изучения уже полученных результатов. Поскольку аппроксимация выступает, по существу, как упрощение исходных данных, а упрощенную версию легче изучать.
Аппроксимация табличных функций в Excel
Основным инструментом, при помощи которого реализуется сглаживание в Excel, является формирование линии тренда. Суть заключается в том, что на базе уже существующих показателей выполняется достраивание графика функции на будущие периоды. Основным предназначением линии тренда очевидно является формирование прогнозов или определение общей тенденции.
Эта линия может быть построена с использованием одного из следующих типов аппроксимации:
линейная,
экспоненциальная,
логарифмическая,
полиномиальная,
* степенная.
Рассмотрим некоторые из этих вариантов более подробно, и начнем с линейной аппроксимации, которая фактически является линейным сглаживанием. Прежде всего, следует рассмотреть наиболее простую версию аппроксимации, то есть, при помощи линейной функции.
Замечание 1
Сначала необходимо построить график, на базе которого будет осуществляться процедура сглаживания.
«Аппроксимация табличных функций в Excel » 👇
Чтобы построить график, необходимо взять таблицу, в которой, например, помесячно указывается себестоимость единицы продукции, выпускаемой организацией, и соответствующая прибыль за данный период. Графическая функция, которую необходимо построить, будет отображать зависимость роста прибыли от уменьшения себестоимости продукции. При построении графика сначала надо выделить столбцы «Себестоимость единицы продукции» и «Прибыль». После этого следует переместиться на вкладку «Вставка». Затем на ленте в блоке инструментов «Диаграммы» выполнить щелчок указателем мыши по кнопке «Точечная». В открывшемся списке нужно выбрать наименование «Точечная с гладкими кривыми и маркерами». Как раз такой вид диаграмм больше всего подходит для работы с линией тренда, а, следовательно, и для использования метода аппроксимации в Excel.
Рисунок 1. Параметры для построения графика. Автор24 — интернет-биржа студенческих работ
Затем будет построен следующий график:
Рисунок 2. Точечная с гладкими кривыми и маркерами. Автор24 — интернет-биржа студенческих работ
Чтобы добавить линию тренда, необходимо выделить график кликом правой кнопки мыши, после чего появится контекстное меню. Следует осуществить выбор в нем пункта «Добавить линию тренда…».
Рисунок 3. Добавить линию тренда на график. Автор24 — интернет-биржа студенческих работ
Имеется и другой вариант добавления линии тренда. В дополнительной группе вкладок на ленте «Работа с диаграммами» следует переместиться во вкладку «Макет». Затем в блоке инструментов «Анализ» необходимо сделать щелчок по кнопке «Линия тренда», после чего откроется список. Поскольку в нашем случае рассматривается применение линейной аппроксимации, то из предложенных позиций следует выбрать «Линейное приближение».
Если же был выбран первый вариант действий с добавлением через контекстное меню, то далее будет открыто окно формата. В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» необходимо установить переключатель в позицию «Линейная». Если это необходимо, то следует поставить галочку около позиции «Показывать уравнение на диаграмме». После данных действий на диаграмме будет отображено уравнение сглаживающей функции.
Кроме того, для сравнения разных вариантов аппроксимации можно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Этот показатель варьируется в диапазоне от нуля до единицы. Чем его значение больше, тем точнее выполнена аппроксимация. Считается, что если величина данного показателя равна 0,85 и выше, то сглаживание может считаться достоверным, а если показатель ниже, то его достоверность ниже допустимой. После проведения всех вышеуказанных настроек, следует нажать на кнопку «Закрыть», размещенную в нижней части окна. Появится линия тренда.
Рисунок 4. Отображение линии тренда. Автор24 — интернет-биржа студенческих работ
При выполнении линейной аппроксимации линия тренда обозначается черной прямой линией. Приведенный тип сглаживания может быть использован в самых простых случаях, когда данные меняются достаточно быстро и зависимость величины функции от аргумента является очевидной. Сглаживание, которое применяется в этом варианте, может быть описано следующей формулой:
y = ax + b.
Для конкретного варианта, приведенного выше, формула будет иметь следующий вид:
y = ‒ 0,1156x + 72,255.
Значение достоверности аппроксимации в рассмотренном случае равняется 0,9418, что считается достаточно приемлемым результатом, который характеризует сглаживание как достоверное.
Далее рассмотрим экспоненциальный тип аппроксимации в Excel. Для изменения типа линии тренда, следует выделить ее кликом правой кнопки мыши и в открывшемся меню нужно выбрать пункт «Формат линии тренда…». После этого будет запущено уже применявшееся ранее окно формата. В блоке выбора типа аппроксимации необходимо установить переключатель в положение «Экспоненциальная». Остальные настройки следует оставить такими же, как и в первом варианте, и затем выполнить щелчок по кнопке «Закрыть». После этого линия тренда будет построена на графике, как показано на рисунке ниже:
Рисунок 5. Экспоненциальный тип аппроксимации. Автор24 — интернет-биржа студенческих работ
При использовании этого метода линия тренда обладает несколько изогнутой формой. Причем уровень достоверности равняется 0,9592, что выше, чем при использовании линейной аппроксимации.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание
- 1 Выполнение аппроксимации
- 1.1 Способ 1: линейное сглаживание
- 1.2 Способ 2: экспоненциальная аппроксимация
- 1.3 Способ 3: логарифмическое сглаживание
- 1.4 Способ 4: полиномиальное сглаживание
- 1.5 Способ 5: степенное сглаживание
- 1.6 Помогла ли вам эта статья?
- 2 Аппроксимация в Excel статистических данных аналитической функцией.
- 3 Итоги.
- 4 P.S. (04.06.2017)
- 5 Высокоточная красивая замена табличных данных простым уравнением.
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Урок: Как построить линию тренда в Excel
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
- График построен.
- Для добавления линии тренда выделяем его кликом правой кнопки мыши. Появляется контекстное меню. Выбираем в нем пункт «Добавить линию тренда…».
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
- Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
- Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
y=ax+b
В конкретно нашем случае формула принимает такой вид:
y=-0,1156x+72,255
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
- После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
- После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.
Общий вид функции сглаживания при этом такой:
y=be^x
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
y=6282,7*e^(-0,012*x)
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
- Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.
В общем виде формула сглаживания выглядит так:
y=a*ln(x)+b
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
y=-62,81ln(x)+404,96
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
- Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
y=a1+a1*x+a2*x^2+…+an*x^nВ нашем случае формула приняла такой вид:
y=0,0015*x^2-1,7202*x+507,01 - Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
- Как видим, после этого наша линия тренда приняла форму ярко выраженной кривой, у которой число максимумов равно шести. Уровень достоверности повысился ещё больше, составив 0,9844.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
- Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
y=bx^n
В конкретно нашем случае она выглядит так:
y = 6E+18x^(-6,512)
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Опубликовано 05 Янв 2014
Рубрика: Справочник Excel | 18 комментариев
(Обратите внимание на дополнительный раздел от 04.06.2017 в конце статьи.)
Учет и контроль! Те, кому за 40 должны хорошо помнить этот лозунг из эпохи построения социализма и коммунизма в нашей стране.
Но без хорошо налаженного учета невозможно эффективное функционирование ни страны, ни области, ни предприятия, ни домашнего хозяйства при любой общественно-экономической формации общества! Для составления прогнозов и планов деятельности и развития необходимы исходные данные. Где их брать? Только один достоверный источник – это ваши статистические учетные данные предыдущих периодов времени.
Учитывать результаты своей деятельности, собирать и записывать информацию, обрабатывать и анализировать данные, применять результаты анализа для принятия правильных решений в будущем должен, в моем понимании, каждый здравомыслящий человек. Это есть ничто иное, как накопление и рациональное использование своего жизненного опыта. Если не вести учет важных данных, то вы через определенный период времени их забудете и, начав заниматься этими вопросами вновь, вы опять наделаете те же ошибки, что делали, когда впервые этим занимались.
«Мы, помню, 5 лет назад изготавливали до 1000 штук таких изделий в месяц, а сейчас и 700 еле-еле собираем!». Открываем статистику и видим, что 5 лет назад и 500 штук не изготавливали…
«Во сколько обходится километр пробега твоего автомобиля с учетом всех затрат?» Открываем статистику – 6 руб./км. Поездка на работу – 107 рублей. Дешевле, чем на такси (180 рублей) более чем в полтора раза. А бывали времена, когда на такси было дешевле…
«Сколько времени требуется для изготовления металлоконструкций уголковой башни связи высотой 50 м?» Открываем статистику – и через 5 минут готов ответ…
«Сколько будет стоить ремонт комнаты в квартире?» Поднимаем старые записи, делаем поправку на инфляцию за прошедшие годы, учитываем, что в прошлый раз купили материалы на 10% дешевле рыночной цены и – ориентировочную стоимость мы уже знаем…
Ведя учет своей профессиональной деятельности, вы всегда будете готовы ответить на вопрос начальника: «Когда!!!???». Ведя учет домашнего хозяйства, легче спланировать расходы на крупные покупки, отдых и прочие расходы в будущем, приняв соответствующие меры по дополнительному заработку или по сокращению необязательных расходов сегодня.
В этой статье я на простом примере покажу, как можно обрабатывать собранные статистические данные в Excel для возможности дальнейшего использования при прогнозировании будущих периодов.
Производственный участок изготавливает строительные металлоконструкции из листового и профильного металлопроката. Участок работает стабильно, заказы однотипные, численность рабочих колеблется незначительно. Есть данные о выпуске продукции за предыдущие 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. После предварительного анализа исходных данных возникло предположение, что суммарный месячный выпуск металлоконструкций существенно зависит от количества уголков в заказах. Проверим это предположение.
Прежде всего, несколько слов об аппроксимации. Мы будем искать закон – аналитическую функцию, то есть функцию, заданную уравнением, которое лучше других описывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а найденное уравнение называется аппроксимирующей функцией для исходной функции, заданной в виде таблицы.
1. Включаем Excel и помещаем на лист таблицу с данными статистики.
2. Далее строим и форматируем точечную диаграмму, в которой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения исходной функции – общий выпуск металлоконструкций в месяц, заданные таблицей.
О том, как построить подобную диаграмму, подробно рассказано в статье «Как строить графики в Excel?».
3. «Наводим» мышь на любую из точек на графике и щелчком правой кнопки вызываем контекстное меню (как говорит один мой хороший товарищ — работая в незнакомой программе, когда не знаешь, что делать, чаще щелкай правой кнопкой мыши…). В выпавшем меню выбираем «Добавить линию тренда…».
4. В появившемся окне «Линия тренда» на вкладке «Тип» выбираем «Линейная».
5. Далее на вкладке «Параметры» ставим 2 галочки и нажимаем «ОК».
6. На графике появилась прямая линия, аппроксимирующая нашу табличную зависимость.
Мы видим кроме самой линии уравнение этой линии и, главное, мы видим значение параметра R2 – величины достоверности аппроксимации! Чем ближе его значение к 1, тем наиболее точно выбранная функция аппроксимирует табличные данные!
7. Строим линии тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.
Лучше всех из выбранных функций аппроксимирует наши данные полином второй степени, у него максимальный коэффициент достоверности R2.
Однако хочу вас предостеречь! Если вы возьмете полиномы более высоких степеней, то, возможно, получите еще лучшие результаты, но кривые будут иметь замысловатый вид…. Здесь важно понимать, что мы ищем функцию, которая имеет физический смысл. Что это означает? Это означает, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только внутри рассматриваемого диапазона значений X, но и за его пределами, то есть ответит на вопрос: «Какой будет выпуск металлоконструкций при количестве переработанных за месяц уголков меньше 45 и больше 168 тонн!» Поэтому я не рекомендую увлекаться полиномами высоких степеней, да и параболу (полином второй степени) выбирать осторожно!
Итак, нам необходимо выбрать функцию, которая не только хорошо интерполирует табличные данные в пределах диапазона значений X=45…168, но и допускает адекватную экстраполяцию за пределами этого диапазона. Я выбираю в данном случае логарифмическую функцию, хотя можно выбрать и линейную, как наиболее простую. В рассматриваемом примере при выборе линейной аппроксимации в excel ошибки будут больше, чем при выборе логарифмической, но не на много.
8. Удаляем все линии тренда с поля диаграммы, кроме логарифмической функции. Для этого щелкаем правой кнопкой мыши по ненужным линиям и в выпавшем контекстном меню выбираем «Очистить».
9. В завершении добавим к точкам табличных данных планки погрешностей. Для этого правой кнопкой мыши щелкаем на любой из точек на графике и в контекстном меню выбираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.
10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.
Аналогичным образом форматируются любые другие объекты диаграммы в Excel!
Окончательный результат диаграммы представлен на следующем снимке экрана.
Итоги.
Результатом всех предыдущих действий стала полученная формула аппроксимирующей функции y=-172,01*ln (x)+1188,2. Зная ее, и количество уголков в месячном наборе работ, можно с высокой степенью вероятности (±4% — смотри планки погрешностей) спрогнозировать общий выпуск металлоконструкций за месяц! Например, если в плане на месяц 140 тонн уголков, то общий выпуск, скорее всего, при прочих равных составит 338±14 тонн.
Для повышения достоверности аппроксимации статистических данных должно быть много. Двенадцать пар значений – это маловато.
Из практики скажу, что хорошим результатом следует считать нахождение аппроксимирующей функции с коэффициентом достоверности R2>0,87. Отличный результат – при R2>0,94.
На практике бывает трудно выделить один самый главный определяющий фактор (в нашем примере – масса переработанных за месяц уголков), но если постараться, то в каждой конкретной задаче его всегда можно найти! Конечно, общий выпуск продукции за месяц реально зависит от сотни факторов, для учета которых необходимы существенные трудозатраты нормировщиков и других специалистов. Только результат все равно будет приблизительным! Так стоит ли нести затраты, если есть гораздо более дешевое математическое моделирование!
В этой статье я лишь прикоснулся к верхушке айсберга под названием сбор, обработка и практическое использование статистических данных. О том удалось, или нет, мне расшевелить ваш интерес к этой теме, надеюсь узнать из комментариев и рейтинга статьи в поисковиках.
Затронутый вопрос аппроксимации функции одной переменной имеет широкое практическое применение в разных сферах жизни. Но гораздо большее применение имеет решение задачи аппроксимации функции нескольких независимых переменных…. Об этом и не только читайте в следующих статьях на блоге.
Подписывайтесь на анонсы статей в окне, расположенном в конце каждой статьи или в окне вверху страницы.
Не забывайте подтверждать подписку кликом по ссылке в письме, которое придет к вам на указанную почту (может прийти в папку «Спам»)!!!
С интересом прочту Ваши комментарии, уважаемые читатели! Пишите!
P.S. (04.06.2017)
Высокоточная красивая замена табличных данных простым уравнением.
Вас не устраивают полученные точность аппроксимации (R2
Подробности Автор: Administrator Родительская категория: Заметки Категория: Компьютерная повседневность Создано: 28 января 2013 Обновлено: 15 мая 2014 Просмотров: 28651
Чтобы приступить к аппроксимации кривой ваших экспериментальных данных в Excel 2003:
1. Создайте диаграмму (график).
2. Выделите линию функции на графике и нажмите правую кнопку мыши, выберите «Добавить линию тренда»
3. Выберите тип аппроксимации во вкладке «Тип» в откурывшемся диалоговом окне «Линия тренда»
4. На вкладке «Параметры» — прогностические параметры, показывать уравнение на графике или нет
Аппроксимация (от лат. approximo — приближаюсь) — это замена одних математических объектов другими, в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В этой нашей статье мы постараемся подробно рассмотреть вопрос о том, как апроксимировать график в офисной программе Excel?
В MS Excel аппроксимация экспериментальных данных осуществляется путем построения их графика (x – отвлеченные величины) или точечного графика (x – имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции (линии тренда).
1. Создайте диаграмму (график).
2. Выделите линию функции на графике и нажмите правую кнопку мыши, выберите «Добавить линию тренда».
3. Выберите тип аппроксимации во вкладке «Тип» в откурывшемся диалоговом окне «Линия тренда».
4. На вкладке «Параметры» — прогностические параметры, показывать уравнение на графике или нет.
Решить задачу аппроксимации экспериментальных данных – значит построить уравнение регрессии. Задача аппроксимации возникает в случае необходимости аналитически, то есть в виде математической зависимости, описать реальные явления, наблюдения за которыми заданы в виде таблицы, содержащей значения показателя в разные моменты времени или при разных значениях независимого аргумента. Например,
— известны показатели прибыли (их можно обозначить Y) в зависимости от размера капиталовложений (X);
— известны объемы реализации фирмы (Y) за шесть недель ее работы. В этом случае, X – это последовательность недель.
Иногда говорят, что требуется построить эмпирическую модель. Эмпирической называется модель, построенная на основе реальных наблюдений. Если модель удается найти, можно сделать прогноз о поведении исследуемого явления и процесса в будущем и, возможно, выбрать оптимальное направление ее развития.
В общем случае задача аппроксимации экспериментальных данных имеет следующую постановку:
Пусть известны данные, полученные практическим путем (в ходе n экспериментов или наблюдений), которые можно представить парами чисел (хi; уi). Зависимость между ними отражает таблица:
| X | х1 | х2 | х3 | … | хn |
| Y | y1 | y2 | y3 | … | yn |
Имеется класс разнообразных функций F. Требуется найти аналитическое (т.е. математическое) выражение зависимости между этими показателями, то есть надо подобрать из множества функций F функцию f, такую что . которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и по возможности точно отражала общую тенденцию зависимости между X и Y, исключая погрешности измерения и случайные отклонения.
Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек (хi; уi) на координатной плоскости.
Графически решить задачу аппроксимации означает, провести такую кривую , точки которой (хi; ŷi) находились бы как можно ближе к исходным точкам (хi; уi), отображающим экспериментальные данные.
Для решения задачи аппроксимации используют метод наименьших квадратов.
При этом функция считается наилучшим приближением к , если для нее сумма квадратов отклонений «теоретических» значений , найденных по эмпирической формуле, от соответствующих опытных значений , имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.
Математическая запись метода наименьших квадратов имеет вид:
(1)
где n — количество наблюдений показателей.
Таким образом, задача аппроксимации распадается на две части.
Сначала устанавливают вид зависимости и, соответственно, вид эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции.
После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим.
Простейшим видом эмпирической модели с двумя параметрами, используемой для аппроксимации результатов экспериментов, является линейная регрессия, описываемая линейной функцией:
где а, b — искомые параметры.
Для модели линейной регрессии метод наименьших квадратов (1) запишется :
(2)
Для решения (2) относительно а и b приравнивают к нулю частные производные:
В итоге для нахождения a и b надо решить систему линейных алгебраических уравнений вида:
(3)
Реализовать метод наименьших квадратов в случае линейной регрессии в Excel можно различными способами.
1 способ. Построить систему линейных алгебраических уравнений, подставив в (3) все известные значения, и решить ее, например, матричным методом (см. зад. 4).
Рис. 25
В формульном виде элемент расчетной таблицы приведен на рис. 26.
Рис.26
2 способ. Решить в Excel задачу оптимизации (2), применив для этого Поиск решения (см. зад. 5).
Рис.27
Замечание 1. Следует обратить внимание, что для целевой функции S удобно применить встроенную математическую функцию СУММКВРАЗН(массив1;массив2), в результате которой как раз и вычисляется сумма квадратов разностей двух массивов. В нашем случае следует в качестве массива1 указать диапазон исходных значений , а в качестве массива2 – «теоретические» значения , рассчитанные по формуле , где a и b – это адреса ячеек с искомыми значениями.
Замечание 2. В диалоговом окне команды Поиск решения следует задать целевую ячейку, направление цели – на минимум и изменяемые ячейки (рис. 28). Данная задача ограничений не содержит.
Рис.28
Замечание3. В качестве эмпирических моделей с двумя параметрами могут использоваться и нелинейные модели вида:
Описанный способ решения метода наименьших квадратов применим и для нелинейных зависимостей.
3 способ. Для нахождения значений параметров a и b в случае линейной регрессии можно использовать следующие встроенные в Excel статистические функции:
НАКЛОН(известные_значения_У; известные_значения_Х)
ОТРЕЗОК(известные_значения_У; известные_значения_Х)
ЛИНЕЙН (известные_значения_У; известные_значения_Х)
Причем, функция НАКЛОН ( ) возвращает значение параметра а, функция ОТРЕЗОК( ) возвращает значение параметра b. Функция ЛИНЕЙН( ) возвращает одновременно оба параметра линейной зависимости, так как является функцией массива. Поэтому для ввода функции ЛИНЕЙН( ) в таблицу надо соблюдать следующие правила:
· выделить две рядом стоящие ячейки
· ввести формулу
· по окончании нажать одновременно комбинацию клавиш Ctrl+ Shift+Enter.
В результате в левой ячейке получится значение параметра а, а в правой – значение параметра b.
Для решения задачи аппроксимации графическим способом в Excel надо построить по исходным данным график, например, точечную диаграмму со значениями, соединенными сглаживающими линиями (см.зад.1). На эту диаграмму Excel может нанести Линию тренда. Линию тренда можно добавить к любому ряду данных, использующему следующие типы диаграмм: диаграммы с областями, графики, гистограммы, линейчатые или точечные диаграммы.
При создании линии тренда в Excel на основе данных диаграммы применяется та или иная аппроксимация. Excel позволяет выбрать один из пяти аппроксимирующих линий или вычислить линию, показывающую скользящее среднее.
Кроме того, Excel предоставляет возможность выбирать значения пересечения линии тренда с осью Y, а также добавлять к диаграмме уравнение аппроксимации и величину достоверности аппроксимации (R2). Также, можно определять будущие и прошлые значения данных, исходя из линии тренда и связанного с ней уравнения аппроксимации.
Чтобы добавить линию тренда к ряду данных надо:
1. Активизировать щелчком мыши диаграмму.
2. Выполнить команду Диаграмма, Добавить линию тренда или переместить указатель на ряд данных, щелкнуть правой кнопкой мыши, а затем в контекстном меню выбрать команду Добавить линию тренда. В появившемся окне Линия тренда раскрыть вкладку Тип (рис. 29)
3. В списке Построен на ряде – выделить ряд данных, к которому нужно добавить линию тренда (Рис.29).
4. В группе Построение линии тренда (аппроксимация и сглаживание) выбрать один из шести типов аппроксимации (сглаживания). – линейная, логарифмическая, полиномиальная, степенная, экспоненциальная, скользящее среднее (Рис.29)
Рис.29
5. Чтобы установить параметры линии тренда надо раскрыть вкладку Параметры диалогового окна Линия тренда(рис. 30)
Рис.30
Показывать уравнение на диаграмме – осуществляет вывод уравнения аппроксимации на диаграмму в виде текстового поля.
Поместить на диаграмму величину достоверности аппроксимации R2– осуществляет вывод на диаграмму достоверности аппроксимации в виде текста.
6. По окончании нажимают экранную кнопку ОК.
Пример результирующей диаграммы приведен на рисунке 31.
Рис.31
Опубликовано 05 Янв 2014
Рубрика: Справочник Excel | 19 комментариев

Учет и контроль! Те, кому за 40 должны хорошо помнить этот лозунг из эпохи построения социализма и коммунизма в нашей стране.
Но без хорошо налаженного учета невозможно эффективное функционирование ни страны, ни области, ни предприятия, ни домашнего хозяйства при любой общественно-экономической формации общества! Для составления прогнозов и планов деятельности и развития необходимы исходные данные. Где их брать? Только один достоверный источник – это ваши статистические учетные данные предыдущих периодов времени.
Учитывать результаты своей деятельности, собирать и записывать информацию, обрабатывать и анализировать данные, применять результаты анализа для принятия правильных решений в будущем должен, в моем понимании, каждый здравомыслящий человек. Это есть ничто иное, как накопление и рациональное использование своего жизненного опыта. Если не вести учет важных данных, то вы через определенный период времени их забудете и, начав заниматься этими вопросами вновь, вы опять наделаете те же ошибки, что делали, когда впервые этим занимались.
«Мы, помню, 5 лет назад изготавливали до 1000 штук таких изделий в месяц, а сейчас и 700 еле-еле собираем!». Открываем статистику и видим, что 5 лет назад и 500 штук не изготавливали…
«Во сколько обходится километр пробега твоего автомобиля с учетом всех затрат?» Открываем статистику – 6 руб./км. Поездка на работу – 107 рублей. Дешевле, чем на такси (180 рублей) более чем в полтора раза. А бывали времена, когда на такси было дешевле…
«Сколько времени требуется для изготовления металлоконструкций уголковой башни связи высотой 50 м?» Открываем статистику – и через 5 минут готов ответ…
«Сколько будет стоить ремонт комнаты в квартире?» Поднимаем старые записи, делаем поправку на инфляцию за прошедшие годы, учитываем, что в прошлый раз купили материалы на 10% дешевле рыночной цены и – ориентировочную стоимость мы уже знаем…
Ведя учет своей профессиональной деятельности, вы всегда будете готовы ответить на вопрос начальника: «Когда!!!???». Ведя учет домашнего хозяйства, легче спланировать расходы на крупные покупки, отдых и прочие расходы в будущем, приняв соответствующие меры по дополнительному заработку или по сокращению необязательных расходов сегодня.
В этой статье я на простом примере покажу, как можно обрабатывать собранные статистические данные в Excel для возможности дальнейшего использования при прогнозировании будущих периодов.
Аппроксимация в Excel статистических данных аналитической функцией.
Производственный участок изготавливает строительные металлоконструкции из листового и профильного металлопроката. Участок работает стабильно, заказы однотипные, численность рабочих колеблется незначительно. Есть данные о выпуске продукции за предыдущие 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. После предварительного анализа исходных данных возникло предположение, что суммарный месячный выпуск металлоконструкций существенно зависит от количества уголков в заказах. Проверим это предположение.
Прежде всего, несколько слов об аппроксимации. Мы будем искать закон – аналитическую функцию, то есть функцию, заданную уравнением, которое лучше других описывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а найденное уравнение называется аппроксимирующей функцией для исходной функции, заданной в виде таблицы.
1. Включаем Excel и помещаем на лист таблицу с данными статистики.
2. Далее строим и форматируем точечную диаграмму, в которой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения исходной функции – общий выпуск металлоконструкций в месяц, заданные таблицей.
О том, как построить подобную диаграмму, подробно рассказано в статье «Как строить графики в Excel?».
3. «Наводим» мышь на любую из точек на графике и щелчком правой кнопки вызываем контекстное меню (как говорит один мой хороший товарищ — работая в незнакомой программе, когда не знаешь, что делать, чаще щелкай правой кнопкой мыши…). В выпавшем меню выбираем «Добавить линию тренда…».
4. В появившемся окне «Линия тренда» на вкладке «Тип» выбираем «Линейная».
5. Далее на вкладке «Параметры» ставим 2 галочки и нажимаем «ОК».
6. На графике появилась прямая линия, аппроксимирующая нашу табличную зависимость.
Мы видим кроме самой линии уравнение этой линии и, главное, мы видим значение параметра R2 – величины достоверности аппроксимации! Чем ближе его значение к 1, тем наиболее точно выбранная функция аппроксимирует табличные данные!
7. Строим линии тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.
Лучше всех из выбранных функций аппроксимирует наши данные полином второй степени, у него максимальный коэффициент достоверности R2.
Однако хочу вас предостеречь! Если вы возьмете полиномы более высоких степеней, то, возможно, получите еще лучшие результаты, но кривые будут иметь замысловатый вид…. Здесь важно понимать, что мы ищем функцию, которая имеет физический смысл. Что это означает? Это означает, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только внутри рассматриваемого диапазона значений X, но и за его пределами, то есть ответит на вопрос: «Какой будет выпуск металлоконструкций при количестве переработанных за месяц уголков меньше 45 и больше 168 тонн!» Поэтому я не рекомендую увлекаться полиномами высоких степеней, да и параболу (полином второй степени) выбирать осторожно!
Итак, нам необходимо выбрать функцию, которая не только хорошо интерполирует табличные данные в пределах диапазона значений X=45…168, но и допускает адекватную экстраполяцию за пределами этого диапазона. Я выбираю в данном случае логарифмическую функцию, хотя можно выбрать и линейную, как наиболее простую. В рассматриваемом примере при выборе линейной аппроксимации в excel ошибки будут больше, чем при выборе логарифмической, но не на много.
8. Удаляем все линии тренда с поля диаграммы, кроме логарифмической функции. Для этого щелкаем правой кнопкой мыши по ненужным линиям и в выпавшем контекстном меню выбираем «Очистить».
9. В завершении добавим к точкам табличных данных планки погрешностей. Для этого правой кнопкой мыши щелкаем на любой из точек на графике и в контекстном меню выбираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.
10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.
Аналогичным образом форматируются любые другие объекты диаграммы в Excel!
Окончательный результат диаграммы представлен на следующем снимке экрана.
Итоги.
Результатом всех предыдущих действий стала полученная формула аппроксимирующей функции y=-172,01*ln (x)+1188,2. Зная ее, и количество уголков в месячном наборе работ, можно с высокой степенью вероятности (±4% — смотри планки погрешностей) спрогнозировать общий выпуск металлоконструкций за месяц! Например, если в плане на месяц 140 тонн уголков, то общий выпуск, скорее всего, при прочих равных составит 338±14 тонн.
Для повышения достоверности аппроксимации статистических данных должно быть много. Двенадцать пар значений – это маловато.
Из практики скажу, что хорошим результатом следует считать нахождение аппроксимирующей функции с коэффициентом достоверности R2>0,87. Отличный результат – при R2>0,94.
На практике бывает трудно выделить один самый главный определяющий фактор (в нашем примере – масса переработанных за месяц уголков), но если постараться, то в каждой конкретной задаче его всегда можно найти! Конечно, общий выпуск продукции за месяц реально зависит от сотни факторов, для учета которых необходимы существенные трудозатраты нормировщиков и других специалистов. Только результат все равно будет приблизительным! Так стоит ли нести затраты, если есть гораздо более дешевое математическое моделирование!
В этой статье я лишь прикоснулся к верхушке айсберга под названием сбор, обработка и практическое использование статистических данных. О том удалось, или нет, мне расшевелить ваш интерес к этой теме, надеюсь узнать из комментариев и рейтинга статьи в поисковиках.
Затронутый вопрос аппроксимации функции одной переменной имеет широкое практическое применение в разных сферах жизни. Но гораздо большее применение имеет решение задачи аппроксимации функции нескольких независимых переменных…. Об этом и не только читайте в следующих статьях на блоге.
С интересом прочту Ваши комментарии, уважаемые читатели! Пишите!
P.S. (04.06.2017)
Высокоточная красивая замена табличных данных простым уравнением.
Вас не устраивают полученные точность аппроксимации (R2<0,95) или вид и набор функций, предлагаемые MS Excel?
Размеры выражения и форма линии аппроксимирующего полинома высокой степени не радует глаз?
Обращайтесь через страницу «Обратная связь» для получения более точного и компактного результата аппроксимации ваших табличных данных и для того, чтобы узнать простую методику решения задач высокоточной аппроксимации функцией одной переменной.
Далее на скриншоте в качестве сравнения представлены результаты поиска аппроксимирующей функции при помощи Excel и при помощи предлагаемой методики.
При использовании предлагаемого алгоритма действий найдена весьма компактная функция, обеспечивающая высочайшую точность аппроксимации: R2=0,9963!!!
Другие статьи автора блога
На главную