На чтение 10 мин Просмотров 64.9к.
Приведем пример формирования инвестиционного портфеля по модели Г. Марковица с помощью программы Excel, разберем достоинства и недостатки данной модели в современной экономике и пути их решения.
Инвестиционный портфель – это совокупность различных финансовых инструментов, удовлетворяющих цели инвестора и, как правило, заключается в создании таких комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска.
Содержание
- Инфографика: Портфельная теория Марковица (основная информация)
- Модель Марковица
- Цели формирования инвестиционного портфеля
- Расчет доходности инвестиционного портфеля Марковица
- Оценка риска инвестиционного портфеля Марковица
- Эконометрический вид модели Марковица
- Пример формирования инвестиционного портфеля Марковица в Excel
- Формирование инвестиционного портфеля минимального риска
- Формирование эффективного инвестиционного портфеля
- Достоинства и недостатки модели Г. Марковица
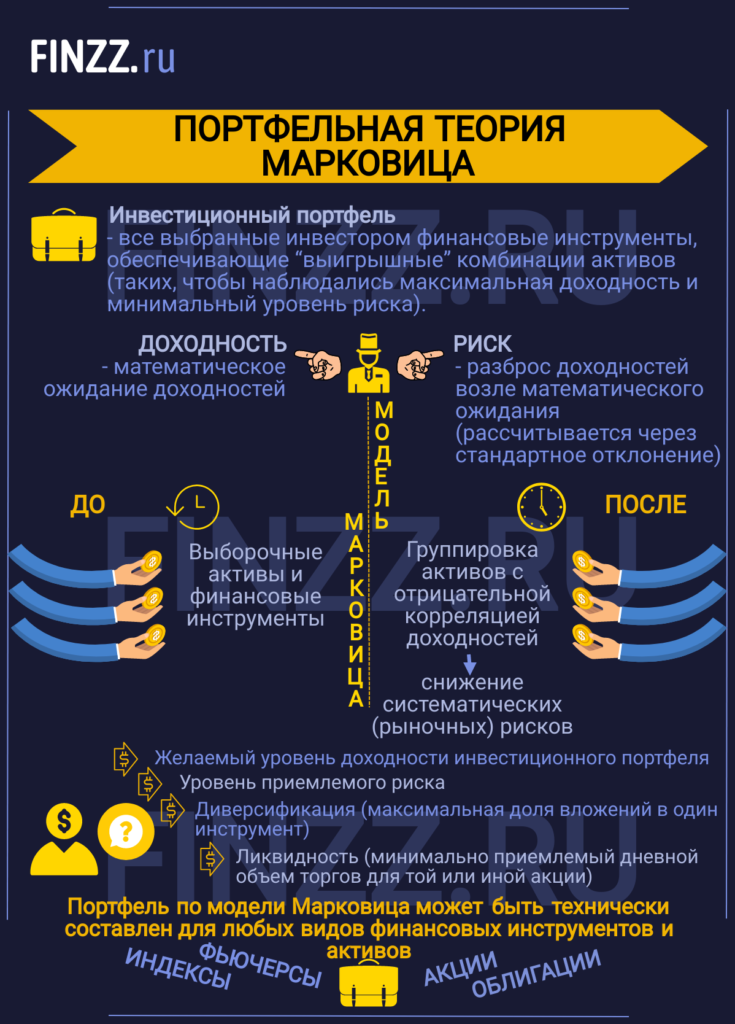
Инфографика: Портфельная теория Марковица (основная информация)
Модель Марковица
Г. Марковиц в 1952 году впервые предложил математическую модель формирования инвестиционного портфеля. В основе его модели лежат два ключевых показателя любого финансового инструмента: доходность и риск, которые были количественно измерены. Доходность по модели представляет собой математическое ожидание доходностей, а риск определяется как разброс доходностей возле математического ожидания и рассчитывается через стандартное отклонение.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
До модели Г. Марковица инвестирование происходило, как правило, в выборочные активы или финансовые инструменты, предложенная же им модель позволила снизить систематические (рыночные) риски за счет группировки активов с отрицательной корреляцией доходностей.
Следует заметить универсальность модели, так инвестиционный портфель может быть технически составлен для любых видов финансовых инструментов и активов: акций, облигаций, фьючерсов, индексов, недвижимости и т.д.
Цели формирования инвестиционного портфеля
Выделяют две инвестиционные стратегии при формировании портфеля:
► Максимизации доходности инвестиционного портфеля при ограниченном уровне риск.
► Минимизация риска инвестиционного портфеля при минимально допустимом уровне доходности.
Расчет доходности инвестиционного портфеля Марковица
Общая доходность портфеля будут представлять собой взвешенную сумму доходностей каждого отдельного финансового инструмента (актива):
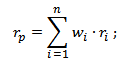
rp – доходность инвестиционного портфеля;
w – доля i-го финансового инструмента в портфеле;
ri – доходность i-го финансового инструмента.
Оценка риска инвестиционного портфеля Марковица
В модели Г. Марковица риск отдельно взятого финансового инструмента рассчитывается как стандартное отклонение доходностей. Для расчета общего риска портфеля необходимо отразить их совокупное изменение и взаимное влияние (через ковариацию), для этого воспользуемся следующей формулой:
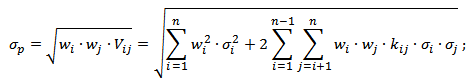
σp – риск инвестиционного портфеля;
σi – стандартное отклонение доходностей i-го финансового инструмента;
kij – коэффициент корреляции между I,j-м финансовым инструментом;
wi – доля i-го финансового инструмента (акций) в портфеле;
Vij – ковариация доходностей i-го и j-го финансового инструмента;
n – количество финансовых инструментов инвестиционного портфеля.
Эконометрический вид модели Марковица
Для того чтобы сформировать инвестиционный портфель необходимо решить оптимизационную задачу. Существует два вида задач: поиск долей акций в портфеле для достижения максимальной эффективности при заданном уровне риска (σp) и минимизация риска при заданном уровне доходности портфеля (rp). Помимо этого на уравнения накладываются дополнительные очевидные ограничения: сумма долей активов должна быть равна 1 и сами доли активов должны быть положительными.
В таблице ниже показаны формулы и наложенные на них ограничения для поиска оптимальных долей финансовых инструментов (акций).
Пример формирования инвестиционного портфеля Марковица в Excel
Рассмотрим наглядный пример формирования инвестиционного портфеля по модели Г. Марковица в программе Excel. Наш портфель будет состоять из четырех отечественных акций: ОАО «Газпром» (GAZP), ОАО «Норильский никель» (GMKN), ОАО «Мечел» (MTLR) и ОАО «Сбербанк» (SBER). Были взяты акции различных секторов: нефтегазового, промышленного и финансового, такой выбор увеличивает диверсификацию портфеля и снижает его рыночный риск.
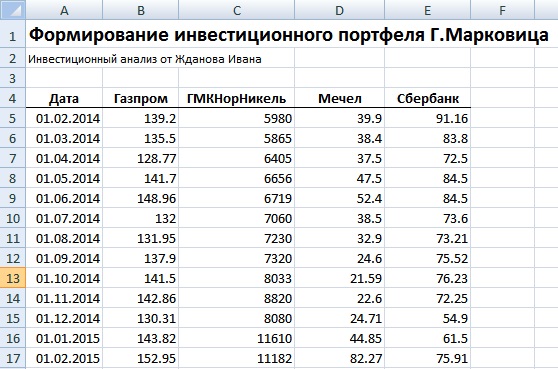
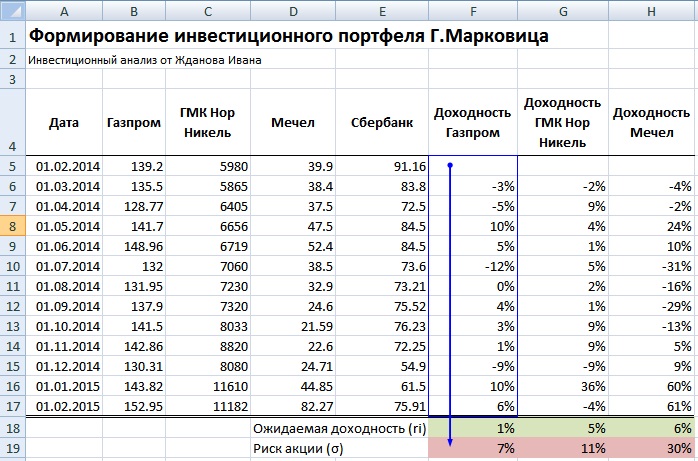
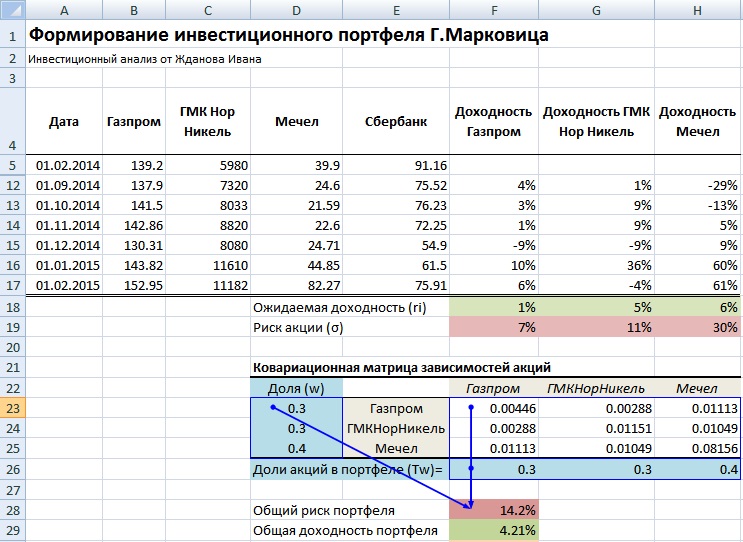
Рекомендуется брать период рассмотрения динамики изменения стоимости акций минимум один год. Это позволяет сделать более точный долгосрочный прогноз доходности и риска портфеля. На рисунке ниже показана ежемесячная стоимость акций за период с 01.02.2014 – 01.02.2015г.
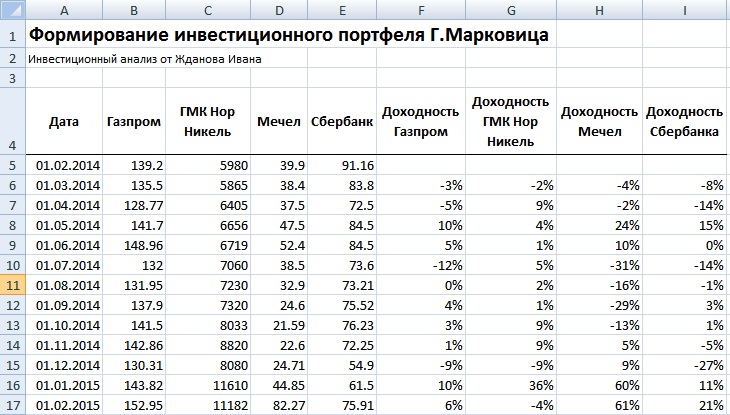
На следующем этапе формирования портфеля необходимо рассчитать ежемесячные доходности по каждой акции. Для этого воспользуемся формулой процентов в Excel:
Доходность Газпром =LN(B6/B5)
Доходность ГМКНорНикель =LN(C6/C5)
Доходность Мечел =LN(D6/D5)
Доходность Сбербанк =LN(E6/E5)
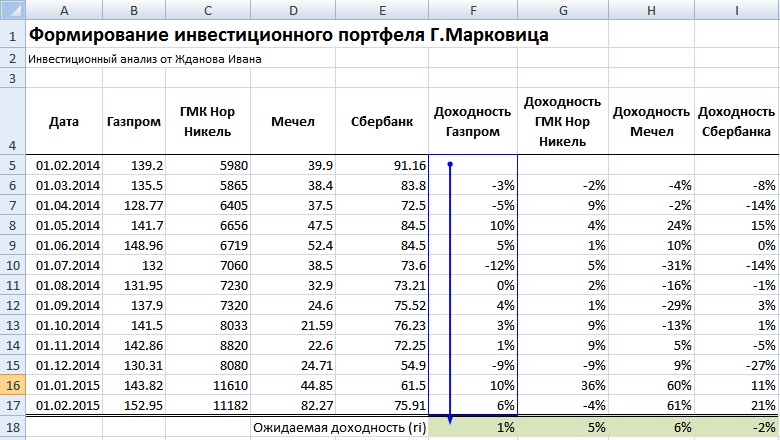
Далее определяем математическое ожидание доходностей по каждой акции, для этого найдем среднеарифметическое значение за весь период. Ожидаемая доходность по каждой акции будет следующая:
Ожидаемая доходность Газпром =СРЗНАЧ(F5:F17)
Ожидаемая доходность ГМКНорНикель =СРЗНАЧ(G5:G17)
Ожидаемая доходность Мечел =СРЗНАЧ(H5:H17)
Ожидаемая доходность Сбербанк =СРЗНАЧ(I5:I17)
Доходность акции ОАО «Сбербанк» имеет отрицательное ожидание доходности, поэтому ее следует исключить из портфеля. Оценка риска каждой акции – это ее изменчивость (волатильность) по отношению к математическому ожиданию доходностей.
Формула расчета риска акций следующая:
Риск Газпром =СТАНДОТКЛОН(F5:F17)
Риск ГМКНорНикель =СТАНДОТКЛОН(G5:G17)
Риск Мечел =СТАНДОТКЛОН(H5:H17)
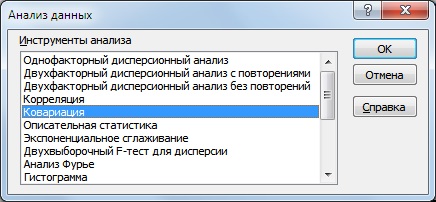
Мы получили первоначальные необходимые данные для оценки долей данных акций в инвестиционном портфеле. Для оценки уровня риска всего инвестиционного портфеля воспользуемся надстройкой в Excel. Для этого зайдем в Главном меню → «Данные» → «Анализ данных» → «Ковариация».
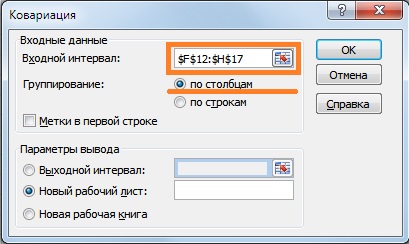
Далее в появившемся окне необходимо найти ковариации между доходностями акций. Указываем входной интервал – ежемесячных доходностей акций, а в опции «Группирование» выбираем функцию «по столбцам».
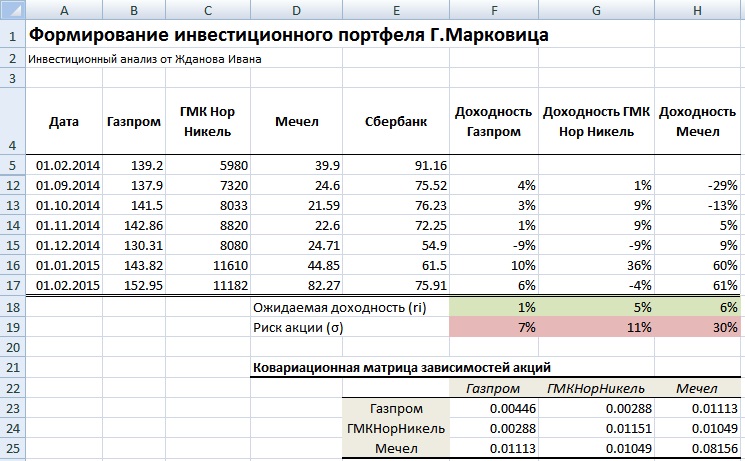
Результатом будет таблица ковариаций доходностей акций между собой. Расположим ее ниже под таблицей. Можно заметить, что диагональные значения представляют собой дисперсию доходностей акций.
Для расчета общего риска портфеля воспользуемся формулой рассмотренной выше и для этого нам необходимо перемножить доли весов акций между собой и значения ковариаций этих акций. Для того чтобы понять принцип расчета, установим доли акций 0.3, 0.3 и 0.4 и рассчитаем общий риск портфеля. Доходность портфеля рассчитывается как средневзвешенная сумма доходностей отдельных акций. Так как мы будем перемножать матрицы необходимо транспонировать столбец с долям (wT). Формула расчета риска инвестиционного портфеля будет иметь следующий вид:
Общий риск инвестиционного портфеля =КОРЕНЬ(МУМНОЖ(МУМНОЖ(F26:H26;F23:H25);D23:D25))
Общая доходность инвестиционного портфеля =F18*F26+G18*G26+H18*H26
Формирование инвестиционного портфеля минимального риска
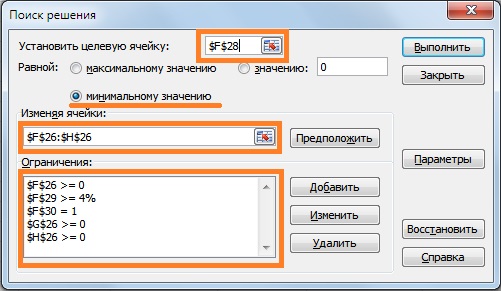
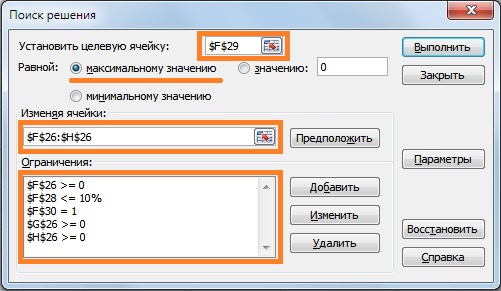
Для данной задачи необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp ≥ 4%. При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню Excel → «Данные» → «Поиск решений», а также введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля), ввести, какие параметры необходимо изменять (доли акций) и текущие ограничения. Целевая ячейка – это ячейка с формулой общего риска инвестиционного портфеля. Программа будет изменять значения долей акций при выставленных ограничениях. Формула ограничения размера доли в портфеле будет иметь следующий вид:
Ограничение на сумму долей акций (F30) =СУММ(F26:H26)
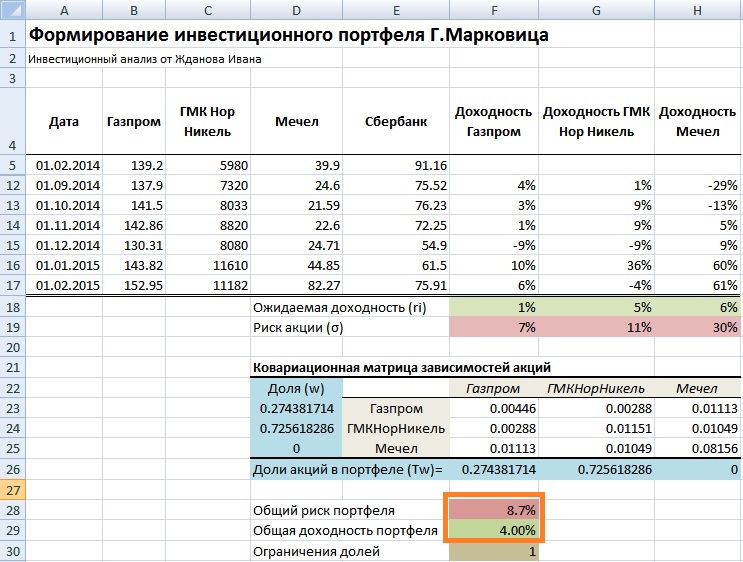
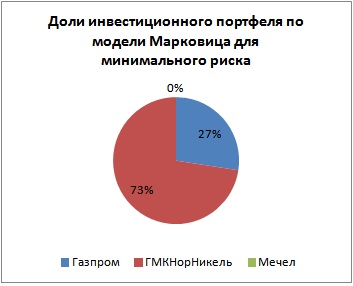
В результате мы получаем следующий расчет общего риска и доходности портфеля. Общий риск портфеля составил 8,7%, тогда как общая доходность 4%. Доли акций Газпрома получились равными 27%, доли ГМКНорНикель 73% и Мечела 0%. При заданных условиях эффективнее будет формирование портфеля из двух акций ОАО «Газпром» и ОАО «ГМКНорНикель».
Визуально доли портфеля будут соотноситься следующим образом.
Формирование эффективного инвестиционного портфеля
Вторая задача, которая решается на основе модели Г. Марковица – посторонние портфеля с максимальным уровнем доходности и ограниченным уровнем риска. Разберем на примере данную задачу. Установим максимально допустимый уровень риска портфеля σp≤10%. С помощью надстройки «Поиск решений» определим доли акций в данной интерпретации задачи. Целевая ячейка будет ячейка с формулой доходности портфеля, ее следует максимизировать, изменяя значения долей акций при ограничениях по риску. На рисунке ниже показаны основные параметры для формирования портфеля с максимальной доходностью.
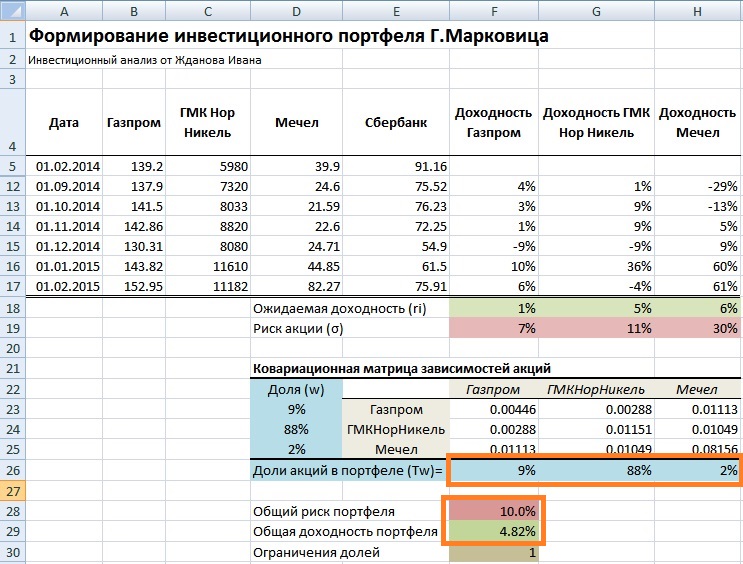
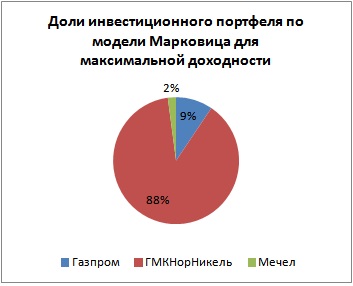
В результате мы получили доли акций в инвестиционном портфеле: 9% акций ОАО «Газпром», 88% акций ОАО «ГМКНорНикель» и 2% акций ОАО «Мечел». Общий риск портфеля не превысил 10%, а доходность составила 4,82%.
Визуально доли инвестиционного портфеля будут соотноситься следующим образом.
Достоинства и недостатки модели Г. Марковица
Рассмотрим ряд недостатков присущих модели Г. Марковица.
- Данная модель была разработана для эффективных рынков капитала, на которых наблюдается постоянный рост стоимости активов и отсутствуют резкие колебания курсов, что было в большей степени характерно для экономики развитых стран 50-80-х годов. Корреляция между акциями не постоянна и меняется со временем, в итоге в будущем это не уменьшает систематический риск инвестиционного портфеля.
- Будущая доходность финансовых инструментов (акций) определяется как среднеарифметическое. Данный прогноз основывается только на историческом значении доходностей акции и не включает влияние макроэкономических (уровень ВВП, инфляции, безработицы, отраслевые индексы цен на сырье и материалы и т.д.) и микроэкономических факторов (ликвидность, рентабельность, финансовая устойчивость, деловая активность компании).
- Риск финансового инструмента оценивается с помощью меры изменчивости доходности относительно среднеарифметического, но изменение доходности выше не является риском, а представляет собой сверхдоходность акции.
Многие из данных недостатков модели были решены последователями: прогнозирование доходности с помощью многофакторных моделей (Ю. Фама, К. Френч, Росс и др.), нейронных сетей; оценка риска на основе моделей ARCH, GARCH и т.д. Следует отметить одно из главных достоинств модели Г. Марковица: систематизация подхода к формированию инвестиционного портфеля и управление его доходностью и риском.
Резюме
В данной статье мы рассмотрели, как с помощью Excel можно сформировать инвестиционный портфель по модели Г. Марковица и решить две классические задачи: максимизация доходности портфеля при минимальном риске и минимизация риска при заданной доходности. Портфель Марковица позволяет снизить систематические риски за счет комбинации различных активов. Несмотря на сложности использования данной модели в современной экономике данная модель применима для таких низковолатильных активов как недвижимость, облигации товарные фьючерсы и т.д. В настоящее время сократился срок пересмотра активов в портфеле, так если раньше он мог составлять год, то сейчас это 2-6 месяцев. С вами был Иван Жданов, спасибо за внимание.
Автор: к.э.н. Жданов Иван Юрьевич
-
EN
EXCELFILES.SPACE
- Home
- Python
- MS Office
- Excel
- Outlook
- About
- Главная
- MS Office
- Excel
- Оптимальный инвестиционный портфель – Теория Марковица
Оптимальный инвестиционный портфель – Теория Марковица
Подробный разбор портфельной теории марковица: предположения, суть, и пример реализации в Excel.
Скачать файл для расчёта оптимального портфеля для любого числа активов
-
Excel-VBA
-
MS Office RU
-
Excel RU
-
MS Office VBA RU
- Главная
- Python
- MS Office
- Excel
- Outlook
- О сайте
Искать…
Если бы вы знали будущее, вам не понадобилась бы Портфельная Теория.
Эти слова принадлежат Гарри Марковицу, лауреату Нобелевской премии по экономике, одному из крупнейших специалистов в академических финансах.
В 1952 году Марковиц написал статью под названием «Выбор портфеля», сформулировав ту самую портфельную теорию, которую используют инвесторы, которые не могут заглянуть в будущее. Но они могут сгладить будущие риски, используя преимущества диверсификации портфеля инвестиций и других ограничений.
Диверсификация означает выбор разрозненных активов, которые ведут себя по-разному в одних и тех же условиях.
Главная идея теории Марковица – доходы напрямую связаны с рисками, которые инвестор должен не только оценивать, но и контролировать.
«Существует компромисс между риском и доходностью. Человек сталкивался с риском еще со времен саблезубого тигра. Если вы не рискуете, то не можете выйти собрать урожай или отстреливать тигров и медведей. Человек рождается в рискованном мире и живет в рискованном мире. И через десять лет этот мир будет рискованным, пока вы хотите зарабатывать деньги и инвестировать деньги». Г.Марковиц
Это примерно то, что я говорю беспокойным инвестором. Мир финансов всегда будет связан с неопределённостью и рисками. С этим придётся жить.
Эволюция человека, или как стать инвестором
Теория портфеля ценных бумаг помогает инвестору увеличить ожидаемую прибыль и сократить риски. То есть решает две задачи:
— максимизация доходности при заданном уровне риска
— минимизация риска при минимально допустимом значении доходности.
Теория Марковица на практике
Если объяснять без построения кривой риска/доходности и выгрузки данных в таблицу Excel, то пример формирования портфеля по Марковицу выглядит так.
После анализа данных доходности и риска инвестиционных инструментов прошлых лет вкладчик приступает к формированию портфеля. При этом для получения минимальных рисков ему нужно в одном портфеле собрать несколько наименее коррелируемых активов: чем выше степень диверсификации портфеля ценных бумаг, тем меньше риски.
Корреляция – это взаимосвязь, похожесть. Снижение корреляции через диверсификацию – это выбор не связанных по своим свойствам активов. А часто – взаимно противоположных.
Например, акции (как доля в бизнесе) и недвижимость в кризис ведут себя по-разному. Падают и те, и те, но степень падения разные: акции самых «подвижных» в цене, или волатильных, бизнесов – могут снижаться до 50%. Недвижимость упадёт при этом процентов на 10. Общая просадка в портфеле при соотношении того и другого 50/50 составит до 30%, что менее рискованно, чем вкладываться просто в акции. И вовсе не факт, что менее доходно! Потому что и недвижимость, и акции в хорошие времена могут расти схожими темпами.
Другой пример. Инвестор может сформировать портфель из акций авиакомпаний и нефтедобывающих компаний, котировки которых напрямую зависят от цены на нефть. Когда стоимость нефти растет, цена на акции авиакомпаний начинает снижаться, а цена на акции нефтедобывающих компаний начинает расти. Таким образом, эти две компании обратно коррелируемы.
Как и все фундаментальные труды, теория Марковица имеет свои плюсы и минусы. К плюсам относят cледующее:
- портфель формируется на принципах стабильности;
- благодаря математическому аппарату процесс формирования инвестиционного портфеля можно довести до автоматизма. Что и сделано через создание рынка индексов и привязанных к ним инвестиционных инструментов – ETF, которые управляются автоматически и поэтому несут очень низкие комиссии за управление.
Минусом теории называют называют то, что хорошо она работает только на растущем рынке, так великолепно изученном Марковицем. Если на рынке ценных бумаг происходит спад — теорию можно считать бесполезной. Если мы видим дефляционный кризис, когда цены падают, как сейчас – тоже непонятно, что делать. Также нет четких критериев для входа или выхода из инструмента и методов прогноза.
Марковиц сделал гениальную для своего времени вещь, продвинув инвестирование вперёд по пути эволюции. Из попыток угадать конкретный актив мир перешёл в новую эпоху пассивного портфельного инвестирования – когда люди вкладываются в классы активов и балансируют портфель по понятным математическим законам. Так инвестирование стало доступно каждому. Так появилась огромная индустрия фондов, которые аккумулировали на сегодня более 50% мирового капитала!
Мы больше не предсказываем будущее. Мы действуем так, чтобы при любом будущем выйти в выигрыш. Портфельная теория развивается в комплексные стратегии инвестирования, где мы комбинируем инструменты таким образом, чтобы они дополняли друг друга и прикрывали от рисков. Так 1+1 становится больше, чем 2. В этом смысле Марковиц стал кем-то вроде Юнга для экономики: из его взглядов выросло целое поколение экономистов, которые взгляды эти расширили и дополнили.
Инвестиционные стратегии простым языком
Однако мир не стоит на месте. Сейчас на дворе не 1952 год, и существуют множество факторов, не учтённых Марковицем. Глобализация. Цифровая экономика. Дефляционный сценарий развития. Да много чего произошло! Последователи Марковица, конечно, расширили его теорию на новые тенденции. Но со временем она работает всё хуже и хуже, это тоже нельзя не признавать.
Сейчас уже существуют математические модели, опровергающие теорию Марковица на современной действительности. Что же, ждём новую теорию, которая продвинет нас и мировые финансы ещё дальше!
Советы Марковица
«Чтобы получить высокую доходность при заданном уровне риска, вам необходимо диверсифицировать», — говорит Марковиц. Но при этом автор теории подчеркивает, что диверсификация означает разные вещи для разных людей.
Иметь диверсифицированный портфель – не означает просто иметь много акций. Портфель должен быть эффективным и состоять, например, из акций крупной капитализации и малой капитализации, акций стоимости и роста, зарубежных и местных бумаг. Из акций, облигаций, фондов недвижимости, золота. Иметь диверсифицированный портфель – значит изучить свойства инструментов и готовить из них «авторские» блюда под себя!
Стратегия инвестора: для чего нужна и как с ней определиться?
«Не обязательно находиться в точности на Границе Эффективности (совокупности всех эффективных портфелей, которые только могут быть — авт.) Но если вы не находитесь где-то рядом с ней, то всякий раз, когда будет происходить кризис, как в 2000 г. или 2008 г., у вас будут проблемы», — считает известный экономист.
Даже продавцу из соседнего магазина лауреат Нобелевской премии с длинным списком корпоративных клиентов (крупнейшим из которых является McDonalds) советует положить половину денег на сберегательный счет, а другую вложить в хорошо диверсифицированный портфель акций.
Если упрощать, для широкого круга клиентов Теория Марковица означает «не класть все яйца в одну корзину», по сути это и будет являться минимизацией риска для заданной доходности через диверсификацию.
Однако умный портфель – это не портфель, собранный из чего попало. Диверсификация ради диверсификации ни к чему хорошему не приводит. Я могу научить Вас самостоятельно составлять инвестиционный портфель! Не откладывайте на потом!
ЗАПИСЫВАЙТЕСЬ НА КОНСУЛЬТАЦИЮ!
Модель Марковица
в данном случае записывается следующим
образом:
целевая функция:

линейные
ограничения:
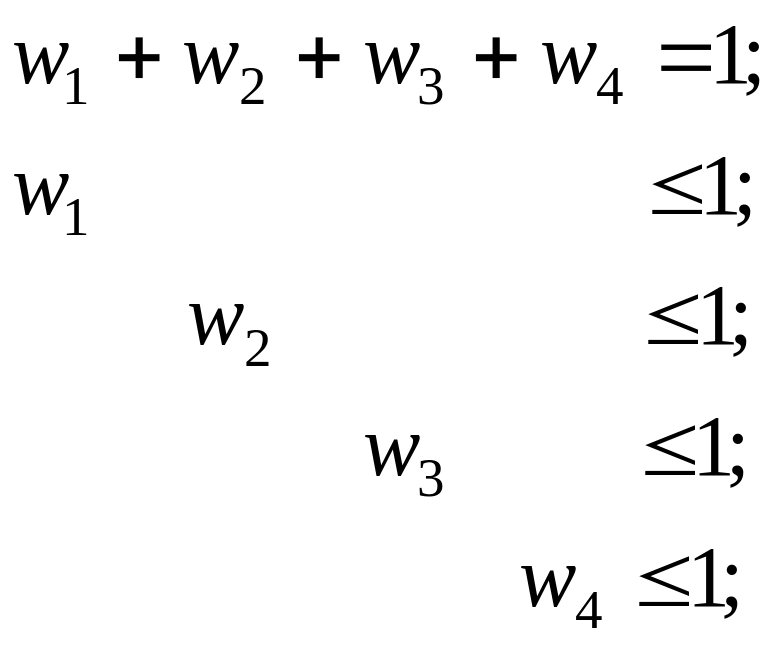
.
-
Подготовка данных
для построения модели с использованием
промежуточных результатов (средних
значений доходности, ковариационной
матрицы, риска), полученных в ходе
аналитического решения задачи. Прежде
всего необходимо эти результаты
разместить на листе MS
Excel
так, как это показано на рис. 4.3. Заметим,
что в ячейке $AP$12
содержится величина дисперсии, т.е.
величина риска, возведенная в квадрат.
Далее следует ввести матрицу из
коэффициентов линейных ограничений
(AJ13:AO19);
строку из нулей, соответствующую
первоначальной структуре портфеля
(AJ24:AO24);
единичный вектор (AP13:AP19). -
Задание целевой
функции путем введения в ячейку AQ12
формулы
=МУМНОЖ(AJ24:AO24;МУМНОЖ(AJ4:AO9;ТРАНСП(AJ24:AO24))).
3. Задание ограничений
путем введения в ячейки (AQ13:AQ20)
формулы
=МУМНОЖ(AJ13:AO20;ТРАНСП(AJ24:AO24)).
4. Вызов модуля
Поиск решения
(Сервис
– Поиск решения).
В результате появится окно, в котором
необходимо:
-
установить целевую
ячейку $AQ$12,
равной минимальному значению (см. рис.
4.4);

Рис. 4.3. Первоначальные
установки при построении модели Марковица

Рис. 4.4. Модуль
Поиск решения
(модель
Марковица)
-
в строке «Изменяя
ячейки» указать диапазон $AJ$24:$AO$24 (см.
рис. 4.4); -
указать
ограничения (см. рис. 4.4):
$AQ$13=$AP$13;
$AQ$14<=$AP$14;
$AQ$15<=$AP$15;
$AQ$16<=$AP$16;
$AQ$17<=$AP$17;
$AQ$18<=$AP$18;
$AQ$19<=$AP$19;
$AQ$20=$AP$20.
-
нажать кнопку
Выполнить.
В результате появится окно, представленное
на рис. 4.5.

Рис. 4.5. Результаты
Поиска решения
(модель
Марковица)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приведем пример формирования инвестиционного портфеля по модели Г. Марковица с помощью программы Excel, разберем достоинства и недостатки данной модели в современной экономике и пути их решения.
Инвестиционный портфель – это совокупность различных финансовых инструментов, удовлетворяющих цели инвестора и, как правило, заключается в создании таких комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Модель Марковица
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Г. Марковиц в 1952 году впервые предложил математическую модель формирования инвестиционного портфеля. В основе его модели лежат два ключевых показателя любого финансового инструмента: доходность и риск, которые были количественно измерены. Доходность по модели представляет собой математическое ожидание доходностей, а риск определяется как разброс доходностей возле математического ожидания и рассчитывается через стандартное отклонение.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
До модели Г. Марковица инвестирование происходило, как правило, в выборочные активы или финансовые инструменты, предложенная же им модель позволила снизить систематические (рыночные) риски за счет группировки активов с отрицательной корреляцией доходностей.
Следует заметить универсальность модели, так инвестиционный портфель может быть технически составлен для любых видов финансовых инструментов и активов: акций, облигаций, фьючерсов, индексов, недвижимости и т.д.
★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности
★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса
Оценка риска инвестиционного портфеля Марковица
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
В модели Г. Марковица риск отдельно взятого финансового инструмента рассчитывается как стандартное отклонение доходностей. Для расчета общего риска портфеля необходимо отразить их совокупное изменение и взаимное влияние (через ковариацию), для этого воспользуемся следующей формулой:
где:
σp – риск инвестиционного портфеля;
σi – стандартное отклонение доходностей i-го финансового инструмента;
kij – коэффициент корреляции между I,j-м финансовым инструментом;
wi – доля i-го финансового инструмента (акций) в портфеле;
Vij – ковариация доходностей i-го и j-го финансового инструмента;
n – количество финансовых инструментов инвестиционного портфеля.
Эконометрический вид модели Марковица
Для того чтобы сформировать инвестиционный портфель необходимо решить оптимизационную задачу. Существует два вида задач: поиск долей акций в портфеле для достижения максимальной эффективности при заданном уровне риска (σp) и минимизация риска при заданном уровне доходности портфеля (rp). Помимо этого на уравнения накладываются дополнительные очевидные ограничения: сумма долей активов должна быть равна 1 и сами доли активов должны быть положительными.
В таблице ниже показаны формулы и наложенные на них ограничения для поиска оптимальных долей финансовых инструментов (акций).
| Портфель Марковица минимального риска | Портфель Марковица максимальной эффективности |
★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса
Калькулятор портфелей Марковица
Всем привет. Я немного вынырнул из небытия. Извиняюсь, что прервал тему про опционы, просто к ней охладел. А так — презентую новый проект, Калькулятор доходности портфелей по Марковицу. Многие видели подобные картинки и знают, что это такое:
Для тех, кто не знает — это кривая риск-доходность портфеля, составленного из 2 инструментов. Марковиц доказал (за что получил Нобеля по экономике), что эта кривая всегда выгнута влево-вверх, и никогда вправо-вниз. То есть, добавление в портфель рисковых высокодоходных инструментов может уменьшить риск портфеля при увеличении прибыльности. Отсюда пошла быть современная портфельная теория.
А теперь можно считать и рисовать на дому! И совершенно бесплатно, в смысле даром!
Давайте по-порядку.
1. Качаем версию с Гитхаба (ссылка в конце поста), распаковываем. Проверяем на вирусы или читаем исходный код, убеждаемся, что все безопасно. Разблокируем calcaa.cmd через свойства файла и запускаем программу. Да, работает под Виндой и Линуксом. На Маках тоже должно, но не проверял из-за наличия отсутствия.
2. Видим примерно такое:
Добавление данных руками пока не доделано (зато удаление работает! гггг), да и не нужно, думаю. Жмем «Открыть» и открываем CSV файл с данными по инструментам. Рядом с программой лежат примеры. Ниже буду показывать «портфель лежебоки», про который многие тоже слышали.
Все примеры данных я сохранил в таком в таком формате:
Разделитель; текст в » десятичная точка, и 1-м столбце везде даты (в примерах).
3. После открытия файла можно посмотреть и подредактировать данные в таблице, посмотреть корреляции и ковариации (вдруг понадобится?).
4. С неинтересной частью закончили, начинаем рисовать! По кнопке «Портфели (Ctrl+Enter)» открывается окно построения графиков. Жамкаем «Нарисовать»!
И видим характеристики портфелей, составленных с разным процентным соотношением инструментов. По горизонтали — риск портфеля (волатильность), по вертикали — доходность.
5. Режим «Только граница» показывает только портфели на границе эффективности. Те, у которых максимальная доходность при данном риске.
6. Режим «Ребалансировки». Мы ведь не просто покупаем постоянный портфель типа «60% акций + 40% облигаций», но и ребалансируем его (скажем, раз в год) для восстановления пропорций активов. И тут есть такой момент, что портфель на границе эффективности вовсе не обязательно самый доходный с учетом ребалансировок. Вот эта кнопка и позволяет раскрасить график и посмотреть доходность портфелей с учетом ребалансировок:
7. Задание ограничений. В таблице над кнопками можно указать минимальные и максимальные веса инструментов для расчета. Допустим, мы «строго по Грэхему» хотим в портфеле акции и облигации в пределах 25-75% каждые. И не более 15% золота на всякий случай. Вводим и смотрим, что получается:
9. Сравнение портфелей и ограничение срока графика. Если такая неприятная штука. Корреляции инструментов в будущих периодах будут не такие, как на истории. Поэтому портфель, который сейчас находится на границе эффективности, в будущем с этой границы уйдет. Допустим, мы в 2005-м году провели расчет и получили такие данные (это уже данные по индексам MSCI развитых рынков — см msci_year_dm.csv). Выбрали портфель на границе эффективности и хотим посмотреть, как он себя повел бы:
Вводим параметры этого портфеля в стоку таблицы «Сравнить» и снова жмем «Нарисовать». Получится так (портфель из строки «Сравнить» нарисован черным):
Теперь меняем даты, и смотрим, как этот портфель повел бы себя с 2006-го по 2015-й:
Видно, что портфель уже больше не на границе, а довольно далеко от нее.
Более подробно, с рисунками и обсуждением, у меня в ЖЖ: https://oppositus.livejournal.com/409878.htmlhttps://oppositus.livejournal.com/410305.htmlhttps://oppositus.livejournal.com/410911.html
10. Напоследок, если кликнуть по портфелю в графике портфелей, можно посмотреть его доходность:
11. Кнопка «Прогноз» (с картинки выше) сравнивает реальную доходность с расчетной. Кнопка «Ребалансировки» переключает график в режим сравнения доходности портфеля «просто купил-и-держу» с портфелем, который ребалансируется раз в период:
Вот основные функции калькулятора на сегодня. Остальное в справке на Гитхабе: https://github.com/Oppositus/CalculatorAA
Качать отсюда: https://github.com/Oppositus/CalculatorAA/tree/master/builds Старые билды качать не имеет смысла, берите 1.5 или более свежие, когда появятся.
Лицензия MIT. Это значит, что можно использовать как угодно и где угодно, в том числе в коммерческой деятельности.
Вопросы, замечания, предложения — пишите сюда, или в ЖЖ. Баги тоже пишите, сюда или в багрекер на Гитхабе.
Надеюсь, кому-нибудь пригодится. Раз уж идут разговоры о том, «что в последнее время стало много инвесторов» — инвестируйте правильно.
Всем чмоки!
Пример формирования инвестиционного портфеля Марковица в Excel
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Рассмотрим наглядный пример формирования инвестиционного портфеля по модели Г. Марковица в программе Excel. Наш портфель будет состоять из четырех отечественных акций: ОАО «Газпром» (GAZP), ОАО «Норильский никель» (GMKN), ОАО «Мечел» (MTLR) и ОАО «Сбербанк» (SBER). Были взяты акции различных секторов: нефтегазового, промышленного и финансового, такой выбор увеличивает диверсификацию портфеля и снижает его рыночный риск.
Рекомендуется брать период рассмотрения динамики изменения стоимости акций минимум один год. Это позволяет сделать более точный долгосрочный прогноз доходности и риска портфеля. На рисунке ниже показана ежемесячная стоимость акций за период с 01.02.2014 – 01.02.2015г.
Котировки акций Газпрома, ГМКНорНикеля, Мечела и Сбербанка
На следующем этапе формирования портфеля необходимо рассчитать ежемесячные доходности по каждой акции. Для этого воспользуемся формулой процентов в Excel:
Доходность Газпром =LN(B6/B5)
Доходность ГМКНорНикель =LN(C6/C5)
Доходность Мечел =LN(D6/D5)
Доходность Сбербанк =LN(E6/E5)
Расчет ежемесячных доходностей акций для модели Марковица в Excel
Далее определяем математическое ожидание доходностей по каждой акции, для этого найдем среднеарифметическое значение за весь период. Ожидаемая доходность по каждой акции будет следующая:
Ожидаемая доходность Газпром =СРЗНАЧ(F5:F17)
Ожидаемая доходность ГМКНорНикель =СРЗНАЧ(G5:G17)
Ожидаемая доходность Мечел =СРЗНАЧ(H5:H17)
Ожидаемая доходность Сбербанк =СРЗНАЧ(I5:I17)
Оценка ожидаемой доходности акций портфеля в Excel
Доходность акции ОАО «Сбербанк» имеет отрицательное ожидание доходности, поэтому ее следует исключить из портфеля. Оценка риска каждой акции – это ее изменчивость (волатильность) по отношению к математическому ожиданию доходностей.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Формула расчета риска акций следующая:
Риск Газпром =СТАНДОТКЛОН(F5:F17)
Риск ГМКНорНикель =СТАНДОТКЛОН(G5:G17)
Риск Мечел =СТАНДОТКЛОН(H5:H17)
Оценка риска по акции инвестиционного портфеля в Excel
Мы получили первоначальные необходимые данные для оценки долей данных акций в инвестиционном портфеле. Для оценки уровня риска всего инвестиционного портфеля воспользуемся надстройкой в Excel. Для этого зайдем в Главном меню → «Данные» → «Анализ данных» → «Ковариация».
Далее в появившемся окне необходимо найти ковариации между доходностями акций. Указываем входной интервал – ежемесячных доходностей акций, а в опции «Группирование» выбираем функцию «по столбцам».
Результатом будет таблица ковариаций доходностей акций между собой. Расположим ее ниже под таблицей. Можно заметить, что диагональные значения представляют собой дисперсию доходностей акций.
Пример расчета ковариационной матрицы для инвестиционного портфеля Марковица в Excel.
Для расчета общего риска портфеля воспользуемся формулой рассмотренной выше и для этого нам необходимо перемножить доли весов акций между собой и значения ковариаций этих акций. Для того чтобы понять принцип расчета, установим доли акций 0.3, 0.3 и 0.4 и рассчитаем общий риск портфеля. Доходность портфеля рассчитывается как средневзвешенная сумма доходностей отдельных акций. Так как мы будем перемножать матрицы необходимо транспонировать столбец с долям (wT). Формула расчета риска инвестиционного портфеля будет иметь следующий вид:
Общий риск инвестиционного портфеля =КОРЕНЬ(МУМНОЖ(МУМНОЖ(F26:H26;F23:H25);D23:D25))
Общая доходность инвестиционного портфеля =F18*F26+G18*G26+H18*H26
Формирование инвестиционного портфеля минимального риска
Для данной задачи необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp ≥ 4%. При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню Excel → «Данные» → «Поиск решений», а также введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля), ввести, какие параметры необходимо изменять (доли акций) и текущие ограничения. Целевая ячейка – это ячейка с формулой общего риска инвестиционного портфеля. Программа будет изменять значения долей акций при выставленных ограничениях. Формула ограничения размера доли в портфеле будет иметь следующий вид:
Ограничение на сумму долей акций (F30) =СУММ(F26:H26)
Расчет долей акций в инвестиционном портфеле в Excel
В результате мы получаем следующий расчет общего риска и доходности портфеля. Общий риск портфеля составил 8,7%, тогда как общая доходность 4%. Доли акций Газпрома получились равными 27%, доли ГМКНорНикель 73% и Мечела 0%. При заданных условиях эффективнее будет формирование портфеля из двух акций ОАО «Газпром» и ОАО «ГМКНорНикель».
Формирование инвестиционного портфеля Марковица в Excel. Пример расчета для минимального риска
Визуально доли портфеля будут соотноситься следующим образом.
Формирование эффективного инвестиционного портфеля
Вторая задача, которая решается на основе модели Г. Марковица – посторонние портфеля с максимальным уровнем доходности и ограниченным уровнем риска. Разберем на примере данную задачу. Установим максимально допустимый уровень риска портфеля σp≤10%. С помощью надстройки «Поиск решений» определим доли акций в данной интерпретации задачи. Целевая ячейка будет ячейка с формулой доходности портфеля, ее следует максимизировать, изменяя значения долей акций при ограничениях по риску. На рисунке ниже показаны основные параметры для формирования портфеля с максимальной доходностью.
Оптимизация инвестиционного портфеля для максимизации доходности
В результате мы получили доли акций в инвестиционном портфеле: 9% акций ОАО «Газпром», 88% акций ОАО «ГМКНорНикель» и 2% акций ОАО «Мечел». Общий риск портфеля не превысил 10%, а доходность составила 4,82%.
Формирование инвестиционного портфеля Марковица в Excel. Пример оценки для максимизации доходности акций
Визуально доли инвестиционного портфеля будут соотноситься следующим образом.
Портфельная теория Марковица суть
Книга «Портфельная теория Марковица» от автора, который в 90 лет взялся за разработку еще одного научного масштабного труда, имеет достаточно простую и одновременно сложную суть. Доходность способа для вложения денег и риск прямо связаны между собой. Математический метод позволил описать принцип так: риск — это функция от разброса значений прибыли за определенные временные интервалы.
Метод необходим не только частным инвесторам; его используют банки, инвестиционные и хэдж фонды.
Ключевая задача — добиться высокой диверсификации портфеля не только по суммам вложений, но и по времени работы инструмента. Это актуально, даже работая с небольшими суммами. В учебниках для ВУЗов по экономике и финансированию портфельная теория Марковица активно описывается и много времени уделяется ее изучению. Для инвестора же важно самому или с помощью доверительного менеджера понять базовые постулаты — учитывать 2 критерия во время вложений: доходность и риски, сравнить, например, прибыль за 2 разных периода или вовсе найти один, но суперкритерий оценки.
Скачав реферат по экономике или финансовому анализу рынка, можно увидеть, что портфельная теория Марковица хоть и эффективна, но требует и знаний, и усердия в расчётах. При этом, стоит понимать, что нужно владеть информацией из рынка, чтобы выбрать правильные стратегии и подобрать пакет акций для вложений. Сегодня такой расчёт, а также упрощенная версия, согласно теории Шарпа, относится к классу иоп — индивидуальной образовательной программы. Знания, как говориться, за плечами не носить и если есть математически проверенный метод уменьшения риска, почему бы его не использовать не только с акциями, но и другими инструментами?
Теория на примере
Если необходимо показать пример, как эффективно работает портфельная теория Марковица, стоит обратить внимание на доходность за определенный период и суммарное время работы. Для простоты восприятия покажу это в виде таблицы.
| Временной интервал в месяцах | 1 | 2 | 3 | 4 |
| Прибыль % | -5 | 5 | 2 | 3 |
Средний показатель дохода равен (-5+5+2+3)/4=1,25. Это суммарная доходность за весь период (у вас могут быть другие значения). Если же (а так грамотно и рационально делать) в портфеле несколько источников, тогда стоит дополнительно провести расчет еще по одной формуле: ∑р (доходность по всему портфелю) представлена как произведение ожидаемой доходности по одному из инструментов и его доли в общем портфеле. Ожидаемая доходность указывается, когда вы покупаете акции на бирже.
Если вы работаете с большим количеством инструментов, тогда можно использовать для простоты расчета введенную формулу в excel, которая поможет согласно портфельной теории Марковица рассчитать: какая доходность в портфеле от сдачи в аренду квартиры, вложений в бизнес, покупки драгоценных металлов или трейдинга криптовалютой. Рассматривая и применяя разные принципы инвестирования, стоит помнить и о доле риска. Согласно работе математика, он рассчитывается как квадратный корень из произведения 1/n, где n — количество периодов и ∑ (среднего значения дохода способа за вычетом одного периода), возведенного в квадрат. Придется вспомнить математические правила возведения в квадрат выражения и порядок проведения действий.
Работают ли школьные знания?
Взглянув на формулы, представляющие комплексную портфельную теорию Марковица, можно немного испугаться, поскольку они сложные. Но понимания, какая позиция за что отвечает, имея данные по ним, смело можно провести расчеты. Будем честны, далеко не все инвесторы таким занимаются, а пользуются интуицией или школьными знаниями (если такая тема преподавалась) или советами наставника (что более эффективно). Фактически, стоит понимать направление работы, чтобы знания работали: если падает цена на золото, то акции ювелирных компаний будут падать, а изделия дешеветь из-за снижения себестоимости металла.
А что, если будут отклонения?
Читая книгу с детально описанной портфельной теорией Марковица, стоит заметить, что сам автор периодически уточняет, что они могут быть. Основной аспект в том, что стоит оценивать исторический сценарий развития, но он повторяется не всегда и не с точной закономерностью. Достаточно вспомнить цены на акции компаний ЮКОС, Фейсбук, Боинг. Отклонения могут быть связаны и с такими аспектами:
- не описанные точки входа и выхода из рынка;
- не предусмотрено использования торгового плеча.
Формируя инвестиционный портфель, можно одновременно использовать несколько теорий, например, дополнительно учитывать коэффициент шарпа, а более делительные рекомендации по формированию стратегии вложения капитала уже на gq-blog.com.
Умение подбирать активы для инвестиций – ключевой навык для извлечения прибыли на бирже. Для решения этой задачи инвесторам необходимо анализировать собственный психологический портрет, ставить реалистичные цели инвестирования и научиться правильно распределять активы разных типов внутри портфеля.
Издание Investopedia опубликовало образовательный материал, в котором рассказывается о том, как построить и поддерживать качественный инвестпортфель. Мы подготовили адаптированную версию этой полезной статьи.
Составление инвестиционного портфеля по Марковицу — 2. Российский рынок
В данном обзоре мы представим простой пример составления оптимального инвестиционного портфеля по Марковицу на примере российских акций.
Введение в портфельную теорию
Портфельная теория Марковица была обнародована в 1952 году. Позже автор получил за нее Нобелевскую премию.
Целью модели является составление оптимального портфеля, то есть с минимальным риском и максимальной доходностью.
Как правило, решается две задачи: максимизация доходности при заданном уровне риска и минимизация риска при минимально допустимом значении доходности.
Доходность портфеля измеряется как средневзвешенная сумма доходностей входящих в него бумаг.
wi — доля инструмента в портфеле;
ri — доходность инструмента.
Риск отдельного инструмента оценивается как среднеквадратичное (стандартное) отклонение его доходности. Для расчета общего риска портфеля необходимо отразить совокупное изменение рисков отдельного инструмента и их взаимное влияние (через ковариации и корреляции — меры взаимосвязи).
σi — стандартное отклонение доходностей инструмента;
kij — коэффициент корреляции между I,j-м инструментом;
Vij — ковариация доходностей i-го и j-го финансового инструмента;
n — количество финансовых инструментов в рамках портфеля.
Таким образом, в рамках правильно подобранного портфеля риски снижаются за счет обратной корреляции инструментов. При этом устраняются не только специфические риски инструмента, но и снижается систематический (рыночный) риск.
Для составления портфеля решается оптимизационная задача. При этом в базовом виде использование заемных средств не предполагается, то есть сумма долей активов равняется единице, а доли эти положительны.
Минимизируем риск при минимально допустимом уровне доходности
Максимизируем доходность при заданном уровне риска
Пример расчетов в Excel
Оптимальный портфель содержит различные группы активов — акции, облигации, товарные фьючерсы и т.д. Так легче подобрать инструменты с отрицательной корреляцией и минимизировать риски.
В нашем примере будет использован более простой подход — составление портфеля из нескольких российских акций. Для этого возьмем бумаги 5 крупных эмитентов с наибольшей форвардной дивидендной доходностью (прогноз экспертов БКС Брокер): Норникель, Северсталь, НЛМК, МТС (присутствуют санкционные риски), ЛСР.
Сразу отмечу, что это лишь пример. Для грамотного составления портфеля необходимо учитывать фундаментальные показатели, включая рыночные мультипликаторы, оценивать технические уровни для входа в позицию.
Этап 1. Выкачиваем котировки. Необходимо взять данные минимум за год. В нашем примере были взяты ежемесячные цены закрытия с 31.05.2017 по 26.06.2018.
Для учета дивидендного фактора указываем выплаты, которые можно взять из дивидендного календаря БКС Экспресс. Чтобы включить годовые дивиденды ЛСР, берем данные за 13 месяцев.
Для увеличения кликните по таблице
Этап 2. Считаем доходности по каждой бумаге с учетом дивидендов.
Считаем доходность за каждый месяц по формуле натурального логарифма. К примеру, доходность Норникеля за май 2021 = LN(B14/B13)
В те месяцы, когда были выплачены дивиденды, добавляем их в числитель. К примеру, доходность Норникеля за октябрь 2021 = LN((B7+C7)/B6)
Для расчета ожидаемой доходности берем среднее значение за рассматриваемый период. В нашем случае это год. Ожидаемая доходность Норникеля = СРЗНАЧ(L3:L15)
Получаем близкую к нулю доходность ЛСР, и убираем бумагу из портфеля. Сразу отмечу, что в этом заключается недостаток модели, ведь просевшие ранее акции в перспективе могут развернуться.
Доходность МТС ниже по сравнению с оставшимися в выборке бумагами, а риск выше. Однако оставим МТС для «чистоты эксперимента».
Этап 3. Расчет риска каждой акции. Производится по формуле стандартного отклонения. К примеру, риск Норникеля =СТАНДОТКЛОН(L3:L15)
Этап 4. Расчет ковариаций между бумагами. Воспользуемся специальной надстройкой в Excel. Для этого выберем в Главном меню → «Данные» → «Анализ данных» → «Ковариация».
Указываем окне входной интервал — ежемесячные доходности акций, а в опции «Группирование» выбираем «по столбцам».
В результате получаем ковариационную матрицу.
Этап 5. Расчет общей доходности портфеля.
Для начала установим произвольные доли бумаг в портфеле. Они положительны, их сумма равна 1. Считаем средневзвешенное значение доходностей отдельных акций. Воспользуемся формулой J26*L16+K26*M16+L26*N16
Этап 6. Расчет общего риска портфеля. Производится по формуле массива КОРЕНЬ(МУМНОЖ(МУМНОЖ(J26:M26;J22:M25); H22:H25))
Этап 7. Портфель минимального риска.
Речь идет о долях отдельных бумаг в портфеле. Для начала необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp >= 3,4%.
При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню → «Данные» → «Поиск решений».
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля, минимизируем), ввести какие параметры, которые необходимо изменять (доли акций), и ограничения. Введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В результате имеем портфель с 43% долей Северстали и 57% долей НЛМК.
Визуально портфель выглядит так:
Этап 8. Портфель максимальной доходности.
Для начала необходимо определить максимальный уровень допустимого риска портфеля (σp). Возьмем σp <= 5%.
В надстройке «Поиск решений» меняем оптимизируемую ячейку на доходность портфеля, ее максимизируем. Меняем ограничение — теперь ограничиваем риск.
В результате имеем портфель на 100% состоящий из акций НЛМК. Так произошло из-за того, что Норникель, Северсталь и НЛМК имеют практически одинаковый показатель риска, но НЛМК имеет более высокую доходность.
Получается, что результаты расчетов предполагают лишь 1 бумагу в портфеле. Это не очень правильно с точки зрения диверсификации. Но не забываем, что перед нами не рекомендация, а лишь пример. В своих расчетах вы можете включить в выборку другие акции, возможно большее их число. Как результат, появится шанс для формирования более сбалансированного портфеля.
Сильные стороны модели Марковица
• Систематизация подхода к формированию портфеля.
• Относительная простота модели. Расчеты может провести любой инвестор в общедоступной программе Excel.
Слабые стороны модели Марковица
• Основная предпосылка модели — эффективные рынки капитала, где действуют рациональные агенты, а значит, не может быть продолжительных иррациональных движений. В реалиях российского рынка не забываем про геополитические риски. Впрочем, они малопрогнозируемы.
• Будущая доходность основывается только на историческом значении доходностей бумаг и не включает влияние макро- и микро- и поведенческих факторов. В реальном мире если акция долго падала, то ожидаемая доходность скорее будет положительной.
• Риск финансового инструмента оценивается с помощью среднеквадратичного отклонения. Однако позитивное изменение доходности выше среднего по факту не является риском.
Начать инвестировать
БКС Брокер
( 1 оценка, среднее 4 из 5 )
Приведем пример формирования инвестиционного портфеля по модели Г. Марковица с помощью программы Excel, разберем достоинства и недостатки данной модели в современной экономике и пути их решения.
Инвестиционный портфель – это совокупность различных финансовых инструментов, удовлетворяющих цели инвестора и, как правило, заключается в создании таких комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Модель Марковица
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Г. Марковиц в 1952 году впервые предложил математическую модель формирования инвестиционного портфеля. В основе его модели лежат два ключевых показателя любого финансового инструмента: доходность и риск, которые были количественно измерены. Доходность по модели представляет собой математическое ожидание доходностей, а риск определяется как разброс доходностей возле математического ожидания и рассчитывается через стандартное отклонение.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
До модели Г. Марковица инвестирование происходило, как правило, в выборочные активы или финансовые инструменты, предложенная же им модель позволила снизить систематические (рыночные) риски за счет группировки активов с отрицательной корреляцией доходностей.
Следует заметить универсальность модели, так инвестиционный портфель может быть технически составлен для любых видов финансовых инструментов и активов: акций, облигаций, фьючерсов, индексов, недвижимости и т.д.
★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности
★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса
Слабые места теории Марковица
При растущем рынке теория Марковица в целом упрощает задачу инвестора. Проблемы появляются при развороте рынка. Основной принцип пассивной стратегии управления капиталом «купить и держать» на медвежьем рынке оборачивается нарастанием убытков. Математическое ожидание доходности зависит от выбранного интервала времени. Чем этот интервал больше, тем медленнее реагирует математическое ожидание на новый ряд значений. В целом, проблема во многом подобна использованию скользящих средних с очень длительным периодом.
Рекомендую прочитать также:
Мошенники в сфере обучения финансовой грамотности
Троянское обучение: как сегодня разводят инвесторов
Теория Марковица не содержит инструментария для определения точек входа и выхода из сделки. В связи с этим приходится всё чаще пересчитывать портфель, постепенно исключая из него лидеров падения. Запрет на короткие сделки означает, что на падающем рынке само понятие эффективного портфеля может терять смысл. Ещё одна проблема связана с тем, что поведение инструмента в прошлом не гарантирует повторения такого поведения в будущем. В настоящее время более популярны активные или комбинированные пассивно-активные стратегии, в которых портфельная теория сочетается с применением технического анализа для более оперативного реагирования на изменения рынка.
Оценка риска инвестиционного портфеля Марковица
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
В модели Г. Марковица риск отдельно взятого финансового инструмента рассчитывается как стандартное отклонение доходностей. Для расчета общего риска портфеля необходимо отразить их совокупное изменение и взаимное влияние (через ковариацию), для этого воспользуемся следующей формулой:
где:
σp – риск инвестиционного портфеля;
σi – стандартное отклонение доходностей i-го финансового инструмента;
kij – коэффициент корреляции между I,j-м финансовым инструментом;
wi – доля i-го финансового инструмента (акций) в портфеле;
Vij – ковариация доходностей i-го и j-го финансового инструмента;
n – количество финансовых инструментов инвестиционного портфеля.
Эконометрический вид модели Марковица
Для того чтобы сформировать инвестиционный портфель необходимо решить оптимизационную задачу. Существует два вида задач: поиск долей акций в портфеле для достижения максимальной эффективности при заданном уровне риска (σp) и минимизация риска при заданном уровне доходности портфеля (rp). Помимо этого на уравнения накладываются дополнительные очевидные ограничения: сумма долей активов должна быть равна 1 и сами доли активов должны быть положительными.
В таблице ниже показаны формулы и наложенные на них ограничения для поиска оптимальных долей финансовых инструментов (акций).
| Портфель Марковица минимального риска | Портфель Марковица максимальной эффективности |
★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса
Безрисковый портфель ценных бумаг
Интересен взгляд на портфель ценных бумаг с так называемым нулевым инвестиционным риском (σ0) и некоторой заданной эффективностью (m0).
На графике этому портфелю соответствует точка A.
Этот портфель более предпочтителен для инвестора, нежели портфель 1, поскольку характеризуется меньшим риском и значительно большей эффективностью (нормой доходности).
Чтобы его сформировать, потребуется включить в него как безрисковые ценные бумаги, так и финансовые вложения в портфель 4 в пропорции [σ0 / σ4] к [(σ4 – σ0)/ σ4].
Пример формирования инвестиционного портфеля Марковица в Excel
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Рассмотрим наглядный пример формирования инвестиционного портфеля по модели Г. Марковица в программе Excel. Наш портфель будет состоять из четырех отечественных акций: ОАО «Газпром» (GAZP), ОАО «Норильский никель» (GMKN), ОАО «Мечел» (MTLR) и ОАО «Сбербанк» (SBER). Были взяты акции различных секторов: нефтегазового, промышленного и финансового, такой выбор увеличивает диверсификацию портфеля и снижает его рыночный риск.
Рекомендуется брать период рассмотрения динамики изменения стоимости акций минимум один год. Это позволяет сделать более точный долгосрочный прогноз доходности и риска портфеля. На рисунке ниже показана ежемесячная стоимость акций за период с 01.02.2014 – 01.02.2015г.
Котировки акций Газпрома, ГМКНорНикеля, Мечела и Сбербанка
На следующем этапе формирования портфеля необходимо рассчитать ежемесячные доходности по каждой акции. Для этого воспользуемся формулой процентов в Excel:
Доходность Газпром =LN(B6/B5)
Доходность ГМКНорНикель =LN(C6/C5)
Доходность Мечел =LN(D6/D5)
Доходность Сбербанк =LN(E6/E5)
Расчет ежемесячных доходностей акций для модели Марковица в Excel
Далее определяем математическое ожидание доходностей по каждой акции, для этого найдем среднеарифметическое значение за весь период. Ожидаемая доходность по каждой акции будет следующая:
Ожидаемая доходность Газпром =СРЗНАЧ(F5:F17)
Ожидаемая доходность ГМКНорНикель =СРЗНАЧ(G5:G17)
Ожидаемая доходность Мечел =СРЗНАЧ(H5:H17)
Ожидаемая доходность Сбербанк =СРЗНАЧ(I5:I17)
Оценка ожидаемой доходности акций портфеля в Excel
Доходность акции ОАО «Сбербанк» имеет отрицательное ожидание доходности, поэтому ее следует исключить из портфеля. Оценка риска каждой акции – это ее изменчивость (волатильность) по отношению к математическому ожиданию доходностей.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Формула расчета риска акций следующая:
Риск Газпром =СТАНДОТКЛОН(F5:F17)
Риск ГМКНорНикель =СТАНДОТКЛОН(G5:G17)
Риск Мечел =СТАНДОТКЛОН(H5:H17)
Оценка риска по акции инвестиционного портфеля в Excel
Мы получили первоначальные необходимые данные для оценки долей данных акций в инвестиционном портфеле. Для оценки уровня риска всего инвестиционного портфеля воспользуемся надстройкой в Excel. Для этого зайдем в Главном меню → «Данные» → «Анализ данных» → «Ковариация».
Далее в появившемся окне необходимо найти ковариации между доходностями акций. Указываем входной интервал – ежемесячных доходностей акций, а в опции «Группирование» выбираем функцию «по столбцам».
Результатом будет таблица ковариаций доходностей акций между собой. Расположим ее ниже под таблицей. Можно заметить, что диагональные значения представляют собой дисперсию доходностей акций.
Пример расчета ковариационной матрицы для инвестиционного портфеля Марковица в Excel.
Для расчета общего риска портфеля воспользуемся формулой рассмотренной выше и для этого нам необходимо перемножить доли весов акций между собой и значения ковариаций этих акций. Для того чтобы понять принцип расчета, установим доли акций 0.3, 0.3 и 0.4 и рассчитаем общий риск портфеля. Доходность портфеля рассчитывается как средневзвешенная сумма доходностей отдельных акций. Так как мы будем перемножать матрицы необходимо транспонировать столбец с долям (wT). Формула расчета риска инвестиционного портфеля будет иметь следующий вид:
Общий риск инвестиционного портфеля =КОРЕНЬ(МУМНОЖ(МУМНОЖ(F26:H26;F23:H25);D23:D25))
Общая доходность инвестиционного портфеля =F18*F26+G18*G26+H18*H26
Формирование инвестиционного портфеля минимального риска
Для данной задачи необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp ≥ 4%. При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню Excel → «Данные» → «Поиск решений», а также введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля), ввести, какие параметры необходимо изменять (доли акций) и текущие ограничения. Целевая ячейка – это ячейка с формулой общего риска инвестиционного портфеля. Программа будет изменять значения долей акций при выставленных ограничениях. Формула ограничения размера доли в портфеле будет иметь следующий вид:
Ограничение на сумму долей акций (F30) =СУММ(F26:H26)
Расчет долей акций в инвестиционном портфеле в Excel
В результате мы получаем следующий расчет общего риска и доходности портфеля. Общий риск портфеля составил 8,7%, тогда как общая доходность 4%. Доли акций Газпрома получились равными 27%, доли ГМКНорНикель 73% и Мечела 0%. При заданных условиях эффективнее будет формирование портфеля из двух акций ОАО «Газпром» и ОАО «ГМКНорНикель».
Формирование инвестиционного портфеля Марковица в Excel. Пример расчета для минимального риска
Визуально доли портфеля будут соотноситься следующим образом.
Формирование эффективного инвестиционного портфеля
Вторая задача, которая решается на основе модели Г. Марковица – посторонние портфеля с максимальным уровнем доходности и ограниченным уровнем риска. Разберем на примере данную задачу. Установим максимально допустимый уровень риска портфеля σp≤10%. С помощью надстройки «Поиск решений» определим доли акций в данной интерпретации задачи. Целевая ячейка будет ячейка с формулой доходности портфеля, ее следует максимизировать, изменяя значения долей акций при ограничениях по риску. На рисунке ниже показаны основные параметры для формирования портфеля с максимальной доходностью.
Оптимизация инвестиционного портфеля для максимизации доходности
В результате мы получили доли акций в инвестиционном портфеле: 9% акций ОАО «Газпром», 88% акций ОАО «ГМКНорНикель» и 2% акций ОАО «Мечел». Общий риск портфеля не превысил 10%, а доходность составила 4,82%.
Формирование инвестиционного портфеля Марковица в Excel. Пример оценки для максимизации доходности акций
Визуально доли инвестиционного портфеля будут соотноситься следующим образом.
Оптимизация финансового портфеля по модели Марковица: идеи нобелевского лауреата на современных рынках
Время на чтение: 14 минут

Гарри Марковиц считается одним из основателей современной портфельной теории. Разработанные им в 1952 г. принципы активно используются инвесторами при формировании портфелей активов и по сей день. Позднее его модель принесет автору Нобелевскую премию.
В данной статье мы рассмотрим механизм создания портфеля по Марковицу с использованием программы Microsoft Excel и покажем, как ее можно использовать даже при самом неблагоприятном стечении событий (и не только на рынке акций).
Содержание
- Принципы формирования финансового портфеля по Марковицу.
- Оптимизация на примере группы акций.
- Оптимизация на примере разносторонних активов.
- Сценарий “Все активы на покупку”
- Сценарий “Невероятный успех”
- Сценарий “Полный провал”
- Заключение.
Принципы формирования финансового портфеля по Марковицу
Портфель активов состоит из множества финансовых инструментов, каждый из которых имеет свой собственный вес. Если говорить современным языком, то портфель включает в себя активы, каждый из которых приобретается с разной лотностью. К примеру, если взять простой портфель из двух акций, то распределение весов со значениями 0,2 и 0,8 может выражаться в приобретении 2 лотов первой акции и 8 лотов второй.
В своей работе Марковиц разработал методологию анализа, позволяющую формировать портфель из оптимально выбранных активов, главным критерием которого является соотношение «доходность/риск». Выбор активов в портфель формируется на основе двух факторов:
- Средней доходности инструмента, рассчитываемой на исторических значениях.
- Риска инструмента, математически определяемого как среднеквадратичное отклонение доходности актива. Другими словами, за риск принимается средняя волатильность торгового инструмента.
Модель Марковица предполагает, что (1) имеются исторические данные по активу, позволяющие высчитать показатели доходности и риска, (2) инвестор заинтересован в том, чтобы максимизировать доходность и минимизировать риск, (3) сравнение портфелей основывается исключительно на соотношении параметров доходности и риска.
Желание инвестора получать максимально возможную доходность при фиксированном риске назовем принципом наивысшей доходности. Стремление инвестора выбрать наименьшее значение риска при заданном уровне доходности назовем принципом наименьшего риска. Именно на этих важных принципах основывается модель Марковица (которые будут полезны и вне его модели). Помимо них, в своей работе Марковиц руководствуется принципом диверсификации активов, который показан ниже.
С целью повышения качества портфеля, Марковиц включает в расчеты степень взаимозависимости активов между собой через коэффициенты корреляции. Данное решение позволяет ему более качественно диверсифицировать активы в портфеле. Если переформулировать выражение «не клади все яйца в одну корзину» в соответствии с данным принципом, то получится «не составляй портфель из высокозависимых друг от друга активов».
К примеру, если при прочих равных условиях необходимо выбрать два актива из трех для составления портфеля, и этими тремя активами являются акции компаний «БМВ» (Германия), «Форд» (США) и «Макдональдс» (США), то, в соответствии с вышеописанным принципом, взаимозависимость «БМВ» и «Форда» значительно выше, чем любые другие сочетания, так как они представляют одну отрасль — машиностроение. Если углубиться и диверсифицировать активы еще и по региональному признаку, то сочетание «Форд» и «Макдональдс» также будет отбрасываться, так как компании относятся к одной стране — США. Таким образом, по принципу отраслевой и региональной диверсификации наш портфель будет состоять из акций «БМВ» (Германия) и «Макдональдс» (США).
Прежде чем начать практическую часть, необходимо показать, каким образом происходит оптимизация параметров в модели Марковица. Оптимизация портфеля активов заключается в решении следующих задач:
- Минимизация риска портфеля при минимально приемлемом уровне доходности.
- Максимизация доходности портфеля при фиксированном уровне риска.
Марковиц проводит две отдельные оптимизации (что будем делать и мы), рассчитанные на нахождение оптимальной лотности активов портфеля, определяющих, в первом случае, на какой наименьший риск может рассчитывать инвестор, желающий иметь конкретный уровень доходности, и дающих, во втором случае, наибольшую доходность при приемлемом для инвестора риске.
Данное теоретическое введение было важным перед тем, как начать составлять математическую модель, так как позволяет понять принципы ее работы и эффективно использовать ее на практике. Перейдем к модели.
За 1 час поможем разобраться с факторами успеха и причинами неудач на финансовых рынках. Бесплатно
Оптимизация на примере группы акций
Ниже мы рассмотрим два примера портфелей: один — составленный исключительно из акций, и второй — сформированный из разнородных активов. В роли данных выступают котировки цен закрытия месячных свечей за период в 13 месяцев с 1 декабря 2017 г. по 31 декабря 2018 г. Акции и другие рассматриваемые в примере активы выбраны случайным образом и не являются рекомендацией к торговле. Котировки могут незначительно отличаться у разных брокеров. Задачей данного примера является иллюстрация принципа оптимизации портфеля, которая позволит проделывать аналогичную работу с любыми другими данными.
Ниже на рисунке 1 в столбцах, помеченных синим цветом, представлены указанные выше котировки акций пяти компаний: Apple, Microsoft, Boeing, Citigroup и Tesla. В правой части таблицы, выделенной оранжевым цветом, по этим котировкам рассчитаны доходности каждого из активов по принципу ежемесячного прироста. То есть, чтобы получить доходность Apple на январь 2018 г. (-1,09%) необходимо посчитать прирост за месяц (167,43-169,27) и определить его долю в значении начального периода (-1,84/169,27). Для повышения точности прогноза можно рассчитывать доходность с помощью натурального логарифма по принципу G6=ln(B6/B5). Однако в данном примере для простоты мы будем пользоваться описанным выше принципом ежемесячного прироста.
Расчет среднемесячной доходности производится методом расчета среднего значения по всем доходностям для конкретной акции, то есть значения суммируются, и сумма делится на их количество — 12 периодов. Как результат, мы получаем, что, к примеру, в среднем за месяц акции Apple имеют отрицательный прирост в -0,12%.

Значение риска рассчитывается методом определения стандартного отклонения по всем доходностям акции. В Excel данная процедура будет выглядеть так: риск для Apple = СТАНДОТКЛОН.В(G6:G17). Напомню, что в данном случает риск характеризует меру изменчивости или волатильности актива.
Следующим шагом после расчета индивидуальных характеристик каждой акции становится расчет доходности и уровня риска всего портфеля. В соответствии с принципами модели Марковица и здравым смыслом, мы убираем из дальнейших расчетов активы, которые дают отрицательную доходность: Apple и Citigroup.
Далее нам необходимо сформировать матрицу ковариаций, которая рассчитывается в Excel через вкладку «Данные» — «Анализ данных» — «Ковариация». Открыв данное окно, необходимо в ячейку «Входной интервал» вставить целевой диапазон (на рисунке 2 это D28:F39) и оставить группирование «по столбцам».

Далее, после формирования матрицы ковариаций, нам необходимо ввести придуманные нами доли активов в портфеле, которые нам кажутся приемлемыми на данный момент и которые в дальнейшем мы и будем оптимизировать. В примере они показаны как 0,2 для Microsoft, 0,3 для Boeing и 0,5 для Tesla.
Расчет совокупной доходности портфеля производится путем суммы произведений ожидаемых месячных доходностей каждого актива с его долей. То есть, J34 = D40*H29 + E40*H30 + F40*H31.
Расчет совокупного риска портфеля производится по формуле J35=КОРЕНЬ(МУМНОЖ(МУМНОЖ(J32:L32; J29:L31); H29:H31)).
Таким образом, мы получаем, что при данном распределении долей в портфеле показатели его совокупной доходности и совокупного риска будут равны 1,37% и 7,74%, соответственно. Возникает вопрос: «как выбрать доли более грамотно, чтобы иметь более приемлемое соотношение доходности к риску?». На помощь приходит оптимизация.
Как было отмечено выше, Марковиц предлагает провести две оптимизации: (1) минимизация риска при заданном значении доходности и (2) максимизация доходности при заданном значении риска.
Проведение оптимизации проводится с помощью инструмента «Поиск решения», расположенного в графе «Данные» рядом с инструментом «Анализ данных». Если по какой-то причине данного инструмента на экране нет, его нужно подключить через «Файл» — «Параметры» — «Надстройки» — «Поиск решения».
На рисунке 3 показан результат оптимизации портфеля акций для минимизации риска при заданном значении доходности. Разберем его пошагово.

Сначала нам необходимо ввести значение минимальной допустимой доходности (в примере она придумана нами и равна 1,50%). Далее мы открываем инструмент «Поиск решения» и заполняем следующие графы:
- «Оптимизировать целевую функцию» — кликаем на ячейку с совокупным риском портфеля (здесь «E57»);
- «До» — нажимаем на «Минимум»;
- «Изменяя ячейки переменных» — выделяем значения долей (здесь «C51:C53»);
- «В соответствии с ограничениями» — ставим ограничения. (1) неотрицательность долей ($C$51 >= 0, $C$52 >= 0, $C$53 >= 0), (2) сумма долей должна равняться единице ($E$58 = 1, при условии, что сама E58 = C51+C52+C53), (3) совокупная доходность портфеля не менее минимальной приемлемой доходности ($E$56 >= $E$47).
В результате оптимизации мы получаем следующие параметры: совокупная доходность портфеля повысилась до 1,57% в месяц, совокупный риск сократился до 5,05% при условии, что 85% портфеля состоит из акций Microsoft и 15% — из акций Tesla.
Аналогичным образом проводится оптимизация для максимизации доходности портфеля при заданном риске. В параметрах «Поиска решений» необходимо заменить ячейку целевой функции на ячейку значения совокупной доходности портфеля, в графе «До» поставить «Максимум» и в ограничениях заменить условие «совокупная доходность портфеля не менее минимальной приемлемой доходности» на «совокупный риск портфеля не более максимально приемлемого риска». Для данного примера результаты представлены на рисунке 4.

Рассмотренный выше пример показывает, как можно с помощью достаточно нетрудных вычислений рассчитать доходности и уровни риска группы активов по историческим данным, а также оптимизировать доли активов в портфеле. При высокой степени повторяемости прошлого результата в будущем (к примеру, при сезонных паттернах) данная модель дает возможность делать расчеты соотношения «доходность/риск» с вполне допустимой точностью и представляться важным элементом анализа.
Статистика алгоритмического трейдинга + новые статьи и новости финансовых рынков в нашем Telegram канале
Оптимизация на примере разносторонних активов
Вторым исследованием данной статьи будет попытка адаптировать модель Марковица под другие биржевые и внебиржевые инструменты. Для данного исследования предполагается взять пять активов из разных сегментов финансовых рынков и проанализировать их по аналогичной выше разобранной схеме. В качестве выбранных активов будут представлены:
- EURUSD (FOREX).
- Нефть марки WTI (Товарный рынок).
- FTSE 100 (Биржевые индексы).
- Microsoft (Акции).
- Bitcoin (Криптовалюты).
Одной из наиболее ярко проявляющихся проблем модели Марковица является то, что она предполагает только приобретение активов в длинные позиции (то есть, расчет исключительно на рост актива). Поэтому для ее адаптации под другие инструменты, которые в современных условиях можно также торговать в шорт (открывать позиции на продажу актива), необходимо усложнить условие модели и ввести в нее параметр продаж.
В качестве аналитической идеи предлагаем три сценария, каждый из которых будет разобран ниже:
- Сценарий «Все активы на покупку» (как в оригинальной модели и в выше разобранном примере с акциями).
- Сценарий «Невероятный успех», который предполагает, что мы угадали все направления (и в покупки, и в продажи) — вариант максимальной прибыли при условии открытия сделки в начале месяца и ее закрытия в конце.
- Сценарий «Полный провал», при котором мы не угадали ни одного направления — полностью обратное направление сценарию «невероятного успеха».
Переходим к рассмотрению каждого из сценариев.
Сценарий «Все активы на покупку»
По аналогии с выше рассмотренным формированием портфеля акций, мы просчитываем доходности и риск пяти новых активов. На рисунке 5 показана помесячная доходность выбранных активов и просчитана ожидаемая средняя месячная доходность и уровень риска для каждого из них. По понятным причинам — только один инструмент (Microsoft) дает положительную доходность — наш портфель на 100% будет состоять из их этих акций.

Дальнейший анализ по этой модели имеет место быть, когда два и более актива показывают положительную ожидаемую доходность. В таком случае анализ проводится по аналогии с выше разобранным примером для акций.
Сценарий «Невероятный успех»
Представим, что мы можем открывать как длинные, так и короткие позиции, и, самое главное, что мы их все закрыли в плюс. Получается, что тогда нам не важен тип актива и характер торговли (открывать только сделки «на покупку» или еще и «на продажу»), а важна лишь его среднемесячная доходность. На рисунке 6 представлены новые данные доходности и риска.

На рисунке 7 показаны новые ковариации и значения совокупной доходности и совокупного риска портфеля, рассчитанные при условии, что каждый актив имеет в портфеле долю в 20%.

Данные по оптимизации портфеля с целью минимизации риска проиллюстрированы на рисунке 8. С заданной минимальной приемлемой доходностью на уровне 10% мы получаем портфель с совокупным риском в 4,64% из трех инструментов: 38% Microsoft, 31% WTI и 31% BTCUSD.

Ниже на рисунке 9 представлен заключительный слайд по данному сценарию, показывающий, что при повышении совокупного риска до 5% мы можем рассчитывать на рост совокупной доходности до 10,47% за счет перераспределения долей активов в следующую сторону: 34% Microsoft, 32% WTI и 34% BTCUSD.

В качестве итога по сценарию «Невероятный успех» можно сказать то, что использование данной модели дает результат при наличии готовых показателей доходности активов (на рисунке 6 — строка «ожидаемая месячная доходность») и не зависит от характера торговли и типа активов. Другими словами, самостоятельный расчет ежепериодных доходностей по каждому активу (на рисунке 6 — данные в оранжевых колонках) позволяет в дальнейшем эффективно использовать принципы составления портфеля по модели Марковица.
В качестве идей для расчета показателя «ожидаемой месячной доходности» можно использовать совокупные данные из собственной торговой истории по любому желаемому активу или идти по аналогии с расчетом в сценарии «Невероятный успех», но с добавлением параметра вероятности успеха (в данном случае вероятность успеха по каждому активу равнялась 100%).
Сценарий «Полный провал»
Перейдем к рассмотрению последнего сценария, при котором ни одно направление движения цены не было определено верно. С точки зрения максимизации прибыли, данный сценарий не представляет из себя интереса, так как она в любом случает будет отрицательной, по причине того, что показанные на рисунке 10 значения ожидаемой месячной доходности меньше нуля.

В данном случае мы можем использовать модель Марковица в обратном режиме: просчитать минимально возможную отрицательную доходность при заданном риске. При этом, все выполняемые действия будут абсолютно идентичными выше приведенным сценариям, однако так как мы заранее формируем портфель из активов с отрицательной доходностью, мы можем сформировать доли таким образом, чтобы потери были минимальны.
На рисунке 11 показаны значения ковариаций и показатели совокупного риска и совокупной доходности портфеля в 2,95% и -7,10%, соответственно. Задача последующей оптимизации — повысить показатель доходности.
На данном этапе важно отметить, что сценарий «Полный провал» можно рассматривать как стресс-тест или реальный риск портфеля. Получив данные на рисунке 11, мы можем предположить, что при сохранении характера торговли и распределения долей между активами наши потери в дальнейшем не будут превышать 7,10% в месяц.

Нашей задачей для данного примера является достижение минимально возможных потерь при заданном риске. Для начала, по аналогии, оптимизируем риск. На рисунке 12 проиллюстрирован портфель, снижающий не только показатели риска, но и показатель совокупной отрицательной доходности до 1,01% и -2,25%, соответственно.

Позволив риску быть выше, чем минимально возможный вариант, мы оптимизируем систему и получаем, что при вложении 100% объема портфеля в один единственный актив (EURUSD), мы бы снизили совокупную отрицательную доходность до -1,35% при незначительном повышении риска на 0,18 п.п., что показано на рисунке 13.

Вызывает сомнение тот факт, что риски минимизируются при вложении всего депозита в один актив, несмотря на математическую обоснованность модели. Не следует беспрекословно использовать ее рекомендации, так как они рассчитываются на исторических данных и не гарантируют повторения ситуации в будущем.
Подытоживая рассмотрение сценария «Полный провал», можно сказать, что с помощью оптимизации торгового портфеля по Марковицу представляется возможным снизить риски и отрицательный результат торговли только за счет перераспределения долей, входящих в портфель активов (хотя можно еще и улучшать качество торговли). Данный метод подразумевает оптимальное распределение портфеля между наиболее неудачными для трейдера торговыми активами таким образом, чтобы совокупные потери были минимальны.
Заключение
Как мы видим, модель оптимизации портфеля активов по Марковицу может использоваться как в классическом стиле для растущих активов, так и в более адаптированном виде, если в нее включить дополнительные условия. Она позволяет определить оптимальное сочетание входящих в портфель активов как для максимизации прибыли при положительных ожидаемых доходностях, так и для минимизации рисков потерь при отрицательных.
Важно помнить, что все модели основаны на исторических данных, поэтому не способны дать гарантий повторения их успеха в будущем. К примеру, если модель показывает, что из пяти активов необходимо вкладывать депозит только в один, следует внимательно присмотреться: либо поискать другие активы, если эти четыре неважного качества, либо изменить модель.
Показанные в статье результаты исследования, в которых модель указывает на вложение всего депозита в один единственны актив, не являются, по мнению авторов, наилучшими вариантами инвестирования. Они получились в результате статистического анализа и показаны в статье исключительно как результаты оптимизации выбранных активов, которые также были выбраны случайным образом, с целью иллюстрации принципов построения модели Марковица. В дальнейшем каждый читатель сам может построить качественные и эффективные портфели на основе данных принципов.
Закончить работу хочется советом самого Гарри Марковица, который он дал в возрасте 90 лет на вопрос от том, как избежать кризисов и разбогатеть: «Диверсифицируйте и ребалансируйте. Ваш портфель должен быть эффективным в любой момент, и тогда вы не будете терять как мелкие инвесторы, а будете расти как большие».
Поделиться статьей
С радостью ответим на ваши комментарии
Читайте также
Алексей Иванов
Магистр мировой экономики. На финансовых рынках с 2016 года. Занимается фундаментальным анализом рынков и портфельной теорией. Создает алгоритмические торговые системы. Email для связи: alexey@empirix.ru