Презентация прогнозирование в excel

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Анализ временных рядов и прогнозирование в Microsoft Excel
  Информационные технологии управления

• 

  2 слайд

  Временные ряды (ВР)
  При практическом изучении ВР
  ставятся следующие цели:
  кратко описать характерные особенности ряда;
  подобрать статистическую модель, описывающую ВР;
  предсказать будущие значения на основе прошлых наблюдений

• 

  3 слайд

  Достижение перечисленных целей позволит управлять процессом, породившим исследуемый ВР
  Стадии анализа временного ряда:
  графическое представление и описание поведения ВР;
  выделение и удаление закономерных составляющих,зависящих от времени;
  выделение и удаление низко- и высокочастотных составляющих процесса;
  построение математической модели для описания оставшейся случайной составляющей и проверка ее адекватности;
  прогнозирование будущего развития процесса, представленного временным рядом.

• 

  4 слайд

  Составляющие временного ряда
  Под детерминированной составляющей ВР x1,,. . . ,.xn мы будем понимать числовую последовательность d1, . . . . .,dn , элементы которой dt вычисляются по определенному правилу как функция времени t.
  Оставшаяся после выделения закономерной составляющей случайная компонента ВР обозначается обычно 1 , . . . ,t , . . . ,n. Для ее описания используют понятия и методы теории вероятностей.

• 

  5 слайд

  Элементы ВР представляют
  либо в виде суммы, либо в виде произведения вышеназванных компонент:
  при t=1, . . . ,n или X=D+E
  при t=1, . . . ,n или X=DxE

• 

  6 слайд

  В экономических приложениях детерминированную компоненту ВР обычно разделяют на три части: тренд trt, сезонную st и циклическую ct составляющие. Так что можно записать следующее:

  при t =1, . . . ,n
  Трендом ВР называют плавно изменяющуюся, нециклическую компоненту, описывающую чистое влияние долговременных факторов, эффект которых сказывается постепенно.
  Сезонная компонента ВР описывает поведение, изменяющееся регулярно в течение заданного периода (года, месяца и т.д.). Она состоит из последовательности почти повторяющихся циклов.
  Циклическая компонента ВР описывает длительные периоды относительного подъема и спада. Она состоит из циклов, которые меняются по амплитуде и протяженности.

• 

  7 слайд

  Модели тренда
  линейная модель
  полином
  экспоненциальная

• 

  8 слайд

  Выделение тренда
  Для оценки и удаления тренда из ВР чаще всего используется метод наименьших квадратов — основу регрессионного анализа временных рядов. При этом значения ВР xt рассматриваются как отклик, а время t — как фактор, влияющий на него:
  x(ti) = f(ti,) + i i=1,…,n

• 

  9 слайд

  Метод наименьших квадратов состоит в том, что мы выбираем функцию тренда так, чтобы

• 

  10 слайд

  Выделение сезонной компоненты
  Предположим, что рассматриваемый ВР может быть описан аддитивной моделью. Пусть p — период последовательности st так что st = st+p для всякого t. Наша задача — оценить значения st по наблюдениям xt при том, что величина p известна.
  Получив оценку тренда по одной из описанных выше методик, рассмотрим для каждого сезона i, 1 i p, все относящиеся к нему разности (предполагая, что n = (m+1)p)

• 

  11 слайд

  Выделение сезонной компоненты
  Усреднение этих разностей дает нам оценку сезонной компоненты, например простое среднее:
  В практических задачах распространена ситуация, когда сезонные колебания пропорциональны среднему значению процесса в рассматриваемый момент времени. Для описания подобных данных следует использовать либо смешанную мультипликативно-аддитивную модель xt = trt  st +t , либо простую мультипликативную модель ВР. Если выбрать первую из них, то при оценке сезонных эффектов удобно рассмотреть частные

• 

  12 слайд

  Выделение сезонной компоненты
  при l = 0,1,2,…,m
  В этом случае оценкой сезонной компоненты или сезонным индексом называют величину
  где 1 i  p
  Получив оценки сезонной компоненты, следует провести ее удаление из рассматриваемого ВР: в случае аддитивной модели, вычитая ее из начальных значений ряда; в случае мультипликативно-аддитивной модели — деля значения исходного ряда на соответствующие сезонные индексы и умножая полученный результат на 100%.

• 

  13 слайд

  Метод скользящих средних (СС)
  Метод СС основан на переходе от исходных значений ряда к их средним значениям на интервале времени, длина которого выбрана заранее. При этом сам выбранный интервал времени скользит вдоль ряда.
  Величина интервала сглаживания должна быть кратна периоду сезонности или равна ему. При этом каждый интервал вычисления СС будет содержать данные, отвечающие всему периоду сезонности.

• 

  14 слайд

  Метод экспоненциального сглаживания
  Основная идея данного метода состоит в том, что каждый новый прогноз получается посредством перемещения предыдущего прогноза в направлении, которое дало бы лучшие результаты по сравнению со старым прогнозом. Базовое уравнение этой модели имеет следующий вид:
  где а — константа сглаживания. Таким образом, каждая новый прогноз представляет собой сумму предыдущего прогноза и поправочного коэффициента, который и передвигает новый прогноз в направлении, делающем оценку более точной.

• 

  15 слайд

  Графические средства анализа
  В Excel существует механизм вставки Линии тренда в диаграмму, построенную на основании базовой линии ВР. Этот способ наиболее нагляден и прост в обращении. Добавление линии тренда к рядам данных производится следующим образом:
  Выберите ряд данных, к которому нужно добавить линию тренда.
  Выберите команду Добавить линию тренда в меню Диаграмма.
  На вкладке Тип выберите нужный тип линии тренда.
  При выборе типа Полиномиальный введите в поле Степень оптимальное на Ваш взгляд значение для независимой переменной.

• 

  16 слайд

  Графические средства анализа
  При выборе типа Скользящее среднее введите в поле Период число периодов, используемых для расчета скользящего среднего.
  На вкладке Параметры можно указать программе, чтобы линия тренда снабжалась уравнением, по которому она строилась и среднеквадратичным отклонением от реального ВР.
  Здесь же можно указать число временных интервалов экстраполирования тренда для построения прогноза.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 212 035 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:
• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»

• Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»

• Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»

• Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»

• Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»

• Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»

• Курс повышения квалификации «Этика делового общения»

• Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС медицинских направлений подготовки»

• Курс профессиональной переподготовки «Организация маркетинга в туризме»

• Курс повышения квалификации «Методы и инструменты современного моделирования»

• Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»

• Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»

• Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»

Слайды презентации

Управление образования Таймырского

Долгано – Ненецкого муниципального района

Таймырское муниципальное казенное образовательное учреждение

«Дудинская средняя общеобразовательная школа №3»

«Золотое перо»

__________________________________________________________________

Исследовательский проект

Социально-гуманитарное направление

(информационные системы и технологии в науке, технике, образовании)

Прогнозирование в Microsoft Excel

Иванов Александр Николаевич

ТМК ОУ «Дудинская средняя школа № 3»

11 а класс

647000 г. Дудинка, ул. Ленина, 38

Серова Елена Леонидовна

Дудинка – 2016

Содержание

Введение        3

Глава 1 Методы прогнозирования        5

1.1 Расчет базовой линии        5

1.2 Методы социально-экономического прогнозирования        6

1.3 Составление линейных прогнозов: функция ТЕНДЕНЦИЯ        7

Глава 2 Составление прогноза средствами программы MicrosoftExcel        9

Глава 3. Проверка и уточнение результатов прогноза        12

Заключение        14

Список использованных источников        15

Приложение        16

Введение

В настоящее время ни одна сфера жизни общества не может обойтись без прогнозов как средства познания будущего. Особое значение имеют прогнозы социально-экономического развития общества, обоснование основных направлений экономической политики, предвидение последствий принимаемых решений. Социально-экономическое прогнозирование является одним из решающих научных факторов формирования стратегии и тактики общественного развития.

Актуальность данной темы определяется тем, что уровень прогнозирования процессов общественного развития обуславливает эффективность планирования и управления экономикой и другими сферами.

Теоретическая и методологическая основы исследования. В развитии методологии прогнозирования социально-экономических процессов большую роль сыграли научные разработки отечественных и зарубежных ученых А.Г. Аганбегяна, И.В. Бестужева-Лады, Л. Клейна, В. Гольдберга. В работах этих ученых рассматривается значение, сущность и функции прогнозирования, его роль и место в системе планирования, исследуются вопросы методологии и организации экономического прогнозирования, показываются особенности научного прогнозирования и реализация их с использованием ЭВМ.

Информационная база исследования. Для написания исследовательской работы были использованы официальные данные органов Федеральной службы государственной статистики России (Росстата), материалы территориального органа Федеральной службы государственной статистики по Таймырскому Долгано-Ненецкому муниципальному району, а также материалы периодической печати, связанные с темой исследования, материалы официального сайта Таймырского Долгано-Ненецкого муниципального района http://www.taimyr24.ru.

Цель и задачи исследования. Целью исследования является уточнение прогноза развития социально-экономической сферы Таймырского Долгано-Ненецкого муниципального района средствами программы MicrosoftExcel.

Для достижения данной цели в ходе работы нами были поставлены и решены следующие задачи:

• провести анализ социально-экономических показателей по Таймырскому Долгано-Ненецкому муниципальному району за последние три года;
• познакомиться с возможностями программы MicrosoftExcel в области построения прогнозов;
• создать прогноз развития социально-экономическойсферы ТДНМР на ближайшие три года;
• проверить результаты прогноза и сделать выводы относительно его точности.

Объект исследования. Объектом исследования является функция прогнозирования программы Microsoft Excel.

Предмет исследования. Предметом исследования является уровень жизни населения Таймырского Долгано-Ненецкого муниципального района.

Гипотеза исследования: будущее состояние экономики в значительной мере предопределяется ее прошлым и настоящим состояниями.

Используемые методы исследования – аналитический, статистический,

Научная новизна исследования. В результате проведенного исследования мы сформулируем и обоснуемследующие предположения:

• программаMicrosoftExcel пригодна для создания реальных социально-экономических прогнозов;
• составление социально-экономического прогноза развития региона может помочь в принятии правильных управленческих решений.

Научно-практическая значимость исследования. Предлагаемая методика анализа ситуации может быть применена для оценки состояния социально-экономических процессов и определения перспектив развития в различных областях.

Структура работы:

Во введении описывается актуальность выбранной темы, выдвигается гипотеза, ставится цель и определяются задачи данной работы.

В первой главе анализируется литература по проблеме исследования, способы и методы социально-экономического прогнозирования средствами программы MicrosoftExcel.

Во второй части приведено описание проведенного исследования, сделан анализ результатов.

В третьей части работы мы проанализировали результаты сделанного ранее прогноза, и продлили прогноз на 2017 г.

В заключении приведены выводы, сделанные в результате проделанной работы.

Глава 1 Методы прогнозирования

Прогнозирование – это своего рода умение предвидеть, умение проанализировать ситуацию и спрогнозировать ожидаемый ход её изменения в будущем. Так как каждое решение – это проекция в будущее, а будущее содержит элемент неопределенности, то важно правильно определить степень рисков, с которыми сопряжена реализация принятых решений. Просчет рисков также является неотъемлемой частью прогнозирования, как системы оценки возможных потерь и выигрышей при принятии данного решения.

Потребность в решении возникает только при наличии проблемы, которая в общем виде характеризуется двумя состояниями – заданным (желаемым) и фактическим (прогнозируемым), и именно прогнозирование будет отправной точкой в процессе принятия управленческого решения.

Социально-экономическое предвидение основных направлений общественного развития предполагает использование специальных вычислительных и логических приемов, позволяющих определить параметры функционирования отдельных элементов производительных сил в их взаимосвязи и взаимозависимости. Систематизированное научно обоснованное прогнозирование развития социально-экономических процессов осуществляется с первой половины 50-х годов, хотя некоторые методики прогнозирования были известны и ранее. К ним относятся: логический анализ и аналогия, экстраполяция тенденций, опрос мнения специалистов и ученых.

Но, не смотря на всю научность вопроса, самые точные прогнозы получаются либо по счастливой случайности, либо потому, что они решают тривиальный вопрос. Реальные системы прогнозирования всегда делают поправку на элемент случайности, и ни один способ прогнозирования не в состоянии предусмотреть случайные события. Если в данных за прошедший период времени имеется некоторая периодичность, то можно использовать прогнозирование для получения довольно точных прогнозов. В любом случае прогноз лучше, чем слепые догадки.

1.1 Расчет базовой линии

Базовая линия представляет собой числовое выражение результатов наблюдений, проводимых на протяжении длительного периода времени. Приведем примеры базовой линии:

• ежедневное количество посещений поликлиники за последние шесть месяцев.
• количество телефонных звонков, полученных сервисной службой за час на прошлой неделе.

С точки зрения прогнозирования, существует четыре важнейших характеристики базовых линий.

Базовая линия включает в себя результаты наблюдений — начиная с самых ранних и заканчивая последними.

Это требование является обязательным и его довольно легко выполнить.

Все временные периоды базовой линии имеют одинаковую продолжительность. На практике незначительные отклонения можно игнорировать. Например, в феврале и марте разное количество дней, однако эта незначительная разница в два-три дня обычно не учитывается в базовых линиях, построенных на основе ежемесячных результатов наблюдений.

Наблюдения фиксируются в один и тот же момент каждого временного периода. Для правильного определения базовой линии следует проводить наблюдения в одно и то же время дня и в один и тот же день недели.

Пропуск данных не допускается. Пропуск даже одного результата наблюдений нежелателен при прогнозировании поэтому, если в наблюдениях отсутствуют результаты за незначительный отрезок времени, нужно восполнить их хотя бы приблизительными данными.

Если базовая линия отвечает всем четырем вышеупомянутым требованиям, то появляется гораздо больше шансов составить точный прогноз.

Кроме данных о самой базовой линии, также необходимо выбрать метод составления прогноза. Excel предлагает три основных подхода к этому процессу: с применением скользящего среднего, регрессии и сглаживания.

1.2 Методы социально-экономического прогнозирования

Все методы прогнозирования (по некоторым оценкам их свыше двух сотен) представляют собой, по существу, различные комбинации элементов перечисленных выше способов получения информации о будущем. В соответствии с этим существуют три дополняющих друг друга способа разработки социально-экономических прогнозов:

– анкетирование (интервьюирование, опрос) – опрос населения, экспертов с целью упорядочить, объективизировать субъективные оценки прогнозного характера. Особенно большое значение имеют экспертные оценки. Опросы населения в практике прогнозирования применяются пока сравнительно редко;

– экстраполирование и интерполирование (выявление промежуточного значения между двумя известными моментами процесса) – построение динамических рядов развития показателей прогнозируемого явления на протяжении периодов основания прогноза в прошлом и упреждения прогноза в будущем (ретроспекции и проспекции прогнозных разработок);

– моделирование – построение поисковых и нормативных моделей с учетом вероятного или желательного изменения прогнозируемого явления на период упреждения прогноза по имеющимся прямым или косвенным данным о масштабах и направлении изменений. Наиболее эффективная прогнозная модель – система уравнений. Однако имеют значение все возможные виды моделей в широком смысле этого термина: сценарии, имитации, графы, матрицы, подборки показателей, графические изображения и т. д.

Экстраполяция означает распространение выводов, касающихся одной части какого-либо явления, на другую часть, на явление в целом, на будущее. Экстраполяция основывается на гипотезе о том, что ранее выявленные закономерности будут действовать в прогнозном периоде. В социальной сфере анализ состояния образования в одном регионе, выявленные тенденции могут «накладываться» на другой регион. В математике и статистике динамический ряд данных продолжается по определенным формулам.

Экстраполяция широко применяется при анализе, прогнозе всех социальных процессов. Например, вывод об уровне развития какой-либо социальной группы можно сделать по наблюдениям за отдельными ее представителями, а о перспективах культуры – по тенденциям в прошлом.

Статистическая экстраполяция – проекция роста населения по данным прошлого – это один из важнейших методов современного научно-технического и социального прогнозирования.

Экстраполяционный метод основан на исследовании объекта прогнозирования (социальная инфраструктура, демографические процессы, состояние образования в историческом плане), ретроспективном анализе количественных временных рядов или тенденций. Этот метод отличается многообразием, насчитывает не менее пяти различных вариантов.

1.3 Составление линейных прогнозов: функция ТЕНДЕНЦИЯ

Использование функции рабочего листа ТЕНДЕНЦИЯ — это самый простой способ вычисления регрессионного анализа. Предположим, результаты наблюдений внесены в ячейки А1:А10, а дни месяца расположены в ячейках В1:В10. Нужно выделитьячейки С1:С10 и ввести следующую формулу, используя формулу массива:

=ТЕНДЕНЦИЯ (А1: А10; В1: В10)

Рассматривая данный метод прогнозирования, следует обратить особое внимание на следующие моменты.

Каждый результат в ячейках С1:С10 получается на основе одной и той же формулы массива, внутри которой «спрятано» более сложное выражение.

Поскольку все значения прогноза составляются на основе одних и тех же показателей отрезка, отсекаемого на оси ординат, и углового коэффициента, прогноз не отражает происходящих изменений во временном ряду.

Функция ТЕНДЕНЦИЯ вычисляет прогнозы, основанные на линейной связи между результатом наблюдения и временем, когда это наблюдение было зафиксировано. Предположим, что вы составляете линейный график данных, на вертикальной оси которого отмечаете результаты наблюдений, а на горизонтальной фиксируете временные моменты их получения. Если эта взаимосвязь носит линейный характер, то линия на графике будет либо прямой, либо слегка наклоненной в одну или другую сторону, либо горизонтальной. Это и будет лучшей подсказкой о том, что взаимосвязь является линейной, и потому в данном случае функция ТЕНДЕНЦИЯ — самый удобный способ регрессивного анализа.

Глава 2 Составление прогноза средствами программы MicrosoftExcel

Случайно увидев отчет социально-экономического развития Таймырского Долгано-Ненецкого муниципального района за 9 месяцев 2013 года, меня заинтересовал вопрос: Если есть отчет, то должен быть какой-то план. А как планируется социально-экономическое развитие нашего региона? Я ведь тоже являюсь жителем Таймыра и мне не безразлично мое будущее.

Для поиска ответа я через поисковую систему задал свой вопрос в Интернете и узнал, что прогноз можно составить при помощи программы MicrosoftExcel.

Проанализировав возможности программы, я понял, что для составления прогноза мне нужны данные за более ранние периоды. Поэтому я нашел аналогичные отчеты за периоды начиная с 2011 года. Таким образом, в моем распоряжении оказались сведения за последние три года.

Социально-экономический отчет – это достаточно большой документ, отражающий множество показателей. Я решил составить прогноз по пяти направлениям:

1. численность работоспособного населения,
2. количество безработных в муниципальном районе,
3. среднемесячный доход на душу населения,
4. количество детей, обучающихся в школах,
5. численность детей, проживающих в социальном приюте.

Свой выбор именно этих показателей я объясняю следующим образом:

• динамика численности населения косвенно отражает динамику развития региона.  Если предприятие не нуждается в рабочих, то оно, возможно, намерено сократить объем производства;
• рост количества безработных, скорее всего, повлечет за собой увеличение числа социально-опасных элементов и, как следствие, рост преступности;
• изменение среднегодового дохода может свидетельствовать об изменении уровня жизни населения;
• количество детей может выступать своего рода показателем стабильности;
• численность детей, проживающих в социальном приюте, расскажет нам о количестве семей «группы риска», что в свою очередь позволит сделать несколько побочных выводов.

Конечно, очень бы хотелось сразу же создать точный и научный прогноз, но для начала нужно научиться работать в программе и попробовать спрогнозировать будущее хотя бы приблизительно.

В практической части своей работы я воспользовался методом скользящего среднего при помощи диаграмм.

Для построения диаграмм мной были созданы соответствующие таблицы (см. Приложение 1).

Следующим этапом работы стало построение диаграмм по известным значениям.

На графиках известные значения выделены синим цветом. Чтобы построить прогноз на ленте Работа с диаграммами открываем вкладку Макет и в меню Линия тренда выбираем команду Линейный прогноз.

Рис. 1 Прогноз изменения численности работоспособного населения до 2017 г.

Рис.2 Прогноз роста безработных в ТДНМР

Рис.3 Прогноз роста среднего дохода на душу населения

Рис. 4 Прогноз изменения численности учащихся школ муниципального района

Рис. 5 Прогноз изменения численности детей, проживающих в социальном приюте

Глава 3. Проверка и уточнение результатов прогноза

Прошло два года, после составления прогноза по пяти направлениям. Пришло время подтвердить или опровергнуть сделанные ранее предположения.

1. Динамика численности населения косвенно отражает динамику развития региона.  Если предприятие не нуждается в рабочих, то оно, возможно, намерено сократить объем производства.

Количество населения, к сожалению, продолжает уменьшаться. И на ближайшее время прогноз тоже имеет отрицательную динамику. Но по прошествии двух лет можно скорректировать сделанный ранее вывод. Численность населения снижается, но производство не снижает объем, а становится более технологичным, автоматизированным. Поэтому однозначно сделать вывод о снижении объемов производства нельзя. Изучая предмет Основы регионального развития, я стал понимать, что по одному параметру судить о социально экономическом развитии региона нельзя.

1. Рост количества безработных, скорее всего, повлечет за собой увеличение числа социально-опасных элементов и, как следствие, рост преступности.

Этот вывод мог бы оказаться верным, но численность безработных в один из исследуемым периодов существенно снизилась и скорректированный прогноз выглядит гораздо оптимистичней. Здесь можно говорить о том, что в районе работают социальные программы переселения граждан «на материк». Таким образом происходит отток населения третьего возраста, за счет чего освобождаются рабочие места.

1. Изменение среднегодового дохода может свидетельствовать об изменении уровня жизни населения.

В численном выражении прогноз сбылся. Действительно, величина дохода на душу населения выросла. Но политическая обстановка вокруг нашего государства сложилась таким образом, что были введены экономические санкции в отношении России, поэтому покупательная способность рубля значительно упала.

1. Количество детей может выступать своего рода показателем стабильности.

Скорректированный прогноз показал, что количество детей в муниципальном районе сокращается быстрее, чем было спрогнозировано ранее. Причин этому тоже может быть несколько. Я не исследовал демографические параметры подробно, поэтому по этой позиции можно только констатировать факт.

1. Численность детей, проживающих в социальном приюте, расскажет нам о количестве семей «группы риска», что в свою очередь позволит сделать несколько побочных выводов.

Скорректированный прогноз показал, что количество детей в социальном приюте уменьшилось менее планируемого. Но радует то, что это число не увеличивается ведь за каждой этой цифрой стоит сломанная детская судьба.

Составив уточненный прогноз, я еще раз убедился, что программа MicrosoftExcel со своей задачей справилась. Прогнозировать с помощью автоматических средств можно с достаточно большой точностью.

Несмотря на то, что прогнозы практически сбылись, новые прогнозы построены, сделать глубокие и правильные выводы о социально-экономическом развитии региона достаточно сложно, потому что данных недостаточно.

Заключение

По ходу работы мною были решены все поставленные ранее задачи:

• провели анализ социально-экономических показателей по Таймырскому Долгано-Ненецкому муниципальному району за последние три года;
• познакомились с возможностями программы MicrosoftExcel в области построения прогнозов;
• создали прогноз развития социально-экономическойсферы ТДНМР на ближайшие три года;
• проверили результаты прогноза и сделали выводы относительно его точности.

Цель работы также была достигнута – уточнен прогноз развития социально-экономической сферы Таймырского Долгано-Ненецкого муниципального района средствами программы MicrosoftExcel.

В результате проведенного исследования мы сформулировали и обосновалиследующие предположения:

• программаMicrosoftExcel пригодна для создания реальных социально-экономических прогнозов,
• составление социально-экономического прогноза развития региона может помочь в принятии правильных управленческих решений.

Кроме того, мы подтвердили гипотезу исследования: будущее состояние экономики в значительной мере предопределяется ее прошлым и настоящим состояниями.

Список использованных источников

1. Кузык, Б. Н. Прогнозирование и стратегическое планирование социально-экономического развития: учебник / Б. Н. Кузык, В. И. Кушлин, Ю. В. Яковец. — М.: Экономика, 2006
2. Лугачев, М. И.    Методы социально-экономического прогнозирования / М. И. Лугачев, Ю. П. Ляпунцов. — М.: ТЕИС, 1999. — 159 с.
3. Просветов, Г. И. Прогнозирование и планирование: задачи и решения: учеб.-метод. пособие / Г. И. Просветов. — М.: РДЛ, 2005.
4. Сиволап, Н. Н. Прогнозирование основных показателей социальной сферы региона / Н. Н. Сиволап // Региональная экономика: теория и практика. — 2007. — № 7.
5. Социальное прогнозирование: рабочая программа, тематика и метод.указания по выполнению курсовых работ для студентов дневной формы обучения: ЭФ: специальность 080103 / сост.: О. Б. Кирик. — Вологда: ВоГТУ, 2007
6. Социальные аспекты экономического развития региона: материалы заседаний регион. секций Третьей Рос. науч.–практ. конф. «Стратегия и тактика реализации соц.-экон. реформ: регион. аспект. Вып. 1, ч. 1 / редкол.: М. Ф. Сычев (отв. ред.) и др.; ВНКЦ ЦЭМИ РАН. – Вологда, 2002
7. http://utmn.ru/docs/3325.pdfДиагностика и прогнозирование социально-экономического развития регионов в рамках нелинейной динамики
8. http://office.microsoft.com/ru-ru/excel-help/HP005209320.aspxТенденция
9. http://office.microsoft.com/ru-ru/excel-help/HP010007461.aspx Добавление, изменение и удаление линии тренда на диаграмме

Приложение

Приложение 1

Таблица 1. Численность работоспособного населения

Год	Факт	Уточненный	Тенденция	Уточненная
2011	21244	21244	21244	21244
2012	21012	21012	21012	21012
2013	20780	20780	20780	20780
2014	20548	20548	20548	20548
2015		20316	20316	20316
2016			20084	20084
2017				19852

Таблица 2. Количество безработных в муниципальном  районе

Год	Факт	Уточненный	Тенденция	Уточненная
2011	318	318	318,00	341,40
2012	325	325	325,00	339,80
2013	332	332	332,00	322,83
2014	339	253	339,00	253,00
2015		229	346,00	229,00
2016			353,00	216,40
2017				191,40

Таблица 3. Среднемесячный  доход на душу населения

Год	Факт	Уточненный	Тенденция	Уточненная
2011	27344,00	27344,00	27344,00	27679,40
2012	29936,00	29936,00	29936,00	30249,20
2013	32758,00	32758,00	32758,00	32733,50
2014	35426,67	34438,00	35426,67	34438,00
2015		36265,00	36265,00	36265,00
2016			38851,40	38851,40
2017				40582,70

Таблица 4. Количество детей, обучающихся в школах

Год	Факт	Уточненный	Тенденция	Уточненная
2011	4845	4845	4845	4885
2012	4906	4906	4906	4871
2013	4778	4778	4778	4751
2014	4776	4660	4776	4660
2015		4702	4743	4702
2016			4709	4619
2017				4506

Таблица 5. Численность детей, проживающих в социальном приюте

Год	Факт	Уточненный	Тенденция	Уточненная
2011	87	87	87	83
2012	73	73	73	73
2013	72	72	72	71
2014	62	65	62	65
2015		65	55	65
2016			47	57
2017				58

Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.

Процедура прогнозирования

Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.

Способ 1: линия тренда

Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.

Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.

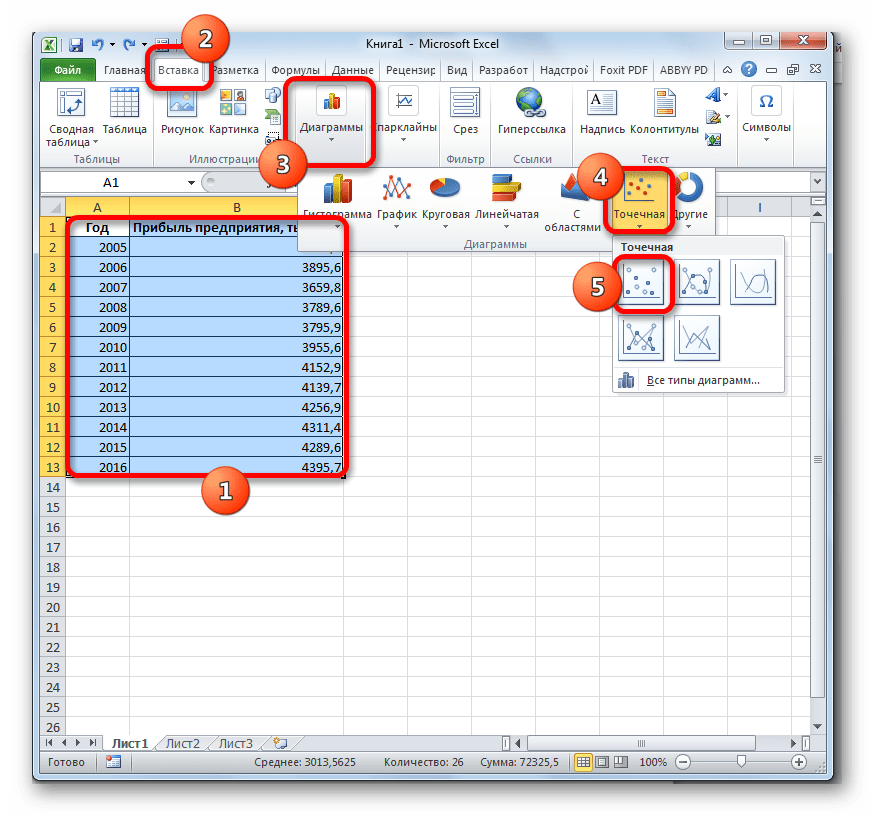
1. Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.



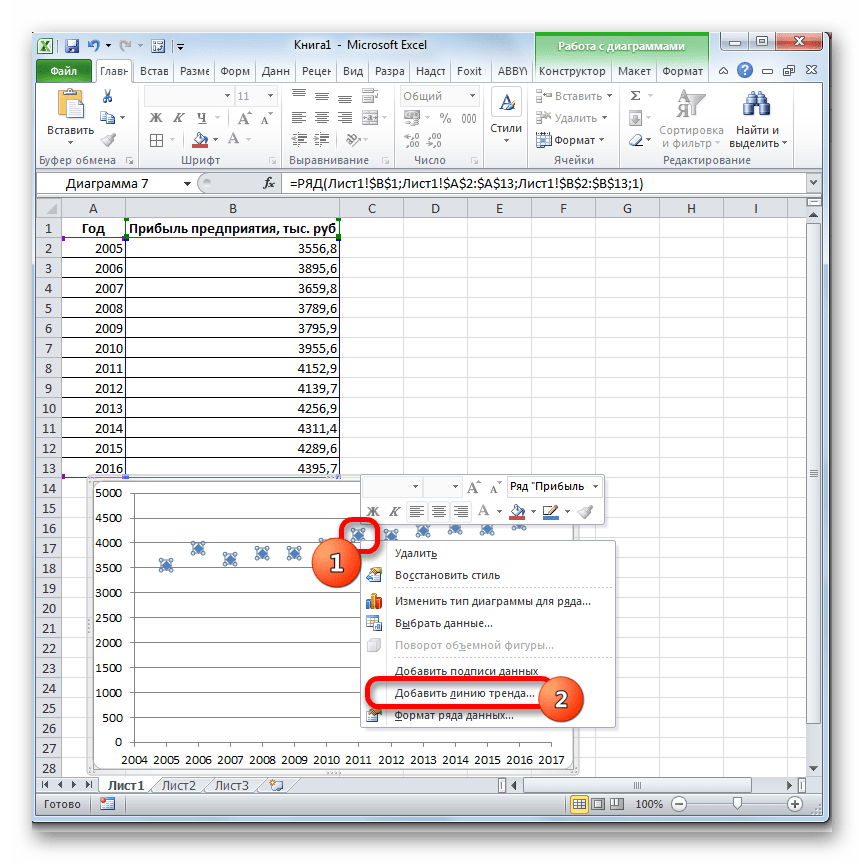
2. Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».



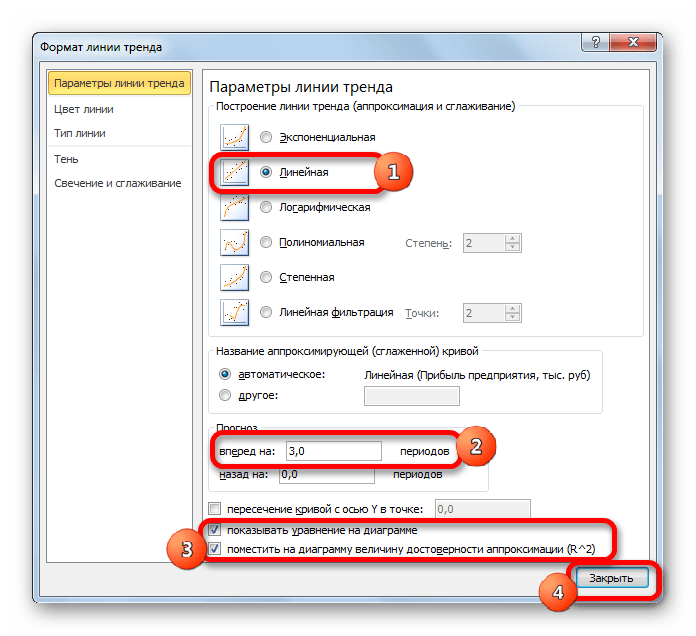
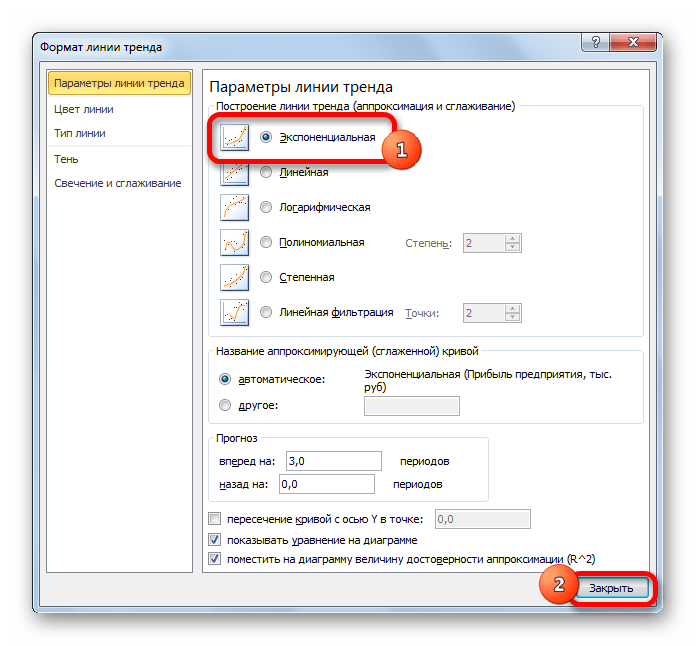
3. Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
   • Линейная;
   • Логарифмическая;
   • Экспоненциальная;
   • Степенная;
   • Полиномиальная;
   • Линейная фильтрация.

   Давайте для начала выберем линейную аппроксимацию.

   В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».



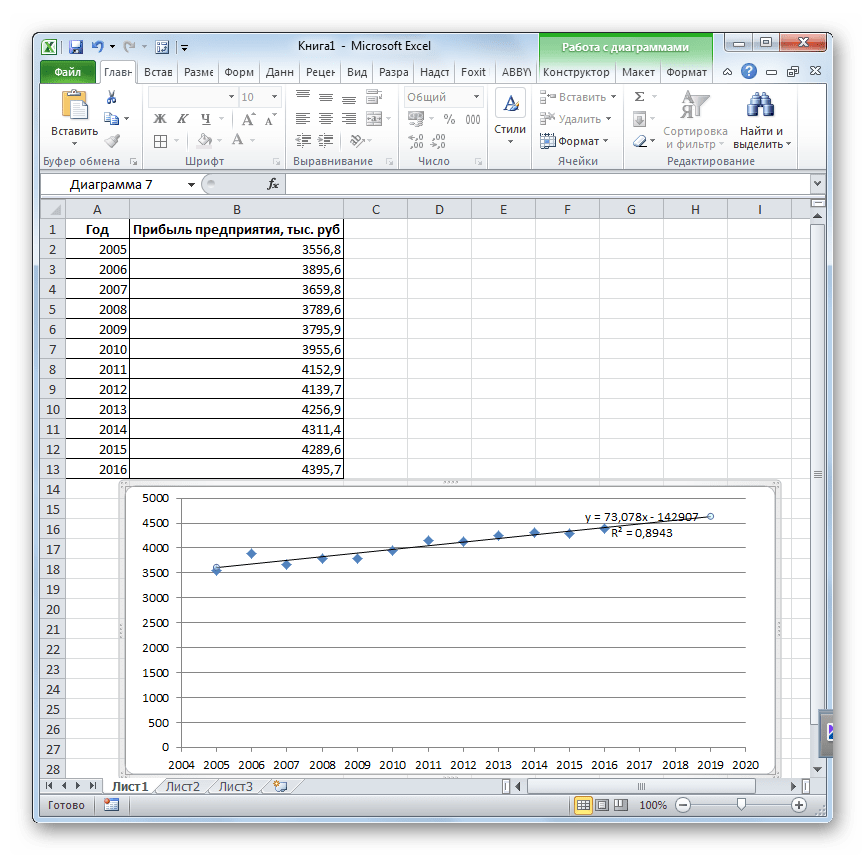
4. Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.



5. Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
   

   Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.

Урок: Как построить линию тренда в Excel

Способ 2: оператор ПРЕДСКАЗ

Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:

=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)

«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.

«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.

«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.

Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.

При вычислении данным способом используется метод линейной регрессии.

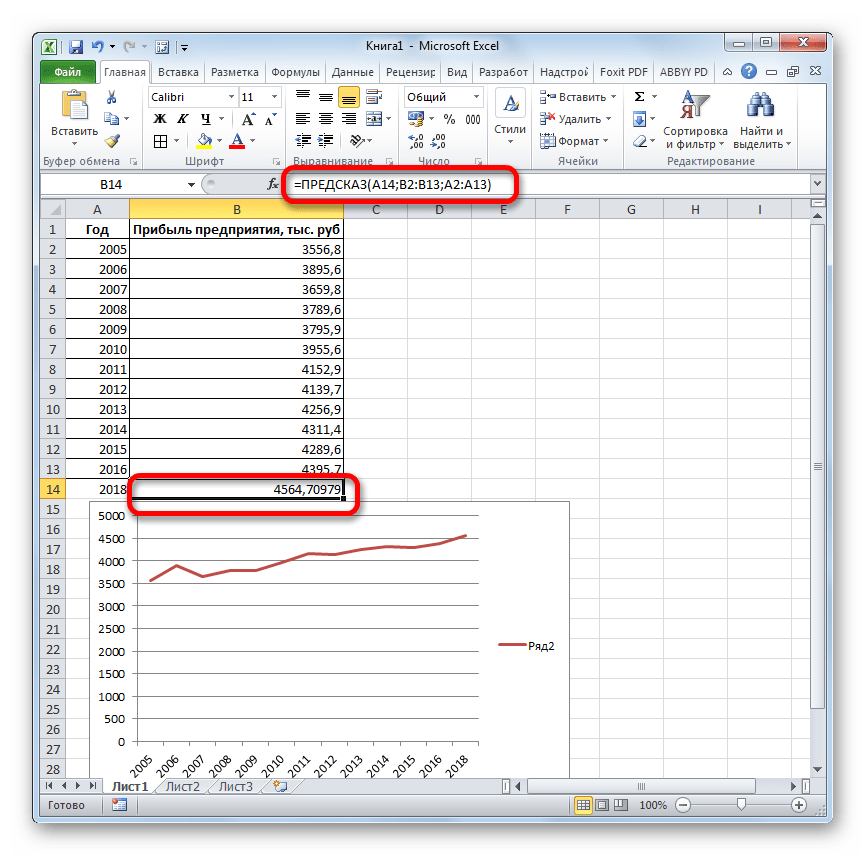
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.

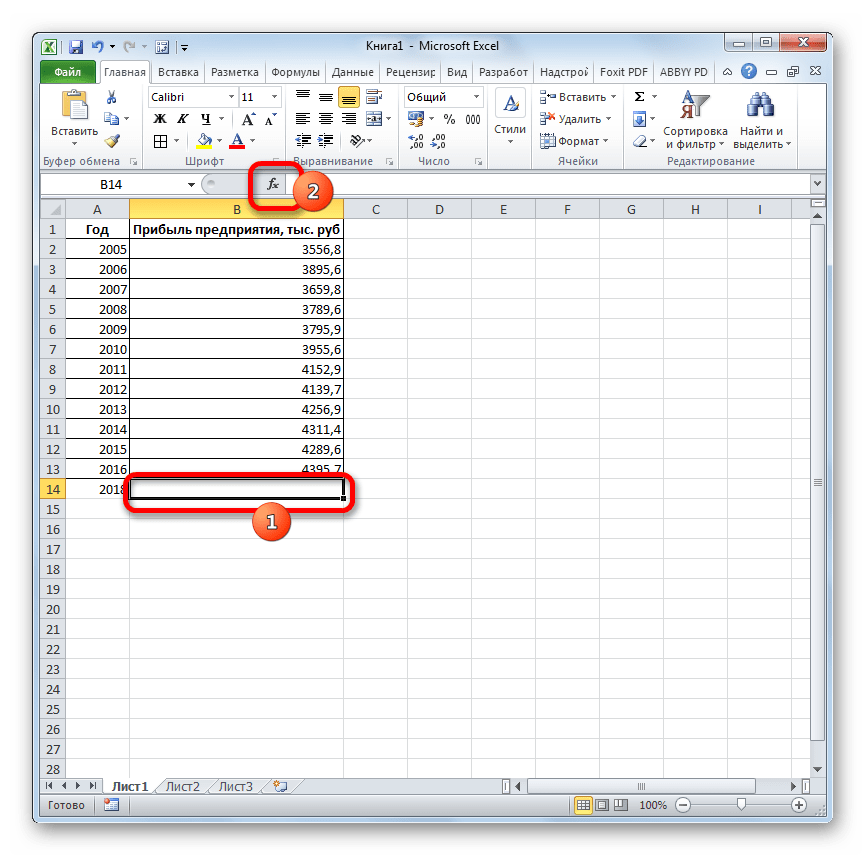
1. Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».



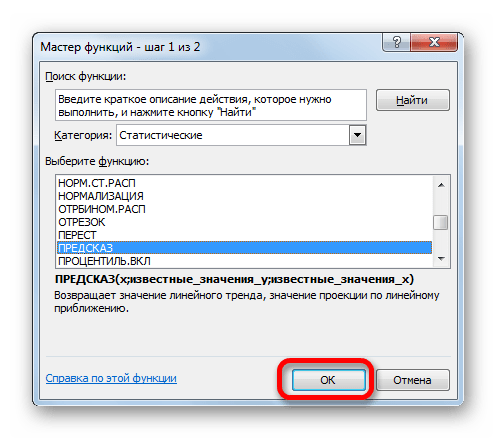
2. Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».



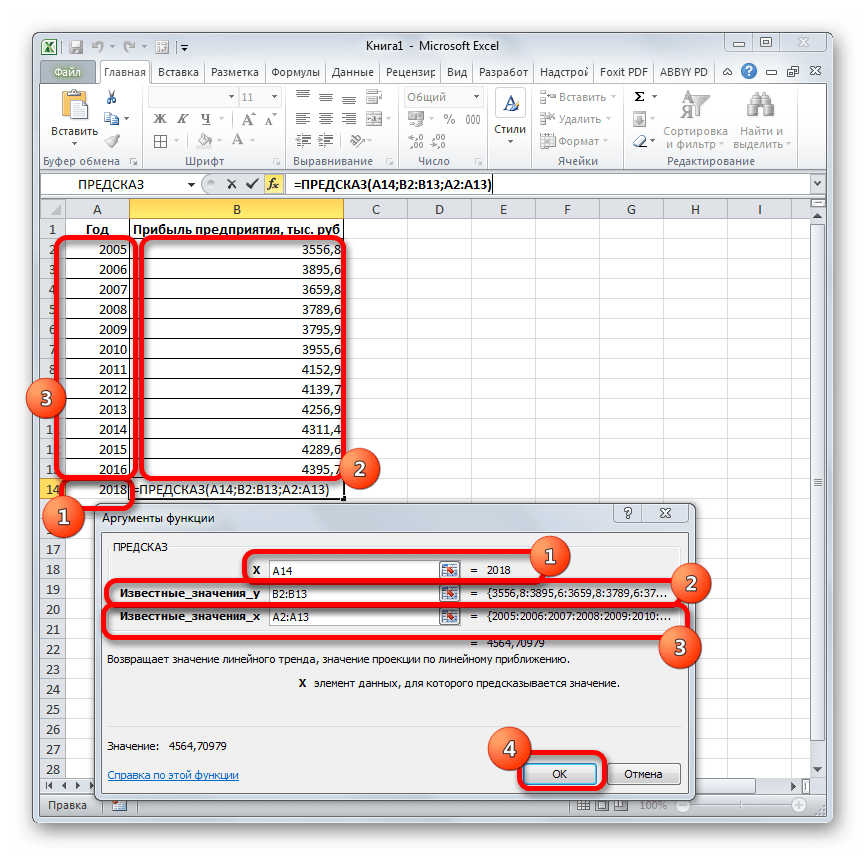
3. Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.

   В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.

   Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.

   После того, как вся информация внесена, жмем на кнопку «OK».



4. Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.



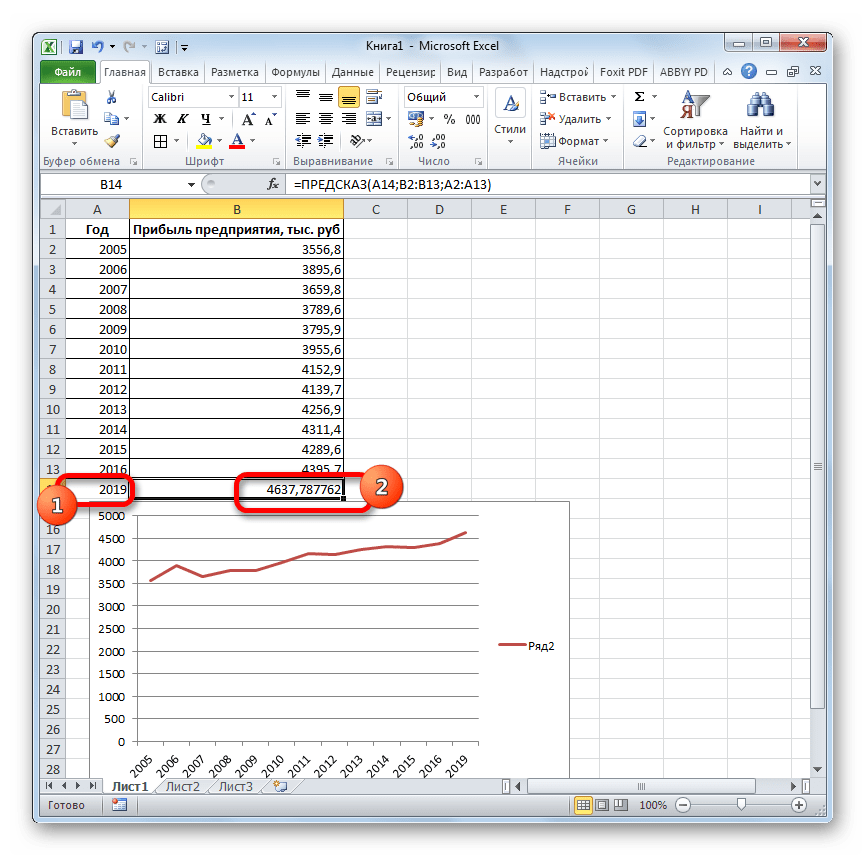
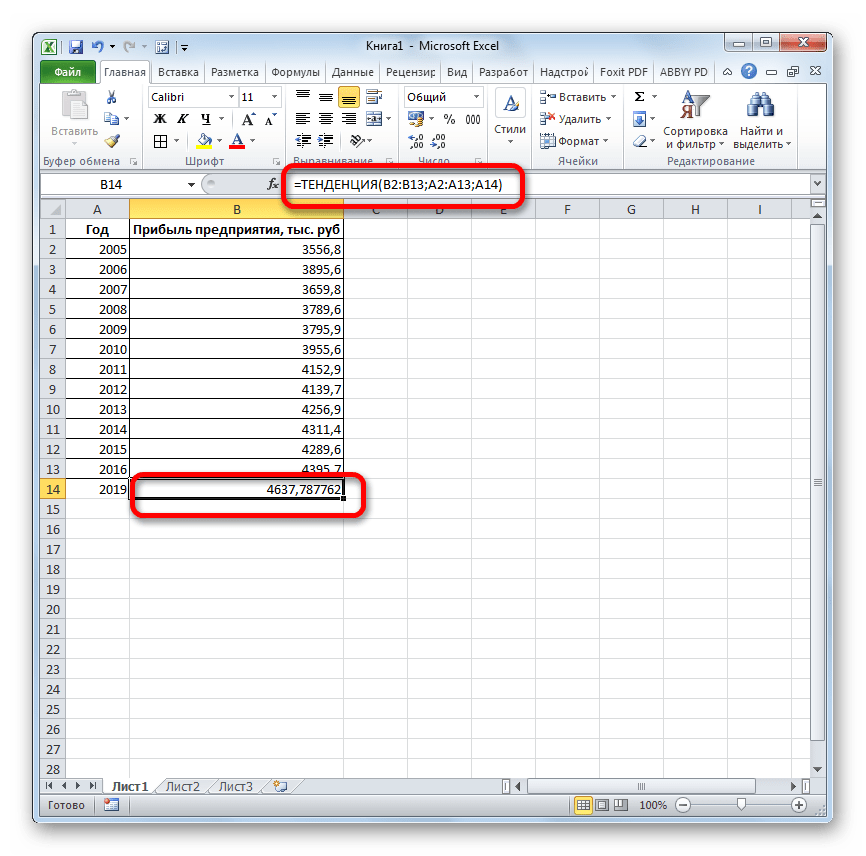
5. Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.

Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.

Урок: Экстраполяция в Excel

Способ 3: оператор ТЕНДЕНЦИЯ

Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:

=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.

Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.

Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.

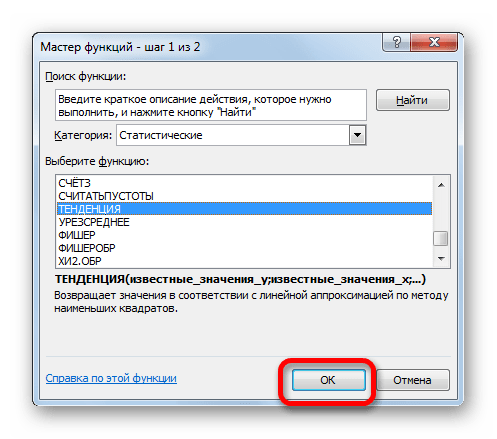
1. Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».



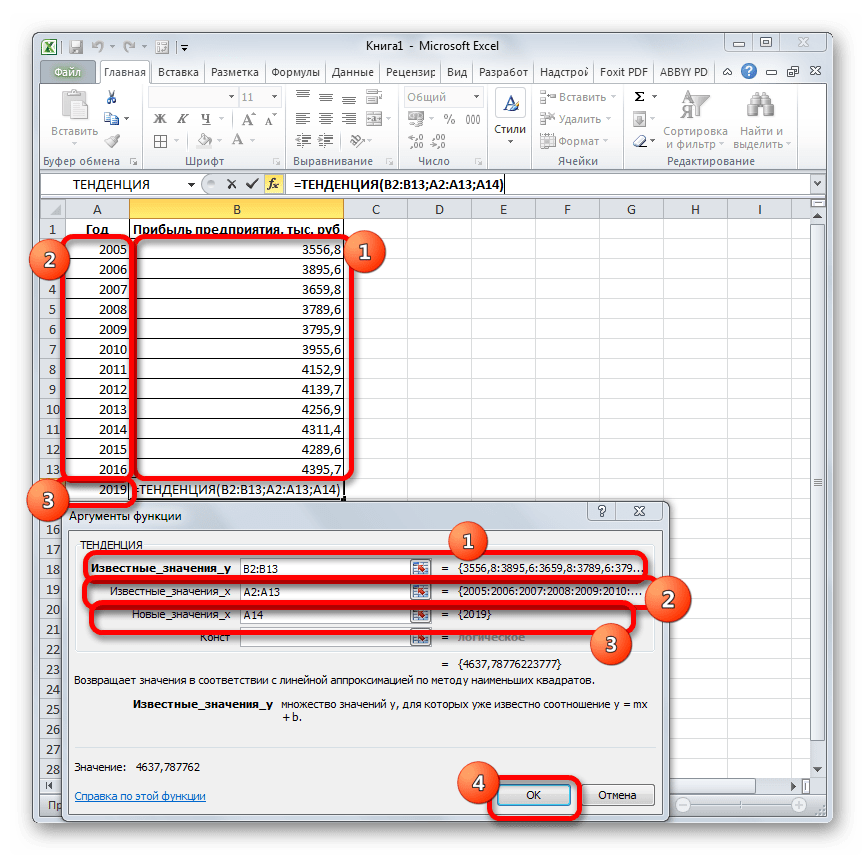
2. Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».



3. Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.

Способ 4: оператор РОСТ

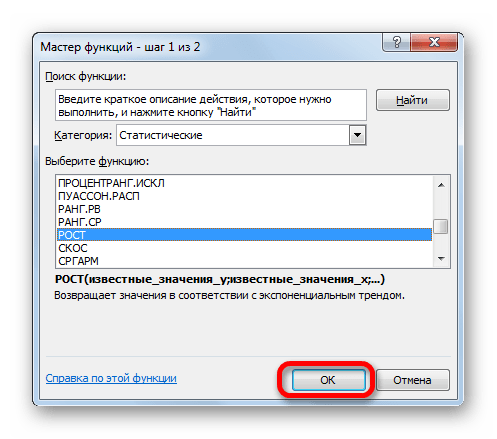
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:

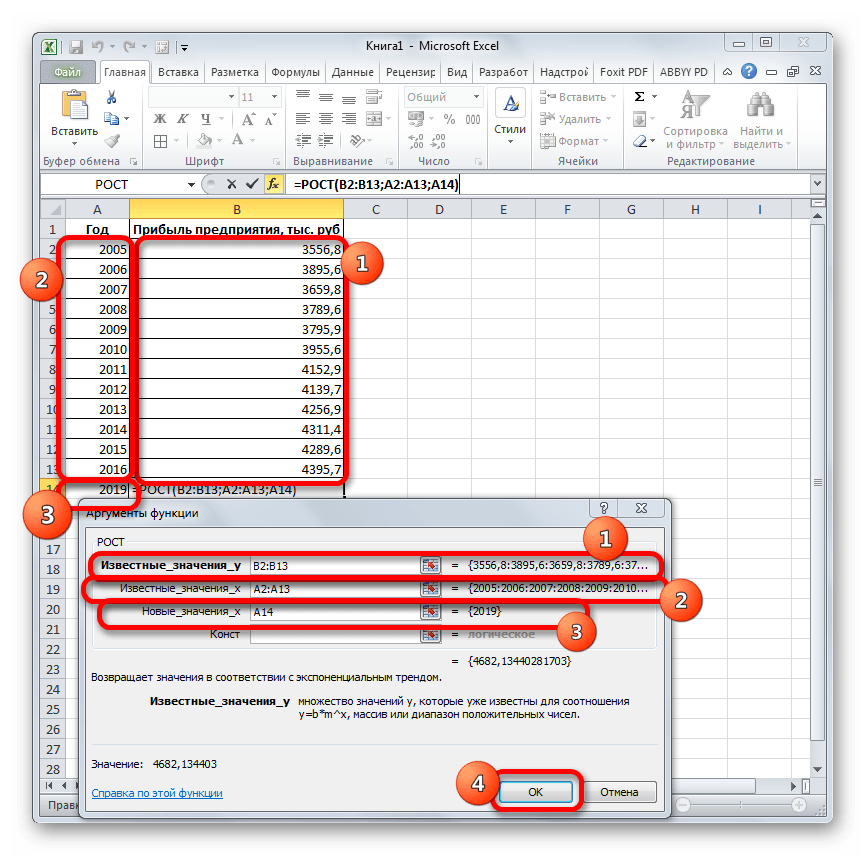
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.

1. Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».



2. Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».



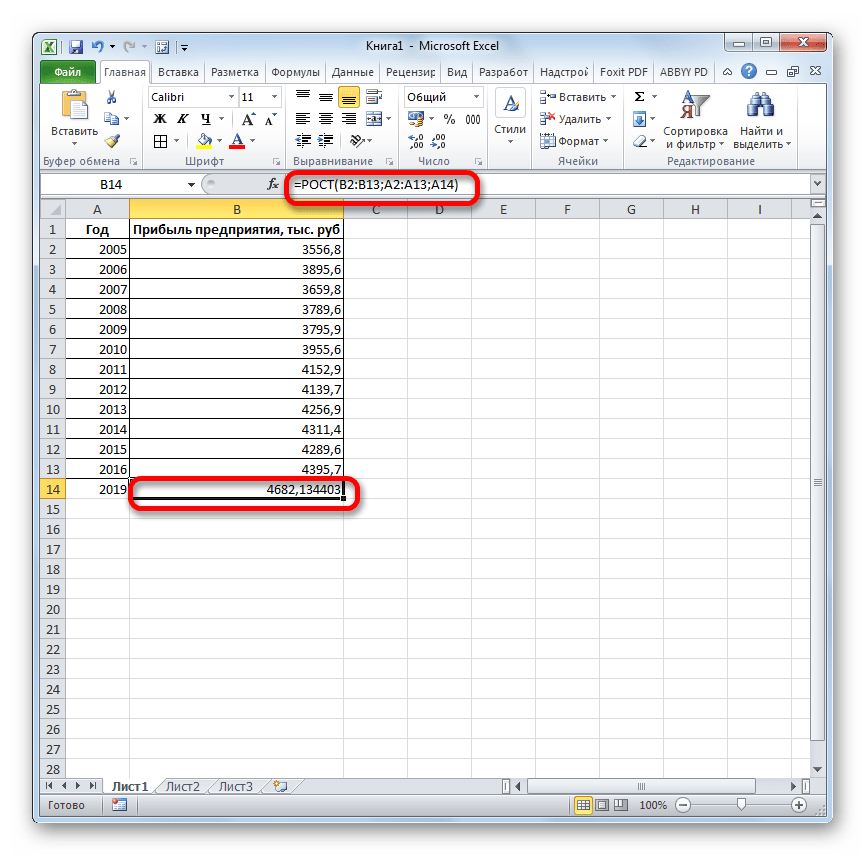
3. Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.

Способ 5: оператор ЛИНЕЙН

Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:

=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.

1. Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».



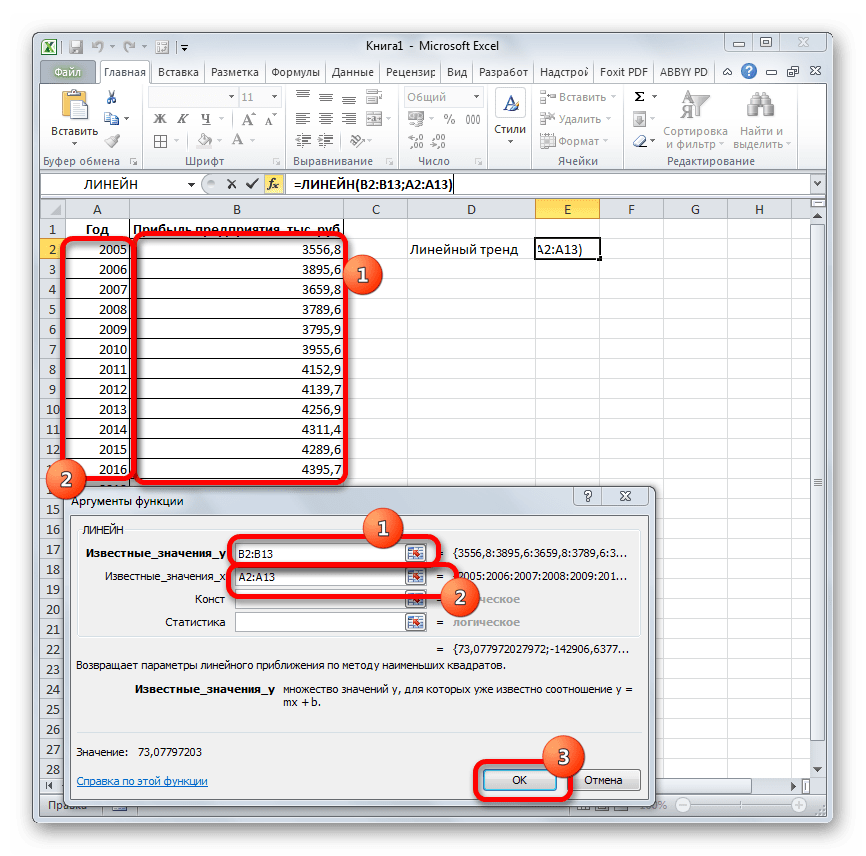
2. В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».



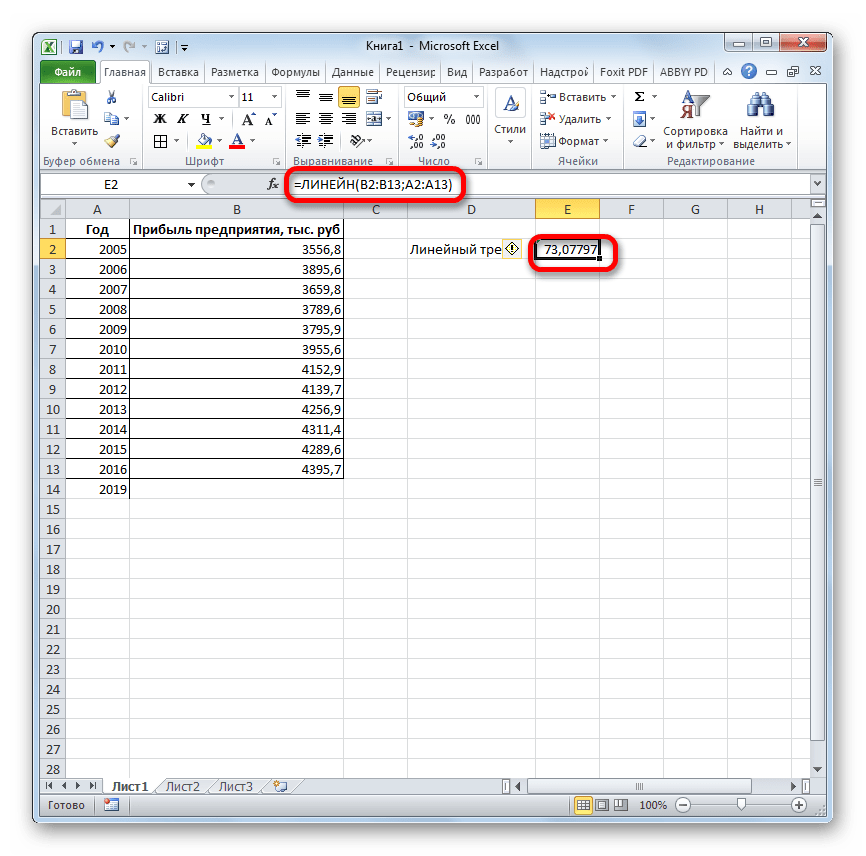
3. Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.



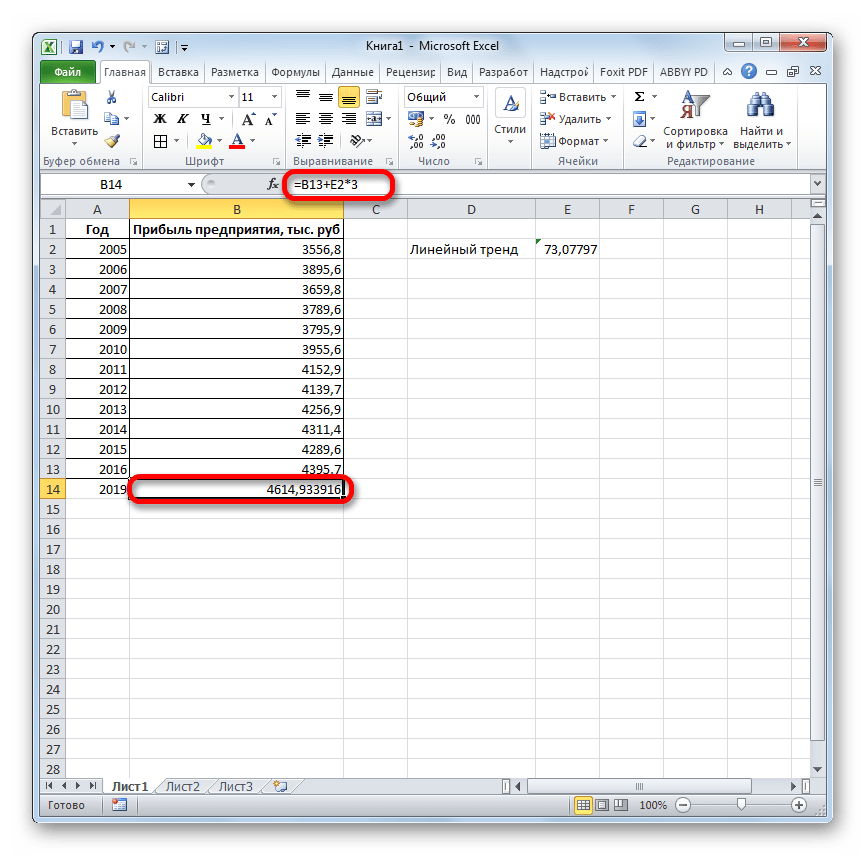
4. Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.

Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.

Способ 6: оператор ЛГРФПРИБЛ

Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:

= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.

1. В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».



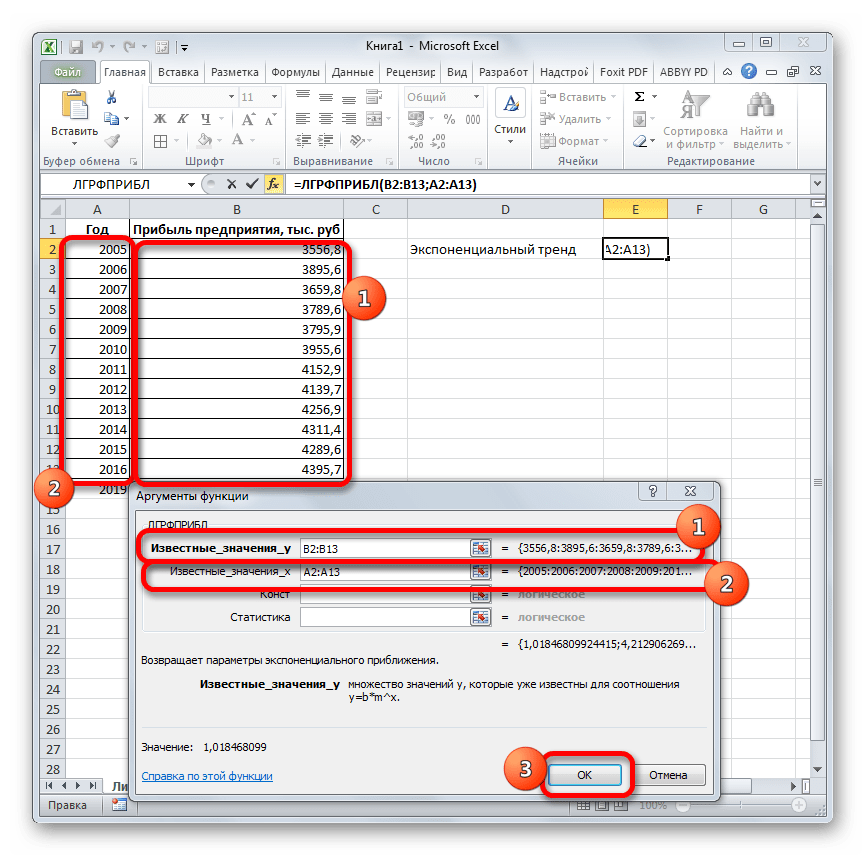
2. Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».



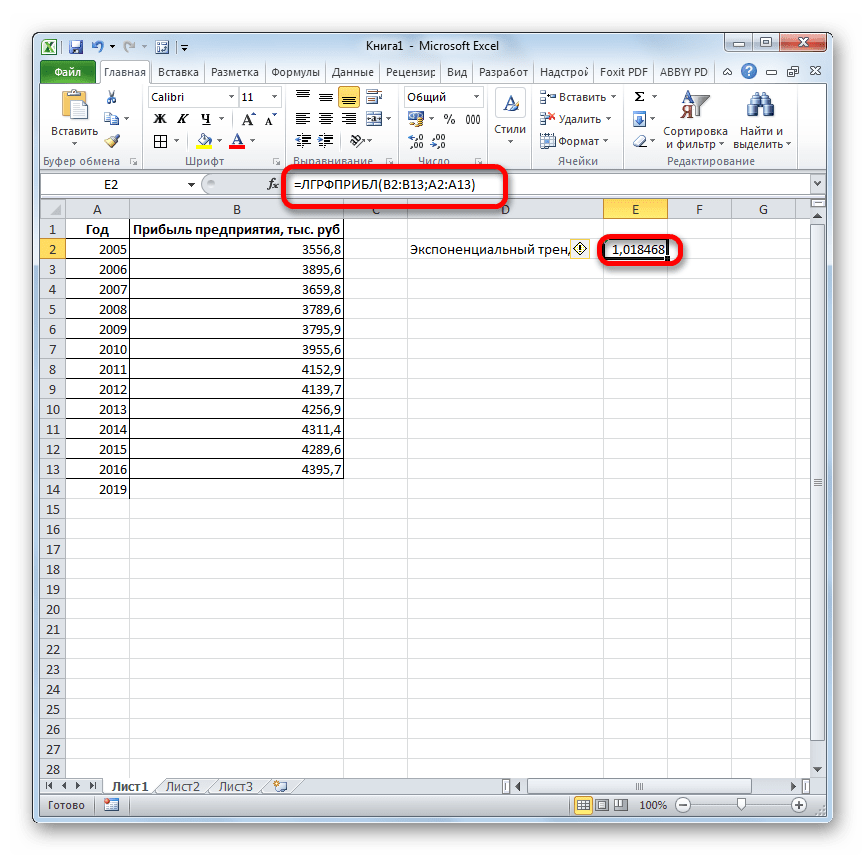
3. Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.



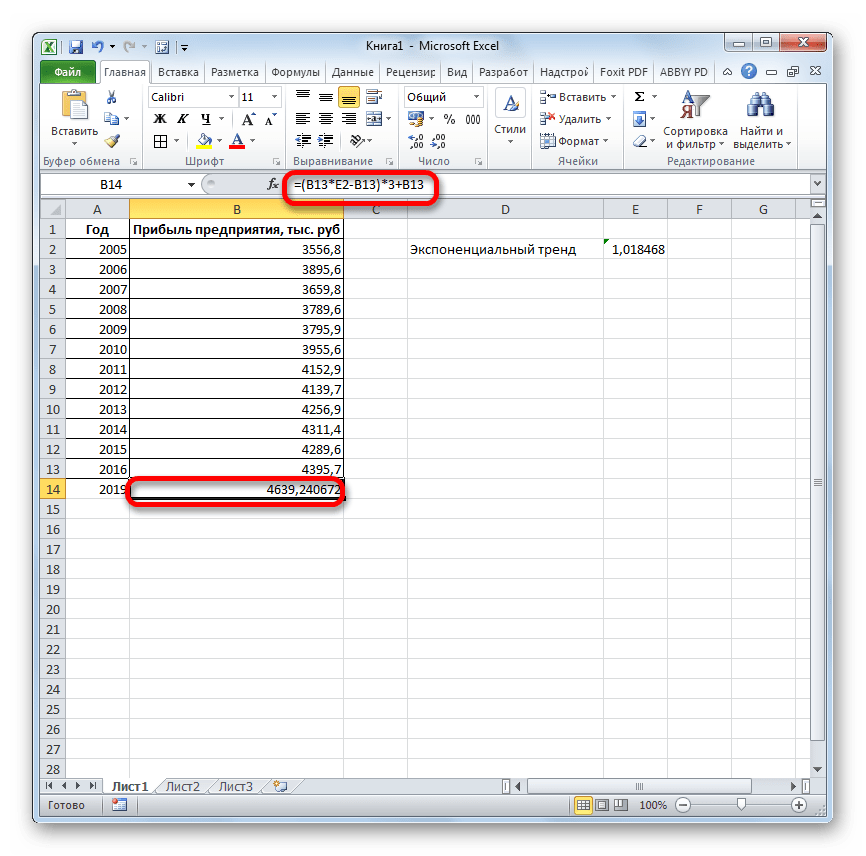
4. Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.

Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.

Урок: Другие статистические функции в Excel

Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.