Цели урока:
- Предметные: повторение основных навыков заполнения расчетной таблицы и построения графиков.
- Метапредметные: развитие общеучебных и общекультурных навыков работы с информацией и визуализацией данных.
- Личностные: представление о сферах применения электронных таблиц в различных предметных областях.
Решаемые учебные задачи:
- систематизировать и расширить представления учащихся о возможностях использования электронных таблиц;
- формировать практические навыки работы с электронной таблицей.
Оборудование: ПК, MS Excel-2010.
Литература:
- Информатика и ИКТ Задачник-практикум 2 т. Под ред. И. Семакина, Е. Хеннера. М.: Бином. Лаборатория Базовых Знаний, 2011.
- Макарычев Ю.Н. и др. Алгебра 9. М.: Просвещение, 2010.
- Семакин И.Г., Залогова Л.А., Русаков С.В., Шестакова Л.В. Информатика. Базовый курс для 7-9 классов. М.: Лаборатория Базовых Знаний, 2012.
Структура урока:
- Мотивационный этап — 3 мин.
- Ориентировочный этап — 15 мин.
- Этап закрепления новых знаний — 18 мин.
- Итог урока — 2 мин.
- Этап информирования учащихся о домашнем задании — 2 мин.
Ход урока
1. Мотивационный этап
В курсе алгебры за 9 класс есть две главы, посвященные решению уравнений и неравенств с одной переменной и решению уравнений и неравенств с двумя переменными. В этих главах рассматриваются в основном алгебраические методы решения, но есть и примеры графического решения. Почему учащиеся с неохотой решают графически уравнения и системы уравнений? Причин несколько: и долго и сложно и решение приближенное. Но если автоматизировать процесс построения графиков, то графический способ является универсальным. Автоматизировать данный процесс можно с помощью табличного процессора MS Excel, хотя бы для того, чтобы всегда можно было проверить правильность ручных вычислений. Наш сегодняшний урок посвящен автоматизации данного процесса.
2. Ориентировочный этап
Рассмотрим задачу 1. Найдите хотя бы один корень уравнения x3 – sinx= 0 с точностью до 0,001.
Для этого рассмотрим функцию у= x3 – sinx, но в 9 классе не знают, как может выглядеть график такой функции, да и с функцией sinx школьники не знакомы. Что делать?
1. С помощью табличного процессора создадим расчетную таблицу, изменяя значение х от -1,4 до 1,4 с шагом 0,2 и построим на ее основе график. Это и будет график функции у= x3 – sinx.
Мы видим, что график пересекает ось X в точках -0,9, 0, 0,9, правда значения -0,9 и 0,9 приближенные.
2. Воспользуемся уточнением корня -0,9 с помощью инструмента «Поиск решения». Для этого подберем значение в ячейке d1 при значении 0 в ячейке d2.
Выполним следующие действия: Данные – Поиск решения. В таблице параметров поиска решения в окне Оптимизировать целевую функцию введем ячейку $d$2 и установим Значение 0. В окне Изменяя ячейки переменных введем адрес ячейки $d$1. Уберем галочку в окне сделать переменные без ограничений неотрицательными. Щелкнем по кнопке Найти решение.
3. В итоге получим результат.
Значение корня уравнения х = — 0,929 найдено с заданной точностью 0,001.
Задача 2. Пушка стреляет ядрами в крепостную стену. Под каким углом и с какой скоростью должно вылетать ядро, чтобы попасть в крепостную стену на заданной высоте.
Разберем задачу с точки зрения физики. Нам известны расстояние до стены и высота стены. Понятно, что если высота полета ядра отрицательна, то ядро не долетит до стены, если же высота больше высоты стены, то ядро перелетит через нее. Путем подбора параметров можно рассчитать скорость и угол вылета ядра.
Для расчета высоты полета ядра воспользуемся формулой
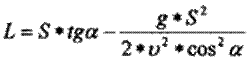
где
- L – высота ядра через определенный промежуток времени,
- S — исходное расстояние,
- u — начальная скорость бросания,
- a — начальный угол бросания,
- g — ускорение свободного падения.
Вывод формулы вы можете рассмотреть на уроках физики.
Для решения задачи ввоспользуемся инструментом «Поиск решения».
В диапазон ячеек b1-b4 вводим исходные данные. В ячейку b6 вводим формулу
=B2*TAN(РАДИАНЫ(B4))-((9,81*B2^2)/(2*B3^2*COS(РАДИАНЫ(B4))^2))
Получаем результат L=0,701017.
Определим минимальный и максимальный углы наклона ствола орудия при которых ядро попадает в стену. Начальная скорость ядра не изменяется.
Выделим ячейку b6 и выполним команду «Поиск решения». В таблице параметров поиска решения в окне Оптимизировать целевую функцию введем ячейку $b$6 и установим Значение 0. В окне Изменяя ячейки переменных введем адрес ячейки $b$4. Щелкнем по кнопке Найти решение.
Получим следующий результат
Минимальный угол = 32,63802°
Выполним аналогичные действия еще раз, установив Значение 1
Максимальный угол бросания = 36,07681°.
3. Этап закрепления новых знаний
Используя инструмент «Поиск решения», решите следующие задачи:
Задача 3: Решите графически уравнение 3х2 — 6х+2 = 0. Один из корней вычислите с точностью до 0,001.
Задача 4: При тренировках теннисистов используют автоматы по выбрасыванию мячика в определенное место площадки. Теннисист находится на определенном расстоянии от автомата. Автомату задаются определенные скорость и угол выбрасывания мячика для подлета к теннисисту на определенной высоте. Определите минимальное и максимальное значение начальной скорости бросания.
4. Итог урока
Сегодня на уроке мы узнали, как с помощью MS Excel можно решить задачи из различных предметных областей.
Какие задачи можно решать с помощью MS Excel? (решение уравнений, физические задачи)
Какими методами можно решить эти задачи? (графическим, поиском решения)
5. Этап информирования учащихся о домашнем задании
Повторить материал по электронному табличному процессору MS Excel.
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Еще…Меньше
Excel — это исключительно мощный инструмент для анализа огромного объема данных. Но он также хорошо работает для простых вычислений и отслеживания практически любых сведений. Ключом для разблокировки всего этого является сетка ячеек. Ячейки могут содержать числа, текст или формулы. Данные помещались в ячейки и групплись в строки и столбцы. Это позволяет сложить данные, отсортировать и отфильтровать их, поместить их в таблицы и создать великолепные диаграммы. Рассмотрим основные этапы, с помощью которые можно начать.
Документы Excel называются книгами. Каждая книга содержит листы. Можно добавить в книгу любое количество листов или создать новую книгу для хранения данных в отдельном месте.
-
Откройте вкладку Файл и выберите команду Создать.
-
В разделе Доступные шаблоны выберите пункт Новая книга.
-
Щелкните пустую ячейку.
Например, щелкните ячейку A1 на новом листе. Ячейки определяются на листе по строке и столбцу. Например, A1 — это ячейка, которая находится в месте пересечения первой строки и столбца A.
-
Введите в ячейке текст или число.
-
Чтобы перейти к следующей ячейке, нажмите клавишу ВВОД или TAB.
-
Вы выберите ячейку или диапазон ячеек, к которые вы хотите добавить границу.
-
На вкладке Главная в группе Шрифт щелкните стрелку рядом с кнопкой Границы и выберите нужный стиль границы.
Дополнительные сведения см. в этойтеме.
-
Вы выберите ячейку или диапазон ячеек, к которые нужно применить затенение.
-
На вкладке Главная в группе Шрифт выберите стрелку рядом с
цвет заливки , а затем в группе Цвета темы или Стандартные цвета выберитенужный цвет.
Дополнительные сведения о том, как применить форматирование к этому формату, см. в теме Форматирование.
После ввода чисел на листе может потребоваться сложить их. Для быстрого сложения чисел можно использовать функцию Сумма.
-
Выберите ячейку, расположенную справа или снизу от чисел, которые необходимо добавить.
-
На вкладке Главная в группе Редактирование нажмите кнопку Автосумма.
Функция «Сумма» выполнит сложение чисел и отобразит результат в выделенной ячейке.
Дополнительные сведения см. в теме Использование авто суммы чисел.
Сложение чисел — лишь одна из доступных в Excel математических операций. Можете поэкспериментировать с формулами вычитания, умножения и деления чисел.
-
Выберите ячейку и введите знак «равно» (=).
Он указывает Excel, что эта ячейка будет содержать формулу.
-
Введите сочетание чисел и знаков операций, таких как «плюс» (+) для сложения, «минус» (-) для вычитания, «звездочка» (*) для умножения и «наклонная черта» (/) для деления.
Например, введите =2+4, =4-2, =2*4 или =4/2.
-
Нажмите клавишу ВВОД.
Будет выполнено вычисление.
Можно также нажать клавиши CTRL+ВВОД, если нужно оставить указатель в активной ячейке.
Дополнительные сведения см. в том, как создать простую формулу.
Для проведения различия между числами разных типов можно применить к ним формат, такой как «денежный», «процентный» или «дата».
-
Выделите ячейки с числами, которые необходимо отформатировать.
-
На вкладке Главная щелкните стрелку в поле Общий.
-
Выберите числовой формат.
Если в списке нет нужного формата, выберите пункт Другие числовые форматы. Дополнительные сведения см. в разделе Доступные числовые форматы.
Для более полного использования полезных функций Excel можно поместить данные в таблицу. Это позволяет быстро фильтровать и сортировать данные.
-
Выделите нужные данные, щелкнув первую ячейку с ними и перетащив область выделения до последней ячейки нужного диапазона.
Для выделения данных с использованием клавиатуры нажмите клавишу SHIFT и расширьте область выделения с помощью клавиш со стрелками.
-
Нажмите кнопку «Быстрый анализ
в правом нижнем углу области выделения.
-
Откройте вкладку Таблицы и наведите указатель мыши на кнопку Таблица, чтобы посмотреть, как будут выглядеть данные. Затем нажмите кнопку Таблица.
-
Щелкните стрелку
в заглавной части столбца.
-
Чтобы отфильтровать данные, снимите флажок Выделить все и выберите данные, которые должны отображаться в таблице.
-
Для сортировки данных выберите пункт Сортировка от А до Я или Сортировка от Я до А.
-
Нажмите кнопку ОК.
Дополнительные сведения см. в Excel таблицы.
Средство быстрого анализа (доступно только в Excel 2016 и Excel 2013 ) позволяет быстро подгонать итоги. Будь то сумма, среднее значение или количество элементов, Excel отображает результаты вычисления непосредственно под числами или рядом с ними.
-
Выделите ячейки с числами, которые нужно сложить или сосчитать.
-
Нажмите кнопку «Быстрый анализ
в правом нижнем углу области выделения.
-
Выберите пункт Итоги, проведите указателем над кнопками, чтобы увидеть результаты вычислений, и нажмите кнопку, чтобы применить итоги.
С помощью условного форматирования или спарклайнов можно выделить наиболее важные данные или отобразить тенденции их изменения. Используйте средство быстрого анализа (доступно только Excel 2016 и Excel 2013 ) для предварительного просмотра в режиме Live Preview.
-
Выделите данные, которые нужно подробно изучить.
-
Нажмите кнопку «Быстрый анализ
в правом нижнем углу области выделения.
-
Изучите параметры на вкладках Форматирование и Спарклайны, чтобы узнать, как они влияют на данные.
Например, выберите в коллекции Форматирование цветовую шкалу, чтобы провести различие между высокой, средней и низкой температурами.
-
Если результат предварительного просмотра вас устраивает, щелкните этот вариант.
Узнайте подробнее, как анализировать тенденции в данных с помощью спарклайнов.
Средство быстрого анализа (доступно только в Excel 2016 и Excel 2013 ) рекомендует диаграмму для ваших данных и позволяет наглядно представить ее несколькими щелчками мыши.
-
Выделите ячейки с данными, которые нужно отобразить в диаграмме.
-
Нажмите кнопку «Быстрый анализ
в правом нижнем углу области выделения.
-
Откройте вкладку Диаграммы, проведите указателем мыши по рекомендуемым диаграммам, чтобы просмотреть их, и выберите наиболее подходящую.
Примечание: В этой коллекции будут показаны только диаграммы, рекомендуемые для ваших данных.
Узнайте о других способах создания диаграмм.
Быстрая сортировка данных
-
Выделите диапазон данных, например A1:L5 (несколько строк и столбцов) или C1:C80 (один столбец). В этот диапазон могут входить и заголовки, созданные для обозначения столбцов или строк.
-
Выделите одну ячейку в столбце, в котором нужно выполнить сортировку.
-
Нажмите
, чтобы выполнить сортировку по возрастанию (от А до Я или от наименьшего числа к наибольшему).
-
Щелкните
, чтобы выполнить сортировку по убытию (от Я до А или от наибольшего числа к наименьшему).
Сортировка по определенным условиям
-
Выделите одну любую ячейку в диапазоне, для которого требуется выполнить сортировку.
-
На вкладке Данные в группе Сортировка & фильтра выберите сортировку.
-
Откроется диалоговое окно Сортировка.
-
В списке Сортировать по выберите первый столбец, по которому нужно выполнить сортировку.
-
В списке Сортировка выберите пункт Значения, Цвет ячейки, Цвет шрифта или Значок ячейки.
-
В списке Порядок выберите порядок сортировки. Можно сортировать текст или числа по возрастанию и по убыванию (соответственно от А до Я и от Я до А для текста или от меньшего к большему и от большего к меньшему для чисел).
Дополнительные сведения о сортировке данных см. в теме Сортировка данных в диапазоне или таблице.
-
Выберите данные, которые нужно отфильтровать.
-
На вкладке Данные в группе Сортировка и фильтр нажмите кнопку Фильтр.
-
Щелкните стрелку
в заглавной области столбца, чтобы отобразить список, в котором можно выбирать фильтры.
-
Чтобы выбрать значения для списка, снимите флажок (Выделить все). При этом снимаются все флажки. Затем выберите только те значения, которые хотите видеть, и нажмите кнопку ОК, чтобы посмотреть результаты.
Дополнительные сведения о фильтрации данных см. в теме Фильтрация данных в диапазоне или таблице.
-
Нажмите кнопку Сохранить на панели быстрого доступа или сочетание клавиш CTRL+S.
Если документ уже сохранялся, никаких дополнительных действий выполнять не нужно.
-
Если вы сохраняете файл впервые, сделайте следующее.
-
В окне Сохранить как выберите расположение для сохранения книги, а затем найдите нужную папку.
-
В поле Имя файла введите имя книги.
-
Нажмите кнопку Сохранить.
-
-
Откройте вкладку Файл и выберите команду Печать или нажмите клавиши CTRL+P.
-
Для предварительного просмотра страниц нажимайте стрелки Следующая страница и Предыдущая страница.
Окно предварительного просмотра отображает страницы в черно-белом или цветном виде в зависимости от настроек принтера.
Если вас не устраивает вид страниц, можно изменить их поля или добавить разрывы страниц.
-
Нажмите кнопку Печать.
-
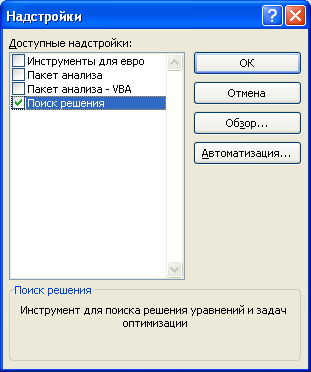
На вкладке Файл выберите параметрыи выберите категорию Надстройки.
-
В нижней части диалогового Excel Параметры выберите Excel в поле Управление и нажмите кнопку Перейти.
-
В диалоговом окне Надстройки выберите нужные надстройки и нажмите кнопку ОК.
Если отобразится сообщение о том, что надстройку не удается запустить, и будет выведено предложение установить ее, нажмите кнопку Да, чтобы установить надстройку.
Дополнительные сведения об использовании надстройок см. в этой теме.
Excel позволяет применять встроенные шаблоны, применять собственные настраиваемые шаблоны и искать их на сайте Office.com. Office.com предлагает широкий выбор популярных шаблонов Excel, включая бюджеты.
Дополнительные сведения о поиске и применении шаблонов см. в этой ссылке.
Нужна дополнительная помощь?
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в
MS EXCEL 2010
(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в
MS EXCEL 2007)
. В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
-
настройку
Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда
Поиск решения
находится в группе
Анализ
на вкладке
Данные
.
Если команда
Поиск решения
в группе
Анализ
недоступна, то необходимо включить одноименную надстройку. Для этого:
-
На вкладке
Файл
выберите команду
Параметры
, а затем — категорию
Надстройки
; -
В поле
Управление
выберите значение
Надстройки Excel
и нажмите кнопку
Перейти;
-
В поле
Доступные надстройки
установите флажок рядом с пунктом
Поиск решения
и нажмите кнопку ОК.
Примечание
. Окно
Надстройки
также доступно на вкладке
Разработчик
. Как включить эту вкладку
читайте здесь
.
После нажатия кнопки
Поиск решения
в группе
Анализ,
откроется его диалоговое окно
.
При частом использовании
Поиска решения
его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт
Добавить на панель быстрого доступа
.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет
. Перед использованием
Поиска решения
настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка
Поиск решения
помогает определить
лучший способ
сделать
что-то
:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
-
Определить
план производства
, при котором доход от реализации произведенной продукции максимальный;
-
Определить
схему перевозок
, при которой общие затраты на перевозку были бы минимальными;
-
Найти
распределение нескольких станков по разным видам работ
, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется
Поиском решения
только по одному показателю
(этот оптимизируемый показатель называется
целевой функцией
). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения
подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание
. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента
Подбор параметра
. Перед первым знакомством с
Поиском решения
имеет смысл сначала детально разобраться с родственным ему инструментом
Подбор параметра
. Основные отличия
Подбора параметра
от
Поиска решения
:
Подбор параметра
работает только с моделями с одной переменной;- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения
оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне
Поиска решения
возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет
. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки
Поиска решения
(см. ниже).
Приведем алгоритм работы с
Поиском решения
, который советуют сами разработчики (
]]>
www.solver.com
]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
-
С помощью диалогового окна
Поиск решения
введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений; -
Запустите
Поиск решения
для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования
Поиска решения
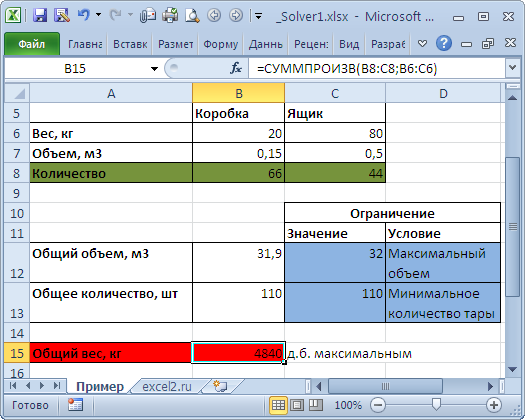
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см.
файл примера
).
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле
=СУММПРОИЗВ(B8:C8;B6:C6)
– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —
=СУММПРОИЗВ(B7:C7;B8:C8)
. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары
=СУММ(B8:C8)
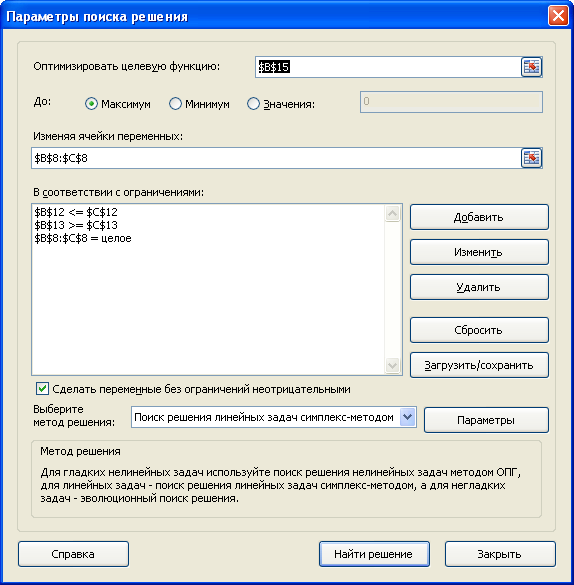
. Теперь с помощью диалогового окна
Поиск решения
введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки
Найти решение
будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет
: в статье »
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью
Поиска решения
является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью
Поиска решения
. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью
Поиска решения
рассмотрено
в этом разделе
.
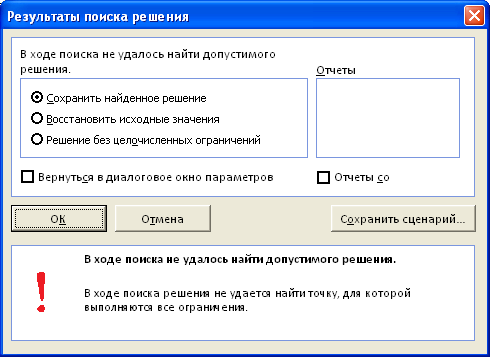
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда
Поиск решения
не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете
Симплекс метод решения линейных задач
, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите
Поиск решения
с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и
Поиск решения
не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,
Поиск решения
может найти решение (если оно действительно существует).
Примечание
. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи
Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства
.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,
Поиск решения
не найдет решения.
При ограничении 17 м3
Поиск решения
найдет решение.
Некоторые настройки
Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Поиска решения
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:
В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.
Кнопки Добавить, Изменить, Удалить
Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.
Кнопка Сбросить
Чтобы удалить все настройки
Поиска решения
нажмите кнопку
Сбросить
– диалоговое окно очистится.
Сохранение и загрузка модели
Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка
Загрузить/ Сохранить,
далее нажмите кнопку
Сохранить
) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку
Параметры
). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку
Загрузить/ Сохранить
, затем, в появившемся диалоговом окне кнопку
Загрузить
, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.
Точность
При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание
ограниченную точность
вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.
Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
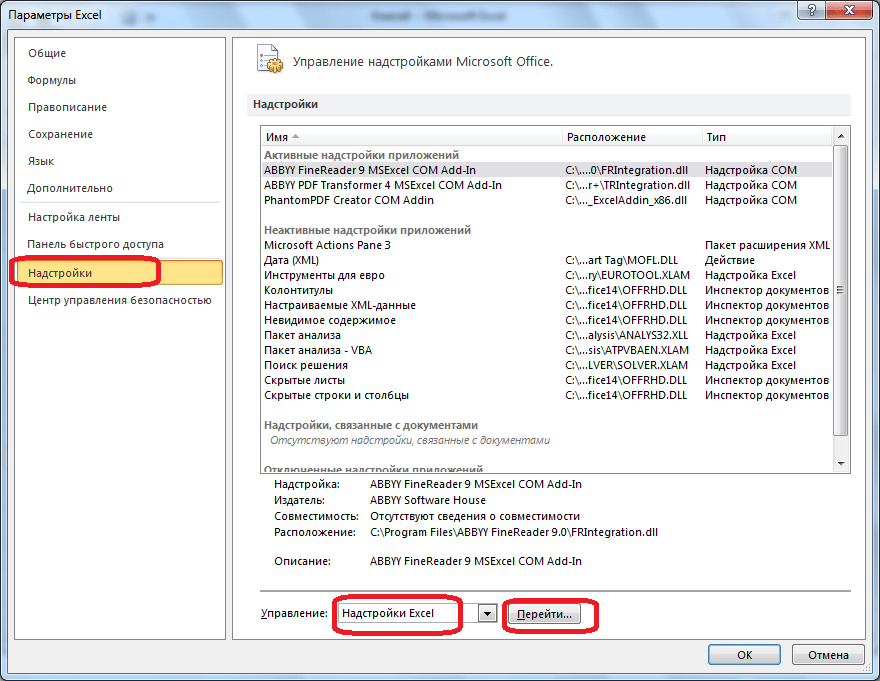
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
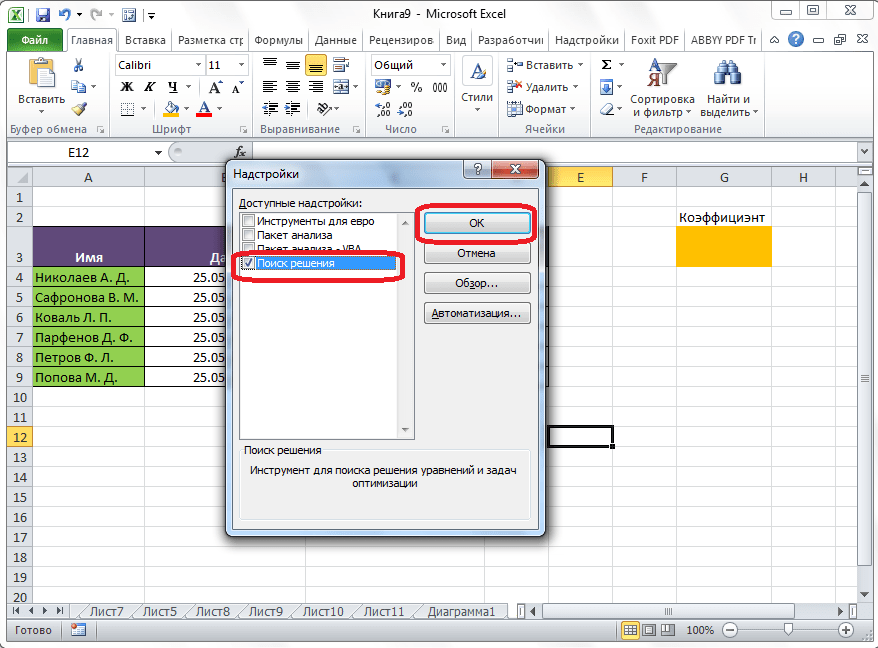
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Подготовка таблицы
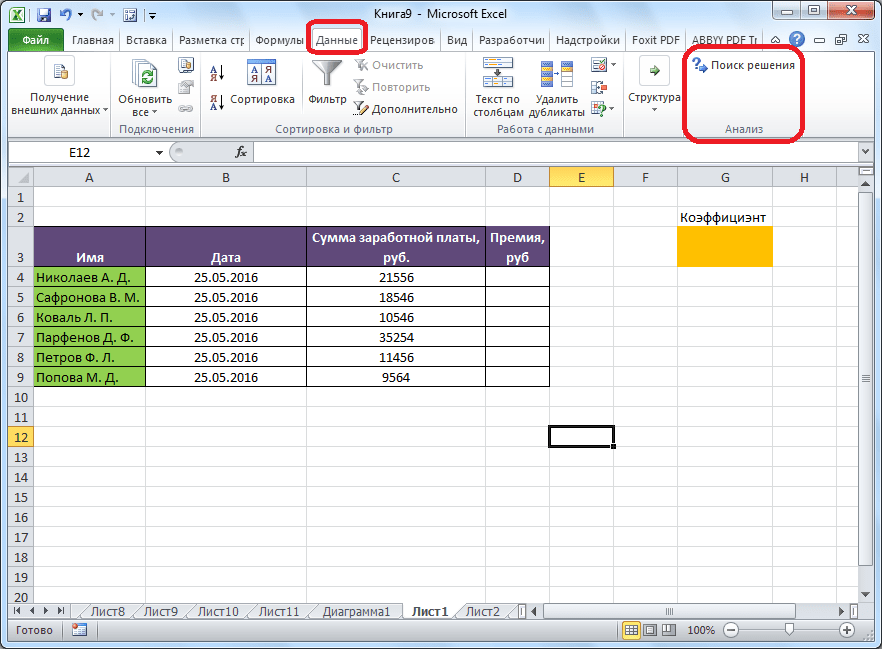
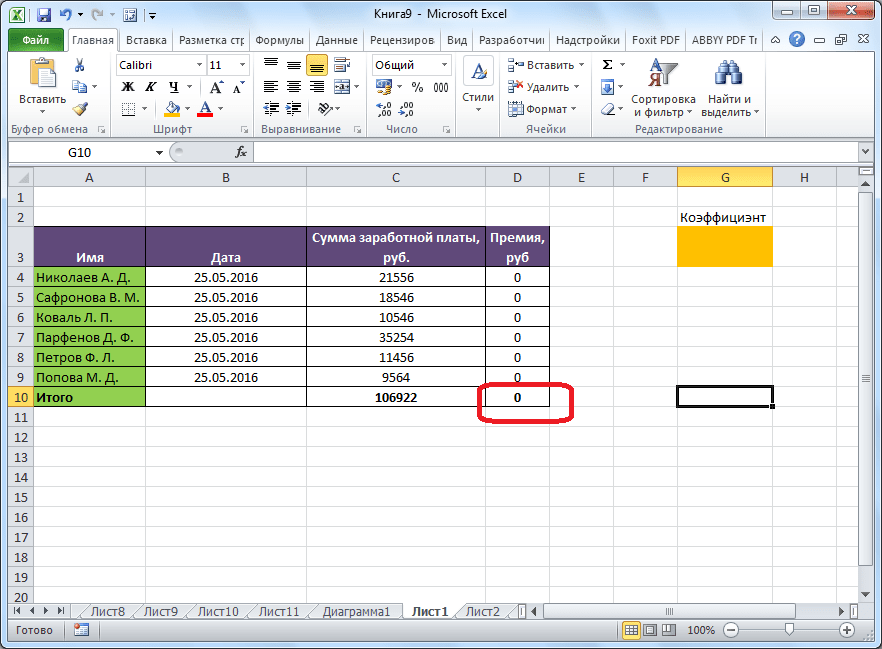
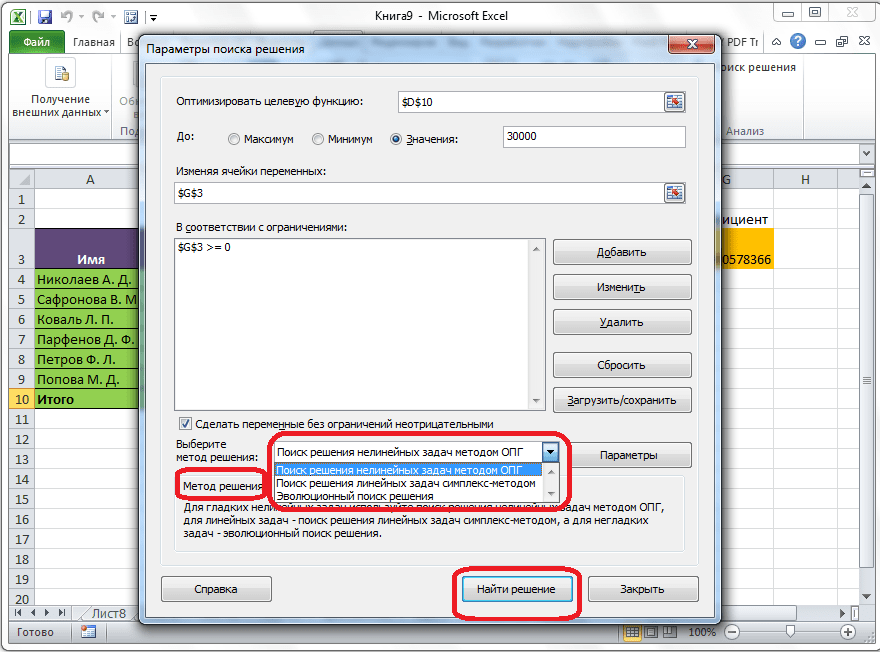
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
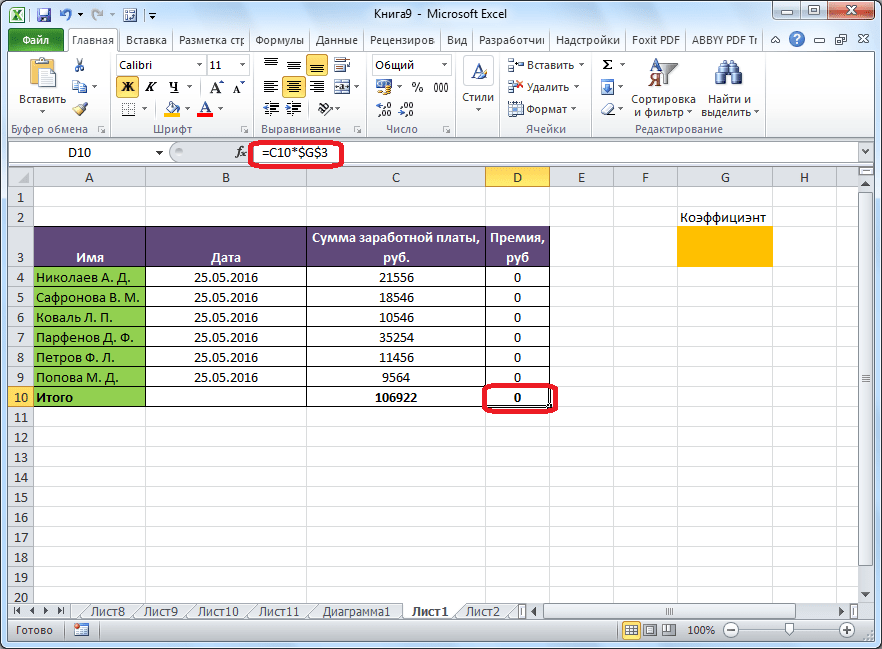
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Запуск инструмента Поиск решения
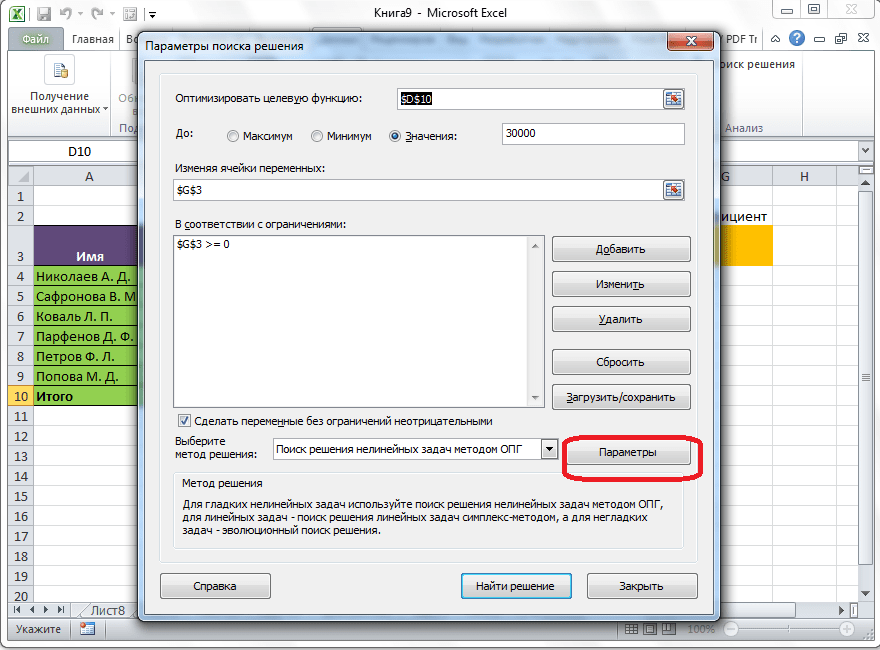
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
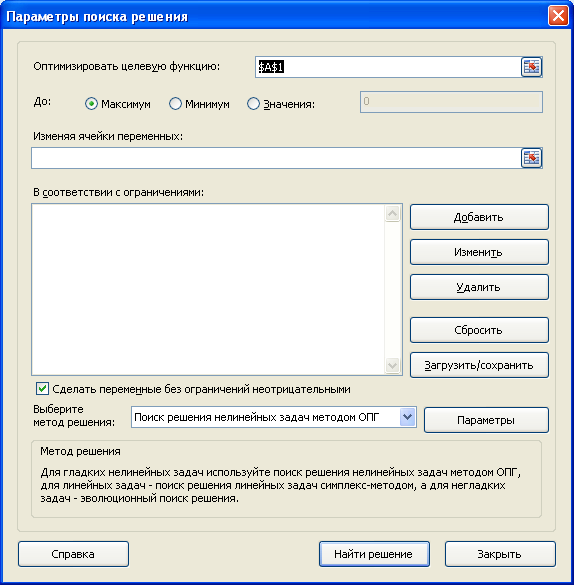
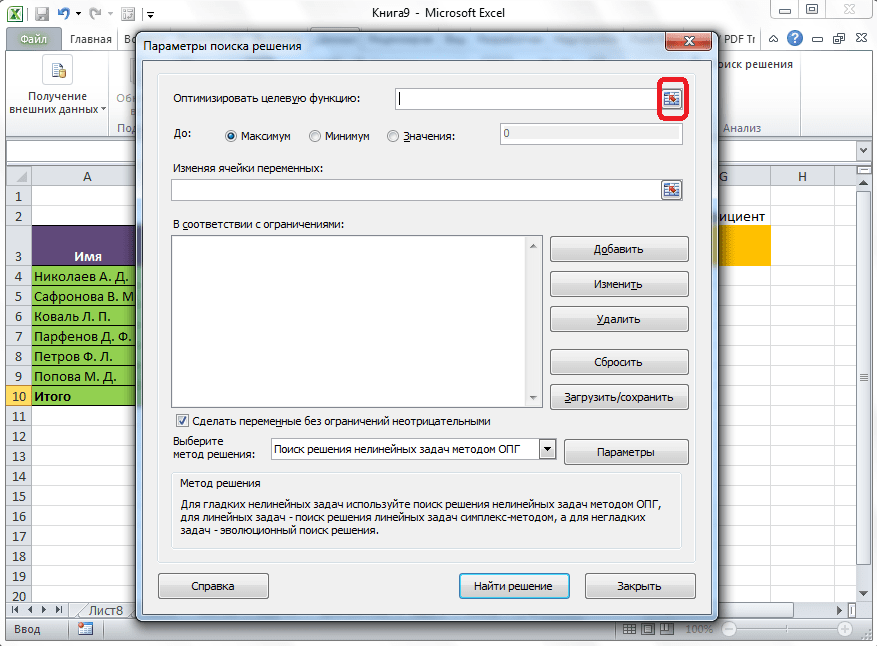
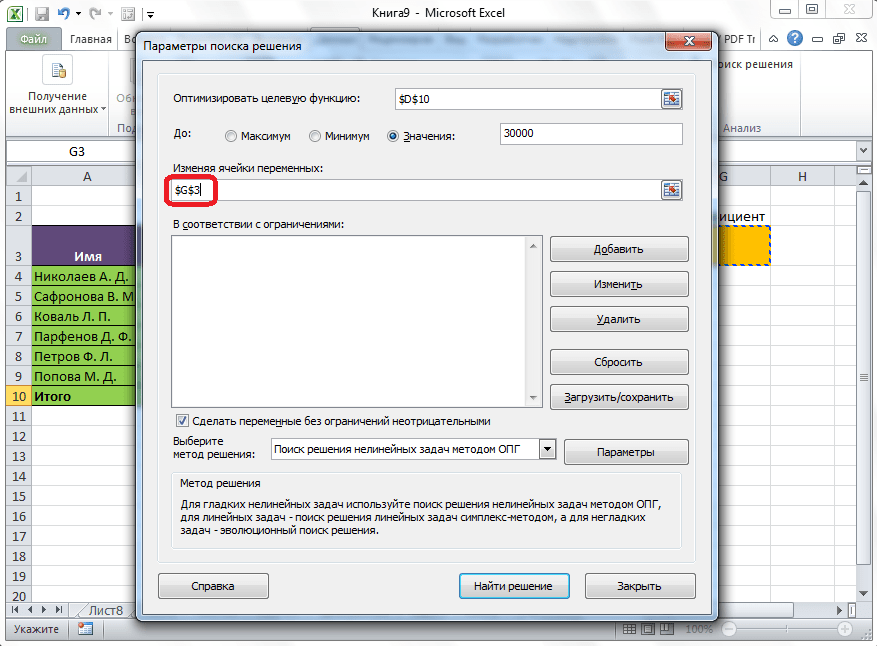
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
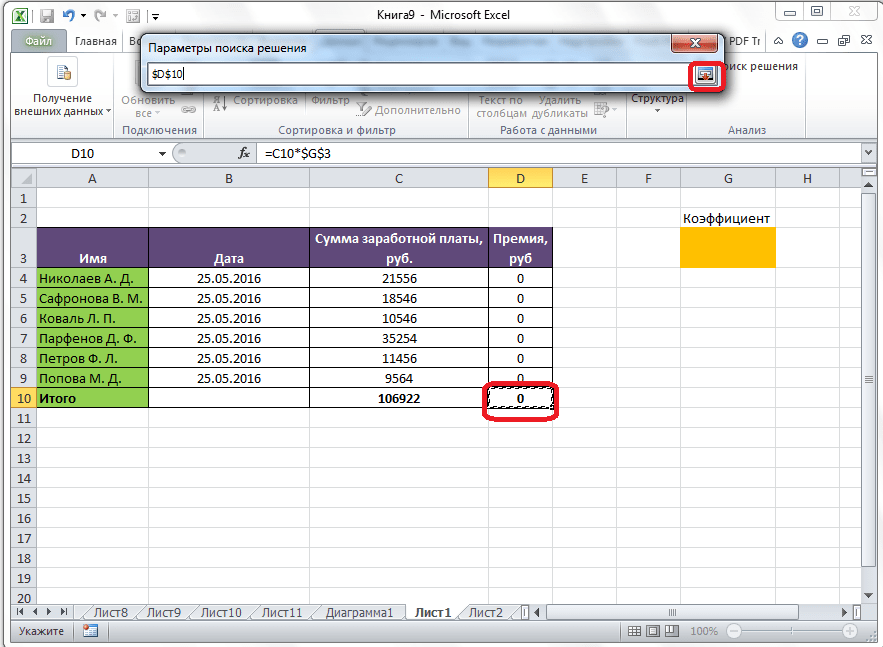
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
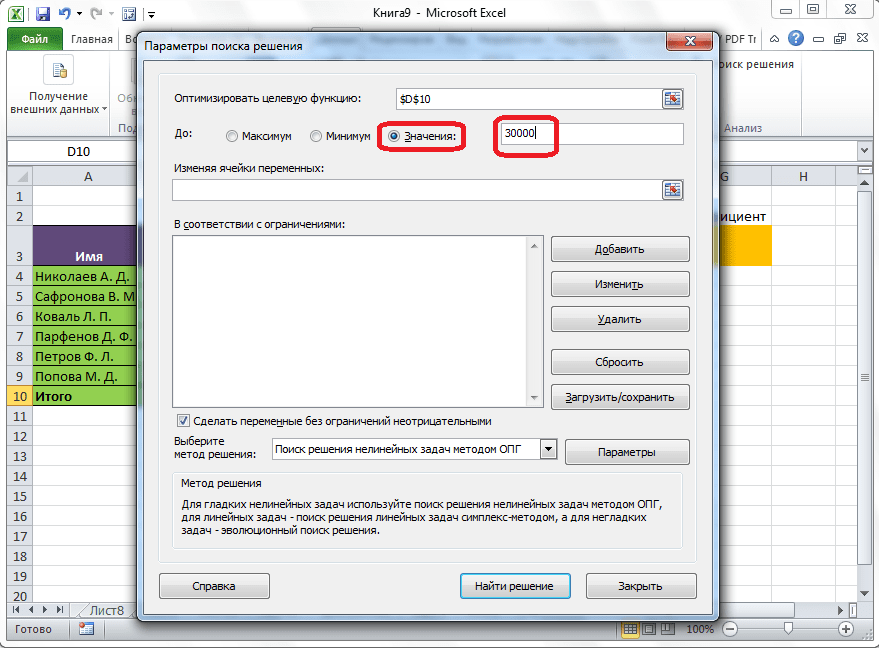
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
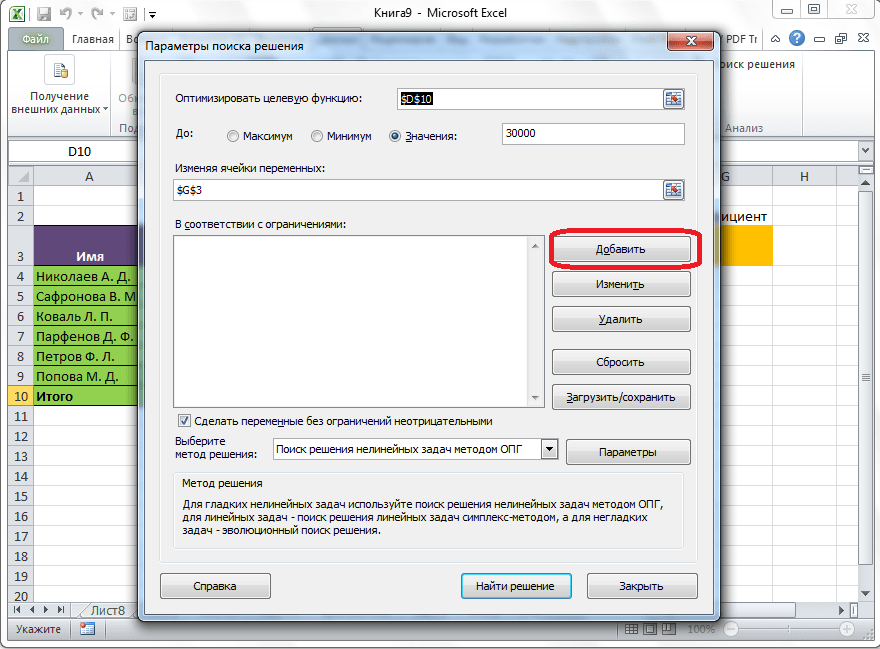
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
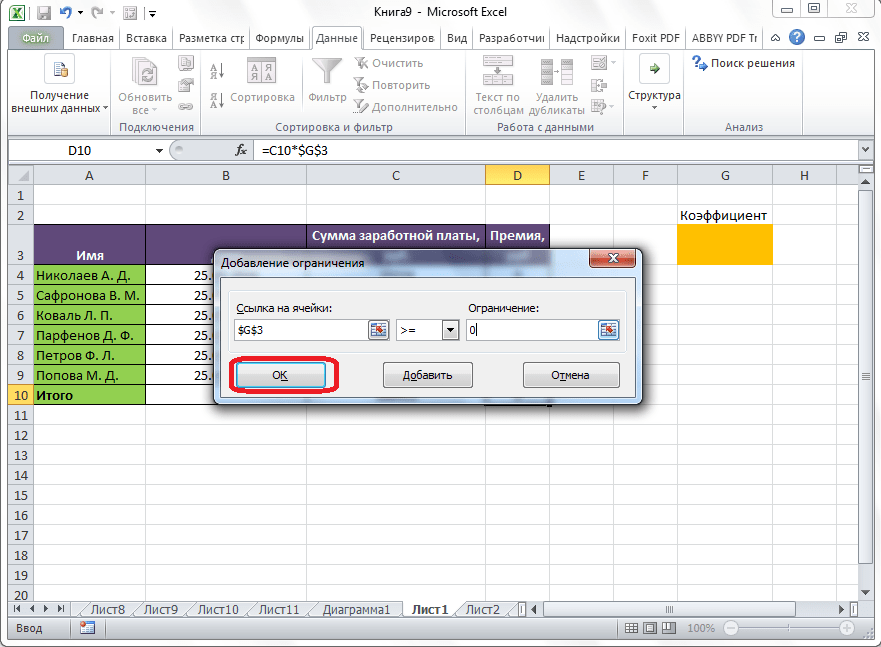
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
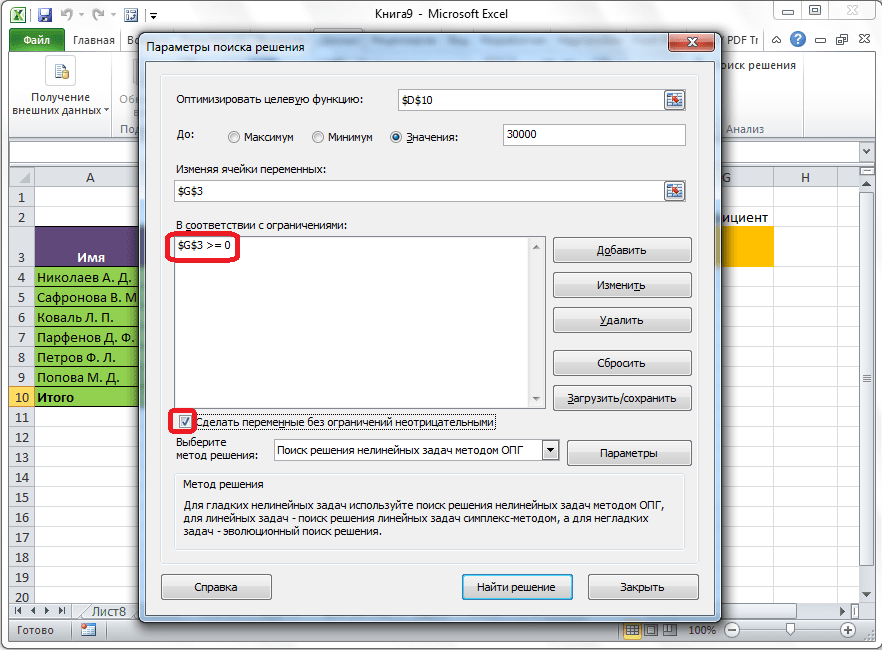
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
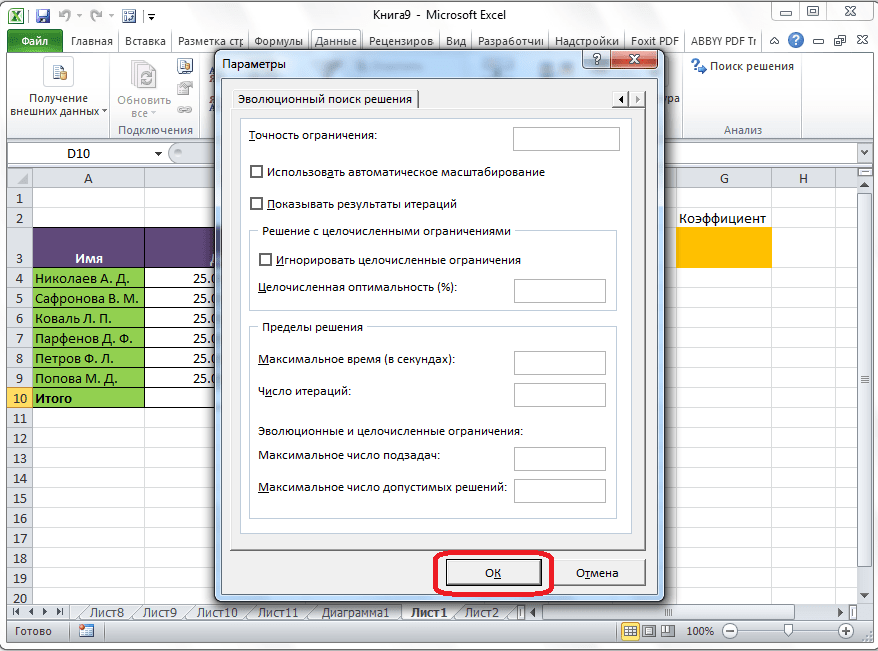
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
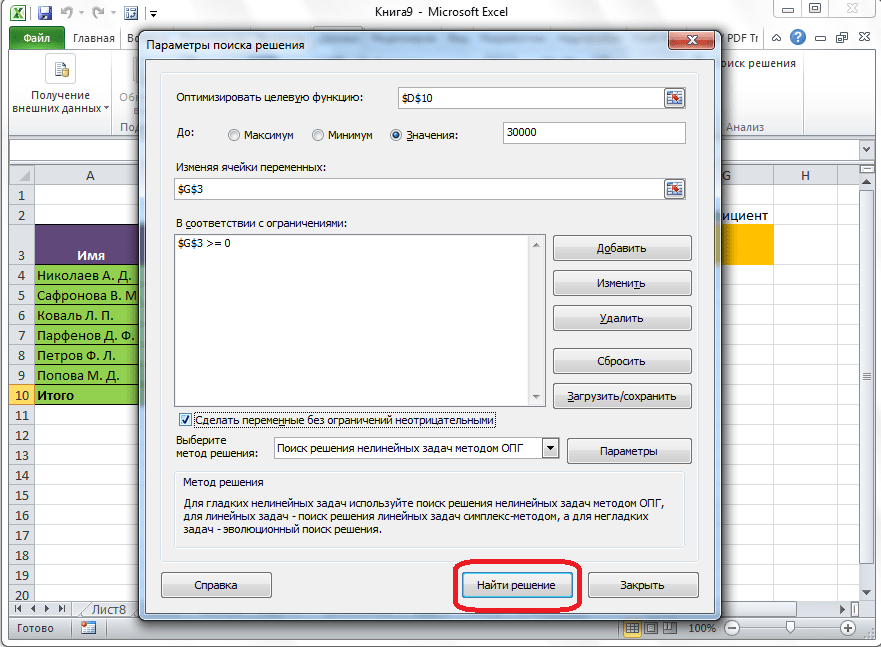
После того, как все настройки установлены, жмем на кнопку «Найти решение».
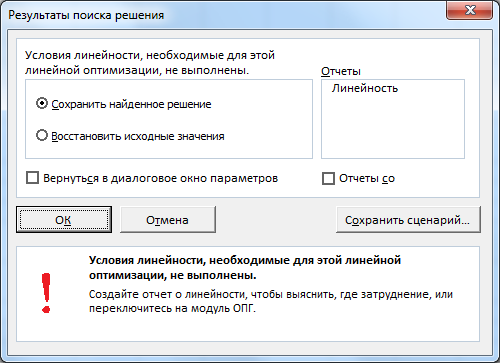
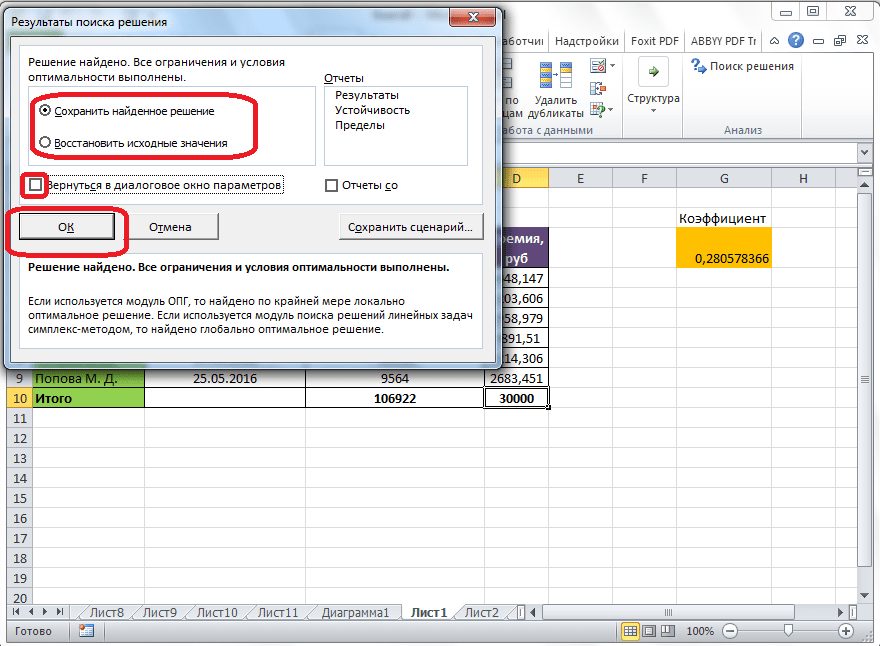
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в MS EXCEL 2010 (эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в MS EXCEL 2007).
В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
- настройку Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда Поиск решения находится в группе Анализ на вкладке Данные.
Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку.
Для этого:
- На вкладке Файл выберите команду Параметры, а затем — категорию Надстройки;
- В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
- В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.
Примечание. Окно Надстройки также доступно на вкладке Разработчик. Как включить эту вкладку читайте здесь.
После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно.
При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет. Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка Поиск решения помогает определить лучший способ сделать что-то:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
- Определить план производства, при котором доход от реализации произведенной продукции максимальный;
- Определить схему перевозок, при которой общие затраты на перевозку были бы минимальными;
- Найти распределение нескольких станков по разным видам работ, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией).
В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра. Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра.
Основные отличия Подбора параметра от Поиска решения:
- Подбор параметра работает только с моделями с одной переменной;
- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул).
Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных.
Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа.
Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).
Приведем алгоритм работы с Поиском решения, который советуют сами разработчики ( ]]> www.solver.com ]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
- С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
- Запустите Поиск решения для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см. файл примера ).
Переменные модели (количество каждого вида тары) выделены зеленым.
Целевая функция (общий вес всех коробок и ящиков) – красным.
Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =СУММПРОИЗВ(B8:C8;B6:C6) – это общий вес всех коробок и ящиков, загруженных в контейнер.
Аналогично рассчитываем общий объем — =СУММПРОИЗВ(B7:C7;B8:C8) . Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков ( =СУММ(B8:C8) .
Теперь с помощью диалогового окна Поиск решения введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки).
Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки Найти решение будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью Поиска решения является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью Поиска решения.
Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу.
Решение классических оптимизационных задач с помощью Поиска решения рассмотрено в этом разделе.
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда Поиск решения не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям.
Если вы используете Симплекс метод решения линейных задач, то можно быть уверенным, что решения действительно не существует.
Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите Поиск решения с другими начальными значениями переменных, то, возможно, решение будет найдено.
Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и Поиск решения не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае, Поиск решения может найти решение (если оно действительно существует).
Примечание. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, =) или граничного значения.
Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.
При ограничении 17 м3 Поиск решения найдет решение.
Некоторые настройки Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2 Похожие задачи
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Ярославский областной
институт повышения квалификации
педагогических и руководящих
работников образования
Творческая работа
“Задачи по моделированию
в среде Excel”
Учителя информатики
средней школы № 58
г.Ярославля
Горбачевой Александры Николаевны
Научный руководитель:
проректор ИПК, руководитель ЦИТ
Смирнова Алевтина Николаевна,
методист ЦИТ ИПК
Потехин Николай Владимирович
г. Ярославль, 2000
Содержание
1. Введение
…………………………………………………………………………………………………….
3
1.1 Психолого-педагогические особенности изучения темы
“Моделирования” в школьном курсе
информатики
1.2 Обязательный
минимум содержания образования по теме
“Моделирование
и формализация”
1.3
Требования к уровню подготовки выпускников по теме
“Моделирование
и формализация”
2. Основные понятия моделирования
……………………………………………….……………. 7
3. Основные этапы моделирования
…………………………………………………..……………. 10
4. Метод математических моделей
………………………………………………….…………….. 13
5. Задачи по моделированию из
различных предметных областей ……….…………. 16
5.1 “Экономика”
……………………………………………………………………… 16
5.2 “Астрономия” ……………………………………………………………………. 24
5.3. “Физика” ………………………………………………………………………… 27
5.4 “Экология” ……………………………………………………………………….. 31
5.5 “Биология” ……………………………………………………………………….. 38
5.6 “География”
……………………………………………………………………… 44
6. Заключение …………………………………………………………………………… 45
7. Список литературы
………………………………………………………………….. 46
8. Приложение
………………………………………………………………………….. 47
1. Введение
1.1 Психолого-педагогические
особенности изучения темы “Моделирования” в школьном курсе информатики
Наиболее важные и
значимые общеобразовательные цели информатики и информатизации — установление и
усиление межпредметных связей, создание условий для восприятия и понимания
информационных процессов в обществе, природе, познании — формирование у
учащихся информационной картины мира.
Современное образование
требует преодоления разрозненности учебных предметов. Каждой научной дисциплине
свойственно свое особое сочетание формализованных и неформализованных методов
моделирования явлений, процедур доказательства и объяснения, и лишь информатика
легко преодолевает межпредметные границы, обогащает все области научного
познания.
Проблема взаимосвязи
школьных дисциплин — математики, информатики, физики, биологии и др. — является
одной из актуальных проблем современной дидактики, психологии и методики преподавания.
Решение задач — конкретных моделей явлений — на уроках информатики является
одним из мощных способов реализации межпредметных связей информатики и других
наук.
Человек издавна
использует моделирование для исследования объектов, процессов, явлений в
различных областях. Результаты этих исследований служат для определения и
улучшения характеристик реальных объектов и процессов; для понимания сути
явлений и выработки умения приспосабливаться или управлять ими; для
конструирования новых объектов или модернизации старых. Моделирование помогает
человеку принимать обоснованные и продуманные решения, предвидеть последствия
своей деятельности.
Компьютерное
моделирование учебных и реальных объектов, ситуаций и процессов в математике,
физике, химии, биологии, экологии ставит учащегося в активную позицию
исследователя, позволяет самостоятельно открывать законы и явления.
Развитие навыков
построения моделей способствует решению задачи, имеющей общеобразовательную
ценность, а именно развитию системного и логического мышления. Ведь процесс
построения моделей требует помимо специальных знаний еще и особым образом
развитого мышления.
Решение задач по
моделированию процессов и явлений развивает мыслительную деятельность учащихся.
Под развитием мышления
учащихся в процессе обучения психологи понимают формирование и
совершенствование всех видов, форм и операций мышления, выработку умений и
навыков по применению законов мышления в познавательной и учебной деятельности,
а также умений осуществлять перенос приемов мыслительной деятельности из одной
области знаний в другую.
Таким образом, развитие
мышления включает в себя:
1. Развитие всех видов мышления
(наглядно-действенного, наглядно-образного, абстрактно-логического) и
одновременно стимуляцию процесса перерастания их из одного вида в другой.
2. Формирование и
совершенствование мыслительных операций.
3. Развитие умений:
·
выделять
существенные свойства предметов и абстрагировать их от несущественных;
·
находить
главные связи и отношения предметов и явлений реального мира;
·
делать
правильные выводы из фактов и проверять их;
·
доказывать
истинность своих суждений и опровергать ложные умозаключения;
·
раскрывать
сущность основных форм правильных умозаключений (индукции, дедукции и по
аналогии);
·
излагать
свои мысли определенно, последовательно, непротиворечиво и обоснованно.
4. Выработку умения осуществлять
перенос операций и приемов мышления из одной области знания в другую;
прогнозирование развития явлений и умение делать выводы.
5. Совершенствование умений и
навыков по применению законов и требований формальной и диалектической логики в
учебной и во внеучебной познавательной деятельности учащихся.
По мнению психологов
схема решения мыслительных задач выглядит следующим образом:
|
Условия возникновения |
Процесс |
Приемы |
Результат |
Формы реализации |
|||||
|
|
Анализ |
Суждения |
|||||||
|
|
Мышление |
Синтез |
Продукт |
Понятия |
|||||
|
|
|||||||||
|
|
Сравнение |
мышления |
Умозаключения |
||||||
|
|
Обобщение |
||||||||
В процессе построения
модели учащиеся, отталкиваясь от общей формулировки задачи, выделяют
существенные части моделируемой системы, исследуют свойства этих объектов,
находят связи между ними, проводят компьютерные эксперименты и анализируют
результаты моделирования. Практически все перечисленные выше процессы мыслительной
деятельности прослеживаются при решении задач на составление моделей.
Умение выделять
необходимую информацию и организовывать ее в структуру — важнейшее качество человеческого
интеллекта.
1.2 Обязательный минимум
содержания образования
по теме “Моделирование и
формализация”
Моделирование как метод познания. Материальные и
информационные модели. Объектно-ориентированное информационное моделирование.
Формализация. Основные типы информационных моделей (табличные, иерархические,
сетевые). Исследование информационных моделей на компьютере.
1.3 Требования к уровню
подготовки выпускников
по теме “Моделирование и
формализация”
Учащиеся должны:
·
уметь
характеризовать сущность моделирования;
·
уметь
характеризовать сущность формализации;
·
знать о
существовании множества моделей для одного и того же объекта;
·
уметь
строить простейшие информационные модели;
·
знать
этапы информационной технологии решения задач с использованием компьютера.
2. Основные понятия моделирования
Понятие модели
Модель —
это некоторое упрощенное подобие реального объекта, явления или процесса.
Модель — это такой
материальный или мысленно представляемый объект, который замещает
объект-оригинал с целью его исследования, сохраняя некоторые важные для данного
исследования типичные черты и свойства оригинала.
Хорошо построенная
модель, как правило, доступнее для исследования, чем реальный объект (например,
такой, как экономика страны, Солнечная система и т.п.). Другое, не менее важное
назначение модели состоит в том, что с ее помощью выявляются наиболее
существенные факторы, формирующие те или иные свойства объекта. Модель также
позволяет учиться управлять объектом, что важно в тех случаях, когда
экспериментировать с объектом бывает неудобно, трудно или невозможно (например,
когда эксперимент имеет большую продолжительность или когда существует риск
привести объект в нежелательное или необратимое состояние).
Таким образом, можно сделать
вывод, что модель необходима для того, чтобы:
·
понять,
как устроен конкретный объект — каковы его структура, основные свойства, законы
развития и взаимодействия с окружающим миром;
·
научиться
управлять объектом или процессом и определить наилучшие способы управления при
заданных целях и критериях (оптимизация);
·
прогнозировать
прямые и косвенные последствия реализации заданных способов и форм воздействия
на объект, процесс.
Структура — это определенный способ
объединения элементов, составляющих единый сложный объект.
Система — это сложный объект,
представляющий собой совокупность взаимосвязанных элементов, объединенных в
некоторую структуру.
В учебнике “Информатика 9
класс” Н.В.Макаровой предложена следующая классификация моделей.
1. Классификация по области использования
|
Модели |
|||||||||||||
|
Учебные |
Опытные |
Научно-технические |
Игровые |
Имитационные |
|||||||||
Учебные: наглядные пособия,
различные тренажеры, обучающие программы.
Опытные: уменьшенные или увеличенные
копии исследуемого объекта для дальнейшего его изучения (модели корабля,
автомобиля, самолета, гидростанции).
Научно-технические модели создают для
исследования процессов и явлений (стенд для проверки телевизоров; синхротрон —
ускоритель электронов и др.).
Игровые: военные, экономические,
спортивные, деловые игры.
Имитационные: отражают реальность с той
или иной степенью точности (испытание нового лекарственного средства в ряде
опытах на мышах; эксперименты по внедрению в производство новой технологии).
2.
Классификация с учетом фактора времени
|
Модели |
|||||||
|
Статические |
Динамические |
||||||
Статическая модель — модель объекта в данный момент
времени.
Динамическая модель позволяет увидеть изменения объекта во времени.
3.
Классификация по способу представления
|
Модели |
|||||||||||||||||||||||
|
Материальные |
Информационные |
||||||||||||||||||||||
|
Знаковые |
Вербальные |
||||||||||||||||||||||
|
Компьютерные |
Некомпьютерные |
||||||||||||||||||||||
Материальная модель — это физическое подобие
объекта. Они воспроизводят геометрические и физические свойства оригинала
(чучела птиц, муляжи животных, внутренних органов человеческого организма,
географические и исторические карты, схема солнечной системы).
Информационная модель — это совокупность
информации, характеризующая свойства и состояния объекта, процесса, явления, а
также взаимосвязь с внешним миром.
Любая информационная
модель содержит лишь существенные сведения об объекте с учетом той цели, для
которой она создается. Информационные модели одного и того же объекта,
предназначенные для разных целей, могут быть совершенно разными.
Вербальная модель — информационная модель в
мысленной или разговорной форме.
Знаковая модель — информационная модель,
выраженная специальными знаками, т.е. средствами любого формального языка.
Знаковые модели — это рисунки, тексты, графики, схемы, таблицы …
Компьютерная модель — модель, реализованная
средствами программной среды.
Прежде чем построить
модель объекта (явления, процесса), необходимо выделить составляющие его
элементы и связи между ними (провести системный анализ) и “перевести”
полученную структуру в какую-либо заранее определенную форму — формализовать
информацию.
Формализация — это процесс выделения и перевода
внутренней структуры предмета, явления или процесса в определенную
информационную структуру — форму.
Процесс построения модели
называется моделированием.
3. Основные этапы моделирования
Моделирование —
творческий процесс. Заключить его в формальные рамки очень трудно. В наиболее
общем виде его можно представить поэтапно в следующем виде.
|
I этап. Постановка задачи Описание задачи Цель моделирования Анализ объекта |
|||
|
|
|||
|
Информационная модель Знаковая модель Компьютерная модель |
|||
|
|
|||
|
эксперимент |
|||
|
|
|||
|
IV этап. Анализ результатов моделирования |
|||
|
|
|||
|
|
Результаты не соответствуют цели |
||
Каждый раз при решении
конкретной задачи такая схема может подвергаться некоторым изменениям: какой-то
блок может быть убран или усовершенствован. Все этапы определяются поставленной
задачей и целями моделирования.
I этап. Постановка
задачи
Под задачей в самом общем
смысле понимается некая проблема, которую надо решить. Главное — определить
объект моделирования и понять, что собой должен представлять результат.
По характеру постановки
все задачи можно разделить на две основные группы. К первой группе можно
отнести задачи, в которых требуется исследовать, как изменяется характеристика
объекта при некотором воздействии на него. Такую постановку задачи принято
называть “что будет, если…”. Вторая группа задач имеет такую обобщенную
формулировку: какое надо произвести воздействие на объект, чтобы его параметры
удовлетворяли некоторому заданному условию? Такая постановка задачи часто
называется “как сделать, чтобы…”.
Цели моделирования
определяются расчетными параметрами модели. Чаще всего это поиск ответа на
вопрос, поставленный в формулировке задачи.
Далее переходят к
описанию объекта или процесса. На этой стадии выявляются факторы, от которых
зависит поведение модели. При моделировании в электронных таблицах учитывать
можно только те параметры, которые имеют количественные характеристики.
Иногда задача может быть
уже сформулирована в упрощенном виде, и в ней четко поставлены цели и
определены параметры модели, которые надо учесть.
При анализе объекта
необходимо ответить на следующий вопрос: можно ли исследуемый объект или
процесс рассматривать как единое целое или же это система, состоящая из более
простых объектов? Если это единое целое, то можно перейти к построению
информационной модели. Если система — надо перейти к анализу объектов, ее
составляющих, определить связи между ними.
II этап. Разработка
модели
По результатам анализа
объекта составляется информационная модель. В ней детально описываются
все свойства объекта, их параметры, действия и взаимосвязи.
Далее информационная
модель должна быть выражена в одной из знаковых форм. Учитывая, что мы будем
работать в среде электронных таблиц, то информационную модель необходимо
преобразовать в математическую. На основе информационной и
математической моделей составляется компьютерная модель в форме таблиц,
в которой выделяются три области данных: исходные данные, промежуточные
расчеты, результаты. Исходные данные вводятся “вручную”. Расчеты, как промежуточные,
так и окончательные, проводятся по формулам, записанным по правилам электронных
таблиц.
III этап. Компьютерный
эксперимент
Чтобы дать жизнь новым конструкторским
разработкам, внедрить новые технические решения в производство или проверить
новые идеи, нужен эксперимент. В недалеком прошлом такой эксперимент можно было
провести либо в лабораторных условиях на специально создаваемых для него
установках, либо на натуре, т.е. на настоящем образце изделия, подвергая его
всяческим испытаниям. Это требует больших материальных затрат и времени. В
помощь пришли компьютерные исследования моделей. При проведении компьютерного
эксперимента проверяют правильность построения моделей. Изучают поведение
модели при различных параметрах объекта. Каждый эксперимент сопровождается
осмыслением результатов. Если результаты компьютерного эксперимента
противоречат смыслу решаемой задачи, то ошибку надо искать в неправильно выбранной
модели или в алгоритме и методе ее решения. После выявления и устранения ошибок
компьютерный эксперимент повторяется.
IV этап. Анализ
результатов моделирования
Заключительный этап
моделирования — анализ модели. По полученным расчетным данным проверяется,
насколько расчеты отвечают нашему представлению и целям моделирования. На этом
этапе определяются рекомендации по совершенствованию принятой модели и, если
возможно, объекта или процесса.
4. Метод математических
моделей
Если попытаться одной
фразой ответить на вопрос: ”Каким образом современная математика применяется к
изучению физических, астрономических, биологических, экономических,
гуманитарных и других явлений?”, то ответ будет таким: ”С помощью построения и
анализа математических моделей изучаемого явления”. Что же такое математическая
модель?
Под математической
моделью понимают систему математических соотношений — формул, уравнений
неравенств и т.д., отражающих существенные свойства объекта или процесса.
При построении
математических моделей далеко не всегда удается найти формулы, явно выражающие
искомые величины через исходные данные. В таких случаях используются
математические модели, позволяющие дать ответы той или иной степени точности.
Изучение явлений с
помощью математических моделей называется математическим моделированием. Схематически
процесс математического моделирования представлен в следующей таблице:
|
внешнего мира |
Его приближенное описание. Запись основных свойств и |
Решение математических задач, исследование решений |
Выводы, новые свойства изучаемого явления, прогнозы, |
Уточнение модели
Хорошо построенная
математическая модель обладает удивительным свойством: ее изучение дает новые,
неизвестные ранее знания об изученном объекте или явлении.
П р и м е р 1. В 1846
г. Французский астроном У.Ж.Ж.Леверье (1811-1877) открыл новую планету
Солнечной системы и назвал ее Нептуном. Открытие этой планеты было сделано
чисто математически, путем вычислений, так сказать, “на кончике пера”.
Анализируя созданную И.Кеплером и И.Ньютоном модель движения планет Солнечной
системы, ученые обнаружили, что фактическая траектория движения планеты Уран
отклонялась от теоретически вычисляемого движения. Ж.Леверье предположил, что
”возмутителем порядка” является неизвестная планета, которая воздействует на
планету Уран. Пользуясь моделью Солнечной системы, он определил массу и закон
движения новой планеты, так что все противоречия и движения планеты Уран были
сняты.
Немецкий астроном
И.Г.Галле в 1846 г. наблюдал новую планету в точно указанном Леверье месте.
Аналогичным методом,
благодаря использованию расхождения теоретически вычисленной траектории Нептуна
с наблюдаемой, в 1930 г. была открыта еще одна планета Солнечной системы,
названная Плутоном.
П р и м е р 2. Знаменитый
английский физик Дж. К. Максвелл (1831 — 1879), изучая построенную им
математическую модель классической электродинамики, из анализа уравнений модели
предсказал существование электромагнитных волн, которые позднее были
экспериментально обнаружены немецким физиком Г.Р.Герцем (1857 — 1894).
П р и м е р 3. Русский
ученый А.А.Фридман (1888 — 1925), анализируя уравнения общей теории относительности,
составленные А.Эйнштейном (1879 — 1955), в 1922
г. обнаружил, что кроме решений, не зависящих от времени, уравнения
А.Эйнштейна имеют еще и другие решения, которые от времени зависят. Это привело
к открытию того, что Вселенная расширяется и сжимается, т.е. пульсирует.
Представление о пульсировании Вселенной стало основой всей современной космологии.
Математические модели, с
помощью которых исследование явлений внешнего мира сводится к решению
математических задач, занимают ведущее место среди других методов исследования
и позволяют не только объяснить наблюдаемые явления, как это было, например, с
движением планеты Уран, но и заглянуть туда, где еще в принципе не могло быть
опытных, экспериментальных данных. Именно так было при проведении первых
атомных и водородных взрывов. И это еще не все. Существуют сферы человеческой
деятельности, где проведение экспериментов, получение экспериментальных
результатов принципиально не возможны!
Например, невозможно
экспериментировать над озоновым слоем Земли. Невозможно определить меру
антропогенного воздействия на ноосферу, достаточную для ее разрушения, —
неизвестно, найдется ли в этом случае на Земле место для человечества.
Развитие математического
аппарата и внедрение мощных современных компьютеров позволили математическому
моделированию, успешно зарекомендовавшему себя в технике, физике, астрономии и
космологии, проникнуть сегодня практически во все области человеческой
деятельности — в экономику и биологию, экологию и лингвистику, медицину и
психологию, историю, социологию и т.д. По мере усложнения объектов
исследования, роль математических моделей изучаемых явлений существенно
возрастает. Появляется целая иерархия математических моделей, каждая из которых
описывает изучаемое явление глубже, полнее, всестороннее.
5. Задачи по моделированию из различных предметных
областей
5.1 Экономика
Задача 1
Машиностроительный завод, реализуя
продукцию по договорным ценам, получил определенную выручку, затлатив на
производство некоторую сумму денег. Определить отношение чистой прибыли к вложенным
средствам.
Постановка задачи
Цель моделирования —
исследовать процесс производства и реализации продукции с целью получения
наибольшей чистой прибыли. Пользуясь экономическими формулами найти отношение
чистой прибыли к вложенным средствам.
Чистая прибыль — это
прибыль после уплаты налога. При расчете налога на прибыль необходимо учитывать
его зависимость от уровня рентабельности. Примем, если уровень рентабельности
не превышает 50%, то с прибыли предприятия взимается налог в 32%. Если же
уровень рентабельности превышает 50%, то с соответствующей суммы прибыли налог
взимается в размере 75%.
Объектом моделирования
является процесс производства и реализации некоторой продукции.
Разработка модели
Основными параметрами объекта
моделирования являются: выручка, себестоимость, прибыль, рентабельность, налог
с прибыли.
Исходные данные:
выручка B;
затраты (себестоимость) S.
Другие параметры найдем, используя
основные экономические зависимости. Значение прибыли определяется как разность
между выручкой и себестоимостью P=B-S.
Рентабельность r вычисляется по
формуле: .
Прибыль, соответствующая предельному
уровню рентабельности 50%, составляет 50% от себестоимости продукции S, т.е.
S*50/100=S/2, поэтому налог с прибыли N определяется следующим образом:
если r<=50, то
N=P*32/100 р., иначе N=S/2*32/100+(P-S/2)*75/100.
Чистая прибыль Рч=Р-N.
И, наконец, результат решения этой
задачи — отношение чистой прибыли к вложенным средствам q= Рч/S.
Так выглядит электронная таблица в
формате отображения формул:
|
A. |
B. |
|
|
1. |
Рентабельность производства |
|
|
2. |
Исходные данные |
|
|
3. |
Выручка (р.) |
|
|
4. |
Себестоимость (р.) |
|
|
5. |
||
|
6. |
Прибыль (р.) |
=B2-B3 |
|
7. |
Рентабельность (%) |
=B4/B3*100 |
|
8. |
Налог (р.) |
=ЕСЛИ(B7<=50;B6*0,32;B4/2*0,32+(B6-B4/2)*0,75) |
|
9. |
Чистая прибыль (р.) |
=B4-B6 |
|
10. |
Отношение чистой прибыли к |
=B7/B3 |
Компьютерный эксперимент
1.
Ввести в
компьютерную модель исходные данные.
Например: B=3000; S=2000.
2. Исследовать, как изменяется
отношение чистой прибыли к вложенным средствам, если менять только выручку,
оставляя постоянной себестоимость.
3. Исследовать, как изменяется
отношение чистой прибыли к вложенным средствам, если менять только
себестоимость, оставляя постоянной выручку.
4.
Как
измениться модель, если налог вычисляется следующим образом:
|
рентабельность |
<=30% |
от 30 до 70% |
>70% |
|
налог |
20% |
40% |
60% |
Изменится
только формула в ячейке B8.
|
8. |
Налог (р.) |
=ЕСЛИ(B7<=30; |
Анализ результатов
Полученная модель
позволяет в зависимости от рентабельности определять налог с прибыли,
автоматически пересчитывать размер чистой прибыли, находить отношение чистой
прибыли к вложенным средствам.
Проведенный компьютерный
эксперимент показывает, что отношение чистой прибыли к вложенным средствам
увеличивается при увеличении выручки и уменьшается при увеличении себестоимости
продукции.
Задача 2
Леспромхоз ведет заготовку деловой
древесины. Известен ее первоначальный объем, ежегодный естественный прирост, а
также годовой план заготовки. Какой объем деловой древесины на данной территории
будет через год, через 2 года и т.д. — до тех пор, пока этот объем не станет
меньше минимально допустимого значения.
Постановка задачи
Цель моделирования —
показать динамику изменения объема деловой древесины, определить время до
которого эти изменения будут происходить.
Объектом моделирования
является процесс ежегодного изменения количества деловой древесины.
Количество деловой
древесины в каждый следующий год вычисляется по количеству древесины
предыдущего года до тех пор пока этот объем не станет меньше минимально
допустимого значения (23000 м3).
Разработка модели
Допустим, исходные данные принимают
следующие значения:
первоначальный объем V (м3)
— 120000;
ежегодный прирост p (%)
— 5,5;
годовой план заготовки R
(м3) — 9500;
миним. допустимое значение
(м3) — 23000.
Результатом является объем древесины через 1, 2, 3, … года.
Объем древесины в каждом следующем
году вычисляется по формуле:
Vi+1 = Vi + Vi*p/100-R
Так выглядит электронная таблица в
режиме отображения формул:
|
A. |
B. |
|
|
1. |
Задача о заготовке древесины |
|
|
2. |
Исходные |
|
|
3. |
Первоначальный |
120000 |
|
4. |
Ежегодный |
5,5 |
|
5. |
Годовой план |
9500 |
|
6. |
Миним. |
23000 |
|
7. |
Объем древесины (м3) |
|
|
8. |
Через 1 год |
=B3+B3*B4/100-B5 |
|
9. |
2 |
=B8+B8*$B$4/100-$B$5 |
|
10. |
3 |
=B9+B9*$B$4/100-$B$5 |
Формулу
копируем.
….
|
27. |
20 |
=B26+B26*$B$4/100-$B$5 |
Вычислительный эксперимент
1. Введите значения исходных
данных и проследите динамику ежегодного изменения количества древесины,
построив график.
2. Разработайте план
использования древесины, так, чтобы данный процесс продолжался в течение 25
лет. (Изменяя значения R.)
|
A. |
B. |
|
|
1. |
Задача о заготовке древесины |
|
|
2. |
Исходные |
|
|
3. |
Первоначальный |
120000 |
|
4. |
Ежегодный |
5,5 |
|
5. |
Годовой план |
9500 |
|
6. |
Миним. |
23000 |
|
7. |
Объем древесины (м3) |
|
|
8. |
Через 1 год |
117100 |
|
9. |
2 |
114041 |
|
10. |
3 |
110813 |
|
11. |
4 |
107407 |
|
12. |
5 |
103815 |
|
13. |
6 |
100025 |
|
14. |
7 |
96026 |
|
15. |
8 |
91807 |
|
16. |
9 |
87357 |
|
17. |
10 |
82661 |
|
18. |
11 |
77708 |
|
19. |
12 |
72482 |
|
20. |
13 |
66968 |
|
21. |
14 |
61152 |
|
22. |
15 |
55015 |
|
23. |
16 |
48541 |
|
24. |
17 |
41710 |
|
25. |
18 |
34505 |
|
26. |
19 |
26902 |
|
27. |
20 |
18882 |
Анализ результатов
В результате эксперимента, видим, что
процесс ежегодного изменения количества деловой древесины будет происходить в
течение 19 лет (до тех пор, пока ее объем не будет меньше минимально
допустимого значения V<23000 м3).
Задача 3
Фирма выпускает прогулочные и
спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600
прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда
проверяется на двух стендах А и В. Каждый прогулочный велосипед проверяется 0,3
ч на стенде А и 0,1 ч — на стенде В, а каждый спортивный велосипед проверяется
0,4 ч на стенде А и 0,3 ч — на стенде В. По технологическим причинам стенд А не
может работать более 240 ч в месяц, а стенд В — более 120 ч в месяц. Реализация
каждого прогулочного велосипеда приносит фирме доход в 50 руб., а каждого
спортивного — 90 руб. Сколько прогулочных и сколько спортивных велосипедов
должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей? [3]
Постановка задачи
Цель моделирования —
составить такой производственный план, который обеспечит максимальную прибыль.
Объект моделирования —
процесс производства и реализации велосипедов
Разработка модели
Исходные данные:
x — количество прогулочных
велосипедов, выпускаемых ежемесячно фирмой;
y — количество спортивных
велосипедов.
Занятость стенда А составляет
0,3х+0,4y, что не должно превышать 240 ч.
Занятость стенда В составляет
0,1х+0,3y, что не должно превышать 120 ч.
Прибыль фирмы составляет S=50х+90у
(руб.)
Итак, мы пришли к следующей модели:
необходимо найти целые значения х и у, удовлетворяющие системе неравенств.
0,3х+0,4y £ 240 О1
0,1х+0,3y £ 120 О2
0 £ x £ 600 О3
0 £ y £ 300 О4
и такие, чтобы прибыль
S=50х+90у была наибольшей.
Таким образом, задача нахождения
наилучшего производственного плана свелась к задаче определения максимального
значения функции S(x,y) при заданных ограничениях. (Такие задачи называются
задачами условной оптимизации)
Электронная таблица в режиме
отображения формул выглядит следующим образом:
|
A. |
B. |
|
|
1. |
Задача планирования |
|
|
2. |
Исходные данные |
|
|
3. |
х |
|
|
4. |
у |
|
|
5. |
Ограничения |
|
|
6. |
=0,3*B3+0,4*B4 |
|
|
7. |
=0,1*B3+0,3*B4 |
|
|
8. |
Результат |
Прибыль |
|
9. |
=50*B3+90*B4 |
Компьютерный эксперимент
В среде электронных таблиц существует
возможность автоматического поиска максимального (минимального) значения
функции. Для этого:
1. введите значения исходных
данных в ячейки В3 и В4 — любые целые числа, учитывая ограничения О3 и О4;
2. выберите команду
[Сервис-Поиск решения…];
3. в появившемся диалоговом окне
введите адрес ячейки, где содержится формула (функция для оптимизации);
4. укажите цель оптимизации
(максимальное значение);
5. введите диапазон ячеек,
посредством изменения значений которых будет достигнуто оптимальное значение
целевой функции;
6. введите все ограничения.
Результат выполнения выглядит так:
|
A. |
B. |
|
|
1. |
Задача планирования |
|
|
2. |
Исходные данные |
|
|
3. |
х |
480 |
|
4. |
у |
240 |
|
5. |
Ограничения |
|
|
6. |
240 |
|
|
7. |
120 |
|
|
8. |
Результат |
Прибыль |
|
9. |
45600 |
Анализ результатов
Значения, находящиеся в ячейках В3,
В4 являются оптимальными для получения максимальной прибыли.
Продолжите компьютерный эксперимент
1. Что будет, если по
технологическим причинам возможность работы стенда В уменьшится до 100 ч. в
месяц.
2. Что будет, если доход от
реализации каждого прогулочного велосипеда увеличится до 60 руб.
3. Что будет, если проверку
спортивного велосипеда на стенде А ограничить до 0,3ч
Задача 4
В городе имеются два склада муки и
два хлебозавода. Ежедневно с первого склада вывозится 50 т муки, со второго —
70 т. Эта мука доставляется на хлебозаводы, причем первый получает 40 т, второй
— 80 т. Допустим, что перевозка одной тонны муки с первого склада на первый
завод составляет 120 руб., с первого склада на второй завод — 160 руб., со
второго склада на первый завод — 80 руб. и со второго склада на второй завод —
100 руб. Как нужно спланировать перевозки, чтобы их общая стоимость за один
день была минимальной? [13]
Задача 5
Для полива трех полей колхоз
использует насосную станцию. На первое поле требуется подать не менее 200
кубометров воды в сутки, на второе — не менее 300, на третье — не менее 350.
Колхоз имеет право расходовать не более 1200 кубометров воды в сутки. Стоимость
подачи одного кубометра воды на первое поле — 1570 руб., на второе поле — 1720
руб., на третье — 1930 руб. Сколько кубометров воды надо подать на каждое поле,
чтобы затраты были наименьшими? [13]
5.2 Астрономия
Задача 1
Определите скорость движения планет
по орбите. Для этого составьте компьютерную модель Солнечной системы.
Постановка задачи
Цель моделирования —
определить скорость движения планет по орбите.
Объект моделирования — Солнечная
система, элементами которой являются планеты. Внутреннее строение планет в
расчет не принимается. Будем рассматривать планеты как элементы, обладающие
следующими характеристиками:
название;
R — удаленность от Солнца (в
астрономических единицах;
астроном. ед. — среднее
расстояние от Земли до Солнца);
t — период обращения вокруг Солнца (в
годах);
V — скорость движения по орбите
(астр.ед./год), предполагая, что планеты
движутся вокруг Солнца по
окружностям с постоянной скоростью.
Разработка модели
Исходные данные:
R — расстояние от планеты до Солнца,
t — период обращения планеты вокруг
Солнца.
Т.к. планеты движутся вокруг Солнца
по окружностям с постоянной скоростью, значение скорости найдем по формуле:
, (1)
Данную модель реализуем в среде
электронных таблиц. Диапазон ячеек D3:D11 содержат формулы. Так выглядит
таблица в формате отображения формул:
|
A. |
B. |
C. |
D. |
|
|
1. |
Модель Солнечной системы |
|||
|
2. |
Планета |
Расстояние от Солнца (астр.ед.) |
Период обращения вокруг (год) |
Скорость движения по орбите (астр.ед./год) |
|
3. |
Меркурий |
0,387 |
0,24 |
=2*ПИ()*B3/C3 |
|
4. |
Венера |
0,723 |
0,62 |
=2* ПИ()*B4/C4 |
|
5. |
Земля |
1,000 |
1,00 |
=2* ПИ()*B5/C5 |
|
6. |
Марс |
1,524 |
1,88 |
=2* ПИ()*B6/C6 |
|
7. |
Юпитер |
5,203 |
11,86 |
=2* ПИ()*B7/C7 |
|
8. |
Сатурн |
9,539 |
29,46 |
=2* ПИ()*B8/C8 |
|
9. |
Уран |
19,18 |
84,02 |
=2* ПИ()*B9/C9 |
|
10. |
Нептун |
30,07 |
164,79 |
=2* ПИ()*B10/C10 |
|
11. |
Плутон |
39,44 |
247,7 |
=2* ПИ()*B11/C11 |
Компьютерный эксперимент
1. Выполните расчеты по формулам.
|
A. |
B. |
C. |
D. |
|
|
1. |
Модель Солнечной системы |
|||
|
2. |
Планета |
Расстояние от Солнца (астр.ед.) |
Период обращения вокруг Солнца (год) |
Скорость движения по орбите (астр.ед./год) |
|
3. |
Меркурий |
0,387 |
0,24 |
10,132 |
|
4. |
Венера |
0,723 |
0,62 |
7,327 |
|
5. |
Земля |
1,000 |
1,00 |
6,283 |
|
6. |
Марс |
1,524 |
1,88 |
5,093 |
|
7. |
Юпитер |
5,203 |
11,86 |
2,756 |
|
8. |
Сатурн |
9,539 |
29,46 |
2,034 |
|
9. |
Уран |
19,18 |
84,02 |
1,434 |
|
10. |
Нептун |
30,07 |
164,79 |
1,147 |
|
11. |
Плутон |
39,44 |
247,7 |
1,000 |
2. Вычислите скорость движения
планет по орбите в км/ч и постройте график в виде столбчатой диаграммы для
скоростей.
В данной модели формула (1)
будет иметь вид:
(1 астрономическая единица = 150 млн.
км.)

Анализ результатов
1. Проанализируйте результаты
расчетов. Можно ли утверждать, что планеты, находящиеся ближе к Солнцу имеют
большую скорость движения по орбите?
2. Представленная модель Солнечной
системы является статической. При построении этой модели мы пренебрегали
изменениями расстояния от планет до Солнца во время их движения по орбите.
Чтобы знать, какая планета дальше и каковы примерные соотношения между
расстояниями, этой информации вполне достаточно. Если же мы хотим определить
расстояние между Землей и Марсом, то пренебрегать временными изменениями
нельзя, и здесь придется использовать уже динамическую модель.
5.3 Физика
Задача 1
При подъеме в гору “заглох” мотор у
машины. Остановится ли машина на горе или же она будет скатываться вниз.
Постановка задачи
Цель моделирования —
пользуясь знакомыми физическими законами движения тела под действием нескольких
сил, исследовать данную ситуацию при различных значениях исходных данных.
Объектом моделирования
является система, состоящая из двух компонентов: машина и дорога.
Разработка модели
Необходимо рассмотреть силы,
действующие на машину в данной системе.


N
Fтр
 |
a
a
x
Fт a
_ _
На машину действуют три силы: сила
тяжести Fт=mg, сила трения Fтр и сила реакции опоры N.
По I закону Ньютона тело находится в
состоянии покоя или движется прямолинейно и равномерно, если равнодействующая
всех приложенных к телу сил равна нулю, т.е. F=0.
_ _ _
II закон Ньютона в векторной форме
записывается так: Fт+N+Fтр=0.
Запишем его в скалярной форме, для
этого рассмотрим проекции сил
|
на ось x: |
на ось y: |
|
(Fт)х=m*g*sina; Nx=0; (Fтр)х=-Fтр Уравнение: m*g*sina-Fтр=0 |
(Fт)y=-m*g*cosa; Ny=N; (Fтр)y=0 Уравнение: -m*g*cosa+N=0 |
Fтр=
m*g*sina
N= m*g*cosa
Так как Fтр=m*N, то m*g*sina=m* m*g*cosa
sina=m* cosa
tga=m
Итак, если tga>m, то машина стоит на месте, в
противном случае она будет скатываться вниз.
Исходными данными
являются:
m — коэффициент трения, 0<m<1;
a — угол наклона, 0<a<90. Так как в электронной
таблице Excel функция tg находит значение tg от угла, выраженного в радианах,
то при записи формулы предусмотрим перевод градусной меры угла в радианную.
Так выглядит таблица в формате
отображения формул:
|
A. |
B. |
|
|
1. |
Задача о дорожном происшествии |
|
|
2. |
Исходные данные: |
|
|
3. |
m |
|
|
4. |
a (град.) |
|
|
5. |
Результат |
=ЕСЛИ(TAN(B4*ПИ()/180)> |
Компьютерный эксперимент
1.
Введите в
компьютерную модель исходные данные.
(Например: m=0,5; a=12)
2. Найти такой коэффициент
трения при котором машина поедет с горы (при данном угле).
3. Найти такой угол при котором
машина будет стоять на горе (при данном коэффициенте трения).
4. Каков будет результат, если
силой трения пренебречь.
Анализ результатов
Данная компьютерная
модель позволяет проводить вычислительный эксперимент, взамен физическому.
Меняя значения исходных данных, можно видеть все изменения происходящие в
системе.
Интересно заметить, что в
построенной модели результат не зависит ни от массы автомобиля, ни от ускорения
свободного падения.
Задача 2
На заданном
расстоянии от пушки находится стена. Известны угол наклона пушки и начальная
скорость снаряда. Попадет ли снаряд в стену?[5]
Постановка задачи
Цель моделирования —
пользуясь знакомыми физическими законами движения тела, брошенного под углом к
горизонту, исследовать данную ситуацию при различных значениях исходных данных.
Объектом моделирования
является система, состоящая из двух компонентов: снаряд, брошенный под углом к
горизонту, и стена. Подобрать начальную скорость и угол бросания так, чтобы
брошенное тело (снаряд) достигло цели.
Разработка модели
Снаряд считаем материальной точкой.
Сопротивлением воздуха и размерами
пушки пренебрегаем.
Исходные данные:
a — угол наклона пушки, 0<a<90 градусов;
V — начальная скорость снаряда (м/с),
0<V<1000;
S — расстояние от пушки до стены (м),
S>0;
h — высота стены (м), h>0.
Результатом является одно из
сообщений: “Снаряд попал в стену”, “Снаряд не попал в стену”.
Для определения попадания
снаряда в стену надо найти высоту L снаряда на расстоянии S от пушки: ведь
попадание снаряда в стену означает, что 0<L<h. Перемещение снаряда по
горизонтали и вертикали:
x=V*t*cosa
y=V*t*sina-g*t2/2, где
g-ускорение свободного падения (9,8 м/с2).
Определим, сколько времени
понадобится снаряду, чтобы преодолеть расстояние S:
t=S/( V*cosa).
Подставив это значение t в выражение
для y, получим значение:
L=S*tga-g*S2/(2*V2*cos2a).
Если L<0, то снаряд до стены не
долетит. Если L>h, то снаряд перелетит через стену.
Так выглядит электронная таблица в
формате отображения формул:
|
A. |
B. |
|
|
1. |
Полет снаряда |
|
|
2. |
Исходные данные: |
|
|
3. |
a (град.) |
35 |
|
4. |
V |
180 |
|
5. |
S |
3000 |
|
6. |
h |
6 |
|
7. |
g |
9,8 |
|
8. |
a (радианы) |
=B3*ПИ()/180 |
|
9. |
L |
=B5*TAN(B8)-B7*B5^2/(2*B4^2*(COS(B8))^2) |
|
10. |
Результат |
=ЕСЛИ(И(B9>0;B9<B6);»Попал»;»Не |
Компьютерный эксперимент
1.
Введите
значения исходных данных:
Например: a=35; V=180; S=3000; h=6; g=9.8 и проанализируйте результат.
(Результат “Не попал”)
2.
Найти
такой угол наклона пушки, не изменяя другие параметры системы, при котором
снаряд попадет в цель. (Результат a=32.6; a=32.7)
3.
Найти
такую скорость снаряда, не изменяя другие параметры системы, при котором снаряд
попадет в цель. (Результат V=177)
4. Усовершенствуйте модель таким
образом, чтобы результатом являлось одно из сообщений: “Снаряд попал в стену”,
“Недолет”, “Перелет”.
Анализ результатов
Данная компьютерная
модель позволяет проводить вычислительный эксперимент, взамен физическому.
Меняя значения исходных данных, можно видеть все изменения происходящие в
системе, производить расчет на поражение цели в зависимости от угла наклона
пушки и скорости снаряда.
Задача 3
Две моторные лодки равномерно
двигались по реке в направлении к озеру, в которое река впадает. Поравнявшись,
они начали двигаться равноускоренно. Какая из лодок раньше дойдет до озера? [11]
5.4 Экология
Задача 1
Представьте себе, что на Земле
останется только один источник пресной воды — озеро Байкал. На сколько лет
Байкал обеспечит население всего мира водой?
Постановка задачи
Цель моделирования —
определить количество лет, в течение которых Байкал обеспечит население всего
мира водой, исследовать построенную модель.
Объектом моделирования
является система, состоящая из двух компонентов: озеро Байкал и население
Земли.
Зная количество воды в
Байкале, численность населения Земли и потребляемость воды на 1 человека, можно
найти на сколько лет ее хватит. При составлении этой модели мы не учитываем
возможные изменения климатических условий. Мы также считаем постоянными численность
населения Земли и потребляемость воды на 1 чел. в день. (Человечество
потребляет на свои нужды огромное количество пресной воды. Основными ее
потребителями являются промышленность, сельское и коммунально-бытовое
хозяйство. Объем потребляемой воды зависит от уровня жизни, составляя от 3 до 700
л на одного человека.)
Разработка модели
Для построения
математической модели определим исходные данные. Обозначим:
V — объем озера Байкал 23000 км3;
N — население Земли 6 млрд. чел.;
p — потребление воды в день на 1
человека (в среднем) 300 л.
Так как 1л. = 1 дм3 воды,
необходимо выполнить перевод V воды озера из км3 в дм3. V
(км3) = V * 109 (м3) = V * 1012 (дм3)
Результат — количество лет, за
которое население Земли использует воды Байкала, обозначим g. Итак,
g=(V*1000000000000)/(N*p*365)
Так выглядит электронная таблица в
режиме отображения формул:
|
A. |
B. |
|
|
1. |
Задача об использовании вод Байкала |
|
|
2. |
Исходные данные |
|
|
3. |
V(км3) |
|
|
4. |
N (чел) |
|
|
5. |
p (л) |
|
|
6. |
g (год) |
=(B3*1000000000000)/(B4*B5*365) |
Компьютерный эксперимент
1.
Введите в
компьютерную модель исходные данные.
|
A. |
B. |
|
|
1. |
Задача об использовании вод Байкала |
|
|
2. |
Исходные данные |
|
|
3. |
V(км3) |
23000 |
|
4. |
N (чел) |
6000000000 |
|
5. |
p (л) |
300 |
|
6. |
g (год) |
35 |
2. Сколько лет можно будет
пользоваться водами Байкала, если потребляемость воды увеличится до 400
литров на человека?
3. Сколько лет можно будет
пользоваться водами Байкала, если население Земли уменьшится до 5,7 млрд. чел.?
Анализ результатов
Построенная модель позволяет
прогнозировать время использования вод Байкала с учетом потребляемости воды на 1
человека, изменения численности населения всего мира. Данную модель можно
уточнить, учитывая изменения климатических условий.
Задача 2
Известны ежегодные показатели
рождаемости и смертности некоторой популяции. Рассчитайте, до какого возраста
могут дожить особи одного поколения.
Постановка задачи
Цель моделирования —
исследовать изменение численности поколения популяции в зависимости от времени,
определить возраст до которого могут дожить особи одного поколения популяции.
Объектом моделирования
является процесс ежегодного изменения количества одного поколения популяции,
который зависит от рождаемости популяции и ее смертности.
Разработка модели
Так как ежегодная рождаемость
популяции соответствует количеству особей одного поколения в популяции, то
исходными данными являются:
x — количество особей в 1 год;
p — ежегодная смертность (%).
Численность популяции в каждом
следующем году рассчитывается по формуле: xi+1=xi — xi*p/100.
Расчет производим до тех пор, пока значение xi не станет <1.
Так выглядит электронная таблица в
режиме отображения формул:
|
A. |
B. |
|
|
1. |
Задача о прогнозировании численности популяции |
|
|
2. |
Исходные данные |
|
|
3. |
смертность (%) |
|
|
4. |
рождаемость |
|
|
5. |
1 год |
B4 |
|
6. |
2 год |
=B5-B5*$B$3/100 |
|
7. |
3 год |
=B6-B6*$B$3/100 |
Формулу копируем.
Компьютерный эксперимент
1. Введите в компьютерную модель
исходные данные p, x (например p=30, x=1000) и проиллюстрируйте зависимость
численности популяции от времени на графике.
Результаты вычислений выглядят
следующим образом:
|
A. |
B. |
|
|
1. |
Задача о прогнозировании численности популяции |
|
|
2. |
% смертности |
30 |
|
3. |
1 год |
1000 |
|
4. |
2 год |
700 |
|
5. |
3 год |
490 |
|
6. |
4 год |
343 |
|
7. |
5 год |
240,1 |
|
8. |
6 год |
168,1 |
|
9. |
7 год |
117,6 |
|
10. |
8 год |
82,4 |
|
11. |
9 год |
57,6 |
|
12. |
10 год |
40,4 |
|
13. |
11 год |
28,2 |
|
14. |
12 год |
19,8 |
|
15. |
13 год |
13,8 |
|
16. |
14 год |
9,7 |
|
17. |
15 год |
6,8 |
|
18. |
16 год |
4,7 |
|
19. |
17 год |
3,3 |
|
20. |
18 год |
2,3 |
|
21. |
19 год |
1,6 |
|
22. |
20 год |
1,1 |
|
23. |
21 год |
0,8 |
|
24. |
22 год |
0,6 |
Анализ результатов
Результаты эксперимента показывают,
что особи одного поколения данной популяции могут дожить до 20 лет.
Продолжите компьютерный
эксперимент
1.
Какова
должна быть рождаемость популяции, чтобы особи одного поколения доживали до 25
лет при той же смертности. (Результат: x=5000)
2.
Каков
должен быть показатель смертности, чтобы при той же рождаемости (x=1000) особи
одного поколения доживали до 35 лет. (Результат: p=18)
Анализ результатов
Модель показывает, что количество
особей одного поколения всегда уменьшается и стремится к нулю, т.е. приводит к
гибели данного поколения популяции.
Задача 3
Определите, как будет меняться
плотность популяции голубя в течение 5 ближайших лет, если предварительные
наблюдения позволили установить, что ее плотность составляет 130 особей/га. За
период размножения (у голубя раз в году) из одной кладки яиц в среднем выживает
1,3 детенышей. Смертность голубя постоянна, в среднем за год погибает 27% особей.
При увеличении плотности популяции до 300 особей/га и выше смертность составляет
50%.
Постановка задачи
Цель моделирования —
исследовать процесс изменения плотности популяции с учетом ее рождаемости и
смертности.
Объект моделирования —
процесс изменения плотности популяции.
Плотность популяции — это
число особей, приходящаяся на единицу площади или объема жизненного
пространства. Измерением плотности пользуются в тех случаях, когда важнее знать
не конкретную величину популяции в тот или иной момент времени, а ее динамику,
то есть ход изменений численности во времени.
Рождаемость характеризует
способность популяции к увеличению численности за счет размножения особей.
Показатель рождаемости — это число новых особей (также яиц, семян), родившихся
(вылупившихся, отложенных) в популяции за определенный промежуток времени.
Смертность — это
показатель, противоположный рождаемости. Смертность, как и рождаемость,
выражается числом особей, погибших за данный период времени, но чаще в виде
относительной или удельной величины. Такой величиной может быть процент особей,
погибших в единичный отрезок времени.
Разработка модели
Известно начальное значение
плотности популяции.
Плотность популяции к
началу следующего года есть ее плотность к началу данного года плюс рождаемость
и минус смертность.
Рождаемость зависит от
плотности самок и плодовитости. Предположим, что в популяции равное количество
самок и самцов, то, зная плотность популяции, можно определить плотность самок
(плотность самок=1/2 плотности популяции). Плодовитость известна по условию
задачи. Число особей, погибших за год — это процент (смертности) от общей
плотности популяции. Смертность популяции зависит так же и от величины
плотности популяции.
Исходные данные:
плотность популяции (P) — 130 особей/га;
плодовитость — 1,3 детеныша в год.
Остальные показатели рассчитываются
следующим образом:
плотность самок = P/2;
рождаемость (R) = плотность самок *
плодовитость;
смертность (S) = P * удельная
смертность;
где удельная
смертность голубя = 27% в год, если P<300,
в противном
случае она равна 50%;
Плотность популяции в каждом следующем году рассчитывается по
формуле:
Pi+1 = Pi + Ri
— Si.
2. По результатам расчетов,
выделив диапазон ячеек B10:E40, постройте общую диаграмму для трех биоритмов.
Анализ результатов
1. Проанализировав диаграмму,
выберите неблагоприятные дни для участия в спортивных соревнованиях.
2. Выберете дни, когда учебная
деятельность будет наиболее (наименее) успешной.
3. Выберете день для посещения
театра.
4. Определите, есть ли у вас
дважды (трижды) критические дни в этом месяце?
5. Как вы думаете, что будет
показывать график, если сложить все три биоритма? Можно ли по нему что-либо
определить?
6. Сторонники селенобиологической
гипотезы (селенобиология исследует влияние Луны на земные организмы)
утверждают, что периоды многодневных ритмов, зависящие от Луны, не должны были
бы представлять собой точно определенные отрезки времени. По их мнению, Луна
диктует некоторый ритм, который не является таким уж регулярным. В связи с этой
гипотезой продолжительность периода такова: физический период — 23,688437
суток, эмоциональный период — 28,426124 суток и интеллектуальный — 33,163812
суток. [8]
Измените модель биоритмов человека в
соответствии с данной теорией.
5.6
География
Задача 1
Какова будет численность населения
России в 2010 году? [16]
Постановка задачи
Объектом моделирования является
процесс изменения численности населения в зависимости от времени. На этот
процесс влияют многие факторы: экология, состояние медицинского обслуживания,
экономическая ситуация в стране, международная обстановка и многое другое.
Обобщив демографические данные, ученые вывели функцию, выражающую зависимость
численности населения от времени:
f(t)=
где коэффициента a и b для каждого
государства свои,
e основание натурального логарифма.
Эта формула лишь приближенно отражает
реальность. Для нахождения значений коэффициентов a и b можно воспользоваться
статистическим справочником. Взяв из справочника значения f(t) (численность
населения в момент времени t), можно приближенно подобрать a и b так, чтобы
теоретические значения f(t), вычисляемые по формуле, не сильно отличались от
фактических данных в справочнике.
6. Заключение
Тема “Моделирование”
является очень важной в курсе информатики, так как дает учащимся возможность
провести исследовательскую работу, выполнить анализ полученных результатов,
обратить внимание на конечность алгоритма, оценить точность модели, столкнуться
с погрешностью приближенных вычислений, увидеть взаимосвязь различных наук и
дисциплин, получить удовлетворение от выполненной работы.
Использование компьютера
как инструмента учебной деятельности дает возможность переосмыслить
традиционные подходы к изучению многих вопросов естественнонаучных дисциплин,
усилить экспериментальную деятельность учащихся, приблизить процесс обучения к
реальному процессу познания, основанному на технологии моделирования.
Решение задач из
различных областей деятельности человека на компьютере базируются не только на
знаниях учащимися технологии моделирования, но, естественно, и на знаниях
данной предметной области. В связи с этим, предложенные уроки по моделированию
целесообразнее проводить после изучения учащимися материала на
общеобразовательном предмете, учителю информатики необходимо сотрудничать с
учителями разных образовательных областей. Известен опыт проведения бинарных
уроков, т.е. уроков, проводимых учителем информатики совместно с
учителем-предметником.
Предложенные задачи можно
использовать при изучении курса информатики в 9-11 классах.
7. Список литературы
1.
Извозчиков
В.А., Бережной Л.Н., Слуцкий А.М. Межпредметные связи и информатика
(методические рекомендации) — Санкт-Петербург, 1992.
2.
Машбиц
Е.И. Психолого-педагогические проблемы компьютеризации обучения — М.,
Педагогика, 1988.
3.
Симонов
А.С. Экономика на уроках математики. — М., Школа-Пресс, 1999.
4.
Учебник
“Информатика. 9 класс.” под ред. Макаровой Н.В. — Санкт-Петербург, ПИТЕР КОМ,
1999.
5.
Гейн
А.Г., Житомирский В.Г. и др. “Основы информатики и вычислительной техники”
пробный учебник для 10-11 классов средней школы — М., Просвещение, 1992.
6.
Семакин
И., Залогова Л., Русаков С., Шестакова Л. «Информатика” учебник по
базовому курсу — М., ООО Лаборатория Базовых Знаний, 1998.
7.
Гисин
В.Б., Коновалов В.П., “Программно-методический комплекс № 4 по курсу
информатики. Элементы компьютерного моделирования” — М., АО КУДИЦ, 1994.
8.
Дагене
В.А., Григас Г.К., Аугутис К.Ф. “100 задач по программированию”, книга для
учащихся, пер. с лит. — М., Просвещение, 1993.
9.
Криксунов
Е.А., Пасечник В.В., Сидорин А.П. “Экология 9 класс”, учебник для
общеобразовательных учебных заведений — М., Дрофа, 1995.
10.Криксунов Е.А., Королев Ю.Б.,
Пасечник В.В., “Экология 9 класс”, рабочая тетрадь — М., Дрофа, 1996.
11. Кикоин И.К., Кикоин А.К. “Физика. 9
класс”, учебник — М., Просвещение,1990.
12.Петросян В.Г., Газарян Р.М.
Межпредметные связи и решение задач//
Информатика и образование. 1998 №8.
13.Островская Е.М. Моделирование на
компьютере// Информатика и образование. 1998 №7, 8; 1999 №1.
14.Пономарева Е.А. Основные
закономерности развития мышления// Информатика и образование. 1999 №8.
15.Бешенков С.А., Лыскова В.Ю., Матвеева
Н.В., Ракитина Е.А. Формализация и моделирование// Информатика и образование.
1999 №6.
16.Гусева О.Л., Миронова Н.Н. Excel для
Windows. Практические работы// Информатика и образование. 1996 №5.
8. Приложение
Рентабельность и вычисление налогов на прибыль
Любое производство не может
существовать, если оно не получает прибыль. Прибыль является важнейшим показателем
финансовой деятельности предприятия. В экономике рассматривают различные формы
прибыли. Под прибылью будем понимать разность между выручкой и себестоимостью.
Выручкой называются доходы от продажи товаров, а себестоимостью — затраты на их
производство и продажу. Обычно прибыль выражают в денежных единицах.
Обозначим выручку от
реализации продукции через B, себестоимость — через S. Тогда
прибыль P будет равна
P = B — S.
Однако величина прибыли
от продажи некоторого продукта безотносительно к тому, сколько затрачено на его
производство, мало что говорит.
На рисунке показаны три
фирмы, имеющие одинаковый доход D, но совершенно различные затраты, этот
доход обеспечивавшие.
фирма I
фирма II фирма III
Затраты З1
фирмы I для получения дохода D достаточно велики, у фирмы II — затраты З2
меньше, чем у фирмы I, а у фирмы III они меньше всех. Очевидно, что фирма III
работает более эффективно, чем фирмы I и II.
Понятие рентабельности
(от нем. rentabel — доходный) и является одним из способов измерения
эффективности деятельности фирмы, отрасли и т.д. за определенный промежуток
времени.
Показателем
рентабельности, или рентабельностью r называют отношение прибыли P
предприятия или фирмы за некоторый промежуток времени к полным затратам
(себестоимости) S за этот же период. Поэтому
или
(1)
Если дробь то это значит, что P>S, т.е.
предприятие работает эффективно, окупает не только все издержки производства,
но и получает определенную прибыль на каждый затраченный рубль.
Если же дробь то это говорит о неэффективности фирмы и
необходимости повышения ее рентабельности путем снижения себестоимости,
повышения качества, уменьшения потерь и т.д. Рисунок показывает, что наибольшая
рентабельность у фирмы III, несколько меньше она у фирмы II, и совсем небольшая
у фирмы I.
Как правило,
рентабельность выражается в процентах:
(2)
Изменение показателя
рентабельности характеризует динамику развития производства, прибыльность или
убыточность хозяйственной деятельности фирм, отраслей и т.д. Еще несколько лет
назад уровень рентабельности играл важнейшую роль при определении налога с
прибыли предприятия или фирм, потому что ставка налога на прибыль существенно
зависела от рентабельности. Дело в том, что в условиях дефицита продукции и
отсутствия конкурентности, некоторые предприятия, особенно
предприятия-монополисты, имели возможность установить непомерно высокие цены на
свою продукцию и тем самым значительно увеличить прибыль без крупных вложений в
производство. Увеличение прибыли вело к повышению рентабельности. Чтобы цены не
росли непомерно, государство принимало различные меры и в том числе установило
так называемый предельный уровень рентабельности. Если рентабельность продукции
предприятия превышала установленный предельный уровень, то налог взимался по
повышенной ставке. Так, в 1991-1993 гг. в России был установлен предельный
уровень рентабельности в 50%. Если уровень рентабельности не превышал этого
значения, то с прибыли предприятия взимался налог в 32%. Если же уровень
рентабельности превышал 50%, то с соответствующей суммы прибыли налог взимался
в размере 75%. (Прибыль, соответствующая предельному уровню рентабельности 50%,
составляет 50% от себестоимости продукции S, т.е. S*50/100=S/2.)
Соотношения , или
позволяют определить любую из величин r, P
или S, если известны две другие.

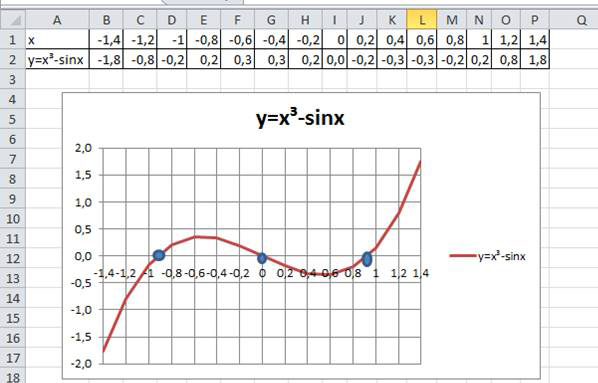
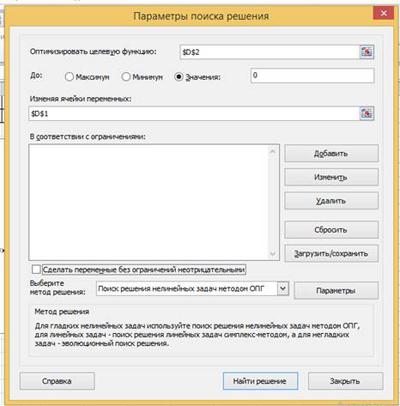
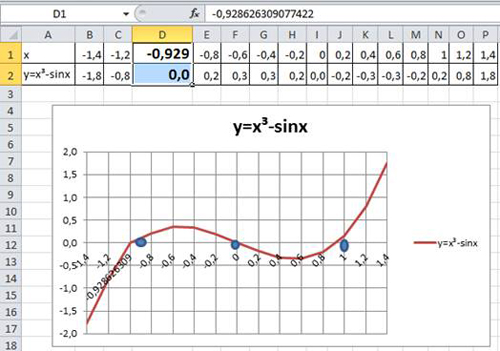
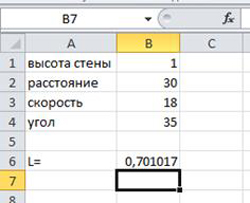
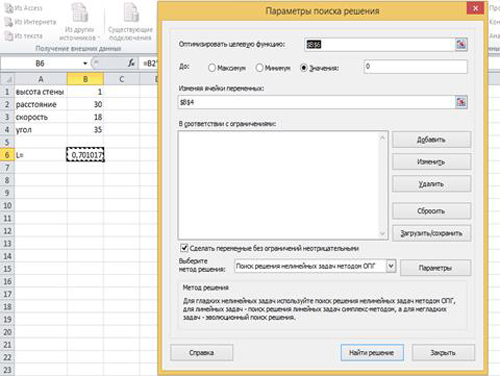
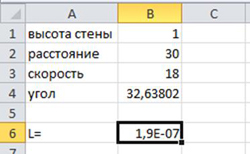
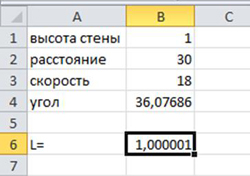
 цвет заливки , а затем в группе Цвета темы или Стандартные цвета выберитенужный цвет.
цвет заливки , а затем в группе Цвета темы или Стандартные цвета выберитенужный цвет.
 в правом нижнем углу области выделения.
в правом нижнем углу области выделения.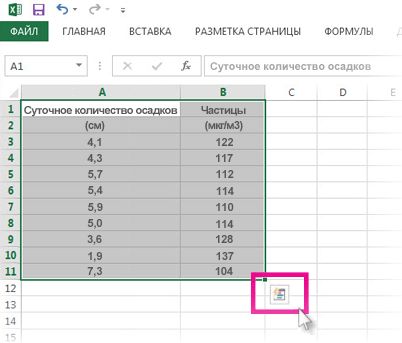
 в заглавной части столбца.
в заглавной части столбца.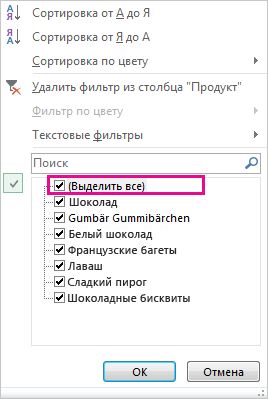
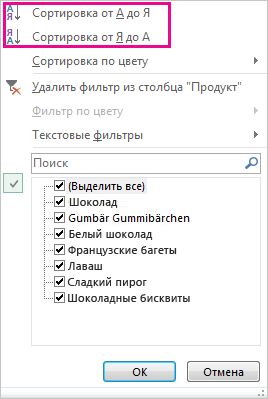
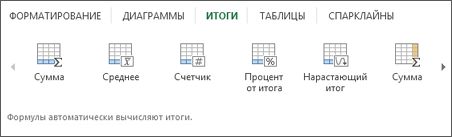
 в правом нижнем углу области выделения.
в правом нижнем углу области выделения.


 , чтобы выполнить сортировку по возрастанию (от А до Я или от наименьшего числа к наибольшему).
, чтобы выполнить сортировку по возрастанию (от А до Я или от наименьшего числа к наибольшему). , чтобы выполнить сортировку по убытию (от Я до А или от наибольшего числа к наименьшему).
, чтобы выполнить сортировку по убытию (от Я до А или от наибольшего числа к наименьшему).