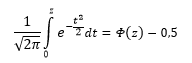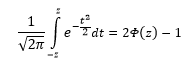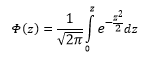Из данной статьи вы узнаете:
-
Что такое доверительный интервал?
-
Как его самостоятельно рассчитать в Excel? Инструкция с пошаговым описанием и файл с примером!
-
В чем суть правила 3-х сигм?
-
Как можно применить эти знания на практике?
В наше время из-за переизбытка информации, связанного с большим ассортиментом товаров, направлений продаж, сотрудников, направлений деятельности и т.д., бывает трудно выделить главное, на что, в первую очередь, стоит обратить внимание и приложить усилия для управления. Определение доверительного интервала и анализ выхода за его границы фактических значений — методика, которая поможет вам выделить ситуации, влияющие на изменение тенденций. Вы сможете развивать позитивные факторы и снизить влияние негативных. Данная технология применяется во многих известных мировых компаниях.
Существуют так называемые «оповещения», которые информируют руководителей о том, что очередное значение в определенном направлении вышло за доверительный интервал. Что это означает? Это сигнал, что произошло какое-то нестандартное событие, которое, возможно, изменит существующую тенденцию в данном направлении. Это сигнал к тому, чтобы разобраться в ситуации и понять, что на неё повлияло.
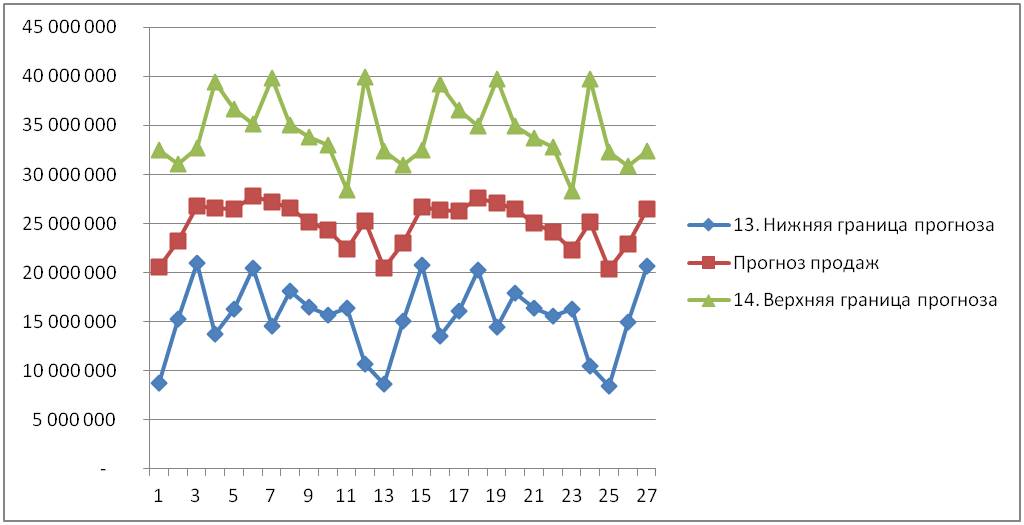
Например, рассмотрим несколько ситуаций. Мы рассчитали прогноз продаж с границами прогноза по 100 товарным позициям на 2011 год по месяцам и в марте фактические продажи:
- По «Подсолнечному маслу» пробили верхнюю границу прогноза и не попали в доверительный интервал.
- По «Сухим дрожжам» вышли за нижнюю границу прогноза.
- По «Овсяным Кашам» пробили верхнюю границу.
По остальным товарам фактические продажи оказались в рамках заданных границ прогноза. Т.е. их продажи оказались в рамках ожиданий. Итак, мы выделили 3 товара, которые вышли за границы, и начали разбираться, что же повлияло на выход за границы:
- По «Подсолнечному маслу» мы вошли в новую торговую сеть, которая дала нам дополнительный объем продаж, что привело к выходу за верхнюю границу. Для этого товара стоит пересчитать прогноз до конца года с учетом прогноза продаж в данную сеть.
- По «Сухим дрожжам» машина застряла на таможне, и образовался дефицит в рамках 5 дней, что повлияло на снижение продаж и выход за нижнюю границу. Возможно, стоит разобраться, что послужило причиной и постараться не повторять данную ситуацию.
- По «Овсяным Кашам» было запущено мероприятие по стимулированию сбыта, которое дало значительный прирост продаж и привело к выходу за границы прогноза.
Мы выделили 3 фактора, которые повлияли на выход за границы прогноза. В жизни их может быть гораздо больше.Для повышения точности прогнозирования и планирования факторы, которые приводят к тому, что фактические продажи могут выйти за границы прогноза, стоит выделить и строить прогнозы и планы по ним отдельно. А затем учитывать их влияние на основной прогноз продаж. Также можно регулярно оценивать влияние данных факторов и менять ситуацию к лучшему за счет уменьшения влияния негативных и увеличения влияния позитивных факторов.
С помощью доверительного интервала мы можем:
- Выделить направления, на которые стоит обратить внимание, т.к. в этих направлениях произошли события, которые могут повлиять на изменение тенденции.
- Определить факторы, которые реально влияют на изменение ситуации.
- Принять взвешенное решение (например, о закупках, при планировании и т.д.).
Теперь рассмотрим, что такое доверительный интервал и как его рассчитать в Excel на примере.
Что такое доверительный интервал?
Доверительный интервал – это границы прогноза (верхняя и нижняя), в рамки которых с заданной вероятностью (сигма) попадут фактические значения.
Т.е. мы рассчитываем прогноз — это наш основной ориентир, но мы понимаем, что фактические значения вряд ли на 100% будут равны нашему прогнозу. И возникает вопрос, в какие границы могут попасть фактические значения, если существующая тенденция сохранится? И на этот вопрос нам поможет ответить расчет доверительного интервала, т.е. — верхней и нижней границы прогноза.
Что такое заданная вероятность сигма?
При расчете доверительного интервала мы можем задать вероятность попадания фактических значений в заданные границы прогноза. Как это сделать? Для этого мы задаем значение сигма и, если сигма будет равна:
-
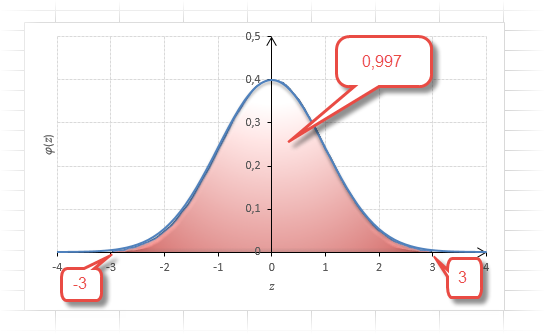
3 сигма — то, вероятность попадания очередного фактического значения в доверительный интервал составят 99,7%, или 300 к 1, или существует 0,3% вероятности выхода за границы.
-
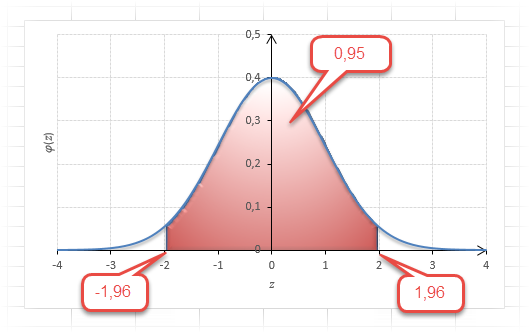
2 сигма — то, вероятность попадания очередного значения в границы составляет ≈ 95,5 %, т.е. шансы примерно 20 к 1, или существует 4,5% вероятности выхода за границы.
-
1 сигма — то, вероятность ≈ 68,3%, т.е. шансы примерно 2 к 1, или существует 31,7% вероятность того, что очередное значение выйдет за пределы доверительного интервала.
Мы сформулировали правило 3 сигм, которое гласит, что вероятность попадания очередного случайного значения в доверительный интервал с заданным значением три сигма составляет 99.7%.
Великим русским математиком Чебышевым была доказана теорема о том, что существует 10% вероятность выхода за границы прогноза с заданным значением три сигма. Т.е. вероятность попадания в доверительный интервал 3 сигма составит минимум 90%, в то время как попытка рассчитать прогноз и его границы «на глазок» чревата куда более существенными ошибками.
Как самостоятельно рассчитать доверительный интервал в Excel?
Расчет доверительного интервала в Excel (т.е. верхней и нижней границы прогноза) рассмотрим на примере. У нас есть временной ряд — продажи по месяцам за 5 лет. См. Вложенный файл.
Для расчета границ прогноза рассчитаем:
- Прогноз продаж (см. статью «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонностью»).
- Сигма — среднеквадратическое отклонение модели прогноза от фактических значений.
- Три сигма.
- Доверительный интервал.
1. Прогноз продаж.
О том, «как рассчитать прогноз продаж с учетом роста и с сезонностью» подробно описано в данной статье. Поэтому для тех, кто еще не изучал данный материал и не знает, как самостоятельно рассчитать прогноз продаж по месяцам с учетом роста и сезонности, рекомендуем для понимания последующих действий изучить данную статью, а затем перейти к дальнейшему изучению данного материала.
2. Для определения сигма рассчитаем среднеквадратическое отклонение модели прогноза от фактических значений.
Для расчета сигма рассчитаем среднеквадратическое отклонение для каждого месяца.
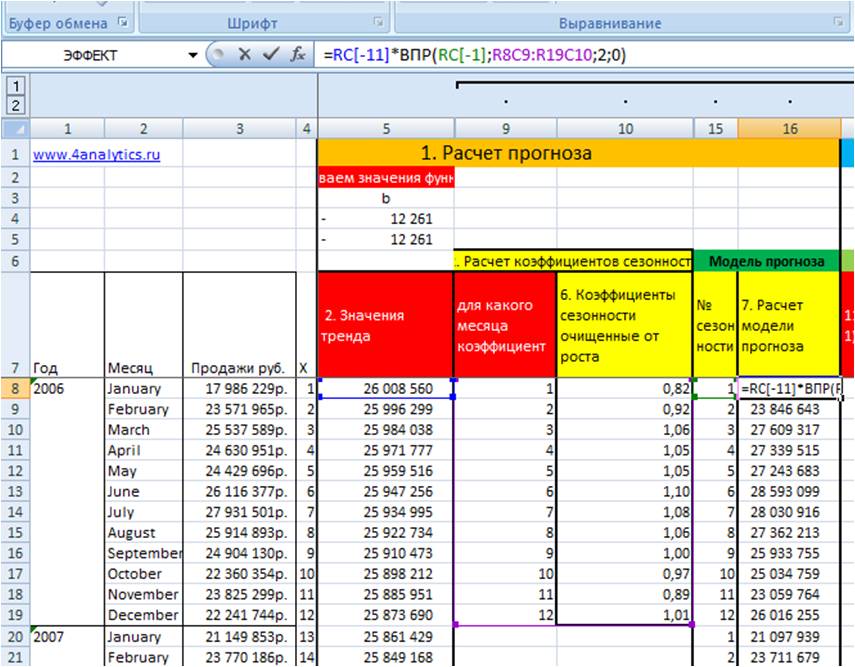
1. Для этого на 7-м шаге во вложенном файле рассчитаем значения прогнозной модели, в нашем случае это прогноз с линейным трендом и сезонностью.
Значение модели = Значение тренда умножим на коэффициент сезонности соответствующего месяца.
В Excel введем формулу:
=RC[-11] (ссылка на тренд)*ВПР(RC[-1];R8C9:R19C10;2;0)(формула ВПР со ссылкой на коэффициент сезонности соответствующего месяца)
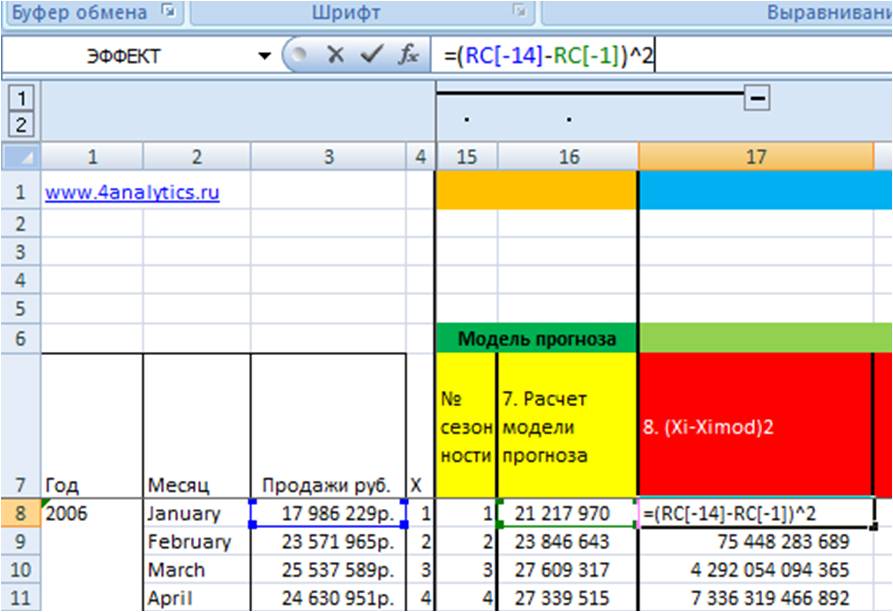
2. Рассчитаем квадрат разницы фактических значений и прогнозной модели (Xi-Ximod)^2 (8 этап во вложенном файле)
=(RC[-14](данные во временном ряду) — RC[-1](значение модели))^2(в квадрате)
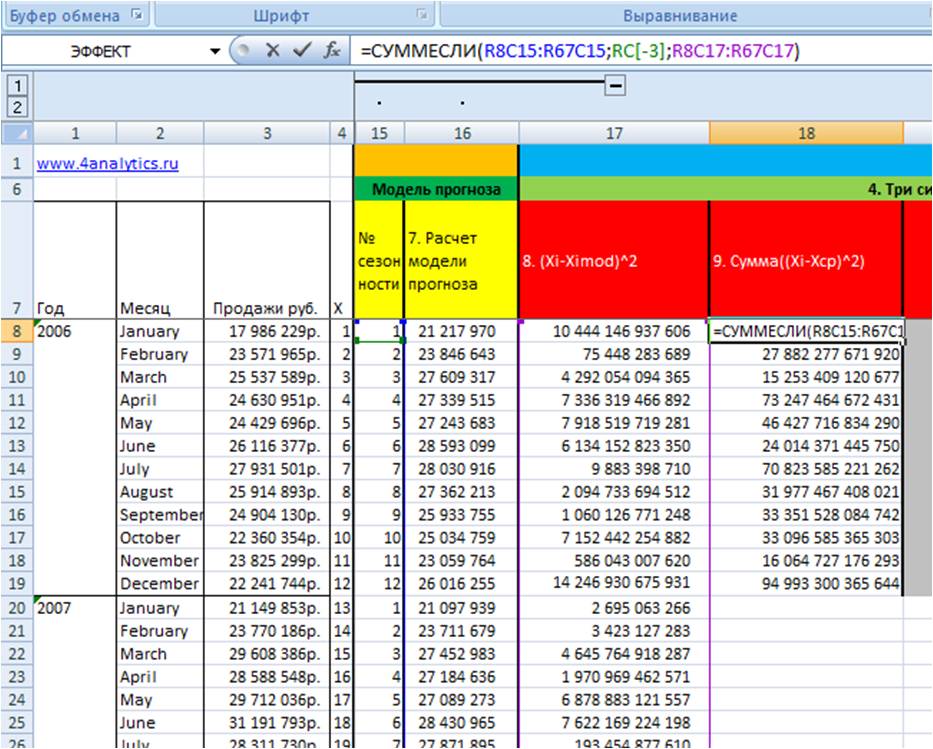
3. Просуммируем для каждого месяца значения отклонений из 8 этапа Сумма((Xi-Ximod)^2), т.е. просуммируем январи, феврали… для каждого года.
Для этого воспользуемся формулой =СУММЕСЛИ()
=СУММЕСЛИ(массив с номерами периодов внутри цикла (для месяцев от 1 до 12);ссылка на номер периода в цикле; ссылка на массив с квадратами разницы исходных данных и значений периодов)
(9 этап во вложенном файле)
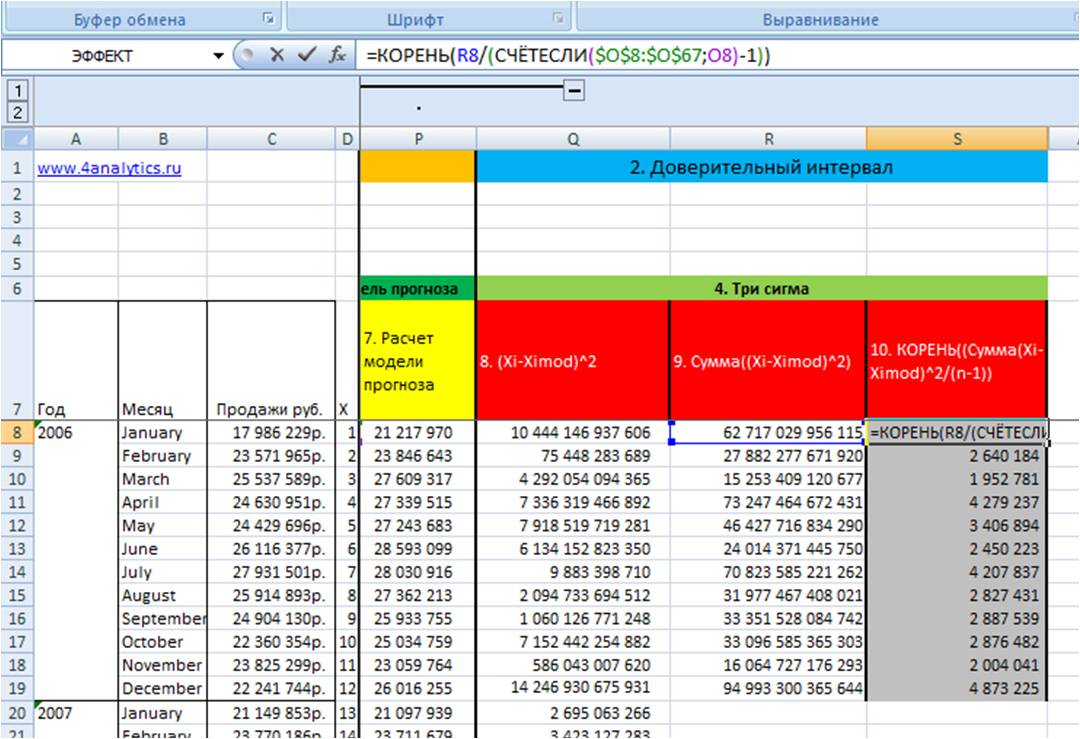
4. Рассчитаем среднеквадратическое отклонение для каждого периода в цикле от 1 до 12 (10 этап во вложенном файле).
Для этого из значения рассчитанного на 9 этапе мы извлекаем корень и делим на количество периодов в этом цикле минус 1 = КОРЕНЬ((Сумма(Xi-Ximod)^2/(n-1))
Воспользуемся формулами в Excel =КОРЕНЬ(R8 (ссылка на (Сумма(Xi-Ximod)^2)/(СЧЁТЕСЛИ($O$8:$O$67 (ссылка на массив с номерами цикла); O8 (ссылка на конкретный номер цикла, которые считаем в массиве))-1))
С помощью формулы Excel = СЧЁТЕСЛИ мы считаем количество n
Рассчитав среднеквадратическое отклонение фактических данных от модели прогноза, мы получили значение сигма для каждого месяца — этап 10 во вложенном файле.
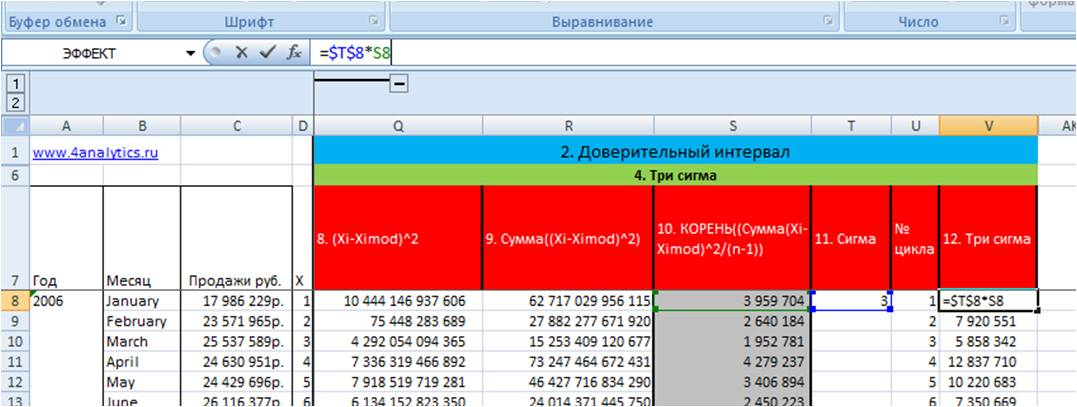
3. Рассчитаем 3 сигма.
На 11 этапе задаем количество сигм — в нашем примере «3» (11 этап во вложенном файле):
Также удобные для практики значения сигма:
1,64 сигма — 10% вероятность выхода за предел (1 шанс из 10);
1,96 сигма — 5% вероятность выхода за пределы (1 шанс из 20);
2,6 сигма — 1% вероятность выхода за пределы (1 шанс из 100).
5) Рассчитываем три сигма, для этого мы значения «сигма» для каждого месяца умножаем на «3».
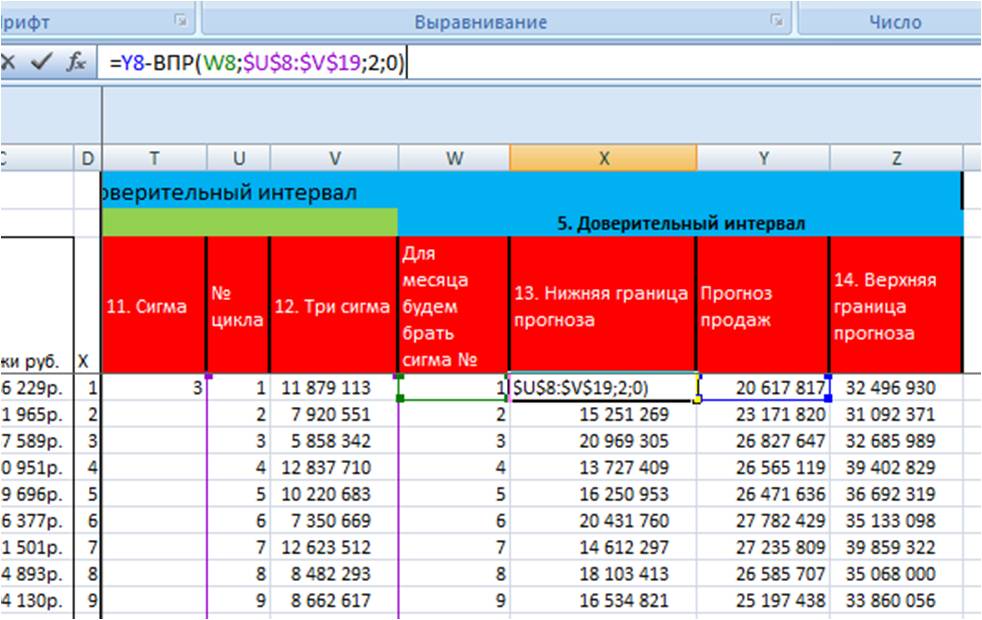
3.Определяем доверительный интервал.
- Верхняя граница прогноза — прогноз продаж с учетом роста и сезонности + (плюс) 3 сигма;
- Нижняя граница прогноза — прогноз продаж с учетом роста и сезонности – (минус) 3 сигма;
Для удобства расчета доверительного интервала на длительный период (см. вложенный файл) воспользуемся формулой Excel =Y8+ВПР(W8;$U$8:$V$19;2;0), где
Y8 — прогноз продаж;
W8 — номер месяца, для которого будем брать значение 3-х сигма;
$U$8:$V$19 — таблица, из которой с помощью функции =ВПР извлекаем значение 3-х сигма, соответствующее данному месяцу, фиксируем ссылку на таблицу с помощью F4, подробнее в статье «Как зафиксировать ссылку в Excel».
Т.е. Верхняя граница прогноза = «прогноз продаж» + «3 сигма» (в примере, ВПР(номер месяца; таблица со значениями 3-х сигма; столбец, из которого извлекаем значение сигма равное номеру месяца в соответствующей строке;0)).
Нижняя граница прогноза = «прогноз продаж» минус «3 сигма».
Итак, мы рассчитали доверительный интервал в Excel.
Теперь у нас есть прогноз и диапазон с границами в пределах, которого с заданной вероятностью сигма попадут фактические значения.
В данной статье мы рассмотрели, что такое сигма и правило трёх сигм, как определить доверительный интервал и для чего вы можете использовать данную методику на практике.
Вы можете скачать файл с примером расчета 3-х сигма и границ прогноза
Точных вам прогнозов и успехов!
Чем Forecast4AC PRO может вам помочь при расчете доверительного интервала?:
-
Forecast4AC PRO автоматически рассчитает верхнюю или нижнюю границы прогноза для более чем 1000 временных рядов одновременно;
-
Возможность анализа границ прогноза в сравнении с прогнозом, трендом и фактическими продажами на графике одним нажатием клавиши;
+ В программе Forcast4AC PRO есть возможность задать значение сигма от 1 до 3.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Функция стандартное отклонение это уже из разряда высшей математики относящейся к статистики. В Excel существует несколько вариантов использования Функции стандартного отклонения это:
- Функция СТАНДОТКЛОНП.
- Функция СТАНДОТКЛОН.
- Функция СТАНДОТКЛОНПА
Данные функции в статистике продаж нам понадобятся для выявления стабильности продаж (анализ XYZ). Эти данные можно использовать как для ценообразования, так и для формирования (корректирования) ассортиментной матрицы и для других полезных анализов продаж, о которых я обязательно расскажу в следующих статьях.
Предисловие
Давайте посмотрим на формулы сначала математическим языком, а после (ниже по тексту) подробно разберем формулу в Excel и как получившийся результат применяется в анализе статистических данных продаж.
Итак, Стандартное отклонение — это оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии )))) Не пугайтесь не понятных слов, потерпите и Вы все поймете!
Чтобы рассчитать Стандартное отклонение, нам нужно выяснить Среднеквадратическое отклонение по формуле
Описание формулы: Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины
Теперь стандартное отклонение — оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии:
Где,
— дисперсия;
— i-й элемент выборки;
— объём выборки;
— среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
Правило трёх сигм () — практически все значения нормально распределённой случайной величины лежат в интервале . Более строго — приблизительно с 0,9973 вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина истинная, а не полученная в результате обработки выборки). Мы же будем использовать округленный интервал 0,1
Если же истинная величина неизвестна, то следует пользоваться не , а s. Таким образом, правило трёх сигм преобразуется в правило трёх s. Именно это правило поможет нам определить стабильность продаж, но об этом чуть позже…
Теперь Функция стандартного отклонения в Excel
Надеюсь я не слишком Вас загрузил математикой? Возможно кому то данная информация потребуется для реферата или еще каких-нибудь целей. Теперь разжуем как эти формулы работают в Excel…
Для определения стабильности продаж нам не потребуется вникать во все варианты функций стандартного отклонения. Мы будем пользоваться всего одной:
Функция СТАНДОТКЛОНП
СТАНДОТКЛОНП(число1;число2;…)
Число1, число2,.. — от 1 до 30 числовых аргументов, соответствующих генеральной совокупности.
Теперь разберем на примере:
Давайте создадим книгу и импровизированную таблицу. Данный пример в Excel Вы скачаете в конце статьи.
Продолжение следует!!!
Подпишитесь на рассылку, что бы не пропустить самое интересное
И снова здравствуйте. Ну что!? Выдалась свободная минутка. Давайте продолжим?
И так стабильность продаж при помощи Функции СТАНДОТКЛОНП
Для наглядности возьмем несколько импровизированных товаров:
В аналитике, будь то прогноз, исследование или еще что то, что связано с статистикой всегда необходимо брать три периода. Это может быть неделя, месяц, квартал или год. Можно и даже лучше всего брать как можно больше периодов, но не менее трех.
Я специально показал утрированные продажи, где не вооруженным глазом видно, что продается стабильно, а что нет. Так проще будет понять как работают формулы.
И так у нас есть продажи, теперь нам нужно рассчитать средние значения продаж по периодам.
Формула среднего значения СРЗНАЧ(данные периода) в моем случае формула выглядит вот так =СРЗНАЧ(C6:E6)
Протягиваем формулу по всем товарам. Это можно сделать взявшись за правый угол выделенной ячейки и протянуть до конца списка. Или поставить курсор на столбец с товаром и нажать следующие комбинации клавиш:
Ctrl + Вниз курсор переместиться в коней списка.
Ctrl + Вправо, курсор переместиться в правую часть таблицы. Еще раз вправо и мы попадем на столбец с формулой.
Теперь зажимаем
Ctrl + Shift и нажимаем вверх. Так мы выделим область протягивания формулы.
И комбинация клавиш Ctrl + D протянет функцию там где нам надо.
Запомните эти комбинации, они реально увеличивают Вашу скорость работы в Excel, особенно когда Вы работаете с большими массивами.
Следующий этап, сама функция стандартного откланения, как я уже говорил мы будем пользоваться всего одной СТАНДОТКЛОНП
Прописываем функцию и в значениях функции ставим значения продаж каждого периода. Если у Вас продажи в таблице друг за другом можно использовать диапазон, как у меня в формуле =СТАНДОТКЛОНП(C6:E6) или через точку с запятой перечисляем нужные ячейки =СТАНДОТКЛОНП(C6;D6;E6)
Ну вот, пол дела сделано. Далее находим вариацию для этого Стандартное отклонение делим на среднее значение.
Вот все расчеты и готовы. Но как понять, что продается стабильно, а что нет? Просто проставим условность XYZ где,
Х — это стабильно
Y — с не большими отклонениями
Z — не стабильно
Для этого используем интервалы погрешности. если колебания происходят в пределах 10% будем считать что продажи стабильны.
Если в пределах от 10 до 25 процентов — это будет Y.
И если значения вариации превышает 25% — это не стабильность.
Что бы правильно задать буквы каждому товару, воспользуемся формулой ЕСЛИ подробнее про функцию ЕСЛИ читайте тут. В моей таблице данная функция будет выглядеть так:
=ЕСЛИ(H6<0,1;»X»;ЕСЛИ(H6<0,25;»Y»;»Z«))
Соответственно все формулы протягиваем по всем наименованиям.
Постараюсь сразу ответить на вопрос, Почему интервалы 10% и 25%?
На самом деле интервалы могут быть иными, все зависит от конкретной задачи. Я специально показал Вам утрированные значения продаж, где разница видна на «глаз». Очевидно, что товар 1 продается не стабильно, но динамика показывает увеличение продаж. Такой товар оставляем в покое…
А вот товар 2, тут уже дистабилизация на лицо. И наши расчеты показывают Z, что говорит нам о не стабильности продаж. Товар 3 и Товар 5 показывают стабильные показатели, обратите внимание, Вариация в пределах 10%.
Т.е. Товар 5 с показателями 45, 46 и 45 показывает вариацию 1%, что является стабильным числовым рядом.
А вот Товар 2 с показателями 10, 50 и 5 показывают вариацию в 93%, что является НЕ стабильным числовым рядом.
После всех расчетов, можно поставить фильтр и отфильтровать стабильность, таким образом если Ваша таблица составляет несколько тысяч наименований вы с легкостью выделите которые не стабильны в продажах или же на оборот, какие стабильны.
В моей таблице не получилось «Y», я думаю для наглядности числового ряда, его нужно добавить. Пририсую Товар 6…
Вот видите, числовой ряд 40, 50 и 30 показывает 20% вариации. Вроде большой погрешности нет, но все же разброс существенный…
И так под итожим:
10,50,5 — Z не стабильность. Вариация более 25%
40,50,30 — Y на этот товар можно обратить внимание, и улучшить его продажи. Вариация меньше 25%, но больше 10%
45,46,45 — X это стабильность, с этим товаром пока ничего делать не надо. Вариация меньше 10%
Правило трёх сигм
«Правило трёх сигм» на самом деле очень приблизительное. Оно даёт хорошее приближение только для определённого объёма выборки. Конечно, есть теория, которая предлагает красивую многоэтажную формулу для распределения показателя размаха вариации. Мы поступим попроще и пойдём путём практического знакомства.
Нас интересует, как размах значений зависит от объёма выборки. Чем больше выборка, тем больше шанс, что может появиться очень редкое значение, которое сильно отклонится от среднего. Гораздо дальше, чем на три сигмы.
Попробуем оценить зависимость размаха от объёма выборки. Используем нормальное распределение с нашими параметрами среднего и сигмы. Сгенерируем выборку размером в миллион значений. Первое, что мы обнаруживаем, — ограничение встроенного генератора случайных чисел надстройки Excel: Integer is not valid. Миллион чисел сгенерировать в надстройке не удаётся.
Попробуем сгенерировать хотя бы десять тысяч чисел. На этот раз попытка удалась. Вычислим размах и выразим его в сигмах.
Размах в сигмах
Построим график: объём выборки — размах в сигмах.
Размах и объём выборки
Рассмотрим начало графика поподробнее. Для этого используем логарифмический масштаб. Вместо объёма выборки используем его логарифм. Вставим новый столбец и вычислим lg (n). Здесь нам пригодится функция LOG10.
Логарифмический масштаб
На графике видно несколько ступенек. Скорее всего, это вызвано недостаточным качеством псевдослучайных чисел. Тем не менее, общая картина просматривается.
При выборке 10 размах равен трём сигмам. При выборке 100 размах 6 сигм. При выборке 10 000 размах равен 13 сигм.
Пользуясь случаем, проверим качество другого генератора случайных чисел Excel. Создадим новый лист и повторим наш эксперимент. Используем метод преобразования — возьмём равномерное распределение и пропустим его через обратное нормальное распределение.
Функция
RAND ()
СЛЧИС ()
позволяет сгенерировать случайное число с равномерным распределением в интервале от 0 до 1. Аргументов у функции нет.
Чтобы из равномерного распределения получить нормальное, вызываем функцию NORM.INV. Формат вызова:
=NORM.INV (probability, mean, standard_dev)
=НОРМ. ОБР (вероятность; среднее; стандартное_откл)
Функция работает по принципу x (p). Это обратное преобразование для функции распределения p (x).
probability — вероятность. В нашем случае это равномерно распределённая величина.
mean — среднее. В нашем примере это 250.
standard_dev — с.к. о. В нашем варианте это 20.
Таким образом, вызываем функция со следующими параметрами
=NORM.INV (B2,250,20)
Используем логарифмический масштаб, как в предыдущем варианте.
Размах в сигмах
Особенность функции генератора случайных чисел в том, что он генерирует новые числа (пересчитывает значение функции) при каждом сохранении файла. Попробуем сохранить файл несколько раз. Сделаем копию графиков и вставим их как рисунки на новый лист.
Запуски генератора
Графики немного отличаются друг от друга. Но при этом общая картина зависимости сохраняется. Чем больше выборка, тем больше размах.
Подведём итоги эксперимента. Правило трёх сигм хорошо работает для выборки объёмом в несколько сотен единиц. Для инженерной работы этого достаточно. А вот если взять хорошую, большую выборку, то размах может вырасти.
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
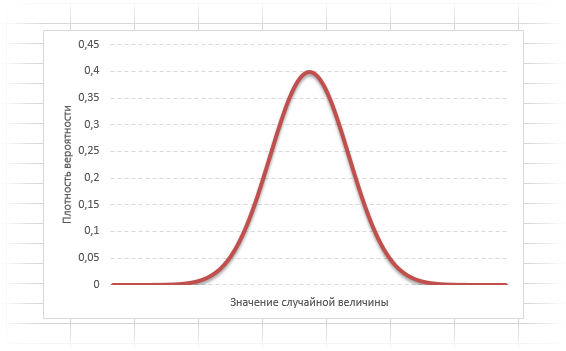
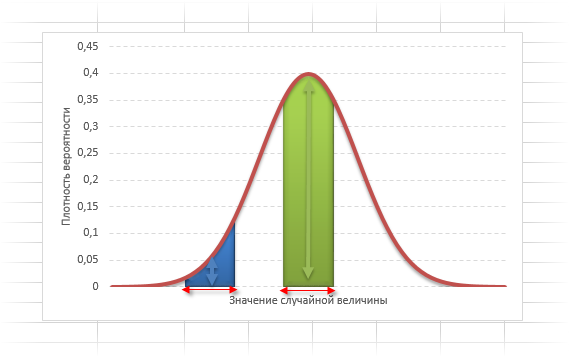
Кривая нормального распределения Гаусса имеет следующий вид.
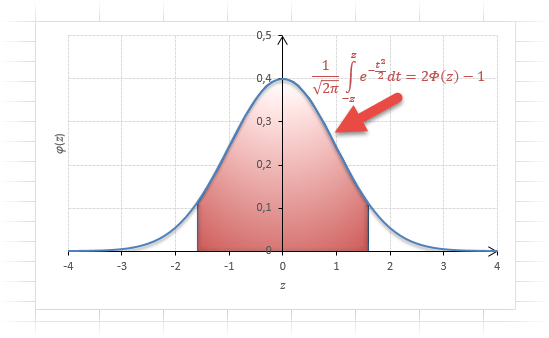
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
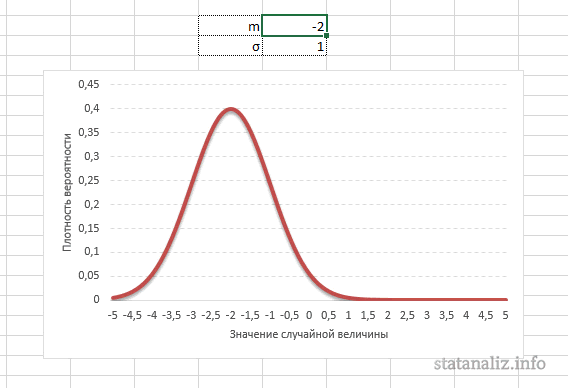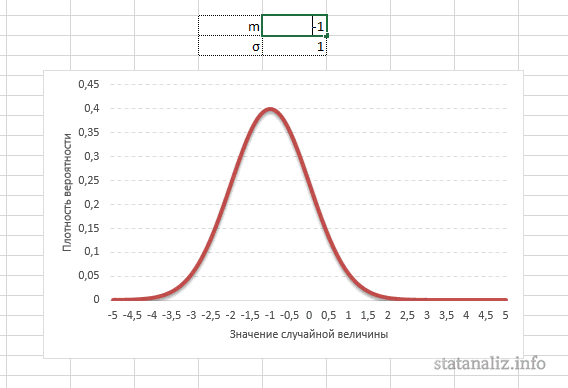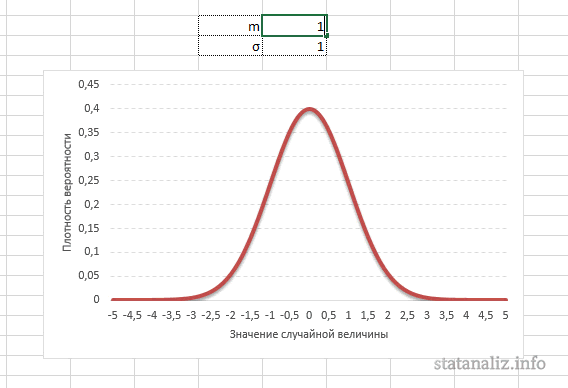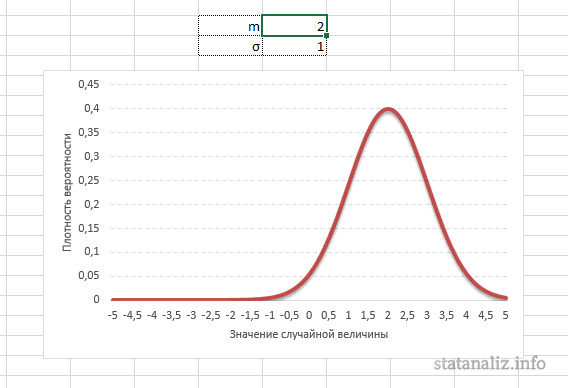
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
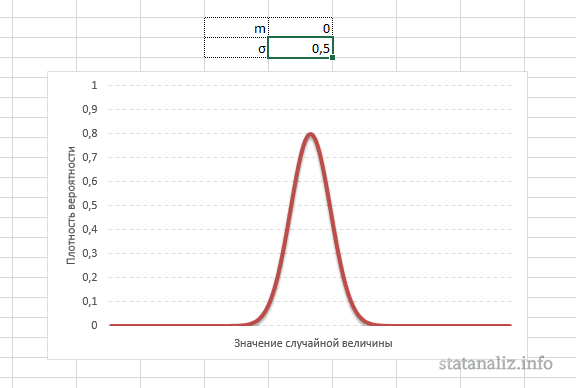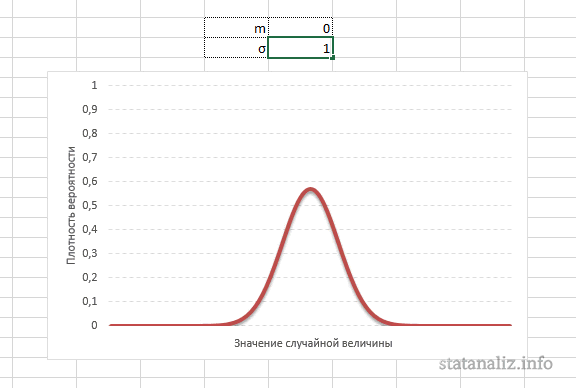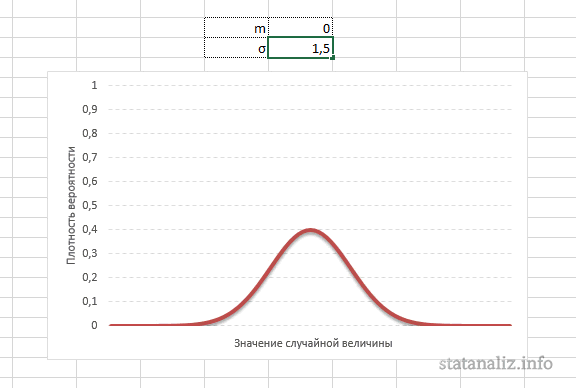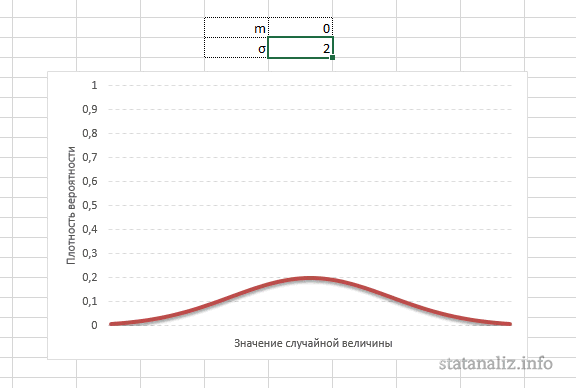
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
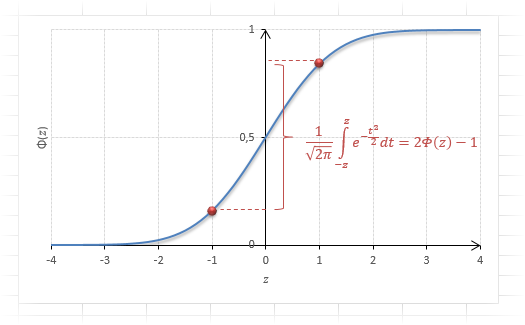
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
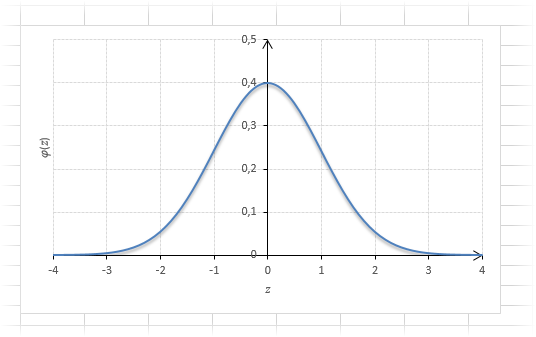
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
График плотности:
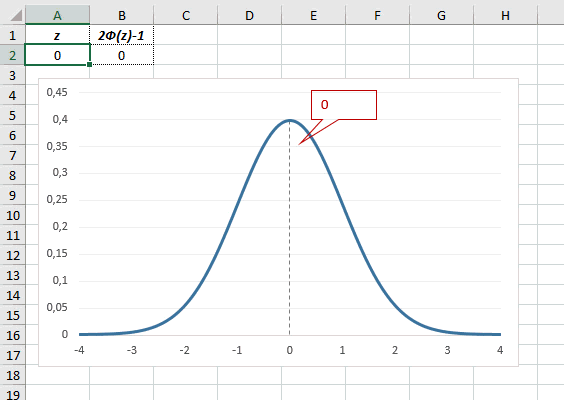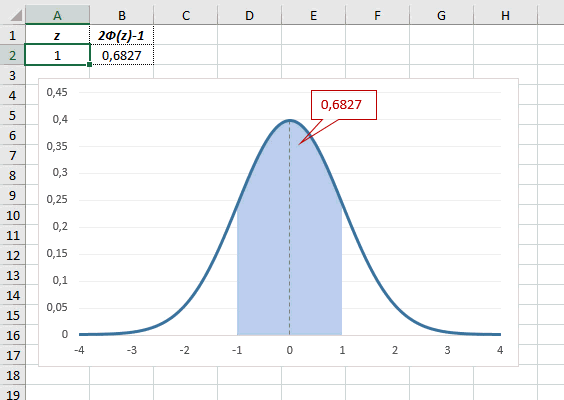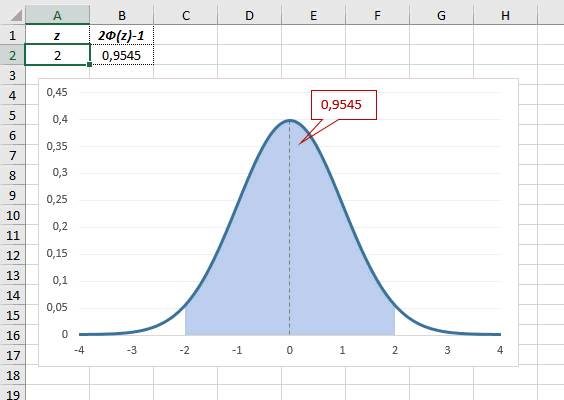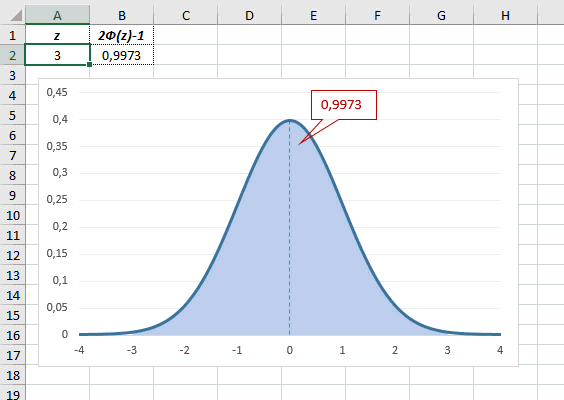
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
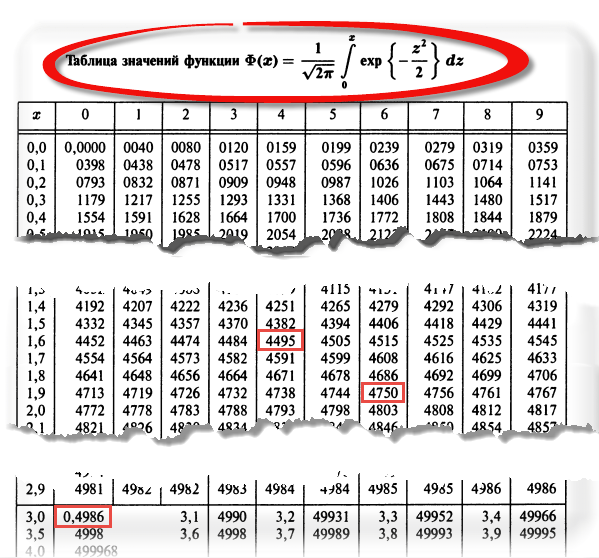
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
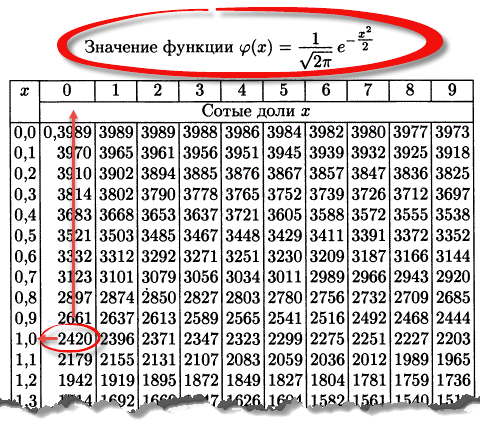
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
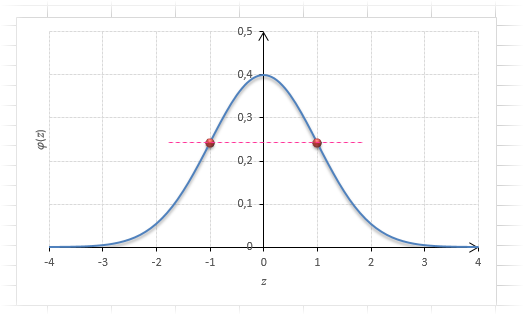
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
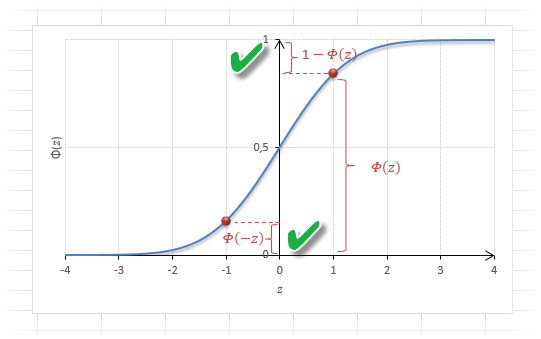
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
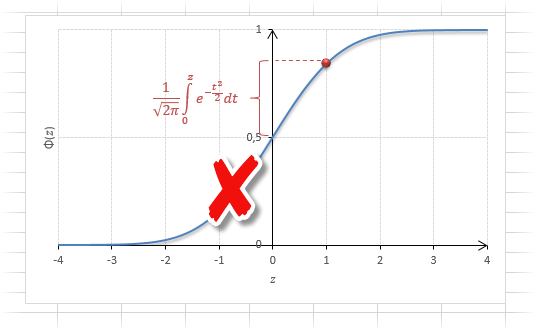
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
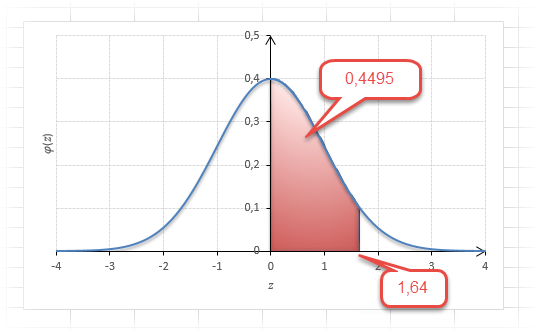
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
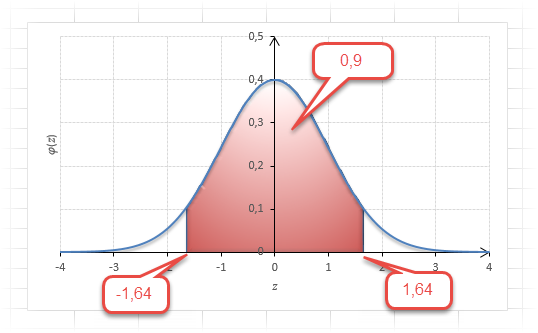
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
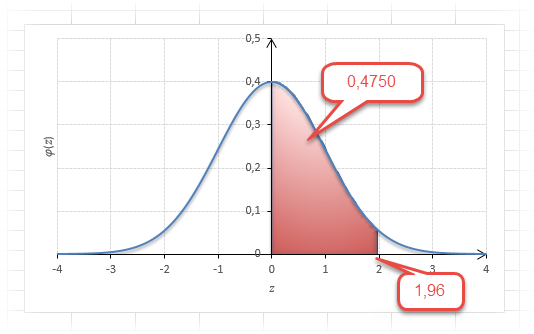
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
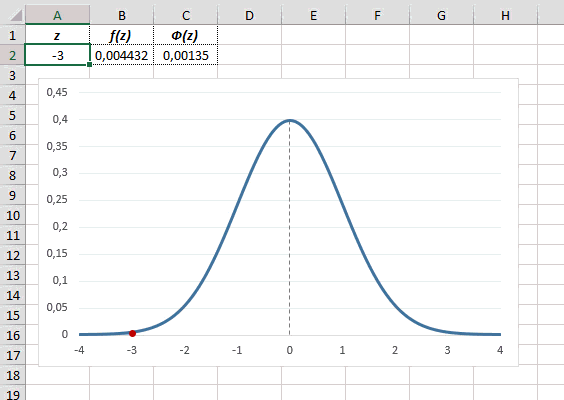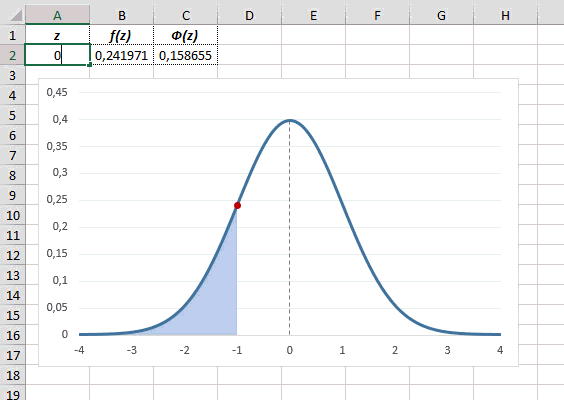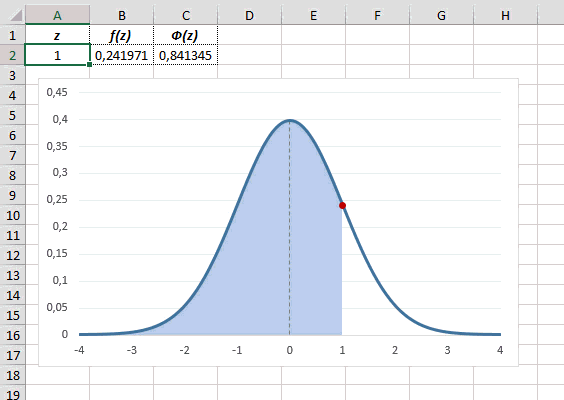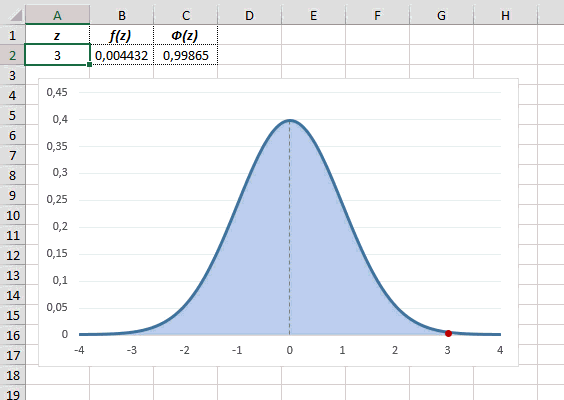
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
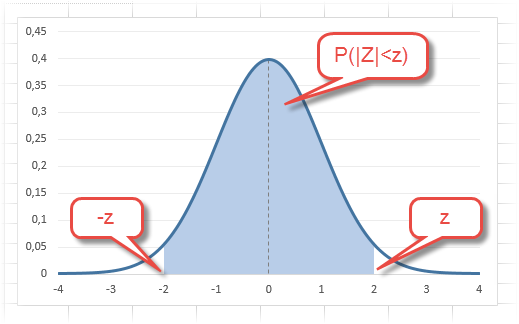
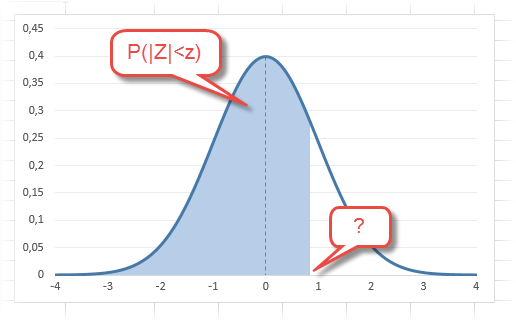
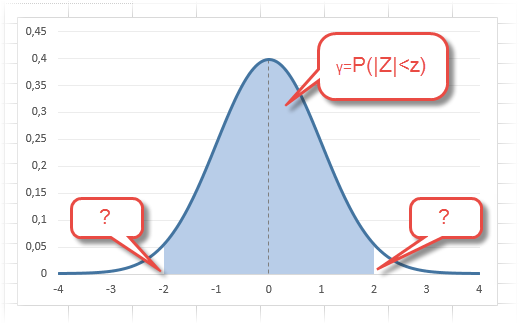
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
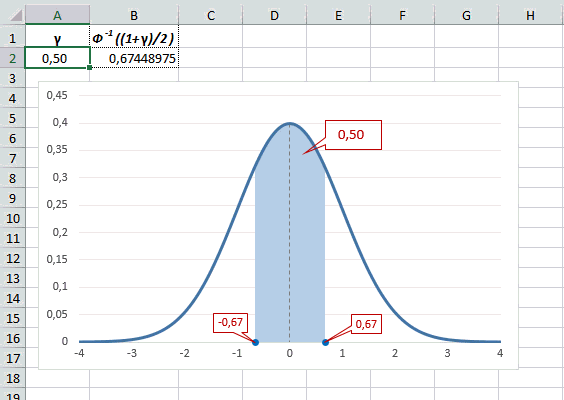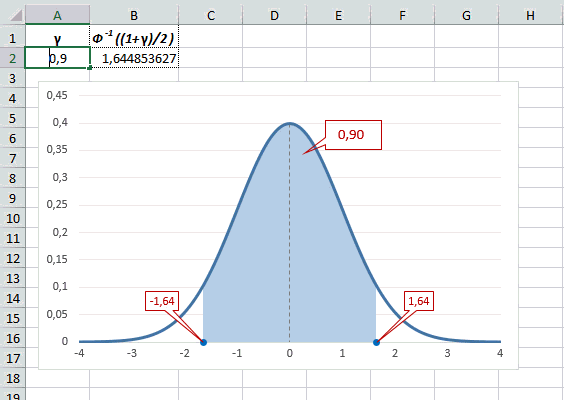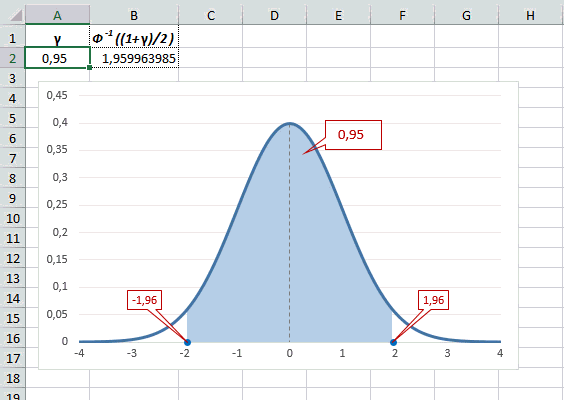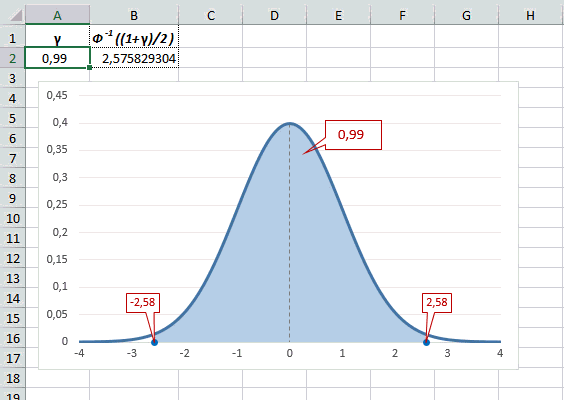
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
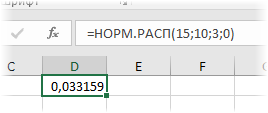
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
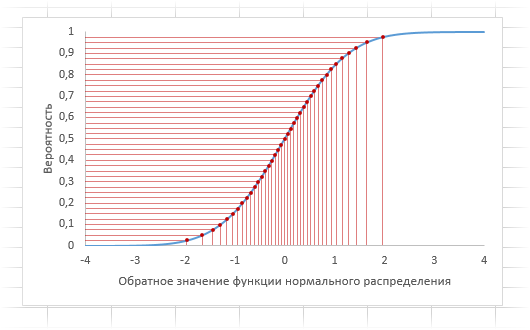
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях:
|
МПМ Пользователь Сообщений: 45 |
Имеется очень много данных. Т.е. Размер выборки не менее 100 значений для 27 разных критериев. Необходимо получить их анализ в виде: Статистику вообще не помню. Очень надо понять…. Откуда берётся 99,7%? И не понимаю что делать с данными числами дальше? Изменено: МПМ — 16.04.2016 18:58:22 |
|
Dima S Пользователь Сообщений: 2063 |
А какое отношение это имеет к екселю?) |
|
МПМ Пользователь Сообщений: 45 |
Dima S,делаю я всё в экселе)) только не понимаю, что делаю) И понятия не имею где спросить. Здесь то уж точно есть профессионалы по статистике. Изменено: МПМ — 16.04.2016 19:28:13 |
|
Jack_Famous Пользователь Сообщений: 10852 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
МПМ
, раз делаете в Excel, приложите файл-пример, чтобы мы тут поняли, что есть, что нужно и какие шаги в данном направлении уже проделаны… Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
|
МПМ Пользователь Сообщений: 45 |
Jack_Famous, таблица огромная. там ничего понятно не будет.
написал анализ от балды: Значения изменялись с вероятностью 99,7% в пределах 13,01%±3*0,0159%. Т.е. доверительный интервал находится в пределах от 8,2% до 17,7%. Но не понимаю что написал. Изменено: МПМ — 16.04.2016 19:52:46 |
||||||||||||||
|
Doober Пользователь Сообщений: 2204 |
#6 16.04.2016 23:16:40
Здесь точно помогут . <#0> |
||
|
Андрей VG Пользователь Сообщений: 11878 Excel 2016, 365 |
#7 16.04.2016 23:21:02
|
||
|
JeyCi Пользователь Сообщений: 3357 |
#8 17.04.2016 07:04:47 тема то Правило трёх сигм (хотя можно было и загуглить)… сигма — это корень из дисперсии… умножайте на 3…
в чём проблема? — найти среднее +/- (3*корень из дисперсии)
выполните от среднего эти действия (+/-) сколько нашли… будет вам доверительный интервал
… вы сначала корень из дисперсии извлеките, а потом называйте это, как хотите… делить не надо… Изменено: JeyCi — 17.04.2016 07:57:56 чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
||||||
|
МПМ Пользователь Сообщений: 45 |
JeyCi,нашёл статью. Пишут: 68,3% площади под нормальной кривой лежит в пределах +/- величины одного стандартного отклонения от значения средней арифметической. Примерно 95,5% площади находится в пределах +/- 2 стандартных отклонения, а 99,7% площади в пределах +/- 3 стандартных Изменено: МПМ — 17.04.2016 09:47:57 |
|
vikttur Пользователь Сообщений: 47199 |
МПМ, с помощью Excel можно решать различные задачи — по статистике, финансовые вычисления, проектирования и прогнозы, матанализ… Но для этого нужно: Если с первым пунктом на этом форуме проблем нет (есть специалисты разного уровня подготовки), то со вторым… Искать иголку в стоге сена? Здесь может не оказаться человека, владеющего статистикой. |
|
МПМ Пользователь Сообщений: 45 |
vikttur,Эх.. Если бы я знал хороший форум по статистике… А этот форум прекрасен и множество умных людей) |
|
JeyCi Пользователь Сообщений: 3357 |
#12 17.04.2016 10:08:17
МПМ . мне статью перепечатывать не надо… я вам высказала, что есть что по вопросу ветки и по данному правилу (хоть это и не относится к тематике данного форума — посему переводить вам всю статистику в рамках этой темы на этом форуме не вижу смысла)… и времени
это интерпретация графика дисперсии (сигма квадрат — график парабола — в зависимости от её вида так и читается, как в вашем посте)… вы же ищите там, где читаете, а не мы будем работать гугл-переводчиками Изменено: JeyCi — 17.04.2016 10:10:18 чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
||||
|
vikttur Пользователь Сообщений: 47199 |
По Вашей логике, на хорошем форуме по Excel должны решать задачи по теормеханике, досконально знать геометрию, быть крутыми финансистами, здесь должны разбираться в работе двигателя внутреннего сгорания и уметь вязать на спицах. А если нет, то обязательно должны найти специализированный форум и дать Вам ссылку. |
|
JeyCi Пользователь Сообщений: 3357 |
#14 17.04.2016 10:25:19 P.S.
Изменено: JeyCi — 17.04.2016 10:39:19 чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
||
|
МПМ Пользователь Сообщений: 45 |
vikttur,самое интересное, что время критиковать есть, а сказать по делу что-то нет. Как умею — так и пытаюсь найти решение вопроса. Так что удаляйте эту тему. Спасибо за конструктивную критику. Очень помогло. |
|
JeyCi Пользователь Сообщений: 3357 |
#16 17.04.2016 10:40:42
зачем я столько вам писала Изменено: JeyCi — 17.04.2016 10:43:09 чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
||
|
vikttur Пользователь Сообщений: 47199 |
#17 17.04.2016 10:44:34 МПМ, позвольте мне самому распоряжаться своим временем.
… не важно, что не в тему и есть определенные правила… На форуме по математике не пробовали поискать? По Word? Тоже как бы связано (и считать, и писать нужно)… По Вашем вопросу сказать нечего, статанализом не владею. |
||
|
МПМ Пользователь Сообщений: 45 |
JeyCi, Спасибо) Ваши ответы — да, полезны) |
|
JeyCi Пользователь Сообщений: 3357 |
#19 17.04.2016 11:32:59
достоверность: чем больше выборка, тем с большей уверенностью можно полагаться на стат. анализ
по правильному это надо не считать, а доказать… это отдельное стат. исследование… если поведение ваших данных подчиняется описанию нормального распределения — так его рассматривали во все времена — можете просто сослаться на любой источник (научную статью)…
сайт по статистике: www.real-statistics.com Изменено: JeyCi — 17.04.2016 11:34:54 чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
||||||
|
МПМ Пользователь Сообщений: 45 |
JeyCi, Например,
скос= 0,705205744 эксцесс= -0,417495757 |
||||||||||||||
|
JeyCi Пользователь Сообщений: 3357 |
может быть нормальным ассимитричным и с эксцессом… не пренебрегайте гуглом Статистический анализ данных в Excel — прокрутить страницу ниже) — но смысл стат. показателей одинаков для любых сфер, к которым применяется стат. анализ… Изменено: JeyCi — 17.05.2016 12:33:39 чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
|
retros Пользователь Сообщений: 3 |
#22 20.07.2018 17:20:23 Не совсем понятна постановка вопроса. Если нужно найти доверительный интервал — см. Точечные и интервальные оценки , но правило трёх сигм к доверительному интервалу имеет косвенное отношение. Если нужно оценить наличие грубых ошибок по критерию трёх сигм — см. Критерий трёх сигм , но надо иметь в виду, что критерий трёх сигм статистически менее обоснован, чем другие критерии грубых ошибок. Изменено: retros — 20.07.2018 17:22:29 |