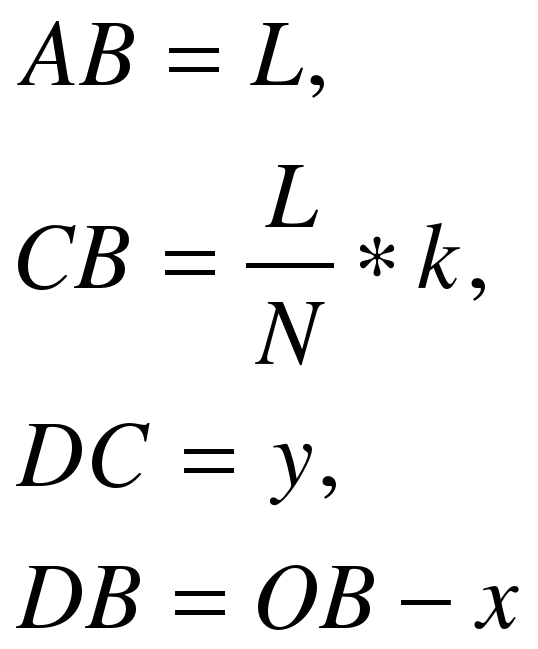ПРАКТИЧЕСКАЯ
РАБОТА №11
Моделирование
случайных процессов в Microsoft Excel
Упражнение 1. ВЕРОЯТНОСТНАЯ МОДЕЛЬ
Цель: Создание
вероятностной модели в электронных таблицах, знакомство с функцией для
генерации случайного числа.
Задание 1. Студенту для
поездки подходит 2 маршрута автобуса. У одного автобуса интервал 10 мин, у
другого — 15 мин. Определить среднее время ожидания и построить в одной системе
координат:
1) график времени ожидания за каждый день года,
2) график среднего времени ожидания для каждого дня
года.
Обоснование задачи. Так как
на остановку студент приходит по-разному, то время ожидания до прибытия
каждого из автобусов будет каждый раз меняться и будет являться случайной
величиной.
СЛУЧАЙНАЯ ВЕЛИЧИНА, СЛУЧАЙНАЯ ПЕРЕМЕННАЯ [random
value, random variable] — всякая наблюдаемая величина, изменяющаяся при
повторении условий, в которых она возникает.
ВЕРОЯТНОСТНАЯ МОДЕЛЬ – это модель, которая содержит
случайные элементы. Таким образом, при задании на входе модели некоторой совокупности
значений, на ее выходе могут получаться различающиеся между собой результаты в
зависимости от действия случайного фактора. Вероятностные модели базируются на
использовании больших серий испытаний со случайными параметрами, причем
точность полученных результатов зависит от количества проведенных опытов.
Для генерации случайной величины в Microsoft Excel
требуется в ячейку ввести формулу =СЛЧИС(). Эта функция возвращает
случайное число из диапазона [0;1).
Чтобы получить случайное вещественное число из
диапазона [0;а), можно использовать следующую формулу: =СЛЧИС()*a.
Если требуется получить случайное вещественное число
между a и b, можно использовать следующую формулу: =СЛЧИС()*(b-a)+a.
Порядок
выполнения.
1. Постройте
в Microsoft Excel таблицу
вида
2. Внесите в
таблицу исходные данные
a –
интервал ожидания 1 автобуса, а=10 минутам;
b –
интервал ожидания 2 автобуса, b=15 минутам;
d – количество
дней в исследуемом периоде (в году) d=365.
3. Заполните
расчетную таблицу формулами в соответствии с математической моделью, используя
абсолютную и относительную адресацию в формулах.
w1 – время
ожидания 1 автобуса (случайное число на отрезке [0;а]);
w2 – время
ожидания 2 автобуса ( случайное число на отрезке [0;b]);
x – время
ожидания за текущий день,
x = min (w1, w2)
t’ср– среднее
время ожидания на текущий день, за n – кол-во дней, для которых
среднее подсчитано;
tср – среднее
время ожидания за год
tср = (x1+x2+…+xn ) / d
4.
Вычислите
время все параметры на исследуемый период (Скопируйте, если это нужно, формулы
вниз на все дни года, используя маркер заполнения)
5.
Построить
на одной диаграмме два графика по заданию (для x и t’ср)
на отдельном листе.
Задание 2. Используя
модель, построенную для решения задачи, определить
·
среднее
время ожидания, если ожидание 1 автобуса 10 мин, 2 автобуса — 60 мин
·
каково
среднее время ожидания, если интервалы автобусов совпадают?
Упражнение
2. БРОСАНИЕ МОНЕТЫ
Цель: моделируя
возможные игровые ситуации (варьируя ставки в данной игре) выяснить, какая
тактика чаще приводит к результату (положительному или отрицательному)
Задание 3. У вас есть 10
монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою
судьбу. Суть игры проста, играя с маклером, вы делаете ставку и бросаете
монету. Если выпадет «орел», маклер выдает вам сумму вашей ставка, в противном
случае – вы ему отдаете сумму. Ставка может быть любой от 1 до 10 монет. Вы
можете назначить самую большую ставку в 10 монет, и тогда за один бросок
выяснится, «сорвали» ли вы банк или, наоборот, обанкротились. Опытные игроки
действуют более осторожно, начиная с маленькой ставки.
Удвоение начального капитала или банкротство приводит
к незамедлительному прекращению этого сеанса игры и расчету. Игра может
продолжиться по вашему усмотрению.
Имитировать результат падения монеты можно с помощью
функции СЛЧИС(). Поскольку вероятность выпадения той или иной стороны 50%,то,
если СЛЧИС()<0,5, то результат «орел» (1), в противном случает – «решка»
(0).
Формула
падения монеты при броске имеет следующий вид:
Бросок
= ЕСЛИ (СЛЧИС()<0,5; 1; 0)
Здесь
«1» на выходе функции означает, что игрок угадал, то есть выпал «орел», а «0» —
не угадал, то есть выпала «решка».
Формула
изменения наличности игрока:
Наличность=
ЕСЛИ(Бросок=1; Наличность+Ставка; Наличность-Ставка)
Формула
определения выигрыша:
Выигрыш=ЕСЛИ(Наличность<2*Начальный
капитал; «-»; «банк»)
Здесь
выдается сообщение «банк» при увеличении наличности вдвое или больше, что
является условием прекращением игры.
Функция
определения проигрыша:
Проигрыш=ЕСЛИ(Наличность>0;
«-»; «банкрот»)
Здесь
выдается сообщение «банкрот» по окончании наличности, что так же является
условием прекращения игры.
Порядок
выполнения работы
1. Создайте в
Microsoft Excel таблицу
вида:
2. Ввести
расчетные данные
3. Провести
следующие исследования
·
Исследовать
выпадения «орла» и «решки» в течение сеанса игры
·
Собрать
статистические данные о выигрыше и проигрыше в течение 10-20 сеансов игры с различными
значениями ставок и исследовать их.
4. Ответьте
на вопросы
·
Кто
чаще выигрывает: казино или игрок?
·
Сколько
в среднем надо сделать бросков до окончания игры?
Упражнение
3. ИГРА В КОСТИ
Цель: Создание игровой
модели, основанной на случайных событиях
Задание 4. Два игрока
бросают по две игральные кости. Сумма очков, выпавших на двух игровых костях,
накапливается. Игра прекращается, когда один из игроков достигает суммы 101.
Игра повторяется до трех побед.
Математическая модель складывается из следующих
рассуждений.
На игровой кости имеется 6 граней с количеством точек
от 1 до 6.
Модель, имитирующая бросание двух костей одним
игроком:
К1=ЦЕЛОЕ (1+6*СЛЧИС())
К2=ЦЕЛОЕ (1+6*СЛЧИС())
Случайные значения суммируются. Суммы бросков по
каждому игроку накапливаются в отдельных столбцах СУММА ПЕРВОГО и СУММА ВТОРОГО
и анализируются после каждого броска в столбце РЕЗУЛЬТАТ
ЕСЛИ (ИЛИ («Сумма первого»>101; «Сумма второго»>101);
«конец игры»; «-»)
Здесь, когда обе суммы меньше 101, в столбце
записывается «-»,а при превышении хотя бы одним игроком порога в столбце
записывается «конец игры». Кто победил, можно определить по соседним столбцам.
Игра прекращается при проявлении сообщения «конец
игры» в столбце РЕЗУЛЬТАТ
Создайте таблицу вида
Заполнить самостоятельно по предложенному материалу,
используя абсолютные и относительные ссылки.
Вопросы:
·
Как
части в нашей жизни происходят случайные процессы?
·
Все
ли случайные процессы можно смоделировать на компьютере?
·
Помогают
ли построенные модели для выбора в жизни?
Литература:
1. Дегтярева
И. Ю. Моделирование процессов. Вероятностные модели [текст] URL: http://www.metod-kopilka.ru/page-2-2-6-11.html
2. Информатика
и ИКТ. Задачник по моделированию. Базовый уровень /Под ред.
Н.В. Макаровой. – Питер. 2007. – 192 с.
Практическая работа
Задание1. «Решение систем уравнений»
Цель: Освоить графический способ решения систем уравнений посредством приложения MS Excel
Ход работы
Решениям уравнения являются значения точек пересечения графика функции с осью абсцисс, а решением системы уравнений являются точки пересечения графиков функций.
Задача.
Найдите решение системы уравнений:
Ответ запишите с точностью до 0,1
Решение:
1.Преобразуем данную систему к виду
Приведенный вид:
2.Произвольно выберем диапазон значений х, например от -10 до 10 с шагом 1 (если на графике не будет точек пересечения, то необходимо подобрать другие значения х). Построим таблицу, состоящую из трех столбцов и заполним ее.
|
x |
y1 |
y2=2x+4 |
|
-10 |
100 |
-16 |
|
-9 |
81 |
-14 |
|
-8 |
64 |
-12 |
|
……. |
…….. |
……… |
|
…… |
……… |
…….. |
3.Для оценки решений воспользуемся точечной диаграммой, на которой отобразим графики обеих функций.
Координаты точек пересечения графиков – решения системы, но получены приближенные значения решений с точностью , равной 1.
4.Для уточнения значений решений построим графики в интервалах от -2 до 0, где находится первое решение , и от 2 до 4, где находится второе решение
5.Составляем новую таблицу для с шагом 0,1 и строим точечную диаграмму для получения первого решения
|
x |
y1 |
y2=2x+4 |
|
-2 |
4 |
0 |
|
-1,9 |
3,61 |
0,2 |
|
-1,8 |
3,24 |
0,4 |
|
…….. |
……… |
……… |
6. Составляем новую таблицу для с шагом 0,1 и строим точечную диаграмму для получения второго решения
|
x |
y1 |
y2=2x+4 |
|
2 |
4 |
8 |
|
2,1 |
4,41 |
8,2 |
|
2,2 |
4,84 |
8,4 |
|
……….. |
………… |
……………. |
7. Решение системы определите самостоятельно
Графическое решение системы уравнений является приближенным.
Задание2 Решите системы уравнений графически с точностью до 0,1
Практическая работа
Тема: Моделирование в среде табличного процессора.
Цель: Демонстрация возможностей моделирования в среде табличного процессора MS Excel.
Развитие творческих способностей у учащихся.
Анализ объекта: Компьютерная модель в среде MS Excel.
Задача /12баллов/. Падение с лестницы.
Электрик Петров приставил к стене лестницу длины L, имеющую 10 ступенек, и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать электрик Петров в зависимости от того, на какой ступеньке он стоит.
Математическая модель:
Обозначим: L – длина лестницы;
N – число ступенек лестницы (по условию задачи N =10);
k – номер ступеньки, на которой стоит электрик и для которой ведется расчет траектории движения.
Для определенности считаем, что ступеньки пронумерованы от 1 до N, начиная снизу. Будем считать, что лестница первоначально занимала вертикальное положение. Это не совсем реально, но удобно для дальнейших расчетов.
При скольжении концов лестницы координата y конца A изменяется от L до 0,
координата x = 0 всегда.
А для конца B наоборот – координата x изменяется от 0 до L, а y = 0.
У промежуточных точек изменяются обе координаты.
В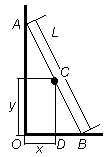
, при этом
Используя эти выражения, получаем:.
Из это пропорции можно получить формулы для координат k-й ступеньки:
(1)
(2)
Расстояния OA и OB связаны с теоремой Пифагора:
Из этой формулы можно выразить OA через OB: , или наоборот. (3)
Траекторию движения ступеньки с электриком будем строить поточечно. Обозначим M – количество точек расчета. В дальнейшем будем вычислять координаты ступеньки для положений лестницы, при которых нижний конец – точка B – перемещается на одну и ту же величину . Изменяя координату x точки B от 0 до L с шагом
, вычисляем длину отрезка OA по формуле (3), а затем координаты ступеньки по формулам (1) и (2).
Задание:
-
Составьте компьютерную модель, проведите расчет координат положения электрика в зависимости от положения лестницы. Пример заполнения электронной таблицы:
| Падение с лестницы | |||
| Исходные данные | |||
|
Длина лестницы, м |
1,8 |
||
|
Количество ступенек |
10 |
||
|
Номер ступеньки, на которой стоит электрик |
8 |
||
|
Количество точек расчета |
20 |
||
| Промежуточные расчеты и результаты | |||
|
Шаг изменения положения точки B |
|||
|
OB |
OA |
Координата x |
Координата y |
|
Заполнить вниз |
Заполнить вниз |
Заполнить вниз |
Заполнить вниз |
-
По результатам вычислений по столбцам C и D постройте диаграмму кривой, по которой движется ступенька с электриком. Убедитесь, что эта кривая похожа на четверть эллипса, сплющенного либо к оси ординат (если номер ступеньки 5), либо к оси абсцисс (если номер ступеньки
-
Проведите расчет и постройте общую диаграмму кривых для всех ступенек. Для построения общей диаграммы надо скопировать результаты проведения экспериментов в соседние столбцы.
Чему научились:
-
Создавать модели в среде табличного процессора MS Excel.
-
Создавать интегрированный документ.
-
Использовать знания, полученные на предыдущих уроках.
2
Лабораторная
работа № 1
Модель
неограниченного роста
Цель работы: Используя компьютерную модель неограниченного роста
исследовать прирост массы живых организмов с течением времени.
Предположения:
Ø
прирост массы живых организмов за
единицу времени пропорционален уже их имеющейся массе;
Ø
регулятором прироста выступает
окружающая среда;
Ø
коэффициент размножения постоянен
Параметры модели:
Ø
начальная масса живых организмов
М(0) = 1 т;
Ø
коэффициент размножения k:
|
Природная зона |
Тундра |
Тайга |
Степь |
Пустыня |
|
Коэффициент k |
0,6 |
1,8 |
1,2 |
0,8 |
Ø
время n.
Связь между параметрами модели задается соотношением:
М(n+1) = (1 +
k) М(n)
Задача:
1)
Определить, через сколько лет
масса растений в различных природных зонах превысит 100 т;
2)
Определить, через сколько лет
масса растений в различных природных зонах превысит 1000 т, 10000 т (т.е.
произойдет ее «удесятерение») ;
3)
Построить график зависимости массы
растений от числа прошедших лет (для каждой природной зоны);
4)
Определить, через сколько лет
масса растений в различных природных зонах превысит
массу Земли (5 976 000 000
000 000 000 000 т).
Ход работы:
|
А |
В |
C |
D |
E |
F |
|
|
1 |
Природная зона |
Год |
Тундра |
Тайга |
Степь |
Пустыня |
|
2 |
Коэффициент размножения k |
0,6 |
1,8 |
1,2 |
0,8 |
|
|
3 |
Начальная масса М(0) |
0 |
1 |
1 |
1 |
1 |
|
4 |
Масса через 1 год |
В3+1 |
C3*(1+C2) |
D3*(1+D2) |
||
|
5 |
Масса через 2 года |
В4+1 |
C4*(1+C2) |
D4*(1+D2) |
||
|
6 |
1.
Загрузите электронную таблицу Excel
и занесите в таблицу 2 исходные данные (они выделены цветом) и формулы.
2.
Измените формулы в блоке ячеек C4:D5 с
учетом того, что номер строки в адресах некоторых ячеек должен быть абсолютным
(неизменным при копировании в последующие строки).
3.
Занесите формулы в ячейки Е4 и F4.
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
4.
Последовательно скопируйте блок
ячеек В4:F4 в последующие строки. Копирование прекратить, как
только во всех четырех столбцах C, D, E и F возникнут числа, большие 100.
Для каждой природной зоны определите,
через сколько лет масса растений
превысит 100 т. Результаты запишите в отчет.
5.
С помощью электронной таблицы вычислить,
через сколько лет масса растений в различных природных зонах превысит 1000 т и
10000 т.
Результаты запишите в отчет.
Для каждой природной зоны сделайте вывод о времени, необходимом для увеличения
массы растений в 10 раз.
6.
С помощью электронной таблицы
вычислить, через сколько лет масса растений в различных природных зонах
превысит массу Земли, равную 5 976 000 000 000 000 000 000 т.
Результаты запишите в отчет.
Для каждой природной зоны сделайте вывод о времени, когда масса растений
превысит массу Земли.
7.
С помощью электронной таблицы для
каждой природной зоны построить график зависимости массы растений от числа
прошедших лет.
Таблицу в режиме отображения
значений и графики приложите к отчету.
Лабораторная
работа № 2
Модель
ограниченного роста
Цель работы: Используя компьютерную модель ограниченного роста
исследовать прирост массы живых организмов с течением времени.
Предположения:
Ø
прирост массы живых организмов за
единицу времени пропорционален уже их имеющейся массе;
Ø
существует некоторое предельное
значение массы живых организмов;
Ø
коэффициент прироста массы живых
организмов за единицу времени пропорционален разности между максимально
возможным значением массы и массой, имеющейся к данному моменту времени.
Параметры модели:
Ø
начальная масса живых организмов
М(0) = 1 т;
Ø
предельное значение массы живых
организмов L = 11000 т.
Ø
коэффициент пропорциональности a
в формуле для коэффициента прироста;
Ø
время n.
Связь между параметрами модели задается соотношением:
М(n+1) = М(n)
+ а М(n) (L — М(n))
k(n) = a (L — M(n))
а = k(n)
/ (L — M(n)),
т.е. при n=0
Þ а = k(0) / (L
— M(0))
|
Природная зона |
Тундра |
Тайга |
Степь |
Пустыня |
|
Коэффициент k |
0,6 |
1,8 |
1,2 |
0,8 |
Задача:
1)
Определить, через сколько лет
масса растений в различных природных зонах превысит 100 т;
2)
Определить, через сколько лет
масса растений в различных природных зонах превысит 1000 т; 10 000 т (т.е.
произойдет ее «удесятерение»)
3)
Построить график зависимости массы
растений от числа прошедших лет (для каждой природной зоны);
Ход работы:
1.
Загрузите электронную таблицу Excel
и занесите в таблицу исходные данные (они выделены цветом) и формулы:
|
А |
В |
C |
D |
E |
F |
|
|
1 |
Природная |
Год |
Тундра |
Тайга |
Степь |
Пустыня |
|
2 |
Коэффициент |
0,6 |
1,8 |
1,2 |
0,8 |
|
|
3 |
Предельное |
11000 |
11000 |
11000 |
11000 |
|
|
4 |
Коэффициент |
|||||
|
5 |
Начальная |
0 |
1 |
1 |
1 |
1 |
|
6 |
Масса через 1 год |
B5+1 |
C5+C4*C5*(C3-C5) |
D5+D4*D5*(D3-D5) |
||
|
Масса через 2 года |
B6+1 |
2.
Измените формулы в блоке ячеек C4:D5
с учетом того, что номер строки в адресах некоторых ячеек должен быть абсолютным
(неизменным при копировании в последующие строки).
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
3.
Последовательно скопируйте блок
ячеек В4:F4 в последующие строки. Копирование прекратить, как только во всех
четырех столбцах C, D, E и F возникнут числа, большие 100.
Результаты занесите в отчет.
Сравните с результатами предыдущей практической работы и сделайте выводы.
4.
С помощью электронной таблицы
вычислить, через сколько лет масса растений в различных природных зонах превысит
1000 т и 10000.
Результаты занесите в отчет.
Сравните с результатами предыдущей практической работы и сделайте выводы.
5.
С помощью электронной таблицы для
каждой природной зоны построить график зависимости массы растений от числа
прошедших лет.
Таблицу в режиме отображения
значений и графики приложите к отчету.
Лабораторная
работа № 3
Границы
адекватности модели неограниченного роста
Цель работы: Найти
границы адекватности модели неограниченного роста.
Предположения и параметры моделей:
Всякая модель имеет ограниченную область адекватности,
и за пределами этой области она перестает удовлетворительно отражать свойства
моделируемого объекта. Модель неограниченного роста остается адекватной, пока
масса живых организмов достаточно мала по сравнению с предельно допустимой
массой этих организмов в данных природных условиях.
Параметры модели неограниченного роста: начальная масса М(0), коэффициент прироста k,
предельное значение массы L, число лет n,
масса живых организмов через n лет М(n);
связь между параметрами модели
определяется формулой:
М(n+1)
= (1 + k) М(n)
Параметры модели ограниченного роста: начальная масса Мо(0), коэффициент
прироста k, число лет n, масса живых организмов через n лет
Мо(n); связь
между параметрами модели определяется формулой:
Мо(n+1) = (1+ k (L – Мо(n))/(L —
M(0)) ) Мо(n)
Поскольку Мо(0)=
М(0), то нетрудно подсчитать, что Мо(1)= М(1), но
вот уже Мо(2)< М(2). И чем дальше, тем больше будет
различие между значениями Мо и М. Будем считать модель
неограниченного роста адекватной, если разница М – Мо
составляет не более 10% от Мо.
Экспериментально
установлено, что предельное значение массы L образует
геометрическую прогрессию относительно границы адекватности n, т.е. L=
b×2n-1, где b – некоторый коэффициент.
Т.к. 2=1+k,
то L= b×(1+k)
n-1.
Отсюда b = L /×(1+k) n-1
Компьютерные эксперименты
показали, что моделью неограниченного роста можно пользоваться с уровнем
погрешности в 10% при выполнении условия L
³ 8×(1+k)
n-1.
Выражение для n полученное при решении показательного неравенства,
показывает, как долго можно пользоваться моделью неограниченного роста при
заданных (предельного уровня массы живых организмов) и (коэффициента
ежегодного прироста):
n £ 1+lg(0,125L)/lg(1+k)
Задание: При начальной массе М(0)=1:
1)
Найти границу адекватности n
при k=1,8 и L=11000.
2)
Исследовать, как граница
адекватности n зависит от величины k (L=11000;
k=1,8; 1,2; 1)
3)
Исследовать, как граница
адекватности n зависит от величины L (k=1; L= 5500; 11000; 22000; 44000)
4)
Исследовать, как коэффициент b зависит от k
(L=5000; k=1; 1,2; 1,5; 2)
Ход работы:
1.
Загрузите электронную таблицу
Excel и занесите в таблицу исходные данные и формулы (при занесении формулы в
ячейку Е2 используйте функцию).
|
A |
B |
C |
D |
E |
|
|
1 |
k |
L |
b |
||
|
2 |
Год (n) |
Неограниченный рост |
Ограниченный рост |
Отклонение, в % |
D1/СТЕПЕНЬ((1+В1);А3-1) |
|
3 |
0 |
1 |
1 |
0 |
|
|
4 |
А3+1 |
(1+В1)*В3 |
(1+В1*(D1-C3)/(D1-C3))*C3 |
(B4-C4)/C4*100 |
|
|
5 |
А4+1 |
(1+В1)*В4 |
(1+В1*(D1-C4)/(D1-C3))*C4 |
(B5-C5)/C5*100 |
2.
Измените формулы в блоке ячеек В4:С5
с учетом того, что номер строки в адресах некоторых ячеек должен быть
абсолютным (неизменным при копировании в последующие строки).
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
3.
Занесите в ячейку В1 значение
коэффициента прироста k=1,8, в ячейку D1 – значение предельной массы живых
организмов L=11000.
4.
Последовательно копируя блок ячеек
А4:D4 в последующие строки найдите, в какой год отклонение
превзойдет границу 10%. Результаты занесите в отчет.
5.
Найдите границу адекватности n
при L=11000 и различных k, равных: 1,8; 1,2 и 1.
Результаты занесите в отчет.
Сделайте выводы об изменении границы
адекватности n с уменьшением k.
6.
Найдите границу адекватности n
при k=1 и различных L, равных: 5500; 11000; 22000 и
44000.
Результаты занесите в отчет.
Сделайте вывод о виде зависимости значения
предельной массы живых организмов L относительно границы адекватности n..
7.
Найдите коэффициент b при L=5000
и различных k, равных: 1; 1,2; 1,5; 2. В ячейке Е2 вместо А3
вставляйте значение года n (или соответствующий номер ячейки), когда отклонение
превзойдет границу 10%. Убедитесь, что во всех случаях b приблизительно
одинаково.
Результаты занесите в отчет.
Сделайте выводы о том, зависит ли коэффициент
b от
коэффициента прироста k .
Лабораторная работа № 4
Метод половинного деления
Цель работы:
Найти значение корня уравнения методом половинного деления.
Задача:
Найти значение корня уравнения:
Вариант №1. x5 — 4x2 + x -2 = 0, с
точностью d=0,001
Вариант №2. x3 — 3x + 3 = 0, с точностью d=0,0005
Вариант №3. 2х = 3х, с точностью d=0,002
Вариант №4. cos(x) = х, с точностью d=0,005
Ход работы:
1.
Загрузите электронную таблицу Excel
и занесите в таблицу исходные данные в выделенные цветом ячейки (в ячейке D1
укажите исследуемую функцию) и необходимые формулы (в вычисляемые ячейки C2, D2, E2).
|
A |
B |
C |
D |
Е |
F |
|
|
1 |
a |
b |
(a+b)/2 |
f(x)= |
b-a |
d |
|
2 |
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
2.
Определите отрезок [ a; b ] длиной
1, значения на концах которого, образуют «вилку» для корня уравнения.
Результат занесите в отчет. Укажите значение функции на концах отрезка.
3.
Вставьте найденные значения a и b в ячейки A2 и B2
соответственно.
4.
Методом половинного деления
найдите значение корня уравнения с заданной точностью d.
Результаты занесите в отчет.
Сделайте выводы.
Коррелляционное моделирование. Практическая работа
27.01.2020 21:04
Практическая работа по теме: «Моделирование корреляционных зависимостей» (11 класс).
Архив содержит: Файл Word с практической работой и Файл Excel с данными и результатами практической работы
Просмотр содержимого документа
«ПР Моделирование корреляционной зависимости»
Практическая работа
Тема: «Моделирование корреляционных зависимостей» (11 класс)
Цель: с помощью электронных таблиц Excel научиться:
-
строить график регрессионной модели;
-
определять наиболее удачную регрессионную модель, используя коэффициент детерминированности,
Ход работы:
-
Соберите данные о средней дневной температуре вашего села (см. Дневник погоды для школьников на https://www.gismeteo.ru/diary/182588/2017/3/).
-
Постройте таблицу данных в ЭТ Excel.
-
Постройте точечную диаграмму температур.
-
Проверьте настройки горизонтальной оси (рис. 1)
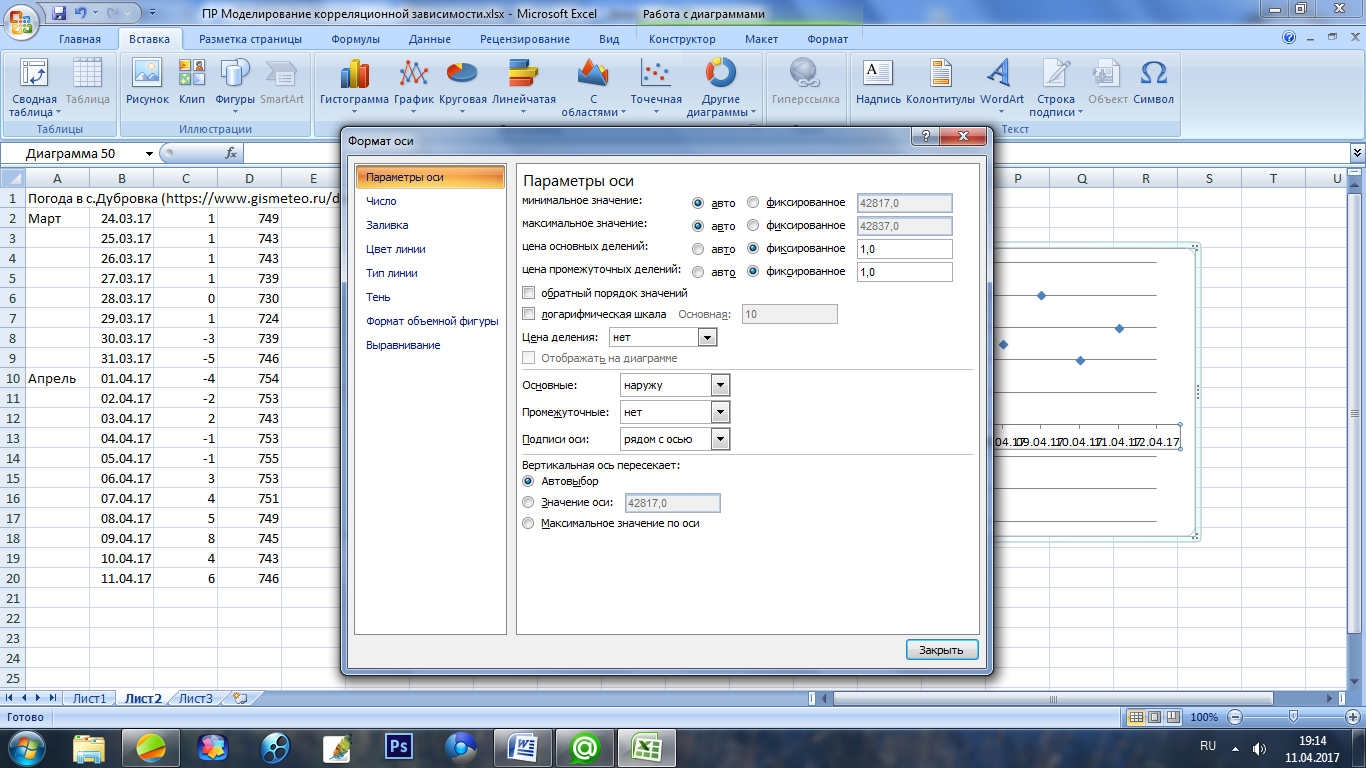

Рис.1. Формат оси (горизонтальной)
-
Аналогично установите настройки вертикальной оси: цена основных и промежуточных делений – 1.
-
Добавьте основные линии сетки, если их нет.
-
Анализируя коэффициент детерминированности, подберите наиболее удачную регрессионную модель (линию тренда).
-
Попробуйте путем графической экстраполяции предсказать температуру через 2-5 дней.
Данные для работы:
|
Месяц |
Дата |
Температура |
|
Март |
24.03.17 |
1 |
|
25.03.17 |
1 |
|
|
26.03.17 |
1 |
|
|
27.03.17 |
1 |
|
|
28.03.17 |
0 |
|
|
29.03.17 |
1 |
|
|
30.03.17 |
-3 |
|
|
31.03.17 |
-5 |
|
|
Апрель |
01.04.17 |
-4 |
|
02.04.17 |
-2 |
|
|
03.04.17 |
2 |
|
|
04.04.17 |
-1 |
|
|
05.04.17 |
-1 |
|
|
06.04.17 |
3 |
|
|
07.04.17 |
4 |
|
|
08.04.17 |
5 |
|
|
09.04.17 |
8 |
|
|
10.04.17 |
4 |
|
|
11.04.17 |
6 |
Рекомендуем курсы ПК и ППК для учителей
Практическая проверочная работа по теме «Моделирование в Excel» для 11 класса
По материалам моих статей по теме «Моделирование» https://урок.рф/library/izuchenie_temi_%C2%ABmodelirovanie%C2%BB_v_11_klasse_chast_1_193503.html
и
https://урок.рф/library/izuchenie_temi_%C2%ABmodelirovanie%C2%BB_v_11_klasse_chast_2_091345.html
составлена практическая проверочная работа в пяти вариантах с ответами.
Вариант 1
1. Дана функция y=5sin2(x+l )-4cos(x-l)+6 . Построить таблицу значений и график функции на интервале [-6.3; 6.7]. Ответить на вопросы:
а) значение функции в точке х=-2,3;
б) количество минимумов функции на данном интервале.
2. Работники предприятия имеют следующую заработную плату: Иванов — 4567руб., Петров 7435руб., Сидоров — 8421руб., Попов — 6872руб., Васина -5994руб. Руководство предприятия выделило на поощрение сотрудников 19000руб., пропорционально их заработной плате. Определите:
а) коэффициент премии; б) премию Попова.
Вариант 2
1. Дана функция y=5cos2(x+1 )-4sin(x-1 )+6 . Построить таблицу значений и график функции на интервале [-6.3; 6.7]. Ответить на вопросы:
а) Значение функции в точке х=2.7;
б) количество максимумов функции на данном интервале.
2. В живом уголке школы есть ёжик, белка, две морские свинки, три хомячка и черепаха. В день ёж съедает 90 г корма по цене 123 руб./кг, белка 130 г по цене 260 руб./кг, морская свинка 160 г по цене 58 руб./кг, хомячок 80 г по цене 186 руб./кг, черепаха 35 г но цене 540 руб./кг. Руководство школы выделило 3000 руб. на содержание животных. Определить:
а) на сколько дней хватит закупленного корма;
б) сколько денег пойдет на содержание белки.
Вариант 3
1. Дана функция y=5cos(2x+1 )-4sin(x-1 )+6 . Построить таблицу значений и график функции на интервале [-6.3; 6.7]. Ответить на вопросы:
а) Значение функции в точке х=-2,3;
б) количество минимумов функции на данном интервале.
2. Детский новогодний подарок содержит 8 шоколадных конфет по 10 руб. 33 коп., 13 карамельных конфет по 7 руб. 85 кои., 5 конфет с мармеладом по 9 руб. 25 коп., I пачку печенья по 36 руб. и шоколадку по 28 руб.
Профсоюзный комитет выделил 15000 рублей. Определить:
а) сколько подарков можно купить;
б) сколько денег потратят на конфеты с мармеладом.
Вариант 4
1. Дана функция y=5sin(2x+1 )-4cos(x-1 )+6 . Построить таблицу значений и график функции на интервале [-6.3; 6.7]. Ответить на вопросы:
а) Значение функции в точке х=2.7;
б) количество максимумов функции на данном интервале.
1. На изготовления одного торта идет 5 яиц по цене 5 руб. 30 коп за штуку, 150 г муки но цене 28 руб/кг, 200 г масла но цене 310 руб./кг, 250 г сахара по цене 34 руб/кг, 600 г сметаны по цене 115 руб./кг. Инвестор выделил 30000 рублей. Определить:
а) сколько тортов можно испечь;
б) сколько денег понадобится на яйца.
Вариант 5
1. Дана функция y=5sin(x+1 )-4cos(3x-1 )+6 . Построить таблицу значений и график функции на интервале [-6.3; 6.7]. Ответить на вопросы:
а) Значение функции в точке х=-2,3;
б) количество максимумов функции на данном интервале.
2. Для обработки полей на I га требуется 135 кг азотных удобрений по цене 789руб/тонна, 76 кг калийных по цене 1239 руб./тонна, 43 кг фосфорных по цене 1523 руб./тонна, 1.5 кг гербицида по цене 355 руб./кг,0,3 кг инсектицидов по цене 890 руб./кг. Фермер планирует потратить 50000 рублей. Определить:
а) сколько гектаров земли может быть обработано;
б) сколько денег требуется для гербицидов.
Ответы
|
Вариант |
Задание 1 |
Задание 2 |
||
|
а) |
б) |
а) |
б) |
|
|
1 |
14,59214 |
4 |
0,570759 |
3922,26 |
|
2 |
5,629709 |
4 |
23 |
798,6138 |
|
3 |
0,885225 |
4 |
50 |
2352,17 |
|
4 |
7,098124 |
5 |
133 |
3546 |
|
5 |
1,366218 |
6 |
46,91893 |
24984,33 |
Практическая работа 3.16-ИКТ-11кл-Семакин.И.Г. (2017-02-21 )
№ 3.16 ПОЛУЧЕНИЕ РЕГРЕССИОННЫХ МОДЕЛЕЙ В MICROSOFT EXCEL
Цель работы: освоение способов построения по экспериментальным данным регрессионной модели и графического тренда средствами Microsoft Excel.
Используемое программное обеспечение: табличный процессор Microsoft Excel.
Задание 1
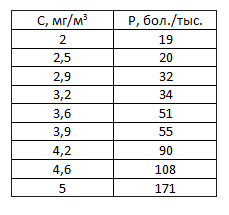
1. Ввести табличные данные зависимости заболеваемости бронхиальной астмой от концентрации угарного газа в атмосфере (см. рисунок).
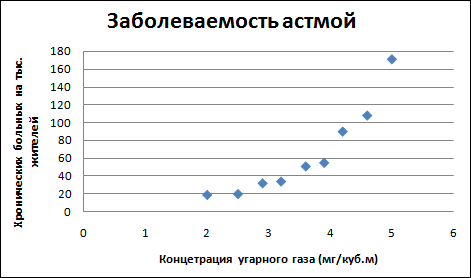
2. Представить зависимость в виде точечной диаграммы (см. рисунок).
Задание 2
Требуется получить три варианта регрессионных моделей (три графических тренда) зависимости заболеваемости бронхиальной астмой от концентрации угарного газа в атмосфере.
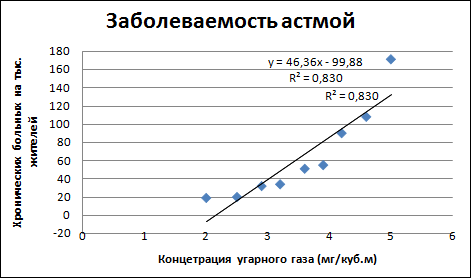
1. Для получения линейного тренда выполнить следующий алгоритм:
=> щелкнуть на поле диаграммы «Заболеваемость астмой», построенной в предыдущем задании;
=> выполнить команду Диаграмма -> Добавить линию тренда;
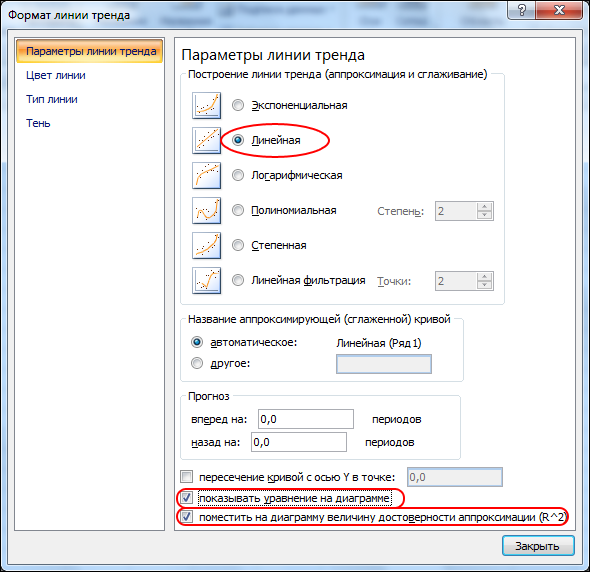
=> в открывшемся окне на вкладке Тип выбрать Линейный тренд;
=> перейти на вкладку Параметры; установить галочки на флажках:
показывать уравнения на диаграмме и поместить на диаграмму величину достоверности аппроксимации R~2;
=> щелкнуть на кнопке ОК.
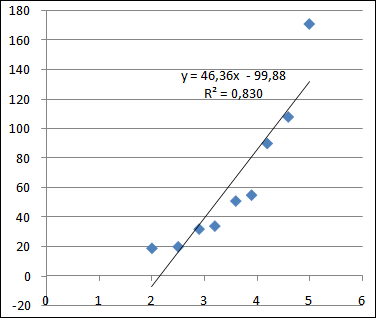
Полученная диаграмма представлена на рисунке:
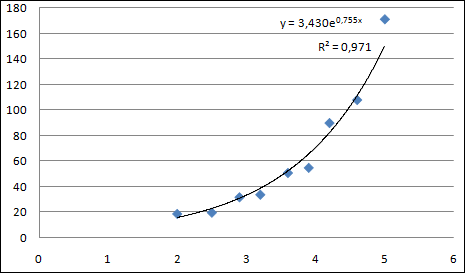
2. Получить экспоненциальный тренд. Алгоритм аналогичен предыдущему. На закладке Тип выбрать Экспоненциальный тренд. Результат представлен на рисунке:
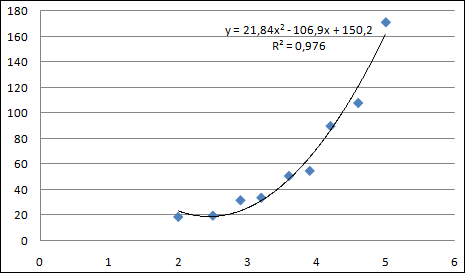
3. Получить квадратичный тренд. Алгоритм аналогичен предыдущему. На закладке Тип выбрать Полиномиальный тренд с указанием степени 2. Результат представлен на рисунке:
После того как вы построили точечную диаграмму зависимости заболеваемости астмой, нужно построить линию тренда.
1. Для этого необходимо выделить диаграмму.
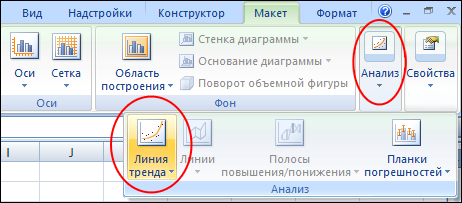
2. В результате выделения в панели инструментов появятся новые разделы. Из этих разделов нам нужно будет перейти в вкладку “Макет”.
3. Из макета нужно перейти в раздел “Анализ”, где мы и найдём операцию построения линии тренда.
Сразу строить линию тренда не советуется, так как нам нужно указать определённые настройки отображения.
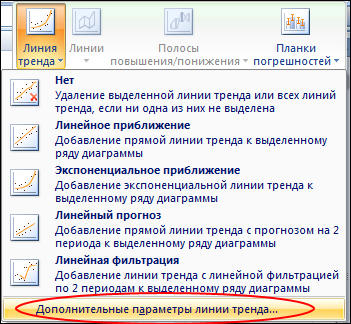
4. Из списка предложенных действий построения линий тренда, выбираем Дополнительные параметры линии тренда.
5. В задании нам говорится:
Цитата
=> в открывшемся окне на вкладке Тип выбрать Линейный тренд;
=> перейти на вкладку Параметры; установить галочки на флажках:
показывать уравнения на диаграмме и поместить на диаграмму величину достоверности аппроксимации R~2;
=> щелкнуть на кнопке ОК.
Устанавливаем настройки согласно запросу:
После выполнения этой операции график примет следующий вид:
6. Остальные пункты делаются по аналогии.