Практическая работа № 2
Тема: Моделирование ситуаций
Задача 2. Обои и комната
1 этап. Постановка задачи
В магазине продаются обои. Наименования, длина и ширина рулона известны. Для удобства обслуживания надо составить таблицу, которая позволит определить необходимое количество рулонов для оклейки любой комнаты.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
D |
Е |
|
|
1 |
Обои и комната |
||||
|
2 |
|||||
|
3 |
Исходные данные |
||||
|
4 |
Комната |
||||
|
5 |
Высота |
2,6 |
|||
|
6 |
Длина |
5 |
|||
|
7 |
Ширина |
3 |
|||
|
8 |
Неоклеив. пов-ть |
15% |
|||
|
9 |
Площадь стен |
Формула 1 |
|||
|
10 |
|||||
|
11 |
Обои |
Промежуточные расчеты |
|||
|
12 |
Обрезки |
10% |
Результаты |
||
|
13 |
Наименования |
Длина |
Ширина |
Площадь рулона |
Количество рулонов |
|
14 |
Образец 1 |
10,5 |
0,5 |
Формула 2 |
Формула 3 |
|
15 |
Образец 2 |
10,5 |
0,6 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
|
16 |
Образец 3 |
10,5 |
0,7 |
||
|
17 |
Образец 4 |
13 |
0,5 |
||
|
18 |
Образец 5 |
13 |
0,6 |
||
|
19 |
Образец 6 |
13 |
0,7 |
Расчетные формулы:
|
Ячейка |
Формула |
|
А10 |
=2*($B$6+$B$7)* $B$5*(1-$B$8) |
|
D14 |
=(1-$B$12)*В14* С14 |
|
Е14 |
=ЦЕЛОЕ($B$9/ D14+1 |
3 этап. Компьютерный эксперимент
Эксперимент 1.
Провести расчет количества рулонов обоев для помещений вашей квартиры
Эксперимент 2.
Изменить данные некоторых образцов обоев и проследить за пересчетом результатов
Эксперимент 3.
Добавить строки с образцами и дополнить модель расчетом по новым образцам.
Задача 3. Компьютерный магазин
1 этап. Постановка задачи
Магазин компьютерных аксессуаров продает товары, указанные в прайс-листе. Стоимость указана в долларах. Если стоимость товара превышает некоторую сумму, покупателю предоставляется скидка. Составить таблицу-шаблон, позволяющую быстро рассчитать стоимость произвольной покупки. В расчете учесть текущий курс доллара.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
D |
Е |
|
|
1 |
Компьютерный магазин |
||||
|
2 |
Дата покупки |
Формула 1 |
|||
|
3 |
|||||
|
4 |
Курс доллара |
30,38 |
|||
|
5 |
Скидки |
5% |
|||
|
6 |
Сумма для учета скидки |
1000 |
|||
|
7 |
Прайс-лист |
||||
|
8 |
Наименование товара |
Цена, $ |
Количества |
Цена, руб. |
Стоимость |
|
9 |
Дискеты 3.5” BASF |
0,12 |
10 |
Формула 2 |
Формула 3 |
|
10 |
Дискеты 3.5” Verbatim |
0,14 |
10 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
|
11 |
Дискеты 3.5”TDK |
0,16 |
0 |
||
|
12 |
CD-R BASF 700 Mb/80 min |
1,7 |
1 |
||
|
13 |
CD-RW Intense 650 Mb/74 min |
2,7 |
0 |
||
|
14 |
Мышь Mitsumi |
5 |
0 |
||
|
15 |
Мышь Genius |
3,5 |
1 |
||
|
16 |
Мышь оптическая |
14 |
0 |
||
|
17 |
Держатель листа (холдер) |
3 |
1 |
||
|
18 |
ИТОГО |
Стоимость покупки без скидки |
Формула 4 |
||
|
19 |
Стоимость покупки со скидкой |
Формула 5 |
Расчетные формулы:
|
Ячейка |
Формула |
|
|
Формула 1 |
B2 |
Команда Вставка – Дата и время |
|
Формула 2 |
D9 |
=B9*$B$4 |
|
Формула 3 |
Е9 |
=С9* D9 |
|
Формула 4 |
Е18 |
=СУММ(Е9:Е17) |
|
Формула 5 |
Е19 |
=ЕСЛИ(Е18$B$6;Е18*(1-$B$5);Е18) |
3 этап. Компьютерный эксперимент
Эксперимент 1.
Ввести курс доллара на текущий день, размер скидки и провести расчет покупки со своим количеством товара.
Эксперимент 2.
Добавить строки другими видами товаров и дополнить модель расчетом по этим данным.
Задача 4. Сберкасса
1 этап. Постановка задачи
За 2 часа до обеденного перерыва 40 бабушек встали в очередь за пенсией. Кассирша обслуживает клиента в среднем одну минуту.
Первая бабушка «мучила» кассиршу вопросами 9 мин. 15 с. Каждая следующая бабушка, частично «мотая на ус» ответы, адресованные предыдущим бабушкам, «мучает» кассиршу на 10 с меньше. Построить модель ситуации и исследовать ее.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
|
|
1 |
Очередь в сберкассе |
||
|
2 |
|||
|
3 |
Исходные данные |
||
|
4 |
Кассир |
||
|
5 |
Время обслуживания одного клиента |
00:01:00 |
|
|
6 |
Очередь |
||
|
7 |
Время общения |
00:09:15 |
|
|
8 |
Уменьшение времени |
00:00:10 |
|
|
9 |
Количество бабушек |
40 |
|
|
10 |
|||
|
11 |
Результаты |
||
|
12 |
№ бабушки |
Время обслуживания бабушки |
Время ожидания бабушки |
|
13 |
1 |
Формула 2 |
Формула 4 |
|
14 |
Формула 1 |
Формула 3 |
Формула 5 |
|
15 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
Расчетные формулы:
|
Ячейка |
Формула |
|
|
Формула 1 |
А14 |
=А13+1 |
|
Формула 2 |
В13 |
=$B$5+$B$7 |
|
Формула 3 |
В14 |
=В13-+$B$8 |
|
Формула 4 |
С13 |
= В13 |
|
Формула 5 |
С14 |
= С13+ В14 |
3 этап. Компьютерный эксперимент
Эксперимент 1.
Изменяя значения ячеек В5, В7, В8, исследовать, влияние этих характеристик на скорость движения очереди.
Проведение исследования
-
Введите в таблицу контрольные исходные данные и скопируйте расчетные формулы в две-три строки.
-
Заполните формулами ячейки на 40 строк.
-
Определите по таблице, сколько времени понадобиться кассиру, чтобы обслужить всю очередь.
-
Найдите в таблице строку, которая соответствует наступлению обеденного перерыва.
Задача 5. Расчет кривой падения электрика
1 этап. Постановка задачи
Электрик Петров приставил к стене лестницу и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать вниз электрик Петров.
2 этап. Разработка модели
Компьютерная модель
|
А |
В |
С |
||
|
1 |
Электрик Петров |
|||
|
2 |
||||
|
3 |
Исходные данные |
|||
|
4 |
Длина лестницы, м |
|||
|
5 |
Количество ступенек |
|||
|
6 |
Номер ступеньки, на которой стоит электрик |
|||
|
7 |
Шаг изменения угла |
|||
|
8 |
Промежуточные расчеты и результаты |
|||
|
9 |
Расстояние между соседними ступеньками |
Формула 1 |
||
|
10 |
Расстояние от ступеньки электрика до пола |
Формула 2 |
||
|
11 |
Расстояние от ступеньки электрика до стены |
Формула 3 |
||
|
12 |
Угол в градусах |
Угол в радианах |
Координата Х |
Координата Y |
|
13 |
Формула 4 |
Формула 6 |
Формула 7 |
Формула 8 |
|
14 |
Формула 5 |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
Заполнить вниз с помощью маркера автозаполнения |
|
15 |
Заполнить вниз с помощью маркера автозаполнения |
Расчетные формулы:
|
Ячейка |
Формула |
|
|
Формула 1 |
C9 |
=$С$4/$С$5 |
|
Формула 2 |
C10 |
=$С$6*$С$9 |
|
Формула 3 |
C11 |
=$С$4-$С$10 |
|
Формула 4 |
А13 |
0 |
|
Формула 5 |
А14 |
= А13+ $С$7 |
|
Формула 6 |
В13 |
=А13/180*ПИ() |
|
Формула 7 |
С13 |
=$С$11*СИН(В13) |
|
Формула 8 |
D13 |
=$С$10*КОС(В13) |
3 этап. Компьютерный эксперимент
Эксперимент 1.
-
Исследовать вид кривой падения электроника в зависимости от номера ступеньки.
-
Исследовать вид кривой в зависимости от номера ступеньки.
Проведение исследования
-
По столбцам С и D постройте диаграмму кривой, по которой движется ступенька с электриком.
ПРАКТИЧЕСКАЯ
РАБОТА №11
Моделирование
случайных процессов в Microsoft Excel
Упражнение 1. ВЕРОЯТНОСТНАЯ МОДЕЛЬ
Цель: Создание
вероятностной модели в электронных таблицах, знакомство с функцией для
генерации случайного числа.
Задание 1. Студенту для
поездки подходит 2 маршрута автобуса. У одного автобуса интервал 10 мин, у
другого — 15 мин. Определить среднее время ожидания и построить в одной системе
координат:
1) график времени ожидания за каждый день года,
2) график среднего времени ожидания для каждого дня
года.
Обоснование задачи. Так как
на остановку студент приходит по-разному, то время ожидания до прибытия
каждого из автобусов будет каждый раз меняться и будет являться случайной
величиной.
СЛУЧАЙНАЯ ВЕЛИЧИНА, СЛУЧАЙНАЯ ПЕРЕМЕННАЯ [random
value, random variable] — всякая наблюдаемая величина, изменяющаяся при
повторении условий, в которых она возникает.
ВЕРОЯТНОСТНАЯ МОДЕЛЬ – это модель, которая содержит
случайные элементы. Таким образом, при задании на входе модели некоторой совокупности
значений, на ее выходе могут получаться различающиеся между собой результаты в
зависимости от действия случайного фактора. Вероятностные модели базируются на
использовании больших серий испытаний со случайными параметрами, причем
точность полученных результатов зависит от количества проведенных опытов.
Для генерации случайной величины в Microsoft Excel
требуется в ячейку ввести формулу =СЛЧИС(). Эта функция возвращает
случайное число из диапазона [0;1).
Чтобы получить случайное вещественное число из
диапазона [0;а), можно использовать следующую формулу: =СЛЧИС()*a.
Если требуется получить случайное вещественное число
между a и b, можно использовать следующую формулу: =СЛЧИС()*(b-a)+a.
Порядок
выполнения.
1. Постройте
в Microsoft Excel таблицу
вида
2. Внесите в
таблицу исходные данные
a –
интервал ожидания 1 автобуса, а=10 минутам;
b –
интервал ожидания 2 автобуса, b=15 минутам;
d – количество
дней в исследуемом периоде (в году) d=365.
3. Заполните
расчетную таблицу формулами в соответствии с математической моделью, используя
абсолютную и относительную адресацию в формулах.
w1 – время
ожидания 1 автобуса (случайное число на отрезке [0;а]);
w2 – время
ожидания 2 автобуса ( случайное число на отрезке [0;b]);
x – время
ожидания за текущий день,
x = min (w1, w2)
t’ср– среднее
время ожидания на текущий день, за n – кол-во дней, для которых
среднее подсчитано;
tср – среднее
время ожидания за год
tср = (x1+x2+…+xn ) / d
4.
Вычислите
время все параметры на исследуемый период (Скопируйте, если это нужно, формулы
вниз на все дни года, используя маркер заполнения)
5.
Построить
на одной диаграмме два графика по заданию (для x и t’ср)
на отдельном листе.
Задание 2. Используя
модель, построенную для решения задачи, определить
·
среднее
время ожидания, если ожидание 1 автобуса 10 мин, 2 автобуса — 60 мин
·
каково
среднее время ожидания, если интервалы автобусов совпадают?
Упражнение
2. БРОСАНИЕ МОНЕТЫ
Цель: моделируя
возможные игровые ситуации (варьируя ставки в данной игре) выяснить, какая
тактика чаще приводит к результату (положительному или отрицательному)
Задание 3. У вас есть 10
монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою
судьбу. Суть игры проста, играя с маклером, вы делаете ставку и бросаете
монету. Если выпадет «орел», маклер выдает вам сумму вашей ставка, в противном
случае – вы ему отдаете сумму. Ставка может быть любой от 1 до 10 монет. Вы
можете назначить самую большую ставку в 10 монет, и тогда за один бросок
выяснится, «сорвали» ли вы банк или, наоборот, обанкротились. Опытные игроки
действуют более осторожно, начиная с маленькой ставки.
Удвоение начального капитала или банкротство приводит
к незамедлительному прекращению этого сеанса игры и расчету. Игра может
продолжиться по вашему усмотрению.
Имитировать результат падения монеты можно с помощью
функции СЛЧИС(). Поскольку вероятность выпадения той или иной стороны 50%,то,
если СЛЧИС()<0,5, то результат «орел» (1), в противном случает – «решка»
(0).
Формула
падения монеты при броске имеет следующий вид:
Бросок
= ЕСЛИ (СЛЧИС()<0,5; 1; 0)
Здесь
«1» на выходе функции означает, что игрок угадал, то есть выпал «орел», а «0» —
не угадал, то есть выпала «решка».
Формула
изменения наличности игрока:
Наличность=
ЕСЛИ(Бросок=1; Наличность+Ставка; Наличность-Ставка)
Формула
определения выигрыша:
Выигрыш=ЕСЛИ(Наличность<2*Начальный
капитал; «-»; «банк»)
Здесь
выдается сообщение «банк» при увеличении наличности вдвое или больше, что
является условием прекращением игры.
Функция
определения проигрыша:
Проигрыш=ЕСЛИ(Наличность>0;
«-»; «банкрот»)
Здесь
выдается сообщение «банкрот» по окончании наличности, что так же является
условием прекращения игры.
Порядок
выполнения работы
1. Создайте в
Microsoft Excel таблицу
вида:
2. Ввести
расчетные данные
3. Провести
следующие исследования
·
Исследовать
выпадения «орла» и «решки» в течение сеанса игры
·
Собрать
статистические данные о выигрыше и проигрыше в течение 10-20 сеансов игры с различными
значениями ставок и исследовать их.
4. Ответьте
на вопросы
·
Кто
чаще выигрывает: казино или игрок?
·
Сколько
в среднем надо сделать бросков до окончания игры?
Упражнение
3. ИГРА В КОСТИ
Цель: Создание игровой
модели, основанной на случайных событиях
Задание 4. Два игрока
бросают по две игральные кости. Сумма очков, выпавших на двух игровых костях,
накапливается. Игра прекращается, когда один из игроков достигает суммы 101.
Игра повторяется до трех побед.
Математическая модель складывается из следующих
рассуждений.
На игровой кости имеется 6 граней с количеством точек
от 1 до 6.
Модель, имитирующая бросание двух костей одним
игроком:
К1=ЦЕЛОЕ (1+6*СЛЧИС())
К2=ЦЕЛОЕ (1+6*СЛЧИС())
Случайные значения суммируются. Суммы бросков по
каждому игроку накапливаются в отдельных столбцах СУММА ПЕРВОГО и СУММА ВТОРОГО
и анализируются после каждого броска в столбце РЕЗУЛЬТАТ
ЕСЛИ (ИЛИ («Сумма первого»>101; «Сумма второго»>101);
«конец игры»; «-»)
Здесь, когда обе суммы меньше 101, в столбце
записывается «-»,а при превышении хотя бы одним игроком порога в столбце
записывается «конец игры». Кто победил, можно определить по соседним столбцам.
Игра прекращается при проявлении сообщения «конец
игры» в столбце РЕЗУЛЬТАТ
Создайте таблицу вида
Заполнить самостоятельно по предложенному материалу,
используя абсолютные и относительные ссылки.
Вопросы:
·
Как
части в нашей жизни происходят случайные процессы?
·
Все
ли случайные процессы можно смоделировать на компьютере?
·
Помогают
ли построенные модели для выбора в жизни?
Литература:
1. Дегтярева
И. Ю. Моделирование процессов. Вероятностные модели [текст] URL: http://www.metod-kopilka.ru/page-2-2-6-11.html
2. Информатика
и ИКТ. Задачник по моделированию. Базовый уровень /Под ред.
Н.В. Макаровой. – Питер. 2007. – 192 с.
Лабораторная
работа № 1
Модель
неограниченного роста
Цель работы: Используя компьютерную модель неограниченного роста
исследовать прирост массы живых организмов с течением времени.
Предположения:
Ø
прирост массы живых организмов за
единицу времени пропорционален уже их имеющейся массе;
Ø
регулятором прироста выступает
окружающая среда;
Ø
коэффициент размножения постоянен
Параметры модели:
Ø
начальная масса живых организмов
М(0) = 1 т;
Ø
коэффициент размножения k:
|
Природная зона |
Тундра |
Тайга |
Степь |
Пустыня |
|
Коэффициент k |
0,6 |
1,8 |
1,2 |
0,8 |
Ø
время n.
Связь между параметрами модели задается соотношением:
М(n+1) = (1 +
k) М(n)
Задача:
1)
Определить, через сколько лет
масса растений в различных природных зонах превысит 100 т;
2)
Определить, через сколько лет
масса растений в различных природных зонах превысит 1000 т, 10000 т (т.е.
произойдет ее «удесятерение») ;
3)
Построить график зависимости массы
растений от числа прошедших лет (для каждой природной зоны);
4)
Определить, через сколько лет
масса растений в различных природных зонах превысит
массу Земли (5 976 000 000
000 000 000 000 т).
Ход работы:
|
А |
В |
C |
D |
E |
F |
|
|
1 |
Природная зона |
Год |
Тундра |
Тайга |
Степь |
Пустыня |
|
2 |
Коэффициент размножения k |
0,6 |
1,8 |
1,2 |
0,8 |
|
|
3 |
Начальная масса М(0) |
0 |
1 |
1 |
1 |
1 |
|
4 |
Масса через 1 год |
В3+1 |
C3*(1+C2) |
D3*(1+D2) |
||
|
5 |
Масса через 2 года |
В4+1 |
C4*(1+C2) |
D4*(1+D2) |
||
|
6 |
1.
Загрузите электронную таблицу Excel
и занесите в таблицу 2 исходные данные (они выделены цветом) и формулы.
2.
Измените формулы в блоке ячеек C4:D5 с
учетом того, что номер строки в адресах некоторых ячеек должен быть абсолютным
(неизменным при копировании в последующие строки).
3.
Занесите формулы в ячейки Е4 и F4.
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
4.
Последовательно скопируйте блок
ячеек В4:F4 в последующие строки. Копирование прекратить, как
только во всех четырех столбцах C, D, E и F возникнут числа, большие 100.
Для каждой природной зоны определите,
через сколько лет масса растений
превысит 100 т. Результаты запишите в отчет.
5.
С помощью электронной таблицы вычислить,
через сколько лет масса растений в различных природных зонах превысит 1000 т и
10000 т.
Результаты запишите в отчет.
Для каждой природной зоны сделайте вывод о времени, необходимом для увеличения
массы растений в 10 раз.
6.
С помощью электронной таблицы
вычислить, через сколько лет масса растений в различных природных зонах
превысит массу Земли, равную 5 976 000 000 000 000 000 000 т.
Результаты запишите в отчет.
Для каждой природной зоны сделайте вывод о времени, когда масса растений
превысит массу Земли.
7.
С помощью электронной таблицы для
каждой природной зоны построить график зависимости массы растений от числа
прошедших лет.
Таблицу в режиме отображения
значений и графики приложите к отчету.
Лабораторная
работа № 2
Модель
ограниченного роста
Цель работы: Используя компьютерную модель ограниченного роста
исследовать прирост массы живых организмов с течением времени.
Предположения:
Ø
прирост массы живых организмов за
единицу времени пропорционален уже их имеющейся массе;
Ø
существует некоторое предельное
значение массы живых организмов;
Ø
коэффициент прироста массы живых
организмов за единицу времени пропорционален разности между максимально
возможным значением массы и массой, имеющейся к данному моменту времени.
Параметры модели:
Ø
начальная масса живых организмов
М(0) = 1 т;
Ø
предельное значение массы живых
организмов L = 11000 т.
Ø
коэффициент пропорциональности a
в формуле для коэффициента прироста;
Ø
время n.
Связь между параметрами модели задается соотношением:
М(n+1) = М(n)
+ а М(n) (L — М(n))
k(n) = a (L — M(n))
а = k(n)
/ (L — M(n)),
т.е. при n=0
Þ а = k(0) / (L
— M(0))
|
Природная зона |
Тундра |
Тайга |
Степь |
Пустыня |
|
Коэффициент k |
0,6 |
1,8 |
1,2 |
0,8 |
Задача:
1)
Определить, через сколько лет
масса растений в различных природных зонах превысит 100 т;
2)
Определить, через сколько лет
масса растений в различных природных зонах превысит 1000 т; 10 000 т (т.е.
произойдет ее «удесятерение»)
3)
Построить график зависимости массы
растений от числа прошедших лет (для каждой природной зоны);
Ход работы:
1.
Загрузите электронную таблицу Excel
и занесите в таблицу исходные данные (они выделены цветом) и формулы:
|
А |
В |
C |
D |
E |
F |
|
|
1 |
Природная |
Год |
Тундра |
Тайга |
Степь |
Пустыня |
|
2 |
Коэффициент |
0,6 |
1,8 |
1,2 |
0,8 |
|
|
3 |
Предельное |
11000 |
11000 |
11000 |
11000 |
|
|
4 |
Коэффициент |
|||||
|
5 |
Начальная |
0 |
1 |
1 |
1 |
1 |
|
6 |
Масса через 1 год |
B5+1 |
C5+C4*C5*(C3-C5) |
D5+D4*D5*(D3-D5) |
||
|
Масса через 2 года |
B6+1 |
2.
Измените формулы в блоке ячеек C4:D5
с учетом того, что номер строки в адресах некоторых ячеек должен быть абсолютным
(неизменным при копировании в последующие строки).
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
3.
Последовательно скопируйте блок
ячеек В4:F4 в последующие строки. Копирование прекратить, как только во всех
четырех столбцах C, D, E и F возникнут числа, большие 100.
Результаты занесите в отчет.
Сравните с результатами предыдущей практической работы и сделайте выводы.
4.
С помощью электронной таблицы
вычислить, через сколько лет масса растений в различных природных зонах превысит
1000 т и 10000.
Результаты занесите в отчет.
Сравните с результатами предыдущей практической работы и сделайте выводы.
5.
С помощью электронной таблицы для
каждой природной зоны построить график зависимости массы растений от числа
прошедших лет.
Таблицу в режиме отображения
значений и графики приложите к отчету.
Лабораторная
работа № 3
Границы
адекватности модели неограниченного роста
Цель работы: Найти
границы адекватности модели неограниченного роста.
Предположения и параметры моделей:
Всякая модель имеет ограниченную область адекватности,
и за пределами этой области она перестает удовлетворительно отражать свойства
моделируемого объекта. Модель неограниченного роста остается адекватной, пока
масса живых организмов достаточно мала по сравнению с предельно допустимой
массой этих организмов в данных природных условиях.
Параметры модели неограниченного роста: начальная масса М(0), коэффициент прироста k,
предельное значение массы L, число лет n,
масса живых организмов через n лет М(n);
связь между параметрами модели
определяется формулой:
М(n+1)
= (1 + k) М(n)
Параметры модели ограниченного роста: начальная масса Мо(0), коэффициент
прироста k, число лет n, масса живых организмов через n лет
Мо(n); связь
между параметрами модели определяется формулой:
Мо(n+1) = (1+ k (L – Мо(n))/(L —
M(0)) ) Мо(n)
Поскольку Мо(0)=
М(0), то нетрудно подсчитать, что Мо(1)= М(1), но
вот уже Мо(2)< М(2). И чем дальше, тем больше будет
различие между значениями Мо и М. Будем считать модель
неограниченного роста адекватной, если разница М – Мо
составляет не более 10% от Мо.
Экспериментально
установлено, что предельное значение массы L образует
геометрическую прогрессию относительно границы адекватности n, т.е. L=
b×2n-1, где b – некоторый коэффициент.
Т.к. 2=1+k,
то L= b×(1+k)
n-1.
Отсюда b = L /×(1+k) n-1
Компьютерные эксперименты
показали, что моделью неограниченного роста можно пользоваться с уровнем
погрешности в 10% при выполнении условия L
³ 8×(1+k)
n-1.
Выражение для n полученное при решении показательного неравенства,
показывает, как долго можно пользоваться моделью неограниченного роста при
заданных (предельного уровня массы живых организмов) и (коэффициента
ежегодного прироста):
n £ 1+lg(0,125L)/lg(1+k)
Задание: При начальной массе М(0)=1:
1)
Найти границу адекватности n
при k=1,8 и L=11000.
2)
Исследовать, как граница
адекватности n зависит от величины k (L=11000;
k=1,8; 1,2; 1)
3)
Исследовать, как граница
адекватности n зависит от величины L (k=1; L= 5500; 11000; 22000; 44000)
4)
Исследовать, как коэффициент b зависит от k
(L=5000; k=1; 1,2; 1,5; 2)
Ход работы:
1.
Загрузите электронную таблицу
Excel и занесите в таблицу исходные данные и формулы (при занесении формулы в
ячейку Е2 используйте функцию).
|
A |
B |
C |
D |
E |
|
|
1 |
k |
L |
b |
||
|
2 |
Год (n) |
Неограниченный рост |
Ограниченный рост |
Отклонение, в % |
D1/СТЕПЕНЬ((1+В1);А3-1) |
|
3 |
0 |
1 |
1 |
0 |
|
|
4 |
А3+1 |
(1+В1)*В3 |
(1+В1*(D1-C3)/(D1-C3))*C3 |
(B4-C4)/C4*100 |
|
|
5 |
А4+1 |
(1+В1)*В4 |
(1+В1*(D1-C4)/(D1-C3))*C4 |
(B5-C5)/C5*100 |
2.
Измените формулы в блоке ячеек В4:С5
с учетом того, что номер строки в адресах некоторых ячеек должен быть
абсолютным (неизменным при копировании в последующие строки).
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
3.
Занесите в ячейку В1 значение
коэффициента прироста k=1,8, в ячейку D1 – значение предельной массы живых
организмов L=11000.
4.
Последовательно копируя блок ячеек
А4:D4 в последующие строки найдите, в какой год отклонение
превзойдет границу 10%. Результаты занесите в отчет.
5.
Найдите границу адекватности n
при L=11000 и различных k, равных: 1,8; 1,2 и 1.
Результаты занесите в отчет.
Сделайте выводы об изменении границы
адекватности n с уменьшением k.
6.
Найдите границу адекватности n
при k=1 и различных L, равных: 5500; 11000; 22000 и
44000.
Результаты занесите в отчет.
Сделайте вывод о виде зависимости значения
предельной массы живых организмов L относительно границы адекватности n..
7.
Найдите коэффициент b при L=5000
и различных k, равных: 1; 1,2; 1,5; 2. В ячейке Е2 вместо А3
вставляйте значение года n (или соответствующий номер ячейки), когда отклонение
превзойдет границу 10%. Убедитесь, что во всех случаях b приблизительно
одинаково.
Результаты занесите в отчет.
Сделайте выводы о том, зависит ли коэффициент
b от
коэффициента прироста k .
Лабораторная работа № 4
Метод половинного деления
Цель работы:
Найти значение корня уравнения методом половинного деления.
Задача:
Найти значение корня уравнения:
Вариант №1. x5 — 4x2 + x -2 = 0, с
точностью d=0,001
Вариант №2. x3 — 3x + 3 = 0, с точностью d=0,0005
Вариант №3. 2х = 3х, с точностью d=0,002
Вариант №4. cos(x) = х, с точностью d=0,005
Ход работы:
1.
Загрузите электронную таблицу Excel
и занесите в таблицу исходные данные в выделенные цветом ячейки (в ячейке D1
укажите исследуемую функцию) и необходимые формулы (в вычисляемые ячейки C2, D2, E2).
|
A |
B |
C |
D |
Е |
F |
|
|
1 |
a |
b |
(a+b)/2 |
f(x)= |
b-a |
d |
|
2 |
Подготовленную таблицу в
режиме отображения формул приложите к отчету.
2.
Определите отрезок [ a; b ] длиной
1, значения на концах которого, образуют «вилку» для корня уравнения.
Результат занесите в отчет. Укажите значение функции на концах отрезка.
3.
Вставьте найденные значения a и b в ячейки A2 и B2
соответственно.
4.
Методом половинного деления
найдите значение корня уравнения с заданной точностью d.
Результаты занесите в отчет.
Сделайте выводы.
Практическая работа
Тема: Моделирование в среде табличного процессора.
Цель: Демонстрация возможностей моделирования в среде табличного процессора MS Excel.
Развитие творческих способностей у учащихся.
Анализ объекта: Компьютерная модель в среде MS Excel.
Задача /12баллов/. Падение с лестницы.
Электрик Петров приставил к стене лестницу длины L, имеющую 10 ступенек, и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать электрик Петров в зависимости от того, на какой ступеньке он стоит.
Математическая модель:
Обозначим: L – длина лестницы;
N – число ступенек лестницы (по условию задачи N =10);
k – номер ступеньки, на которой стоит электрик и для которой ведется расчет траектории движения.
Для определенности считаем, что ступеньки пронумерованы от 1 до N, начиная снизу. Будем считать, что лестница первоначально занимала вертикальное положение. Это не совсем реально, но удобно для дальнейших расчетов.
При скольжении концов лестницы координата y конца A изменяется от L до 0,
координата x = 0 всегда.
А для конца B наоборот – координата x изменяется от 0 до L, а y = 0.
У промежуточных точек изменяются обе координаты.
В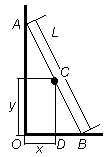
, при этом
Используя эти выражения, получаем:.
Из это пропорции можно получить формулы для координат k-й ступеньки:
(1)
(2)
Расстояния OA и OB связаны с теоремой Пифагора:
Из этой формулы можно выразить OA через OB: , или наоборот. (3)
Траекторию движения ступеньки с электриком будем строить поточечно. Обозначим M – количество точек расчета. В дальнейшем будем вычислять координаты ступеньки для положений лестницы, при которых нижний конец – точка B – перемещается на одну и ту же величину . Изменяя координату x точки B от 0 до L с шагом
, вычисляем длину отрезка OA по формуле (3), а затем координаты ступеньки по формулам (1) и (2).
Задание:
-
Составьте компьютерную модель, проведите расчет координат положения электрика в зависимости от положения лестницы. Пример заполнения электронной таблицы:
| Падение с лестницы | |||
| Исходные данные | |||
|
Длина лестницы, м |
1,8 |
||
|
Количество ступенек |
10 |
||
|
Номер ступеньки, на которой стоит электрик |
8 |
||
|
Количество точек расчета |
20 |
||
| Промежуточные расчеты и результаты | |||
|
Шаг изменения положения точки B |
|||
|
OB |
OA |
Координата x |
Координата y |
|
Заполнить вниз |
Заполнить вниз |
Заполнить вниз |
Заполнить вниз |
-
По результатам вычислений по столбцам C и D постройте диаграмму кривой, по которой движется ступенька с электриком. Убедитесь, что эта кривая похожа на четверть эллипса, сплющенного либо к оси ординат (если номер ступеньки 5), либо к оси абсцисс (если номер ступеньки
-
Проведите расчет и постройте общую диаграмму кривых для всех ступенек. Для построения общей диаграммы надо скопировать результаты проведения экспериментов в соседние столбцы.
Чему научились:
-
Создавать модели в среде табличного процессора MS Excel.
-
Создавать интегрированный документ.
-
Использовать знания, полученные на предыдущих уроках.
2
Сборник заданий в среде электронных таблиц Excel. Охвачены темы ввода данных, форматирования, создания диаграмм и графиков, работы с формулами и функциями. Можно пользоваться, как практикумом по работе в Excel в 9 — 11 классах
В электронных таблицах можно выполнять задачи поиска, сортировки данных. Можно фильтровать инфориацию по заданным критериям.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Контрольное задание»
Задание 1
|
Температура воздуха в городах мира за неделю |
|||||||
|
№ |
Дата |
Москва |
Рим |
Париж |
Лондон |
Мадрид |
Макс. темпер. |
|
1 |
22.09.2009 |
16 |
21 |
14 |
12 |
22 |
|
|
2 |
23.09.2009 |
15 |
22 |
15 |
11 |
23 |
|
|
3 |
24.09.2009 |
12 |
19 |
12 |
13 |
21 |
|
|
4 |
25.09.2009 |
17 |
18 |
13 |
12 |
20 |
|
|
5 |
26.09.2009 |
15 |
19 |
15 |
14 |
19 |
|
|
6 |
27.09.2009 |
14 |
22 |
17 |
15 |
20 |
|
|
7 |
28.09.2009 |
11 |
20 |
16 |
12 |
22 |
|
|
Ср. темпер. |
|||||||
|
|||||||
Задание 2
Имеется ведомость успеваемости учебной группы по четырем предметам. Обработайте исходные данные с помощью электронных таблиц и получите ответы на следующие вопросы.
-
Какой средний балл имеет каждый учащийся?
-
Какой средний балл получила группа по каждому предмету?
-
Постройте столбиковую гистограмму для средних баллов по предметам.
Исходные данные:
|
№ |
Фамилия И.О. |
Физика |
Матема-тика |
Инфор-матика |
История |
Ср. балл |
|
1 |
Иванов И.И. |
4 |
3 |
5 |
4 |
|
|
2 |
Петров П.П. |
4 |
5 |
4 |
5 |
|
|
3 |
Сидоров С.С. |
5 |
5 |
4 |
4 |
|
|
4 |
Семенов С.С. |
3 |
3 |
4 |
3 |
|
|
5 |
Степанов С.С. |
4 |
4 |
4 |
4 |
|
|
6 |
Николаев Н.Н. |
5 |
5 |
5 |
5 |
|
|
7 |
Никитин Н.Н. |
3 |
4 |
4 |
5 |
|
|
8 |
Сергеев С.С. |
3 |
4 |
3 |
3 |
|
|
9 |
Александров А.А. |
5 |
4 |
3 |
3 |
|
|
10 |
Алексеев А.А. |
4 |
5 |
4 |
5 |
|
|
Ср.балл |
Задание 3.
РАСЧЕТ ПОВРЕМЕННОЙ ЗАРАБОТНОЙ ПЛАТЫ
|
ФАМИЛИЯ |
Ставка за час, руб. |
Количество отработанных часов |
начис-лено, руб. |
Налог (14%), руб. |
Итого к выдаче, руб. |
|
Иванов |
5694 |
157 |
|||
|
Петров |
4121 |
134 |
|||
|
Сидоров |
2312 |
162 |
|||
|
Козлов |
4557 |
278 |
|||
|
Михайлов |
3782 |
115 |
|||
|
Дубинин |
2677 |
219 |
Формат ячеек денежный в рублях.
Ввести соответствующие формулы:
-
начислено = ставка*количество отработанных часов
-
налог = начислено*0,14
-
к выдаче = начислено — налог
Задание 4
-
В табличном процессоре Excel выполнить табуляцию функции
на отрезке [-4;4] с некоторым шагом (шаг вводится с клавиатуры). Построить график данной функции. На графике указать названия осей и подписи значений функции
Время реализации практикума – 4 часа.
Основой практикума стала статья “Построение и исследование вероятностных
(стохастических) моделей”, опубликованная в [1, с.45–47].
Тип урока: урок-исследование
Цели урока:
- Формирование умений и навыков общенаучного, общеинтеллектуального
характера - Формирование общеучебных и исследовательских навыков работы с
компьютером. - Развитие творческого мышления.
- Умение использовать дополнительные источники информации (литература,
справочную информацию о программе, и т.д.) - Развитие навыков интерпретации (истолковывания) информации, анализа
результатов.
Задачи урока:
- Воспитательная – развитие познавательного интереса, осознание своей
значимости в образовательном процессе. - Учебная – углубление знаний по компьютерному моделированию в среде MS
Excel - Развивающая – развитие исследовательского и аналитического мышления,
нестандартного решения возникающих проблем, расширение кругозора.
Оборудование: компьютеры с операционной системой Windows 9x и выше,
проектор, экран, программные средства: пакет Microsoft Office, MS PowerPoint, MS
Excel
В практической работе поставлена задача:
Проверить, действительно ли датчик случайных чисел в электронных таблицах
подчиняется закону равномерного распределения. [1, с.45]
Компьютерный эксперимент состоял в моделировании проверки распределения
значений, получаемых с помощью датчика случайных чисел: [1, с.45–46]
- “Выбросить” N чисел в каком-либо интервале [a, b]
- разбить интервал на M частей
- подсчитать количество чисел, попавших в каждую часть. Если доля попавших
чисел для каждой части близка к N/M, то распределение равномерное.
Предполагаемое оформление работы в среде электронных таблиц [1, с.46]
<Рисунок 1>
Выполнение практической работы в среде MS Excel требует от учащихся следующих
умений и навыков:
- Вводить и редактировать данные всех трёх типов (числа, текст и формулы).
- Объединять ячейки.
- Форматировать данные.
- Оформлять ячейки и диапазоны ячеек.
- Использовать автозаполнение ячеек.
- Использовать копирование диапазонов ячеек.
- Применять встроенные функции MS Excel категорий Логические,
Математические. - Строить диаграммы с помощью Мастера.
- Применять условное форматирование ячеек.
- Уметь интерпретировать (истолковывать) информацию.
Технически выполнение учащимися практической работы не вызывает затруднений.
Но само понятие случайности, а тем более равномерности распределения учащимся
трудно представить. Поэтому большинство учащихся выполняет действия формально,
не задумываясь о содержательной интерпретации результатов.
Автор данной разработки счёл необходимым дополнить практическое занятие
основными теоретическими сведениями и углубить компьютерный эксперимент в части
наглядного изображения результатов работы датчика случайных чисел.
План занятия по теме “Построение и исследование вероятностных
(стохастических) моделей”:
- Понятие случайной величины <презентация>.
- Практическая работа с датчиком случайных чисел в среде MS Excel.
- Практическая работа “Построение и анализ диаграмм по результатам работы
датчика случайных чисел”.
Ход занятия
1. Понятие случайной величины <презентация>
Понятие и наглядное представление случайной величины (Слайды 4–8
презентации) представляют вводную часть практического занятия.
Выборка букв русского алфавита не велика по объёму, составлена произвольно,
но с повтором нескольких букв.
| Буква | Номер (по алфавиту) |
| Ь | 30 |
| О | 16 |
| М | 14 |
| Т | 20 |
| Г | 4 |
| А | 1 |
| Ы | 29 |
| С | 19 |
| Ч | 25 |
| Ь | 30 |
| В | 3 |
| М | 14 |
Далее объявляется Статистическая пауза, во время которой учащиеся проводят
мини-исследование.
Статистическая пауза.
Каждому учащемуся выдаётся лист с текстовым фрагментом. <Приложение
1>
Текст выбран произвольно, с учётом его познавательного характера [2, с.45]
Задание 1. Посчитать количество появлений каждой буквы из выборки в
текстовом фрагменте.
Для более рационального использования времени и быстрого получения
результатов каждый учащийся считает появление одной буквы в текстовом фрагменте.
Задание 2. Построить гистограмму частоты появлений в текстовом фрагменте
каждой буквы из выборки
Учащиеся строят гистограммы в среде MS Excel.
<Рисунок 2>, <Рисунок
3>, <Рисунок 4>
Результаты выводятся на экран для совместного обсуждения. В ходе обсуждения
возникают естественные вопросы:
Изменятся ли результаты подсчётов, если:
- Выбрать другие буквы алфавита
- Увеличить выборку букв алфавита
- Выбрать другой текст
Ответ очевиден. Эксперимент требует многократного проведения.
Для лучшего понимания равномерности распределения учащимся предлагается
привести примеры объектов, процессов, которые могут быть равномерными (Слайд
14 презентации). (Более простая форма задания: привести словосочетания, в
которых используется слово равномерный).
Наиболее часто приводятся примеры:
Равномерная скорость.
Равномерное развитие (движение).
Равномерно распределить что-либо.
Примеры позволяют обобщить понятие равномерного процесса.
Равномерный процесс как одинаковый, постоянный в каком-нибудь отношении,
на всём протяжении, во всех частях чего-нибудь.
Приведённая часть занятия является вводной для последующей практической
работы.
В Слайдах 16–18 презентации раскрывается основное содержание
компьютерного эксперимента – тест на равномерность. <Рисунок
5>
В Сайдах 19–22 представлены части практической работы на основе
изложенного теоретического материала.
<Рисунок 6>, <Рисунок
7>
2. Выполнение практической работы с датчиком случайных чисел в среде MS Excel
Каждый учащийся получает лист с описанием практической работы. <Приложение
2>
Результат работы, выполненной учащимися. <Рисунок 8>
Проблема.
Анализ результатов практической работы показал недостаточную наглядность
распределения случайных чисел.
Наглядным средством для отображения зависимости между данными в электронных
таблицах являются диаграммы.
Следующая часть практической работы носит экспериментальный исследовательский
характер.
Начало работы по эксперименту 1 может быть предложено в качестве домашнего
задания. В ходе обсуждения идей на следующем занятии учащиеся могут себя
проверить и выполнить практическую часть.
3. Практическая работа “Построение и анализ диаграмм по результатам работы
датчика случайных чисел”.
Эксперименты строятся на основе предложений, возникающих во время “мозгового
штурма”.
Результаты каждого эксперимента выводятся на экран для выявления недостатков и
обсуждения дальнейших шагов.
Эксперимент 1.
Учитель ставит более простую задачу: Наглядно представить результаты работы
датчика случайных чисел в MS Excel.
Функция СЛЧИСЛ () возвращает равномерно распределенное случайное число, большее
либо равное 0 и меньшее 1. Новое случайное число возвращается каждый раз, когда
рабочий лист (или формула) вычисляются повторно.
Для наглядности учащиеся предлагают цветовое решение:
Если значение случайной величины больше 0,5, то в ячейку заносится 1 и ячейка
закрашивается одним цветом, в противном случае – значение ячейки равно 0, и она
закрашивается контрастным цветом.
Реализация такого предложения требует применения условной функции.
Учащимся предлагается самостоятельно разобраться в том, как работает условная
функция. Для этого используются справочные возможности программы MS Excel.
Один из примерных результатов этого небольшого исследования приведён на рисунке.
<Рисунок 9>
Эксперимент 2.
Обсуждение вместе с учащимися результатов эксперимента 1 выявляет недостаток:
наряду с цветом желательно использовать автоматический подсчёт 0 и 1.
В ячейке E21 – функция, подсчитывающая сумму (а значит, количество) “единиц”:
=СУММ(E2:E20). Соответственно, в ячейке D21 – функция, подсчитывающая количество
чисел в диапазоне за вычетом результата ячейки E21: =СЧЁТ(A2:A20)-E21.
К недостаткам результата эксперимента 2 учащиеся отнесли наличие двух
отдельных столбцов для 1 и для 0. Даже цветовое решение не помогает сделать
более наглядным вывод о приблизительно равном появлении “1” и “0”.
<Рисунок 10>
Эксперимент 3.
Блочное размещение “1” и “0” в одном столбце.
Реализация поставленной цели потребовала использования двух моделей: на основе
модели из эксперимента 2 строится следующая, в которой количество “1” и “0”
представлено цветовыми блоками.
Числовые значения в ячейках показывают разность между количеством “1” и числом
закрашенных ячеек. С увеличением номера ячейки разность уменьшается. Эти
числовые значения затрудняют восприятие “равномерности”
<Рисунок 11>
Эксперимент 4.
Использование Мастера диаграмм.
С помощью Мастера диаграмм учащиеся самостоятельно строят гистограмму и круговую
диаграмму по результатам работы датчика случайных чисел.
Анализ результатов эксперимента 4 показал, что гистограмма и круговая диаграмма
дают наиболее наглядные и простые модели.
<Рисунок 12>
Окончательный результат.
Гистограмма, круговая диаграмма и график выбраны для окончательного
представления результатов практической работы.
Самым неожиданным для учащихся стала простота окончательного решения по
сравнению с первыми экспериментами.
<Рисунок 13>
Литература.
- С.А. Бешенков, Е.А. Ракитина Решение типовых задач по
моделированию// Журнал Информатика в школе, № 1, 2005, с.45-47. – М.:
“Образование и Информатика”, 2005. - Н.В. Семакова Методические разработки уроков по сетевым
технологиям. Изучение сетевых технологий в VII–XI классах// Журнал
Информатика в школе, № 7, 2010, стр. 85, М.: – Информатика и образование,
2010.
Федеральное
государственное бюджетное образовательное учреждение высшего образования
«Саратовский
государственный технический университет имени Гагарина Ю.А.»
Кафедра «Экспертиза и управление недвижимостью»
Компьютерное моделирование в MS EXCEL
Задания
для практических занятий по курсу «ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В СТРОИТЕЛЬСТВЕ»
для студентов направления «строительство
Одобрено:
Зав.каф. ЭУН
__________Я.С.Стрельцин
Председатель УМКН
«Строительство»
____________
САРАТОВ
2016
Оглавление
ВВЕДЕНИЕ
ЗАДАЧИ ОПТИМИЗАЦИИ.. 2
ЗАДАЧА О
РАЗМЕЩЕНИИ СТРОЯЩЕГОСЯ ОБЪЕКТА.. 3
МАТЕМАТИЧЕСКАЯ
ПОСТАНОВКА ЗАДАЧИ О МЕСТОПОЛОЖЕНИИ ВНОВЬ СТРОЯЩЕГОСЯ ОБЪЕКТА.. 4
РЕШЕНИЕ
ЗАДАЧИ О МЕСТОПОЛОЖЕНИИ СТРОЯЩЕГОСЯ ОБЪЕКТА С ПОМОЩЬЮ MS EXCEL.. 5
ЗАДАЧА ОБ
ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ.. 9
ПОСТАНОВКА ЗАДАЧИ ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ.. 10
МАТЕМАТИЧЕСКАЯ
ПОСТАНОВКА ЗАДАЧИ ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ.. 10
РЕШЕНИЕ
ЗАДАЧИ ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ С ПОМОЩЬЮ MS EXCEL.. 12
ЗАДАНИЕ 1
МЕСТОПОЛОЖЕНИЕ СТРОЯЩЕГОСЯ ОБЪЕКТА.. 15
ЗАДАНИЕ 2
ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ ОПРЕДЕЛЕННЫХ РАЗМЕРОВ ИЗ ЦЕЛЫХ ЗАГОТОВОК С ПОМОЩЬЮ MS
EXCEL.. 17
Задача
оптимизации перевозок. 19
Постановка задачи.. 19
Варианты заданий.. 19
Рекомендации по
математической модели и решению… 21
Задача
оптимизации плана выпуска продукции. 22
Постановка задачи.. 22
Варианты заданий.. 23
Рекомендации по
математической модели и решению… 24
ВВЕДЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ
В методических указаниях
рассматриваются задачи оптимизации для инженерных задач и решение их в среде MS Excel для строительных специальностей.
Интерес к этим задачам обусловлен спецификой их
формализации и прикладной значимостью.
Функции MS Excel обладают развитым аппаратом
численного анализа данных, позволяющим решать сложные задачи линейного и
нелинейного программирования со многими неизвестными и ограничениями, что
делает его очень удобным инструментом решения задач оптимизации.
В MS Excel для решения различных задач
оптимизации есть средство Поиск решения. Эта команда находится в меню Сервис.
Если команда не обнаруживается, это значит, надстройка Поиск решения не
загружена. Для загрузки надо выбрать Надстройки из меню Сервис.
Из списка диалогового окна выбирается Поиск решения и в квадратике
устанавливается флажок. В случае отсутствия в списке надстройки Поиск
решения, запускается








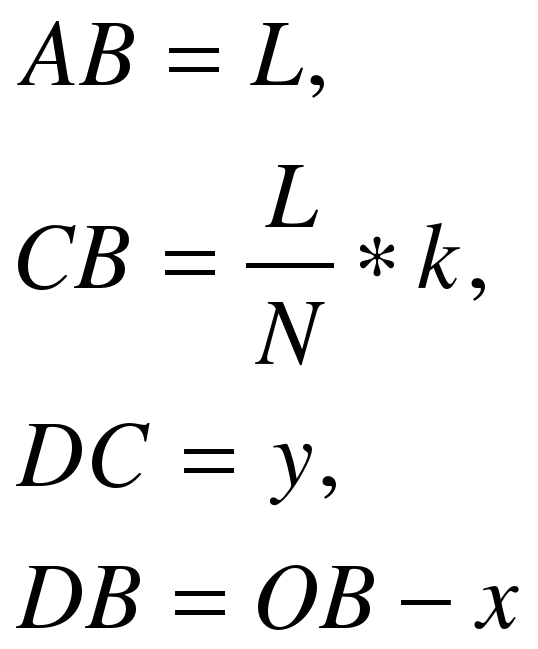
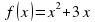 на отрезке [-4;4] с некоторым шагом (шаг вводится с клавиатуры). Построить график данной функции. На графике указать названия осей и подписи значений функции
на отрезке [-4;4] с некоторым шагом (шаг вводится с клавиатуры). Построить график данной функции. На графике указать названия осей и подписи значений функции