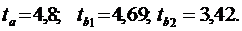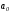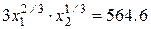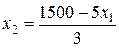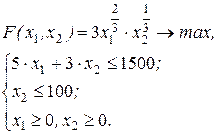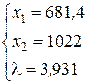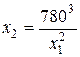Ппп ms office excel - Word и Excel - помощь в работе с программами

Содержание

Решение с помощью ППП Excel
Запуск надстройки Power Pivot для Excel
Откройте окно Power Pivot.
Устранение неполадок: исчезновение ленты Power Pivot
Решение задач с помощью ППП Excel (инструмент Регрессия)

Решение с помощью ППП Excel

Задача 3.3 Динамика выпуска продукции Швеции характеризуется данными (млн. долл.), представленными в табл. 3.3.1.

1. Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда – ЛГРФПРИБЛ. В качестве зависимой переменной в данном примере выступает время (t = 1, 2, …, n). Приведем результаты вычисления функции ЛИНЕЙН и ЛГРФПРИБЛ (рис. 3.1 и 3.2).

Рис. 3.1 Результат вычисления функции ЛИНЕЙН

Рис. 3.2 Результат вычисления функции ЛГРФПРИБЛ

Запишем уравнение линейного и экспоненциального тренда, используя данные рис. 3.1 и 3.2:

2. Построение графиков осуществляется с помощью Мастера диаграмм.

Порядок построения следующий:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2) активизируйте Мастер диаграмм любым из следующих способов:

а) в главном меню выберите Вставка / Диаграмма;

б) на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм;

3) в окне Тип выберите График (рис. 3.3); вид графика выберите в поле рядом со списком типов. Щелкните по кнопке Далее;

Рис. 3.3 Диалоговое окно Мастера диаграмм: тип диаграммы

4) заполните диапазон данных, как показано на рис. 3.4. Установите флажок размещения данных в столбцах (строках). Щелкните по кнопке Далее;

Рис. 3.4 Диалоговое окно Мастера диаграмм: источник данных

5) заполните параметры диаграммы на разных закладках (рис. 3.5): название диаграммы и осей, значение осей, линии сетки, параметры легенды, таблица и подписи данных. Щелкните по кнопке Далее;

Рис. 3.5 Диалоговое окно Мастера диаграмм: параметры диаграммы

6) укажите место размещения диаграммы на отдельном или имеющемся листе (рис. 3.6). Щелкните по кнопке Далее. Готовая диаграмма, отражающая динамику уровня изучаемого ряда, представлена на рис. 3.7.

Рис. 3.6 Диалоговое окно Мастера диаграмм: размещение диаграммы

Рис. 3.7 Динамика выпуска продукции

В ППП MS Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:

1) выделите область построения диаграммы; в главном меню выберите Диаграмма / Добавить линию тренда;

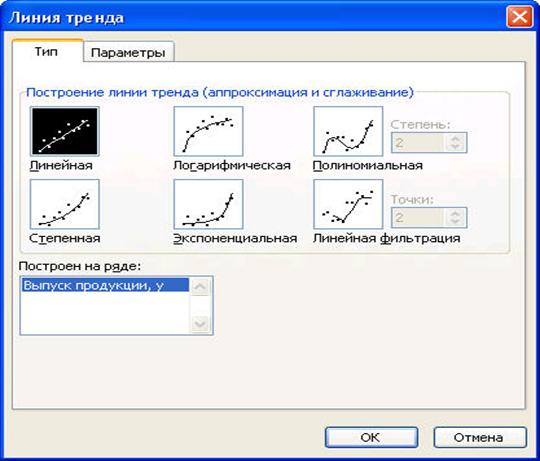
2) в появившемся диалоговом окне (рис. 3.8) выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимирующего полинома, для скользящего среднего – количество точек усреднения.

Рис. 3.8 Диалоговое окно типов линий тренда

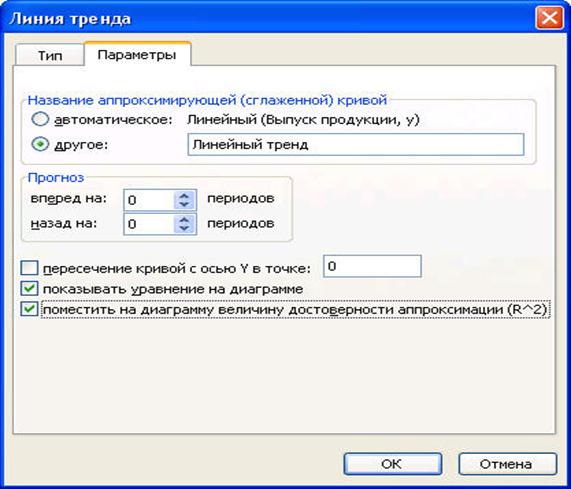
В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение среднеквадратического отклонения, установив соответствующие флажки на закладке Параметры (рис. 8.9). Щелкните по кнопке ОК.

Рис. 3.9 Диалоговое окно параметров линии тренда

На рис. 3.10-3.14 представлены различные виды трендов, описывающие исходные данные задачи.

Рис.3.10 Линейный тренд

Рис.3.11 Логарифмический тренд

Рис.3.12 Полиномиальный тренд

Рис.3.14 Экспоненциальный тренд

3. Сравним значения (или R 2 ) по разным уравнениям трендов:

полиномиальный 6-й степени — =0,9728; экспоненциальный — =0,9647;

линейный — =0,8841; степенной — =0,8470; логарифмический — =0,5886.

Исходные данные лучше всего описывает полином 6-й степени. Следовательно, в рассматриваемом примере для прогнозных значений следует использовать полиномиальное уравнение.

Контрольные вопросы

1. Каковы основные элементы временного ряда?

2. В чем состоит задача эконометрического анализа временного ряда?

3. Перечислите основные виды трендов.

4. Что представляют собой параметры линейного и экспоненциального трендов?

5. Что такое аддитивная модель временного ряда? Перечислите этапы ее построения.

6. Как строится мультипликативная модель временного ряда?

7. Что такое скорректированная сезонная компонента и для чего она применяется?

8. Как выбрать наиболее предпочтительный тренд?

9. Пояснить особенности применения аддитивных и мультипликативных моделей.

10. Поясните расчет сезонной компоненты в аддитивных и мультипликативных моделях временных рядов.

Пример варианта промежуточного тестирования

1. Прогнозное значение уровня временного ряда в аддитивной модели равно:

а) разности трендового значения и значения сезонной компоненты;

б) трендовому значению;

в) случайному значению;

г) сумме трендового значения, случайного значения и значения сезонной компоненты.

д) сумме трендового и случайного значения.

2. На основе помесячных данных о числе раскрытых преступлений за последние два года была построена аддитивная модель временного ряда. Скорректированное значение сезонной компоненты за январь – S=-2, уравнение тренда: . На основе модели число раскрытых преступлений на январь следующего года составит:

3. Для описания темпов роста заработной платы были рассмотрены следующие виды трендов: экспоненциальный, полиномиальный 8 степени, линейный, степенной и логарифмический. Значения коэффициентов детерминации для каждого тренда составляют соответственно:

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Запуск надстройки Power Pivot для Excel

Power Pivot — это надстройка, с помощью которую можно выполнять мощный анализ данных в Excel. Надстройка встроена в определенные версии Office, но по умолчанию не включена.

Список версий Office, которые включают Power Pivot, а также список версий, в которых их нет, см. в вопросе Где Power Pivot?

Вот как можно включить Power Pivot перед первым использованием.

Перейдите на вкладку Файл > Параметры > Надстройки.

В поле Управление выберите Надстройки COM и нажмите Перейти.

Установите флажок Microsoft Office Power Pivot и нажмите кнопку ОК. Если установлены другие версии Power Pivot, то они будут также перечислены в списке надстроек COM. Выберите надстройку Power Pivot для Excel.

На ленте появится вкладка Power Pivot.

Откройте окно Power Pivot.

Щелкните Power Pivot.

На этой вкладке можно работать со сводными таблицами, вычисляемыми полями и ключевыми показателями эффективности Power Pivot, а также создавать связанные таблицы.

Нажмите кнопку Управление.

Откроется окно Power Pivot. Здесь вы можете нажать кнопку «Внешние данные», чтобы использовать мастер импорта таблиц для фильтрации данных при их добавлении в файл, создания связей между таблицами, обогащения данных вычислениями и выражениями и создании сводных таблиц и сводных диаграмм на их основе.

Устранение неполадок: исчезновение ленты Power Pivot

В редких случаях лента Power Pivot исчезает из меню, когда Excel определяет, что надстройка нарушает его работу. Это может произойти, если Excel неожиданно завершает работу при открытом окне Power Pivot. Чтобы восстановить меню Power Pivot:

Выберите Файл > Параметры > Надстройки.

В поле Управление выберите Отключенные объекты > Перейти.

Выберите Microsoft OfficePower Pivot и нажмите кнопку Включить.

Если не удается восстановить ленту Power Pivot, выполнив указанные выше действия, или лента исчезает, когда вы закрываете и снова открываете Excel, сделайте следующее:

откройте меню Пуск > Выполнить и введите команду regedit;

В редакторе реестра разверните следующий раздел:

Для Excel 2013: HKEY_CURRENT_USER > Software > Microsoft > Office > 15.0 > User Settings.

Для Excel 2016: HKEY_CURRENT_USER > Software > Microsoft > Office > 16.0 > User Settings

щелкните правой кнопкой мыши PowerPivotExcelAddin, а затем нажмите Удалить;

вернитесь в верхнюю часть редактора реестра;

разверните раздел HKEY_CURRENT_USER > Software > Microsoft > Office > Excel > Addins;

щелкните правой кнопкой мыши PowerPivotExcelClientAddIn.NativeEntry.1, а затем нажмите Удалить;

закройте редактор реестра;

включите надстройку, выполнив действия, описанные в начале этой статьи.

Источник

Решение задач с помощью ППП Excel (инструмент Регрессия)

Эта операция проводится с помощью инструмента анализа данных Регрессия. Для этого:

1. В главном меню последовательно выберите пункты Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;

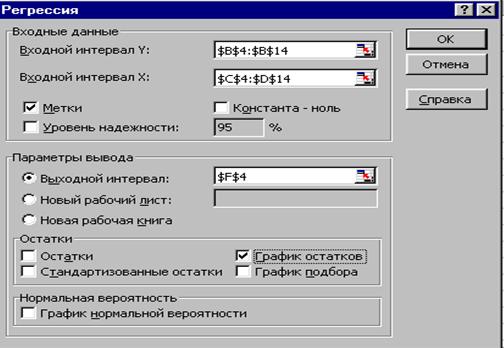
2. Заполните диалоговое окно ввода данных и параметров вывода (рис.1.7):

Входной интервал У – диапазон, содержащий данные результативного признака;

Входной интервал Х – диапазон, содержащий данные факторов независимого признака;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона.

Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне.

Щелкните по кнопке ОК.

Рис. 1.7. Диалоговое окно ввода параметров инструмента Регрессия

Результаты регрессионного анализа для данных вышеприведенного примера представлены на рис 1.8.

Рис. 1.8. Результат применения инструмента Регрессия

По результатам вычислений составим уравнение множественной регрессии вида

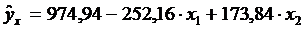
Критерий Стьюдента t — статистики имеют расчетные значения:

Табличное значение критерия Стьюдента составляет t_табл. = 2,31 при 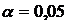. Расчетные значения критерия Стьюдента больше его табличных значений, следовательно, можно сделать вывод о существенности параметров уравнения.

Контрольные задания

Задание к задачам 1- 6.

Используя ППП Exsel:

1. Рассчитайте парные коэффициенты корреляции и сделайте по ним вывод.

2. Постройте множественное уравнение регрессии с полным перечнем факторов и сделайте экономическую интерпретацию его параметров.

3. Оцените статистическую значимость множественного уравнения в целом и его параметров.

4. Оцените качество построенной модели, используя ошибку аппроксимации и коэффициент множественной детерминации.

5. Рассчитайте средние и частные коэффициенты эластичности, а также частные коэффициенты корреляции, выполните анализ.

Имеются данные о рентабельности производства шерсти по 18 административным районам области за год:

х₁ — настриг шерсти с одной овцы, кг;

х₂ — затраты на 1 центнера шерсти, человеко – часов;

х₃ — себестоимость 1 центнера, руб;

у – уровень рентабельности, %.

Таблица 1.24 – Рентабельность производства шерсти

№ района	х₁	х₂	х₃	у
1	1,3	574,1	7815,3	64,2
2	1,4	1156,3	8441,9	76,9
3	0,5	1333,3	5604,2	67,7
4	1,9	712,1	4862,7	83,9
5	1,6	1276,9	8817,3	81,0
6	1,3	563,8	9301,8	100,0
7	0,4	1000,0	11200,0	87,4
8	1,7	516,5	11312,5	78,2
9	0,4	285,7	8550,3	88,3
10	1,5	428,6	19521,7	90,0
11	0,9	725,0	5417,6	86,4
12	0,7	328,4	5709,5	90,0
13	1,4	738,5	14660,4	92,9
14	1,0	556,8	7301,2	52,1
15	1,8	193,5	9052,8	92,6
16	0,5	729,7	20157,9	90,5
17	1,2	322,8	16052,6	94,8
18	1,1	403,5	9034,5	72,1

Имеются данные об уровне убыточности производства мяса птицы по 20 административным районам области за год:

х₁— затраты на 1 центнера прироста, человеко – часов;

х₂ — затраты на 1 центнера прироста, руб.;

х₃ — себестоимость 1 центнера, руб.;

у – уровень убыточности, %.

Таблица 1.25 – Уровень убыточности производства мяса птицы

№ района	х₁	х₂	х₃	у
1	46,9	3517,7	3655,1	42,7
2	136,3	4432,6	3047,2	36,1
3	114,8	3878,0	3243,6	35,3
4	247,4	8324,7	5839,9	52,5
5	192,4	5162,6	1546,5	23,2
6	10,1	2860,8	2976,0	39,7
7	108,5	4290,6	2562,5	31,7
8	142,7	8046,7	4600,4	57,3
9	99,1	3370,8	4888,9	63,6
10	153,8	5547,4	3871,4	31,4
11	115,3	4599,7	2806,9	14,2
12	63,0	2589,3	2852,1	53,2
13	107,1	5902,9	2904,8	35,9
14	111,3	6754,1	3178,3	25,7
15	86,9	4904,2	4702,1	59,0
16	110,8	4719,2	7122,3	61,6
17	200,6	8462,1	2871,8	36,8
18	136,7	5830,3	6070,3	53,7
19	87	2619,6	4711,3	61,4
20	107,4	2198,2	4400,0	30,3

Имеются данные об уровне рентабельности и удельном весе продукции собственного производства и покупной в товарообороте 15 предприятий общественного питания за год:

х₁— удельный вес в товарообороте продукции собственного производства, %;

х₂ — удельный вес в товарообороте покупной продукции, %;

у – уровень рентабельности, %.

Таблица 1. 26 – Уровень рентабельности предприятий общественного питания

Имеются данные об уровне рентабельности и показателям хозяйственной деятельности по 15 торговым предприятиям за год:

х₁— производительность труда, у. е.;

х₃ – относительный уровень издержек обращения, %;

у – уровень рентабельности, %.

Таблица 1. 27 – Уровень рентабельности торговых предприятий

№ предпр.	х₁	х₂	х₃	у
1	7134	149	14,91	5,2
2	5415	142	15,05	4,41
3	7633	151	14,77	5,23
4	10259	165	11,55	6,72
5	14620	175	9,21	7,14
6	8736	155	14,2	4,4
7	5590	144	16,23	3,78
8	10212	165	11,97	6,83
9	11586	171	13,05	6,07
10	9156	161	13,45	6,1
11	12501	173	10,13	7,1
12	11274	168	12,33	6,21
13	7700	150	15,23	3,7
14	9383	160	13,95	5,55
15	12255	170	10,17	6,9

Имеются данные об уровне рентабельности и показателям хозяйственной деятельности по 15 предприятиям общественного питания за год:

х₁— удельный вес в товарообороте продукции собственного производства, %;

х₂ — удельный вес в товарообороте покупной продукции, %;

х₃ – трудоемкость в расчете на 100000 у. е. товарооборота, чел.;

х₄– относительный уровень издержек обращения, %;

у – уровень рентабельности, %.

№ пред.	Х₁	х₂	х₃	х₄	у
1	56,6	43,4	28	31,51	7,92
2	51,6	48,4	27	30,2	8,17
3	48,5	51,5	22	29,1	8,0
4	63,2	36,8	38	32,79	7,04
5	47,6	52,4	30	26,44	9,14
6	60,8	39,2	35	37,16	9,0
7	32,2	67,8	24	26,04	9,13
8	53,2	46,8	25	31,91	7,81
9	41,6	58,4	29	27,13	9,17
10	76,1	23,9	43	29,3	9,01
11	43,6	56,4	31	33,7	6,43
12	52,8	47,2	30	36,44	5,64
13	50,0	50,0	37	31,3	7,75
14	43,4	56,6	28	31,65	7,7
15	47,6	52,4	24	27,09	7,02

Имеются данные об уровне трудоемкости товарооборота и показателям хозяйственной деятельности по 15 предприятиям общественного питания за год:

х₁— удельный вес в товарообороте продовольственных товаров, %;

х₂ – удельный вес в товарообороте непродовольственных товаров, %;

х₃ – удельный вес товарооборота общественного питания, %;

у – уровень трудоемкости товарооборота, %.

Таблица 1. 29 – Уровень трудоемкости товарооборота

№ пред.	Х1	х2	х3	у
1	82,1	17,9	5,9	9
2	76,2	23,8	10,6	10
3	80,3	19,7	5,5	12
4	84,9	15,1	15,0	14
5	81,2	18,8	7,0	8
6	81,5	18,5	12,7	9
7	85,2	14,8	11,3	14
8	77,8	22,2	6,9	10
9	82,2	17,8	8,1	12
10	82,3	17,7	17,0	12
11	80,1	19,9	6,9	11
12	76,0	24,0	5,7	10
13	77,3	22,7	9,7	11
14	74,5	25,5	12,7	9
15	73,5	26,5	7,4	8

Контрольные вопросы

1. Назовите, в чем состоит спецификация модели множественной регрессии.

2. Сформулируйте требования, предъявляемые к факторам для включения их в модель множественной регрессии.

3. К каким трудностям приводит мультиколлинеарность факторов, включенных в модель, и как они могут быть разрешены?

4. Назовите методы устранения мультиколлинеарности факторов.

5. Что означает взаимодействие факторов и как оно может быть представлено графически?

6. Назовите способы оценки параметров множественной регрессии?

7. Приведите порядок вычисления параметров множественной модели методом наименьших квадратов.

8. В чем заключается метод оценки параметров уравнения множественной регрессии с использованием стандартизованных переменных?

9. Как интерпретируются коэффициенты множественной регрессии степенной модели?

10. Как интерпретируются коэффициенты множественной регрессии линейной модели?

11. Какие эконометрические параметры используются для оценки сравнительной силы воздействия факторов на результат?

12. Как рассчитываются коэффициенты множественной корреляции и детерминации?

13. Для чего используются частные коэффициенты эластичности и как их рассчитать?

14. Каково назначение частной корреляции при построении множественного уравнения регрессии?

15. Составьте матрицу частных коэффициентов корреляции разного порядка для регрессионной модели с четырьмя факторами.

16. Как оценить статистическую значимость множественной модели в целом?

17. Как оценить статистическую значимость параметров уравнения множественной регрессии?

18. Что такое частный критерий Фишера и для чего он рассчитывается?

19. Как связаны между собой критерий Стьюдента, используемый для оценки статистической значимости коэффициентов регрессии, и частные критерии Фишера?

20. При каких условиях строится уравнение множественной регрессии с фиктивными переменными?

21. Как трактуются коэффициенты модели, построенной только на фиктивных переменных?

22. Сформулируйте основные предпосылки применения МНК для построения регрессионной модели.

23. Как можно проверить наличие гомо – или гетероскедастичности остатков?

24. Как оценивается отсутствие автокорреляции остатков при построении статистической регрессионной модели?

Тесты

1. Частные коэффициенты (или индексы) корреляции характеризуют

а) тесноту связи между у и всеми факторами, включенными в модель;

б) качество построенной модели;

в) тесноту связи между у и соответствующим фактором х при устранении

влияния других включенных в модель факторов;

г) статистическую значимость коэффициентов чистой регрессии.

2. Коэффициент чистой регрессии признается статистически значимым, если:

а) F част х_i F табл.;

в) F част х_i = 1; г) F част х_i> 0.

3. Модель вида y = f (x₁,x₂, …, x_n)представляет собой:

а) множественную регрессию;

б) одномерный временной ряд;

в) простую регрессию;

г) аддитивную модель временного ряда.

4. Допустимый предел средней ошибки аппроксимации ( 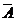) составляет

а) от – 1 до +1; б) от 0 до + 1; в) от – 1 до 0; г) до (8-10)%.

5. Средний коэффициент эластичности ( 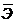) показывает

а) долю дисперсии, объясненную регрессией, в общей дисперсии результативного признака;

б) средний процент изменения результата от своего среднего значения при изменении фактора на 1% от своего среднего значения;

в) статистическую значимость уравнения регрессии;

г) нет правильного ответа.

6. Известно, что при фиксированном значении х₃ ме6жду величинами х₁ и х₂ существует положительная связь. Какое значение имеет частный коэффициент корреляции r _x₁_x_2,_x₃?

а) — 0,8; б) 0; в) 0,4; г) 1,3.

7. Множественный коэффициент корреляции для двухфакторного уравнения, построенного по 20 наблюдениям, равен 0,85. Чему равен критерий Фишера?

а) 8,74; б) 12,13; в) 22,13; г) 122,14.

8. Имеется уравнение в линеаризованном виде ln y = 0,1274 -0,2143* ln x₁ +2,8254* ln x₂. Естественная форма данного уравнения будет иметь вид:

в) у = 1,136*х₁ -0,2143 * х₂ 2,8254 ; г) у = 1,136*0,2143х₁ * 2,8254х₂.

9. Оцените статистическую значимость коэффициентов регрессии в уравнении у = 30 +10*х₁ + 8* х₂, построенном по 19 наблюдениям, если их стандартные ошибки равны m_b₁ = 2.5; m_b₂= 4.

а) коэффициент регрессии b₁ статистически значим, а b₂ — нет;

б) оба коэффициента регрессии статистически значимы;

в) коэффициент регрессии b₂ статистически значим, а b₁ — нет;

г) оба коэффициента регрессии статистически незначимы.

10. Множественный коэффициент корреляции r_yx₁_x₂ = 0,963, парные коэффициент корреляции r_yx₁ = 0,428 и r_yx₂ = 0,962. чему равны частные критерии Фишера F_x₁ и F_x₂? 7

11. Множественный коэффициент детерминации R 2 = 0.927. парные коэффициент корреляции r_yx₁ = 0,428 и r_yx₂ = 0,962. Чему равны критерии Стьюдента t_b₁ и t_b₂, рассчитанные для 10 наблюдений?

в) t_b = 9,44 ; t_b₂ = 1,44; г) t_b = 8,94 ; t_b₂ = 0.74.

12. Производственная функция характеризуется уравнением ln Р = 0,552 + 0,2761 ln Z + 0.5211 ln K. Средние коэффициенты эластичности равны

а) Э(Z) = 0,552 ; Э(K) = 0,2761; б) Э(Z) = 0,2761 ; Э(K) = 0,5211;

в) Э(Z) = 0,5211 ; Э(K) = 0,522; г) Э(Z) = 0,2761 ; Э(K) = 0,522.

13. Как интерпретируются коэффициенты множественной регрессии степенной функции?

а) являются средними коэффициентами эластичности;

б) являются коэффициентами чистой регрессии;

в) являются свободными членами;

г) нет правильного ответа.

14. Имеются данные Σу = 8,564; Σх₁ = 743,5; Σх₂ = 32606; Σх₁*у = 639,393; Σх₂*у = 27983; Σх₁ 2 = 55451; . Σх₂ 2 = 1,07*10 8 ; +Σх₁* х₂ = 2428731. Чему равны параметры двухфакторной модели, построенной по 10 наблюдениям?

а) а= 2,5; b₁ = 0,164; b₂= -0,0034; б) а=-0,25; b₁=1,64; b₂= 0,034;

в) а= — 0,25; b₁ = 0,0164; b₂=-0,000034; г) а=-0,78; b₁=0,164; b₂=0,064.

15. В чем смысл средней ошибки аппроксимации?

а) Абсолютное отклонение расчетного значения результативного признака от его фактического значения;

б) среднее отклонение расчетного значения результативного признака от его фактического значения, выраженного в %;

в) среднее отклонение расчетного значения результативного признака от его среднего значения;

г) среднее отклонение расчетного значения результативного признака от его среднего значения, выраженное в %.

16. Назовите методы устранения мультиколлинеарности факторов.

а) исключение из модели одного или нескольких факторов; преобразование факторов; переход к совмещенным уравнениям регрессии;

б) исключение из модели одного или нескольких факторов; преобразование факторов; переход к совмещенным уравнениям регрессии или к уравнениям регрессии приведенной формы;

в) исключение из модели одного или нескольких факторов; переход к совмещенным уравнениям регрессии или к уравнениям регрессии приведенной формы;

г) исключение из модели одного или нескольких факторов; преобразование факторов; переход к уравнениям регрессии приведенной формы.

17. С какой целью рассчитываются частные коэффициенты эластичности для уравнения множественной регрессии?

а) они могут быть использованы для принятия решений относительно развития конкретных регионов;

б) они могут быть использованы для определения спроса и потребления;

в) они могут быть использованы для принятия решений в среднем по регионам;

г) нет полного ответа.

18. Сформулируйте требования, предъявляемые к факторам для включения их в модель множественной регрессии

а) факторы не должны быть мультиколлинеарны; факторы не должны быть фиктивными;

б) они должны быть количественно измеримы; факторы не должны быть интеркоррелированы;

в) факторы не должны находиться в тесной линейной зависимости; факторы не должны быть фиктивными;

г) факторы должны находиться в тесной линейной зависимости ; факторы должны быть количественно измеримы.

19. Каким образом оценивается статистическая значимость мультиколлинеарности факторов?

а) по критерию Фишера; б) по критерию Стьюдента;

в) по величине χ 2 ; г) все ответы правильные.

20. Каков смысл коэффициентов регрессии в логарифмической регрессионной модели?

а) коэффициенты регрессии являются эластичностями переменной у по переменных х₁, х₂ … х_n.;

б) коэффициенты регрессии показывают среднее изменение переменной у при изменении переменным х₁, х₂ … х_n на единицу;

в) коэффициенты регрессии показывают среднее изменение переменной у при изменении соответствующей переменной на единицу и неизменном среднем уровне других факторов;

г) коэффициенты регрессии показывают темпы прироста переменной у по переменных х₁, х₂ … х_n.

21. Средние коэффициенты эластичности для уравнения у(х) = -294 +44,15х₁+13,21х₂ составят … при условии, что средние значения признаков равны :х₁ = 4,45; х₂ = 19,5; у=160.

а) 1,23; 1,61; б) 0,77; 1,45;

в) 2,43; 3,56; г) 3,42; 2,71.

22. Мультиколлинеарность – это связь между …

а) векторами; б) процессами; в) признаками; г) явлениями.

23. После расчета неизвестных параметров модели следует:

а) определить состав включенных в модель регрессии переменных;

б) оценить адекватность и точность модели;

в) выбрать функцию, связывающую результативный признак и факторные признаки;

г) рассчитать интервальные прогнозные оценки.

24. В каких случаях во множественной регрессии используются фиктивные переменные?

а) если фактор имеет количественные уровни;

б) если фактор имеет качественные уровни;

в) если в уравнение вводится 2 и более факторов;

г) если факторы мультиколлинеарны.

25. Адекватность эконометрической модели – это …

а) способность модели описывать выходные параметры с относительной погрешностью не более некоторого заданного значения δ;

б) возможность модели обеспечить минимальное совпадение фактических и теоретических значений;

в) способность отразить в достаточной мере выходные параметры, которые отвечают поставленной цели;

г) возможность установить соотношения между внешними и выходными параметрами путем исследования на внешние воздействия.

26. Множественная корреляция – это …

а) связь между двумя показателями;

б) связь между несколькими факторами и одним результативным признаком;

в) связь между одним фактором и результативным признаком при исключении других факторов;

г) связь между одним фактором и несколькими результативными признаками.

27. Система нормальных уравнений вида 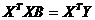используется для оценки

а) коэффициентов регрессионного уравнения;

б) временного сдвига двух переменных;

в) коэффициента детерминации;

г) статистической значимости параметров модели.

Дата добавления: 2018-02-15 ; просмотров: 856 ; Мы поможем в написании вашей работы!

Источник

1. Настройка пакета для выполнения регрессионного анализа

Процедуры корреляционно-регрессионного анализа выполняются в табличном процессоре с помощью модуля «Пакет анализа». Для подключения этого модуля с помощью команды СЕРВИС – НАДСТРОЙКИ выведите окно НАДСТРОЙКИ и включите надстройку ПАКЕТ АНАЛИЗА.

Рис. 11. Диалоговое окно Надстройки меню Сервис.

После выполнения этой процедуры в ниспадающем меню пункта СЕРВИС появится команда АНАЛИЗ ДАННЫХ.

Рис. 12. Лист ППП «Excel» пункт меню Сервис команда Анализ данных.

2. Расчет показателей описательной статистики

Для проверки требований, предъявляемых к исходным данным, следует рассчитать ряд показателей, характеризующих эти данные (среднее значение, дисперсия и т. д.). Эти характеристики данных можно получить, воспользовавшись функцией СЕРВИС — АНАЛИЗ ДАННЫХ – ОПИСАТЕЛЬНАЯ СТАТИСТИКА.

Рис. 13. Диалоговое окно АНАЛИЗ ДАННЫХ.

После выбора требуемой функции откроется окно ОПИСАТЕЛЬНАЯ СТАТИСТИКА.

Рис. 14. Диалоговое окно ОПИСАТЕЛЬНАЯ статистика.

Для расчета показателей описательной статистики в окне «Входной интервал» укажите область ячеек электронной таблицы, где расположены анализируемые данные (исследуемый показатель и все факторы). Желательно в эту область включить ячейки с обозначениями переменных (Х0, Х1, …, Хр) для комфортного восприятия результатов вычислений. Если метки данных (обозначения переменных) учтены, то в области ВХОДНЫЕ ДАННЫЕ включите опцию «Метки в первой строке». Затем в области «Параметры вывода» укажите, куда должны быть выведены результаты расчетов (Новый лист либо Выходной интервал И верхняя левая ячейка области электронной таблицы, где должны быть размещены результаты).

В области «Параметры вывода» включите опцию «Итоговая статистика» и выполните процедуру.

В полученных результатах расчетов удалите повторяющуюся информацию (многократное повторение названий статистик) и рассчитайте для каждого показателя коэффициенты вариации (по среднему значению и стандартному отклонению).

3. Выявление тесноты связи и закона зависимости между факторами и результирующим показателем (анализ полей корреляции)

Для построения полей корреляции (диаграмм рассеивания) используйте команду ВСТАВКА – ДИАГРАММА – ТОЧЕЧНАЯ (вариант без соединения точек) либо мастер диаграмм. В результате выполнения этой команды появится окно МАСТЕР ДИАГРАММ (шаг 2 из 4):

Рис. 15. Диалоговое окно Мастера диаграмм.

В окне Диапазон укажите область столбца электронной таблицы, где находится массив данных для фактора, и через точку с запятой область данных по результирующему показателю. Щелкните мышкой по кнопке ДАЛЕЕ. В результате появится окно следующего 3 шага. В соответствующих окнах введите заголовок графика и названия осей; разместите график на рабочем листе. Постройте графики, отражающие влияние каждого фактора на исследуемый показатель.

Рис. 16. Диалоговое окно Мастера диаграмм – Параметры диаграммы.

Элементы корреляционной матрицы получите, воспользовавшись функцией СЕРВИС — АНАЛИЗ ДАННЫХ — КОРРЕЛЯЦИЯ. В результате будет открыто окно АНАЛИЗ ДАННЫХ.

Рис. 17. Диалоговое окно Анализ данных.

После выбора требуемой функции откроется окно КОРРЕЛЯЦИЯ.

Рис. 18. Диалоговое окно Корреляция.

В окне «Входной интервал» задайте область ячеек электронной таблицы, где расположены анализируемые данные (исследуемый показатель и все факторы). В эту область так же включите ячейки с обозначениями переменных (Х0, Х1, …, Хр). Если метки учтены в области данных, то в окне КОРРЕЛЯЦИЯ включите опцию «Метки в первой строке». Затем в области «Параметры вывода» укажите левую верхнюю ячейку области электронной таблицы, куда должна быть выведена корреляционная матрица.

Анализируя корреляционную матрицу, сделайте выводы о том, как сильно связаны факторы между собой и с исследуемым показателем. Если обнаружены коллинеарные (мультиколлинеарные) факторы, то для дальнейшего анализа следует оставить только один из этих факторов. Проводя анализ взаимосвязей показателей по корреляционной матрице, необходимо помнить о том, что парные коэффициенты корреляции — это показатели тесноты связи для линейных зависимостей.

4. Расчет параметров регрессионной модели

Вид регрессионной модели обосновывают двумя путями: теоретическим и эмпирическим. В первом случае используют качественные рассуждения о законе связи между исследуемым показателем и каждым из факторов, а также результаты других исследователей по построению аналогичных регрессионных моделей. При эмпирическом подходе выводы о форме связи делают на основе анализа фактических данных, представленных в виде первичных полей корреляции.

Чаще всего для анализа используют линейный вид модели или модель, которую можно привести к линейному виду путем некоторых преобразований и замены переменных.

Для расчета параметров регрессионной модели воспользуйтесь функцией СЕРВИС — АНАЛИЗ ДАННЫХ — РЕГРЕССИЯ. В результате появится окно АНАЛИЗ ДАННЫХ. В этом окне выберите инструмент анализа РЕГЕРССИЯ.

Рис. 19. Диалоговое окно Анализ данных.

После щелчка мышкой по кнопке ОК на экране появится окно РЕГРЕССИЯ.

Рис. 20. Диалоговое окно Регрессия.

В этом окне в области «Входной интервал Y» укажите область ячеек, где находятся данные исследуемого показателя, в области «Входной интервал X» — область ячеек с данными по всем факторам. Желательно при этом учитывать обозначения переменных. Если метки данных включены при определении области переменных, то включите опцию «Метки».

Чтобы получить данные для расчета средней относительной ошибки аппроксимации, в этом диалоговом окне поставьте флажок рядом с опцией ОСТАТКИ.

В результате использования функции СЕРВИС — АНАЛИЗ ДАННЫХ — РЕГРЕССИЯ будут получены не только параметры модели, но и показатели, позволяющие оценить надежность построенной модели.

5. Исключение из модели факторов, оказывающих несущественной влияние

Все факторы, влияние которых на исследуемый показатель несущественно, должны быть исключены из модели. Влияние фактора следует считать несущественным, если соответствующий коэффициент регрессии статистически не значим, то есть его можно приравнять нулю. Коэффициент регрессии следует считать статистически значимым (не равным нулю), если фактическая величина критерия Стьюдента будет больше табличного значения этого критерия. Табличное значение критерия Стьюдента можно найти, воспользовавшись в Excel мастером функций .

После обращения к мастеру функций на экране появится окно «Мастер функций – шаг 1 из 2».

Рис. 21. Диалоговое окно Мастера функций.

В левой части этого окна выберите категорию функций «Статистические», в правой части, используя бегунок, выберите функцию «СТЬЮДРАСПРОБР» и щелкните мышкой по кнопке ОК. В результате появится окно для задания параметров этой функции. В этом окне «Вероятность» – уровень значимости (= 1-, где — доверительная вероятность).

Рис. 22. Диалоговое окно функции Стьюдраспобр.

Уровень значимости обычно принимают равным 0,05; число степеней свободы = (где — число наблюдений, — число параметров регрессионной модели).

Если в модели присутствует несколько несущественных факторов, то первым следует исключить тот фактор, для которого табличное значение критерия Стьюдента намного больше . Несущественно влияющий фактор убирают из совокупности наблюдений и пересчитывают параметры регресcионной модели и ее характеристики. Для модели, полученной на втором шаге, заново проверяют статистическую значимость коэффициентов регресcии. Если вновь обнаружен фактор, оказывающий несущественное влияние на анализируемый показатель, то этот фактор также исключают из модели. Отсев факторов из модели выполняют до тех пор, пока в ней останутся только факторы, оказывающие сильное влияние на .

Чтобы убедиться в том, что из модели были исключены факторы, оказывающие слабое влияние на исследуемый показатель, сравните величины коэффициентов детерминации первого и последнего шагов. Их различие будет незначительным.

6. Проверка надежности регрессионной модели

Вывод о статистической значимости модели в целом делают по — критерию. Если фактическая величина критерия Фишера окажется больше табличного значения, то полученная модель статистически значима и полно описывает изменение исследуемого показателя под действием факторов, присутствующих в модели.

Теоретическое значение — критерия также можно получить с помощью мастера функций . Для этого в окне «Мастер функций – шаг 1 из 2» следует выбрать функцию FРАСПОБР.

Рис. 23. Диалоговое окно Мастера функций.

В окне выбранной функции задайте требуемые параметры.

Рис. 24. Диалоговое окно функции Fраспобр.

«Вероятность» – уровень значимости (обычно принимают равным 0,05); «Число_степеней свободы1» — это число факторов, присутствующих в модели, «Число_степеней свободы2» определяют как разность между числом наблюдений и числом параметров модели.

Если Fрасч > Fтабл, то построенная модель считается статистически надежной, а следовательно, правильно отражает закон изменения исследуемого показателя под действием факторов, присутствующих в модели.

7. Проверка адекватности регрессионной модели

Среднюю относительную ошибку аппроксимации пользователь должен рассчитать самостоятельно по формуле , где фактические (расчетные) значения исследуемого показателя.

Если модель используют для целей анализа, допустима величина средней относительной ошибки до 10%, при применении модели для прогнозирования ошибка не должна быть больше 4%.

Для этого рядом с остатками следует добавить столбец фактических значений исследуемого показателя и выполнить ряд промежуточных расчетов.

8. Интерпретация полученных результатов

На этом этапе разрабатывают рекомендации об использовании результатов регрессионного анализа. Анализируют коэффициенты регрессии в натуральном и стандартизованном масштабе, а также коэффициенты эластичности.

Коэффициент регрессии в натуральном масштабе показывает, на сколько своих единиц измерения в среднем изменится исследуемый показатель при увеличении — го фактора на единицу своего измерения. При этом влияние остальных факторов находится на среднем уровне; свободный член уравнения характеризует изменение показателя за счет изменения факторов, неучтенных в модели.

В связи с тем, что факторы имеют различный физический смысл и различные единицы измерения, коэффициенты регрессии нельзя сравнивать между собой и, следовательно, невозможно определить, какой из факторов оказывает наибольшее влияние. Для устранения различий в единицах измерения применяют частные коэффициенты эластичности, рассчитываемые по формуле: , где — средние значения — го фактора и исследуемого показателя, — коэффициент регрессии, стоящий при переменной в многофакторном уравнении регрессии. Как известно, коэффициент эластичности характеризующие на сколько % в среднем изменится При увеличении j-го фактора на 1% при фиксированном положении других факторов.

При определении степени влияния отдельных факторов необходим показатель, который бы учитывал влияние анализируемых факторов с учетом различий в уровне их колеблемости. Таким показателем является коэффициент регрессии в стандартизированном масштабе Коэффициент показывает на какую часть своего среднеквадратического отклонения изменится при изменении j-го фактора на одно свое среднеквадратическое отклонение при фиксированном значении остальных факторов. Уравнение регрессии в стандартизированном масштабе : где

Границы влияния фактора на исследуемый показатель рассчитываются по формуле (левая граница) (правая граница), где — доверительные полуинтервалы.

< Предыдущая		Следующая >

Источник

В ППП EXCELдля определения
параметров линейного тренда и показателей
его качества используется статистическая
функция ЛИНЕЙН. Порядок вычисления
следующий:

1. введите исходные данные

2. выделите область (5 строк. 2 столбца)
для вывода результатов.

3. Активизируйте мастер функций.

4. В окне Категория выберите Статистические,
в окне Функция — ЛИНЕЙН. Щелкните по
кнопке ОК.

5. Заполните аргументы функции.

Известные значения у— диапазон,
содержащий данные уровней временного
ряда.Известные значения х —диапазон,
содержащий показатели времени.Константа
—1.Статистика-1.

Рис1. Входная панель
статистической функции ЛИНЕЙН

Щелкните по кнопке ОК. Чтобы раскрыть
итоговую таблицу результатов нажмите
на клавишуF2, а затем
последовательно на комбинацию клавиш
<CTRL>+<SHIFT>+<ENTER>.

Рис. 2. Результат
вычисления функции ЛИНЕЙН.

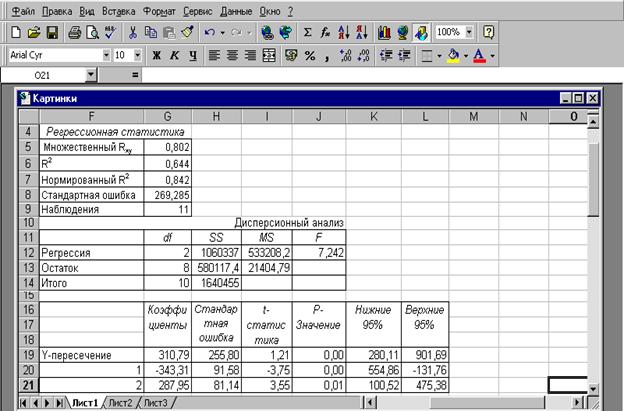
Результат вычисления функции ЛИНЕЙН
выводится в следующем порядке:

Значение коэффициента	Значение коэффициента
Среднеквадратическое отклонение	Среднеквадратическое отклонение
Коэффициент детерминации	Среднеквадратическое отклонение у
Критерий Фишера	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

В типовом примере:
,.
Следовательно, в течение анализируемого
периода курс возрастал ежемесячно на
25 копеек. Чтобы подтвердить достоверность
такого вывода, следует оценить качество
уравнения рассмотренными в задании 1
способами проверки статистических
гипотез. Имеются три направления оценки
качества уравнения: общая оценка качества
(коэффициент детерминации, критерий
Фишера), оценка качества коэффициентов
регрессии (стандартные ошибки
коэффициентов, t-статистика), проверка
выполнения предпосылок МНК. В типовом
примере коэффициент детерминации
составил 0,7828, критерий Фишера – 79,29. Это
означает, что 78,28% дисперсии курса доллара
объясняется его динамикой во времени,
а 21,72% — независящими от времени факторами.
Наблюдаемое значение критерия Фишера
при критическом 4,30 (см. таблицу значений
критерия Фишера в приложении) подтверждает
статистическую значимость уравнения
в целом.

Часто во временных рядах нарушением
предпосылки МНК о независимости случайных
отклонений является автокорреляция
остатков. Ряд остатков будет получен
как отклонения фактических уровней
временного ряда от полученных по
уравнению:

(43)

В условиях автокорреляции остатковэффективность оценок будет снижаться.
Для обнаружения автокорреляции применяют
критерий Дарбина-Уотсона. Значение
критерия определяется по формуле:

(44)

При отсутствии автокорреляции d=2,d=0при сильной
положительной автокорреляции,d=4при отрицательной автокорреляции.
Критерий имеет границыи,
позволяющие принять или отвергнуть
гипотезу об отсутствии автокорреляции.
(См. таблицу значений критерия в
приложении) При сравнении величиныdсивозможны следующие варианты:

Если d<,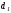
то гипотеза об отсутствии автокорреляции
отвергается. Еслиd>,
то гипотеза об отсутствии автокорреляции
не отвергается. Если<d<,
то нет достаточных оснований дня принятия
решений, то есть величина попадает в
область «неопределенности».

В нашем случае, критерий Дарбина-Уотсона
для линейного тренда
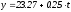
равен0,25. Границы критерия:=1,27и=1,45.d<,
0,25<1,27— гипотеза об отсутствии
автокорреляции отвергается. В остатках
присутствует автокорреляция.

Рис. 3. Входящая
панель инструмента РЕГРЕССИЯ

Для расчета критерия Дарбина-Уотсона
с помощью инструмента анализа данных
Регрессияв ПППMSEXCELможно получить остатки и графики остатков
по линейной регрессии. Порядок работы
следующий:

1. В главном меню выберите Сервис/Надстройки»Установите флажокПакет анализа.ЩелкнитеОК.

2. В главном меню выберите Сервис/Анализ
данных/ Регрессия. ЩелкнитеОК.

3. Заполните диалоговое окно ввода
данных. Установите соответствующие
флажки. Щелкните ОК.

В ППП EXCELдля построения
графика в главном меню выберите опцию
Вставка/Диаграммаи затем, после
построения линейного графика, в главном
меню опцию Диаграмма/Добавить треид.В появившемся диалоговом окне выберите
тип линии тренда и задайте соответствующие
параметры на закладке Параметры.ЩелкнитеОК.

Рис. 4. Входная
панель инструмента ЛИНИЯ ТРЕНДА.

Результаты решения в пакете Excel:

Линейный тренд:

Степенной тренд:

Ошибка прогноза— величина,
характеризующая расхождение между
фактическим и прогнозным значением
показателя. Абсолютная ошибка прогноза
определяется по формуле:

(45)

Средняя абсолютная ошибка по модулю:

(46)

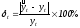
Определим показатели точности прогноза,
зная, что официальный курс доллара в 1
полугодии 2001 года составил:

Месяц	Официальный	Линейный	Степенной
	курс. руб.	тренд (прогноз)	тренд (прогноз)
Январь	28,37	29,52	28,62
Февраль	28,72	29,77	28,72
Март	28,74	30,02	28,82
Апрель	28,83	30,27	28,92
Май	29,09	30,52	29,01
Июнь	29,07	30,77	29,10

Показатели точности прогноза

	Линейный	степенной	Линейный	степенной
Январь	1,15	0,25	4,05	0,88
Февраль	1,05	0.00	3,66	0,00
Март	1,28	0,08	4,45	0,28
Апрель	1,44	0,09	4,99	0,31
Май	3,43	-0,08	4,92	-0,28
Июнь	1,70	0,03	5,85	0,10
Средняя	1,34	0,09	4,65	0,31

Очевидно, что линейный тренд завышает
прогнозные оценки, логарифмический их
занижает, наименьшие ошибки прогноза
имеет степенной тренд.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Для решения поставленной задачи воспользуемся возможностями среды электронных таблиц Excel модулем «Поиск решения», предназначенным для решения задач нелинейного программирования (команда основного меню «Сервис/Поиск решения»). Применим следующую технологию.

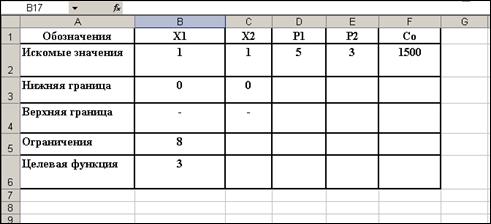
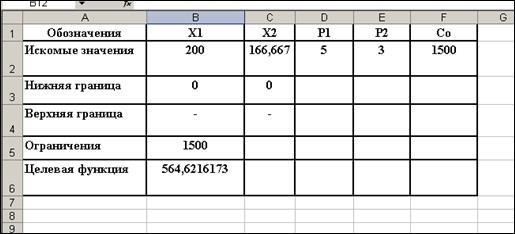
Процесс решения начинается с создания формы и ввода исходных данных. Откроем рабочий лист и создадим форму согласно рисунку 1.

Дадим ряд комментариев по заполнению формы. Ячейки В2-C2 содержат любое допустимое решение задачи, выбор которого осуществляется на основе априорной информации с учетом особенностей, как задачи, так и методов решения. В третьей и четвертой строках заданы соответственно верхняя и нижняя границы вовлекаемых ресурсов, что может диктоваться как особенностями производства, так и возможностями фирмы. В пятой строке задается ограничение, связанное с лимитированием совокупных затрат в рассматриваемом периоде (указанные ограничения будут использованы для решения задачи в краткосрочном периоде).

Рисунок 1 – Форма для ввода исходной информации в ЭТ «MS Excel»

В ячейке В6 формируется целевая функция, реализующая заданный критерий оптимальности и зависящая от ячеек, в которых находятся начальные значения. Курсор необходимо установить в ячейку с целевой функцией и вызвать команду «Сервис/Поиск решения», в диалоговом окне которой заполняются все текстовые поля. Пример заполнения окна приведен на рисунке 2.

Рисунок 2 – Диалоговое окно «Поиск решения» ЭТ «MS Excel»

После назначения параметров, активизируется команда «Выполнить» и в дополнительном диалоговом окне сообщается информация о результатах решения задачи и возможностях формирования автоматических отчетов.

В случае положительного решения (рисунок 3) на рабочем листе в ячейках, которые были разрешены для изменения (искомые значения), отражаются результаты – искомые оптимальные значения. В случае если решение найти не удается, показывается соответствующее текстовое сообщение с указанием причины.

Рисунок 3 – Сообщение о результатах и дополнительные возможности

Результаты решения задачи представлены на рисунке 4:

Рисунок 4 – Результаты решения задачи в ЭТ «MS Excel»

Помимо результатов с помощью стандартных отчетов находится значение множителя Лагранжа, который в данном случае имеет четкую экономическую интерпретацию: величина, обратная множителю Лагранжа, определяет нижнюю границу цены выпускаемой продукции. Фирма может установить цену не ниже 2,64 денежных единиц.

Далее проиллюстрируем взаимное расположение изокванты и изокосты в оптимальной точке.

Оптимальное значение выпуска равно 564,6 единиц, следовательно, построим изокванту, определяемую уравнением:

Полученное уравнение разрешим относительно х ₁: .

Далее построим изокосту для уровня издержек С =1500:

Протабулируем функции (Таблица 1), изменяя аргумент х ₁ в окрестности оптимальной точки и построим графики с помощью «Мастера диаграмм» (Рисунок 5).

Таблица 1 – Исходные данные для построения изокосты и изокванты

х ₁	Изокванта	Изокоста
160,00	260,39	233,33
170,00	230,65	216,67
180,00	205,74	200,00
190,00	184,65	183,33
200,00	166,65	166,67
210,00	151,15	150,00
220,00	137,73	133,33
230,00	126,01	116,67
240,00	115,73	100,00
250,00	106,65	83,33
260,00	0,52	66,67

Рисунок 5 – Взаимное расположение изокванты и изокосты в точке локального рыночного равновесия в ЭТ «MS Excel»

Построив изокосту и изокванту убеждаемся, что в оптимальной точке наблюдается касание изокосты и изокванты.

Решим задачу для краткосрочного периода.

В краткосрочном периоде математическая модель будет дополнена ограничением на использование второго ресурса в объеме не более 100 единиц. Это может быть связано с отсутствием возможности увеличения рабочих мест или с недостатком квалифицированной рабочей силы.

В результате модель примет вид:

Решая задачу для краткосрочного периода, получим следующие результаты: фирма полностью использует ресурс х ₂ в количестве 100 единиц, затраты первого ресурса составят 240 единиц, при этом объем выпуска сократится до 537,77 единиц при заранее обусловленных совокупных затратах в 1500 единиц. Решение и взаимное расположение изокосты и изокванты представлено на рисунках 8-11. В краткосрочном периоде уже не наблюдается касания, а изокоста и изокванта пересекаются.

Сопоставляя результаты можно сделать вывод, что в краткосрочном периоде при одинаковых издержках фирмы объем выпускаемой продукции ниже, чем объем выпуска в долгосрочном периоде. Следовательно, прибыль фирмы в долгосрочном периоде не ниже краткосрочного.

Рисунок 8 – Результаты решения задачи в краткосрочном периоде в ЭТ «MS Excel»

Рисунок 10 – Взаимное расположение изокванты и изокосты в точке локального рыночного равновесия для краткосрочного периода в ЭТ «MS Excel»

Решение задачи максимизации выпуска при ограничении на совокупные затраты существенно зависит от величины затрат, следовательно, при изменении С изменится и положение точки локального рыночного равновесия (x ₁⁰(C), x ₂⁰ (C)). Множество точек, соответствующих различным значениям С, образуют линию L, которая называется долговременной (стратегической) линией развития фирмы. Проведем анализ влияния величины издержек на оптимальную стратегию фирмы, предполагая, что цены на ресурсы остаются неизменными. Для этого решается семейство задач с возможным диапазоном изменения совокупных издержек и строится стратегическая (долговременная) линия развития фирмы. Результаты анализа представлены в таблице 2 и на рисунке 13. На основе аппроксимации результатов может быть построена аналитическая зависимость объема выпуска от затрат.

Таблица 2 – Вариантный анализ

Вариант	С	х ₁	х ₂	У
			166,667	564,62
		213,33	177,77	602,26
		226,66	188,88	639,9
				677,55
		253,33	211,11	715,19

Рисунок 12 – Стратегическая линия развития фирмы

Исследуем возможность решения задачи аналитически.

Заданная производственная функция является неоклассической, то есть непрерывной, возрастающей, строго квази-вогнутой и дифференцируемой во всех точках. Фирма может вовлекать в производство только неотрицательные количества каждого ресурса. Кроме того, множество производственных возможностей является ограниченным, замкнутым, непустым и выпуклым. В этой ситуации предпосылка о строгой вогнутости (выпуклости) производственной функции позволяет переписать ограничение-неравенство на совокупные затраты в виде равенства. Экономически это означает, что так как издержки ограничены величиной 1500 единиц, то имеет смысл использовать производственные возможности в полном объеме, то есть зафиксировать С на уровне 1500, и перейти к следующей задаче:

Построенная модель представляет собой задачу нелинейного программирования с ограничениями в форме равенств, для решения которой можно применить метод Лагранжа. Функция Лагранжа имеет вид:

Найдем частные производные по всем переменным и приравняем их к нулю, затем решим полученную систему нелинейных уравнений.

Решая систему, получим, что решением является точка х ₁=200; х ₂=166,6; λ =0,38. Максимальный выпуск составит Y =564,6 единиц при издержках С =1500 единиц.

В целом, анализируя различные варианты поведения фирмы в области управления ресурсами, фирма должна учитывать не только производственные возможности, но и ограничения, связанные со сбытом произведенной продукции, возможные ограничения по мощности поставщиков ресурсов, а также доступность финансовых ресурсов.

Перейдем к решению второй задачи — задачи минимизации издержек производства при фиксированном объеме выпускаемой продукции.

Для случая долговременного промежутка построим математическую модель минимизации издержек производства при фиксированном объеме выпускаемой продукции:

Построенная модель представляет собой задачу нелинейного программирования с ограничениями в форме равенств, для решения которой можно применить метод Лагранжа.

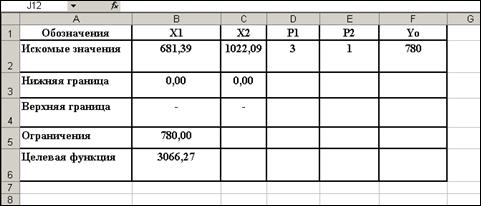
Получим, что решением является точка х ₁=681.4; х ₂=1022. Минимальные издержки производства составят С =3066,27 ед. Выпуск Y =780 единиц. Результаты решения в ППП представлены на рисунках 13 и 14.

Значение множителя Лагранжа имеет четкую экономическую интерпретацию: величина множителя Лагранжа равна нижней границе цены единицы выпускаемой продукции. Таким образом, фирма может устанавливать цену реализации не ниже 3,93 д.е. за единицу продукции.

Рисунок 13 – Результаты решения задачи в долгосрочном периоде в MS Excel

Далее проиллюстрируем взаимное расположение изокванты и изокосты в оптимальной точке (рисунки 15 и 16).

Построим изокванту для объема выпускаемой продукции Y =780, то есть .

Полученное уравнение разрешим относительно х ₁:

Построим изокосту для оптимального значения издержек производства С =3066.27, что может быть записано как или .

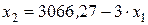
Рисунок 15 – Взаимное расположение изокванты и изокосты в точке локального рыночного равновесия

Для построения стратегической линии развития фирмы (рисунок 17) будем варьировать значение объема выпуска продукции Y в интервале от 760 единиц до 800 ед. Результаты сведем в таблицу 3. На основе аппроксимации результатов может быть построена аналитическая зависимость издержек производства от объема выпуска.

Таблица 3 – Вариантный анализ влияния объема выпуска

Вариант	Y	х ₁	х ₂

Рисунок 17 – Стратегическая линия развития фирмы

Анализируя решение основных задач можно сделать следующие выводы. Стратегические задачи должны иметь приоритет перед тактическими, так решение в долгосрочном периоде всегда соответствует большей величине прибыли, что является целью фирмы. По результатам решения можно определить не только оптимальные значения ресурсов, вовлекаемых в производство, но и определить нижнюю границу цены продукции. Если сложившаяся цена рыночного равновесия превосходит рассчитанную, то фирме выгодно производить и реализовывать продукцию, в противном же случае следует изменить стратегию, либо отказаться от заведомо убыточной продукции.

Таблица А.1 Варианты для индивидуальных заданий

№	Производственная функция	Цена ресурса x ₁	Цена ресурса x ₂	Издерж-ки производ-ства	Объем выпуска	Ограничения на ресурсы в краткосрочном периоде
Обозна-чения	F (x ₁, x ₂)	p ₁	p ₂	C0	Y0	х ₁	х ₂

	5x₁^1/3x₂^2/3			min
	2x₁^3/4x₂^1/4				max		—
	3x₁^2/3x₂^1/3			min
	5x₁^1/2x₂^1/2				max	—
	4x₁^1/3x₂^2/3			min
	3x₁^2/3x₂^1/3				max
	5x₁^1/5x₂^4/5			min
	6x₁^2/3x₂¹^/3				max
	4x₁²^/⁵x₂³^/⁵			min
	3x₁^1/⁴x₂³^/⁴				max
	5x₁^1/3x₂^2/3			min
	2x₁³^/⁴x₂¹^/⁴				max
	4x₁²^/3x₂¹^/3			min
	5x₁^1/²x₂¹^/²				max
	6x₁^1/3x₂^2/3			min
	7x₁^2/3x₂^1/3				max
	3x₁³^/⁴x₂¹^/⁴			min
	2x₁^1/3x₂^2/3				max
	4x₁^2/3x₂^1/3			min
	5x₁^1/4x₂^3/4				max
	2x₁^1/²x₂^2/3			min
	3x₁^1/3x₂^1/3				max
	6x₁^1/3x₂^2/3			min
	5x₁^2/3x₂^1/2				max
	5x₁^1/3x₂^2/3			min

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности…

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями…

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм…

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени…

Источник

Курс повышения квалификации

«Применение MS Word, Excel в финансовых расчетах»

Среднее время обучения наших слушателей на данном курсе:
89
дней (минимальное время обучения:
21 день)

В настоящий момент курс проходит
27 обучающихся из 14
регионов

Обращаем Ваше внимание, что в период действия подписки Вы одновременно можете проходить 3
курса (2 ПК и 1 ПП).

Предусмотрена возможность ускоренного обучения по индивидуальному графику.

Срок обучения по программе

36 часов — от 2 недель
72 часа — от 2 недель
108 часов — от 3 недель

Источник