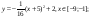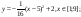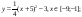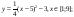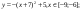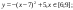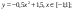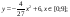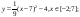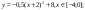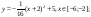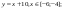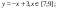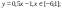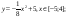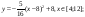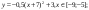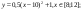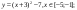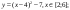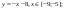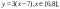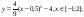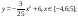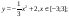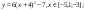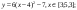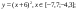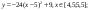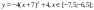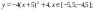Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
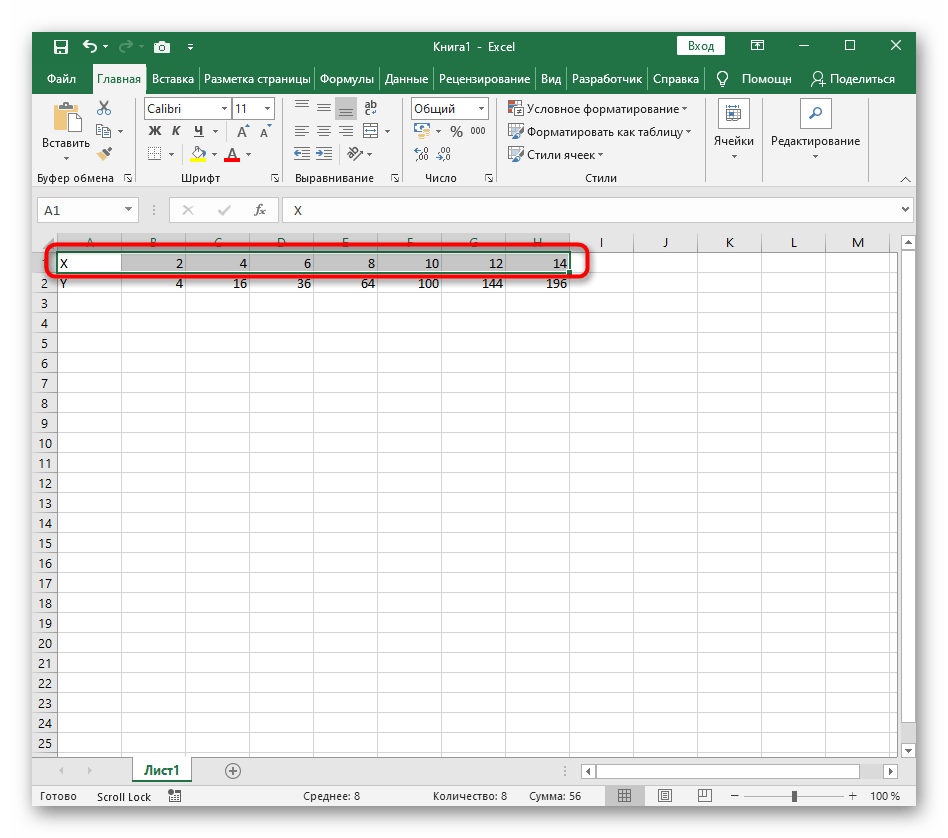
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
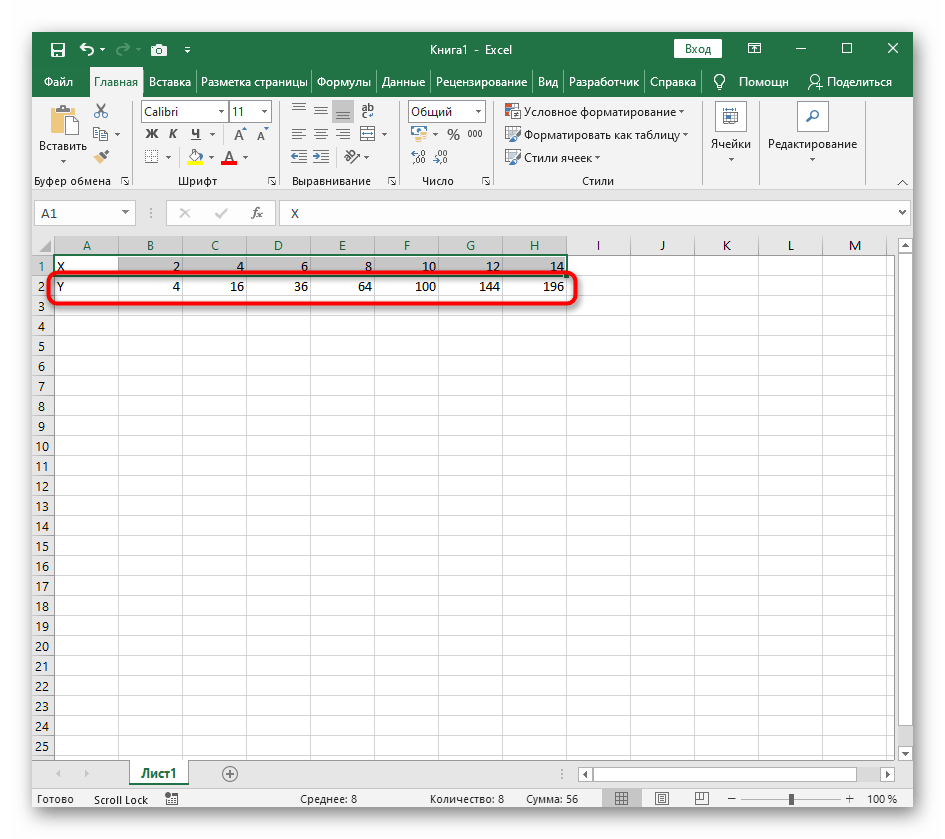
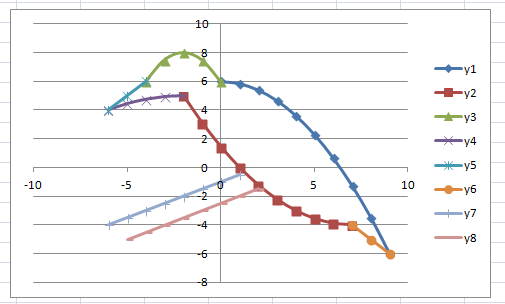
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Построение графиков функций
1. Построить в разных системах координат при x [− 2, 2] графики функций
|
1 + x2 |
3 |
|||||||||||||||||
|
1 + x |
2 |
, x < 0 |
||||||||||||||||
|
, x ≤ 0 |
||||||||||||||||||
|
1 + x |
1 + x |
4 |
||||||||||||||||
|
2 |
−2x |
|||||||||||||||||
|
y = sin |
(x) + |
, |
g = |
, z |
= 2e |
, |
x [0;1] |
|||||||||||
|
1 + cos2 (x) |
||||||||||||||||||
|
2x |
x >1 |
|||||||||||||||||
|
1 + |
, x > 0 |
2sin(3x), |
||||||||||||||||
|
2 |
||||||||||||||||||
|
1 |
+ x |
|||||||||||||||||
|
В ячейки A1:D1 записываем заголовки |
||||||||||||||||||
|
таблицы x, y, g ,z. |
||||||||||||||||||
|
Графики нужно |
построить |
в пределах |
||||||||||||||||
|
x [− 2, 2], возьмём шаг 0,2. |
Тогда x будет принимать значения -2, -1,8, -1,6, -1,4 и так далее до 2
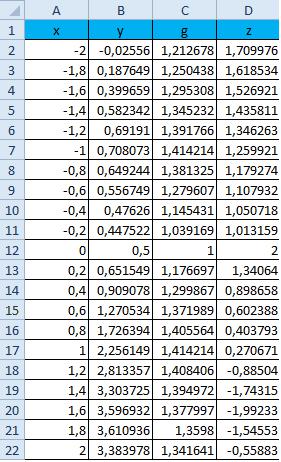
В ячейку A2 введем первое значение -2, в ячейку A3 введем следующее значение — 1,8. Выделим эти две ячейки и протянем их до значения 2.
Вячейку B2 введем формулу для вычисления y(x) =SIN(A2)^2+(1+A2)/(1+COS(A2)^2)
Вячейку C2 введем формулу для вычисления g(x) =ЕСЛИ(A2<=0;(1+A2^2)/(1+A2^4)^(1/2);(1+2*A2/(1+A2^2))^(1/2))
Вячейку D2 введем формулу для вычисления z(x) =ЕСЛИ(A2<0;(1+A2^2)^(1/3);ЕСЛИ(A2<=1;2*EXP(-2*A2);2*SIN(3*A2)))
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
1 |
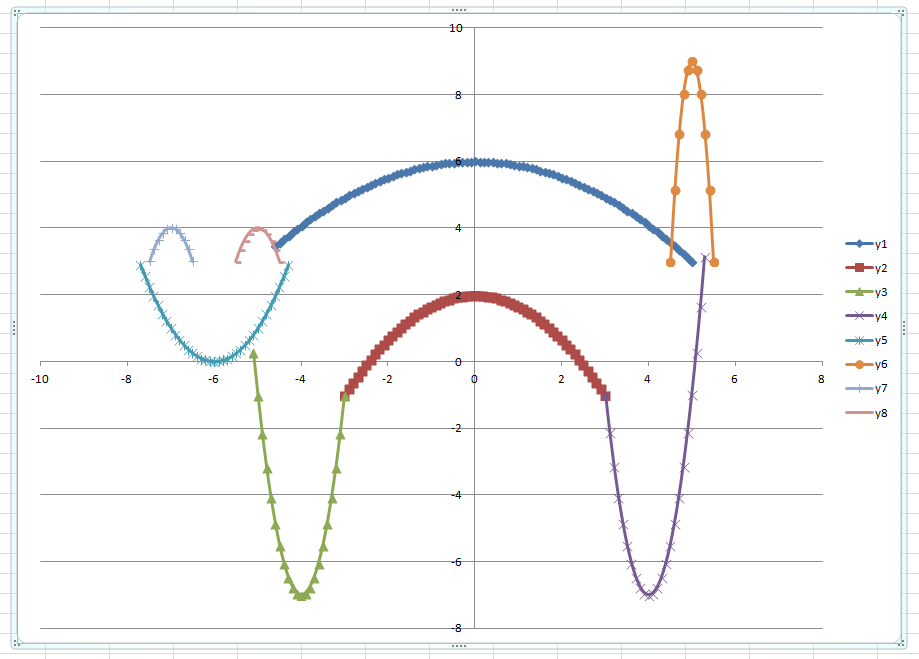
Ячейки B2, C2, D2 протянем вниз до значения x равного 2, в данном случае до 22 строчки. В результате, получим
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
2 |
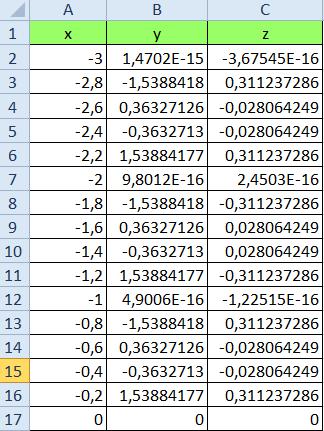
2. Построить в одной системе координат при x [− 3;0] графики функции
Y =2sin(2πx)cos(4πx) Z =cos3 (4πx)sin(πx)
На новом листе Excel в столбце A, протабулируем значения x в пределах от -3 до 0 с шагом 0,2.
В ячейку B2 введем формулу =2*SIN(2*ПИ()*A2)*COS(4*ПИ()*A2)
В ячейку C2 введем формулу =COS(4*ПИ()*A2)^3*SIN(ПИ()*A2)
Ячейки B2, C2 протянем вниз до значения x равного 0, в данном случае до 17 строчки.
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
3 |
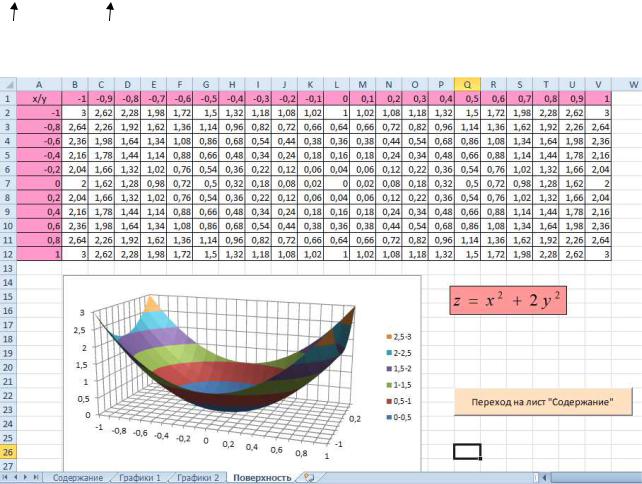
3. Построить поверхность z = x2 + 2y 2 при x [−1;1] В ячейку B2 введем формулу
=$A2^2+2*B$1^2
|
фиксируем |
фиксируем |
|
номер столбца |
номер строки |
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
4 |

Пользовательские функции.
Сохранить файл в формате *.xlsm (тип файла Книга Excel с поддержкой макросов)
Открыть редактор Visual Basic (Alt+F11) Добавить модуль Insert → Module
|
sin 2 (x) + |
1 + x |
||||||||||
|
1 + cos2 (x) |
|||||||||||
|
1 + x |
2 |
x ≤ 0 |
|||||||||
|
, |
|||||||||||
|
1 + x4 |
|||||||||||
|
1 + |
2x |
, x > 0 |
|||||||||
|
2 |
|||||||||||
|
1 + x |
|||||||||||
|
3 |
|||||||||||
|
1 + x |
2 , |
x < 0 |
|||||||||
|
2e−2x, |
x [0;1] |
||||||||||
|
x >1 |
|||||||||||
|
2sin(3x), |
|||||||||||
Y =2sin(2πx)cos(4πx)
Z =cos3 (4πx)sin(πx)
z = x2 + 2y 2
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
5 |
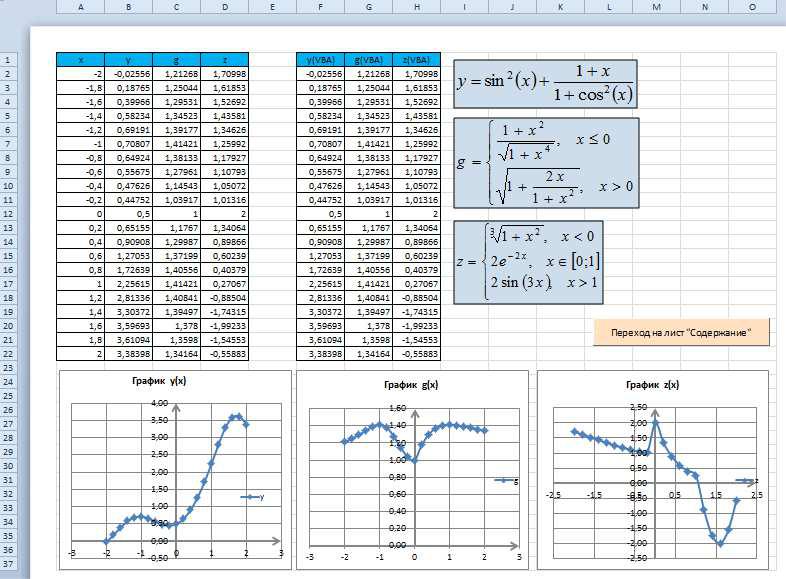
Построение графиков функций y(x), g(x), z(x) в разных системах координат
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
6 |
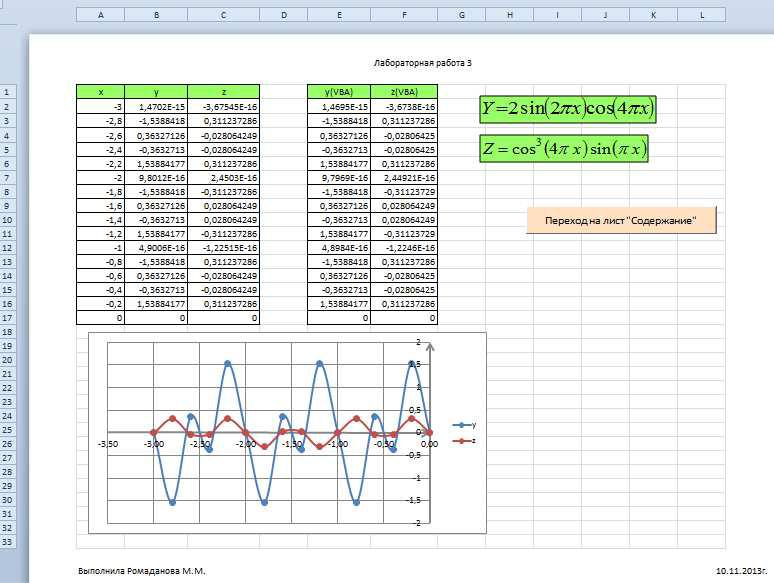
Построение графиков функций y(x), z(x) в одной системе координат
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
7 |
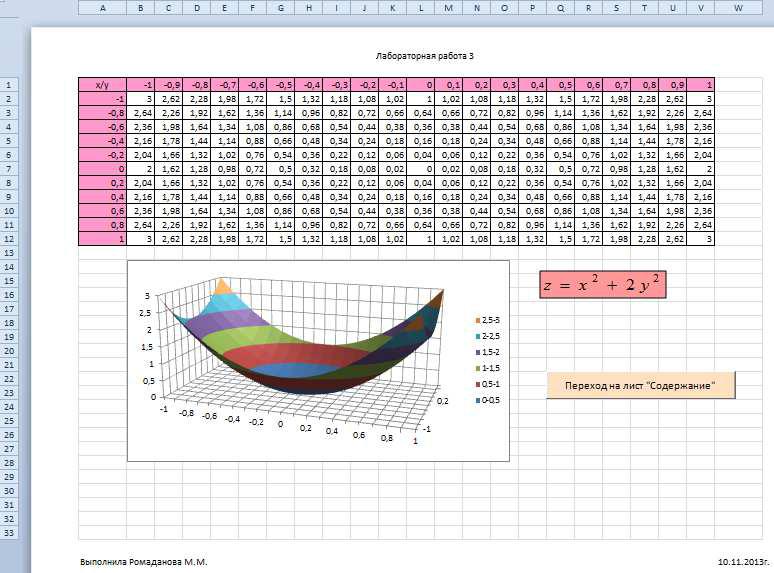
Построение поверхности z(x,y)
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
8 |
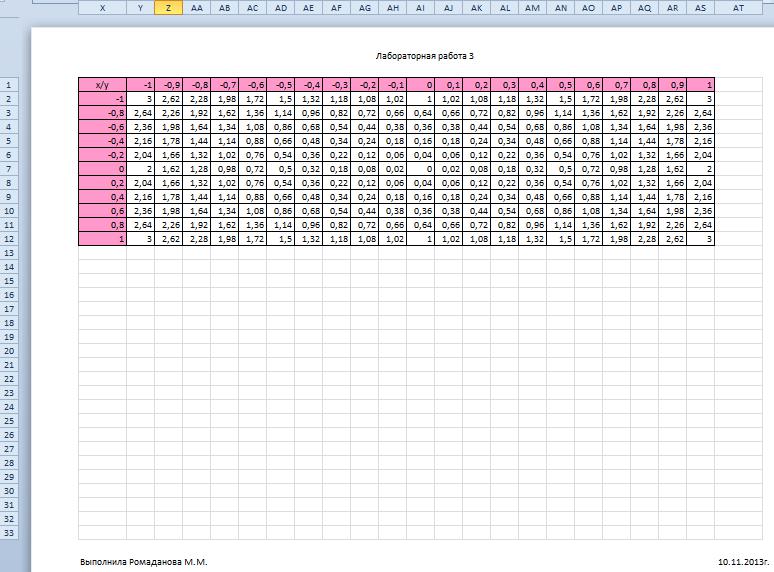
Поверхность z(x,y), построенная с помощью пользовательских функций. Должны получиться такие же значения, как и в предыдущей таблице.
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
9 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
29.03.2015511.29 Кб43.pdf
- #
Содержание |
Назад |
Далее
9.7. Построение графиков и функций
Рассмотрим построение графика функции на примере функции
y = cos2
(px), x
Î[0,1]. Для построения графика функции необходимо сначала построить таблицу её значений
при различных значениях аргумента с фиксированным шагом. Выберем шаг равным 0,1.
Необходимо найти y(0), y(0,1),
y(0,2), … , y(1). С этой целью в диапазон ячеек
А1:А11 введем следующие значения переменной
x: 0, 0.1, 0.2, …, 1. Выбранные
значения образуют арифметическую прогрессию. Заполнение ячеек членами арифметической
прогрессии в Excel можно осуществить двумя способами.
Первый способ. В ячейки А1
и А2 вводим первый и второй члены арифметической
прогрессии и выделяем эти ячейки. После этого устанавливаем указатель мыши на
маркер заполнения выделенного диапазона и протаскиваем его вниз до тех пор, пока
не получится числовой ряд нужной длины.
Второй способ. В ячейку А1 вводим
первый член арифметической прогрессии. Выбираем команду Правка
/ Заполнить / Прогрессия и в открывшемся диалоговом окне
Прогрессия в группе Расположение
устанавливаем переключатель в положение По столбцам,
а в группе Тип – в положение Арифметическая
. В поле Шаг вводим значение 0.1, а в поле
Предельное значение – 1. После нажатия кнопки
ОК будет выполнено построение прогрессии.
С помощью команды Правка / Заполнить / Прогрессия
можно создавать также геометрические прогрессии.
Ввод формул в ячейку можно производить с клавиатуры или с помощью диалогового окна
Мастер функций, вызываемого командой
Вставка / Функция или нажатием кнопки
панели инструментов Стандартная. Мастер функций содержит
список всех встроенных в Excel функций, а также справки
по синтаксису функций и примеры их применения.
Выделим ячейку В1 и нажмем кнопку 
На экране появится первое диалоговое окно Мастер функций. Это окно
содержит два списка: Категория – список, включающий 11 категорий
функций, и Функция – список имен функций, входящих в выбранную категорию.
Функция cos относится к категории
Математические. Выберем эту функцию и нажмем кнопку
ОК. На экране появится второе диалоговое окно
Мастер функций. В поле Число
введем аргумент функции. В рассматриваемом случае это ПИ()*А1. После нажатия
кнопки ОК в ячейку В1 будет
введена формула =COS(ПИ()*A1).
Отметим, что при использовании мастера функций перед вводом формулы в ячейку
не надо вводить знак «=», т.к. мастер функций введет его сам.
Теперь с помощью клавиатуры добавьте в эту формулу операцию возведения в квадрат.
После всех описанных действий в ячейку В1 будет введена
формула
=COS(ПИ()*A1)^2.
Для того чтобы завершить процесс табулирования функции, выделим ячейку В1
, установим указатель мыши на маркере заполнения этой ячейки и протащим
его вниз до ячейки В11.
Для построения графика используется Mастера диаграмм (рис. 19).
Вызов мастера диаграмм производится
или с помощью команды Вставка / Диаграмма, или нажатием кнопки
панели инструментов Стандартная (рис. 19).
Рис. 19. Первый шаг мастера диаграмм.
Работа с мастером диаграмм осуществляется по шагам. На первом шаге в открывшемся
диалоговом окне на вкладке Стандартные выбираем тип диаграммы
График, её вид и нажимаем кнопку Далее.
На втором шаге на вкладке Диапазон данных
необходимо указать диапазон данных, по которому строится график (рис. 20).
Рис. 20. Второй шаг мастера диаграмм. Вкладка
Диапазон данных.
Для этого надо установить переключатель Ряды в столбцах. После
этого в окне Диапазон надо указать диапазон данных
$B$1:$B$11. Однако проще указать диапазон, протягивая по нему мышь.
На вкладке Ряд в окне Подписи оси Х аналогичным
образом надо указать диапазон значений переменной
x: =$A$1:$A$11 (рис. 21).
Значения из этого диапазона используются в качестве меток оси X.
Выполнив эти действия, нужно нажать кнопку Далее.
Рис. 21. Второй шаг мастера диаграмм. Вкладка Ряд.
На третьем шаге устанавливаются параметры диаграммы, такие
как Подписи данных, Таблица данных, Заголовки, Оси, Линии сетки,
Легенда (рис. 22).
Рис. 22. Третий шаг мастера диаграмм.
На четвертом шаге указывается место размещения диаграммы: на отдельном листе или
на имеющемся (рис. 23).
Рис. 23. Четвертый шаг мастера диаграмм.
Построение графика функции завершается нажатием кнопки Готово
(рис. 24).
Рис. 24. Результат построения графика функции.
Рассмотрим пример построения графика функции
при x
Î[0, 1].
Этот график строится также, как и предыдущий, за одним исключением – в ячейку
В1 вводится формула
=ЕСЛИ(A1<0,5; (1+ABS(0,2-A1))/(1+A1+A1^2); A1^(1/3)).
Функция ЕСЛИ используется для проверки значений формул и организации переходов в
зависимости от результатов проверки.
Синтаксис функции ЕСЛИ
ЕСЛИ(лог_выражение; значение_если_истина;
значение_если_ложь)>
Лог_выражение – любое значение или
выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ.
Значение_если_истина – значение, которое
возвращается, если лог_выражение имеет
значение ИСТИНА.
Значение_если_ложь – это значение, которое
возвращается, если лог_выражение
имеет значение ЛОЖЬ.
Результат построения графика функции показан на рис. 25.
Рис. 25. Результат построения графика функции с помощью функции ЕСЛИ.
Рассмотрим пример построения в одной системе координат графиков следующих двух функций:
y = 2sinx
z = 3cos2x —
sinx
при
x
Î[–3,0].
В диапазон ячеек А2:А17 вводим значения переменной
x от –3 до 0 с шагом 0,2.
В ячейки В1 и С1 вводим
y и
z, соответственно.
В ячейки В2 и С2 вводим формулы
=2*SIN(A2),
=3*COS(2*A2)–SIN(A2).
Выделим диапазон В2:С2, установим указатель мыши на маркере
заполнения этого диапазона и протащим вниз так, чтобы заполнить диапазон В2:С17
.
На первом шаге мастера диаграмм на вкладке Стандартные
выберем тип График и вид График с маркерами,
помечающими точки данных.
На втором шаге на вкладках Диапазон данных и
Ряд указываем диапазон ячеек B1:C17, по которому
строятся графики функций, и диапазон A2:A17, по которому
стоятся надписи по оси X. Заголовки столбцов
Y и Z в ячейках В1
и С1 должны быть включены в диапазон данных, поскольку они
используются при построении легенды.
На третьем шаге указываем название диаграммы и надписи на осях. Если необходимо,
наносим на график линии сетки, таблицу данных и легенду.
На четвертом шаге указываем место размещения диаграммы. Результат построения приведен
на рис. 26.
Рис. 26. Результат построения графиков двух функций.
Содержание |
Назад |
Далее
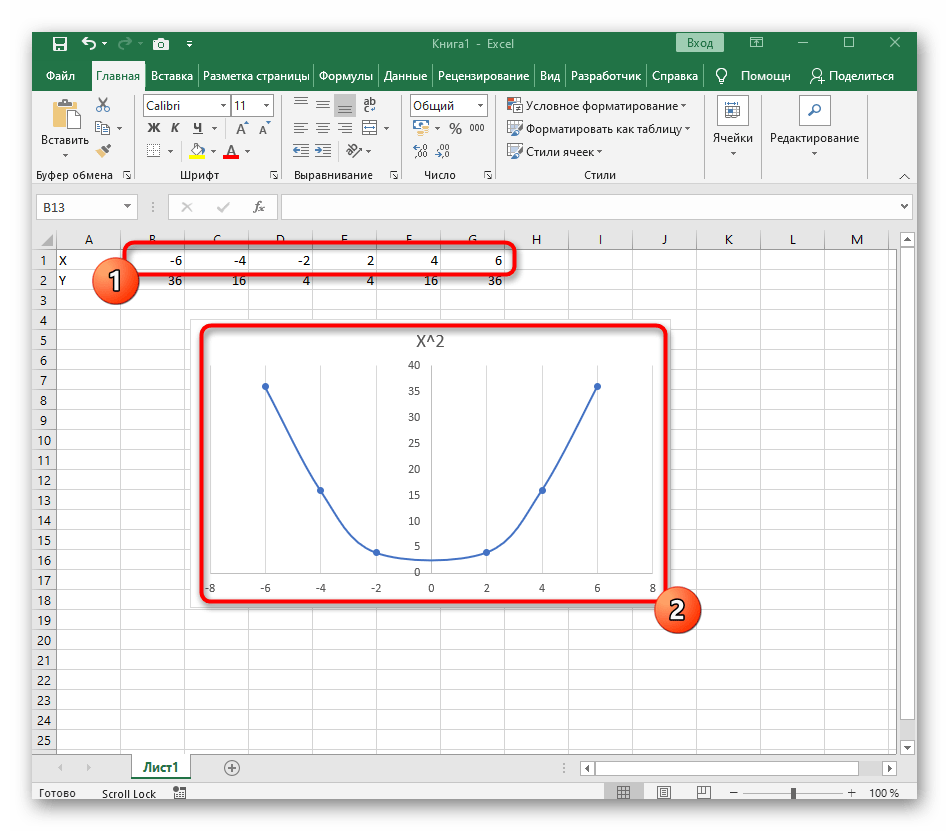
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
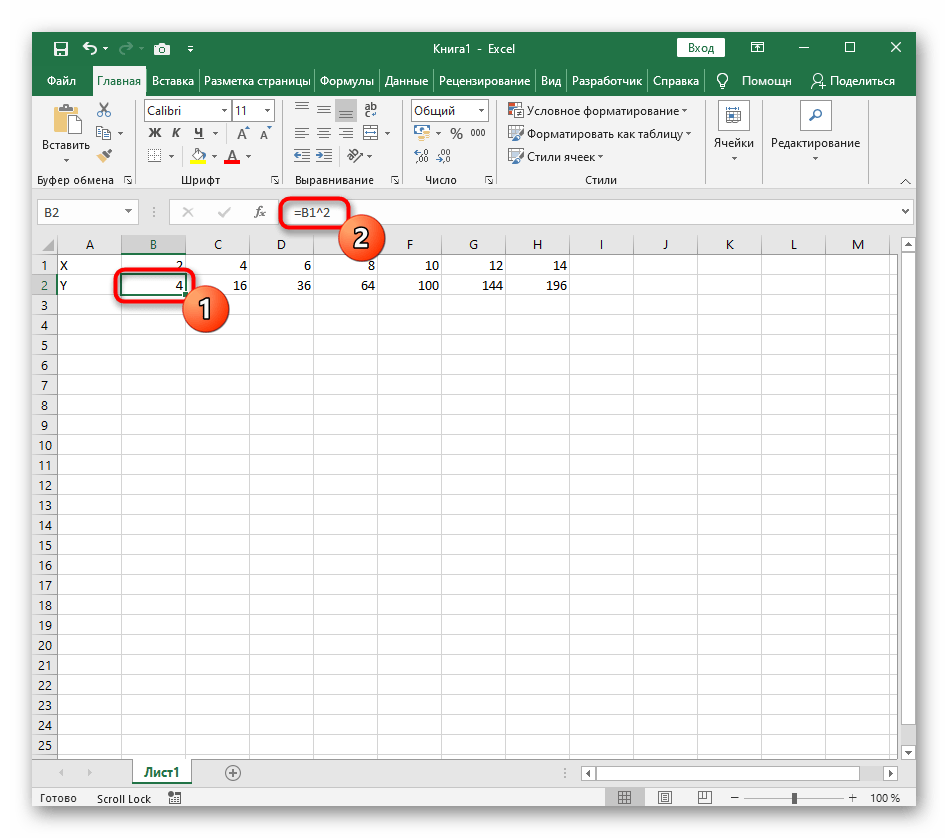
- Нажмите по первой ячейке и впишите
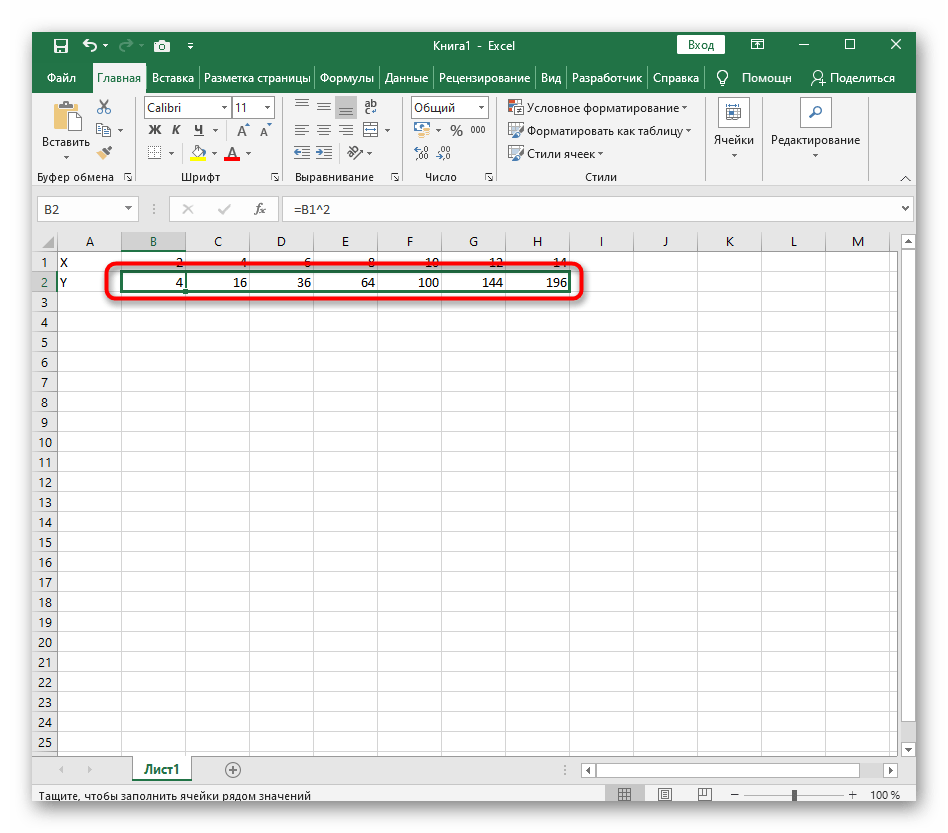
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
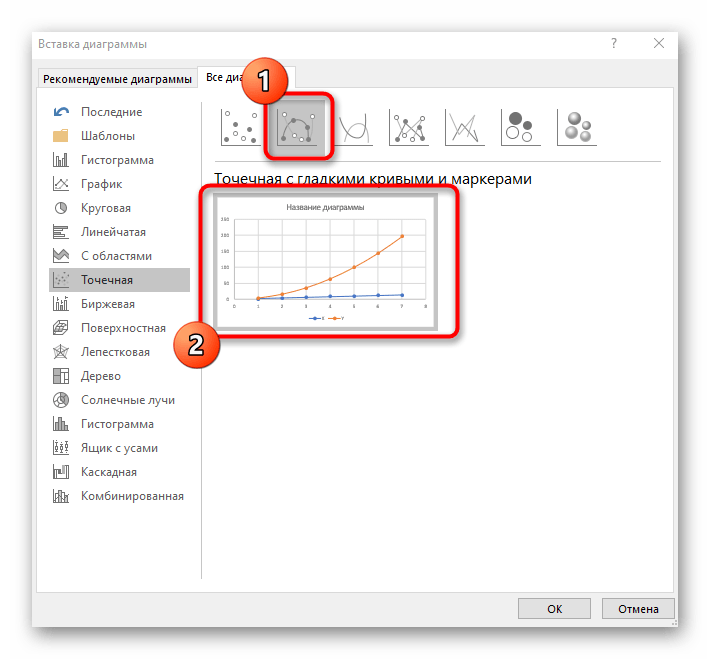
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
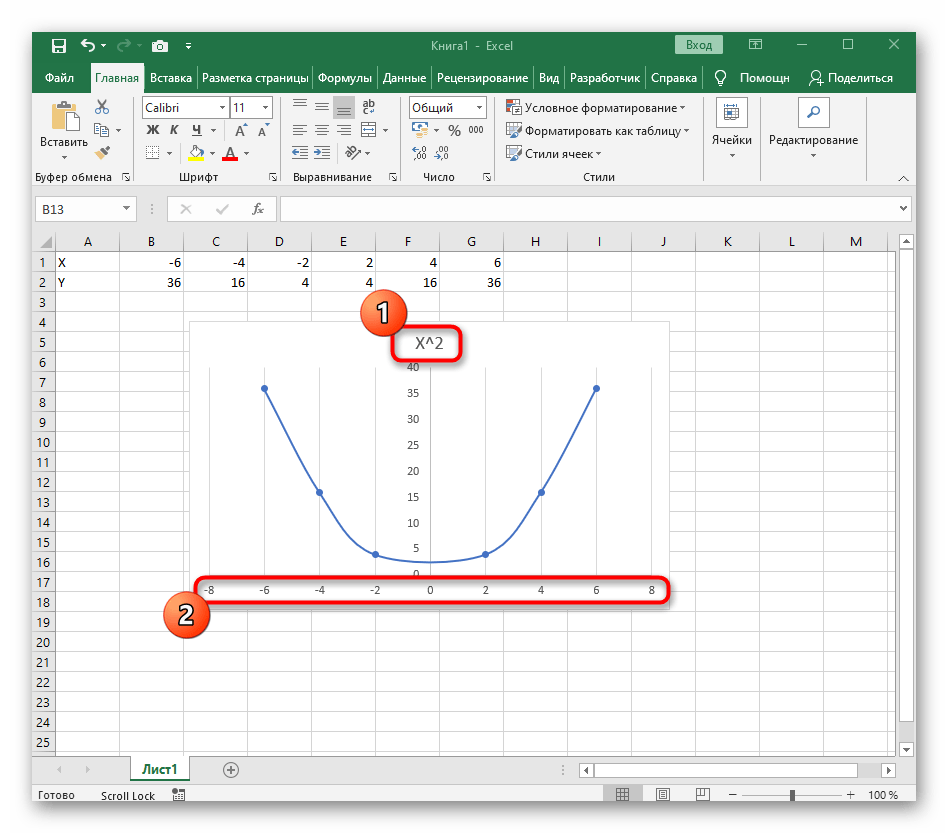
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
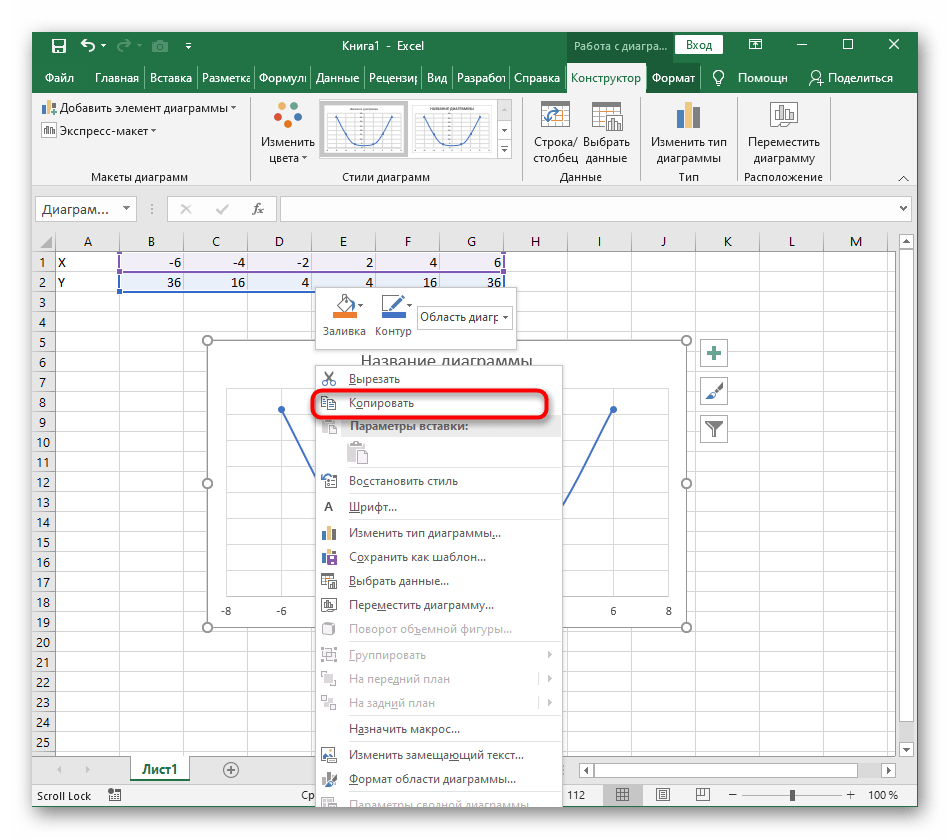
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
Практическая работа в MS Excel по теме
ПОСТРОЕНИЕ ДИГРАММ И ГРАФИКОВ
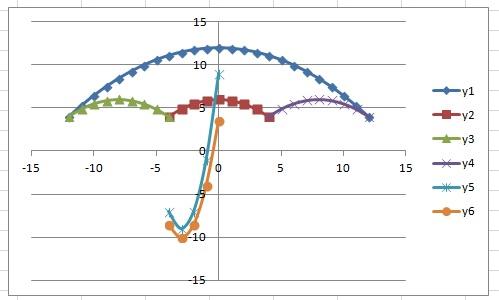
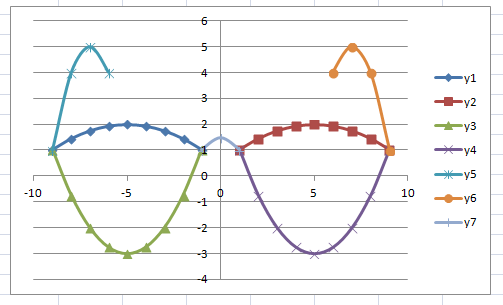
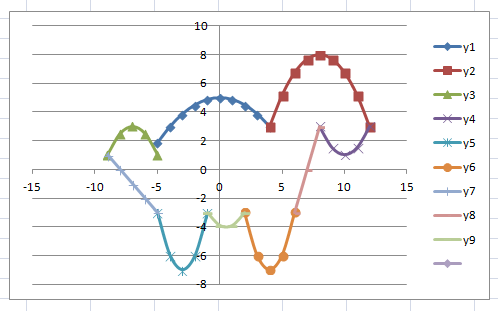
Задание: Построение рисунка «ЗОНТИК»
Приведены функции, графики которых участвуют в этом изображении:
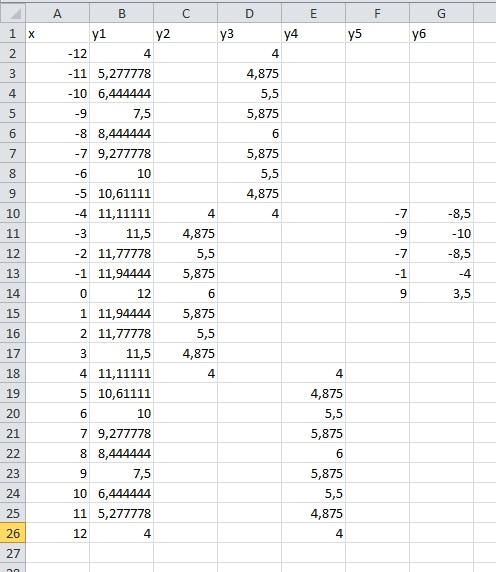
у1= -1/18х2 + 12, х[-12;12]
y2= -1/8х2 +6, х[-4;4]
y3= -1/8(x+8)2 + 6, х[-12; -4]
y4= -1/8(x- 
y5= 2(x+3)2 – 9, х[-4;0]
y6=1.5(x+3)2 – 10, х[-4;0]
-
Запустить MS EXCEL
-
В ячейке А1 внести обозначение переменной х
-
Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х2 + 12, х[-12;12]
Порядок выполнения действий:
-
Устанавливаем курсор в ячейку В1 и вводим у1
-
В ячейку В2 вводим формулу
Нажимаем Enter на клавиатуре
Автоматически происходит подсчет значения функции.
Растягиваем формулу до ячейки В26
Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х[-4;4]) вводим формулу для графика функции y2= -1/8х2 +6.
И.Т.Д.
В результате должна получиться следующая ЭТ
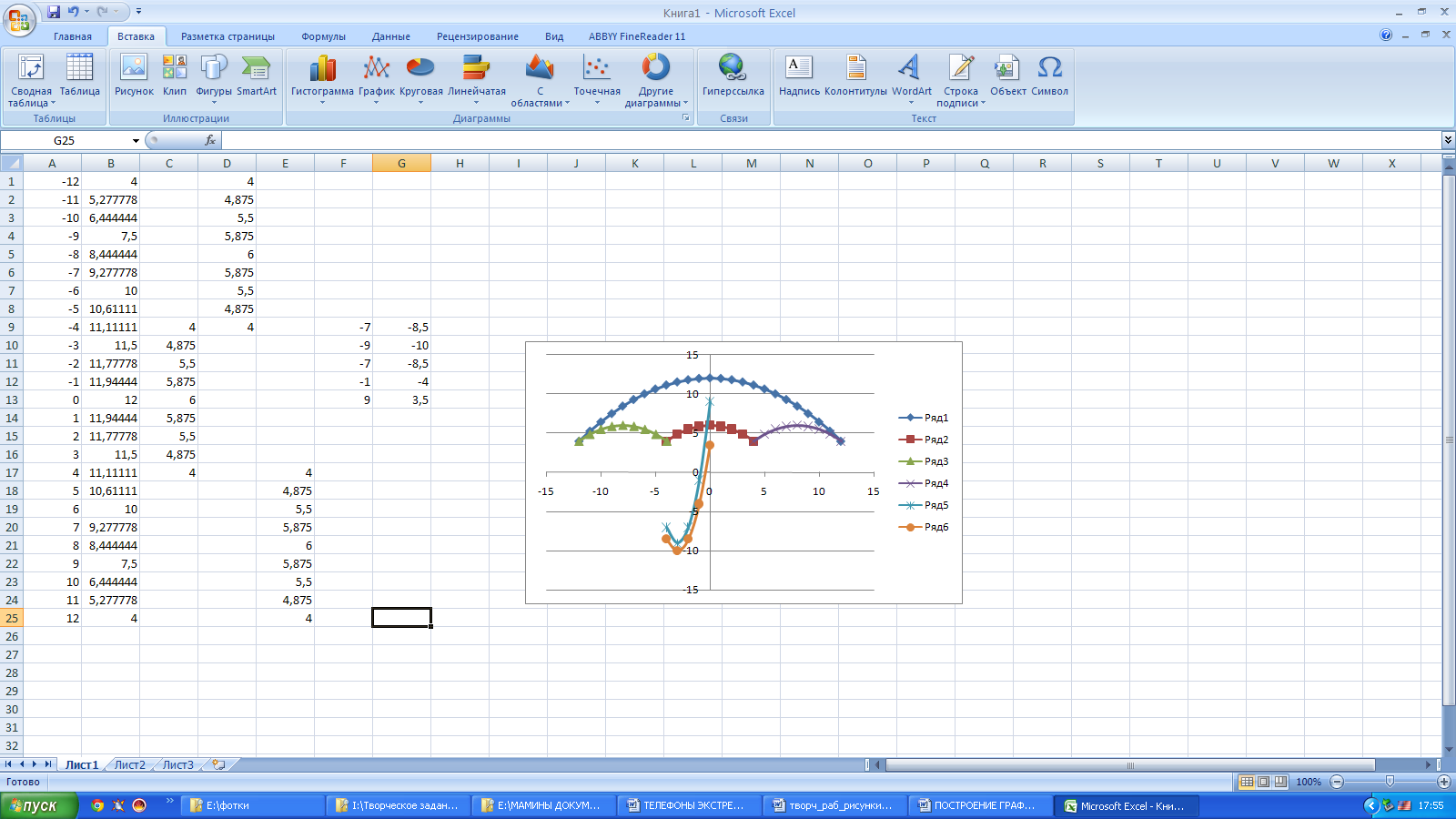
После того, как все значения функций подсчитаны, можно строить графики этих функций.
-
Выделяем диапазон ячеек А1:G26
-
На панели инструментов выбираем меню Вставка → Диаграмма.
-
В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok.
В результате должен получиться следующий рисунок:
Самостоятельная работа:
Построить графики функций в одной системе координат. Получить рисунок.
|
1. «Очки» 1) 2) 3) 4) 5) 6) 7) |
|
|
2. «Птица» 1) 2) 3) 4) 5) 6) 7) |
|
|
3. «Динозаврик» 1) 2) 3) 4) 5) 6) 7) 9) |
|
|
4. «Кошка» 1) 2) 3) 4) 5) 6) 7) |
|
1