Практическая
работа
Тема:
Построение диаграмм и графиков в электронных таблицах MS Excel.
Цель:
закрепление практических навыков по теме «Построение диаграмм и графиков в электронных
таблицах MS Excel».
Задачи:
Образовательная: формирование глубоких и прочных знаний по построению диаграмм и
графиков, формирование умений и навыков, носящих в современных условиях общенаучный
и общекультурный характер;
Развивающая:
развитие у школьников
теоретического, творческого мышления; формирования операционного мышления,
направленного на выбор оптимальных решений; развить навыки мыслительной
деятельности, включая каждого учащегося в учебно – познавательный процесс и
создание условия для работы каждого в индивидуальном темпе;
Воспитательная:
развитие
познавательной активности и интереса к предмету, воспитание информационной
культуры.
Программное
обеспечение: Windows, Microsoft Office.
Ход
работы:
Задание
1.
Представить данные
в виде круговой диаграммы:
 |
|||
 |
|||
Задание
2.
Представить данные в виде
гистограммы:
Задание
3. Построить
графики функций: у = х3, у = 2х для х в диапазоне
[-4;4] с шагом 1и у = -2х2-2х+5 для х в диапазоне [-4;3] с шагом
0,5.
Задание 4. Представить
данные в виде двухрядной линейчатой диаграммы:
Задание
5. Построение
рисунка «Зонтик»
Приведены
функции, графики которых участвуют в этом изображении:
у1=
-1/18х2 + 12, хÎ[-12;12]
y2= -1/8х2
+6, хÎ[-4;4]
y3= -1/8(x+8)2
+ 6, хÎ[-12; -4]
y4= -1/8(x-8)2
+ 6, хÎ[4; 12]
y5=
2(x+3)2
– 9, хÎ[-4;0]
y6=1.5(x+3)2
– 10, хÎ[-4;0]
Порядок
выполнения действий:
1. Запустить
MS EXCEL
2. В ячейке А1
внести обозначение переменной х
3. Заполнить
диапазон ячеек А2:А26 числами от -12 до 12 с шагом 1, используя меню
(ЗАПОЛНИТЬ-ПРОГРЕССИЯ-ПО СТОЛБЦАМ).
4. Последовательно
для каждого графика функции будем вводить формулы.
Для у1= -1/18х2
+ 12, хÎ[-12;12]
5. Устанавливаем
курсор в ячейку В1 и вводим у1
6. В ячейку В2
вводим формулу
7. 
Нажимаем
Enter
на
клавиатуре
8. Автоматически
происходит подсчет значения функции.
9. Растягиваем
формулу до ячейки В26
10. 
Аналогично
в ячейку С10 (т.к значение функции находим только на отрезке хÎ[-4;4]) вводим
формулу для графика функции y2= -1/8х2 +6.
и.т.д.
В
результате должна получиться следующая ЭТ
После
того, как все значения функций подсчитаны, можно строить графики этих функций.
1. Выделяем
диапазон ячеек А1:G26
2. На панели
инструментов выбираем меню Вставка → Диаграмма.
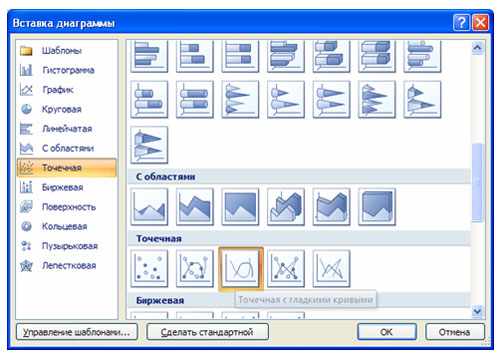
3. В окне
Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok.
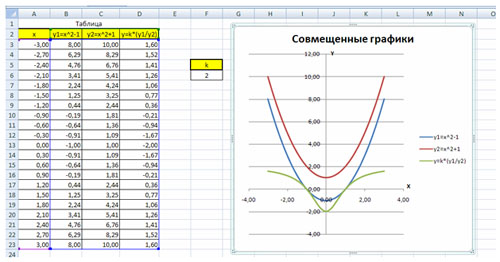
В
результате должен получиться следующий рисунок:
Выполнение
проекта:
Выберите себе один
из вариантов заданий на карточках и выполните проект по образцу, описав ход
выполнения работы по алгоритму, похожему на алгоритм выполнения Проекта
«Зонтик». Карточки с заданиями проектов для самостоятельного выполнения (обучающимся
таблица с решением не видна, доступны только уравнения функций, и изображение,
которое должно получиться в ходе выполнения работы, построения графиков фукций).
Домашнее
задание:
 |
Итог
урока:
Укажите в ВЫВОДЕ
после практической работы, достигли ли вы целей и задач нашего урока, получили
ли результат, удовлетворены ли вы результатом своей работы?
Список
литературы:
1.
И.Семакин, Е.К. Хеннер.
Задачник – практикум. Информатика и ИКТ в двух томах — М.: БИНОМ. Лаборатория
знаний, 2012;
2.
И.Семакин, Е.К. Хеннер.
Информатика, 11 класс-М.: БИНОМ. Лаборатория знаний, 2015
ВАРИАНТ№1
Задание
. Выполнить Проект «Очки» по образцу
1. y=-116(x+5)*(x+5)+2,
xЄ [-9;-1];
2. y=-116(x-5)*(x-5)+2,
xЄ [1;9];
3. y=-14(x+5)*(x+5)-3,xЄ[-9;-1];
4. y=-14(x-5)*(x-5)-3,xЄ[1;9];
5. y=–(x+9)*(x+9)+1,
xЄ[-9;-6];
6. y=–(x-9)*(x-9)+1,
xЄ[6;9];
7. y=-0,5*x*x+1,5,xЄ[-1;1];
|
x |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
|
-9 |
1 |
1 |
1 |
||||
|
-8 |
1,4375 |
-0,75 |
0 |
||||
|
-7 |
1,75 |
-2 |
-3 |
||||
|
-6 |
1,9375 |
-2,75 |
-8 |
||||
|
-5 |
2 |
-3 |
|||||
|
-4 |
1,9375 |
-2,75 |
|||||
|
-3 |
1,75 |
-2 |
|||||
|
-2 |
1,4375 |
-0,75 |
|||||
|
-1 |
1 |
1 |
1 |
||||
|
0 |
1,5 |
||||||
|
1 |
1 |
1 |
1 |
||||
|
2 |
1,4375 |
-0,75 |
|||||
|
3 |
1,75 |
-2 |
|||||
|
4 |
1,9375 |
-2,75 |
|||||
|
5 |
2 |
-3 |
|||||
|
6 |
1,9375 |
-2,75 |
-8 |
||||
|
7 |
1,75 |
-2 |
-3 |
||||
|
8 |
1,4375 |
-0,75 |
0 |
||||
|
9 |
1 |
1 |
1 |
ВАРИАНТ
№2
Задание
. Выполнить Проект «Лицо» по образцу
1. y=0,25*x*x-5,xЄ
[-6;6];
2. y=0,25*x*x-3,xЄ[-2;2];
3. y=-x*x+2,xЄ[-1;1];
4. y=0,33333*(x+3)*(x+3)+2,
хЄ[-5;-1];
5. y=0,2*(x-3)*(x-3)+2,хЄ[1;5];
6. y=-0,2*(x+3)*(x+3)+4,хЄ[-5;-1];
7. y=-0,2*(x-3)*(x-3)+4,хЄ[1;5];
8. y=-0,2*(x+3)*(x+3)+5,хЄ[-5;-1];
9. y=-0,2*(x-3)*(x-3)+5,хЄ[1;5];
10. y=-0,2*x*x+10,xЄ[-6;6];
|
x |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y9 |
y10 |
|
-6 |
4 |
2,8 |
||||||||
|
-5 |
1,25 |
3,333333 |
3,2 |
4,2 |
5 |
|||||
|
-4 |
-1 |
2,333333 |
3,8 |
4,8 |
6,8 |
|||||
|
-3 |
-2,75 |
2 |
4 |
5 |
8,2 |
|||||
|
-2 |
-4 |
-2 |
2,333333 |
3,8 |
4,8 |
9,2 |
||||
|
-1 |
-4,75 |
-4,75 |
1 |
3,333333 |
3,2 |
4,2 |
9,8 |
|||
|
0 |
-5 |
-3 |
2 |
10 |
||||||
|
1 |
-4,75 |
-4,75 |
1 |
2,8 |
3,2 |
4,2 |
9,8 |
|||
|
2 |
-4 |
-2 |
2,2 |
3,8 |
4,8 |
9,2 |
||||
|
3 |
-2,75 |
2 |
4 |
5 |
8,2 |
|||||
|
4 |
-1 |
2,2 |
3,8 |
4,8 |
6,8 |
|||||
|
5 |
1,25 |
2,8 |
3,2 |
4,2 |
5 |
|||||
|
6 |
4 |
2,2 |
3,2 |
2,8 |
ВАРИАНТ№3
Цель работы:
- научиться строить графики в Excel;
- развить самостоятельность;
- развить навыки мыслительной деятельности, включая каждого учащегося в учебно – познавательный процесс и создавая условия для работы каждого в индивидуальном темпе;
Оборудование:
- ПЭВМ, сеть, проектор;
- опорный конспект, план практической работы, варианты для самостоятельной работы учащихся.
| Этапы | План урока + опорный конспект | Средства обучения |
| I | Подготовительный. Постановка учебных задач. Устное разъяснение порядка работы на уроке, тема урока. |
— |
| II | Повторение.
Фронтальный опрос изученного материала. Вопросы:
|
проектор |
| III | Объяснение нового материала и подготовка к практической работе:
|
Проектор, раздаточный материал |
| IV | Выполнение проектной практической работы:
|
Компьютер |
| V | Итоги:
|
Проектор, раздаточный материал, компьютер |
Опорный конспект
Построение совмещенных графиков в Microsoft Office Excel -2007.
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:
Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя переменными, при проведении сравнения анализа значений y при одних и тех же значениях x.
ПРИМЕР.
(Используется при объяснении материала через проектор.)
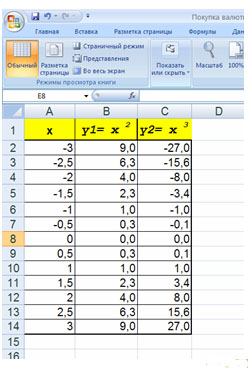
Построить графики функций y1= x 2 и y2= x 3 на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:
2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
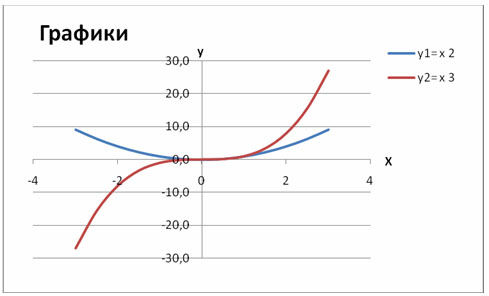
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y
5. Должен получиться график:
P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.
Раздаточный материал
Варианты
ВАРИАНТ 1
Построить графики функций y1= x 2 -1, y2= x 2+1 иy=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.
ВАРИАНТ 2
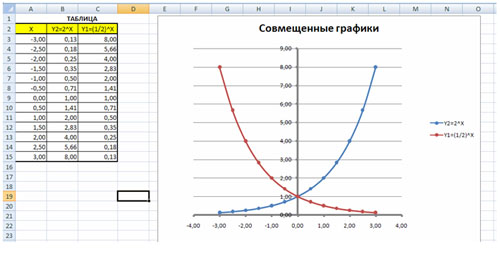
Построить графики функций y1=
и y2= 2х на интервале [- 3 ; 3] с шагом 0,5.
ВАРИАНТ 3
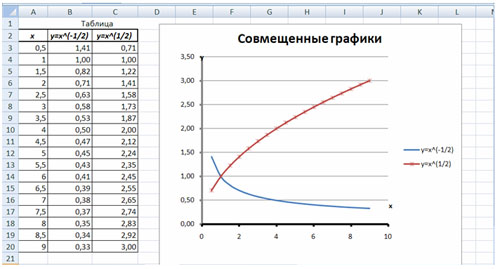
Построить графики функций y1= 
, y2=
на интервале [- 0,5 ; 9] с шагом 0,5.
ВАРИАНТ 4
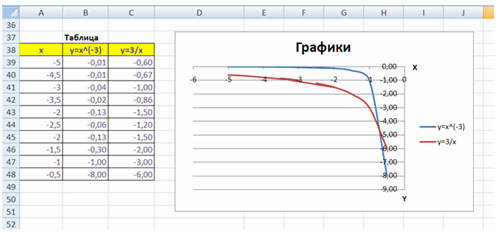
Построить графики функций y1=
, y2= 
на интервале [- 5 ; -0,5] с шагом 0,5.
ВАРИАНТ 5
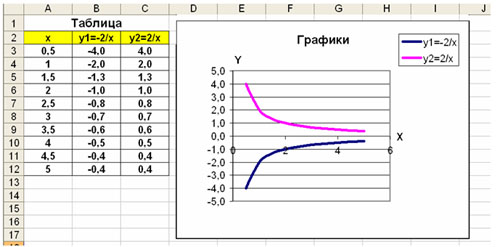
Построить графики функций y1= 
, y2=
на интервале [0,5 ; 5] с шагом 0,5.
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
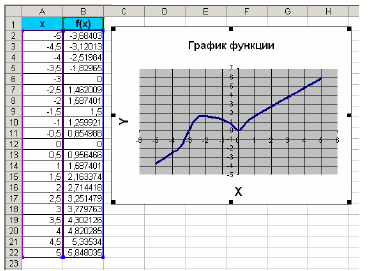
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:
Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
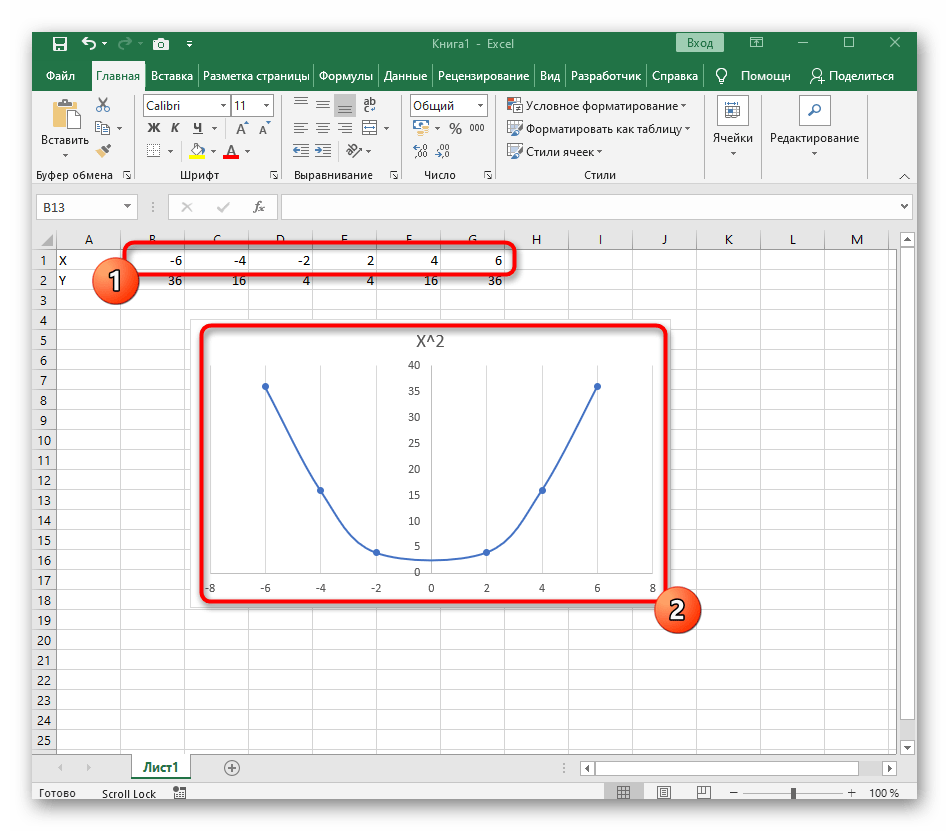
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
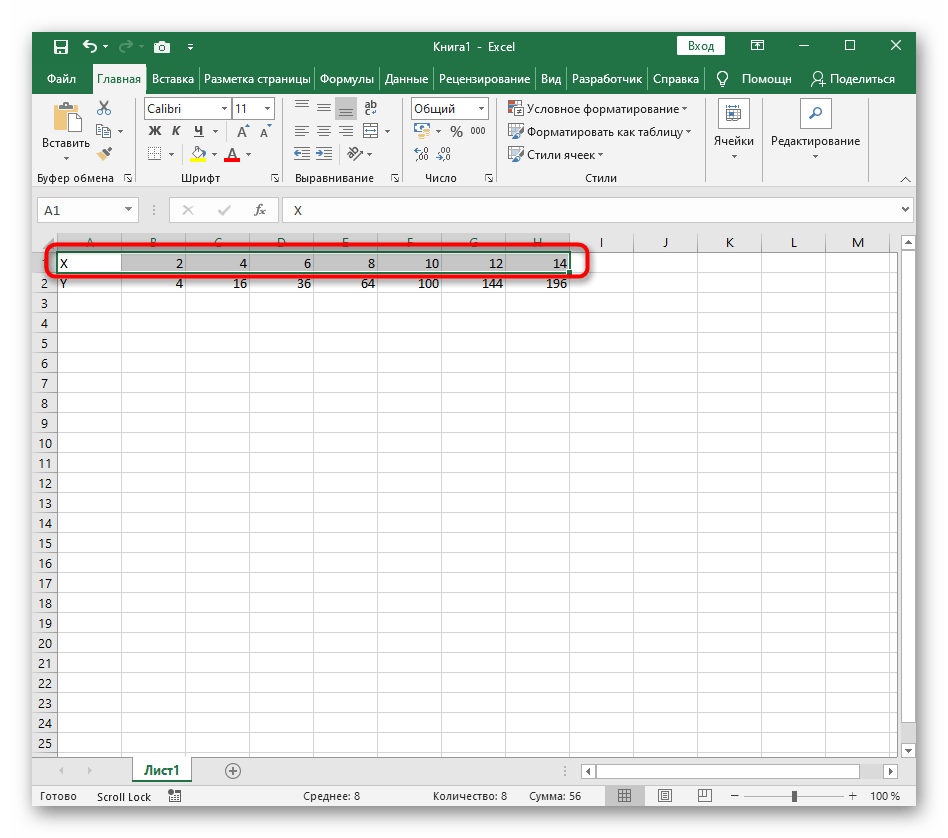
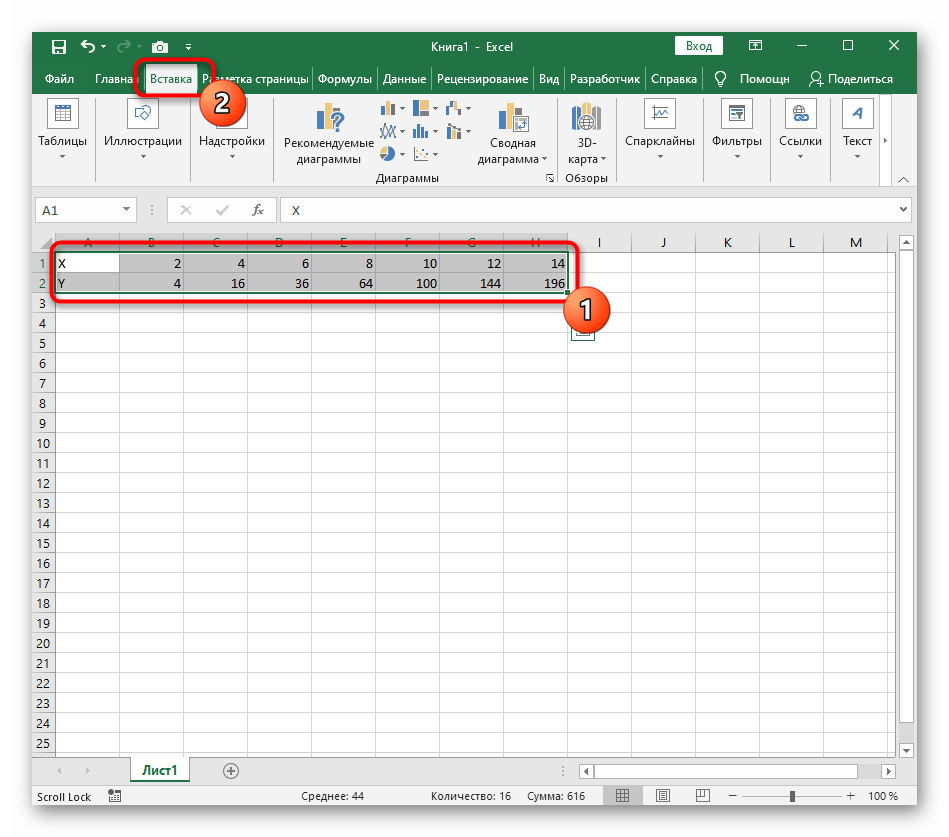
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
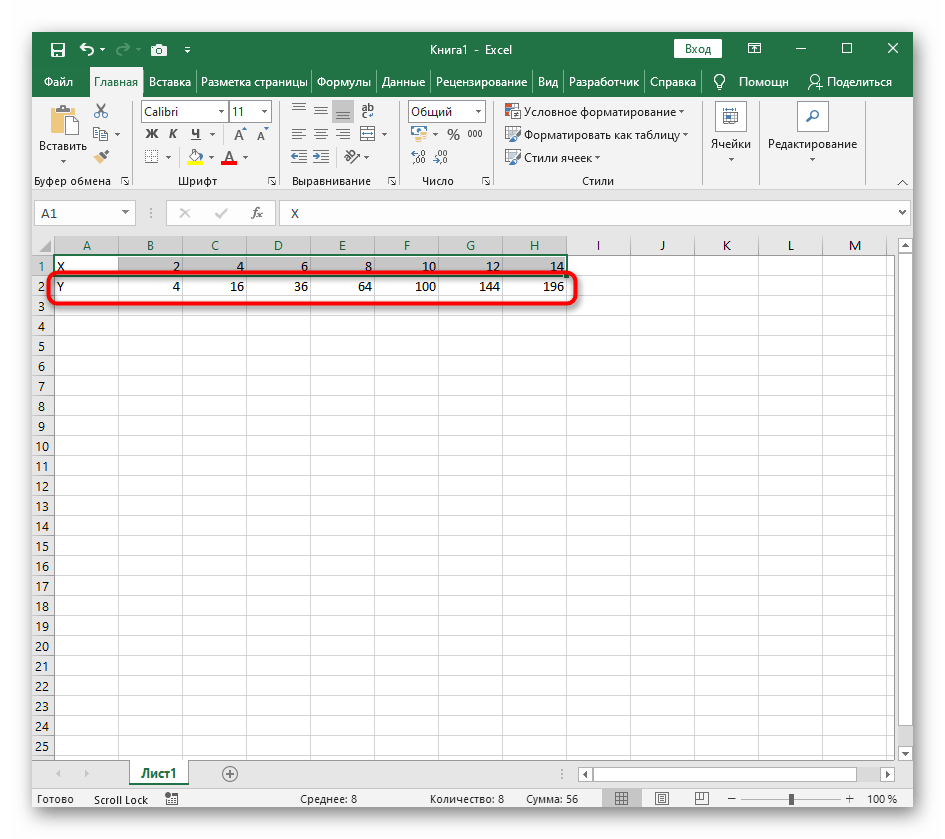
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
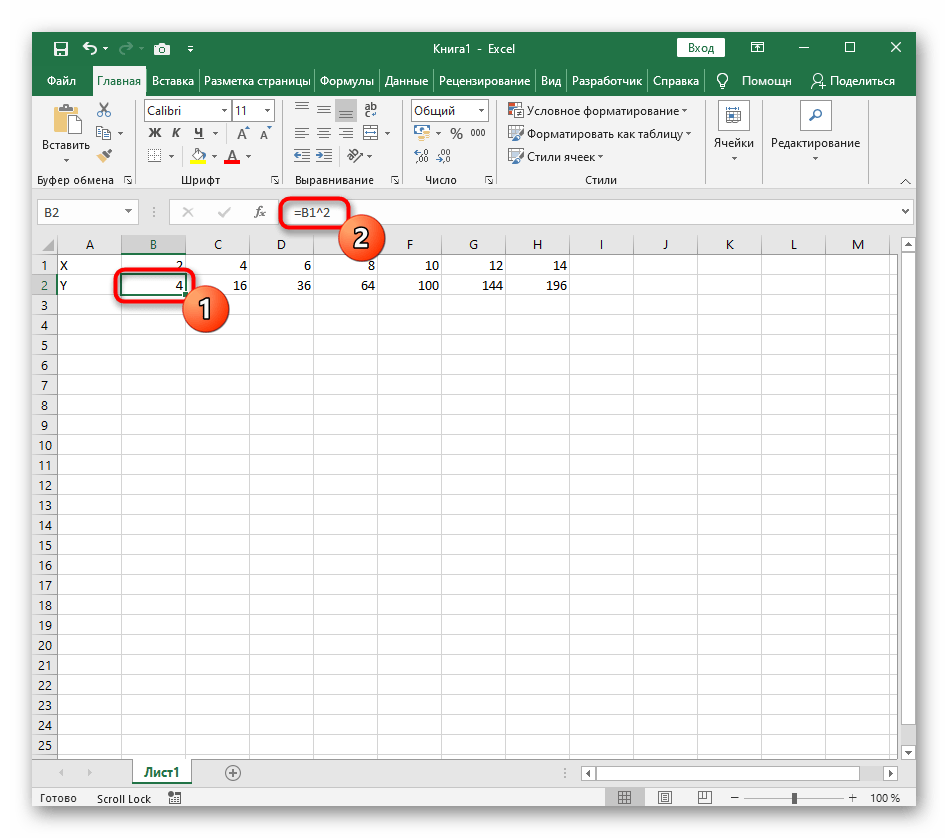
- Нажмите по первой ячейке и впишите
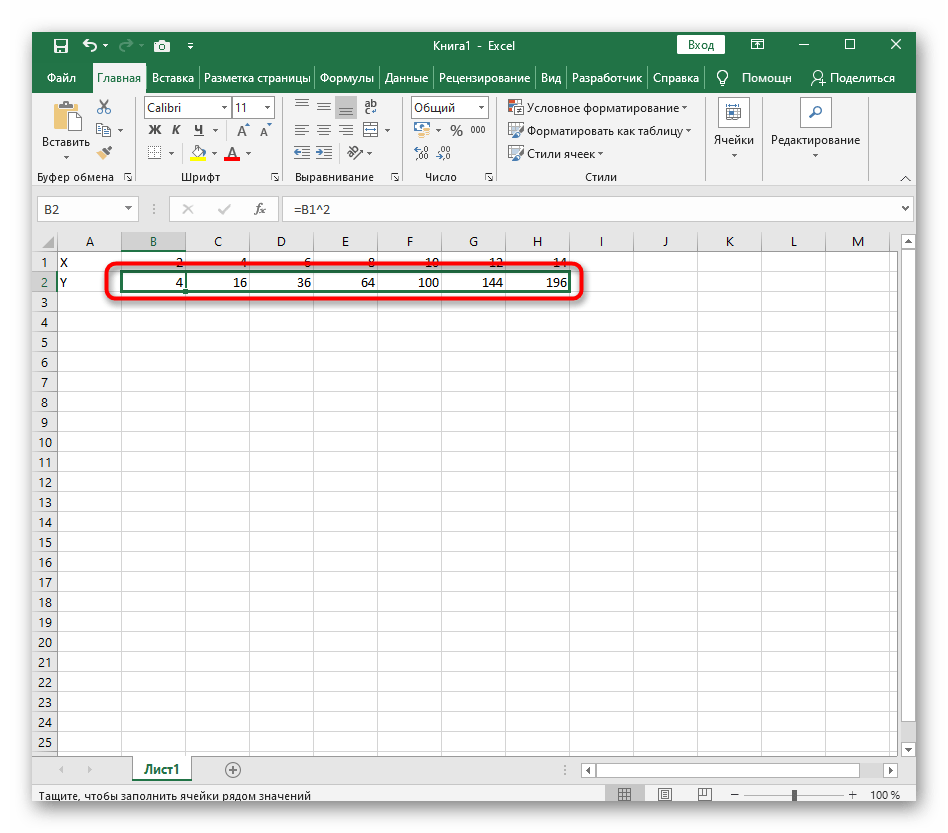
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
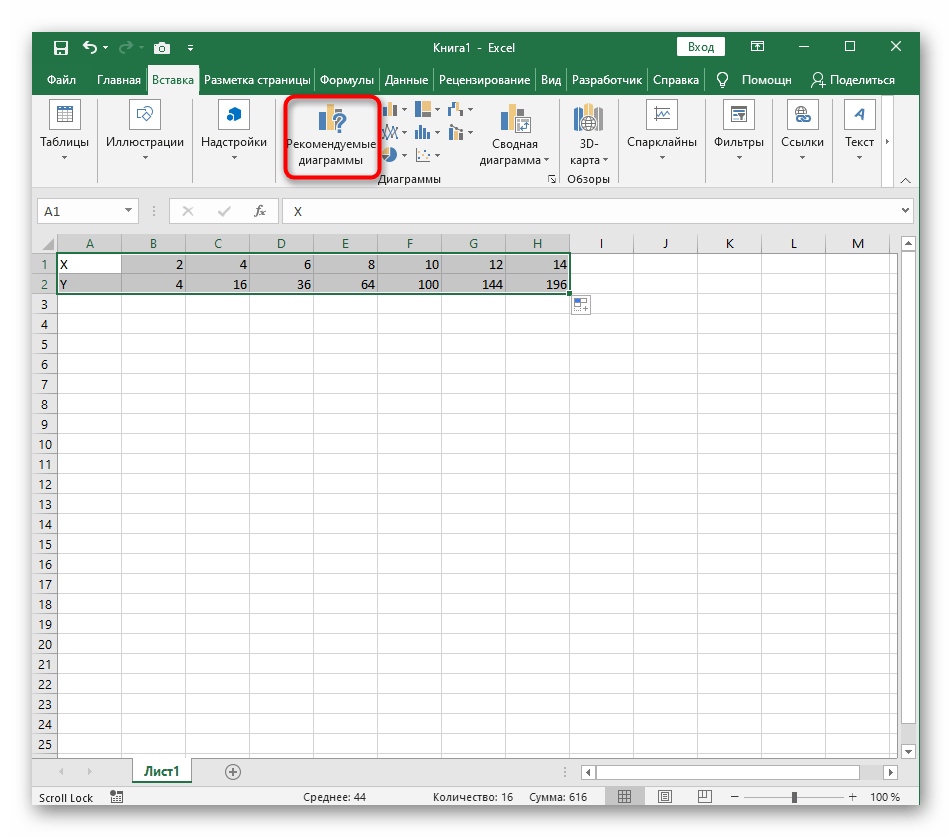
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
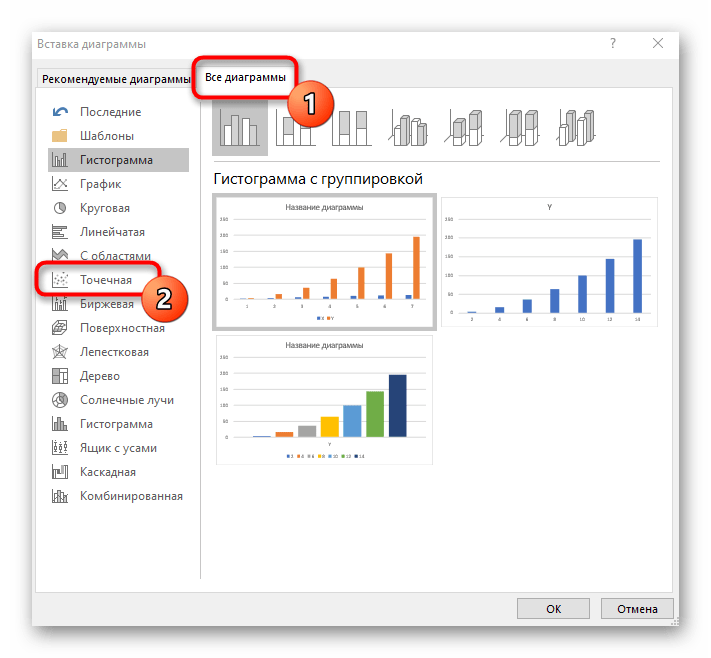
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
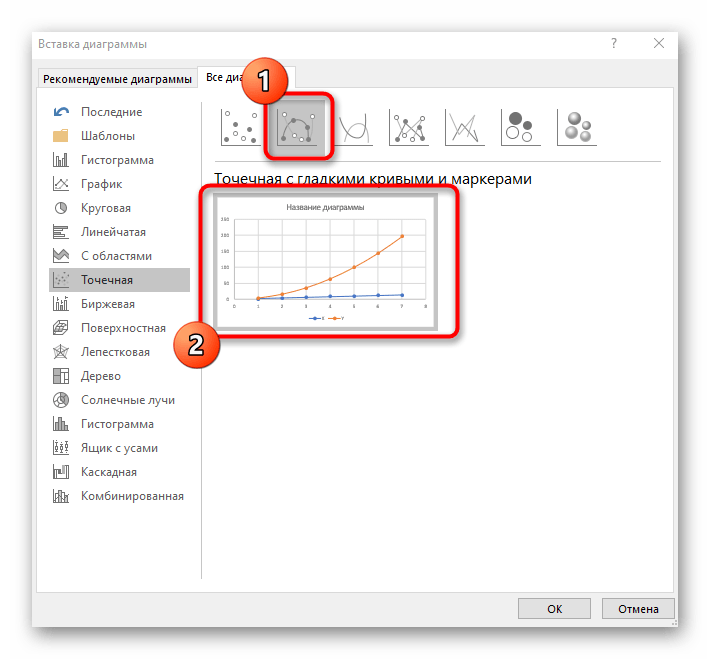
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
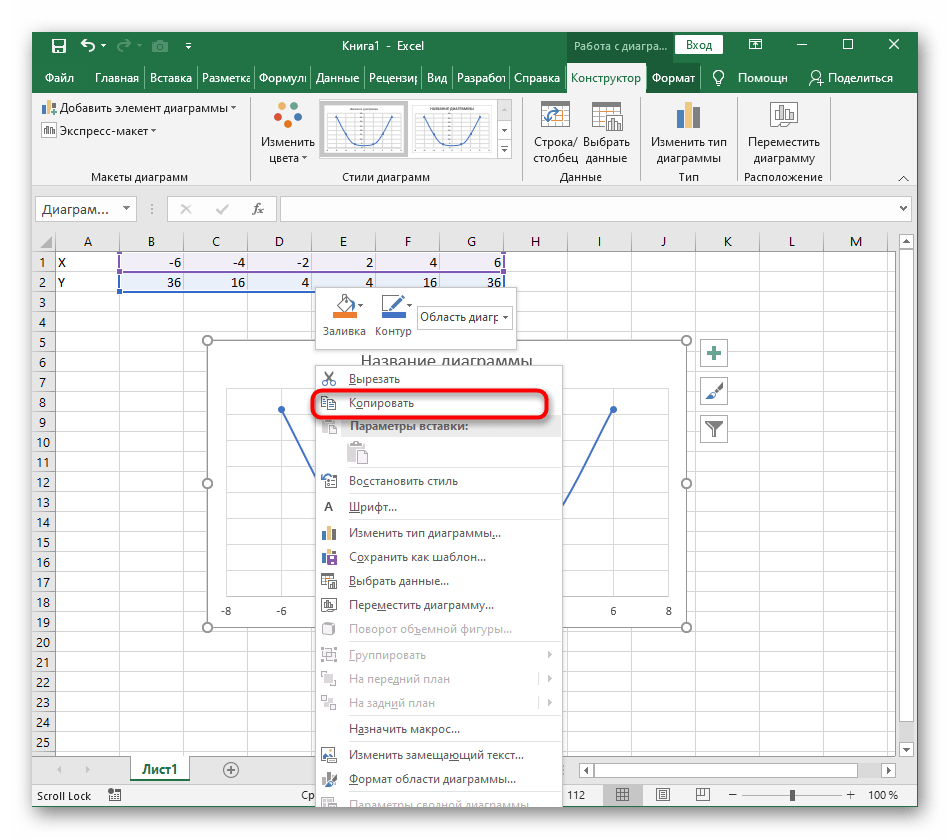
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
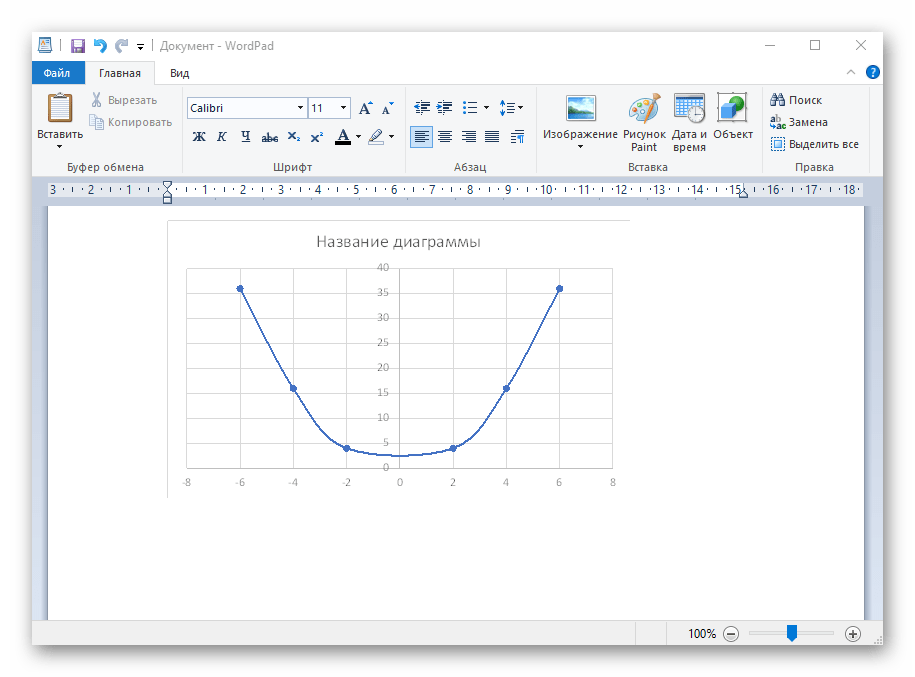
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
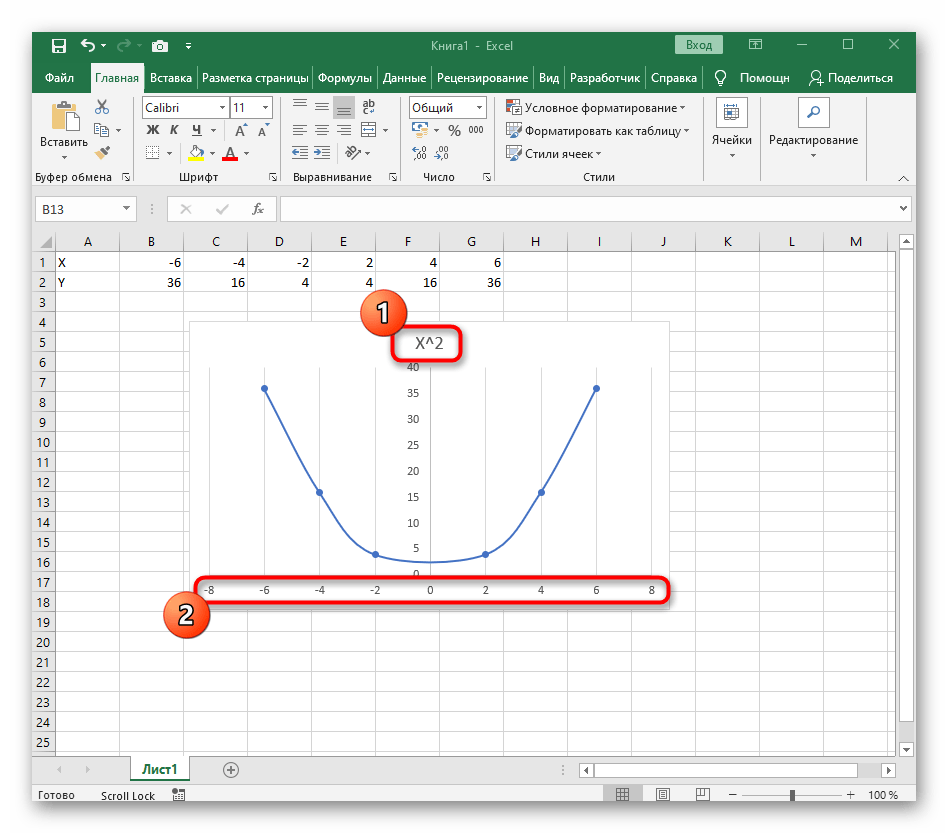
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.
Еще статьи по данной теме:
Помогла ли Вам статья?
Цель
работы:
Приобретение навыков построения графиков
функций на плоскости и в трехмерном
пространстве. Изучение графических
возможностей пакета MS Excel.
Задание
1.
Построить графики функций f(x) и g(x) для
x∈[-5;5]
с шагом 0,5. Задание выполняется на первом
листе рабочей книги MS Excel. Лист переименовать
в «Задание 1».
Варианты
задания 1
Порядок
работы:
Построить
график функции f(x)=
3 x2
⋅(x+3).
Определим функцию f(x).
Для этого в ячейки А2:А22 необходимо
ввести значение аргумента при помощи
автозаполнения.
Маркер
автозаполнения
В
ячейку В2 вводится значение функции,
вычисляемое по формуле =(A2^2*(A2+3))^(1/3).
Ячейки В3:В22 заполняются также при помощи
автозаполнения. Далее выделим диапазон
А2:В22 и воспользуемся «Мастером диаграмм».
Для построения графика функции лучше
выбрать точечную диаграмму, со значениями,
соединенными сглаживающими линиями
без маркера.
Рис.
3.2. Построение графика функции с помощью
мастера диаграмм
Чтобы
график получился выразительным,
необходимо определить промежуток
изменения аргумента, увеличить толщину
линий, выделить оси координат, нанести
на них соответствующие деления, сделать
подписи на осях и вывести заголовок.
График
функции f(x)
При
построении графика функции
следует
обратить внимание на область определения
функции. В данном случае функция не
существует при обращении знаменателя
в ноль.
Решим
уравнение
Следовательно,
при определении значений аргумента
следует помнить, что при (-2) функция не
определена.
График
функции g(x)
Задание
2.
Построить график функций q(x) для x∈[-2;2]
с шагом 0,1. Задание выполняется на втором
листе рабочей книги MS Excel. Лист переименовать
в «Задание 2».
Варианты
задания 2
Порядок
работы:
Построить
график функции q(x) для x∈[-2;2]
с шагом 0,2:
При
построении этого графика используется
встроенная функция ЕСЛИ. Например, в
ячейке А2 (см. рис. 3.5) находится начальное
значение аргумента, тогда в ячейку В2
необходимо ввести формулу:
=ЕСЛИ(A2<0;1+A2+A2^2;ЕСЛИ(A2>=1;2*ABS(0,5+SIN(A2));КОРЕНЬ(1+2*A2))).
График
функции q(x)
В
том случае если при задании формулы не
требуется использовать функцию Если
дважды, удобнее вводить формулу в
диалоговом окне «Мастера функций».
Эта функция находится в категории
логические. Для вызова мастера
воспользуемся пунктом меню Вставка
Пункт
меню «Вставка» и Диалоговое окно Мастера
функций
Задание
3.
Построить поверхность Z(x,y) при x, y∈[-1;1]
с шагом 0.1. Задание выполняется на третьем
листе рабочей книги MS Excel. Лист переименовать
в «Задание 3».
Варианты
задания 3
Построить
поверхность
.
Приступим
к построению поверхности. В диапазон
C2:W2 введем последовательность значений
переменной x: -1, -0,9 … 1, а в диапазон ячеек
B3:B23 последовательность значений
переменой y: -1, -0,9 … 1. В ячейку C3 введем
формулу =2*EXP(C$2)-$B3*EXP($B3)
При
вводе формулы обратите внимание на то,
что необходимо сослаться на строку с
номером 2 и столбец с именем В. Для этого
при написании формулы следует использовать
абсолютные ссылки. Знак $, стоящий перед
буквой в имени ячейки, дает абсолютную
ссылку на столбец с данным именем, а
знак $, стоящий перед цифрой – абсолютную
ссылку на строку с этим именем. Поэтому
при копировании формулы из ячейки С3 в
ячейки диапазона С3:W23 в
них
будет найдено значение z при соответствующих
значениях x, y. Т.о. создается таблица
значений z(x,y).
Фрагмент
таблицы значений Z
Перейдем
к построению поверхности. Выделим
диапазон ячеек С3:W23, содержащий таблицу
значений функции и ее аргументов, вызовем
Мастер диаграмм и выберем тип диаграммы
Поверхность, далее заполним диалоговые
окна.
Построение
поверхности с помощью мастера диаграмм
После
нажатия кнопки Готово получим изображение
заданной поверхности.
Поверхность
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #