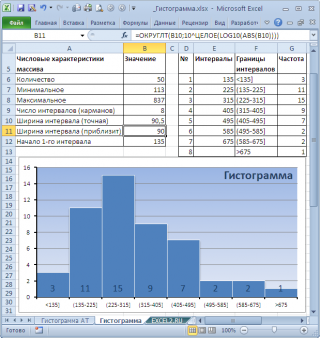
Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
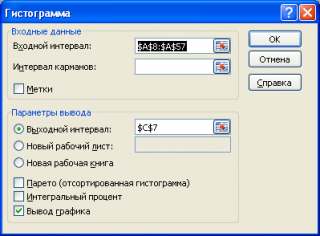
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
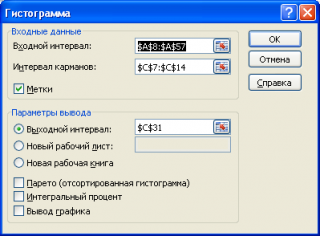
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
Перед тем как анализировать полученный результат —
отсортируйте исходный массив данных
.
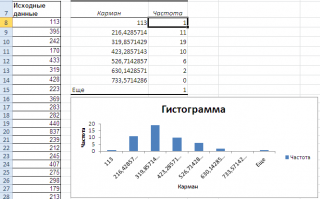
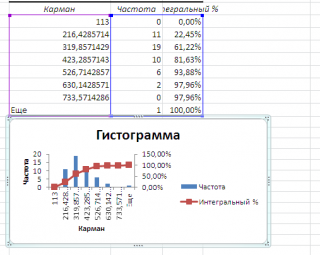
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
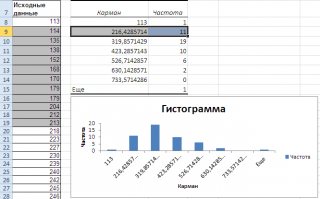
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
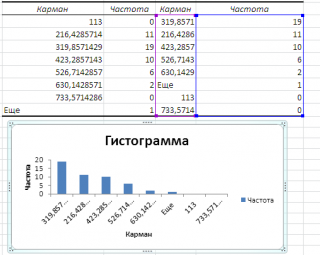
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
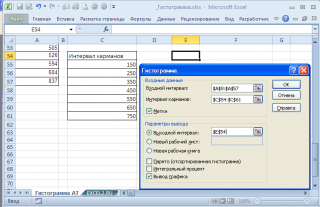
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
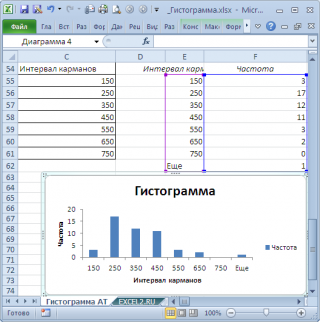
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
В итоге можно добиться вот такого результата.
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
Одной из разновидностей гистограмм является
график накопленной частоты
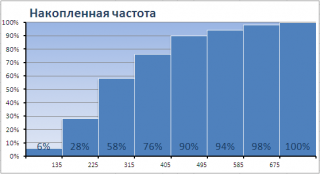
(cumulative frequency plot).
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).
17 авг. 2022 г.
читать 3 мин
Выборочное распределение — это вероятностное распределение определенной статистики , основанное на множестве случайных выборок из одной совокупности .
В этом руководстве объясняется, как выполнить следующие действия с выборочными распределениями в Excel:
- Сгенерируйте выборочное распределение.
- Визуализируйте распределение выборки.
- Рассчитайте среднее значение и стандартное отклонение выборочного распределения.
- Рассчитайте вероятности относительно выборочного распределения.
Создание выборочного распределения в Excel
Предположим, мы хотим сгенерировать выборочное распределение, состоящее из 1000 выборок, в каждой из которых размер выборки равен 20 и происходит от нормального распределения со средним значением 5,3 и стандартным отклонением 9 .
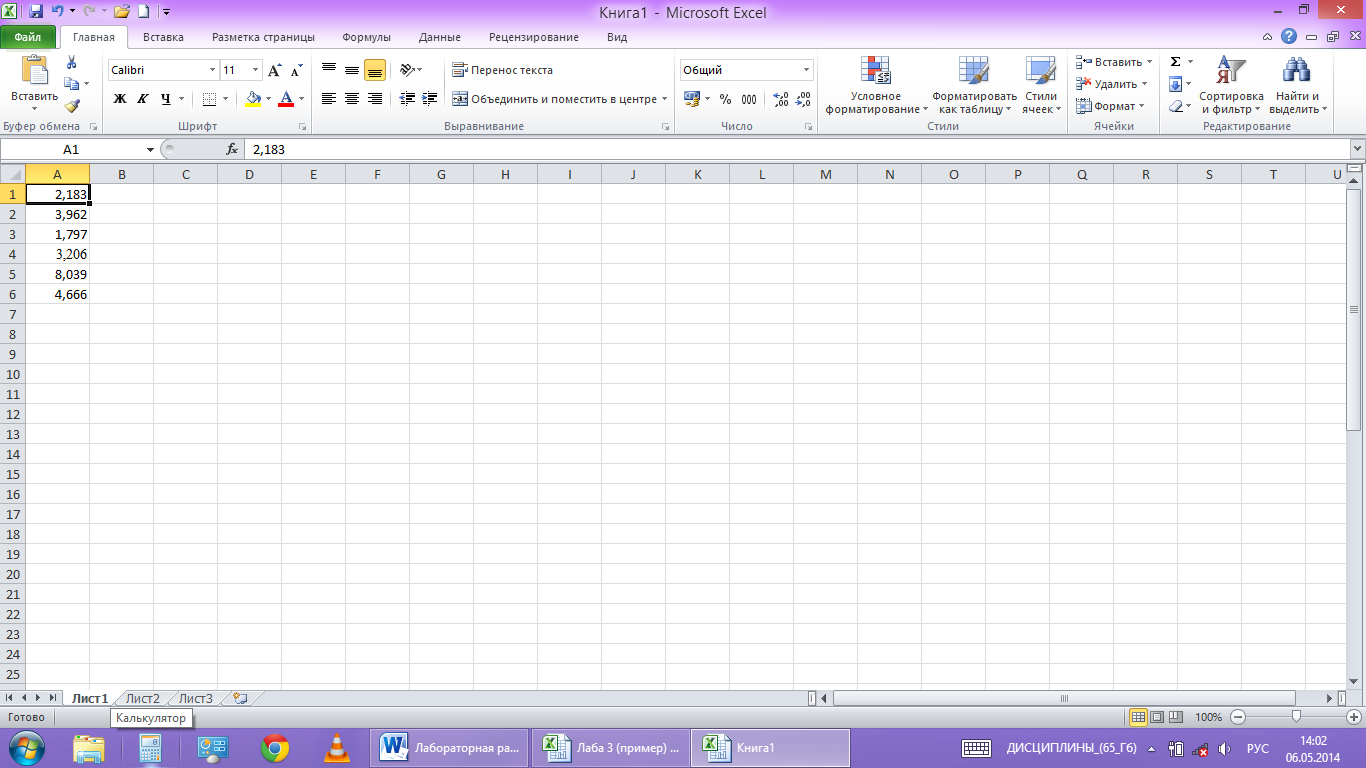
Мы можем легко сделать это, введя следующую формулу в ячейку A2 нашего рабочего листа:
= NORM.INV ( RAND (), 5.3, 9)
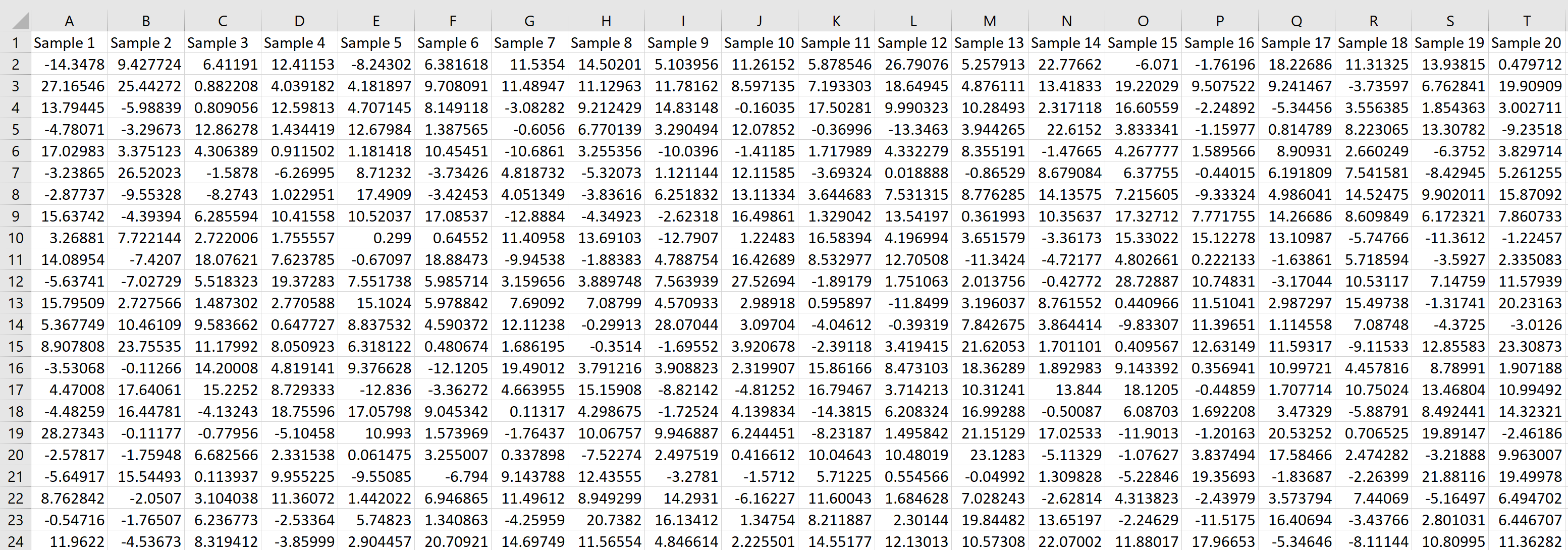
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и перетащить формулу на 20 ячеек вправо и на 1000 ячеек вниз:
Каждая строка представляет выборку размера 20, в которой каждое значение получено из нормального распределения со средним значением 5,3 и стандартным отклонением 9.
Найдите среднее значение и стандартное отклонение
Чтобы найти среднее значение и стандартное отклонение этого выборочного распределения средних значений выборки, мы можем сначала найти среднее значение каждой выборки, введя следующую формулу в ячейку U2 нашего рабочего листа:
= AVERAGE (A2:T2)
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и дважды щелкнуть, чтобы скопировать эту формулу в каждую другую ячейку в столбце U:
Мы видим, что первая выборка имела среднее значение 7,563684, вторая выборка имела среднее значение 10,97299 и так далее.
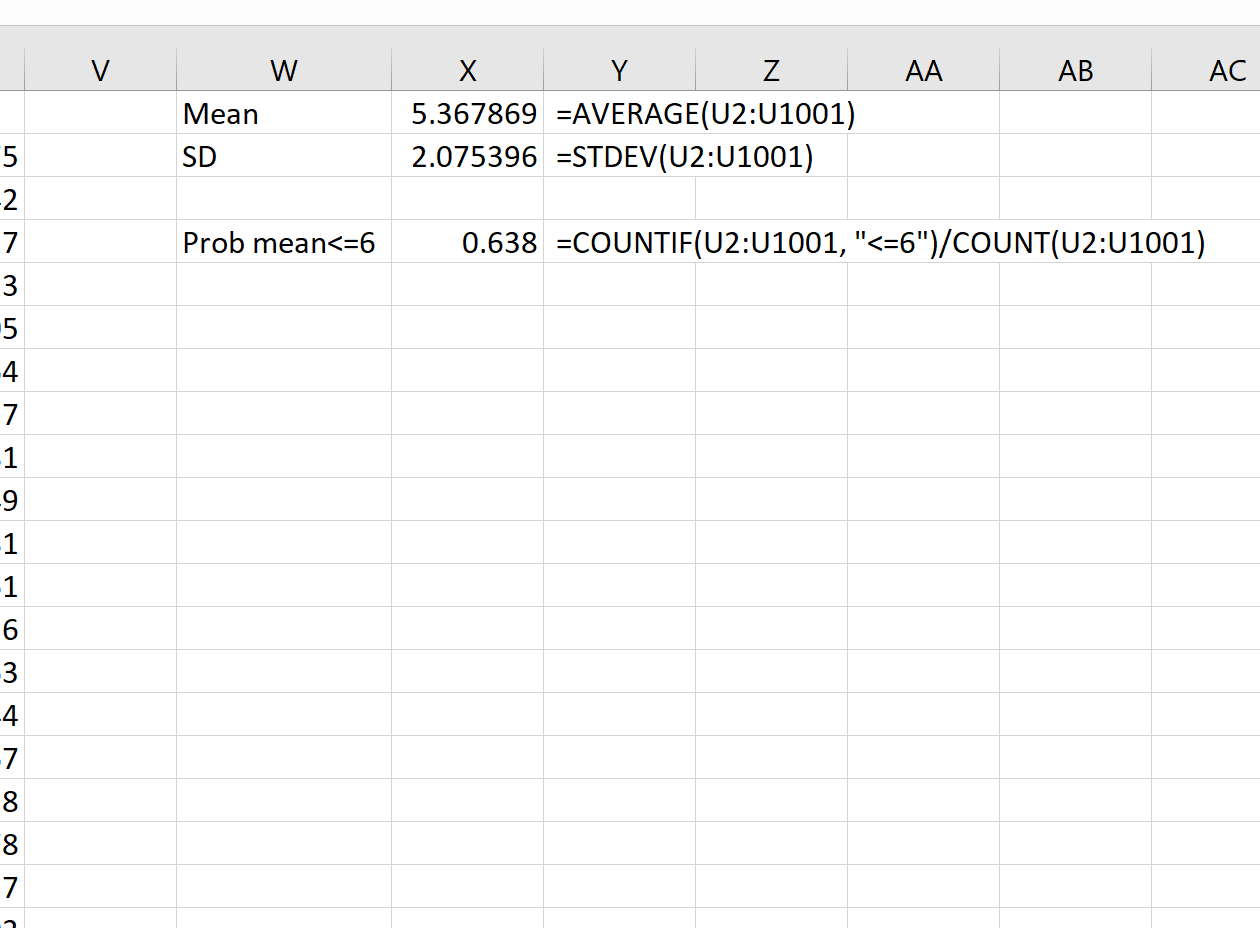
Затем мы можем использовать следующие формулы для расчета среднего значения и стандартного отклонения среднего значения выборки:
Теоретически среднее значение выборочного распределения должно быть 5,3. Мы видим, что фактическое среднее значение выборки в этом примере равно 5,367869 , что близко к 5,3.
И теоретически стандартное отклонение выборочного распределения должно быть равно s/√n, что будет равно 9/√20 = 2,012. Мы видим, что фактическое стандартное отклонение выборочного распределения составляет 2,075396 , что близко к 2,012.
Визуализируйте распределение выборки
Мы также можем создать простую гистограмму для визуализации выборочного распределения выборочных средних.
Для этого просто выделите все средние значения выборки в столбце U, щелкните вкладку « Вставка », затем выберите параметр « Гистограмма » в разделе « Диаграммы ».
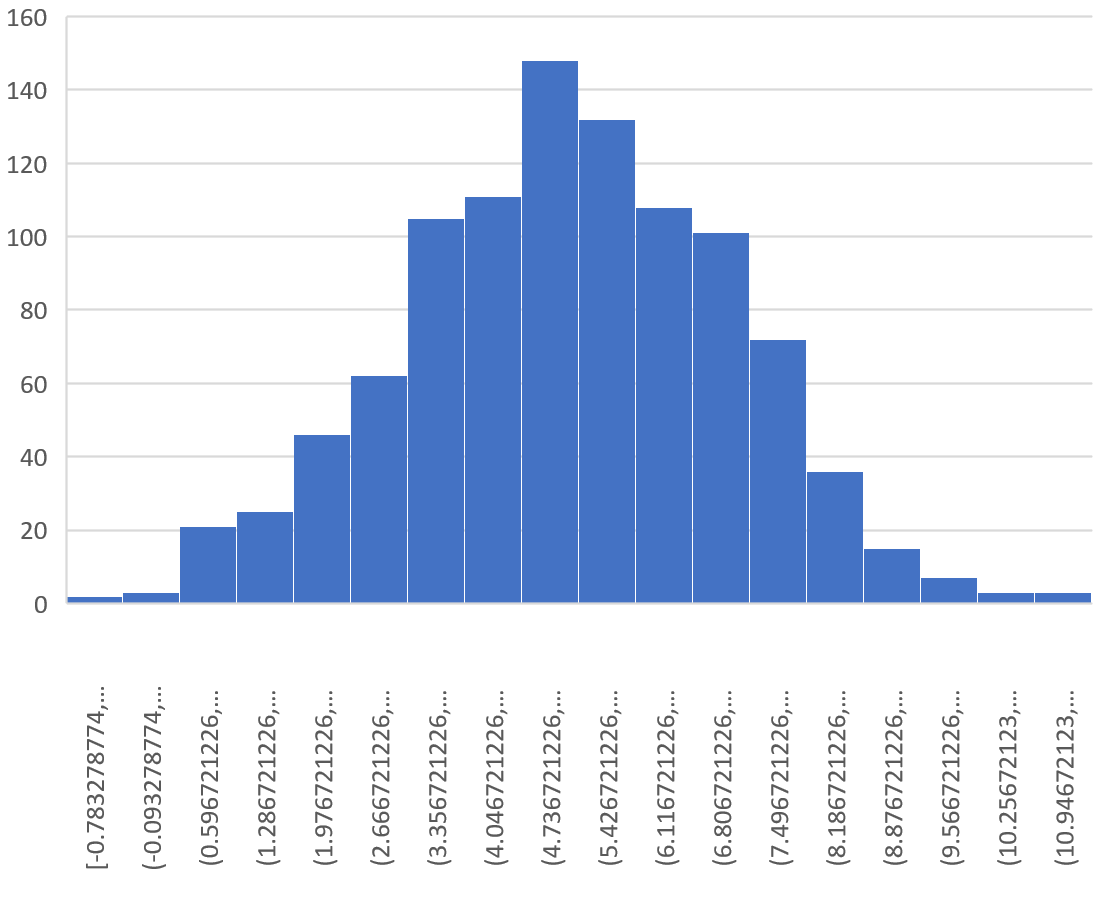
В результате получается следующая гистограмма:
Мы видим, что распределение выборки имеет форму колокола с пиком около значения 5.
Однако из хвостов распределения мы можем видеть, что некоторые выборки имели средние значения больше 10, а некоторые — меньше 0.
Рассчитать вероятности
Мы также можем рассчитать вероятность получения определенного значения среднего значения выборки на основе среднего значения совокупности, стандартного отклонения совокупности и размера выборки.
Например, мы можем использовать следующую формулу, чтобы найти вероятность того, что среднее значение выборки меньше или равно 6, учитывая, что среднее значение генеральной совокупности равно 5,3, стандартное отклонение генеральной совокупности равно 9 и размер выборки равен:
= COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)
Мы видим, что вероятность того, что среднее значение выборки меньше или равно 6, составляет 0,638.
Это очень близко к вероятности, рассчитанной Калькулятором распределения выборки :
Дополнительные ресурсы
Введение в выборочные распределения
Калькулятор распределения выборки
Введение в центральную предельную теорему
Задание
Для
случайной выборки объемом n=50
с несовпадающими числами выполнить
следующую последовательность действий:
1.Вывести
на лист Excel
исходные статистические данные.
2. Построить
вариационный ряд.
3. Вычислить
статистические характеристики.
4. Построить
интервальный статистический ряд.
5.Построить
гистограмму частот.
6. Составить
статистическую функцию распределения
статистического ряда.
7.
Составить и постоить статистическую
функцию распределения группированного
статистического ряда.
В качестве примера
рассмотрим следующую выборку
Порядок выполнения работы
1.Ввод исходных статистических данных.
Вводим данные в
первый столбец таблицы (рис.1).
рис.1
2. Построение вариационного ряда.
Производим
сортировку данных в порядке возрастания.
Для этого:
а) выделяем первый
столбец;
б)
на ленте
во вкладке «Данные» выбираем «Сортировка
и фильтр» (рис.2)
рис. 2
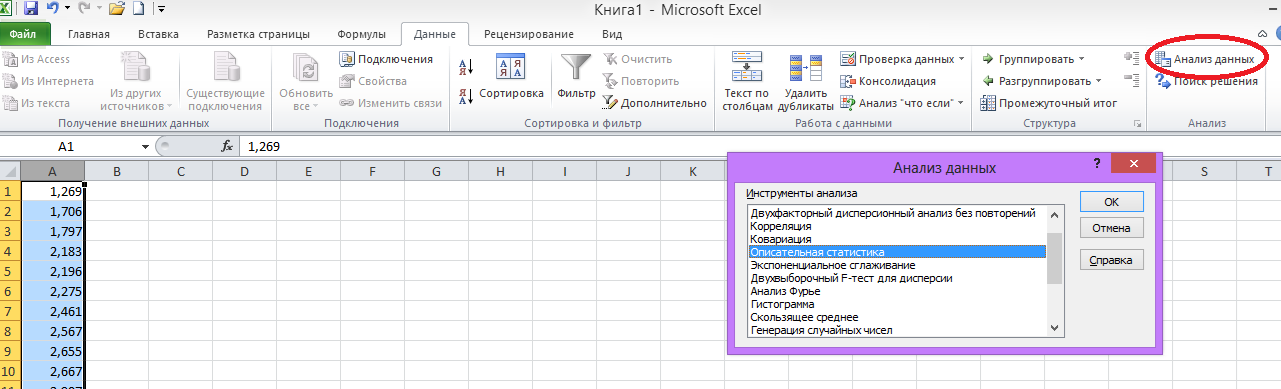
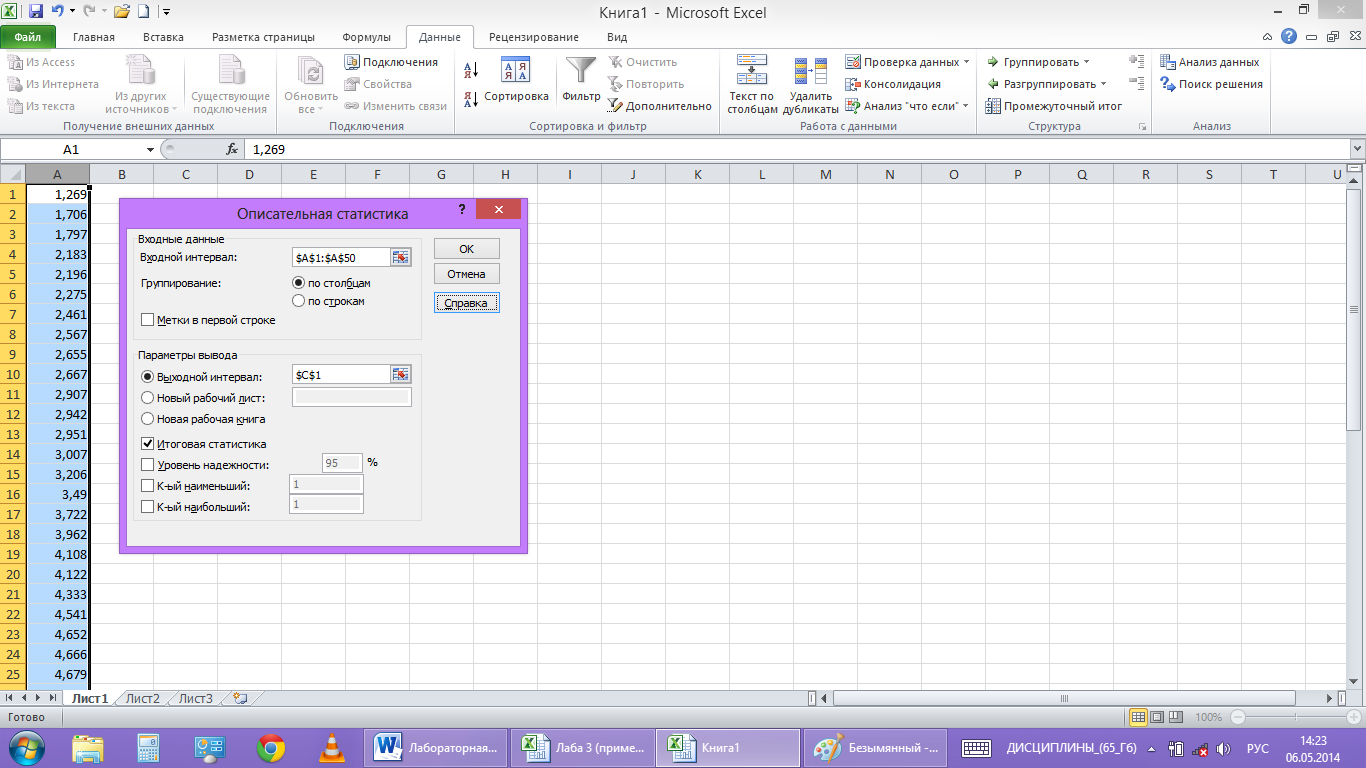
3. Вычисление статистических характеристик.
На ленте
во вкладке «Данные» выбираем «Анализ
данных» меню «Описательная статистика»
нажимаем ОК.
рис. 3
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
а в пункте «Выходной интервал» обозначим
первую ячейку для записи результаов
$C$1.
Ставим флажок напротив пункта «Итоговая
статистика» и нажимаем ОК.(рис.4)
рис. 4
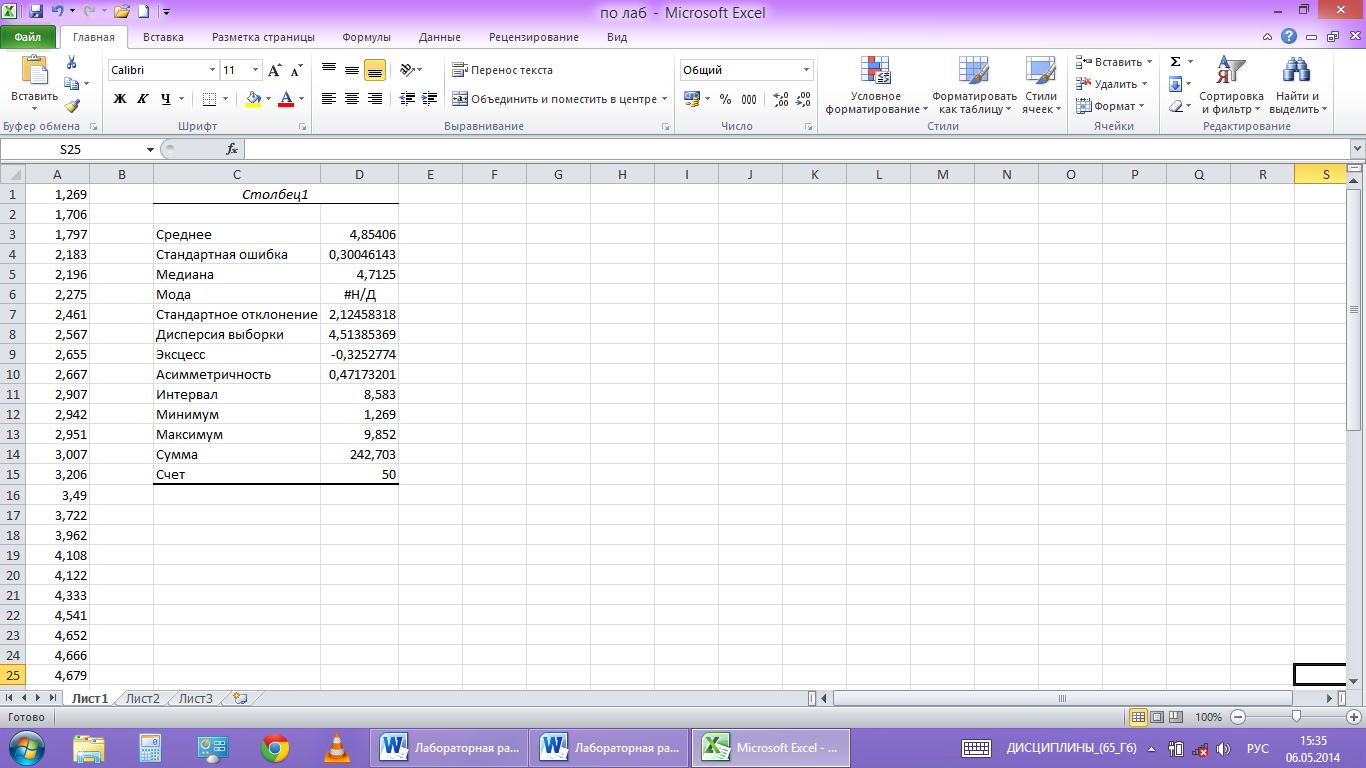
На
рабочем листе появляется таблица с
вычисленными значениями числовых
характеристик выборки (рис.5)
рис. 5
Здесь
«Среднее»означает математическое
ожидание выборки, а «Стандартная ошибка»
— погрешность ее значения. «Дисперсия
выборки» означает исправленную выборочную
дисперсию, а «Стандартное отклонение»
— исправленное среднее квадратичное
отклонение. Положительное значение
«Асимметричности» означает, что «длинная
часть» кривой лежит правее моды.
Отрицательное значение «Эксцесса»
означает, что кривая имеет более низкую
и «плоскую» вершину, чем нормальная
кривая. «Интервал» равен разности
Xmax−Xmin.
«Сумма»
дает результат суммирования всех
элементов выборки. «Счет» задает общее
число элементов выборки.
4. Построение интервального статистического ряда.
Длину интервала
группировки определяем по формуле
Необходимые данные
имеем в таблице: Xmax
– в ячейке D13,
Xmin–
в ячейке D12,
число элементов выборки n
— в ячейке D15.
В ячейку С16 вводим
слово «Интервал», в ячейку D16
вводим формулу
в ячейке D16
появится значение числа h.
В ячейку C17
вводим букву h.
В ячейку D17
вводим формулу
В ячейке
D17
получаем округленное до одного знака
после запятой значение интерала h.
Проведем формирование
интервалов. Для этого от Xmin
отступим влево примерно на h/2
и получим начальную точку отсчета.
Последовательно прибавляя к ней целое
число отрезков h,
получим все граничные точки интервалов.
В ячейку
F1
вводим формулу
В этой
ячейке появляется значение начальной
точки отсчета. В ячейку F2
вводим формулу
В этой
ячейке появляется значение второй
граничной точки первого интервала.
Возвращаемся в ячейку F2,
ставим курсор в правый нижний угол рамки
и двигаем его вниз, не отпуская левую
кнопку мыши. В результате такой процедуры
(протяжка) столбец F
заполнят граничные точки интервалов.
Самый нижний интервал должен включать
Xmax
(рис.6).
Проведем подсчет
числа вариант, попавших в каждый интервал,
определим относительные частоты и
серединные точки этих интервалов.
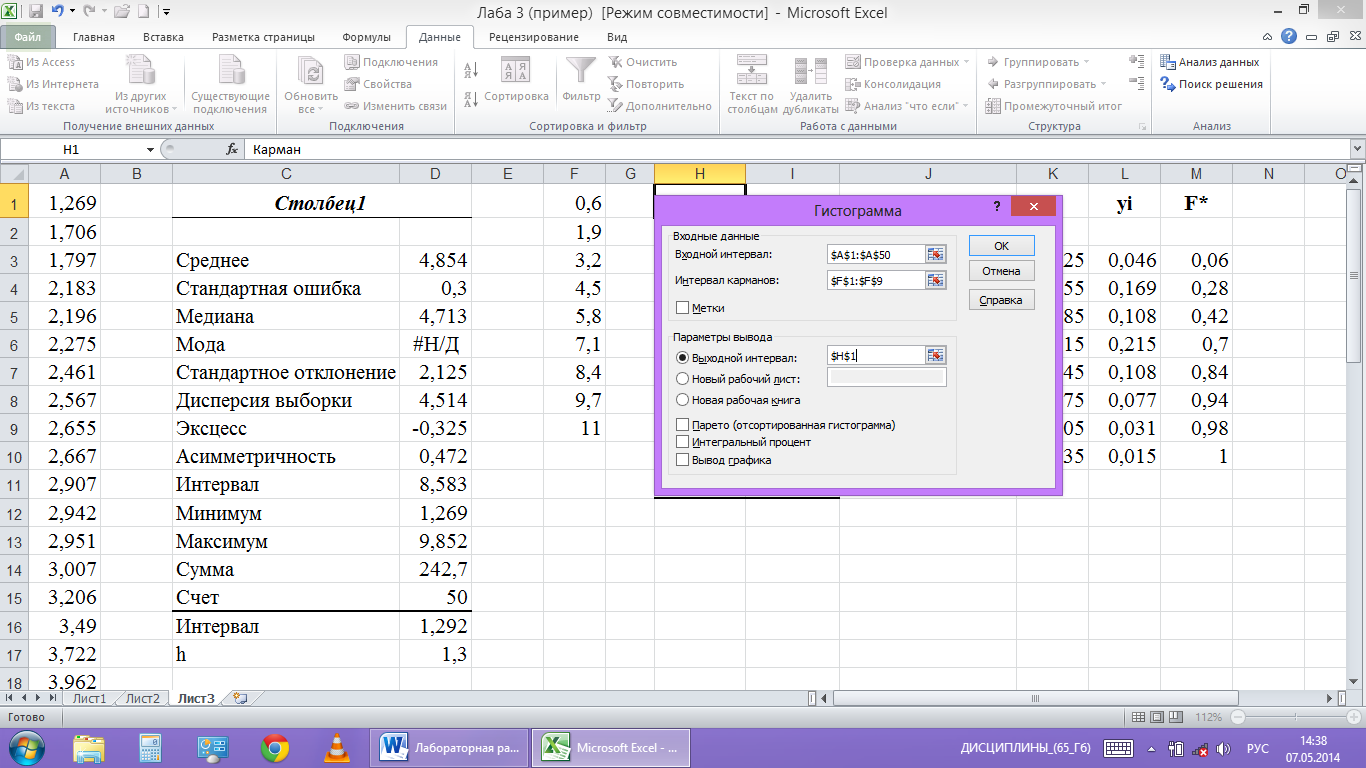
Для
этого на ленте во вкладке «Данные»
выбираем «Анализ данных» меню
«Гистограмма». (рис.
7)
|
|
|
|
рис. 6 |
рис. 7 |
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
в пункт «Интервал карманов» — диапазон
ячеек с границами интервалов $F$1:$F$9.
Отметим точкой пункт «Выходной интервал»
и введем в него адрес первой ячейки для
записи результатов $Н$1. Появится таблица
из двух столбцов с обозначениями «Карман»
и «Частота» (рис.8).
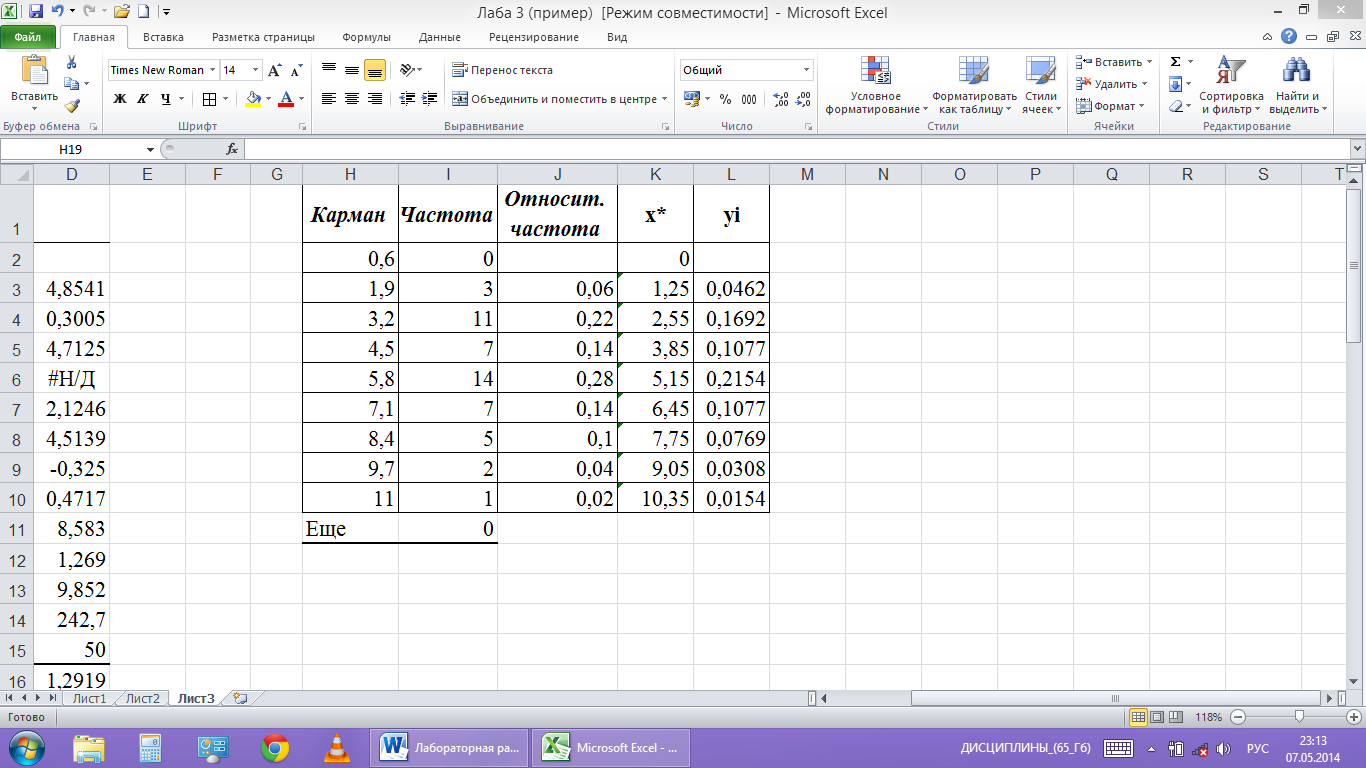
Определим
относительные частоты рi*,
значения серединных точек интервалов
и высоты
прямоугольников
Для этого
-
в ячейку
J1
введем заголовок «Относительная
частота»; -
В ячейку
J3
введем формулу
и
протягиваем её вниз до ячейки J10.
В результате к таблице из двух столбцов
добавится третий столбец (рис.8). В этой
таблице частота появления случайной
величины в каждом интервале записана
в одной строке с концом интервала;
-
в ячейку
K1
введем заголовок столбца Х*; -
в ячейку
К3 введем формулу
Протягиваем
эту формулу до ячейки К10. В результате
в четвертом столбце таблицы (рис.8)
появятся значения серединных точек
интервалов;
-
в ячейку
L1
введем заголовок столбца Уi; -
в ячейку
L3
введем формулу
Протягиваем
её вниз до ячейки L10.
В
результате в пятом столбце таблицы
(рис.8) появятся значения Уi.
рис.8
Соседние файлы в папке Лаб.работы
- #
- #
- #
- #
- #
- #
- #
Построение рядов распределения
Любой ряд распределения характеризуется двумя элементами:
— варианта(хi) – это отдельные значения признака единиц выборочной совокупности. Для вариационного ряда варианта принимает числовые значения, для атрибутивного – качественные (например, х=«государственный служащий»);
— частота (ni) – число, показывающее, сколько раз встречается то или иное значение признака. Если частота выражена относительным числом (т.е. долей элементов совокупности, соответствующих данному значению варианты, в общем объеме совокупности), то она называется относительной частотойили частостью.
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Интервальный ряд может строиться как с интервалами равной длины (равноинтервальный ряд) так и с неодинаковыми интервалами, если это диктуется условиями статистического исследования. Например, может рассматриваться ряд распределения доходов населения со следующими интервалами:
где k – число интервалов, n – объем выборки. (Конечно, формула обычно дает число дробное, а в качестве числа интервалов выбирается ближайшее целое к полученному число.) Длина интервала в таком случае определяется по формуле
При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:
— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.
Проиллюстрируем процесс первичной обработки данных на следующих примерах.
Пример 1.1. имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Теперь построим полигон: выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Пример 1.2. Имеются данные о выбросах загрязняющих веществ из 50 источников:
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Составить равноинтервальный ряд, построить гистограмму
Внесем массив данных в лист Excel, он займет диапазон А1:J5 Как и в предыдущей задаче, определим объем выборки n, минимальное и максимальное значения в выборке. Поскольку теперь требуется не дискретный, а интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу =1+3,322*LOG10(B7).
Рис.1.4. Пример 2. Построение равноинтервального ряда
Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(В9-В8)/С10.
Рис.1.5. Пример 2. Построение равноинтервального ряда
Теперь заполним массив «карманов» при помощи функции ЧАСТОТА, как это было сделано в примере 1.
Рис.1.6. Пример 2. Построение равноинтервального ряда
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Расчет ширины интервала и таблица интервалов приведены в файле примера на листе Гистограмма . Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() . О вводе этой функции см. статью Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL .
Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Стиль и внешний вид гистограммы
После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:
- добавить заголовок и другие дополнительные данные для отображения. Для того, чтобы добавить данные на график, кликните на пункт “Добавить элемент диаграммы”, затем, выберите нужный пункт из выпадающего списка:
Вы также можете использовать кнопки быстрого доступа к редактированию элементов гистограммы, стиля и фильтров:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Например:
Для распределения учеников по росту получаем: begin S^2=fraccdot 104,1approx 105,1\ sapprox 10,3 end Коэффициент вариации: $ V=fraccdot 100textapprox 6,0textlt 33text $ Выборка однородна. Найденное значение среднего роста (X_)=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
- если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
Рассмотренные в лабораторной работе 2 распределения вероятностей СВ
опираются на знание закона распределения СВ. Для практических задач такое
знание – редкость. Здесь закон распределения обычно неизвестен, или известен с
точностью до некоторых неизвестных параметров. В частности, невозможно
рассчитать точное значение соответствующих вероятностей, так как нельзя
определить количество общих и благоприятных исходов. Поэтому вводится статистическое
определение вероятности. По этому определению вероятность равна отношению
числа испытаний, в которых событие произошло, к общему числу произведенных
испытаний. Такая вероятность называется статистической частотой.
Связь
между эмпирической функцией распределения и функцией распределения
(теоретической функцией распределения) такая же, как связь между частотой события
и его вероятностью.
Для
построения выборочной функции распределения весь диапазон изменения случайной
величины X (выборки)
разбивают на ряд интервалов (карманов) одинаковой ширины. Число интервалов
обычно выбирают не менее 3 и не более 15. Затем определяют число значений
случайной величины X, попавших
в каждый интервал (абсолютная частота, частота интервалов).
Частота интервалов – число, показывающее сколько раз значения,
относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти
числа на общее количество наблюдений (n), находят относительную частоту (частость) попадания
случайной величины X в заданные
интервалы.
По
найденным относительным частотам строят гистограммы выборочных функций
распределения. Гистограмма распределения частот – это графическое
представление выборки, где по оси абсцисс (ОХ) отложены величины интервалов, а
по оси ординат (ОУ) – величины частот, попадающих в данный классовый интервал.
При увеличении до бесконечности размера выборки выборочные функции
распределения превращаются в теоретические: гистограмма превращается в график
плотности распределения.
Накопленная частота интервалов – это число, полученное
последовательным суммированием частот в направлении от первого интервала к
последнему, до того интервала
включительно, для которого определяется накопленная частота.
В Excel для построения выборочных функций распределения
используются специальная функция ЧАСТОТА
и процедура Гистограмма из пакета анализа.
Функция ЧАСТОТА (массив_данных,
двоичный_массив) вычисляет частоты появления случайной величины в интервалах
значений и выводит их как массив цифр, где
•
массив_данных
— это массив или ссылка на
множество данных, для которых
вычисляются частоты;
•
двоичный_массив
— это массив интервалов, по
которым группируются значения выборки.
Процедура
Гистограмма из Пакета анализа выводит
результаты выборочного распределения в виде таблицы и графика. Параметры диалогового окна Гистограмма:
•
Входной диапазон — диапазон исследуемых данных
(выборка);
•
Интервал карманов — диапазон ячеек или набор граничных
значений, определяющих выбранные интервалы (карманы). Эти значения должны быть
введены в возрастающем порядке. Если
диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и
максимальным значениями данных, будет создан
автоматически.
•
выходной диапазон предназначен для ввода ссылки на левую верхнюю ячейку выходного диапазона.
•
переключатель
Интегральный процент позволяет установить режим включения в
гистограмму графика интегральных
процентов.
•
переключатель
Вывод графика позволяет установить режим автоматического создания встроенной диаграммы на листе, содержащем
выходной диапазон.
Пример 1. Построить эмпирическое распределение веса
студентов в килограммах для следующей
выборки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.
Решение
1. В ячейку А1 введите слово Наблюдения,
а в диапазон А2:А21 — значения веса
студентов (см. рис. 1).
2.
В
ячейку В1 введите названия интервалов Вес, кг. В диапазон В2:В8 введите
граничные значения интервалов (40, 45,
50, 55, 60, 65, 70).
3.
Введите
заголовки создаваемой таблицы: в ячейки С1 — Абсолютные частоты, в ячейки D1 — Относительные
частоты, в ячейки E1 — Накопленные частоты.(см. рис. 1).
4.
С
помощью функции Частота заполните столбец абсолютных частот, для этого
выделите блок ячеек С2:С8. С
панели инструментов Стандартная
вызовите Мастер функций (кнопка fx). В появившемся диалоговом окне
выберите категорию Статистические и функцию
ЧАСТОТА, после чего нажмите кнопку ОК. Указателем мыши в рабочее поле Массив_данных
введите диапазон данных наблюдений (А2:А8). В рабочее поле Двоичный_массив
мышью введите диапазон интервалов (В2:В8). Слева на клавиатуре последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце C должен появиться массив абсолютных частот (см. рис.1).
5.
В
ячейке C9 найдите общее количество
наблюдений. Активизируйте ячейку С9, на
панели инструментов Стандартная нажмите кнопку Автосумма.
Убедитесь, что диапазон суммирования указан правильно и нажмите клавишу Enter.
6.
Заполните столбец относительных частот. В ячейку введите формулу
для вычисления относительной частоты: =C2/$C$9.
Нажмите клавишу Enter. Протягиванием (за правый
нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон и получите массив относительных частот.
7.
Заполните
столбец накопленных частот. В ячейку D2 скопируйте значение относительной
частоты из ячейки E2. В ячейку D3 введите формулу: =E2+D3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу
в диапазон D3:D8. Получим массив накопленных
частот.
Рис. 1. Результат вычислений из
примера 1
8.
Постройте диаграмму относительных и накопленных частот. Щелчком указателя
мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите закладку Нестандартные
и тип диаграммы График/гистограмма. После
редактирования диаграмма будет иметь такой вид, как на рис. 2.
Рис. 2
Диаграмма относительных и накопленных частот из примера 1
Задания для самостоятельной работы
1. Для данных из примера 1 построить выборочные функции распределения, воспользовавшись процедурой Гистограмма из пакета Анализа.
2. Построить выборочные функции распределения
(относительные и накопленные частоты) для роста
в см. 20 студентов: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181,
183, 172, 176.
3. Найдите распределение по абсолютным частотам для
следующих результатов тестирования в
баллах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (используйте границы интервалов 70, 80, 90).
4. Рассмотрим любой из критериев оценки качеств педагога-профессионала,
например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос
анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку
такого измерения, необходимо увеличить число возможных ответов на конкретный
критериальный вопрос. В табл. 1 представлены возможные варианты ответов.
Обозначим
этот параметр через х. Тогда в процессе ответа на вопрос величина х
примет дискретное значение х, принадлежащее определенному интервалу значений.
Поставим в соответствие каждому из ответов определенное числовое значение
параметра х (см. табл. 1).
Табл. 1 Критериальный вопрос: успешное решение задач обучения и воспитания
|
№ п/п |
Варианты ответов |
Х |
|
1 |
Абсолютно неуспешно |
0,1 |
|
2 |
Неуспешно |
0,2 |
|
3 |
Успешно в очень |
0,3 |
|
4 |
В определенной |
0,4 |
|
5 |
В среднем успешно, |
0,5 |
|
6 |
Успешно с |
0,6 |
|
7 |
Успешно, но |
0,7 |
|
8 |
Достаточно успешно |
0,8 |
|
9 |
Очень успешно |
0,9 |
|
10 |
Абсолютно успешно |
1 |
При проведении анкетирования в каждой отдельной
анкете параметр х принимает случайное значение, но только в пределах числового
интервала от 0,1 до 1.
Тогда в результате измерений мы получаем
неранжированный ряд случайных значений (см. табл. 2).
Таблица 2.
Результаты опроса ста учителей
Сгруппируйте полученную выборку, рассчитайте среднее
значение выборки, стандартное отклонение, абсолютную и относительную частоту
появления параметра, а также постройте график плотности вероятности f(x)=
где
W(x) – относительная частота наступления события;
— стандартное
отклонение;
=3,14.
Постройте график функции f(x) и сравните его с
нормальным распределением Гаусса.
Решение математических задач
средствами Excel: Практикум/ В.Я. Гельман. – СПб.: Питер, 2003 — с. 168-172