17 авг. 2022 г.
читать 2 мин
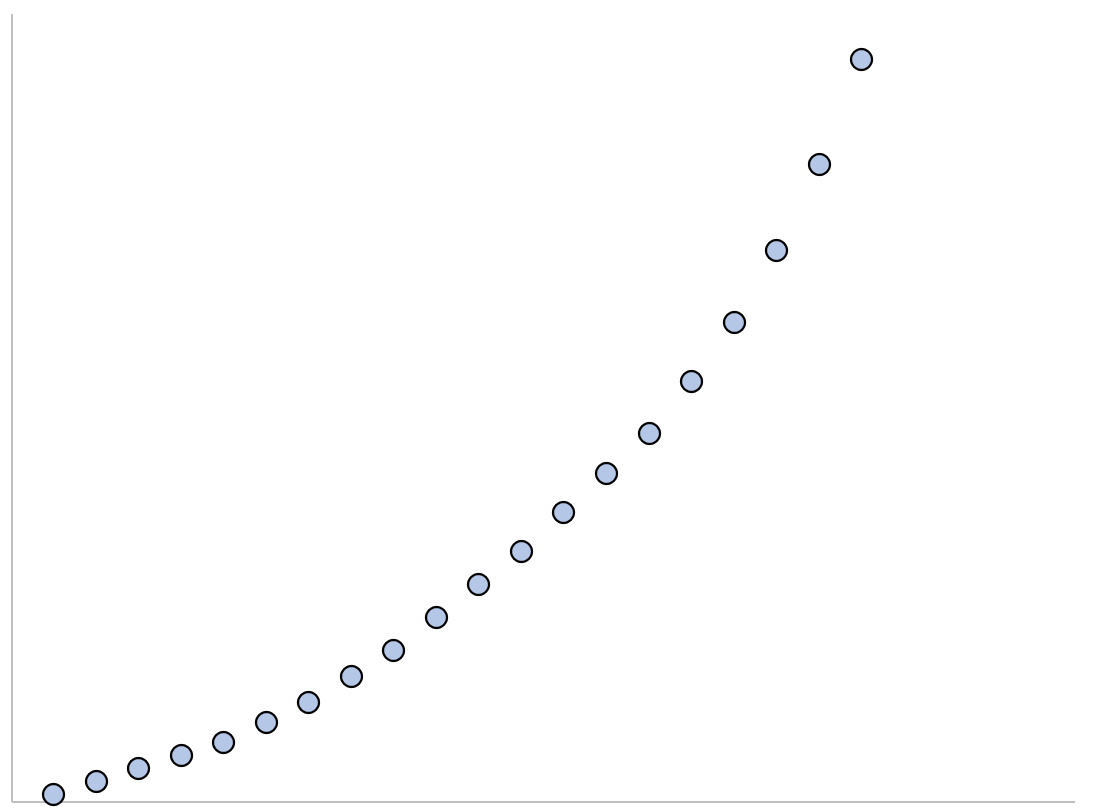
Экспоненциальная регрессия — это тип модели регрессии, который можно использовать для моделирования следующих ситуаций:
1. Экспоненциальный рост: рост начинается медленно, а затем стремительно ускоряется без ограничений.
2. Экспоненциальное затухание: затухание начинается быстро, а затем замедляется, приближаясь к нулю.
Уравнение модели экспоненциальной регрессии принимает следующий вид:
у = аб х
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить экспоненциальную регрессию в Excel.
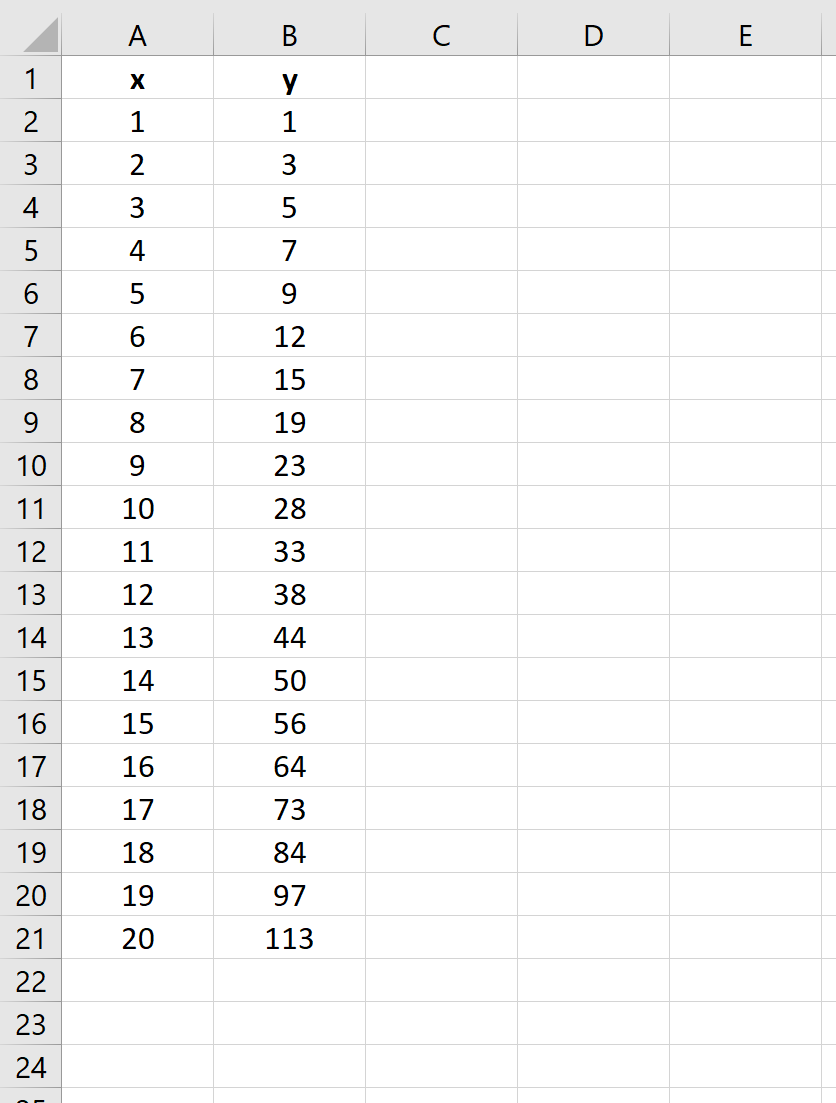
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных, содержащий 20 наблюдений :
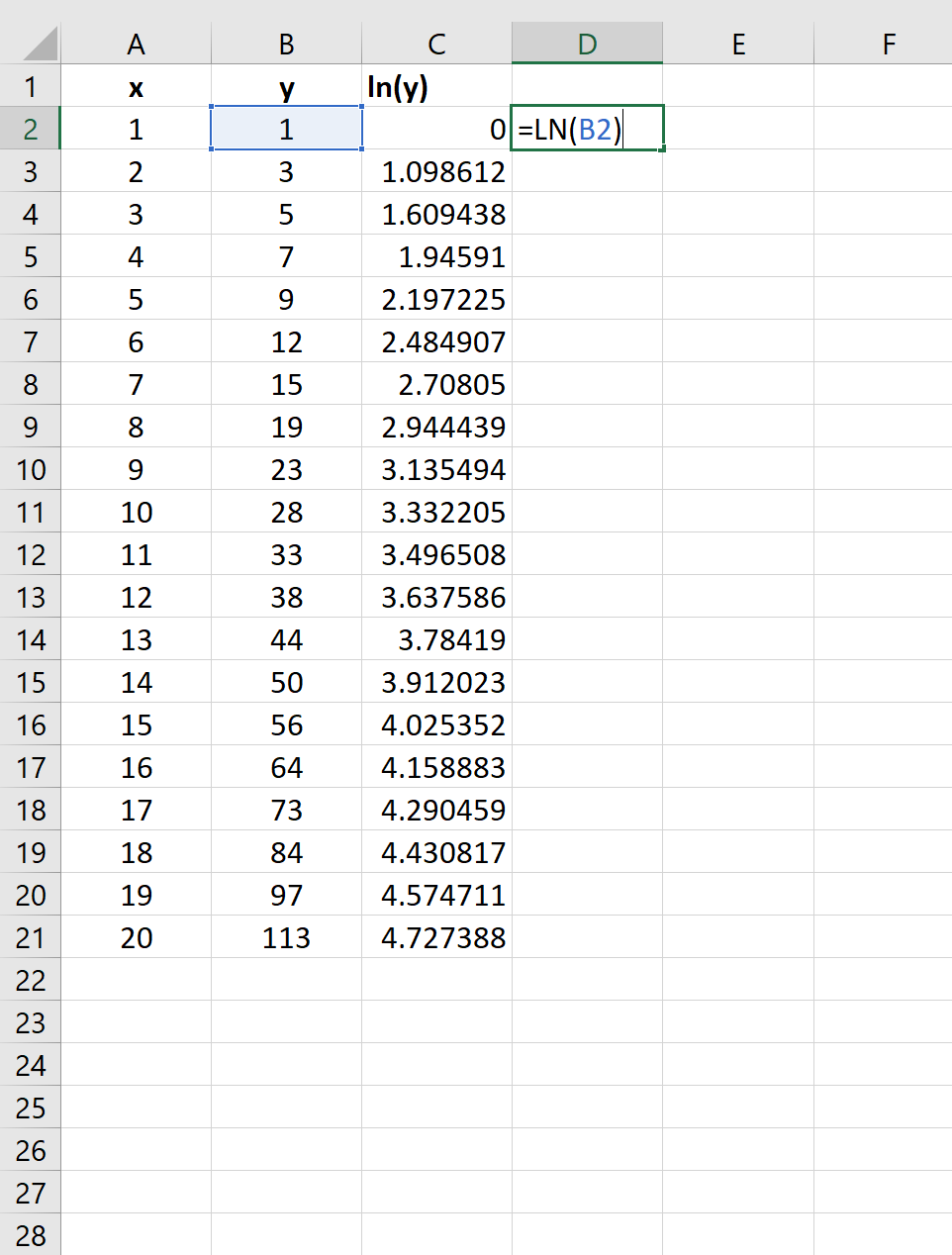
Шаг 2: возьмите натуральный логарифм переменной отклика
Далее нам нужно создать новый столбец, представляющий естественный журнал переменной ответа y :
Шаг 3: Подберите модель экспоненциальной регрессии
Далее мы подгоним модель экспоненциальной регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
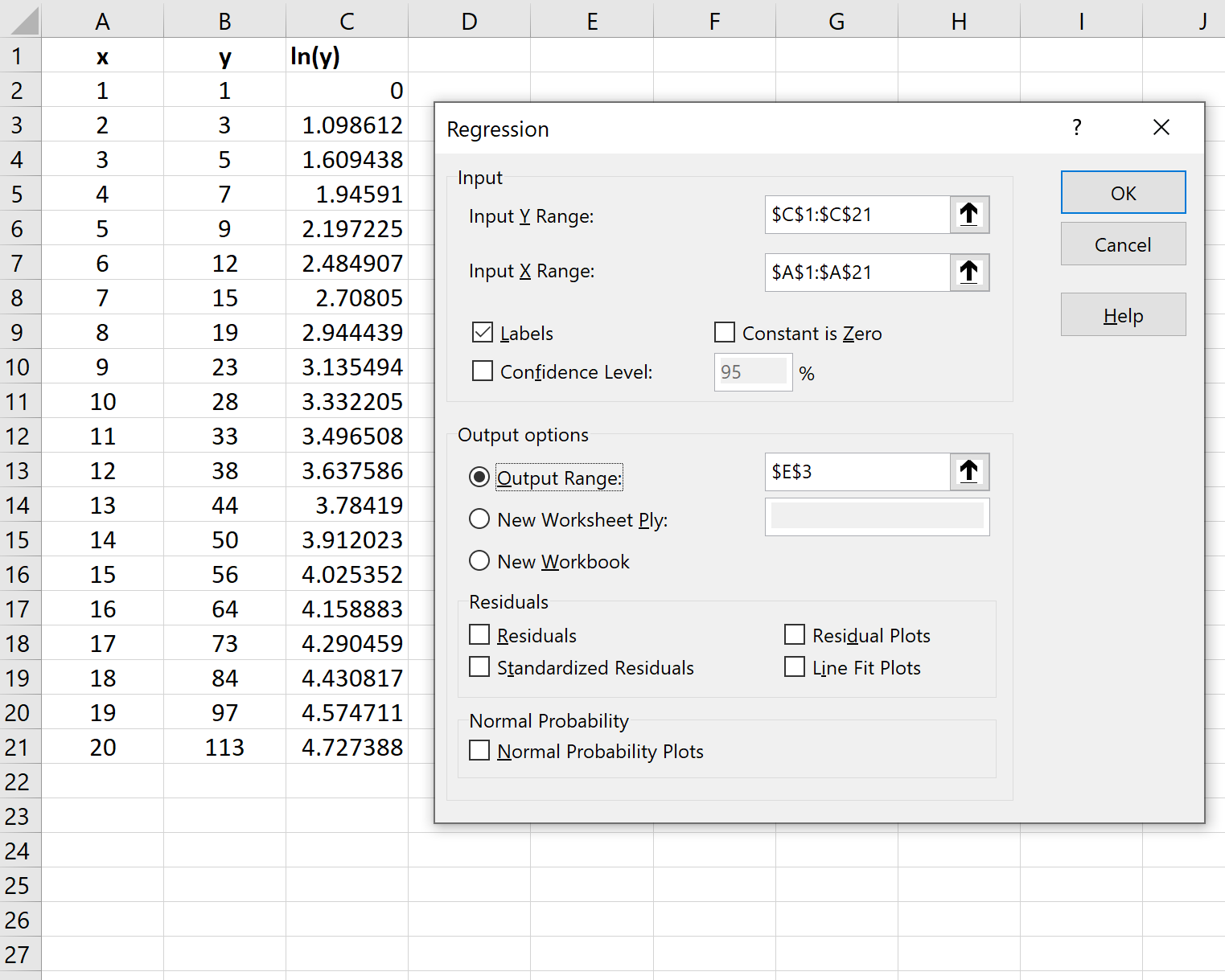
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
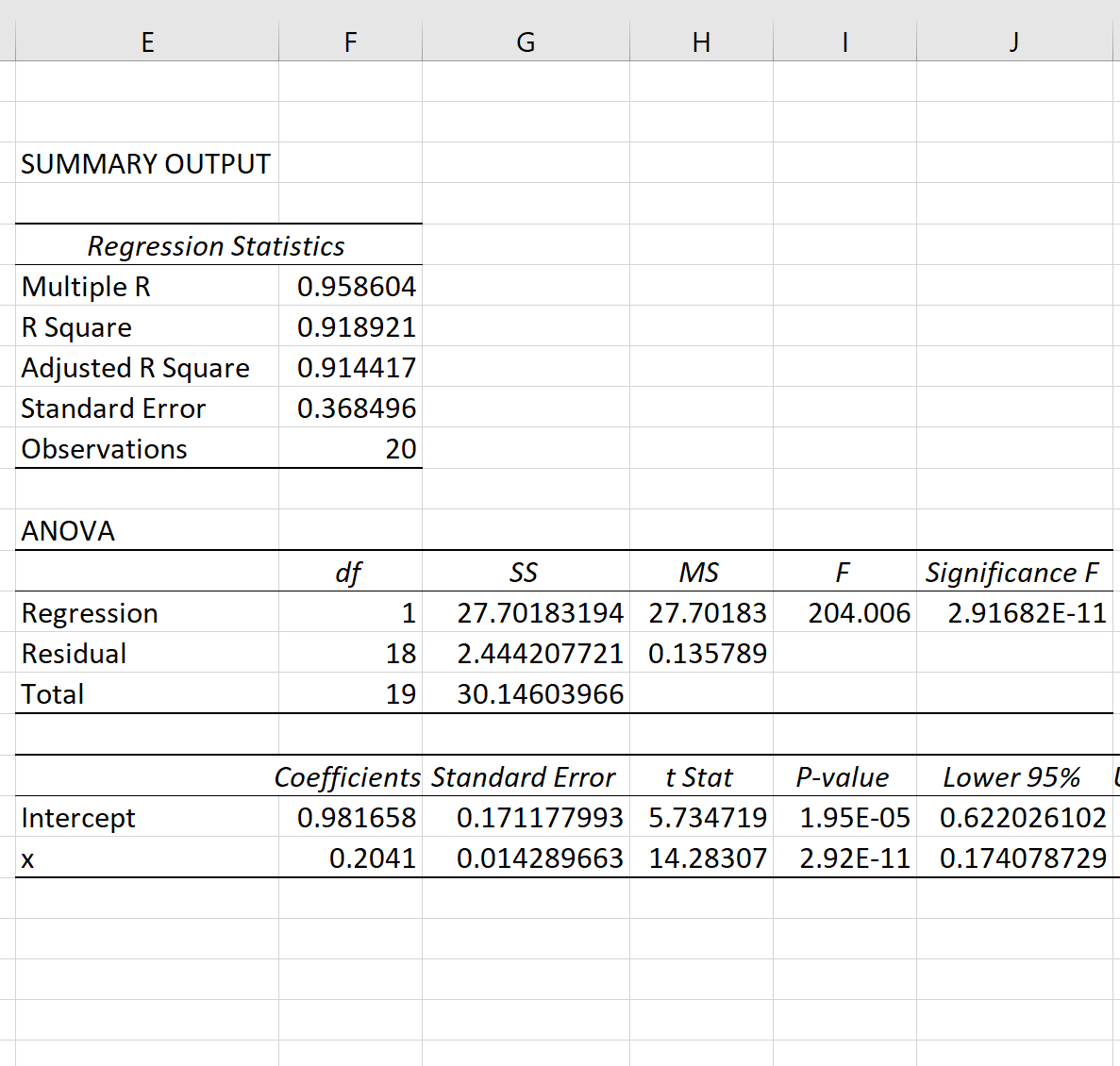
Как только вы нажмете OK , будут показаны результаты модели экспоненциальной регрессии:
Общее значение F модели составляет 204,006, а соответствующее значение p чрезвычайно мало, что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение экспоненциальной регрессии:
ln(у) = 0,9817 + 0,2041(х)
Применив e к обеим частям, мы можем переписать уравнение как:
у = 2,6689 * 1,2264 х
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 14, то мы можем предсказать, что y будет равно 46,47 :
у = 2,6689 * 1,2264 14 = 46,47
Бонус: не стесняйтесь использовать этот онлайн- калькулятор экспоненциальной регрессии для автоматического вычисления уравнения экспоненциальной регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Перейти к контенту
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 18. Модели статистического прогнозирования ГДЗ по Информатикe. 11 класс. Базовый уровень. ФГОС Семакин И.Г.
По данным из следующей таблицы постройте с помощью Excel линейную, квадратичную, экспоненциальную и логарифмическую регрессионные модели. Определите параметры, выберите лучшую модель.

Ответ

Скачать файл Excel
- Информатика
- Математика
- Алгебра
- Геометрия
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной
функции.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным. Основная статья про МНК —
МНК: Метод Наименьших Квадратов в MS EXCEL
.
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m
x
=a*(e
ln(m)
)
x
= a*e
x*ln(m)
=a*e
bx
, где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю
линейной зависимости
с помощью замены переменных (см.
файл примера
).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента
a
необходимо выполнить обратное преобразование a=
EXP(A)
.
Примечание
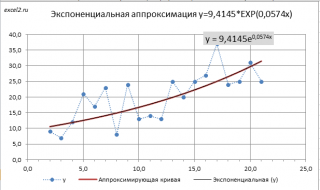
: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы
Линия тренда
(
Экспоненциальная линия тренда
). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью
Основы построения диаграмм в MS EXCEL
.
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больш
и
х по модулю отрицательных чисел) соответствующее значение
y
асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы
Линия тренда.
Если среди значений
y
есть отрицательные, то с помощью инструмента
Линия тренда
экспоненциальную линию тренда построить не удастся.
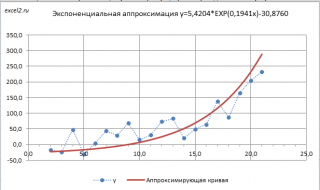
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте
х
значения
y
также будут увеличиваться. В качестве
с
можно взять некую заранее известную нижнюю границу для
y
, ниже которой
у
не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см.
файл примера лист Экспонента2
).
Если при росте
х
значения
y
уменьшаются по экспоненциальной кривой, т.е. a<0 (существует некая верхняя граница
с
для
у
), то к линейному случаю Y=b*x+A свести задачу позволит замена переменных Y=ln(c-y) и A=ln(-a) (см.
файл примера лист Экспонента3
).
Функция РОСТ()
Еще одним способом построить линию экспоненциального тренда является использование функции
РОСТ()
, английское название GROWTH.
Синтаксис функции следующий:
РОСТ(
известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст]
)
Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент
известные_значения_y
) и на массив значений переменной Х (аргумент
известные_значения_x
). Функция рассчитает прогнозные значения Y для Х, указанных в
аргументе новые_значения_x
. Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент
конст
должен быть установлен равным ЛОЖЬ (или 0).
Если среди значений
y
есть отрицательные, то с помощью функции
РОСТ()
аппроксимирующую кривую построить не удастся.
Безусловно, использование функции
РОСТ()
часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.
Наконец, покажем как с помощью функции
РОСТ()
вычислить коэффициенты уравнения y=
a
*EXP(
b
*x).
Примечание
: В MS EXCEL имеется специальная функция
ЛГРФПРИБЛ()
, которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.
Чтобы вычислить коэффициент
a
(значение Y в точке Х=0) используйте формулу
=РОСТ(C26:C45;B26:B45;0)
. В диапазонах
C26:C45
и
B26:B45
должны находиться массивы значений переменной Y и X соответственно.
Чтобы вычислить коэффициент
b
используйте формулу:
=
LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/
РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/
(МИН(B26:B45)-МАКС(B26:B45))
Функция ЛГРФПРИБЛ()
Функция
ЛГРФПРИБЛ()
на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты
а
и
m
уравнения y=
a
*
m
^x.
Используя свойство степеней a
mn
=(a
m
)
n
приведем уравнение экспоненциального тренда y=
a
*EXP(
b
*x)=
a
*e
b
*x
=
a
*(e
b
)
x
к виду y=
a
*
m
^x, сделав замену переменной m= e
b
=EXP(
b
).
Чтобы вычислить коэффициенты уравнения y=
a
*EXP(
b
*x) используйте следующие формулы:
=
LN(ЛГРФПРИБЛ(C26:C45;B26:B45))
— коэффициент
b
=
ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2)
— коэффициент
a
Примечание
: Функция
ЛГРФПРИБЛ()
, английское название LOGEST, является
формулой массива, возвращающей несколько значений
. Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в
Строке формул
ввести =
ЛГРФПРИБЛ(C26:C45;B26:B45)
, затем для ввода формулы вместо обычного
ENTER
нажать
CTRL
+
SHIFT
+
ENTER
.
Функция
ЛГРФПРИБЛ()
имеет линейный аналог – функцию
ЛИНЕЙН()
, которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции (
статистика
) установлен ИСТИНА, то
ЛГРФПРИБЛ()
возвращает регрессионную статистику:
стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов:
SSR
,
SSE
и др.
Примечание
: Особой нужды в функции
ЛГРФПРИБЛ()
нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=
a
*
m
^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=
a
*EXP(
b
*x).
Содержание
- Выполнение аппроксимации
- Способ 1: линейное сглаживание
- Способ 2: экспоненциальная аппроксимация
- Способ 3: логарифмическое сглаживание
- Способ 4: полиномиальное сглаживание
- Способ 5: степенное сглаживание
- Вопросы и ответы
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Урок: Как построить линию тренда в Excel
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
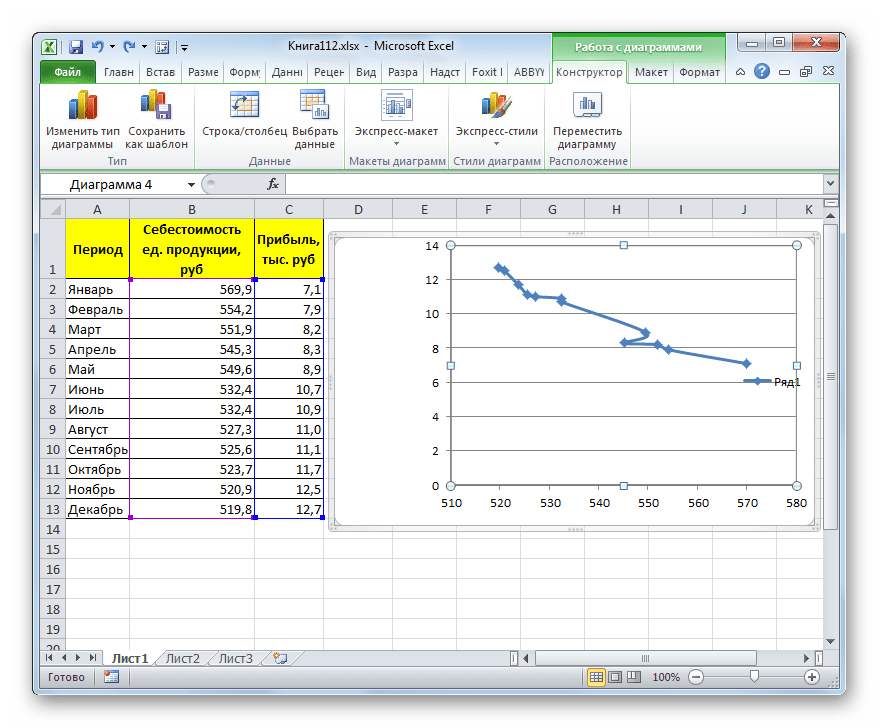
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
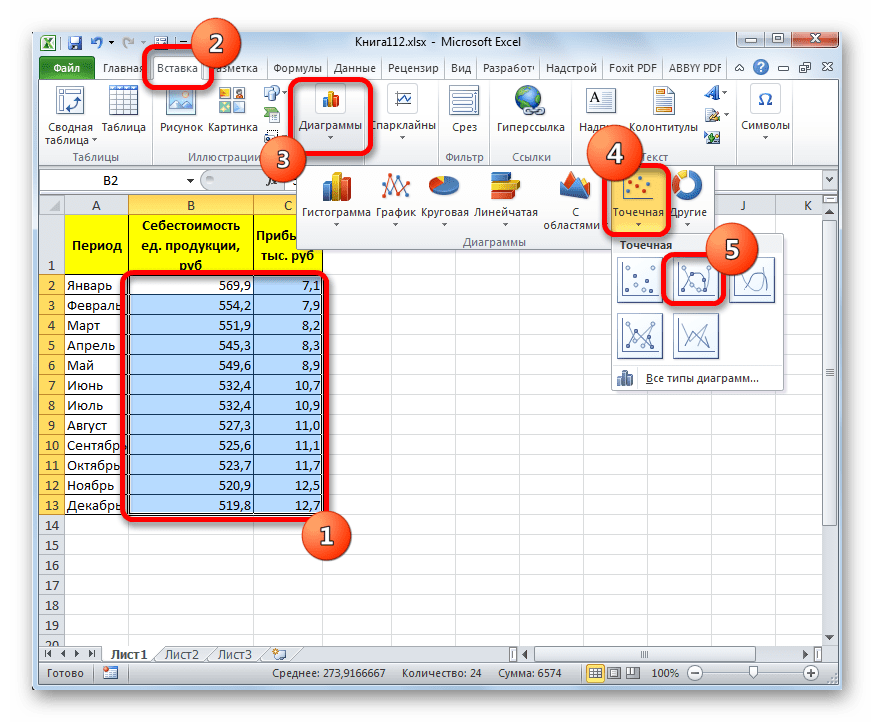
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
- График построен.
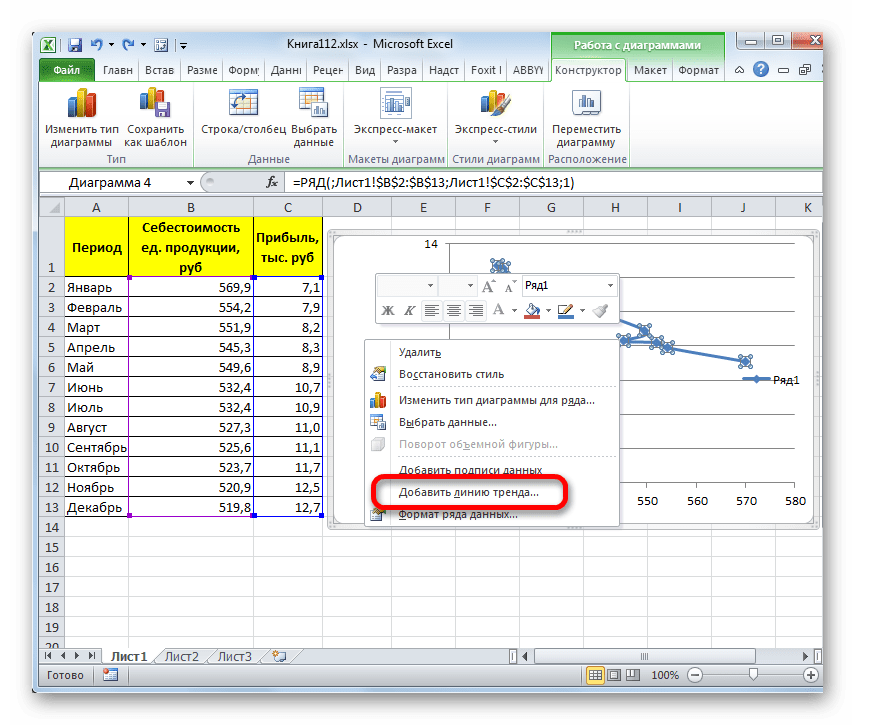
- Для добавления линии тренда выделяем его кликом правой кнопки мыши. Появляется контекстное меню. Выбираем в нем пункт «Добавить линию тренда…».
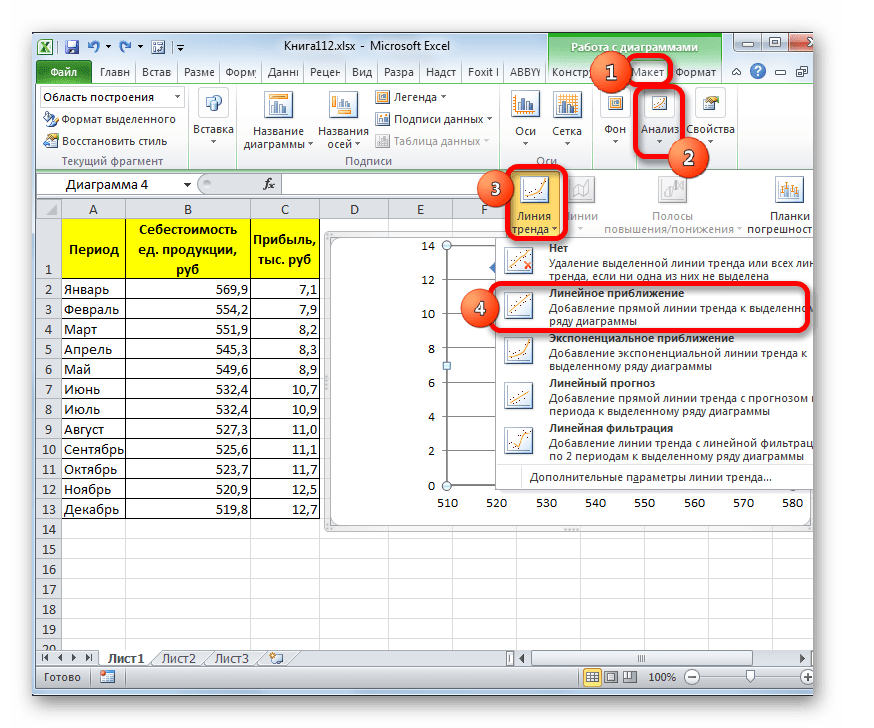
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
- Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
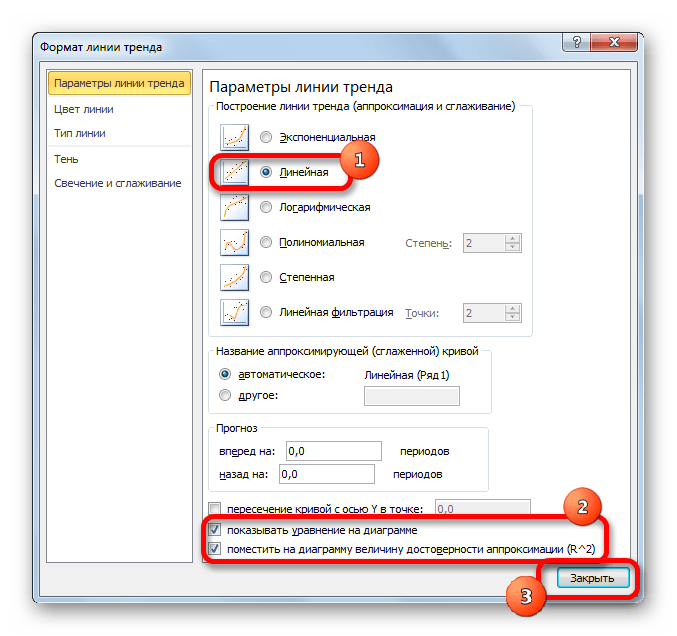
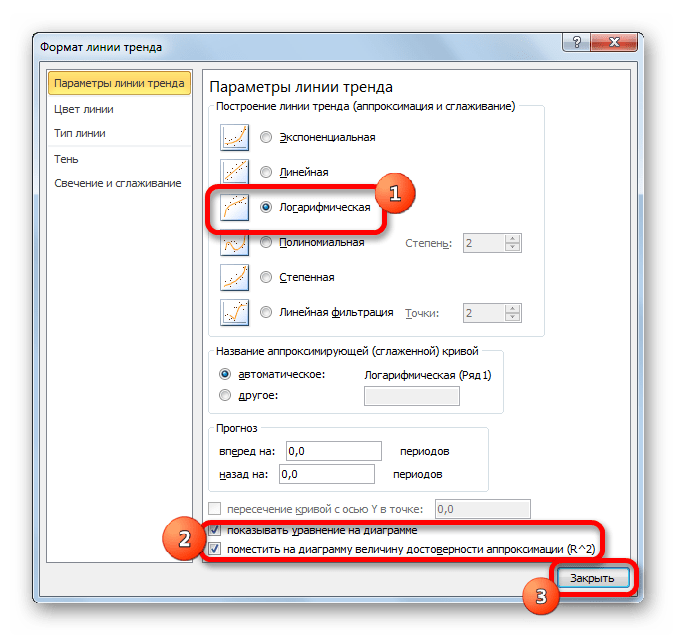
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
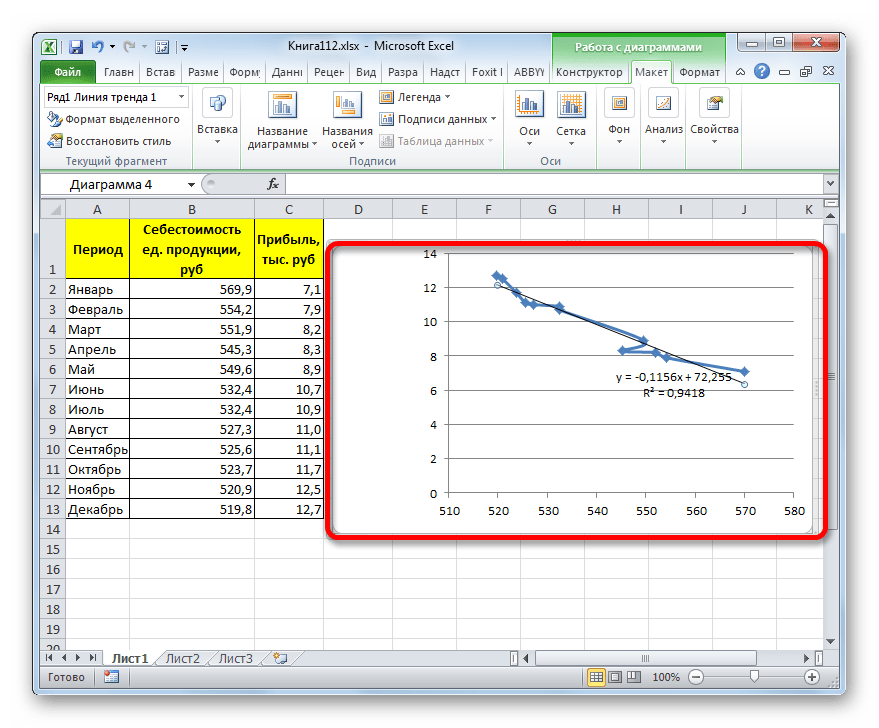
- Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
y=ax+b
В конкретно нашем случае формула принимает такой вид:
y=-0,1156x+72,255
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
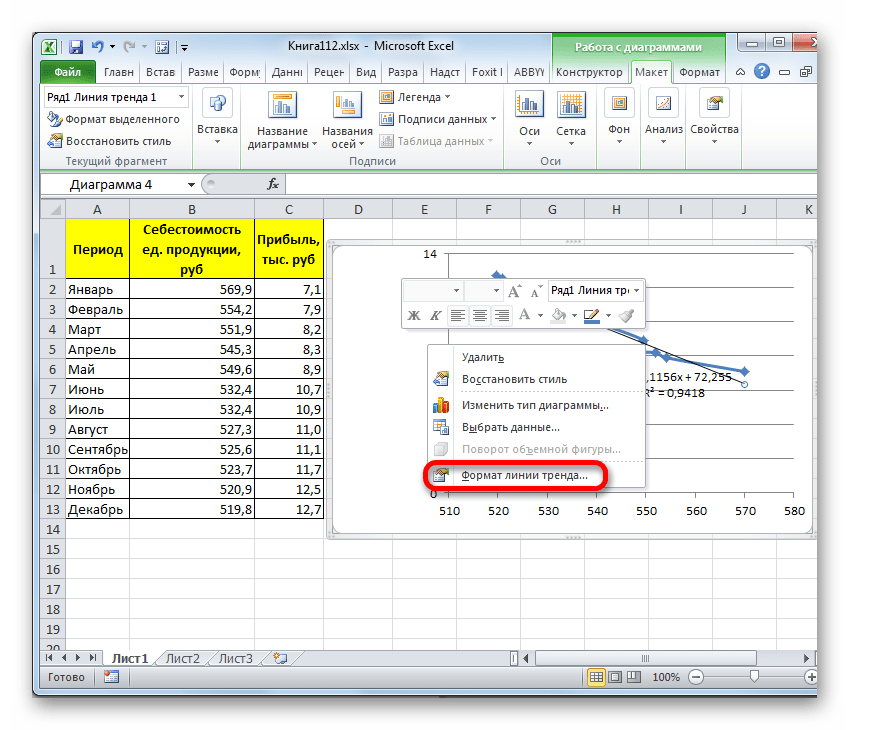
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
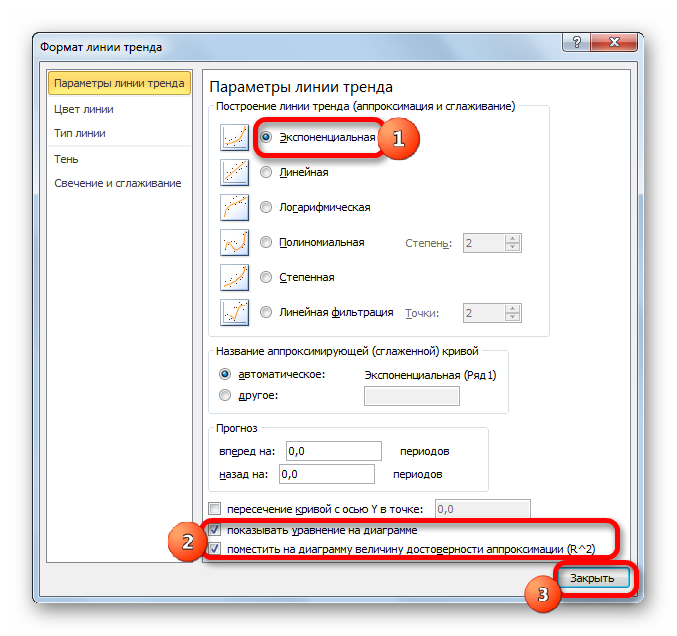
- После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
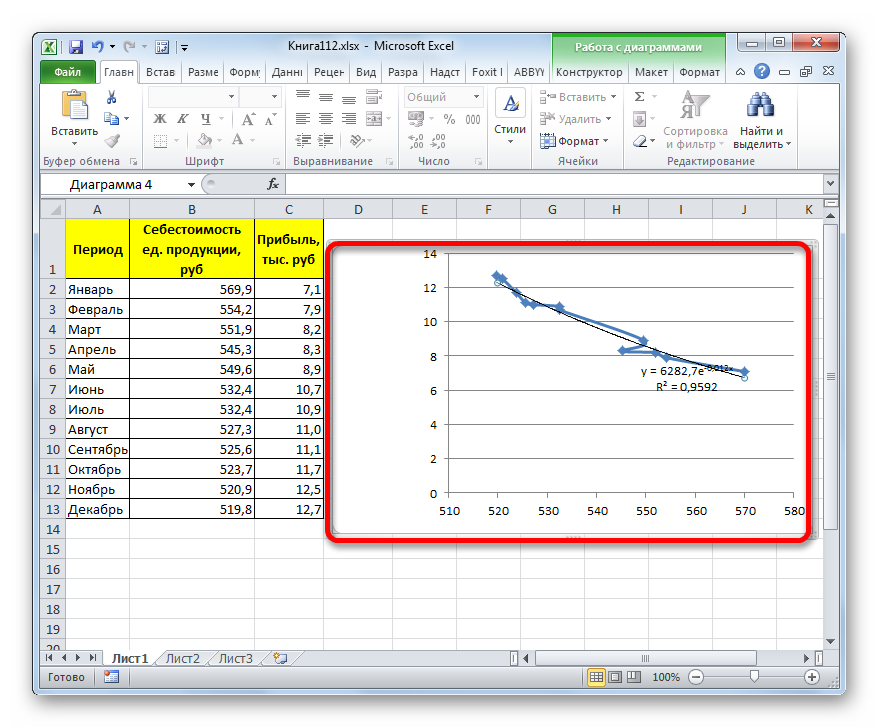
- После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.
Общий вид функции сглаживания при этом такой:
y=be^x
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
y=6282,7*e^(-0,012*x)
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
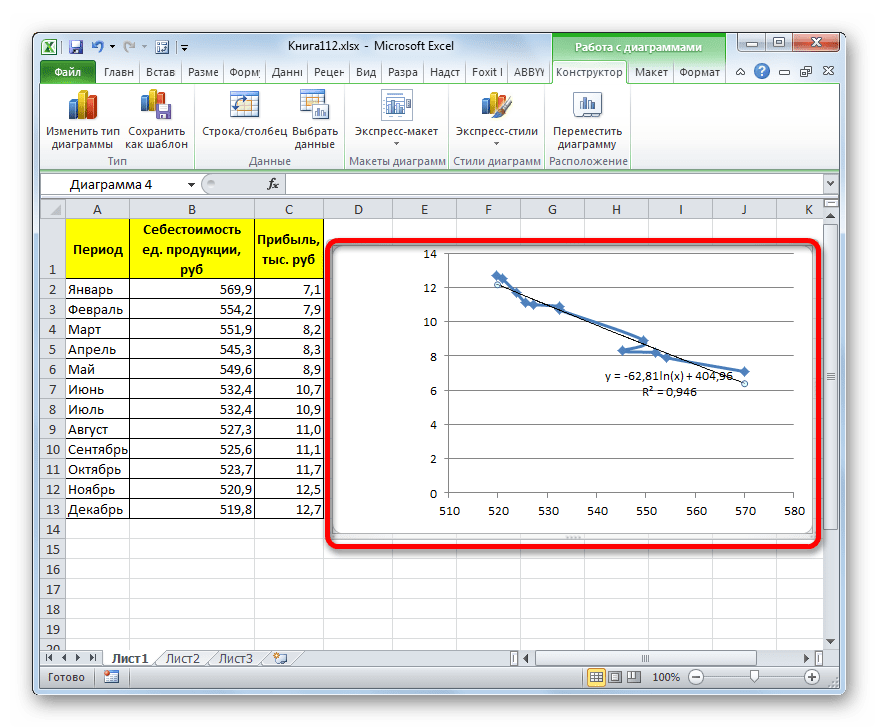
- Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.
В общем виде формула сглаживания выглядит так:
y=a*ln(x)+b
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
y=-62,81ln(x)+404,96
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
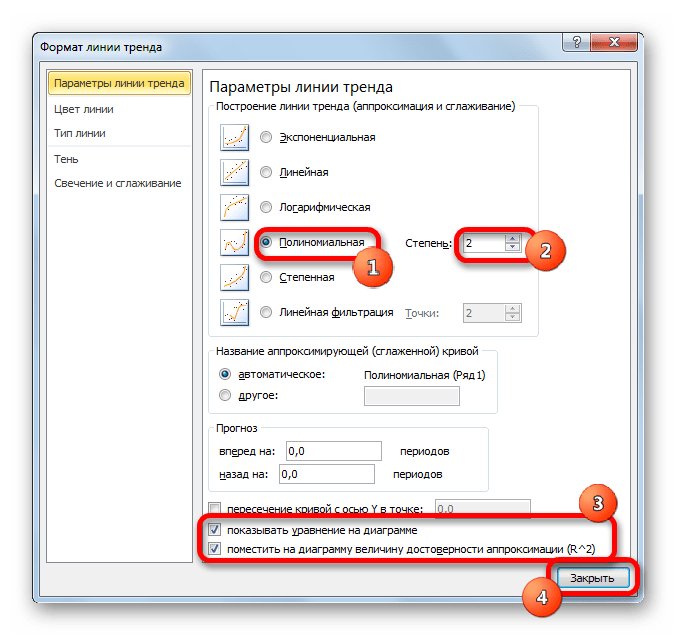
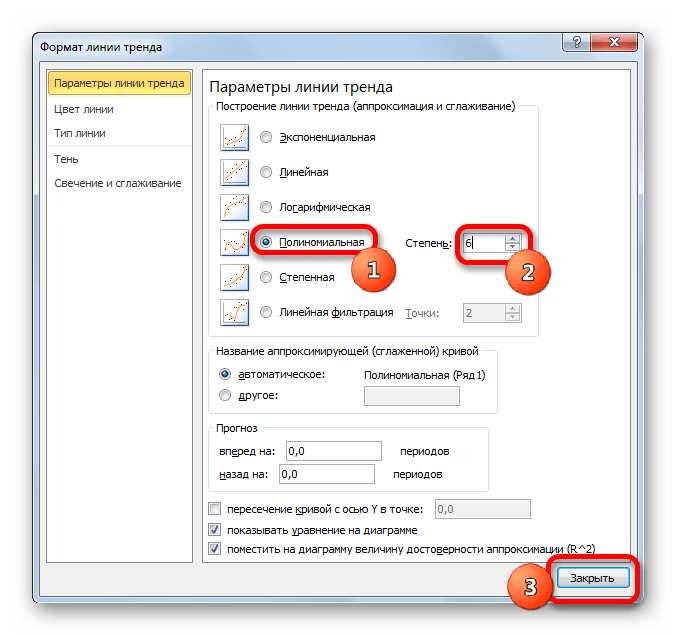
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
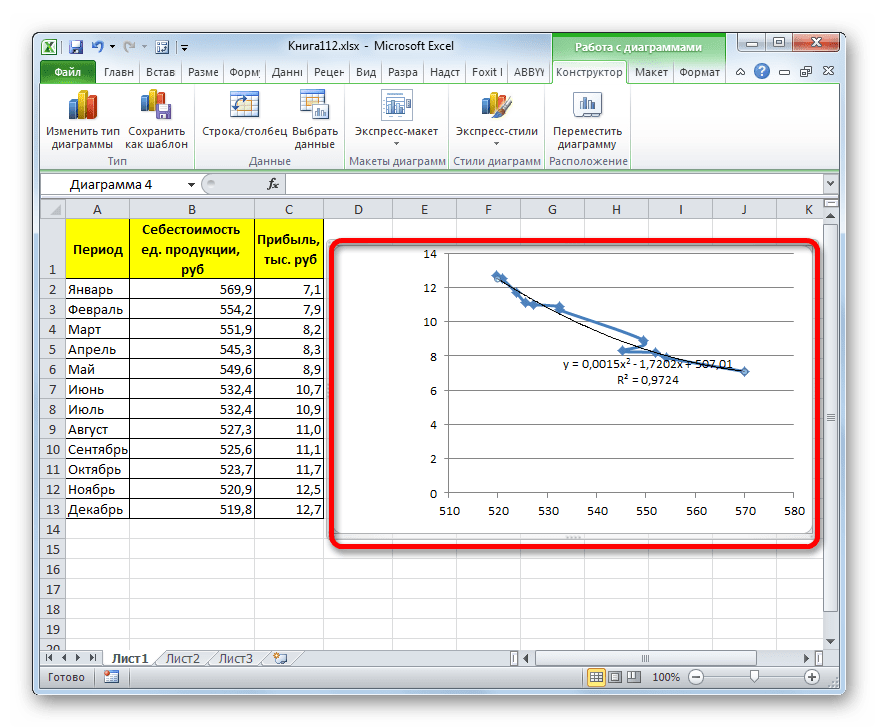
- Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
y=a1+a1*x+a2*x^2+…+an*x^nВ нашем случае формула приняла такой вид:
y=0,0015*x^2-1,7202*x+507,01 - Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
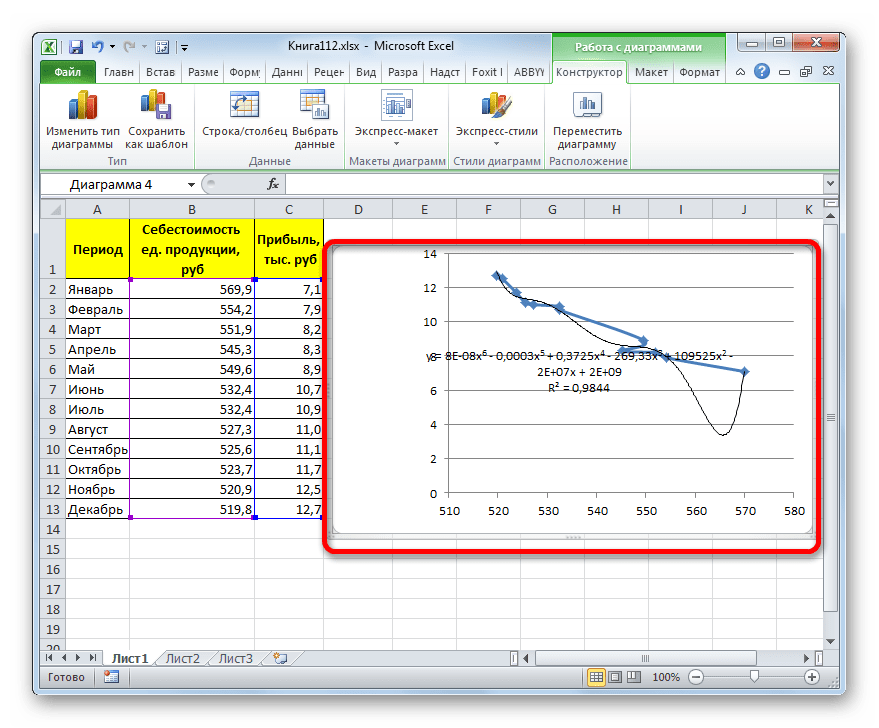
- Как видим, после этого наша линия тренда приняла форму ярко выраженной кривой, у которой число максимумов равно шести. Уровень достоверности повысился ещё больше, составив 0,9844.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
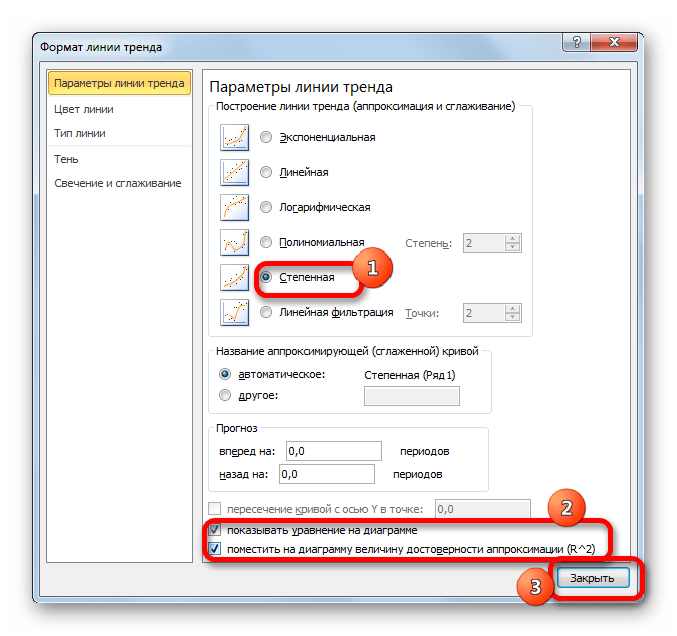
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
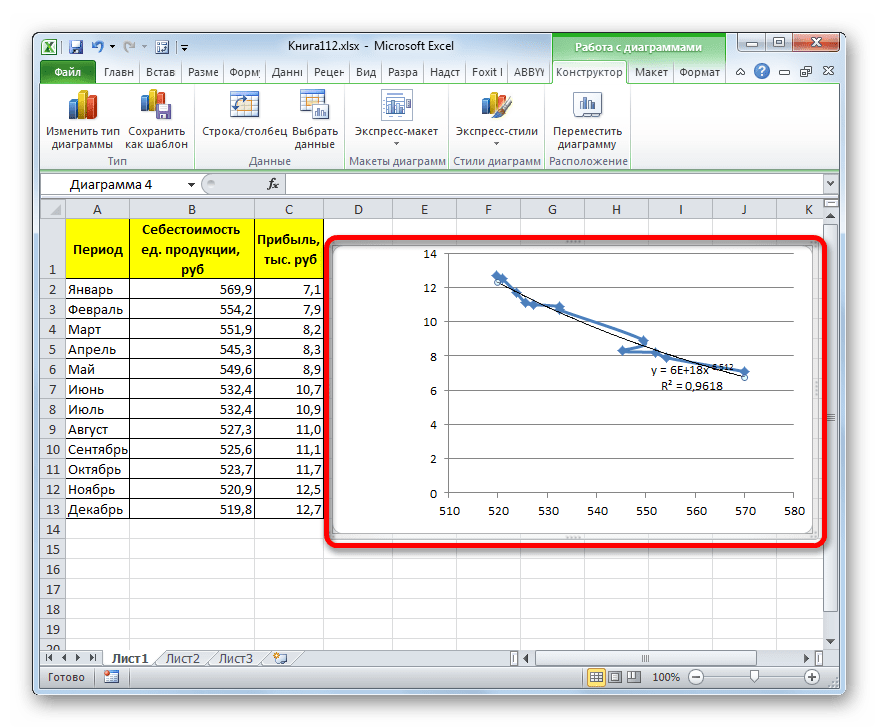
- Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
y=bx^n
В конкретно нашем случае она выглядит так:
y = 6E+18x^(-6,512)
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Построение регрессионных моделей с помощью табличного процессора
Опишем алгоритм получения с помощью MS
Excel регрессионных моделей по МНК с
построением тренда.
Сначала следует ввести табличные данные
и построить точечную диаграмму, как это
показано на рис. 2.12 (можно игнорировать
все лишние детали — надписи, легенду,
— чтобы получилось так, как на рис. 2.14
а, в качестве подписи к оси ОХ выбрать
текст «Линейный тренд»). Далее следует:
=> щелкнуть мышью по полю диаграммы
(по одной из точек диаграммы); => выполнить
команду => Диаграмма => Добавить линию
тренда;
:=> в открывшемся окне на закладке «Тип»
выбрать «Линейный тренд»;
=> перейти к закладке «Параметры»;
установить галочки на флажках «показывать
уравнения на диаграмме» и «поместить
на диаграмму величину достоверности
аппроксимации R2», щелкнуть по
кнопке ОК.
Диаграмма готова. Она будет точно такой,
как на рис. 2.14 а. Аналогично можно получить
и другие типы трендов. Квадратичный
тренд получается путем выбора
полиномиального типа функции с
указанием степени 2.
Заметим, что MS Excel дает возможность
пользователю самому задавать тип
регрессионной модели, а не ограничиваться
предлагаемым меню из шести функций.
Однако для большого числа практических
ситуаций этих функций бывает вполне
достаточно.
Продолжение линии тренда за границы
области данных, приведенных в исходной
таблице, называется экстраполяцией.
Для получения такого рисунка нужно
добавить в описанный в описанный
выше алгоритм еще одно действие: => на
вкладке «Параметры» в области «Прогноз»
в строке «вперед на» установить 2 единицы.
Здесь имеются в виду единицы используемого
масштаба по горизонтальной оси.
Задание для самостоятельного выполнения
-
По данным из следующей таблицы постройте
с помощью MS Excel линейную, квадратичную,
экспоненциальную и логарифмическую
регрессионные модели. Определите
параметры, выберите лучшую модель.
Произвести прогнозирование по полученной
модели: получить значение Y
для Х=1, 17, 19, 29.
|
X |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
|
Y |
44 |
32 |
35 |
40 |
30 |
27 |
21 |
25 |
20 |
23 |
18 |
19 |
20 |
16 |
-
В следующей таблице приводится прогноз
средней дневной температуры на последнюю
неделю мая в различных городах европейской
части России. Города упорядочены по
алфавиту. Указана также географическая
широта этих городов. Построить несколько
вариантов регрессионных моделей (не
менее трех), отражающих зависимость
температуры от широты города. Выбрать
наиболее подходящую функцию. Произвести
прогнозирование по полученной модели:
рассчитать прогноз средней температуры
для следующих городов: Сочи — 43,5 гр. с.
ш., Москва — 55,7 гр. с. ш., Санкт-Петербург
— 60 гр. с. ш., Мурманск — 69 гр. с. ш.
|
Город |
Широта, гр. с. ш. |
Температура |
|
Воронеж |
51,5 |
16 |
|
Краснодар |
45 |
24 |
|
Липецк |
52,6 |
12 |
|
Новороссийск |
44,8 |
25 |
|
Ростов на Дону |
47,3 |
19 |
|
Рязань |
54,5 |
11 |
|
Северодвинск |
64,8 |
5 |
|
Череповец |
59,4 |
7 |
|
Ярославль |
57,7 |
10 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #