Трехмерные диаграммы (поверхности и изолинии) в EXCEL
history 16 мая 2015 г.
-
Группы статей
- Диаграммы и графики
Рассмотрим трехмерные диаграммы в MS EXCEL 2010. С помощью трехмерных диаграмм отображают поверхности объемных фигур (гиперболоид, эллипсоид и др.) и изолинии.
Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
При попытке построить диаграмму типа Поверхность на основе одного ряда данных, MS EXCEL может сказать, что ему требуется как минимум 2 ряда. На самом деле, для более или менее наглядной поверхности потребуется как минимум 10 рядов (лучше 20 – для сложных поверхностей). К счастью, ряды не нужно создавать в ручную – достаточно правильно сформировать таблицу с исходными данными.
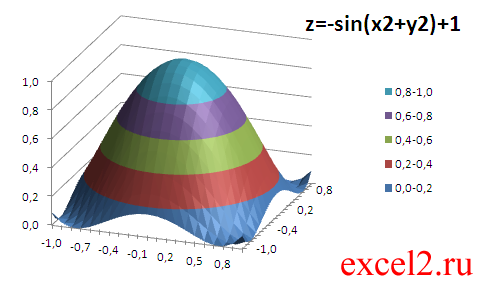
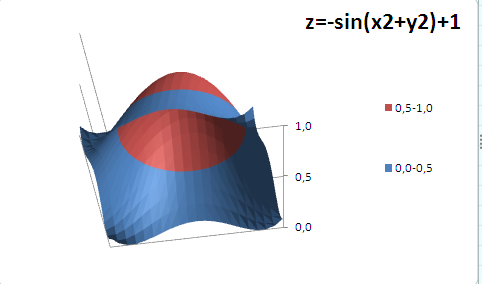
Построим график функции z=-sin(x*х+y*y)+1 (см. файл примера ).
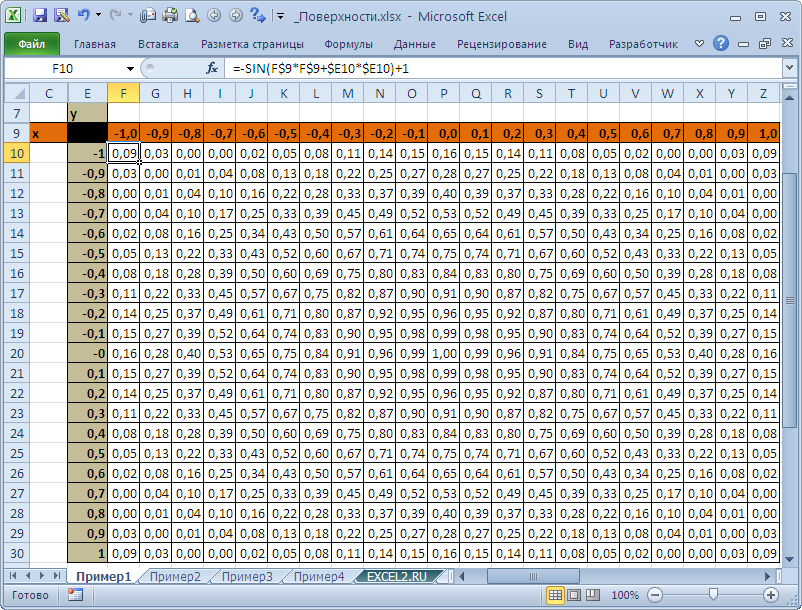
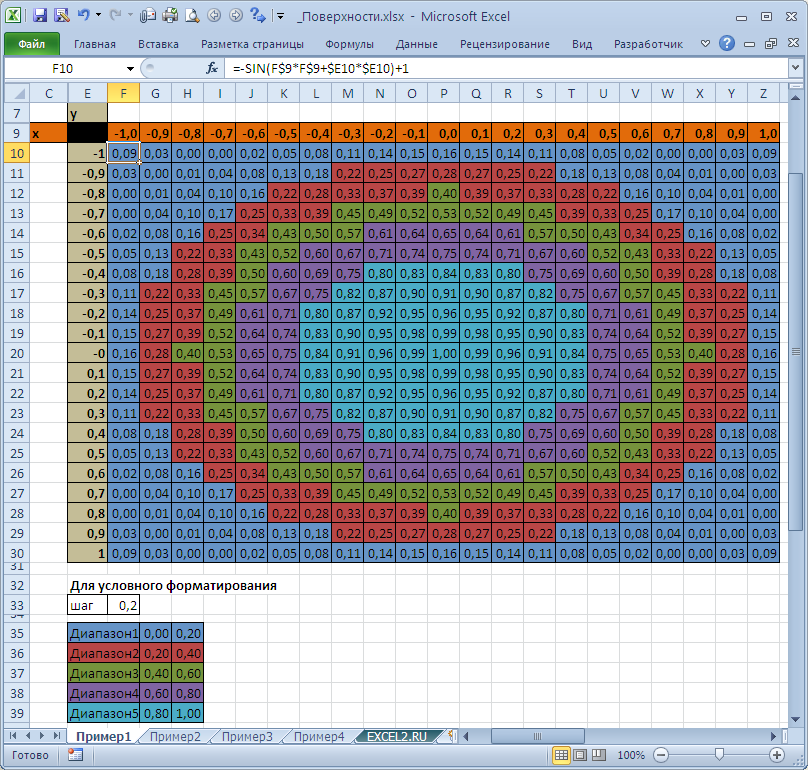
В качестве источника данных используем таблицу, в которой в верхней строке указаны значения Х, а в левом столбце Y. В остальных ячейках – значения Z для всех пар (Х,Y)
Чтобы значения Z были более информативны — можно использовать Условное форматирование .
Условное форматирование показывает некий вариант изолиний (см. ниже): близкие значения Z выделены одним цветом. Это также позволяет предварительно оценить вид создаваемой диаграммы.
Теперь выделите любую ячейку таблицы и постройте диаграмму типа Поверхность (вкладка Вставка , группа Диаграммы , Кнопка Другие ).
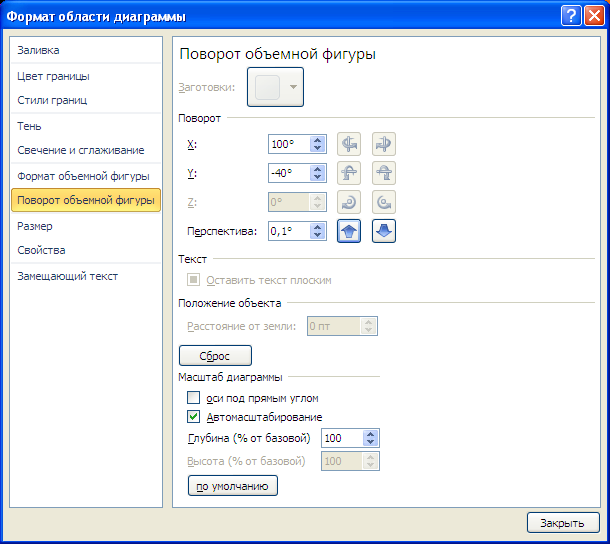
Полученную фигуру можно повращать (кнопка Поворот объемной фигуры на вкладке Макет ).
Для построения диаграммы используется 3 оси: горизонтальная ось (категорий), вертикальная ось (значений), ось Z (рядов значений). Все 3 названия осей требуют пояснения.
Во-первых, ось Z на самом деле является нашей осью Х и отображает имена рядов. Если имена рядов убрать, то изменятся и подписи оси (убрать имена рядов можно нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор ).
Этот факт роднит диаграмму Поверхность с Диаграммой График , где по Х отображаются лишь подписи. Т.е. при попытке построить поверхность с неравномерным шагом по Х (например, 1, 2, 5, 9, 77, 103, ..) получим искажения масштаба: значения по Х будут откладываться последовательно 1, 2, 3, … (конечно, Z будет рассчитаны правильно). Интересно, что формат подписей по оси Z можно настроить только изменяя формат ячеек, на которые ссылаются имена рядов (изменение формата на вкладке Число (в окне Формат Оси) ни к чему не приводит).
Во-вторых, по вертикальной оси (значений) на самом деле откладываются значения Z (это очевидно из рисунка).
И, наконец, в-третьих, горизонтальная ось (категорий) – это значения Y (на самом деле опять только подписи). Подписи, как и для Графика можно удалить или изменить нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор (на этот раз нужно нажать кнопку расположенную справа).
Так как диаграмма Поверхность – это по сути трехмерный График , в котором одному Х соответствует один Y, то некоторые объемные фигуры отобразить на диаграмме Поверхность не удастся. Например, не удастся отобразить гиперболоид, т.к. каждой паре (Х;Y) на диаграмме Поверхность соответствует только один Z, а для гиперболоида это не так (каждой паре соответствует 2 значения Z). Поэтому, в MS EXCEL придется довольствоваться только половиной гиперболоида.
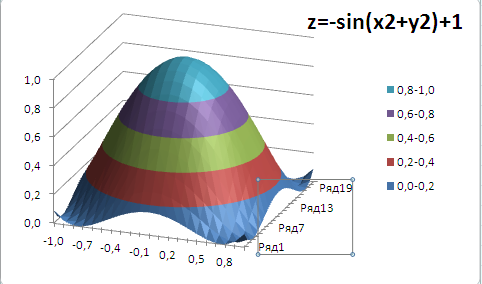
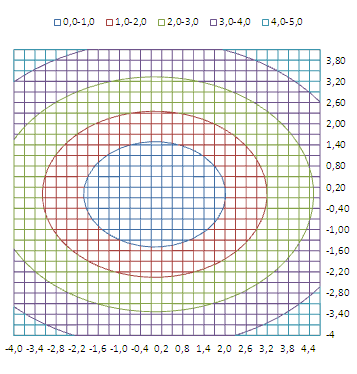
Как видно из диаграммы, близкие значения Z выделены одним цветом, которые указаны в Легенде. К сожалению, в MS EXCEL невозможно управлять этими уровнями (даже при повороте фигуры количество уровней и диапазоны значений существенно изменяются). Это приводит к тому, что построение изолиний ( линии уровня, контурный график, англ. Contour plot ) реализовано в MS EXCEL в достаточно ограниченном виде: невозможно указать на диаграмме значение изолинии (диапазоны цветов указаны на Легенде), разбиение на диапазоны по Z производится MS EXCEL автоматически и нет возможности на это повлиять. Ниже приведены изолинии для упомянутого выше гиперболоида. Это особый вид диаграммы – Проволочная контурная .
Практически такой же картинки можно добиться простым поворотом фигуры на диаграмме Поверхность .
Построение поверхностей второго порядка в excel
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
3. .Уравнение плоскости, проходящей через три точки
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
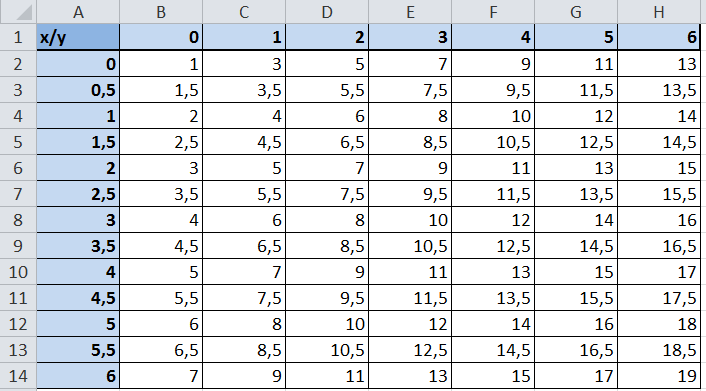
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица (рис. 1).
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
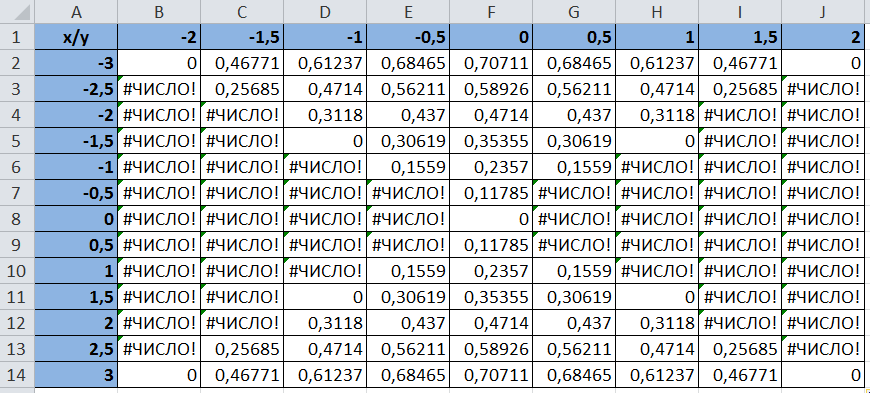
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
| | | следующая лекция ==> |
| | | Решите задачи с использованием диаграммы Эйлера-Венна. |
Дата добавления: 2017-02-25 ; просмотров: 2062 | Нарушение авторских прав
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
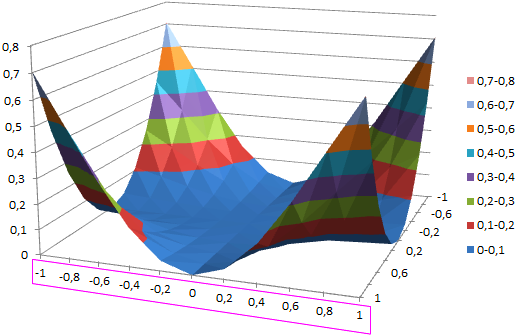
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
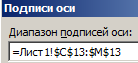
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
by Ирина Кяршис
ГЛАВА 1. Возможности табличного процессора Microsoft Excel
1.1.Ввод данных в Excel
Электронная таблица – это программа, позволяющая автоматизировать табличные расчеты. Документ Microsoft Ехсел является рабочей книгой, состоящей из листов. Таблица состоит из 65536 строк и 256 столбцов. Строки нумеруются числами, столбцы – буквами латинского алфавита (А, В …, Z, АА, АВ …). На пересечении строки и столбца расположена ячейка, которая имеет адрес, состоящий из имени столбца и номера строки (А4). Одна из ячеек всегда является активной.
Прямоугольная группа смежных ячеек называется диапазоном ячеек. Примеры диапазонов – А2: С4, В2: К40.
Ячейки могут содержать данные трех типов:
1) Текстовые данные – это строка текста произвольной длины.
2) Числовые данные – это отдельное число. Может быть целым, дробным (зап.). Если ширина ячейки мала, то число записывается в экспоненциальной форме, например 125 000 000 → 1,25Е + 8 или вместо числа ставятся символы ###. При этом число сохраняется.
3) Формула – это арифметическое выражение. Он представляет собой последовательность чисел, ссылок на ячейки и функций, объединенных знаками арифметических операций: +, -, /, *. Excel предлагает несколько сотен встроенных функций, которые разделены на категории.
Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.
Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.
Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).
1.2.Типы диаграмм
В зависимости от типа диаграммы данные отображаются на ней разным способом.
Можно отметить несколько стандартных типов:
1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.
2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.
3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.
4. С областями . Диаграмма с областями похожа на график.
5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.
Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.
6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)
7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.
8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.
Подробнее о типах диаграмм здесь
1.3 Основы построения диаграмм в Excel
Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.
Совокупность этих элементов определяет макет диаграммы.
Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).
Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.
Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.
6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.
Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).
Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.
ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2.1 Уравнения поверхностей второго порядка и их графики
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.
Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=1, где a и b – действительные полуоси, с – мнимая полуось.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=-1,где с – действительная полуось, a и b – мнимые полуоси.
Поверхностная диаграмма в Excel и пример ее построения
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
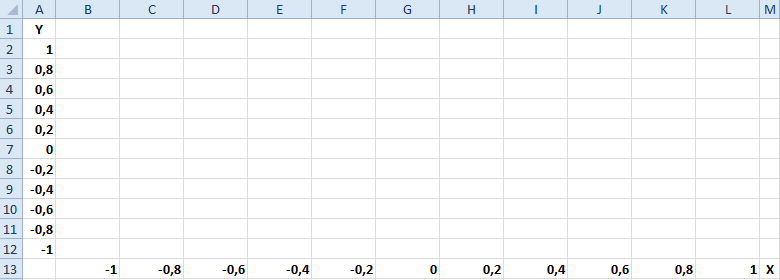
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
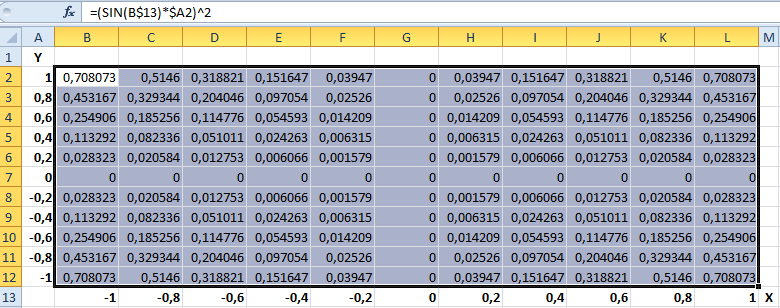
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
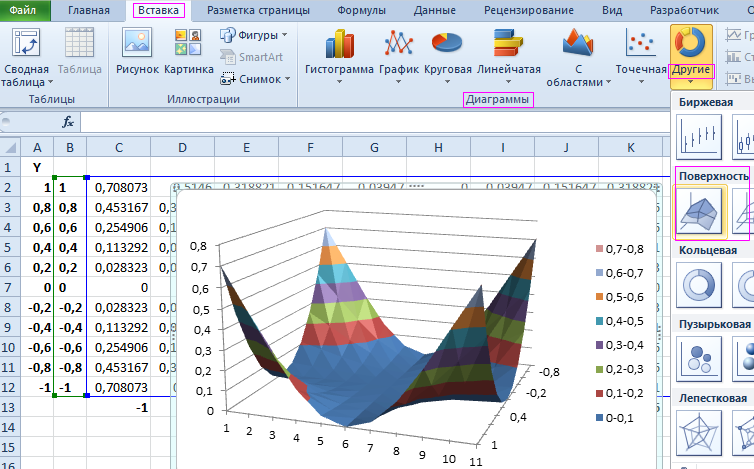
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
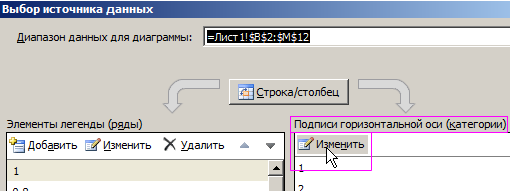
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
источники:
http://4systems.ru/inf/postroenie-poverhnostej-vtorogo-porjadka-v-excel/
http://exceltable.com/grafiki/poverhnostnaya-diagramma
Примечания:
-
Примеры из Excel, хотя диаграммы также доступны в Word, PowerPoint и Outlook word. Если вы используете одну из этих программ, функции одинаковы, но при этом могут быть небольшие различия при получении исходных диаграмм.
-
Следующие процедуры применимы Office 2013 и более новых версиях. Office шаги 2010 г.?
Создание 3-D chart
-
Выберем на нем ячейки, содержащие данные, которые вы хотите использовать для диаграммы.
-
На вкладке Вставка щелкните Диаграммы, если вы видите только значок, или выберите диаграмму, которая вам нужна.
Вы также можете щелкнуть значок Просмотр всех диаграмм в правом нижнем разделе Диаграммы. Откроется диалоговое окно Диаграмма, в котором можно выбрать любой тип диаграммы. В каждой категории обычно есть как двух-, так и трехугодные. Выберите один из них.
Изменение 3-D формата элементов диаграммы
-
На 3-D chart щелкните элемент диаграммы, например полосы или линии, который вы хотите изменить формат 3-D, или сделайте следующее, чтобы выбрать его из списка элементов диаграммы.
-
Щелкните диаграмму.
Отобразит вкладку «Средства работы с диаграммами»с вкладками «Конструктор» и «Формат». -
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Область диаграммы, а затем выберите нужный элемент диаграммы.
-
-
Сочетания клавиш. Вместо этого можно щелкнуть элемент диаграммы, для которого нужно изменить формат, и нажать клавиши CTRL+1. Переступить к шагу 3.
-
В группе Текущий выделение нажмите кнопку Формат выделения.
-
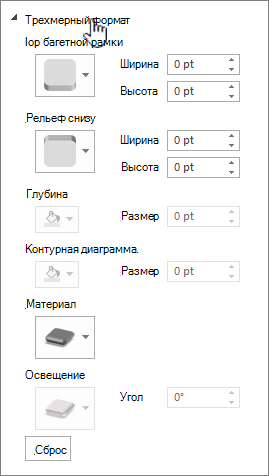
Нажмите кнопкуЭффекты, выберите формат 3-D, а затем выберите один или несколько из следующих параметров.
-
Нажмите кнопку Верхнее илиНижнее, а затем выберите нужный формат.
В полях Ширинаи Высота выберите нужный размер.
-
ЩелкнитеМатериальный и выберите нужный эффект.
Примечание: Доступность этих параметров зависит от выбранного элемента диаграммы. Некоторые параметры, представленные в этом диалоговом окне, доступны не для всех диаграмм.
Параметры этого диалогового окна работают с выбранным элементом диаграммы. При выборе всей диаграммы создаются рамки, а при выборе ряда данных она работает только с элементами этого ряда.
-
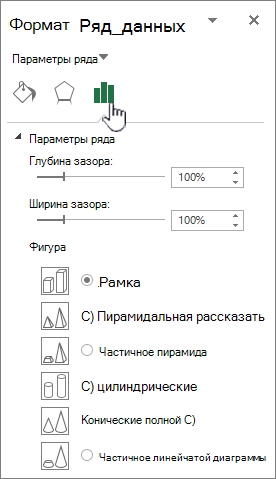
Изменение глубины и интервалов в 3-D chart
Вы можете изменить глубину диаграммы в трехмерных диаграммах с осями, глубину зазора в трехмерных перспективных диаграммах и ширину зазора в трехмерных линеек или гограммах.
-
Щелкните трехуголевую диаграмму, которую вы хотите изменить.
-
В меню Формат выберите пункт Выбранный ряд данных.
-
На вкладке Формат ряда данных нажмите кнопку Параметрыряда и выберите нужные параметры глубины и ширины.
Примечание: Доступность этих параметров зависит от выбранного элемента диаграммы. Некоторые параметры, представленные в этом диалоговом окне, недоступны для диаграмм.
Изменение поворота трехуголной диаграммы
-
Щелкните область диаграммы для 3-D chart, которую вы хотите повернуть, или выберите Область диаграммы в списке Элементы диаграммы в списке Текущий выделение на вкладке Формат.
-
Сочетания клавиш. Вместо этого можно щелкнуть область диаграммы и нажать клавиши CTRL+1. Переступить к шагу 3.
-
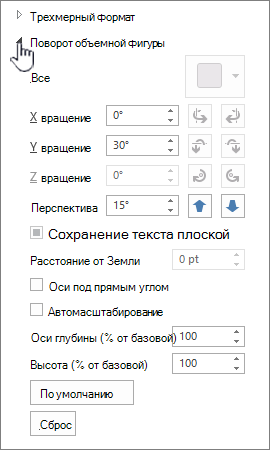
На вкладке Формат области диаграммы нажмите кнопку Эффекты и выберите поворот 3-D.
-
Выполните одно или несколько из указанных ниже действий:
-
Чтобы изменить угол поворота, щелкните нужный угол поворота в полях Поворот X и Поворот Y.
Примечание: Диаграммы можно повернуть вокруг горизонтальной и вертикальной осей, но не вокруг оси глубины. Поэтому в поле Z нельзя указать угол поворота.
-
Чтобы изменить поле представления на диаграмме, щелкните нужный уровень перспективы в поле Перспектива или нажимайте кнопки Узкие поля представления или Расширить, пока не доймете до нужного результата.
Примечание: Некоторые параметры, представленные в этом диалоговом окне, недоступны для диаграмм. Сбросить прежние параметры невозможно.
-
Изменение масштаба 3-D chart
Масштаб трехуголной диаграммы можно изменить, указав ее высоту и глубину в процентах от ее основания.
-
Щелкните область диаграммы на диаграмме, которую вы хотите изменить, или выберите область диаграммы в списке Элементы диаграммы в списке Текущий выделение на вкладке Формат.
-
Сочетания клавиш. Вместо этого можно щелкнуть область диаграммы и нажать клавиши CTRL+1. Переступить к шагу 3.
-
В диалоговом оке Формат области диаграммы нажмите кнопку Поворот 3-D.
-
В свойствах поворота 3-D (Поворот 3-D) сделайте следующее:
-
Чтобы изменить глубину диаграммы, укажите процент глубины в поле Глубина (% от базового).
-
Чтобы изменить как глубину, так и высоту диаграммы, в полях Глубина (% от базового) и Высота (% от базового) сужайте флажки Автосметка, а затем укажите процент глубины и высоты.
-
Чтобы использовать представление осей с прямым углом, выберите поле Оси под прямым углом, а затем укажите нужный процент глубины в поле Глубина (% от базовой оси).
-
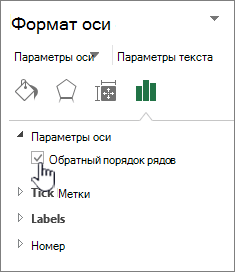
Изменить порядок рядов данных на объемной диаграмме
Вы можете изменить порядок печати рядов данных, чтобы крупные объемные маркеры данных не блокировали их меньше.
-
На диаграмме щелкните ось глубины или выберите Ось глубины в списке Элементы диаграммы в списке Текущий выделение на вкладке Формат.
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
-
В категории Параметры оси в области Параметры осивыберите вариант Ряд в обратном порядке.
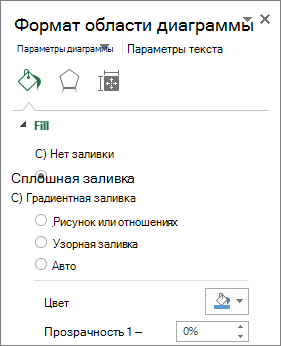
Использование прозрачности в 3-D chart
Хотя прозрачность можно использовать в объемных и двухмерных диаграммах, она особенно полезна на объемных диаграммах, где крупные маркеры данных могут скрыть более мелкие.
-
На объемной диаграмме щелкните ряд данных или точку данных, которые вы хотите сделать прозрачными, или выберите ряд данных из списка Элементы диаграммы в списке Текущий выделение на вкладке Формат.
-
Сочетания клавиш. Вместо этого можно щелкнуть элемент диаграммы, для которого нужно изменить формат, и нажать клавиши CTRL+1. Переступить к шагу 3.
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
-
Щелкните Заливка &линия ,нажмите кнопку Заливка и выберите Сплошная заливка ,Градиентнаязаливка или Рисунок или текстура.
-
Щелкните и выберите цвет, если вы хотите изменить цвета элемента.
-
Щелкните его, а затем проведите по нужному проценту прозрачности.
Создание точечная диаграммы или графика в Office 2010 г.
-
Выберем на нем ячейки, содержащие данные, которые вы хотите использовать для диаграммы.
-
На вкладке Вставить в группе Диаграммы выполните одно из указанных ниже действий.
-
Чтобы создать 3-D column chart, щелкните Столбец ,а затем в столбце 3-Dщелкните 3-D Column.
-
Чтобы создать трехлинометрную цилиндровую диаграмму, щелкните Г столбец,а затем в области Цилиндр выберитеТрехуголовый цилиндр.
-
Чтобы создать трехмерную конусную диаграмму, щелкните Г столбец, а затем в области Coneвыберите трехмерную конус.
-
Чтобы создать трехуголевую пирамиду, щелкните Гограмма, а затем в области Пирамида выберитетрехуголовая пирамида.
-
Чтобы создать трех d line chart, щелкните Линия, а затем в области 3-D Lineщелкните 3-D Line.
-
Чтобы создать трехуголную диаграмму с областью, щелкните Область,а затем в области 3-Dвыберите 3-D Area.
-
Чтобы создать трехмерную поверхностную диаграмму, щелкните Другие диаграммы ,а затем в области Surfaceвыберите трехмерную поверхностную диаграмму или проволо 3-D Surface.
Совет: При наведении указателя мыши на тип или подтип диаграммы появляется всплывающая подсказка с его названием. Дополнительные сведения о поддерживаемых типах диаграмм см. в статье Типы диаграмм.
-
-
На 3-D chart щелкните элемент диаграммы, для которого вы хотите изменить формат 3-D, или выберите его в списке элементов диаграммы сделайте следующее:
-
Щелкните диаграмму.
Отобразит вкладку Средства работы с диаграммами,добавив вкладки Конструктор,Макет и Формат. -
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Область диаграммы, а затем выберите нужный элемент диаграммы.
-
-
Сочетания клавиш. Вместо этого можно щелкнуть элемент диаграммы, для которого нужно изменить формат, и нажать клавиши CTRL+1. Переступить к шагу 3.
-
На вкладке Макет в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
-
Щелкните Формат 3-Dи выберите один или несколько из следующих параметров:
-
В области Безувеликащелкните Сверху иснизу , а затем выберите нужный формат. В полях Ширинаи Высота выберите нужный размер.
-
В области Surfaceщелкните Материальныйи выберите нужный эффект.
Примечание: Доступность этих параметров зависит от выбранного элемента диаграммы. Некоторые параметры, представленные в этом диалоговом окне, недоступны для диаграмм.
-
Совет: Эту процедуру также можно использовать для изменения формата элементов диаграммы.
Вы можете изменить глубину диаграммы в трехмерных диаграммах с осями, глубину зазора в трехмерных перспективных диаграммах и ширину зазора в трехмерных линеек или гограммах.
-
Щелкните трехуголевую диаграмму, которую вы хотите изменить.
-
В меню Формат выберите пункт Выбранный ряд данных.
-
На вкладке Параметры выберите нужные параметры глубины и ширины.
-
Щелкните область диаграммы для 3-D chart, которую вы хотите повернуть, или выберите ее в списке элементов диаграммы сделайте следующее:
-
Щелкните диаграмму.
Отобразит вкладку Средства работы с диаграммами,добавив вкладки Конструктор,Макет и Формат. -
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Область диаграммы, а затем выберите нужный элемент диаграммы.
-
-
Сочетания клавиш. Вместо этого можно щелкнуть область диаграммы и нажать клавиши CTRL+1. Переступить к шагу 3.
-
На вкладке Макет в группе Фон нажмите кнопку Поворот 3-D.
-
В категории Повороты 3-D в области Поворотсделайте следующее:
-
Чтобы изменить угол поворота, щелкните нужный угол поворота в полях Xи Y.
Примечание: Диаграммы можно повернуть вокруг горизонтальной и вертикальной осей, но не вокруг оси глубины. Поэтому в поле Z нельзя указать угол поворота.
-
Чтобы изменить поле представления на диаграмме, щелкните нужный уровень перспективы в поле Перспектива или нажимайте кнопки Узкие поля представления или Расширить, пока не доймете до нужного результата.
Примечание: Некоторые параметры, представленные в этом диалоговом окне, недоступны для диаграмм. Сбросить прежние параметры невозможно.
-
Масштаб трехуголной диаграммы можно изменить, указав ее высоту и глубину в процентах от ее основания.
-
Щелкните область диаграммы для 3-D диаграммы, которую вы хотите изменить, или выберите ее из списка элементов диаграммы сделайте следующее:
-
Щелкните диаграмму.
Отобразит вкладку Средства работы с диаграммами,добавив вкладки Конструктор,Макет и Формат. -
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Область диаграммы, а затем выберите нужный элемент диаграммы.
-
-
Сочетания клавиш. Вместо этого можно щелкнуть область диаграммы и нажать клавиши CTRL+1. Переступить к шагу 3.
-
На вкладке Макет в группе Фон нажмите кнопку Поворот 3-D.
-
В категории Повороты 3-D в области Шкаладиаграммы сделайте одно из следующих:
-
Чтобы изменить глубину диаграммы, укажите процент глубины в поле Глубина (% от базового).
-
Чтобы изменить как глубину, так и высоту диаграммы, в полях Глубина (% от базового) и Высота (% от базового) сужайте флажки Автосметка, а затем укажите процент глубины и высоты.
-
Чтобы использовать представление осей с прямым углом, выберите поле Оси под прямым углом, а затем укажите нужный процент глубины в поле Глубина (% от базовой оси).
-
Вы можете изменить порядок печати рядов данных, чтобы крупные объемные маркеры данных не блокировали их меньше.

-
На диаграмме щелкните ось глубины или выберите ее из списка элементов диаграммы, вы можете сделать следующее:
-
Щелкните диаграмму.
Отобразит вкладку Средства работы с диаграммами,добавив вкладки Конструктор,Макет и Формат. -
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Область диаграммы, а затем выберите нужный элемент диаграммы.
-
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
-
В категории Параметры оси в области Параметры осивыберите вариант Ряд в обратном порядке.
Хотя прозрачность можно использовать в объемных и двухмерных диаграммах, она особенно полезна на объемных диаграммах, где крупные маркеры данных могут скрыть более мелкие.
-
На объемной диаграмме щелкните ряд данных или точку данных, которые вы хотите сделать прозрачными, или выберите его из списка элементов диаграммы, вы можете сделать следующее:
-
Щелкните диаграмму.
Отобразит вкладку Средства работы с диаграммами,добавив вкладки Конструктор,Макет и Формат. -
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Область диаграммы, а затем выберите нужный элемент диаграммы.
-
-
Сочетания клавиш. Вместо этого можно щелкнуть элемент диаграммы, для которого нужно изменить формат, и нажать клавиши CTRL+1. Переступить к шагу 3.
-
На вкладке Макет в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
-
Нажмите кнопкуЗаливка и выберите сплошная заливка,Градиентнаязаливка или Рисунок или текстура.
-
Щелкните его на панели прозрачность, а затем сдвиньте его до нужного процента прозрачности.
|
0 / 0 / 0 Регистрация: 28.04.2021 Сообщений: 1 |
|
|
1 |
|
Построить Конус с поверхностной диаграммой28.04.2021, 15:10. Показов 4460. Ответов 2
Здравствуйте ! Нужно уравнение для построение конуса в excel . Единственное что у меня вышло это пирамида с прямыми углами (картинку прикрепил) Миниатюры
0 |
|
1062 / 506 / 137 Регистрация: 27.02.2013 Сообщений: 1,451 |
|
|
29.04.2021, 02:20 |
2 |
|
РешениеBlackNet, уравнение конуса в excel Код z=КОРЕНЬ(x^2/a^2+y^2/b^2)*c^2)
1 |
|
1062 / 506 / 137 Регистрация: 27.02.2013 Сообщений: 1,451 |
|
|
29.04.2021, 03:32 |
3 |
|
А у меня конус получился Миниатюры
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
29.04.2021, 03:32 |
|
Помогаю со студенческими работами здесь
Построить вращающийся усеченный конус Построить стереометрический рисунок: срезанный конус Как построить в matlab усеченный конус
Построить конус, заданный уравнением, в matlab. Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 3 |
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
3. .Уравнение плоскости, проходящей через три точки
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица (рис. 1).
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
| | | следующая лекция ==> |
| | | Решите задачи с использованием диаграммы Эйлера-Венна. |
Дата добавления: 2017-02-25 ; просмотров: 2062 | Нарушение авторских прав
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
by Ирина Кяршис
ГЛАВА 1. Возможности табличного процессора Microsoft Excel
1.1.Ввод данных в Excel
Электронная таблица – это программа, позволяющая автоматизировать табличные расчеты. Документ Microsoft Ехсел является рабочей книгой, состоящей из листов. Таблица состоит из 65536 строк и 256 столбцов. Строки нумеруются числами, столбцы – буквами латинского алфавита (А, В …, Z, АА, АВ …). На пересечении строки и столбца расположена ячейка, которая имеет адрес, состоящий из имени столбца и номера строки (А4). Одна из ячеек всегда является активной.
Прямоугольная группа смежных ячеек называется диапазоном ячеек. Примеры диапазонов – А2: С4, В2: К40.
Ячейки могут содержать данные трех типов:
1) Текстовые данные – это строка текста произвольной длины.
2) Числовые данные – это отдельное число. Может быть целым, дробным (зап.). Если ширина ячейки мала, то число записывается в экспоненциальной форме, например 125 000 000 → 1,25Е + 8 или вместо числа ставятся символы ###. При этом число сохраняется.
3) Формула – это арифметическое выражение. Он представляет собой последовательность чисел, ссылок на ячейки и функций, объединенных знаками арифметических операций: +, -, /, *. Excel предлагает несколько сотен встроенных функций, которые разделены на категории.
Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.
Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.
Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).
1.2.Типы диаграмм
В зависимости от типа диаграммы данные отображаются на ней разным способом.
Можно отметить несколько стандартных типов:
1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.
2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.
3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.
4. С областями . Диаграмма с областями похожа на график.
5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.
Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.
6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)
7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.
8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.
Подробнее о типах диаграмм здесь
1.3 Основы построения диаграмм в Excel
Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.
Совокупность этих элементов определяет макет диаграммы.
Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).
Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.
Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.
6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.
Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).
Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.
ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2.1 Уравнения поверхностей второго порядка и их графики
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.
Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=1, где a и b – действительные полуоси, с – мнимая полуось.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=-1,где с – действительная полуось, a и b – мнимые полуоси.
|
Excel 2013, Горизонтальная коническая диаграмма |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |




























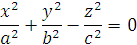







 Сообщение было отмечено BlackNet как решение
Сообщение было отмечено BlackNet как решение
