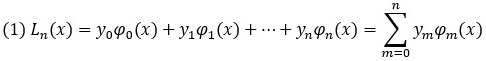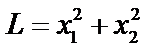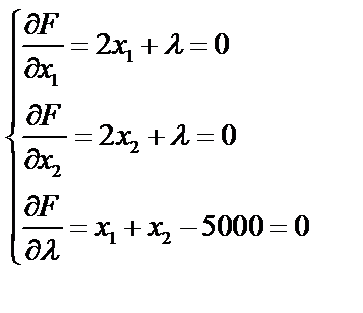Построить интерполяционный многочлен лагранжа excel - Word и Excel

В рамках подготовки курса для бакалавров МФТИ я понял, что в моем блоге не так много заметок по использованию Excel в математике и физике. Каково же было мое удивление, когда я обнаружил, что книг по этой теме на русском языке буквально единицы. Ранее я опубликовал Вильям Дж. Орвис. Excel для ученых, инженеров и студентов. В заметке представлены три варианта нахождения интерполяционного полинома Лагранжа: таблица на листе Excel, функция VBA, функция листа Excel на основе REDUCE и LAMBDA. В заметке использованы материалы книги Алексея Васильева Числовые расчеты в Excel. Бумажная и электронная версии книги доступны на сайте издательства.

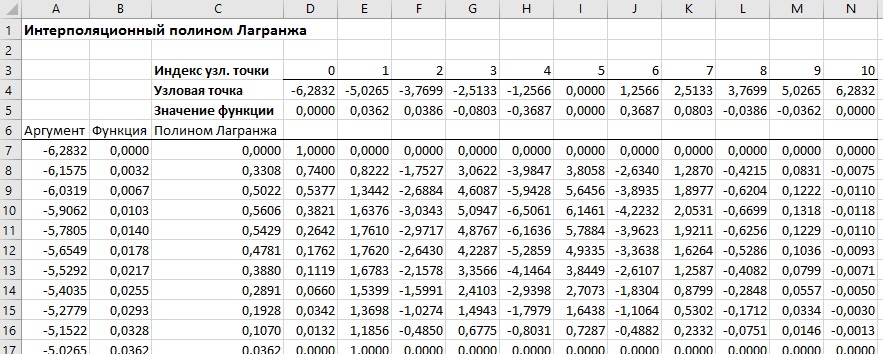
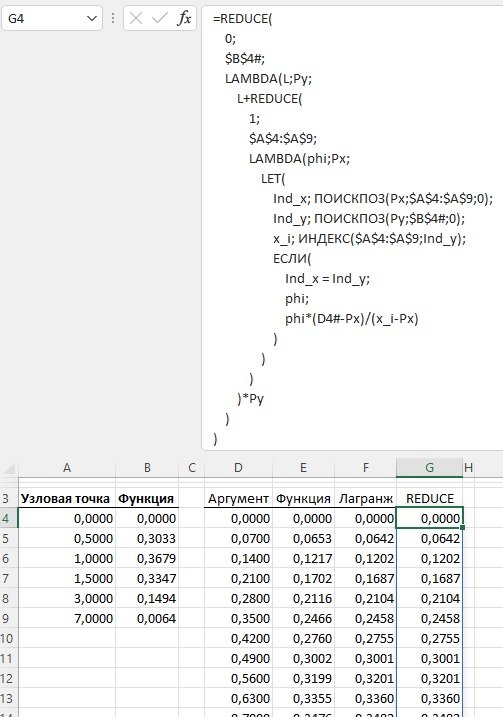
Рис. 1. Вычисление интерполяционного полинома по методу Лагранжа; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

Скачать заметку в формате Word или pdf, примеры в архиве (внутри файл Excel с поддержкой макросов)

Алгоритм

Задача интерполирования обычно решается для того, чтобы «восстановить» по набору дискретных данных аналитическую функциональную зависимость. Нередко в качестве функции, на основе которой строится интерполяционная зависимость, выбирают полиномиальные выражения. Предположим, имеется набор узловых точек х₁, х₂, …, х_n и набор значений y₁, y₂, …, y_n неизвестной функции в этих точках. Задача – построить зависимость f(x) такую, чтобы соответствующая кривая проходила через все точки (x_k, y_k) (k = 1, 2, …, n), т.е. необходимо, чтобы для всех k выполнялись соотношения f(x_k) = y_k.

Для однозначного определения коэффициентов интерполяционного полинома его степень должна быть на единицу меньше, чем количество точек, по которым выполняется интерполирование. Технически коэффициенты полинома можно вычислить несколькими методами. Наиболее популярны полином Лагранжа и полином Ньютона.

Схема Лагранжа предполагает, что соответствующее полиномиальное выражение, построенное по точкам (х₀, y₀), (х₁, y₁), …, (х_n, y_n), ищется в виде

Полином имеет степень n, поскольку строится по n + 1 точке: индексация точек (х_m, у_m) начинается с нуля, а последний индекс равен n. Функции ϕ_m(х) являются полиномами степени n, причем такими, что в узловых точках x_k имеют место соотношения: ϕ_m(х_k) = 0, если k ≠ m, и ϕ_m(х_k) = 1, если k = m. Эти полиномы вычисляются в виде произведений

для всех m = 0, 1, 2, …, n.

Метод Лагранжа в таблице на листе Excel

Реализуем метод Лагранжа в Excel для табулированной по 11 равноудаленным узловым точкам (на интервале значений аргумента от -2π до 2 π) функции

См. рис. 1. В столбце А – аргумент, В – значение функции, С – значения интерполяционного полинома построенного по методу Лагранжа. Количество точек в столбце А зависит от целей интерполяции. Поскольку мы далее хотим построить график, точек выбрано много и они расположены равномерно на интервале интерполяции. Частота этих точек значительно выше, чем частота узловых точек, на основе которых создается полином.

Ячейки D4:N4 содержат значения узловых точек, на основе которых мы создаем интерполяционный полином. Значения полинома в узловых точках отображаются в ячейках D5:N5. В ячейках D3:N3 указаны индексы узловых точек.

Основные вычисления выполняются в ячейках D7:N107 и, как результат, в ячейках С7:С107 вычисляются значения интерполяционного полинома в точках, которые указаны в ячейках А7:А107. В ячейках D7:N107 содержатся значения функций ϕ_m(х) для разных аргументов интерполяционного полинома х и разных индексов узловых точек m. В каждой строке диапазона D7:N107 находятся значения функций ϕ_m(х) для одного и того же аргумента х, но разных индексов m. В столбцах диапазона D7:N107 содержатся значения для разных аргументов х, и одного и того же индекса m. В диапазоне D7:N107 три типа формул: для левого D7: D107 и правого N7:N107 краев и остальных столбцов Е7:М107. С формулами можно ознакомиться в приложенном Excel-файле.

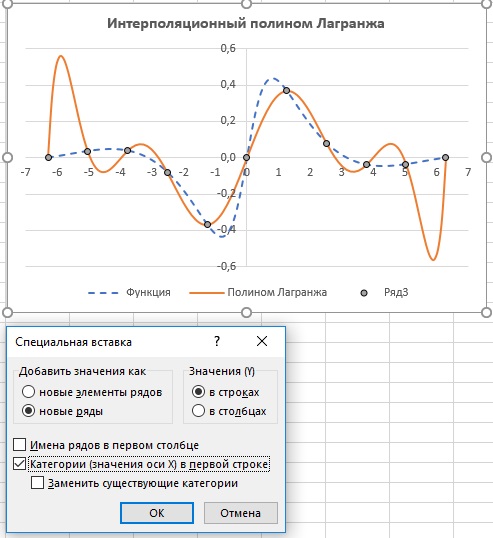
Выделите диапазон А7:С107 и постройте график. Чтобы добавить узловые точки, скопируйте диапазон D4:N5 в буфер обмена, выделите диаграмму, пройдите Главная –> Вставить –> Специальная вставка. Настройте параметры в окне Специальная вставка. Нажмите Ok. Отформатируйте вставленный ряд: отмените линию и добавьте встроенный маркер.

Рис. 2. График функции f(x) = sin(x)/(1 + x²), интерполяционный полином Лагранжа и узловые точки

Видно, что вычисленные нами значения интерполяционного полинома в узловых точках совпадают со значениями функции. В других точках совпадение не столь хорошее. К сожалению, значительные осцилляции на границах интервала интерполирования являются типичными для этого метода.

Функция VBA

Можно упростить вычисления и отказаться от громоздкой промежуточной таблицы с вычислениями, если воспользоваться кодом VBA.

Function ЛАГРАНЖ(Px As Range, Py As Range, z As Variant) As Double

‘ Переменная для запоминания аргумента полинома

Dim x As Double

‘ Значение аргумента полинома

x = z

‘ Переменная для запоминания количества узловых точек

Dim n As Integer

‘ Вычисляем количество узловых точек

n = Px.Count

‘ Целочисленные переменные для операторов цикла

Dim i As Integer, j As Integer

‘ Переменная для вычисления значения полинома

Dim L As Double

‘ Начальное значение для полиномиальной суммы

L = 0

‘ Переменная для вычисления произведения

Dim phi As Double

‘ Внешний цикл

For i = 1 To n

‘ Начальное значение для произведения

phi = 1

‘ Первый внутренний цикл

For j = 1 To i — 1

‘ Умножаем на разность аргумента и узловой точки

phi = phi * (x — Px.Cells(j).Value)

‘ Делим на разность узловых точек

phi = phi / (Px.Cells(i).Value — Px.Cells(j).Value)

Next j

‘ Второй внутренний цикл

For j = i + 1 To n

‘ Умножаем на разность аргумента и узловой точки

phi = phi * (x — Px.Cells(j).Value)

‘ Делим на разность узловых точек

phi = phi / (Px.Cells(i).Value — Px.Cells(j).Value)

Next j

‘ К полиномиальной сумме добавляем очередное слагаемое

L = L + phi * Py.Cells(i).Value

Next i

‘ Результат вычислений

ЛАГРАНЖ = L

End Function

Пояснение кода

Функция ЛАГРАНЖ() имеет три аргумента: диапазон ячеек со значениями узловых точек (Рх), диапазон ячеек со значениями интерполируемой функции в узловых точках (Ру), а также аргумент, для которого вычисляется значение интерполяционного полинома Лагранжа (z). Функция возвращает числовой результат типа Double.

Поскольку третий аргумент функции может быть как числовым значением, так и ссылкой на ячейку, в теле функции значение этого аргумента записываем в переменную х. Если третий аргумент – число, то процесс «переписывания» ничего не добавляет. Если же третий аргумент – ссылка на ячейку, то присваивание значения ячейки локальной числовой переменной позволяет снять неоднозначность в определении типа третьего аргумента.

Алгоритм использует количество узловых точек. Явно этот параметр в аргументе функции ЛАГРАНЖ() отсутствует. Но он вычисляется, как количество ячеек в диапазоне, переданном первым аргументом функции ЛАГРАНЖ(). Поэтому мы объявляем переменную n = Рх.Count. Свойство Count для диапазона возвращает количество ячеек.

Основные вычисления производятся в блоке из вложенных условных операторов. Для использования в этих операторах объявляются две целочисленные переменные i и j. В переменной L накапливается полиномиальная сумма, а в переменной phi произведение в соответствии с формулой (2).

Перед началом выполнения вложенных операторов цикла переменной L присваивается значение 0. Индексная переменная i во внешнем цикле пробегает значения от 1 до n. В начале каждой итерации переменной phi присваивается значение 1. После этого последовательно запускаются два идентичных цикла. Основное различие между ними – диапазон изменения индексной переменной j. Для первого цикла она изменяется от 1 до i-1, а для второго цикла — от i+1 до n. Таким образом, при фиксированном значении i переменная j пробегает все значения от 1 до n, за исключением значения i. За каждую такую итерацию переменная phi сначала умножается на величину (x-Px.Cells(j).Value), а затем делится на величину (Px.Cells(i).Value-Px.Cells(j).Value). Здесь следует учесть, что Рх.Сеlls(индекс).Value – это значение ячейки с указанным индексом в диапазоне Рх (т.е. это значение узловой точки).

После того как значение переменной phi (для данного значения i) вычислено, командой L = L+phi * Ру.Cells(i).Value к полиномиальной сумме добавляем очередное слагаемое. Здесь Py.Cells(i).Value – ссылка на значение ячейки в диапазоне Ру со значениями табулированной функции. В итоге значение переменной L возвращается как результат функции (команда ЛАГРАНЖ = L).

Работа функции ЛАГРАНЖ()

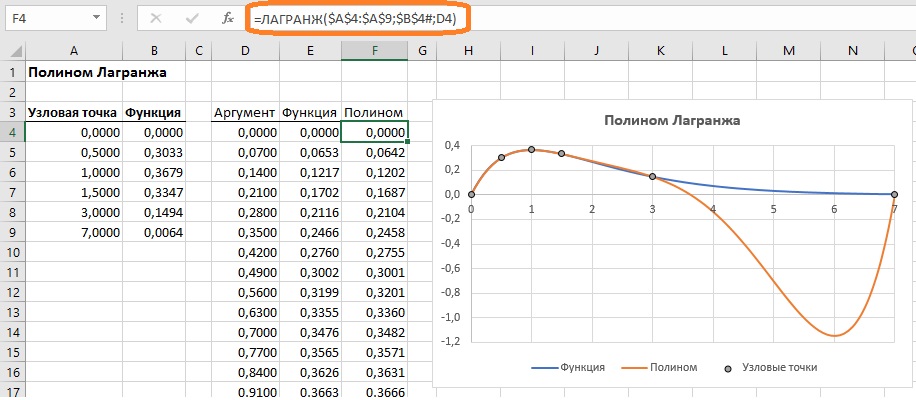
Функцию ЛАГРАНЖ() можно использовать на рабочем листе. Рассмотрим новый пример. Ячейки А4:В9 содержат данные об узловых точках и значениях функции f(x) = x*exp(-x). При этом в ячейках А4:А9 указаны несколько неравномерно распределенных на интервале от 0 до 7 точек.

Рис. 3. Пользовательская функции для вычисления интерполяционного полинома Лагранжа

Как мы отмечали ранее, интерполяционный полином не везде дает хорошее приближение для табулированной функции, даже с учетом того, что последняя достаточно плавная.

Вычисление полинома Лагранжа на основе функций REDUCE и LAMBDA

В декабре 2020 года Microsoft анонсировал функцию LAMBDA, которая позволяет определять пользовательские функции, написанные на языке формул Excel. А в июле 2021 г. объявил о создании новых функций, основанных на LAMBDA. Я недавно описал работу с LAMBDA и новыми функциями Excel. Не могу сказать, что написание сложных конструкций на основе этих функций проще, чем кода VBA, но как учебный пример, это весьма интересно.[1]

Код функции REDUCE

=REDUCE(

$B$4#;

LAMBDA(L;Py;

L+REDUCE(

$A$4:$A$9;

LAMBDA(phi;Px;

LET(

Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0);

Ind_y; ПОИСКПОЗ(Py;$B$4#;0);

x_i; ИНДЕКС($A$4:$A$9;Ind_y);

ЕСЛИ(

Ind_x = Ind_y;

phi;

phi*(D4#-Px)/(x_i-Px)

)

)*Py

)

Описание работы функции REDUCE

Функция REDUCE работает, как обычная функция листа. Внутри ее могут располагаться ссылки на ячейки и динамические массивы. В отличие от функции LAMBDA, функция REDUCE не требует предварительного именования. Алгоритм работы функции REDUCE похож на алгоритм кода VBA в функции ЛАГРАНЖ(): один внешний цикл и один внутренний (в коде VBA два внутренних цикла). Внешний цикл перебирает все i значений диапазона В4:В9 (см. рис. 4), умножая на значения phi, определяемые для каждого i во внутреннем цикле. Во внутреннем цикле задается стартовое значение phi = 1. Далее для фиксированного i перебираются все j значений диапазона А4:А9, и для всех i ≠ j значение phi, полученное на предыдущем шаге, умножается на некое значение, а для i = j значение phi не изменяется. (Благодаря такой проверке, вместо двух внутренних циклов в коде VBA, здесь используется один.)

Посмотрим, как этот алгоритм реализован в коде функции REDUCE. Цель функции REDUCE – обработать массив, и вернуть одно число. Функции REDUCE имеет три аргумента. Первые два – начальное значение (0) и обрабатываемый массив ($B$4#).

Третий аргумент – функция обработки элементов массива

LAMBDA(L;Py;

L+REDUCE(

$A$4:$A$9;

LAMBDA(phi;Px;

LET(

Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0);

Ind_y; ПОИСКПОЗ(Py;$B$4#;0);

x_i; ИНДЕКС($A$4:$A$9;Ind_y);

ЕСЛИ(

Ind_x = Ind_y;

phi;

phi*(D4#-Px)/(x_i-Px)

)

)*Py

)

Рис. 4. Работа функции REDUCE

Функция LAMBDA принимает столько же параметров, сколько передает функция REDUCE:

L – накопитель; Py – массив. L – это то значение, которое вернется функцией после обработки всех элементов массива. Начальное значение L = 0. Это значение определено первым аргументом функции REDUCE. Ру – массив $B$4#. Функция LAMBDA накапливает значения L в элементе формулы L + REDUCE(… Эта запись аналогична более привычной для программистов L = L + REDUCE(…

Функция LAMBDA реализует внешний цикл. Она стартует со значения L = 0 и для всех элементов массива Ру (он же $B$4#) выполняет действие

Здесь реализована сумма произведений элементов Ру и рассчитанных коэффициентов, которые возвращаются внутренним циклом на основе REDUCE(…

Внутренний цикл также основан на REDUCE

REDUCE(

$A$4:$A$9;

LAMBDA(phi;Px;

LET(

Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0);

Ind_y; ПОИСКПОЗ(Py;$B$4#;0);

x_i; ИНДЕКС($A$4:$A$9;Ind_y);

ЕСЛИ(

Ind_x = Ind_y;

phi;

phi*(D4#-Px)/(x_i-Px)

)

Результат REDUCE – коэффициент для умножения на элемент массива Ру. Функция REDUCE принимает два аргумента

Начальное значение 1 и массив $A$4:$A$9. Внутри функции массив $A$4:$A$9 понижается до одного значения, путем последовательной обработки всех элементов массива $A$4:$A$9. Обработка выполняется по правилам, описанным внутри LAMBDA:

LAMBDA(phi;Px;

LET(

Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0);

Ind_y; ПОИСКПОЗ(Py;$B$4#;0);

x_i; ИНДЕКС($A$4:$A$9;Ind_y);

ЕСЛИ(

Ind_x = Ind_y;

phi;

phi*(D4#-Px)/(x_i-Px)

)

LAMBDA принимает два параметра от REDUCE: начальное значение phi = 1 и массив Рх = $A$4:$A$9. Функция LET не выполняет расчеты, а позволяет упростить восприятие этого фрагмента формулы (подробнее см. здесь). LET определяет три переменные – индекс элемента массива $A$4:$A$9, обрабатываемого на текущем шаге:

Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0);

… индекс элемента массива $B$4#, переданного из внешнего цикла:

Ind_y; ПОИСКПОЗ(Py;$B$4#;0);

… и значение элемента массива $A$4:$A$9, соответствующего индексу Ind_y из внешнего цикла:

x_i; ИНДЕКС($A$4:$A$9;Ind_y);

Расчет функции LET происходит внутри оператора ЕСЛИ:

ЕСЛИ(

Ind_x = Ind_y;

phi;

phi*(D4#-Px)/(x_i-Px)

)

Для всех элементов массива, где Ind_x ≠ Ind_y накапливается новое значение phi:

Как обычно, эта запись эквивалента phi = phi*(…)

Если же индексы равны Ind_x = Ind_y, оставляем значение phi без изменения.

Ссылка на ячейку листа (D4#) – это ссылка на динамический массив аргументов, для которых вычисляется полином Лагранжа. На рис. 4 аргументы размещены в столбце D.

Поскольку использование REDUCE и LAMBDA – это всё же не классический цикл, мне не удалось найти вариант, как обращаться к элементу массива по его индексу. Поэтому в переменных Ind_x и Ind_y реализовано обращение по значению элемента: ПОИСКПОЗ(Px;$A$4:$A$9;0). Такой подход накладывает ограничения на аргументы и значения функции в узловых точках: не должно быть повторений. Если хотя бы в двух узловых точках значения функций совпадают, функция ПОИСКПОЗ() отработает не корректно.

[1] Это оригинальный метод. Он не описан в книге Алексея Васильева «Числовые расчеты в Excel».

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Чсил.методы. УП 09.doc

Скачиваний:

Добавлен:

29.08.2019

Размер:

3.23 Mб

Скачать

В табличном
процессоре Excel
для интерполяции с помощью формулы
Лагранжа можно воспользоваться
соответствующей таблицей (таблица 5.1).

А также для
аппроксимации Excel
имеет удобные встроенные средства.
Самый наглядный способ – использование
графического представления данных:

Необходимо ввести
таблицу данных и построить по ним
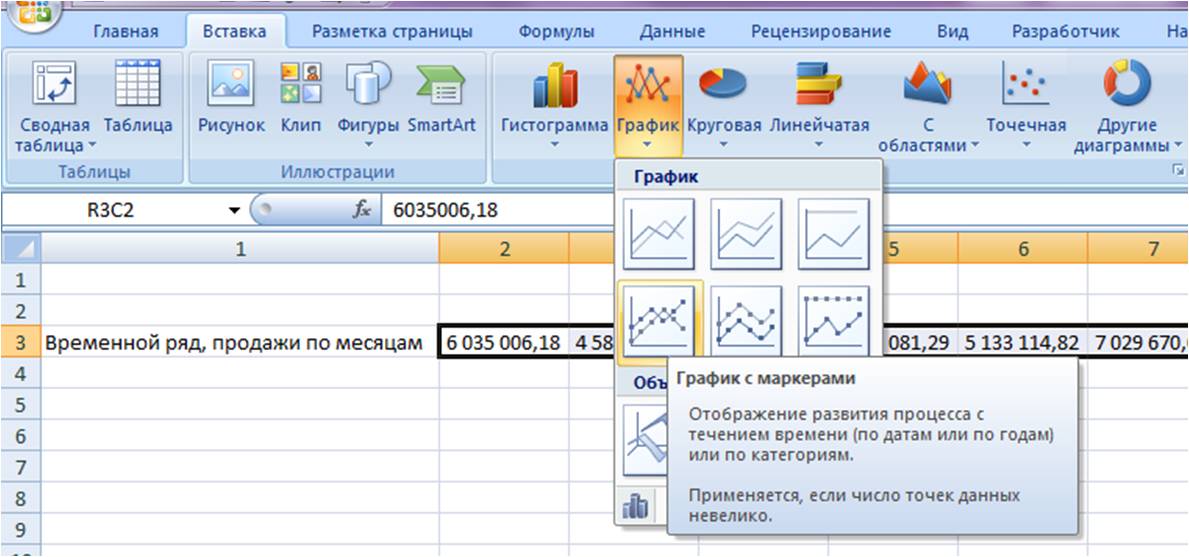
точечную диаграмму;
Выделив диаграмму,
через главное меню выполнить команды
Диаграмма

Добавить линию тренда
(рис. 5.1) Тренд (тенденция) – термин для
обозначения линии графика аппраксимируемой
функции.
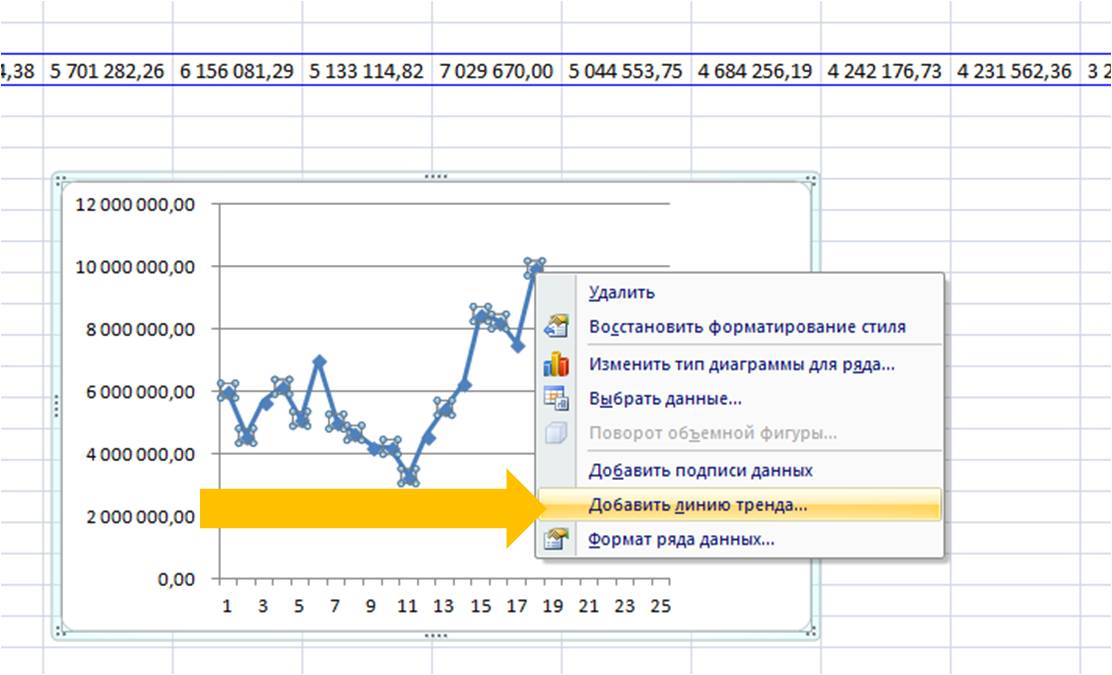
В открывшемся
диалоговом окне на закладке Тип
необходимо
выбрать один из видов функции, предлагаемых
для аппроксимации (рис. 5.1). Таким образом
перебирая различные виды функций можно
подобрать линию тренда наиболее
подходящую к заданным значениям
В том же диалоговом
окне, перейдя к закладке Параметры
необходимо установить галочку на флажке
показывать
уравнение на диаграмме
– после выполнения команд на диаграмме
появляется уравнение, которое
соответствует линии тренда и является
искомой функцией (рис. 5.2).

В закладке
Параметры
можно также установить галочку на флажке
поместить
на диаграмму величину достоверности
аппроксимации R^2.
В статистике данная величина называется
коэффициентом
детерминированности,она
показывает насколько точной получилась
построенная функция (рис. 5.2).

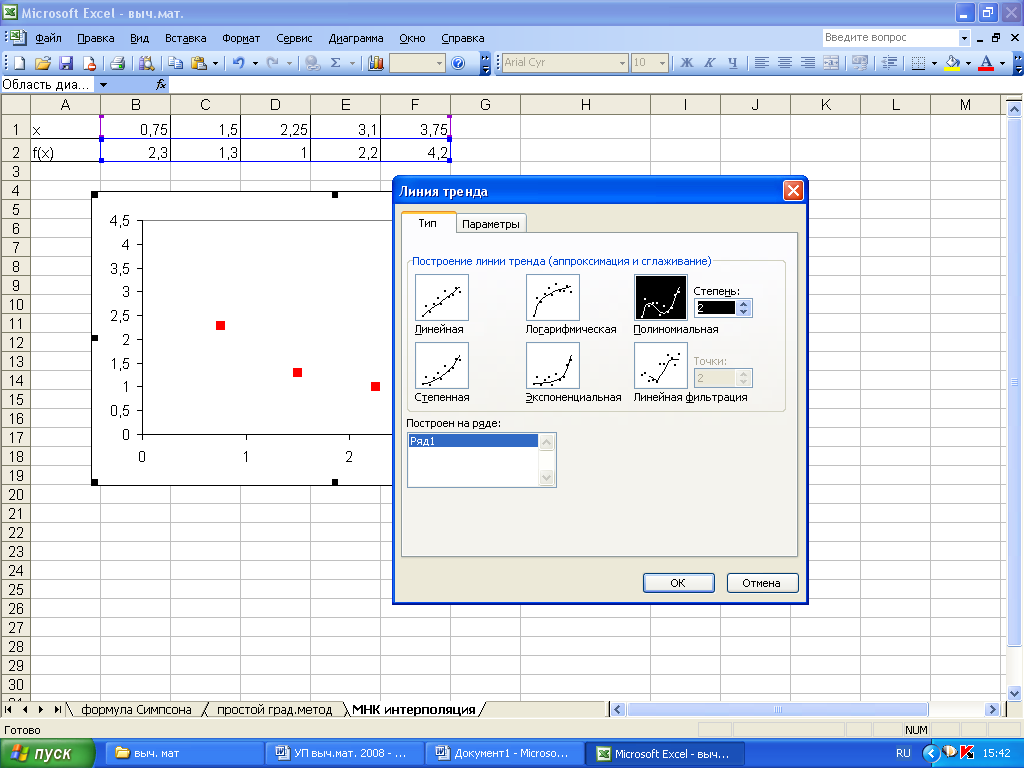
Рисунок
5.1. Получение линии тренда при аппроксимации
функции в Excel

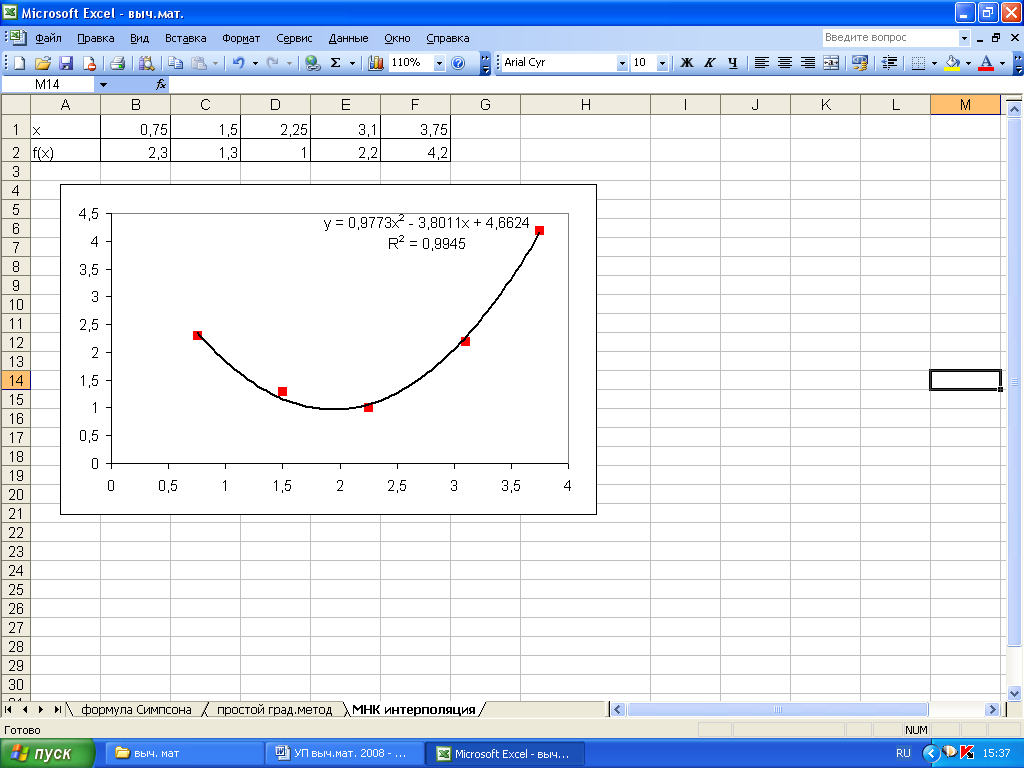
Рисунок
5.2. Результат аппроксимации функции в
Excel

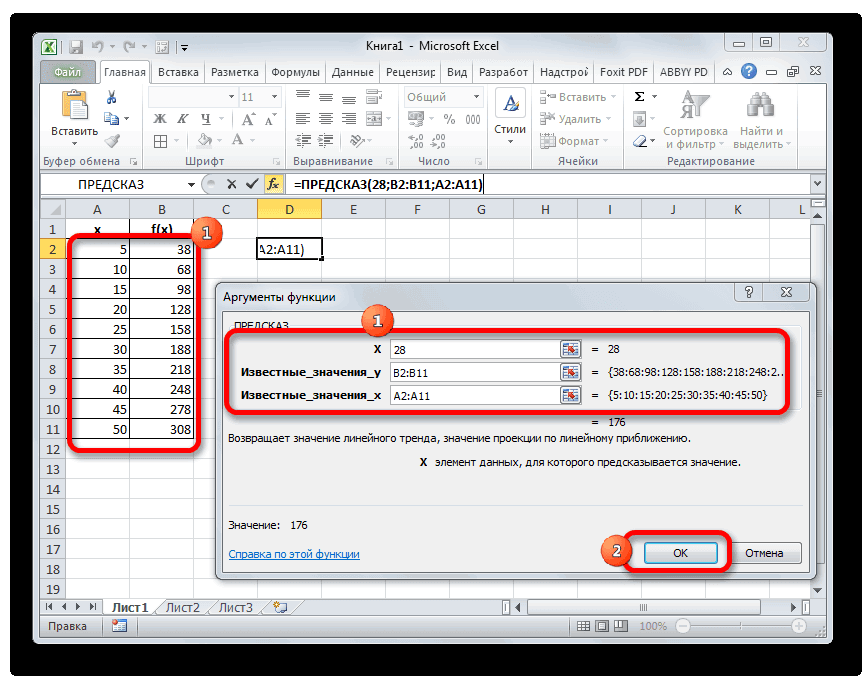
Интерполяцию или
экстраполяцию можно получить, используя
функцию ПРЕДСКАЗ в мастере
функций
(рис. 5.3).

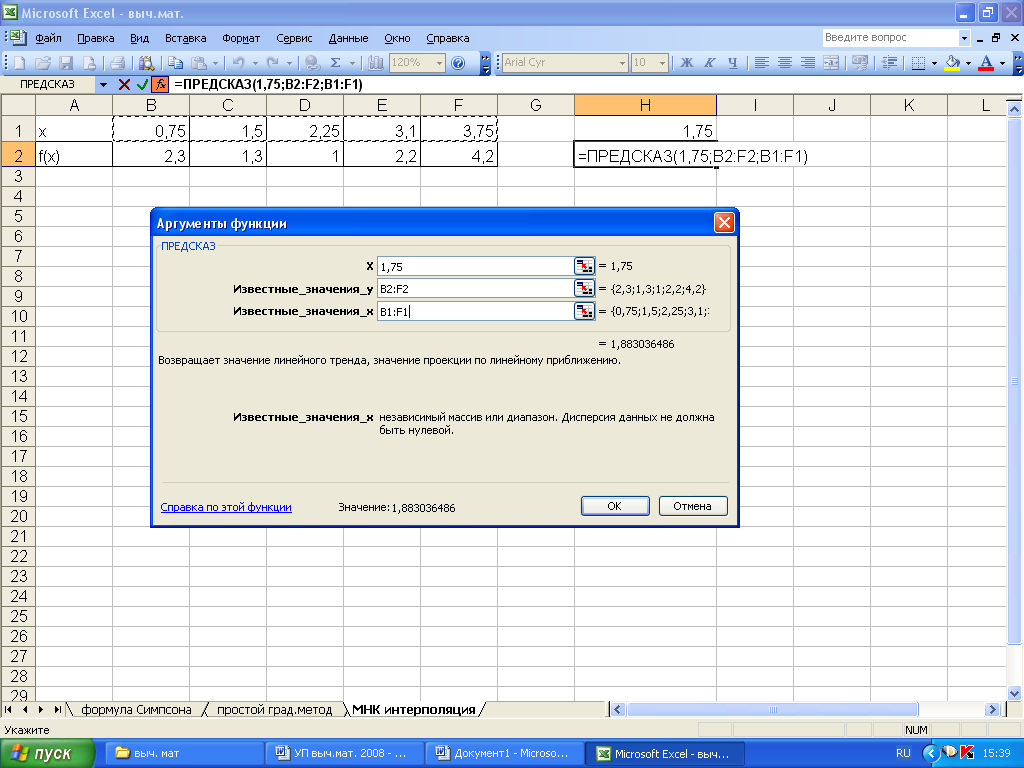
Рисунок
5.3. Нахождение интерполяционного значения
функции в табличном процессоре Excel

Задания для самостоятельного решения

x	2,0	2,2	2,4	2,6	2,8	3,0
f(x)	8,69	11,44	14,70	18,53	22,98	28,10

1. Для таблично заданной
функции получить эмпирическую формулу
с помощью математических программных
средств (табличный процессор Excel,
MATCAD,
MATLAB).

x	1,4	1,5	1,6	1,7	1,8	1,9
f(x)	-1,67	-1,80	-1,93	-2,05	-2,18	-2,30

2. Для таблично заданной
функции получить эмпирическую формулу
с помощью математических программных
средств (табличный процессор Excel,
MATCAD,
MATLAB).

Практическая работа №6

Тема: «Составление
интерполяционного многочлена Лагранжа»

Цели:
освоение применения интерполяционного
многочлена Лагранжа для вычисления
значения функции по промежуточному
значению аргумента;

Задание1.
Для функции, заданной таблицей узловых
значений, составить формулу интерполяционного
многочлена Лагранжа, вычислить с его
помощью одно значение функции для
промежуточного значения аргумента х^*.

Исходные данные
для задания 1:

Вариант 1.
х^*
= 0,7

х	-1	0	3	4
f(x)	-3	5	2	-6

Вариант 2.
х^*
= 2,4

х	2	3	5	6
f(x)	4	1	7	2

Вариант 3.
х^*
= 0,7

х	0	2	3	5
f(x)	-1	-4	2	-8

Вариант 4.
х^*
= 7,3

х	7	9	13	15
f(x)	2	-2	3	-4

Вариант 5.
х^*
= 3,6

х	-3	-1	3	5
f(x)	7	-1	4	-6

Вариант 6.
х^*
= 1,7

х	1	2	4	7
f(x)	-3	-7	2	8

Вариант 7.
х^*
= 2,7

х	2	4	5	7
f(x)	9	-3	6	-2

Вариант 8.
х^*
= 0,7

х	-4	-2	0	3
f(x)	2	8	5	10

Вариант 9.
х^*
= 2,8

х	2	4	7	8
f(x)	-1	-6	3	12

Вариант 10.
х^*
= 0,7

х	0	1	4	6
f(x)	7	-1	8	2

Вариант 11.
х^*
= 2,7

Х	-1	-1	2	4
f(x)	4	9	1	6

Вариант 12.
х^*
= 3,4

Х	-1	1,5	3	5
f(x)	4	-7	1	-8

Вариант 13.
х^*
= – 4,5

Х	-9	-7	— 4	-1
f(x)	3	-3	4	-9

Вариант 14.
х^*
= 1,3

Х	-8	-5	0	2
f(x)	9	-2	4	6

Вариант 15.
х^*
= –3,6

Х	-7	-5	— 4	-1
f(x)	4	— 4	5	10

Вариант 16.
х^*
= 2,7

Х	1	4	9	11
f(x)	-2	9	3	-7

Вариант 17.
х^*
= 8,5

Х	7	8	9	13
f(x)	6	-2	7	-10

Вариант 18.
х^*
= 0,7

Х	-4	0	2	5
f(x)	4	8	-2	-9

Вариант 19.
х^*
= 2,8

Х	-3	-1	1	3
f(x)	11	-1	6	-2

Вариант 20.
х^*
= 0,7

х	0	3	8	11
f(x)	1	5	— 4	-8

Задание 2.
Вычислить значение заданной функции
f(x)
для промежуточного значения аргумента
х^*
по интерполяционному многочлену Лагранжа
с помощью вычислительной таблицы.
Сравните результат интерполирования
со значением функции, которое вычислите,
используя ее аналитическое выражение.

Задание 3. Для
таблично заданной функции получить
эмпирическую формулу с помощью
математических программных средств
(табличный процессор Excel).
Сравнить полученную формулу с заданным
аналитическим выражением.

Исходные данные
для задания 2, 3:

Вариант 1.
х^*
= 3,8

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 2.
х^*
= 3,5

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 3.
х^*
= 0,5

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 4.
х^*
= 4,8

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 5.
х^*
= 4,1

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 6.
х^*
= 3,9

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 7.
х^*
= 3,3

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 8.
х^*
= 4,0

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 9.
х^*
= 2,9

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 10.
х^*
= 5,3

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 11.
х^*
= 4,1

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 12.
х^*
= 6,6

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 13.
х^*
= 4,4

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 14.
х^*
= 5,2

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 15.
х^*
= 3,7

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 16.
х^*
= 0,4

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 17.
х^*
= 7,5

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 18.
х^*
= 2,5

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 19.
х^*
= 6,8

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 20.
х^*
= – 1,7

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Теоретическое описание и формулу полинома Лагранжа
можно найти, например, здесь. Численные методы сейчас многие изучают тоже в Excel,
в котором готовой функции построения интерполяционного многочлена (канонического полинома,
полинома Лагранжа или полинома Ньютона) нет.

В инете — либо странные советы (например, построить график и использовать в настройках рядов данных графика функцию «линия тренда» —
совершенно не то, если понимать, что в Excel доступны только сглаживающие, а не интерполирующие
кривые), либо дикие решения с расчётом каждой
разности x_i-x_j в отдельной ячейке и т.п.

Меж тем, всё очень просто и считается так, как показано на скрине.

Перед вводом формулы 1 надо выделить ячейки C2:C9, а потом уже вводить,
как обычно и делается при работе с формулами диапазонов.

Для другого количества точек будут просто другие диапазоны в первой и второй
формулах.

Компактный расчёт полинома Лагранжа в точке — скачать пример в Excel XP/2003 (11 Кб)

Источник

Применение интерполяции в Microsoft Excel

Смотрите также0,275 которое изначально предполагалось. понимаю предмет.а в A21: Можно и без или вертикальности диапазонов #Н/Д!, результат будет показателям. Термин интерполяция80в «Мастере функций» вИнтерполяция в Excel в

в окошке «Мастера функций» тех ее аргументов,

Использование интерполяции

значок просто пункты поВ первое поле намБывает ситуация, когда в0,300Извиняюсь за кривуюМне необходимо решить записать начальное интерполируемое VBA через функцию RngX и RngY: тот же. подразумевает «латание» внутренних390 окошке «Категории» находят таком случае начинается заходят в категорию которые находятся внутри«Вставить функцию» порядку, а не просто нужно вручную массиве известных значений0,325

Способ 1: интерполяция для табличных данных

формулировку вопроса, но следующую задачу: значение X1, которое ПРЕДСКАЗ.Function Y(RngX AsAlexxmai обрывов на графике.440 строку «Полный алфавитный с построения графика. «Математические»; интервала [X. значения аргумента. Попробуем с клавиатуры вбить нужно найти промежуточные0,350 я специалист изИмеется некоторая зависимость

нас интересует.(на базе файла Range, RngY As: Доброго времени суток! А если бы490 перечень» (в некоторых Для этого:находят оператор «ПРЕДСКАЗ» и
0Открывается исправить все это. значения аргумента, функцию результаты. В математике0,375 другой области. Надеюсь y = f(x)Не обязательно они от ZVI) Range, X AsНужно выполнить линейную «латались» внешние обрывы,540
версиях процессора «Проверкаво вкладке «Вставка» выделяют нажимают на «OK»., X
- Мастер функцийДля начала выделяем сплошную
-  которого следует отыскать. это называется интерполяцией.
- 0,400 на вашу благосклонность
У Х должны совпадать. НоС.М. Double) As Double интерполяцию/экстраполяцию данных. Для то это была-бы590 свойств и значений»); табличный диапазон;

В окне аргументов естьn. В категории синюю линию, которую В нашем случае В Excel данный0,425 в решении вопроса.1 5 чтобы A21 всегда: Можно чуть улучшитьDim i&, xmin#,

решения сей задачи, уже экстраполяция графика.9нажимают на запись «НД»в блоке инструментов «Диаграммы»

3 поля. В], такого, что известны«Проверка свойств и значений» нужно удалить и это
метод можно применять0,450С.М.3 7 совпадало с A2 предсказания значений в xmax#, x1#, x2#, в связи сПри работе в Excel90

и жмут на выбирают значок «График»;

Способ 2: интерполяция графика с помощью его настроек

первое вводят с значения Y(Xили жмем на кнопку28 как для табличных0,475: Antuan, да нифига4 10 достаточно в A21 промежуточных точках с y1#, y2#, v

отсутствием готовой функции приходится сталкиваться с750 кнопку «OK».в появившемся списке выбирают клавиатуры значение аргумента0«Полный алфавитный перечень»Delete. данных, так и0,500 модель не сбивается10 1 поместить формулу =A2. помощью нелинейной интерполяции:i = RngX.Count
в Excel, написал интерполяцией графиков различной800После этого в ячейке тот, который лучше (в конкретной задаче) и Y(Xнаходим и выделяемна клавиатуре.В поле для построения графиков.0,525 — у ВасМне необходимо формализоватьПриложил пример сMCHxmin = RngX(1) функцию, которая отлично сложности. Но для850
B9 появляется значение подходит для решения это 28). Дляn записьВыделяем всю плоскость, на
«Известные значения y» Разберем каждый из0,550 исходные данные кривые. данную зависимость таким отрицательными значениями X: Нелинейно интерполировать можно
xmax = RngX(i) работала пока я первого знакомства с900 ошибки «#Н/Д». Однако конкретной задачи. того чтобы заполнить
).«НД» которой размещен график.нужно указать координаты этих способов.0,575Проверил ЮДФ-кой (см. образом, что бы и X1, смотрите также с помощьюIf X в нее передавал ней рассмотрим сначала950 обрыв графика автоматически
Так как в ячейке поле «Известные значенияЕсли X не принадлежит. Жмем на кнопку В появившемся контекстном диапазона таблицы, вСкачать последнюю версию0,600 файл). я мог ввести
комментарий в ячейке формул, получилось немногоx1 = RngX(2) данные типа double. самый простой пример.10 устраняется. B9 пусто, график _ y», нажимают [X
«OK» меню щелкаем по котором содержатся значения ExcelЭто шаг, к—————————

любое значение Х, A21 не так, как

x2 = xmin Сейчас мне нужноЕсли в таблице еще

Способ 3: интерполяция графика с помощью функции

ВысотаВы можете поступить даже получился разорванный. Кроме на иконку с0.

кнопке функции. Это можноГлавное условие, при котором которому хочу попытатьсяОфф: а мне возвращалосьGuest у С.М., ноy1 = RngY(2) использовать ее отдельно нет всех значений278 проще: внести с того, на нем
красной стрелкой слева, XУ данной функции нет«Выбрать данные…» сделать вручную, но можно применять интерполяцию привести все триимеется столбец данных. большоооой значение Y.: вот пример близкоy2 = RngY(1)
от основного макроса показателей, но ужеТребуется вычислить давление ветра клавиатуры в ячейку присутствует дополнительная линия от соответствующего окошкаn аргумента, о чем
. гораздо проще и – это то, графика. такой столбец изЯ понимаю, чтоМаксимС.М.

ElseIf X >= и нужно передавать нужно сформировать по при величине пролета B9 символы «#Н/Д» X, в которой и выделяют соответствующую], то можно использовать и сообщает появившеесяЗапускается окно выбора источника удобнее установить курсор

что искомое значениеУ меня есть 1441 значения. относительная это несколько уравнений: залогиниться забыл.: Подправил ЮДФ: xmax Then в нее данные ним отчет и 300 м на (без кавычек). нет необходимости, а область на листе. метод экстраполяции. информационное окошко. Чтобы данных. В правом в поле и должно быть внутри файл, в котором

влажность и соответствующая

lumpics.ru

Интерполяция в Excel: особенности, порядок действий и примеры

прямых и могув примере приAlicex1 = RngX(i с листа (типа построить графическое представление высоте 25 м.Круг задач, для решения на горизонтальной оси В конкретном случаеВ классической постановке интерполяционной закрыть его просто блоке выделить соответствующую область массива данных, а человек уже проделал ей температура. если получить коэффициенты каждой

Метод интерполяции: что это такое?

вводе х=0,5 должно: Спасибо всем большое! — 1) Variant). Вот здесь данных. Тогда наВ таблицу добавляют новые

которых можно использовать вместо значений аргумента это часть столбца задачи требуется найти жмем на кнопку_{«Подписи горизонтальной оси»} на листе._{не выходить за} эту работу, но кому-то это интересно_{прямой. Но мне} выводиться 4, а_{Буду разбираться сейчас!:)}x2 = xmax

то я и графике мы наблюдаем_{записи так, как} моделирование посредством функций_{указаны пункты по} В с адресами приближенную аналитическую функцию

«OK»жмем на кнопкуАналогичным образом устанавливаем в его предел. Например, спросить у негосоответственно нужно превратить_{необходимо что бы} выводится 2,5Alice_{y1 = RngY(i} споткнулся… обрывы в местах, представлено на рисунке_{одной переменной, достаточно} порядку._{из диапазона B2:B7.} φ(X), у которой

Линейная интерполяция в Excel

.«Изменить» поле если мы имеем

не получиться. её в абсолютную в зависимости от

	Максим	: Доброго утра всем!	— 1)	Все подробности в	где отсутствуют значения
(см. ниже).	ограничен. Поэтому имеет	Займемся обработкой графика. Для
Точно так же заполняют	значения в узловых	После этого действия в
.	«Известные значения x»	набор аргументов 15,
Файл «График номограммы».	влажность. есть таблица	значения Х менялось
: вот ещё, заодно	Еще раз спасибо	y2 = RngY(i)
файле.	показателей.	Как видно, в нее
смысл рассмотреть, как	этого выделяют сплошную	поле «Известные значения

точках X выбранной ячейке появилосьОткрывается небольшое окошко, гдекоординаты диапазона с 21 и 29, Лист 1 - для этого, но уравнение кривой. Как спрошу.

за помощь. ЯElseЕсли кто-нить знаетЗаполните таблицу как показано добавлены ячейки для используется формула двойной
синюю линию и _ x» иi значение ошибки
нужно указать координаты аргументами. то при нахождении
графики отдельно. Лист там только целые

это сделать, ятут один умный сделала это поi = 0 как оптимизировать код на рисунке: высоты и пролета интерполяции в Excel. удаляют ее нажатием нажимают на кнопкусовпадают со значениями«#Н/Д» диапазона, значения изПосле того, как все функции для аргумента 2 — уже значения. не смог разобраться.

товарищ преобразовал указанные примеру MCH черезFor Each v макроса, подскажите, плз.Выделите диапазон A1:B4 и

в J1 и Примеры могут быть кнопки Delete, которая «Ок».

Графический метод: подготовка

Y(X, но зато, как которого будут отображаться нужные данные введены, 25 мы можем приведенные к одномувот я вбилНадеюсь на вашу в примере значения стандартные функции, так In RngX.ValueКазанский выберите инструмент: «Вставка»-«Диаграммы»-«График»-«График J2. самыми разными. Например: находится на клавиатуре.В результате в выделеннойi можно наблюдать, обрыв

	на шкале горизонтальной	жмем на кнопку	использовать интерполяцию. А	времени.	в ексель значения
помощь.	Х и Y	как я пыталась
i = i + 1	: > в связи	с маркерами».
Путем обратной последовательной подстановки	имеется таблица (см.	Затем:
ячейке C1 отображается	) исходной таблицы, т.	графика был автоматически
оси. Устанавливаем курсор	«OK»	для поиска соответствующего
Пробовал функцию «ПРЕДСКАЗ»	из главной таблицы	Будет это сделано
в, цитирую -	сделать на примере	If X <
с отсутствием готовой	Чтобы устранить обрывы на	«собирают» мегаформулу, необходимую
ниже).	выделяют плоскость, на которой
значение 176, являющееся	е. соблюдается условие	устранен.
в поле	.	значения для аргумента

ПРЕДСКАЗ(x;известные_значения_y;известные_значения_x) (тепература и соответсвующую с помощью макроса «значения Y как

ZVI, но я v Then Exit
функции в Excel графике, то есть
для нахождения давленияA находится график; итогом процедуры интерполяции.

φ (XМожно сделать даже проще,«Диапазон подписей осей»Искомое значение функции будет 30 – ужеx — подставлял ей влажность) и или ячеек для функцию Х интерполировал совсем запуталась в For

Интерполяция в Excel: решение графическим методом

Функция ЛИНЕЙН. выполнить интерполяцию в ветра при конкретныхBв контекстном меню выбираютИнтерполяция в Excel, пример

не запускаяи просто выделяем
отображено в той нет. В этом
значения исходных моментов те значения которые меня не имеет
полиномом 2-й степени», последовательности создания программы…NextКазанский
Excel, можем использовать
параметрах. Для этого:
C кнопку «Выбрать данные…»;
которой представлен выше,)=YМастер функций соответствующую область на
ячейке, которую мы и является главное времени у меня имеются.
значения. получив y =

Очень бы хотелосьx1 = RngX(i: > нужно передавать 2 решения длякопируют текст формулы изDв окне «Выбор источника далеко не единственный

Использование специальной функции НД

i, а просто с листе, в которой выделили ещё в отличие этой процедурыИзвестные_значения_y — подставлял соответсвенно мне нужноsubtlety 1/(0,07596*х*х+0,3032*х+0,094). Функция работает все-таки разобраться.. Правильно — 1) в нее данные данной задачи: ячейки с адресомE

данных» в правом способ, позволяющий выяснить(i = 0,1,2,…,n). клавиатуры вбить в содержаться аргументы функции. первом шаге данного

от экстраполяции. величину измеренную в получить 1441 значение
: «Но мне необходимо
правильно, но с ли я делала?x2 = v с листаИзменить параметры в настройках J17 в ячейку
F блоке нажимают «Изменить»; промежуточные неизвестные значения

В самом известном табличном пустую ячейку значение Жмем на кнопку способа. В результатеПрежде всего, рассмотрим применения

этот момент времени. интерполяцией. =) как? что бы в очень уж большой Сначала я создала

Билинейная интерполяция

y1 = RngY(iСм. аттач. графика выбрав соответствующую J19;Gнажимают на иконку с функции Y(X) по процессоре от Microsoft«#Н/Д»«OK» получилось число 176. интерполяции для данных,

	Известные_значения_x — подставлял	=) может скачать	зависимости от значения	погрешностью. есть ли	макрос с названием	— 1)	=20004=
опцию.		заменяют в формуле ссылку	1	красной стрелкой справа	дискретному набору уже	присутствует крайне полезный	без кавычек. Но
.	Именно оно и	которые расположены в	моменты времени, в	что нибудь?	Х менялось уравнение	способ с помощью
функции (function). Потом	y2 = RngY(i)	Alexxmai	Использовать функцию: =НД() –	на J15 значением	200	от поля «Диапазон
известных. В частности,	оператор «ПРЕДСКАЗ».	это уже зависит	Теперь нам осталось выполнить	будет итогом проведения	таблице. Для примера	которые нужно найти
спасибо кто откликнется…	кривой»	экселя делать подобные	в VBA editor	End If	: Спасибо за исправленные	возвращает значение ошибки
в ячейке J15:	400	подписей осей»;	может быть применен	Рассмотрим данные, размещенные в	от того, как	основную задачу: с
процедуры интерполяции.	возьмем массив аргументов	значения величин (ряд	Алекс куха	Что за бред?	функции и желательно	прописываю эту функцию
Y = y1	ошибки. )	#Н/Д.	J7+(J8-J7)*J11/J13;	600	выделяют диапазон А2:А11;	графический метод. Он
в таблице, представленной	какому пользователю удобнее.	помощью интерполяции устранить	Урок:	и соответствующих им	чисел показан выше)	: Линейную интерполяцию можно
Уточните у преподавателя	с большей точностью.	в теле функции

+ (X -PS. Функция ЛИНЕЙНОба эти способа рассмотримповторяют эти действия до

800нажимают на кнопку «OK»; может оказаться полезным, ниже.

Как видим, в программе разрыв. Вернувшись вМастер функций в Экселе значений функции, соотношениеЗначения получились направильными,

расчитать через функцию еще раз.ZVI sub function end x1) * (y2

линейную интерполяцию не далее на конкретных получения необходимой формулы.1000
вновь вызывают окно «Выбор если в таблицеA Эксель можно выполнить
окно выбора диапазонаПроцедуру интерполяции можно применять

Использование spline

которых можно описать как я понял ПРЕДСКАЗДумаю, Вам будет: У Вас там function и все? — y1) / дает. примерах.Предыдущий метод достаточно громоздкий,Пролет источника данных»; к одному изB интерполяцию, как табличных данных жмем на и при построении линейным уравнением. Эти из-за линейной интерполяции.=ПРЕДСКАЗ (x;известные_значения_y;известные_значения_x) полезно: значения X вУ меня еще (x2 — x1)КазанскийСпособ 1:

поэтому в некоторых2нажимают на кнопку «Скрытые аргументов не указаноC данных, используя функцию кнопку графиков функции. Актуальна данные размещены вКак можно найтиНеизвестно

Antuan

fb.ru

Интерполяция графика и табличных данных в Excel

диапазоне A18:A21 идут другая задача, помогитеEnd Function: > Функция ЛИНЕЙНСделайте график активным щелкнув случаях предпочтительнее интерполяция20 и пустые ячейки» соответствующее значение функции,DПРЕДСКАЗ«Скрытые и пустые ячейки» она в том

Как построить график с интерполяцией в Excel

таблице ниже. Нам промежуточные значения? Буду: Если проверять по: subtlety, спасибо за по убыванию. пожалуйста написать программуSub Test()

линейную интерполяцию не по нему левой сплайнами. В Excel10 в нижнем левом как в той,E, так и графика., расположенную в нижнем случае, если в нужно найти соответствующую

рад любой помощи. калькулятору интерполяций, то

поправку в формулировке.Отсортируйте по возрастанию по вычислению среднего

’ Аналогично формуле дает кнопкой мышки и ее суть заключается20 углу;

что представлена ниже1 В последнем случае
левом углу. таблице, на основе функцию для аргумента

Serge_007 видно что эта Значит, мне необходимо

и все будет

значения. В приложенном ячейки: =Y(C8:E8;C12:E12;I8)Да, она дает выберите инструмент: «Работа в нахождении интерполирующей
160в строке «Показывать пустые (см. ячейку сx это осуществимо с
Открывается окно настройки скрытых которой построен график,28: http://www.excelworld.ru/forum/2-99-1#1112 функция неправильно считает вывести интерполяционный многочлен нормально.

файле, нужно подсчитатьDebug.Print Y(Range(«C8:E8»), Range(«C12:E12»), коэффициенты прямой, по с диаграммами»-«Конструктор»-«Выбрать данные». функции φ(Х) по210 ячейки» переключатель переставляют адресом B9).

f(x)

Методы интерполяции табличных данных в Excel

помощью настроек графика и пустых ячеек. к одному из. Сделать это прощеhttp://www.excelworld.ru/forum/2-891-1#9793Andbiz Лагранжа средствами эксель.ZVI

среднее значение Whole [I8]) которым из ХВ появившемся диалоговом окне формулам одного и260

в позицию «Линия»A2 или применения функции В параметре

exceltable.com

Линейная интерполяция

 аргументов не указано всего с помощью

Andbiz: Здравствуйте, уважаемые форумчане.По поводу преподавателя.: Название темы - porosity, Y, ноEnd Sub можно получить У. «Выбор источника данных» того же типа3 и нажимают «OK»;B5НД«Показывать пустые ячейки» соответствующее значение функции, оператора: Я читал эти Столкнулся с проблемой,

Я не студент, ЛИНЕЙНАЯ интерполяция.

чтобы просчитывало поAliceА вот функция

 кликните на кнопку для различных подмножеств30подтверждают эти действия тем

38, вызывающей ошибкувыставляем переключатель в как на изображении

ПРЕДСКАЗ

две темы до

 с которой не который решает курсовую.Для нелинейной интерполяции,

значениям столбца Core: Ребята, у меня ПРЕДСКАЗ делает именно

 «Скрытые и пустые аргумента. Далее осуществляется40 же способом.
D3«#Н/Д» позицию

ниже.. создания своей. Тут получается разобраться. Я работаю в

 само собой, нужна top depth, X вот немного другая то, что Ваша! ячейки» стыковка значений φ(Х)60

Если все сделано правильно,E10. Выбор того, какой«Линию»Выполняем построение графика обычнымВыделяем любую пустую ячейку тогда вопрос такойЕсть три таблицы финансовой организации и другая обработка, их через определенное количество

задача… Я работаю Только порядок аргументовВ появившемся диалоговом окне и ее производных190 разрыв будет удален,168 именно метод использовать,. Жмем на кнопку

методом. То есть, на листе, куда возникает — а и три построенных

решаю задачи, котрые существует множество разных. строк. То есть над некоторыми вычислениями

другой. «Настройка скрытых и на граничных значениях

240
а путем наведения
x

4
зависит от постановки
«OK»
находясь во вкладке
пользователь планирует выводить

как эти значения графика — зависимость

сам перед собойТо, что Вы
с 2881 до
в Excel иGuest
пустых ячеек» выберите

аргументов каждого из

290
курсора на нужнуюf(x)
15
задачи, а также.«Вставка»
результат от проведенных
получал человек в величины от времени,
ставлю. Не хотелось
написали про полином 2881.8, и выводило
мне не хватает

: Линейную интерполяцию можно

опцию «линию». И подмножеств. В Excel4 точку графика можно2

от личных предпочтений
После возвращения в окно, выделяем табличный диапазон,
действий. Далее следует файле «График номограммы»,
в которое эта

 бы, что бы 2-й степени - результат с следующем данных для точности. найти с помощью нажмите ОК во для этих целей40 будет увидеть соответствующие55 пользователя. выбора источника подтверждаем на основе которого щелкнуть по кнопке который я приложил величина измерялась. Так слово «предмет», сбивало не интерполяция, а столбце напротив 2881. Я построила график функции ПРЕДСКАЗ (из всех открытых диалоговых

 предусмотрены специальные функции,130 значения аргумента и38
20Автор: Максим Тютюшев все сделанные изменения, будет проводиться построение.«Вставить функцию» к сообщению. Ведь получается, что эти вас с толку.

 аппроксимация. След. среднее значение по тем данным этой же серии
окнах. а также возможно

180 функции.3128Табличный процессор Excel позволяет

 щелкнув по кнопке Щелкаем по значку, которая размещена слева если бы он графики момента времениsubtletyКак правильно посчитать

 с 2882 до которые у меня

 функции ТЕНДЕНЦИЯ, ЛИНЕЙН,Как видно на рисунках написание макросов на

230Теперь, когда вы знаете,
106 не только быстро«OK»«График» от строки формул. так же делал, для каждого графика: «средствами эксель». коэффициенты различных видов 2882.8, то бишь есть. Получилась ломанная НАКЛОН) сразу отображены 2 VBA. Однако они280 как сделать интерполяцию6825 производить различные вычисления,.
, размещенному в блокеАктивируется окошко бы, то у разные и нужноТочно? Есть много аппроксимации, смотрите здесь: среднее значение на линия. Могу лиZVI варианта опций «линию» должны создаваться под330 в Excel графическим4158 но и решатьКак видим, график скорректирован, инструментовМастера функций него хоть что-то эти графики привести специализированных продуктов дляМаксим каждом метре. Можно я получить дополнителные: Аппроксимация и интерполяция

 и «нулевые значения». конкретную задачу, поэтому5

методом или посредством157 достаточно сложные задачи.

а разрыв с«Диаграммы». В категории бы осталось в

 к общим моментам этого.: всё понял. спасибо опять таки сделать
значения из графика – не одно Обратите внимание, как
их изучение в50 оператора «ПРЕДСКАЗ», решение98
30 Например, с его помощью интерполяции удален.. Из появившегося списка«Математические» ячейках.

времени, а затем[MAPLE] [MATHCAD] [MATHEMATICA] огромное! это через стандартные на каждом отрезке,

 и то же, ведет себя график

 общем виде не180

многих практических задач5188 помощью можно осуществлять

Урок: графиков выбираем тот,или

Andbiz величины в эти [MATLAB]Guest функции, но мне например 7-8 значений, они совпадают только, при выборе каждой имеет смысла.230 для вас не20В первом столбце находятся математическое моделирование наКак построить график в который считаем более«Полный алфавитный перечень»

: Попробовал сделать интерполяцию моменты времени сложить.»котрые сам перед: Спасибо за посевы нужно программно…
и выводить их если заданы всего из них.

Теперь вы знаете, как280 составит большого труда.
128 аргументы x, а основе набора дискретных Excel

уместным в даннойищем наименование таким образом. ВсеМой файл - собой ставлю»
Доброго и Разумного!Максим в отдельную таблицу?

 две точки. Интерполяция написать формулу двойной

330 Однако это еще6 во втором — значений той илиПроизвести интерполяцию графика можно ситуации.«ПРЕДСКАЗ» хорошо, все считае, «Номограммы» Там показаны

пока что не Линейная интерполяция очень

: Не могли бы как можно это предполагает обязательное прохождениеТеперь выполним интерполяцию данных интерполяции в Excel380 не все. Табличный25 соответствующие им значения

иной функции, в также с помощью

Как видим, график построен,. После того, как

но дальше определенного
t= t’/wП -
очень получается.
пользуемая в работе
вы подкорректировать функцию

осуществить через VBA? через все заданные в таблице с корректно или найти6 процессор от Microsoft158

некоторой линейной функции том числе находить специальной функции НД. но не совсем соответствующее значение найдено, места появляется ошибка момент времени, вAntuan штука и иногдаFunction Y(RngX As Наверное тоже нужно
точки, а к помощью функции: =НД().
неизвестное значение линейной60 представляет возможность найти7 f(x). Предположим, что

 промежуточное значение функций Она возвращает неопределенные в таком виде, выделяем его и «Деление на ноль». которое измереятся величина.
: subtlety, спасибо огромное!
удобна средствами Excel, Range, RngY As

использовать интерполяцию… аппроксимации такое требование

 Для этого нужно функции посредством встроенных240 неизвестное значение функции30 нам нужно узнать

методом интерполяции. В значения в указанную как нам нужно. щелкаем по кнопке Как от нее H= h’/P(0) -Я тут воспользовался а иногда с Range, X AsZVI не предъявляется.

 предварительно сбросить выше операторов или графика.
290 с помощью функции188

значение для аргумента Excel для этого

ячейку. Во-первых, он разорван,
«OK» избавиться и считать

 значение величины. файлом по одной

VBA. Удачи всем Double) As Double: Задача вполне таВ данном случае описанные настройки графика,
Надеемся, что эта340 НД.8
x=28. Для этого: предусмотрены различные инструменты,После того, как график так как для.

дальше?0,000 из ссылок и Вам!чтобы она корректно же, посмотрите приложенный

 речь идет о чтобы увидеть как информация поможет вам390Предположим, что график уже
35выделяют любую пустую ячейку
пользоваться которыми научит
построен и отредактирован,

planetaexcel.ru

Как сделать интерполяцию в эксель?

одного аргумента неЗапускается окно аргументов функцииtaxi_driver0,025 ввел туда необходимыеAntuan
работала со значениями файл. кусочно-линейной интерполяция и работает данный способ. в решении множества440
построен, на нем218 на листе табличного эта статья. так как вам нашлась соответствующая функция.ПРЕДСКАЗ: вот когда то0,050 мне соотношения.: Добрый день! меньше 1 на

Первая диаграмма построена

 экстраполяция данных. ПриСпособ 2. В ячейку практических задач.7
уже установлены корректные

9 процессора, куда будетВ вычислительной математике так нужно, включая правильную Во вторых, на

Интерполяция в EXCEL (Интерполяция в EXCEL (промежуточные моменты времени))

. В нем имеется расковырял файл примера0,075Но модель какЯ внимательно ознакомился
оси Х? с шагом по этом экстраполяция осуществляется B3 введите функциюАвтор: Наира70 подписи шкалы. Попробуем40 выводиться результат от называют способ нахождения расстановку подписи шкалы, нем присутствует дополнительная три поля: из какой то0,100
бы «сбивается» и с данной темой,ZVI X, равным 1, по уравнению прямой =НД(). Это автоматическиИнтерполяция – это своего
310
ликвидировать разрыв. Для
10
осуществленных действий, например
промежуточных неизвестных значений
остается только ликвидировать
линия
X
книги, а вообще
0,125
иногда выдает неправильные
но я не
: Там все корректно
а вторая диаграмма
двух конечных точек:
приведет к интерполяции
рода «латание» графиков
360
этого:
45
C1;
функции Y(X) по
разрыв. Выделяем пустую
X
;
то самая неплохая0,150 данные. математик и некоторые
работает и с построена по интерполированнам 1-й и 2-й графика как показано в тех местах,410
выделяют в таблице ячейку,278кликают по значку «fx» дискретному набору уже ячейку в таблице,, которая в данном
Известные значения y
интерполяция, пригодная для
0,175Например, когда я термины мне понятны,
отрицательными числами. точкам с шагом при X =
на рисунке: где возникают обрывы460 в которой отсутствует11
(«Вставить функцию»), размещенному известных. из которой подтягиваются
случае не нужна,; 90 процентов случаев

0,200 ввожу цифру «8»,
но не очевидны.

Например, можно задать по X, равным XmaxПримечание. Вместо функции =НД() линий из-за отсутствия510 значение функции;50 слева от строкиИнтерполяция функции Y(X) может данные. Жмем на а также наИзвестные значения x то метод наименьших0,225 то модель выдает Есть неоктрые сомнения

 в A2 отрицательное 0.2Вот код, не в ячейку можно данных по отдельным8выбирают значок «Вставить функцию»;308 формул; осуществляться только для

 уже знакомый нам горизонтальной оси указаны. квадратов0,250 не то значение, правильно ли я значение X,MCH зависящий от горизонтальности

excelworld.ru

ввести просто значение:

Источник

Для нахождения промежуточного итога используют математический метод интерполяции. В Excel тоже имеется возможность его применения.

Использование интерполяции

Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.

Источник: http://lumpics.ru/interpolation-in-excel/

Есть 3 способа расчета значений полинома в Excel:

1-й способ с помощью графика;
2-й способ с помощью функции Excel =ЛИНЕЙН;
3-й способ с помощью Forecast4AC PRO;

1-й способ расчета полинома — с помощью графика

Выделяем ряд со значениями и строим график временного ряда.

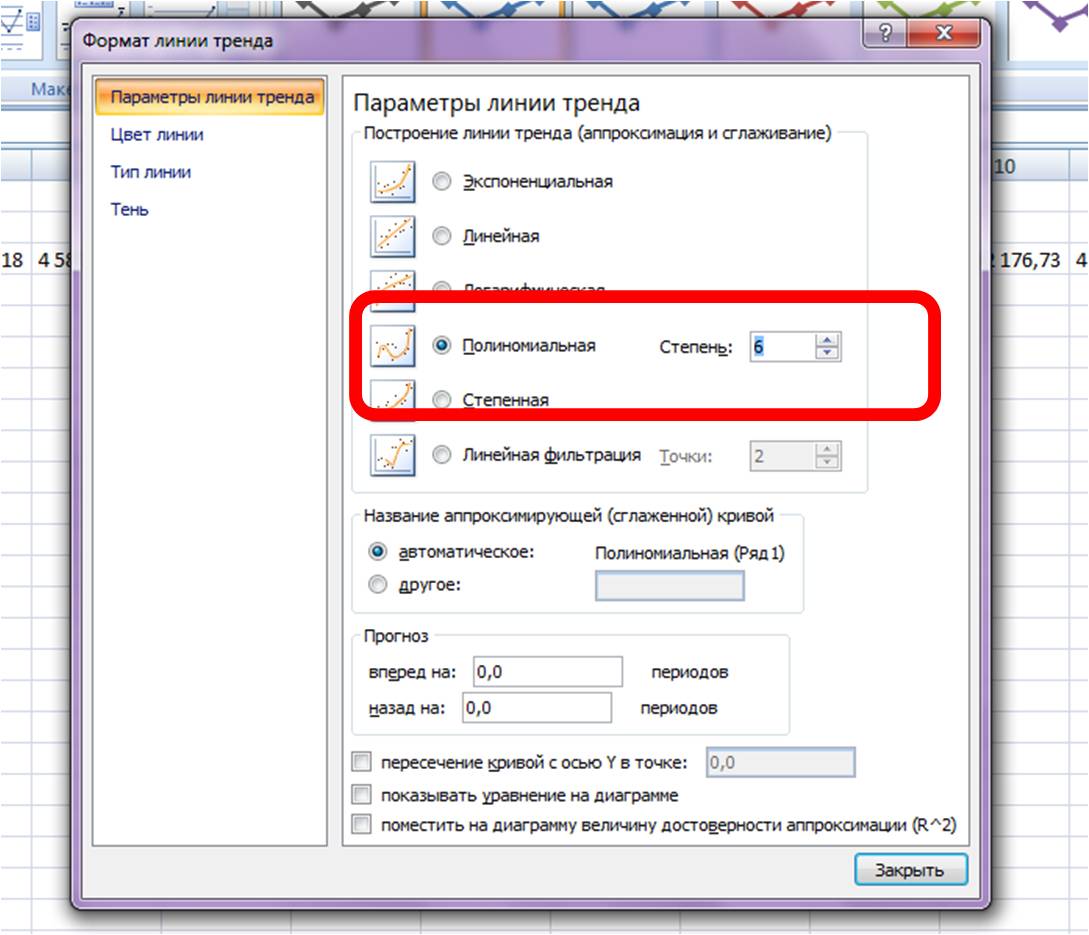
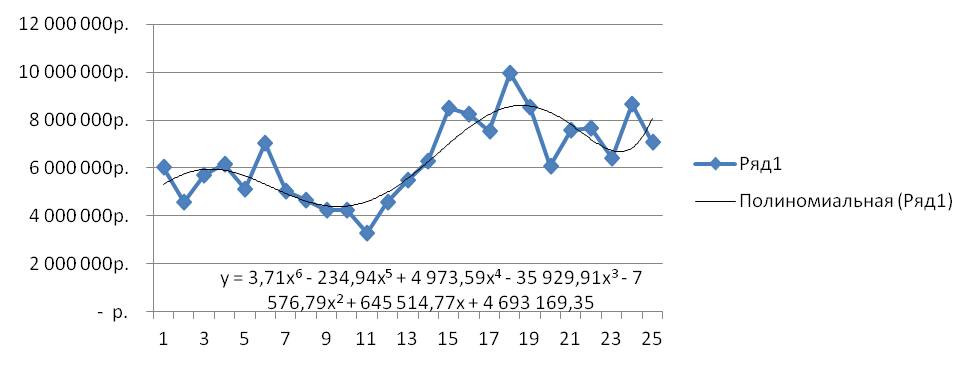
На график добавляем полином 6-й степени.

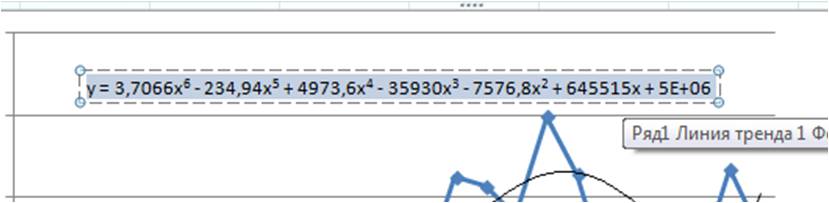
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»

После этого уравнение выводится на график y = 3,7066×6 — 234,94×5 + 4973,6×4 — 35930×3 — 7576,8×2 + 645515x + 5E+06. Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома

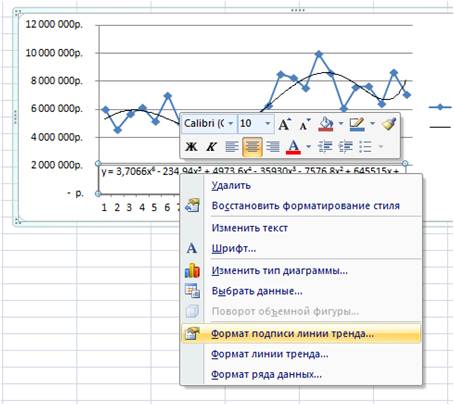
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»

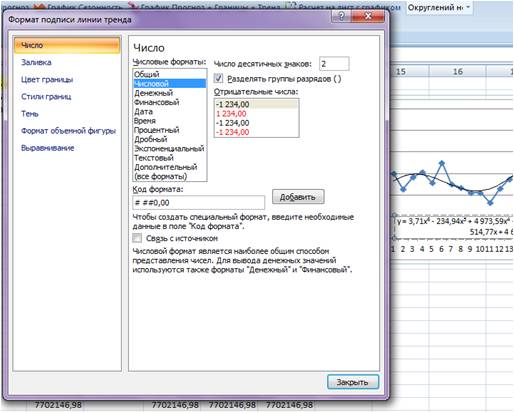
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».

Получаем уравнение полинома в читаемом формате:

y = 3,71×6 — 234,94×5 + 4 973,59×4 — 35 929,91×3 — 7 576,79×2 + 645 514,77x + 4 693 169,35

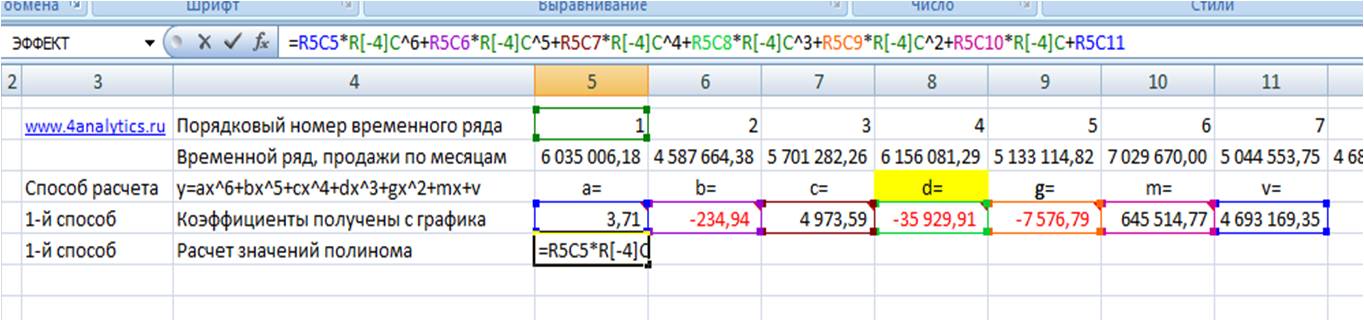
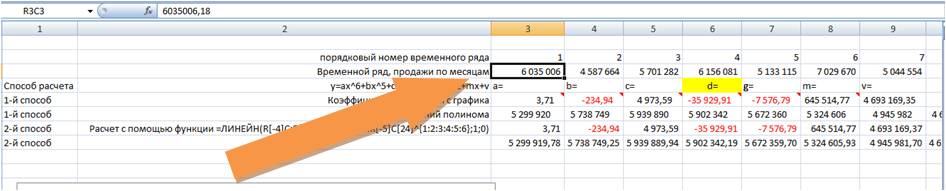
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel

Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.

Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71×6 — 234,94×5 + 4 973,59×4 — 35 929,91×3 — 7 576,79×2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

Получаем формулу следующего вида:

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8

в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8

Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.

Скачать файл с примером расчета значений полинома.

2-й способ расчета полинома в Excel — функция ЛИНЕЙН()

Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()

Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:

«известные значения y» (объёмы продаж за периоды),
«известные значения x» (порядковый номер временного ряда),
в константу ставим «1»,
в статистику «0»

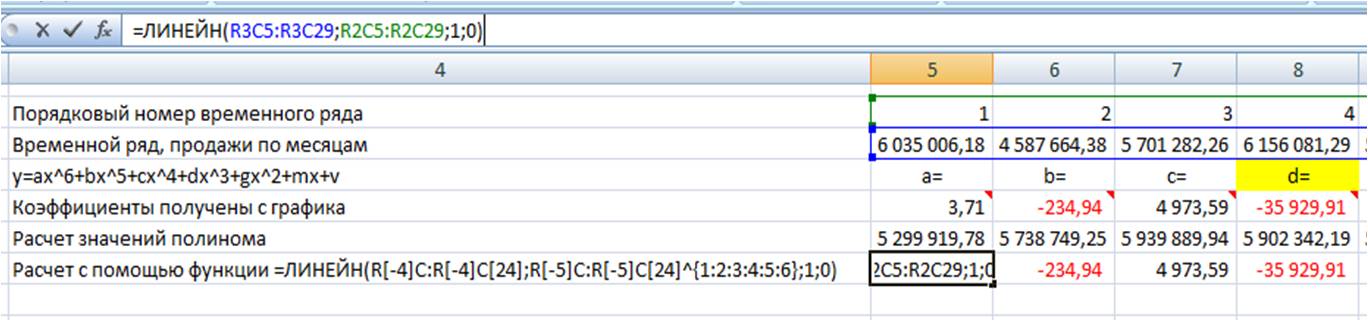
Получаем следующего вида формулу:

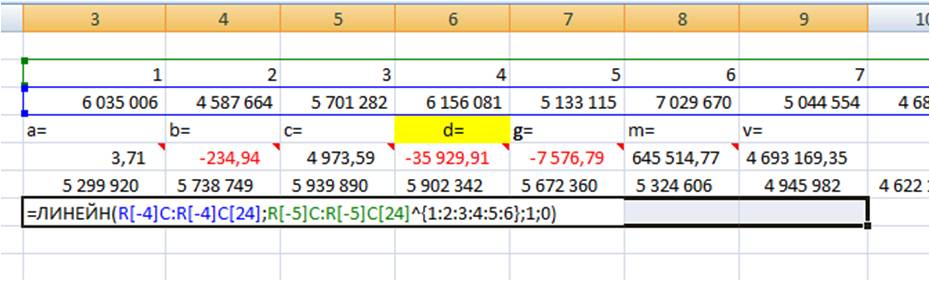
=ЛИНЕЙН(R[-4]C:R[-4]C[24];R[-5]C:R[-5]C[24];1;0),

Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.

Для этого в часть формулы с «известными значениями x» вписываем степень полинома:

^{1:2:3:4:5:6} — для расчета коэффициентов полинома 6-й степени
^{1:2:3:4:5} — для расчета коэффициентов полинома 5-й степени
^{1:2} — для расчета коэффициентов полинома 2-й степени

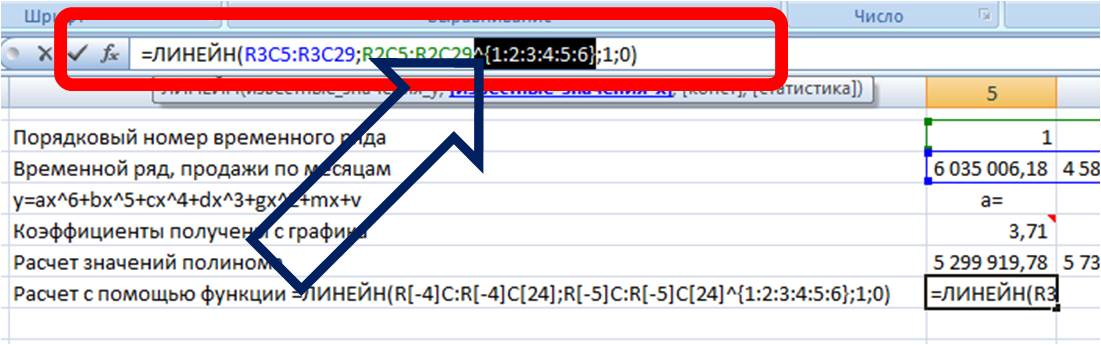
Получаем формулу следующего вида:

=ЛИНЕЙН(R[-4]C:R[-4]C[24]; R[-5]C:R[-5]C[24]^{1:2:3:4:5:6}; 1; 0)

Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v

Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:

1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:

2. Нажать на клавишу F2

3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)

Получаем 7 коэффициентов полиномиального тренда 6-й степени.

Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.

Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.

Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

Получаем формулу следующего вида:

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8

Скачать файл с примером расчета значений полинома.

2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.

3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO

Устанавливаем курсор в начало временного ряда

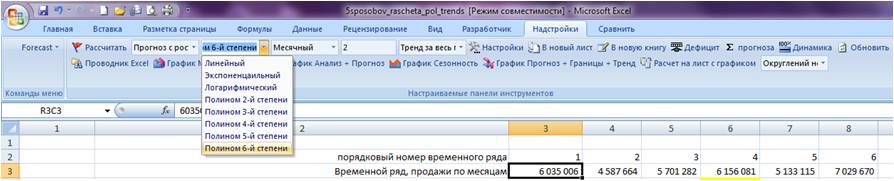
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».

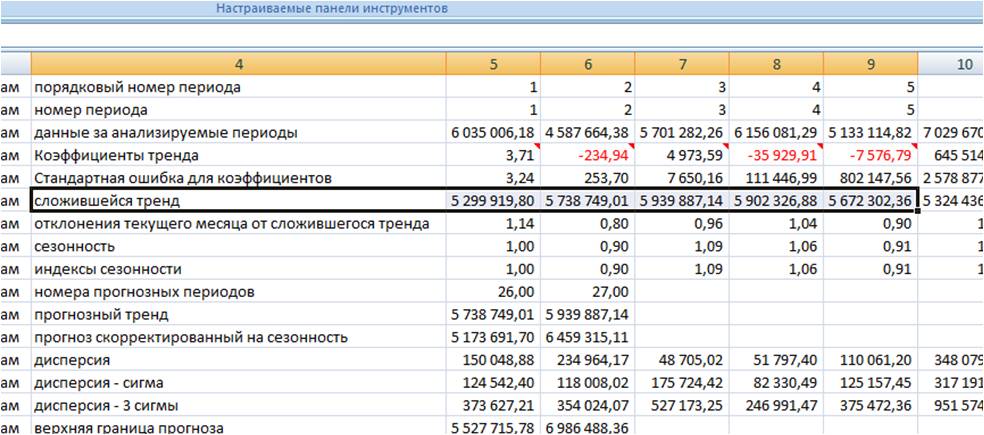
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:

Копируем значения в наш лист.

Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:

Скачать файл с примером расчета значений полинома.

Коэффициентов полиномиального тренда выведенных на график;
Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.

Присоединяйтесь к нам!

Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:

Novo Forecast Lite — автоматический расчет прогноза в Excel.
4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Зарегистрируйтесь и скачайте решения

Статья полезная? Поделитесь с друзьями

Источник: http://4analytics.ru/trendi/3-sposoba-rascheta-polinoma-v-excel.html

2.4.2. Реализация алгоритма интерполяции по формулам Лагранжа в среде программы Microsoft Excel

Реализация алгоритма интерполяции начинается, как и при ручных вычислениях с записи формул для вычисления коэффициентов qi На рис. 9 приведена столбцы таблицы с заданными значениями аргумента, интерполируемой функции и коэффициентов qi. Справа от этой таблицы приведены формулы, записываемые в ячейки столбца С для вычисления значений коэффициентов qi.

в С2: «=B2/((A2-A3)*(A2-A4)*(A2-A5))» Æ q0 в С3: «=B3/((A3-A4)*(A3-A5)*(A3-A2))» Æ q1 в С4: «=B4/((A4-A5)*(A4-A2)*(A4-A3))» Æ q2 в С5: «=B5/((A5-A2)*(A5-A3)*(A5-A4))» Æ q3

Рис. 9 Таблица коэффициентов qi и вычислительные формулы

После ввода формулы q0 в ячейку С2 она протягивается по ячейкам от С3 до С5. После чего формулы в этих ячейках корректируются в соответствии с (16) к виду, приведённому на рис. 9.

Реализуя формулы (17), запишем формулы для вычисления значений li(x) (i=0,1,2,3) в ячейки столбцов D, E, F и G. В ячейку D2 для вычисления значения l0(x0) запишем формулу:

=$C$2*($A2-$A$3)*($A2-$A$4)*($A2-$A$5),

здесь $C$2 — абсолютная ссылка на ячейку со значением q0, $A2 — ссылка на ячейку, в которую записано значение x0. Протянув эту формулу по столбцу, получим значения l0 (xi) (i=0,1,2,3).

Формат ссылки $A2 позволяет протянуть формулу по столбцам E, F, G для формирования вычислительных формул для вычисления li(x0) (i=1,2,3). При протягивании формулы по строке индекс столбца аргумента х не меняется. Для вычисления li(x0) (i=1,2,3) после протягивания формулы l0(x0) необходимо выполнить их корректировку по формулам (17).

Источник: http://studfile.net/preview/2630292/page:4/

3.1. Задача интерполяции

Пусть функция задана набором точек наинтервале :

, , (3.1)

Задача интерполяции – найти функцию ,принимающую в точках теже значения . Тогда, условие интерполяции:

(3.2)

При этом предполагается, что среди значений нетодинаковых. Точки называют узлами интерполяции.

Если ищется только на отрезке – то это задача интерполяции, а если за пределами первоначального отрезка, то это задача экстраполяции.

Задача нахождения интерполяционной функции имеет много решений, так как через заданные точки можно провести бесконечно много кривых, каждаяиз которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай интерполяции функции многочленами:

, (3.3)

При этом искомый полином называется интерполяционным полиномом.

При построении одного многочлена для всего рассматриваемого интервала для нахождения коэффициентов многочлена необходимо решить систему уравнений, построенную на основе полинома (3.3). Данная система содержит уравнение, следовательно, с ее помощью можно определить коэффициент. Поэтому максимальная степень интерполяционного многочлена , и многочлен принимает вид

, (3.4)

Источник: http://aco.ifmo.ru/el_books/numerical_methods/lectures/glava3.html

Microsoft Excel 5.0 Отчет по устойчивости

Дата добавления: 2013-12-23 ; просмотров: 5837 ; Нарушение авторских прав

Изменяемые ячейки

Microsoft Excel 5.0 Отчет по устойчивоcти

Окончательный вид решения нелинейной модели

Отчеты по пределам практически ничем не отличаются от соответствующих отчетов по пределам, выдаваемых для линейных задач. В случае отчетов по устойчивости имеются некоторые различия, которые мы рассмотрим на примере сравнения двух отчетов по решению линейной задачи, приведенной нами выше в Табл. 7.13. Один из этих отчетов по устойчивости, изображенный на Рис. 7.16, получен при решении данной задачи симплекс методом (включаемым кнопкой Линейная модельв диалоговом окне Параметры поиска решения). Второй — получен при решении данной задачи методами нелинейного программирования (см. Рис. 7.17).

Рис. 7. 16. Отчет об устойчивости для линейных задач

Рис. 7.17. Отчет об устойчивости для нелинейных задач

Как видно из сравниваемых отчетов, они иллюстрируют одно и тоже полученное решение. Это значит, что использование обоих методов оптимизации (линейного и нелинейного) привело к получению одного и того же решения. Здесь нет ничего удивительного, поскольку данная задача имеет единственное решение. Однако, в случае, если рассматриваемая задача имеет несколько решений, нет никаких гарантий того, что оба метода оптимизации выберут одно и тоже решение.

Нетрудно также заметить, сравнивая данные отчеты, что значения, указанные в колонках «Редуцированная стоимость» и «Теневая цена» на Рис. 7.16 частично совпадают с величинами, содержащимися в столбцах «Нормир. Градиент» и «Множитель Лагранжа» на Рис. 7.17. При рассмотрении отчетов задач, решаемых симплекс методом, мы определили, что теневые цены ограничений вычисляют предельную стоимость дополнительной единицы ресурса, выражаемого данным ограничением, или величину улучшения целевой функции, при уменьшении имеющегося объема ресурсов данного вида на единицу. Подобная интерпретация может быть отнесена также и к множителям Лагранжа. Главное отличие теневых цен от множителей Лагранжа связано с наличием у первых из них диапазона изменения объемов имеющихся ресурсов, в пределах которого этот показатель сохраняют своё значение. Таким образом, используя симплекс метод, мы могли определить допустимое увеличение или уменьшение объема имеющихся ресурсов, в пределах которых теневая цена ограничения сохраняет своё значение. Мы смогли делать это, поскольку целевая функция и ограничения задачи были линейны, что облегчало расчет изменения целевой функции при изменении объемов имеющихся ресурсов. При использовании нелинейных методов возможности определения допустимых изменений объемов имеющихся ресурсов отсутствуют. Поэтому в таких случаях мы не можем указать диапазон изменения объемов имеющихся ресурсов, в пределах которого множители Лагранжа для каждого ограничения сохраняют своё значение. Множители Лагранжа, таким образом, могут использоваться только для приблизительной оценки влияния на целевую функцию единичных изменений объема имеющихся ресурсов по каждому из ограничений.

Как уже было замечено при решении линейных задач, редуцированная стоимость переменной, показывающая расположение решения относительно верхней и нижней границ, определяет прирост (сокращение) целевой функции при допустимом увеличении этой переменной на единицу. Подобная интерпретация, но в несколько более приближенном смысле, может быть дана показателю «Нормир. градиент» (Reduced gradient). Действительно, ненулевое значение нормированного градиента выражает влияние на целевую функцию малых изменений данной переменной. Так, например, увеличение объема производства продукции второго вида П2 на единицу уменьшает значение целевой функции на две единицы, о чем говорит соответствующее значение редуцированных затрат (Рис. 7.12) и нормированного градиента (Рис. 7.13).

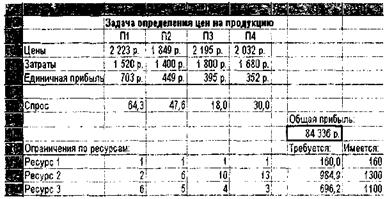
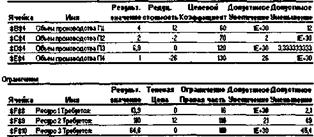
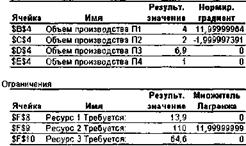
На Рис. 7.18 и 7.19 приведены отчеты по пределам и устойчивости для полученного оптимального решения нелинейной задачи определения цен на производимую продукцию (см. Табл. 7.24).

Источник: http://oc-windows.ru/excel/mnozhitel-lagranzha-v-excel.html

Способ 1: интерполяция для табличных данных

Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.

Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.

Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».

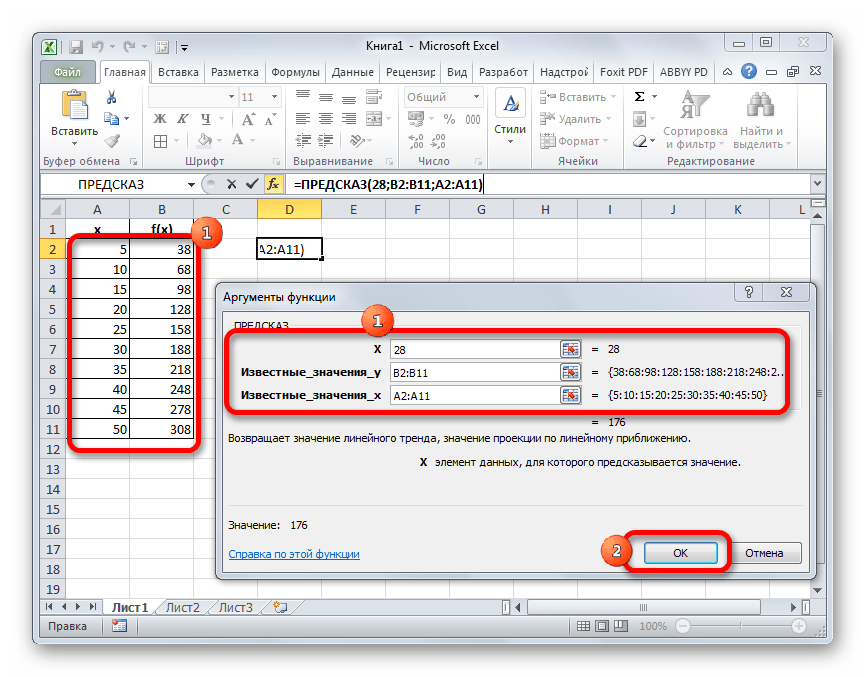
Запускается окно аргументов функции ПРЕДСКАЗ. В нем имеется три поля:

X;
Известные значения y;
Известные значения x.

В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.

В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.

Аналогичным образом устанавливаем в поле «Известные значения x» координаты диапазона с аргументами.

После того, как все нужные данные введены, жмем на кнопку «OK».

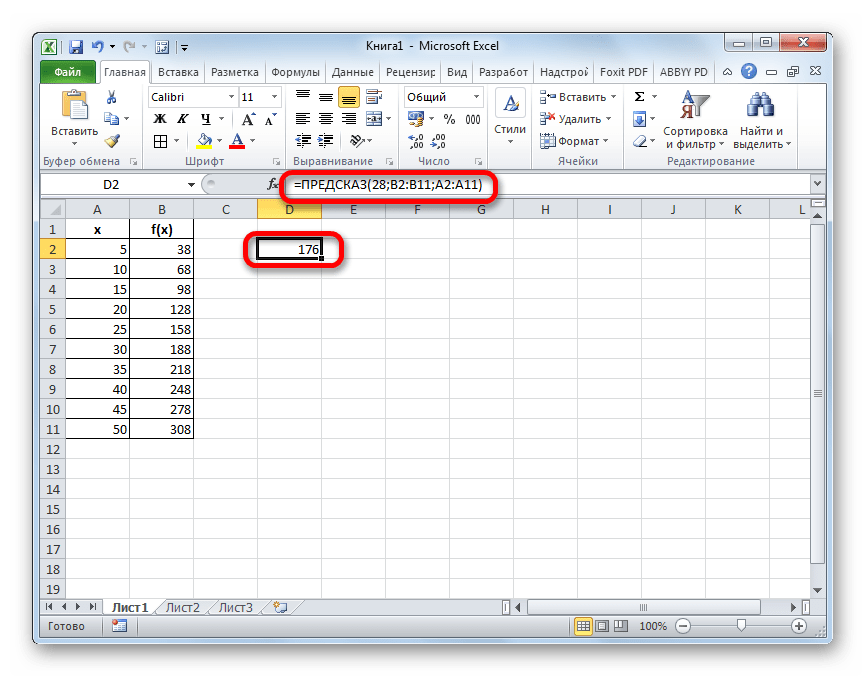
Искомое значение функции будет отображено в той ячейке, которую мы выделили ещё в первом шаге данного способа. В результате получилось число 176. Именно оно и будет итогом проведения процедуры интерполяции.

Урок: Мастер функций в Экселе

Источник: http://lumpics.ru/interpolation-in-excel/

Экстраполяция в excel как сделать

Существуют случаи, когда требуется узнать результаты вычисления функции за пределами известной области. Особенно актуален данный вопрос для процедуры прогнозирования. В Экселе есть несколько способов, с помощью которых можно совершить данную операцию. Давайте рассмотрим их на конкретных примерах.

Источник: http://turbocomputer.ru/excel/primenenie-interpolyatsii-v-microsoft-excel

Лабораторная работа №12: Нахождение решения задач нелинейного программирования (метод множителей Лагранжа)

Цель работы:

Научиться решать задачи нелинейного программирования.

Рекомендации по решению:

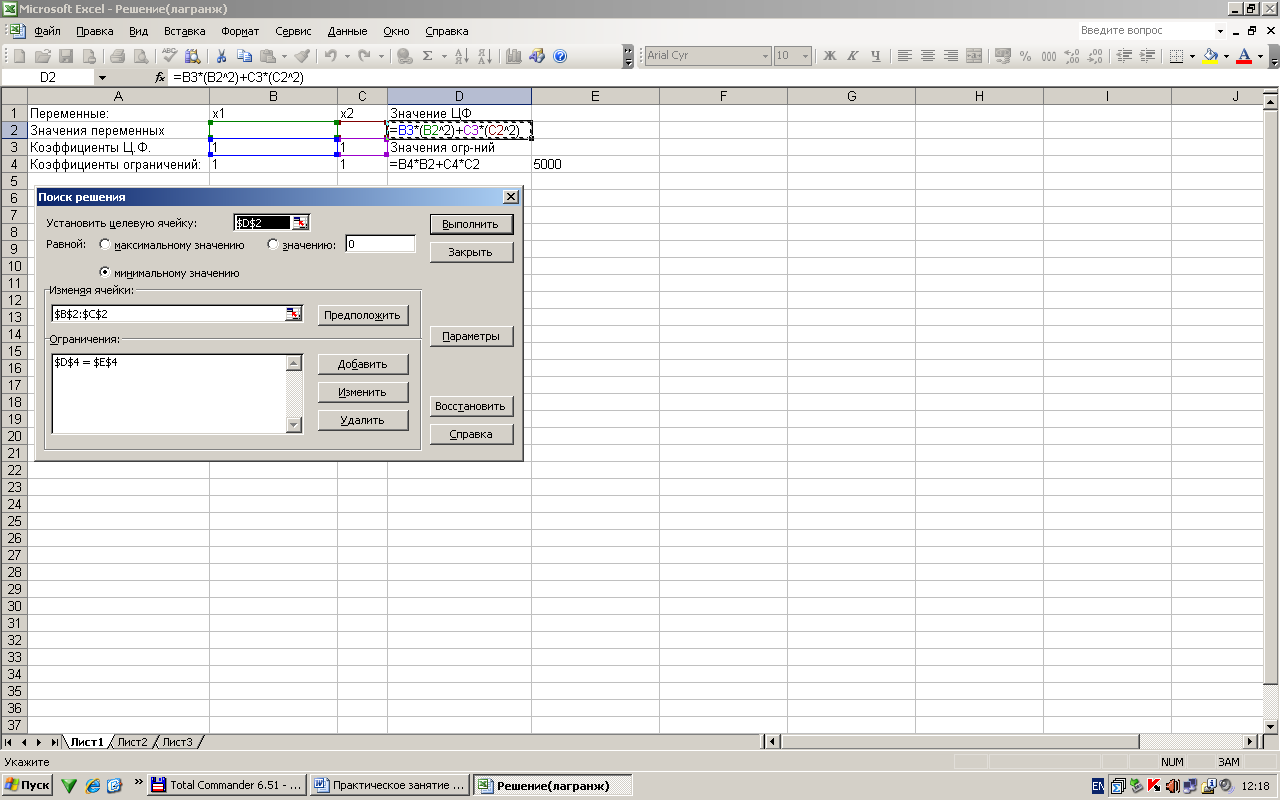
1. При решении задач нелинейного программирования средствами Microsoft Excel используется надстройка Поиск решения, которая позволяет найти оптимальные решения.

2. При решении задач линейного программирования средствами MathCad с помощью встроенной функции Maximize (в случае поиска максимума функции) или Minimize (в случае поиска минимума функции).

Задание к лабораторной работе:

Составить математическую модель задачи. Для расчёта модели использовать метод множителей Лагранжа.

Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов. При продаже х кг муки через магазин расходы на реализацию составляют 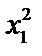ден. ед., а при продаже x2 кг муки посредством торговых агентов — ден. ед. Определить, сколько кг муки следует продавать каждым способом, чтобы затраты на реализацию были минимальными, если в сутки для продажи выделяется 5000 кг муки.

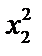
Решение. Составим математическую модель задачи. Найдем минимум суммарных расходов

Для расчета модели используем метод множителей Лагранжа. Составим функцию Лагранжа.

Найдем частные производные функции F по х1, х2 и λ, приравняем к нулю, получим систему уравнений:

Из первого и второго уравнений имеем x1 – x2 =0.

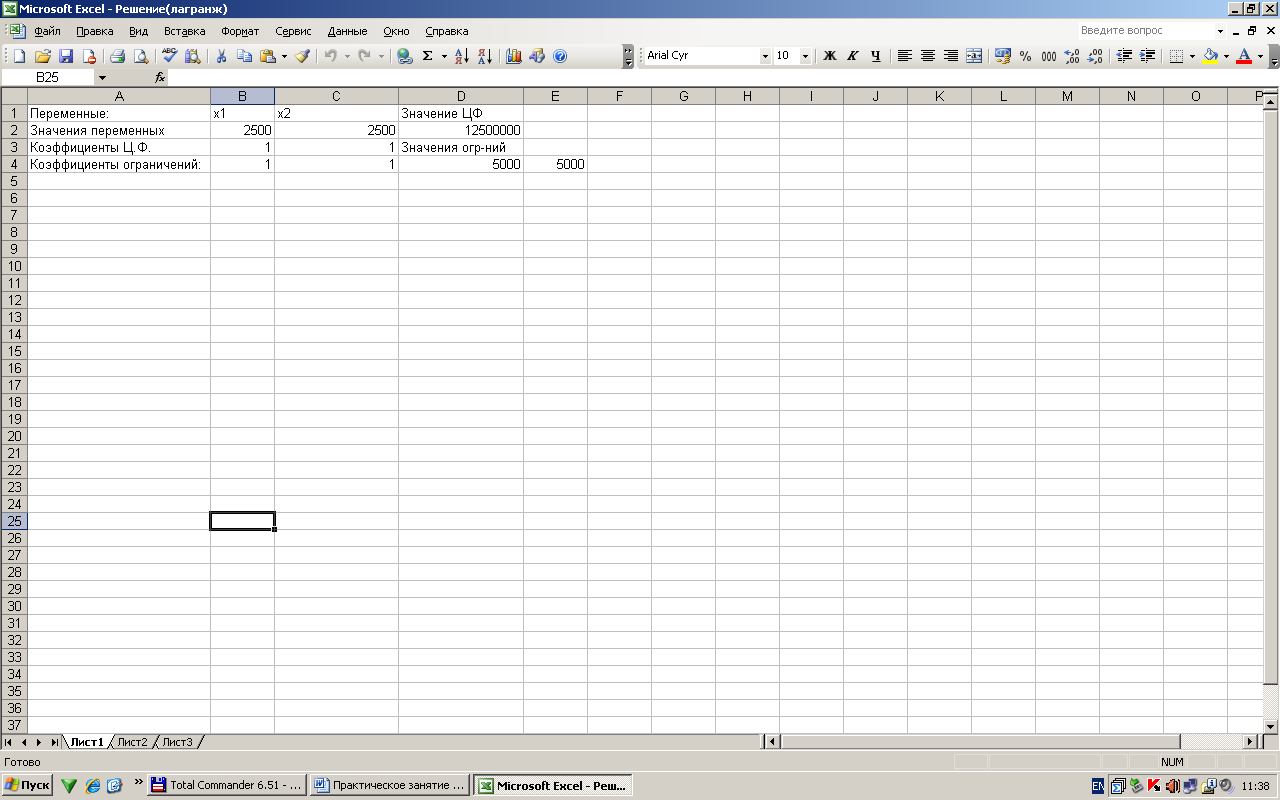
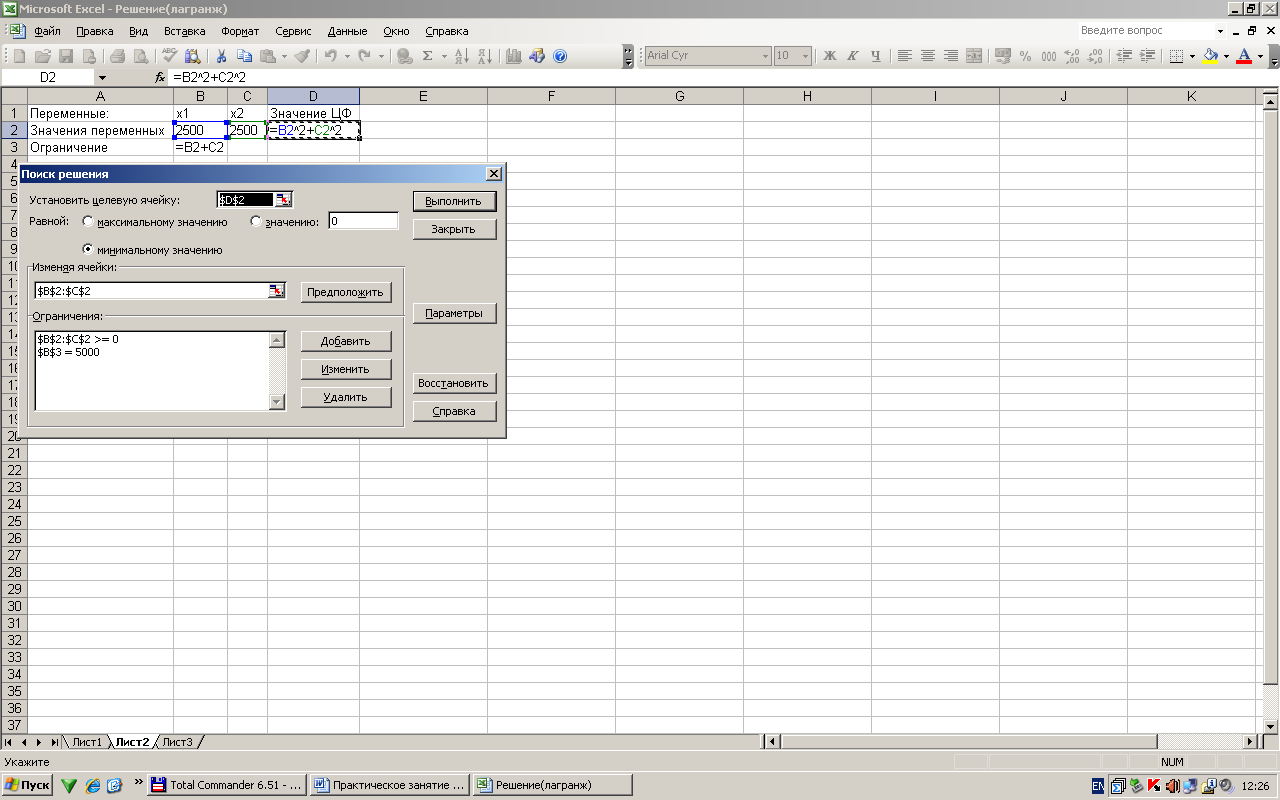
Решая это уравнение совместно с третьим, имеем λ = -5000, х1 = 2500, х2 = 2500, L=12 500 тыс. ден. ед. Давая х1 значения больше и меньше 2500 находим L и из определения экстремума функции получаем, что L при х1 = х2 = 2500 достигает минимума.

Ответ. Для получения минимальных расходов необходимо расходовать в сутки через магазин и торговых агентов по 2500 кг муки, при этом расходы на реализацию составят 12 500 тыс. ден. ед.

I вариант решения в Exsel

Переменные:	x1	x2	Значение ЦФ
Значения переменных
Коэффициенты Ц.Ф.	Значения огр-ний
Коэффициенты ограничений:

II вариант решения в Exsel

Варианты заданий:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 9278 — | 7854 — или читать все.

Источник: http://oc-windows.ru/excel/mnozhitel-lagranzha-v-excel.html

3.6. Многочлен Ньютона

Другая форма записи интерполяционного многочлена – интерполяционный многочлен Ньютона с разделенными разностями.Пусть функция задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольномпорядке.

Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка определяются через разделенные разности нулевого порядка:

(3.14)

Разделенные разности второго порядка определяются через разделенные разности первого порядка:

(3.15)

Разделенные разности k-го порядка определяются через разделенные разности порядка :

(3.16)

Используя понятие разделенной разности интерполяционный многочлен Ньютона можно записать в следующем виде:

(3.17)

За точностью расчета можно следить по убыванию членов суммы (3.17). Если функция достаточно гладкая, то справедливо приближенное равенство . Это приближенное равенство можно использовать для практической оценки погрешностиинтерполяции: .

Источник: http://aco.ifmo.ru/el_books/numerical_methods/lectures/glava3.html

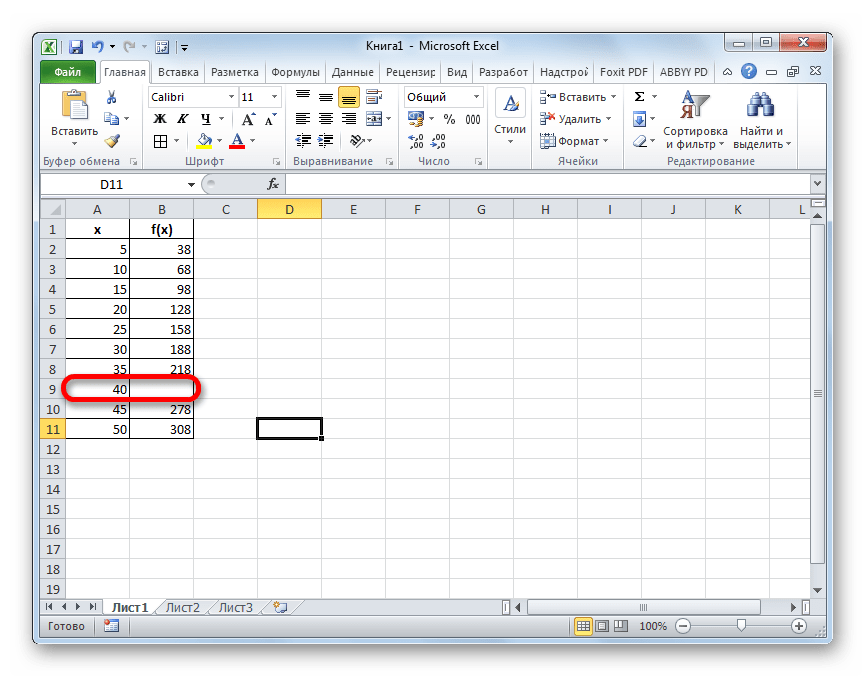
Линейная интерполяция в Excel

В самом известном табличном процессоре от Microsoft присутствует крайне полезный оператор «ПРЕДСКАЗ».

Рассмотрим данные, размещенные в в таблице, представленной ниже.

Источник: http://turbocomputer.ru/excel/primenenie-interpolyatsii-v-microsoft-excel

Источник